Long-Term Dynamics of Institutions: Using ABM as a Complementary Tool to Support Theory Development in Historical Studies

, , , , ,
and
aDelft University of Technology, Netherlands; bLinnaeus University, Sweden; cLund University, Sweden; dUtrecht University, Netherlands; eErasmus University, Netherlands
Journal of Artificial
Societies and Social Simulation 24 (4) 7

<https://www.jasss.org/24/4/7.html>
DOI: 10.18564/jasss.4706
Received: 29-Jan-2021 Accepted: 29-Sep-2021 Published: 31-Oct-2021
Abstract
Historical data are valuable resources for providing insights into social patterns in the past. However, these data often inform us at the macro-level of analysis but not about the role of individuals’ behaviours in the emergence of long-term patterns. Therefore, it is difficult to infer ‘how’ and ‘why’ certain patterns emerged in the past. Historians use various methods to draw hypotheses about the underlying reasons for emerging patterns and trends, but since the patterns are the results of hundreds if not thousands of years of human behaviour, these hypotheses can never be tested in reality. Our proposition is that simulation models and specifically, agent-based models (ABMs) can be used as complementary tools in historical studies to support hypothesis building. The approach that we propose and test in this paper is to design and configure models in such a way as to generate historical patterns, consequently aiming to find individual-level explanations for the emerging pattern. In this work, we use an existing, empirically validated, agent-based model of common pool resource management to test hypotheses formulated based on a historical dataset. We first investigate whether the model can replicate various patterns observed in the dataset, and second, whether it can contribute to a better understanding of the underlying mechanism that led to the observed empirical trends. We showcase how ABM can be used as a complementary tool to support theory development in historical studies. Finally, we provide some guidelines for using ABM as a tool to test historical hypotheses.Introduction
Large historical datasets are increasingly being used to reveal sociological patterns of human behaviour throughout history (Mace 2000), particularly in the domains of social and economic history. Whether these trends are about migration patterns across continents (Hatton & Williamson 2005), or the relation between sanctioning and the survival of common-pool resources (CPRs) (De Moor et al. 2021), they all share one common feature: these patterns are the emerging results of the interplay between institutions and other macro-level entities, on the one hand and micro-level individual decisions and behaviour, on the other (Coleman 1990).
Given the increasing use of large datasets among historians, the description of historiography as “a selection of details from the past, placed in a particular order, to provide a meaningful interpretation of the past” (Noll 2012) has become too limited. This is because it does not go beyond the primarily descriptive approach of historiography. But even with currently used analytical approaches, often supported by solid statistical methods, insights into recurrent patterns that can be derived from historical data are often general, abstract and usually only pertain to the macro-level of analysis. In addition, historical data are difficult to use to produce causal explanations about ‘how’ and ‘why’ these patterns occurred in the past due to lack of detailed information regarding individual behaviour (Kwok 2017). Of course, the data themselves limit any possibilities of retrieving the individual motivations underlying long-term patterns. There simply is too little information available about these motivations, as we can only in very exceptional cases rely on, for example, biographies or interviews that shed light on individual behaviour. Systematic registration of individual biographical events (e.g., births, deaths and marriages,) does not start until the 19th century, and even then only in some countries. In terms of methodology, however, there may be more so far unexplored opportunities that could allow us to study causal relationships in more depth, and as such, contribute to our understanding of past evolutions.
Given these limitations, simulation models, and especially agent-based models (ABMs) can be designed to replicate observed patterns and hence, represent an instrument to develop theories and virtually test historical hypotheses (Edmonds 2017; Romanowska et al. 2019). More specifically, ABMs allow the identification of specific patterns of individual behaviour at a micro level that may have resulted in recorded historical patterns at the macro level. This in turn, allows us to infer whether the hypothesized causalities are actually possible and, in the best of case, likely to be true. In other words, by comparing emerging patterns from historical datasets to emerging patterns from simulation models, one can explore the plausibility of the underlying mechanisms that have led to those patterns.
The goal of this paper is to show how historical hypotheses can be tested with agent-based models. The dataset that we use is a unique historical dataset on CPRs in several Western and Southern European countries from the Middle Ages until the 19th century (De Moor et al. 2016). The dataset includes detailed descriptions of the systems of rules and enforcement mechanisms—i.e., institutions for collective action (Ostrom 1990a)—that commoners established or modified during the life-cycle of each CPR in order to manage appropriation of resources and to prevent their overuse. On the basis of these data, historians have already suggested hypotheses that can be built upon. For example, De Moor et al. (2016) hypothesized that the reason for the longevity of Dutch CPRs is that they paid more attention to collaboration between commoners rather than sanctioning. Such conclusions can never be tested in reality, as the patterns are the results of hundreds if not thousands of years of human behaviour and any interaction is influenced by numerous parameters (Vahdati et al. 2019).
Here, we extend an existing, empirically validated, agent-based model of CPR management to test hypotheses that were previously generated through the analysis of the above-mentioned dataset. The ABM simulates the emergence of institutions for the management and use of CPRs, where agents collectively exploit a resource using both individual strategies and endogenously generated institutional rules (Ghorbani et al. 2017).
More specifically, we check under which conditions the model can replicate various patterns observed in the dataset of historical CPRs, and whether it can contribute to a better understanding of the causal mechanisms at play in creating specific historical trends. We focus on historical data for CPRs in the UK and the Netherlands for which previous work has already proposed hypotheses that can be tested with our model (De Moor et al. 2016). By configuring the model to represent a particular country, we can compare the generated patterns and trends with the historical ones and hence check whether the hypothesized mechanisms are sufficient to generate the observed pattern.
This article is organized as follows: Section 2 describes the literature on using historical data in ABM. Section 3 describes our historical dataset. Section 4 presents the agent-based model and the specifications. Section 5 presents parameter setups. Section 6 shows how the model can replicate some patterns and provide explanations. Section 7 provides methodological steps for testing historical hypotheses and Section 8 concludes the article.
Related Research
Historical data has mainly been used in agent-based modelling practices to either produce more realistic simulation models or to validate them. For example, Carley et al. (2006) base their ABM on historical data in order to build a realistic biological attack (disease outbreak) model, while Bert et al. (2014) validate their land-use ABM by comparing their model output with historical data. Most of this research considers short-term horizons, such as population growth over seven years (Ligmann-Zielinska & Jankowski 2007) or household and housing information during a 10-year period (Geanakoplos et al. 2012).
Nonetheless, there are also a limited number of articles that have looked into longe- term horizons. For example, historical data has been used to calibrate and validate models in order to make them more reliable for testing contemporary scenarios. Sattenspiel et al. (2019), for instance, calibrate an ABM, modelling a specific epidemic event in the early 20th century by using historical data on fishing villages in Newfoundland and Labrador. Historical data is used to calibrate and validate the model, to ensure that the simulated data can reasonably represent real situations, to be used to develop disease transmission scenarios. Historical data is collected from newspaper articles, government reports, photos, and other materials. In addition, the ABM was previously developed using several ethnographic, culture, and historical sources on the specification of the pandemic and early 20th century Newfoundland and Labrador (Dimka et al. 2014). This model presents a small community and its disease transmission during the early 20th century, but not the specific place that provided the data.
In addition to calibrating and validating models, historical data has also been used to replicate and explain historical patterns. Harrison et al. (2002), for example, model the historical trajectory of vowel harmony. They use ABM to reveal how individual changes influence the instability of vowel harmony systems in Turkic (Altaic) languages. The goal was to identify a set of input drivers of this change by systematically varying these inputs and comparing the corresponding ABM output with empirical observations (the process of language change has the shape of an S-curve). In this research, the historical data of a dozen Turkic language corpora were used. The simulation results however were unable to show a downward S-curve. As authors mention, the reason might be the impact of demographic and language contact factors, which have not been implemented in the model.
Furthermore, ABMs have been used to study social phenomena such as cultural evolutions (Derex et al. 2018; Kandler et al. 2012; Turchin & Currie 2016). Turchin et al. (2018) used ABM as a micro model of individual behavior and decisions to explain observed patterns and determine why certain conditions result in disruptive emergent events, using data on the social and political organizations of human societies. Turchin et al. (2013) apply ABM to build a cultural evolutionary model to predict under which conditions large-scale complex societies appeared in history. They compared the results of the model with a dataset consisting of spatiotemporal information of societies in Afroeurasia between 1,500 BCE and 1,500 CE.
Likewise, ABM has been applied in the archaeology field (Cioffi-Revilla 2014; Kohler et al. 2005; Romanowska et al. 2019; Saqalli & Vander Linden 2019; Wurzer et al. 2015). For example, Axtell et al. (2002) use ABM to reproduce spatial and demographic parameters of the Anasazi community in Long House Valley from A.D. 800 to 1300. The agents in the model represent households and are able to decide where to locate their settlements and fields. Households derive their demographic and nutritional characteristics from ethnographic studies of historic Pueblo groups. The goal was to generate “the history” to explain observed spatiotemporal characteristics of the ancient society. Its focus lies in the environmental account of the development of this society, which in fact goes a long way towards explaining its rise and fall (Axtell et al. 2002).
Additionally, Bowles & Choi (2013) present the evolution of property rights during the Holocene. They model the characteristic of Pleistocene ethnolinguistic period using an ABM, where individuals are in groups and the model has three phases: production, distribution and cultural updating. The goal of the model was to study the emergence of farming systems and property right and cultural evolution to create private ownership during the early Holocene period. The data (climate, archaeological, etc.) is used to calibrate the model and the model outcomes are checked to see whether they replicate the known patterns of the emergence of farming.
More recently, Frantz et al. (2014) used agent-based simulation to model the informal interactions of cheating merchants between Genoese traders, based on game theory. They used several data sources of Genoese perspectives in the 12th century. Different topologies of trust-based networks and two communication modes are used to test their model. The result showed that the communication between the Genoese is not sufficient to detect cheating merchants.
Our work builds on the limited account of research that make use of long-term historical data to explain social phenomena (Axtell et al. 2002; Sattenspiel et al. 2019). Here, we focused on the emergence and dynamics of “institutions as rules” and not cultural evolution of societies. Our goal was to generalize and extend the practices and show the value of ABM for historians and scholars interested in studying historical patterns. By showing how ABM provides insights into the patterns found in our dataset, we aim to provide guidelines for using ABM in historical studies.
A Historical Dataset of CPRs
Common pool resources and their management
The dataset used in this article covers the management of CPRs in European countries over seven centuries. CPRs are resources shared among a group of people. These resources are often large enough that many individuals can use them simultaneously (Ostrom 2002), and they risk depletion as a result of over-use. In this situation, where CPRs are not governed well and individual interests are not properly balanced with the optimal use of the resource, they may be over-used, resulting in the “Tragedy of the commons” (Hardin 1968). To avoid this, users can collectively build management institutions: systems of rules and enforcement mechanisms (Ostrom 1990b).
The set of rules defining a socio-ecological system can be formal or informal (Hodgson 2006; North 1991). Formal rules include political and economic regulations, contracts, and governmental rules; informal rules include norms, taboos, customs, and traditions (Jepperson 1991; Ostrom 2000). Generally speaking, institutions define a set of incentives that structure human communications and affect individual decisions (North 1993). Institutions for the management of CPRs are the rules-in-use that commonly emerge through people’s collective behaviour (Koontz et al. 2015; Ostrom 2000). For CPRs to be successful, most individuals have to recognize, accept and abide by institutional rules even when they conflict with their self-interest (Koppenjan & Groenewegen 2005; Streeck & Thelen 2005).
A dataset of CPR management over seven centuries
In this study, we used a subset of a dataset1 including an extensive collection of management institutions (5000 rules) of 900 CPRs (i.e., the CPR and the social system surrounding it) across several countries in Europe (Belgium, Germany, Italy, the Netherlands, Spain, and the United Kingdom) between 1283 and 1972 (De Moor et al. 2016), all coded and translated into English. The dataset consists of information on the use, governance and management of these CPRs. It captures the institutional rules which commoners established, updated, or changed during the life span of each CPR to foster cooperation and to protect natural resources from over-exploitation. The commoners had regular meetings, often once per year, where they developed and amended the institutional rules to facilitate the maintenance and use of the resources they held collectively. More information about the dataset can be found in De Moor et al. (2016) and Forsman et al. (2021).
This dataset was analysed by Farjam et al. (2020) to extract long-term historical patterns of institutional rules. They extracted cases that included extensive and reliable information and selected the CPRs that were functional for at least 200 years. This subset of the dataset, which will be used as a reference in this paper, includes 3,775 institutional rules for ten Dutch CPRs and eight UK CPRs across six centuries. The Dutch CPRs were recorded from 14th century to the early 20th century; the United Kingdom CPRs were recorded from 16th century to the 19th century. On average, the CPRs survived for 245 years across this subset of dataset.
Extracting historical patterns from the dataset
Farjam et al. (2020) found that the pattern of institutional change in the CPRs follows a U-shape for both the UK and the Netherlands (Figure 1). This implies frequent institutional changes at the beginning of the establishment of the CPRs, followed by a period of stability, and finally another burst of changes right before the dissolution of the CPRs.
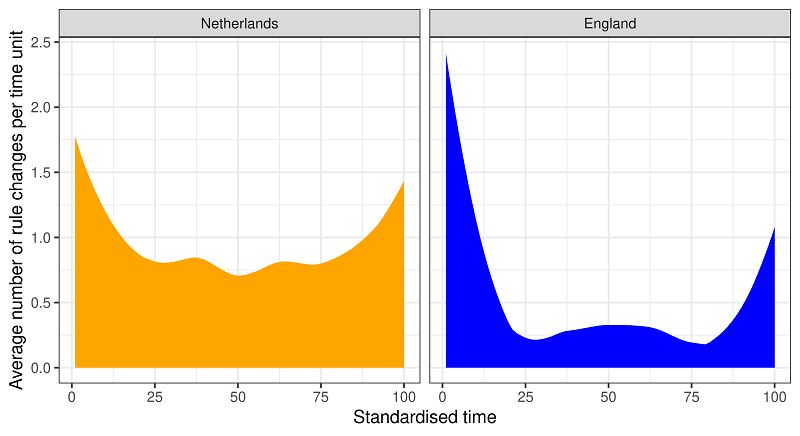
We can consider the first period of rapid changes a “training phase”, where the users of the CPRs try to discover, possibly by trial-and-error, rules that are well adapted to local conditions (Ostrom 1990b). This is often followed by a period of stability, where the institutional rules seem to work in preserving the resources from overuse, organizing their maintenance and guaranteeing the longevity of the CPRs in general.
This period of stability often ends with another burst of changes in the rules, and finally the dissolution of the CPRs. De Moor et al. (2016) advanced an explanation for the latter pattern. During the 19th century, and especially in the period between 1830 and 1850, when most CPRs were dissolved, the modification of regulations, legislation and incentives for privatization by governments put pressure on the commoners, who often faced financial difficulty as well. Commoners often tried to react to these pressures and to adapt to the new situation by changing their rules, even if their efforts were not always sufficient to prevent the dissolution of the CPRs. At the same time, historical accounts suggest that environmental pressures (e.g., droughts) could also be determining factors for the dissolution of CPRs and the collapse of entire societies (Axtell et al. 2002; Diamond 2005). To summarize, the reasons behind a U-shaped pattern observed in the institutional change of historical CPRs can be hypothesized as below. Note that H2 is not based on the historical dataset that is the subject of this paper but a more general historical account.
H1. The U-shaped pattern of institutional change in the 19th century is the result of an institutional learning phase based on trial and error, followed by a period of stability during which commoners are satisfied with the current institutional setting, and a final period of rapid change as a result of a social shock, such as increased external pressure on commoners through escalating taxation.
H2. The U-shaped pattern of institutional change in the 19th century is the result of an institutional learning phase based on trial and error, followed by a period of stability during which commoners are satisfied with the current institutional setting, and a final period of rapid change as a result of an environmental shock, e.g., a drought.
On another account, De Moor et al. (2021) observed that Dutch CPRs have had a much longer life span than those in the UK. They claim that longer-lived CPRs are associated with fewer rules, including formal sanctions and, vice-versa, that CPRs with short life spans tend to focus more on providing sanctions with the rules. The third hypothesis therefore, focuses on the relation between CPRs’ life spans and the number of institutions including formal sanctions.
H3. Less focus on sanctioning has had a positive effect on the CPRs’ longevity.
A fourth pattern in the dataset worth further investigation is the link between the CPRs longevity and the frequency of meetings between commoners. De Moor et al. (2016) claim that longer-lasting CPRs are the ones that made incremental institutional changes by meeting frequently to adjust previously formulated rules. They highlight the importance of members’ involvement, rule internalization, and the frequency of meetings to establish such institutions. This leads to our fourth hypothesis.
H4. Having frequent meetings among commoners has had a positive effect on CPRs’ longevity.
In this paper, we explore these four hypotheses using an ABM to check which ones can emerge in a simulated CPR’s setting that confirm the observed historical patterns.
An Agent-Based Model of CPR Institutional Dynamics
Model overview
The model presented here was initially developed by Ghorbani & Bravo (2016) and validated with extensive contemporary data on irrigation, fishery and forestry cases in Ghorbani et al. (2017). The model represents a CPR management setting consisting of one resource, a set of agents who exploit it, and endogenously generated institutional rules. Here, we briefly present the model; a full description is available in the Appendix and the model is available on CoMSES.2
Agents in the model represent commoners. There are two independent sets of possible actions and possible conditions that agents use to define their individual resource-exploitation strategies. At the beginning of each run, agents randomly select an action-condition pair as their strategy and follow the strategy to extract "yield" from the resource. If agents are not satisfied with their yield (i.e., their yield balance is negative), they change their strategy in subsequent rounds. This change of strategy can be completely random (representing innovative behaviour) or done by copying successful neighbours. At specific points in time determined by a parameter specifying frequency of meetings; if a majority of agents are unsatisfied, they “meet” to vote on an institutional rule, which was basically the most common individual strategy. Once in place, all agents have to comply with the institutional rule, although under certain settings they can “cheat” and follow their own individual strategy instead. During the “meeting”, agents also decide on monitoring intensity and fines for any agent caught cheating.
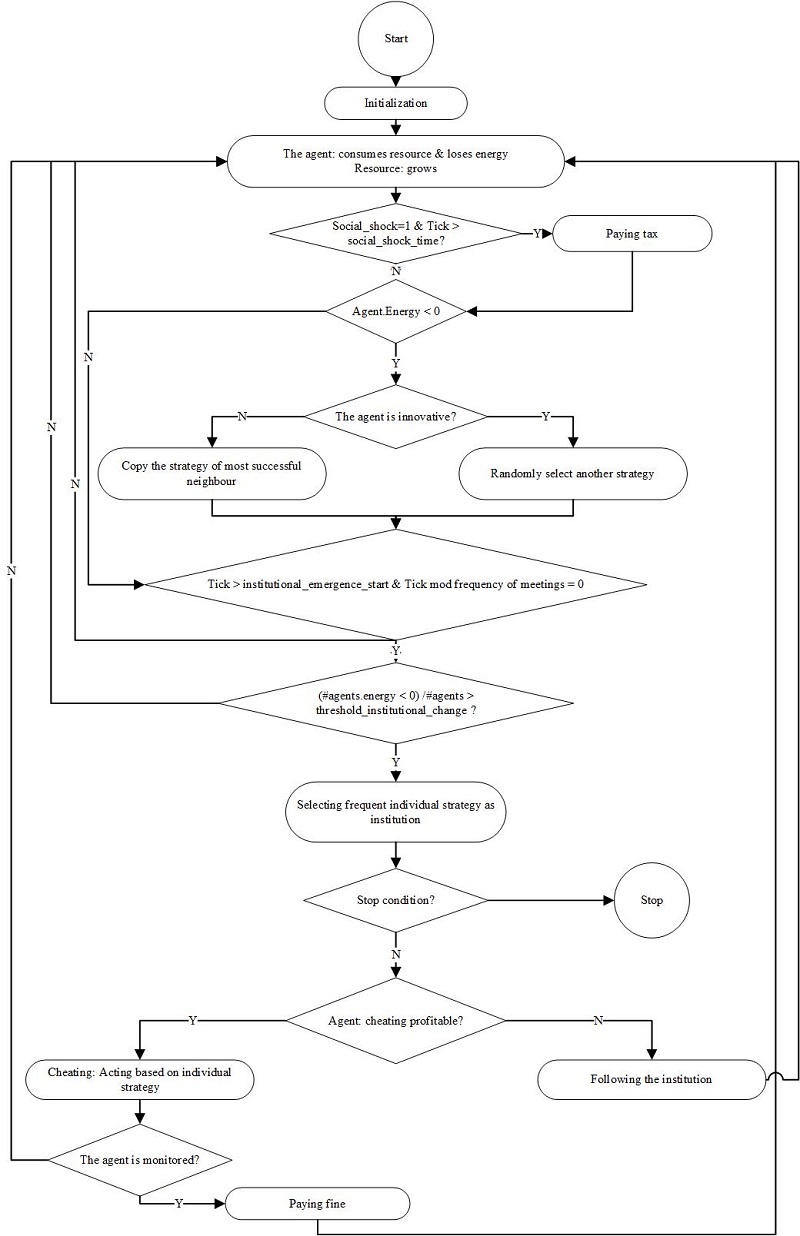
Figure 2 provides an overview of the model. In the initialization phase, the agents are created, the network is set up and agents are initialized with a random action and random condition pair (a.k.a. strategy). The agents consume resource units based on their individual strategy. For example, an individual strategy might look like this: eat 5 units of resource every 2 ticks. In addition, agents gain a fixed amount of yield in each tick, representing their needs. The resource is renewed in each time step according to a logistic growth function. The simulation stops if there are no resource units left, the portion of agents with very low is higher than a certain threshold, or simply after a certain number of ticks.
Conceptualization
The CPR-model consists of four main components: agents, institutional rules, social and environmental shocks and the resource.
- Agents: An initial yield value (resource unit) is assigned to all agents. Each agent records its current strategy, neighbours, and the yield level.
- Individual strategy: Any possible combination of an action and a condition shapes a strategy, and agents only have one strategy at a time. An action represents how many units of resource the agent can consume, and each condition shows when or under which condition the agent can gain that amount of yield (‘true’ means at every ticks). At the beginning the individual strategy3 is chosen randomly and assigned to the agents. For example, an individual strategy might look like this: eat 4 units from the resource every 3 ticks (i.e., when ticks mod 3 = 0).
- Strategy change: When the agent’s yield is below a certain threshold the strategy changes according to one of the two following procedures and the innovativeness of the agent (a parameter of the model): 1) when the innovativeness is less than a certain threshold: copy from the most successful neighbour who currently has the maximum amount of yield, or 2) when the innovativeness is greater than a threshold: randomly select a new combination of action and condition as new strategy.
- Institutional Rules: Institutions have the same structure as individual strategies (i.e., action and condition). In addition to that, each institutional rule also specifies the intensity of the monitoring and the amount of the fine the cheaters must pay.
- Cheating: The agents do not all comply with the institution. If they have the propensity to cheat, and their own individual strategies provide more gain for them than the current institution, they will follow their own strategy instead of following the institution. The management of the resource also includes monitoring activities, where a certain percentage of cheaters are sanctioned.
- Voting: Agents vote on institutional rules. The most frequent individual strategy is chosen as the institutional rule. After the institutional rule is established, agents must obey it. Besides the action-condition pair, the agents also vote on the monitoring intensity and the amount of the fine.
- Social and Environmental Shocks: There are two types of shocks that can take place in the system. An environmental shock is when a large amount of the resource is suddenly lost during some time interval and a social shock is when the agents lose more units per tick (yield is increased). The former represents environmental incidents such as diseases that destroy natural resources and the latter represents taxation where agents pay more for the same number of units they previously received.
- Resource: The resource grows according to \(\Delta R = rR(1-\frac{R}{K})\), where \(K\) is the carrying capacity and r is the reproduction rate.
Model validation
The model was implemented in NetLogo. A dataset consisting of 66 irrigation, 56 fishery, and two forestry cases and one sea vegetable case4 were used to empirically inform the model (Ghorbani et al. 2017). To conduct this empirical information, the relationships between the outputs of the model were compared to the relationships between representative variables in the dataset. For instance, the institutional component has negative coefficients on individual income in both the ABM and the dataset, which means that, on average, the agents gain less yield when the frequency of institutional change is higher. Overall, the analysis of Ghorbani et al. (2017) shows that the model was able to reproduce the observed institutional patterns in the data to a great extent.
Experimental Setup
The experiments were designed to test the hypotheses presented in Section 3.3. For Hypotheses 1 and 2, regarding patterns of institutional change, the model was calibrated to mimic the UK setting (right side of Figure 1). For Hypothesis 3 and Hypothesis 4, related to the longevity of the CPRs and its correlation with meeting frequency and sanctioning, the Dutch setting was used for calibration. The reason for that was that the Dutch CPRs survived substantially longer than UK CPRs (De Moor et al. 2021). Therefore, by extending parameter ranges for sanctioning, varying the frequency of meetings in the simulation, and relaxing the conditions for the end of the simulation, we were able to model experiments that were similar to the Dutch setting.
For all experiments, we first calibrated the model to produce the desired historical pattern and then tried to identify the limits of parameter space able to reproduce such a pattern. This procedure allows us to establish whether the underlying reasons for an observed historical pattern are consistent with the ones (i.e., parameters) that determine the same output from the simulation. This process will be better illustrated in Section 6. We take each simulation run as representing one CPR and each time step, one month of its life span in order to cover five to seven centuries for a simulation run. Each experiment includes 500 independent simulation runs.
The shared parameter setups across all experiments are shown in Table 1, similar to those in Ghorbani et al. (2017). Note that the values used for the parameters were based on sensitivity analysis of the model.
| Parameter | Value(s) |
|---|---|
| Actions | consume [0, 2, 4, 6, 8, 10, 12, 14, 16, 18], [-5] (negative value stands for loss) |
| Conditions | true (ticks mod 250) = 0, (ticks mod 2) = 0; (ticks mod 3) = 0, yield \(\leq\) 0, (ticks mod 20) = 0 |
| Social influence | 0.9 – 1 (uniform random float) |
| Monitoring cost weight | 50 – 60 (uniform random integer) |
| Carrying capacity (\(K\)) | 10000 – 20000 (uniform random integer) |
| Growth rate (\(r\)) | 0.25 – 0.35 (uniform random float) |
| Number of agents | 100 (fixed) |
| Consumption unit | 1 (fixed) |
| (personal) Innovation rate | 0.01 – 0.2 (uniform random float) |
| Threshold for institutional change | 0.5 – 0.75 (uniform random float) |
| Rewire prop | 0.1 (fixed) |
| Type of network | Random network (fixed) |
| Institutional-emergence-start | 500 – 1000 (uniform random integer) |
Experiment 1 – Impact of environmental and social shock on institutional change patterns
The first experiment included three scenarios. The primary scenario did not have any shock throughout the simulation. The second scenario included a social shock, and the third an environmental shock (Table 2). Each of these scenarios encompassed 500 independent simulation runs. For all these scenarios, the stop condition (which is adjusted from the original model in Ghorbani et al. 2017) is shown in Algorithm 1:
Since the United Kingdom CPRs were recorded from the 16th to the 19th century (Farjam et al. 2020), and as we assumed one tick to be one month, we choose the stop condition in the range of 5000-6000 to be sure it covered the life span of the UK CPRs.
In the second scenario, the social shock was modelled in the form of “taxation”, i.e., a certain amount of extra yield subtracted from the agents’ budget in each tick. This happened at ticks greater than “Social shock time” (Table 2). The rationale behind choosing a relatively high number for this parameter was to allow the system to reach a stable state ahead of the introduction of the shocks. The shock was introduced once in the model and continued to the end of the simulation to represent the historical incidence.
In the third scenario, we modelled environmental shock as a sudden change in the amount of the resource stock. This happens at each “Environmental shock interval”, in the range of 1000-2000 ticks. In other words, in each “Environmental shock interval”, the amount of resource decreased based on the “Resource loss percentage”.
Note that for all three scenarios, we looked at full parameter ranges to see whether the U-shape pattern can emerge from the simulation.
| Parameter | Scenario 1 | Scenario 2 | Scenario 3 |
| Individual cheating propensity | 0.1 – 0.35 (uniform random float) | 0.1 – 0.35 (uniform random float) | 0.1 – 0.35 (uniform random float) |
| Max fine | 20 (fixed) | 20 (fixed) | 20 (fixed) |
| Frequency of meetings | 12 | 12 | 12 |
| Environmental shock | False | False | True |
| Social shock | False | True | False |
| Environmental shock interval | - | - | 1000 – 2000 (uniform random integer) |
| Resource loss percentage | - | - | 20 – 70 (uniform random integer) |
| Social shock time | - | 4000 – 4500 (uniform random integer) | - |
| Taxation amount | - | 5 – 10 (uniform random integer) | - |
Experiment 2: Impact of sanctioning on the longevity of the CPRs
A remarkable feature of the Dutch data is that, unlike other countries where sanctioning was extensively used, nearly half of the existing institutional rules did not have any sanction attached to them. This suggests that a no-sanction condition can also be sustainable in the long run, contradicting the current literature that assumes sanctioning to be the primary method to avoid freeriding (De Moor et al. 2016). Therefore, we set the probabilities in the model in such a way that at least half of the institutions emerge without any sanctioning attached to them, and the other half follow the same algorithm for choosing a sanction as described in 4.2. The stop condition is based on Algorithm 2:
We used the Dutch parameter settings for this experiment with the same parameter setup of Experiment 1, but expanded ranges for cheating and fining-related parameters (‘Individual cheating propensity’: a uniform random float in the range of 0.1 – 1, and ‘Max fine’: a uniform random integer in the range of 20 – 100) and also extended the simulation period to 7000 ticks. This allowed us to better test our fourth hypothesis (H4) by increasing the agents’ opportunity to cheat, which better mimics the condition of Dutch CPRs. Additionally, since commoners usually met at least once annually, we chose the frequency of meeting as 12 (ticks), similar to the previous experiment.
Experiment 3: Impact of meeting frequency on the CPRs’ longevity
To analyze the impact of meeting frequency on the CPRs’ longevity (H4), we designed four scenarios, each one including 500 independent runs, with frequency of meetings in {6, 12, 18, 24} ticks, i.e., meetings every six months, every year, every one and a half years, and every two years, respectively. The reason behind choosing these periods is the fact that the commoners usually met at least once a year. At these meetings, agents could change their managing institutions, provided that a certain percentage of them (parameter: institutional change threshold) were unsatisfied (i.e., had negative yield).
Results
Testing H1: Social shock and institutional change trends over the lifetime of the CPRs
The goal here is to test whether it is possible to obtain a U-shaped pattern of institutional change in our abstract model and if so, under which parameter settings and in which scenario. The recorded outcome is the frequency of institutional changes over time, which is compared with the one in Farjam et al. (2020), reported in Figure 1.
In the first scenario of Experiment 1 (without environmental or social shocks) the pattern of institutional change in the simulation shows a high level of activity at the beginning, followed by a long period of low activity, hence forming something similar to an L-shape (Figure 3), in contrast to the U-shape observed empirically.
Based on Farjam et al. (2020), we used standardized time \(t_{c,a}\) by changing the tick in which a given institution emerged (\(y_{c,a}\)) using the formula:
| \[ t_{c,a} = \frac{y_{c,a} - y_{c}^{F}}{y_{c}^{L}- y_{c}^{F}}\] | \[(1)\] |
The second scenario introduced a social shock. Recall that the goal here is to mimic the historical conditions where commoners had financial issues in the 19th century due to the new taxes introduced in the country. Our goal is to see whether having a social shock (i.e., tickly taxes) results in institutions rapidly changing after a period of stability. This can indeed be observed in Figure 4. This outcome primarily depends on the fact that the yield balance of the agents is now more often negative (due to paying “taxes” every tick), making them more prone to changing the existing institution. Consistent with the historical data (De Moor et al. 2016), despite the commoners attempt to adapt, their average yield becomes lower than the stopping condition for the simulation, leading to the dissolution of the CPRs.
Testing H2: Environmental shock and institutional change trends over the lifetime of the CPRs
Another hypothesis could be that environmental shocks may have an impact similar to that of social shocks (H2). The goal here was to reproduce the historical U-shaped pattern of institutional change by introducing an environmental shock (in the form of sudden resource scarcity) into the system (Scenario 3). The result of the model with environmental shock (and without social shock) is shown in Figure 5. Similar to the no-shock setting, we observed an L-shaped pattern of institutional change, implying that the sudden loss of a resource does not really cause agents to enter the final phase of the CPR’s life (rapid institutional change) that is empirically observed.
Surprisingly, the time of the environmental shock was not even observable in the institutional change diagram (Figure 5): it seems that the agents only changed the institution to a limited extent to compensate for the loss, but the average yield of the agents was eventually not low enough for the CPR to dissolve. In fact, previous model outcomes showed that at times of resource scarcity, the agents tended to extend the time intervals between their consumption of the resource to allow it to be replenished (Ghorbani & Bravo 2016). Therefore, considering the full parameter range, we can conclude that environmental shock did not result in agents entering a period of rapid institutional change followed by the dissolution of the CPR, which does not support H2.
It is interesting to note here the main difference between a social shock and environmental shock. For the former, the agents continuously require more energy (demand) per time interval, while for the latter, the agents are not able to take from the resource at a certain moment in time, making them temporarily unsatisfied with the situation. This dissatisfaction will however diminish as the resource replenishes over time. This situation is similar to a resource scarcity situation (Ghorbani & Bravo 2016), where the agents adapt to the environmental shock by taking less resource units over longer intervals of time (e.g. every 100 ticks, this is emergent from the model). Another reason to observe L-shaped pattern is the fact that the agents were not aware of the state of the resource. They are only conscious about their yield level and act accordingly. Therefore, when there was an environmental shock, the agents did not react significantly. Although in the case of sudden reduction of the resource (as an environmental shock), we have indirect impact on the yield level of agents, it seems that they can adapt themselves with the sudden changes of the resource and the impact is not as much as when their yield level have been continuously reduced (social shock). However, when we had a social shock, since their yield continuously reduced and they sensed the changes, their reacted by repeatedly changing the institutions and U-shaped pattern has been emerged.
It is worth mentioning that Figures 3 to 5 show a short "warming-up phase", which cannot be found in Figure 1 (i.e., in the dataset). Since the institutions in the model are emerging from agent behaviour, this warm-up period allows the agents to select their individual strategies which eventually become the collective strategy. The time for the institution to emerge is also conditioned on the satisfaction of the agents and therefore varies between simulation runs and also in the diagrams.
By comparing the implementations of environmental and social shocks, one may argue that the two shocks are related in the sense that one is a decline in the availability of the resource, while the other is simply increase in metabolisms (see Blom 2019). This makes the results even more insightful as they do not lead to the same outcome in terms of institutional change. The reason behind the difference is in the way the shock continues to affect agents: after the environmental shock, the resource gradually recovers, while in the social shock situation there is a continuous burden on the agents.
Testing H3: Sanction-oriented institutions and longevity of the CPRs
To test H3, we tested whether having no sanctions in the modelled institutions significantly affected the simulated CPRs life span. As shown in Figure 6, a significant positive correlation exists between the number of institutions without sanctioning in one run (representing one CPR and standardized based on the total number of institutional changes) and the age of CPR (\(r = 0.68\)), which supports H3. In other words, the figure shows the relation between the number of institutions without sanctioning (normalized based on the number of institutions) and the age of CPR. The cluster of observations at \(age\_common = 7000\) is due to the stop condition of the simulation where all runs that have not finished yet are terminated.
This suggests that institutions lacking sanctions have a positive impact on the longevity of commons. This implies that the CPRs which lasted longest mostly had many institutions with \(fine=0\) (and therefore the ratio is close to 1). Although the amount of a sanction is relatively low compared to the income of agents per tick, and the probability of sanctioning is also low. The explanation behind this may be related to agents losing more yield per tick and therefore, being more frequently unhappy with the institution in place, thus attempting to change it.
Testing H4: Frequency of meetings and longevity of the CPRs
To test H4, we ran four experiments, each including 500 independent runs, with frequency of meetings in {6, 12, 18, 24} ticks.
Given that the data were right-censored— i.e., simulations that were still running after 7,000 time steps were stopped—we analysed the effect of the frequency of meetings using maximum likelihood estimation of censored regressions (Messner et al. 2016). We considered the predictor variable as ordinal, since only four possible meeting frequencies (namely 6, 12, 18, and 24 time steps) were considered, and controlled for the resource regeneration rate \(r\) and carrying capacity \(K\) (Table 3). Note that the interpretation of the model remains similar if the meeting frequency is introduced as a numerical variable. Table 3 shows censored regression estimations on CPRs’ life spans. The reference class for meeting frequency is six time steps.
The results clearly show a significant effect of meeting frequency, with less frequent meetings leading to shorter life spans for CPRs, that is, providing the opportunity for agents to change the institution more frequently increases the CPR’s longevity, which supports H4. Neither the carrying capacity nor the regeneration rate coefficients, however, are significant.
| Coefficients (location model): | |||||
| Estimate | Std. Error | z value | Pr(>|z|) | ||
| (Intercept) | 9,88E+06 | 1,50E+06 | 6.581 | 4.67e-11 | *** |
| Frequency of meetings: 12 | -1,86E+06 | 3,69E+05 | -5.053 | 4.34e-07 | *** |
| Frequency of meetings: 18 | -2,10E+06 | 3,68E+05 | -5.704 | 1.17e-08 | *** |
| Frequency of meetings: 24 | -2,28E+06 | 3,67E+05 | -6.205 | 5.45e-10 | *** |
| \(K\) | 4,97E+01 | 4,25E+01 | 1.168 | 0.243 | |
| \(r\) | -1,56E+06 | 4,32E+06 | -0.361 | 0.718 | |
| Coefficients (scale model with log link:) | |||||
| Intercept | 8.44860 | 0.03165 | 267 | <2e-16 | *** |
| Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 | |||||
| Distribution: Gaussian | |||||
| Log-likelihood: -7557 on 7 Df | |||||
| Number of iterations in BFGS optimization: 196 | |||||
To summarize, we used an empirically tested model to explore some historical hypotheses on the development of CPRs’ management institutions. By replicating the observed historical patterns, we aimed to identify parameters that help to explain their emergence. Our results were consistent with three hypotheses previously proposed in the literature on the subject: social shock results in the dissolution of CPRs, less focus on sanctioning has a positive effect on the CPRs’ longevity and having frequent meetings among commoners has a positive effect on the CPRs’ longevity. We also tested an additional explanation for the dissolution of the CPRs, based on the effect of environmental shocks on institutions, but found no support for it.
Summarizing Methodological steps for Testing Historical Hypotheses Using ABM
In this section we present a set of guidelines that can support the process of testing historical hypotheses as shown in Figure 7.
- Hypotheses on historical patterns and trends. The first step in the process of studying historical patterns using agent-based modelling is to extract the patterns that are of interest in a particular historical context, such as the ones described in this article. These historical patterns are commonly accompanied by hypotheses that explain possible causalities. These hypotheses can be extracted from already published articles, but can also be formalized by statistically analysing historical datasets related to that specific context (here the CPRs). Here, we primarily used a historical dataset to extract the patterns, and used existing articles based on the same dataset to define the hypotheses.
- An agent-based model representing the historical setting. An agent-based model is built that represents the historical context and that can reproduce the historical trends and patterns. This model needs to be validated to make sure that it is sufficiently representative of the context. Here, the dataset that was used to validate the model was completely independent of the dataset that showed the historical trends that were to be studied.
- Parameter configuration of the model. The experiments are set up in such a way as to be able to reproduce the historical pattern. Therefore, the experimentation process is a repetitive task that aims to configure the parameters in the model so that the model produces specific outcomes.
- Finding causal links between model parameters and historical patterns. By reproducing patterns that resemble patterns observed in history, we compare model parameters that were the cause of the emerging pattern to variables in the hypothesis to confirm or reject the hypothesis.
With this practice, we simply used ABM as a complementary tool to support theory development in historical studies.
Discussion and Conclusion
In this research, we used agent-based modelling as a complementary tool to support theory development in historical studies. By building models that produce historical patterns, we aimed to identify parameters that explain patterns and that are present in hypothesized causalities in historical studies. This practice allowed us to confirm existing hypotheses found in the literature. For the particular case of institutions in CPR management, we used an existing and already validated agent-based model and identified patterns in a historical dataset that were important in explaining institutional dynamics for this management. Three out of the four hypotheses that were extracted from published articles on the same historical dataset were corroborated:
- Our model corroborated the fact that institutions that are endogenously built to manage CPRs faced rapid changes at the beginning, as agents were trying to find an acceptable institution that satisfied their needs, essentially based on trial and error. After that, the CPRs faced a period of institutional stability, as the agents were satisfied with the situation. However, social interruptions that lead to agents’ loss lead to rapid institutional change, as the agents tried to adapt to the new situation with higher consumption (resembling personal demand with added taxation). They were not successful in their endeavours and the CPR died out as it was not able to meet the commoners’ demand.
- The model showed that sanctioning had a negative impact on the longevity of CPRs. Institutions without sanctioning mechanisms seemed to have been more effective in the long run, leading to longer CPR lifetime.
- The model corroborated the fact that involving agents in institutional development in more frequent meetings contributed to the longevity of the CPRs. If commoners could change institutions more frequently, adjustments lead to more stable and longer lived CPRs.
- The hypothesis that was rejected concerned the influence of environmental shock as the emerging pattern from the simulation was an “L” shape, suggesting that the agents were in fact able to recover from the shock and remained in a relatively stable institutional setting.
An important point to emphasize here is that the model used to the hypotheses was completely independent of the dataset used to generate those hypotheses. As such, we did not have any pre-specified relationships in the model that would bias our results. We do not claim here that testing historical hypotheses should be done by using an independent model that does not use associated data, but that this independence could increase the reliability of this type of research. The strategy of having independent datasets for training and testing models is also the gold standard in machine learning literature.
Moreover, rather than trying to focus on input data that represent reality, we considered the output of the model to replicate the investigated pattern. This helped us calibrate the model to represent the desired emerging patterns, rather than being fully data-driven. We were interested in qualitative representations of reality in the form of patterns and trends (Grimm et al. 2005), rather than quantitative accounts of reality. This supports the claim that abstract models that are not necessarily data-driven in nature, can generate important insights which otherwise may have been invisible.
This modelling practice, however, also has some limitations. First, the model that we used as the basis to test the hypotheses was quite abstract and missed certain important concepts in the CPR settings s. For example, agents were homogenous (apart from choosing different strategies) and therefore a power structure in which some agents had more rights than others was missing. We did not change the model to be able to test its existing validity. However, future extensions of the model could bring more in-depth insights. Second, the agents do not have any learning behaviour, which implies that even if we made new generations of agents, as they would be very similar to existing ones, and did not learn from experience, we would most probably observe the same behaviour. More intelligence and learning behaviour might therefore lead to other insightful explanations about the type of historical patterns we observed in our experiments. Third, the dataset has an implicit bias, as it included only CPRs that survived for over 200 years and had changed their regulations at least three times over this 200-year period. Short-lived CPRs, long-lived CPRs that used the same regulation over their entire life span, and other CPRs not meeting these criteria were therefore excluded and may have shown different results. Finally, related to model parameterization, given that the model was very abstract, there were minimal empirical basis for many of the parameters, requiring us to look into full parameter ranges. The current model was quite simple, therefore, looking at the whole parameter spectrum was feasible. Adding these details and complexities to the model however, would make parameter sweeping difficult, if not infeasible, calling for more linkage to real-world data.
Acknowledgements
This work is supported by the Riksbankens Jubileumsfond, project MIDI: Modelling institutional dynamics in historical commons (https://lnu.se/en/research/searchresearch/forskningsprojekt/project-modelling-institutional-dynamics-in-historical-commons/). Additional support and access to computing facilities were provided by the Linnaeus University Center for Data Intensive Sciences and Applications, DISA (https://lnu.se/disa).
Notes
- The dataset is a part of the Common Rules Project (De Moor et al. 2016).
- https://www.comses.net/codebase-release/10eeafa9-f5d4-4534-8109-ffeae0d00b5d/.
- To define individual strategies, we use ADICOgrammar (Crawford & Ostrom 1995). In the ADICOgrammar of institutions A denotes Attributes: specifies subject towhoma strategy, norm or rule applies; D refers to Deontic: determines how an action is done (prohibition, obligation, and permission or, in other words must not, may, and must; Frantz et al. 2013); I represents Aims: identifies the actions toward which Deontic applies; C indicates Conditions: under which conditions or, in other words, when, where, and how a strategy, norm or rule applies; and O denotes Or Else: determines specific punishments to be applied when an agent acts in violation of the institutional rules.
- This dataset used in Ostrom’s (1990a) book.
Appendix: The Model Description
This section describes the model in more detail using the ODD + D (Müller et al. 2013) standard for describing agent-based models.
Model overview
Purpose
This model is an agent-based model of common pool resources (CPRs) management to test hypotheses that were previously generated through a historical dataset. The ABM simulates the emergence of institutions for the management and use of CPRs. The goal of this work is to show how historical hypotheses can be tested with agent-based models. In other words, by comparing emerging patterns from historical datasets to emerging patterns from simulation models, one can explore the plausibility of the underlying mechanisms that have led to those patterns.
State variables and scales
The model includes a number of appropriators and one shared resource. Appropriators select an institution at a specific time after the start of the simulation. Furthermore, we introduce two types of shocks in the model: social shock and environmental shock.
Appropriators
| Variable | Description |
|---|---|
| Yield | Captures the amount of yield that the agents currently have. It decreases every tick based on consumption needs and increases based on appropriation activities. |
| Current action | the number of resource units the agents are consuming/appropriating at a point in time |
| Current condition | Under what condition the agents take action (e.g., every x ticks) |
| Cheated | A Boolean variable that shows whether the agent cheated in the previous tick |
| Cheating profitable | s the outcome of the decision of the agent on whether it should cheat in this round or not. (Boolean) |
| Cheating propensity | The probability of cheating |
Resource
| Variable | Description |
|---|---|
| Resource Growth (\(r\)) | In each round of the simulation, the amount of resource is increased by this value given a particular growth function. |
| Initial amount (\(K\)) | This is the amount of resource given at the beginning of the simulation |
| Resource type | The type of resource is fishery or irrigation in the model. |
Institution
| Variable | Description |
|---|---|
| Action | The action that has to be executed by every agent in the simulation. This is selected by the agents. |
| Condition | The condition under which the agents appropriate from the resource (execute action). This is selected by the agents. |
| Frequency of meetings | The number of ticks after which the institution is formed by the agents. |
| Threshold for institutional change | The threshold needed to establish an institution. |
| Fine | The amount of penalty paid by agents in case they cheat, and in case their cheating is caught. This is selected by the agents. |
| Monitoring | The percentage of agents who will be monitored for cheating. This is selected by the agents |
| Institutional_emergence_start | The trial and error phase of CPR before going to emerge the institutions |
Shocks
| Variable | Description |
|---|---|
| Environmental shock interval | The interval that environmental shock happens. |
| shock happens. | |
| Resource loss percentage | The percentage of resource that will be decreased in each environmental shock intervals. |
| Social shock time | When a social shock is introduced. |
| Taxation amount | The amount of penalty paid by agents in each tick after social shock time. |
Process overview and scheduling
The simulation model consists of two general processes which are depicted in Figure 2:
- The initial appropriation process: during the initialization phase, the agents are created, the network is set up and agents are initialized with a random action and random condition pair as their individual strategy. The agents consume resource units based on their individual strategy. For example, an individual strategy might look like this: eat 5 units of resource every 2 ticks. In addition, agents consume a fixed amount of yield in each tick, representing their needs. The resource is renewed in each time step according to a logistic growth function. If agents are not satisfied with their energy level (i.e., their energy balance is negative), they change their strategy. This change of strategy can be completely random (representing innovative behaviour) or done by copying successful neighbours.
- Appropriation based on institutional rules. At specific points in time if a majority of agents are unsatisfied, they come together to vote on an institutional rule, which is basically the most common individual strategy. Once in place, all agents have to follow the institutional rule, although under certain settings they can “cheat” and follow their individual strategy instead. While following the institution, the opinion of the agents about their individual strategy is continuously updated. If they cheat, monitoring and fine mechanisms will be applied. If a certain proportion of agents are unsatisfied with the current institution, the meet again to vote on a new institution. In addition to the threshold for satisfaction, another parameter determining the meeting frequency also influences how often the agents change the institution. The simulation stops if there are no resource units left, or when the portion of agents with very low energy is higher than a certain threshold, or simply after a certain number of ticks. Environmental shock and social shock take place during this phase.
Design concepts
Theoretical and empirical background
The model is primarily based on the concepts proposed in IAD framework for management institutions in CPR system. It uses the ADICO grammar of institutions to build institutions which follow a pseudo-evolutionary process, i.e., mutation of institutions (innovation) and copying behaviour.
Individual decision-making and sensing
The agents follow a basic decision-making process. They look at their yield level to make decision. The agents also decide whether they would comply with the institutional rule, or follow their own strategy. They do this by comparing the potential yield gain from each action and select the most profitable one, depending on the cheating propensity. This is also the only “prediction mechanism” in the model.
Learning
The agents do not have learning abilities. They only check their current yield level to decide whether they want to continue their existing strategy or select a new one.
Interaction and collective action
Each agent is placed in a network (random). The agents may copy the strategy of the successful neighbor in terms of energy level. Furthermore, the agents come together and collectively vote on the institution by proposing their own strategy. The most common strategy is selected as the new institution.
Heterogeneity
Agents are heterogeneous with respect to their behavioral strategies and homogeneous with respect to all other parameters.
Details
Implementation details
The details of the implementation are explained in Section 4.2 of the paper.
Initialization
The model starts by all agents having 0 amount of energy. This amount will decrease based on a given constant value (energy consumption) and will increase (or decrease) based on the strategy that the agent is choosing then following
References
AXTELL, R. L., Epstein, J. M., Dean, J. S., Gumerman, G. J., Swedlund, A. C., Harburger, J., Chakravarty, S., Hammond, R., Parker, J., & Parker, M. (2002). Population growth and collapse in a multiagent model of the Kayenta Anasazi in Long House Valley. Proceedings of the National Academy of Sciences, 99(suppl 3), 7275–7279. [doi:10.1073/pnas.092080799]
BERT, F. E., Rovere, S. L., Macal, C. M., North, M. J., & Podestá, G. P. (2014). Lessons from a comprehensive validation of an agent based-model: The experience of the Pampas Model of Argentinean agricultural systems. Ecological Modelling, 273, 284–298. [doi:10.1016/j.ecolmodel.2013.11.024]
BLOM, P. (2019). Nature’s Mutiny: How the Little Ice Age of the Long Seventeenth Century Transformed the West and Shaped the Present. New York, NY: Liveright Publishing.
BOWLES, S., & Choi, J. K. (2013). Coevolution of farming and private property during the early Holocene. Proceedings of the National Academy of Sciences, 110(22), 8830–8835. [doi:10.1073/pnas.1212149110]
CARLEY, K. M., Fridsma, D. B., Casman, E., Yahja, A., Altman, N., Chen, L. C., Kaminsky, B., & Nave, D. (2006). BioWar: Scalable agent-based model of bioattacks. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 36(2), 252–265. [doi:10.1109/tsmca.2005.851291]
CIOFFI-REVILLA, C. (2014). A formal theory of politogenesis: Towards an agent simulation of social complexity origins. [doi:10.2139/ssrn.2429322]
COLEMAN, J. S. (1990). Foundations of Social Theory. Cambridge, MA: Harvard University Press.
CRAWFORD, E. S., & Ostrom, E. (1995). A grammar of institutions. The American Political Science Review, 89(3), 582–600. [doi:10.2307/2082975]
DE MOOR, T., Farjam, M., van Weeren, R., Bravo, G., Forsman, A., Ghorbani, A., & DEhkordi, M. A. E. (2021). Taking sanctioning seriously: The impact of sanctions on the resilience of historical commons in Europe. Journal of Rural Studies, 87, 181–188. [doi:10.1016/j.jrurstud.2021.08.009]
DE MOOR, T., Laborda-Pemán, M., Lana-Berasain, J. M., van Weeren, R., & Winchester, A. (2016). Ruling the commons. Introducing a new methodology for the analysis of historical commons. International Journal of the Commons, 10(2), 529–588. [doi:10.18352/ijc.760]
DEREX, M., Perreault, C., & Boyd, R. (2018). Divide and conquer: Intermediate levels of population fragmentation maximize cultural accumulation. Philosophical Transactions of the Royal Society B: Biological Sciences, 373(1743), 20170062. [doi:10.1098/rstb.2017.0062]
DIAMOND, J. (2005). Collapse: How Societies Choose to Fail or Succeed. New York, NY: Viking.
DIMKA, J., Orbann, C., & Sattenspiel, L. (2014). Applications of agent-based modelling techniques to studies of historical epidemics: The 1918 flu in newfoundland and labrador. Journal of the Canadian Historical Association, 25(2), 265–296. [doi:10.7202/1032848ar]
EDMONDS, B. (2017). 'Different modelling purposes.' In B. Edmonds & R. Meyer (Eds.), Simulating Social Complexity: A Handbook (pp. 39–58). Berlin/Heidelberg Springer. [doi:10.1007/978-3-319-66948-9_4]
FARJAM, M., De Moor, T., van Weeren, R., Forsman, A., Dehkordi, M. A. E., Ghorbani, A., & Bravo, G. (2020). Shared patterns in long-term dynamics of commons as institutions for collective action. International Journal of the Commons, 14(1), 78–90. [doi:10.5334/ijc.959]
FORSMAN, A., De Moor, T., van Weeren, R., Farjam, M., Dehkordi, M. A. E., Ghorbani, A., & Bravo, G. (2021). Comparisons of historical Dutch commons inform about the long-term dynamics of social-ecological systems. PLoS ONE, 16(8), e0256803. [doi:10.1371/journal.pone.0256803]
FRANTZ, C., Purvis, M. K., & Nowostawski, M. (2014). Agent-based modeling of information transmission in early historic trading. Social Science Computer Review, 32(3), 393–416. [doi:10.1177/0894439313511931]
FRANTZ, C., Purvis, M. K., Nowostawski, M., & Savarimuthu, B. T. R. (2013). nADICO: A nested grammar of institutions. International Conference on Principles and Practice of Multi-Agent Systems [doi:10.1007/978-3-642-44927-7_31]
GEANAKOPLOS, J., Axtell, R., Farmer, J. D., Howitt, P., Conlee, B., Goldstein, J., Hendrey, M., Palmer, N. M., & Yang, C. Y. (2012). Getting at systemic risk via an agent-based model of the housing market. American Economic Review, 102(3), 53–58. [doi:10.1257/aer.102.3.53]
GHORBANI, A., & Bravo, G. (2016). Managing the commons: A simple model of the emergence of institutions through collective action. International Journal of the Commons, 10(1), 200–219.
GHORBANI, A., Bravo, G., Frey, U., & Theesfeld, I. (2017). Self-organization in the commons: An empirically-tested model. Environmental Modelling & Software, 96, 30–45. [doi:10.1016/j.envsoft.2017.06.039]
GRIMM, V., Revilla, E., Berger, U., Jeltsch, F., Mooij, W. M., Railsback, S. F., Thulke, H. H., Weiner, J., Wiegand, T., & DeAngelis, D. L. (2005). Pattern-oriented modeling of agent-based complex systems: Lessons from ecology. Science, 310(5750), 987–991. [doi:10.1126/science.1116681]
HARDIN, G. (1968). The tragedy of the commons. Science, 162(3859), 1243–1248. [doi:10.1126/science.162.3859.1243]
HARRISON, K. D., Dras, M., & Kapicioglu, B. (2002). Agent-based modeling of the evolution of vowel harmony. Proceedings-NELS, 1(32), 217–236.
HATTON, T. J., & Williamson, J. G. (2005). Global Migration and the World Economy: Two Centuries of Policy and Performance. Cambridge, MA: MIT Press. [doi:10.7551/mitpress/3303.001.0001]
HODGSON, G. M. (2006). What are institutions? Journal of Economic Issues, 40(1), 1–25.
JEPPERSON, R. (1991). Institutions, institutional effects, and institutionalism. The New Institutionalism in Organizational Analysis, 6, 143–163. [doi:10.1017/9781139939744.004]
KANDLER, A., Perreault, C., & Steele, J. (2012). Cultural evolution in spatially structured populations: A review of alternative modeling frameworks. Advances in Complex Systems, 15(01n02), 1203001. [doi:10.1142/s0219525912030014]
KOHLER, T. A., Gumerman, G. J., & Reynolds, R. G. (2005). Simulating ancient societies. Scientific American, 293(1), 76–84. [doi:10.1038/scientificamerican0705-76]
KOONTZ, T. M., Gupta, D., Mudliar, P., & Ranjan, P. (2015). Adaptive institutions in social-ecological systems governance: A synthesis framework. Environmental Science & Policy, 53(B), 139–151. [doi:10.1016/j.envsci.2015.01.003]
KOPPENJAN, J., & Groenewegen, J. (2005). Institutional design for complex technological systems. International Journal of Technology, Policy and Management, 5(3), 240–257. [doi:10.1504/ijtpm.2005.008406]
KWOK, R. (2017). Historical data: Hidden in the past. Nature, 549(7672), 419–421. [doi:10.1038/nj7672-419]
LIGMANN-ZIELINSKA, A., & Jankowski, P. (2007). Agent-based models as laboratories for spatially explicit planning policies. Environment and Planning B: Planning and Design, 34(2), 316–335. [doi:10.1068/b32088]
MACE, R. (2000). Evolutionary ecology of human life history. Animal Behaviour, 59(1), 1–10. [doi:10.1006/anbe.1999.1287]
MESSNER, J. W., Mayr, G. J., & Zeileis, A. (2016). Heteroscedastic censored and truncated regression with crch. The R Journal, 8(1), 173–181. [doi:10.32614/rj-2016-012]
MÜLLER, B., Bohn, F., Dreßler, G., Groeneveld, J., Klassert, C., Martin, R., Schlüter, M., Schulze, J., Weise, H., & Schwarz, N. (2013). Describing human decisions in agent-Based models ODD + D, An extension of the ODD protocol. Environmental Modelling & Software, 48, 37–48.
NOLL, K. L. (2012). Canaan and Israel in Antiquity: A Textbook on History and Religion. Edinburgh: T&T Clark.
NORTH, D. C. (1991). Institutions. Journal of Economic Perspectives, 5(1), 97–112.
NORTH, D. C. (1993). 'Institutional change: A framework of analysis.' In S. E. Sjöstrand (Ed.), Institutional Change: Theory and Empirical Findings (pp. 35–46). London, UK: Routledge.
OSTROM, E. (1990a). Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge, MA: Cambridge University Press.
OSTROM, E. (1990b). The Evolution of Institutions for Collective Action. Edición En Español: Fondo de Cultura Económica, México.
OSTROM, E. (2002). 'Common-pool resources and institutions: Toward a revised theory.' In B. L. Gardner & G. C. Rousser (Eds.), Handbook of Agricultural Economics (Vol. 2, pp. 1315–1339). Amsterdam, NL: North-Holland. [doi:10.1016/s1574-0072(02)10006-5]
OSTROM, E. (2017). Collective action and the evolution of social norms. Journal of Economic Perspectives, 14(3), 137–158. [doi:10.1257/jep.14.3.137]
ROMANOWSKA, I., Crabtree, S., Harris, K., & Davies, B. (2019). Agent-based modeling for archaeologists: Part 1 of 3. Advances in Archaeological Practice, 0(0), 1–7. [doi:10.1017/aap.2019.6]
SAQALLI, M., & Vander Linden, M. (2019). Integrating Qualitative and Social Science Factors in Archaeological Modelling. Berlin Heidelberg: Springer.
SATTENSPIEL, L., Dimka, J., & Orbann, C. (2019). Using cultural, historical, and epidemiological data to inform, calibrate, and verify model structures in agent-based simulations. Mathematical Biosciences and Engineering: MBE, 16(4), 3071–3093. [doi:10.3934/mbe.2019152]
STREECK, W., & Thelen, K. (2005). 'Introduction: Institutional change in advanced political economies.' In W. Streeck & K. Thelen (Eds.), Institutional Change in Advanced Political Economies. New York, NY: Oxford University Press.
TURCHIN, P., & Currie, T. E. (2016). Cultural group selection is plausible, but the predictions of its hypotheses should be tested with real-world data. Behavioral and Brain Sciences, 39. [doi:10.1017/s0140525x15000278]
TURCHIN, P., Currie, T. E., Turner, E. A., & Gavrilets, S. (2013). War, space, and the evolution of Old World complex societies. Proceedings of the National Academy of Sciences, 110(41), 16384–16389. [doi:10.1073/pnas.1308825110]
TURCHIN, P., Witoszek, N., Thurner, S., Garcia, D., Griffin, R., Hoyer, D., Midttun, A., Bennett, J., Næss, K. M., & Gavrilets, S. (2018). A history of possible futures: Multipath forecasting of social breakdown, recovery, and resilience. Cliodynamics, 9(2). [doi:10.21237/c7clio9242078]
VAHDATI, A. R., Weissmann, J. D., Timmermann, A., de León, M. S. P., & Zollikofer, C. P. E. (2019). Drivers of Late Pleistocene human survival and dispersal: An agent-based modeling and machine learning approach. Quaternary Science Reviews, 221, 105867.
WURZER, G., Kowarik, K., & Reschreiter, H. (2015). Agent-Based Modeling and Simulation in Archaeology. Cham Heidelberg: Springer International Publishing.