Egalitarian Sharing Explains Food Distributions in a Small-Scale Society

N/A, Brazil
Journal of Artificial
Societies and Social Simulation 25 (3) 5
<https://www.jasss.org/25/3/5.html>
DOI: 10.18564/jasss.4835
Received: 27-Jul-2020 Accepted: 17-Jun-2022 Published: 30-Jun-2022
Abstract
Among social anthropologists, there is virtual consensus that the food-sharing practices of small-scale non-agricultural groups cannot be understood in isolation from the broader repertoire of leveling strategies that prevent would-be dominants from exercising power and influence over likely subordinates. In spite of that widespread view, quantitatively rigorous empirical studies of food sharing and cooperation in small-scale human groups have typically ignored the internal connection between leveling of income and political power, drawing inspiration instead from evolutionary models that are neutral about social role asymmetries. In this paper, I introduce a spatially explicit agent-based model of hunter-gatherer food sharing in which individuals are driven by the goal of maximizing their own income while minimizing income asymmetries among others. Model simulation results show that seven basic patterns of inter-household food transfers described in detail for the Hadza hunters of Tanzania can be simultaneously reproduced with striking accuracy under the assumption that agents selectively support and carry on sharing interactions in ways that maximize their income leveling potential.Introduction
Small-scale societies where individuals and families meet their daily subsistence needs by consuming wild foods and cultigens usually place a strong cultural emphasis on the virtues of giving to those in need. Among people as diverse in geographical location and cultural background as the Batek of Malaysia (Endicott 1988), the !Kung of Botswana (Lee 1979), and the Yanomami of Venezuela (Hames 2000), sharing of food is understood as an obligation of the giver and a right of the receiver, and those who refuse to share are invariably faced with accusations of stinginess and other forms of diffuse social pressure to grant the request. Such food-sharing practices may be understood as egalitarian to the extent that their leveling outcomes arise from the interactions of individuals proximately driven by leveling concerns to keep in check the asymmetric accumulation of valued resources within the group. Social anthropologists generally concur that food-sharing arrangements in small-scale societies are part and parcel of the broader repertoire of leveling strategies that prevent would-be dominants from exercising authority over potential subordinates (Boehm 1999, 2012; Clastres 1989; Endicott 1988; Fried 1967; Lee 1988; Wiessner 1996; Woodburn 1982). In the words of Boehm (1994, p. 180), such arrangements “would not be likely to work if decisive political power remained in the hands of a few”, while if valuable food items were not shared “it could be difficult to equalize power”.
In their empirical studies of human food sharing, however, evolutionary anthropologists rarely contemplated egalitarian motivations, drawing inspiration from sociobiological models in which sharing behavior is driven by various dispositions toward reciprocal risk-reduction, maximization of kindred benefits or status-seeking through signaling of individual qualities (see Gurven 2004; Hawkes et al. 2018; Kelly 2013 for reviews). The problem with these theories is that they ignore social role asymmetries: assortativity in cooperation is just as likely to include dominant as subordinate members of the social hierarchy (Gavrilets 2012). Consequently, they fail to accommodate the prevalent anthropological view of food sharing as a power leveling mechanism.
As a response to the insufficiency of traditional sociobiological models of cooperation, recent years have seen fundamental advances in evolutionary research that copes with the particular mechanisms leading to the evolution of egalitarian behavior and derived traits in humans (Boyd et al. 2011; Gavrilets & Richerson 2017; Hill et al. 2011; Silk & House 2016). Two prominent approaches are now well-established in the literature. The first suggests that dominant behavior can be suppressed to the extent that individuals are able to build and sustain reputations for their skills, knowledge and generosity that may bring about favorable relationships with social partners. If adaptive benefits such as social support, advantageous alliances, political influence or access to mating opportunities are more effectively obtained through freely conferred deference of followers rather than violent coercion over subordinates, dominance hierarchies may be expected to at least partly subside in favor of more stable status hierarchies (Cheng 2020; Henrich & Gil-White 2001). Reputation-based mechanisms for the evolution of cooperation are well-studied analytically (Gintis et al. 2001; Panchanathan & Boyd 2004), and associations between measures of social status and reproductive success have been consistently found in nonindustrial societies (von Rueden & Jaeggi 2016). A recent study among Tsimane forager-horticulturalists of Bolivia (von Rueden et al. 2019) provides the best example to date of how cooperative assortativity through status-seeking can play a role in the maintenance of relatively egalitarian relationships within a small-scale social group.
Although it offers a plausible alternative for the explanation of human egalitarianism, the reputational approach should be taken with a grain of salt. Theoretically, it seems to share some of the basic issues of earlier sociobiological accounts of cooperation. Status-seeking is at best an indirect motivation underlying the leveling of power asymmetries, which fails to account for the widespread view that egalitarian social relationships are primarily sustained by conscious choice of leveling strategies in small-scale societies. Besides, none of the available mathematical models of reputation-based cooperation is framed on an explicit representation of asymmetric social roles. Empirical research, on the other hand, repeatedly failed to find support for status-seeking accounts of human cooperation in egalitarian settings. The major proxy of social status in hunter-gatherer studies – hunting reputation – is probably too costly and noisy to serve as an effective reputational index (Stibbard-Hawkes et al. 2018). More generally, status-seeking strategies require that favorable relationships accumulated by well-reputed individuals be relatively stable in time. However, longitudinal data from a field experiment suggest that stable partnerships and dispositions have little to do with how cooperation is maintained in an egalitarian society (Smith et al. 2018); rather, cooperative assortativity in this social setting depends on the cooperativeness of one’s current residence group, which suggests a role for local norms in sustaining cooperation. Finally, in at least two well-studied egalitarian societies no evidence was found to support the notion that skillful, knowledgeable or well-reputed individuals accumulate adaptive advantages. Kraft et al. (2019) found that measures of foraging performance, prosociality and kin presence fail to predict lifetime reproductive success among the Batek of Malaysia; and Smith (2019) reported that being a preferred social partner or having stronger reciprocal ties with partners is not associated with higher reproductive success among the Hadza of Tanzania. All these findings agree with observations on the successful leveling of status-seeking behaviors in hunter-gatherers (Wiessner 1996), which suggests that human egalitarian tendencies do not easily yield to reputation-based accounts of cooperation.
A more promising approach emphasizes the role of leveling strategies in supporting the capacity of human groups to enforce strong egalitarian norms among its members and punish antisocial behaviors like dominance, aggrandizing, and hoarding (Boehm 1993; Erdal & Whiten 1996; Power 2009). A rich set of mathematical models now provide a comprehensive picture of how cooperation can evolve in socially asymmetric settings either through third-party punishment performed by leveling coalitions (Boyd et al. 2010) or second-party punishment such as in shunning and withdrawing from cooperative relationships with dominant individuals (Hooper et al. 2021). Most notably, the role of food sharing as a power leveling mechanism that could lead to the disruption of primate-like dominance hierarchies has been mathematically modeled (Gavrilets 2012). Considering the theoretical power and empirical plausibility of this approach, it is surprising that it remains unexplored in quantitative empirical studies of human food sharing.
In this paper, I begin by discussing an evolutionary theory that makes full sense of the anthropological view of leveling behavior as the main driver of hunter-gatherer sharing interactions. Next, I use an agent-based modeling approach to constructively test three theoretical predictions about the institutional architecture of decentralized food sharing systems. The agent-based model uses quantitative data on Hadza hunters’ population and individually heterogeneous food production patterns to track the aggregate results of spatially explicit sharing interactions across several empirically relevant dimensions. By means of a set of evolutionarily plausible sharing interaction rules, I show that Hadza patterns of inter-household food distributions can be accurately predicted under the assumption that agents selectively support and carry on sharing interactions in ways that maximize their income leveling potential within the group. Finally, I discuss model results in relation to previous evolutionary accounts of food sharing and cooperation in small-scale societies and consider opportunities for improvement in its theoretical basis and construction.
Evolution of the Egalitarian Social Instinct
The rationale behind the idea that sharing constitutes an intentional leveling device is pretty straightforward. Given that leveling of political power is a fundamental aspect of social organization in most small-scale human groups and that power leveling requires leveling of material resources that may be used strategically to disrupt the balance of power among individuals and families, then it makes sense to explain distributions of all such strategic resources based on the egalitarian hypothesis that sharing individuals are intentionally committed to the goal of reducing political inequalities that may arise from resource inequalities. Food sharing understood as consumption leveling is of course just a particular application of this rationale.
A more difficult challenge is to understand the evolutionary trajectories that could have lead to the emergence of egalitarian sharing behavior in the human species. Among non-human primates, most certainly, intentional leveling of food consumption is nowhere to be found. It would seem natural therefore to hold culture accountable for this radical innovation (Boehm 1993; Knauft 1991). But it so happens that sharing constitutes part of a common core of leveling devices found in very disparate cultural settings within an environment that is likely to have characterized early human evolution (Boehm 2012; Shultziner et al. 2010; Whiten & Erdal 2012). Besides, the very functionality of those leveling institutions seems to depend on flexible cognitive capacities and motivational dispositions that go beyond what is merely required by norm conformity or cultural adaptation. As Lee (1990) persuasively argues, the institution of sharing cannot simply amount to a set of cultural norms stipulating the ceiling of accumulation above which one cannot rise and the floor of destitution below which one cannot sink; rather, the idea is that ceiling and floor are closely articulated through a series of decentralized interactions that yield consumption leveling as their social outcome. For this process to be set in motion, individuals should be able to gather and process relevant information available in their social environment in order to correctly gauge the extent to which decentralized food distributions promote consumption leveling in the group as a whole. More than conformity to cultural norms, then, hunter-gatherer food sharing depends upon evolved psychological dispositions toward egalitarian behavior.
Such dispositions are predicted by Gavrilets (2012) in his evolutionary account of the egalitarian social instinct. The author starts from the assumption that human egalitarian tendencies evolved in a context of dyadic costly disputes over resource ownership. He describes the fitness \(w_{i}\) of a focal agent \(i\) is a function of resources \(R_{i}\) accumulated by \(i\) as well as resources \(R_{j}\) accumulated by every agent \(j\) who has a stake in the conflict:
| \[ w_{i} = \frac{f(R_{i})}{\sum_{j}f(R_{j})}\] | \[(1)\] |
Individual behavior optimized by natural selection under these assumptions leads to a couple of compelling evolutionary scenarios. First, in the absence of coalitions, modeling dyadic ownership disputes as a hawk-dove interaction (Hamilton 1981) generates a stable dominance structure in which weaker individuals usually give up their resources without fighting and only few males father most of the group offspring. Consistent with dominance hierarchies generally observed in non-human primates, this initial scenario provides an acceptable baseline from which to explore other evolutionary possibilities. Gavrilets expands the basic model by allowing doves to receive help from a leveler who incurs helping costs without deriving any direct benefits from cooperation. Even in this restricted coalition of only two members, it is shown that the population of levelers can become stable and generate substantial increases in group-level equality regarding both food distributions and male reproductive success. Key to this egalitarian outcome is that coalition synergy – the strength of coalitions above and beyond the sum of the strengths of individual members – be sufficiently high, while group size and strength assessment error by parties involved in the dispute be sufficiently low. As long as these conditions are fulfilled, levelers can successfully explore interdependent gains from intervening in costly disputes as third-parties.
This evolutionary account of the egalitarian social instinct obviously cannot be directly extrapolated to the ritualized, culturally elaborate, consciously intentional food sharing practices of evolved human societies. However, available empirical evidence suggests that its main assumptions succeed in capturing culturally-invariant regularities in food-sharing behavior observed in small-scale societies. First, the theoretical assumption that self-interested psychological motives are not easily suppressed by the egalitarian drive to share is well documented by ethnographic reports. Intense arguments and jealousies over food distributions, as well as occasional attempts at stealing and cheating, attest against any simple predisposition to share (Erdal & Whiten 1996). Second, that these recurring self-interested behaviors are successfully suppressed by coordinated action of group-members directed at the leveling of power and resource asymmetries within the group is a widely held view among anthropologists (Boehm 1999, 2012; Clastres 1989; Endicott 1988; Fried 1967; Lee 1988; Wiessner 1996; Woodburn 1982). In their descriptions of the hunter-gatherer "sharing ethos", ethnographers have long observed that command of social support is paramount and that interactions are framed in terms of entitlement of those in need to receive shares. Refusing to share food is usually not an option, since individuals can help themselves to it and take resources from unwilling givers without violating property norms (Endicott 1988; Peterson 1993). Even so, those who acquire a reputation for stinginess tend to elicit the anger of other group members and become subject to various forms of social pressure that can go from rough jokes to more serious sanctions like ostracism.
If such a combination of individual self-interest in resource accumulation and successful coordinated action toward its suppression were drivers of the egalitarian equilibrium in early human societies, at least three predictions about the general normative structure of sharing interactions in extant egalitarian hunter-gatherer groups should hold:
- Entitlement to receive shares. Social support should be granted to poorer individuals in sharing interactions based not on considerations about their level of destitution, but rather on the extent to which helping them contributes toward maximizing group-level equality.
- Giver choice. Poorer individuals who are socially supported in sharing interactions should preferentially seek to receive shares from the wealthiest among potential givers, thereby maximizing not only direct gains to themselves but also indirect gains to others upon which their social support relies.
- Equality. Because any resulting income asymmetry is detrimental to every interested party except for the eventual hoarder, the outcome of a sharing interaction should tend toward the pooling and equal division of the total amount of resources held by all those directly involved.
None of these predictions is easy to test against quantitative data collected in the field. Nevertheless, they can be jointly implemented within a modeling environment designed to simulate food-sharing patterns like those reported in field studies. In the next section, I describe a spatially explicit agent-based model of food distributions in which sharing interactions follow a plausible set of rules derived from each of the predictions above.
Model Design
To investigate which distribution patterns can be generated from a set of egalitarian sharing interaction rules, an agent-based model incorporating key aspects of an extant hunter-gatherer population was developed (see Model Documentation). The model consists of three components, the first of which sets out the main structural features of an agent population, while the others are designed to track changes in caloric incomes of each individual agent as they acquire wild foods and then engage in give-and-take of acquired resources with group co-residents from other households. Together, the three model components allow us to investigate aggregate distribution patterns that emerge from structured, rule-governed interactions among individuals given the most salient features of their social and economic environment, which include group size, individual heterogeneity and variability in acquisition. A full run of the model comprises a number of time-steps, each corresponding to a “foraging day” in which caloric returns are stochastically assigned to agents before spatially explicit sharing interactions take place. See Appendix B for a detailed model description.
Population
The main simulations and analyses presented below revolve around a small local group of seven agents representing their respective households. The size of this population is not arbitrary, but reflects the average number of married hunters studied by Wood & Marlowe (2013) across seven different Hadza camps. Because individual heterogeneity in food acquisition among these agents is key to understanding their sharing behavior, the group was further divided into three types consisting of one top, three regular, and three poor agents. This division is intended to take advantage of Wood and Marlowe’s data on food production and distribution relative to a sample of the best, median and poorest married Hadza hunters from each camp. The distribution of agents across types is the result of an educated guess based on average group size together with the fact that hunting success follows a right-skewed distribution among the Hadza.
Foraging
In groups like the Hadza, where hunting is predominantly a solitary activity, the returns of an individual hunter generally depend on his level of skill and luck, both of which are closely associated with the particular resource types he targets. Accordingly, total daily acquisitions for each agent are recorded anew at the beginning of every time-step of the model. These values are defined as the sum of calories each agent obtains according to his success probabilities and average returns in foraging for two types of resources: large game and other foods. Success probabilities and average returns of an individual agent for both resource types depend on whether he is a top, regular or poor hunter, and are modeled after empirical values recorded for the Hadza. While this approach simplifies day-to-day variability in sizes and amounts of food items targeted by Hadza hunters, it adequately represents individual heterogeneity in success and returns. Table 1 displays the food acquisition data used in the foraging component of the model.
| Daily acquisition rates | |||
|---|---|---|---|
| Top hunters | Regular hunters | Poor hunters | |
| Large game | 15,800 kcal | 1,000 kcal | - |
| Other foods | 1,000 kcal | 1,700 kcal | 1,350 kcal |
| Daily success rates | |||
| Top hunters | Regular hunters | Poor hunters | |
| Large game | 2 % | 2 % | - |
| Other foods | 37% | 43% | 40% |
Sharing
After foods are brought into Hadza camps, members from different households typically approach the households of successful acquirers to receive a share. Large game meat tends to attract the attention of crowds, but individuals often also receive shares from other food types, which they may take to their own households for later consumption or else eat on the spot in a shared meal. Following the spatial organization of Hadza camps, agent households are more or less evenly spaced from each other and are positioned at the center of a round-shaped area where sharing interactions take place. At each time-step of the model, after individual foraging returns are assigned, agents proceed to the sharing of the available bounty following three basic rules that describe the structure of a decentralized hunter-gatherer food distribution system according to the predictions of the theoretical model discussed above.
The first rule defines which agents are granted decisive social support to claim shares from others and are therefore entitled to receive shares. Following the first theoretical prediction, entitlement to receive shares is operationalized in terms of an individual’s need relative to the current level of group inequality:
- Let \(S\) be the set including the incomes of all group members. For each agent \(i\) whose income is lower than the highest income in \(S\), let \(S_{-i}\) be the subset of \(S\) formed by excluding \(i\)’s income. Then find the Gini-index of income inequality for the set \(S\) and for its subset \(S_{-i}\). If the former inequality measure exceeds the latter, then agent \(i\) is entitled to receive shares.
- For each agent \(i\) who is found entitled to receive shares, let \(A\) be the set including every other agent with income greater than \(i\). Then select one member \(j\) of the set \(A\) randomly with probability given by the ratio between \(j\)’s income and the total summed incomes of all \(A\) members. Last, move \(i\) to the household area of \(j\).
- For each agent \(i\) who belongs to the group, let Ri be the set including every other agent located in the household area of \(i\). If \(R_{i}\) is non-empty, pool the incomes of \(i\) and every \(R_{i}\) member together and divide the total sum equally among them.
Results
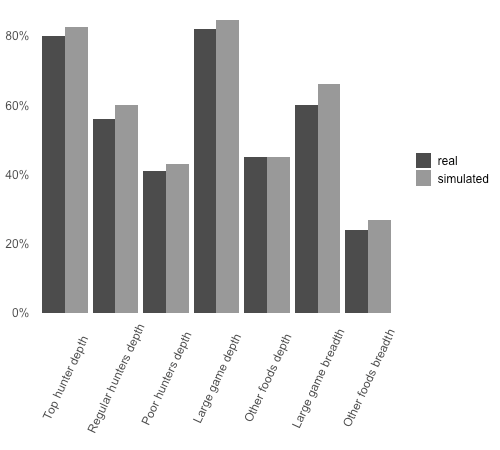
Wood & Marlowe (2013) datasets for primary distributions of large game meat and complete distributions of other food types can be directly compared to a total of seven different outcome variables of the model describing the following dimensions of Hadza food distributions: sharing depth by hunter type – mean percentage of total kilocalories acquired by individual hunters and shared with other households, disaggregated by hunter type (top, regular, poor hunters); sharing depth by food type – mean percentage of total kilocalories acquired by individual hunters and shared with other households, disaggregated by food type (large game meat and other types of foods); sharing breadth by food type – mean percentage of potential receiving households that actually receive shares from individual hunters, disaggregated by food type (large game meat and other types of foods). Model outputs for the seven outcome variables were averaged over 100 independent model runs of 1,000 time-steps each (see Operational details in Appendix A).
Figure 1 compares Hadza food-sharing patterns and simulation outcomes. The striking proximity between real and simulated values emerging spontaneously from the model’s sharing interaction rules is sufficient to validate the underlying theoretical predictions on the evolution of the egalitarian social instinct. Appendix A shows that there is little variation in outcome variables across independent simulations and that model results are fairly robust to variation in population and other parameter values within plausible ranges. Appendix D introduces random variations to each sharing interaction rule and discusses the results of a total of seven alternative models implementing different levels of randomization to the original model design. These results help to further validate the egalitarian model by showing that each of its interaction rules has independent positive impact on the model’s fit to the empirical data.
Discussion
This study represents the first attempt to test the predictions of an evolutionary model that explains food sharing as a power leveling mechanism in small-scale human groups. The agent-based simulations reported here show that seven key food-sharing patterns described in detail for the Hadza hunters of Tanzania can be simultaneously reproduced with striking accuracy under the assumption that individuals selectively favor and carry-on sharing interactions in such a way as to maximize the equality of income distribution within their residential groups.
The appeal to traditional sociobiological theories of cooperation in the context of small-scale human groups has been frequently criticized for sacrificing ethnographic realism in the name of evolutionary plausibility (Boehm 2012; Henrich 2018; Woodburn 1998). Among the most prominent of the theories originally developed by biologists and then adapted to the food-sharing realities of the Hadza and other small-scale societies, kin selection (Hamilton 1964) explains the evolution of cooperation through the inclusive fitness benefits of cooperating with kin; reciprocity (Trivers 1971) suggests that short-term fitness losses in cooperation can be offset by more substantial long-term fitness gains if individuals are able to favor reciprocators in their repeated interactions; and costly signaling (Gintis et al. 2001; Zahavi 1977) assumes that widespread cooperation works as an honest signal of individual qualities to an audience, thereby increasing the fitness-enhancing social support and attention cooperators receive from others. Among the Hadza, kin selection and reciprocity received limited support from empirical data. Wood & Marlowe (2013) report in their study that Hadza food transfers flow more often to close kin than to non-kin. Based on data collected in a previous field study, it has also been shown that there is modest but significant correlation between meat shares given and received among the Hadza (Jaeggi & Gurven 2013). Apart from consistency with these patterns, neither theory seems to afford an ethnographically plausible pathway to integrate substantial bodies of observations on food sharing among the Hadza or small-scale societies in general.
Kin selection does not explain widespread distributions of food to genetically unrelated others in small-scale societies. This is especially true about mobile hunter-gatherers, who are notable both for their prodigious food sharing and low intra-group relatedness (Hill et al. 2011; Walker 2014). Besides, pervasive cultural institutions like partible paternity (Walker et al. 2010), reflected in the lack of correspondence between kin terms and genetic relatedness typically observed in human societies (Cronk et al. 2019), also contribute to undermine the theory’s plausibility. Although potentially able to account for cooperation with non-kin, reciprocity cannot accommodate the outstanding imbalances documented in human food transfers. Among the Hadza studied by Wood & Marlowe (2013), best hunters who succeeded in large game hunting shared six times more food than median hunters each day on average (see ESM Table S4). Were this outstanding contribution disparity primarily sustained by reciprocal cooperation, one would expect best hunters and their families to be helped more often and more substantially than other group members on a daily basis. Yet this is likely not the case. For example, there has been found no evidence of nutritional advantage to being or marrying a well-reputed Hadza hunter (Stibbard-Hawkes et al. 2020).
Kin selection and reciprocity theories also beg the question of producer control over acquired resources. In spite of countless ethnographic accounts suggesting the opposite (Endicott 1988; Hawkes et al. 2001; Kent 1993; Woodburn 1982), supporters of both theories and associated hypotheses have often argued in favor of producer control based on the quantitative observation that individuals in small-scale societies tend to keep substantially larger portions of their production than the portions they give to others (Gurven 2004). In a recent contribution, I showed that this argument is misleading (Pinheiro 2021). Because income leveling entails net resource flows from the wealthier to the poorer, the average contribution rate for the population as a whole will tend toward the relatively low rates of the poorer whenever they outnumber the wealthier. Consequently, just about any successful income leveling strategy should be consistent with the observation that individuals keep larger average portions of their production to themselves than the portions they give to others.
Costly signaling theory provides an alternative explanation of why male hunters engage in widespread sharing of meat with unrelated non-reciprocators among the Hadza and other foragers (Hawkes et al. 2001, 2014; Hawkes & Bird 2002). However, signaling motives do not explain why individuals in small-scale societies often share reliable and easy-to-acquire food items that would seem to have little appeal to an audience. For example, what could be the signaling value of various fruits that Hadza hunters share with other households in a relatively modest but still significant proportion, usually in the context of one-on-one interactions removed from the eyes of others? Another difficulty with signaling theory is that interested audiences will be on the look out for both successes and failures of signalers, with the consequence that less capable producers should invest relatively less time and energy in subsistence activities with signaling potential (Stibbard-Hawkes et al. 2018). This is inconsistent with the low inter-individual variance in hunting effort generally observed among hunters. Finally, supporters of signaling theory have not been able to show that their assumed indirect benefits from cooperation are associated with any actual fitness gains. On the contrary, evidence shows that being a preferred social partner is not associated with higher reproductive success among the Hadza (Smith 2019), so that the point of signaling to gain favorable attention of others is moot in this empirical setting.
In contrast, the constructive agent-based modeling approach adopted here integrates a substantial sum of ethnographic observations within a sound evolutionary framework. By deriving its central assumptions from a plausible theory on the evolution of leveling coalitions and operationalizing the notion of entitlement to receive shares, the model makes sense of the prevalent anthropological view of food sharing as leveling behavior contingent upon coordinated group effort rather than the outcome of an individualized willingness to give shares. The agent-based approach developed here is also the first to reproduce patterns of both widespread large-game meat distributions and distributions of other food types based on a single coherent set of sharing interaction rules. Since givers are chosen randomly based on probabilities weighted by their income, receivers tend to flock around the households of large game meat acquirers – whose incomes are outstandingly larger than anyone else’s – even on days when most agents also acquired other foods. Conversely, on days when no large game is available, receivers are more likely to scatter around the households of agents who acquired other foods and whose incomes are therefore relatively undifferentiated from each other. This realistic spatial patterning of food distributions is reflected in the gap between the sharing breadth of large game meat and other foods reproduced by the model.
A potential objection that can be leveled against the present approach is that it relies on excessively demanding cognitive assumptions. In order to effectively determine who is entitled to receive shares, it is implicitly assumed that agents have accurate information about each other’s holdings, use that information to assess each other’s relative needs in ways consistent with Gini-index computations of inequality, correctly update all the relevant information at each sharing interaction, and do not face serious coordination problems in giving or withholding social support to potential beneficiaries. Although the model is neutral about how these informational, cognitive and organizational processes are proximally implemented, there are a number of reasons to believe they are effective in the context of small-scale egalitarian societies.
First, evidence from neurobiology and developmental psychology shows that inequality aversion is wired into the human brain’s reward circuitry (Tricomi et al. 2010) and is displayed by young children from an early age (Fehr et al. 2008; McAuliffe et al. 2017; Rizzo & Killen 2016), so that the capacity to correctly assess unequal distributions is likely part of the evolved human cognitive repertoire. When development of this capacity is encouraged through social learning, such as is certainly the case in small-scale egalitarian societies (Lew-Levy et al. 2018), individuals may come to age with a robust sense of fairness (Erdal & Whiten 1994) that equips them to make reliable judgments about distributive equality. Second, much of the monitoring costs and coordination problems involved in acquiring and updating information on resource distributions in a small-scale group may be mitigated through linguistic communication and gossip (Smith 2010), which allow the rapid acquisition and diffusion of fine-grained information at a low cost. Third, an interdependent psychology that instantiates common interest in group-level equality among all except the occasional hoarders has the potential to greatly facilitate the coordination of decentralized sharing interactions. Ethnographic accounts of the various gains to cooperation as well as the strong sense of interdependence associated with human small-scale group living suggest that these are privileged contexts for development of interdependent psychologies (Tomasello et al. 2012).
To the extent that food sharing is one from a diverse set of leveling strategies deployed in small-scale societies, it is unsurprising that it requires "a political capacity to operate in large coalitions and a cognitive capacity to arrive at a shared plan of action" (Boehm 1993, 1999). Granting and withholding social support to potential receivers in ways that effectively reduce group-level inequality may be a less daunting task if it is performed collectively rather than individually. Future studies should gain insight on proximate mechanisms that have the potential to engage collectivities in otherwise decentralized interactions and examine the possibilities and constraints related to social scale and organization. For example, future elaborations of the present model could represent the mechanism by which entitled receivers are identified as a process of social problem-solving engaging the collective intelligence of observers (Carletti et al. 2020).
Sharing rules derived from the theoretical predictions explored here do not exhaust the diversity of patterns and correlates documented by anthropologists in their field work among small-scale human groups. Yet one of the advantages of agent-based models is that they can be relatively easily expanded to generate more complex interactions and integrate larger datasets. Future developments of this egalitarian model should attempt to reproduce other documented features of sharing behavior in small-scale societies, like preferential sharing with kin. My provisional take on the matter is that most of the evidence on food sharing left aside in the present elaboration could be elucidated by taking into account the social embeddedness of sharing behavior. In this way, even if individuals preferentially seek high-income resource holders as sharing partners, the fact that they generally interact more often with relatives on a daily basis would suffice to explain a kin bias in their resource distributions. A similar constructive agent-based approach has been successfully applied to the study of patterns of social affiliation in primates (Puga-Gonzalez et al. 2009, 2015). At the ultimate level of evolutionary causation, an expanded theory of fitness interdependence has the potential to account not only for the human egalitarian social instinct but also for evolved patterns of preferential interaction with genetically related and fictive kin as well as friends (Aktipis et al. 2018). Further explorations of the fitness interdependence hypothesis therefore hold great promise to advance the study of sharing and cooperation in small-scale human groups as well as the understanding of decentralized resource distribution systems in general.
Model Documentation
A detailed model description, following the ODD (Overview, Design concepts, Details) protocol (Grimm et al. 2006) is provided in Appendix B. The ABM was developed using the NetLogo modeling environment (Wilensky 1999). The source code is available at: https://www.comses.net/codebase-release/3d57536d-df94-4581-bc13-86a663a33331/.Acknowledgements
A first rudimentary version of the model developed in this paper was presented at the 2017 Complexity Economics seminar at the Post-Graduate Economics Department of Universidade de Brasília. I am grateful to Professor Bernardo Mueller and all participants at the seminar for their patience and active engagement with my work. I would also like to thank the anonymous referees of JASSS for their careful revision and invaluable suggestions to the first version of the manuscript.Appendix
Appendix A: Sensitivity Analysis
Operational details
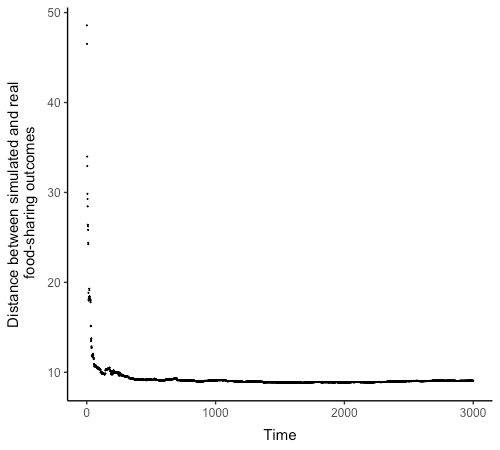
All analyses reported in this study were carried out in R (R Core Team 2017). Sample points for the main simulation experiment and sensitivity analysis were generated in R, with NetLogo model runs performed through the RNetLogo package (Thiele et al. 2012) using codes adapted from Thiele et al. (2014). I first conduct a pre-test to determine the number of time-steps required for model convergence to a steady-state behavior. The pre-test consists of 10 model runs at parameter values drawn from uniform distributions within the ranges listed in Table 2. A Latin hypercube technique was used to avoid uneven sampling of the parameter space. The outputs of all model outcome variables are recorded at every time-step. Figure 2 shows the change in aggregate model output (measured as the root mean squared error between simulated outcomes and real sharing patterns) across time. The output quickly converges to a mean within the first few hundred time-steps. It remains definitely stable from around 500 time-steps onwards.
Next, I use the main simulation experiment dataset derived from 100 replicate runs in the default parameter set to estimate distribution of the output. Each replicate was run for 1,000 time-steps and the outputs of all outcome variables were collected at the end. Sharing breadth of large-game meat is by far the most spread variable, with standard deviation of 3 and range of 14 percent points approximately (Figure 3). Together, the remaining six outcome variables have mean standard deviation of 0.8 and mean range of 4 percent points approximately. Therefore, with the exception of large-game sharing breadth, model outputs display almost deterministic behavior given enough time-steps for hunter acquisition rates to stabilize around their mean values.
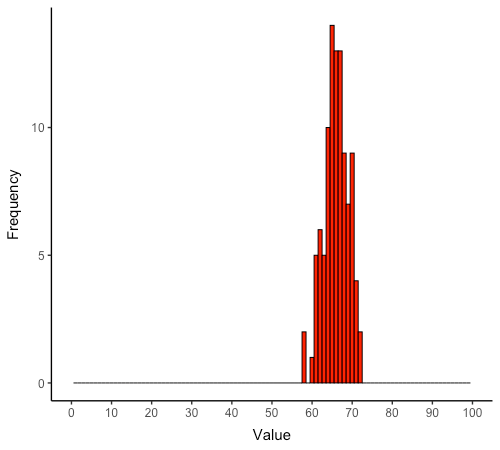
Large-game sharing breadth constitutes an exception for two combined reasons. First, hunters acquire large game at a success rate of 2% each day, which means large-game acquisitions take longer to stabilize around their mean than acquisitions of other food types. Second, although sharing breadth is represented in a continuous percentage scale to facilitate comparability, it is not a continuous variable. Thus, within the small hunter population considered (\(n=7\)), the smallest possible deviation in sharing breadth outputs would be of 1/6 or approximately 16.6 percent points. This means that minimal deviations in sharing breadth each time-step can contribute to a relatively large spread of the output at the end of a model run.
In the main simulation experiment and sensitivity analysis, respectively, 100 replicates and 10 replicates were used per parameter set to estimate output means. Each replicate was run for 1,000 time-steps and the outputs of all outcome variables were collected at the end.
OFAT and LHS analyses
The model used in this study has 13 parameters describing the number, success and acquisition rates of three types of agents representing hunters in a small-scale society. In the main simulation experiment reported here, I kept the 13 model parameters fixed at values that correspond to Hadza hunters’ population and food acquisition data. Under these default assumptions, the model’s spatially explicit sharing interaction rules were sufficient to reproduce Hadza food distribution patterns.
What remains to be verified are the conditions under which results obtained from the main simulation experiment hold. To do that, I now let the model parameters vary away from default values one at a time and over comprehensive ranges. This OFAT (One-factor-at-a-time) method of sensitivity analysis has proven to be an efficient way to gain insight on model response to variation in its parameters (ten Broeke et al. 2016). A major disadvantage is that it leaves interaction effects generated by simultaneous variation in parameters unexplored. However, as non-linearities involved in agent-based models make it difficult even for costlier regression-based methods to capture interaction effects reliably, the advantages of OFAT analysis are considerable and it provides an essential first step to further explorations of model sensitivity.
The default values and ranges of parameter variation are listed in Table 2. The number of simulated hunter types varied in intervals of one within their respective range, while the other parameters varied away from their nominal values in equidistant intervals of 10% up to a maximum variation of 30% (above and below). This means that the effects of 70 different parameter sets over 7 outcome variables were recorded for a total of 490 model outputs. To measure parameter sensitivity, I calculate the difference between simulated outcomes and real food-sharing patterns. Following this approach, one finds that simulated outcomes deviate more than 5 percent points from real patterns in 85 out of the total 490 model outputs. Among these potentially significant outputs, only 8 deviate more than 10 percent points from real patterns. All these strongly significant deviations relate to the effects of population parameters over sharing breadth variables.
| Parameter | Description | Default value | Simulated ranges |
|---|---|---|---|
| bests_number | Number of top hunters | 1 | 1-3 |
| regs_number | Number of regular hunters | 3 | 1-5 |
| poors_number | Number of poor hunters | 3 | 1-5 |
| m_chance_bests | Success rate / top / large game | 2% | 1.4-2.6% |
| m_amount_bests | Acquisition rate / top / large game | 15,800 kcal | 11,060-20,540 kcal |
| o_chance_bests | Success rate / top / other foods | 37% | 26-48% |
| o_amount_bests | Acquisition rate / top / other foods | 1,000 kcal | 700-1,300 kcal |
| m_chance_regs | Success rate / reg. / large game | 2% | 1.4-2.6% |
| m_amount_regs | Acquisition rate / reg. / large game | 1,000 kcal | 700-1,300 kcal |
| o_chance_regs | Success rate / reg. / other foods | 43% | 30-56% |
| o_amount_regs | Acquisition rate / reg. / other foods | 1,700 kcal | 1,190-2,210 kcal |
| o_chance_poors | Success rate / poor / other foods | 40% | 28-52% |
| o_amount_poors | Acquisition rate / poor / other foods | 1,350 kcal | 945-1755 kcal |
Thus, any reduction in the number of either regular or poor hunters is associated with a substantial increase in the sharing breadth of large game meat and a relatively lesser, but also significant, increase in the sharing breadth of other foods. This is fully expected since sharing breadth is calculated as the number of receiving households divided by the number of total households. As total households decrease in the population, sharing breadth of all foods tends to increase. This effect is particularly strong for the sharing breadth of large game meat because a reduction in the number of either regular or poor hunters means the probability of anyone interacting with a wealthy large game acquirer increases relatively. For the same reason, any increase in the number of top hunters also leads to a significant increase in the sharing breadth of large game.
The OFAT analysis thus suggests that the model is considerably robust to variation in its parameters. To further validate this result, I performed 100 randomized model runs in which parameters were drawn from uniform distributions within the same ranges using Latin hypercube sampling. To keep results consistent with the fact that hunter efficiency follows a right-skewed distribution, only model runs in which the random number of top hunters was strictly less than both the number of regular and poor hunters were considered. Mean outputs for all outcome variables were not significantly different from outputs derived from the default parameter set (Figure 4).
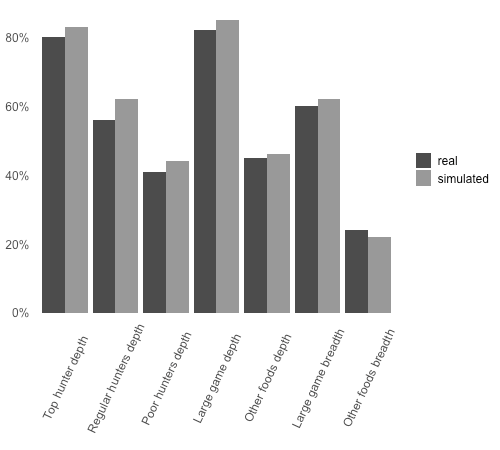
Overall, 83% of simulated outcomes generated in the OFAT analysis tests matched real Hadza sharing patterns by a difference of less than 5 percent points. Virtually the same results derived from the default set were replicated by using random parameter sets with values drawn from comprehensive ranges. Given the extent to which evolutionary studies have focused on the sharing of large-game meat, ignoring other types of foods or dealing with them in ad hoc fashion, it is highly significant that a single, coherent set of equality maximization rules was able to reproduce core observations on food sharing in a small-scale society under a comprehensive range of plausible variation in underlying assumptions about hunter population, success and acquisition rates.
Appendix B: Model description
The model description follows the ODD (Overview, Design concepts, Details) protocol for describing individual- and agent-based models (Grimm et al. 2006), as updated by Grimm et al. (2020).
Purpose and patterns
The purpose of the model is to test the extent to which food distribution patterns in an extant hunter-gatherer group can be reproduced by means of a set of spatially explicit sharing interaction rules derived from a theory on the evolution of the egalitarian social instinct (Gavrilets 2012).
The model is evaluated by its ability to reproduce seven patterns along three different dimensions of hunter-gatherer food distributions:
- Sharing depth by hunter type – mean percentage of total kilocalories acquired by individual hunters and shared with other households, disaggregated by hunter type (top, regular, poor hunters);
- Sharing depth by food type – mean percentage of total kilocalories acquired by individual hunters and shared with other households, disaggregated by food type (large game meat and other types of foods);
- Sharing breadth by food type – mean percentage of potential receiving households that actually receive shares from individual hunters, disaggregated by food type (large game meat and other types of foods).
Entities, state variables and scales
Agents of the model are hunters who forage for and share food that will be consumed within their households. Hunters are further divided into top, regular, and poor as per foraging efficiency (following Wood and Marlowe’s data on best, median and poorest married Hadza hunters observed in seven different camps). State variables of agents are as follows:
- own-income – kilocalories in possession of a hunter that he produced by himself;
- share-income – kilocalories in possession of a hunter that were produced by others and then transferred to him in a sharing interaction;
- total-income – sum of a hunter’s own-income and share-income at any time;
- meat-number – list of other hunters who receive shares from a hunter on a day when he acquires large-game meat;
- share-number – list of other hunters who receive shares from a hunter on a day when he does not acquire large-game meat.
Each agent is also associated with a unique patch where his household is located and next to which food transfers occur. The time-step of the model represents one day and simulations were run for 1,000 days.
Process overview and scheduling
At the beginning of a model run, success and acquisition rates for two food types (large-game meat and other foods) are set for each individual hunter according to his foraging efficiency (top, regular, poor). At each time step, if a hunter succeeds in acquiring one or both food types, the total sum of kilocalories obtained are added to his own-income.
The initial assignment of caloric incomes is followed by food distributions. First, each individual hunter who is entitled to receive shares chooses a giver randomly based on income-weighted probabilities and moves to the household area of the chosen giver. After receivers are positioned in the household area of their respectively chosen givers, sharing interactions take place: the giver and all receivers located in his household area pool their caloric incomes together and divide the sum equally. Kilocalories shared by a giver are first deducted from the giver’s share-income and then from his own-income, while kilocalories obtained by each receiver are added to the receiver’s share-income. Besides, each receiver located in a giver’s household area is added without repetition to the giver’s meat-number or to his share-number (depending on whether the giver did or did not acquire large-game meat that day).
If there are no more hunters who meet the entitlement condition for receiving shares, the information stored in each hunters’ state variables is collected. Then these variables are reset, hunters go back to their households and the model proceeds to the next time-step.
Design concepts
Basic principles
Gavrilets (2012) theory on the origins of the egalitarian social instinct provides a solid evolutionary foundation for the kind of intentional leveling behavior observed in small-scale societies and vastly discussed and documented by social anthropologists over the years. This theory shows how fitness interdependence among individuals can trigger an egalitarian drive to help the weaker obtain resources from the stronger even when the helper bears sunken costs. The emerging psychology is such that individuals who have a stake in the outcome of sharing interactions face an incentive to maximize their own income (when acting as participants) and to minimize income asymmetries among the participants (when acting as observers). Because each individual’s interest in hoarding resources is destined to be countered by the common interest of the many in reducing income asymmetries, this interdependent psychology has the potential to account for successful suppression of hoarding behavior through the coordinated action of leveling coalitions.
Emergence
The model generates spatial patterns of both widespread large game distributions and restricted distributions of other food types observed in hunter-gatherer societies. These patterns are not directly imposed on the model but result predictably from (i) the wide quantitative gap between acquisitions of large-game meat versus other food types and (ii) the fact that hunters who are entitled to receive shares preferentially choose high-income resource holders as givers.
The model also reproduces seven patterns describing the depth and breadth of hunter-gatherer food distributions by tracking and comparing information stored in the agents’ state variables. Because these results are driven by sharing interaction rules derived from predictions of a theory that has never been tested against quantitative data, their emergence is neither intuitive nor in any sense predictable.
Adaptation
Hunters are assumed to have an interest in maximizing their own total-incomes while minimizing asymmetries in the total-incomes of others. Accordingly, for each individual hunter who might attempt to obtain food from someone else, the adaptive behavior of observers is to either grant or withhold social support to the potential receiver in a way that minimizes group-level income asymmetries. Social support to a potential receiver is modeled as direct objective seeking: a hunter is considered entitled to receive shares based on how his total-income affects group-level equality (see Objectives below). The adaptive behavior for a socially supported hunter is to maximize his own total-income: he preferentially chooses the wealthiest among all potential givers based on a stochastic process described below ("giver selection" submodel) and then moves to the household area of the chosen giver to claim resource shares.
Objectives
The objective criterion used by observers to decide if a focal hunter is entitled to receive shares consists in a comparison of Gini-index inequality measures. The script used for computing the Gini-index of a set of values was adapted from Wilensky (1998). If the Gini-index for total-incomes of all hunters exceeds the Gini-index for total-incomes of all hunters except the focal hunter, then the focal hunter is entitled to receive shares. An entitled receiver then selects a wealthier hunter randomly with probability weighted by the latter’s total-income.
Learning
Agents do not change their adaptive traits over time.
Prediction
It is implicitly assumed that observers grant social support to an individual hunter by estimating whether his total-income negatively affects group-level equality.
Sensing
It is implicitly assumed that observers have all the information and cognitive capacity to identify which hunters are entitled to receive shares. This includes accurate information about the total-income of every hunter, the capacity to assess the relative needs of each hunter in ways consistent with Gini-index computations of inequality, and the capacity to correctly update the relevant information after each food distribution cycle. Although these implicit assumptions are cognitively demanding, they are not unrealistic if sharing is to be modeled as a leveling device in ways consistent with ethnographic observations on hunter-gatherer distributions. In future elaborations, the proximate mechanism by which entitled receivers are identified could be modeled as a process of social problem-solving engaging the collective intelligence of all interested observers (Carletti et al. 2020).
Stochasticity
Both foraging and sharing are represented by stochastic processes. The total amount of kilocalories acquired by an individual hunter each day varies stochastically according to the acquisition and success rates of top, regular and poor hunters (following Wood and Marlowe’s data on best, median and poorest married Hadza hunters observed in seven different camps). When it comes to food distributions, a hunter who is found entitled to receive shares selects a partner randomly with probability given by the ratio between the partner’s income and the summed incomes of all potential partners.
Collectives
No collectives of agents are represented in the model.
Observation
Graphical output on the model interface shows hunters and their households, as well as the displacement of hunters to each other’s household areas when sharing interactions take place. Summary statistics on mean acquisition, total-income and sharing breadth for each hunter type (top hunters in red, regular hunters in green, poor hunters in blue), as well as the mean percentage of acquisitions consumed within producer households versus mean percentage given to non-producers’ households are updated via interface plots at each time step. Summary statistics on the seven outcome variables of interest (see Purpose and Patterns above) are provided at the end of each model run.
Initialization
Model runs start with a population of one top, three regular, and three poor hunters located at the center of their respective household areas. Each individual hunter differs in daily success rates and average daily acquisition rates for two different resource types (large game and other foods) based on their foraging efficiency (whether they are top hunters in red, regular hunters in green or poor hunters in blue). The number and distribution of hunter types, as well as other default parameter values defining success and acquisition rates for each hunter type, follow Wood and Marlowe’s data on married Hadza hunters observed in seven different camp sites. See Table 2 for descriptions, default values and simulated ranges of model parameters.
Input data
The model does not use input data to represent time-varying processes.
Submodels
Forage
At the beginning of each time-step, hunters have zero calories in both their own-income and share-income. The own-income of an individual hunter of given foraging efficiency is then updated through the following procedures:
- Add \(\frac{a_{m}}{p_{m}}\) kilocalories to the hunter’s own-income with probability \(p_{m}\);
- Add \(\frac{a_{o}}{p_{o}}\) kilocalories to the hunter’s own-income with probability \(p_{o}\).
where:
\(p_{m}\) = daily probability of acquiring large-game meat;
\(p_{o}\) = daily probability of acquiring other food types;
\(a_{m}\) = mean daily caloric acquisition of large-game meat;
\(a_{o}\) = mean daily caloric acquisition of other food types.
Take a regular hunter who (a) has a 2% daily chance of acquiring large-game meat and acquires 1,000 kilocalories of large game meat each day on average and (b) has a 43% daily chance of acquiring other foods and acquires 1,700 kilocalories of other foods each day on average. Following the first procedure above, an amount of 1,000/0.02 = 50,000 kilocalories of large game meat will be added to his own-income with a probability of 2%; each day; following the second procedure above, an amount of 1,700/0.43 \(\approx\) 3,950 kilocalories will be added to his own-income with a probability of 43% each day. Over the course of time, consequently, the hunter’s acquisition of large game meat and other foods will stabilize around their daily averages.
The own-income each hunter takes to the sharing round of the model is the sum total of kilocalories from food types he successfully acquired that day. After the own-income of each individual hunter is thus updated, go to the Associate sub-model.
Associate
The first step of a sharing interaction cycle is defining who is entitled to receive shares. Social support is granted to potential receivers only if helping them contributes toward maximizing group-level equality. Let \(G(\cdot)\) be a function that computes the Gini-index for a set of values, \(S\) the set of total-incomes of all hunters in the group, and \(S_{-i}\) the set of total-incomes of all hunters in the group except for the total-income of a focal hunter \(i\). Then hunter \(i\) is entitled to receive shares if and only if the following condition obtains:
| \[G(S) > G(S_{-i})\] | \[(2)\] |
If no hunters are found entitled to receive shares, the information stored in the state variables of each individual hunter is collected, quantitative state variables are zeroed and list state variables are emptied. The sharing round is over and the model proceeds to the next time-step. However, if at least one hunter is found entitled to receive shares, each entitled receiver chooses his respective giver.
A receiver preferentially chooses the wealthiest among all potential givers. Define \(x\) as a hunter’s total-income and let \(A_{k > i}\) be the set of hunters \(k\) whose total-income is strictly higher than the total-income of hunter \(i\). The probability \(P\) that \(i\) chooses \(j\) as a giver is:
| \[P_{ij} = \frac{x_{j}}{\sum_{k}x_{k}}\] | \[(3)\] |
where \(j\) is a member of set \(A_{k > i}\) and the sum is taken over all members of set \(A_{k > i}\).
The giver choice algorithm works as follows. First, pick a random number n within the interval \([0,1]\) and then pick a random hunter \(j\) from set \(A_{k > i}\). Next update the value of \(n\):
| \[n^{'} = n - P_{ij}\] | \[(4)\] |
If \(n^{'}\) is less than or equal to 0, hunter \(j\) is chosen as a giver; if not, repeat the procedure: pick another hunter from set \(A_{k > i}\) randomly without repetition, then update the value of \(n^{'}\) and check if the result is less than or equal to 0. The chance of a hunter being chosen as a giver is therefore directly proportional to his total-income \(x\). Also, because the sum of probabilities \(P\) over all members of set \(A_{k > i}\) is equal to one, the algorithm ensures that hunter \(i\) will choose one and only one other hunter as a giver. Finally, move hunter \(i\) to the household area of his giver and repeat the procedure for each other hunter who is found entitled to receive shares. Then go to the Share sub-model.
Share
After receivers are positioned in the household area of their respectively chosen givers, decentralized food transfers take place. Given the equitable nature of food distributions, the giver and each receiver in a local sharing interaction should end up with the same total-income. Let \(R_{j}\) be the set of receivers located in the household area of giver \(j\). After food transfers take place, the total-income \(x^{*}\) of each party in the sharing interaction is expressed by the equation:
| \[x^{*} = \frac{x_{j} + \sum_{k \in R_{j}}x_{k}}{\mid R_{j}\mid + 1}\] | \[(5)\] |
This formula makes room for all possibilities of local interactions that go from dyadic to group-wide food transfers. Note that giver \(j\) transfers \(x_{j} - x^{*}\) kilocalories to others, while each receiver \(k\) obtains \(x^{*} - x_{k}\) kilocalories from his giver. This is how the state variables of participants are updated.
- If giver j acquired large-game meat and this is his first interaction in the day, add every member of set \(R_{j}\) to his meat-number list; otherwise, add every member of set \(R_{j}\) without repetition to his share-number list.
- Subtract \(x_{j} - x^{*}\) kilocalories from the share-income of hunter \(j\) until it equals zero, then subtract the remaining amount from his own-income.
- Add \(x^{*}-x_{k}\) kilocalories to the share-income of every hunter \(k\) included in set \(R_{j}\).
Repeat the procedure for each hunter whose household area is occupied by at least one other hunter. After food transfers take place, receivers return to their households and a new cycle of sharing interactions begins. Go back to the Associate sub-model.
Appendix C: Example of a Sharing Round
For clarity of exposition, consider how the sharing interaction rules described above are implemented for agents \(\{a, b, c\}\) and their respective total-incomes \(\{100, 500, 1500\}\).
First cycle
Agent \(c\) is not entitled to receive shares since she is the group member with the highest total-income. The Gini-index of the full income set \(\{100, 500, 1500\}\) is 0.44. Excluding the total-income of agent \(a\) from the full set, the Gini-index of the resulting subset \(\{500, 1500\}\) is 0.25, which means that \(a\) makes the group more unequal and is thus entitled to receive shares. On the other hand, excluding the total-income of agent \(b\) from the full set, the Gini-index of the resulting subset \(\{100, 1500\}\) is 0.44, which means that \(b\) does not make the group more unequal and is thus not entitled to receive shares.
Next, agent \(a\) randomly chooses one group member with total-income higher than her own as a giver. She will choose \(b\) with probability \(500 / (500 + 1500) = 0.25\) or \(c\) with probability \(1500 / (500 + 1500) = 0.75\). Assume the highest probability wins and she chooses the latter. Agent \(a\) then moves to the household area of agent \(c\).
Finally, food transfers take place in the household areas occupied by at least one agent from another household. Since agent \(a\) is positioned in the household area of agent \(c\), these two agents pool their respective total-incomes together and divide the total sum equally, each ending up with 800.
Second cycle
The updated income set is \(\{800, 500, 800\}\). Because both agents \(a\) and \(c\) now have the highest total-income, they are not entitled to receive shares. The Gini-index of the full income set is 0.1. Excluding the total-income of agent \(b\) from the full set, the Gini-index of the resulting subset \(\{800, 800\}\) is 0, so that \(b\) is entitled to receive shares.
Agent \(b\) chooses either agent \(a\) or \(c\) with probability 0.5. Assume she chooses the former. Agent \(b\) then moves to the household area of agent \(a\). Finally, agents \(a\) and \(b\) pool their respective total-incomes together and divide the total sum equally, each ending up with 650.
Third cycle
The updated income set is \(\{650, 650, 800\}\). Agent \(c\) is not entitled to receive shares and the Gini-index of the full income set is 0.05. Excluding the total-income of either agent \(a\) or \(b\) from the full set, the Gini-index of the resulting subset \(\{650, 800\}\) is again 0.05, so that no one is found entitled to receive shares. The sharing round of the simulation is over.
Appendix D: Alternative Models
In this section, I introduce a random variation for each of the three sharing interaction rules of the egalitarian model described above (see Sharing subsection in Model Design). This allows for the construction of seven alternative models reflecting different levels of randomization to the original model design. By comparing the egalitarian model with its randomized versions, one can assess the extent to which the original sharing rules – and therefore the theoretical assumptions they convey – contribute to the model’s goodness of fit.
Random designs
There follows a brief description of the set of rules used to generate the models studied in this section.
Entitlement. Both in the original model design and in the random treatment, the richest agent is never entitled to receives shares. However, in the original model design, agents are considered entitled to receive shares according to a condition that explicitly seeks to maximize group-level equality. By contrast, in the random entitlement treatment agents are randomly selected to receive shares each day until a maximum limit is reached. The maximum number of agents who are allowed to receive shares each day is controlled by a global variable.
Giver choice. Both in the original model design and in the random treatment, an entitled agent chooses a giver randomly from among all agents who have a higher income than herself. However, in the original model design, the probability of a potential giver being selected is proportional to her income, while in the random giver choice treatment it is equally likely that any one of the potential givers be selected.
Sharing. Both in the original model design and in the random treatment, resources of an agent and all other agents who chose her as a giver are pooled together for the sake of sharing. However, in the original model design, each member of the pool receives an equal "slice" of the pooled amount, while in the random sharing treatment each member of the pool is assigned a random-sized "slice" of the pooled amount.
Table 3 below shows the models that can be generated by all possible combinations of the original sharing interaction rules and the random variations just described. To study how these different levels of randomization affect model performance, I ran a total of 400 simulations with parameters set to their default values listed in Table 2 and each of the three sharing interaction rules sampled randomly from among their original or random versions.
| Model | Entitlement | Giver choice | Sharing |
|---|---|---|---|
| Alternative Model 1 | random | random | random |
| Alternative Model 2 | random | random | equal |
| Alternative Model 3 | random | probabilistic | random |
| Alternative Model 4 | random | probabilistic | equal |
| Alternative Model 5 | income-leveling | random | random |
| Alternative Model 6 | income-leveling | random | equal |
| Alternative Model 7 | income-leveling | probabilistic | random |
| Egalitarian Model | income-leveling | probabilistic | equal |
In models that adopt the random entitlement treatment (Alternative Models 1 to 4), the maximum number of agents allowed to receive shares each day was set equal to the mean daily frequency of interactions obtained in simulations of the Egalitarian Model. This is analogous to the procedure used by Aktipis et al. (2011) to test an agent-based model of risk-pooling among Maasai pastoralists. Given the random sampling of sharing rules, each of the eight models listed in Table AII were simulated approximately 50 times. To reduce the potential for accidental error in model performance, individual simulations were run for 3,000 time-steps.
Evaluation metrics
Root Mean Squared Error (RMSE) is a convenient approach to summarizing the errors of a model relative to observational data when outcome variables are expressed in the same measurement unit. One of the advantages of RMSE is that it allows for a relatively easy interpretation: it is the number that would obtain if all outcome variables of the model deviated from their respective observational value by the same absolute amount. Therefore, in the present modeling environment, a RMSE of 10 would be equivalent to a situation in which each outcome variable describing Hadza food distribution patterns deviated from its respective observational value by 10 percent points above or below.
However, because RMSE assigns equal weights to all of a model’s errors, it is prone to distortions when outcome variables present different levels of inter-correlation. In the present modeling environment, for example, most kilocalories acquired by top hunters are from large game, while most available large-game meat kilocalories are acquired by top hunters; consequently, a model’s failure to predict one of these outcome variables will most certainly be associated with failure to predict the other, thus inflating model error on account of correlation between variables.
To correct for such potential distortions, model performance is evaluated in this section by means of Weighted Root Mean Squared Error (WRMSE) between simulated outcome variables and actual observations, with each outcome variable being assigned a unique weight according to its level of inter-correlation with all the other variables. To arrive at those unique weights, the following steps were followed:
- Generate a \(7 \times 7\) matrix of Spearman correlation coefficients \(\rho\) and their respective significance levels \(p\) for the seven outcome variables of interest;
- For each coefficient \(\rho\) in the matrix that is statistically significant at \(p < 0.05\), convert the coefficient into a partial weight by applying the function \(1 - \mid \rho \mid\);
- For each coefficient \(\rho\) in the matrix that is statistically non-significant at \(p \geq 0.05\), substitute the coefficient by a "balanced" partial weight of 0.5;
- Sum the partial weights of each row in the matrix and normalize the results between 0 and 1 to obtain a 1 X 7 vector of unique weights for each outcome variable.
By using the weights generated through this procedure in the calculation of the WRMSE values, one is assured that model errors due to strongly inter-correlated variables are relatively less penalized than errors due to weakly inter-correlated variables. Besides the calculation of WRMSE values, categorical criteria were also used to find simulations in which all outcome variables generated by a model deviate less than 5 percent points from their respective observational value.
Results
Figure 5 shows the distributions of WRMSE values generated across 400 simulations for the eight models examined in this section. With median WRMSE values of 27 and 24, respectively, Alternative Models 5 and 7 call attention for the grossly inaccurate results they generate. What both models have in common is that they combine the income-leveling entitlement rule with a random sharing rule; because the income-leveling rule constantly attempts to "correct" unequal distributions generated by the random sharing rule, the average frequency of daily sharing interactions in these models tends to be inordinately high, thus leading to severe errors in the outcome variables.
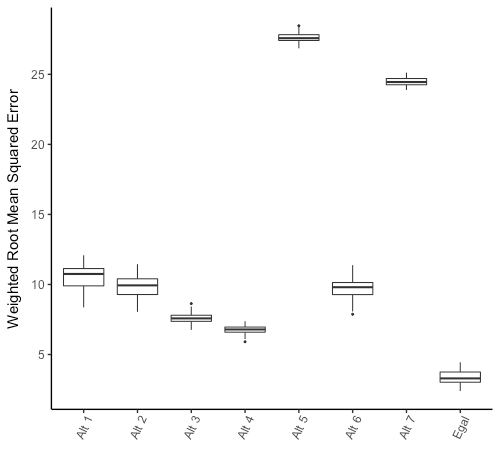
These distortions are not observed in Alternative Models 1 to 4 because the random entitlement rule limits the number of daily interactions by design and does not force the model to "correct" unequal distributions. Otherwise, they are spontaneously reduced by coupling the income-leveling entitlement rule with the equal sharing rule, which brings the frequency of daily sharing interactions to realistic levels in Alternative Model 6 and the Egalitarian Model. However, combining the income-leveling and equal sharing rules alone is not sufficient to justify the adoption of either, since the distribution of WRMSE values generated by Alternative Model 6 (median 9.8, range 7.9-11.4) is only slightly lower than the error distribution generated by the fully randomized Alternative Model 1 (median 10.7, range 8.4-12.1).
Models implementing the probabilistic giver choice rule invariably perform better than identical models adopting random giver choice, since the latter strongly underestimate the gap between the sharing breadth of large game meat and other foods. Nevertheless, within the random entitlement treatment, adoption of the equal sharing rule improves model performance only slightly (Alternative Model 2 versus Alternative Model 1, and Alternative Model 4 versus Alternative Model 3). This is because random-sized "slices" of the pooled amounts distributed among agents in the random sharing treatment tend to approach their central tendency over the course time, thus producing a result that is roughly similar to equal sharing.
With a median WRMSE value of 6.8, Alternative Model 4 offers the best fit to empirical data among alternative models. This is expected given that this model is identical to the Egalitarian Model except for adoption of the random entitlement rule, which in turn was deliberately designed to reproduce the Egalitarian Model’s mean interaction frequency. Therefore, the only significant difference between the Egalitarian Model and Alternative Model 4 is that the former selects entitled receivers in such a way as to promote sharing interactions that maximize group-level equality. This qualitative difference is sufficient to noticeably improve the Egalitarian Model’s performance, bringing its median WRMSE value down to 3.3. In fact, only 16 of the 400 simulations examined here were such that each outcome variable deviated from its respective observational value by less than 5 percent points; all of these sharp matches between model results and empirical data were obtained in the Egalitarian Model, accounting for a significant 33% of simulations run for this model. Together with the WRMSE value distributions, these results suggest that each sharing interaction rule implemented by the Egalitarian Model plays a unique role in explaining the model’s fit to the empirical data.
References
AKTIPIS, A., Cronk, L., Alcock, J., Ayers, J. D., Baciu, C., Balliet, D., Boddy, A. M., Curry, O. S., Krems, J. A., Muñoz, A., Sullivan, D., Sznycer, D., Wilkinson, G. S., & Winfrey, P. (2018). Understanding cooperation through fitness interdependence. Nature Human Behaviour, 2(7), 429–431. [doi:10.1038/s41562-018-0378-4]
AKTIPIS, C. A., Cronk, L., & de Aguiar, R. (2011). Risk-Pooling and herd survival: An agent-Based model of a Maasai gift-Giving system. Human Ecology, 39(2), 131–140. [doi:10.1007/s10745-010-9364-9]
BOEHM, C. (1993). Egalitarian behavior and reverse dominance hierarchy. Current Anthropology, 34(3), 227. [doi:10.1086/204166]
BOEHM, C. (1994). Reply to: “On Human Egalitarianism: An Evolutionary Product of Machiavellian Status Escalation?”. Current Anthropology, 35(2), 178–180.
BOEHM, C. (1999). Hierarchy in the Forest: The Evolution of Egalitarian Behavior. Cambridge, MA: Harvard University Press.
BOEHM, C. (2012). Moral Origins: Social Selection and the Evolution of Virtue, Altruism and Shame. New York, NY: Basic Books.
BOYD, R., Gintis, H., & Bowles, S. (2010). Coordinated punishment of defectors sustains cooperation and can proliferate when rare. Science, 328(5978), 617–620. [doi:10.1126/science.1183665]
BOYD, R., Richerson, P. J., & Henrich, J. (2011). The cultural niche: Why social learning is essential for human adaptation. Proceedings of the National Academy of Sciences, 108(2), 10918–10925. [doi:10.1073/pnas.1100290108]
CARLETTI, T., Guarino, A., Guazzini, A., & Stefanelli, F. (2020). Problem solving: When groups perform better than teammates. Journal of Artificial Societies and Social Simulation, 23(3), 4: https://www.jasss.org/23/3/4.html. [doi:10.18564/jasss.4292]
CHENG, J. T. (2020). Dominance, prestige, and the role of leveling in human social hierarchy and equality. Current Opinion in Psychology, 33, 238–244. [doi:10.1016/j.copsyc.2019.10.004]
CLASTRES, P. (1989). Society Against the State: Essays in Political Anthropology. New York, NY: Zone Books.
CRONK, L., Steklis, D., Steklis, N., van den Akker, O. R., & Aktipis, A. (2019). Kin terms and fitness interdependence. Evolution and Human Behavior, 40(3), 281–291. [doi:10.1016/j.evolhumbehav.2018.12.004]
ENDICOTT, K. M. (1988). 'Property, power, and conflict among the Batek of Malaysia.' In T. Ingold, D. Riches, & J. Woodburn (Eds.), Hunters and Gatherers 2: Property, Power, and Ideology. Oxford: Berg, pp. 110–127.
ERDAL, D., & Whiten, A. (1994). On human egalitarianism: An evolutionary product of Machiavellian status escalation? Current Anthropology, 35(2), 175–183. [doi:10.1086/204255]
ERDAL, D., & Whiten, A. (1996). 'Egalitarianism and Machiavellian intelligence in human evolution.' In P. Mellars & K. Gibson (Eds.), Modelling the Early Human Mind. Cambridge: McDonald Institute Monographs, pp. 139–150.
FEHR, E., Bernhard, H., & Rockenbach, B. (2008). Egalitarianism in young children. Nature, 454(7208), 1079–1083. [doi:10.1038/nature07155]
FRIED, M. H. (1967). The Evolution of Political Society. New York, NY: Random House.
GAVRILETS, S. (2012). On the evolutionary origins of the egalitarian syndrome. Proceedings of the National Academy of Sciences, 109(35), 14069–14074. [doi:10.1073/pnas.1201718109]
GAVRILETS, S., & Richerson, P. J. (2017). Collective action and the evolution of social norm internalization. Proceedings of the National Academy of Sciences, 114(23), 6068–6073. [doi:10.1073/pnas.1703857114]
GINTIS, H., Smith, E. A., & Bowles, S. (2001). Costly signaling and cooperation. Journal of Theoretical Biology, 213(1), 103–119. [doi:10.1006/jtbi.2001.2406]
GRIMM, V., Berger, U., Bastiansen, F., Eliassen, S., Ginot, V., Giske, J., Goss-Custard, J., Grand, T., Heinz, S. K., Huse, G., Huth, A., Jepsen, J. U., Jørgensen, C., Mooij, W. M., Müller, B., Pe’er, G., Piou, C., Railsback, S. F., Robbins, A. M., … DeAngelis, D. L. (2006). A standard protocol for describing individual-based and agent-based models. Ecological Modelling, 198(1–2), 115–126. [doi:10.1016/j.ecolmodel.2006.04.023]
GRIMM, V., Railsback, S. F., Vincenot, C. E., Berger, U., Gallagher, C., DeAngelis, D. L., Edmonds, B., Ge, J., Giske, J., Groeneveld, J., Johnston, A. S. A., Milles, A., Nabe-Nielsen, J., Polhill, J. G., Radchuk, V., Rohwäder, M. S., Stillman, R. A., Thiele, J. C., & Ayllón, D. (2020). The ODD protocol for describing agent-based and other simulation models: A second update to improve clarity, replication, and structural realism. Journal of Artificial Societies and Social Simulation, 23(2), 7: https://www.jasss.org/23/2/7.html. [doi:10.18564/jasss.4259]
GURVEN, M. (2004). To give and to give not: The behavioral ecology of human food transfers. Behavioral and Brain Sciences, 27(4), 543–583. [doi:10.1017/s0140525x04000123]
HAMES, R. B. (2000). 'Reciprocal altruism in Yanomamo food exchange.' In L. Cronk, N. Chagnon, & W. Irons (Eds.), Adaptation and Human Behavior: An Anthropological Perspective. Berlin: de Gruyter. [doi:10.4324/9781351329200-23]
HAMILTON, W. D. (1964). The genetical evolution of social behaviour. Journal of Theoretical Biology, 7(1), 1–16.
HAMILTON, W. D. (1981). The role of asymmetries in animal contests. Animal Behaviour, 29(1), 193–205. [doi:10.1016/s0003-3472(81)80166-2]
HAWKES, K., & Bird, R. B. (2002). Showing off, handicap signaling, and the evolution of men’s work. Evolutionary Anthropology, 11(2), 58–67. [doi:10.1002/evan.20005]
HAWKES, K., O’Connell, J. F., & Blurton Jones, N. G. (2001). Hadza meat sharing. Evolution and Human Behavior, 22, 113–142. [doi:10.1016/s1090-5138(00)00066-0]
HAWKES, K., O’Connell, J. F., & Blurton Jones, N. G. (2014). More lessons from the Hadza about men’s work. Human Nature, 25, 596–619. [doi:10.1007/s12110-014-9212-5]
HAWKES, K., O’Connell, J. F., & Blurton Jones, N. G. (2018). Hunter-gatherer studies and human evolution: A very selective review. American Journal of Physical Anthropology, 165(4), 777–800. [doi:10.1002/ajpa.23403]
HENRICH, J. (2018). Human cooperation: The hunter-Gatherer puzzle. Current Biology, 28(19), 1143–1145. [doi:10.1016/j.cub.2018.08.005]
HENRICH, J., & Gil-White, F. J. (2001). The evolution of prestige: Freely conferred deference as a mechanism for enhancing the benefits of cultural transmission. Evolution and Human Behavior, 22(3), 165–196. [doi:10.1016/s1090-5138(00)00071-4]
HILL, K., Walker, R. S., Bozicevic, M., Eder, J., Headland, T., Hewlett, B., Hurtado, A. M., Marlowe, F., Wiessner, P., & Wood, B. M. (2011). Co-Residence patterns in hunter-Gatherer societies show unique human social structure. Science, 331(6022), 1286–1289. [doi:10.1126/science.1199071]
HOOPER, P. L., Kaplan, H. S., & Jaeggi, A. V. (2021). Gains to cooperation drive the evolution of egalitarianism. Nature Human Behaviour, 5(7), 847–856. [doi:10.1038/s41562-021-01059-y]
JAEGGI, A. V., & Gurven, M. (2013). Reciprocity explains food sharing in humans and other primates independent of kin selection and tolerated scrounging: A phylogenetic meta-analysis. Proceedings of the Royal Society B, 280(1768). [doi:10.1098/rspb.2013.1615]
KELLY, R. L. (2013). The Lifeways of Hunter-Gatherers: The Foraging Spectrum. Cambridge: Cambridge University Press.
KENT, S. (1993). Sharing in an egalitarian Kalahari community. Man, 28(3), 479–514. [doi:10.2307/2804236]
KNAUFT, B. M. (1991). Violence and sociality in human evolution. Current Anthropology, 32(4), 391.
KRAFT, T. S., Venkataraman, V. V., Tacey, I., Dominy, N. J., & Endicott, K. M. (2019). Foraging performance, prosociality, and kin presence do not predict lifetime reproductive success in Batek hunter-Gatherers. Human Nature, 30, 71–97. [doi:10.1007/s12110-018-9334-2]
LEE, R. B. (1979). The!Kung San: Men, Women and Work in a Foraging Society. Cambridge: Cambridge University Press.
LEE, R. B. (1988). 'Reflections on primitive communism.' In T. Ingold, D. Riches, & J. Woodburn (Eds.), Hunters and Gatherers: History, Evolution and Social Change. Oxford: Berg, pp. 252–268.
LEE, R. B. (1990). 'Primitive communism and the origin of social inequality.' In S. Upam (Ed.), Evolution of Political Systems: Sociopolitics in Small-Scale Sedentary Societies. Cambridge: Cambridge University Press, pp. 225–246.
LEW-LEVY, S., Lavi, N., Reckin, R., Cristóbal-Azkarate, J., & Ellis-Davies, K. (2018). How do hunter-Gatherer children learn social and gender norms? A meta-Ethnographic review. Cross-Cultural Research, 52(2), 213–255. [doi:10.1177/1069397117723552]
MCAULIFFE, K., Blake, P. R., Steinbeis, N., & Warneken, F. (2017). The developmental foundations of human fairness. Nature Human Behaviour, 1(0042), 2017. [doi:10.1038/s41562-016-0042]
PANCHANATHAN, K., & Boyd, R. (2004). Indirect reciprocity can stabilize cooperation without the second-order free rider problem. Nature, 432, 499–502. [doi:10.1038/nature02978]
PETERSON, N. (1993). Demand sharing: Reciprocity and the pressure for generosity among foragers. American Anthropologist, 95(4), 860–874. [doi:10.1525/aa.1993.95.4.02a00050]
PINHEIRO, M. P. (2021). On some recent confusions in the study of Hadza food sharing. American Anthropologist, 174(3), 389–391. [doi:10.1002/ajpa.24185]
POWER, C. (2009). 'Sexual selection models for the emergence of symbolic communication: Why they should be reversed.' In R. Botha & C. Knight (Eds.), The Cradle of Language: Studies in the Evolution of Language. Oxford: Oxford University Press, pp. 257–280.
PUGA-GONZALEZ, I., Hildenbrandt, H., & Hemelrijk, C. K. (2009). Emergent patterns of social affiliation in primates, a model. PLoS Computational Biology, 5(12), e1000630. [doi:10.1371/journal.pcbi.1000630]
PUGA-GONZALEZ, I., Hoscheid, A., & Hemelrijk, C. K. (2015). Friendship, reciprocation, and interchange in an individual-based model. Behavioral Ecology and Sociobiology, 69(3), 383–394. [doi:10.1007/s00265-014-1850-4]
R Core Team. (2017). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing<./p>
RIZZO, M. T., & Killen, M. (2016). Children’s understanding of equity in the context of inequality. The British Journal of Developmental Psychology, 34(4), 569–581. [doi:10.1111/bjdp.12150]
SHULTZINER, D., Stevens, T., Stevens, M., Stewart, B. A., Hannagan, R. J., & Saltini-Semerari, G. (2010). The causes and scope of political egalitarianism during the Last Glacial: A multi-disciplinary perspective. Biology & Philosophy, 25(3), 319–346. [doi:10.1007/s10539-010-9196-4]
SILK, J. B., & House, B. R. (2016). The evolution of altruistic social preferences in human groups. Philosophical Transactions of the Royal Society B: Biological Sciences, 371(20150097). [doi:10.1098/rstb.2015.0097]
SMITH, E. A. (2010). Communication and collective action: Language and the evolution of human cooperation. Evolution and Human Behavior, 31(4), 231–245. [doi:10.1016/j.evolhumbehav.2010.03.001]
SMITH, K. M. (2019). Hadza hunter-Gatherers and the evolution of human cooperation: Evidence against partner choice models. Publicly Accessible Penn Dissertations. 3535. Available at: https://repository.upenn.edu/cgi/viewcontent.cgi?article=5321&context=edissertations.
SMITH, K. M., Larroucau, T., Mabulla, I. A., & Apicella, C. L. (2018). Hunter-Gatherers maintain assortativity in cooperation despite high levels of residential change and mixing. Current Biology, 28(19), 3152–3157. [doi:10.1016/j.cub.2018.07.064]
STIBBARD-HAWKES, D. N. E., Attenborough, R. D., Mabulla, I. A., & Marlowe, F. W. (2020). To the hunter go the spoils? No evidence of nutritional benefit to being or marrying a well-reputed Hadza hunter. American Journal of Physical Anthropology, 173(1), 61–79.
STIBBARD-HAWKES, D. N. E., Attenborough, R. D., & Marlowe, F. W. (2018). A noisy signal: To what extent are Hadza hunting reputations predictive of actual hunting skills? Evolution and Human Behavior, 39(6), 639–651. [doi:10.1016/j.evolhumbehav.2018.06.005]
TEN Broeke, G., van Voorn, G., & LigTENberg, A. (2016). Which sensitivity analysis method should I use for my agent-based model? Journal of Artificial Societies and Social Simulation, 19(1), 5: https://www.jasss.org/19/1/5.html. [doi:10.18564/jasss.2857]
THIELE, J. C., Kurth, W., & Grimm, V. (2012). RNETLOGO: An R package for running and exploring individual-based models implemented in NETLOGO. Methods in Ecology and Evolution, 3(3), 480–483. [doi:10.1111/j.2041-210x.2011.00180.x]
THIELE, J. C., Kurth, W., & Grimm, V. (2014). Facilitating parameter estimation and sensitivity analysis of agent-Based models: A cookbook using NetLogo and ’R’. Journal of Artificial Societies and Social Simulation, 17(3), 11: https://www.jasss.org/17/3/11.html. [doi:10.18564/jasss.2503]
TOMASELLO, M., Melis, A. P., Tennie, C., Wyman, E., & Herrmann, E. (2012). Two key steps in the evolution of human cooperation. Current Anthropology, 53(6), 673–692. [doi:10.1086/668207]
TRICOMI, E., Rangel, A., Camerer, C. F., & Odoherty, J. P. (2010). Neural evidence for inequality-averse social preferences. Nature, 463(7284), 1089–1091. [doi:10.1038/nature08785]
TRIVERS, R. L. (1971). The evolution of reciprocal altruism. The Quarterly Review of Biology, 46(1), 35–57. [doi:10.1086/406755]
VON Rueden, C. R., & Jaeggi, A. V. (2016). Men’s status and reproductive success in 33 nonindustrial societies: Effects of subsistence, marriage system, and reproductive strategy. Proceedings of the National Academy of Sciences, 113(39), 10824–10829. [doi:10.1073/pnas.1606800113]
VON Rueden, C. R., Redhead, D., O’Gorman, R., Kaplan, H., & Gurven, M. (2019). The dynamics of men’s cooperation and social status in a small-scale society. Proceedings of the Royal Society B: Biological Sciences, 286(1908). [doi:10.1098/rspb.2019.1367]
WALKER, R. S. (2014). Amazonian horticulturalists live in larger, more related groups than hunter-gatherers. Evolution and Human Behavior, 35(5), 384–388. [doi:10.1016/j.evolhumbehav.2014.05.003]
WALKER, R. S., Flinn, M. V., & Hill, K. R. (2010). Evolutionary history of partible paternity in lowland South America. Proceedings of the National Academy of Sciences, 107(45), 19195–19200. [doi:10.1073/pnas.1002598107]
WHITEN, A., & Erdal, D. (2012). The human socio-cognitive niche and its evolutionary origins. Philosophical Transactions of the Royal Society B: Biological Sciences, 367(1599), 2119–2129. [doi:10.1098/rstb.2012.0114]
WIESSNER, P. (1996). 'Leveling the hunter: Constraints on the status quest in foraging societies.' In P. Wiessner & W. Schiefenhövel (Eds.), Food and the Status Quest. New York, NY: Berghahn Books, pp. 171–192.
WILENSKY, U. (1998). NetLogo wealth distribution model. Evanston, IL: Northwestern University.
WILENSKY, U. (1999). NetLogo. Center for connected learning and computer-based modeling, Northwestern University, Evanston, IL. Available at: http://ccl.northwestern.edu/netlogo/.
WOOD, B. M., & Marlowe, F. W. (2013). Household and kin provisioning by Hadza men. Human Nature, 24(3), 280–317. [doi:10.1007/s12110-013-9173-0]
WOODBURN, J. (1982). Egalitarian societies. Man, 17(3), 431–451. [doi:10.2307/2801707]
WOODBURN, J. (1998). '“Sharing is not a form of exchange”: An analysis of property-sharing in immediate-return hunter-gatherer societies.' In C. M. Hann (Ed.), Property Relations: Renewing the Anthropological Tradition. Cambridge: Cambridge University Press, pp. 48–63.
ZAHAVI, A. (1977). 'Reliability in communication systems and the evolution of altruism.' In B. Stonehouse & C. M. Perrins (Eds.), Evolutionary Ecology. London: McMillan, pp. 253–259. [doi:10.1007/978-1-349-05226-4_21]