How Culture Influences the Management of a Pandemic: A Simulation of the COVID-19 Crisis

, , , , , ,
and
aDelft University of Technology, Netherlands; bUmeå University, Sweden
Journal of Artificial
Societies and Social Simulation 25 (3) 6
<https://www.jasss.org/25/3/6.html>
DOI: 10.18564/jasss.4877
Received: 30-Nov-2020 Accepted: 20-Jun-2022 Published: 30-Jun-2022
Abstract
Since its first appearance in Wuhan (China), countries have been employing, to varying degrees of success, a series of non-pharmaceutical interventions aimed at limiting the spread of SARS-CoV-2 within their populations. In this article, we build on scientific work that demonstrates that culture is part of the explanation for the observed variability between countries in their ability to effectively control the transmission of SARS-CoV-2. We present a theoretical framework of how culture influences decision-making at the level of the individual. This conceptualization is formalized in an agent-based model that simulates how cultural factors can combine to produce differences across populations in terms of the behavioral responses of individuals to the COVID-19 crisis. We illustrate that, within our simulated environment, the culturally-dependent willingness of people to comply with public health related measures might constitute an important determinant of differences in infection dynamics across populations. Our model generates the highest rates of non-compliance within cultures marked as individualist, progressive and egalitarian. Our model illustrates the potential role of culture as a population-level predictor of infections associated with COVID-19. In doing so, the model, and theoretical framework on which it is based, may inform future studies aimed at incorporating the effect of culture on individual decision-making processes during a pandemic within social simulation models.Introduction
The outbreak of the novel Corona Virus Disease in 2019 (‘COVID-19’) continues to have a tremendous impact on the daily lives of people around the globe. Although the scale at which SARS-CoV-2 (the virus that causes COVID-19) has been able to spread across the globe is unprecedented, this is certainly not the first pandemic the world has witnessed (Huremović 2019). Such global epidemics are inevitable and are expected to occur more often given our increasingly connected lives. To illustrate, in our modern connected and urbanized world the outbreak of an infectious disease can move from a remote village to a major city on the other side of the world in less than 36 hours (Sands et al. 2019). This highlights the importance of finding ways that facilitate the effective management of the impact of such disease outbreaks.
While at the time of writing this article, enormous efforts have been geared towards mass vaccination of populations, altering the behavior of individuals and the consequent patterns of social interaction by means of non-pharmaceutical measures remains the main approach to limit viral transmission. For instance, restricting physical contacts, increasing the frequency of hand washing, wearing face masks in public and maintaining a sufficient physical distance from others all help to exert a downward pressure on the transmission potential of the virus. Crucially, the readiness of people to comply to these public health related measures is dependent upon prevailing cultural beliefs. Gelfand et al. (2021) show that nations with ‘tight’, rather than ‘loose’ cultures have been most effective in limiting the mortality of COVID-19. Moreover, Gokmen et al. (2021), Erman & Medeiros (2021) and Lu et al. (2021) support the claim that the cultural characteristics of societies affect how behavioral measures are applied and the extent to which they are effective in curbing infection and/or mortality rates across the globe.
The cumulative evidence, therefore, suggests that strategies aimed at limiting the spread of any contagious virus ought to account for the prevailing cultural context within which those strategies are formulated and put into practice. Hence, gaining a better understanding of how culture might influence the response of individuals to the implementation of non-pharmaceutical measures that are aimed at limiting the transmission of SASRS-CoV-2 is a valuable objective to pursue.
In this paper, we present an agent-based simulation model of culturally-influenced decision-making at the level of individuals within the context of a pandemic. We experiment with this model as an ‘illustration’ practice (Edmonds 2017). This means that our modeling purpose is to provide an illustration of how the observed cross-cultural differences in the development of COVID-19 infections might arise. Thus, we do not intend to offer an explanatory or predictive model of these cross-cultural differences, nor is it our intention to provide an exhaustive account of the model's mechanisms.
The current paper starts with a description of our theoretical representation of how culture can influence the behavior of individuals during a pandemic. Next, we describe the research methodology and give a description of the model. The paper subsequently describes the outcomes of a series of model experiments. We conclude by discussing the experimental outcomes and presenting avenues for further research.
Theoretical Framework
We first present the definitions and theories that are combined to model culturally-influenced decision-making behavior during a pandemic. The closest concept to culture at an individual level is that of ‘values’ (Schwartz 2014). The connection between individual values and culture is already established in various seminal publications both theoretically and empirically (Hofstede et al. 2010; Schwartz 2011). We argue that the culture of a population is reflected in the characteristics of the value systems of the people within that population. A person’s values orient him/her toward performing certain types of behavior. The concept of needs is introduced to explain the process of how behavior ultimately manifests itself. In the following paragraphs we introduce and describe the theories underlying the assumed relationships included within our model.
Culture
Our conception of culture is predominantly informed by Schwartz (2014) who argues that culture should be thought of as a latent, normative collective value system that is external to the individual, and which underlies and justifies the functioning of a society. Schwartz (2014) proposes that culture works as a ‘press’ to which people are exposed; a press that takes on many forms. It is through the exposure to a wide variety of daily stimuli that culture shapes the content and distribution of an individual’s values (Schwartz 2014). Note that culture influences every individual in a unique way; this is because no two people are exposed to the cultural press in the exact same way, and no two people are genetically predisposed to react to the cultural press in the exact same way.
In line with Schwartz (2014) and Hofstede (2001), we propose that culture can be formalized as a set of cultural dimensions whose scores are thought of as a population’s cultural profile. Cultural dimensions thus orient the formation of a person’s values through his/her day-to-day exposure to the aforementioned cultural press (see Figure 1). Differences between societies on these cultural dimensions reflect the differences in latent value emphases between these societies.
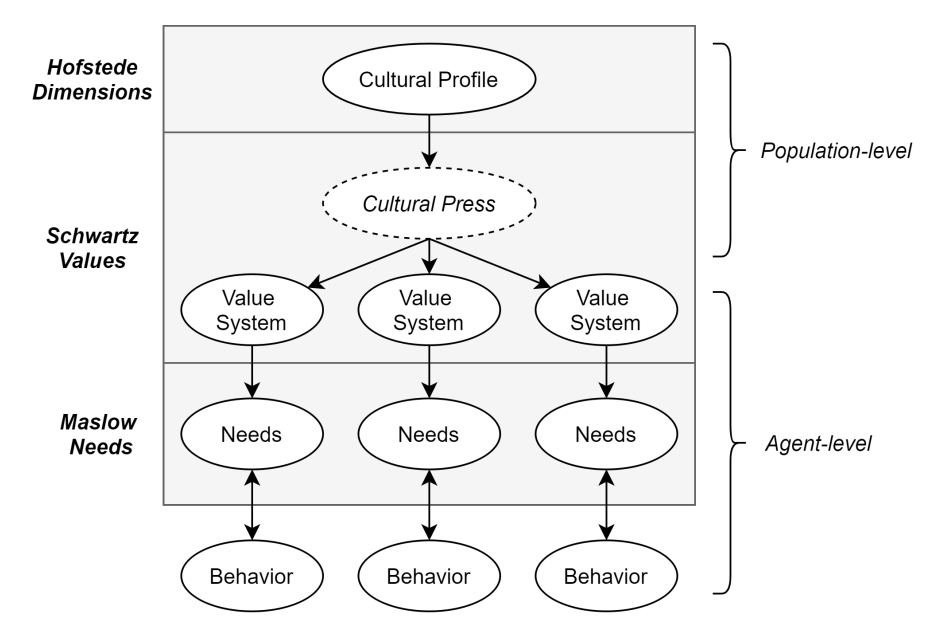
The current study utilizes the Hofstede Cultural Dimensions (HCDs) framework (Hofstede et al. 2012; Minkov & Hofstede 2011) to formalize a nations’ cultural profiles because of its unique position of earned respect within the field of cross-cultural research (Taras et al. 2009). The 6 HCDs are: (1) Power-Distance vs Egalitarianism (PDI), (2) Individualism vs Collectivism (IDV), (3) Uncertainty Avoidance vs Uncertainty Tolerance (UAI), (4) Masculinity vs Femininity (MAS), (5) Long-term vs Short-term Orientation (LTO), and (6) Indulgence vs Restraint (IVR). A detailed description of these dimensions can be found in Appendix A.1.
The Hofstede framework is one of several ways in which culture may be formalized; see e.g. Taras et al. (2009). One alternative formalization of culture that competes with the HCD-framework is presented by Schwartz’s notion of Cultural Value Orientations (CVOs) (Schwartz 2011). The HCDs are favoured over the CVOs because of the availability of extensive and up-to-date empirical data (Hofstede-Insights 2020). For a detailed comparison of the HCDs with Schwartz’s CVOs the interested reader is referred to Tekeş et al. (2019), Fischer et al. (2010), Ng et al. (2007), Ng & Lim (2019).
Values
Prior attempts at conceptualizing values have produced a large number of definitions. From this pool of definitions, a set of at least three common features can be extracted (Schwartz 2012). First, values are relatively stable affectively-laden beliefs about desirable end-states of reality (i.e., how the world 'ought to be') that motivate action. Second, values serve as general guiding principles for behaviour and decisions over a wide range of contexts (Anderson 2019). Third, a person’s values are ordered based on their relative importance to that person (Schwartz 2012).
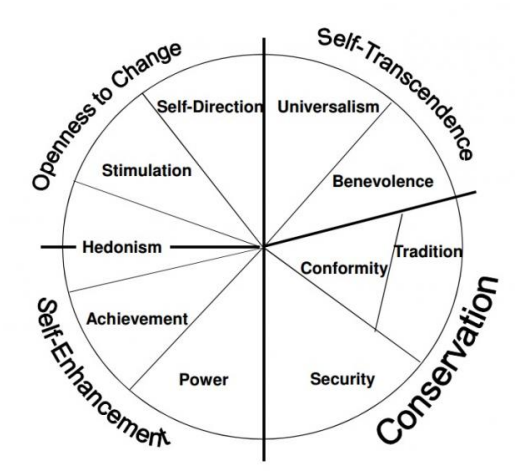
Basic Value Theory (BVT) (Schwartz 2012) distinguishes ten values that are universally present within the value systems of humans (Figure 2). Although the nature and structure of the Schwartz BVT Values may be universal, individuals and groups differ substantially in the relative importance they ascribe to each value. The BVT summarizes the relations between each of the values within the value circumplex (Figure 2). Values placed close to one another in the circumplex are considered mutualistic (tend to harmonize with one another) and values placed further away from one another become increasingly antagonistic (are generally in conflict with each other). The circumplex implies that actions in pursuit of any particular value will have consequences for a person’s ability to cater to the fulfillment of the other values (Schwartz 2012). Similar to Hofstede’s Cultural Dimensions, the Schwartz’s BVT framework has received an extensive amount of attention and empirical validation (Rokeach 2008).
Culture and values
We build on previous research conducted by Vanhée & Dignum (2018) to couple Schwartz values with the HCDs by introducing the notion of a Dominant Cultural Correlate (DCC). A ‘DCC’ denotes the cultural (i.e., macro-level) concept that shows the strongest fit with a particular value at the micro-level. Specifically, each Schwartz BVT Value is assigned one or more DCCs on the basis of theoretical descriptions provided by Schwartz (2012) and Hofstede (2020). Note that a DCC can be positively (\(DCC^+\)) or negatively correlated (\(DCC^-\)) with a given Schwartz Value. Appendix A.1 presents a detailed argumentation for the theoretical linkages depicted in Table 1.
| Value | \(\mathbf{DCC^+}\) | \(\mathbf{DCC^-}\) |
|---|---|---|
| Hedonism (HED) | IVR | - |
| Stimulation (STM) | - | UAI |
| Self-Direction (SD) | IDV | - |
| Universalism (UNI) | - | MAS, PDI |
| Benevolence (BEN) | - | MAS |
| Conformity & Tradition (CT) | PDI | IDV, LTO, IVR |
| Security (SEC) | UAI | - |
| Power (POW) | PDI, MAS | - |
| Achievement (ACH) | MAS | - |
In this paper, we primarily focus on the cross-cultural differences in value emphases (i.e., the inter-cultural variation of values) and not on differences in the intra-cultural variation of values. Although our model includes a parameter for specifying intra-cultural variation, we chose to control for its effects during the model experiments presented in this paper.
Values and needs
Although values give direction to behavior, they are too abstract to directly determine the choice of action in every situation. In our model we therefore couple values and actions through the needs of an agent. We loosely base our conceptualization of how values, needs and actions relate to one another on the archetypical Beliefs-Desires-Intention (BDI) model of agency (Balke & Gilbert 2014). Table 2 explicates how values, needs and actions are connected through the reflective questions one may ask oneself during decision-making.
| Construct | Deliberation Processes |
|---|---|
| Values [Beliefs] | How should the world be? What state(s) of reality is/are desirable? |
| Needs [Desires] | What discrepancies do I currently perceive between how the world is and how it should be? |
| Actions [Intentions] | What can I do at this moment within the constraints posed by my current contextual circumstances that bring the world as it appears closer to how I think it should be? |
The implemented needs within our model are derived from the renowned Maslow framework (McLeod 2007) and can be grouped into two classes: psychological and physiological. Building on the concept of value trees (Heidari et al. 2020; van der Weide 2011), we propose that the Schwartz BVT Values inform the prioritization of an individual’s psychological needs. This implies that whatever one values in life determines what he/she desires. We presume that people work towards the fulfillment of their values through satisfying their psychological needs. The associations between the psychological needs and Schwartz BVT Values presented in Table 3 derive from the description of ‘exemplary values’ by Schwartz (1994).
In line with Self-Determination Theory (SDT) (Deci & Ryan 2004), we assume that a person’s values exerts an influence only on the prioritization of psychological needs. The prioritization of physiological needs are therefore presumed to be the same for everyone. Importantly, we presume that a basic satisfaction level of physiological needs must be met before an individual becomes concerned with meeting her psychological needs (Tay & Diener 2011). Physiological needs have to do with obtaining and maintaining a healthy physical state of being; that is, a state devoid of hunger, thirst, and/or other physical threats. Psychological needs, on the other hand, are related to obtaining and maintaining a healthy psychological state of being; that is, a state of devoid of anxiety, confusion, depression, and/or mental conflict.
Note that the ordering in the satisfaction of needs in our model is not strictly hierarchical but rather statistical; that is, when a physical and psychological need are both depleted, an agent is more likely to tend to the physical need rather than the psychological need, in case it has to make a choice between the two. Moreover, by linking needs to values, and values to cultural dimensions, we make the ordering of agent’s needs culturally sensitive. A detailed description of needs is found in Appendix A.4.
| Need | Type | Values |
|---|---|---|
| Food | Physiological | N/A |
| Health | Physiological | N/A |
| Sleep | Physiological | N/A |
| Financial Survival | Physiological | N/A |
| Financial Stability | Psychological | Power |
| Risk Avoidance | Psychological | Security |
| Compliance | Psychological | Conformity & Tradition, Security |
| Conformity | Psychological | Conformity & Tradition |
| Belonging | Psychological | Benevolence, Conformity & Tradition |
| Leisure | Psychological | Hedonism, Stimulation |
| Luxury | Psychological | Power, Hedonism |
| Autonomy | Psychological | Achievement, Self-Direction |
Decision-making
Values have a reliable, albeit weak, effect on behavior (Mercuur et al. 2019) which is generally indirect and/or contingent upon contextual factors (Hitlin & Piliavin 2004). In the current study, the effect of values on behavior is influenced by, inter alia, a person’s needs, the actions of one’s peers, and contextual factors.
At any given moment in time, the relative importance an individual ascribes to its values determines the priority assigned towards satisfying particular needs. Thus, needs are assigned ‘priority-weights’ according to the structure of one’s value system. These priority-weights remain static over the course of a simulation. Although an individual’s values may change over the course of a lifetime (van de Poel 2018), this process lies beyond the scope of this study.
What varies over the course of a simulation is the satisfaction level of needs. The dynamism of satisfaction levels is modelled using the ‘water tank’ approach as presented by Dörner et al. (2006) and modelled by Di Tosto & Dignum (2012) and Heidari et al. (2020).
The activities that an individual performs alter the satisfaction levels of its needs. During decision-making, individuals form expectations regarding how much satisfaction will likely be obtained by performing certain actions. Agents are expected to choose among alternative courses of action in a manner that maximizes the potential satisfaction to be gained from executing the action. This expectation-based selection of activities builds on the process-based motivation theory of Vroom (Miner 2005).
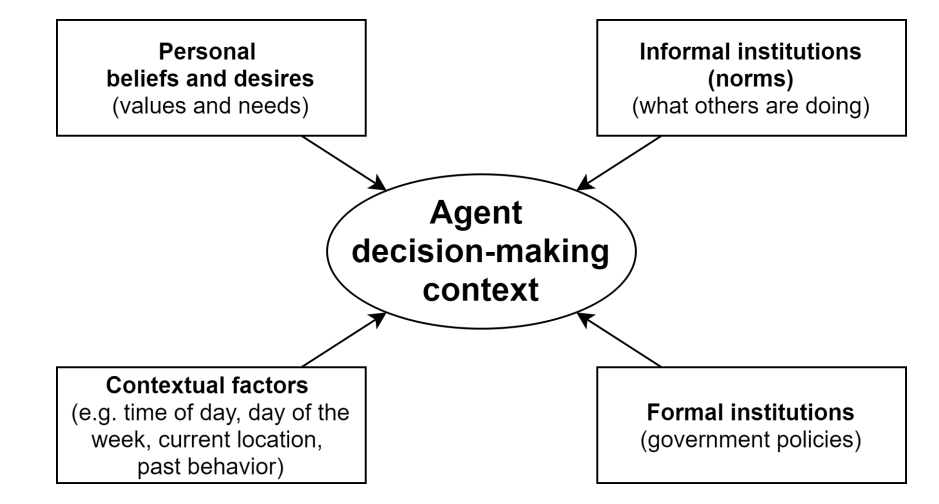
The current model involves many agents, each possessing a unique value system, making decisions on what activity to perform during a particular time-step. The decisions of agents are influenced by global and local contextual factors. Global contextual factors are the same for all agents, such as the time of the day and day of the week. Local contextual factors, on the other hand, are unique to the agent. Examples are the occupation of the agent, its past behavior, the location in which it currently finds itself, and with whom it is befriended. Other determinants in the decision-making process are institutions. We make a distinction between formal and informal institutions. Formal institutions are considered to be rules that are legally enforced (e.g., government policies). Informal institutions (i.e., social norms) are behavioral rules whose legitimacy lies in facilitating social interactions and cohesion (Ghorbani et al. 2012). At any given instance, these factors combine to form a unique decision-making context for each agent (see Figure 3). Faced with these constraining or enabling factors, an agent then decides upon a particular course of action that it considers most satisfying.
To recapitulate, individuals choose to engage in activities that generate the highest expected level of satisfaction for the most urgent needs. The urgency of a need is defined as a function of that need’s satisfaction level (dynamic component) and its value-based priority-weight (static component).
In the following section we describe how the theoretical framework presented in this section is operationalized within an agent-based model.
Model Description
The current research uses and builds on an existing model of COVID-19 called ASSOCC.1 The ASSOCC project is an extensive multi-dimensional simulation model that aims to increase understanding of the short- and long-term effects of the COVID-19 pandemic on individuals, societies and economies (ASSOCC 2020; Dignum et al. 2020). We extend the ASSOCC model by adding a cultural dimension to it.
The original ASSOCC model and our ‘cultural’ version are developed in NetLogo (Wilensky 1998). The statistical analysis of simulation outcomes is conducted in RStudio (RStudio 2020). Data on nation’s cultural dimensions is taken from the Hofstede Insights database (Hofstede 2020).
ASSOCC: Model narrative
Below we provide a brief overview and description of the various sub-models that constitute the ASSOCC model. We focus on describing the components of ASSOCC that are not endogenous to our cultural model, but that do constitute the underlying architecture upon which our cultural model is built. A full ODD+D description (Müller et al. 2013) of the model is available at ASSOCC (2020). A full description of the model and its implementation is provided in Dignum (2021).
Entities, variables and scales
With the ASSOCC model a city of around 1000 inhabitants can be simulated. The agents are divided into four age-groups; young (4-18 years), student (18-25 years), worker (25-65 years) or retired (65+ years). The agents live in different household compositions varying from family households (2 youngsters and 2 workers), students/workers/retirees households (max 2 residents) and multi-generational households (2 youngsters, 2 workers and 2 retirees). Moreover, the simulated city contains schools, universities, office buildings, essential shops, non-essential shops, public leisure places (e.g. parks, squares) and private leisure places (e.g. cafes, bars) that agents may choose to visit their walking hours. The total number of all these places is proportional to the number of agents living within the city. A day in the simulated world is divided into 4 time-steps: morning, afternoon, evening and night. During each of these time-steps, the agents choose to perform one single activity at a specific location.
Process overview & scheduling
During the simulation, agents wake up in their homes and start their days by choosing a morning-activity from the activity-set that is presented to them. Table 8 in Appendix A.2 provides an overview of the activities that are included in the activity-sets presented to agents over the course of a simulation. The activity with the highest expected satisfaction gain is chosen from the activity-set. The activities that are available to an agent at a particular time-step depend on (i) the type of day (weekday or weekend-day), (ii) the type of time-step (morning, afternoon, evening, night), (iii) the age-group of the agent and (iv) the non-pharmaceutical measures that may or may not be active at that moment. The activities within the activity-set are represented as a list consisting of a motive, location and social distancing behavior (binary); e.g. \(\langle Study, University, TRUE \rangle\). Agents that choose the same location for performing their activity are able to interact. It is through these interactions that the virus is able to transmit itself from one agent to another. When agents switch activities, they move from one location to the next using different modes of transportation. Agents that share the same mode of transportation may also interact, which leads to an increased risk of viral transmission.
Social network
Upon setup, each agent is randomly ascribed a set of locations (e.g., a home, private-leisure places, essential- and non-essential shops etc.) which constitutes in a personal list of places that it can visit during a simulation. Agents that share the same home location become family members, while agents with the same working locations become colleagues. Where the configuration of family members and colleagues is straightforward, the establishment of friendly ties consist of a tripartite process. First, the subset of agents are selected that hold the same location of the type ‘work’ and/or ‘private-leisure’ in their places-to-visit lists. This is done to ensure that agents only befriend other agents when they are able to meet with each other professionally, as in the case of colleagues, or socially, as in the case of non work-related friends. Next, a second filter is to only select those agents from the same age-group, as it is assumed that people tend to befriend others that have a similar age. The last step involves selecting friends from the previous subset, based on how similar their value systems are to the target-agent (see Paragraph 3.23 for a formal description of how the degree of similarity between value systems is determined). This tendency to befriend like-minded others is based on the principle of homophily (McPherson et al. 2001).
Due to the aforementioned selection criteria, it can happen that the subset of potential friends for some agents becomes rather small; these agents will have relatively few friends and therefore hold a comparatively marginalized position within the social network. Conversely, a given agent whose age is similar to many others and whose places-to-visit list exhibits a high degree of overlap with those of others will frequently appear in the set of potential links of others. Such agents will be chosen as friends relatively often. As a consequence, these agents will be well-connected and hold a more centralized position within the social network.
To ensure that the social network topology displays a realistic combination of clusters and wide bridges (i.e., ties between agents belonging to different social clusters), we introduce the random-link parameter which specifies the proportion of agents that randomly befriend another agent within the network. It must be stressed that the current study does not experiment with the influence of different network topologies on the spread and fatality of COVID-19. This study focuses on providing and illustration of how the observed differences in infection rates across populations with different cultural profiles might occur. Hence, the variables tied to the topology of the social network are controlled for in the simulation outcomes presented in this paper. Moreover, the topology of the social network remains static, which means agents are not able to be- or defriend others over the course of a simulation.
The virus
In our simulation, the virus spreads through bilateral social interactions between an agent that is infected (the ‘carrier’) and an agent that is not infected (the ‘recipient’). The disease sub-model within ASSOCC is parameterized and calibrated on the basis of a validated epidemiological model developed by scientists from the Oxford University’s Nuffield Department of Medicine (Hinch et al. 2020). Appendix A.3 presents a detailed description of the transmission process. In short, the probability that a carrier infects a recipient is a function of the contagiousness of the carrier, the susceptibility of the recipient, the social distancing behavior of both agents, and the ‘density-factor’ of the location where the interaction is taking place.
The moment an agent becomes infected, its disease may progress through various stages, namely: asymptomatic, mild symptoms, severe symptoms, life-threatening symptoms, recovery, and death.2 The ASSOCC model contains five types of disease progressions (note that \(\mu\) indicates the typical or average length of each distinct cycle):
- \(\text{infected}\rightarrow\text{asymptomatic}\rightarrow\text{recovery}\) (\(\mu\) = 15 days)
- \(\text{infected}\rightarrow\text{mild symptoms}\rightarrow\text{recovery}\) (\(\mu\) = 18 days)
- \(\text{infected}\rightarrow\text{severe symptoms}\rightarrow\text{recovery}\) (\(\mu\) = 18 days)
- \(\text{infected}\rightarrow\text{symptomatic}\rightarrow\text{life-threatening symptoms} \rightarrow\text{recovery}\) (\(\mu\) = 22 days)
- \(\text{infected}\rightarrow\text{ symptomatic}\rightarrow\text{life-threatening symptoms} \rightarrow\text{dead}\) (\(\mu\) = 15.5 days)
Once an agent recovers from the virus, it is assumed that it becomes immune to the disease which means it can no longer contribute to its transmission. Note that when agents become aware of their infection status - such as when they start experiencing symptoms - they may choose to adjust their behavior by, for instance, quarantining at home and thereby isolating themselves from all agents except those that reside in the same house.
Implementing and lifting behavioral measures
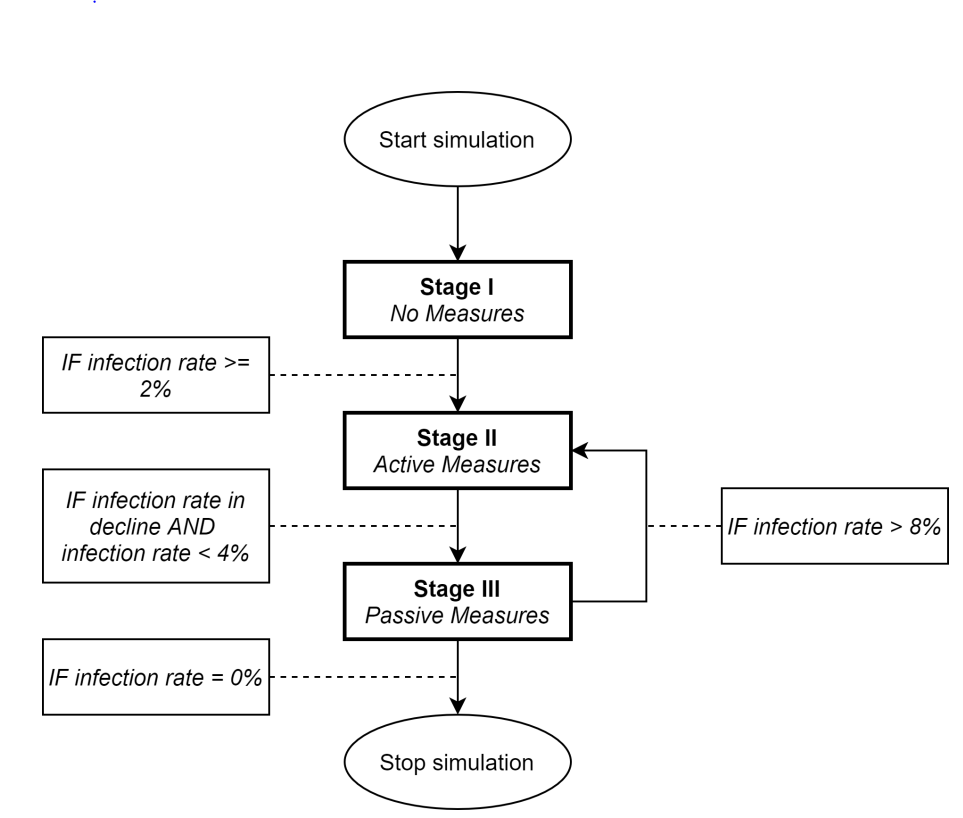
The seeding of model executions happens by randomly selecting three agents from the agent-set and setting their infection-status to ‘TRUE’. This is done to ensure a reliable start of the spread of the virus. At the start of a simulation, none of the agents are aware of the virus and there are no measures active that aim to limit the spread of the virus. Once the number of infected agents relative to the total agent population exceeds a pre-specified critical threshold (set by the parameter infection-rate-based-trigger), various non-pharmaceutical measures are triggered within the model. A description of these measures is provided in Table 4.
The measures included in Table 4 are designed to resemble common classes of non-pharmaceutical measures observed in the real world (ACAPS 2020). We model only non-pharmaceutical measures that involve placing a demand on the discipline and personal responsibility of individuals. We refer to this class of non-pharmaceutical measures as behavioral measures. Other non-pharmaceutical measures, such as restricting the opening hours of non-essential locations, make less of an appeal to individual responsibility by simply enforcing certain behaviors (in this case, preventing people from visiting such locations). Experimenting with the response of individuals to such authoritarian measures falls beyond the scope of the current study.
Within the model, there are three stages of severity with respect to the measures taken to curb viral transmission; these are described in Table 4. During the first stage the agents are unaware of the existence of the virus. The second stage involves the enforcement of various behavioral measures that restrict agents’ freedom of movement. This stage is called the ‘active measures’ stage. This stage becomes active when the number of infections (relative to the total population) exceeds a pre-specified threshold set by the modeller. Once the number of infections has decreased sufficiently to allow for the relaxation of measures, a third stage becomes activated; this stage is referred to as the ‘passive measures’ stage. In this third stage, everyone is still aware of the existence of the virus and advised to adhere to the measures introduced in the ‘active measures’ stage. However, the measures are no longer actively enforced by the government. Whether agents choose to comply to the measures or not is in this stage is a choice made purely on the basis of one’s own risk perceptions.
In reality, governments are forced to make a continuous trade-off between restricting the freedom of their citizens and controlling the growth of the virus. By introducing these three theoretical stages of virus control, we try to emulate how governments give back freedoms to citizens when the prevalence of the virus shrinks, and constrain it when the presence of the virus within the population increases.
| Stage | Description |
|---|---|
| No measures | In this stage agents are unaware of the existence of the virus. As a consequence, people go about their daily activities without knowing they might be infected or become infected. People who experience symptoms at this stage do not know that it is due to the coronavirus and therefore will not alter their behavior because of it. |
| Active measures |
|
| Passive measures | All the measures implemented and enforced by the government in the ‘active measures’ stage are lifted. Despite the government lifting the measures in this phase, agents can still choose to adhere to certain measures because they know the risk of contamination is lower as a result. Thus, agents can still practice social distancing and/or self-isolation when the government is not actively enforcing this behavior. The choice agents make about whether or not to act in accordance with the behavioral measures introduced is therefore not influenced by a sense of duty to the government. In this ‘passive’ stage of virus control, agents know about the virus and how to limit the risks of becoming infected; whether they act in accordance with this knowledge is purely dependent on the outcome of the risk assessment each individual agent makes when deciding on which activity to perform next. |
It is important to stress that agents can decide, at any time, to disobey any of the implemented behavioral measures, even when these are actively enforced by the government. Whether or not an agent decides to comply with any of the active measures depends on the satisfaction of its needs (see Section 3.26 and the way in which these are prioritized based on its values (see Section 3.25). In our model experiments, we focus on the differences across cultural contexts in agents’ propensity to disobey behavioral measures introduced by the government. Thus, we focus explicitly on the cross-cultural differences in compliance behavior of agents within the ‘active measures’ stage.
As noted, the moments that mark the transition between each of the three stages are determined by various thresholds set by the modeller that are related to the infection rate. By default, these thresholds are specified in such way that the number of infection ‘waves’ generated by the model is maximized (see Figure 4 for the default settings). This is done to obtain as much information as possible with regards to the motives and behaviors of agents during the different stages of virus control.
The cultural model
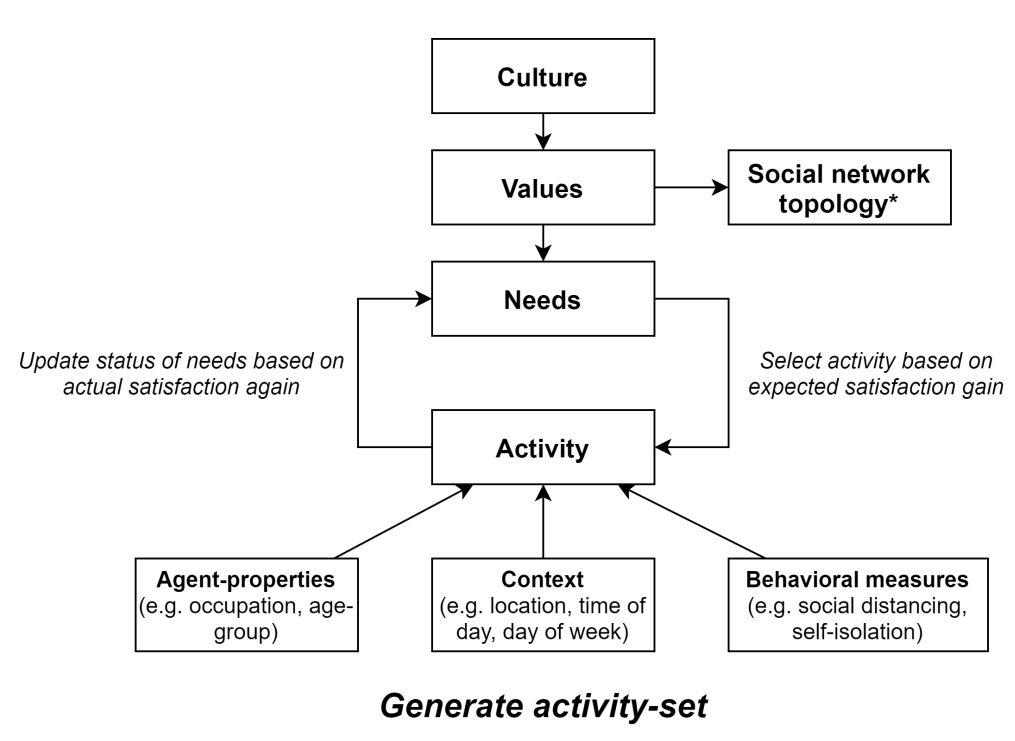
Figure 5 provides a conceptual overview of how our cultural model is fitted into the larger ASSOCC architecture. It is important to stress that the scope of our cultural model is confined to a representation of culture and its formative influence on the value systems of people constituting a population. That is to say that we intentionally exclude other population-level factors that are of influence on the course of a pandemic and that may correlate with the characteristics of a population’s cultural profile. Examples of such factors are demographic composition, infrastructural features, political regime and governance systems. Furthermore, Figure 5 shows that the social network topology is partly determined by the values that people hold. We do not, however, experiment with this relationship since the effect of various social network topologies on the management of a pandemic falls beyond the scope of this paper. The components in Figure 5 marked with an asterisk are part of the larger ASSOCC modelling architecture but are not included as a part of current model experiments.
The following sections describe each relationship depicted in Figure 5. In Section 3.20 we describe how culture influences the configuration of people’s value systems. Section 3.22 explains how people’s value systems are configured so as to ensure that they are logically consistent. The influence of values on the social network topology is described in Section 3.23, and on needs in Section 3.25. A description of the formation of the activity-set and the needs-based selection of activities from this set can be found starting in Section 3.26.
Cultural clusters
We implement a formal representation of culture on the basis of a cluster analysis of data present in the Hofstede database (Hofstede 2020). The Hofstede database contains data on the cultural profiles of 112 countries. 65 countries remain after filtering out countries with incomplete data. The extraction of clusters from this data enables us to construct meaningful cultural blocs that can be fed into the model for experimentation (see Table 12 in Appendix C.1). The construction of these blocs allows us to forego the complexity of experimenting with country-level data whilst retaining the bulk of the information that is present within the Hofstede database. Importantly, we simulate populations with hypothetical cultures that do not display a one-to-one correspondence to any particular country in the real world. For a description of the clustering procedure see Appendix C.1.
Culture-based value formation
We compute the population means of the Schwartz BVT Values (\(\mu[Val_i]\)) as linear combinations of HCD scores. In Section 2.7 we present which HCDs are mapped onto which Schwartz BVT Values. The values of agents are drawn from a normal distribution with \(\mu[Val_i]\) as the mean and \(\sigma[Val_i]\) as the standard-deviation. This standard-deviation is set to 7.5 to make a spread around the mean that is not too narrow nor wide. The parameter \(\sigma[Val_i]\) is controlled for during current experimentation (see Table 5). It can, however, be used to experiment with intra-cultural differences (i.e. cultural consensus) in future experiments. Appendix C.2 presents the distribution of value levels for each cultural bloc resulting from the current procedure.
One must be wary of the fact that our results are conditioned on the assumption that agent values are normally distributed in a way that is depicted in Appendix C.2. Inferring individual properties from aggregated population-level tendencies could, in principle, take on many different forms (other than a Gaussian distribution) and still satisfy the condition that they average out in a particular way. The possible space- and network-based distribution heterogeneity that arises from varying the way in which individual characteristics are inferred from aggregate statistics is likely to have an influence on the dynamics of virus diffusion. However, experimenting with the various ways in which individual values can be deduced from cultural dimensions and assessing the effect this has on viral transmission falls beyond the scope of our study.
Structure of value systems
Value-based social network
Modelling the value circumplex of the BVT (Schwartz 2012) is done on the basis of a procedure presented by Heidari et al. (2020). A detailed description of how this procedure is implemented in our model can be found in Appendix B.1. We ensure that values placed close to one another within the circumplex will be constrained in their dissimilarity (i.e., their importance levels will be similar), whereas values placed further apart will be less constrained in their dissimilarity (see Appendix B.1). To account for the effect of age on the structure of agent value systems3, a procedure is implemented that performs a linear transformation of an agent’s values according to a set of coefficients taken from Schwartz (2020) (see Appendix B.1).
The structural properties of agent value systems determine how they link up with one another to form a particular type of social network. There are two global parameters that change the topology of the network: (i) the number of ‘friend links’ each agent tends to make (specified by friend-links), which is set to 7 by default, and (ii) the proportion of agents that makes a random link with another agent in the population (specified by random-links), which is set to 0.15 by default. The default settings for these global parameters are decided upon by means of a visual inspection of the type of social network topologies they generate. The desired network topology is one that exhibits a realistic combination of weak ties, social clusters, and wide bridges (Centola 2015).
As described in depth in Paragraph 1.1.3.2, agents link up with others whose value systems exhibit similar characteristics. The similarity of value systems that exists between two agents is determined by computing the Euclidian Distance (\(d\)) between a targeted pair of value systems; i.e., value system \(X\) and value system \(Y\), see Equation 1.
| \[ d_{X,Y}=\sqrt{\sum_{Val=1}^{9}(X_{Val}-Y_{Val})^2}\] | \[(1)\] |
Value-based needs prioritization
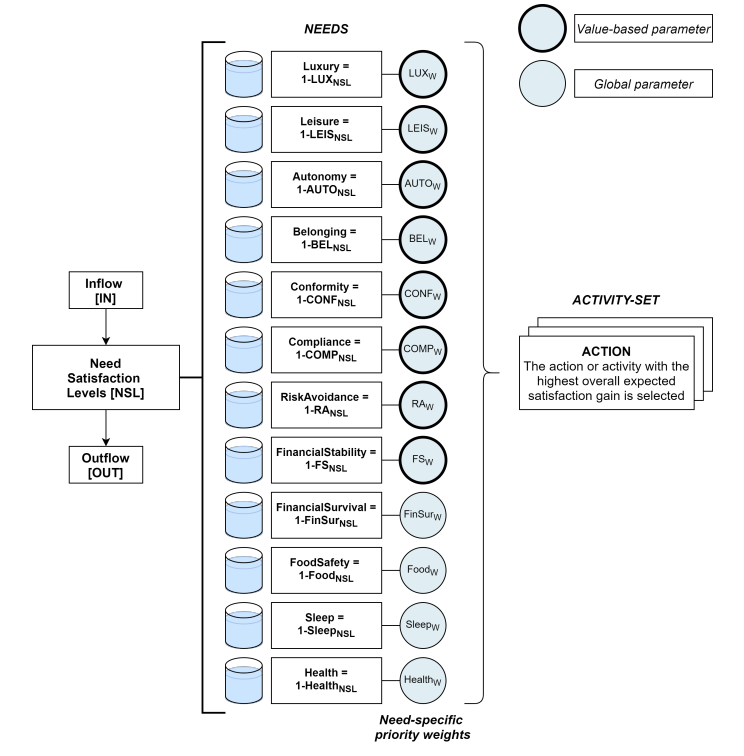
As described in Section 2.9, the values of an agent determine the priority-weights ascribed to its 8 psychological needs (see Table 10 in Appendix A.4 for a description of needs). The priority-weights of the physiological needs are set globally and are therefore the same for all agents. Agent needs are indexed as \(n\), where \(n \in \{1 \ldots 12\}\). The priority-weight of a need is denoted as \(\omega_n\). After having computed the priority-weight for all needs, they are normalized to ensure that their sum equals 1 (see Equation 2). Normalized priority-weights are denoted as \(\omega^\prime_n\), where \(\sum_{n=1}^{12}\omega^\prime_n=1\). Figure 6 visualizes our value-based needs model.
| \[ \omega^\prime_n=\frac{\omega_n}{\sum_{n=1}^{12}\omega_n}\] | \[(2)\] |
Needs-based activity selection
During an instance of decision-making, agents are presented a set of activities (\(Activities\)) from which they select the activity (\(A\)) that grants them the highest Total Satisfaction Gain (TSG) (denoted as \(\alpha\)); see Equation 3. The content of \(Activities\) is dependent upon the time of day, the current location of the agent, and the agent’s properties such as its age and occupation-type. The gains and penalties agents incur to their need satisfaction levels when performing activities are formalized in a pay-off structure. This pay-off structure was calibrated on the basis of a series of unit test which involved an iterative and careful tweaking of the pay-off matrix under various model settings to ensure that agents display natural-looking behavior; that is, we avoid agents from obsessively choosing to perform one and the same activity as this would indicate that this activity has too high a payoff relative to other activities. Note that the assessment of what counts as ‘normal’ or ‘natural looking’ behavior in this context is not backed by empirical data on the statistical distribution of people’s daily activities.
| \[ \alpha = \max_{A \in Activities} TSG(A)\] | \[(3)\] |
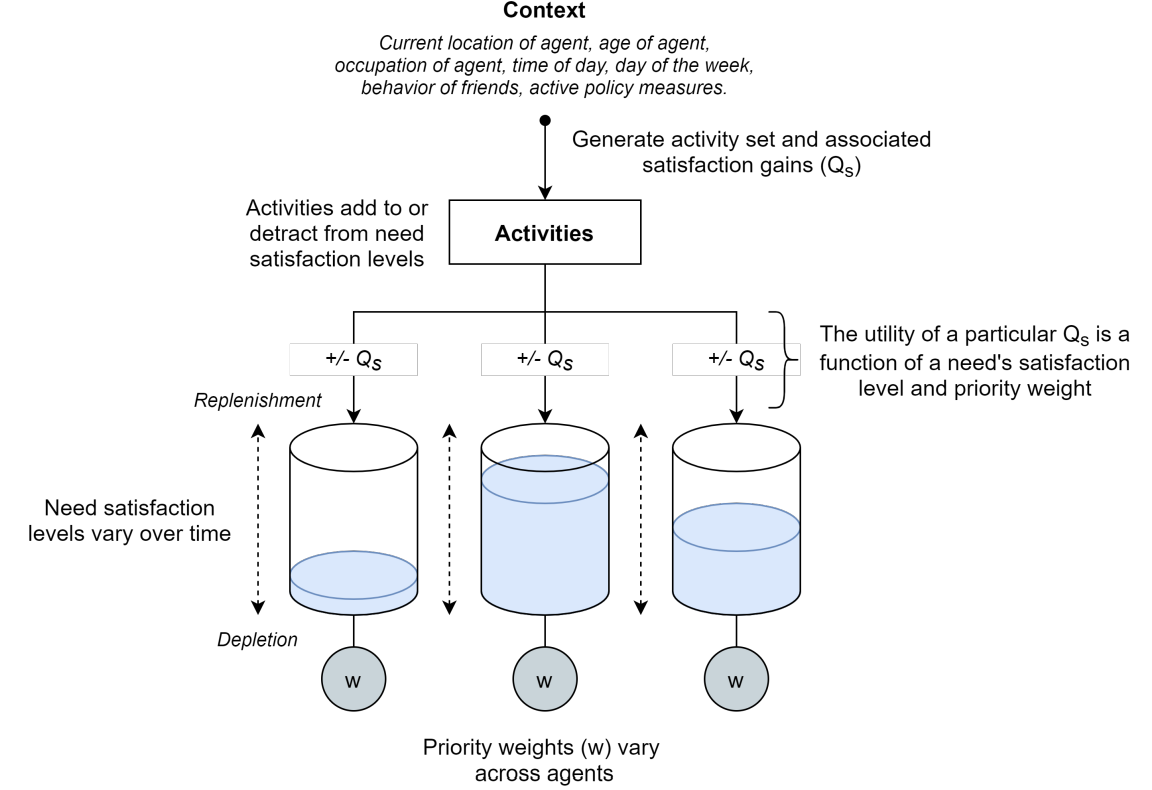
An agent assesses the satisfaction it expects to gain by performing a particular action based on the Diminishing Marginal Utility (DMU) model. The DMU proposes a sublinear monotonic relationship between the quantity of resources available to an agent (i.e., the satisfaction levels of its needs) and the relative utility (\(U\)) of the resources (i.e., satisfaction) to be gained from performing a particular activity (Goetz 2013). This implies that, in general, gaining a particular quantity of satisfaction (\(Q_s\)) holds a higher value (or utility) for an agent whose satisfaction levels are depleted versus one whose levels are maxed out. Note, however, that \(U(Q_s)\) also depends on the priority an agent ascribes to a particular need; specifically, the utility of replenishing the satisfaction level of a depleted need increases in proportion to the priority ascribed to that need by a given agent. To summarise, \(U(Q_s)\) is a function of need satisfaction levels (which vary over time) and the priority ascribed to needs (which are determined on the basis of an agent’s value system and remain fixed over the course of a simulation).
The need satisfaction levels of agents vary over time as performing activities may detract from or add to these levels. Moreover, the need satisfaction levels of agents are subject to a decay rate, implying that agents who refrain from doing anything will see their satisfaction levels drop slowly but surely to the point of depletion. The dynamics of satisfaction levels is modelled using the ‘water tank’ approach as presented by Dörner et al. (2006) and modelled by Di Tosto & Dignum (2012) and Heidari et al. (2020); where each need is represented as a water tank that can be filled with certain quantities of satisfaction. A full water tank represents a need that is fully met, whereas an empty water tank represents one that has been fully neglected. Agents are continuously driven to keep their water tanks filled up to a certain extent and within certain limits. Due to external circumstances and/or lack of internal capacities, agents often are not able to attain an ideal state of overall satisfaction. This means agents are always motivated to engage in activities that help them approach, but never reach, a maximal state of satisfaction.
Rather than maximizing their overall satisfaction, agents have to make trade-offs and, as a consequence, display ostensibly irrational behavior; that is, preferring one thing over another in one moment, while changing preferences in the next. This process of working towards maintaining a relatively stable and well-balanced status of need satisfaction levels in the face of changing environmental conditions resembles that of homeostasis.
Social decision-making
Agents within our model base their decision about what activities to engage in partly on what their peers are doing. We implement a simple form of ‘social imitation’ (Bandura 1962; Rilling & Sanfey 2011) by having agents track the actions of their peers, and obtaining a satisfaction boost in their need for conformity if they choose to engage in an activity that is similar to the activity that the majority of their peers have engaged in the past.
As noted, actions, or activities, are defined by a motive, a location and whether one chooses to engage in social distancing (represented as a Boolean). An instance of an action could look like this: \(\langle Study, University, TRUE \rangle\). During decision-making, agents reflect on what their peers did during that moment of the day (e.g. morning, afternoon or evening), the day before. An agent can obtain gains in the satisfaction level of its need for conformity by choosing to perform an action that is ‘similar’ to the one previously chosen by the majority of its peers. More specifically, at a given \(t\), agents look at the activities chosen by the majority of their peers at \(t-4\) and may choose an activity that is defined, either fully or partly, by the same three activity-related characteristics. The degree of overlap in the characteristics of activities chosen by agents defines the ‘similarity’ of their actions. The greater this similarity, the greater the satisfaction gains that can be realized with respect to their need for conformity. Consequently, agents that place a higher priority on satisfying their need for conformity will tend to imitate the actions of their peers more frequently.
Model Evaluation
The ASSOCC model is the result of extensive collaboration between a group of researchers, making sure that unit tests were performed each time the model was expanded upon. In doing so, continuous efforts have been allocated towards verifying the model. With regard to model validation, the current cultural model relies on the ASSOCC validation processes and extends those by focusing on (1) reflecting on the empirical underpinnings of the theoretical assumptions embedded in the culture model (see Section 4.2), and (2) investigating the robustness of model behavior in response to perturbations in the settings of input parameters (see Section 4.3).
Model calibration
When possible, the calibration of model parameters was performed using empirical data. In case empirical data was not available, calibration of model parameters was done on the basis of a series of model tests where theoretically valid outcomes were obtained mainly through a process of trial & error. Appendix C.3 presents the parameters of our model and how they are calibrated.
Global sensitivity analysis
The evaluation of our model comprises of an exploration and quantification of the sensitivity of model outputs with respect to marginal changes in the settings of model input parameters (henceforth referred to as factors). In doing so, we assess the robustness of model outcomes to marginal changes in core and ancillary assumptions embedded within the model (ten Broeke et al. 2016) (see Appendix C.3 for an overview of model parameters). To reach this objective, we execute a Global Sensitivity Analysis (GSA) that varies all selected factors simultaneously and analyzes the consequent model behaviour.
We adhere to a non-parametric (i.e., ‘model-free’ or ‘variance-based’) approach as it circumvents the assumption of linearity inherent in regression-based approaches that is ill-suited for modelling complex dynamic systems (Ligmann-Zielinska et al. 2014; Ligmann-Zielinska & Sun 2010). See Appendix C.4 for a detailed description of this GSA approach and the results of the sensitivity analysis.
Model Experimentation
The goal of our experimentation is to illustrate how different cultural contexts influence the transmission of SARS-CoV-2 within our model given the implementation of various behavioral measures aimed at limiting the spread of the virus. The experiments are built on our conceptualization of how culture influences the value systems of individuals within a population, and how these value systems in turn affect the needs of individuals and consequently their decision-making and interactions.
Experiment design
A total of 18 experiments is performed to explore the emergent patterns of viral transmission. Each experiment is replicated 150 times for each cultural bloc resulting in a total of 900 model executions. The length of the simulations is determined by how long it takes for none of the agents to be infected anymore. This means that the duration of our simulation runs are of different lengths. Under default settings, simulation runs do not seem to last longer than around 1500 time-steps, which translates to 375 days in our simulated world. As a precaution, we define a maximum number of time-steps (2000 ‘ticks’) to be sure that our model does not get stuck in an infinite loop. Appendix C.5 gives a detailed explanation for choosing this experimental design and Appendix C.3 provides a detailed description of the functionality of model parameters and their calibration.
| Parameter | Settings | Function |
|---|---|---|
| cultural-bloc | A, B, C, D, E, Neutral | Independent variable |
| cultural-consensus | 7.5 | Control variable |
| country-specific-settings | World | Control variable |
| social-distancing-factor | 0.3 | Control variable |
| contagion-factor | 5 | Control variable |
| friend-links | 7 | Control variable |
| random-links | 0.15 | Control variable |
| Replications | 150 | Experimental design parameter |
| Max ticks | 2000 | Experimental design parameter |
Experimental Results
To illustrate the influence of cultural parameters on the spread of the virus, we first look at the infection curves across cultural contexts. We then turn our attention to illustrating what might be the causal mechanisms underlying cross-cultural differences in infection rates.
Infections
Figure 8 and Figure 9 show the infection curves and cumulative infections per cultural bloc, respectively. The data represent the mean values as computed on the basis of 150 replications. Simulations run for as long as there are infected agents present within the population. Figure 8 shows that, at this stopping criterion, our model runs do not exceed the 1,500 time-steps. Because of computational constraints, our Netlogo-based model is not able to simulate populations of more than approximately 1,200 agents. This means that at some point the virus generally dies out because all agents have become immune to it.
Figure 9 shows that bloc A reports the highest measurement of cumulative infections, and blocs C and D the lowest. As can be seen in Table 12, Appendix C.1, bloc A holds the highest ranked score for Individualism and the lowest ranked score for Power Distance and Masculinity. This finding suggests that, within our model, individualist and egalitarian cultures experience more difficulty in successfully managing the spread of the virus under the introduced measures in the model. Blocs C and D perform best in terms of curbing infections. Bloc D holds the lowest ranked scores for Individualism and Long-term Orientation, and the highest ranking for Indulgence (see Table 12, Appendix C.1). Bloc C holds a top ranking for Uncertainty Avoidance. These results illustrate how the values espoused in conservative and collectivist cultural contexts lend themselves well for an effective management of the pandemic within our model.
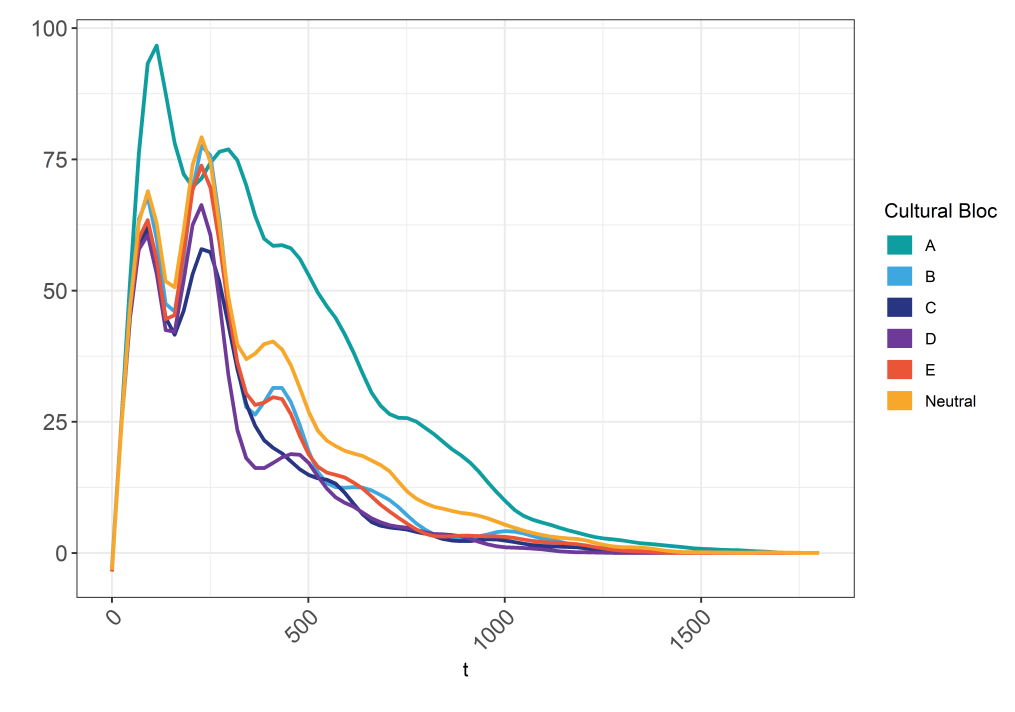
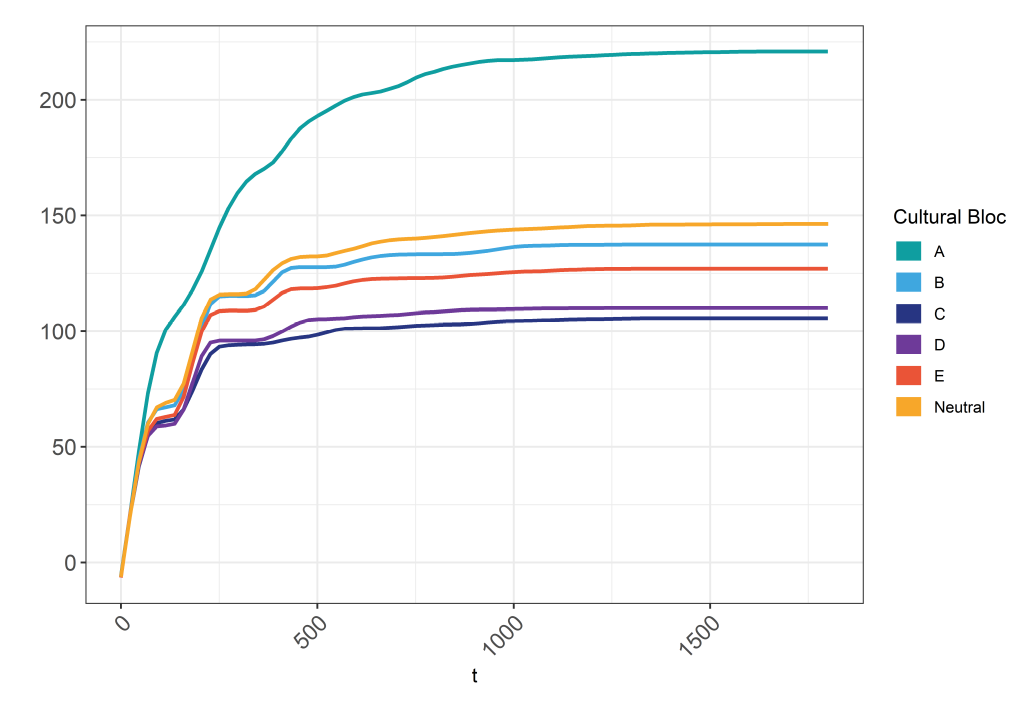
The cross-cultural differences depicted in Figure 8 and Figure 9 can be explained by zooming in on how agents are behaving over the course of a simulation. Since viral transmission is propelled by agent interaction (see Appendix A.3), it is logical to look at how often agents come together to interact and what the characteristics of these interactions are. Differences in the frequency and nature of these interactions across cultural contexts may explain, in part, how and why we observe the cross-cultural differences in the patterns of infections that the model generates.
Agent behaviour
Quantity of interactions
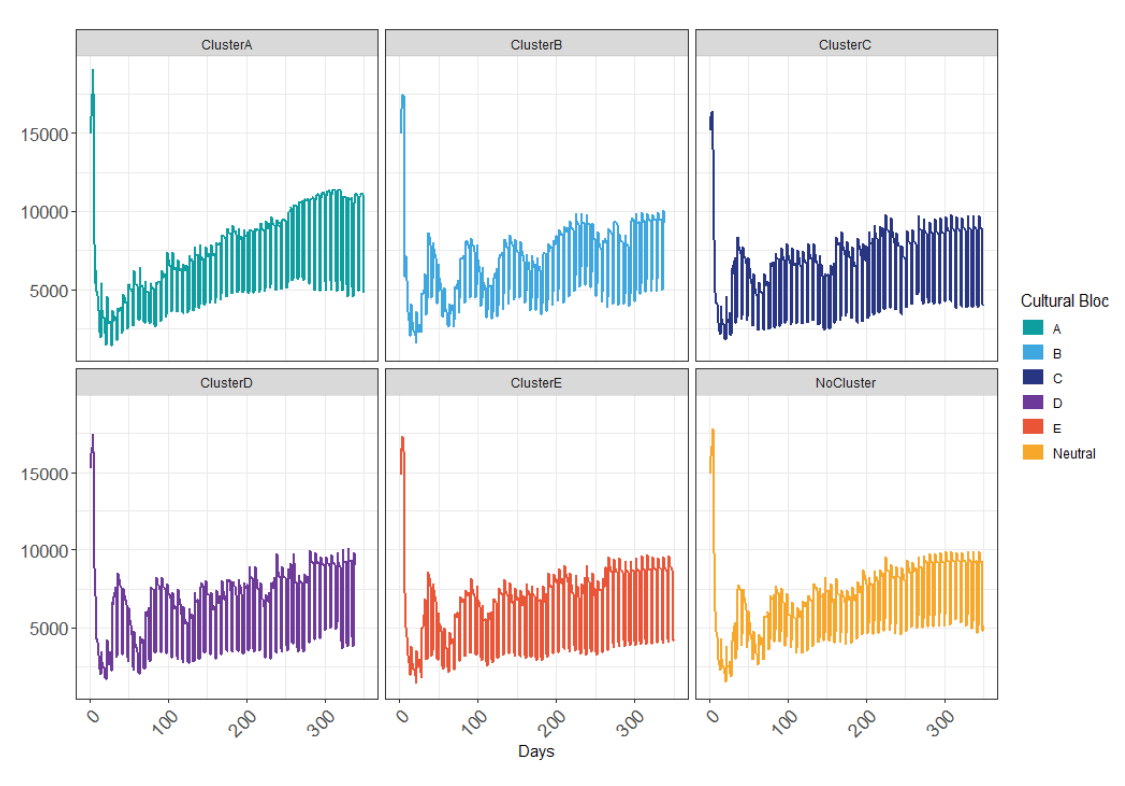
To understand how and why the observed cross-cultural differences in infections are generated by the model, we focus first on analyzing the number of contacts that occur between agents over the course of a simulation. Cross-cultural differences in the number of contacts between agents could explain the differences observed between cultural contexts in terms of infections; after all, the higher the number of contacts between agents, the higher the transmission potential of the virus, which ultimately translates into higher infection rates.
Figure 10 shows how the number of interactions or moments of contact between pairs of agents develops over the course of a simulation. The plot shows an explosive growth of contacts during the first few time-steps across cultural contexts. The high number of contacts allows the virus to spread easily among the agent population. The rapid increase in the number of infections leads to the first phase being initiated fairly quickly across model runs. The ‘active measures’ stage is generally triggered around 30 time-steps (which amounts to approximately 7 days in our simulated world), after which the number of contacts steeply decreases.
It can be seen that, after the active measures phase is invoked for the first time, the number of contacts does not reach the same heights it did during the first few time-steps. This illustrates that agents are more likely to stay home than before they knew of the existence of the virus, regardless of whether behavioral measures are actively enforced.
Furthermore, there are roughly two fluctuation patterns that can be discerned from the plots. The first pattern involves a high-intensity (short period) oscillation resulting from the differences in the frequency of contacts that occur between day and night, as well as between weekdays and weekends. The second type of fluctuation is characterized by longer periods and is due to changes in the virus control stages (see Table 4). Specifically, when behavioral measures are actively enforced, the frequency of contacts decreases; when enforcement is lifted, the interaction between agents increases, creating an oscillation in the frequency of contacts as governments switch back and forth between the active and passive stages of virus control in their efforts to control viral transmission.
Regarding cross-cultural differences, some subtle differences can be observed. Most notably, the fluctuations in the number of contacts that results from changes in the intensity of virus control are least pronounced for bloc A, and most visible for bloc B. Apparently agents in bloc A hardly respond to the active enforcement of behavioral measures. This could explain, in part, why bloc A performs worse in curbing infections than bloc B. Moreover, bloc A shows slightly higher peaks in the number of contacts during simulations, illustrating that these agents are less risk-averse than those in the other blocs.
It must be noted that, in epidemiological models, the agent network topology is an important determinant of the nature of the relationship between the number of contacts that occur between agents and the infections that take place. This means that even though the frequency of interactions between agents may look similar for two blocs, their infection rates may differ because of differing network topologies. Analyzing the ways in which the network topology affects this relationship, however, falls beyond the scope of this paper.
In addition to the number of interactions, the nature or quality of these interactions plays an important role in driving viral dynamics within our model. The next section discusses this in more detail.
Quality of interactions
As described in Section 3.26, agents are programmed to maximally satisfy their needs whilst taking into account the existence of constraining and/or enabling factors in their environments. Depending on the state of its needs, an agent may, therefore, decide not to obey the behavioral measures implemented by the government. The degree of non-compliance within a population affects the likelihood of infected agents coming into contact with healthy ones, will ultimately determine infection rates.
During the most stringent stage (i.e., the ‘active measures’ stage; see Section 3.11), a collection of actively enforced non-pharmaceutical measures is implemented. It is interesting to see whether rates of compliance with these behavioral measures differs across cultural contexts during this phase as this could explain why some blocs outperform others in terms of curbing infections (see Figure 9).
To study this, we first register all the moments a given agent (an ‘infector’) infects another agent while the ‘active measure’ phase is in effect. During such an instance, the model registers whether the infector is complying with any of the behavioral measures implemented and enforced by the government. For this analysis, we group all behavioral measures related to staying home and isolating oneself from others under the heading of ‘self-isolation’; this includes (compulsory) hybrid working, self-quarantining and curfew (see Table 4). Social istancing is a behavioral measure that forms its own category in this context.
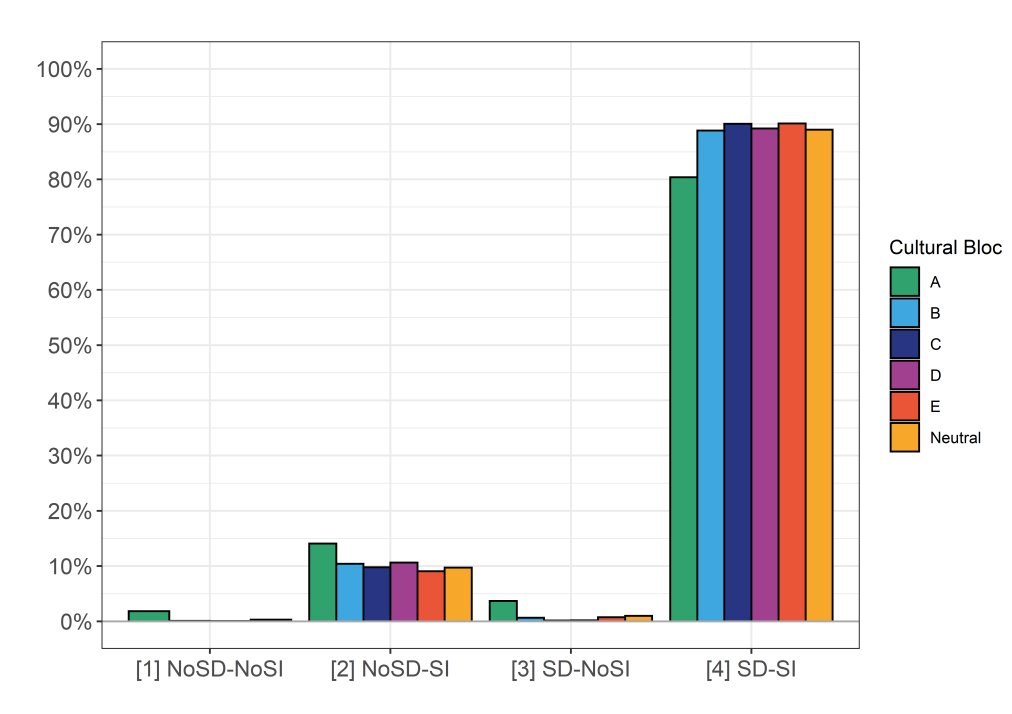
As described in Section 3.4, agents pick an activity to perform during each time-step which consists of a motive (specifying what the agent is doing, e.g. ‘working’), a location (specifying where the agent is doing it, e.g. ‘the office’) and whether the agent decides to engage in social distancing or not whilst performing the activity (implemented as a Boolean). Agents choose activities that, based on which non-pharmaceutical measures are active, can be classified as being in conflict or in accordance with the prevailing rules regarding social distancing and/or self-isolation. We therefore distinguish four types of compliance behavior. These types are depicted in Table 6. Any instance of agent behavior can be mapped onto one of the four positions within this 2x2 matrix. The quality of contacts, therefore, can be defined in terms of the decisions of interacting agents to comply to social distancing (or not) and/or to self-isolate (or not) (see Table 6). To facilitate interpretation of the results we chose to apply the following acronyms referring to the various compliance behavior types: Type 1 = NoSD-NoSI, Type 2 = NoSD-SI, Type 3 = SD-NoSI, Type 4 = SD-SI. Where SD stands for Social-Distancing, and SI for Self-Isolation. The prefix ‘No’ indicates non-compliance.
| Self isolation | |||
| Not-comply | Comply | ||
| Social distancing | Not-comply | Type 1 | Type 2 |
| Comply | Type 3 | Type 4 | |
Table 7 illustrates how agents displaying various types of compliance behavior may infect someone else within our simulated world.
| Compliance behavior type | Description |
|---|---|
| Type 1 | Agents who fail to comply with any of the active behavioral measures are most likely to infect someone else. |
| Type 2 | Since these agents are complying with the measure of self-quarantining and/or the curfew, they generally stay at home when they are infected. Thus, an agent that is infected by one that exhibits Type 2 compliance behavior is usually the housemate. |
| Type 3 | These agents are leaving the house although they are aware that they or one of their housemates is infected and/or when a curfew is in effect. Although these agents are social distancing when they are leaving the house, they are still likely to infect others. This is because social distancing reduces, but does not negate, the likelihood of infecting others. |
| Type 4 | Although these agents comply with all active behavioral measures, they may still infect others. For instance, infections can occur through agents going about their daily business without being aware that they are carrying the virus (such as when they are pre- or asymptomatic). Moreover, social distancing does not completely reduce the risk of infecting another person; especially when many people are gathered in, for example, a supermarket, the risk of viral spread may still be high even if everyone maintains some measure of physical distance from others. |
Figure 11 shows that agents display different forms of compliance behavior during a pandemic across cultural contexts. Each time an agent infects someone, the model records whether it is engaging in social distancing and/or whether it is self-isolating when it should be. The plots in Figure 11 are constructed by counting the number of recorded infections within each category of compliance behavior across the 150 replications. These numbers are subsequently divided by the total number of recorded infections. This means that Figure 11 shows the relative frequency distribution of the four types of compliance behavior (Table 6) that agents display upon infecting someone else.
The figure shows that the vast majority of infecting agents across all cultural blocs are classified as SD-SI (Type 4); which means that they are compliant to the prevailing rules of social distancing and self-isolation. This finding can be explained by the fact that despite adhering to behavioral measures, agents often still infect those with whom they frequently come in contact (e.g., housemates). Bloc A stands out as having 1 out of 5 agents displaying some form of non-compliance during the most stringent stages of virus control. This finding could explain why bloc A displays such remarkable infection rates (see Figure 9).
Agent motives
Figure 11 shows what type of compliance behavior (see Table 6) agents tend to display upon infecting another agent across cultural contexts. To better understand why agents are behaving the way they are when they are infecting someone else, it is instructive to look at what their motives are.
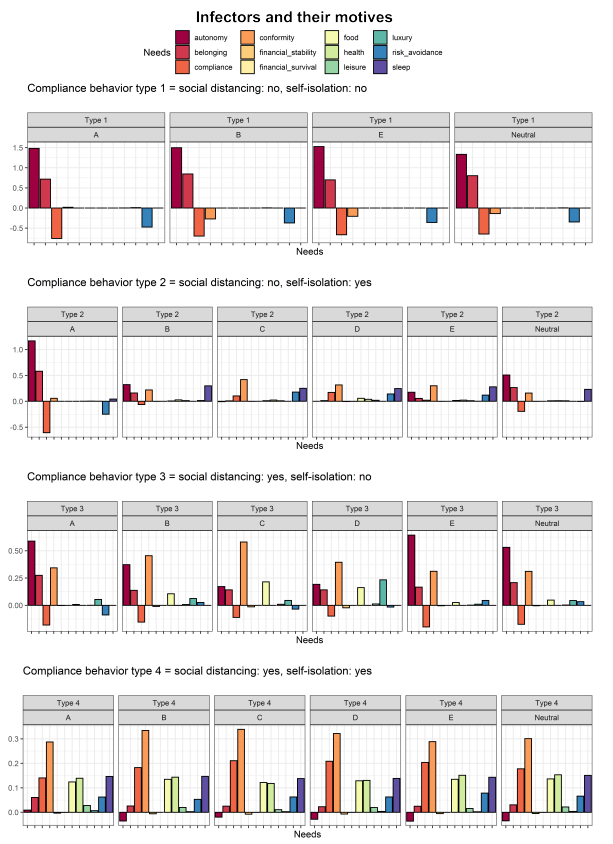
The plots in Figure 12 show how each need contributes to an agent’s decision to engage in a particular type of compliance behavior upon infecting someone (see Table 10 in Appendix A.4 for a detailed description of needs). We call the contribution of a need to an agent’s behavior its motivational force. The motivational force of a need reflects the anticipated change in the satisfaction level of that need resulting from the behavior of an agent. Hence, if the motivational force is a positive one, it should be interpreted as a replenishment of a need’s satisfaction level. If the motivational force is negative, then this means a need is depleted by the behavior of the agent. Positive motivational forces thus encourage an agent to act in a certain manner, whereas negative forces discourage an agent to do so. The magnitude of the motivational force of a need in comparison to those of other needs corresponds to its relative influence on the behavior of an agent. The plots in Figure 12 show the tug-of-war between a multitude of motivational forces at play within agents during moments of decision-making, ultimately resulting in the manifestation of certain behaviors.
Agent motives are calculated by registering the expected satisfaction gain (or loss) for each need for each agent during instances of decision-making. These values are normalized so that their sum equals 1; this is done by dividing each satisfaction gain (or penalty) by the total sum of satisfaction gains. In this way, we gain insight into the relative contribution of each need to an agent’s decision outcome. Moreover, because the absolute satisfaction gains differ across activities and over time, we scale the data so that all satisfaction gains of different activities at different times converge on a common scale. This enables us to compute meaningful averages of each need’s ‘motivational force’ over the 150 replications.
Motives type 1 infectors
Looking at the plots for ‘Type 1’ compliance behavior in Figure 12, it is generally the case that the need for autonomy and belonging push agents towards non-compliance (as indicated by the strong positive motivational force of these needs). Conversely, the need for compliance and risk-avoidance tend to discourage rule violation (as indicated by their negative motivational force). However, the gains in autonomy and belonging tend to outweigh the losses incurred in compliance and risk-avoidance, which results in agents breaking the rules.
Strikingly, bloc C and D do not report any Type 1 infectors, which means that the agents in these blocs are reluctant to be (strongly) disobedient to the demands placed upon them by the government. Moreover, it can be observed that ‘Type 1’ infectors in blocs B, E and Neutral experience penalties in the satisfaction of their need for conformity, while in bloc A this is not the case. Type 1 infectors thus behave less in a non-conformist manner in bloc A than in the other blocs; which indicates that Type 1 non-compliance behavior is more commonly observed or more ‘socially accepted’ in bloc A than in the other blocs (see Paragraph 3.30 for a description of conformity-driven behavior in our model).
Motives type 2 infectors
Figure 12 shows that agents in blocs A, B and Neutral are driven towards non-compliance with social distancing primarily by the need for autonomy and belonging. This suggests that the individuals in these blocs find it rewarding to be free to make their own decisions and to meet others in their physical proximity because it gives them a greater sense of belonging and togetherness. In bloc C, D and E, agents are receiving gains in their need for conformity by not engaging in social distancing. This indicates that agents are pushed towards this form of non-compliance because most of their peers are doing the same thing.
The small gains that can be observed in the need for physical sustenance (food and drinks) and sleep (which also involves resting and relaxation) across cultural blocs indicate that Type 2 agents tend to be at essential shops or at home when they are infecting others.
It stands out that infectors in some blocs tend to obtain gains in compliance and risk-avoidance for not complying to social distancing, which may seem counter-intuitive at first. However, one must keep in mind that NoSD-SI (Type 2) compliance behavior involves complying to self-isolation, which presents satisfaction gains for the needs for compliance and risk-avoidance. So although social distancing may lead to negative pay-offs for compliance and/or risk-avoidance, these losses can be offset by the gains in these needs through compliance with the measures pertaining to self-isolation.
Motives type 3 infectors
Figure 12 shows that Type 3 infectors in all blocs tend to incur costs to the satisfaction levels of their need for compliance. Across the board, these costs are offset by gains in autonomy, belonging and conformity, indicating that agents are generally driven to disobey the self-isolation rule because they want to be with friends and/or because significant others are behaving in the same manner. Blocs A, E and Neutral are driven towards non-compliance with self-isolation measures primarily by their need for autonomy. Blocs B, C and D mostly by their need for conformity.
The need for food and luxury also seems to play an important role as driver of SD-NoSI (Type 3) compliance behavior in some blocs, which implies that agents in those blocs are often driven to break from self-isolation to go shopping for (non-)essential goods.
Motives type 4 infectors
Figure 12 shows that complying to the rule of social distancing and self-isolation presents agents with large gains for compliance, conformity, risk-avoidance and health. The need for autonomy is generally depleted when agents act in compliance with behavioral measures because they tend to be constrained in their actions by obeying these rules. This depletion of autonomy may at some point lead to rule violation (as can be seen in the motive plots for Types 1, 2 and 3 in Figure 12). The gains in the need for sleep that can be observed are explained by the fact that when agents are sleeping or resting, they are always at home and thus compliant to the self-isolation measures.
Discussion & Conclusion
The current study provides an illustration of the cross-cultural differences observed in COVID-19 infection rates and the effectiveness of behavioral measures implemented by governments to manage the pandemic. We illustrate how agents within populations with different cultural profiles show a varying propensity to comply with behavioral measures such as social distancing and/or self-isolation, which in turn determines the effectiveness of these behavioral measures to curb infection rates. The following paragraphs describe some of the insights that our model-based illustration provides.
We illustrate that populations whose cultural profile is individualist, egalitarian and feminine, tend to suffer from relatively high infection rates. Conversely, populations characterized by a collectivist, hierarchical and masculine cultural profile display a higher efficacy at limiting the spread of the virus. It must be stressed that our model has only been tested for a restricted range of possible parameter settings, which means our results may therefore be quite brittle to marginal changes in any of the assumptions embedded within the model. Nevertheless, our simulations generated some noteworthy results that illustrate how cross-cultural differences in infection rates may arise when agents have different value prioritizations.
We show how, across cultural contexts, particular differences emerge regarding not only how often agents come together to interact, but also the ways in which they do so. By doing so we show how agents with different value priorities in our model are more (or less) likely to comply with non-pharmaceutical measures implemented by the government. Some interesting patterns were observed when zooming in on why agents within our model decide to (dis)obey the government.
In general, the highest rates of non-compliance within our model occur in cultures marked as individualistic, progressive and egalitarian. We illustrate that individuals tend to break the rules of social distancing and/or self-isolation when they feel overly constrained in their freedom to decide on how to act. This is especially the case for people in individualist cultures. Moreover, our model shows that individuals may come to feel isolated or socially disconnected, driving them towards non-compliance as to cater to their need for connection and belonging. Another significant driver of compliance behavior was shown to be the need for conformity, illustrating that individuals within our model are often socially motivated to comply to the rules or not. Some patterns in the motives of agents were not directly deducible from experimental settings, such as the cross-cultural variability in the propensity of agents to comply to or disregard behavioral measures on the basis of social conformity (i.e., acting in ways because others are doing so also), authoritative pressures (i.e., acting in ways because one is being told to do so), or a combination of both.
Limitations & recommendations
The current study has some limitations that deserve attention. A first point of criticism can be made regarding our assumption that people’s values remain static over the course of a simulation. Although values are relatively stable constructs, the context of a pandemic may expose people to extreme events that could potentially lead to a drastic revision of one’s beliefs. For instance, recovering from a near-death case of COVID-19 may lead a person that was initially risk-seeking or tolerant to become more conservative and risk-avoidant. In contrast, someone that recovered from a very mild case of COVID-19 may become more risk-tolerant and even suspicious of the need for public-health related measures which could potentially lead to a lower valuation of compliance to authority. In addition to these first-hand experiences, people may adjust their beliefs based on the information they receive from others. Conversely, they may feel the urge to proclaim their own beliefs and try to convince others of their views. Cultures may differ with respect to promoting resistance versus openness to change in people’s belief systems. Some cultures promote a more friendly stance towards the spread of new, potentially disruptive, ideas than others. People living in these tolerant cultures may change their values more easily, and therefore more frequently. An interesting avenue for future research would be to include a representation of the dynamics of processes that explain how individuals acquire, utilize and mutate their cultural assumptions and habits, as well as those that describe how cultural beliefs spread and change over time during a pandemic across cultural contexts.
As noted in the chapter presenting our cultural model, we chose to control for the effect of within-population variability in people’s value systems (i.e. cultural consensus) on the management of the COVID-19 pandemic. Societies may differ from each other in terms of how strong the influence of culture is on the formation of people’s values. Generally, the formative influence of culture on people’s beliefs is more pronounced in ‘tight’ than in ‘loose’ societies (Gelfand et al. 2006). Studying the effect of cultural consensus on the management of a pandemic presents an interesting extension to the experiments currently presented. It is important to stress here that drawing inferences about the structure of value systems at the level of individuals from population-level cultural dimensions exposes one to the risk of making an ecological fallacy. When it comes down to specifying how values are distributed within a population based on a set of cultural dimensions it becomes difficult to avoid making such a fallacy. To assess how robust model outcomes are to the ecological fallacy, one could analyze the behavior of the model whilst exploring how the distribution of values is allowed to vary within a population under the condition that the differences in cultural dimensions between populations remain unchanged.
Another point that should be discussed is the fact that our model presumes that each time persons are engaged in decision-making, they enjoy unobstructed access to the structural properties of their value systems and the satisfaction to be gained from performing a broad range of activities. It is then assumed that they consistently choose the activity that gives them the most satisfaction, given the environmental constraints they face during decision-making. A large body of research points out that humans do not make decisions in such a rational manner (Klein et al. 1993; Simon 1997). Incorporating more realistic representations of bounded rationality and cognitive biases into the decision-making process would therefore enhance the external validity of our theoretical framework.
Finally, the execution time of our model is rather slow due to the computational complexity that characterizes it. Due to limitations in the availability of computing power disposable to us, it was not possible to run simulations with populations of larger than approximately 1,200 agents. This cap on the number of agents that could be simulated, combined with the assumptions that an agent becomes immune once it recovers from the virus, often led to the situation wherein the virus ‘burnt through all of the wood available to it’ during model executions. That is, at some point either all agents are immune or have passed away, leaving none of them susceptible to become infected anymore. As a consequence, the current NetLogo-based version of the model is not able to simulate many waves of infections.
Notes
ASSOCC: Agent-based Social Simulation of the Coronavirus Crisis.↩︎
Older agents are more likely to find themselves developing severe of life-threatening symptoms than younger agents (see Appendix A.3).↩︎
Across cultures, older people tend to exhibit a lower endorsement of agentic personal values and higher endorsement of communal personal values than younger people (Fung et al. 2016).↩︎
Originally, Conformity & Tradition are considered to be distinct values; Tradition being a more extreme version of Conformity. For the sake of simplicity, these values are currently thought of as constituting a mild - i.e., conformity - and a more extreme - i.e., tradition - case of the same type of value.↩︎
https://cran.r-project.org/web/packages/NbClust/NbClust.pdf.↩︎
Appendix
Appendix A: Conceptualization Details
Appendix A.1: Hofstede cultural dimensions & Schwartz BVT values
- Power-Distance (PDI): High-PDI cultures prescribe decision-making power to be concentrated in the hands of figures of authority rather than to be distributed equally across the members of a society as in the case of low-PDI cultures (Hofstede et al. 2012). High-PDI cultures are designed around aristocratic principles that promote social exclusivity. Hence, individual value systems within high-PDI cultures will be biased towards ascribing a high importance to the Power value of Schwartz which is characterized by a motivation to pursue and obtain a high-ranked social status and proprietary control over resources and decision-making power (Schwartz 2012). Moreover, high-PDI cultures promote values of obedience, and discipline, which corresponds to the Conformity & Tradition value of Schwartz (Vanhée & Dignum 2018). Therefore, the \(DCC^+\) of the Power and Conformity & Tradition values is PDI. Conversely, PDI constitutes the \(DCC^-\) of Universalism (see Table 1). This is because Universalism is concerned with promoting egalitarianism (Schwartz 1994).
- Masculinity (MAS): High-MAS cultures are organized around meritocratic principles and prescribe assertiveness, mastery, toughness and competition (Hofstede et al. 2012; Vanhée & Dignum 2018). Low-MAS cultures are characterized by promoting consensus-building, compromise, modesty, compassion and social equality (Hofstede et al. 2012; Vanhée & Dignum 2018). Based on these characteristics it is proposed that individuals in high-MAS (vs low-MAS) societies tend to value Achievement and Power. This is because Achievement promotes the acquisition of prestige through the display of ability and success, and Power endorses the importance of striving for high social status and acquiring positions of power. Conversely, high-MAS societies suppress the valuation of Benevolence and Universalism since these two values combine to promote cooperation and social equality (Schwartz 1994). MAS therefore constitutes the \(DCC^+\) of the Achievement and Power values and the \(DCC^-\) of Benevolence and Universalism (see Table 1).
- Uncertainty Avoidance Index (UAI): The UAI-HCD is about how societies cope with the unknowable (Hofstede et al. 2012). High-UAI cultures are intolerant and/or dismissive of things that challenge the status quo. High-UAI cultures tend to have strict rules and rituals that suppress change by enhancing predictability and order (Hofstede et al. 2012). On the contrary, low-UAI cultures promote curiosity, exploration and experimentation (Hofstede et al. 2012). It is hypothesized that the Security and Stimulation values are the ones most closely related to the UAI-HCD. People that value Security seek to promote stability, order and safety (Schwartz 1994). People that value Stimulation find it important to live a life that is exciting and loaded with novel experiences. High-UAI societies are therefore presumed to promote Security and demote Stimulation. Thus, UAI forms the \(DCC^+\) of Security and the \(DCC^-\) of Stimulation.
- Long-Term Orientation (LTO): This dimension is about the extent to which a society looks forward to the future rather than resorting to the past to solve problems (Hofstede et al. 2012). High-LTO cultures promote planning, foresight and perseverance (Hofstede et al. 2012). Low-LTO cultures, on the other hand, prescribe time-honoured traditions and are suspicious of societal change. Stability is important to low-LTO societies, leading them to stick to conventions that uphold the status quo. With regard to the LTO-HCD, it seems that the value Conformity & Tradition is most relevant. People that value Conformity & Tradition find it important to obey to social norms, to respect a society’s traditions and orient oneself to the past to obtain the information to deal with problems occurring in the present and future (Schwartz 1994). Based on these descriptions, it is hypothesized that low-LTO cultures promote the valuation of Conformity & Tradition, whereas high-LTO societies will tend to suppress the importance ascribed to this value. The LTO-HCD therefore forms the \(DCC^-\) of Conformity & Tradition.
- Individualism (IDV): This dimension is essentially about affiliation (Hofstede et al. 2012). Low-IDV societies view humans as fixed members of a single well-defined group in which all members are interdependent (Hofstede 2020). Low-IDV cultures promote loyalty, harmony and a general promotion of the collective over the individual. In contrast, high-IDV societies promote self-sufficiency, self-actualization and self-expression (Hofstede et al. 2012). We propose that the Self-Direction and Conformity & Tradition values relate most closely to the IDV-HCD. Self-Direction is concerned with the valuation of individual freedom, independent thought and autonomy. It is hypothesized that people in high-IDV societies will tend to ascribe high importance to Self-Direction. On the contrary, high-IDV cultures will demote Conformity & Tradition, since this value prescribes the restraint of individual freedom for the sake of the collective. Thus, IDV forms the \(DCC^+\) of Self-Direction and the \(DCC^-\) of Conformity & Tradition.
- Indulgence (IVR): High-IVR societies allow a relatively free gratification of basic and natural human drives related to enjoying life and having fun (Hofstede 2020). Low-IVR cultures suppress instant gratification and promote tight regulation of individual behavior by means of strict social norms. We propose that the characteristics of high-IVR societies harmonize with the goals promoted by the Hedonism value. Hedonism prescribes pleasure and sensuous gratification for oneself (Schwartz 1994). Low-IVR societies, on the other hand, promote the value of Conformity & Tradition as it prescribes self-restraint and discipline. The IVR-HCD therefore constitutes the \(DCC^+\) of Hedonism and the \(DCC^-\) of Conformity & Tradition.
Appendix A.2: Description of activities
| Activity | Location | Age-Group | Type of Day (Time of Day) | Present in Activity Set? |
|---|---|---|---|---|
| Resting | Home | Youngsters, Students, Workers | Weekday & Weekend (Morning, Afternoon, Evening, Night) | Always |
| Relaxing | Public Leisure | Youngsters, Students, Workers | Weekday (Evening), Weekend (Morning, Afternoon, Evening) | Always |
| Retirees | Weekday & Weekend (Morning, Afternoon, Evening) | Always | ||
| Private Leisure | Youngsters, Students, Workers | Weekday (Evening), Weekend (Morning, Afternoon, Evening) | Always | |
| Retirees | Weekday & Weekend (Morning, Afternoon, Evening) | Always | ||
| Shopping | Essential Shop | Students, Workers | Weekday (Evening), Weekend (Morning, Afternoon, Evening) | Always |
| Retirees | Weekday & Weekend (Morning, Afternoon, Evening) | Always | ||
| Non-Essential Shop | Students, Workers | Weekday (Evening), Weekend (Morning, Afternoon, Evening) | Always | |
| Retirees | Weekday & Weekend (Morning, Afternoon, Evening) | Always | ||
| Learning | School | Youngsters | Weekday (Morning, Afternoon) | Always |
| University | Students, Workers | Weekday (Morning, Afternoon) | Always | |
| Home | Youngsters, Students | Weekday (Morning, Afternoon) | Always | |
| Working | Workplace | Workers | Weekday (Morning, Afternoon) | Always |
| Home | Workers | Weekday (Morning, Afternoon) | Always | |
| Getting tested | Hospital | Youngster, Students, Workers, Retirees | Weekday & Weekend (Morning, Afternoon, Evening, Night) | Can be removed from activity set when testing capacity is met |
| Getting treated | Hospital | Youngster, Students, Workers, Retirees | Weekday & Weekend (Morning, Afternoon, Evening, Night) | Can be removed from activity set when all hospital beds are taken |
Appendix A.3: Viral transmission
Agent interaction
The interactions between agents in our model take the form of discrete moments of contact between pairs of agents. All agents that are located in the same location at the same time come into contact with each other. The number of contacts (\(N\)) that takes place at a certain location (\(l\)) during a particular time-step (\(t\)) is therefore determined by Equation 4, where \(n\) is the size of the agent-set that is present at \(\langle l, t \rangle\), and \(r\) is the number of agents that are allowed to interact with each other during moments of contact. Note that \(r = 2\) because interactions are only allowed to take place between pairs of agents.
| \[ N_{l,t}=C(n,r)=\frac{n!}{(r!(n-r)!)}\] | \[(4)\] |
Each agent holds a personal list of locations (think of this as a ‘places-I-tend-to-visit’ list) from which they select, based on their needs, the places to visit over the course of a simulation. This list is randomly constructed for each agent upon the setup of a simulation. Moreover, the contents of the list do not change during a simulation. The list contains locations of various types; i.e., (non-) essential shops, public & private leisure places, and labor locations (working places, schools, universities, shops, hospitals). Agents whose lists overlap in terms of their content may come into contact with each other if they decide to visit the same location during the same time-step. Agents whose lists do not contain identical elements will never come into contact with each other. The size of the agent-set that an agent can potentially interact with is dependent on the agent/location ratio; the higher this ratio (i.e., the more agents relative to the number of locations) the higher the number of contacts that will take place during a simulation. If an interacting pair of agents happens to consist of one that is infected (a ‘carrier’) and one that is not (a ‘recipient’), then an infection can take place. Whether a contact results in the transmission of the virus from the carrier to the recipients depends on four different components: i) the contagiousness of the carrier, ii) the susceptibility of the recipient, iii) social distancing behavior of the recipient, and iv) the density factor of the location.
The contagiousness of the carrier from the moment that it was infected is modelled using a Gamma distribution which specifies how the contagiousness of a carrier develops as the disease progresses and is calibrated on the basis of findings presented by Ferretti et al. (2020). The susceptibility of agents is modelled after Hinch et al. (2020). Whether viral transmission takes place also depends on the social distancing behavior of the interacting agents. Whether agents are social distancing reduces the likelihood that a carrier infects a recipient: Appendix A.5 provides a detailed description of how social distancing is modelled. Lastly, the density-factor of a location is positively related to transmission of the virus. The density-factor of a location (which remains static over the course of a simulation) summarises how crowded, ventilated and sterile a particular location, on average, tends to be. Specifically, the higher the density-factor of a location the more crowded, the less ventilated and non-sterile it is.
Density factors for locations
Table 9 shows how the raw density-factors are determined for each location present within the model. The raw density-factors are subsequently fed into Equation 6 to compute the final density-factors for each location. These location-specific density-factors play an important role in the transmission of the virus; in general, the higher the density-factor of a location the more likely it is that infections take place at that particular location over the course of a simulation. Each location category is given a discrete score \([0, 0.5, 1]\) on four dimensions, a higher score on any of these dimension means that it contributes positively to the transmission potential of the virus at that location. Since dimensions differ in their relative influence on the transmission potential of the virus, they are allocated dimension-specific influence weights, denoted here as \(\omega\). The influence weights are calibrated as follows: \(\omega_{Dim1} = 4\), \(\omega_{Dim2} = 2\), \(\omega_{Dim3} = 1\), \(\omega_{Dim4} = 3\).
The first dimension (Dim1) indicates whether agents at a particular location are typically situated inside or outside, where 1 = inside, and 0 = outside. The second dimension (Dim2) represents the sterility of the environment; that is, whether the environment is cleaned rigorously and frequently, here 0 = yes, 0.5 = neutral, 1 = no. The third dimension (Dim3) relates to the typical length of an agent’s visit to the location in question, where 0 = short, 0.5 = medium and 1 = long. The fourth dimension (Dim4) relates to the typical degree of crowdedness at a particular location, where 0 = low, 0.5 = medium and 1 = high.
The raw density-factors (\(DF^{Raw}_{L}\)), where \(L\) functions as an index for Location type, are computed according to .
| \[ DF^{Raw}_{L}=\sum_{i=1}^{4}{\omega_{Dim_i}\cdot Dim_i}\] | \[(5)\] |
The final density-factors (\(DF^{Final}_{L}\)) are computed according to Equation 6 where the following condition holds \(0.01 \leq DF^{Final}_{L} \leq 0.9\).
| \[ DF^{Final}_{L}=\frac{DF^{Raw}_{L}}{\max[DF^{Raw}]}\] | \[(6)\] |
| ID | Location | Dim1 | Dim2 | Dim3 | Dim4 | \(DF^{Raw}\) | \(DF^{Final}\) |
|---|---|---|---|---|---|---|---|
| 1 | Hospital | 1 | 0 | 1 | 0 | 5 | 0.5 |
| 2 | Workplace | 1 | 0.5 | 1 | 0.5 | 7.5 | 0.75 |
| 3 | School | 1 | 1 | 1 | 0.5 | 8.5 | 0.85 |
| 4 | Home | 1 | 1 | 1 | 1 | 10 | 0.9 |
| 5 | Private-Leisure | 1 | 1 | 1 | 1 | 10 | 0.9 |
| 6 | Public-Leisure | 0 | 0 | 1 | 0 | 1 | 0.1 |
| 7 | University | 1 | 0.5 | 1 | 0.5 | 7.5 | 0.75 |
| 8 | Essential Shops | 1 | 1 | 0 | 1 | 9 | 0.9 |
| 9 | Non-Essential Shops | 1 | 1 | 0 | 1 | 9 | 0.9 |
| 10 | Walking Outside | 0 | 0 | 0 | 0 | 0 | 0.01 |
| 11 | Queuing | 0 | 0 | 0 | 1 | 3 | 0.3 |
| 12 | Public Transport | 1 | 1 | 0.5 | 1 | 9.5 | 0.9 |
Appendix A.4: Description of needs
| Need | Description |
|---|---|
| Health | Health is modelled as the urgency to stay at home when experiencing mild symptoms \(\langle Rest, Home \rangle\) and going to the hospital whenever experiencing critical symptoms \(\langle Get Treated, Hospital \rangle\). |
| Sleep | Sleep is modelled as the urgency to relax after a long day at work: \(\langle Relax, Home \rangle\), or to rest in bed during the night: \(\langle Rest, Home \rangle\). |
| Food Safety | This need encompasses the desire to possess over enough provisions to feed the members of one’s household for a period of two weeks. The activity related to food safety is: \(\langle Shopping, Essential Shop \rangle\). This action cannot be performed by youngsters as it is assumed that only parents are responsible for ensuring the availability of a sufficient amount of food at home. |
| Financial Survival | includes the desire to have sufficient financial resources to provide one’s household with the essential provisions needed to survive. The satisfaction level of this need decreases when agents perform the following activities:\(\langle Shopping, Essential Shop\rangle\), \(\langle Shopping, Non Essential Shop\rangle\). The satisfaction level of this need is replenished when agents go to work or receive social support payments from the government. |
| Risk Avoidance | This need relates to the desire to avoid situations that threatens one’s well-being (e.g. avoiding contamination with the virus, getting treated when sick). Risk avoidance is also related to the crowdedness of locations where activities may be performed. Performing activities in crowded locations without conforming to social distancing will result in lower satisfaction gains for risk avoidance. Conforming to social distancing and/or self-isolation, avoiding crowded locations and/or getting treated at the hospital will all result in higher satisfaction gains for risk avoidance. |
| Compliance | This need involves the desire to behave in a way that is prescribed by authorities (i.e., government, parents, employers). For youngsters, students and workers, the satisfaction level of compliance is increased by working and/or studying, and/or complying with actively enforced behavioral measures. Not working, studying or complying with behavioral measures results in diminished satisfaction gains or penalties for compliance. |
| Conformity | This need relates to the desire to feel accepted and recognized by the peers in one’s social network (i.e., friends, family, colleagues). Conformity is modelled such that engaging in the same activities as those performed by one’s social peers will result in higher satisfaction gains. With regard to social peers, a distinction is made between colleagues and friends & family. During time-steps in which agents work or study, the social reference group consists only of colleagues or fellow students. During non-working hours, the reference group consists of friends and family. |
| Financial Stability | This need involves the desire to acquire a stable financial status. Agents compare their current amount of capital with the target amount of capital they need to live a comfortable live. Whenever the current amount of a capital drops below the target amount of capital, individuals will experience a decrease in the satisfaction level of financial stability when spending capital. Increasing the satisfaction level of one’s financial stability is done through working. |
| Belonging | This need expresses the desire to feel connected with significant others. Agents increase the satisfaction of this need by being near friends or family whilst performing activities. Social distancing reduces the potential satisfaction that can be gained from being with peers as it prohibits agents from being physically close to one another. |
| Leisure | This need relates to the desire to exercise or relax during non-working hours. Within the model the need for leisure can be satisfied by relaxing at home or at private and/or public leisure places. |
| Luxury | This need expresses the desire to buy and possess non-essential goods. The need for luxury can be satisfied by purchasing non-essential items in non-essential shops: i.e., \(\langle Shopping, Non Essential Shop\rangle\). |
| Autonomy | This need involves the desire to be in control of one’s decisions. Autonomy is modelled such that anything restricting the ability of agents to freely choose their activities will result in a loss of satisfaction. The satisfaction level of this need increases when agents are able to choose the activities that they find most appealing. |
Appendix A.5: Social distancing
Once the social distancing measure becomes activated, agents are offered the choice to either engage in social distancing while performing their daily activities or not. Specifically, the moment an agent decides to perform a particular activity, it simultaneously reflects upon whether it will perform the activity in such a way so that it conforms to the rule of social distancing. This involves putting in effort to maintain a safe physical distance from other agents carrying out the same activity at the same location. Engaging in social distancing leads to a lower contamination risk, but it also lowers the frequency and quality of interpersonal contact. Humans are social creatures that seek to be meaningfully connected to others; maintaining a strict physical distance from others makes it more difficult to establish such connections. Thus, choosing to engage in social distancing also comes at a cost to one’s psychological well-being.
We propose that agents differ in how they perceive the trade-off between the positive and negative pay-offs presented by choosing to engage in social distancing or not. That is, some agents may find that the physical proximity of their friends outweighs the increased risk of becoming infected, while other agents find the health risks of close interpersonal contact too great to not engage in social distancing. We implement these agent-specific valuations of social distancing by assigning each of them a particular social-distancing-profile (SDP). An agent’s social-distancing-profile dictates the degree to which it feels the urge to be in close physical contact with other agents. It is presumed that agents that are (highly) extrovert will have more difficulty maintaining physical distance from their friends and family (Park 2015). It is shown that one’s personality type and the structure of one’s value system are closely related to one another (Roccas et al. 2002). On this basis, we propose that agents that ascribe a relatively high importance to Achievement, Stimulation and Hedonism will be extrovert, whereas agents scoring high on Conformity & Tradition and Security are introvert (Roccas et al. 2002). Agent social-distancing-profiles are drawn from a normal distribution with a mean that is higher for extroverts than for introverts. The standard-deviation used is set by the global parameter std-dev-social-distancing-profile, which is denoted as \(\sigma[SDP]\) and is set to 0.1 by default. Agent SDP’s are capped to fall within a range of \([0,1]\).
Agents with a relatively low SDP experience higher satisfaction gains from engaging in their activities whilst complying to social distancing measures than agents with a relative high SDP. This implies that low-SDP agents will tend to engage in social distancing more often than high-SDP agents. Note that an agent’s decision to engage in social distancing or not is also dependent upon the status of its needs’ satisfaction levels at a current time-step \(t\). For instance, critically low levels of Belonging and/or Autonomy may incite an agent to elicit a preference for not engaging in social distancing. Thus, the SDP of an agent represents a static proclivity to (dis)obey to the measure of social distancing. The status of its needs induce a dynamic component to the decision to comply to social distancing.
The decrease in P(Y infects X) due to X engaging in social distancing, i.e., P(Y infects X | Xsocial-distancing-status = Active) < P(Y infects X | Xsocial-distancing-status = Not active), is modulated by the global parameter social-distancing-factor. The lower the setting of the social-distancing-factor, the stronger the decrease in the probability of becoming infected (or infecting someone else) upon engaging in social distancing.
Appendix B: Implementation Details
Appendix B.1: Structural properties of agent value systems
We define a set of \(Values = \{ V_1 \ldots V_9 \}\), where V1 = Hedonism (HED), V2 = Stimulation (STM), V3 = Self-Direction (SD), V4 = Universalism (UNI), V5 = Benevolence (BEN), V6 = Conformity & Tradition (CT)4, V7 = Security (SEC), V8 = Power (POW), and V9 = Achievement (ACH). The second set relevant to this procedure contains the importance levels (\(Val_i\)) tied to each value (\(V_i\)). Suppose we define a function (\(f\)) that takes as an input the value index \(v\) and outputs the importance level of that value such that \(Val_i = f(V_i)\). If \(Val_i\) = 100, then the agent in question will ascribe maximum priority to satisfying needs related to the fulfillment of \(V_i\). If \(Val_i\) = 0, then the fulfillment of \(V_i\) is assigned the lowest possible priority by an agent during decision-making.
The following condition ensures that any two instances of \(Values\) whose indices are sufficiently close to one another hold similar importance levels: \(0\leq|Val_i-Val_j|\leq UB_{i,j}\), \(\forall i,j \in \{1 \ldots 9\}\). Where \(UB_{i,j}\) serves as an upper boundary to the dissimilarity between the importance levels of \(V_i\) and \(V_j\) (see Equation 7). This way, values placed close to one another within the circumplex will be constrained in their dissimilarity (i.e., their importance levels will be similar), whereas values placed further apart will be less constrained in their dissimilarity. Parameter \(c\) in Equation 7 is an integer ranging from \([1,100]\).
By default, the \(c\) parameter is set to 20 as testing pointed out that this lead to a desirable re-calibration of value systems.
| \[ UB_{i,j} = \begin{cases} |i-j|*c & \text{if $|i-j| \leq 5$} \\ (9-|i-j|)*c & \text{if $|i-j| > 5$} \end{cases}\] | \[(7)\] |
Figure 14 visualizes how values placed close to one another on the Schwartz circumplex are positively correlated (as indicated by the green bidirectional arrows). Values that are placed further apart - e.g. on opposites sides of the circular structure - are negatively correlated (as visualized using red bidirectional arrows).
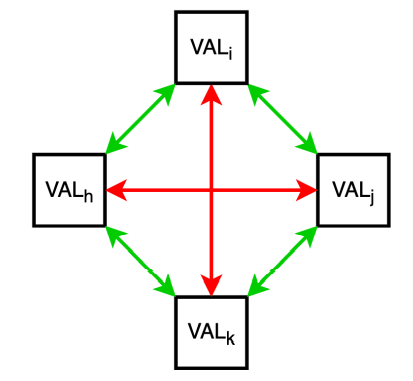
The global parameter influence-of-age-on-value-system modulates the strength of the age-dependent transformation; it is set to 5 by default. The age-group dependent weights are denoted as \(\omega_{Age}\), and the value-specific coefficients are symbolized as \(C_i\). The re-calibrated value importance levels (\(Val_i^\prime\)) are computed by applying Equation 8 where \(\forall Age \in AgeGroups\) and \(\forall i \in \{1 \ldots 9\}\), and \(AgeGroups = \{Young, Student, Worker, Retired\}\).
| \[ Val_i^\prime = Val_i - (C_i \cdot \omega_{Age})\] | \[(8)\] |
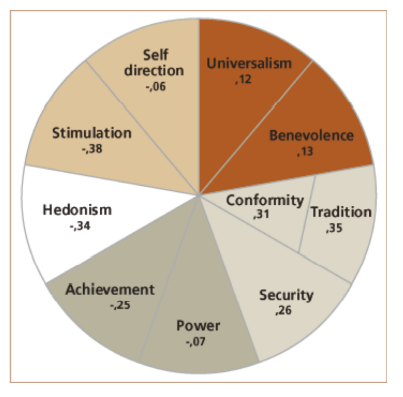
Appendix B.2: Computing satisfaction gains of activities
An activity’s total satisfaction gain, i.e., \(TSG(A)\), is computed as the sum of the ‘discounted expected satisfaction gains’ (\(eSG^\prime\)) of that activity for all of the agent’s needs (\(n\)) (see Equation 9).
| \[ TSG(A) = \sum_{n=1}^{12}eSG_n^\prime(A)\] | \[(9)\] |
A distinction is made between four different types of satisfaction gains, namely: expected vs actual and undiscounted vs discounted; Table 11 presents a quadrant that shows how these various satisfaction gains relate to one another. Undiscounted Satisfaction Gains (\(SG\)) can be conceived of as ‘raw’ estimates of the satisfaction potential of an activity. A \(SG\) is used to compute a Discounted Satisfaction Gain (\(SG^\prime\)) by incorporating information about the urgency status of an agent’s needs (see Equations 10 and 11). Expected Satisfaction Gains (\(eSG(A)\)) are those the agent expects to incur before performing an activity, whereas the Actual Satisfaction Gains (\(aSG(A)\)) represent the satisfaction gained from an activity after it has occurred (Equation 13). Often times \(eSG_n(A) = aSG_n(A)\), but this need not always be the case. For instance, when an agent decides to go shopping for groceries, it expects to be able to buy all that it needs and bases its \(eSG_n\) for that activity on that assumption. However, when shops are under-stocked, the agent in question may not be able to buy all that it intended to do, resulting in a situation where \(eSG_n(A) > aSG_n(A)\). The discrepancy between \(eSG_n(A)\) and \(aSG_n(A)\) is denoted by \(\epsilon\), which represents the error in an agent’s expectations (see Equation 13).
| Satisfaction Gains | Expected | Actual |
|---|---|---|
| Undiscounted | \(eSG(A)\) = raw satisfaction gained from performing an activity. | \(aSG(A)\) = the raw actual satisfaction gained from performing an activity (generally the same as \(eSG(A)\)). |
| Discounted | \(eSG^\prime(A)\) = the satisfaction gained from an activity weighted by the urgency of the need(s) addressed by that particular activity. | \(aSG^\prime(A)\) = the actual satisfaction gained from performing an activity corrected for mistakes in agent’s expectations. |
Assume a function (\(\tau\)) is defined that takes as input an activity (\(A\)) and returns the \(eSG\) for each of the agent’s needs (\(n\)); \(\tau(A) : Activity \rightarrow eSG_n\). Each \(eSG_n(A)\) is then multiplied by the urgency of that need (\(Urgency_n\)) to obtain \(eSG_n^\prime(A)\) (see Equation 11). As can be seen in Equation 10, the urgency of a need is a function of that need’s satisfaction level (\(SatLevel^t_n\)) and priority-weight (\(\omega_n\)). Note that \(SatLevel^t_n\) varies over time, whereas \(\omega_n\) remains static over the course of a simulation. This implies that needs with a high urgency will have a relatively large influence on the action that is selected by an agent during decision-making. Thus, the activities that are most likely to be picked from \(Activities\) during decision-making are those that present a satisfaction gain for needs that are ascribed a high priority-weight and whose satisfaction levels are depleted.
| \[ Urgency^t_n = \omega_n \cdot (1 - SatLevel^t_n)\] | \[(10)\] |
| \[ eSG_n^\prime(A) = \tau(A) \cdot (\omega_n \cdot Urgency^t_n)\] | \[(11)\] |
As time passes, the satisfaction level of needs diminishes until one of them reaches a status of depletion that becomes so critical that it comes to dominate the decision-making process. The magnitude by which \(SatLevel_n\) decreases is modulated by the decay rate, which is denoted as \(r\) and is subject to the condition: \(r < 1\). The decay rate is static but differs across needs, hence it is denoted as \(r_n\). Some needs are depleted faster than others as to ensure agents display natural looking behavior; such as going to bed every night or shopping for food regularly. Note that the multiplicative effect of the decay rate in Equation 12 leads full water tanks to leak relatively higher quantities of satisfaction than emptier tanks.
| \[ SatLevel^t_n=(r \cdot SatLevel^{t-1}_n) + aSG_n^\prime(A)\] | \[(12)\] |
| \[ aSG_n^\prime(A) = eSG_n^\prime(A) \cdot \epsilon\] | \[(13)\] |
Appendix C: Model Experimentation and Parameterization
Appendix C.1: Description of cluster analysis
Clusters are determined by applying the ‘K-means clustering’ technique which is one of the most commonly used unsupervised machine learning algorithms for partitioning a given data set into a set of \(k\) groups (i.e., \(k\) clusters), where \(k\) represents the number of groups prespecified by the researcher. The algorithm groups data together so as to ensure that countries within clusters are as similar as possible (i.e., high intra-cluster similarity) and countries across clusters are as dissimilar as possible (i.e., low inter-cluster similarity). (Appendix C.1) shows which countries are grouped together in each of the cultural blocs.
To determine the number of clusters to extract from the data, we apply the NbClust package5 in R. This package provides 30 indices for determining the optimal number of clusters and proposes the best clustering scheme from the different results obtained by varying all combinations of number of clusters, distance measures, and clustering methods. In doing so, we find that the optimal number of clusters is 5 with a score of 8 out of 30. The 5 clusters are depicted in Figure 16.
In K-means clustering, each cluster is represented by its center (i.e, the centroid) which corresponds to the mean of all data points assigned to a particular cluster. As the dimensionality of the data is determined by the number of Hofstede dimensions, each cluster is defined by a 6-dimensional centroid. This centroid represents the cultural profile of a particular bloc (see Table 12). Note that we add a bloc termed ‘Neutral’ as a baseline reference point. This bloc helps us to assess how the other blocs (A to E) affect the model’s behavior in comparison to a situation where all cultural parameters are calibrated to a neutral setting.
| Cultural Bloc | PDI | IDV | MAS | UAI | LTO | IVR |
|---|---|---|---|---|---|---|
| A | 32.09 | 77.82 | 39.64 | 43.45 | 38.09 | 67.64 |
| B | 82.90 | 27.70 | 59.20 | 37.60 | 58.20 | 33.30 |
| C | 67.39 | 34.70 | 43.17 | 83.57 | 40.17 | 39.48 |
| D | 69.83 | 18.33 | 58.33 | 73.50 | 15.83 | 87.83 |
| E | 46.93 | 58.73 | 54.27 | 73.87 | 75.27 | 39.00 |
| Neutral | 50 | 50 | 50 | 50 | 50 | 50 |
| Lowest rank | A | D | A | B | D | B |
| Highest Rank | B | A | B | C | E | D |
| Mean | 58.19 | 44.55 | 50.77 | 60.33 | 46.26 | 52.88 |
| St.Dev. | 18.47 | 21.94 | 8.03 | 19.00 | 20.14 | 20.99 |
| Country | PDI | IDV | MAS | UAI | LTO | IVR | Cultural Bloc |
|---|---|---|---|---|---|---|---|
| Australia | 38 | 90 | 61 | 51 | 21 | 71 | A |
| Canada | 39 | 80 | 52 | 48 | 36 | 68 | A |
| Denmark | 18 | 74 | 16 | 23 | 35 | 70 | A |
| Finland | 33 | 63 | 26 | 59 | 38 | 57 | A |
| Great Britain | 35 | 89 | 66 | 35 | 51 | 69 | A |
| Ireland | 28 | 70 | 68 | 35 | 24 | 65 | A |
| Netherlands | 38 | 80 | 14 | 53 | 67 | 68 | A |
| New Zealand | 22 | 79 | 58 | 49 | 33 | 75 | A |
| Norway | 31 | 69 | 8 | 50 | 35 | 55 | A |
| Sweden | 31 | 71 | 5 | 29 | 53 | 78 | A |
| U.S.A. | 40 | 91 | 62 | 46 | 26 | 68 | A |
| Country | PDI | IDV | MAS | UAI | LTO | IVR | Cultural Bloc |
|---|---|---|---|---|---|---|---|
| Bangladesh | 80 | 20 | 55 | 60 | 47 | 20 | B |
| China | 80 | 20 | 66 | 30 | 87 | 24 | B |
| Hong Kong | 68 | 25 | 57 | 29 | 61 | 17 | B |
| India | 77 | 48 | 56 | 40 | 51 | 26 | B |
| Indonesia | 78 | 14 | 46 | 48 | 62 | 38 | B |
| Malaysia | 104 | 26 | 50 | 36 | 41 | 57 | B |
| Philippines | 94 | 32 | 64 | 44 | 27 | 42 | B |
| Singapore | 74 | 20 | 48 | 8 | 72 | 46 | B |
| Slovak Rep | 104 | 52 | 110 | 51 | 77 | 28 | B |
| Vietnam | 70 | 20 | 40 | 30 | 57 | 35 | B |
| Country | PDI | IDV | MAS | UAI | LTO | IVR | Cultural Bloc |
|---|---|---|---|---|---|---|---|
| Africa East | 64 | 27 | 41 | 52 | 32 | 40 | C |
| Arab countries | 80 | 38 | 53 | 68 | 23 | 34 | C |
| Argentina | 49 | 46 | 56 | 86 | 20 | 62 | C |
| Brazil | 69 | 38 | 49 | 76 | 44 | 59 | C |
| Bulgaria | 70 | 30 | 40 | 85 | 69 | 16 | C |
| Chile | 63 | 23 | 28 | 86 | 31 | 68 | C |
| Croatia | 73 | 33 | 40 | 80 | 58 | 33 | C |
| Greece | 60 | 35 | 57 | 112 | 45 | 50 | C |
| Iran | 58 | 41 | 43 | 59 | 14 | 40 | C |
| Malta | 56 | 59 | 47 | 96 | 47 | 66 | C |
| Morocco | 70 | 46 | 53 | 68 | 14 | 25 | C |
| Pakistan | 55 | 14 | 50 | 70 | 50 | 0 | C |
| Peru | 64 | 16 | 42 | 87 | 25 | 46 | C |
| Poland | 68 | 60 | 64 | 93 | 38 | 29 | C |
| Portugal | 63 | 27 | 31 | 104 | 28 | 33 | C |
| Romania | 90 | 30 | 42 | 90 | 52 | 20 | C |
| Russia | 93 | 39 | 36 | 95 | 81 | 20 | C |
| Serbia | 86 | 25 | 43 | 92 | 52 | 28 | C |
| Slovenia | 71 | 27 | 19 | 88 | 49 | 48 | C |
| Spain | 57 | 51 | 42 | 86 | 48 | 44 | C |
| Thailand | 64 | 20 | 34 | 64 | 32 | 45 | C |
| Turkey | 66 | 37 | 45 | 85 | 46 | 49 | C |
| Uruguay | 61 | 36 | 38 | 100 | 26 | 53 | C |
| Country | PDI | IDV | MAS | UAI | LTO | IVR | Cultural Bloc |
|---|---|---|---|---|---|---|---|
| Africa West | 77 | 20 | 46 | 54 | 9 | 78 | D |
| Colombia | 67 | 13 | 64 | 80 | 13 | 83 | D |
| El Salvador | 66 | 19 | 40 | 94 | 20 | 89 | D |
| Mexico | 81 | 30 | 69 | 82 | 24 | 97 | D |
| Trinidad and Tobago | 47 | 16 | 58 | 55 | 13 | 80 | D |
| Venezuela | 81 | 12 | 73 | 76 | 16 | 100 | D |
| Country | PDI | IDV | MAS | UAI | LTO | IVR | Cultural Bloc |
|---|---|---|---|---|---|---|---|
| Austria | 11 | 55 | 79 | 70 | 60 | 63 | E |
| Belgium | 65 | 75 | 54 | 94 | 82 | 57 | E |
| Czech Rep | 57 | 58 | 57 | 74 | 70 | 29 | E |
| Estonia | 40 | 60 | 30 | 60 | 82 | 16 | E |
| France | 68 | 71 | 43 | 86 | 63 | 48 | E |
| Germany | 35 | 67 | 66 | 65 | 83 | 40 | E |
| Hungary | 46 | 80 | 88 | 82 | 58 | 31 | E |
| Italy | 50 | 76 | 70 | 75 | 61 | 30 | E |
| Japan | 54 | 46 | 95 | 92 | 88 | 42 | E |
| Korea South | 60 | 18 | 39 | 85 | 100 | 29 | E |
| Latvia | 44 | 70 | 9 | 63 | 69 | 13 | E |
| Lithuania | 42 | 60 | 19 | 65 | 82 | 16 | E |
| Luxembourg | 40 | 60 | 50 | 70 | 64 | 56 | E |
| Switzerland | 34 | 68 | 70 | 58 | 74 | 66 | E |
| Taiwan | 58 | 17 | 45 | 69 | 93 | 49 | E |
Appendix C.2: Distribution of values across cultural blocs
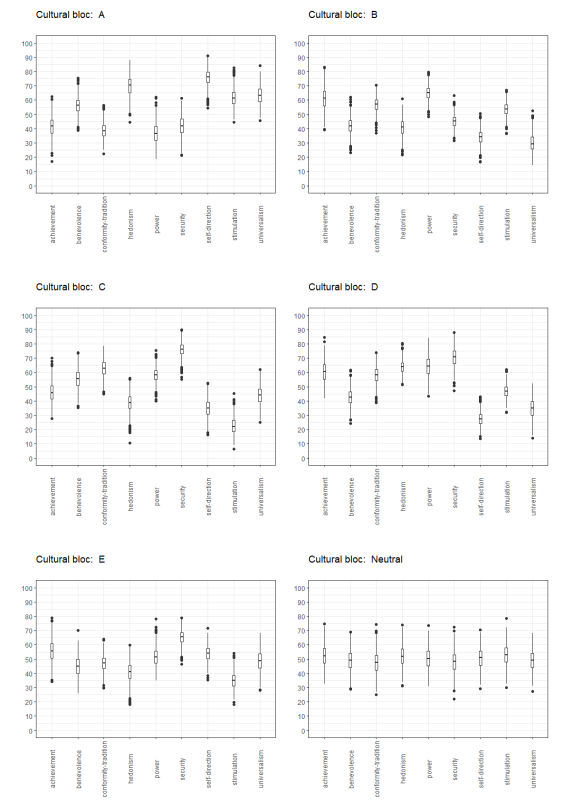
Appendix C.3: Description of model parameters
The ASSOCC model consists of several modules. The focus of this paper lies on the culturally-extended version of the model. The parameters contained within the cultural sub-model can be classified as core or ancillary. Core parameters are those that are manipulated in model experimentation (see Table 19), whereas ancillary parameters exist to ensure that the model functions properly (see Table 20). With regard to the core parameters, the ‘cultural’ category contains the HCDs and cultural consensus parameters (marked with thick boundary in Figure 18), and the ‘non-cultural’ category relates to those parameters that are included in model experimentation but do not play a focal role in current model experiments.
| Model Parameter | Default Setting [Range] | Description |
|---|---|---|
| CULTURAL-BLOC | A, B, C, D, E, Neutral | This categorical parameter specifies which cultural bloc is selected for an execution of the model. Each cultural bloc has its own Hofstede cultural profile which, when selected, is used to calibrate the Hofstede dimension variables in the model. |
| COUNTRY-HOFSTEDE-SCORES | "Custom" | This categorical parameter specifies which country-based Hofstede Cultural Dimension scores are to be loaded into the model. |
| VALUE-SYSTEM-CALIBRATION-FACTOR | 20 [0,40] | This continuous parameter determines the degree to which agent-level value systems are re-calibrated according to the inter-value relationships specified in the Schwartz circumplex model (Schwartz 2012). Increasing this parameter leads mutualistic values to obtain more similar importance levels and antagonistic values to beget more dissimilar importance levels. The default setting for this parameter was set on the basis of a sensitivity analysis. |
| INFLUENCE-OF-AGE-ON-VALUES | 5 | This continuous parameter determines the magnitude of the differences between age-groups in terms of the structural properties of agents’ value systems. Increasing this parameter leads to bigger differences in the value systems of agents belonging to different age-groups. The default setting for this parameter was set on the basis of a sensitivity analysis. |
| HOFSTEDE-SCHWARTZ-MAPPING-MODE | "Theoretical" | This categorical parameter specifies the mode by which HCDs are mapped onto the Schwartz BVT Values. By default, all hypothesized linkages are included within the specification of agent values. |
| Model Parameter | Default Setting [Range] | Description |
|---|---|---|
| contagion-factor | 5 [1,20] | This continuous parameter models the contagiousness of the virus. It modulates the likelihood that the virus is transmitted during social interaction. Turning this parameter up leads to a more infectious virus. The calibration of this parameter is done on the basis of a sensitivity analysis. |
| social-distancing-factor | 0.3 [0,1] | This continuous parameter modulates the effect that social distancing has on the contagiousness of the virus. Turning this parameter down dampens the contagiousness of the virus when an agent is engaging in social distancing. The default setting for this parameter is determined on the basis of a sensitivity analysis. |
| friend-links | 7 | This parameter determines the number of friends selected from the set of potential friend links by agents upon setup of the model. It is set to 7 by default since we presume that people tend to have, on average, 7 friends. |
| random-links | 0.15 | This parameter determines the proportion of agents that randomly links up with another agent within the social network. Its default setting was set via a series of unit tests making sure that it produces a network topology that displays wide bridges between clusters of agents. |
| country-hofstede-scores | "Custom" | This categorical parameter specifies which country-based Hofstede Cultural Dimension scores are to be loaded into the model. |
| country-demographic-settings | "Custom" | This categorical parameter specifies the country-level demographic data to be loaded into the model. Demographic data includes distribution of age-groups, distribution of households (e.g. persons per household, number of households segmented by household types), workforce characteristics (e.g. employment segmented by various occupations) and transportation modality (e.g. usage of transport segmented by various transportation modes). |
| Model Parameter | Default Setting [Range] | Description |
|---|---|---|
| initial-active-measures-trigger | 0.02 [0, 1] | This continuous parameter specifies the infection rate at which the ‘active measures’ phase is triggered for the first time. |
| active-measures-trigger | 0.08 [0, 1] | This continuous parameter specifies the infection rate at which the ‘active measures’ phase is triggered for the Nth time. |
| active-measures-lifter | 0.04 [0, 1] | This continuous parameter specifies the infection rate at which the ‘active measures’ phase is lifted. When the ‘active measures’ stage is lifted, the ‘passive measures’ phase is automatically triggered. |
| stdev-social-distancing-profile | 10 [0,25] | This continuous parameter modulates the variance in social distancing profiles. Increasing this parameter leads to more variability in social distancing profiles and therefore in agent’s decisions to comply or not to social distancing. The default setting for this parameter was set on the basis of a sensitivity analysis. |
| maslow-multiplier | 0 [0,2] | This continuous parameter modulates the degree to which the priority of needs are ordered according to the one posited by the Maslow HON theory. Increasing this parameter leads to a more pronounced hierarchical ordering. This parameter is deactivated by default. |
| survival-multiplier | 2.5 [0,5] | This continuous parameter regulates the priority assigned to the needs included in the Survival category. Dialing up this parameter leads agents to assign increasing levels of priority to fulfilling their physiological needs. The default setting for this parameter was set on the basis of a sensitivity analysis. |
Appendix C.4: Global sensitivity analysis
Time-dependent Sobol variance decomposition
Variance-based GSA partitions the variance (\(V\)) of model output (\(Y\)) that is attributed to changes in \(k\) factors represented individually as \(V_i\) and in combinations with an increasing level of dimensionality (Ligmann-Zielinska & Sun 2010) (see Equation 14). For instance, \(V_{ij}\) represents the sensitivity of model outputs to the interaction between factors \(X_i\) and \(X_j\).
| \[ V=\sum_{i}^{}V_i+\sum_{i<j}^{}V_{ij}+\ldots+\sum_{i<\ldots<k}^{}V_{i<\ldots<k}\] | \[(14)\] |
These variance statistics are used to compute first-order (\(Si\)) indices for every factor (see Equation 15). An \(Si\) quantifies the partial contribution of a factor to the variance in \(Y\) independently from the other \(k-1\) factors (Ligmann-Zielinska & Sun 2010). The higher the \(Si\) of a factor relative to others, the more influential it is in determining a model’s behaviour. The numerator in Equation 15 can be interpreted as follows: it is the variance (\(V\)) in the expected value of \(Y\) conditional upon \(X_i\) which is denoted as \(E(Y|X_i)\). An instance of \(E(Y|X_i=x_i)\), where \(x_i\) represents a particular setting of \(X_i\), is computed by varying all factors but \(X_i\) (\(X_{\sim i}\)) and computing the average value for \(Y\) across the drawn samples of \(X_{\sim i}\). This procedure is repeated many times for many unique settings of \(X_i\) so that at some point we obtain a credible estimate of \(V_{X_i}[E_{X_\sim i}(Y|X_i)]\).
| \[ S_i=\frac{V_i}{V}=\frac{V_{X_i}[E_{X_\sim i}(Y|X_i)]}{V(Y)}\] | \[(15)\] |
We compute a \(Si\) statistic for each factor \(k\) for each time-step \(t\) of an executed model simulation. This approach is coined Time-Dependent Sobol Variance Decomposition (t-SVD) (Ligmann-Zielinska & Sun 2010). Note that the outcome of the sum of the \(Si\) of all factors corresponds to the percentage of output variability attributed to variability in the factors whilst treating them independently from one another. The remainder - that which makes the output variability sum up to 100% - is the proportion of output variance that must be attributed to the interactions among factors (Ligmann-Zielinska & Sun 2010). By applying t-SVD we gain a better understanding of how the sensitivity of the model to factor variability evolves over the course of a simulation.
Results of global sensitivity analysis
The t-SVD is executed by drawing a large number of random samples of factor settings from the factor space. The samples are drawn using Latin Hypercube Sampling (LHS) (van Dam et al. 2012). Factor settings are sampled using a uniform probability distribution as to avoid imposing unnecessary restrictions on the sampling process. The selection of factors included in the GSA is limited to the ‘non-cultural’ (denoted as \(X^\prime_i\)) and ‘ancillary’ (symbolized as \(X^{\prime\prime}_i\)) parameters that fall within the scope of the cultural model (for an overview of model parameters, see Table 19 and Table 20 in Appendix C.3). The factors and their sampling ranges are depicted in Table 21. Factor samples are fed into the model to execute simulations. The model’s sensitivity to a factor is then measured as the proportion of variance in model outputs that can be attributed to changes (i.e., variance) in that factor (Ligmann-Zielinska et al. 2014; ten Broeke et al. 2016).
| ID | Factor | Default Value | Min | Max |
|---|---|---|---|---|
| \(X^\prime_1\) | contagion-factor | 10 | 5 | 15 |
| \(X^\prime_2\) | social-distancing-factor | 0.45 | 0.2 | 0.7 |
| \(X^{\prime\prime}_1\) | std-dev-social-distancing-profile | 0.1 | 0.05 | 0.15 |
| \(X^{\prime\prime}_2\) | min-random-value-generator | 20 | 20 | 40 |
| \(X^{\prime\prime}_3\) | max-random-value-generator | 60 | 60 | 80 |
| \(X^{\prime\prime}_4\) | survival-multiplier | 2.5 | 1.25 | 3.75 |
| \(X^{\prime\prime}_5\) | maslow-multiplier | 0 | 0 | 1 |
As can be seen in Figure 19, the model tends to produce three waves of infections under default model settings (see Appendix C.3 for an overview of default model settings). Figure 19 depicts the relative contribution of each factor to this emergent outcome over the course of a simulation. Notably, contagion-factor (\(X^\prime_1\)) and social-distancing-factor (\(X^\prime_2\)) are shown to have the greatest influence on the variability of infections. The influence of the \(X^{\prime\prime}_5\) seems to swell during the third wave of infections. The influence of \(X^{\prime\prime}_2\) and \(X^{\prime\prime}_3\) is negligible, which is desirable since the sole purpose of these parameters is to fill in the gaps left behind by unsupported ‘Hofstede-Schwartz linkages’ (see (???) Appendix E: Calibration of Model Parameters). The conclusion drawn on the basis of this GSA is that the parameters \(X^\prime_1\) and \(X^\prime_2\) are the most important non-cultural parameters within our model. The empirical calibration of these parameters would therefore have the strongest positive impact on the external validity of our model.
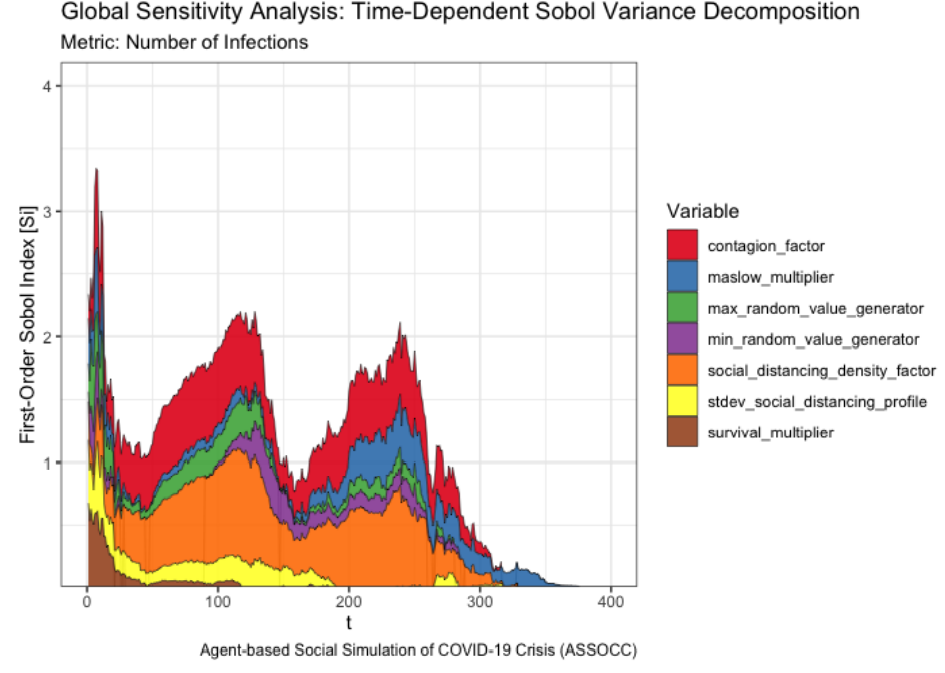
Appendix C.5: Coefficient of variation analysis
When running simulations one ought to be aware of the possible existence of ‘nuisance factors’ (Lorscheid et al. 2012). Nuisance factors are defined here as model inputs that are not classified as independent variables but that do affect model outcomes. Controllable nuisance factors, or control variables, are controlled for by fixing their settings during model experimentation. Uncontrollable nuisance factors, or noise factors, require a different approach. An example of a noise factor is the application of the pseudo-random number generator during simulation runs. The pseudo-random number generator enables the execution of stochastic process elements, but it also induces variability in the distribution of model outcomes corresponding to simulation runs with identical parameter settings. This undesirable variability is henceforth referred to as experimental error. To assess whether there exist other noise factors apart from the pseudo-random number generator, the model is run twice with identical parameter settings and with a fixed seed. Since the outcomes are identical, we conclude that the pseudo-random number generator constitutes the only noise factor in our model.
One way to come to grips with experimental error is to estimate its impact on the variance of model outputs (Lorscheid et al. 2012). Declaring that ‘a metric’s experimental error is large’ is the same as stating that the variability in the variance (\(\sigma^2\)) of a particular metric across identical simulation runs is high. In other words, experimental error occurs when the spread (i.e., standard-deviation) of a metric behaves erratically vis-à-vis a measure of its centrality (i.e., arithmetic mean) across identical simulation runs. Hence, the higher a metric’s experimental error, the higher the number of replicate simulations needed to obtain a meaningful estimation of the statistical distribution of a metric. An estimation is meaningful when it is not, or to a minimal extent, obfuscated by experimental error. According to Lorscheid et al. (2012), the behaviour of a metric’s Coefficient of Variation (CV) (see Equation 16) across duplicate simulation runs provides a sound indication of the degree of experimental error that is involved in its computation.
| \[ CV = \frac{\sigma_{metric}}{\mu_{metric}}\] | \[(16)\] |
A metric’s CV typically stabilizes as the number of replications increases, as dictated by the law of large numbers. The point at which increasing the number of replications does not drastically alter a metric’s CV anymore can be used to gauge the number of runs (N) required for obtaining meaningful results (Lorscheid et al. 2012). Figure 20 shows how the CV of various metrics behaves as the number of replicate model runs increases. Specifically, the first-order difference is shown on the Y-axis which corresponds subtracting \(CV_{metric}\) at \(t-1\) from \(CV_{metric}\) at \(t\). The point of inflection after which the first-order difference of the CV tends to stabilize around zero indicates the minimum number of replications needed to obtain meaningful results. We consider 150 replications to meet this requirement (see Figure 20).
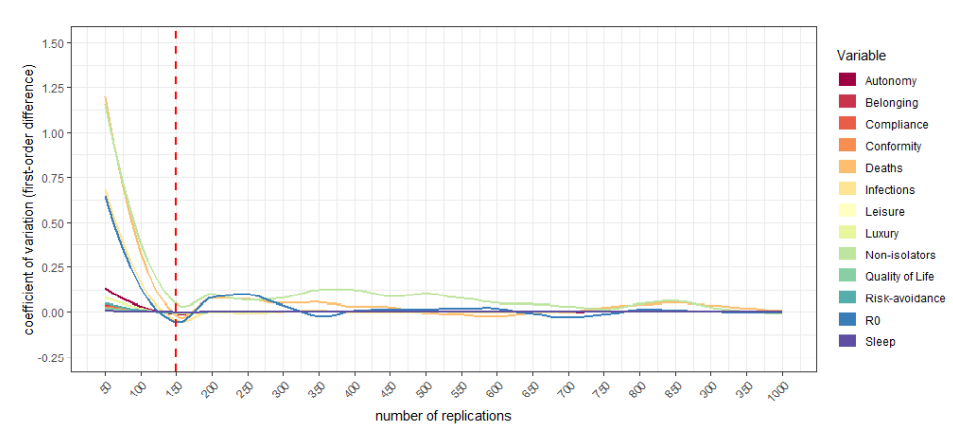
References
ACAPS. (2020). COVID-19 government measures dataset. Available at: https://web.archive.org/web/20201105193821/https://www.acaps.org/covid-19-government-measures-dataset.
ANDERSON, E. (2019). 'Dewey’s moral philosophy.' In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
ASSOCC. (2020). Agent-Based social simulation of the coronavirus crisis. Archived at: https://web.archive.org/web/20201106094701/https://simassocc.org/.
BALKE, T., & Gilbert, N. (2014). How do agents make decisions? A survey. Journal of Artificial Societies and Social Simulation, 17(4), 13: https://www.jasss.org/17/4/13.html. [doi:10.18564/jasss.2687]
DECI, E. L., & Ryan, R. M. (2004). Handbook of Self-Determination Research. Rochester: University Rochester Press.
DIGNUM, F. (2021). Social Simulation for a Crisis - Results and Lessons from Simulating the COVID-19 Crisis. Berlin Heidelberg: Springer International Publishing.
DIGNUM, F., DIGNUM, V., Davidsson, P., Ghorbani, A., van der Hurk, M., Jensen, M., Kammler, C., Lorig, F., Ludescher, L. G., Melchior, A., Mellema, R., Pastrav, C., Vanhee, L., & Verhagen, H. (2020). Analysing the combined health, social and economic impacts of the corovanvirus pandemic using agent-based social simulation. Minds and Machines, 30, 177–194. [doi:10.1007/s11023-020-09527-6]
DI Tosto, G., & DIgnum, F. (2012). Simulating social behaviour implementing agents endowed with values and drives. International Workshop on Multi-Agent Systems and Agent-Based Simulation. [doi:10.1007/978-3-642-38859-0_1]
DÖRNER, D., Gerdes, J., Mayer, M., & Misra, S. (2006). A simulation of cognitive and emotional effects of overcrowding. Proceedings of the Seventh International Conference on Cognitive Modeling.
EDMONDS, B. (2017). 'Different modelling purposes.' In B. Edmonds & R. Meyer (Eds.), Simulating Social Complexity (pp. 39–58). Berlin Heidelberg: Springer. [doi:10.1007/978-3-319-66948-9_4]
ERMAN, A., & Medeiros, M. (2021). Exploring the effect of collective cultural attributes on COVID-19-related public health outcomes. Frontiers in Psychology, 12, 884. [doi:10.3389/fpsyg.2021.627669]
ESS. (2020). The European Social Survey (ESS). Available at: https://web.archive.org/web/20201101015551/http://www.europeansocialsurvey.org/.
FERRETTI, L., Wymant, C., Kendall, M., Zhao, L., Nurtay, A., Abeler-Dörner, L., Parker, M., Bonsall, D., & Fraser, C. (2020). Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science, 368(6491). [doi:10.1126/science.abb6936]
FISCHER, R., Vauclair, C.-M., Fontaine, J. R. J., & Schwartz, S. H. (2010). Are individual-level and country-level value structures different? Testing Hofstede’s legacy with the Schwartz Value Survey. Journal of Cross-Cultural Psychology, 41(2), 135–151. [doi:10.1177/0022022109354377]
FUNG, H. H., Ho, Y. W., Zhang, R., Zhang, X., Noels, K. A., & Tam, K.-P. (2016). Age differences in personal values: Universal or cultural specific? Psychology and Aging, 31(3), 274. [doi:10.1037/pag0000082]
GELFAND, M. J., Jackson, J. C., Pan, X., Nau, D., Pieper, D., Denison, E., Dagher, M., van Lange, P. A., Chiu, C.-Y., & Wang, M. (2021). The relationship between cultural tightness-looseness and COVID-19 cases and deaths: A global analysis. The Lancet Planetary Health, 5(3), e135–e144. [doi:10.1016/s2542-5196(20)30301-6]
GELFAND, M. J., Nishii, L. H., & Raver, J. L. (2006). On the nature and importance of cultural tightness-looseness. Journal of Applied Psychology, 91(6), 1225. [doi:10.1037/0021-9010.91.6.1225]
GHORBANI, A., Aldewereld, H., Dignum, V., & Noriega, P. (2012). Shared strategies in artificial agent societies. International Workshop on Coordination, Organizations, Institutions, and Norms in Agent Systems. [doi:10.1007/978-3-642-37756-3_5]
GOETZ, M. K. (2013). The paradox of value: Water rates and the law of diminishing marginal utility. Journal of American Water Works Association, 105(9), 57–59. [doi:10.5942/jawwa.2013.105.0147]
GOKMEN, Y., Baskici, C., & Ercil, Y. (2021). The impact of national culture on the increase of COVID-19: A cross-country analysis of European countries. International Journal of Intercultural Relations, 81, 1–8. [doi:10.1016/j.ijintrel.2020.12.006]
HEIDARI, S., Jensen, M., & Dignum, F. (2020). 'Simulations with values.' In H. Verhagen, M. Borit, G. Bravo, & N. Wijermans (Eds.), Advances in Social Simulation (pp. 201–215). Berlin Heidelberg: Springer. [doi:10.1007/978-3-030-34127-5_19]
HINCH, R., Probert, W., Nurtay, A., Kendall, M., Wymant, C., Hall, M., & Fraser, C. (2020). Effective configurations of a digital contact tracing app: A report to NHSX. Available at: https://cdn.theconversation.com/static_files/files/1009/Report_-_Effective_App_Configurations.pdf?1587531217.
HITLIN, S., & Piliavin, J. A. (2004). Values: Reviving a dormant concept. Annual Review of Sociology, 30, 359–393. [doi:10.1146/annurev.soc.30.012703.110640]
HOFSTEDE, G. (2001). Culture’s Consequences: Comparing Values, Behaviors, Institutions and Organizations Across Nations. Thousand Oaks, CA: Sage.
HOFSTEDE, G. (2020). The 6D model of national culture. Available at: https://geerthofstede.com/culture-geert-hofstede-gert-jan-hofstede/6d-model-of-national-culture/.
HOFSTEDE, G., HOFSTEDE, G. J., & Minkov, M. (2010). Cultures and Organizations: Software of the Mind. New York, NY: McGraw-Hill.
HOFSTEDE, G. J., Jonker, C. M., & Verwaart, T. (2012). Cultural differentiation of negotiating agents. Group Decision and Negotiation, 21(1), 79–98. [doi:10.1007/s10726-010-9190-x]
HOFSTEDE-INSIGHTS. (2020). The Hofstede 6D model: Comparing countries. Available at: https://web.archive.org/web/20201106105630/https://www.hofstede-insights.com/product/compare-countries/.
HUREMOVIĆ, D. (2019). 'Brief history of pandemics (pandemics throughout history).' In D. Huremović (Ed.), Psychiatry of Pandemics (pp. 7–35). Berlin Heidelberg: Springer. [doi:10.1007/978-3-030-15346-5_2]
KLEIN, G. A., Orasanu, J., & Calderwood, R. (1993). Decision Making in Action: Models and Methods. Santa Barbara, CA: Praeger.
LIGMANN-ZIELINSKA, A., Kramer, D. B., Cheruvelil, K. S., & Soranno, P. A. (2014). Using uncertainty and sensitivity analyses in socioecological agent-based models to improve their analytical performance and policy relevance. PloS ONE, 9(10), e109779. [doi:10.1371/journal.pone.0109779]
LIGMANN-ZIELINSKA, A., & Sun, L. (2010). Applying time-dependent variance-based global sensitivity analysis to represent the dynamics of an agent-based model of land use change. International Journal of Geographical Information Science, 24(12), 1829–1850. [doi:10.1080/13658816.2010.490533]
LORSCHEID, I., Heine, B.-O., & Meyer, M. (2012). Opening the “black box”of simulations: Increased transparency and effective communication through the systematic design of experiments. Computational and Mathematical Organization Theory, 18(1), 22–62. [doi:10.1007/s10588-011-9097-3]
LU, J. G., Jin, P., & English, A. S. (2021). Collectivism predicts mask use during COVID-19. Proceedings of the National Academy of Sciences, 118(23), e2021793118. [doi:10.1073/pnas.2021793118]
MCLEOD, S. (2007). Maslow’s hierarchy of needs. Simply Psychology, 1(1–18).
MCPHERSON, M., Smith-Lovin, L., & Cook, J. M. (2001). Birds of a feather: Homophily in social networks. Annual Review of Sociology, 27(1), 415–444. [doi:10.1146/annurev.soc.27.1.415]
MERCUUR, R., Dignum, V., & Jonker, C. (2019). The value of values and norms in social simulation. Journal of Artificial Societies and Social Simulation, 22(1), 9: https://www.jasss.org/22/1/9.html. [doi:10.18564/jasss.3929]
MINER, J. B. (2005). Organizational Behavior 1: Essential Theories of Motivation and Leadership. London: Routledge.
MINKOV, M., & Hofstede, G. (2011). The evolution of Hofstede’s doctrine. Cross Cultural Management: An International Journal, 8(1), 10–20. [doi:10.1108/13527601111104269]
MÜLLER, B., Bohn, F., Dreßler, G., Groeneveld, J., Klassert, C., Martin, R., Schlüter, M., Schulze, J., Weise, H., & Schwarz, N. (2013). Describing human decisions in agent-based models–ODD+ D, an extension of the ODD protocol. Environmental Modelling & Software, 48, 37–48.
NG, S. I., Lee, J. A., & Soutar, G. N. (2007). Are Hofstede’s and Schwartz’s value frameworks congruent? International Marketing Review, 24(2), 164–180.
NG, S. I., & Lim, X. J. (2019). Are Hofstede’s and Schwartz’s values frameworks equally predictive across contexts? Revista Brasileira de Gestão de Negócios, 21(1), 33–47. [doi:10.7819/rbgn.v0i0.3956]
PARK, J. H. (2015). Introversion and human-contaminant disgust sensitivity predict personal space. Personality and Individual Differences, 82, 185–187. [doi:10.1016/j.paid.2015.03.030]
ROCCAS, S., Sagiv, L., Schwartz, S. H., & Knafo, A. (2002). The big five personality factors and personal values. Personality and Social Psychology Bulletin, 28(6), 789–801. [doi:10.1177/0146167202289008]
ROKEACH, M. (2008). Understanding Human Values. New York, NY: Simon & Schuster.
RSTUDIO. (2020). Open source & professional software for data science teams. Available at: https://web.archive.org/web/20201106105126/https://rstudio.com/.
SANDS, P., El-Turabi, A., Saynisch, P., & Morhard, R. (2019). Outbreak readiness and business impact: Protecting lives and livelihoods across the global economy. Available at: https://www3.weforum.org/docs/WEF%20HGHI_Outbreak_Readiness_Business_Impact.pdf.
SCHWARTZ, S. H. (1994). Are there universal aspects in the structure and contents of human values? Journal of Social Issues, 50(4), 19–45. [doi:10.1111/j.1540-4560.1994.tb01196.x]
SCHWARTZ, S. H. (2011). Values: Cultural and Individual. Cambridge: Cambridge University Press.
SCHWARTZ, S. H. (2012). An overview of the Schwartz theory of basic values. Online Readings in Psychology and Culture, 2(1), 2307–0919. [doi:10.9707/2307-0919.1116]
SCHWARTZ, S. H. (2014). Rethinking the concept and measurement of societal culture in light of empirical findings. Journal of Cross-Cultural Psychology, 45(1), 5–13. [doi:10.1177/0022022113490830]
SCHWARTZ, S. H. (2020). How age influences values. Available at: https://web.archive.org/web/20200216043738/http://essedunet.nsd.uib.no/cms/topics/1/2/2.html.
SIMON, H. A. (1997). Models of Bounded Rationality: Empirically Grounded Economic Reason. Cambridge, MA: MIT Press. [doi:10.7551/mitpress/4711.001.0001]
TARAS, V., Rowney, J., & Steel, P. (2009). Half a century of measuring culture: Review of approaches, challenges, and limitations based on the analysis of 121 instruments for quantifying culture. Journal of International Management, 15(4), 357–373. [doi:10.1016/j.intman.2008.08.005]
TAY, L., & Diener, E. (2011). Needs and subjective well-being around the world. Journal of Personality and Social Psychology, 101(2), 354. [doi:10.1037/a0023779]
TEKEŞ, B., Üzümcüoğlu, Y., Hoe, C., & Özkan, T. (2019). The relationship between Hofstede’s cultural dimensions, Schwartz’s cultural values, and obesity. Psychological Reports, 122(3), 968–987.
TEN Broeke, G., van Voorn, G., & Ligtenberg, A. (2016). Which sensitivity analysis method should i use for my agent-based model? Journal of Artificial Societies and Social Simulation, 19(1), 5: https://www.jasss.org/19/1/5.html. [doi:10.18564/jasss.2857]
VAN Dam, K. H., Nikolic, I., & Lukszo, Z. (2012). Agent-Based MXodelling of Socio-Technical systems. Berlin Heidelberg: Springer Science & Business Media.
VAN de Poel, I. (2018). Design for value change. Ethics and Information Technology, 23, 27–31. [doi:10.1007/s10676-018-9461-9]
VAN der Weide, T. L. (2011). Arguing to motivate decisions. Utrecht University, PhD Thesis.
VANHÉE, L., & Dignum, F. (2018). Explaining the emerging influence of culture, from individual influences to collective phenomena. Journal of Artificial Societies and Social Simulation, 21(4), 11: https://www.jasss.org/21/4/11.html.
WILENSKY, U. (1998). NetLogo wealth distribution model. Evanston, IL: Northwestern University.