Introduction and Background

Social identity and collective action problems

Organizational control aims at ensuring that organizational actors contribute to collective or organizational goals (Cardinal et al. 2017; Sitkin et al. 2010) which is a fundamental problem in organizations and may be considered a “problem of collective action” (Coleman 1989), a “problem of commons” (Hartman 1994), or an “agency problem” (Eisenhardt 1989). In particular, organizational control is aimed “to direct attention, motivate, and encourage individuals to act in ways that support the organization’s objectives” (Cardinal et al. 2017 p. 559). Organizational control suggests a multitude of mechanisms, for example, pay-for-performance systems for rewarding or boundary systems for delimiting the behavior of organizational members (Merchant & Van der Stede 2017; Simons 1994).

It has long been recognised that shared social identity is a basis for social influence and coordination in organizational contexts (Haslam 2004). Social identity weakens the distinction between the individual and the group – or, in other terms, lets the group be a part of the self. In an organizational context, the identification of an organizational member with the organization could be termed organizational identity as “a particular form of social identity – one associated with the membership of a given organization or organizational unit” as Cornelissen et al. (2007 p. S5) put it. (While here we adopt this definition, according to another understanding, organizational identity means the identity of an organization as if, in a metaphorical sense, an organization is a single organism on its own. For a comprehensive discussion of the term “organizational identity”, also considering social identity and corporate identity, the reader can refer to Cornelissen et al. 2007.) Individuals perceiving themselves as being a member of the same group, e.g., of a particular organization, are (more) motivated to coordinate their behavior in relation to those issues that are relevant for the shared identity (Cornelissen et al. 2007; Haslam, Eggins, et al. 2003). As Haslam, Postmes, et al. (2003) put it, organizational identity becomes a “mental and material building block” (p. 361) as cognitive categorization and identification processes of individuals lead to collective actions and products (Postmes et al. 2005). In particular, identification with the group may contribute to cooperation, group performance, trust and organizational citizenship. For overviews, see Hogg & Terry (2000), van Knippenberg & Ellemers (2003), Wegge & Haslam (2003), Ellemers et al. (2004), Haslam & Ellemers (2005), Charness & Chen (2020). Hence, when the organizational identity of organizational members – or “we thinking” as Akerlof (2016) puts it – is activated, personal self-interest is expected to lose relative relevance compared to the interest of the collective, which mitigates collective action problems.

However, there is also evidence that identification with the organization can have its own tensions and downsides and that it may not be universally beneficial (Alvesson & Willmott 2002; Bernard et al. 2016; Caprar et al. 2022; Ellemers et al. 2004; van Knippenberg & Ellemers 2003). In this vein, based on insights from social psychology, Bernard et al. (2016) show that social identification may be accompanied by “social free-riding” and conflicts of interests among group members which allow distinct groups to emerge. The main argument here is that individuals with low contribution to a group’s status, do identify with the group; while, at the same time, individuals who provide a high contribution to a group’s status seek to segregate themselves from that group, as they experience a loss of group status by low-contribution individuals.

The “claim”, that organizational identity may mitigate collective action problems, directly translates into issues of organizational control (Kärreman & Alvesson 2004; van Knippenberg & Ellemers 2003). In particular, the question arises in how far could the social identity of individual decision-makers as organizational members complement or even substitute “established” mechanisms employed for organizational control. This constitutes the research issue studied in this paper by means of an agent-based simulation.

Social identity as control mechanism?

According to Merchant & Van der Stede (2017)’s classification, four types of control mechanisms can be distinguished (for other classifications and a discussion, see Simons 1994; Kruis et al. 2016; Strauß & Zecher 2013):

  • Results controls focus on the outcome of organizational members’ behaviour. Results controls typically create meritocracies where the highest reward is given to the individual or organizational unit with the best results.
  • Action controls intend to directly affect behaviour in that they set behavioural constraints by defining rules and procedures to comply. For example, a decision may require seeking consent from a superior or within a committee.
  • Personnel controls refer to employees’ self-motivation to “do a job properly”. These controls focus, among others, on selection and placement.
  • Cultural controls encourage mutual monitoring and rely on some pressure on individuals who deviate from group norms and values.

Control mechanisms also are classified into formal and informal controls. Formal controls are officially sanctioned, institutionalized mechanisms and often get codified (e.g., in contracts, organizational handbooks); in contrast, informal controls comprise values, norms, and beliefs which guide the behaviour of organizational members (Cardinal et al. 2010). There is some correspondence of informal controls to “cultural controls” according to the classification of Merchant & Van der Stede (2017), while formal controls correspond to results, action and personnel controls. Moreover, the relation of social identity to cultural controls appears nearly self-evident: identification with a group is assumed to let individuals internalize group norms. Hence, the more individuals identify with the group, the more their behavior may be shaped by the group norms (Alvesson & Kärreman 2004; Kärreman & Alvesson 2004; van Knippenberg & Ellemers 2003).

The balance between formal vs. informal controls (Cardinal et al. 2004) and the question of the conditions when informal controls could complement or substitute formal controls have been studied in previous research. In particular, the measurability of the task (Eisenhardt 1985), the uncertainty of the task (Kirsch et al. 2010), or the novelty of the knowledge required to accomplish a task (Kreutzer et al. 2016; Lechner et al. 2010) were found to be relevant contingencies for informal controls complementing formal mechanisms. The trait of identity as a component of control is elaborated by Kärreman & Alvesson (2004). They distinguish between technocratic control (addressing results, action and personnel controls in the classification of Merchant & Van der Stede (2017)) and socio-ideological forms of control. Socio-ideological controls target “social relations, emotions, identity formation, and ideology” (Kärreman & Alvesson 2004 p. 152). From this angle, organizational identity may be regarded a type of control which may be purposefully designed with “identity work” (Alvesson & Kärreman 2004; Alvesson & Willmott 2002; Brown 2015).

However, research has also shown that individuals have several social identities and that the salience, i.e., activation, of a specific social identity depends on the context and particular situation (Stets & Burke 2000). For example, mergers or hostile takeovers tend to be perceived as threatening and to activate the identification with the overall firm (Hogg & Terry 2000; Terry 2003).

Moreover, social identity is not only a cause for certain phenomena at the group level, e.g., organizational performance, but may also be a consequence of these phenomena. For example, the distance between an individual’s performance and the collective’s performance may affect the activation of the individual’s social identity (Bernard et al. 2016; Shayo 2020; van Knippenberg & Ellemers 2003). At the same time, several control mechanisms (i.e., results controls according to Merchant & Van der Stede (2017) or technocratic controls as Kärreman & Alvesson (2004) called them) aim at enhancing the collective’s performance. Hence, organizational identity (as a “cultural” or “socio-ideological” control) may also interfere with these other control mechanisms. For example, in an in-depth case study of a consultancy firm, Alvesson and Kärreman find that loosening technocratic control allows for more behavioral discretion while employees’ orientation towards the collective via socio-ideological control is tightened (Alvesson & Kärreman 2004; Kärreman & Alvesson 2004). They conclude, “that the technocratic and socio-ideological layers of control do not so much complement or supplement, as feed upon and inform each other” (Kärreman & Alvesson 2004 p. 171).

Endogeneity of social identity and agent-based simulation

The relevance of the context for social identity becoming salient and the two-fold role as “cause and effect” indicates both the contingent and dynamic character of individuals’ organizational identity (Charness & Chen 2020; Haslam 2004; Pratt 2001; Stets & Burke 2000; van Knippenberg & Ellemers 2003). Moreover, regarding social identity a control mechanism (be it named cultural, informal or socio-ideological) highlights the potential interference with other control mechanisms employed in an organization.

However, the emergence and effects of organizational identity of organizational members in interference with contingency factors like task complexity and mechanisms employed for organizational control poses remarkably methodological challenges, especially for empirical research (Ashforth et al. 2008; Brown 2015; Cardinal et al. 2017). These challenges result, among other reasons, from the different levels (individual vs. organizational) to be studied in a long-term perspective for which agent-based modelling appears to be a promising research method (Wall & Leitner 2021). This also corresponds to Cardinal et al. (2017) who suggest the study of organizational control from a complexity theory perspective, i.e., formal and informal controls interacting in complex environments with lower-level agents interacting and creating feedback loops thus causing even more interactions (Cardinal et al. 2017).

Here, we adopt this perspective and consider social identity as endogenously emerging from interactions between agents and (other) control mechanisms under environmental complexity employing an agent-based simulation. In particular, the paper pursues two objectives:

  • First, the paper seeks to contribute to the understanding of the emergence of organizational identification and its performance effects in interaction with major traits of the organizational context including (other) organizational controls.
  • Second, it aims to highlight the potential of agent-based simulation as a research method for studying the emergence and effects of social identity in organizations.

In the agent-based model, the organizational identification of managerial decision-makers emerges endogenously based on various “mechanisms” for the activation (salience) of organizational identity. The complexity of the organizations’ overall task affects the interdependencies between subordinate decision-makers’ tasks and the coordination needed. Organizations may employ various control mechanisms to align subordinate decision-makers’ behaviour with the organization’s objective. In the simulation experiments, decision-makers’ emerging identification with the organization and the organizational performance are observed.

The structure of the paper is as follows: The paper proceeds with an agent-based model, with particular focus on modelling the organizational identification of decision-makers within the organizations against the background of previous research. Section 3 provides an overview of the simulation experiments. Section 4 presents a detailed analysis of results. Section 5 discusses the findings from a broader perspective and points out avenues for future research, followed by concluding remarks.

An Agent-Based Model of Social Identity in Organizational Control

Model overview and modelling choices

This section aims to outline the major building blocks of the agent-based model. The model captures artificial organizations that seek superior performance to their overall multi-dimensional decision problem. This overall decision-making task is decomposed into equal-sized sub-problems, and each sub-problem is delegated to a distinct decision-making agent who may represent a manager of the first management line below the headquarters, e.g., the head of a business unit. The organization’s task could be of different levels of complexity, and the organizations may employ various mechanisms to coordinate the managers’ decisions with respect to the overall organizational performance. In each time step, each manager searches for options that promise to increase the objective function, which captures the manager’s preferences, including those related to social identity. The managers’ organizational identity may be activated by three different “mechanisms” that have been intended to convert previous research on the salience of social identity in organizational settings into the model. These mechanisms capture the threat by performance declines and distance to fellow managers – may it be in terms of input (i.e., effort) or output (i.e., a unit’s performance) level. Details on how managers’ activation of social identity is modelled against the background of previous research are given in paragraphs 2.24 to 2.44.

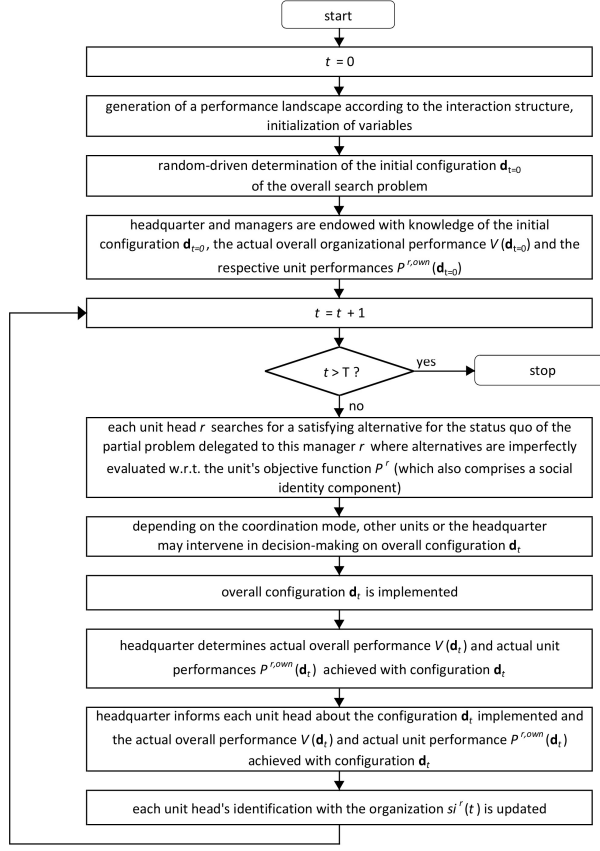
Figure 1 provides an overview of the model’s conceptual framework, while Figure 2 outlines the process structure of the model. However, before the model is described in more detail, the major modelling choices deserve some comments.

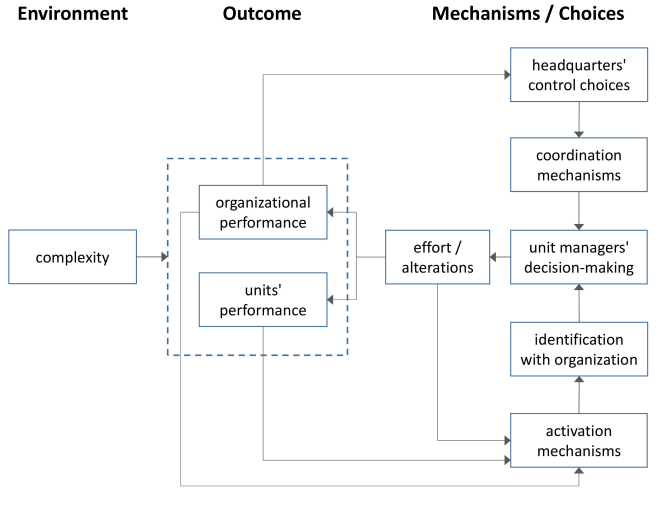
First, the model builds on the framework of NK fitness landscapes, initially introduced in evolutionary biology (Kauffman 1993; Kauffman & Levin 1987), which has been widely used in managerial science (Ganco & Hoetker 2009; Wall 2016). A major advantage of the NK framework is that it allows to conveniently “tune” the complexity in terms of the interactions among elements - may they represent the genes of a genome, the modules of a new product (Ethiraj & Levinthal 2004) or the single choices of a multi-dimensional decision-problem (Li et al. 2006).

Second, for capturing managers’ search behaviour, the model does not build on hill-climbing algorithms as widely used in agent-based models of organizations (Baumann et al. 2019; Chang & Harrington 2006). These algorithms have recently been criticized for not appropriately reflecting managerial behaviour (Billinger et al. 2014; Puranam et al. 2015; Tracy et al. 2017). Therefore, the model employs an algorithm (Wall 2021) that captures key elements of so-called satisficing1 behaviour – initially described by Simon (1955, 1959) – which can build on considerable empirical evidence (Caplin et al. 2011; Güth 2010; Johnson et al. 2012; Misuraca & Fasolo 2018; Parker et al. 2007). Among the key elements of satisficing behaviour is that agents search until they find a satisfying alternative and adapt the aspiration level to the difficulty of their task.

Third, as for capturing social identity in our model of hierarchical organizations, a modelling choice is to focus primarily on identification as one of the three social-psychological processes that – building on the original foundations of social identity theory (Tajfel 1974, 1975; Tajfel & Turner 1979) – are relevant for social identity (Ellemers et al. 2003): (1) categorization, i.e., the tendency to perceive themselves and others as members of groups rather than separate individuals; (2) comparison, i.e., the tendency to assess groups and individuals based on dimensions related to groups, which also leads to (different) valuations of ingroup vs. outgroup members; (3) identification, i.e., the extent to which an individual conceives the self as a group member rather than an individual with personal characteristics. The model’s focus is on the unit managers’ conceived membership of the overall organization, i.e., managers’ identification with the overall organization. The higher the identification, the more likely an individual acts in line with the group identity to which the membership refers (van Knippenberg & Ellemers 2003). As argued in the introduction, this refers to major concerns of organizational control, i.e., aligning organizational members’ behaviour with organizational objectives, which is at the centre of our research question. However, among the activation mechanisms studied, there are two that build on a manager’s distance from fellow managers at the same hierarchical level. As will be explained in more detail below, these mechanisms could be regarded as capturing comparisons between groups in terms of the social identity approach (see paragraph 2.41).

Fourth, as mentioned above, in the model managers’ social identity is reflected in managers’ preference functions. Hence, the model presented here follows the stream of economic models on social identity which are preference-based as opposed to believe-based models (Charness & Chen 2020). In preference-based models, identification with a group is a component of an agent’s utility where the relevance (or even salience) of the social identity may be given exogenously (Akerlof & Kranton 2005) or emerge endogenously (Bernard et al. 2016). In believe-based models, agents invest in social identity in order to find out “who they are” (Bénabou & Tirole 2011). In this vein, pro-social behaviour is regarded as an identity investment that may inform the individual about the self, i.e., forming beliefs about the self and eventually inducing further identity re-investments. Taken to an extreme, in belief-based models, individuals seek to learn about their own social nature. In contrast, in preference-based models, an individual weighs its social utility components against individual-centred components. This paper’s research question focuses on the role of social identity in the context of organizational control: organizational control boils down to how to affect behaviour so that organizational members behave in favour of organizational goals rather than individual interests. This refers to the weighting of components in individuals’ utility and corresponds to the above-mentioned preference-based models of social identity with their focus on weighting social and individual components of utility. Hence, in a nutshell, the rationale for employing a preference-based modelling approach of social identity for our purpose is its correspondence to the key problem of organizational control.

The agent-based model is presented in two steps. First, the principal organizational setting and managerial decision-making are outlined briefly (pars. 2.8 to 2.23). For more extensive descriptions of the hierarchical organizations, the reader can refer to Wall (2016, 2017, 2021). Subsequently, the model’s description focuses on managers’ social identity which is described in paragraphs 2.24 to 2.44.

A Model of hierarchical decision-making organizations

Overall task, delegation and agents

The artificial organizations face an overall task which is specified according to the framework of NK fitness landscapes (Kauffman 1993; Kauffman & Levin 1987). The organizations’ overall task is an \(N\)-dimensional binary decision problem \(\vec{d_t}={(d_{1t},...,d_{Nt})}\) with \(d_{it}\in \left\{0,1\right\}\), \(i=1,...N\). Each of the two states of every single choice \(d_{it}\) of the \(N\)-dimensional problem \(\vec{d_t}\) provides a contribution \(C_{it}\) to the overall performance \(V_t\) of the organization. The overall performance \(V_t\) achieved in period \(t\) results as normalized sum of contributions \(C_{it}\) from

\[V_{t}=V(\vec{d_t})=\frac{1}{N}\sum^{N}_{i=1} {C_{it}}.\] \[(1)\]

While the contributions \(C_{it}\) are randomly drawn from a uniform distribution with \(0\leq{C_{it}}\leq1\), they are a function of choices and the interactions among choices:

\[C_{it}=f_{i}(d_{it};d_{i_{1}t},...d_{i_{K}t}) \] \[(2)\]
with \(\left\{i_1,...,i_K\right\} \subset\left\{1,...,i-1,i+1,...,N\right\}\). With this, parameter \(K\) (with \(0\leq K\leq N-1\)) captures the complexity of the decision problem in terms of the number of those choices \(d_{jt}\), \(j\neq{i}\) which also affect the performance contribution \(C_{it}\) of choice \(d_{it}\). In case of no interactions among choices, \(K\) equals 0. In contrast, \(K=N-1\) reflects the maximum level of complexity where each single choice \(i\) affects the performance contribution of each other binary choice \(j\neq i\).

The organizations comprise two types of decision-making agents: (1) a headquarter and (2) \(M\) subordinate decision-makers \(r\), each of which being the head of a respective unit (or department) \(r\in \left\{1,...,M\right\}\). The organizations make use of division of labor. In particular, the \(N\)-dimensional overall decision problem is decomposed into \(M\) disjoint, equal-sized2 partial problems, and each of these sub-problems is exclusively delegated to one decision-manager being the head of unit \(r \left\{1,...,M\right\}\). The headquarter is responsible for the coordination of the \(M\) unit heads. This includes informing the unit managers about performances achieved, rewarding them and – depending on the coordination mode – eventually intervening in decision-making.

Shaped by the level \(K\) and the structure of interdependencies, indirect interactions among the units may result (e.g., Figure 3III). Let \(K^{ex}\) denote the level of cross-unit interdependencies. In case that cross-unit interactions exist (i.e., if \(K^{ex}>0\)), then the performance contributions of unit head \(r\)’s choices to overall performance \(V\) are affected by choices made by other units \(q \neq r\) and vice versa.

Given the decomposition of the overall decision problem, the contribution of each unit head \(r\) to overall performance (Equation 1) from those \(N^r\) decisions assigned to that manager results from

\[P^{r,own}_{t}(\vec{d^r_t})=\frac{1}{N}\sum^{N^r}_{i=1+w} {C_{it}} \] \[(3)\]
with \({w}=0\) for manager \({r}=1\) and \({w}={\sum^{r-1}_{m=1} {N^m}}\) for department heads \(r>1\). From the perspective of unit head \(r\)
\[P^{r,res}_{t}=\sum^{M}_{q=1,q\neq{r}} {P^{q,own}_{t}} \] \[(4)\]
gives the performance achieved in the “rest” of the organization, i.e., from decisions of the other managers. From this, it also follows that for the organizational performance as given in Equation 1 it holds that
\[V_{t}(\vec{d^r_t}) = P^{r,own}_{t}(\vec{d^r_t}) + P^{r,res}_{t}(\vec{d^r_t})\] \[(5)\]
which we will take up when modelling managers’ identification with the organization.
Managers’ search and decision-making

At each time step, the organizations search for a superior solution of an \(N\)-dimensional binary decision problem \(\vec{d_t}={(d_{1t},...,d_{Nt})}\) with \(d_{it}\in \left\{0,1\right\}\), \(i=1,...N\). The headquarters’ objective function corresponds with the organizational performance given in Equation 1. However, with the decomposition of the overall decision problem, search and decision-making is delegated to the \(M\) subordinate managers (with eventual intervention by the headquarters). Let \(P^r(\vec{d_t})\) denote unit head \(r\)’s objective function which is elaborated in more detail in paragraphs 2.24 to 2.44) with particular respect to managers’ social identity.

The model assumes that managers prefer higher levels for their respective objective functions. Hence, they seek solutions to their partial decision problems that promise higher levels of \(P^r\). As is common in agent-based modelling, unit heads show some form of bounded rationality (with further references, Katsikopoulos 2014; Wall & Leitner 2021) which the model reflects in three aspects of managers’ cognitive limitations:

  • Managers cannot survey the entire search space and, hence, cannot “locate” the optimal solution of their partial decision problems “at once” but have to search stepwise for superior solutions.
  • Unit heads cannot anticipate the other managers’ choices; instead, each manager \(r\) assumes that the fellow managers \(q\neq{r}\) will stay with the status quo, i.e., opt for \(\vec{d}^{q*}_{t-1}\).
  • The model assumes that unit heads cannot perfectly ex-ante evaluate the performance contributions of newly discovered solutions; rather, their ex-ante evaluations are afflicted with noise which is, for the sake of simplicity, a relative error imputed to the actual performances (Levitan & Kauffman 1995; Wall 2016). The error terms follow a Gaussian distribution \(N(0;\sigma)\) with expected value \(0\). The standard deviations differ according to whether the performance of the “own” unit, i.e., \(P^{r,own}\) (see Equation 3) or the residual performance \(P^{r,res}\) (see Equation 4) is evaluated. In particular, we assume that the manager can more precisely assess the performance of the “own” unit than of the rest of the organization, i.e., \(\sigma^{r,own} < \sigma^{r,res}\), which reflects specialization in the own field of competence. All errors are assumed to be independent of each other. However, regarding the status quo option, we assume that unit head \(r\) gets informed about the actual performance of the status quo \(\vec{d}^{r*}_{t-1}\) at the end of period \(t-1\), and, from this, also infers the actual performance \({P}^{r}_{t}\) should the status quo be kept in \(t\). Information about the actual performance of the overall organization and the respective unit’s performance may be generated by accounting techniques. Informing subordinates accordingly broadly refers to what in organizational control is captured by “results controls” (e.g., Merchant & Van der Stede 2017 see Introduction) or “diagnostic and interactive control systems” (Simons 1994, 2014).

As argued above (see paragraph 2.4), managers perform search and decision-making processes in the spirit of satisficing with the algorithmic representation following Wall (2021). A core idea of satisficing is that decision-makers discover and evaluate new options sequentially: the agent discovers one novel option \(\vec{d}^{r}_t\) and evaluates whether it is satisfactory. If so, the search stops; otherwise, the next alternative is searched and evaluated, and so forth.

For being satisfactory, an option has to promise meeting the aspiration level \(a^r(t)\) relevant at that time. Hence, for manager \(r\) seeking to find a superior solution, an alternative is satisfactory if it promises a favourable change \(\Delta P^r_t\) compared to what the status quo \(\vec{d}^{r*}_{t-1}\) yields, i.e., if the following criterion is met:

\[\Delta P^r_t \geq a^r(t) \] \[(6)\]
If a newly discovered option appears satisfactory – let us call a satisfactory alternative \(\vec{d}^{r^s}_{t}\) – search is stopped for this time step \(t\). Otherwise, the next option is searched and evaluated against the aspiration level as far as a maximum number of options \(s^{max,r}(t)\) is not reached yet. If no satisfactory alternative to the status quo \(\vec{d}^{r*}_{t-1}\) is found, then unit head \(r\) prefers keeping this configuration also in period \(t\).

The model of satisficing behaviour comprises three further aspects which deserve some remarks (for more details, see Wall 2021).

  • The sequence of search, i.e., of agent’s discoveries of new options is to be specified. The model presented here employs a “closest-first” search policy: a manager \(r\) starts searching in the immediate “neighborhood” of the status quo \(\vec{d}^{r*}\). Should this not lead to a satisfactory option, manager \(r\) extends the “circle” of search around the status quo. The sequence follows increasing Hamming distances of newly discovered alternatives \(\vec{d}^{r}_t\) to the status quo given by \(h(\vec{d}^{r}_t) = \sum^{N^r}_{i=1} {\left|\vec{d}^{r*}_{t-1} - \vec{d}^{r}_t\right|}\). Hence, the search starts with options of Hamming distance \(h(\vec{d}^{r}_t)=1\), then followed by options with a Hamming distance of two and so forth, as long as either the aspiration level is met or the maximum number of options \(s^{max,r}\) to be considered is reached.3 A rationale for a “closest-first” search policy is based on considerations of cost of search and change and the idea of stepwise improvement. Small steps could be assumed to show lower cost than more distant options which require more changes.
  • A core element in satisficing is the adaptation of the aspiration level based on experience: The aspiration level may increase (decrease) depending on how easy (difficult) it was to find a satisfactory alternative in the past. In the model, subordinate managers adjust their aspiration levels according to the experience, i.e., the improvement or deterioration for the objective achieved over time. In particular, the aspiration level \(a^r\) is captured as an exponentially weighted moving average of past changes in the attainment of objective \(P^r\) (Börgers & Sarin 2000; Levinthal 2016; Levinthal & March 1981), i.e.,
    \[a^r(t+1) = \alpha^r\cdot \Delta P^{r*}_{t} +(1-\alpha^r)\cdot a^r(t). \] \[(7)\]
    where \(\alpha^r\) denotes the speed of adjustment for manager \(r\), and \(\Delta P^{r*}_{t}\) is the change in the actual attainment from time step \(t-1\) to \(t\), i.e., \(\Delta P^{r*}_{t} = P(\vec{d}^{r}_{t})-P(\vec{d}^{r}_{t-1})\). Hence, the aspiration level could also become negative, i.e., a decline in the goal attainment becoming acceptable – if declines happened in the past.
  • Another aspect of satisficing is the adaptation of the maximum number of options searched. The decision-maker dynamically adjusts the space for searching options. When it was difficult (easy) to find satisfactory options in the past, the search space for alternatives is broadened (narrowed). In the model, this idea is captured as an adjustment of the maximum number \(s^{max,r}(t)\) of options that the unit head \(r\) may search for in the next time step. For this, an exponentially weighted moving average of past search spaces is employed where \(\beta^r\) denotes the speed of adjustment for manager \(r\).
Coordination of managers’ decision-making

Once the unit heads \(r\) have searched and formed their preferences on their partial decision problems, the next step is coming to a decision on the organization’s overall decision problem \(\vec{d_t}\). For this, the model comprises four different mechanisms of how the unit heads’ preferences on \(\vec{d^r_t}\) are transformed into the overall configuration \(\vec{d_t}\). These coordination mechanisms refer to what in management control has been named “action controls” (Merchant & Van der Stede 2017) (see paragraph 1.5) or “boundary systems” with the aim “to set limits on opportunity-seeking behaviour” (Simons 1994 p. 7) and to “delineate the acceptable domain of activity for behaviour of organizational participants” (Simons 1994 p. 39), (Simons 2014).

The following outlines the main ideas of the coordination mechanisms, while a description in detail is given in Wall (2017). In particular, the types of coordination captured in the model differ in the communication channels4, the information employed in decision-making, the locus of final decision-making, and, in the end, the tightness of coordination provided (for an overview and further modes see, for example, Malone 1987; de Vries et al. 2016; Malone & Crowston 1994; Siggelkow & Rivkin 2005).

The decentralized mode grants the highest possible level of autonomy to the \(M\) unit heads since each of them is allowed to choose the most preferred option which is either the satisfactory alternative \(\vec{d}^{r^s}_{t}\) or the status quo \(\vec{d}^{r*}_{t-1}\). The overall organizational configuration \(\vec{d_t}\), hence, results from a mere “combination” of the unit heads’ preferred options. Obviously, this does not require any form of communication. The headquarter does not intervene in decision-making directly, and its role is limited to registering the achieved performances \(\vec{d_t}\) and \(P^{r}_{t}(\vec{d^r_t})\) at the end of each period \(t\), informing and rewarding unit heads accordingly. [par:decentralized]

The sequential mode captures the idea of “sequential planning”: units make their final choices sequentially, taking the “preceding” choices into account with, for the sake of simplicity, the sequence being given by the index \(r\) of the units. In particular, in time step \(t\), unit \(r\) with \(1\leq{r}< M\) informs unit \(r+1\) about the choices made so far, i.e., made by the “preceding” units \(\leq{r}\). Unit \(r+1\) re-evaluates its “own” options, i.e., an eventually found satisfactory alternative \(\vec{d}^{r^s}_{t}\) and the status quo \(\vec{d}^{r*}_{t-1}\) taking these “prior” choices into account. This will potentially result in a revision of preferences: the status quo may now appear more favourable than the newly found option regarded as satisfactory before re-evaluation. Hence, units’ \(r>1\) choices are a function of the choices of the preceding units. The headquarter’s role corresponds to that of the decentralized mode.

In the lateral veto mode, unit heads mutually inform each other about their preferences. Next, each unit head individually evaluates – according to the own objective function – the “composite configuration” \(\vec{d^C}\), resulting from the preferences of all \(M\) units. The unit heads are endowed with mutual veto power. A unit head \(r\) will veto against the composite vector \(\vec{d^C}\) if it promises a lower attainment than the status quo. Hence, to be accepted, the composite vector \(\vec{d^C}\) has to promise the same or a higher attainment than the status quo \(\vec{d}^{r*}_{t-1}\) to the objective \(P^r\) of each single unit head. Even with one unit head vetoing, the status quo is kept. As with the two preceding coordination modes, the headquarter does not intervene in decision-making.

In the proposal mode the final choice is made by the headquarter. For this, each unit transfers its preferences to the headquarter, which compiles the preferences to a composite vector \(\vec{d^C}\) and then evaluates the overall performance \(V(\vec{d^C})\) (see Equation 1) which this solution promises. The headquarter favours the composite vector if it promises the same or a higher organizational performance \(V(\vec{d^C})\) than the status quo; otherwise, the organization stays with the status quo, i.e., then \(\vec{d_{t}}=\vec{d_{t-1}}\). However, as with unit heads, the model assumes that the headquarter cannot ex-ante evaluate new options perfectly, i.e., other solutions than the status quo. Instead, also the headquarters suffers from some relative noise following a Gaussian distribution with expected value \(0\) and standard deviation \(\sigma^{head}\).

Modelling social identity in managerial decision-making

Principal representation of organizational identity in the model

In the model, social identity is conceptualized as of how much unit heads identify with the overall organization which captures “organizational identity” following Cornelissen et al. (2007), i.e., an employee’s social identity associated with the membership of an organization or organizational unit (for this, see also paragraph 1.2). In particular, a manager’s identification with the organization is regarded high if this manager’s objective function \(P^r\) corresponds with the organization’s objective \(V^r\) – or, as Akerlof & Kranton (2005) put it in their seminal paper on social identity in organizations: if the manager acts in the interest of the firm.

As argued above (see paragraph 2.6), the model employs a preference-based approach for capturing managers’ identification with the organization. In the preference-based approach, social identity boils down to the weight an individual puts on social in relation to individual components in the spirit of Akerlof & Kranton (2005). Hence, for our modelling effort, the first question is what the individual and the social components are in a unit manager \(r\)’s objective function. The model considers the unit performance \(P^{r,own}\) (see Equation 3), i.e., the sum of performances obtained from a manager \(r\)’s “own” decisions as the individual component. The rationale for this is that the unit performance reasonably enters the performance evaluation of the respective unit head: it may serve as value base for the manager’s monetary compensation (results controls) or may affect the manager’s future career perspectives (personnel controls) (see paragraph 1.5). In contrast, the performance achieved "outside’’ of manager \(r\)’s unit, \(P^{r,res}_{t}(\vec{d^r_t})\)), as given in Equation 4, is regarded the social component in the model.

Following the preference-based view of social identity, the weight of the social in relation to the individual component is at the centre of modelling social identity (see paragraph 2.6). In the model, for the sake of simplicity, we normalize the weight of the individual component \(P^{r,own}\) in a manager’s objective function to 1 and capture the weight the manager puts on her/his respective social component in time step \(t\) by a factor \(si^r (t) \geq 0\). With this, manager \(r\)’s objective function is modelled as:

\[P^r_{t}(\vec{d^r_t}) = P^{r,own}_{t}(\vec{d^r_t}) + si^r(t)\cdot P^{r,res}_{t}(\vec{d^r_t})\] \[(8)\]
The weight \(si^r(t)\) of the “social” component in a manager’s objective function (Equation 8) reflects the level of salient identification of manager \(r\) with the overall organization at time step \(t\). For this, please, compare the manager’s objective function in Equation 8 with Equation 5 which reflects the organizational performance from the perspective of manager \(r\) as it corresponds (with Equations. 3 and 4) with the organizational performance as given in Equation 1. In particular, if in Equation 8 the weight on the social component is \(si^r(t) = 1\), then manager \(r\)’s objective is perfectly in line with the organizational objective \(V\) (see Equation 5). In contrast, if \(si^r(t) = 0\), manager \(r\) does not identify at all with the overall organization and will decide in favour of the “own” performance only (please, recall that it depends on the interactions among choices \(d_i\) whether a manager’s “own’’ decisions affect the performance achieved in the”rest’’ of the organization.)

The representation of managers’ salient social identification as weight \(si^r(t)\) in Equation 8 in the model deserves some comments on, first, the dynamics and, second, the magnitudes to be expected. The magnitudes that \(si^r\) make take are considerably low shaped by the activation mechanisms reflected in the model, which is why this is discussed below (see paragraph 2.43 and 2.44).

The dynamic nature of social identity (Charness & Chen 2020; Haslam 2004; Pratt 2001; Stets & Burke 2000; van Knippenberg & Ellemers 2003) is captured in the model as \(si^r(t)\) changes over time and is endogenously set by managers (Shayo 2020) according to the activation mechanisms that are described in the following. However, the model assumes that a manager’s organizational identification may be subject to some “memory effect”, i.e., that the identification level in period \(t\) might be affected to some extent by the past. For capturing this, an exponential weighting is employed with \(\gamma^r\) denoting the speed of adjustment for manager \(r\) while ensuring that \(si^r(t+1)\) cannot get negative. This leads to

\[si^r(t+1) = \max (0; \gamma^r\cdot S^{r}_{t} +(1-\gamma^r)\cdot si^r(t)) \] \[(9)\]
where \(S^{r}_{t} \in \{ S^{r\textrm{, c-org-perf}}_{t}, S^{r\textrm{, d-unit-perf}}_{t}, S^{r\textrm{, d-effort}}_{t}, S^{r\textrm{, combined}}_{t}\}\) is the base for social identity according to the four activation mechanisms for managers’ social identity introduced in the following paragraphs.
Activation mechanisms of managers’ social identity

Among the insights from prior research on social identity is that, first, an individual’s behaviour only responds to identification with a group to that extent as the membership is salient and, second, the salience is affected by the immediate context (Hogg & Terry 2000; Shayo 2020; van Knippenberg & Ellemers 2003). In our model, the context is shaped exogenously (e.g., task complexity, coordination) and subject to endogeneous changes within the organizations’ search processes, which affect and also are affected by the activation of managers’ social identity \(si^r\).

For reflecting main sources for the activation of social identity in organizational settings as identified in prior research, the model captures four mechanisms where the fourth is a combination of the others:

  • (a) changes in organizational performance (c-org-perf)
  • (b) distance in unit’s performance (d-unit-perf)
  • (c) distance in effort among managers (d-effort)
  • (d) combination of mechanisms (a) to (c) (combined)

The mechanism based on (a) changes in organizational performance reflects what one may also call "activation from threats". For example, it has been found that, in situations of perceived threats like a merger or hostile takeover, identification with the overall firm tends to be activated (Hogg & Terry 2000; Terry 2003). Modelling the various situations (e.g., hostile takeover) that could be perceived as threats in detail is beyond the level of abstraction of the model introduced. However, the model assumes that the unit heads, at the end of each period, get informed about the actual organizational performance \(V_t\) achieved in that period and compare it to the level \(V_{t-1}\) achieved in the previous period. A decline (incline) in organizational performance is perceived as a threat and, thus, leads to an effect to \(r\)’s organizational identity \(>0\) (\(<0\)) as given by
\[S^{r\textrm{, c-org-perf}}_{t} = - \frac {{V_t} - V_{t-1}}{V_{t-1}}\] \[(10)\]
(The change in organizational performance is computed as a relative metric; the same applies to the other activation mechanisms in order to avoid problems of incommensurable dimensions across the mechanisms.) Hence, in the end of period \(t\), \(S^{r,\textrm{c-org-perf}}\) as computed in Equation 10 is employed to update the level of identification according to Equation 9.

However, it is worth mentioning that the activation mechanism (a) changes in organizational performance produces the same levels of identification across unit heads since the base is the actual performance of the overall organization, which is the same for each unit. This is in contrast with the other mechanisms which produce heterogeneity in organizational identity across managers, as shown in the following.

In particular, the activation mechanisms “distance in unit’s performance” (d-unit-perf) and “distance in effort among managers” (d-effort) build on the distances among unit heads – be it regarding the “outcome” in terms of units’ performance or the “input” as the units’ effort incurred. These activation mechanisms are based on insights from social psychology and their reflection in economic models of social identity (Akerlof & Kranton 2005; Bernard et al. 2016; Shayo 2009, 2020) according to which two interrelated aspects affect individuals’ choices on the identification with a group: First, individuals prefer identifying with high-status groups. Second, individuals dislike the distance between their own characteristics and the stereotype of the group they identify with.

According to Bernard et al. (2016), this leads to what the authors call “social free-riding”: An individual with characteristics below the group’s “average” identifies with that group. This group’s status is affected by the characteristics of its members. In this sense, the low-type members socially free-ride on the high-type members of the group, which has two adverse effects for the high-type group members: First, since the status of the group depends on the contributions of its members, the group’s status is reduced. Second, the group’s stereotype is reduced, increasing the distance of the high-type members and making it less favourable for them to identify with the group.

For capturing these interrelated aspects in the model, the questions arise of how the status of the group of decision-makers (the “management circle”) is defined and how an individual manager’s distance in our artificial organizations is operationalized. The model reflects two approaches.

First, the units’ performances may be a reasonable criterion for the management group’s status in organizations where performance orientation plays an important role. For example, performance orientation may be a dominant personality trait of the managers in the organization (e.g., with further references Matzler & Mueller 2011). Performance orientation could also be a characteristic of an organization’s culture emphasizing the organization’s mission which entails a clear set of goals linked to the mission and providing a concise direction for subordinate’s work (for an overview Denison et al. 2014). Moreover, the already mentioned results controls as the most characteristic means of management control (Merchant & Van der Stede 2017) seek to provide decision-makers with a clear focus on performance.

The “d-unit-perf” activation mechanism builds on the distance of a particular unit’s performance against the average performance level provided by the other units in the organization. For reflecting organizational identification based on distance in unit performance of manager \(r\), we have the following:
\[S^{r\textrm{, d-unit-perf}}_{t} = - \left(\frac {P^{r,own}_t}{V_{t}} -\frac{1}{M}\right) \] \[(11)\]
where the expression in brackets indicates whether unit \(r\)’s performance is above or below the average relative units’ contributions to overall performance. (Please, recall that the partial decision problems are equal-sized which is why \(1/M\) with \(M\) being the number of units gives the (relative) average of performance contribution.) Should a unit \(r\)’s relative performance be lower (higher) than this average relative contribution, the identification \(S^{r,\textrm{d-unit-perf}}_{t}\) with the organization is increased (decreased) (which is why the term in brackets is multiplied by \((-1)\)). This captures the dynamics from “social free-riding” (Bernard et al. 2016) as outlined above.

Second, in a similar vein, managers may regard the alterations (effort) as a relevant aspect of group status in organizational cultures that stress adaptability. According to the widely accepted definition of organizational cultures of Denison et al. (2014) adaptability, among others, refers to employees’ ability to learn and change in response to demand. In this vein, the “d-effort” activation mechanism builds on the distance of a particular unit’s effort (in terms of the number of single choices altered in the partial decision problem) against the average effort provided by the other units in the organization.

To depict the units’ organizational identification based on distance in effort, the model employs a structurally similar approach as for the distance by unit performance. In particular, the Hamming distances of the configurations implemented for unit \(r\)’s partial problem in periods \(t\) and \(t-1\), i.e., \(h(\vec{d}^{r}_t) = \sum^{N^r}_{i=1} {\left|\vec{d}^{r}_{t} - \vec{d}^{r}_{t-1}\right|}\) and the distances of the organization-wide configurations implemented, respectively, \(h(\vec{d}_t) = \sum^{N}_{i=1} {\left|\vec{d}_{t} - \vec{d}_{t-1}\right|}\) are relevant. If the organization alters, at least, one single choice \(d_i\), i.e., if \(h(\vec{d}_t) > 0\) this leads to
\[S^{r\textrm{, d-effort}}_{t} = - \left(\frac{h(\vec{d}^{r}_t)}{h(\vec{d}_t)} -\frac{1}{M}\right) \] \[(12)\]
and otherwise to \(S^{r\textrm{, d-effort}} =0\).

Similar to Equation 11, the expression in brackets indicates whether unit \(r\)’s relative effort is above or below the average relative units’ effort. Again, the simple term \(1/M\) is feasible since the partial decision problems are equal-sized for the sake of simplicity. Should a unit \(r\)’s relative effort be lower (higher) than the average relative effort, the identification \(S^{r\textrm{, d-effort}}\) with the organization increases (decreases). This allows capturing the identification dynamics from “social free-riding” (Bernard et al. 2016), now based on the relative effort.

The two activation mechanisms that build on the “distance” of a manager to the other unit heads could also be viewed in terms of an inherent comparison between groups which is one of the three social-psychological processes of social identity (Ellemers et al. 2003): The model regards the organization as the group with which a manager may more or less identify, while the model does not explicitly depict a unit as a group of particular organizational members assigned to that unit. Instead, in the model, the unit is only represented by the unit head. However, one may see the two distance mechanisms also as an implicit comparison between two groups – namely the unit and the overall organization: a unit head identifies more (less) with her/his unit as a group when the unit’s performance or effort, respectively, is above (below) the average of the organization as the group.

Fourth, in addition to the three activation mechanisms outlined above, the “combined” mechanism is studied, which is simply an additive combination of the others. In particular, we have
\[S^{r\textrm{, combined}}_{t}=S^{r\textrm{, c-org-perf}}_{t}+S^{r\textrm{, d-unit perf}}_{t}+S^{r\textrm{, d-effort}}_{t} \] \[(13)\]
The idea behind is prior research suggesting that the salience of an individual’s organizational identity may be affected by different mechanisms at a time (Hogg & Terry 2000; Pratt 2001; van Knippenberg & Ellemers 2003).

With the activation mechanism introduced, the description of the model deserves some comments on the magnitude of the weight \(si^r(t)\) of the social component in manager \(r\)’s objective function (Equation 8). The main point here is that – given the above modelling of the activation mechanisms – we should expect relatively low levels of the bases for social identity \(S^r_t\) which then propagate to relatively low levels of the emerging weight \(si^r(t)\) according to Equation 9. This holds for each of the "single’’ activation mechanisms:

  • (a) changes in organizational performance (c-org-perf): According to Equation 10, the percentage change of overall performance in time step \(t\) against the previous period \(t-1\) affects managers’ identification with the organization. However, first, in the simulations organizations seek to stepwise increase their performance while according to this mechanism performance declines increase identification which may result from false positive alterations due to information errors. Second, while the first search periods usually show many alterations of the configurations \(\vec{d}\), and thus higher rates of change in \(V(\vec{d})\), the later search stages show less movements – even up to inertia. These aspects let expect rather low levels of \(S^{r\textrm{, c-org-perf}}_{t}\) and \(si^r(t)\) accordingly.
  • (b) distance in unit’s performance (d-unit-perf): This activation mechanism builds on the deviation of a unit’s relative performance from the average relative performance. Hence, \(S^{r\textrm{, d-unit-perf}}_{t}\) also is a percentage. For example, assume a manager \(1\) contributes 20 percent to overall performance \(V\) while, with \(M=4\) managers as in our experiments, the average relative performance per manager is 25 percent; then, according to Equation 11, the basis \(S^{1\textrm{, d-unit-perf}}_{t}\) for social identify of manager 1 is 0.05.
  • (c) distance in effort among managers (d-effort): This mechanism also builds on a relative deviation from the average effort. Hence, the basis \(S^{r\textrm{, d-effort}}_{t}\) also is a percentage number. (For example, let us assume that in period \(t\), in the overall configuration \(V(\vec{d})\), five alterations have happened (i.e., five bits flipped) with manager 1 being responsible for one alteration; then, as specified in Equation 12, a basis \(S^{1\textrm{, d-effort}}_{t}=0.05\) for social identify enters the update of manager 1’s weight of the social component in Equation 9. [par:magnitude1]

The preceding remarks intend to illustrate the magnitudes of the weight \(si^r(t)\) of the social component in the unit heads’ objective function to be expected from the activation mechanisms captured in the agent-based model. However, it is worth mentioning that also the particular parameter settings affect the magnitude of the emerging weights: For example, low precision in ex-ante evaluations of options makes performance declines more likely (c-org-perf) while homogeneity of unit heads’ traits and task characteristics (as in our experiments), in tendency, results in lower distances in unit performance and effort across units ((d-unit-perf) and (d-effort). Section 5 discusses influencing factors of the magnitude, the respective modelling choices, and avenues for empirical foundations from a broader perspective.

Simulation experiments and parameter settings

This section introduces the simulation experiments and the related parameter settings. The upper part of Table 1 displays the parameter settings that apply to all experiments; the lower part of the table informs about the settings that vary across experiments.

Table 1:Parameter Settings
Parameter Values / Types
Applying to all experiments
Observation period \(T=240\)
Simulation runs per scenario 5,000 runs with 50 runs on 100 distinct
fitness landscapes
Number of choices \(N=12\)
Number of managers \(M=4\)
Managers’ decision problem size \(N^r=3\) for all managers \(r=(1,...,4)\),
problem i.e., \(\vec{d}^{1}=(d_{1},d_{2},d_{3}), \vec{d}^{2}=(d_{4},d_{5},d_{6})\),
\(\vec{d}^{3}=(d_{7},d_{8},d_{9}),\vec{d}^{4}=d_{10},d_{11},d_{12})\)
Precision of ex-ante evaluations
- managers \(\sigma^{r,own}=0.05\) for all managers \(r=(1,...,4)\)
\(\sigma^{r,res}=0.15\) for all managers \(r=(1,...,4)\)
- headquarters \(\sigma^{head}=0.1\)
Aspiration level
- in the beginning \(a^r(t=0)=0\) for all managers \(r=(1,...,4)\)
- speed of adjustment \(\alpha^r = 0.5\) for all managers \(r=(1,...,4)\)
Max. number of alternatives
- in the beginning \(s^{max,r}(t=0)=2\) for all managers \(r=(1,...,4)\)
- speed of adjustment \(\beta^r = 0.5\) for all managers \(r=(1,...,4)\)
Managers’ identification with organization
- in the beginning \(si^{r}(t=0)=0\) for all managers \(r=(1,...,4)\)
- speed of adjustment for activation mechanisms (a) to (d):
\(\gamma^r = 0.5\) for all managers \(r=(1,...,4)\)
for activation mechanism (e):
\(\gamma^r = 0\) for all managers \(r=(1,...,4)\)
- activation mechanisms a. c-org-perf: by change of organizational performance
b. d-unit-perf: by distance of unit performance
c. d-effort: by distance of effort
d. combined: additive combination of mechanisms a. to c.
e. no SI: no activation of social identity
Subject to variation across experiments Experiments
Type A Type B Type C
(lr)3-5 Interaction structures decomposable, \(K=2, K^{ex}=0\), Figure 3.I x x x
near-decomposable, \(K=3, K^{ex}=1\), Figure 3.II - x x
non-decomposable medium, \(K=5, K^{ex}=3\), Figure 3.III - x x
non-decomposable high, \(K=8, K^{ex}=6\), Figure 3.IV - x x
Coordination modes decentralized x x x
sequential planning - - x
lateral veto - - x
proposal - - x

The experiments aim to study the emergence and performance effects of organizational identification in different organizational contexts. For this purpose, following the idea of factorial design of simulation experiments (Lorscheid et al. 2012), three types of simulation experiments are conducted, which differ in respect of the organizational context as indicated in the lower part of Table 1:

  • Type A experiments intend to provide a basic understanding of the dynamics unfolding from the different activation mechanisms of managers’ organizational identification. Thus, these experiments reflect organizations facing a perfectly decomposable overall task, i.e., a situation without interactions across units (\(K^{ex}=0\), Figure 3.I) which may represent organizations with strict product diversification (Galbraith 1974; Rivkin & Siggelkow 2007; Thompson 1967). Moreover, managers have autonomy in decision-making ("decentralized’’ mode). The rationale for these baseline scenarios is to study the dynamics emerging from organizational identification with as little as possible interference from the organizational context.
  • Type B experiments aim to provide a deeper understanding of the emergence and performance effects of organizational identification when interdependencies across units exist, i.e., when the overall task is not decomposable (\(K^{ex}>0\)). Experiments for low, medium and high levels of cross-unit interactions are conducted (Figure 3.II to IV). Interaction structures with many cross-unit interactions may capture what – according to the prominent classification of Thompson (1967) – is called reciprocal interdependencies occurring in organizations with functional specialization.
  • In Type C experiments, the prevailing coordination mechanism of the organizations is varied and, in particular, the level of discretion granted to the subordinate decision-makers by the action controls is modified (see paragraphs 2.20 to 2.23). Hence, while in Type A and B experiments decision-makers have full discretion about the sub-tasks assigned to them, in the type C experiments, action controls that delimit in some ways decision-makers’ autonomy are simulated. The rationale is to study whether tighter coordination may, for example, “overrule” the emergence of organizational identification and its effects on overall performance.

Taking the three types of experiments together, 80 scenarios are simulated, i.e., five activation mechanisms (including the “no social identity” case) in four structures of cross-unit interactions and four types of coordination. Some parameters are fixed for the three types of experiments, as indicated in the upper part of Table 1. In particular, in all experiments, organizations are observed for 240 periods5 of searching for superior solutions to an \(N=12\) dimensional decision problem, starting from a randomly chosen initial position. For each scenario, 5000 simulations are run.

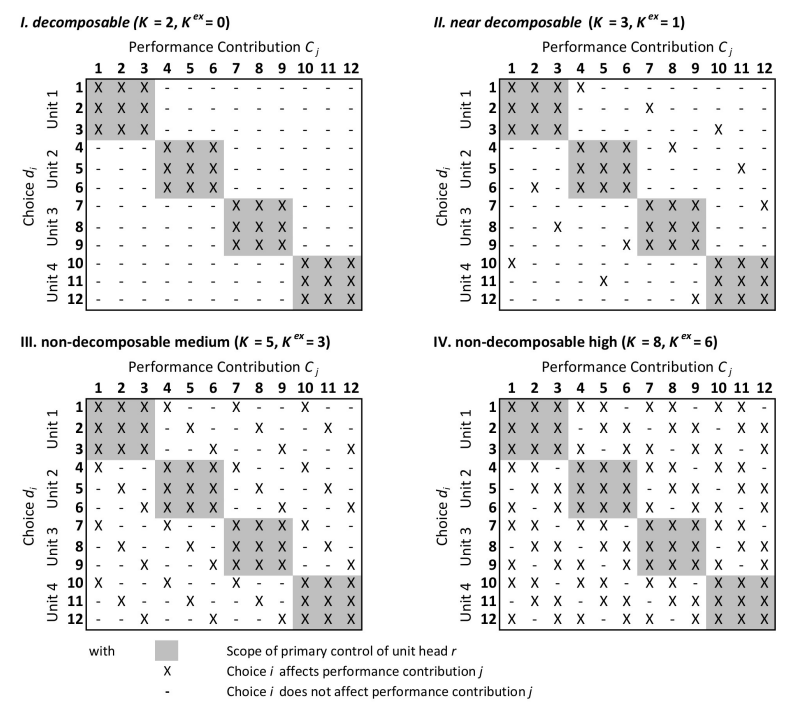
Regarding the organizational structure, the headquarter decomposes the overall decision problem into \(M=4\) equal-sized sub-problems, each delegated exclusively to a subordinate manager (unit head). When ex-ante evaluating options, the agents suffer from noise following a Gaussian distribution: The mean equals zero for any agent; as for the standard deviations, the managers’ error levels are 0.05 for the “own’’ and 0.15 for ”residual’’ performance, reflecting the idea of specialization (i.e., more precise forecasts for the own domain). The headquarter ex-ante evaluates the overall performance of options with an error of 0.1. These settings are in line with some empirical evidence according to which error levels around 10 percent may be a realistic estimation (Redman 1998; Tee et al. 2007). Further parameters refer to managers’ satisficing behaviour: The aspiration levels of performance enhancements start at a level of zero which captures the desire to avoid, at least, situations of not sustaining an already achieved performance level. The maximum search space starts at a moderate level of just two alternatives. The speed of adjustment for both the aspiration level of performance enhancements and the maximum number of alternatives is set to 0.5, i.e., present and past are weighted equally.

The experiments are conducted for the four activation mechanisms of managers’ organizational identification introduced in paragraphs 2.24 to 2.44 and for the case where no identification gets activated. It is worth mentioning that, in each experiment, managers are homogeneous regarding the activation mechanism. While managers’ levels of organizational identity may differ in the course of a simulation, they all start at a level of zero organizational identification. The speed of adjustment is 0.5 for all managers, i.e., putting equal weight on presence and past (see Equation 9).

Results

This section presents the results obtained from the simulation experiments. In the foreground is analysing the dynamics and performance effects unfolding from endogenously emerging organizational identification. Hence, the focus is on analysing the model – following the line of experiment types A to C. For each type of experiments, the analysis starts with summarizing the simulation output in “observations” which are numbered consecutively from 1 to 7 across the experimental types.

Baseline analysis of activation mechanisms (Type A experiments)

This first step of analysis focuses on how the different activation mechanisms of decision-makers’ identification with the organization affect the organizational search processes. Thus, the baseline scenarios (type A experiments, Table 1) capture situations without cross-unit interdependencies (Figure 3.I) and without coordination, i.e., organizations employing the “decentralized” mode.

Preliminary Remarks on the Metrics, Tables and Figures

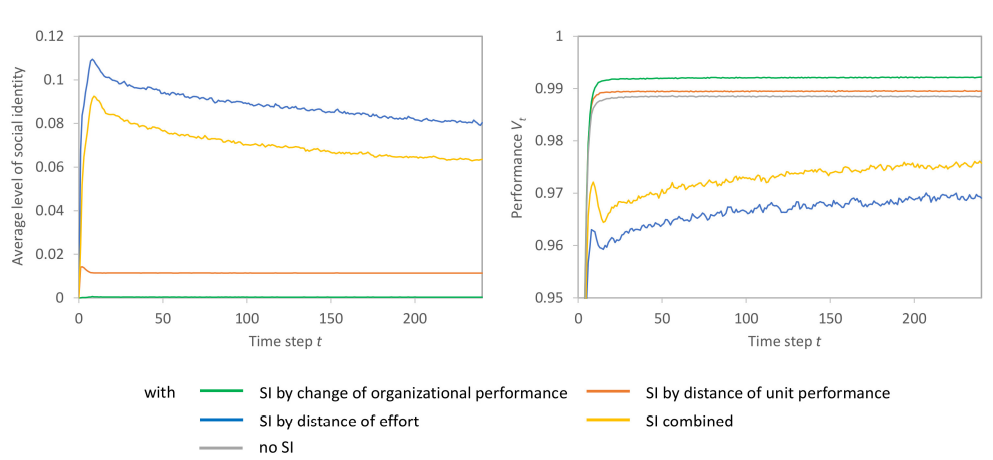
Results for the type A experiments are given in Figure 4 and in Tables 2 to 4. Figure 4 displays the levels of social identity averaged for the \(M=4\) decision-making managers and the organizational performance \(V_t\) obtained for the different types of social identity activation in the baseline-scenarios. Table 2 displays condensed results for the baseline scenarios I.a to I.e in the upper lines. In particular, Table 2 provides the following metrics:

  • The average level of social identity of the four decision-makers and over the observation time serves as a condensed metric for decision-makers’ identification with the organization. In terms of the formal description of the model, this measure averages the \(si^r(t)\) (see Equation 8 and 9 ) of the four decision-makers over the \(T=240\) time steps of observation (and in average over simulation runs per scenario). This leads us to expect rather low levels of this metric. In the course of the search processes, the units move towards higher levels of performance while the alterations decline. In consequence, performance changes (c-org perf) and also distances across units (d-unit perf and d-effort ) decline over time.
  • Two metrics inform about the effectiveness of the search: (1) the mean of the final performance, \(\overline{V}_{t=240}\), achieved in the 5000 simulation runs for a particular scenario6, and (2) the relative frequency of how often the global maximum of the respective performance landscape is found at the end of the observation period.
  • Three metrics are employed to gain a deeper understanding of the organizations’ search processes: The average effort per period informs about the average extent of change (in terms of bits flipped in the binary decision problem) per period. The ratio of periods in which the status quo is altered may indicate the diversity of search. In contrast, the ratio of periods with false-positive alterations, i.e., alterations in favour of a false-positive option (i.e., reducing \(V_t\)), to the \(T=240\) observation periods gives an idea of the quality of alterations.

Table 3 displays the average levels of social identity for the different levels of task complexity and coordination modes, i.e., for experiments types A to C. Table 4 reports the performance differences of scenarios where managers’ organizational identity may get activated against the respective scenario without activation. The baseline scenarios I.a.1 to I.d.1 (Type A experiments, i.e., decomposable structure with “decentralized” mode) are displayed in the upper left block of these tables.

Observations from Type A experiments

The results for the baseline scenarios allow the following observations:

  • Observation 1: Among the “single” activation mechanisms, the “distance of effort” mechanism induces the highest level of organizational identification, while the “change of organizational performance” leads to a very low identification. The level of organizational identity emerging with the “combined” mechanisms is below the sum of averages from the single activation mechanisms.
  • Observation 2: The level of managers’ identification with the organization tends to be associated with the average effort level provided per period, the ratio of periods with alterations, and the false-positive moves accordingly.
  • Observation 3: Identification based on “distance of effort” leads to significant performance losses, while the “change of organizational performance” induces low but significant performance gains – both compared against the scenario without managers’ organizational identification. The “distance of unit performance” has slightly positive performance effects.
Performance-based activation mechanisms (“c-org-perf” and “d-unit-perf”)

For explaining the observations, it is helpful to recall that no interactions among the managers’ sub-problems exist in the decomposable structure. Hence, if all managers were able to evaluate alternatives perfectly, they would find their respective local optima within a few time steps, which – due to perfect decomposability – would also result in the optimal solution at the organizational level.

Table 2:Condensed results of Type A (baseline scenarios) and Type B (variation of task complexity) experiments. Confidence intervals (CI) are given at a confidence level of 0.99 percent. For parameter settings see Table 1.
Scenario Avg. SocId per decision-maker and period (\(\pm\)CI) Final performance \(\overline{V}_{t=240}\) (\(\pm\)CI) Frequency of global maximum in \(t=240\) Average effort per period Ratio of periods with altered configs. \(\vec{d}\) Ratio of false-positive alterations
I. Decomposable (\(K^{ex}=0\))
a. c-org perf. 0.00039 \(\pm\)0.00003 0.9922 \(\pm\)0.0008 57.76% 0.3861 21.05% 9.70%
b. d-unit perf. 0.01148 \(\pm\)0.00017 0.9895 \(\pm\)0.0009 52.24% 0.4483 23.77% 11.51%
c. d-effort 0.08856 \(\pm\)0.00171 0.9691 \(\pm\)0.0018 28.90% 1.2151 64.65% 31.91%
d. combined 0.07056 \(\pm\)0.00171 0.9757 \(\pm\)0.0017 39.80% 0.9502 50.71% 24.96%
e. no SI 0 \(\pm\)0 0.9885 \(\pm\)0.001 49.68% 0.4321 25.43% 12.00%
II. Near decomposable (\(K^{ex}=1\))
a. c-org perf. 0.00440 \(\pm\)0.00023 0.9462 \(\pm\)0.0026 23.60% 0.5191 25.98% 12.84%
b. d-unit perf. 0.01233 \(\pm\)0.00017 0.9388 \(\pm\)0.0031 20.62% 0.5776 27.77% 13.88%
c. d-effort 0.06735 \(\pm\)0.00141 0.9047 \(\pm\)0.0043 14.52% 1.3308 61.83% 31.01%
d. combined 0.05748 \(\pm\)0.00131 0.9265 \(\pm\)0.0038 25.18% 1.0615 49.22% 24.65%
e. no SI 0 \(\pm\)0 0.9375 \(\pm\)0.003 21.08% 0.5644 27.08% 13.41%
III. Non-decomposable medium (\(K^{ex}=3\))
a. c-org perf. 0.02612 \(\pm\)0.00048 0.8203 \(\pm\)0.0063 10.72% 1.8051 71.72% 36.38%
b. d-unit perf. 0.01605 \(\pm\)0.00015 0.8636 \(\pm\)0.0055 9.44% 1.407 55.39% 28.00%
c. d-effort 0.06534 \(\pm\)0.00075 0.8019 \(\pm\)0.0061 7.04% 2.0278 81.08% 41.18%
d. combined 0.06134 \(\pm\)0.00095 0.8484 \(\pm\)0.0063 13.68% 1.6553 65.83% 33.14%
e. no SI 0 \(\pm\)0 0.8457 \(\pm\)0.0062 8.40% 1.5833 63.13% 31.98%
IV. Non-decomposable high (\(K^{ex}=6\))
a. c-org perf. 0.04112 \(\pm\)0.00037 0.7071 \(\pm\)0.0065 2.10% 2.4424 90.40% 45.88%
b. d-unit perf. 0.01969 \(\pm\)0.00011 0.7405 \(\pm\)0.0071 3.98% 2.2044 82.24% 41.79%
c. d-effort 0.05986 \(\pm\)0.00047 0.7048 \(\pm\)0.0065 3.38% 2.4061 90.26% 45.92%
d. combined 0.07096 \(\pm\)0.00059 0.7188 \(\pm\)0.0069 4.54% 2.3913 87.54% 44.34%
e. no SI 0 \(\pm\)0 0.7182 \(\pm\)0.0067 2.40% 2.3317 88.09% 44.72%

From this, an explanation for the low levels of identification observed for the “c-org-perf” and the “d-unit-perf” activation mechanism (observation 1) could start. The performance inclines that unit heads reasonably achieve – and this, in principle, independent from each other – lets the “distance of unit performance” be at low levels, which induces low identification. In consequence, unit heads put low focus on the “rest” of the organization, which here does not only reflect the decomposable structure but also prevents unit heads from being affected by (imperfect) evaluations of the residual performance (Equation 8). However, it is worth noticing that the identification from the “d-unit-perf” mechanism remains at a low positive level (see left plot in Figure 4). This results from unit heads’ cognitive limitations: as our unit heads cannot perfectly ex-ante evaluate their options and are not endowed with memory, they repeatedly implement promising options that turn out as false positive alterations after implementation. A false positive alteration, in turn, tends to let a unit’s performance go below the average of the units and, thus, increases organizational identification according to the “distance of unit performance” mechanism.

For the decomposable structure, also organizational performance shows quick enhancements (i.e., by units independently locating the local optima), which leads to low levels of identification from the “changes of organizational performance” mechanism. Moreover, it is notable that performance declines and inclines of unit performances may level off in summing up for the organizational performance. This further dampens changes in overall performance, and, thus, the identification level from this mechanism is close to zero (observation 1).

Effort-based activation (“d-effort”)

However, in the model, managers cannot correctly evaluate their options in advance. For example, they may also consider interactions among sub-problems that, in fact, do not exist (“phantom” cross-unit interactions). Moreover, decision-makers cannot anticipate their fellow decision-makers’ choices but assume that these will stay with the status quo. Hence, a manager \(r\) that identifies more with the organization and, thus, with the overall objective will even more likely react to decisions by other managers \(q \neq r\), which affects the \(r\)’s residual performance component in Equation 8. Mutual adjustments are the consequence, which relates to observation 2.

These considerations explain the high levels of identification resulting from the “distance of effort” mechanism in some kind of interrelated “chain reactions”: In tendency, past low-effort managers show the highest level of organizational identification and, according to Equation 8, they will then put more emphasis on the “residual” performance and, with that, due to imperfect ex-ante evaluations, in the decomposable structure also on “phantom” interactions. This reasonably leads to adjustments (observation 2), so that these past below-average-effort managers are then above the average and, hence, according to the “distance of effort” mechanism, next a reduction of these managers’ identification follows; in contrast, those managers with, so far, low level of identification due to past above-average effort will then increase their identification for the following period and so forth. It is worth emphasizing, that each adjustment in the organizational identification induces that managers (imperfectly) evaluate the status quo and their options against a modified objective function, which induces further alterations and, thus, destabilizes search processes. Moreover, the frequent alterations are ineffective since, in the decomposable structure, they are made in consideration of “phantom” interactions which lead the units astray from the local maxima of their decision problems. This further explains, the low frequency of global maximum found (about 29 percent, see Table 2) compared to the other scenarios. These considerations also relate to observation 3 and, in the next section, will be further developed for the type B experiments on effects of task complexity.

Combination of activation mechanisms (“combined”)

Based on the preceding analysis of the “single” activation modes, next, we turn to the combination of mechanisms. In particular, the observation (1) that the identification induced by the “combined” mechanism is below the sum of identification levels from the single mechanisms deserves attention (see Table 2, scenario I.d. versus scenarios I.a. to I.c. and left plot in Figure 4). This observation suggests that interactions among the single activation mechanisms occur, should they be effective in combination with each other. Figure 5 illustrates the interactions with an example of only two managers: manager 1 decides to switch one of the binary choices assigned to her/him, while manager 2 chooses to keep the status quo. Moreover; manager 1’s choice might be false positive – due to imperfect ex-ante evaluations – and, thus, reduce unit 1’s performance. As Figure 5 illustrates, for both managers, the emerging effects from the single activation mechanisms on their respective organizational identification go in different directions, i.e., (partially) offsetting the single mechanisms’ effects in combination.

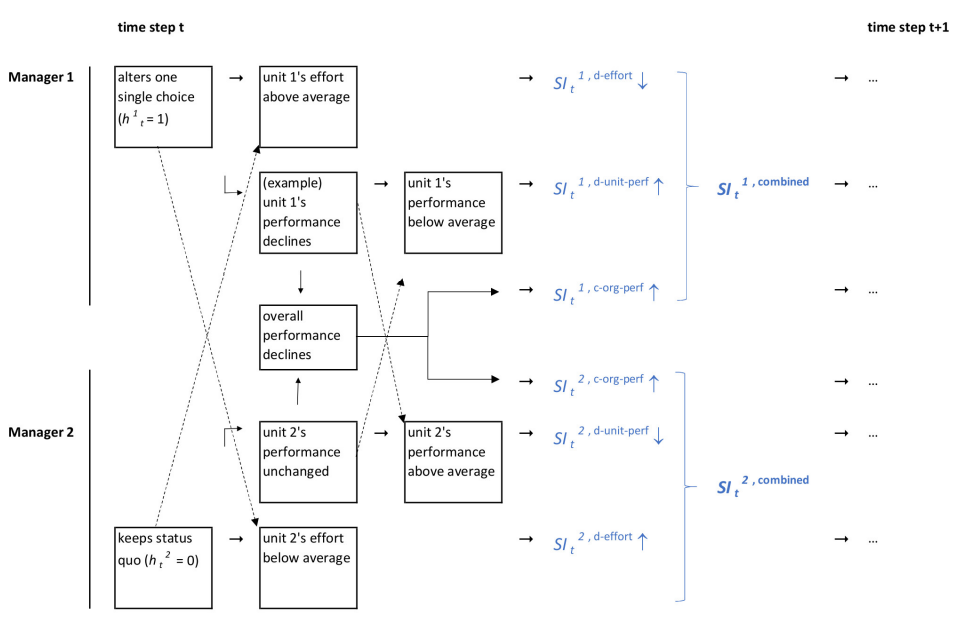
Effects of task complexity (Type B experiments)

Observations from Type B experiments

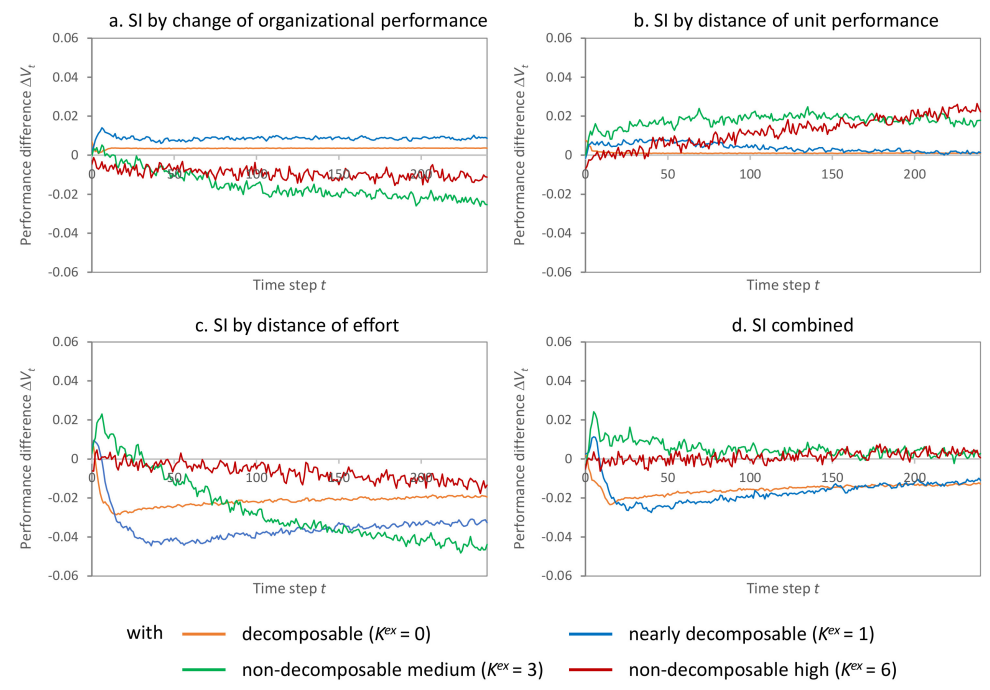
In the next step of the analysis, we turn to scenarios where interactions across units’ partial decision problems exist. Table 2 also reports simulation results for scenarios with cross-unit interdependencies of levels \(K^{ex} \in \{1, 3, 6\}\) (for the metrics see paragraph 4.3). In column “1. Decentralized” of Table 3 the average levels of social identity per decision-maker and over time are displayed. Moreover, the respective column in Table 4 reports the performance differences achieved with the different activation mechanisms against the respective “no social identity” scenario. The plots in Figure 6 show the differences of performance against the respective “no social identity” scenarios for the activation mechanisms and levels of task complexity under investigation. The results may be summarized in the following observations:

  • Observation 4: As for the organizational identification of decision-makers, the activation mechanisms are differently sensitive to task complexity. With the “distance of effort” mechanism, the identification declines with increasing complexity. In contrast, the “distance of unit performance” and the “change of organizational performance” mechanisms lead to an incline of identification with increasing task complexity.
  • Observation 5: Organizational identification per se is neither universally beneficial nor detrimental for the organizational performance compared to “no social identity”. Instead, the activation mechanism shapes the direction of effects: The activation by “distance of effort” appears to be detrimental for all levels of complexity; in contrast, the “distance by unit performance” mechanism has positive effects for all levels of complexity. The “change of organizational performance” is detrimental when task complexity is high.
Table 3:Average levels of social identity during search processes for different activation mechanisms and coordination modes. Half-lengths of confidence intervals at a confidence level of 0.99 percent. For parameter settings see Table 1
1. Decentralized 2. Sequential 3. Lateral Veto 4. Proposal
I. Decomposable (\(K^{ex}=0\))
a. c-org perf. 0.00039 \(\pm\)0.00003 0.00048 \(\pm\)0.00003 0.00001 \(\pm\)0 0.00009 \(\pm\)0.00001
b. d-unit perf. 0.01148 \(\pm\)0.00017 0.01144 \(\pm\)0.00017 0.01635 \(\pm\)0.00027 0.01112 \(\pm\)0.00017
c. d-effort 0.08856 \(\pm\)0.00171 0.02027 \(\pm\)0.00131 0.00139 \(\pm\)0.00019 0.01139 \(\pm\)0.00086
d. combined 0.07056 \(\pm\)0.00171 0.03561 \(\pm\)0.00142 0.01701 \(\pm\)0.00033 0.02029 \(\pm\)0.00071
II. Near decomposable (\(K^{ex}=1\))
a. c-org perf. 0.0044 \(\pm\)0.00023 0.00397 \(\pm\)0.0002 0 \(\pm\)0 0.00031 \(\pm\)0.00004
b. d-unit perf. 0.01233 \(\pm\)0.00017 0.01204 \(\pm\)0.00017 0.01985 \(\pm\)0.00036 0.01485 \(\pm\)0.00022
c. d-effort 0.06735 \(\pm\)0.00141 0.03607 \(\pm\)0.0015 0.00041 \(\pm\)0.00003 0.0049 \(\pm\)0.00034
d. combined 0.05748 \(\pm\)0.00131 0.04314 \(\pm\)0.00136 0.01965 \(\pm\)0.00035 0.01733 \(\pm\)0.00034
III. Non-decomposable medium (\(K^{ex}=3\))
a. c-org perf. 0.02612 \(\pm\)0.00048 0.01164 \(\pm\)0.00035 0 \(\pm\)0 0.00029 \(\pm\)0.00002
b. d-unit perf. 0.01605 \(\pm\)0.00015 0.01416 \(\pm\)0.00016 0.02348 \(\pm\)0.00043 0.01691 \(\pm\)0.00025
c. d-effort 0.06534 \(\pm\)0.00075 0.06014 \(\pm\)0.00148 0.0002 \(\pm\)0.00001 0.00271 \(\pm\)0.00014
d. combined 0.06134 \(\pm\)0.00095 0.05323 \(\pm\)0.0013 0.0233 \(\pm\)0.00041 0.01834 \(\pm\)0.00027
IV. Non-decomposable high (\(K^{ex}=6\))
a. c-org perf. 0.04112 \(\pm\)0.00037 0.02466 \(\pm\)0.00043 0 \(\pm\)0 0.00029 \(\pm\)0.00002
b. d-unit perf. 0.01969 \(\pm\)0.00011 0.01679 \(\pm\)0.00014 0.02502 \(\pm\)0.00044 0.02026 \(\pm\)0.00029
c. d-effort 0.05986 \(\pm\)0.00047 0.07761 \(\pm\)0.00131 0.00013 \(\pm\)0.00001 0.00194 \(\pm\)0.00008
d. combined 0.07096 \(\pm\)0.00059 0.0725 \(\pm\)0.0013 0.02477 \(\pm\)0.00044 0.02091 \(\pm\)0.00029
Table 4:Mean differences of final performance \(V_{t=240}\) achieved with different activation of social identity against the respective “no social identity” scenario for different coordination modes. Half-lengths of confidence intervals at a confidence level of 0.99 percent; * indicates a significant performance difference. For parameter settings see Table 1
Scenario 1. Decentralized 2. Sequential 3. Lateral Veto 4. Proposal
I. Decomposable (\(K^{ex}=0\))
no SI (base) 0.9885 0.9912 0.9221 0.9776
a. c-org perf. 0.0036 \(\pm\)0.0009* -0.0015 \(\pm\)0.0009* -0.0015 \(\pm\)0.0031 0.001 \(\pm\)0.0015
b. d-unit perf. 0.001 \(\pm\)0.001 -0.0032 \(\pm\)0.0009* 0.0021 \(\pm\)0.003 0.0011 \(\pm\)0.0015
c. d-effort -0.0195 \(\pm\)0.0015* -0.0024 \(\pm\)0.0009* 0.0053 \(\pm\)0.003* 0.0026 \(\pm\)0.0015*
d. combined -0.0128 \(\pm\)0.0014* -0.0019 \(\pm\)0.0009* 0.0061 \(\pm\)0.003* 0.0051 \(\pm\)0.0014*
II. Near decomposable (\(K^{ex}=1\))
no SI (base) 0.9375 0.943 0.8401 0.9323
a. c-org perf. 0.0087 \(\pm\)0.0028* 0.0024 \(\pm\)0.0024* 0.0072 \(\pm\)0.0042* -0.0021 \(\pm\)0.0025
b. d-unit perf. 0.0013 \(\pm\)0.003 0.0039 \(\pm\)0.0025* 0.0029 \(\pm\)0.0042 -0.0044 \(\pm\)0.0026*
c. d-effort -0.0328 \(\pm\)0.0037* 0.0047 \(\pm\)0.0025* 0.0033 \(\pm\)0.0043 0 \(\pm\)0.0025
d. combined -0.011 \(\pm\)0.0034* 0.0021 \(\pm\)0.0025 0.0073 \(\pm\)0.0042* 0.0059 \(\pm\)0.0026*
III. Non-decomposable medium (\(K^{ex}=3\))
no SI (base) 0.8457 0.8941 0.7853 0.8907
a. c-org perf. -0.0254 \(\pm\)0.0063* 0.0013 \(\pm\)0.0041 0.0015 \(\pm\)0.0046 -0.0025 \(\pm\)0.0029
b. d-unit perf. 0.0179 \(\pm\)0.0058* 0.0165 \(\pm\)0.004* 0.0053 \(\pm\)0.0047* 0.003 \(\pm\)0.003*
c. d-effort -0.0438 \(\pm\)0.0061* 0.0066 \(\pm\)0.004* 0.0051 \(\pm\)0.0046* 0.0042 \(\pm\)0.0029*
d. combined 0.0027 \(\pm\)0.0062 0.0225 \(\pm\)0.0039* 0.0008 \(\pm\)0.0046 0.0035 \(\pm\)0.0029*
IV. Non-decomposable high (\(K^{ex}=6\))
no SI (base) 0.7182 0.8233 0.7511 0.8502
a. c-org perf. -0.0112 \(\pm\)0.0066* -0.0023 \(\pm\)0.0059 -0.004 \(\pm\)0.0045 -0.0009 \(\pm\)0.003
b. d-unit perf. 0.0222 \(\pm\)0.0069* 0.0206 \(\pm\)0.0058* 0.003 \(\pm\)0.0045 -0.0064 \(\pm\)0.003*
c. d-effort -0.0135 \(\pm\)0.0066* 0.0124 \(\pm\)0.0056* -0.0023 \(\pm\)0.0045 0.0001 \(\pm\)0.003
d. combined 0.0006 \(\pm\)0.0068 0.034 \(\pm\)0.0055* 0.0024 \(\pm\)0.0045 0.0013 \(\pm\)0.003
Frequent mutual adjustments and activation mechanisms

The interactions among units’ decision problems serve as a starting point for explaining these observations. In particular, in non-decomposable structures, the choices of a manager \(r\) also affect the performance contributions of other decision-makers \(q\neq r\). In the model, decision-makers cannot anticipate their fellow managers’ choices perfectly but assume that they will stay with their status quo. Hence, at the end of each time step \(t\), managers may experience surprises due to fellow managers’ choices (see Figure 2), which lets managers mutually adjust their choices in the next period – though based on imperfect evaluations. This effect is the more pronounced the higher the task complexity as the average effort per period, and the ratio of alterations in Table 2 indicate.

Given that these dynamics also apply to search in the “no-identity scenario", for a start, the question arises what the”distance of effort" mechanism may add to the level of effort, or alterations respectively. This mechanism induces high (low) identification with the organization when the differences between the decision-makers’ effort (i.e., number of single choices altered in a period) are high (low). However, non-decomposability leads to frequent mutual adjustments by decision-makers as argued above and, hence, higher levels of intra-unit interactions \(K^{ex}\) induce less identification from the “distance of effort” mechanism (observation 4). In contrast, frequent mutual adjustments – based on imperfect ex-ante evaluations – also mean that the unit’s performances fluctuate. This may lead to altered distances of unit performance which is why identification based on the “distance of unit performance” mechanism inclines with the task complexity (observation 4). In a similar vein, alterations due to frequent mutual adjustments by decision-makers also induce fluctuations in the overall organizational performance. This translates into organizational identification from the “change of organizational performance” mechanism increasing with task complexity (observation 4).

Destabilization vs. productive “entrenchment”

With respect to the performance effects of organizational identification in conjunction with task complexity (observation 5), it is helpful to start with a general consideration on task complexity and decision-makers’ objective functions: With cross-unit interactions (i.e., \(K^{ex}>0\)), the global maximum cannot be found by locating the maxima of units’ decision-problems. In this sense, unit heads taking the “external” effects of their choices into account appropriately reflect the interaction structure. Hence, identification with the organization (i.e., levels \(si^{r}(t)>0\) in decision-makers’ objective function as given in Equation 8) promises to be beneficial with respect to overall performance when cross-unit interactions exist. This conjecture is also in line with prior research (Bushman et al. 1995; Siggelkow & Rivkin 2005; Wall 2017).

However, the results (Figure 6 and column 1 in Table 4) indicate that organizational identification based on the “distance of effort” mechanism is significantly detrimental for non-decomposable structures compared to the “no social identity” scenario. The “change of organizational performance” is detrimental when task complexity is high (i.e., \(K^{ex}=3\) and \(K^{ex}=6\)). In these cases, contrary, the “distance of unit performance” mechanism is significantly beneficial for organizational performance. These results indicate that the activation mechanisms studied unfold different dynamics in conjunction with task complexity. Regarding the “d-effort” and the “ch-org perf” mechanisms, it was argued above, that these mechanisms lead to many alterations (see paragraph 4.14), which induces a destabilization of search. For example, solutions with high levels of organizational performance may be abandoned “accidentally”. This may happen since a unit head’s objective function has changed (because her/his identification \(si^{r}(t)\) is modified) and/or since the fellow managers’ did no stay with their status quo.

The question remains why the “distance of unit performance” mechanism results in such significant performance excesses of around 2 points of percentage against the “no social identity” scenarios for higher levels of complexity (see also Figure 6.b). We argue, that this mechanism unfolds a temporary “entrenchment” effect that stabilizes search: Let us assume that unit 1’s performance is above average, and, consequently, unit 1’s organizational identification decreases. Hence, in the next period, unit 1 puts less or no focus on the rest of the organization, making it less likely that this momentarily high-performing unit abandons its status quo solution – including moves in favour of false-positive options. (Please, recall that in the model, units’ ex-ante evaluations on the “rest” of the organization are noisier than on the own decision problem.) Consequently, the below-average performing decision-makers are less likely to experience surprises from their fellow above-average managers’ choices, which further stabilizes search. Hence, the “distance of unit performance” mechanism stabilizes search in that momentarily above-average performing decision-makers are more likely to keep their status quo which propagates to the other units in terms of fewer surprises. This is the more relevant, the higher the level of cross-unit interactions. This explanation is supported by the ratio of alterations (and of false-positive moves, correspondingly), which, with the “d-unit perf” mechanism, is considerably below the levels obtained in the “no social identity” scenarios for \(K^{ex}=3\) and \(K^{ex}=6\) as reported in Table 2.

Effects of the coordination mode (Type C experiments)

Observations from Type C experiments

In the scenarios analysed so far, the organizations merely employ “results controls” (see paragraph 1.5): at the end of every time step, each unit head is informed about the overall organizational performance and the respective unit’s performance contribution, which may serve as a basis for a unit head’s rewards. In the experiments introduced now, the organizations also make use of “action controls”, i.e., coordination mechanisms that delimit in some way the discretion of unit heads (see paragraph 2.20 to 2.23). Results are reported in Tables 3 and 4 and for “sequential planning” in Figure 7 – particularly in comparison to Figure 6 for the “decentralized” mode. The results allow for the following observations:

  • Observation 6: As for the organizational identification, the activation mechanisms show different sensitivity to the coordination mode. With tight coordination (lateral veto, proposal), the “change of organizational performance” and “distance of effort” mechanisms lead to low organizational identification. In contrast, the “distance of unit performance” mechanism appears to be less sensitive to the coordination mode.
  • Observation 7: The performance effects of organizational identification vary with the coordination mode: With tight coordination (lateral veto, proposal), organizational identification has low effects on final performance. In contrast, with “sequential planning”, organizational identification has predominantly positive performance effects when, at least, some interactions across units exist, which holds for all activation mechanisms.
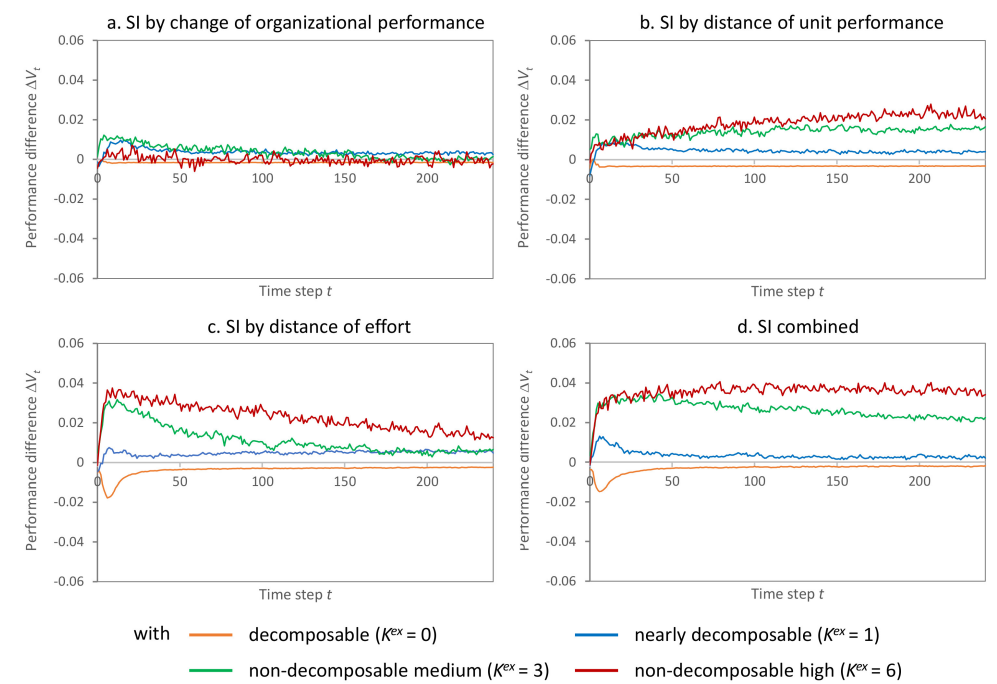
Coordination and performance losses (“c-org-perf”)

For a deeper analysis, recalling the purpose of action controls may serve as a starting point. To ensure that decisions are made in favour of the overall organizational objectives, a purpose is to “delineate the acceptable domain of activity for behaviour of organizational participants” (Simons 1994 p. 39). With cross-unit interdependencies, detrimental “external” effects of one unit’s choices may occur that reduce overall performance, which is why the need for coordination increases with task complexity.

This directly refers to the activation of organizational identification by “change of organizational performance” (observation 6): If coordination is effective, at least, losses in overall performance should be less likely and, hence, organizational identification from this activation mechanism is rather low. For example, in the “proposal” mode, the identification based on the “c-org-perf” mechanism is about one to two magnitudes smaller compared against the “decentralized” mode (see Table 3), and, with “lateral veto” power, identification is (close to) zero. In the proposal mode, the headquarter evaluates the option resulting from unit heads’ proposals against the status quo and only decides in favour of an alteration if it promises an increase in overall performance. Hence, an identification-inducing performance decline only could happen in case of false-positive evaluations by the headquarter (Sah & Stiglitz 1986; Wall 2016). With lateral veto power, whenever one unit head expects to experience a decline for her/his objective from the first preference of one of the fellow managers, this unit head vetoes so that no alterations at all happen in that time step and the status quo is kept. With this, an alteration that may reduce organizational performance is rather unlikely and could only happen in case of false-positive evaluations by all other unit heads. Hence, the “c-org-perf” activation mechanism of organizational identification is fairly ineffective when units have lateral veto power, as the results reflect.7. And even with “sequential planning” the “c-org-perf” activation induces low identification, since the potential “surprises” from fellow managers’ choices are stepwise reduced.

In this sense, coordination “reduces” (sequential planning) or “withdraws” (proposal, lateral veto) the basis, i.e., performance losses, for inclining organizational identification based on the “c-org perf” activation mechanism (observation 6). Accordingly, the performance effects are low (observation 7).

Tight coordination (“lateral veto”, “proposal”) and effort (“d-effort”)

These considerations also contribute to explain the relatively low identification and performance effects emerging from the “distance of effort” mechanism for the “lateral veto” and the “proposal” mode. As argued above, these types of action controls reduce the alterations and, correspondingly, the effort per period since the criteria to be met for any change of the status quo are relatively strict. (For example, for \(K^{ex}=6\), the average effort per period is about 0.5 in the proposal mode, about 0.08 with lateral veto power, compared to around 2.4 in the decentralized mode, i.e., when unit heads have full autonomy). Hence, the units do not differ that much for the effort taken, and, in consequence, the identification resulting from the “distance of effort” mechanism is relatively low when coordination is tight (observation 6). This also explains the relatively low performance effects that this activation mechanism induces for the lateral veto and the proposal mode (observation 7).

Lateral veto power and (polarization by) unit performance (“d-unit perf”)

In contrast, with lateral veto power, the “distance of unit performance” mechanism tends to induce a higher identification for a given interaction structure, while similar levels of identification emerge for the decentralized, the sequential, and the proposal mode (observation 6).

Of particular interest is the high level of identification induced by the “d-unit-perf” mechanism with lateral veto power. An explanation lies in the persistence of differences between units that this coordination mechanism reasonably evokes: Let us assume a unit \(r\) in time step \(t-1\) has an above-average unit performance (\(P^{r,own}\)). This means that, in period \(t\), \(r\)’s identification with the organization is relatively low, and \(r\) focuses (even more) on the own performance (see Equation 8). Unit head \(r\) will veto against an alteration preferred by a below-average performing unit \(q\) which \(r\) regards detrimental for her/his objective – may the other unit’s alteration be of actual or only perceived harm to \(r\)’s objective. This, in turn, means that unit \(q\) cannot improve the solution for her/his own partial decision problem, while unit \(r\) remains at its above-average performance. In consequence, with the “d-unit perf” mechanism, below-average unit head \(q\)’s organizational identification further inclines. At the same time, above-average manager \(r\)’s identification with the organization declines (delimited to zero), which means that, in the next period \(t+1\), unit \(r\) will focus (even more) on the own performance (see Equation 8 and fn. fn7). It is worth mentioning that the differences in unit performance in the model are random driven (namely by the initial configuration, the alternative options discovered, noise in ex-ante evaluations) since, in the experiments, the unit heads are homogeneous, for example, in their information processing capabilities, search behaviour, scope of competencies.

These considerations suggest that lateral veto power combined with the “distance of unit performance” mechanism tends to perpetuate – even random-driven – performance differences between units and, in this sense, also to “polarize” between units: low-performing units with high identification and higher-performing units with low identification.

Sequential planning and horizontal information flows

While the organizational identification and performance effects are relatively low when tight coordination (lateral veto power or hierarchy in the proposal model) is employed, the emerging effects are notable for “sequential planning” (observation 7). As can be seen from Figure 7 – also in comparison to Figure 6 – for each activation mechanism performance excesses compared to “no identification” are achieved if at least minimal cross-unit interactions (i.e., \(K^{ex}\geq 1\)) exist. Performance excesses from the two “distance-based” activation mechanisms tend to increase with the level of task complexity. In the vast majority of scenarios, the respective excesses in final performance compared to the respective “no-identity” scenarios are significant (Table 4).

For explaining these effects, it is helpful to start with the particular traits of this coordination mode. Sequential planning partially mitigates the unit head’s imperfect knowledge about the fellow managers’ choices. Due to sequential decision-making, a manager \(r>1\) is informed about the choices of those managers preceding in the sequence and can revise her/his preferences accordingly. Hence, fewer surprises from fellow managers’ choices occur, and, from this, mutual adjustments are reduced considerably compared to the decentralized mode (by a third to a half). At the same time, those alterations that happen, in tendency, are more beneficial for unit heads’ \(r>1\) respective objectives: choices in favour of leaving the status quo build on better knowledge. The horizontal information flow about choices made so far in the sequence is the more relevant, the higher task complexity due to cross-unit interactions. As for the “distance of effort” mechanism, those units managers \(r>1\) with below-average effort in the past will identify more with the organization and, hence, will put more focus on overall performance – and this with better information than in the decentralized structure which is particularly relevant when complexity is high. In a similar vein, the “distance of unit performance” mechanism lets below-average performing managers \(r>1\) – via increased identification – consider overall performance even more and based on better information than available in the decentralized mode.

Hence, the driving force behind the remarkable beneficial performance effects of the two distance-based activation mechanisms is that sequential planning causes horizontal information flows across units. This is particularly relevant when task complexity is high and, hence, local decision-making without considering externalities is inappropriate.

Discussion and future research

A particular feature of the agent-based simulation model on social identity in organizations introduced in this paper is that decision-makers’ identification with the organization is endogenously emerging. Decision-makers’ organizational identification – governed by different activation mechanisms – is a cause and a consequence of the dynamics unfolding in the organizations’ search for superior performance (Figure 1). Overall, the simulations suggest that the activation mechanisms in conjunction with organizational contingencies considerably shape the emerging dynamics of identification and performance effects. The results could be condensed into three key findings:

  • First, the results indicate that organizational identification is not universally beneficial, which supports findings of prior research (Alvesson & Willmott 2002; Bernard et al. 2016; Caprar et al. 2022; Ellemers et al. 2004; van Knippenberg & Ellemers 2003).
  • Second, the agent-based model allows to vary organizational contingencies which reveals that the task complexity and the prevailing coordination mode may considerably affect both organizational members’ identification and the performance effects thereof.
  • Third, the results highlight that not only the level of organizational identification but also the cause, i.e., the activation mechanisms for identification, shape the performance effects of organizational identity.

The following aims at discussing these results and highlighting avenues for future research. We focus on four aspects, i.e., activation mechanisms, traits of organizational members, the prevailing type of coordination, and its meaning for empirical research in organizational control.

Towards a comparative perspective on activation mechanisms

An important aspect highlighted by the model is that the activation mechanisms of identification differ in the unfolding dynamics and performance effects, which may induce further consequences in the organization in terms of, for example, entrenchment or polarization across units.

The activation by “change of organizational performance”, taken together, has the lowest and, if at all, primarily adverse performance effects. This mechanism neither builds on nor enhances temporary heterogeneity across decision-makers and, in the experiments, has the same effect on every decision-maker’s objective function. In contrast, the two activation mechanisms that are driven by the mutual comparisons across decision-makers build on endogenous heterogeneity across actors (“distance”) that may have emerged in the course of search (even though the decision-makers are homogeneous apart from the sub-tasks which, however, are equal-sized and symmetric regarding interactions).

The “distance of unit performance” mechanism is relatively insensitive to the organizational context in terms of task complexity and coordination mode and has predominantly positive effects on organizational performance in the vast of majority of contexts studied. This is of particular interest as the “distance of unit performance” mechanism may arise out of an organizational culture emphasizing mission orientation according to Denison et al. (2014) and also is closely related to “results controls” (Merchant & Van der Stede 2017) (see paragraph 1.5). In this sense, one may regard organizational identification based on the “distance of unit performance” mechanism as an informal control that effectively complements the formal results controls (Cardinal et al. 2004; Kreutzer et al. 2016; Lechner et al. 2010).

However, the dynamics resulting from the “distance of unit performance” mechanism also direct to considerations on long-term power dynamics. This mechanism not only builds on temporary heterogeneity (“distance”) of actors but also may even increase heterogeneity. The simulations suggest that organizational units with above-average performance contributions may show some "entrenchment’’ which may be temporal (when task complexity is high) or, with lateral veto power, even may persist. In consequence, above-average and below-average units in terms of parochial performance emerge. While it is beyond the scope of the model presented here to study the organizational consequences of performance differences between organizational units, there is evidence on the potential long-term power effects as, for example, the allocation of resources or formal power in organizations (Li et al. 2017). Hence, an interesting avenue for future research may also be to study the power dynamics resulting from activation mechanisms that explicitly build on performance differences across organizational members or units.

The “distance of effort” mechanism induces an exceptionally high level of alterations in the search processes, which could reflect a high focus on adaptability as one of the five cultural dimensions in the widely accepted framework of organizational culture introduced by Denison et al. (2014). The results highlight that adaptability may have its downside for organizational performance due to a destabilization of search. However, among the limitations of the model presented here is that it does not comprise any long-run returns from adaptability itself (for example, increased customer loyalty from responsiveness or flexibility valued by customers). Moreover, a limitation of the simulation experiments presented here is that the effort (or diversity of search in terms of alterations) comes at no cost for the unit heads. Hence, an obvious extension of this simulation study is adding “cost of effort” to decision-makers’ objective functions. This may be particularly relevant for the dynamics emerging from the “distance of effort” mechanism since this type of activation induces, by far, the highest effort levels.

The simulations for the “combined” mechanism have uncovered that the “single” activation mechanisms may interact in a non-trivial way if individuals’ identification with the organization is subject to these activation rules simultaneously. However, it is worth mentioning that the model builds on a simple – for not to say: simplistic – additive combination of activation mechanisms. Hence, an exciting avenue for future research is to study other forms of combining activation rules for social identity.

Moreover, future research may wish to study further activation mechanisms – separately and in combination with each other. This appears particularly relevant as the simulations have uncovered that the activation mechanisms may remarkably affect the emerging dynamics and consequences for the organization.

Heterogeneity of organizational members

These considerations also refer to the homogeneity versus heterogeneity of decision-makers in the simulation experiments presented here: As mentioned above, the simulation experiments are conducted for a population of unit heads that are homogeneous concerning various attributes – namely the principal structure of their objective functions, the effective activation mechanism for organizational identification, the size of their respective partial decision-problems, the intra- and cross-unit interactions of choices, (zero) cost of effort, the precision of ex-ante evaluations and (lack of) memory. Nonetheless, heterogeneity may emerge endogenously in decision-makers’ objective functions from the two activation mechanisms driven by a comparison (“distance”) within the management circle – based on random effects, i.e., units’ initial configurations, noisy information, and options discovered. In particular, certain decision-makers may (temporarily) identify more than the fellow managers with the organization or the particular “own” sub-unit (or the self, depending on how the distance-mechanisms are interpreted, see paragraph 2.41.

Future work may consider to study the emergence of organizational identification for situations where decision-makers are (exogenously) heterogeneous, for example, with respect to their information-processing capabilities or their costs of effort. An interesting question then is how organizational identification, for example, affects behavioural and performance differences across organizational members. For example, reasonably, heterogeneous cost of effort across units would increase the distances in effort and, thus, the emerging identification of “high-cost” units from the “d-effort” mechanism. Correspondingly, differences in units’ accuracy of ex ante-evaluations would enhance the identification from the “d-unit perf” mechanism. Moreover, also the activation mechanisms could differ across decision-makers. This may reflect that, for example, some actors are more oriented towards innovation and change, while others focus on performance, capturing the personal traits of the individuals in the management circle. The emerging dynamics of and from organizational identification may also be of interest in regard of the so-called personnel controls. In particular, simulations for management teams that are diverse in these and potentially other personality traits may provide insights on favourable compositions in the management circle.

The considerations about the composition of the management team direct to another dimension of unit heads’ homogeneity (implicitly) captured in our agent-based model: At the beginning of the observation period, all unit heads “start’’ without any identification with the organization, and they all remain in the organization. In more general terms, this corresponds to a situation where all unit heads get hired at the same time, have the same organizational”memory’’ and where, later on, there is no turnover. This directs to the simulation models of organizational culture of Harrison and Carroll (Carroll & Harrison 1998; Harrison & Carroll 1991, 2006). They focus on cultural transmission in terms of maintenance of organizational culture over time which is of particular interest regarding demographic heterogeneity vs. cultural heterogeneity or homogeneity of organizational members: in practice, organizational culture is often highly persistent over time while members enter and exit the organization which poses an interesting tension regarding cultural transmission. For studying the dynamics resulting from turnover and socialization of organizational members, Harrison and Carroll’s models capture three processes, namely (1) new members entering an organization, (2) enculturation of organizational members, and (3) members departing from the organization.

Following Halloran & Kashima (2006), culture and social identity are in a "reciprocal relationship: culture enables and influences social identity processes whereas social identity salience regulates the aspects of cultural knowledge that are emphasized in the context’’ (p. 150). Against this background, an exciting extension of the model presented here would include turnover processes in the management team and the enculturation of new members in the spirit of Harrison and Carroll. This would also mean integrating further activation mechanisms for social identification and including additional social interactions and effects such as alienation and susceptibility to socialization (Harrison & Carroll 2006) in the model.

A comparative view on coordination modes and identification

The simulations have uncovered that the dominant coordination mode – captured in action controls – together with task complexity and the activation mechanism considerably affects organizational identification and performance effects.

In particular, the effects of the coordination mode on the emergence of identification appear worth some further consideration here. The prevailing coordination mode remarkably shapes the “character” of an organization – for example, whether it is regarded “bureaucratic”, “hierarchical” or “organic” and, thus, the autonomy granted to subordinates or the information flows for mentioning just a few prominent characteristics attributed to organizations (Greenwood & Hinings 1993; Mintzberg 1980). The coordination mode is among the major organizational design options, which propagates to the configuration of action controls in management control systems (Merchant & Van der Stede 2017). Roughly speaking, one may say that action controls shape subordinates’ discretion based on a “top-down” organizational design choice.

The results of our simulation experiments suggest that these “top-down” means non-trivially affect the emerging identification of organizational members, i.e., a “bottom-up” emerging informal control mechanism. In particular, depending on the activation mechanism, tight coordination (i.e., hierarchical or lateral veto power) either considerably reduces organizational identification or – due to polarization in the organization – tight coordination may even increase identification compared to the “decentralized” mode (where, in fact, no action controls are employed). Regarding the performance effects, tight coordination overrides organizational identification regardless of the level of task complexity. In contrast, “sequential planning” – providing autonomy to subordinates while enforcing horizontal information flows and adaptation – induces notable identification with the organization; moreover, if, at least, the task is of some complexity, “sequential planning” leads to remarkable performance excesses for the vast majority of cases studied. Hence, organizational identification apparently complements coordination by “sequential planning”

These results suggest that organizational identification may be particularly effective and productive when the prevailing type of coordination grants some decision-making autonomy to subordinates and lets subordinates interact via information transfer. This conjecture relates to Haslam (2004) who states: “Conditions that allow for social identity-based interaction should also allow group productivity to exceed that of individuals working in isolation by means of its capacity to foster, among other things, information exchange, transactive memory systems and mutual influence” (Haslam 2004 p. 181).

In sum, these results let us conjecture an association between subordinates’ autonomy and information transfer among subordinates on the one side and productive effects of organizational identification on the other side.

This conjecture, nonetheless, calls for further research efforts. First, it is worth mentioning that the endogeneity of organizational identification in this simulation study builds on a few activation mechanisms, which, of course, are neither meant to be exhaustive nor generally valid. Hence, studying other mechanisms for the activation of organizational identity appears a worthwhile extension. Second, an obvious extension is also to analyze further action controls in conjunction with organizational identity. Based on the findings of this study, those coordination mechanisms that leave considerable discretion at the site of subordinate decision-makers while relying on shared knowledge appear particularly promising. Third, should these extensions support the conjecture that organizational identification is particularly productive in settings granting autonomy and fostering knowledge transfer between subordinates, it is an obvious next step to seek for empirical evidence – whether that is in field studies or laboratory experiments. Moreover, future research may also wish to expand the context: an association between autonomy and identification with an overall system may not only be of interest in organizations (firms); it may also be of interest for broader societal contexts.

Avenues towards empirical research in organizational control

This paper primarily focuses on the agent-based model and the analysis of results obtained from the simulation experiments. Hence, a question is what this research effort and the results could mean for empirical research in organizational design, particularly organizational control.

A first partial response to this question lies in a general view of what a simulation model of social identity in organizations could contribute to the “empirical’’ side of control systems research. As outlined by Wall & Leitner (2021), formal models (analytical and simulation models) force the researcher to specify variables and functional relations, and the”solution’’ of a formal model – i.e., proofs in analytical models and numerical results in simulations (Chang & Harrington 2006) – may then reveal novel connections among variables.

Newly discovered connections could then be transferred into hypotheses to be tested in empirical research (for overviews of empirical research methods in management control, the reader may refer to Langfield-Smith (2006) or Speklé & Widener (2018)). In this vein, from the simulation results obtained in this study, hypotheses on the emergence and effects of social identification could be derived – taking, for example, the following type:

  • “With tight action controls, decision-makers’ identification with the organization is low.”
  • “The activation mechanism non-trivially affects the performance effects of decision-makers’ identification with the organization.”
  • “Lateral information flow among decision-makers fosters positive effects of identification with the organization in complex task environments.”

The empirical testing of hypotheses derived from this simulation study could then contribute to a design-oriented or practical perspective. Decision-makers’ identification with the organization refers to the “cultural controls’’ according to the classification of control mechanisms of Merchant & Van der Stede (2017) (see paragraph 1.5). It has for long been recognized that organizational control should not be seen as a mere”collection’’ of control mechanisms. Instead, while taking contingencies into account, internal consistency among an organization’s various control mechanisms (Grabner & Moers 2013) is the design goal for "management control systems’’ (Bedford & Malmi 2015; Malmi & Brown 2008; Merchant & Van der Stede 2017). In this sense, our results suggest combining action controls that grant high autonomy and enforce horizontal information flow with cultural controls that foster decision-makers’ organizational identity when the organizational task shows at least some complexity.

These considerations also refer to what has been named “identity work’’ (Alvesson & Willmott 2002): Organizations may take several actions to purposefully foster and affect the identification of organizational members with the organization. However, according to our results, employing tight coordination”overrides’’ organizational identification – with the consequence that resource-consuming “identity work’’ may be disputable. Moreover, our results also indicate that the”cause’’ for identification with the organization shapes the effects which may be relevant for "identity work’‘. For example, as argued above, social identification based on the relative unit performance (i.e., the “d-unit perf’’ mechanism in the model) corresponds to a strong mission orientation. However, according to our results, entrenchment and polarization effects are on the downside. Hence, designers of organizational controls and”identity workers’’ may consider whether they should seek to activate managers’ identification with the organization by building on other mechanisms.

Conclusion

This paper used an agent-based simulation to study the emergence and performance effects of subordinate decision-makers’ identification with the organization in conjunction with formal control mechanisms. The contributions of the paper are two-fold.

First, from a methodological perspective, the model presented may provide some evidence for the potential of agent-based modelling and simulation for studying social identity. A particular feature of the agent-based model introduced here is that subordinate decision-makers’ organizational identification is modelled as an endogenous variable – being a cause and a consequence of the dynamics unfolding in the artificial organizations. In particular, in the model, the activation mechanisms for decision-makers’ identification with the organization are fed by decision-makers’ efforts and performance effects – which are affected by the decision-makers’ organizational identity. As indicated in the discussion, various extensions of the simulations experiments could further highlight the potential of agent-based approaches for studying social identity. This includes, for example, investigating the effects of other activation mechanisms or organizations in which agents have heterogeneous activation mechanisms. However, the study may prove that agent-based modelling allows studying the contingent, emergent and dynamic traits of social identity, which could pose particular challenges for other research methods (Wall & Leitner 2021).

Second, the study contributes to the understanding of the dynamics and effects of social identity. In this vein, the results suggest that the activation mechanism of organizational identification in conjunction with contingencies like task complexity and formal control mechanisms subtly affect the performance effects and emerging organizational dynamics. Organizational identification appears particularly relevant when the control mechanisms employed grant some autonomy to subordinates. Moreover, the results suggest that identification with the organization may have its downsides: in interference with the control mechanisms, organizational identification may lead to temporal entrenchment or even pertinent polarisation between subordinates. While these results have to be considered against the background of the modelled activation mechanisms, they could pave the way for forming hypotheses that could ideally be tested in empirical research. Moreover, results may also be considered in contexts beyond the inner of organizations. In this vein, the interference between autonomy granted and individuals’ identification with an entirety also directs to broader societal contexts.

Acknowledgements

The author thanks the editorial team of this Special Issue for their initiative and the careful paper development process they organized. Namely, Bruce Edmonds, Geeske Scholz, and Nanda Wijermans provided helpful comments in the SIAM workshop, and Martin Neumann gave constructive feedback on previous versions of the paper. The comments of two anonymous reviewers further helped to improve the paper.

Notes

  1. The term satisficing results from merging satisfying and sufficing in the sense that, in a search process, a solution is found which is both satisfying and sufficing (Hoffrage & Reimer 2004).↩︎

  2. This requires that \(N \in \mathbb{N}\) is divisible by \(M\) without remainder. In the simulation experiments, \(N=12\) and \(M=3\), so that each partial problem comprises \(N^*=4\) single choices, see Table 1.↩︎

  3. For example, for a manager’s decision problem of size \(N^r=3\), three alternatives to the status quo with a Hamming distance \(h(\vec{d}^{r}_t)=1\), three alternatives with \(h(\vec{d}^{r}_t)=2\) and one with \(h(\vec{d}^{r}_t)=3\) exist. A manager first discovers nearest neighbors; next, options with \(h(\vec{d}^{r}_t)=2\) are found etc. where the sequence among equal-distanced options is randomly given.↩︎

  4. The model assumes that communication in the course of coordination works perfectly. For an investigation of the effects of unintended communications errors see Wall (2019).↩︎

  5. The observation period \(T\) was fixed based on pretests which indicate that the results do not principally change for more extended observation periods.↩︎

  6. Metrics related to the organizational performance \(V_t\) is given relative to the global maxima of the respective performance landscapes: otherwise, the results were not comparable across different performance landscapes.↩︎

  7. Moreover, it is worth mentioning that the lower a unit head’s organizational identification (i.e., the lower \(si^{r}(t)\)), the less likely it gets that alterations happen (which could turn out as false-positive and, thus, increase identification via the “c-org-perf” mechanism). This is because with lower \(si^{r}(t)\) a compensation of a lower “own” by a higher “residual” performance in \(r\)’s objective function (see Equation 8) gets less likely (Siggelkow & Rivkin 2005; Wall 2017).↩︎

References

AKERLOF, G. A., & Kranton, R. E. (2005). Identity and the economics of organizations. Journal of Economic Perspectives, 19(1), 9–32. [doi:10.1257/0895330053147930]

AKERLOF, R. (2016). “We thinking” and its consequences. American Economic Review, 106(5), 415–419. [doi:10.1257/aer.p20161040]

ALVESSON, M., & Kärreman, D. (2004). Interfaces of control: Technocratic and socio-ideological control in a global management consultancy firm. Accounting, Organizations and Society, 29(3), 423–444. [doi:10.1016/s0361-3682(03)00034-5]

ALVESSON, M., & Willmott, H. (2002). Identity regulation as organizational control: Producing the appropriate individual. Journal of Management Studies, 39(5), 619–644. [doi:10.1111/1467-6486.00305]

ASHFORTH, B. E., Harrison, S. H., & Corley, K. G. (2008). Identification in organizations: An examination of four fundamental questions. Journal of Management, 34(3), 325–374. [doi:10.1177/0149206308316059]

BAUMANN, O., Schmidt, J., & Stieglitz, N. (2019). Effective search in rugged performance landscapes: A review and outlook. Journal of Management, 45(1), 285–318. [doi:10.1177/0149206318808594]

BEDFORD, D. S., & Malmi, T. (2015). Configurations of control: An exploratory analysis. Management Accounting Research, 27, 2–26. [doi:10.1016/j.mar.2015.04.002]

BERNARD, M., Hett, F., & Mechtel, M. (2016). Social identity and social free-riding. European Economic Review, 90, 4–17. [doi:10.1016/j.euroecorev.2016.01.001]

BÉNABOU, R., & Tirole, J. (2011). Identity, morals, and taboos: Beliefs as assets. The Quarterly Journal of Economics, 126(2), 805–855.

BILLINGER, S., Stieglitz, N., & Schumacher, T. R. (2014). Search on rugged landscapes: An experimental study. Organization Science, 25(1), 93–108. [doi:10.1287/orsc.2013.0829]

BÖRGERS, T., & Sarin, R. (2000). Naive reinforcement learning with endogenous aspirations. International Economic Review, 41(4), 921–950.

BROWN, A. D. (2015). Identities and identity work in organizations. International Journal of Management Reviews, 17(1), 20–40. [doi:10.1111/ijmr.12035]

BUSHMAN, R. M., Indjejikian, R. J., & Smith, A. (1995). Aggregate performance measures in business unit manager compensation: The role of intrafirm interdependencies. Journal of Accounting Research, 33, 101–129. [doi:10.2307/2491377]

CAPLIN, A., Dean, M., & Martin, D. (2011). Search and satisficing. American Economic Review, 101(7), 2899–2922. [doi:10.1257/aer.101.7.2899]

CAPRAR, D. V., Walker, B. W., & Ashforth, B. (2022). The dark side of strong identification in organizations: A conceptual review. Academy of Management Annals, 16(2). [doi:10.5465/annals.2020.0338]

CARDINAL, L. B., Kreutzer, M., & Miller, C. C. (2017). An aspirational view of organizational control research: Re-invigorating empirical work to better meet the challenges of 21st century organizations. Academy of Management Annals, 11(2), 559–592. [doi:10.5465/annals.2014.0086]

CARDINAL, L. B., Sitkin, S. B., & Long, C. P. (2004). Balancing and rebalancing in the creation and evolution of organizational control. Organization Science, 15(4), 411–431. [doi:10.1287/orsc.1040.0084]

CARDINAL, L. B., Sitkin, S. B., & Long, C. P. (2010). A configurational theory of control. In S. B. Sitkin, L. B. CARDINAL, & K. M. Bijlsma-Frankema (Eds.), Organizational Control (pp. 51–79). Cambridge: Cambridge University Press. [doi:10.1017/cbo9780511777899.004]

CARROLL, G. R., & Harrison, J. R. (1998). Organizational demography and culture: Insights from a formal model and simulation. Administrative Science Quarterly, 43(3), 637–667. [doi:10.2307/2393678]

CHANG, M.-H., & Harrington, J. E. (2006). Agent-based models of organizations. In L. Tesfatsion & K. L. Judd (Eds.), Handbook of Computational Economics: Agent-Based Computational Economics (Vol. 2, pp. 1273–1337). Amsterdam: Elsevier. [doi:10.1016/s1574-0021(05)02026-5]

CHARNESS, G., & Chen, Y. (2020). Social identity, group behavior, and teams. Annual Review of Economics, 12(1), 691–713. [doi:10.1146/annurev-economics-091619-032800]

COLEMAN, J. S. (1989). Rationality and society. Rationality and Society, 1(1), 5–9.

CORNELISSEN, J. P., Haslam, S. A., & Balmer, J. M. T. (2007). Social identity, organizational identity and corporate identity: Towards an integrated understanding of processes, patternings and products. British Journal of Management, 18(s1), 1–16. [doi:10.1111/j.1467-8551.2007.00522.x]

DENISON, D., Nieminen, L., & Kotrba, L. (2014). Diagnosing organizational cultures: A conceptual and empirical review of culture effectiveness surveys. European Journal of Work and Organizational Psychology, 23(1), 145–161. [doi:10.1080/1359432x.2012.713173]

DE Vries, T. A., Hollenbeck, J. R., Davison, R. B., Walter, F., & van DEr Vegt, G. S. (2016). Managing coordination in multiteam systems: Integrating micro and macro perspectives. Academy of Management Journal, 59(5), 1823–1844. [doi:10.5465/amj.2014.0385]

EISENHARDT, K. M. (1985). Control: Organizational and economic approaches. Management Science, 31(2), 134–149. [doi:10.1287/mnsc.31.2.134]

EISENHARDT, K. M. (1989). Agency theory: An assessment and review. The Academy of Management Review, 14(1), 57–74. [doi:10.5465/amr.1989.4279003]

ELLEMERS, N., De Gilder, D., & Haslam, S. A. (2004). Motivating individuals and groups at work: A social identity perspective on leadership and group performance. Academy of Management Review, 29(3), 459–478. [doi:10.5465/amr.2004.13670967]

ELLEMERS, N., Haslam, S. A., Platow, M. J., & van Knippenberg, D. (2003). Social identity at work: Developments, debates, directions. In S. A. Haslam, D. van Knippenberg, M. J. Platow, & N. Ellemers (Eds.), Social Identity at Work: Developing Theory for Organizational Practice (Vol. 29). London: Taylor & Francis.

ETHIRAJ, S. K., & Levinthal, D. (2004). Modularity and innovation in complex systems. Management Science, 50(2), 159–173. [doi:10.1287/mnsc.1030.0145]

GALBRAITH, J. R. (1974). Organization design: An information processing view. Interfaces, 4(3), 28–36. [doi:10.1287/inte.4.3.28]

GANCO, M., & Hoetker, G. (2009). NK modeling methodology in the strategy literature: Bounded search on a rugged landscape. In D. D. Bergh & D. J. Ketchen (Eds.), Research Methodology in Strategy and Management (pp. 237–268). Bingley: Emerald. [doi:10.1108/s1479-8387(2009)0000005010]

GRABNER, I., & Moers, F. (2013). Management control as a system or a package? Conceptual and empirical issues. Accounting, Organizations and Society, 38(6–7), 407–419. [doi:10.1016/j.aos.2013.09.002]

GREENWOOD, R., & Hinings, C. R. (1993). Understanding strategic change: The contribution of archetypes. Academy of Management Journal, 36(5), 1052–1081. [doi:10.5465/256645]

GÜTH, W. (2010). Satisficing and (un)bounded rationality — A formal definition and its experimental validity. Journal of Economic Behavior & Organization, 73(3), 308–316.

HALLORAN, M. J., & Kashima, E. S. (2006). Culture, social identity and the individual. In T. Postmes & J. Jetten (Eds.), Individuality and the Group: Advances in Social Identity (pp. 137–154). London: Sage. [doi:10.4135/9781446211946.n8]

HARRISON, J. R., & Carroll, G. R. (1991). Keeping the faith: A model of cultural transmission in formal organizations. Administrative Science Quarterly, 36(4), 552–582. [doi:10.2307/2393274]

HARRISON, J. R., & Carroll, G. R. (2006). Culture and Demography in Organizations. Princeton, NJ: Princeton University Press.

HARTMAN, E. M. (1994). The commons and the moral organization. Business Ethics Quarterly, 4(3), 253–269. [doi:10.2307/3857446]

HASLAM, S. A. (2004). Psychology in Organizations. Thousand Oaks, CA: Sage.

HASLAM, S. A., Eggins, R. A., & Reynolds, K. J. (2003). The ASPIRe model: Actualizing social and personal identity resources to enhance organizational outcomes. Journal of Occupational and Organizational Psychology, 76(1), 83–113. [doi:10.1348/096317903321208907]

HASLAM, S. A., & Ellemers, N. (2005). Social identity in industrial and organizational psychology: Concepts, controversies and contributions. In G. P. Hodgkinson & J. K. Ford (Eds.), International Review of Industrial and Organizational Psychology (Vol. 20, pp. 39–118). Hoboken, NJ: Wiley. [doi:10.1002/0470029307.ch2]

HASLAM, S. A., Postmes, T., & Ellemers, N. (2003). More than a metaphor: Organizational identity makes organizational life possible. British Journal of Management, 14(4), 357–369. [doi:10.1111/j.1467-8551.2003.00384.x]

HOFFRAGE, U., & Reimer, T. (2004). Models of bounded rationality: The approach of fast and frugal heuristics. Management Revue, 15(4), 437–459. [doi:10.5771/0935-9915-2004-4-437]

HOGG, M. A., & Terry, D. I. (2000). Social identity and self-Categorization processes in organizational contexts. Academy of Management Review, 25(1), 121–140. [doi:10.5465/amr.2000.2791606]

JOHNSON, E. J., Shu, S. B., Dellaert, B. G. C., Fox, C., Goldstein, D. G., Häubl, G., Larrick, R. P., Payne, J. W., Peters, E., Schkade, D., Wansink, B., & Weber, E. U. (2012). Beyond nudges: Tools of a choice architecture. Marketing Letters, 23(2), 487–504. [doi:10.1007/s11002-012-9186-1]

KATSIKOPOULOS, K. V. (2014). Bounded rationality: The two cultures. Journal of Economic Methodology, 21(4), 361–374. [doi:10.1080/1350178x.2014.965908]

KAUFFMAN, S. A. (1993). The Origins of Order: Self-Organization and Selection in Evolution. Oxford: Oxford University Press.

KAUFFMAN, S. A., & Levin, S. (1987). Towards a general theory of adaptive walks on rugged landscapes. Journal of Theoretical Biology, 128(1), 11–45. [doi:10.1016/s0022-5193(87)80029-2]

KÄRREMAN, D., & Alvesson, M. (2004). Cages in tandem: Management control, social identity, and identification in a knowledge-Intensive firm. Organization, 11(1), 149–175.

KIRSCH, L. J., Ko, D.-G., & Haney, M. H. (2010). Investigating the antecedents of team-based clan control: Adding social capital as a predictor. Organization Science, 21(2), 469–489. [doi:10.1287/orsc.1090.0458]

KREUTZER, M., Cardinal, L. B., Walter, J., & Lechner, C. (2016). Formal and informal control as complement or substitute? The role of the task environment. Strategy Science, 1(4), 235–255. [doi:10.1287/stsc.2016.0019]

KRUIS, A.-M., Speklé, R. F., & Widener, S. K. (2016). The levers of control framework: An exploratory analysis of balance. Management Accounting Research, 32, 27–44. [doi:10.1016/j.mar.2015.12.002]

LANGFIELD-SMITH, K. (2006). A review of quantitative research in management control systems and strategy. In C. S. Chapman, A. G. Hopwood, & M. D. Shields (Eds.), Handbooks of Management Accounting Research (Vol. 2, pp. 753–783). Amsterdam: Elsevier. [doi:10.1016/s1751-3243(06)02012-8]

LECHNER, C., Frankenberger, K., & Floyd, S. W. (2010). Task contingencies in the curvilinear relationships between intergroup networks and initiative performance. Academy of Management Journal, 53(4), 865–889. [doi:10.5465/amj.2010.52814620]

LEVINTHAL, D. A. (2016). Learning and adaptation. In M. Augier & D. J. Teece (Eds.), The Palgrave Encyclopedia of Strategic Management (pp. 1–5). London: Palgrave Macmillan UK. [doi:10.1057/978-1-349-94848-2_787-1]

LEVINTHAL, D. A., & March, J. G. (1981). A model of adaptive organizational search. Journal of Economic Behavior & Organization, 2(4), 307–333. [doi:10.1016/0167-2681(81)90012-3]

LEVITAN, B., & Kauffman, S. A. (1995). Adaptive walks with noisy fitness measurements. Molecular Diversity, 1(1), 53–68. [doi:10.1007/bf01715809]

LI, J., Matouschek, N., & Powell, M. (2017). Power dynamics in organizations. American Economic Journal: Microeconomics, 9(1), 217–241. [doi:10.1257/mic.20150138]

LI, R., Emmerich, M. M., Eggermont, J., Bovenkamp, E. P., Bäck, T., Dijkstra, J., & Reiber, J. C. (2006). Mixed-Integer NK landscapes. In T. P. Runarsson, H.-G. Beyer, E. Burke, J. Merelo-Guervós, L. D. Whitley, & X. Yao (Eds.), Parallel Problem Solving From Nature - PPSN IX (Vol. 4193, pp. 42–51). Berlin Heidelberg: Springer. [doi:10.1007/11844297_5]

LORSCHEID, I., Heine, B.-O., & Meyer, M. (2012). Opening the “black box” of simulations: Increased transparency and effective communication through the systematic design of experiments. Computational and Mathematical Organization Theory, 18(1), 22–62. [doi:10.1007/s10588-011-9097-3]

MALMI, T., & Brown, D. A. (2008). Management control systems as a package — Opportunities, challenges and research directions. Management Accounting Research, 19(4), 287–300. [doi:10.1016/j.mar.2008.09.003]

MALONE, T. W. (1987). Modeling coordination in organizations and markets. Management Science, 33(10), 1317–1332. [doi:10.1287/mnsc.33.10.1317]

MALONE, T. W., & Crowston, K. (1994). The interdisciplinary study of coordination. ACM Computing Surveys, 26(1), 87–119. [doi:10.1145/174666.174668]

MATZLER, K., & Mueller, J. (2011). Antecedents of knowledge sharing – Examining the influence of learning and performance orientation. Journal of Economic Psychology, 32(3), 317–329. [doi:10.1016/j.joep.2010.12.006]

MERCHANT, K. A., & Van der Stede, W. A. (2017). Management Control Systems: Performance Measurement, Evaluation and Incentives. New York, NY: Pearson Education.

MINTZBERG, H. (1980). Structure in 5’s: A synthesis of the research on organization design. Management Science, 26(3), 322–341. [doi:10.1287/mnsc.26.3.322]

MISURACA, R., & Fasolo, B. (2018). Maximizing versus satisficing in the digital age: Disjoint scales and the case for “construct consensus”. Personality and Individual Differences, 121, 152–160. [doi:10.1016/j.paid.2017.09.031]

PARKER, A. M., de Bruin, W. B., & Fischhoff, B. (2007). Maximizers versus satisficers: Decision-making styles, competence, and outcomes. Judgment and Decision Making, 2(6), 342. [doi:10.1017/s1930297500000486]

POSTMES, T., Haslam, S. A., & Swaab, R. I. (2005). Social influence in small groups: An interactive model of social identity formation. European Review of Social Psychology, 16(1), 1–42. [doi:10.1080/10463280440000062]

PRATT, M. G. (2001). Social identity dynamics in modern organizations: An organizational psychology. In M. A. Hogg & D. I. Terry (Eds.), Social Identity Processes in Organizational Contexts (pp. 13–30). London: Taylor & Francis.

PURANAM, P., Stieglitz, N., Osman, M., & Pillutla, M. M. (2015). Modelling bounded rationality in organizations: Progress and prospects. Academy of Management Annals, 9(1), 337–392. [doi:10.5465/19416520.2015.1024498]

REDMAN, T. C. (1998). The impact of poor data quality on the typical enterprise. Communications of the ACM, 41(2), 79–82. [doi:10.1145/269012.269025]

RIVKIN, J. W., & Siggelkow, N. (2007). Patterned interactions in complex systems: Implications for exploration. Management Science, 53, 1068–1085. [doi:10.1287/mnsc.1060.0626]

SAH, R. K., & Stiglitz, J. E. (1986). The architecture of economic systems: Hierarchies and polyarchies. American Economic Review, 76(4), 716–727. [doi:10.3386/w1334]

SHAYO, M. (2009). A model of social identity with an application to political economy: Nation, class, and redistribution. American Political Science Review, 103(2), 147–174. [doi:10.1017/s0003055409090194]

SHAYO, M. (2020). Social identity and economic policy. Annual Review of Economics, 12(1), 355–389. [doi:10.1146/annurev-economics-082019-110313]

SIGGELKOW, N., & Rivkin, J. W. (2005). Speed and search: Designing organizations for turbulence and complexity. Organization Science, 16(2), 101–122. [doi:10.1287/orsc.1050.0116]

SIMON, H. A. (1955). A behavioral model of rational choice. Quarterly Journal of Economics, 69(1), 99–118. [doi:10.2307/1884852]

SIMON, H. A. (1959). Theories of decision-Making in economics and behavioral science. The American Economic Review, 49(3), 253–283.

SIMONS, R. (1994). Levers of Control: How Managers Use Innovative Control Systems to Drive Strategic Renewal. Cambridge, MA: Harvard Business Press.

SIMONS, R. (2014). Performance Measurement and Control Systems for Implementing Strategy. Harlow: Pearson International.

SITKIN, S. B., Cardinal, L. B., & Bijlsma-Frankema, K. M. (2010). Organizational Control. Cambridge University Press.

SPEKLÉ, R. F., & Widener, S. K. (2018). Challenging issues in survey research: Discussion and suggestions. Journal of Management Accounting Research, 30(2), 3–21.

STETS, J. E., & Burke, P. J. (2000). Identity theory and social identity theory. Social Psychology Quarterly, 63(3), 224–237. [doi:10.2307/2695870]

STRAUSS, E., & Zecher, C. (2013). Management control systems: A review. Journal of Management Control, 23(4), 233–268.

TAJFEL, H. (1974). Social identity and intergroup behaviour. Social Science Information, 13(2), 65–93. [doi:10.1177/053901847401300204]

TAJFEL, H. (1975). The exit of social mobility and the voice of social change: Notes on the social psychology of intergroup relations. Social Science Information, 14(2), 101–118. [doi:10.1177/053901847501400204]

TAJFEL, H., & Turner, J. C. (1979). An intergrative theory of intergroup conflict. In W. G. Austin & S. Worchel (Eds.), The Social Psychology of Intergroup Relations (pp. 33–47). Monterey, CA: Brooks/Cole.

TEE, S. W., Bowen, P. L., Doyle, P., & Rohde, F. H. (2007). Factors influencing organizations to improve data quality in their information systems. Accounting and Finance, 47(2), 335–355. [doi:10.1111/j.1467-629x.2006.00205.x]

TERRY, D. J. (2003). A social identity perspective on organizational mergers. In S. A. Haslam, D. van Knippenberg, M. J. Platow, & N. Ellemers (Eds.), Social Identity at Work: Developing Theory for Organizational Practice (Vol. 29). London: Taylor & Francis.

THOMPSON, J. D. (1967). Organizations in Action. Social Science Bases of Administrative Theory. New York, NY: McGraw-Hill.

TRACY, W. M., Markovitch, D. G., Peters, L. S., Phani, B. V., & Philip, D. (2017). Algorithmic representations of managerial search behavior. Computational Economics, 49(3), 343–361. [doi:10.1007/s10614-015-9559-7]

VAN Knippenberg, D., & Ellemers, N. (2003). Social identity and group performance. In S. A. Haslam, D. VAN Knippenberg, M. J. Platow, & N. Ellemers (Eds.), Social Identity at Work: Developing Theory for Organizational Practice (Vol. 29). London: Taylor & Francis.

WALL, F. (2016). Agent-based modeling in managerial science: An illustrative survey and study. Review of Managerial Science, 10(1), 135–193. [doi:10.1007/s11846-014-0139-3]

WALL, F. (2017). Learning to incentivize in different modes of coordination. Advances in Complex Systems, 20(2–3), 1–29. [doi:10.1142/s0219525917500035]

WALL, F. (2019). Coordination with erroneous communication: Results of an agent-based simulation. Knowledge and Information Systems, 61(1), 161–195. [doi:10.1007/s10115-018-1292-9]

WALL, F. (2021). Modeling managerial search behavior based on Simon’s concept of satisficing. Computational and Mathematical Organization Theory. [doi:10.1007/s10588-021-09344-x]

WALL, F., & Leitner, S. (2021). Agent-Based computational economics in management accounting research: Opportunities and difficulties. Journal of Management Accounting Research, 33(3), 189–212. [doi:10.2308/jmar-19-073]

WEGGE, J., & Haslam, S. A. (2003). Group goal setting, social identity, and self-categorization. In S. A. Haslam, D. van Knippenberg, M. J. Platow, & N. Ellemers (Eds.), Social Identity at Work: Developing Theory for Organizational Practice (Vol. 29). London: Taylor & Francis.