Evolutionary Model Discovery of Human Behavioral Factors Driving Decision-Making in Irrigation Experiments

,
and
aHuman-Centered Artificial Intelligence Research Lab, University of Central Florida, United States; bDepartment of Industrial Engineering and Management Systems, University of Central Florida, United States; cUniversity of Central Florida, UCF Coastal: National Center for Integrated Coastal Research, United States
Journal of Artificial
Societies and Social Simulation 26 (2) 11
<https://www.jasss.org/26/2/11.html>
DOI: 10.18564/jasss.5069
Received: 11-Nov-2022 Accepted: 20-Mar-2023 Published: 31-Mar-2023
Abstract
Small farms are thought to produce around a third of the global crop supply. But, in the wake of the climate crisis, their existence is increasingly vulnerable to changes in the spatial and temporal availability of water. The small-scale irrigation systems which water these farms present a social-ecological dilemma: Upstream farms have prevailing access to a canal's resources, but all farms along the canal must contribute to maintaining the irrigation infrastructure. Thus, it is key to assess the social mechanisms which promote resilience in these systems and, more widely, in complex social-ecological dilemmas under changing conditions. Toward this, we build on previous work in which a stylized irrigation dilemma was simulated via a social lab experiment. Studies of the data produced from this experiment modeled participants' behavior with multiple, theoretically grounded agent-based models (ABMs). These models encode causal, human-interpretable hypotheses of decision making which generates the real-world behavior observed in the experiment. However, the accuracy of these models in fitting the experimental data is limited. Using Evolutionary Model Discovery, a recent algorithm for inverse generative social science (iGSS), we show the ability to automatically generate a wide variety of unique new ABMs which fit the experimental data more accurately and robustly than the original, manually-constructed ABMs. To do this, we algorithmically explore the space of possible behavioral rules for agents choosing how to contribute to the maintenance of the irrigation infrastructure. We find that, in contrast to the original models, our best-performing models typically have an additional element of stochasticity and favor factors such as other-regarding preferences and perceived relative income. Given that this change in just a small part of the original model has yielded such an advance, our results suggest that iGSS methods have great potential for continuing to derive more accurate models of complex social-ecological dilemmas.Introduction
As the climate crisis continues to cause ecological upset across our Earth (Michelozzi & De’Donato 2021), an increasing number of communities have grown ever more vulnerable to once-rare environmental events such as droughts, changing temperatures, storms, and extreme weather (Michelozzi & De’Donato 2021). Political, technological, and social changes are required in order to lessen the human cost of climate change and prevent collapse in the agricultural systems on which we all rely on. The study of social-ecological commons dilemmas, therefore, has grown more important than ever as we work to study the mechanisms which will allow us to best understand–and therefore intervene–in these systems. Increasing understanding on this front allows us to engineer and govern sustainable, antifragile systems (Taleb 2012): systems that not only can cope, but thrive under changing conditions and increased disturbances.
These mechanisms driving human behavior in such commons dilemmas have been a focus of scholars for decades (Anderies et al. 2011, 2013; Baggio et al. 2015; Cifdaloz et al. 2010; Dawes 1980; Dietz et al. 2003; Gutiérrez et al. 2011; Janssen et al. 2012; Janssen & Baggio 2017; Ostrom 1990), yet the precise mechanisms governing peoples’ behavior in many types of systems are still largely a mystery. Irrigation systems are one such commons dilemma; In river and canal-based irrigation systems, upstream farmers have greater access and control of the system’s resources than downstream farmers by the simple nature of their physical location. Yet, contributions are required from all users of the system in order to maintain and repair the irrigation infrastructure, as individual upstream farmers do not typically have the resources to maintain only their section of full-scale irrigation infrastructure alone (see e.g., Cifdaloz et al. 2010). To date, many qualitative understandings have been derived from the study of such systems, but no unified model exists describing the factors contributing to human decision making which are more likely to increase the resilience of these systems.
We contribute further to the study of irrigation systems by reanalyzing data collected from participants engaging in a simulated irrigation system in an experimental laboratory setting (Anderies et al. 2013). In this experiment, participants were given charge of virtual fields which required regular watering via an irrigation canal shared by three other participants. The simulation was formulated in a round-based game-like format. Participants were rewarded tokens for successfully supplying their fields with water; however, the canal’s efficiency would also degrade each round, requiring participants to invest their earnings into the canal’s upkeep in order to keep the system in working order.
The original experimenters gathered time series through collecting information on the participants’ behavior each round such as investment amounts and water extraction levels. They deduced various macro-scale metrics from the participants’ behavior such as Gini coefficients for participants’ earnings and average group level investments over the entire game. Traditional statistical analysis was able to gather some mechanistic insights on the data (Anderies et al. 2013; Baggio et al. 2015; Janssen et al. 2015), but it was unable to fully explain the dynamics of each time series. Pursuant to this, scholars constructed agent-based models in attempt to better explain behavioral characteristics of the individuals in these irrigation common pool resource games (Baggio & Janssen 2013; Janssen & Baggio 2017). Each hypothesized model of agent behavior was carefully formulated based on existing theories on human decision making in relevant environments (Baggio & Janssen 2013; Janssen & Baggio 2017), in line with the current best practice of drawing from cognitive science to inform agent architectures for generative social science (Miranda 2022; Miranda & Garibary 2022). However, no single model offered an especially accurate or robust explanation of the data. Each model was, at best, a partial fit.
Inverse generative social science
Recently, problems such as this have become a ripe opportunity to employ a related family of advancements in agent-based modelling known as inverse generative social science (iGSS). To conceptualize iGSS, consider: On a fundamental level, an ABM is a tacit hypothesis that a given set of micro-scale rules for agent interaction work together to produce an observed macro-scale emergent phenomena. Naturally, it is desirable to test multiple different multiple possible hypotheses. Traditionally, modellers’ intuitions and qualitative domain literature have been the primary sources in forming such hypotheses. Since constructing each hypothesis requires a considerable amount of manual work, testing variation has primarily been limited to adjusting numeric parameters or testing only a limited selection of rules. Researchers have therefore been very limited in the number of alternative rule hypotheses that they are able to test, and the space of plausible, alternative rules often goes largely unexplored.
Inverse generative social science (iGSS) serves to remedy this issue by leveraging machine learning to automate the exploration of the space of possible rules (Epstein 1999; Vu et al. 2019). Rather than building up entire models, the iGSS modeller begins by specifying possible subsets of models. That is, the modeller defines a set of primitive agent constituents and operator functions capable of combining them. They then define an appropriate fitness function or selection pressure used to be able to evaluate how good a given model is, typically seeking the generation of a known macro-scale phenomenon or a precise fit to real-world data. Then, a specialized iGSS machine learning algorithm combines and recombines the model primitives into new models, evaluates them, and converges towards optimal models in an evolutionary fashion. To do this, we utilize evolutionary model discovery (EMD), a recent framework for iGSS (Gunaratne 2019; Gunaratne et al. 2021). Our results take the form of a variety of different agent token-investment strategies and an analysis of the possible causal factors which contribute to this behavior.
In this study, we leverage advances in iGSS and evolutionary model discovery in order to devise which sets of rules are more likely to give rise to the outcomes observed in the original irrigation experiments. Our results indicate that a missing key to previously formulated models may have been an additional element of stochasticity which was not accounted for. Our analysis also indicates that other factors, such as utility maximization and perceived relative income, are also important in increasing model fitness.
In light of this and the evidence presented from other works, we argue that iGSS has powerful potential for deriving more accurate and robust inferences on the relationship between micro-level elements and observed macro-phenomena.
Research questions
- RQ1: Is there a model or class of models that can outperform the current state-of-the-art in explaining human decision making in irrigation experiments?
- RQ2: Can inverse generative social science be utilized as a sound methodology in producing such a model or class of models?
Background
The irrigation experiment
In 2010-2012, a series of experiments were run at Arizona State University with undergraduate student participants that were presented either a digitally or paper-based simulated irrigation system (Anderies et al. 2013; Baggio et al. 2015; Janssen et al. 2015). The irrigation system requires maintenance and provides water. Participants then, at each round, needed to decide how much to invest in maintaining the infrastructure and how much water they wanted to extract. Depending on the level of the group investment, a specific amount of water was available for extraction. Upstream participants had a natural priority in their access to the water versus downstream participants. At the end of the game, the five participants were rewarded with a direct conversion of tokens to US dollars.
The experiments were first statistically analyzed via regression models which discovered some correlations in the data (Anderies et al. 2013; Baggio et al. 2015; Janssen et al. 2015). Data from irrigation experiments were also analyzed by constructing multiple, competing agent based models in which agents follow rules dictated by theoretical considerations (i.e. selfish, altruistic, utilitarian, random etc.) (Baggio & Janssen 2013). Further, this approach was refined on another set of irrigation experiments in Janssen & Baggio (2017). The analysis via agent based models in Baggio & Janssen (2013) and Janssen & Baggio (2017) shed some light on potential rules governing the overall irrigation system, but, of the handful of competing rules, no one model was found to clearly outperform all others.
Evolutionary Model Discovery
We leverage evolutionary model discovery (EMD), a framework for iGSS,(Gunaratne 2019; Gunaratne et al. 2021) to derive possible behavioral rules in an inverse fashion. The algorithm on which EMD is based combines provided model subsets/primitives (henceforth referred to as factors) and operators into syntactic trees which encode new models of agent behavior. Using genetic programming, generations of these trees are formulated, mutated, and evaluated according to a provided fitness function. The best-performing rules are then allowed to cross-breed and generate successive generations.
After obtaining the data encoding model performance from the genetic program, the modeler may use it to analyze the importance and efficacy of individual factors and their interactions. Using this information, the modeller may analyze the automatically-generated models and use the insights gained therein to manually create new models and test whether they improve the overall fitness. These models can then be assessed in order to provide new scientific insights about the causal relationships which lead to observed macro-scale phenomena.
EMD and related approaches in iGSS have been successfully used in automating the discovery of sophisticated models in domains such as archaeology (Gunaratne & Garibay 2020), social media analysis (Gunaratne et al. 2021), and public health (Vu et al. 2019).
Methods
Here, we specifically examine the irrigation experiment performed and analyzed in Baggio et al. (2015) and Baggio & Janssen (2013). We begin with the highest-performing model derived in Baggio & Janssen (2013): The other-regarding preferences (utilitarian) model, a model based on findings from behavioral economics. In a nutshell, each agent is imbued with either a competitive, egalitarian, or altruistic disposition. The probability of an agent having any one of these decisions is determined by parameters. Each agent then incorporates information on the environment and their neighbors’ behavior to make decisions which maximize some notion of utility which is congruent with their disposition.
In order to place more precise bounds on our scope and search-space, we concentrate on agent investment behavior and leave extraction behavior unchanged. In place of the investment behavior, we allow the insertion of new models generated from a set of hypothesized alternate factors.
Hypothesized alternate factors influencing investment decision
To capture a more realistic space of human behavior, we utilize the paradigm introduced by Agent_Zero (Epstein 2014) of ensuring factors represent three dimensions of human decision-making: rational, social, and emotional. We indicate the hypothesized factors in Table 1. Of these, \(F_\text{self}, F_\text{heur}, F_\text{pseu}, F_\text{alt},\) and \(F_\text{util}\) represent factors originally hypothesized in Baggio & Janssen (2013). We introduce the factors: \(F_\text{rand}\) to serve both as a “null” model and allow additional stochasticity; \(F_\text{up}\) and \(F_\text{down}\) to allow for dynamics more directly related to neighbors’ investments; and \(F_\text{inc}\) to add an emotional dimension, as prior work has shown that perceived income relative to others affects investment behavior (Anderies et al. 2013; Baggio et al. 2015; Janssen et al. 2012) and serves a proxy for emotions such as envy, superiority, generosity, etc. Note that considering each of these dimensions of human decision-making is simply a conceptual modeling tool, and factors may indeed be arbitrarily argued to belong to more than one dimension or a different dimension than l in Table 1.
| Factor | Name | Description |
|---|---|---|
| Rational factors | ||
| \(F_\text{self}\) | Selfishness | Higher probability for investments closer to 0 tokens |
| \(F_\text{rand}\) | Random | Uniform random probability |
| \(F_\text{pseu}\) | Pseudorandom | Pseudorandom “trembling hand” model from Baggio & Janssen (2013); The first investment is randomly chosen, and subsequent investments are the same as the first investment plus or minus a noise term |
| Social factors | ||
| \(F_\text{alt}\) | Altruism | Higher probability for investments closer to the maximum token investment |
| \(F_\text{util}\) | Other-regarding preferences (utilitarian) | Investment behavior of the original base model, introduced in Baggio & Janssen (2013) based on findings from behavioral economics |
| \(F_\text{up}\) | Upstream homophily | Higher probability for investments more similar to upstream neighbor’s last investment |
| \(F_\text{down}\) | Downstream homophily | Higher probability for investments more simliar to downstream neighbor’s last investment |
| Emotional factors | ||
| \(F_\text{inc}\) | Relative income | Greater weight for below-average-income agents to invest less and above-average-income agents to invest more. |
We formulate each factor as a function \(F_i(x) : [0..10] \rightarrow [0,1]\). This represents the probability of investing \(x\) tokens (an integer between 0 and 10) due to the given factor \(F_i\). These factors can then be combined using addition (+), subtraction (-), multiplication (*), and division (/) into a combined rule \(R(x)\). For example, a given \(R(x)\) may be \(R(x) = 2*F_\text{self}+ F_\text{up}- F_\text{down}\).
Agents then decide the number of tokens to invest, \(x'\), using argmax over the possible investment amounts:
| \[\begin{aligned} x' = \underset{x \in [1..10] }{\text{argmax}}\ R(x)\end{aligned}\] | \[(1)\] |
Or, alternatively, using argmin to allow for the probabilistic complement of \(R(x)\). Note also that, with the inclusion of the subtraction operator, the probabilistic complement of each individual factor is also encoded. For example, while \(F_\text{up}\) produces a more positive value for \(x\) more similar to the upstream neighbor’s last investment, \(-F_\text{up}\) produces a more negative value.
We model factors concerned with higher probability centered on a particular value \(v\) with the linear probability density \(P(v,x) = -\left| \frac{v - x}{\omega} \right| + 1\) where \(\omega\) is a parameter controlling the “width” of the probabilization.
Evolutionary model discovery
Our function \(fit\) for evaluating model fitness, separate from the agent decision functions detailed in the previous section, is identical to that used in Baggio & Janssen (2013). It is defined as: \(fit = fit_1 \cdot fit_2 \cdot fit_3 \cdot fit_4 \cdot fit_5\) where each \(fit_i\) is defined as the normalized squared difference between simulated data, \(d_s\), and experimentally observed data, \(d_e\), for a particular metric \(fit_i = 1 - (d_e - d_e)^2\). The metrics are defined as the average group level investments in the public infrastructure level over the 10 rounds (\(fit_1\)), the average contribution per position (\(fit_2\)), the average collection per position (\(fit_3\)), the average Gini coefficient of contributions (\(fit_4\)), and the average Gini coefficient of collected tokens (\(fit_5\)).
Hence, higher \(fit\) represents a better fit to the experimental data with a maximum fitness of \(fit=1\) and minimum of \(fit=0\). This fitness function is useful, in that it effectively achieves a single aggregated function encompassing multiple optimization objectives. Through multiplying each metric, low fitness in one metric is more heavily penalized than if the metrics were simply summed and normalized.
For example, comparing one case with all \(fit_i = 0.9\) versus another case of \(fit_1 = fit_2 = fit_3 = fit_4 = 0.9\) but \(fit_5 = 0.5\), the penalty for the lower \(fit_5\) is a reduction of fitness of \(0.08\) if using a summed and normalized fitness (\((\sum_i fit_i)/5\)), but the reduction is \(0.262\) if using a product fitness (\(\prod_i fit_i\)).
Janssen et al. (2012) compared different configurations of fitness measures (including product, normalized sum, and others still), but they ultimately did not find a qualitative difference in them. Hence, we choose the product \(fit\) for its slight quantitative advantages described above.
We initialize all model parameters to a random value uniformly distributed between plus-or-minus 0.05 the optimal values reported in Table 3 of Baggio & Janssen (2013). This initialization allows us to alleviate over-fitting to arbitrarily precise parameters which allows the discovery of more robust models (Gunaratne & Garibay 2020).
We chose the hyperparameters for evolutionary model discovery based on Gunaratne & Garibay (2020): We set the mutation rate to 0.2, and we allowed the crossover rate to vary between 0.6 and 0.8. We set the minimum tree depth to 2, as this is the minimum depth for a valid rule in the formulation of the problem (allowing for the first layer to be the argmax/argmin function and the second layer to be a single factor). To encourage the exploration of the possibility of more complex rules, we set the maximum tree depth to 64.
In total, we ran the algorithm until it had evolved approximately 10,000 models. Of these, based on fitness, we selected the top 100 models and sampled each of them 100 times to obtain a fitness distribution under the randomly initialized parameters. For all of this, we used the NetLogo/Python implementation of EMD provided by Gunaratne & Garibay (2020).
Results
We begin showcasing the results by assessing all 10,000 evolved models/rules. Our analysis follows the methodological footsteps put forth by prior EMD analyses such as Gunaratne & Garibay (2020) and Gunaratne et al. (2021). That is, we begin by analyzing the importance of individual and joint factors in terms of their impact on the fitness of each model. We then analyze the best-fitness models themselves. This allows us to paint a larger picture of not only the best models, but the general significance and robustness of including factors in any given model. This allows us to more precisely see what contributes to a given models success, and in theory also allows the manual construction of new models based on insights garnered from the algorithmic construction.
The factor analysis is important for more precisely deducing the dynamics of each factor, as evolutionary model discovery was successful in evolving a great variety of rules with varying complexity in factor interaction. The set of evolved rules range from from rules with just one or two factors to the most complex model evolved, \(\text{argmin} ((F_{rand} + F_{alt} - F_{rand} - F_{up}) * F_{down}) * (((F_{heur} + F_{self}) * (F_{self} + F_{heur})) + (F_{heur} * F_{heur}))\), incorporating eleven factor presences (although its fitness is only 0.218).
To further assess the factors using this importance information, we conduct a pairwise analysis comparing the importance of each factor with every other factor. Results from systematic Mann-Whitney U tests comparing the permutation importance of each factor A against every other factor B confirm (\(p < 0.0001\)) that all factors except for \(F_\text{up}\) and \(F_\text{down}\) show significant difference and can be ordered from highest to lowest permutation accuracy importance as: \(F_\text{rand}, F_\text{util}, F_\text{alt}, F_\text{inc}, F_\text{heur}, F_\text{pseu},F_\text{self}\).
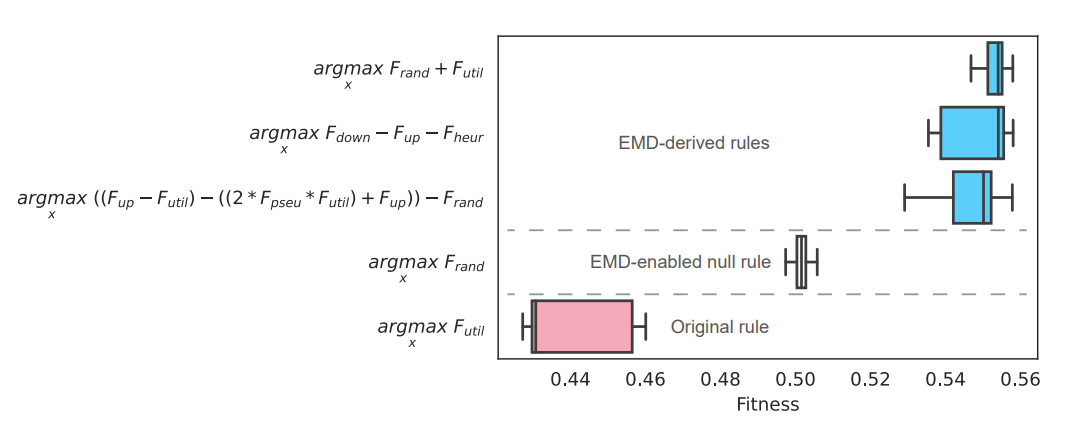
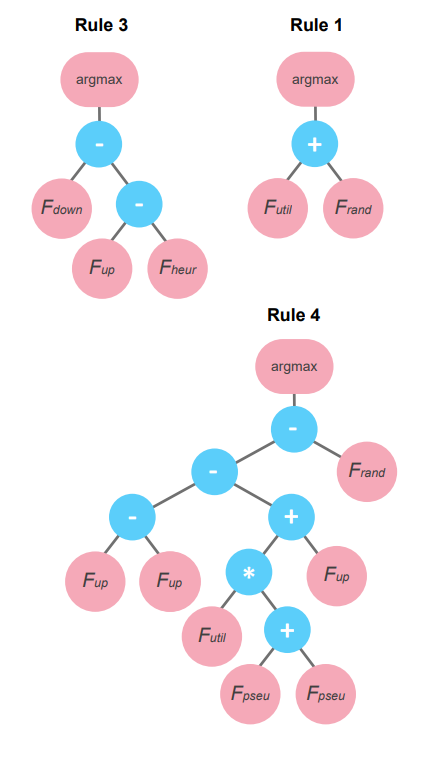
Finally, the 10 best-fit candidate models evolved by the genetic program are reported in Table 2 along with their mean fitness score. As expected from the factor analysis, \(F_\text{rand}\) is the most frequently appearing factor. Figure 1 displays a selection of these top models (rules 1, 3, and 4) compared against a model consisting of just \(F_\text{rand}\) (as a kind of null model) and the original utilitarian model. The EMD-derived models score considerably higher in fitness. We show visualizations of the evolved syntax trees of these models in Figure 2. These may be read as typical abstract syntax trees; Visualizing them in this manner eases the conceptualization of evolutionary processes such as branch crossover and mutation.
| # | Rule | Mean fitness |
|---|---|---|
| 0 | \(\underset{x}{\text{argmin}}F_{pseu1} - F_{rand} + F_{util} - F_{pseu2}\) | 0.5534 |
| 1 | \(\underset{x}{\text{argmax}}F_{rand} + F_{util}\) | 0.5533 |
| 2 | \(\underset{x}{\text{argmin}}F_{rand} - F_{util}\) | 0.5531 |
| 3 | \(\underset{x}{\text{argmax}}F_{down} - F_{up} - F_{heur}\) | 0.5497 |
| 4 | \(\underset{x}{\text{argmin}}((F_{up} - F_{util}) - ((2*F_{pseu}*F_{util}) + F_{up})) - F_{rand}\) | 0.5471 |
| 5 | \(\underset{x}{\text{argmax}}F_{rand1} + (F_{util} * F_{rand2})\) | 0.5459 |
| 6 | \(\underset{x}{\text{argmin}}F_{pseu} + F_{down} - F_{rand1} - F_{rand2}\) | 0.5442 |
| 7 | \(\underset{x}{\text{argmin}}(F_{up} * F_{inc}) + F_{rand}\) | 0.5368 |
| 8 | \(\underset{x}{\text{argmin}}- F_{rand1} - F_{rand2} - F_{pseu} + 2*F_{inc}\) | 0.5342 |
| 9 | \(\underset{x}{\text{argmin}}F_{rand1} - F_{rand2} + F_{pseu}\) | 0.5341 |
Discussion
In this study, we built upon previous work in the study of irrigation systems social dilemmas. We reanalyzed and augmented a set of agent-based models designed to model behavior in a stylized irrigation dilemma as simulated via a behavioral laboratory experiment. We focused on an individual facet of the model: agents’ behavior in contributing to the collective upkeep of irrigation infrastructure. Utilizing evolutionary model discovery, we algorithmically explored a much larger space of possible rules for this behavior than was previously possible. We find that, in contrast to the original models, our best-performing rules typically have an additional element of stochasticity and favor factors such as other-regarding preferences and perceived relative income.
This idea of baseline behavior augmented with a small amount of additional stochasticity was, in fact, expressed and hypothesized in the models’ original introduction (Baggio & Janssen 2013). For example, rule 1 in Table 2 is a simple addition of the baseline utilitarian model with a random term. Baggio and Jannsen conceptualized this idea as the “wavering hand:” Agents have some idea of how to reason about the system and make decisions, but incomplete understandings and/or uncertainty can cause an amount of stochasticity about a more clearly explained behavior. However, we suspect that the discovery of the robustness of this fact may not have originally occurred as exploring additional rule configuration possibilities was simply too labor-intensive a process prior to modern iGSS methods.
There are additional insights to be had from the models generated and subsequent factor analysis. We note that rule 3 in Table 2 represents an interesting outlier in the top performers, as it defies the factor composition which would be expected from the importance analysis. This interaction between the heuristic and both up- and down-stream homophily may belie a particular strategy where upstream farmers are especially motivated to match the investments of downstream farmers. This insight may be used to inform further research on related irrigation dilemma strategies.
Further, we would like to note that, in this current formulation, all agents homogeneously follow the same strategy. This may be a contributing factor to the appearance of disparate rules with similar fitness in Table 2. Further research may find additional fitness gains through exploring increasingly heterogeneous agents. Additionally, a clear direction forward may also involve allowing the extraction behavior to vary as well as the investment behavior.
Ultimately, given our results and those of other works (Garibay et al. 2021; Gunaratne 2019), we argue that iGSS methods pave a clear path forward for agent-based modelling and represent a natural evolution of the practice. We anticipate that further developments of iGSS will serve to bring about a new era of generative social science models which are not only more accurate and robust, but may aid in uncovering causal mechanisms that otherwise would have remained un-discovered.
References
ANDERIES, J. M., Janssen, M. A., Bousquet, F., Cardenas, J. C., Castillo, D., Lopez, M. C., Tobias, R., Vollan, B., & Wutich, A. (2011). The challenge of understanding decisions in experimental studies of common pool resource governance. Ecological Economics, 70(9), 1571–1579. [doi:10.1016/j.ecolecon.2011.01.011]
ANDERIES, J. M., Janssen, M. A., Lee, A., & Wasserman, H. (2013). Environmental variability and collective action: Experimental insights from an irrigation game. Ecological Economics, 93, 166–176. [doi:10.1016/j.ecolecon.2013.04.010]
BAGGIO, J. A., & Janssen, M. A. (2013). Comparing agent-based models on experimental data of irrigation games. 2013 Winter Simulations Conference (WSC), Washington, DC, USA. [doi:10.1109/wsc.2013.6721555]
BAGGIO, J. A., Rollins, N. D., Pérez, I., & Janssen, M. A. (2015). Irrigation experiments in the lab: Trust, environmental variability, and collective action. Ecology and Society, 20(4), 12. [doi:10.5751/es-07772-200412]
CIFDALOZ, O., Regmi, A., Anderies, J. M., & Rodriguez, A. A. (2010). Robustness, vulnerability, and adaptive capacity in small-scale social-ecological systems: The Pumpa Irrigation System in Nepal. Ecology and Society, 15(3), 39. [doi:10.5751/es-03462-150339]
DAWES, R. M. (1980). Social dilemmas. Annual Review of Psychology, 31(1), 169–193.
DIETZ, T., Ostrom, E., & Stern, P. C. (2003). Struggle to govern the commons. Science, 302(5652), 1907–1912. [doi:10.1126/science.1091015]
EPSTEIN, J. M. (1999). Agent-Based computational models and generative social science. Complexity, 4(5), 41–60. [doi:10.1002/(sici)1099-0526(199905/06)4:5<41::aid-cplx9>3.0.co;2-f]
EPSTEIN, J. M. (2014). Agent_Zero: Toward Neurocognitive Foundations for Generative Social Science. Princeton, NJ: Princeton University Press. https://doi.org/10.1515/9781400848256 [doi:10.23943/princeton/9780691158884.001.0001]
GARIBAY, I., Epstein, J. M., & Rand, W. (2021). Inverse generative social science workshop. Available at: https://www.igss-workshop.org
GUNARATNE, C. (2019). Evolutionary model discovery: Automating causal inference for generative models of human social behavior. PhD Thesis, University of Central Florida
GUNARATNE, C., & Garibay, I. (2020). Evolutionary model discovery of causal factors behind the socio-agricultural behavior of the Ancestral Pueblo. PloS ONE, 15(12), e0239922. [doi:10.1371/journal.pone.0239922]
GUNARATNE, C., Rand, W., & Garibay, I. (2021). Inferring mechanisms of response prioritization on social media under information overload. Scientific Reports, 11(1), 1–12. [doi:10.1038/s41598-020-79897-5]
GUTIÉRREZ, N. L., Hilborn, R., & Defeo, O. (2011). Leadership, social capital and incentives promote successful fisheries. Nature, 470(7334), 386–389.
JANSSEN, M. A., Anderies, J. M., Pérez, I., & Yu, D. J. (2015). The effect of information in a behavioral irrigation experiment. Water Resources and Economics, 12, 14–26. [doi:10.1016/j.wre.2015.09.001]
JANSSEN, M. A., & Baggio, J. A. (2017). Using agent-based models to compare behavioral theories on experimental data: Application for irrigation games. Journal of Environmental Psychology, 52, 194–203. [doi:10.1016/j.jenvp.2016.04.018]
JANSSEN, M. A., Bousquet, F., Cardenas, J.-C., Castillo, D., & Worrapimphong, K. (2012). Field experiments on irrigation dilemmas. Agricultural Systems, 109, 65–75. [doi:10.1016/j.agsy.2012.03.004]
MICHELOZZI, P., & De’Donato, F. (2021). IPCC sixth assessment report: Stopping climate change to save our planet. Epidemiologia E Prevenzione, 45(4), 227–229.
MIRANDA, L. (2022). Humans in algorithms, algorithms in humans: Understanding cooperation and creating social AI with causal generative models. University of Central Florida Electronic Theses and Dissertations
MIRANDA, L., & Garibary, O. O. (2022). Approaching (super)human intent recognition in stag hunt with the Naïve Utility Calculus generative model. Computational and Mathematical Organization Theory, 2022. [doi:10.1007/s10588-022-09367-y]
OSTROM, E. (1990). Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge: Cambridge University Press.
TALEB, N. N. (2012). Antifragile: Things That Gain From Disorder. New York, NY: Random House.
VU, T. M., Probst, C., Epstein, J. M., Brennan, A., Strong, M., & Purshouse, R. C. (2019). Toward inverse generative social science using multi-objective genetic programming. Proceedings of the Genetic and Evolutionary Computation Conference, New York, NY, USA. [doi:10.1145/3321707.3321840]