Dyadic Interaction Shapes Social Identity in the Axelrod Model Using Empirical Data

,
,
,
and
aUniversity of Limerick, Ireland; bDepartment of Mathematics & Statistics, Mathematics Applications Consortium for Science and Industry (MACSI), University of Limerick, Ireland; cDepartment of Psychology, University of Limerick, Ireland
Journal of Artificial
Societies and Social Simulation 26 (2) 2
<https://www.jasss.org/26/2/2.html>
DOI: 10.18564/jasss.4992
Received: 03-May-2022 Accepted: 23-Nov-2022 Published: 31-Mar-2023
Abstract
Group dynamics and inter-group relations influence the self-perception. The Social Identity Approach explains the role of multiple identities, derived from categories or group memberships, in social interaction and individual behaviour. In agent-based models, agents interact with their environment to make decisions and take actions. Thus, we examine to what extent the interaction in an agent-based model natively captures core principles of the Social Identity Approach. To do so, we extend the Axelrod model and the agreement-threshold model with explicit aspects of the Social Identity Approach to assess their influence on the simulation outcomes. We study the variants of the Axelrod model by using Monte Carlo simulations and compare the simulation results with longitudinal survey data of opinions. These extensive simulations favour the Axelrod model and the agreement-threshold model. These models fit, without the explicit embedding of features from the Social Identity Approach, the volatility of the opinion-based features better for the given data sets. Our two extensions of the Axelrod model formalise elements of the Social Identity Approach; however, they do not support the fitness of the model to the data. In the simulations, even in the standard Axelrod model, the social identity affects the development of the agents' identity through the homophily principle, and the agents, in turn, shape their own social identity by social influence. We argue that the Axelrod model and the agreement-threshold model implicitly include social identities as emerging properties of evolving opinion-based groups. In addition to that, the attitudinal data captures the hidden group structure in the attitude positions of the participants. In this way, core features of the Social Identity Approach already implicitly play a role in these empirically-driven agent-based models.Introduction
Social psychological theories explain how individuals experience themselves and interact, employing mechanisms at varying levels of abstraction. For example, the Social Identity Approach (SIA) articulates how individual identities, perceptions, and behaviour are informed by groups and resulting social identities (Reicher et al. 2010). A groups describes a more abstract entity from an individual perspective that receives additional evaluations on a group-level. Crucially, entities such as groups and individuals are mutually constitutive, and reciprocally influence each-other: individuals can collectively influence group identity; and group identity shapes individuals. Although the SIA is frequently applied only to explain how existing social structure (like group categories, ingroup bias, and so on) shapes individual cognition and behaviour, Reicher (2004) warns against “reductionist misreadings” of the SIA that only consider one-way influence of social structure on individuals. Instead, to understand social identity as a dynamic system, we also need to understand how individuals’ behaviour shapes the system that shapes them. In other words, we need to consider individual and group levels of analysis as different views on a recursive dynamical system (Lüders et al. 2022).
Agent-based models often aim to incorporate these theories to build up macro-level outcomes from micro-level interactions. The understanding of complex emergence through agent-based model simulations relies on capturing theories of interaction and their simpler formalisation (Epstein 2008). Within society, groups form through social interactions among individuals, and, at the same time, define the individual’s identity by transmitting common group values, beliefs and behaviours. Our goal is to explore roles of in- and out-group categorisation through the Social Identity Approach in variations of an agent-based model. In particular, we consider cases of opinion-based categorisation, in which social groups can form around shared attitudes.
An important element of group identification is agreement on core attitudes (Bliuc et al. 2007; Maher et al. 2020) and, in turn, this agreement can result in the formation of opinion-based groups (Dinkelberg et al. 2021). These groups can be represented in Axelrod’s model of cultural dissemination (Axelrod 1997) as emerging features of social identity, where homophily and social influence shape the agents’ attitude positions and, therefore, who they align with. In the model, agents have a number of attitudes which, to maintain consistency with Axelrod’s original description, we refer to as traits. Each trait can take the value of one of a fixed set of cultural features. The agents interact with other agents who are similar by copying one of their traits; the higher the mutual similarity, the higher the tendency to interact. This model reveals the dynamics of the opinion-based group formation in an early stage – clusters of people’s shared opinions characterise social groups (Kruglanski et al. 2006). Importantly, opinion-based social identities exist as emergent features at the macro level whilst shaping decisions and trajectories at the micro level without any explicit parameterization or perception of identity. A disadvantage of the Axelrod model in this respect it that it tends to converge to one cluster where every agent ends up with the same opinion vector. This feature contradicts what we see in society where multiple groups form and polarise on a number of different dimensions.
The Axelrod model has been extended with an agreement threshold to allow the use of opinions and to seed it with survey data (see MacCarron, Maher, et al. 2020a). The core idea in the agreement-threshold model is that people will only adopt a different opinion if it’s reasonably close to their own views which describes a concept loosely related to the "latitude of acceptance" (Sherif 1963). MacCarron, Maher, et al. (2020a) later demonstrate that the simulations with an agreement threshold result in various opinion clusters rather than in the single cluster which we would normally observe in the standard Axelrod model.
The Axelrod model is usually seeded uniformly at random (e.g., Klemm et al. 2003; Pinto & Balenzuela 2020; Stivala et al. 2014) and shows how the progressive coordination of attitudes structures social groups (i.e., clustering). In this paper, we seed both the Axelrod model and agreement-threshold model with empirical opinion data from surveys randomly on a connected lattice. This allows us to explore how the structured attitudinal data provides macro-level social identities through embedded group properties that, at the same time, shape micro-level interaction dynamics. We also show how simple agent-based models can provide insights on the potential evolution pathways of opinion-based identities using longitudinal empirical data.
Our simplest model is the Axelrod model, which is a multi-dimensional opinion dynamics model that is based on simple interaction mechanisms. We test extensions of this model with aspects of the Social Identity Approach to uncover its impact on the model’s outcome. We compare the outcome of two additional mechanisms derived from the Social Identity Approach with the standard Axelrod model and the agreement-threshold model. Both mechanisms rely on an additional explicit parameter. This parameter determines the group structure (i.e., party affiliation of an agent), so that the agents are able to distinguish between in- and out-group members. The group categories determine the agents’ behaviour. To evaluate the formalisation of the Social Identity Approach, we conduct an analysis on randomly-generated data and extend this to empirical attitudinal data.
We apply three longitudinal survey data sets to seed the opinion dynamics models (see Dinkelberg et al. 2021b). By having data in two or more time points, we know the previous and later stages of the participants. We draw the estimated features changes between the states with the help of the agent-based models. The relative number of changes per feature indicates their expected volatility (likelihood of change) between two time points and show us how likely a position change is, under the models that we test. We run Monte Carlo simulations from the initial time step allowing for approximately the same number of changes as observed in the empirical data. From the average of many simulations, we can identify to what extent the Axelrod model replicates the outcome in the emerging opinion-based groups. The purpose of the model is explanatory as we compare simulation results to empirical data; however, by doing this, we take the first step to shift the model’s purpose to prediction (Edmonds et al. 2019).
In Section 2, we outline briefly the two base models that already exist in the literature, the Axelrod model and the agreement-threshold model. We then discuss to what extent the Social Identity Approach is already, natively, captured by these base models. From there, we draw parallels from the Social Identity Approach to newly introduced mechanisms for in- and out-group interaction. We further evaluate the aspects of the Social Identity Approach in the various versions of the Axelrod model by running simulations on randomly seeded models and validate then the models’ functionality with empirical data. Finally, we conclude the influence of the Social Identity Approach on the models’ outcomes and its role for the model’s fitness.
The Base Axelrod Models
Axelrod (1997) model of cultural dissemination is an agent-based model that addresses the phenomenon of global divergence and local convergence in a system of agents that exert social influence due to similarity (Flache et al. 2017). Two principles are core to the model’s dynamics: (1) homophily as the tendency of people to prefer interaction with more similar people and (2) social influence which results in mutual assimilation (Castellano et al. 2009). In the system, each agent has number of features (vector), each of which can take the value of several available traits. Each feature is defined by a fixed number of traits. This so called cultural vector has the length of the number of features. Interaction between the agents can unfold discretely in time, such that, two neighbours are selected at random and interact with a probability proportional to their cultural similarity. The similarity of cultural traits considers the number of traits that are the same in the each of the agents’ cultural vectors. Interaction results in higher cultural similarity of the interaction partners and, by that mechanism, cultural regions in the model can evolve. The model has been applied in various areas of research such as Complex Systems, Social Simulations, Physics and Opinion Dynamics and still is topical over 20 years after its inception (e.g., Nguyen et al. (2021) for Axelrod-based social influence model or Macy et al. (2021) for a homophily-based model of polarisation).
In the Axelrod model, the agents are arranged on a 2D-lattice, each connected to four neighbours. Each agent has a vector of features with different characteristics (traits). The agents’ features can chance via exposure to social influence by other, neighbouring agents. The probability of an agent being influenced in the system follows the principle of homophily. The greater the similarities in their vectors, the higher the interaction probability. The influence mechanism in the model consists of three steps: (1) randomly select two interaction partners; (2) compute the chance to interact, as a function of their shared number of traits; and (3) if an agent is influenced, it copies randomly a trait of its interaction partner on which they previously differed, and thereby become more similar to each other. A possible outcome of Axelrod’s model are cultural regions of linked agents, in which all share the same cultural vectors.
Previous work shows that the Axelrod model is well-suitable for use with attitudinal survey data (Dinkelberg et al. 2021b; MacCarron, Maher, et al. 2020b). The number of survey items from the survey corresponds to the features in the model, whereas the number of response options on a scale defines the number of traits. Therefore, one agent in the model represents a participant from the survey initialized with their responses to the survey items. However, an issue with using Axelrod’s model to represent survey data is that, if the number of features is larger than the number of traits, then the Axelrod model will always converge to a single dominate feature vector (referred to as a culture) given long amounts of time. As a result, extensions often allow different cultures to emerge in a broader set of parameters (Centola et al. 2007; MacCarron, Maher, et al. 2020b; Shibanai et al. 2001; Ulloa et al. 2016).
One notable extension is the agreement-threshold model, which incorporates an agreement threshold, limiting the flexibility of feature adaption and social influence (MacCarron, Maher, et al. 2020a). The agreement threshold allows the agent to adopt features that are within a certain range and rejects adaption of traits that fall outside of it. To introduce an agreement threshold, the traits of each feature are placed on an ordinal scale instead of a nominal scale (for a more detailed description, see SI).
The ordinal scale for the traits in this agreement-threshold model makes it particularly suitable to seed with attitudinal survey data. MacCarron, Maher, et al. (2020b) show how attitude-related items (survey questions) can be represented as features and response options as traits. The traits describe an opinion along a scale (e.g., steps on a Likert-scale, often used for capturing opinions in surveys, Croasmun & Ostrom (2011)). Further, the limitation due to the agreement threshold prevents an agent from a sudden reversal of its opinion position, for example, switching from an extremely negative to an extremely positive opinion. Instead, an agent can only switch to a trait that is positioned directly next to it on the ordinal scale. The underlying social network in survey data is generally unknown and, therefore, we cannot know who can influence who. However, in recent work on placing the Axelrod model on different topologies (e.g., random network; complete graph), it was shown that the topology does not affect the behaviour of the model; rather the homophily parameter of the agents outweighs the topology of the underlying network (Dinkelberg et al. 2021b). As in MacCarron, Maher, et al. (2020b), we soften the assumption of cultural regions and explicitly observe here the forming of opinion-based groups (groups around shared attitudes (Bliuc et al. 2007), based on similar or identical feature vectors). The higher the alignment in feature and traits, the higher the likelihood of sharing the same cultural identity.
In our approach, we seed the Axelrod model, the agreement-threshold model and some model extensions, which formalise additional elements of the Social Identity Approach. We then introduce the model’s input, empirical, attitudinal survey data, to observe the opinion changes in the system. We use three longitudinal data sets, a study on public health attitudes in the UK, data from two periods of the American National Election Studies, and a data set on political attitudes before and after the 2020 US election.
Social Identity Approach in the (Extended) Axelrod Model
Social Identity Approach
We introduce the foundation of additional mechanism in the Axelrod model that determines the role of groups. The Social Identity Approach (SIA) loosely combines the social identity theory (Tajfel et al. 1979) and the self-categorisation theory (Tajfel & Turner 1986; Turner et al. 1987) to understand how individual and social identity intersect, and shape group dynamics. Social identity, as a complementary concept to personal identity, describes the group memberships and group relations of a person. The social identity theory outlines the relations between in-group and out-group and their values for identity construction (Abrams & Hogg 1990). To obtain in- and out-groups in a social setting, people are divided into categorical social groups, for example gender or political affiliation, etc. To the extent that people identify with their group membership, they adopt behaviour, attitudes and values to conform with the group identity. The members of an in-group identify with the in-group, and distinguish between in-group and out-group in perception and behaviour, thus making the identities psychologically and materially real (Hornsey 2008). These aspects of social categorisation, social identification and social comparison of the social identity theory are placed into a dynamic context by the self-categorisation theory (Reicher et al. 2010). Due to social categorisation, individuals divide the social world into groups and select group memberships. The process of group identification and alignment with the group identity is described as social identification (Smaldino et al. 2012). The distinction between in-group and out-group generally leads to a positive affinity for their in-group. This social comparison influences the inter-group relations and its dynamics. The self-categorisation theory emphasises the contextual variability of the manifold social identities which a person incorporates and in which situation these become salient (Jenkins 2014). The SIA broadens this identity concept from an individual and draws parallels to group behaviour and values.
In the Axelrod model and the agreement-threshold model, we formalise aspects of this fusion of social psychological theories to consider group identification in the social dynamics. Scholz et al. (2021) examine the representation of SIA in agent-based models, uncovering that only a few studies implement an agent-based model with all aspects of SIA (see e.g., Mekni 2013). Up to this time point, most of the agent-based modeling studies focus on one or few aspects of SIA such as group norms and social identities (Scholz et al. 2021). The authors underline that a translation from this social psychological framework into an agent-based model requires further interpretation from the modellers. Hence, in this paper, the examination and use of SIA in the Axelrod model supports this to implement SIA and to improve the reflection of real-world processes in agent-based models.
Embedded elements of the Social Identity Approach in the base Axelrod models
We stated previously that the Axelrod model involves aspects of SIA, as does the agreement-threshold model (MacCarron, Maher, et al. 2020a). The standard Axelrod model only explicitly incorporates one aspect of the SIA: that people are motivated to maintain, and intensify, connections to people with whom they identify (where identification is represented as consensus across a vector of features – the opinions that they hold). The model does not explicitly allow the agents to classify others by social categories and, at the beginning of the simulation runs, there exists no explicit distinction between in- and out-group. However, different cultural regions (defined by agents that can no longer change their opinion due to their neighbour all sharing the same feature vectors) can emerge and indicate group structure due to attitude alignment. The group structure is not embedded in the decision process of the agents except as it is expressed in dyadic interactions between neighbouring agents. Given that, the model excludes many aspects of social comparison, for example, ranking the own group higher in value than out-groups to enhance self-esteem (Martiny & Rubin 2016). Nonetheless, through the multi-dimensional component of the cultural vectors, the agents’ interactions are dependent on their similarities and, therefore, on their emerging opinion-based groups. These emerging groups direct the agents to common social identities which get more homogeneous over time. All in all, the standard Axelrod model captures some aspects of the SIA, but misses explicit definitions of in-group and out-group as well as group-dependent behaviour.
In our analysis, we aim to reveal further elements of the SIA such as social identification that the agreement-threshold model contains as well as their influence on the opinion dynamics. MacCarron, Maher, et al. (2020a) extension to the Axelrod model above involves the addition of an agreement threshold. The emerging opinion-based groups are defined by gradually approaching agents in their opinion vectors. The simulations build upon survey data which define the model’s starting conditions. In real-world attitudinal survey data, we expect to capture existing opinion-based group structure; and expect that these opinions reflect aspects of social identities (Hogg & Smith 2007). The similarities lead to a higher probability of interaction and have therefore a direct influence on consequent social identity formation.
The agreement threshold operationalizes the social identification of the SIA, since it draws a line between the in- and out-group from an agent’s position, based on dyadic comparison. An agent adapts its attitudes towards a perceived in-group (within the agreement threshold), and will not be influenced by agents from a perceived out-group (outside the agreement threshold). The model shows an opinion space with different opinion-based groups which are set implicitly by an agent’s social categorisation. These opinion-based groups are defined by agents’ features and, at the same time, they represent parts of the agents’ social identity. In-group interactions shape the social identities. If the original or extended Axelrod models are shown to capture social identity processes, then we have made some progress towards a (minimal) representation of Turner & Oakes (1986) vision of social identity, capturing "the continuous reciprocal (dialectical) interaction and functional interdependence between the psychological processes of individuals and their activity, relations and products as society" (p. 240). Here, they explicitly reject reductionist versions of social identity, arguing that social structure and individual agency are irreducibly intertwined.
Mechanisms to enhance the role of social identity approach in the Axelrod model
We next discuss further aspects of SIA which could be integrated as mechanisms and foster its representation in the model. The distinction between in- and out-group plays an essential role in the SIA. The group-dependent social identity drives the individual behaviour and values. As an additional mechanism, we adjust the agent’s perception of the in- and out-group members. Therefore, we integrate the out-group homogeneity effect into our model, which has been widely observed (Boldry et al. 2007; Park & Rothbart 1982; Quattrone & Jones 1980). This effect derives from social comparison and underlines the situational importance of group membership. The interaction will be influenced by an inter- or intra-group relation. The individual perceives the members of the out-group and the in-group, in an inter-group comparison both as homogeneous. Despite potential individual alignments, the focus lies on the differences between the groups. Therefore, in the inter-group interaction, the role of being group members is salient.
Nevertheless, when focusing only on the in-group, we can expect the opposite, an in-group heterogeneity effect (Frederic & Falomir-Pichastor 2018). Although in-group members share a common social identity, they are perceived as more heterogeneous from an in-group member. In the intra-group context, the individual’s positions is set in contrast to the group and differences are emphasised here.
The social identity theory underlines the influence of the group membership on interaction. Brewer (1979) detects an in-group bias that fosters a positive in-group relation. This bias shifts the interaction preference from inter-group towards intra-group. The idea is related to the "echo chambers" in online social media, where opinions are circulated among like-minded individuals and it works as a divisive factor for inter-group relations (Baumann et al. 2020).
The agreement threshold already encapsulates aspects of SIA. To implement differences in the perception of the in- and out-group, we introduce and test two new mechanisms to enhance the dynamics of the model.
Additionally implemented mechanisms in the Axelrod model
Specifically, we use reported political affiliation as an indicator of group membership. For instance, a Democrat is able to identify other Democrats (in-group) or Republicans (out-group). Therefore, we further extend the model with a group affiliation parameter that indicates the agents’ group.
- Group-dependent perception: The members from out-groups are perceived as relatively homogeneous, while in-group members are perceived as more heterogeneous. We implement these two perceptions into our model by defining a group-dependent agreement threshold. The interaction between in-group members takes place without the limitation of the agreement threshold (same as in the standard Axelrod model). The in-group members are perceived as more diverse; however, the intention to align with the in-group members is still prevailing. The inter-group interaction involves an agreement threshold, which in turn just allows attitude changes within a certain range. Only out-group members who are perceived as close to agent’s in-group (within the agreement threshold) are able to influence the agents’ attitudes. Due to their attitude alignment, they can be perceived as an in-group member of an emerging opinion-based group.
- In-group preference: The group parameter defines the group membership of the agents and represents a salient social identity by creating a preference for interaction with in group members. We achieve this by decreasing the probability of interaction with out-group members. Note that this probability is still non-zero, thus inter-group interaction can still take place. If the two neighbours do not belong to the same group, the probability of interaction is 10 percent.
Simulations
Synthetic data
Initialisation of models with randomly seeded simulations
Axelrod (1997) shows that local convergence and global diversity are possible in the same model within a range of parameters. Nevertheless, global convergence with a low number of features and traits is the usual outcome. Compared to the standard Axelrod model, the agreement-threshold model can obtain the global diversity with the same parameters (MacCarron, Maher, et al. 2020a). The dynamics and outcomes of the Axelrod model with the additional mechanisms is unknown. We therefore construct a simulation case with synthetic data which is comparable to the given data sets. We set up a model with 100 agents that are divided into two equally sized groups. The length or the number of features of the cultural vector varies from 2 to 15. The number of traits is set to 5.
Results from randomly seeded simulations
In Figure 1, we show the mean relative size of the biggest cluster as a macro outcome of the model assessing the global convergence or diversity. A cluster is defined as a set of agents that share identical cultural vectors. The standard Axelrod model converges rapidly with an increasing number of features towards a relative size of the largest cluster equals the system size1, whereas the agreement-threshold model allows only a very limited cluster size near the minimum (one single agent). The agreement-threshold model with the in-group preference mechanism aligns with the outcomes of the agreement-threshold model. However, the same mechanism on the standard Axelrod model produces a relatively large cluster around 85% of the total system size, and is more similar to the standard Axelrod model. The Axelrod model with the group-dependent perception aligns even more with the standard Axelrod model and produces from 5 to 15 features a dominant cluster which is very close to the system size.

The results show that the in-group preference mechanism only partly influences the models dynamics in the long run, considering the relative size of the biggest cluster. The group-dependent perception mechanism does not change the model dynamics and behaves like the standard Axelrod model.
Longitudinal data sets
The usual approach is to initialise the model with cultural vectors that are uniformly randomly distributed (Axelrod 1997). The agreement-threshold model has already been tested with the uniformly randomly distributed conditions (Dinkelberg et al. 2021b; MacCarron, Maher, et al. 2020b). Here, we change the initial conditions and seed the model with longitudinal data sets on political and health-related attitudes, but keep the agreement threshold the same. We rely on the following three data sets:
- Data set 1: Survey data was collected around the 2020 US presidential election (Dinkelberg et al. 2021), with eight items on political attitudes derived from the ANES data set (see data set 2). The data was collected online via Prolific (www.prolific.co) in four waves: three weeks before, two days before, two days after, and three weeks after the 2020 US presidential election. The number of participants who responded to all questions and took part in all four time points was \(N=290\).
- Data set 2: The American National Election Studies (ANES) are surveys collected in each US presidential election cycle on a wide range of attitudes. From the ANES data set 2016 (ANES 2017) and 2020 (ANES 2021), we use a subset of eight items that refer to political, cultural and economic attitudes and relate to eight politically-relevant topics, identified by Malka et al. (2014). While the number of participants per cycle are usually over \(N=4000\), we selected only participants who took part in both 2016 and 2020 and responded to all relevant items. The number of selected participants was \(N=1635\).
- Data set 3: Maher et al. (2020) (Study 1a) provide a longitudinal data set on public health attitudes from 2020 in the United Kingdom. The items were taken from the Wellcome Trust health survey (Wellcome Trust and Ltd, The Gallup Organization 2019): eight items on trust in people and institutions (4-point scale) and three items on vaccines (5-point scale). The items are an assessment of trust in institutions and people. The size of this data set was \(N=195\).
Initialisation with empirical data
The goal is to investigate which of the models reproduces feature dynamics with volatility most similar to those observed in the actual survey. The model describes the relative number of changes between two time points for each feature. We allow the simulations to run for the same number of changes as we observe in the data sets between time points, i.e. the overall number of changes in the model stays the same but the number of changes per feature varies. We then compare the number of changes for each feature in the longitudinal data sets between time points with the cumulative results from the simulation runs.
With each one of the three data sets, we initialise all Axelrod models with the participants as agents and their survey answers as their cultural vectors. The participants are randomly allocated to a grid (lattice) as normal within model. The number of items per time point defines the number of features for the cultural vector and the traits are the responses to the particular item. We use the 2D-Lattice as there is no information about the social network or any additional information on how the participants are related. The size of the 2D-lattice depends on the number of valid participants in the data set. The parameter settings are therefore fixed by the data sets as the base Axelrod model does not allow any other parameter settings.
Measurement to quantify the differences between the model variations
We use the L2 distance as a numerical summary for these models, comparing each model variation to the observed data (see Tables 1- 3). The closeness of each model variation to the data is given by the mean euclidean distance:
| \[d(f_1,f_2) = \frac{1}{N} %\cdot \sum_{k=1}^N \sqrt{\sum_{i=1}^{M}{(f_{1,i} - f_{2,i})^2}} \; , \] | \[(1)\] |
Results from empirical data
The variations of the Axelrod model describe the relative number of changes between time points. The box plots in Figures 2 and 3 show the distribution of the accumulated changes for the US presidential election data from time point one to time point four for each item for the Axelrod simulations. The red bars indicate the relative number of changes per feature in the empirical data set and act as a benchmark for the simulation results.
In Figure 2, we focus on the simulations without agreement threshold: (1) the standard Axelrod model and (2) the standard Axelrod model with in-group preference. Overall, the relative number of changes is always close to the region between the 25\(^{th}\) and 75\(^{th}\) percentile of the simulations. The standard Axelrod model has a lower standard deviation and the means are closer to the observed number of changes.
In Figure 3, we compare the changes from the empirical data set (red bars) to three different simulation settings with an agreement threshold: (1) the agreement-threshold model (purple); (2) the agreement-threshold model with the group-dependent perception (orange) and (3) the agreement-threshold model with in-group preference (green). It is striking that the estimated changes for all three variations are close to the actual changes over time. The relative number of changes from the empirical data lies in 7 of 8 features within the 25\(^{th}\) and 75\(^{th}\) percentile of the agreement-threshold model. The agreement-threshold model outperforms all the other variations in their fitness and the variance, while including less additional parameters. The in-group preference version of the model estimates close to all feature ranks like in the empirical data, as well as the agreement-threshold version. The group-dependence preference performance is similar to the standard Axelrod model in Figure 2.
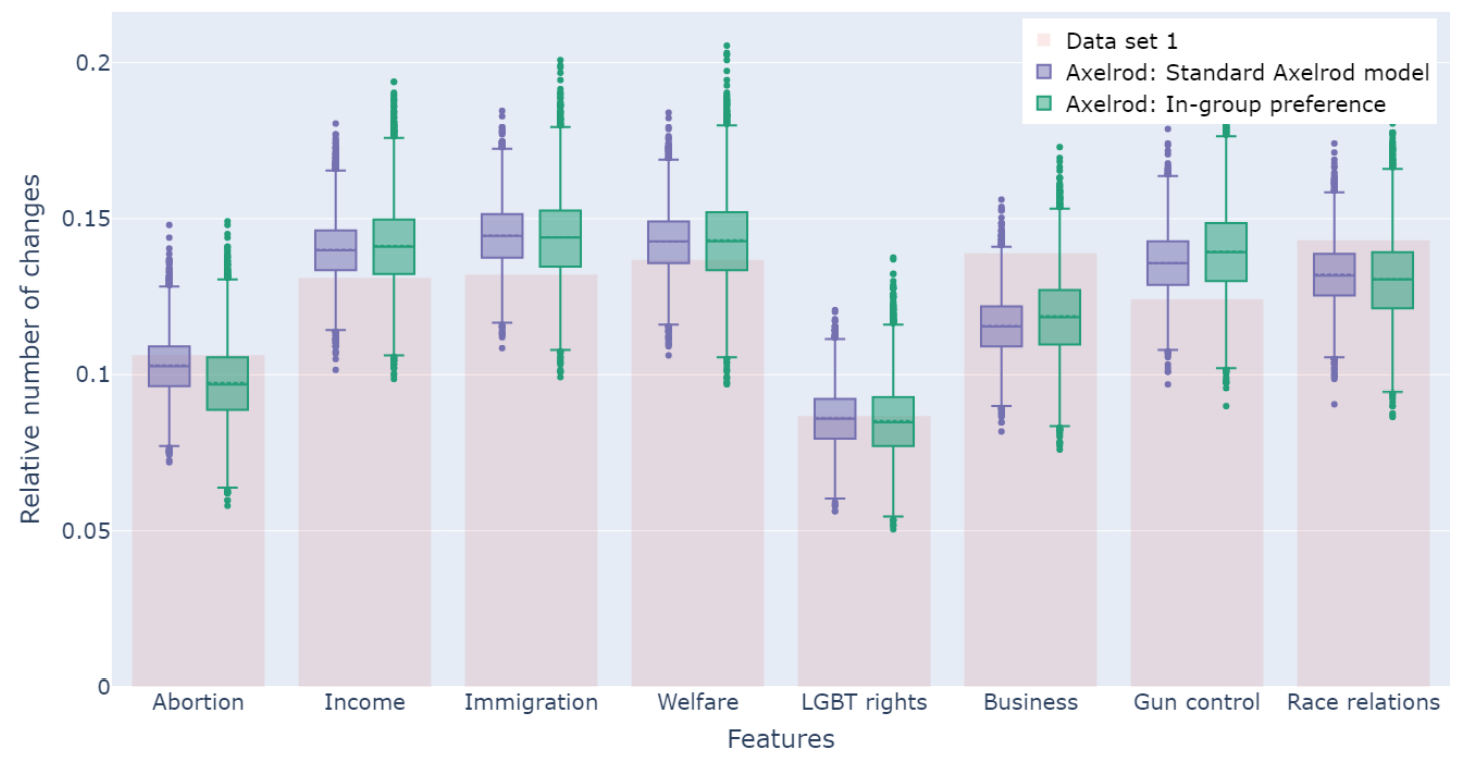
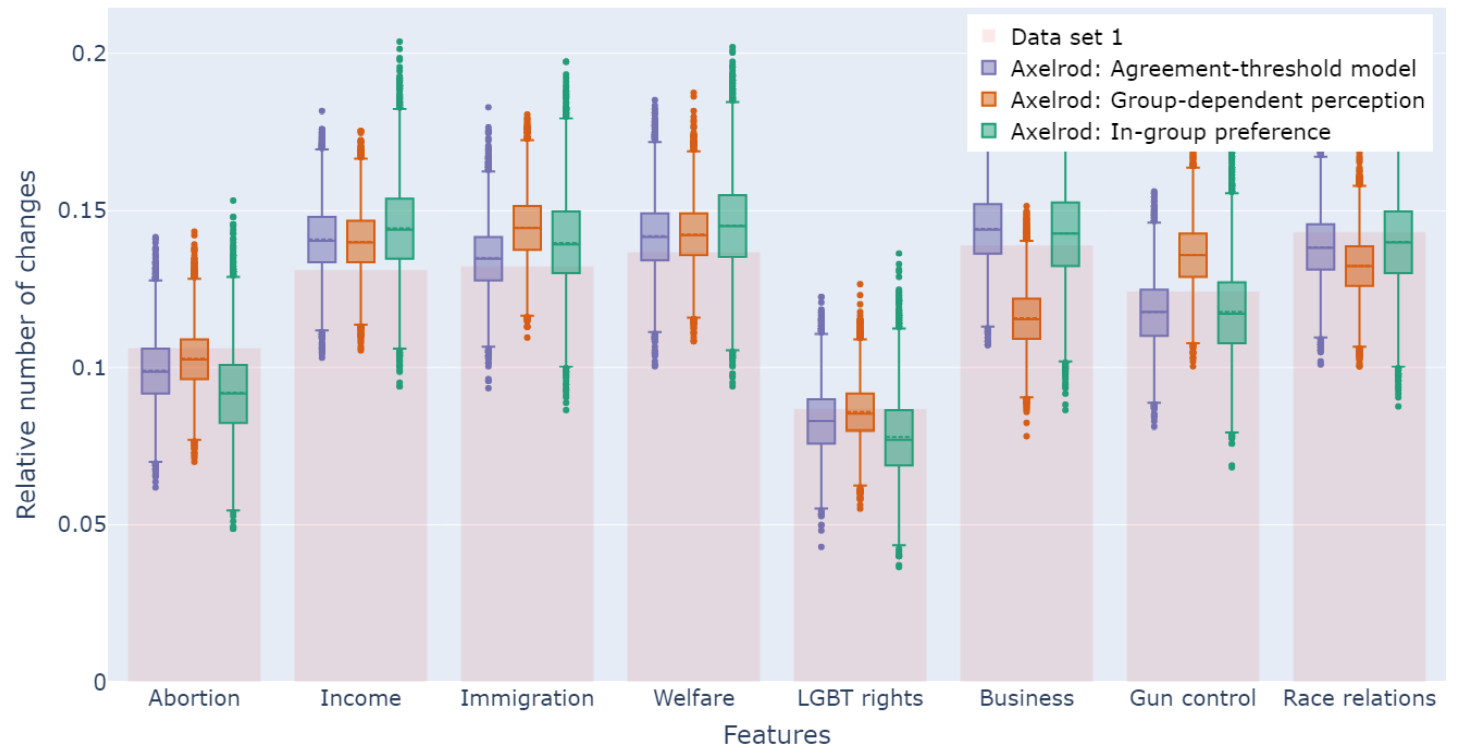
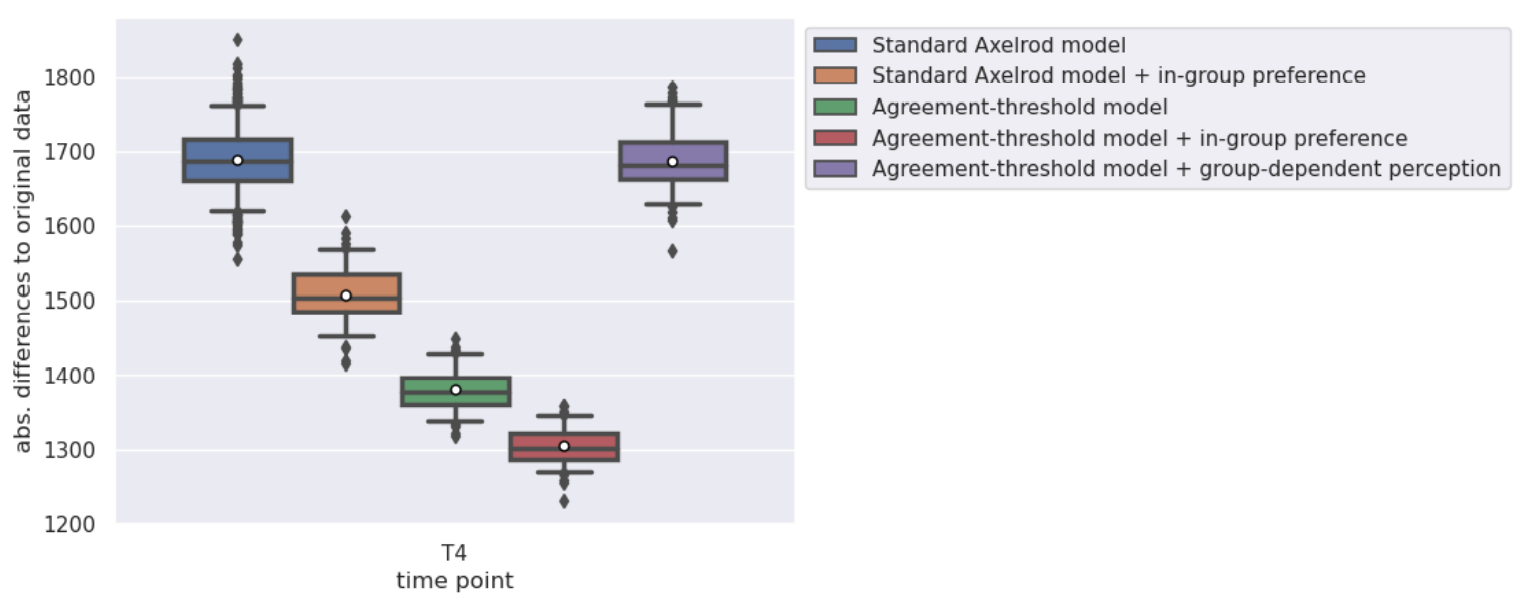
The L2 mean distance quantifies what is depicted by the box plots: the agreement-threshold performs best for the US presidential election data. The Table 1 summarises the results for the first data set (and the results for the remainder data can be found Table 2 and 3 in the SI).
| Name | Time point | Agreement threshold | Model variation | L2 mean distance | Std. deviation |
|---|---|---|---|---|---|
| Data set 1 | T4 | no | Standard Axelrod model | 96.97 | 12.01 |
| Data set 1 | T4 | no | In-group preference | 105.85 | 16.71 |
| Data set 1 | T4 | yes | Agreement-threshold model | 85.41 | 10.26 |
| Data set 1 | T4 | yes | Group-dependent perception | 96.55 | 11.84 |
| Data set 1 | T4 | yes | In-group preference | 99.94 | 15.76 |
The simulations on the data sets 2 and 3 (SI, Figure 6, 4 and 5) replicate the strong fitness from the standard Axelrod model. The agreement-threshold model and the agreement-threshold model with the in-group preference mechanism show high standard deviation in their model fitness. The standard Axelrod model, the model with the in-dependent preference mechanism and the model with the group-dependent perception show similar number of changes per feature (see SI, Table 2). This aligns with the results on the synthetic data, where these variations of the model also depict the same macro outcomes as the base models (see Figure 1).
Discussion
Social identity processes are thought to play a key role in attitude maintenance and change, especially in relation to political events and social crises (Maher et al. 2020). A key challenge for efforts to model this is that social group relations and identification are emergent phenomenon, which themselves are partially determined by the structure of attitudes in society. In the Axelrod model, with attitudes as features, opinion-based groups can emerge as features at the macro level and shape attitude change at micro level. In some cases, additional mechanisms can improve this aspect of the model (MacCarron, Maher, et al. 2020a), but it was previously unclear how a explicit social identity related parameterisation would improve the explanatory power of the attitude changes.
Our theoretical analysis suggests that elements of the SIA are represented in all variations of the Axelrod model but to a different extent. However, none of the model variations captures the SIA to a full extent. We integrated the distinction between in- and outgroup and re-adjusted the viewpoints and behaviour for in- and outgroup members. Reicher et al. (2010) evaluate the SIA to be a flexible theory of perception and impacts of social groups that is applicable to various circumstances. In the outlined model(s), the model’s mechanisms are fixed and its agents are missing decision-making power and adaption to different social situations.
The Axelrod models are missing relevant elements of SIA. The salience of social identities decides which social identity is present and it changes dependent on the environmental circumstances. Preferences and positive emotional association with a group provokes the salience of a social identity. Thus, an individual holds multiple social identities, connected with behaviours, beliefs and norms. The positive association to groups influences the motivation of categorisation and the definition of in- and outgroups by the individuals. In the Axelrod models, there are no overlapping group memberships, so that also the concept of salience is obsolete here. The social identity eclipses with the personal identity or is determined by the group parameter. We focus in the models more on the processes of SIA, i.e., the reaction of group members and the different treatment for in- and outgroup members. For a further extension of these models, the multi-dimensionality of social identities and concept of salience should play a more influential role. In the end, the empirical data limits our models, providing no information on salience and multiple group categorisation.
Using three different longitudinal data sets, we investigated the performance of the Axelrod model in describing attitude change over time, with and without explicit mechanism of social identification and attitude change resistance. Our results highlight an overall strong performance of the original model in imitating the feature changes between time points, given the approximate number of observed changes. Although not every feature change falls into the region between the 25\(^{th}\) and 75\(^{th}\) percentile, the approximation of the features’ changes reflect their high variability. The standard Axelrod model indicates the expected changes per feature over the three data sets to a better extent than the models with additional mechanisms and parameters.
The explicit inclusion of a group parameter and the introduction of two additional mechanisms from the SIA does not improve the ability to reproduce number of changes. The group-dependent preference mechanism introduces a blend of the Axelrod model and the agreement-threshold model. For showing the expected number of changes, it lags behind the performance for the Axelrod model with or without agreement threshold. Without a significant increase in the explanatory power of the model the increase in complexity is not warranted.
The introduction of the second mechanism, in-group preference, introduces a group-based limitation of interaction. The agents preselect their potential interaction partner and rely heavily on this group parameter. This forces the groups to move into a more coherent opinion space within the group without being influenced much by outgroup members. The changes are primarily within items in which the in-group members do not agree on. Therefore, these items may not play an essential role for the group parameter and the social identity of the group.
The determined in- and out-group structure, defined by the group parameter, could be irrelevant for the accounted changes in the data. In that case, the group parameter might reflect differences based on social categories that are not relevant to the identity reflected in this item set. Nonetheless, the items were particularly selected as a subset for the political identity (Dinkelberg et al. 2021). From the data perspective, it could be advantageous to try various social categories. For a detection of possible opinion-based groups and selection of relevant items in the data set (Dinkelberg et al. 2021).
It is noteworthy that the base Axelrod models performed as well as, or better than, the models that explicitly included social categories and explicit SIA mechanisms. This is because the additional group parameter overlaps elements of the SIA that are already implicitly embedded in the Axelrod model (especially when it is initialized with naturalistic data), specifically, the homophily-dependent social influence mechanism which makes dyadic interactions contingent on emergent social structure. If we apply the Axelrod model to attitudinal data, the opinions, which then form the agents’ culture, indicate group structure. The alignment of attitudes in multiple dimensions marks the evolving group identity due to either the formation of opinion-based groups or the group structure that is already incorporated in the data. Additionally, the possible members of the opinion-based groups, in return, act as group members because they influence primarily other in-group members and shape the social identity. Hence, the group parameter might interfere with this and shift the agents into alternative group structures.
The agreement-threshold model expands the implicit opinion-based group structure. The distinction between the in-group (within the agreement threshold) and the out-group (outside the agreement threshold) integrates a sharper social identification for the agents. The agreement threshold fosters the collective group formation and adds a factor of identification between groups. The limitation on the opinion change has essential influence on the agents’ behaviour as they do not interact with an agent outside their opinion space which is defined by their agreement threshold.
The number of changes between two time points are based on data. If the number of changes in the model runs towards unlimited time, the Axelrod model reaches, with a high probability, a global consensus state. The Axelrod model with the agreement threshold would obtain a broader opinion landscape. Nguyen et al. (2021) provide a possible explanation of conservation of multiple states for an Axelrod-based model with an increased probability of interaction. The agents are faster in aligning with their local environment and get dynamically fixed to local attitudes, which in turn provides the system to reach a global consensus state. Only one of the two additional mechanisms (in-group preference), based on the explicit formalisation of SIA, behaves like the agreement-threshold model. This extension of the model allows a more realistic representation of future states of the presented data in an unlimited time frame.
The explicit formalisation of the SIA performs worse, or only as good as, the standard Axelrod model over all three data sets. The additional mechanisms and the group parameter increase the model’s complexity without substantial performance gain. Nevertheless, the differences in the results between the mechanisms and the Axelrod model lead to starting points of a possible interpretation of the model results. For example, the in-group preference shows a similar behaviour as the Axelrod model when the feature changes are mainly to be found within the selected group structure. This room for analysis fosters the motivation to integrate further elements of the SIA to evaluate which elements of it drive the model or which of them are not relevant.
The fact that the Axelrod model alone works has some key advantages: the model is well studied and it is a model that takes no parameters, it just uses the number of survey items and their scales. The agreement threshold and SIA additions all take additional parameters thus increasing their complexity. While we state earlier a key disadvantage of the standard Axelrod model is that everyone ends up agreeing with everyone else, that is in “infinite” time. Here we observe the actual number of changes in four years is nowhere near the large time-scales required for Axelrod to converge. We cannot say that if all the participants were to live forever, in an isolated system, that they will not eventually all agree with one another.
Conclusion
Social identities and the group structure are salient in the attitudinal data sets. The Axelrod model implicitly includes these aspects in simulations of evolving opinion-based groups. The multi-dimensional representation of the opinions chains the personal identity and the social identity together. Social identity affects the development of the personal identity through the homophily principle, and the agents, in turn, shape the own social identity by social influence. This provides a minimal operationalisation of Turner and Oakes’ vision of a recursive dynamic theory of social identity, where individual psychology and social structure are irreducibly intertwined (Turner & Oakes 1986). Specifically, in the Axelrod model, agents’ attitude vectors capture their position in the social identity space; and an inter-group structure emerges through homophily-preserving dyadic interactions. Indeed, the Social Identity Approach is in so far present in the Axelrod model that the data on opinions and its structure leads to empirically valid simulation results.
Of course, the Axelrod model excludes various aspects of the Social Identity Approach such as the salience of multiple identities and the agents’ need to choose between them in specific situations. The flexibility of the social identities and the motivation to act as a group member are complex but essential mechanisms that should be addressed in future work.
Overall, the results allow the conclusion that the Axelrod model captures some aspects of social identity, and is able to detect volatility and future changes in opinion-based features. This addresses a common criticism of the agent-based models (Garcia & Jager 2011), which tend to not be validated with empirical data. Here, we elevate the Axelrod model from being pure conceptual ("toy model") to a empirically-driven agent-based model to fit feature volatility in attitudinal data sets. Indeed, using the empirical data is essential because it provides a starting point already imbued with emergent social identity.
Acknowledgements
The authors would like to thank Alina Dubovskaya for discussions on the Axelrod model and interpretation of the results and the Social Dynamics Lab in UL for discussions of models and results. Furthermore, we want to express our thanks to the organisers of SIAM special issue author workshop Geeske Scholz, Nanda Wijermans, Martin Neumann, Rocco Paolillo, and Anne Templeton, and for the fruitful discussion with our reviewers and other workshop participants. AD and MQ are funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 802421). PMC is funded by Science Foundation Ireland, grant number 16/IA/4470.Supplementary Information
Agreement-threshold model
The agreement-threshold model (MacCarron, Maher, et al. 2020a) enhances the Axelrod model to measure opinion dynamics and to allow more opinion diversity. The additional feature, the agreement threshold, limits the agents’ ability to jump between extreme opinions. The restriction is set on the copying process, whereas in the standard Axelrod model random copying of traits was allowed, in the agreement-threshold model only features that are closer from the agent’s actual position than the agreement threshold can be copied. The influence of agents far away from the own opinion is limited and reflects commonly acknowledged constraints on social influence (Deffuant et al. 2000; Sherif & Hovland 1962). Two individuals \(i\) and \(j\) can copy feature \(k\), if \(|\nu_{i,k}-\nu_{j,k}| \leq a\). This is similar to the idea of bounded confidence (Hegselmann & Krause 2002); however, it takes the threshold into account before and not just after interacting. In MacCarron, Maher, et al. (2020b), the agreement threshold with \(a=1\) (distance of opinion which is perceived similar) was used and we will keep this parameter setting for our simulations. The agreement threshold adjusts two mechanisms: likelihood of interaction and the possible features which can be copied by an agent during an interaction. The likelihood of interaction now includes positions where the agents have identical values and where the features are within the agreement threshold. The new mechanism is similar to the latitude of acceptance from the Social Judgement Theory set up by Sherif & Hovland (1962) (for a more detailed description, see SI in Dinkelberg et al. 2021b).
Results on empirical data
Data set 2: American National Election Studies
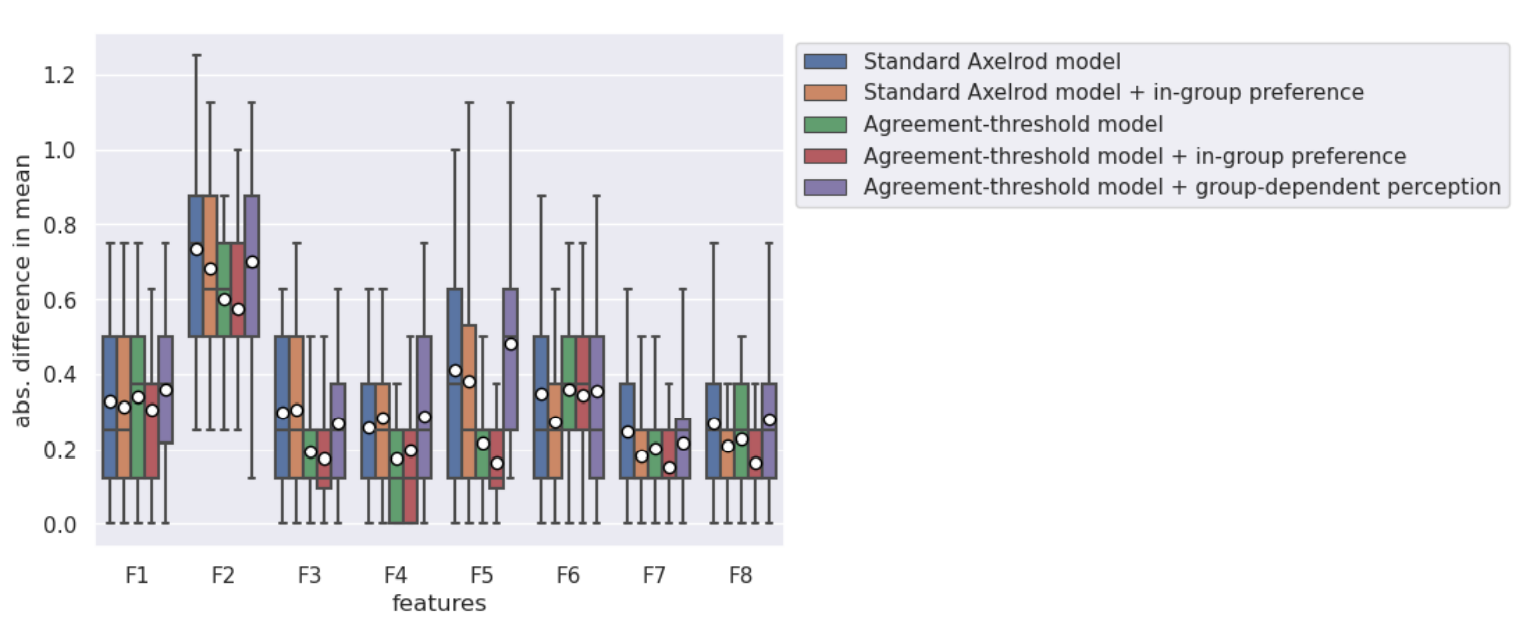
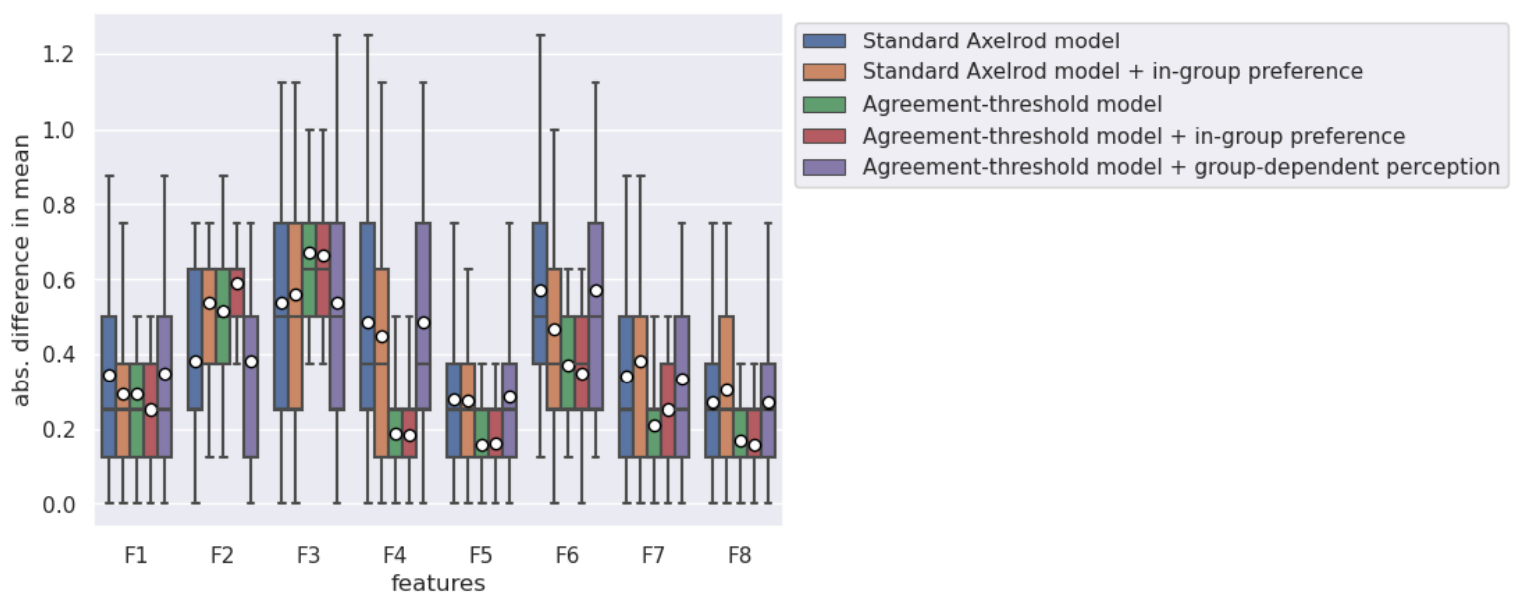
The explanatory power of the relative number of changes for the ANES data set is worse in comparison to the other two data sets. In Figure 4 and Figure 5, we measure the relative number of changes for the eight features of the ANES data set. The relative numbers are shown as bars. The results from the Axelrod simulation are displayed as box plots, first, to distinguish and, second, to display the distribution in more detail. Figure 4 holds the results for the simulation runs without agreement threshold and Figure 5 includes all simulations with an agreement threshold. The level of fitness is the same for the standard Axelrod, the in-group preference (no agreement threshold) and the group-dependent preference model. The relative number of changes are in 3 out of 8 times within the 25\(^{th}\) and 75\(^{th}\) percentile. The variations with an agreement threshold do not provide information on the volatility of the features.
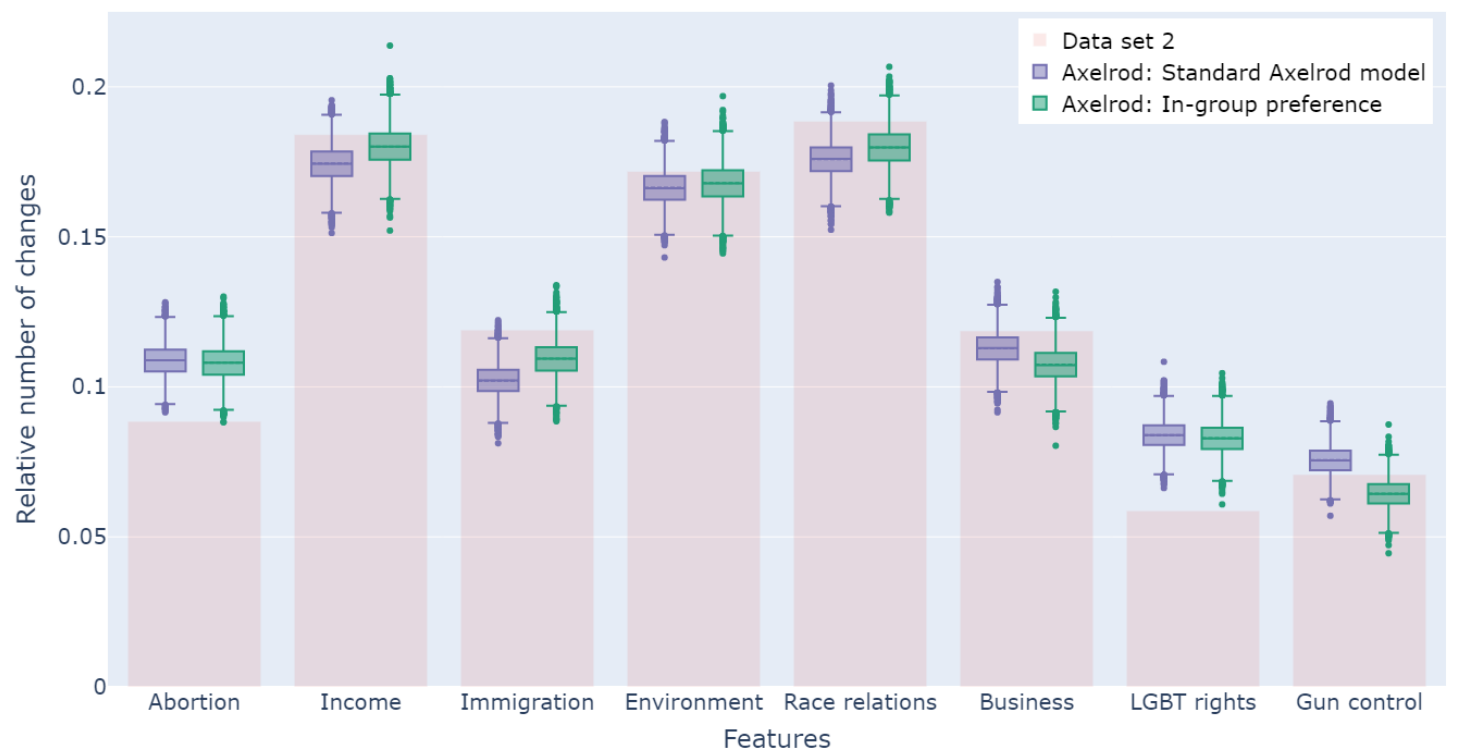
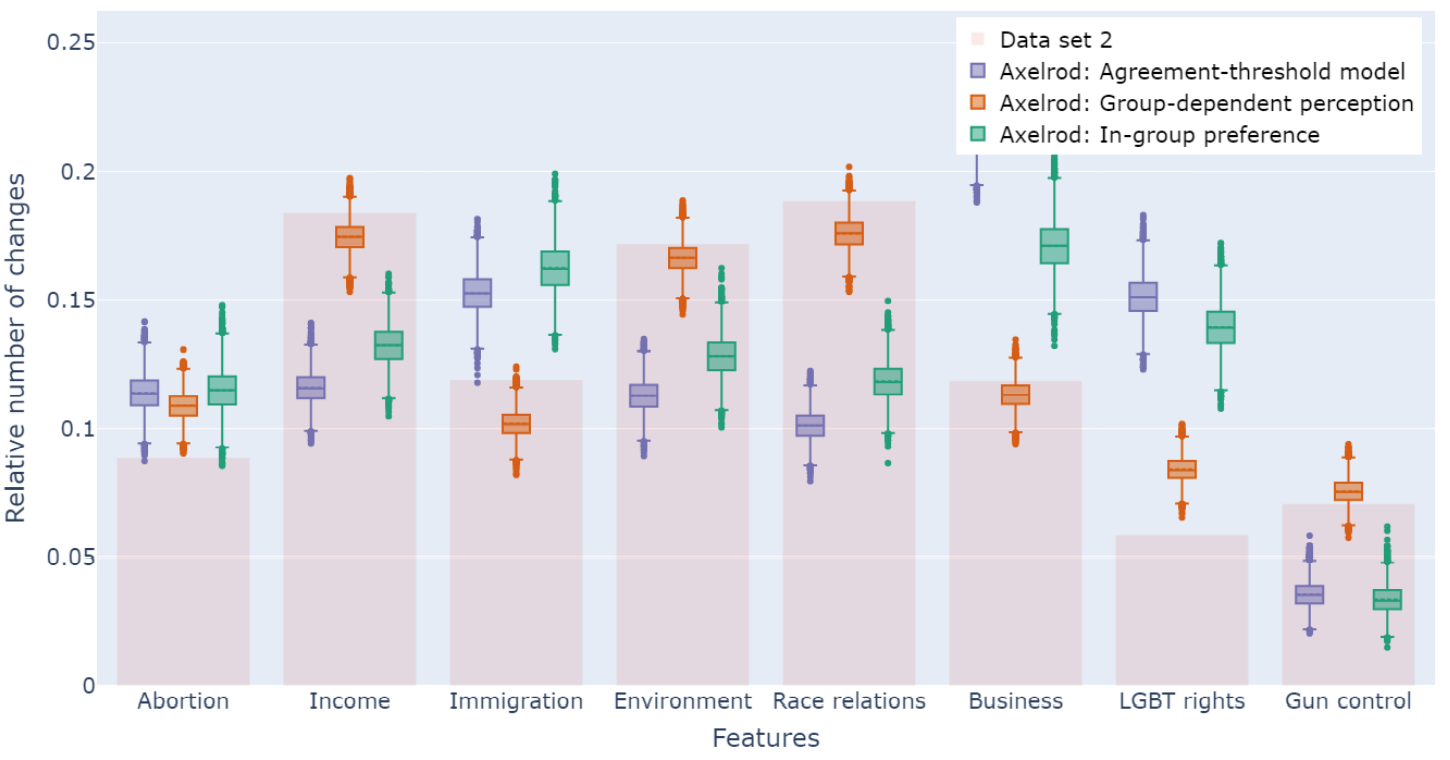
There are two major constraints in the data set. The number of changes, measured as a differences between the two time points, can only be an approximation. In the two other data sets, we observe changes in opinions over a time period from less than 3 weeks. This limits the precision of the time parameter. The second limitation is given by the number of response options as they vary between the items. The items are based on a Likert-scale and range from 1 to 3, 1 to 4 or 1 to 7 response options. The issue is primarily of relevance for the integration of an agreement threshold (\(a=1\)). The agreement threshold constraint is stricter for the items with more response options. The agreement-threshold model and the ingroup-preference model show a very high variance in their simulation results. For example, for the 6th item, the results ranges from around 5% to 70% of relative number of changes. The standard Axelrod model and the group-dependent preferences model as well as the in-group preference model (without agreement threshold) demonstrate the tendency of changes for the features. They accurately describe the most changes for the three features with the highest changes in the data.
Data set 3: Trust health survey in UK (2020)
The longitudinal data set on trust in people and institutions as well as opinions on vaccines from Maher et al. (Maher et al. 2020) reveals opinions at three different time points. The time of the data collection is the early phase of the COVID-19 pandemic in 2020. Here, we simulate volatility in the features during this phase.
We compute the number of changes between the time points and determine in this way the number of changes for the simulations. Unlike the other data sets, there is no additional information for a group parameter. Therefore, the simulations runs include only the standard Axelrod model and the agreement-threshold model. The model is seeded with 11 features for each agent, where as the data allows us \(N=195\) different agents. The simulations run for 1207 changes, which are number of changes between time point 1 and 3. We run each model for 10,000 times.
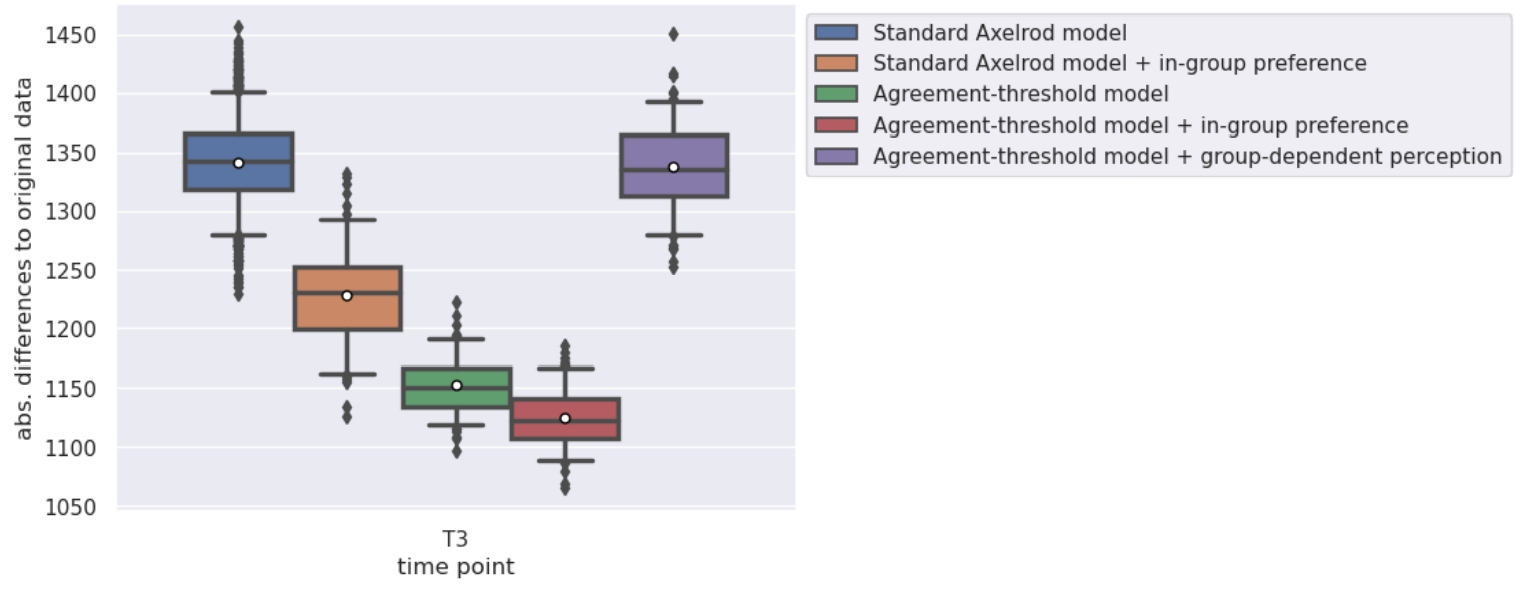
Figure 6 shows a comparison of the relative number of changes in the data set (red bars) and the distributions of the simulation results on box plots for the standard Axelrod model (purple) and the agreement-threshold model. The trend of the relative number of changes for each feature is picked up by the standard Axelrod model, whereas the fitness of the agreement-threshold model show a high variability in their results.
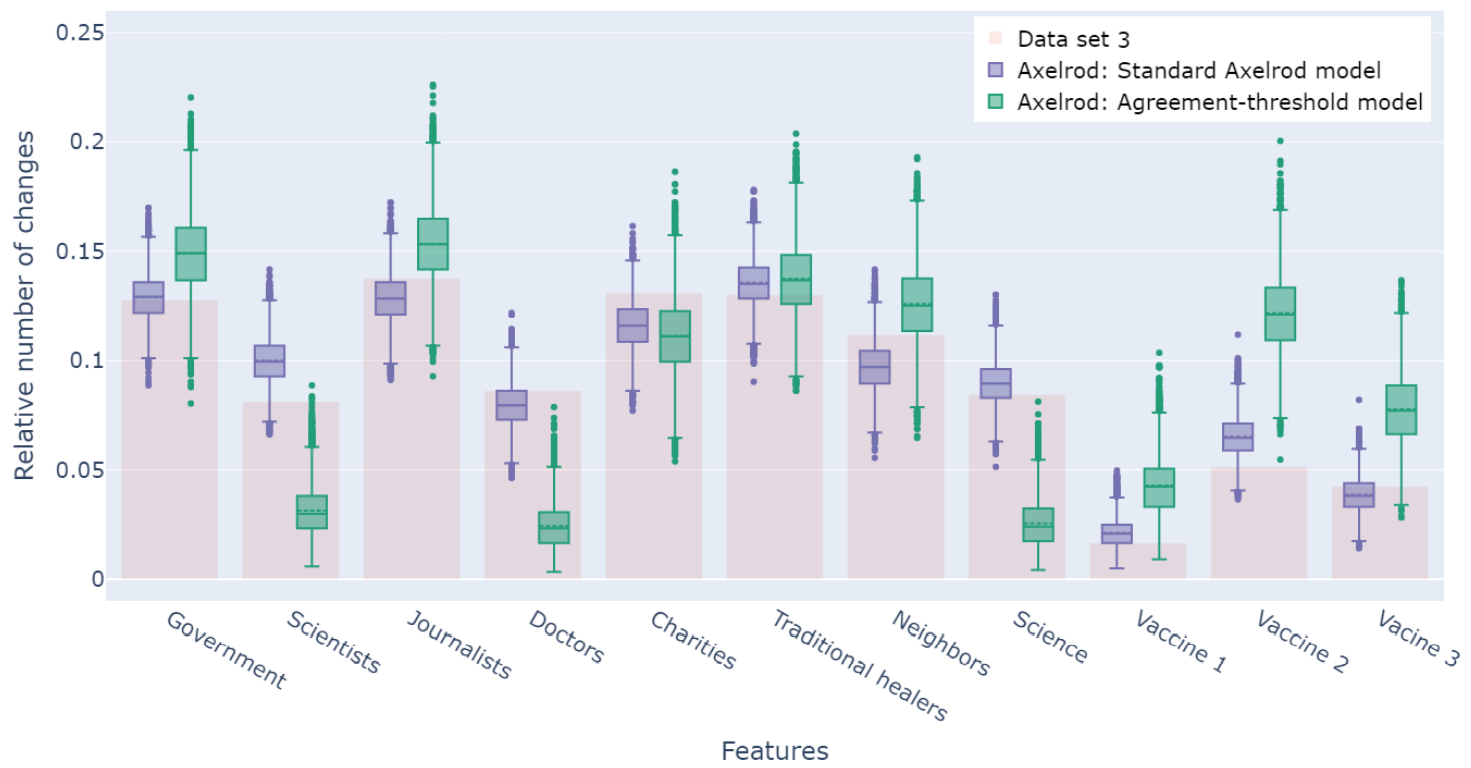
The standard Axelrod model’s means are closer to the empirical number of changes and the variations are much more narrow than for the agreement-threshold model. The differences between the two models are striking for the features 2, 4 and 8 where the 95% confidence intervals do not overlap. The items display the trust in scientists (2), the trust in doctors (4) and the trust in Science (8). The agreement threshold allows only changes within the threshold, whereas the standard Axelrod model accounts for changes outside the agreement threshold. This could be particularly important as the items show the trust in health and scientific community during a start of an epidemic. The attitudes towards could be influenced by an external shock, and usually stable attitudes change.
Closeness of the model variations to results from the three data sets
The results in Table 2 and 3 show the L2 mean distance (see Equation 1) for data set 2 and 3. In Table 3, we only compare the standard Axelrod model and the agreement-threshold model due to the fact that there was no group parameter given in the data set. The standard Axelrod model, as already seen in the Figure 6, outperforms the agreement-threshold model. Its L2 mean distance and the standard deviation are much lower.
Concerning the L2 mean distance for the simulations in data set 2 (see Table 2), three classes of different performance are present. The best fitness of volatility has the standard Axelrod model with ingroup-preference whereby the standard Axelrod model as well as the agreement-threshold model with group-dependent perception are very close it. The results of the agreement-threshold model with in-group preference is further away from the observed data, and the agreement-threshold model performs worst. The standard deviation of worst two performances is also much higher.
| Name | Time point | Agreement threshold | Model variation | L2 mean distance | Std. deviation |
|---|---|---|---|---|---|
| Data set 2 | T2 | no | Standard Axelrod model | 859.79 | 10.60 |
| Data set 2 | T2 | no | In-group preference | 845.14 | 10.85 |
| Data set 2 | T2 | yes | Agreement-threshold model | 1200.55 | 22.03 |
| Data set 2 | T2 | yes | Group-dependent perception | 859.71 | 10.72 |
| Data set 2 | T2 | yes | In-group preference | 1090.56 | 23.79 |
| Name | Time point | Agreement threshold | Model variation | L2 mean distance | Std. deviation |
|---|---|---|---|---|---|
| Data set 3 | T3 | no | Standard Axelrod model | 56.8 | 11.61 |
| Data set 3 | T3 | yes | Agreement-threshold model | 172.31 | 16.6 |
Closeness of the aggregated results of the simulations and the fitted data points
The Axelrod model and the variations replicate, to a certain degree, the relative number of changes in the features for the given data sets (see Simulations, Section 4.4). Nevertheless, the replication of the next states of the data on a macroscopic level is not achieved by the simulations. Through the general conceptualisation of the Axelrod model is as a "toy model", the model does not seek to accurately predict the underlying dynamics of a social data set. Therefore, we did not expect the simulations to match the average level of the features from the simulated data points. On the contrary, we expected the model to be very distinct to the data on the individual level. To underline this, we compared the following:
- For the overall level, we compared the average level of each feature at the fitted time point to the average level of each feature from the simulations. The absolute difference between the average level of the data point and the simulation shows to what extent the simulations deviate from the fitted data point.
- To measure the difference between the data point and the simulations, we inspect the deviations on the individual level. Hence, we calculate the Manhattan distance of the feature vector from every individual for the simulated and the fitted time point. We then sum up the individual differences of the simulations.
The results in Figures 7-12 show for all three data sets that the overall results of the simulations highly deviate from the fitted time points. If we focus on the individual level where we compare each participant to its simulated counterpart, the differences are more noticeable.


Notes
We report here a normalised order parameter (\(S_\rm{{max}}\) \(/N\)) that describes the size of the largest cluster (\(S_{max}\)) in relation to the system size (\(N\)). It is widely used to describe the Axelrod model dynamics (Battiston et al. 2017; Castellano et al. 2009; Flache & Macy 2011; Klemm et al. 2003)↩︎
References
ABRAMS, D., & Hogg, M. (1990). An introduction to the social identity approach. In Social identity theory: Constructive and critical advances (pp. 1–9). Harvester-Wheatsheaf.
ANES. (2017). ANES 2016 time series study.
ANES. (2021). ANES 2020 Time SeriesStudy Full Release [dataset and documentation].
AXELROD, R. (1997). The dissemination of culture. Journal of Conflict Resolution, 41(2), 203–226.
BATTISTON, F., Nicosia, V., Latora, V., & San Miguel, V. (2017). Layered social influence promotes multiculturality in the Axelrod model. Scientific Reports, 7(1). [doi:10.1038/s41598-017-02040-4]
BAUMANN, F., Lorenz-Spreen, P., Sokolov, I. M., & Starnini, M. (2020). Modeling echo chambers and polarization dynamics in social networks. Physical Review Letters, 124(4). [doi:10.1103/physrevlett.124.048301]
BLIUC, A. M., McGarty, C., Reynolds, K., & Muntele, D. (2007). Opinion-based group membership as a predictor of commitment to political action. European Journal of Social Psychology, 37(1), 19–32. [doi:10.1002/ejsp.334]
BOLDRY, J. G., Gaertner, L., & Quinn, J. (2007). Measuring the measures. Group Processes & Intergroup Relations, 10(2), 157–178. [doi:10.1177/1368430207075153]
BREWER, M. B. (1979). In-group bias in the minimal intergroup situation: A cognitive-motivational analysis. Psychological Bulletin, 86(2), 307–324. [doi:10.1037/0033-2909.86.2.307]
CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81, 591–646. [doi:10.1103/revmodphys.81.591]
CENTOLA, D., González-Avella, J. C., Eguíluz, V. M., & San Miguel, M. (2007). Homophily, cultural drift, and the co-Evolution of cultural groups. Journal of Conflict Resolution, 51(6), 905–929. [doi:10.1177/0022002707307632]
CROASMUN, J. T., & Ostrom, L. (2011). Using likert-Type scales in the social sciences. Journal of Adult Education, 40, 19–22.
DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(01n04), 87–98. [doi:10.1142/s0219525900000078]
DINKELBERG, A., MacCarron, P., Maher, P. J., & Quayle, M. (2021). Homophily dynamics outweigh network topology in an extended Axelrod’s cultural dissemination model. Physica A: Statistical Mechanics and Its Applications, 578, 126086. [doi:10.1016/j.physa.2021.126086]
DINKELBERG, A., O’Reilly, C., MacCarron, C., Maher, P. J., & Quayle, M. (2021). Multidimensional polarization dynamics in US election data in the long term (2012-2020) and in the 2020 election cycle. Analyses of Social Issues and Public Policy, 21(1), 284–311. [doi:10.1111/asap.12278]
DINKELBERG, A., O’Sullivan, D. J., Quayle, M., & MacCarron, P. (2021). Detecting opinion-based groups and polarization in survey-based attitude networks and estimating question relevance. Advances in Complex Systems, 24(02). https://doi.org/10.1142/s0219525921500065 [doi:10.1142/s0219525921500065]
EDMONDS, B., Le Page, C., Bithell, M., Chattoe-Brown, E., Grimm, V., Meyer, R., Montañola-Sales, C., Ormerod, P., Root, H., & Squazzoni, F. (2019). Different modelling purposes. Journal of Artificial Societies and Social Simulation, 22(3), 6. [doi:10.18564/jasss.3993]
EPSTEIN, J. M. (2008). Why model? Journal of Artificial Societies and Social Simulation, 11(4), 12.
FLACHE, A., & Macy, M. W. (2011). Local convergence and global diversity. Journal of Conflict Resolution, 55(6), 970–995. [doi:10.1177/0022002711414371]
FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2. [doi:10.18564/jasss.3521]
FREDERIC, N. S., & Falomir-Pichastor, J. M. (2018). Heterogeneity of ingroup identity and anti-Immigrant prejudice: The moderating role of RWA and outgroup homogeneity. International Review of Social Psychology, 31(1). [doi:10.5334/irsp.152]
GARCIA, R., & Jager, W. (2011). From the special issue editors: Agent-based modeling of innovation diffusion. Journal of Product Innovation Management, 28(2), 148–151. https://doi.org/10.1111/j.1540-5885.2011.00788.x [doi:10.1111/j.1540-5885.2011.00788.x]
HEGSELMANN, R. & Krause, U. (2002). Opinion dynamics and bounded confidence: Models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2
HOGG, M. A., & Smith, J. R. (2007). Attitudes in social context: A social identity perspective. European Review of Social Psychology, 18(1), 89–131. [doi:10.1080/10463280701592070]
HORNSEY, M. J. (2008). Social identity theory and self-categorization theory: A historical review. Social and Personality Psychology Compass, 2(1), 204–222. [doi:10.1111/j.1751-9004.2007.00066.x]
JENKINS, R. (2014). Social identity. Routledge.
KLEMM, K., Egu, V. M., Toral, R., & San Miguel, M. (2003). Nonequilibrium transitions in complex networks: A model of social interaction. Physical Review E, 67(2), 026120. [doi:10.1103/physreve.67.026120]
KRUGLANSKI, A. W., Pierro, A., Mannetti, L., & De Grada, E. (2006). Groups as epistemic providers: Need for closure and the unfolding of group-centrism. Psychological Review, 113(1), 84. [doi:10.1037/0033-295x.113.1.84]
LÜDERS, A., Dinkelberg, A., & Quayle, M. (2022). Becoming "us" in digital spaces: How online users creatively and strategically exploit social media affordances to build up social identity. Acta Psychologica, 228, 103643.
MACCARRON, P., Maher, P. J., Fennell, S., Burke, K., Gleeson, J. P., Durrheim, K., & Quayle, M. (2020a). Agreement threshold on Axelrod’s model of cultural dissemination. PLoS One, 15(6), e0233995. [doi:10.1371/journal.pone.0233995]
MACCARRON, P., Maher, P. J., & Quayle, M. (2020b). Identifying opinion-based groups from survey data: A bipartite network approach.
MACY, M. W., Ma, M., Tabin, D. R., Gao, J., & Szymanski, B. .. (2021). Polarization and tipping points. Proceedings of the National Academy of Sciences, 118(50), e2102144118. [doi:10.1073/pnas.2102144118]
MAHER, P. J., MacCarron, P., & Quayle, M. (2020). Mapping public health responses with attitude networks: The emergence of opinion-based groups in the UK’s early COVID-19 response phase. British Journal of Social Psychology, 59(3), 641–652. https://doi.org/10.1111/bjso.12396 [doi:10.1111/bjso.12396]
MALKA, A., Soto, C. J., Inzlicht, M., & Lelkes, Y. (2014). Do needs for security and certainty predict cultural and economic conservatism? A cross-national analysis. Journal of Personality and Social Psychology, 106(6), 1031–1051. [doi:10.1037/a0036170]
MARTINY, S. E., & Rubin, M. (2016). Towards a clearer understanding of social identity Theory’s Self-Esteem hypothesis. In Peace psychology book series (pp. 19–32). Springer International Publishing. [doi:10.1007/978-3-319-29869-6_2]
MEKNI, M. (2013). Crowd simulation using informed virtual geospatial environments.
NGUYEN, N., Chen, H., Jin, B., Quinn, W., Tyler, C., & Landsberg, A. (2021). Cultural dissemination: An agent-Based model with social influence. Journal of Artificial Societies and Social Simulation, 24(4), 5. [doi:10.18564/jasss.4633]
PARK, B., & Rothbart, M. (1982). Perception of out-group homogeneity and levels of social categorization: Memory for the subordinate attributes of in-group and out-group members. Journal of Personality and Social Psychology, 42(6), 1051–1068. [doi:10.1037/0022-3514.42.6.1051]
PINTO, S., & Balenzuela, P. (2020). Erdós-Rényi phase transition in the Axelrod model on complete graphs. Physical Review E, 101(5), 052319. [doi:10.1103/physreve.101.052319]
QUATTRONE, G. A., & Jones, E. E. (1980). The perception of variability within in-groups and out-groups: Implications for the law of small numbers. Journal of Personality and Social Psychology, 38(1), 141–152. [doi:10.1037/0022-3514.38.1.141]
REICHER, S. (2004). The context of social identity: Domination, resistance, and change. Political Psychology, 25(6), 921–945. [doi:10.1111/j.1467-9221.2004.00403.x]
REICHER, S. D., Spears, R., & Haslam, S. A. (2010). The social identity approach in social psychology. In M. Wetherell & C. Talpade Mohanty (Eds.), The sage handbook of identities. Sage. [doi:10.4135/9781446200889.n4]
SCHOLZ, G., Eberhard, T., Ostrowski, R., & Wijermans, N. (2021). Social identity in agent-Based models - Exploring the state of the art. In Springer proceedings in complexity (pp. 59–64). Springer International Publishing. [doi:10.1007/978-3-030-61503-1_6]
SHERIF, C. W. (1963). Social categorization as a function of latitude of acceptance and series range. The Journal of Abnormal and Social Psychology, 67(2), 148–156. [doi:10.1037/h0043022]
SHERIF, M., & Hovland, C. I. (1962). Social judgment: Assimilation and contrast effects in communication and attitude change. American Journal of Sociology, 68(1), 126–127.
SHIBANAI, Y., Yasuno, S., & Ishiguro, I. (2001). Effects of global information feedback on diversity: Extensions to Axelrod’s adaptive culture model. The Journal of Conflict Resolution, 45(1), 80–96. [doi:10.1177/0022002701045001004]
SMALDINO, P., Pickett, C., Sherman, J., & Schank, J. (2012). An agent-Based model of social identity dynamics. Journal of Artificial Societies and Social Simulation, 15(4), 7. [doi:10.18564/jasss.2030]
STIVALA, A., Robins, G., Kashima, Y., & Kirley, M. (2014). Ultrametric distribution of culture vectors in an extended Axelrod model of cultural dissemination. Scientific Reports, 4(1). [doi:10.1038/srep04870]
TAJFEL, H. & Turner, J. C. (1986). The social identity theory of intergroup behavior. Psychology of Intergroup Relations, 2, 7–24 [doi:10.4324/9780203505984-16]
TAJFEL, H., Turner, J. C., Austin, W. G. & Worchel, S. (1979). An integrative theory of intergroup conflict. Organizational Identity: A Reader, 56(65), 94–109
TURNER, J. C., Hogg, M. A., Oakes, P. J., Reicher, S. D., & Wetherell, M. S. (1987). Rediscovering the social group: A self-categorization theory. Basil Blackwell.
TURNER, J. C., & Oakes, P. J. (1986). The significance of the social identity concept for social psychology with reference to individualism, interactionism and social influence. British Journal of Social Psychology, 25(3), 237–252. [doi:10.1111/j.2044-8309.1986.tb00732.x]
ULLOA, R., Kacperski, C., & Sancho, F. (2016). Institutions and cultural diversity: Effects of democratic and propaganda processes on local convergence and global diversity. PLoS One, 11(4), e0153334. [doi:10.1371/journal.pone.0153334]
WELLCOME Trust and Ltd, The Gallup Organization. (2019). Wellcome Global Monitor, 2018.