Social Simulation Models as Refuting Machines

Introduction

Social simulation models have been used increasingly in recent years, but their role in the scientific method remains the subject of intense debate (see e.g. Axelrod 1997a; Anzola 2019, 2021a; Arnold 2019, 2014; Davidsson et al. 2017; Edmonds 2001, 2010; Edmonds et al. 2019; Edmonds & Hales 2005; Epstein 2006b; Epstein 2008; Galán et al. 2009; Gilbert & Ahrweiler 2009; Gilbert & Terna 2000; Leombruni & Richiardi 2005; Squazzoni et al. 2014; Troitzsch 1997). Nowadays there seems to be broad consensus that understands models as tools designed to achieve a certain purpose (Davidsson et al. 2017; Edmonds et al. 2019; Epstein 2008). This view highlights the purpose of the model as a key factor to determine how the model should be interpreted and evaluated. Edmonds et al. (2019) review seven distinct purposes for social simulation models (prediction, explanation, description, theoretical exposition, illustration, analogy, and social interaction), acknowledging the fact that their list is not exhaustive.

In this paper we elaborate on the role of (some) social simulation models as refuting machines. Under this role, models are interpreted as formal machines that allow us to explore the logical implications of some of the assumptions contained in a certain empirical theory. (Here we use the term ‘empirical theory’ in a rather loose sense, as a shortcut to denote a set of beliefs about how certain aspects of the real world work, which are often not made explicit.) Under this interpretation, the important point is not whether the formal model is an adequate representation of any real-world system, but rather, whether it fulfils the assumptions of a prevailing empirical theory, so the formal model can be used to explore the logical consequences of the empirical theory. In this case, if the model produces something that is at odds with the predictions of the theory, this can be understood as an indication that something may be wrong with the theory.

The role of models as refuting machines can be subsumed in Edmonds et al.'s (2019) list of common modelling purposes under the illustration category or, often more appropriately, under the theoretical exposition category, depending mainly on the extent to which the model has been thoroughly analysed and proved to be robust and sufficiently general.

To explain the role of social simulation models as refuting machines, let us first clarify some of the terminology we will use. We say that a theory has been refuted if it has been proven wrong. If the refutation occurs within the empirical realm (i.e., by an empirical observation), we say that the theory has been falsified (Popper 2005). For example, the observation of a white raven falsifies the empirical statement ‘All ravens are black’. If the refutation occurs within the realm of formal statements (devoid of empirical content), we say that the theory has been disproved. For example, proving that number 3 is odd disproves the statement ‘All integers are even’.

In our view, social simulations cannot directly falsify scientific theories since they cannot produce genuinely new empirical evidence,¹ but they may disprove them by providing (new) formal statements that are inconsistent with some of the theory’s assumptions or implications. In this way, social simulation models can be seen as refuting machines of scientific theories with empirical content.

The basic framework we wish to put forward in this paper is sketched in Figure 1. An empirical theory is created from a certain real-world process by identifying key entities, individual variables, interaction rules and aggregate variables. The empirical theory is defined by a certain set of assumptions (‘shared assumptions + other assumptions’ in Figure 1). Now let us consider a computer model that contains some of the assumptions in the empirical theory (‘shared assumptions’ in Figure 1) plus potentially some other assumptions that are not significant (‘non-significant assumptions’ in Figure 1). Non-significant assumptions are those that do not affect the logical consequences of the computer model significantly. If the computer model generates (formal) evidence that contradicts some of the assumptions in the empirical theory or some of its implications, then the empirical theory is shown to be inconsistent. This is because the computer model would be producing logical consequences of the shared assumptions, which are contained in the empirical theory.

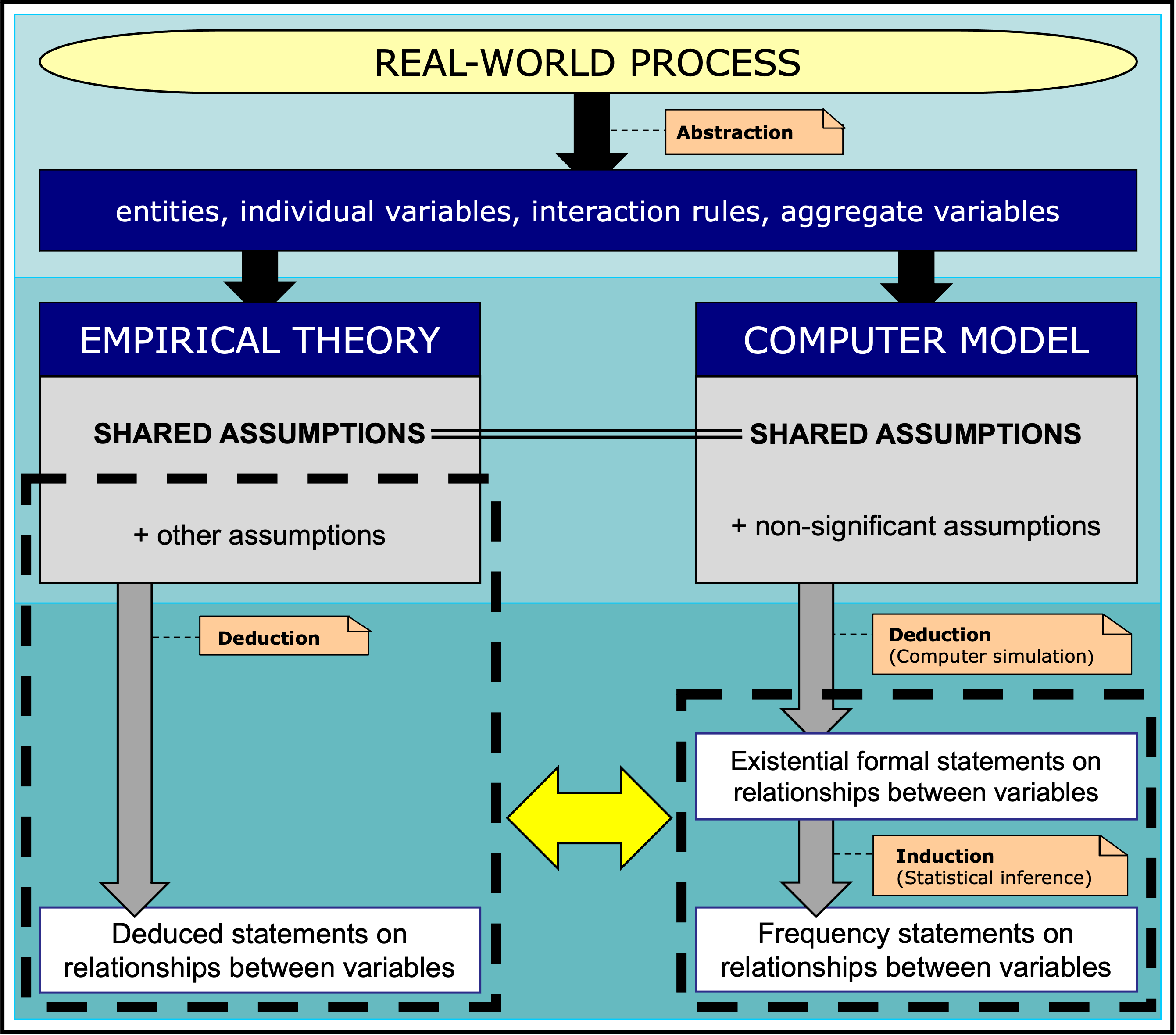
We believe that many of the most celebrated models in the social simulation literature have played this refuting role, i.e., they were able to disprove a theory that was widely believed to be true at the time of publishing. To test this hypothesis, we examined several popular models in the social simulation literature and found that most of these models are most naturally interpreted, not as scientific theories that could be falsified by empirical observations, but rather as providers of compelling (computer-generated) logical statements that refuted a prevailing belief or assumption (see Appendix B for various examples). Rather than falsifiable theories, these models were refuting machines. And by refuting prevailing theories, these models greatly advanced science and, in many cases, they even opened a new field.

The remainder of the paper is organized as follows. In the next section, we present in broad terms the different types of statements that we may find in science (empirical vs. formal; and existential vs. universal), and we explain that simulation models can produce formal existential statements. In section 3, we discuss a key aspect of the scientific method: refutation by using a counter-example. Section 4 explains how formal models can indeed refute empirical theories by providing a counter-example that reveals an inconsistency within them. However, it should be noted that this type of refutation is in principle impossible if the empirical theory allows for exceptions. Thus, section 5 explains how formal models can refute, in practice, empirical theories that allow for exceptions. In section 6, we turn to empirical theories that are vaguely specified. Here, we argue that a necessary condition for a formal model to be able to refute a prevailing and vaguely specified empirical theory is that the significant assumptions in the formal model must be credible. In section 7, we note that most social simulation models that have played the role of refuting machines tend to be strikingly simple, and we offer an explanation within our framework of why that may be the case. The final section summarizes our view of social simulation models as refuting machines.

The paper has two appendices. Appendix A includes a NetLogo (Wilensky 1999) implementation of the Schelling-Sakoda model which can be run online, and Appendix B includes a review of some emblematic models to illustrate our view.

Simulation models as tools to produce formal existential statements

Empirical vs formal statements. Existential vs universal statements

To fully understand the role of social simulation models in science, we have to understand that statements can be of different types. In particular, we have to distinguish between empirical and formal statements, and between existential and universal statements (Popper 2005, originally published in 1934).²

Empirical statements convey information about the real world, obtained from observation or experimentation. An example could be: ‘There exists a black raven’. Formal statements, on the other hand, are expressed in a formal language devoid of meaning or context and say nothing about the real world. An example would be: ‘\(1 + 1 = 2\)’. Some formal statements –called axioms– are postulated as being true by assumption, while others are logically derived applying rules of inference to the axioms and to previously derived statements.

Independent of the distinction between empirical and formal statements, we can distinguish between existential and universal statements. Existential statements refer to one particular individual of a class (e.g., ‘There exists a black raven’), while universal statements refer to all members of a class (e.g., ‘All ravens are black’). More precisely, a universal statement refers to all members of a universe. In the raven example, the universe is composed of all current ravens. Using mathematical language, a universal statement can be written as follows:

\[\forall \; x \in \Omega : Cx\]

\[(1)\]

Here, the symbol \(\forall\) means ‘for all’, \(C\) denotes a property, and \(Cx\) means that \(x\) possesses this property. If \(C\) means ‘being black’ and \(\Omega\) is the universe of all ravens, then we have ‘All ravens are black’. The statement is universal because it pertains to all members of a class.

In contrast, an existential statement can be written as follows:

\[\exists \; x \in \Omega : Cx\]

\[(2)\]

Here, the symbol \(\exists\) means ‘There exists’. Thus, the statement becomes ‘There exists a raven which is black’. The statement is existential because it does not necessarily pertain to all members of a class, but at least to one.

Examples of the different combinations of formal/empirical and universal/existential statements are shown in Figure 2.

What type of statements can social simulation models provide? It seems clear that they cannot produce genuinely new empirical statements because they are not part of the natural world (though they can generate empirical hypotheses). They are formal models –since they are expressed in a programming language and can be run on a computer (Suber 2007)– and, as such, can only provide formal statements. In this sense, they do not differ substantially from other formal models expressed in mathematical formalism. Indeed, social simulation models expressed in a programming language can be perfectly expressed using mathematics (Epstein 2006a, 2006b; Leombruni & Richiardi 2005; Richiardi et al. 2006). This means that the exact same function that a social simulation model implements can be expressed in mathematical language, in the sense that both implementations would lead to exactly the same output if given the same input. Thus, the language in which a formal model is expressed is rather immaterial for our purposes.

In particular, the type of formal statement (existential or universal) that can be derived from a formal model does not depend on the language in which it is expressed. It depends, rather, on the approach followed to derive the statements.

In general, one can derive statements from formal models using two approaches: the mathematical analysis approach or the computer simulation approach (Izquierdo et al. 2013).³ The mathematical approach to analyse formal models consists in examining the rules that define the model directly. Its aim is to deduce the logical implications of these rules for any particular instance to which they can be applied, i.e., for the whole domain of the model. Thus, using the mathematical approach we can derive universal statements about the formal model, i.e., statements that are true for all parameter values of the model (including initial conditions), or at least for all parameter values within a certain class.

However, most social simulation models are not analysed using mathematics, but rather following the so-called computer simulation approach. In contrast with mathematical analysis, the computer simulation approach does not consider the rules that define the formal model directly, but instead applies these rules to particular instances of the input space, by running the model on a computer (after having assigned a particular value to each parameter of the model). Each individual run of a model constitutes a formal existential statement, since it refers to one particular instance of the input space. In this sense, running a computer model once can be seen as the formal counterpart of conducting an empirical experiment or observation: observations provide direct information about empirical systems, while simulations provide direct information about computer models. Nonetheless, if a simulation model is based on an empirical theory and there is an equivalence between the assumptions of both systems (the theory and the computer model), then information about a computer model can provide information about the associated theory, as well as hypotheses about empirical systems.

Before presenting a more detailed example, let us introduce a formalism that is particularly useful to describe and analyse social simulation models, namely time-homogeneous Markov chains. Markov chains are stochastic processes that are useful to describe systems which evolve in discrete time steps and which, at each time step, find themselves in one of a set of possible states. The key property of a time-homogeneous Markov chain is that the probability that a system that is in state \(i\) at time step \(t\) will be in state \(j\) at the following time step \(t+1\) depends exclusively on the states \(i\) and \(j\) (i.e., this probability does not depend on the particular time step \(t\) at which the transition takes place, or on the states that the system visited before reaching state \(i\)).

Given that most social simulation models are stochastic and run in discrete time steps, it is convenient to see them as time-homogeneous Markov chains (Gintis 2013; Izquierdo et al. 2009). When we run the model in a computer, we are effectively sampling one specific realisation of that stochastic process, i.e., we obtain just one sequence of states in time. The following section presents an example to clarify these arguments.

An example of a model and of formal statements derived with it

Consider the following model, which implements the main features from a family of models proposed by Sakoda (1949, 1971) and –independently– by Schelling (1969, 1971, 1978). Specifically, we focus on the model described in Schelling (1971 pp. 154–158). A NetLogo (Wilensky 1999) implementation of this model can be found (and run online) in Appendix A, together with some instructions on how to use it. Let us call this model \(\textbf{M}\). The assumptions of \(\textbf{M}\) are (see Figure 3):

• There is a 13x16 grid containing \(n\) agents. The number of agents \(n\) is assumed to be even. Half of the agents are blue and the other half orange. We assume \(n \in [100, 200]\).
• Initially, agents are distributed at random in distinct grid cells.
• Agents may be content or discontent.
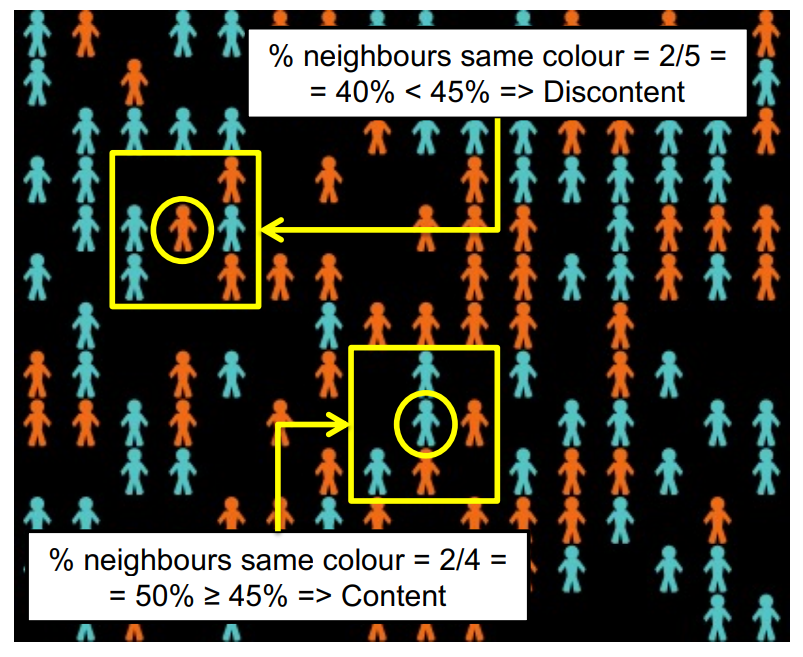
• Each individual agent is content if it has no Moore neighbours, or if at least \(\alpha \%\) of its neighbours are of its same colour. Otherwise, the agent is discontent.
• In each iteration of the model, if there are any discontent agents, one of them is randomly selected to move to the closest empty cell where the moving agent would be content, if there is any available. If there is no such cell, the discontent agent will move to a random empty cell. If there is more than one closest cell where the agent would be content, one of them is chosen at random. We use taxicab (aka Manhattan) distance.

This is a stochastic model with two parameters: the number of agents, \(n\), and the intolerance threshold \(\alpha\). Figure 3 shows a snapshot where \(n=138\) and \(\alpha = 45\%\).⁴ This value of \(\alpha\) means that agents are content as long as \(45\%\) of their neighbours (or more) are of their same colour.

Model \(\textbf{M}(n,\alpha)\) is completely specified and could be implemented in many different programming languages and also studied mathematically. To see it as a Markov chain, we can define the state of the system as a vector of dimension \(13*16=208\), where each component corresponds to a certain cell in the grid. Every component of this vector can take 3 different values to denote whether the cell is empty, occupied by a blue agent or occupied by an orange agent. With this definition, the number of possible states is \(L = \binom{208}{\frac{n}{2}, \frac{n}{2}, 208-n}\); the two snapshots in Figure 4 show two different states for a model where \(n=138\) (which implies \(L=6.87382\times 10^{96}\), a number greater than the estimated number of atoms in the observable universe).

What is interesting about the Schelling-Sakoda model \(\textbf{M}(n,\alpha)\) is that its dynamics most often lead to situations with clearly distinctive segregation patterns, even if agents are not particularly intolerant (i.e., \(\alpha \ge 35\%\)). Figure 4 shows two end states of \(\textbf{M}(n=138,\alpha= 45\%)\), where every agent is content and therefore no more changes occur in the model.

To quantify the level of segregation, let us define –for each realisation of the model– the long-run segregation index \(w\) as the long-run average percentage of neighbours of the same colour across agents with at least one neighbour. Most realisations of the model reach an absorbing state, such as the two shown in Figure 4 for \(\textbf{M}(n=138,\alpha= 45\%)\); in that case, the long-run segregation index is just the average percentage of neighbours of the same colour at that final state.

Thus, each simulation run \(i\), parameterized with a fixed number of agents \(n_f\) and a fixed intolerance threshold \(\alpha_f\), will have a certain long-run segregation index \(w_i\) associated with it.⁵ Note that two runs parameterized with the same values of \(n_f\) and \(\alpha_f\) could perfectly have different values of the long-run segregation index, since each simulation run \(i\) involves a certain realisation of stochastic events \(\phi_i\) –for a start, the initial distribution of agents in the grid, which is random, is most likely going to be different in each run. Thus, each run of the model \(i\) constitutes a formal existential statement of the following type:

\[\langle \textbf{M}(n_f,\alpha_f), \phi_i \rangle \implies w= w_i,\]

\[(3)\]

where the arrow \((\implies)\) denotes logical implication.⁶ This is an existential statement in the sense that we are saying that there exists a realisation of model \(\textbf{M}(n_f,\alpha_f)\) for which the segregation index is \(w_i\). To be clear, using \(\Phi\) to denote the set of all possible realisations of a model, we could write the statement above using the existential quantifier \(\exists\) as:

\[\exists \; \phi\in \Phi: \langle \textbf{M}(n_f,\alpha_f), \phi\rangle \implies w= w_i.\]

\[(4)\]

By running many simulation runs of parameterized model \(\textbf{M}(n_f,\alpha_f)\), we can gather many formal statements of the type \(\{\langle\textbf{M}(n_f,\alpha_f), \phi_i\rangle \implies w=w_i\}\), where each value of \(i\) corresponds to a different simulation run. Each run would be showing us how model \(\textbf{M}(n_f,\alpha_f)\) can behave, while, by the law of large numbers, a sufficiently large set of simulation runs would show us how model \(\textbf{M}(n_f,\alpha_f)\) usually behaves.⁷

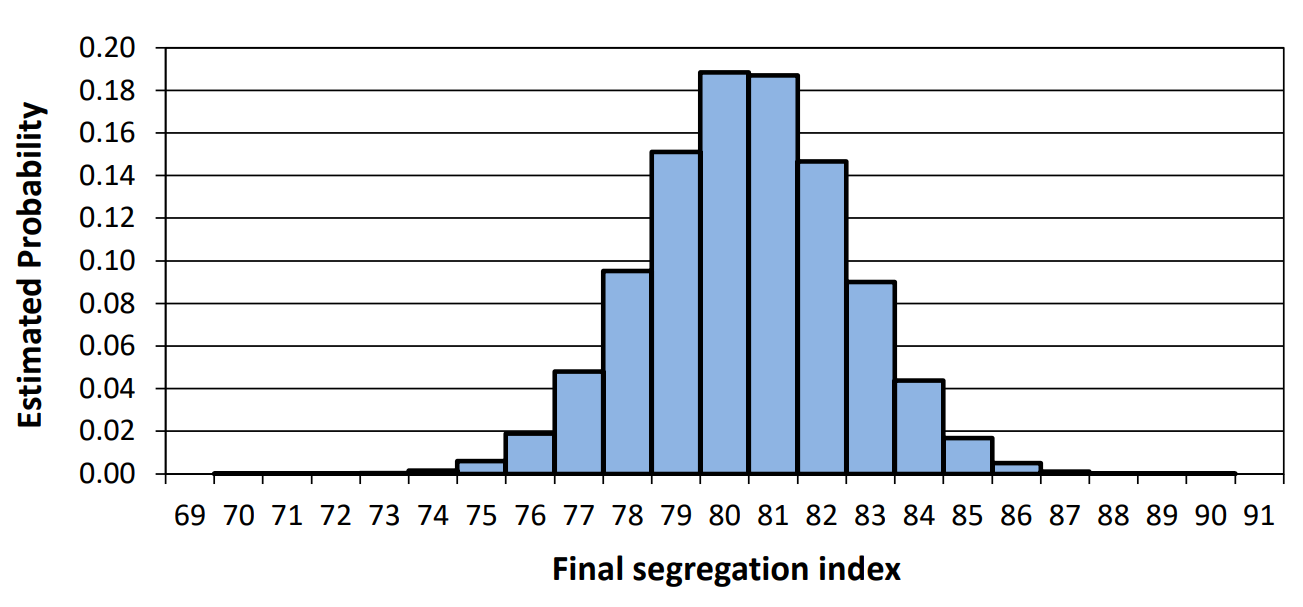
Note that the long-run segregation index of the stochastic Schelling-Sakoda model \(\textbf{M}(n_f,\alpha_f)\) –and any other well-defined statistic of the model– follows a certain probability distribution which, in principle, could be derived exactly. Let \(\mathbb{W}(n_f,\alpha_f)\) denote this distribution. We do not know the exact expression of \(\mathbb{W}(n_f,\alpha_f)\), but we know the distribution exists, and we can approximate it to any degree of confidence by running simulations. Figure 5 offers an approximation to \(\mathbb{W}(n=138,\alpha=45\%)\), computed with \(10^6\) simulation runs, which we call \(\mathbb{\hat{W}}(n=138,\alpha=45\%)\).

Therefore, given some specific values \(n_f\) and \(\alpha_f\) for parameters \(n\) and \(\alpha\) respectively, we can establish two types of logical implications:

• Using the mathematical approach, in principle we could deduce the logical implication:

  \[\textbf{M}(n_f,\alpha_f) \implies w\sim \mathbb{W}(n_f,\alpha_f)\]

  \[(5)\]

  The problem here is that we may not be able to derive the exact distribution \(\mathbb{W}(n_f,\alpha_f)\). In any case, note that this type of logical implication can lead to universal statements. For instance, if distribution \(\mathbb{W}(n_f,\alpha_f)\) placed all its mass on values of \(w\) greater than \(50\%\), then we could state that all realisations of \(\textbf{M}(n_f,\alpha_f)\) lead to segregation indices greater than \(50\%\).
• Using the computer simulation approach, we can derive sets of formal existential statements such as the following:

  \[\{\langle\textbf{M}(n_f,\alpha_f), \phi_i \rangle \implies w=w_i\}_{i=1,\dots,10^6}\]

  \[(6)\]

  We summarize the set of \(10^6\) implications above as:

  \[\textbf{M}(n_f,\alpha_f) \xrightarrow{10^6} w\sim \mathbb{\hat{W}}_{10^6}(n_f,\alpha_f),\]

  \[(7)\]

  where distribution \(\mathbb{\hat{W}}_{10^6}(n_f,\alpha_f)\) is the finite-sample distribution corresponding to sample\(\{w=w_i\}_{i=1,\dots,10^6}\), and the single arrow \((\xrightarrow{})\) does not denote logical implication. Instead, \(\textbf{X} \xrightarrow{m} s\) denotes that statement \(s\) is true for a random sample of \(m\) simulation runs of model \(\textbf{X}\). In particular, \(\textbf{X} \xrightarrow{m} y \sim \mathbb{Y}\) denotes ‘Distribution \(\mathbb{Y}\) for statistic \(y\) has been obtained by running \(m\) simulations of model \(\textbf{X}\)’; this is the type of ‘frequency statement’ that can be derived using the computer simulation approach (see Figure 1). Naturally, this type of relation \((\xrightarrow{m})\) is weaker than the logical implication \((\implies)\) derived with the mathematical approach.

Falsifications, disproofs and refutations

In the previous section we have seen that, following the computer simulation approach, we can use social simulation models to generate formal existential statements. Existential statements are useful because they can refute universal statements, both in the empirical realm (in which case we use the term ‘falsification’) and in the realm of formal statements (and then we use the term ‘disproof’).

As an example, consider the empirical statement ‘A prokaryote has been found on Mars’. This existential statement is enough to falsify the universal empirical hypothesis ‘There is no extra-terrestrial life’. An example within the realm of formal systems is the existential statement ‘Number 3 is not even’, which disproves the universal statement ‘All integers are even’. A less obvious example –involving the use of computer simulation– is the disproof of Polya’s conjecture, which reads ‘more than half of the natural numbers less than any given number have an odd number of prime factors’. This statement gained popularity over the years because it was unknown whether it was true or not, despite the fact that a single counter-example would have sufficed to settle the issue. Science had to wait... until computer simulations became available. Using this new approach, Haselgrove established in 1958 the existence of an integer that disproved Polya’s conjecture, benefiting from the fact that ’now that electronic computers are available it is possible to calculate [...] over large ranges with considerable accuracy’ (Haselgrove 1958).

Another beautiful example was provided by Lander & Parkin (1966). This article is famous for being one of the shortest papers ever published, with only two sentences (Figure 6). Indeed, it can take just one (possibly very concise) formal existential statement to disprove a theoretical hypothesis. Mertens’ conjecture is another case of a mathematical hypothesis disproved using computer simulation (Odlyzko et al. 1984).

To put all this in the context of social simulation, let us go back to our version of the Schelling-Sakoda model. Running this model once, we can obtain the following existential statement:

\[\exists \; \phi\in \Phi: \langle \textbf{M}(n = 138, \alpha = 45\%), \phi\rangle \implies w= 82.16\%.\]

\[(8)\]

This statement can also be written as:

\[\textbf{M}(n = 138, \alpha = 45\%) \xrightarrow{\;1\;} w= 82.16\%.\]

\[(9)\]

This existential statement can disprove statements such as ‘The long-run segregation index of model \(\textbf{M}(n = 138, \alpha = 45\%)\) is necessarily less than 75%’. Such a universal statement refers to all possible realisations of the model and could be formalized as:

\[\forall \; \phi\in \Phi: \langle \textbf{M}(n = 138, \alpha = 45\%), \phi\rangle \implies w< 75\%.\]

\[(10)\]

Another example of a (more general) universal statement that would be disproved by the same simulation run would be:

\[\forall n \in [100, 200] \text{ and } \forall \alpha \in [0, 50\%] \text{ and } \forall \phi\in \Phi,\,\,\, \textbf{M}(n, \alpha) \implies w< 75\%.\]

\[(11)\]

The universal statement above includes all possible realisations of the model and also various combinations of parameter values.

How can formal statements refute empirical theories? A matter of consistency

It is clear that computer simulations can provide counter-examples to formal conjectures. But what about empirical conjectures? Very often, an empirical theory can be considered a story that captures, to some degree, the relationship between empirical entities by combining assumptions about these empirical entities and their interactions, and by showing some of the logical consequences of these assumptions. This last step, finding the logical consequences of some assumptions, is shared with computer simulations (see Figure 1).

Computer models can disprove empirical theories by showing that they are internally inconsistent, i.e., that they contain or imply statements that are logically incompatible. For instance, if a theory contains the statement ‘all ravens are black’, and it also contains the statement ‘Austrian ravens are white’, then the theory is inconsistent. Inconsistency is the worst flaw that a theory can have (Popper 2005 sec. 24): a theory with flawed reasoning may still produce conclusions that are true, but if a theory is inconsistent, then any conclusion and its negation can be logically deduced from the theory, making the theory totally useless.⁸

Crucially, to prove the inconsistency of an empirical theory, one does not necessarily require an empirical statement, a formal one may do just as well. Formal statements can refute empirical theories by uncovering inconsistencies in their logical foundations. This is the role that some simulation models have been able to play in the literature. They did not falsify any theory –since, being formal, that would be impossible–, but they refuted an empirical theory by revealing certain formal inconsistencies within it (see Figure 1). In layman terms, social simulations can provide counter-examples to formal preconceptions that lay the ground for an empirical explanation of the world.

As an example, consider an empirical theory which, implicit or explicitly, rests on the truthfulness of

constitutes evidence that seems to be at odds with Assumption 1, and it therefore challenges, at least to some extent, the consistency of any empirical theory that contains such an assumption. (Here, we are considering that being content in a neighbourhood where \((1-\alpha) = 55\%\) of your neighbours are unlike you can be considered a ‘tolerant preference’, but some people may prefer the term ‘mildly segregationist individual preferences’.)

However, there is a crucial condition that must be checked before we can say that Formal statement 1 constitutes evidence that refutes Assumption 1: the significant assumptions used to produce Formal statement 1 must be a subset of the assumptions implied in Assumption 1 (i.e., tolerant individual preferences and free movement).

In general, if a computer model is to challenge the consistency of an empirical theory or belief, the assumptions of the model responsible for the statements that challenge the empirical theory must be contained in the empirical theory. Galán et al. (2009) define significant assumptions as those that are the cause of some significant result obtained when running the model. Using this terminology, our first principle states that the significant assumptions of the model must be contained in the empirical theory. In other words, any assumption of the computer model that is not shared with the empirical theory must be non-significant (see Figure 1).

Let us elaborate on this important issue. Note that the formal model may contain assumptions that are not present in the empirical theory it aims to refute. An example of such an assumption in our computer implementation of model \(\textbf{M}\) would be the use of floating-point arithmetic, instead of real arithmetic. Naturally, the results obtained with the model can contradict the empirical theory only if they are a logical consequence of the assumptions that are also present in the empirical theory, and not of other auxiliary assumptions that are not in the empirical theory (such as the use of floating-point arithmetic in our example). Thus, in our example, we would have to make sure that the use of floating-point arithmetic is not driving the results.⁹

Interestingly, in this view, the model does not have to be a simplification or an abstraction of any real-world system. It may just be a description of some of the assumptions or beliefs used in the empirical theory, which, ideally, would be shown to contradict some other assumptions used by the theory, or some other statements that can be deduced from the theory. We believe that many well-known social simulation models are most naturally interpreted in this way, i.e., not necessarily as simplifications of any real-world system, but as counter-examples that disprove assumptions widely believed to be true. The following quote by Schelling about his own model offers some support for this interpretation:

“What can we conclude from an exercise like this? We may at least be able to disprove a few notions that are themselves based on reasoning no more complicated than the checkerboard. Propositions beginning with ‘It stands to reason that...’ can sometimes be discredited by exceedingly simple demonstrations that, though perhaps true, they do not exactly ‘stand to reason.’ We can at least persuade ourselves that certain mechanisms could work, and that observable aggregate phenomena could be compatible with types of ‘molecular movement’ that do not closely resemble the aggregate outcomes that they determine.” (Schelling 1978 p. 152)

Refuting empirical theories that allow for exceptions

We have seen that social simulations (or, more generally, formal statements) can reveal the inconsistency of a formal system that forms the basis of an empirical theory: Assumption 1 above establishes that some aggregate event follows necessarily from certain individual behaviour –as a logical implication, not as an empirical fact–, but Formal statement 1 is not consistent with Assumption 1.

Note, however, that social theories hardly ever rest on assumptions expressed in terms as definite as those in Assumption 1. It is far more common to encounter assumptions that allow for exceptions or are expressed in statistical terms, such as:

Clearly, adding ‘in most cases’ changes the game completely. Formal statement 1 above could be said to refute Assumption 1 because both statements are incompatible, but it clearly does not refute Assumption 2. This second assumption leaves room for situations where tolerant preferences could indeed lead to distinctive patterns of segregation. Such situations may be exceptional, according to Assumption 2, but they can exist. Since Assumption 2 does not rule out any specific event, it is clearly non-refutable (i.e., there is no existential statement that could ever contradict it).

A more formal example would be the following,

In plain words, Probability statement 1 says that, when running model \(\textbf{M}(n = 138, \alpha = 45\%)\), the probability of obtaining a segregation index \(w\) smaller than \(75\%\) is greater than \(0.9\). Since this is a probability statement that can accommodate any possible outcome, there is no single observation that could contradict it. The same issue arises when dealing with the (empirical) falsifiability of probability statements:

“Probability hypotheses do not rule out anything observable; probability estimates cannot contradict, or be contradicted by, a basic statement; nor can they be contradicted by a conjunction of any finite number of basic statements; and accordingly not by any finite number of observations either.” (Popper 2005 originally published in 1934, section 65, p. 181)

Popper examined the problem of randomness at great length (Popper 2005 pp. 133–208) and proposed a methodological rule according to which we could falsify probability statements in practice. The criterion is ‘reproducibility at will’. If we are able to show an effect that (i) is unlikely according to a probability statement and (ii) it is ‘reproducible at will’ (i.e., we can repeat it as many times as we like), we may consider the probability statement falsified in practice. The rationale is that the probability of observing a very large series of consecutive unlikely events is extremely unlikely (and the larger the series, the more unlikely it is). So, if we observe a series of events which, according to a certain probability statement, is extremely unlikely, then there is reason to doubt the truthfulness of the probability statement.

This type of reasoning is in line with Fisher’s foundations for hypothesis testing and statistical significance,¹⁰ and we can adopt the same ‘statistical’ approach for refuting (formal) assumptions via computer simulations.

“[...] no isolated experiment, however significant in itself, can suffice for the experimental demonstration of any natural phenomenon; for the ‘one chance in a million’ will undoubtedly occur, with no less and no more than its appropriate frequency, however surprised we may be that it should occur to us. In order to assert that a natural phenomenon is experimentally demonstrable we need, not an isolated record, but a reliable method or procedure. In relation to the test of significance, we may say that a phenomenon is experimentally demonstrable when we know how to conduct an experiment which will rarely fail to give us a statistically significant result.” (Fisher 1971 pp. 13–14, originally published in 1935)

Returning to our running example, it is clear that a single simulation run like Formal statement 1, i.e. \(\textbf{M}(n = 138, \alpha = 45\%) \xrightarrow{\;1\;} w= 82.16\%\), is not enough to refute Probability statement 1, but if, when running model \(\textbf{M}(n = 138, \alpha = 45\%)\), we systematically and consistently obtain evidence that is considered unlikely according to Probability statement 1, then there is much reason to doubt the truthfulness of Probability statement 1.

This is actually the case with model \(\textbf{M}(n = 138, \alpha = 45\%)\), since it rarely fails to give us the following result:

The reader is invited to check how ‘reproducible at will’ this statement is by running the online model provided in Appendix A.

The fact that we can reproduce the formal statement above ‘at will’, constitutes evidence strong enough to refute Probability statement 1 in practice. But, is that enough to refute a more general (and vague) statement, such as Assumption 2 (i.e., ‘In most cases, when individuals can choose their location freely, tolerant individual preferences for segregation lead to weakly segregated societies’)? We believe it is not, since Reproducible-at-will statement 1, which imposes \(n = 138\) and \(\alpha = 45\%\), seems too specific to contradict a statement that refers to ‘most cases’. After all, the ‘in most cases’ in Assumption 2 could well mean that it applies to all but a few special parameter combinations such as the one we have found.

A much more convincing case can be put forward noting that model \(\textbf{M}(n, \alpha)\) consistently leads to distinctive patterns of segregation not only in \(13\times16\) artificial worlds populated by \(n = 138\) agents with \(\alpha = 45\%\) moving according to the ‘closest-content-cell’ rule, but also for a wide range of different conditions. In particular, we consistently obtain strong patterns of segregation in any artificial world that is neither too sparse nor too crowded (i.e., for all \(n \in [40\%, 90\%]\) of the number of cells in the world), populated by agents who have ‘mildly segregationist preferences’ (i.e., for all \(\alpha \in [35, 50]\)), and move according to different rules (such as ‘random-content-cell’, ‘random-cell’, or ‘best-cell’ –see Appendix A; all these rules lead to even greater segregation). The reader can check that this is the case by running the online model provided in Appendix A. The model is also robust to various other changes in its assumptions, like e.g. the use of rectangular grid cells (Flache & Hegselmann 2001).¹¹

The fact that model \(\textbf{M}\) and its multiple variations can consistently produce evidence against Assumption 2 over such a wide range of situations suggests that Assumption 2 (and any empirical theory that includes such an assumption) may not be adequate, and further investigation is needed.

In general, we consider a formal model useful to refute an empirical theory that allows for exceptions if it covers a sufficiently important range of the situations to which the theory can be applied, and produces evidence that contradicts a logical assumption or deduced statement of the theory at will. This second principle should be understood in relative terms, as it contains a number of graded concepts. Specifically, we do not see ‘refutability’, ‘importance’, or ‘reproducibility as will’ as all-or-nothing properties. Rather, we believe that these properties are a matter of degree. The model will be able to better refute the empirical theory (i) the greater the range, diversity and importance of the situations over which it offers contradicting evidence, and (ii) the more reproducible and compelling this contradicting evidence is.

In this regard, with hindsight, the refutation of an empirical theory is often best attributed not to one single model only, but also to the whole set of models that derive from the original model, complementing it by making slight variations on its assumptions, and proving that the refuting inference is robust to such variations.¹² This is Ylikoski & Aydinonat's (2014) family of models thesis:

“The implication of these observations is that a more appropriate unit of analysis is the ongoing research initiated by Schelling’s papers. It would be arbitrary to focus only on early models in this tradition or to limit one’s attention only to models that have been proposed by Schelling himself. The research concerning Schelling’s original insights is extensive both in a temporal and a social sense: checkerboard models have been studied for over forty years by a multitude of scholars in various disciplines. The research has produced many surprising findings that should not be read back to the original models. It is by analyzing the whole continuum of such models that one can make better sense of the real epistemic contribution of this family of models. This is our first cluster thesis: abstract models make better sense when understood as a family of related models, not as isolated representations.” (Ylikoski & Aydinonat 2014 pp. 22–23)

How to refute unspecified empirical theories?

The point we want to make in this paper is that social simulation models can refute, and have been able to refute, empirical theories widely believed to be true by revealing certain formal inconsistencies in them. However, the empirical theory to be refuted is hardly ever made explicit, so how can a model refute an empirical theory that is not even fully specified? In the following paragraph we argue that for a model to have a chance to refute a prevailing empirical theory, its significant assumptions (i.e., those that are driving the results) must be credible. For an assumption to be credible, it must be coherent with our background knowledge, with our intuition and with our experience (Sugden 2000 sec. 11).

The fact that an empirical theory, whatever it may be, is widely believed to be true implies that its assumptions must be credible, i.e., they must cohere with the background knowledge of the time.¹³ On the other hand, if the model is to refute this theory on logical grounds, the assumptions in the model that are responsible for producing contradicting evidence (i.e., the significant assumptions) must be present in the empirical theory. Thus, for a model to refute the empirical theory, the significant assumptions in the model must be credible.

Let us discuss this last principle in the context of the Schelling-Sakoda model M. We saw that there are many assumptions in M that are not responsible for the emergence of segregation (e.g., the size of the world and the movement rule). Since these assumptions are not ‘doing the work’, there is no need to worry about them. In contrast, there are other assumptions that are crucial, like that \(\alpha\) must be in the interval \([35, 50]\) –something that could be interpreted as agents having ‘mildly segregationist preferences’. Since assuming this type of preferences is significant to obtain the results of the model, if the model is going to have some practical relevance, then we must make sure that such preferences are credible. In this regard, note that Schelling (1978 pp. 143–147) offers a number of stories whose “[...] purpose, surely, is to persuade us of the credibility of the hypothesis that real people – it is hinted, people like us – have mildly segregationist preferences” (Sugden 2000 p. 10). Even though Schelling does not make explicit the empirical theory he is refuting with his model, he makes sure that the assumptions in his model that are leading to the unexpected results seem credible. Otherwise, the model would not be telling us anything about the real world.

“Furthermore, its implications have been buttressed by accumulated findings on preferences in multicultural settings which show that all major racial and ethnic groups hold preferences that are as strong as or stronger than the relatively mild preferences Schelling considered in his original two-group formulation.” (Clark & Fossett 2008 p. 4109)

In Appendix B, we discuss several popular social simulation models which have been able to –at least partially– refute a prevailing belief:

• Schelling's (1971) ‘Dynamic models of segregation’
  Prevailing belief it refutes: Pronounced social segregation is the result of either deliberate public policy or strongly segregationist preferences.
• Epstein & Axtell's (1996) ‘Growing artificial societies: social science from the bottom up’
  Prevailing belief it refutes: To explain complex social phenomena such as trade or wealth distributions, one needs to consider complex patterns of individual behaviour and social interaction.
• Nowak & May's (1992) ‘Evolutionary games and spatial chaos’
  Prevailing belief it refutes: Sustaining cooperation in social dilemmas requires repetition and memory.
• Conway’s ‘Game of life’ (Gardner 1970)
  Prevailing belief it refutes: Systems governed by a small number of very simple rules (for their individual agents and interactions) have a limit on the aggregate complexity that they can explain or generate.
• Gode & Sunder's (1993) ‘Allocative Efficiency of Markets with Zero-Intelligence Traders: Market as a Partial Substitute for Individual Rationality’
  Prevailing belief it refutes: The efficiency of competitive markets rests on the rationality of economic agents.
• Reynolds's (1987) ‘Flocks, herds and schools: A distributed behavioral model’
  Prevailing belief it refutes: Complex phenomena such as the synchronized motion of a flock of birds require complex individual rules of coordination.
• Arthur's (1989) ‘Competing technologies, increasing returns, and lock-in by historical events’
  Prevailing belief it refutes: When there are several competing technologies, a market competition mechanism ensures that the most efficient technology will be the surviving one.
• Axelrod's (1997b) model of ‘dissemination of culture’
  Prevailing belief it refutes: Individuals’ tendency to agree with social neighbours leads to global consensus in a society.

The value of toy models and emergence

In our review of popular social simulation models, we have noticed that models (or families of models) that have successfully refuted a prevailing belief tend to be strikingly simple and idealized (see Appendix B). This kind of models are often called ‘toy models’ (Reutlinger et al. 2018). Is this a coincidence? Or is simplicity a desirable feature for models that are meant to refute an empirical theory? Here we explain why, ceteris paribus, toy models are in better conditions than complex and less idealized models to play the role of refuting machines.

First, note that the kind of refutation we are proposing here is by no means strict. It is a subjective matter of degree, influenced by the perceived credibility of the significant assumptions of the model, the perceived strength of the contradicting evidence they provide, and the perceived importance and variety of the situations to which they apply. Now, the simpler and more idealized the model, the easier it is to understand both its assumptions and how these assumptions lead to its logical implications.¹⁴ This understanding enables the reader to gain intuition, or knowledge, about which assumptions are significant, and therefore should be perceived as credible. Simplicity also helps us to assess the extent to which the assumptions of the model collectively cover a sufficiently important range of situations over which the empirical theory can be applied. Without developing this intuition or knowledge, it would not be clear what sort of empirical theory the model is refuting, if any. Thus, to refute an empirical theory, simpler models seem to be favoured, even though they are not necessarily more general (see e.g. Evans et al. (2013; Edmonds 2018)).¹⁵

Another feature shared by most refuting machines in the social simulation literature is that they show some kind of emergent phenomenon. This is the case, in particular, for all the models reviewed in Appendix B, and it makes plenty of sense in our framework. Let us consider why. Emergent phenomena are macroscopic patterns that arise from the decentralized interactions of simpler individual components (Holland 1998). What characterizes emergent phenomena is that their appearance is not evident from a description of the system consisting of the specification of the behaviour of its individual components and the rules of interaction between them (Epstein 1999; Gilbert 2002; Gilbert & Terna 2000; Squazzoni 2008). In the most striking examples of emergent phenomena, rather complex macroscopic patterns arise from the interactions of very simple individual components. These emergent phenomena are, by definition for many scholars, surprising, i.e., counter-intuitive, i.e., they refute a prevailing belief. Thus, it is natural that models showing surprising emergent phenomena are likely to be able to play the role of a refuting machine.

A typical example of an emergent phenomenon is the formation of differentiated groups in the Schelling-Sakoda model; the emergence of clear segregation patterns is not explicitly imposed in the definition of the model, but emerges from the local interactions of individuals with surprisingly weak segregationist preferences.

Conclusions

In this paper we have argued that a prominent way in which social simulations can contribute (and have contributed) to the advance of science is by refuting some of our incorrect beliefs about how the real world works. More precisely, social simulations can produce counter-examples that reveal a logical inconsistency in a prevailing empirical theory. To do so, there are two conditions that the social simulation model should fulfil. Firstly, all the significant assumptions of the model (i.e., the assumptions that are leading to the contradicting results) must be included in the empirical theory, so they should be credible. Secondly, when trying to refute an empirical theory that allows for exceptions, the model should produce compelling evidence against the theory in a sufficiently important range of situations over which the empirical theory can be applied.

Naturally, many of the terms used in the two conditions above, such as ‘refutability’, ‘credibility’, or ‘importance’, should be understood as graded concepts that can be fulfilled to a partial extent. The model will be able to better refute the empirical theory (i) the more credible its significant assumptions are, (ii) the greater the range, diversity and importance of the situations over which it offers contradicting evidence, and (iii) the more reproducible and compelling this contradicting evidence is. This implies that refutation often builds up in time (as more assumptions are explored and more contradicting evidence is obtained), and it is best attributed to a whole family of models, rather than just to the first model that illustrated some counter-intuitive phenomenon.

We have also argued that simpler models are often in a better position to refute a prevailing belief, compared with more complex models. One reason for this is that in simple models it is easier to check the conditions that the model must fulfil so it can convincingly refute an empirical theory, i.e., the extent to which its significant assumptions are credible, and the extent to which they collectively cover a sufficiently important range of situations over which the empirical theory can be applied.

In the appendix, we show that many well-known models in the social simulation literature seem to have been able to –at least partially– refute a prevailing empirical theory, and they have done so with a strikingly simple model. In essence, these models are simple credible stories with an unexpected end.

References

ALVARADO, R. (2022). Computer simulations as scientific instruments. Foundations of Science, 27(3), 1183–1205. [doi:10.1007/s10699-021-09812-2]

ANZOLA, D. (2019). Knowledge transfer in agent-based computational social science. Studies in History and Philosophy of Science, 77, 29–38. [doi:10.1016/j.shpsa.2018.05.001]

ANZOLA, D. (2021a). Capturing the representational and the experimental in the modelling of artificial societies. European Journal for Philosophy of Science, 11(3), 63. [doi:10.1007/s13194-021-00382-5]

ANZOLA, D. (2021b). Social epistemology and validation in agent-Based social simulation. Philosophy & Technology, 34(4), 1333–1361. [doi:10.1007/s13347-021-00461-8]

ARNOLD, E. (2019). Validation of computer simulations from a Kuhnian perspective. In C. Beisbart & N. J. Saam (Eds.), Computer Simulation Validation: Fundamental Concepts, Methodological Frameworks, and Philosophical Perspectives (pp. 203–224). Cham: Springer International Publishing. [doi:10.1007/978-3-319-70766-2_8]

ARNOLD, E. (2014). What’s wrong with social simulations? The Monist, 97(3), 359–377. [doi:10.5840/monist201497323]

ARTHUR, W. B. (1989). Competing technologies, increasing returns, and lock-in by historical events. The Economic Journal, 99(394), 116–131. [doi:10.2307/2234208]

ARTHUR, W. B. (1994). Increasing Returns and Path Dependence in the Economy. Ann Arbor, MI: University of Michigan Press.

AXELROD, R. (1997a). Advancing the art of simulation in the social sciences. In R. Conte, R. Hegselmann, & P. Terna (Eds.), Simulating Social Phenomena (pp. 21–40). Berlin Heidelberg: Springer. [doi:10.1007/978-3-662-03366-1_2]

AXELROD, R. (1997b). The dissemination of culture: A model with local convergence and global polarization. Journal of Conflict Resolution, 41(2), 203–226. [doi:10.1177/0022002797041002001]

AYDINONAT, N. E. (2007). Models, conjectures and exploration: An analysis of Schelling’s checkerboard model of residential segregation. Journal of Economic Methodology, 14(4), 429–454. [doi:10.1080/13501780701718680]

BARBEROUSSE, A., & Vorms, M. (2014). About the warrants of computer-based empirical knowledge. Synthese, 191(15), 3595–3620. [doi:10.1007/s11229-014-0482-6]

CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Review of Modern Physics, 81(2), 591–646. [doi:10.1103/revmodphys.81.591]

CHALMERS, A. F. (1999). What Is This Thing Called Science? New York, NY: Open University Press.

CLARK, W. A. V., & Fossett, M. (2008). Understanding the social context of the Schelling segregation model. Proceedings of the National Academy of Sciences, 105(11), 4109–4114. [doi:10.1073/pnas.0708155105]

COLANDER, D. (2008). Review of "The Economy as an Evolving Complex System III: Current Perspectives and Future Directions", Edited by Lawrence E. Blume and Steven N. Durlauf. Economica, 75(297), 191–192. [doi:10.1111/j.1468-0335.2007.00641.x]

COOK, M. (2004). Universality in elementary cellular automata. Complex Systems, 15(1), 1–40.

DAVIDSSON, P., Klügl, F., & Verhagen, H. (2017). Simulation of complex systems. In L. Magnani & T. Bertolotti (Eds.), Springer Handbook of Model-Based Science. Cham: Springer International Publishing. [doi:10.1007/978-3-319-30526-4_35]

DAWKINS, R. (2009). The Greatest Show on Earth: The Evidence for Evolution. New York, NY: Free Press.

EDMONDS, B. (2001). The use of models - Making MABS more informative. In S. Moss & P. Davidsson (Eds.), Multi-Agent-Based Simulation (Vol. 1979, pp. 15–32). Berlin Heidelberg: Springer. [doi:10.1007/3-540-44561-7_2]

EDMONDS, B. (2010). Bootstrapping knowledge about social phenomena using simulation models. Journal of Artificial Societies and Social Simulation, 13(1), 8. [doi:10.18564/jasss.1523]

EDMONDS, B. (2018). A Bad Assumption: A Simpler Model Is More General. Review of Artificial Societies and Social Simulation. Available at: https://rofasss.org/2018/08/28/be-2/

EDMONDS, B., & Hales, D. (2005). Computational simulation as theoretical experiment. The Journal of Mathematical Sociology, 29(3), 209–232. [doi:10.1080/00222500590921283]

EDMONDS, B., Le Page, C., Bithell, M., Chattoe-Brown, E., Grimm, V., Meyer, R., Montañola-Sales, C., Ormerod, P., Root, H., & Squazzoni, F. (2019). Different modelling purposes. Journal of Artificial Societies and Social Simulation, 22(3), 6. [doi:10.18564/jasss.3993]

EPSTEIN, J. M. (1999). Agent-based computational models and generative social science. Complexity, 4(5), 41–60. [doi:10.1002/(sici)1099-0526(199905/06)4:5<41::aid-cplx9>3.0.co;2-f]

EPSTEIN, J. M. (2006a). Generative Social Science: Studies in Agent-Based Computational Modeling. Princeton, NJ: Princeton University Press. [doi:10.23943/princeton/9780691158884.003.0003]

EPSTEIN, J. M. (2006b). Remarks on the foundations of agent-Based generative social science. In L. Tesfatsion & K. L. Judd (Eds.), Handbook of Computational Economics (Vol. 2, pp. 1585–1604). Amsterdam: North-Holland. [doi:10.1016/s1574-0021(05)02034-4]

EPSTEIN, J. M. (2008). Why model? Journal of Artificial Societies and Social Simulation, 11(4), 12.

EPSTEIN, J. M., & Axtell, R. (1996). Growing Artificial Societies: Social Science From the Bottom Up. Washington, DC: Brookings Institution Press.

EVANS, M. R., Grimm, V., Johst, K., Knuuttila, T., de Langhe, R., Lessells, C. M., Merz, M., O’Malley, M. A., Orzack, S. H., Weisberg, M., Wilkinson, D. J., Wolkenhauer, O., & Benton, T. G. (2013). Do simple models lead to generality in ecology? Trends in Ecology & Evolution, 28(10), 578–583. [doi:10.1016/j.tree.2013.05.022]

FARMER, J. D., Patelli, P., & Zovko, I. I. (2005). The predictive power of zero intelligence in financial markets. Proceedings of the National Academy of Sciences, 102(6), 2254–2259. [doi:10.1073/pnas.0409157102]

FISHER, R. A. (1971). The Design of Experiments. London: Macmillan.

FLACHE, A., & Hegselmann, R. (2001). Do irregular grids make a difference? Relaxing the spatial regularity assumption in cellular models of social dynamics. Journal of Artificial Societies and Social Simulation, 4(4), 6.

GALÁN, J. M., Izquierdo, L. R., Izquierdo, S. S., Santos, J. I., del Olmo, R., López-Paredes, A., & Edmonds, B. (2009). Errors and artefacts in Agent-Based modelling. Journal of Artificial Societies and Social Simulation, 12(1), 1.

GARCÍA, J., & van Veelen, M. (2016). In and out of equilibrium I: Evolution of strategies in repeated games with discounting. Journal of Economic Theory, 161, 161–189.

GARCÍA, J., & van Veelen, M. (2018). No strategy can win in the repeated Prisoner’s Dilemma: Linking game theory and computer simulations. Frontiers in Robotics and AI, 5, 102.

GARDNER, M. (1970). Mathematical games. The fantastic combinations of John Conway’s new solitaire game "life". Scientific American, 223(4), 120–123.

GIBBARD, A., & Varian, H. R. (1978). Economic models. The Journal of Philosophy, 75(11), 664–677. [doi:10.5840/jphil1978751111]

GILBERT, N. (2002). Varieties of emergence. Proceedings of the Agent 2002 Conference on Social Agents: Ecology, Exchange, and Evolution.

GILBERT, N., & Ahrweiler, P. (2009). The epistemologies of social simulation research. In F. Squazzoni (Ed.), Epistemological Aspects of Computer Simulation in the Social Sciences (Vol. 5466, pp. 12–28). Berlin Heidelberg: Springer-Verlag [doi:10.1007/978-3-642-01109-2_2]

GILBERT, N., & Terna, P. (2000). How to build and use agent-based models in social science. Mind & Society, 1(1), 57–72. [doi:10.1007/bf02512229]

GINTIS, H. (2013). Markov Models of social dynamics: Theory and applications. ACM Transactions on Intelligent Systems and Technology, 4(3), 19. [doi:10.1145/2483669.2483686]

GODE, D. K., & Sunder, S. (1993). Allocative efficiency of markets with zero-Intelligence traders: Market as a partial substitute for individual rationality. Journal of Political Economy, 101(1), 119–137. [doi:10.1086/261868]

GOTTS, N. M., Polhill, J. G., & Law, A. N. R. (2003). Agent-Based simulation in the study of social dilemmas. Artificial Intelligence Review, 19(1), 3–92. [doi:10.1023/a:1022120928602]

HARTMAN, C., & Benes, B. (2006). Autonomous boids. Computer Animation and Virtual Worlds, 17(3–4), 199–206. [doi:10.1002/cav.123]

HASELGROVE, C. B. (1958). A disproof of a conjecture of Pólya. Mathematika, 5(02), 141. [doi:10.1112/s0025579300001480]

HATNA, E., & Benenson, I. (2012). The Schelling Model of ethnic residential dynamics: Beyond the integrated - segregated dichotomy of patterns. Journal of Artificial Societies and Social Simulation, 15(1), 6. [doi:10.18564/jasss.1873]

HEGSELMANN, R. (2017). Thomas C. Schelling and James M. Sakoda: The Intellectual, Technical, and Social History of a Model. Journal of Artificial Societies and Social Simulation, 20(3), 15. https://doi.org/10.18564/jasss.3511 [doi:10.18564/jasss.3511]

HINDERSIN, L., Wu, B., Traulsen, A., & García, J. (2019). Computation and simulation of evolutionary game dynamics in finite populations. Scientific Reports, 9(1), 6946. [doi:10.1038/s41598-019-43102-z]

HOLLAND, J. H. (1998). Emergence. From Chaos to Order. Reading, MA: Addison-Wesley.

IZQUIERDO, L. R., IZQUIERDO, S. S., Galán, J. M., & Santos, J. I. (2009). Techniques to understand computer simulations: Markov chain analysis. Journal of Artificial Societies and Social Simulation, 12(1), 6.

IZQUIERDO, L. R., IZQUIERDO, S. S., Galán, J. M., & Santos, J. I. (2013). Combining mathematical and simulation approaches to understand the dynamics of computer models. In B. Edmonds & R. Meyer (Eds.), Simulating Social Complexity (pp. 235–271). Berlin, Heidelberg: Springer [doi:10.1007/978-3-540-93813-2_11]

IZQUIERDO, L. R., IZQUIERDO, S. S., Galán, J. M., Santos, J. I., & Sandholm, W. H. (2022). Schelling-Sakoda model of spatial segregation. Software available at: https://luis-r-izquierdo.github.io/schelling-sakoda-refuting-machine/.

IZQUIERDO, L. R., IZQUIERDO, S. S., & Sandholm, W. H. (In progress). Agent-Based Evolutionary Game Dynamics. University of Wisconsin Pressbooks.

IZQUIERDO, L. R., IZQUIERDO, S. S., & Sandholm, W. H. (2019). An introduction to ABED: Agent-based simulation of evolutionary game dynamics. Games and Economic Behavior, 118, 434–462. [doi:10.1016/j.geb.2019.09.014]

IZQUIERDO, L. R., & Polhill, J. G. (2006). Is your model susceptible to floating-Point errors? Journal of Artificial Societies and Social Simulation, 9(4), 4.

KENNEDY, J., & Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN’95 - International Conference on Neural Networks. [doi:10.1109/icnn.1995.488968]

LADLEY, D. (2012). Zero intelligence in economics and finance. The Knowledge Engineering Review, 27(2), 273–286. [doi:10.1017/s0269888912000173]

LANDER, L. J., & Parkin, T. R. (1966). Counterexample to Euler’s conjecture on sums of like powers. Bulletin of the American Mathematical Society, 72(6), 1079. [doi:10.1090/s0002-9904-1966-11654-3]

LEOMBRUNI, R., & Richiardi, M. (2005). Why are economists sceptical about agent-based simulations? Physica A: Statistical Mechanics and Its Applications, 355(1), 103–109. [doi:10.1016/j.physa.2005.02.072]

NOWAK, M. A., & May, R. M. (1992). Evolutionary games and spatial chaos. Nature, 359, 826–829. [doi:10.1038/359826a0]

ODLYZKO, A. M., te Riele, H. J., & ODLYZKO, A. (1984). Disproof of the Mertens Conjecture. Centrum voor Wiskunde en Informatica.

PARKER, W. S. (2017). Computer simulation, measurement, and data assimilation. The British Journal for the Philosophy of Science, 68(1), 273–304. [doi:10.1093/bjps/axv037]

PEREZGONZALEZ, J. D. (2015). Fisher, Neyman-Pearson or NHST? A tutorial for teaching data testing. Frontiers in Psychology, 6, 2015. [doi:10.3389/fpsyg.2015.00223]

POLHILL, J. G., Izquierdo, L. R., & Gotts, N. M. (2006). What every agent-based modeller should know about floating point arithmetic. Environmental Modelling & Software, 21(3), 283–309. [doi:10.1016/j.envsoft.2004.10.011]

POPPER, K. R. (2005). The Logic of Scientific Discovery. Routledge.

REUTLINGER, A., Hangleiter, D., & Hartmann, S. (2018). Understanding (with) toy models. The British Journal for the Philosophy of Science, 69(4), 1069–1099. [doi:10.1093/bjps/axx005]

REYNOLDS, C. W. (1987). Flocks, herds and schools: A distributed behavioral model. Computer Graphics (ACM SIGGRAPH ’87 Conference Proceedings of the 14th annual conference on Computer graphics and interactive techniques) [doi:10.1145/37401.37406]

RICHIARDI, M., Leombruni, R., Saam, N., & Sonnessa, M. (2006). A common protocol for agent-Based social simulation. Journal of Artificial Societies and Social Simulation, 9(1), 15.

ROBERTS, S. (2020). The lasting lessons of John Conway’s Game of Life. The New York Times, December, 28. Available at: https://www.nytimes.com/2020/12/28/science/math-conway-game-of-life.html

ROCA, C. P., Cuesta, J. A., & Sánchez, A. (2009). Effect of spatial structure on the evolution of cooperation. Physical Review E, 80(4), 046106. [doi:10.1103/physreve.80.046106]

ROSEN, R. (2012). Anticipatory Systems: Philosophical, Mathematical, and Methodological Foundations. Springer New York.

SAKODA, J. M. (1949). Minidoka: An analysis of changing patterns of social behavior. PhD Thesis, University of California.

SAKODA, J. M. (1971). The checkerboard model of social interaction. The Journal of Mathematical Sociology, 1(1), 119–132. [doi:10.1080/0022250x.1971.9989791]

SCHELLING, T. C. (1969). Models of segregation. The American Economic Review, 59(2), 488–493.

SCHELLING, T. C. (1971). Dynamic models of segregation. The Journal of Mathematical Sociology, 1(2), 143–186.

SCHELLING, T. C. (1978). Micromotives and Macrobehavior. Norton.

SERI, R. (2016). Analytical approaches to agent-Based models. In D. Secchi & M. Neumann (Eds.), Agent-Based Simulation of Organizational Behavior (pp. 265–286). Springer International Publishing. [doi:10.1007/978-3-319-18153-0_13]

SERI, R., & Secchi, D. (2017). How many times should one run a computational simulation? In B. Edmonds & R. Meyer (Eds.), Simulating Social Complexity: A Handbook (pp. 229–251). Springer International Publishing. [doi:10.1007/978-3-319-66948-9_11]

SQUAZZONI, F. (2008). The micro-Macro link in social simulation. Sociologica, 1, 2008.

SQUAZZONI, F. (2012). Agent-Based Computational Sociology. John Wiley & Sons.

SQUAZZONI, F., Jager, W., & Edmonds, B. (2014). Social simulation in the social sciences: A brief overview. Social Science Computer Review, 32(3), 279–294. [doi:10.1177/0894439313512975]

SUBER, P. (2007). Formal Systems and Machines: An Isomorphism.

SUGDEN, R. (2000). Credible worlds: The status of theoretical models in economics. Journal of Economic Methodology, 7(1), 1–31. [doi:10.1080/135017800362220]

SZUCS, D., & Ioannidis, J. P. A. (2017). When null hypothesis significance testing is unsuitable for research: A reassessment. Frontiers in Human Neuroscience, 11, 2017. [doi:10.3389/fnhum.2017.00390]

THOMPSON, N. S., & Derr, P. (2009). Contra Epstein, Good Explanations Predict. Journal of Artificial Societies and Social Simulation, 12(1), 9. https://www.jasss.org/12/1/9.html. https://www.jasss.org/12/1/9.html

TROITZSCH, K. G. (1997). Social science simulation - Origins, prospects, purposes. In R. Conte, R. Hegselmann, & T. P. (Eds.), Simulating Social Phenomena (Vol. 456, pp. 41–54). Springer. [doi:10.1007/978-3-662-03366-1_3]

WIKIPEDIA contributors. (2022a). Boids. Available at: https://en.wikipedia.org/w/index.php?title=Boids&oldid=1094517009.

WIKIPEDIA contributors. (2022b). Conway’s Game of Life. Available at: https://en.wikipedia.org/w/index.php?title=Conway%27s_Game_of_Life&oldid=1102145663.

WILENSKY, U. (1999). NetLogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL. Available at: http://ccl.northwestern.edu/netlogo/.

WINSBERG, E. (2009). A tale of two methods. Synthese, 169(3), 575–592. [doi:10.1007/s11229-008-9437-0]

WOLFRAM, S. (1983). Statistical mechanics of cellular automata. Reviews of Modern Physics, 55(3), 601. [doi:10.1103/revmodphys.55.601]

WOLFRAM, S. (2002). A New Kind of Science. Wolfram Media.

YLIKOSKI, P., & Aydinonat, N. E. (2014). Understanding with theoretical models. Journal of Economic Methodology, 21(1), 19–36. [doi:10.1080/1350178x.2014.886470]