The Wisdom of the Small Crowd: Myside Bias and Group Discussion

Edoardo Baccini; Zoé Christoff; Stephan Hartmann; Rineke Verbrugge

doi:10.18564/jasss.5184

Introduction

Group discussion in general, and argumentation in particular, often plays a critical role in political, social, and scientific communities and can play a key role in decision making and scientific research. Therefore, the understanding of argumentation is the subject of numerous scientific investigations in different research areas in the cognitive and social sciences (Hornikx & Hahn 2012; Oaksford & Chater 2020). These investigations have shown that argumentative contexts are very complex and that it can be more difficult than expected to convince other people with one’s arguments. This is especially true when the participants in a discussion have different prior assumptions about the topic under discussion. Indeed, research has shown that participants in a discussion are influenced by their prior beliefs to such a degree that they favor them over alternatives both in finding new arguments and in evaluating other people’s arguments (Čavojová et al. 2018; Edwards & Smith 1996; Kuhn 1991; McKenzie 2004; Nickerson 1998; Perkins 1985; Stanovich 2021; Taber & Lodge 2006; Wolfe & Britt 2008).

In this paper, following Stanovich (2021), we use the term “myside bias" to refer to the influence of an agent’s prior beliefs on the evaluation and production of information in general, and of arguments in particular. By using this term, we aim to bring together the extensive body of work that has been conducted on the topic of prior belief biases, displaying a variety of terms to refer to such bias in one or another specific context, e.g., either argument production or argument evaluation or information search. Among others, some of the most closely related terms that are in use are: ”confirmation bias" (Gabriel & O’Connor 2022; Rabin & Schrag 1999), “biased assimilation" (Corner et al. 2012; Dandekar et al. 2013; Lord et al. 1979), ”biased/selective processing" (Newman et al. 2018; Shamon et al. 2019), “attitude congruence bias" (Taber et al. 2009), ”refutational processing" (Liu et al. 2015), “defensive processing" (Wood et al. 1995), and ”motivated cognition" (Lorenz et al. 2021). The existence of such a diverse terminology risks concealing the common subject-matter. We hope that our work will contribute to a more unified terminology in the field.

The main focus of this paper is myside-bias in the evaluation of arguments. In this context, research has uncovered the following two effects. On the one hand, discussants overestimate the strength of arguments that support their own prior beliefs or that attack opposing beliefs; on the other hand, discussants underestimate arguments that attack their own prior beliefs or that support opposing beliefs (Corner et al. 2012; Liu et al. 2015; Lord et al. 1979; Newman et al. 2018; Nickerson 1998; Shamon et al. 2019; Stanovich et al. 2013; Stanovich 2021; Stanovich & West 2007; Stanovich & West 2008; Taber et al. 2009; Taber & Lodge 2006; Toplak & Stanovich 2003).

For these reasons, it has been argued that myside-biased individuals risk becoming overconfident in their beliefs and are less willing to revise them, regardless of the truth value of the beliefs in question (Mercier 2017; Mercier & Sperber 2017; Stanovich 2021). Moreover, it has been argued that myside bias contributes to undesirable social phenomena such as attitude polarization (Lord et al. 1979; Newman et al. 2018; Stanovich 2021; Taber et al. 2009). Accordingly, myside bias is expected to have a detrimental effect on the ability of groups of discussants to get to the truth, i.e., on their ability to collectively find the correct answer to a given question.

However, this account ignores the fact that group discussions can provide a deceptive platform for unbiased reasoners who are easily led to hold false beliefs. This point is central to recent theories of reasoning that focus on reasoning in the context of human evolution (Mercier & Sperber 2017; Sperber et al. 2010). From an evolutionary perspective, cognitive devices such as the myside bias, which tests how new information fits with pre-existing beliefs, may provide agents with a mechanism that prevents them from falling prey to deceptive information (Mercier & Sperber 2011; Mercier & Sperber 2017).

The debate about the effects of myside bias also touches on the related and very timely debate about the extent to which group discussions enhance or diminish the collective wisdom derived from the wisdom-of-the-crowds tradition (Surowiecki 2005), and is currently a focus of researchers using both empirical methods (Claidière et al. 2017; Mercier & Claidière 2022; Navajas et al. 2018; Trouche et al. 2014) and formal methods (Hahn et al. 2019, 2020; Hahn 2022; Hartmann & Rafiee Rad 2018, 2020).

The main starting point of this debate is Condorcet’s Jury Theorem (Condorcet 1785), which is about the ability of groups of voters to find the true answer to a binary problem by majority voting. This theorem shows that the probability of the group finding the true answer by majority voting converges to $1$ as a function of group size, provided a number of conditions are met. In the simplest case, voters should vote non-strategically and independently, and individually vote for the correct answer with probability greater than $1/2$ (i.e., better than chance). For an overview of jury theorems, see Dietrich & Spiekermann (2022).

Most notably, any communication among a group of discussants destroys the independence of their opinions, thus violating a crucial assumption of Condorcet’s Jury Theorem. As a consequence, one would expect that, all other things being equal, group discussion decreases the ability of groups to track the truth. In this regard, a number of studies have shown that communication does indeed harm collective wisdom (Hahn et al. 2019; Lorenz et al. 2011). In other words, collectives can better track the truth if they simply aggregate their opinions into a single answer without discussing. This would imply that there is a higher chance for a collective to cast a majority of correct votes if the members of the collective do not communicate.

Recently, however, discussions were found, on the contrary, to improve group answers, compared to simply aggregating the opinions that group members originally held. In particular, Mercier & Claidière (2022) found that discussions led to better overall answers for mathematical or factual problems in large groups. This suggests that correct majorities are more likely after discussions than when agents’ original opinions are simply aggregated.

In this regard, researchers have suggested that the myside bias constitutes a driving mechanism that makes group discussions beneficial for collective wisdom. Some have indeed argued that the myside bias can improve the truth-tracking ability of a group of discussants, by increasing the agents’ stubbornness, preventing correct agents from abandoning their correct belief too early and thus fostering a thorough exploration of the different beliefs under considerations (Gabriel & O’Connor 2022). Indeed, while non-biased discussants might easily fall prey to false beliefs, the myside-biased agent attentively assesses external arguments and is only convinced by good enough arguments, checking them against their prior beliefs. Others have suggested that, during a discussion, the myside bias could prompt a fruitful cognitive division of labor between agents at the opposite sides of an issue (Landemore 2012; Mercier 2016; Mercier & Sperber 2017): agents from each side can carefully evaluate arguments that attack their own view and produce counterarguments, thus reducing the likelihood of incorrect beliefs to spread among the discussants.

The above considerations outline two parallel debates, the first one on the effects of myside bias and the second one on the effects of group discussion on collective wisdom, suggesting that there is not yet a clear answer to either of the following two questions:

Does myside bias help or hinder the ability of groups to track the truth via discussion?
Does group discussion help or hinder the ability of groups to track the truth?

This paper starts from a modified version of Baccini & Hartmann’s (2022) model of individual myside bias and extends it to develop an agent-based model for group discussions between myside-biased agents that allows us to answer these two questions in detail.

In this regard, our paper provides an epistemic analysis of group discussion, i.e., an analysis of the belief/opinion dynamics of agents in a group, that is primarily concerned with the correctness or incorrectness of the agents’ opinions/beliefs, similar to, for instance, the analyses in Hegselmann & Krause (2006), Zollman (2007), Douven & Kelp (2011), Brousmiche et al. (2016), Hahn et al. (2020), Gabriel & O’Connor (2022). This also means that our main focus will not be around opinion polarisation or opinion clustering, even though they constitute an important research direction in the study of opinion dynamics (see, e.g., Hegselmann & Krause 2002; Alvim et al. 2021; Flache et al. 2017; Kopecky 2022; Kurahashi-Nakamura et al. 2016; Schweighofer et al. 2020; Urbig et al. 2008).

We proceed in a twofold way. First, we propose a Bayesian model that adequately captures three important features of myside bias in argument evaluation at the individual level and provides a Bayesian justification of this model, thus showing that myside bias has a rational Bayesian explanation under certain conditions. In doing so, this paper fills a gap in the literature, because despite the ever-growing literature on Bayesian approaches to reasoning and argumentation (for overviews, see (Chater & Oaksford 2008; Oaksford & Chater 2020; Zenker 2013)), there is still no systematic Bayesian model of myside bias in argument evaluation.

Second, we implement this Bayesian model of myside bias into an agent-based model of group discussion in order to study the impact of myside bias on the ability of groups to track the truth. In this respect, we are particularly interested in deliberative contexts, where agents have to produce and evaluate arguments to reach a collective conclusion. Our perspective is motivated by a number of recent empirical and formal studies that investigate whether group discussion improves on the initial aggregate answers of the agents to a binary decision problem (Claidière et al. 2017; Hartmann & Rafiee Rad 2018; Mercier & Claidière 2022; Trouche et al. 2014).

The paper is structured as follows. In Section 2, we review a number of empirical studies and formal models that are directly concerned with group discussion or myside bias or both. In Section 3, we present a Bayesian model of myside bias, discuss its implications for argument evaluation and provide an epistemic justification for it. In Section 4, we present an agent-based model of group discussion with myside-biased agents, and explain in detail the notion of group truth-tracking that we want to investigate with it. In Section 5, we present and discuss the results of a number of experiments that we performed using the agent-based model, varying the ways in which the myside bias is distributed across the group of discussants. In Section 6, we discuss the implications of our findings in the context of the relevant literature, as well as some limitations of our work and directions for further research. Finally, in Section 7, we draw our conclusions.

Related Work

In this section, we provide an overview of some relevant work. First, we present empirical findings on the characteristics of myside bias in argument evaluation. We then discuss a number of formal models of opinion dynamics in groups that involve some form of myside bias.

Myside bias in argument evaluation

Myside bias in argument evaluation has been studied both in the context of formal argumentation, in which participants are asked to evaluate the conclusions of inferences that have a clear logical structure, and in the context of informal argumentation, in which subjects are asked to evaluate informal arguments that resemble real-world discussions (Čavojová et al. 2018). Overall, both lines of research show that the correspondence between arguers’ prior beliefs and the content of a conclusion or proposition influences how arguers perceive the truth value of a conclusion or the strength of an argument.

In the case of the study of formal arguments, early research on belief bias shows that the prior credibility of the conclusion of a deductive inference influences the arguer’s judgment about the validity of the inference (Evans 1989, 2002, 2007; Evans et al. 1993). Further research has shown that the credibility of an argument’s conclusion in light of one’s prior beliefs is a predictor of whether an actor judges a conclusion to be true or false. For example, Čavojová et al. (2018) found that participants had difficulty accepting the conclusions of logically valid arguments about abortion whose content conflicted with their prior beliefs about abortion. At the same time, participants had difficulty rejecting invalid arguments with the conclusions of which they agreed (Čavojová et al. 2018).

Much of the experimental research on myside bias has been conducted in an informal argumentation framework (Čavojová et al. 2018), and myside bias in argument evaluation has been documented in a substantial number of experiments (Corner et al. 2012; Edwards & Smith 1996; Liu et al. 2015; Lord et al. 1979; Newman et al. 2018; Nickerson 1998; Shamon et al. 2019; Stanovich et al. 2013; Stanovich & West 2007, 2008; Stanovich & West 2008; Taber et al. 2009; Taber & Lodge 2006). A commonly used experimental paradigm consists in initially letting participants express their opinions on a particular issue, such as abortion or public policy; afterwards, participants are exposed to a set of arguments relevant to the issue and asked to rate the strength of arguments from a set of arguments both for and against the participants’ positions on an issue (Edwards & Smith 1996; Liu et al. 2015; Shamon et al. 2019; Stanovich et al. 2013; Stanovich & West 2007; Stanovich & West 2008; Taber & Lodge 2006).

Within this framework, the myside bias has been studied in relation to a variety of research topics in the cognitive and social sciences, such as individual and group reasoning (Mercier 2017; Mercier 2018), scientific thinking (Evans 2002; Mercier & Heintz 2014), intelligence and cognitive abilities (Stanovich et al. 2013; Stanovich & West 2007; Stanovich & West 2008), human evolution (Mercier & Sperber 2011; Mercier & Sperber 2017; Peters 2020), public policies and political thinking (Mercier & Landemore 2012; Shamon et al. 2019; Stanovich 2021; Taber et al. 2009; Taber & Lodge 2006), and climate change (Corner et al. 2012; Newman et al. 2018). Overall, this body of work provides us with a rather coherent picture of how an agent’s prior beliefs impact on the agent’s judgement about the persuasiveness of different arguments.

As briefly mentioned above, an agent judges the strength of an argument depending on whether the argument is compatible or not with the agent’s prior position on the issue that is considered. For instance, in line with Edwards & Smith (1996), Taber et al. (2009) found that arguments compatible with the participants’ prior political stances were deemed stronger than incompatible ones; in addition, participants with increasingly stronger initial attitude commited a stronger bias, and participants with more prior knowledge would spend more time in analysing and counter-arguing constrastive arguments to their prior beliefs.

Recently, Liu et al. (2015) developed what they called a congruence model, according to which an agent’s judgement about the strength of an argument is determined by two dimensions: the compatibility of the argument with the agent’s prior view, and the intrinsic quality of the argument. Liu et al. (2015), and more recently Shamon et al. (2019), found that both these dimensions, and not just the compatibility with prior beliefs, are relevant for explaining people’s assessment of argument strength. In addition, Shamon et al. (2019) also found that arguments judged as familiar are rated as stronger than less familiar arguments.

A number of studies also support the claim that the myside bias in argument evaluation is a driving mechanism of attitude polarisation, i.e., the fact that participants' prior attitudes become more extreme after exposure to conflicting arguments (Lord et al. 1979; Newman et al. 2018; Stanovich 2021; Taber et al. 2009). In this regard, experiments in Corner et al. (2012) and (Shamon et al. 2019) suggest that attitude polarisation is not a necessary consequence of myside bias in argument evaluation, and that mysided reasoners might not always end up entertaining more extreme beliefs after discussion.

Overall, three salient features of myside bias in the evaluation of arguments stand out:

Arguments that favor their own prior beliefs and disfavor opposing views are overweighted (Liu et al. 2015; Lord et al. 1979; Shamon et al. 2019; Stanovich et al. 2013; Stanovich 2021; Stanovich & West 2007; Stanovich & West 2008). At the same time, an argument that attacks the prior opinion of the arguer or confirms contrary views is generally classified as a weak argument (Nickerson 1998).
Reasoners who are neutral toward the topic under discussion tend not to exhibit a myside bias in evaluation tasks (Shamon et al. 2019; Taber & Lodge 2006).
The myside bias occurs in various gradations: Proponents who believe more firmly in their point of view tend to have a stronger bias than proponents who hold a milder view (Shamon et al. 2019; Stanovich & West 2008; Taber et al. 2009). In other words, two arguers who are on the same side of an issue may show stronger or weaker bias depending on their beliefs.

In summary, myside bias can be interpreted as a difference of opinion about the extent to which an argument confirms (or refutes) a belief (or its opposite) between an agent who is neutral toward the belief and the case in which the agent supports either the truth or falsity of the belief. Finally, note that the model we develop in Section 3 accounts for all three empirically observed features of the bias described above.

Formal models of myside bias

A number of formal frameworks has been developed to study the effect of myside bias at the individual level. For instance, Rabin & Schrag (1999) developed a Bayesian model of belief update with confirmation bias. In their framework, confirmation bias works in the following way: agents that are more convinced of either the truth or the falsity of a proposition can mistakenly evaluate contrasting signals as supporting signals of their favoured alternative with a fixed probability. While representing the first approach to modelling myside bias within a Bayesian framework, their model falls short of giving a sufficiently fine-grained formal representation of myside bias. Admittedly, there is no prior-dependent modulation of the bias: the bias has the same intensity independently of the agents’ priors. Furthermore, agents do not underweight or overweight arguments, but only mistake disconfirming arguments for confirming ones with a fixed probability.

More recently, Nishi & Masuda (2013) have implemented the model of Rabin & Schrag (1999) in a multi-agent context, and studied the emergence of macro-level phenomena such as consensus and bi-polarisation as a result of a myside bias in the evaluation of evidence. As such, their work suffers from the same limitations we identified above in the work of Rabin & Schrag (1999). The model that we propose retains the Bayesian approach of Rabin & Schrag (1999) while also allowing for a more realistic representation of the myside bias, taking into account the three above-mentioned empirically observed properties.

Other models of myside-biased individual argument evaluation have been proposed. For instance, building on the Argument Communication Framework of Mäs & Flache (2013) and on the empirical findings in Shamon et al. (2019), Banisch & Shamon (2021) developed an individual-level model of myside bias which accounts for the representation of an attitude-dependent gradation of the bias via a strength of biased processing parameter. In their model, an agent accepts/rejects arguments with a certain probability that depends on whether the arguments cohere or not with the prior attitude of an agent, with coherent arguments being more likely to be accepted. On top of this, the strength of biased processing parameter controls how much more likely it is for an agent to accept arguments that cohere with its prior attitude, compared to accepting arguments that do not.

Starting from the work of Hunter et al. (1984), Lorenz et al. (2021) develop a very general model of individual attitude that combines a variety of cognitive mechanisms driving an agent’s attitude dynamics. Among other mechanisms, the model incorporates what they call motivated cognition, which makes an agent’s evaluation of a received piece of information dependent on the absolute value of the difference between the agent’s attitude and the message, where both attitude and message are real numbers.

Let us highlight some relevant distinctions between the model that we will propose on the one hand, and the models in Banisch & Olbrich (2021) and Lorenz et al. (2021) on the other. First, neither of these two models is Bayesian: in Banisch & Olbrich (2021), the opinion of an agent is the sum of the arguments that it accepts, where arguments can take either value $1$ or $-1$, and the changes in an agent’s opinion are determined by changes in the set of arguments that it accepts or rejects after interacting with others; in Lorenz et al. (2021), the agents’ attitudes are real numbers (positive or negative) and the pieces of information that they exchange are the values of their attitudes, rather than pieces of evidence or arguments.

Second, as for the case of Mäs & Flache (2013), the agents in Banisch & Shamon (2021) can only exchange arguments that, although of possibly different polarity (i.e., supporting either one of two sides of an issue), are all equally strong. In this regard, the Bayesian setting that we employ allows for a more fine-grained representation of arguments, where each argument is associated with a diagnostic value that specifies how much the argument supports one side of the issue against the other.

Both Banisch & Shamon (2021) and Lorenz et al. (2021) also implemented their individual-level models in a multi-agent environment and studied the opinion patterns emerging at the collective level as a result of the interaction between myside-biased agents. In this regard, Banisch & Shamon (2021) found that, if the agents’ bias is weak, the group converges to a consensus more rapidly; conversely, as the agents’ bias becomes stronger, a persistent state of bi-polarisation at the collective level is reached, i.e., a state where agents can be divided into two groups characterised by extreme but mutually opposed beliefs. Similarly, Lorenz et al. (2021) found that motivated processing produces patterns of bi-polarisation. Note that neither of these models is concerned with the problem of truth-tracking.

Other multi-agent models of belief formation implement some form of myside bias in evaluation and investigate its relation to macro-level societal patterns, such as convergence to consensus or polarisation. For instance, Alvim et al. (2019, 2021) propose a model of polarisation in social networks with confirmation bias, which is inspired by the work on bounded confidence models of Hegselmann & Krause (2002). These models in turn generalise the studies on iterative opinion pooling (DeGroot 1974; French Jr 1956; Lehrer & Wagner 1981), where agents update their opinions by a weighted average of the opinions of neighbouring agents.

The models in Alvim et al. (2019), Alvim et al. (2021) embed a confirmation bias factor as a function of the distance between the prior beliefs of two neighbouring agents. When updating their beliefs, agents compute a weighted average of their neighbours, where the weights of the underlying network structure are themselves weighted by the confirmation bias factor. Note, however, that Alvim et al. (2019), Alvim et al. (2021) are concerned with group polarization, and not group truth-tracking. While a number of generalizations of bounded-confidence models have been proposed to address problems of truth-tracking (see, e.g., Hegselmann & Krause 2006, 2015; Douven & Riegler 2009), we believe that other formal frameworks are more apt to specifically model group discussion, in particular with respect to agents exchanging stronger or weaker arguments in support of alternatives to an issue.

Let us conclude this section by discussing the very recent Bayesian model of group learning in social networks with confirmation bias developed by Gabriel & O’Connor (2022). Their model builds on the two-armed bandit model developed in Bala & Goyal (1998) and on the network models of Zollman (2007), Zollman (2010) to study group learning. Without going into the details of the two-armed bandit model, it should be said that agents in the learning process can learn both by receiving signals from the world and by communicating with their neighbours. Within this framework, Gabriel & O’Connor (2022) consider two different ways of modeling confirmation bias. First, moderately biased agents are given an intolerance parameter that sets for each agent the probability of ignoring information from its neighbours, based on the likelihood of the information in light of its prior beliefs. Second, agents that are strongly biased completely ignore information received from neighbours for which the probability of the information in light of their own beliefs is less than a certain threshold.

Gabriel & O’Connor (2022) found that moderate confirmation bias increases the probability that agents converge to the correct consensus; this effect is attributed to the fact that a moderate bias allows agents to explore different relevant options for a longer time, thus making more likely that truth will ultimately result from the group learning process. On the other hand, with strong confirmation bias, as the strength of the bias increases, consensus becomes less likely, and more agents in the network stabilise on choosing the wrong option.

Our model differs from Gabriel & O’Connor’s (2022) approach in three respects: First, neither the moderate nor the strong confirmation bias in Gabriel & O’Connor (2022) correspond to a prior-dependent underweighting or overweighting of argument strength. In both their moderate and their strong bias case, agents either update on the evidence as they receive it, or completely ignore the evidence received. Therefore, their model omits what was considered one of the key elements of myside bias.

Second, while the analysis in Gabriel & O’Connor (2022) focuses on groups of relatively small size (up to $25$ agents), we want to explore the effect of myside bias on larger groups as well. This is motivated by our interest in deliberative contexts that can involve larger groups, such as interaction in social media groups or state legislatures.

Third and finally, while Gabriel & O’Connor (2022) focus only on homogeneously biased groups, much of our analysis relies on modeling heterogeneous groups in which the myside bias is distributed differently across the group of discussants. We will show that a number of interesting types of group dynamics emerge in these groups that are important for finding the truth in a discussion.

A Bayesian Model of Myside Bias in Argument Evaluation

To provide a Bayesian model of myside bias, we introduce binary propositional variables $A$ and $B$ (in italic script) which have the values A and $\neg$A, and B and $\neg$B (in roman script), respectively, with a prior probability distribution $P$ defined over them. In the present context, B is the target proposition and A is an argument in support of B. A and B are contingent propositions and we assume that $P({\rm A}), P({\rm B}) \in (0,1)$. Here, $(0,1)$ is the interval containing all real numbers between 0 and 1, excluding the endpoints. $P$ represents the subjective probability function of an agent and $P({\rm A})$ measures how strongly they believe in A. See Sprenger & Hartmann (2019) for a philosophical justification of the Bayesian framework.

Next, we are interested in the posterior probability of B after learning A. According to Bayes’ theorem, it is given by $P^{\ast}({\rm B}) := P({\rm B \vert A})$ which can also be written as:

\[ P^{\ast}({\rm B}) = \frac{P({\rm B})}{P({\rm B}) + x\cdot P({\rm \neg B})} .\]

\[(1)\]

Here the likelihood ratio $x$ is given by

\[ x := \frac{P({\rm A \vert \neg B})}{P({\rm A \vert B})},\]

\[(2)\]

where we follow the convention used in Bovens & Hartmann (2003). Then the following proposition holds:

Proposition 1. Let $A$ and $B$ be two binary propositional variables with a prior probability distribution $P$ and a posterior distribution $P^{\ast}$ defined over them. Then Equation (1) implies that (i) $P^{\ast}({\rm B}) > P({\rm B})$ iff $0 \leq x < 1$, (ii) $P^{\ast}({\rm B}) = P({\rm B})$ iff $x = 1$, and (iii) $P^{\ast}({\rm B}) < P({\rm B})$ iff $x > 1$.

This proposition directly relates confirmation and disconfirmation of one’s own beliefs to the likelihood ratio $x$: if $x < 1$, then the agent’s degree of belief in B increases, and therefore the argument A confirms the target belief B; if $x > 1$, then the agent’s degree of belief in B decreases, and therefore the argument A disconfirms the target belief B (“A attacks B”); if $x = 1$, then learning A does not make any difference for the agent’s degree of belief in B, which means that A is not relevant for the truth or falsity of B. The likelihood ratio $x$ is also referred to as the diagnosticity of an argument A relative to a belief B. Here the term “diagnosticity” refers to the fact that the likelihood ratio measures how much A specifically supports the truth of B against its falsity. For instance, consider a case in which an argument A is more likely to be true if B is true than if $\neg$B is true, i.e., when $P({\rm A \vert B}) > P({\rm A \vert \neg B})$: then $x < 1$ and, by Proposition 1, the argument A will increase the degree of belief in the target proposition B. The more likely it is that an argument A is true if B is true, compared to the case where $\neg$B is true, the smaller $x$ is and the higher the confirmation of B is.

Another important property to be spelled out is the following:

Proposition 2. Let $A$ and $B$ be two binary propositional variables, and let $P,Q$ be two prior probability distribution such that $P({\rm B})=Q(\neg{{\rm B}})$. Let $x$ and $y$ be two likelihood ratios such that $x, y > 0$ and define $\Delta_B := P^{\ast}({\rm B})-P({\rm B})$, where $P^{\ast}({\rm B})$ is the posterior probability obtained by updating $P({\rm B})$ on $x$ with Equation (1), and define $\Delta_{Q} := Q^{\ast}({\rm \neg B})-Q({\rm \neg B})$, where $Q^{\ast}({\rm \neg B})$ is the posterior probability obtained by updating $Q({\rm \neg B})$ on $y$ with Equation (1). Then Equation (1) implies that $\Delta_P = \Delta_{Q}$ iff $y=1/x$.

This proposition captures the notion that the change in an agent’s degree of belief in B triggered by argument $x$ is, in absolute value, the same as the change triggered in an agent’s equally strong degree of belief in the alternative $\neg$B triggered by the inverse of $x$. In other words, if we take two agents with equally strong degrees of beliefs, but towards opposite alternatives of an issue, the likelihood ratio $x$ and its inverse $1/x$ determine equal changes in their degrees of beliefs.

The perceived likelihood ratio

The central idea of the proposed model is that the myside bias affects the way an agent judges the diagnosticity of an argument A relative to B. This, in turn, affects the way the agent updates the strength of their belief in B based on the argument A. See also Nickerson (1998).

Therefore, we model the myside bias as a distortion of the (pure) likelihood ratio $x$ of A relative to B, via a perceived likelihood ratio function $x'$. If an agent assigns a high degree of belief to B, then using $x'$ yields more confirmation than using the (pure) likelihood ratio $x$, provided that $x$ is confirmatory (i.e., $x < 1$); on the other hand, if $x$ is disconfirmatory (i.e., $x > 1$), then $x'$ yields less confirmation than $x$. More specifically, we propose the following functional form:

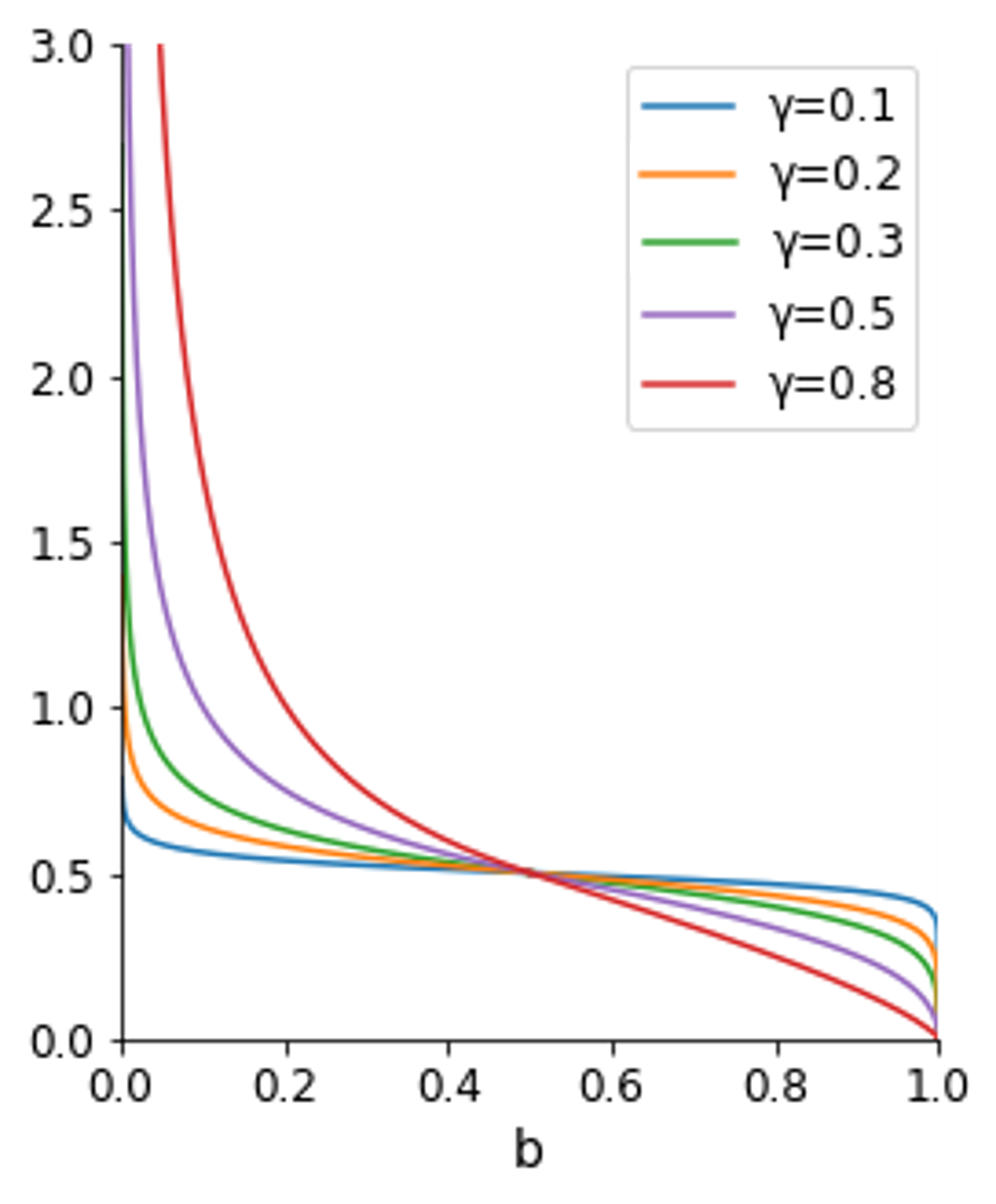
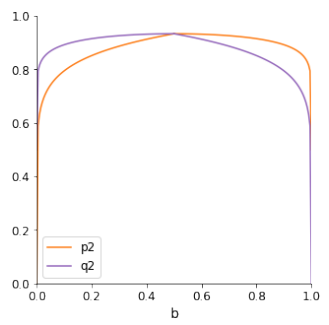
Definition 1. An agent considers the propositions A (= the argument) and B (= the target belief) with a probability distribution $P$ defined over the corresponding propositional variables. $x$ is the (pure) likelihood ratio defined in Equation (2) and $b:= P({\rm B})$ is the agent’s prior degree of belief in $B$. Then the agent’s perceived likelihood ratio $x'$ is given by \[ x’(x,b) = \begin{cases} 2 \, x \cdot \frac{\bar{b}^\gamma}{b^\gamma + \bar{b}^\gamma} & {\rm for} \ b\geq 1/2 \\ \\ \frac{x}{2} \cdot \frac{b^\gamma + \bar{b}^\gamma}{b^\gamma} & {\rm otherwise,} \\ \end{cases}\] with $\bar{b} := 1-b$ and $0 < \gamma <1$.

**Figure 1.** $x'$ as a function of $b$ for $x = 1/2$ and different values of $\gamma$.

Note that the perceived likelihood ratio $x'$ is a function of the prior probability of the target proposition, as opposed to the pure likelihood ratio $x$, which is considered independent of the prior probability. Figure 1 shows the perceived likelihood ratio $x'$ as a function of the agent’s prior degree of belief $b$. We see that $x' < x$ if $b > 1/2$ and $x' > x$ if $b < 1/2$. Furthermore, we take the parameter $\gamma$, which determines the convexity of the function, to characterise different ways in which agents can be more or less radically biased. This is motivated by the fact that, for a fixed agent’s prior belief $b$, as the value of $\gamma$ increases, the distortion of the (pure) likelihood ratio becomes stronger. In other words, $\gamma$ can account for the agents’ individual differences in the way they more or less strongly distort arguments, which are independent from the agents’ prior degrees of belief. We will refer to $\gamma$ also as the radicality parameter. We will see below that $\gamma$ has to be in the open interval $(0, 1)$. Then the distortion is much stronger for values of $b$ close to the extremes (i.e., $0$ and $1$), than for middling values of $b$.

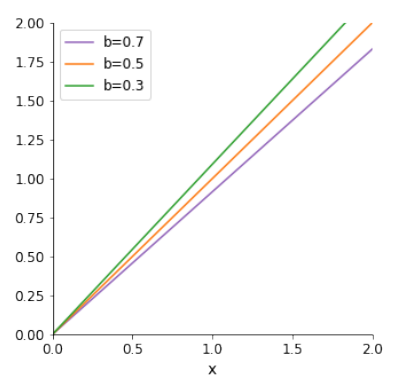
Figure 2 plots the perceived likelihood ratio $x'$ as a function of the (pure) likelihood ratio $x$ for fixed values of $b$ and $\gamma$. In this case, $x'$ is a linear function of $x$, where $x' > x$ if $b > 1/2$. Similarly, $x' < x$ if $b < 1/2$.

**Figure 2.** $x'$ as a function of $x$ for $\gamma=0.2$ and different values of $b$.

We summarise our findings in three propositions:

Proposition 3. The perceived likelihood ratio $x'(x,b)$ has the following features: (i) If $b > 1/2$, then $x' < x$, (ii) if $b = 1/2$, then $x'=x$, and (iii) if $b < 1/2$, then $x' > x$.

Proposition 4. The perceived likelihood ratio $x'(x,b)$ is strictly monotonically decreasing in $b$.

Proposition 5. Fix two (pure) likelihood ratios $x,y>0$ such that $x \cdot y = 1$, and two probability distributions $P$ and $Q$ over a propositional variable $B$, such that $P(\rm B)=Q({\rm \neg B})$. Then $x'(x, P({\rm B})) \cdot y'(y, Q({\rm B})) =1$.

Propositions 3 and 4 demonstrate that the perceived likelihood ratio $x'(x,b)$ is adequate to represent the myside bias, because it incorporates the three salient features of myside biased identified above. In particular, Proposition 3 shows that if the agent is more convinced of B than of $\neg$B, any argument will be perceived as more confirmatory or less disconfirmatory compared to the evaluation of a neutral observer (who uses the pure likelihood ratio $x$). On the other hand, if an agent is prone to believe that the target proposition is false, they will tend to perceive arguments as less confirmatory or more disconfirmatory than a neutral observer. Furthermore, an agent who is indifferent between B and $\neg$B will not be biased towards either of the two sides. This is consistent with the first two salient features of myside bias.

In addition, Proposition 4 shows that, all things being equal, the perceived likelihood ratio decreases as the strength of belief in B increases, and increases as the strength of belief in B decreases. Intuitively, this means that myside bias gets more pronounced as the degree of belief in the target proposition increases, in accordance with the third salient feature of myside bias.

Proposition 5 guarantees that the distortion preserves the property described in Proposition 2, according to which a likelihood ratio $x$ determines the same change in an agent’s degree of belief in, say, $\rm B$, as the change determined by the inverse of $x$ in an agent whose degree of belief in $\neg{\rm B}$ is equally strong. If this were not the case and our function would map two pure likelihood ratios $x,y$ such that $x=1/y$ to values that are not the inverse of one another, this would determine an asymmetry in the way agents with equally strong degrees of belief in opposite sides of an issue distort equally strong (pure) likelihood ratios. This would be equivalent to unjustifiably assuming that the distortion of arguments can be stronger or weaker dependently on which side of the issue an agent is on.

The myside bias update

An agent who commits the myside bias does not update with the (pure) likelihood ratio $x$, but with the perceived likelihood ratio $x'(x, b)$ provided in Definition 1. Using Bayes’ theorem with $x'$ instead of $x$, the posterior degree of belief in the target proposition B, after updating on the argument A, is then given by:

\[ P^{\ast \ast}({\rm B}) = \frac{b}{b + x'(x, b) \cdot \bar{b}} .\]

\[(3)\]

From Equation (1) and (3) and Proposition 3 we then obtain:

Proposition 6. The following claims hold: (i) If $b > 1/2$, then $P^{\ast \ast}({\rm B}) > P^{\ast}({\rm B})$; (ii) if $b = 1/2$, then $P^{\ast \ast}({\rm B}) = P^{\ast}({\rm B})$, and (iii) if $b < 1/2$, then $P^{\ast \ast}({\rm B}) < P^{\ast}({\rm B})$.

Therefore, our model predicts that agents’ posterior degrees of belief will be more extreme than those of an agent who uses Equation (1) to calculate their posterior degree of belief (unless they are indifferent to the target statement). More specifically, agents who rate $\neg$B as more likely than B will have a lower posterior degree of belief than that obtained using Equation (1). Conversely, agents who believe B more strongly than $\neg$B will have a higher posterior degree of belief than an agent who uses Equation (1). This prediction is consistent with recent findings presented in Bains & Petkowski (2021).

Another interesting consequence of the proposed model is that the new updating rule (i.e., Equation 3) is non-commutative, i.e., the result of an update on two or more arguments depends on the order in which the update takes place. Figure 3 illustrates this point. Here we consider an agent who is initially indifferent between B and $\neg$B (and therefore sets $b= 1/2$). Subsequently, the agent is presented with two arguments, ${\rm A_1}$ (with the pure likelihood ratio $x_1$) and ${\rm A_2}$ (with the pure likelihood ratio $x_2$), such that $x_1 < 1 < x_2$, i.e., the first argument (${\rm A_1}$) is confirmatory and the second argument (${\rm A_2}$) is disconfirmatory. If the agent first updates on ${\rm A_1}$, then their degree of belief in B will increase; in turn, this will determine an underweighting of the disconfirmatory strength of ${\rm A_2}$, since $P^{\ast \ast}({\rm B}) > 1/2$, by Proposition 3. However, if the agent first updates on ${\rm A_2}$, then $P^{\ast \ast}({\rm B}) < 1/2$ and their second update (on ${\rm A_1}$) uses the perceived likelihood ratio $x_1' > x_1$, again by Proposition 3. Thus, the agent assigns a higher posterior degree of belief to B if they first update on the stronger argument ${\rm A_1}$, followed by a second update on the weaker argument ${\rm A_2}$.

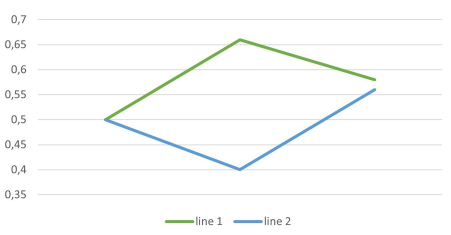
**Figure 3.** The result of the update on two arguments, ${\rm A_1}$ (with likelihood ratio $x_1$) and ${\rm A_2}$ (with likelihood ratio $x_2$) for $b = 1/2$ and $\gamma = 0.2$. Line 1: first update on ${\rm A_1}$, then on ${\rm A_2}$. Line 2: first update on ${\rm A_2}$, then on ${\rm A_1}$.

Mathematically, the reason for the non-commutativity of the new updating rule is the fact that the perceived likelihood ratio is a function of the prior probability. (While updating by Bayes’ theorem is commutative, it is well known that updating by Jeffrey conditionalisation is non-commutative, however, for a different reason.) It is worth noting that likelihood ratios that depend on the prior probability of the hypothesis being tested, while unusual, are not uncommon in the literature. See, e.g., Chapter 5 of Bovens & Hartmann (2003) for a discussion.

We summarise our findings on the non-commutativity of myside-biased updating in the following proposition.

Proposition 7. An agent considers the propositions ${\rm A_1, A_2}$ and ${\rm B}$ with a prior probability distribution $P$ defined over them. The corresponding likelihoods are $x_1$ and $x_2$, respectively. Let $P^{†} ({\rm B})$ be the posterior probability of B after updating first on ${\rm A_1}$ and then on ${\rm A_2}$, and let $P^{‡} ({\rm B})$ be the posterior probability of B after updating first on ${\rm A_2}$ and then on ${\rm A_1}$. Then $P^{‡} ({\rm B}) > P^{†} ({\rm B})$ iff $x_1 > x_2$.

Hence, it is epistemically advantageous for a myside-biased agent to first update on the stronger argument, i.e., on the argument with the smaller (pure) likelihood ratio.

Our model also predicts that reasoners are easily persuaded of their own position and harder to change. For instance, the stronger an agent’s prior degree of belief becomes, the stronger contrasting arguments need to be in order to sway the reasoner. In contrast with this view, Mercier (2017), Mercier (2020) and Mercier & Sperber (2017) argue that myside bias does not directly affect an agent’s evaluation of external arguments, and that reasoners are able to accept good arguments even when they challenge their own view. Within this framework, one would not expect to observe differences in argument evaluation between reasoners differing in their prior degrees of beliefs. This contrasts with our prediction that argument evaluation changes as a function of an arguer’s prior degree of belief.

While the correctness of one or the other of these predictions remains an open question, our model has the advantage that it intuitively explains harmful group-level phenomena, such as polarization in peer groups and communication difficulties between polarized groups as an effect of one-sided exchanges and evaluations of arguments (Stanovich 2021).

Justifying the model

So far, we have presented a model that is consistent with the three salient features of myside bias. The model is Bayesian because it models the bias in a Bayesian way: The agent assigns a prior probability to B, is then presented with an argument A, and updates B accordingly. This requires specifying a likelihood ratio, and our model identifies an appropriate choice, viz., $x'(x,b)$. However, this choice must be justified. Otherwise, the model would be a purely ad hoc solution. So how can the choice and the proposed functional form of $x'(x,b)$ be justified?

To address this question, we introduce a new propositional variable $E$ and argue that the agent does not only learn A, but also E. In the present context, the appropriate posterior probability of B is therefore $P^{\ast \ast \ast}({\rm B}) = P({\rm B \vert A, E})$. We will then see that, under certain conditions, $P^{\ast \ast \ast}({\rm B}) = P^{\ast \ast}({\rm B})$.

The new propositional variable $E$ has the values E: “The target belief coheres with the background beliefs” and $\neg$E: “The target belief does not cohere with the background beliefs” We take E to be supporting evidence for B. That is, it is rational to assign a higher degree of belief to a proposition that fits well to one’s background beliefs than to a proposition that does not. Hence, it is rational that $P({\rm B \vert E}) > P({\rm B \vert \neg E})$.

It has already been suggested that the link between an agent’s beliefs and their background beliefs justifies their putative bias in evaluating arguments (Evans 2002; Evans & Over 1996). For example, Evans (2002) argues that a broadly coherent system of beliefs is necessary to make sense of the world, and that this justifies an individual’s biased attitude toward her or his own view and toward alternatives. Our proposal is in line with this research.

Before proceeding, it is important to note that the agent considers proposition E on the basis of the argument A put forward. Considerations of coherence with background beliefs also play a role, of course, in an agent’s determination of the prior probability of B. Here, however, the focus is on the following question: does B cohere with the agent’s background beliefs in light of A?

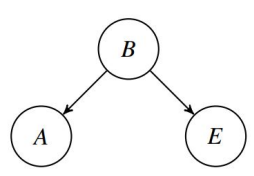
Next, we note that $A \perp \!\!\! \perp E \vert B$. That is, once we know that B, learning E will not change the degree of belief an agent assigns to A: The truth (or falsity) of the argument only depends on the target belief. This plausible assumption then suggests the Bayesian network represented in Figure 4. Note that there are arcs from $B$ to $A$ and from $B$ to $E$, indicating that the corresponding propositional variables are directly probabilistically dependent on each other. For an introduction to the theory of Bayesian networks, see Hartmann (2021) and Neapolitan (2003).

**Figure 4.** The Bayesian network for the myside bias.

To complete the Bayesian network, we have to specify the prior probability of the root node $B$, i.e.,

\[ P({\rm B}) = b,\]

\[(4)\]

and the conditional probabilities of the child nodes (i.e., $A$ and $E$) given the values of their parent (i.e., $B$). These likelihoods are given by:

\[ \begin{eqnarray} \label{prior2} P({\rm A \vert B}) := p_1 \quad &,& \quad P({\rm A \vert \neg B}) := q_1 \nonumber \\ P({\rm E \vert B}) := p_2 \quad &,& \quad P({\rm E \vert \neg B}) := q_2 . \end{eqnarray} \]

\[(5)\]

Using this, we can calculate the posterior probability of B after learning A and E.

Proposition 8. An agent considers the propositions ${\rm A, B}$ and ${\rm E}$. The corresponding propositional variables satisfy the conditional independencies encoded in the Bayesian network in Figure 3 and the prior probability distribution $P$ is defined in Equations (4) and (5). Then \[P({\rm B \vert A, E}) = \frac{b}{b + x'' \cdot \bar{b}},\] with $x'' = x \cdot x_E$ and $x := q_1/p_1$ and $x_E := q_2/p_2$.

To establish that $P^{\ast \ast \ast}({\rm B}) = P({\rm B \vert A, E}) = P^{\ast \ast}({\rm B})$, we need to show that

\[ x_E := q_2/p_2 = \begin{cases} \frac{2 \, \bar{b}^\gamma}{b^\gamma + \bar{b}^\gamma} & {\rm for} \ b\geq 1/2 \\ \\ \frac{b^\gamma + \bar{b}^\gamma}{2 \, b^\gamma} & {\rm otherwise} \\ \end{cases}\]

This obtains if one sets

\[ \begin{eqnarray} p_2 &:=& \begin{cases} 1/2 \cdot \left(b^\gamma + \overline{b}^\gamma \right) & \textrm{ for } b\geq 1/2 \\ \\ b^\gamma & \textrm{ otherwise, and} \end{cases} \label{p2q2like1} \end{eqnarray} \]

\[(6)\]

\[ \begin{eqnarray} q_2 &:=& \begin{cases} \bar{b}^\gamma & \textrm{ for } b\geq 1/2 \\ \\ 1/2 \cdot \left(b^\gamma + \overline{b}^\gamma \right) & \textrm{ otherwise} \label{p2q2like2} \end{cases} \end{eqnarray} \]

\[(7)\]

We will now argue that this is a good choice. And indeed, the assignments (6) and (7) are plausible. First, we mentioned already that a prior dependence of the likelihoods has already been used in other contexts. Second, an agent who believes B more strongly than $\neg$B (i.e., who assigns $b >1/2$) expects the target belief to cohere more with their background beliefs under the assumption that B is true than under the assumption that it is false. Likewise, an agent who believes $\neg$B more strongly than B (i.e., who assigns $b <1/2$) expects the target belief to cohere less with their background beliefs under the assumption that B is true than under the assumption that it is false. It is easy to see that Equations (6) and (7) account for this. See also Figure 5.

**Figure 5.** The likelihoods $p_2$ and $q_2$ as a function of $b$ for $\gamma = 0.1$.

Third, both $p_2$ and $q_2$ have a maximum at $b =1/2$ if $\gamma <1$. See also Figure 4. This is plausible, because a proposition with a middling prior probability is most “flexible” and one would expect it to easily fit into a system of background beliefs. This is not to be expected with a proposition of whose truth or falsity one is much more convinced. For $\gamma > 1$, $p_2$ has a minimum at $b =1/2$. Because this is not plausible (given the above considerations), we restrict the range of $\gamma$ to the open interval $(0,1)$ (see Definition 1)).

The crucial idea of the present proposal is that an agent who holds a belief B and who is confronted with an argument A for or against B does not only update their strength of belief in A but also investigates, prompted by the argument A, whether B fits to their background beliefs. This will lead to an increase or decrease of the agent’s strength of belief in B—the myside bias—which then, under these assumptions, turns out to be a rational response. The suggestion we make here thus bears similarity with other proposals in the literature that tie the notion of coherence to prior-belief effects in the evaluation of arguments, evidence and information, e.g., Thagard (2006), Rodriguez (2016), Wolf et al. (2015).

In closing this section, let us shortly comment on the notion of coherence that is used here. “Coherence” is a notoriously vague term that plays a key role in the coherence theory of justification in epistemology (see, e.g., BonJour (1985)). It refers to the property of an information set to “hang together well” which is often taken to be a sign of its truth. Witness reports in murder cases are good illustrations of this. But while we have a good intuitive sense of which information sets are coherent and which are not (and which of two information sets is more coherent), it is notoriously hard to make precise what coherence means and to substantiate the claim that coherence is, under certain conditions, truth-conducive (or at least probability-conducive) in the sense that a more coherent set is, given certain conditions, more likely to be true (or has a higher posterior probability). These questions have been addressed in the literature in formal epistemology. See, e.g., Bovens & Hartmann (2003), Douven & Meijs (2007) and Olsson (2022). It will be interesting to relate the qualitative proposal made in this paper to that literature. This will allow for a more fundamental derivation of the perceived likelihood ratio proposed in this paper. We leave this task for another occasion.

An Agent-Based Model of Myside Bias in Group Discussion

To investigate the effects of myside bias in group discussions, we created an agent-based model in NetLogo (Wilensky 1999). This model simulates a group discussion in which the agents debate a binary issue. The debated issue has a correct/true alternative and an incorrect/false alternative. Our goal is to evaluate the impact of myside bias by determining what effect it has on the ability to track the truth in discussions between agents with a myside bias compared to agents without this bias. The model code is available at https://www.comses.net/codebases/68a53ba2-8cfd-4805-bb16-5e8bd6840d25/releases/1.1.0/.

The setup

Our model consists of $n$ agents and a unique propositional variable, which can either assume value "true" or value "false". This propositional variable represents the issue that the agents have to settle during their discussion. Note that we assume that the issue has only one correct answer, namely "true", while the other answer is incorrect.

At the start, each agent is randomly assigned a prior probability distribution over the propositional variable, by randomly generating, for each agent, its prior degree of belief in the correct alternative of the variable from a uniform probability distribution. In this paper, we will be concerned with groups of decision makers that are competent on average, and thus we will assume that at the beginning of the discussion, the average belief of the discussants in the correct answer to the question is strictly above chance. We do this by generating distributions of priors over the agents whose average is strictly greater than $1/2$.

This choice is inspired by some variants of the Condorcet’s Jury Theorem, which we briefly mentioned in Section 1. While the simplest version of this theorem considers groups of voters that all have the same competence (i.e., the same probability of casting a correct vote), these variants focus on more realistic scenarios in which voters may have different competences, and in which some voters might possibly be incompetent, i.e., more likely to vote for the wrong option (probability < $0.5$) (Dietrich 2008; Owen et al. 1989).

Discussion groups that are competent on average have particularly interesting features to analyse from a truth-tracking perspective. First, such groups can contain agents that have a higher degree of belief in the incorrect answer: in the context of tracking truth, we can then investigate under which conditions group discussion leads those initially incorrect agents to strengthen, weaken or reverse their prior incorrect beliefs. Second, on average competent groups can contain an initial majority of agents that support the incorrect side of the issue: this will allow us to investigate under which conditions initially incorrect majorities are overturned or retained as a result of discussion.

Since we mentioned Condorcet’s Jury Theorem, it is important to note that we do not interpret agents’ degrees of belief as competence in the sense of this theorem, i.e., competence as a person’s probability of voting for the correct answer. In our setting, we take an agent’s degree of belief as an indicator of accurate voting, namely correct if their belief level is higher than $1/2$, otherwise incorrect.

Before the start of the discussion, each agent is also assigned a specific positive number strictly smaller than $1$, representing its individual radicality parameter $\gamma$ discussed in the previous section. The model encodes three distinct procedures for assigning values of $\gamma$ to the discussants. The first option consists in assigning the same value for $\gamma$ to all agents; this way the resulting group of individuals is homogeneous with respect to the radicality parameter.

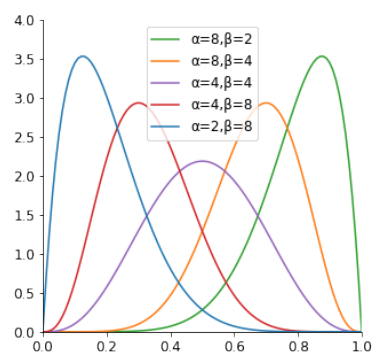
The second option is to assign agents values drawn from a $\beta$-distribution, that can be fixed by assigning values to the parameters $\alpha$ and $\beta$. In this way, we can generate a group of discussants that is heterogeneous with respect to the radicality parameter, where the values for $\gamma$ are drawn from a distribution which is the same for the entire group of discussants. Figure 6 plots examples of $\beta$-distributions produced by different values for the parameters $\alpha$ and $\beta$.

**Figure 6.** This figure plots some examples of different $\beta$-distributions, determined by different values of the parameters $\alpha,\beta$.

The third option is to generate two distinct $\beta$-distributions, one fixing the distribution of the radicality parameter in the group of agents having a higher prior degree of belief in the correct alternative, and the other fixing the distribution of the parameter in the group of agents with a stronger degree of belief in the incorrect answer. This option allows us to model situations in which the correct/incorrect subgroups of discussants show different radicality of the myside bias.

The discussion process

Discussion among agents is modelled in a novel way compared to the preexisting models that we have mentioned in Section 2. This is so for two reasons. First, the existing models are often enriched with a multiplicity of aspects characterising real-world argumentative dynamics (e.g., different network topologies Zollman 2007; Alvim et al. 2021; Gabriel & O’Connor 2022, or the reliability of agents and information Hartmann & Rafiee Rad 2018; Hahn 2022). Including these refinements in our modelling could hinder our scope to specifically analyse the effect of myside bias on group discussion, and therefore a simpler model may better serve our purpose.

Second, our model can provide a novel basic framework within which to study argumentative dynamics in groups. As mentioned in the previous section, in our framework, arguments are propositional random variables, each of which is associated with a likelihood ratio representing its diagnostic value. In our model, the agents discuss by directly exchanging these likelihood ratios with one another. This approach is rather novel compared to other computational models of group discussion or information exchange between agents, where they typically exchange positive/negative signals of equal strength (see, e.g., Ding & Pivato 2021; Mäs & Flache 2013), or simply take as information one another’s beliefs (see, e.g., Hegselmann & Krause 2002 and Alvim et al. 2019).

The discussion begins by randomly drawing a first speaker. The first speaker draws an argument and presents it to the other agents. Depending on its prior beliefs, the agent presents:

an argument in support of the correct alternative (likelihood ratio strictly smaller than $1$), if the agent’s prior is $b> 1/2$;
an argument in support of the incorrect alternative (likelihood ratio strictly bigger than $1$) if the agent’s prior is $b< 1/2$;
no argument if the agent’s prior is $b= 1/2$.

In our setting, agents pick their arguments by drawing the corresponding likelihood ratio from a distribution that is fixed at the start, and that is common for all agents. We can think of a specific distribution over the space of likelihood ratios as determining the argumentative competence of the agents, i.e. the ability of an agents to present stronger or weaker arguments in support of their preferred alternative. Indeed, the distribution determines which likelihood ratios are more likely to occur and which are less likely: this way, stronger arguments might be made more frequent than weaker arguments, or vice versa, by manipulating the parameters of the distribution.

For the specific results that we present in this paper, we assume that stronger and weaker arguments are equally likely to be drawn by a given agent; to put it differently, very convincing arguments can occur as often as weakly convincing arguments. We furthermore assume that this is the case for both initially correct and initially incorrect agents, i.e., agents with $b>0.5$ can pick any argument confirming the correct side of the issue, and agents with $b<0.5$ can pick any argument disconfirming the correct side of the issue. Furthermore, we do not assume any difference in competence between agents with $b>0.5$ and agents with $b<0.5$, i.e., we ensure that the likelihood for a correct agent to pick a confirming argument with corresponding likelihood ratio $x<1$, is the same as the likelihood for an incorrect agent to draw a disconfirming argument with corresponding likelihood ratio $1/x>1$. We will have more to say about these specific choices in Section 6.

Let us now comment on our modelling choice concerning the mechanism with which agents present arguments relevant for the issue under discussion. In particular, note that agents that prefer either one of the alternatives to the target issue will exclusively present arguments in favour of the alternative they prefer. Note that, modelled this way, argument production is itself subjected to a form of myside bias: the prior beliefs of an agent determine the set of possible arguments that an agent can share with the other discussants (Mercier 2017; Mercier & Sperber 2017).

Our choice to model argument production in this way is rooted in the argumentative theory of reasoning developed in Mercier & Sperber (2017), which claims that participants in a discussion aim at persuading others of their own belief, rather than cooperatively evaluating reasons in favour and against the target issue together with the other discussants.

As a consequence, this theory predicts that participants in a discussion only present arguments that favour their own prior position (or disfavour contrasting positions) on the discussion topic, while avoiding contrasting arguments. Indeed, by presenting this latter type of arguments, an agent would risk swaying the rest of the discussants towards opposite views to its own, thus not serving the purposes to convince other discussants of its own view. This prediction has been observed in a number of empirical studies (Mercier 2017; Mercier & Sperber 2017; Trouche et al. 2014).

As already mentioned in Banisch & Olbrich (2021), we remark that a more general way to model argument production would be to implement a parameter that regulates how much more likely an agent is to present prior-compatible arguments than to present prior-incompatible arguments. Furthermore, this parameter could be made prior-dependent so as to model different degrees of biased argument production, where, for instance, agents with more extreme opinions are more biased than agents with milder opinions. Including such a mechanism of argument production in our model would allow for a more fine-grained analysis of the interaction between myside-bias in argument evaluation and myside-bias in argument production. We leave an extension of our model in this direction for future work.

After the argument is presented, all the other agents update their prior belief in light of the given argument, according to the update rule given in Equation 3. The discussion proceeds by repeating this process, until any further change in the agents’ beliefs is highly unlikely to occur. More precisely, we stop the simulation when: all agents with $b > 1/2$ have degree of belief $b>0.99999$; and all agents with $b < 1/2$ have degree of belief $b < 0.00001$; and there is no agent with degree of belief $b = 1/2$.

Tracking truth and monitoring discussion

As mentioned earlier, we are primarily interested in the truth-tracking ability of groups of myside-biased agents, and on whether group discussion is epistemically detrimental or beneficial.

Note that, in our framework, the truth-tracking ability of a group cannot simply be defined as its ability to converge unanimously to the correct answer such as in the case of the moderate bias in Gabriel & O’Connor (2022), or in Zollman (2007), Hegselmann & Krause (2002). Indeed, in our setting, a group discussion might end up in one of the following three states: correct consensus, in which all agents agree on the correct answer; incorrect consensus, in which all agents agree on the incorrect answer; no consensus, in which all agents strongly believe in different alternatives. By consequence, there might be situations in which some agents entertain extremely high degrees of belief in the correct answer, while other agents simultaneously entertain extremely high degrees of belief in the incorrect answer.

Directly mirroring the experiments in Mercier & Claidière (2022), and in the spirit of Condorcet, we decide to focus on the effect of myside-biased discussion on belief aggregation via the majority rule. In other words, we investigate under which condition discussion is beneficial or detrimental for a majority of the agents to entertain the correct belief. Within this perspective, we can think of our model as a model of collective decision making in the sense of Dryzek & List (2003), Dietrich & Spiekermann (2022), where agents undergo a deliberation phase, during which they communicate and revise their beliefs, and a post-deliberation phase, during which the agents’ revised beliefs are aggregated according to a decision rule, the majority rule in our case.

From the perspective of belief aggregation via majority rule, we will investigate the following: first, under which conditions initially correct majorities are retained and, simultaneously, initially incorrect majorities overturned; second, under which conditions correct majorities are more likely before or after discussion.

To explain the epistemic effects of discussion in biased groups at the level of belief aggregation via the majority rule, it is also crucial to monitor some more general aspects of group discussion. In particular, we consider how many agents change their mind, both among agents initially holding correct beliefs and among those initially holding incorrect beliefs. This is crucial, because it allows us to understand what types of conversation produce the epistemic effects observed at the level of belief aggregation via the majority rule. For instance, this type of information enables us to know whether, for a given discussion group, changes in the likelihood of correct/incorrect majorities after discussion are to be attributed to an effective and virtuous group argument exchange of the kind envisioned by Mercier & Sperber (2017) and Gabriel & O’Connor (2022), or to an effective but vicious group discussion where correct agents are swayed to prefer the incorrect beliefs as in Hahn et al. (2019), or to a context of ineffective argument exchange in which agents do not change their minds and simply strengthen their initial stance.

Results

In this section, we present the results of a number of experiments performed using the agent-based model of group discussion that we have just presented. We will proceed in the following three steps. First, we present the results of experiments of groups in which the radicality parameter $\gamma$ is distributed homogeneously among the agents, i.e., all agents are assigned the same value of $\gamma$. Second, we present a number of results from experiments on heterogeneous groups in which the parameter $\gamma$ is distributed according to a given initial distribution that is the same across the group of initially correct agents, i.e., those agents that hold the correct belief before the discussion, as well as across the group of initially incorrect agents, i.e., those agents that initially hold the incorrect belief. Finally, we present results performed on heterogeneous groups of agents in which the parameter $\gamma$ is distributed differently across initially correct agents and initially incorrect agents.

Let us briefly recall that in the experiments below, we considered on average competent groups of agents, whose prior beliefs are drawn from a uniform distribution. This implies that already at the start of the conversation some agents might be rather opinionated, i.e., their beliefs might be closer to the extremes $0$ or $1$ than to the neutral point $0.5$. In this regard, we remark that a preliminary exploratory analysis conducted on groups whose priors are drawn from a $\beta$-distribution more or less sparse around the average $0.5$ suggested qualitatively alike results to the ones we present below. As an example of a difference in magnitude, let us mention that groups whose priors are drawn from a $\beta$-distribution less sparse around the average $0.5$ are more likely to reach a consensus after discussion compared to the groups that we consider below. This is an unsurprising consequence of the fact that, as the agents’ priors become more similar and approach the neutral point $0.5$, the disagreement between agents in the evaluation of the evidence decreases.

**Figure 7.** Examples of a converging macro-level dynamic (a), and of a bipolarising macro-level dynamic (b).

Two kinds of pattern can characterise the macro-level dynamics of group discussion for all types of groups that we considered (homogeneous groups, heterogeneous groups with a common radicality distribution, and heterogeneous groups with two distinct radicality distributions). The first kind of macro-level pattern is characterised by the convergence of the agents’ beliefs towards very high or very low degrees of belief in the correct answer. This pattern typically results from discussion in groups of smaller size with only mildly radical agents; for instance, as illustrated in Figure 7(a), in homogeneous groups this pattern is frequent for small group sizes where the radicality parameter $\gamma$ is smaller than $0.3$.

The second pattern that we registered is that of bipolarisation, illustrated in Figure 7(b), which occurs in larger discussion groups, or in groups with strongly biased agents. For the case of homogeneous groups, bipolarisation becomes the most frequent pattern, for instance, if a group of mildly biased agent (generally, $\gamma<=0.3$) is large enough, or if agents become more radical.

We also note that in the experiments we conducted, conversations can be rather short also in larger groups and they can converge to a consensus or a non-consensus state quite fast. This is an unsurprising consequence of the fact that agents are as likely to present stronger arguments as to present weaker arguments in support of their case: when very strong reasons are presented, then conversations can be rather quick and sway many discussants to support the arguer’s side. On the other hand, when less decisive arguments are provided, the conversation can last longer and be more divisive. Again, we found that simulations where weaker or stronger arguments (confirmatory and disconfirmatory) were made more or less frequently showed qualitatively alike trends to the cases we analyse below, in which arguments of different strength are equally likely to occur.

In each of the experiments below, we analyse the data taken from 30,000 iterations of the simulation for each given pair of group size and distribution of the radicality parameter $\gamma$.

Experiment 1: Homogeneous groups

As stated above, we conducted a first experiment on homogeneous groups of agents, where all agents are assigned the same value of the radicality parameter $\gamma$. Recall also that the priors of the agents are drawn from uniform distributions, and that arguments of all strengths are equally likely to be drawn. We run simulations for groups of different sizes ($11, 21, 31, 51, 101, 301$ and $501$) and different values of $\gamma$ ($0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8$ and $0.9$), where $0$ means ‘no bias’. Note indeed that Equation (3) and Equation (1) are equivalent if we assign the value $0$ to $\gamma$. Indeed, if we plug in $0$ for $\gamma$ in the expression of the perceived likelihood ratio $x'$ given in Definition 1, we obtain that $x'(x,b) = x$, for any value of $b$. In turn, by plugging in $x$ for $x'(x,b)$ in Equation (3), we obtain Equation (1). Thus the case of a non-biased update can be recovered as a myside-biased update where $\gamma$ is assigned value $0$.

Effects of myside bias and group size on the discussion

Let us now analyse the effects of myside bias on several features of the discussions that agents conduct. We start by looking at the distribution of correct, incorrect and no consensuses for each combination of group size and value of $\gamma$, which is summarised in Figure 8.

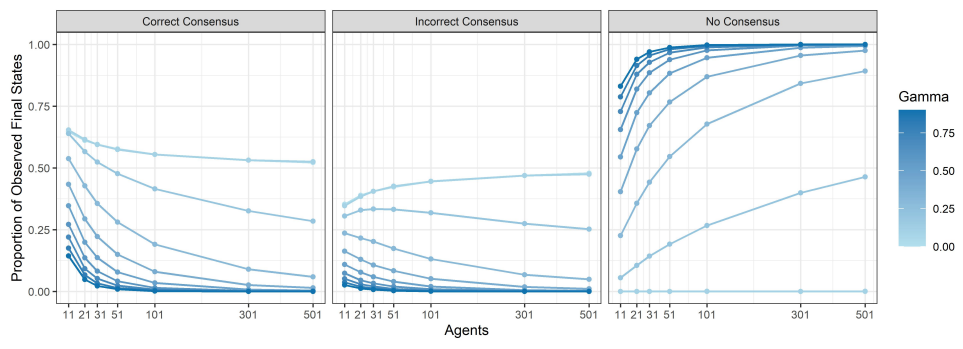
**Figure 8.** Proportions of correct consensus (left), incorrect consensus (center), and no consensus (right), for each group size (horizontal axis) and value of $\gamma$, with increasingly darker shades of blue indicating higher values of $\gamma$. The results are proportions over 30000 repetitions for each combination of group size and value of $\gamma$.

Two effects can be clearly observed, one determined by the parameter $\gamma$ and the other determined by group size. First, for a fixed value of group size, as the value of $\gamma$ increases (moving from lighter to darker shades of blue), non-consensus states become generally more frequent. It is, however, worth noticing that there is no substantial difference between the no-bias case and the case in which $\gamma=0.1$ (the two lines overlap), although for $\gamma=0.1$, a minuscule number of non-consensus states has been observed. This is consistent with the fact that cases without bias and cases with $\gamma > 0$ are qualitatively different in that if there is no bias, then a consensus state will always be reached.

Second, for a fixed value of $\gamma > 0$, as group size increases, non-consensus states become more likely, with both correct consensuses and incorrect consensuses becoming less frequent. Nevertheless, if we look at the case of $\gamma = 0.1$, non-consensus states are hardly ever reached. In such a case, as group size increases, the number of correct consensuses decreases, while the number of incorrect consensuses increases.

The considerations above suggest the following picture. First, the more radical actors become, the more difficult it is for them to agree on one side of the issue, whether it is the right side or the wrong side. Moreover, this inability to reach consensus seems to have a similar effect on the ability to converge to a correct answer as it does on the ability to converge to an incorrect answer, i.e., for a fixed group size, there is no noticeable difference in the way the number of correct consensuses and incorrect consensuses decreases with increasing radicality. On the other hand, at least for low levels of radicality, it appears that increasing the group size of discussants gives the incorrect consensus an advantage over the correct consensus.

We can better understand these effects by considering how discussion changes for different values of $\gamma$ and group sizes, which we summarise in Figure 9. Figure 9 shows, for each combination of $\gamma$ and group size, the proportion of correct and incorrect discussants at the beginning of the conversation who maintained their initial position on the topic at the end of the discussion.¹ Again, two clear effects can be seen, one determined by the value of $\gamma$ and one by group size.

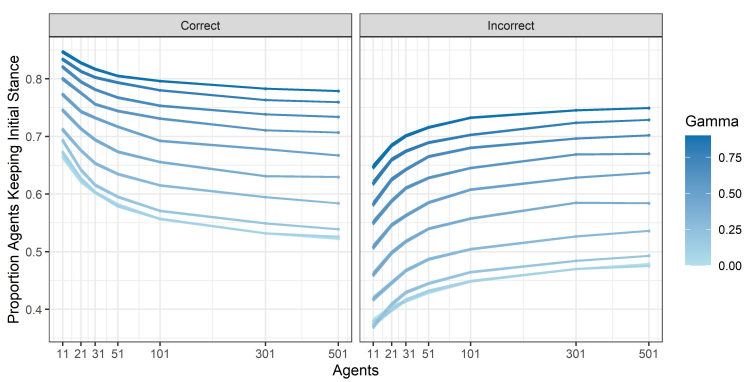
**Figure 9.** Proportion of agents that do not change their initial position on the issue at the end of a discussion, for each combination of group size ($x$-axis) and value of radicality $\gamma$, with increasingly darker shades of blue indicating higher values of $\gamma$. The left panel plots the proportion for the agents that are correct at the start, and the right panel plots the proportion for the agents that are incorrect at the start. Values of the proportions are on the $y$-axis, and the thickness of lines represents the $99\%$ confidence interval around the observed value. The proportions are computed over $30,000$ repetitions for each combination of group size and value of $\gamma$.

First, it is clear that, for fixed group size, as the value of $\gamma$ increases (moving from lighter to darker shades of blue), more and more agents keep their initial stance. This is true for both those agents that are initially correct and for those agents that are initially incorrect.

So far, it seems that the effect of increasing the radicality of the agents mainly impacts the effectiveness of the discussion to actually change the agents’ minds. As agents become more radical, arguments become less of a determinant factor in the way agents form their beliefs.

The second effect has to do with group size. In particular, we observe that, for a fixed value of $\gamma$, as group size increases, the proportion of initially correct agents that mantain their initial correct belief decreases (left panel of Figure 9). This means that, as group size increases, the proportion of initially correct agents that are swayed into adopting the incorrect belief increases; at the same time, the proportion of initially incorrect agents that stick with their initially incorrect belief increases (right panel of Figure 9).

As the size of the discussion group increases, no matter how radical in their bias the agents are, increasingly more agents that are correct are persuaded of the incorrect alternative, while less incorrect agents are persuaded to switch to the correct alternative. This is an effect of the fact that, while in smaller groups, the proportion of initially correct agents is often considerably larger than that of the initially incorrect agents, on average competent groups of larger sizes do not have this feature. Thus, as group size increases, incorrect agents become increasingly more likely to speak at the beginning of the conversation. As a consequence, in larger groups, initially incorrect agents are more often able to anchor agents with milder preferences for the correct side of the issue into favouring the incorrect side of the issue. This anchoring effect is a result of the non-commutativity of the update rule determined by Equation 3, which we will discuss in more detail in the Section 6.

To sum up, our findings on the results of myside bias and group size in group discussions were two-fold: first, we noticed that increasing the radicality of the bias leads on average more agents to stick with their initial beliefs, which in turns translates into non-consensus states being the increasingly more frequent outcome of a discussion; second, we found that as group size increases, initially correct agents tend on average to be more often swayed to the incorrect side of the issue, which has the effect of making correct consensuses increasingly less frequent in favour of incorrect consensuses.

The effects on truth-tracking

Recall that we are interested in the impact of group discussion on belief aggregation based on majority rule. In particular, we are interested in understanding whether discussion is detrimental or beneficial to collective decisions determined by majority rule. In this direction, we start by looking at the average proportion of correct majorities that are retained after discussions, and the number of correct majorities that are lost after discussions. We do the same for those majorities that are incorrect at the start, i.e., for those cases in which the majority of the group favours the incorrect alternative. This way we obtain an overview of the ability or inability of group discussion to retain old correct majorities and acquire new correct majorities.

Results are shown in Figure 10. As for the case of the feature of the discussion, we unsurprisingly observe a clear effect of group size on the proportion of retained correct majorities. Indeed, for a fixed value of the radicality of the bias, we see that, as group size increases (from the leftmost panel to rightmost), the proportion of initially correct majorities that are retained decreases. On the other hand, increasing group size seemingly leaves the proportion of the retained incorrect majorities almost unaltered, except for high values of $\gamma$.

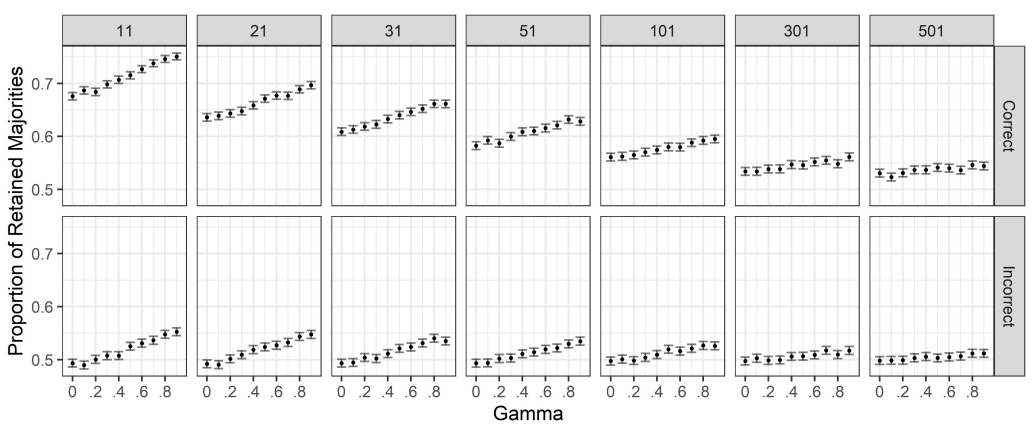
**Figure 10.** The proportion of correct majorities at the start (Correct) and the proportion of incorrect majorities at the start (Incorrect) that are retained after discussion, for each combination of group size (on top) and value of $\gamma$ ($x$-axis). Proportions ($y$-axis) are computed over $30,000$ repetitions for each combination of majority type (Correct, Incorrect), group size and value of $\gamma$, and are plotted with the $99\%$ confidence interval around the observed value.

This suggests that larger groups perform worse than smaller groups when it comes to obtaining correct majorities during a discussion. This is consistent with the fact mentioned above that as group size increases, it becomes more likely that an originally correct representative with a less strong conviction will switch to the wrong alternative.

We also find that for smaller group sizes, the number of correct majorities that are retained increases as the bias of the agents becomes more radical; simultaneously, we observe that this effect disappears in larger groups. Similarly, the number of false majorities that are retained also appears to increase with the same trend. Again, this points to the fact observed above that the discussion becomes less effective as the representatives become more radical. On the other hand, as group size increases, the proportion of both correct and incorrect majorities that are retained does not change with the value of $\gamma$.

Finally, we measured the proportion of correct majorities after discussion (Figure 11), and we then compared it with the proportion of correct majorities before discussion. Comparing the proportion of correct majorities before discussion to the proportion of correct majorities after discussion is useful in giving us an indication of how likely it is to have a correct majority before the conversation versus after the conversation. This helps us to check under which conditions, if any, discussion in groups is more beneficial than mere belief aggregation via majority rule before discussion.

In order to estimate the likelihood of correct majorities before discussion, we calculated, for each group size, the proportion of correct majorities before the start of the discussion and checked whether there were statistically significant differences in their values across different group sizes. The proportions of correct majorities shows a decreasing tendency with increasing group size; the difference in the proportions across group sizes was found to be significant between groups of $11$ agents and group sizes greater than or equal to $31$ agents, and between groups of $21$ agents and group sizes greater than or equal to $101$.²

We then noticed that the range of the values assumed by the proportion of correct majorities before discussion across different group sizes is very small ($0.842\pm0.002$ ($99\%$ confidence) for $11$ agents, and $0.833\pm0.002$ ($99\%$ confidence) for $501$ agents), while the range of the values assumed by the proportion of correct majorities after discussion across different group-sizes is much larger (for instance, for $\gamma=0$, $0.647\pm0.007$ ($99\%$ confidence) for $11$ agents, and $0.522\pm0.007$ ($99\%$ confidence) for $501$ agents). For these reasons, in order to simplify our analysis, we computed the proportion of correct majorities at the start over the aggregate data of all group sizes, and found it to be approximately $0.836$ ($\pm0.001$, $99\%$ confidence). We then took this aggregate value to represent the likelihood of a correct majority before discussion for any group size, and used it as a benchmark against which to compare the likelihood of correct majorities after discussion. Indeed, given the much larger scale of the differences in the proportion of correct majorities after discussion (compared to the differences before discussion) across different group sizes, this aggregate value still allowed us to meaningfully detect group-size dependent effects on the likelihood of correct majorities after discussion compared to their likelihood before discussion.

The proportion of correct majorities after discussion is reported in Figure 11. First, note that for all combinations of group size and radicality of the bias, the proportion of correct majorities after discussion is never above the aggregate average value of $0.836$. This means that correct majorities are always less likely after a discussion than before the discussion. This is true for groups with unbiased discussants as well as for groups with biased discussants.

Second, the proportion of correct majorities after discussion decreases significantly as the group size increases (from the plots on the left to the plots on the right). This suggests that in homogeneous groups, discussions not only cause correct majorities to become less frequent, but they become less frequent as the size of the deliberating group increases. This is consistent with what we said above about the detrimental effect of discussions in larger groups.

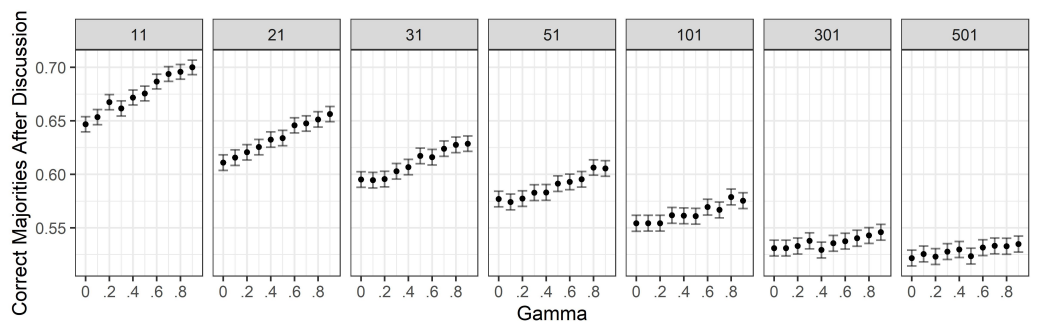
**Figure 11.** This figure plots, for each group size (top) and value of $\gamma$ ($x$-axis), the proportion of correct majorities after the discussion, with $99\%$ confidence intervals around the observed value. Values of the proportions are on the $y$-axis. The proportions are computed over $30,000$ repetitions for each combination of group size and value of $\gamma$.

As for the radicality of the agents, the data suggest a clear pattern. Increasing radicality among the discussants determines an increase in the proportion of correct majorities after discussion. In other words, the more radically biased the discussants, the more likely correct majorities become. This effect gradually fades away in increasingly larger groups of agents, where no statistically significance difference is observed among different values of $\gamma$: this is consistent with the pattern observed in Figure 10.

Should we conclude from this that the myside bias is beneficial for collective truth-tracking via discussion, at least in smaller groups? On the one hand, it is true that increasing the radicality of the agents increases the likelihood of a correct majority after discussion in small groups of agents; however, our analysis above suggests that this happens at the expenses of effective communication. In particular, we found above that, as agents become more radically biased, fewer agents change minds during the discussion, while more and more agents retain their initial positions, regardless of the information shared by the other agents. This, in turn, reflects at the collective level in the fact that fewer majorities that were correct at the start are lost during a discussion.

In summary, the pictures of the effects of myside bias in group discussion depicted above is multi-faceted. First, group discussion per se is rather detrimental to collective truth-tracking via majority rule, regardless of the radicality of agents’ biases, with discussion in bigger groups being significantly more detrimental than discussion in smaller groups. Second, while having no epistemic effects on bigger groups, the myside bias slightly increases the likelihood of correct majorities after discussion in smaller groups, but does so for the wrong reasons: the higher number of correct majorities observed after discussion is not the result of a virtuous argument exchange as envisioned in Mercier & Sperber (2017), but it rather results from an inhibition of mind-changing communication, which reduces the overall loss of correct majorities that group discussion seems to bring about. Finally, any effect of myside bias on truth-tracking via majority aggregation fades away as discussion groups become larger, and, overall, group discussion is a better truth-tracker in smaller than in bigger groups.

Experiment 2: Heterogeneous groups with a single common radicality distribution

The second set of experiments is conducted with groups in which the radicality parameter $\gamma$ is heterogeneously distributed across agents and follows a single distribution that we specify at the beginning of the simulation. This set of experiments is motivated by the idea that discussions in the real world might take place between discussants who differ in how radically they are biased.

As mentioned above, we used $\beta$-distributions to determine how the radicality parameter $\gamma$ is distributed across agents. We did this by setting three different mean values for the radicality that a group can have ($0.2, 0.5$ and $0.8$), and we then generated sets of $5$ different $\beta$ distributions for each given mean (by setting the parameters $\alpha,\beta$ to produce distributions with the given mean). In this way, we were able to compare distributions with different means as well as distributions with the same mean that differ in dispersion (measured by the variance).

Our results regarding the frequency of correct, incorrect, and non-consensus states are shown in Figure 12. A number of clear effects emerge, each related to the mean of the $\beta$ distributions, the dispersion around the mean of the $\beta$-distributions, and the group size.

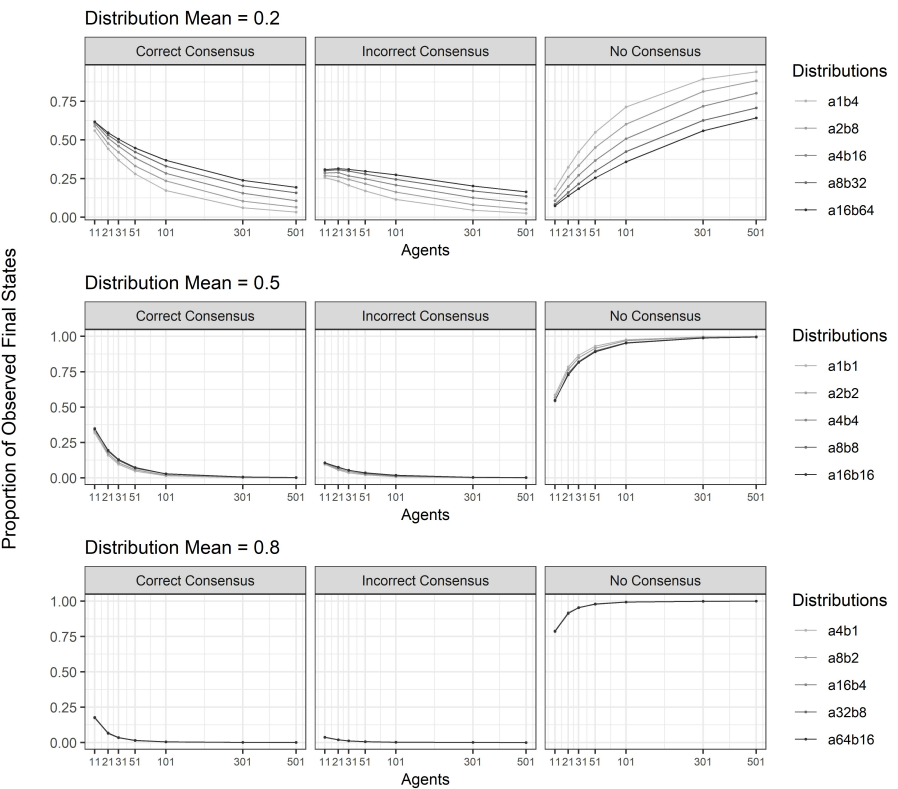
**Figure 12.** Each group of three horizontally adjacent panels reports the proportions of correct consensus (left), incorrect consensus (centre), and no consensus (right) for a set of distributions of radicality $\gamma$ (legend on the right of each group of three horizontal plots) with the same mean (top left of each each group of three horizontal plots). Within each set of distributions with the same mean, the distributions are ordered in descending order of variance (the top distribution has the highest variance and the bottom distribution has the lowest variance). Proportions ($y$-axis) are results of $30,000$ repetitions for each group size and distribution of $\gamma$.

Let us proceed in order. First, for fixed group size, $\beta$-distributions of $\gamma$ with higher averages (from the top plot to the bottom plot) are overall characterised by a higher proportion of discussions ending in non-consensus states. This means that as a group of discussants becomes on average more radically biased, they will agree less often on either side of the issue.

Second, looking at $\beta$-distributions with average $0.2$ (blocking the top three panels), we see that as the dispersion around the mean decreases (moving from lighter to darker lines), the proportion of non-consensus states decreases. This effect is robust across different group sizes. This effect becomes weaker as the average of the $\beta$-distributions becomes higher, with distributions with mean $0.8$ seemingly showing no effect.

The effect of decreasing dispersion around the mean can be explained by the fact that a larger dispersion of radicality $\gamma$ means a higher probability that some discussants are very radical. This, in turn, leads to a higher probability that the discussion will end in a state where the discussants still disagree on which side of the issue is the correct one. This is true for distributions with lower average, as decreasing dispersion equates to increasingly weaker radicality among discussants, who are thus more likely to change their minds during the discussion. However, this is not to be expected for distributions with a high average: in such cases, a decrease in dispersion actually means that weakly radical discussants are rarer and the discussion is led by more and more agents who have a stronger radical bias.

Third, we see that, as for the case of homogeneous groups, increasing group size determines a clear decrease in correct consensus states for heterogeneous groups as well. This effect is stable across distributions with different dispersion and different averages. We also notice that, for low-enough dispersion around the mean $0.2$, the proportion of incorrect consensus initially increases with group size, and then decreases. In addition, we observe overall that, as group size increases, there is a larger loss in correct consensuses than in incorrect consensuses.

In these experiments, we do not plot the mean proportion of agents retaining or changing their initial position for a given distribution of $\gamma$ and limit ourselves to making the following two observations, which are in line with what we observed above about the effects of dispersion on the reachability of different consensus states. First, for distributions of $\gamma$ with the same mean, as the dispersion around the mean decreases, the proportion of agents retaining or changing their initial position (for both initially correct and initially incorrect agents) tends to approximate the proportion observed in the case of homogeneous groups in which the radicality parameter $\gamma$ of all agents is the mean of the distributions. Second, the effects of decreasing dispersion around the same mean on the proportion of agents retaining their initial beliefs vary with the mean of the distribution. In general, decreasing dispersion around lower values of $\gamma$ will tend to decrease the proportion of agents that keep their initial stance, due to the elimination of higher values of $\gamma$. On the other hand, decreasing dispersion around higher mean values of $\gamma$ generally produces an increase in agents retaining their initial beliefs, due to the exclusion of more moderate values of $\gamma$.³

What about truth-tracking? In Figure 13 we plot the proportion of correct majorities after discussion, for each distribution of the $\gamma$ with mean $0.2$, for each group size. We included for each group size the data point corresponding to the cases where $\gamma = 0.2$ is homogeneously distributed across the agents (red point in each plot). Results are qualitatively the same for the sets of distributions with mean $\gamma = 0.5$ and $\gamma = 0.8$.

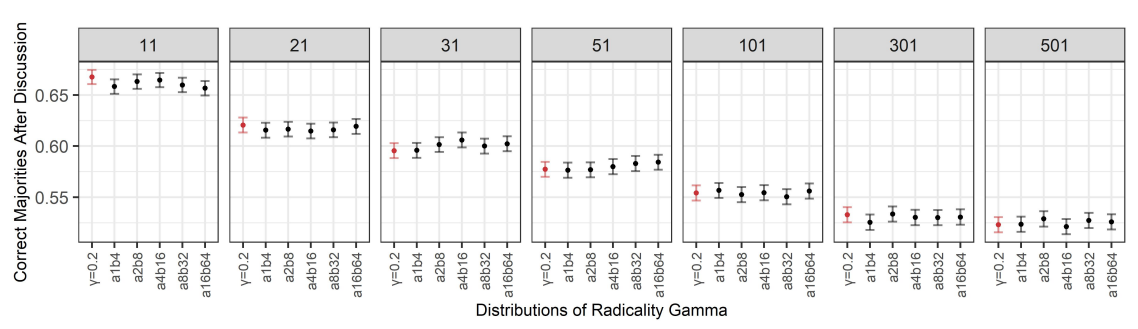
**Figure 13.** A comparison of the proportion of correct majorities after discussion of homogeneous groups with $\gamma=0.2$ with those of groups with different $\beta$-distributions with mean $0.2$ applying to both initially correct and initially incorrect arguers, for each group size (top). The specific $\beta$-distributions are indicated on the $x$-axis, with the label $\gamma=0.2$ indicating homogeneous groups. Again, data are taken from $30,000$ repetitions of the simulation for each combination of group size and distribution of $\gamma$.

Considering the proportion of correct majorities after discussion, we see that heterogeneously distributing the radicality parameter does not affect the proportion of correct majorities after discussion, and even that the likelihood of a correct majority after discussion for cases of heterogeneous groups with radicality mean $0.2$, does not differ from the case where agents in the group are homogeneously biased with radicality parameter $0.2$. This effect is robust across all group sizes.

The absence of an epistemic effect of different dispersions for distributions with the same mean fits well with our observations on homogeneous groups, namely that the myside bias primarily affects the extent to which the discussion is able to change opinions. We therefore have reason to believe that as long as the distribution of the bias is the same for all agents, regardless of whether they were initially right or wrong, changes in radicality affect all agents in the same way. As a consequence, also in this case, an increase in radicality inhibits mind-changing communication, while possibly minimizing the loss in correct majorities that group discussion seems to produce.

Experiment 3: Heterogeneous groups with different distributions among initially correct and incorrect agents

In the first and second set of experiments, we showed that the myside bias in the evaluation of arguments tends to inhibit discussants and makes them less likely to change their minds, and that initially wrong and initially right agents are similarly affected. In addition, we saw that, in smaller groups, this inhibitory effect can increase the probability of a correct majority at the end of a discussion in smaller discussion groups, by reducing the loss in correct majorities that group discussion creates. We also found that this effect tends to disappear with increasing group size. Accordingly, a larger group appears to disadvantage correct reasoners while favoring incorrect ones by making correct reasoners more prone to switch to the wrong side of the issue.

In light of these results, we conjecture that myside bias can produce mind-changing argument exchange, in those cases where its radicality is distributed differently across initially correct reasoners and initially incorrect reasoners. In turn, we then expect to observe epistemically beneficial or detrimental effects on collective truth-tracking via majority rule, depending on whether the bias is more radical among agents that are initially correct agents or agents that are initially incorrect.

We tested this hypothesis with a number of experiments where we differentially varied the distributions of radicality of the agents that are correct at the start, and of those that are incorrect at the start. This was done by running the simulation using pairs of $\beta$-distributions (one for the initially correct agents and one for the initially incorrect agents) whose means are progressively further apart. For doing this, we used pairs of distributions whose parameters $\alpha$ and $\beta$ are inverted from one distribution to the other (e.g., $\alpha_1=5$ and $\beta_1=2$, and $\alpha_2 = 2$ and $\beta_2 = 5$, where the subscripts denote two different distributions).

In the analysis that follows, as well as in the plots, we denote the pair of distributions by writing first the parameter $\alpha_{cor}$ followed by the parameter $\beta_{cor}$ fixing the distribution of $\gamma$ across initially correct agents, then the parameter $\alpha_{inc}$ followed by the parameter $\beta_{inc}$ of the distribution of $\gamma$ for initially incorrect agents. For example, if the distribution for the initially correct agents has $\alpha_{cor} = 5$ and $\beta_{cor} = 2$, and the distribution for the initially incorrect agents is $\alpha_{inc} = 2$ and $\beta_{inc} = 5$, then we denote the pair as $(5, 2, 2, 5)$.

We report results of the experiments for the following pairs of distributions $(5, 2, 2, 5)$, $(9, 2, 2, 9)$, $(17, 2, 2, 17)$, $(2, 5, 5, 2)$, $(2, 9, 9, 2)$ and $(2, 17, 17, 2)$. Note that the first three pairs $(5, 2, 2, 5)$, $(9, 2, 2, 9)$, and $(17, 2, 2, 17)$ model cases in which the average radicality of agents that are initially correct is higher than that of the agents that are initially incorrect. Moreover, as $\alpha_{cor},\beta_{inc}$ assume higher values, the average of the distributions for initially correct agents becomes higher, and the average of the distributions for initially incorrect agents becomes lower. The second three pairs $(2, 5, 5, 2)$, $(2, 9, 9, 2)$ and $(2,17,17,2)$ model cases in which the average radicality of the agents that are incorrect at the start is higher than that of the initially correct agents; furthermore, as $\beta_{cor},\alpha_{inc}$ assume higher values, the distribution of $\gamma$ for initially incorrect agents has a higher average and the distribution of $\gamma$ for the initially incorrect agents has a lower average.

The remainder of this section considers results based on $30,000$ repetitions for each combination of distribution pair and group size.

Case 1: Initially correct discussants are more radically biased

We start by comparing the effects of the pairs of distributions $(5, 2, 2, 5)$, $(9, 2, 2, 9)$, $(17, 2, 2, 17)$ on the kind of discussions that the agents conduct. Results are summarised in Figure 14 and Figure 15.

**Figure 14.** Proportions of correct consensus (left panel), incorrect consensus (central panel), and no consensus (right panel), for different combinations of group size ($x$-axis) and pair of distinct $\beta$-distributions for the parameter $\gamma$ across initially correct and initially incorrect agents. Each pair of distributions is labelled reporting, in order, the values of $\alpha$ and $\beta$ for the distribution of $\gamma$ in the initially correct subgroup of agents, and $\alpha$ and $\beta$ for the incorrect subgroup of agents. Darker shades of green indicate that distributions in a pair have a higher mean for initially correct agents and a lower mean for initially incorrect agents.

**Figure 15.** Proportion of agents that do not change their initial position on the issue at the end of a discussion, for each combination of group size ($x$-axis) and distribution pairs of radicality $\gamma$ (reported in the legend on the right of the figure). The left panel plots the proportion for the agents that are correct at the start, and the right panel plots the proportion for the agents that are incorrect at the start. Values of the proportions are on the $y$-axis, and the thickness of lines represents the $99\%$ confidence interval around the observed value. The proportions are computed over $30,000$ repetitions for each combination of group size and distribution pairs.

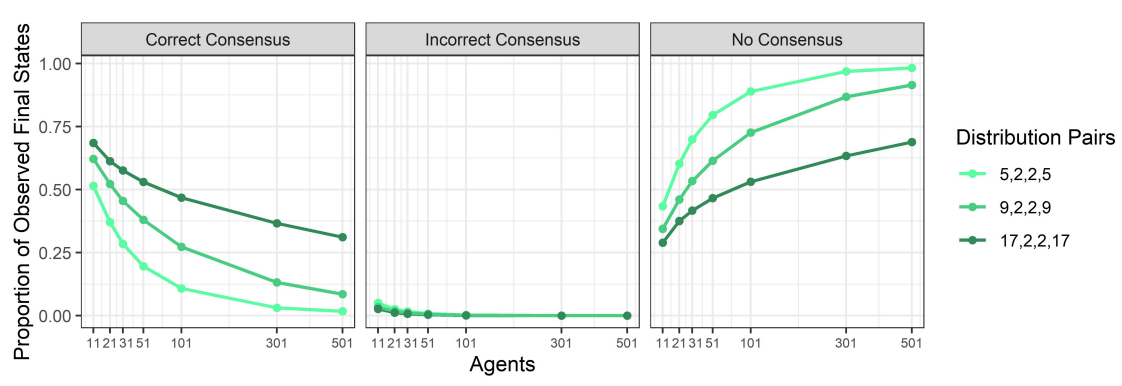
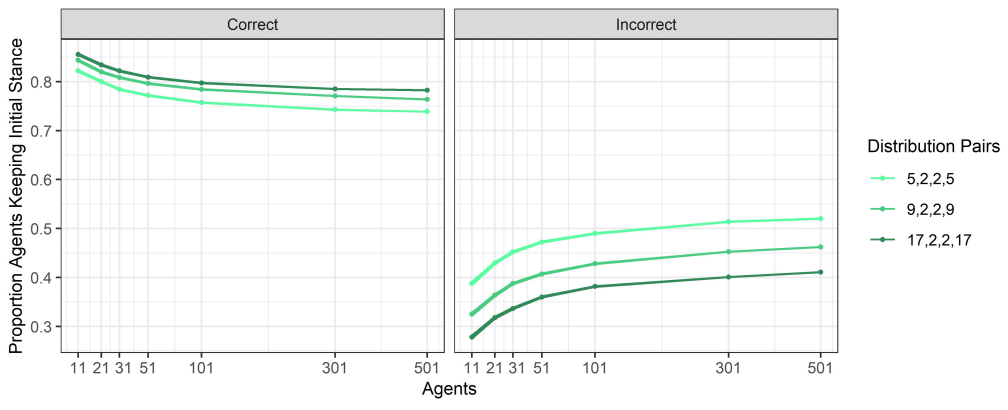
In Figure 14, for a given group size, as the distributions of radicality across initially correct agents moves closer to higher values, and the distribution for the initially incorrect agents moves closer to lower values (moving from lighter to darker shades of green), the numbers of non-consensus states and incorrect consensus states decrease in favour of a higher number of correct consensuses. This suggests that agents not only agree more often, but that they agree more often on the correct answer.

Figure 15 suggests that this is an effect of initially correct discussants being able to sway initially incorrect reasoners on the right side of the issue, and simultaneously to avoid being anchored into endorsing the incorrect side of the issue. Note indeed that, for a fixed group size, the proportion of correct reasoners that stick with their starting correct belief increases (moving from lighter to darker shades of green), while the proportion of incorrect reasoners that stick with the incorrect belief decreases. This means that, as initially correct discussants become more radically biased and initially incorrect discussants become less radically biased, discussions become truth-conducive, making agents more likely to stick with or switch to the correct side of the issue.

Again, we notice that both the effect on consensus and the effect on the discussion reduce significantly with an increase in group size. In Figure 14, we see indeed that, while discussions in groups of $11$ agents terminate in a correct consensus more often than in no consensus, as group size increases, for all three pairs of distributions, correct consensus still remains less likely than no consensus for groups of larger size. Similarly, in Figure 15, as group size increases, an increasingly larger proportion of initially correct agents switches to the incorrect side of the issue, and an increasingly smaller proportion of initially incorrect agents switches to the correct side of the issue, for all three pairs of distributions.

Overall, it seems that by making the initially correct agents more radical than the rest of the agents, we break the symmetry with which the myside bias was affecting correct and incorrect agents in homogeneous groups and in heterogeneous groups with a common radicality distribution. Indeed, while for these groups, increasing radicality would similarly determine an increase in the proportion of agents sticking with their initial opinion across both initially correct and initially incorrect ones, we now see that the behaviors of these two groups differ: while initially correct agents on average stick more often with their initial opinion, initially incorrect agents switch more often to the correct side. By consequence, we would expect this asymmetrical effect of the bias to positively reflect on the truth-tracking abilities of groups. We found that this is indeed the case.

Turning to belief aggregation with majority rule, we again looked at the mean proportion of majorities (correct and incorrect) that are lost or retained in Figure 16, and found two effects. We immediately notice that, for a fixed group size, as the radicality increases among initially correct agents and decreases among initially incorrect agents ($x$-axis of each subplot), we see that increasingly more correct majorities are retained and that increasingly more incorrect majorities are lost. These asymmetric effects on correct and incorrect majorities directly mirror the asymmetric effect on initially correct and initially incorrect discussants.

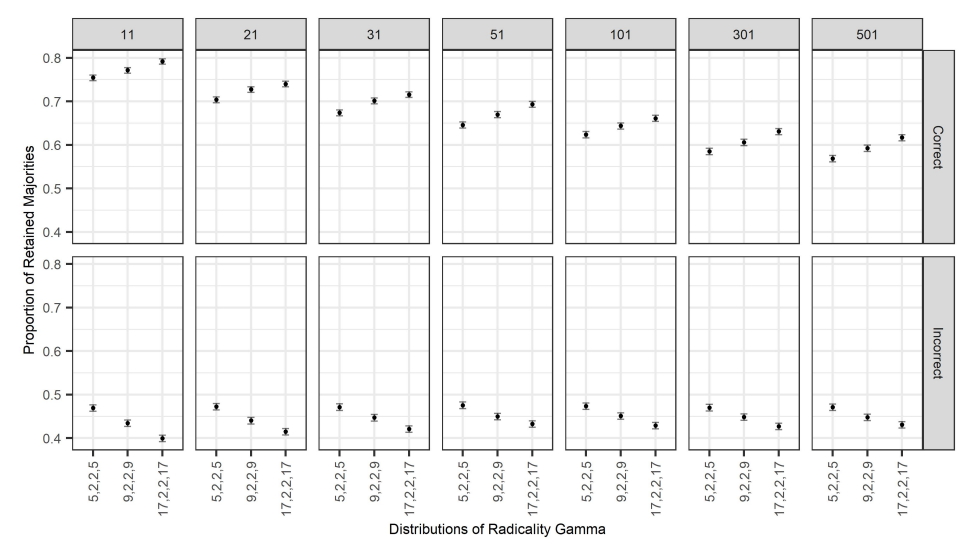
**Figure 16.** The proportion of correct majorities at the start (Correct), and the proportion of incorrect majorities at the start (Incorrect) that are retained at the end of the discussion, for each combination of group size (on top) and pair of $\beta$-distributions for initially correct and initially incorrect agents ($x$-axis), with $99\%$ confidence intervals around the observed values. Values of the proportions are on the y-axis. The mean proportions are averages over $30,000$ repetitions for each combination of majority type (Correct, Incorrect), group size and distribution pairs.

The second effect that emerges is again the harmful effect of discussing in bigger groups, which we have consistently found throughout all experiments so far. For each of the pairs of distributions, as group size increase, the proportion of correct majorities that are retained decreases, while the proportion of incorrect majorities that are retained increases. Again, this is due to the fact that in bigger groups, agents that are initially incorrect are more likely to speak first and anchor mildly radical initially correct agents and make them switch to the incorrect side of the issue.

Increasing the radicality of correct agents and decreasing the radicality of incorrect agents also reflects on the likelihood of correct majorities after discussion, as shown in Figure 17. Indeed, for a given group size (fixing one plot), as the radicalities of correct agents grow further apart from those of the incorrect agents at the start, the proportion of correct majorities at the end of discussion increases, and it also increases compared to the case where agents have no bias.

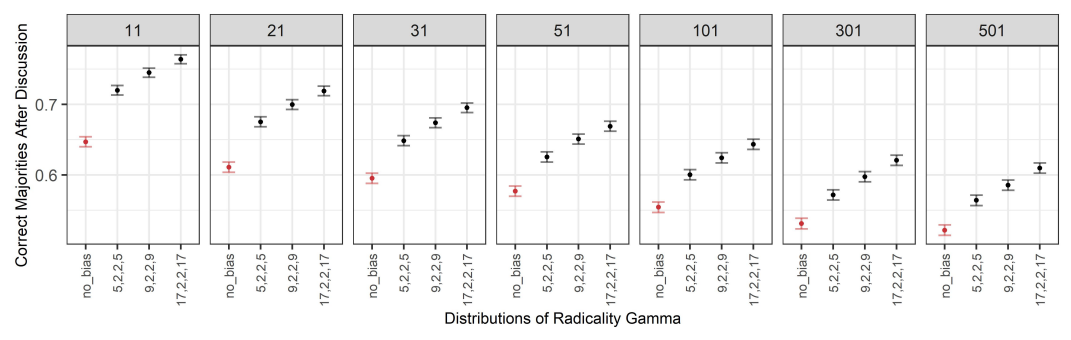
**Figure 17.** This figure compares, for each group size (on the top), the proportion of correct majorities after discussion of homogeneous groups without bias (red data point) with those of groups with different pairs of $\beta$-distributions, for the case in which the $\beta$-distribution for the correct group has a higher mean, with $99\%$ confidence intervals around the observed values. The specific pairs of $\beta$-distributions are reported on the $x$-axis. Again, data are taken from $30,000$ repetitions of the simulation for each combination of group size and distribution of $\gamma$.

In other words, groups of agents in which the initially correct agents are radically more biased than the initially incorrect agents perform better than groups of agents who are not biased at all. In particular, in one experiment in which we varied the agents’ competence in argument production, we also found that, for small groups ($11$ agents), the proportion of correct majorities after discussion can surpass the proportion of correct majorities before discussion, showing that, at least in some specific circumstances, discussion can actually increase the number of correct majorities in groups where the initially correct agents are radically biased. Nevertheless, this finding was only observed in one experiment in which initially correct agents were assigned extremely high values of $\gamma$ and initially incorrect agents were assigned extremely low values of $\gamma$, thus pointing to the fact that the general detrimental effect of group discussion that we observed is a robust and frequent outcome.

In sum, myside bias seems to provide an epistemic advantage in heterogeneous groups where radicality is stronger among initially correct agents than among initially incorrect agents. Deliberative truth-tracking thus benefits from the effects of the radicality distribution of myside bias in these groups, so much so that, across all group sizes, such groups perform better than groups with unbiased discussants. Nevertheless, the harmful effects of discussing in larger groups persist in these heterogeneous groups. In Figure 17, the proportion of correct majorities after discussion decreases with group size.

Case 2: Initially incorrect agents are more radically biased

We now look at the pairs of distributions $(2, 5, 5, 2)$, $(2, 9, 9, 2)$ and $(2, 17, 17, 2)$, which model cases where the agents that are initially incorrect become progressively more radical than those agents that are initially correct.

In these cases, the distributions of consensus states in Figure 18 show that incorrect consensus states become more frequent as initially incorrect agents become more radical than initially correct agents (from lighter to darker shades of red). Simultaneously, both correct consensus states and no consensus states become less frequent.

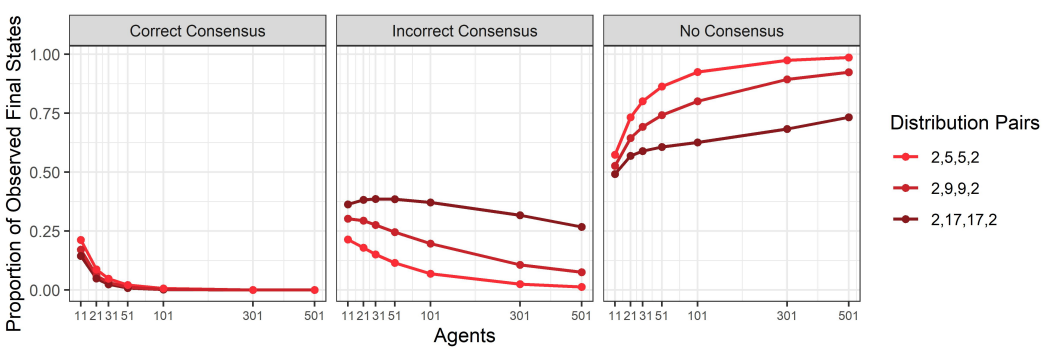
**Figure 18.** Proportions of correct consensus (left panel), incorrect consensus (central panel), and no consensus (right panel), for different combinations of group size ($x$-axis) and pair of distinct $\beta$-distributions for the parameter $\gamma$ for initially correct and initially incorrect agents, respectively. Again, each pair of distributions is labelled reporting, in order, the values of $\alpha$ and $\beta$ for the distribution of $\gamma$ in the initially correct subgroup of agents, and $\alpha$ and $\beta$ for the incorrect subgroup of agents. Darker shades of red indicate that distributions in a pair have a higher mean for initially correct agents and a lower mean for initially incorrect agents.

This effect is robust across different group sizes, with larger discussion groups ending more often in no consensus states. Let us also point out that there is an important difference concerning the way differential distributions of radicality among initially correct agents and initially incorrect agents affect consensus in smaller and larger groups. Indeed, if we compare the distribution of consensus states in smaller groups ($11, 21, 31$ agents) in Figure 14 with that of smaller groups in Figure 18, we see that when the initially correct agents are more radical, incorrect consensus is much less likely, compared to correct consensus in cases in which initially incorrect reasoners are more radical. This seems to suggest that in smaller groups, increasing radicality among correct agents determines a larger gain in reaching correct consensus than the gain in incorrect consensus determined by increasing radicality among incorrect reasoners at the start. Note that this difference seems to disappear as group size increases, thus suggesting again that the epistemic advantage that correct reasoners have in smaller groups is lost in larger discussion groups.

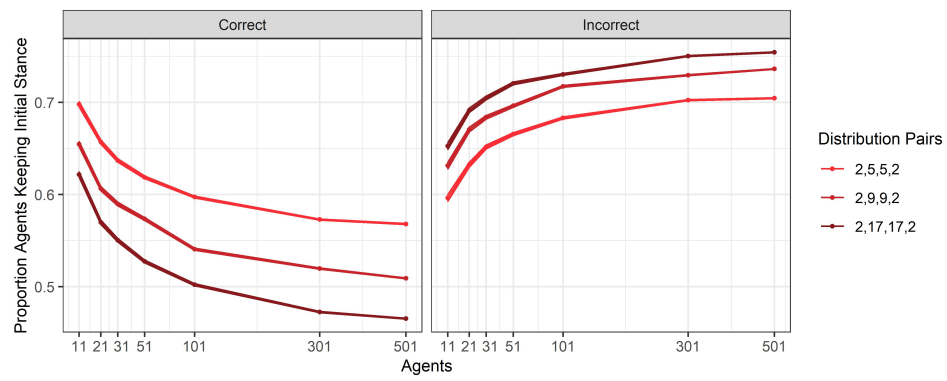
**Figure 19.** Proportion of agents retaining their initial position on the issue after discussion, for each combination of group size ($x$-axis) and distribution pairs of radicality $\gamma$. The left panel plots the proportion for the agents that are correct at the start, and the right panel plots the proportion for the agents that are incorrect at the start. Values of the proportions are on the $y$-axis, and the thickness of lines represents the $99\%$ confidence interval around the observed value. Proportions are computed over $30,000$ repetitions for each combination of group size and distribution pairs.

We observe a similar pattern in the way discussion affects retention and change of opinion in Figure 19. With the increasingly higher radicality among incorrect reasoners at the start and the lower radicality among correct reasoners at the start, more agents among those initially correct are swayed to the incorrect side of the issue. Simultaneously, more initially incorrect agents stick to their incorrect opinion. This effect can become stronger to the point that the proportion of initially correct agents that switch to supporting the incorrect side of the issue is higher than the proportion of initially incorrect agents that switch to the correct side of the issue, with groups of bigger size amplifying this effect. Note that this was never the case for any of the other experiments that we performed, if we compare Figure 19 with Figure 9 or 15.

Summing up, increasing radicality among initially incorrect agents has detrimental effects on the nature of the discussion, and detrimentally affects belief aggregation with the majority rule.

Figure 20 shows indeed that the proportion of retained correct majorities decreases as the distributions assign higher radicality to initially incorrect agents and lower radicality to initially correct ones. Again, this effect can cause the proportion of lost correct majorities to be higher than the proportion of lost incorrect majorities, as opposed to what we observed in all previous experiments (compare Figure 10 and 16). In turn, this reflects on the likelihood of correct majorities after discussion, Figure 21, which not only assumes lower values for distributions with higher radicality among initially incorrect agents, but it is always lower than that of groups of non-biased discussants. These effects are robust across different group sizes.

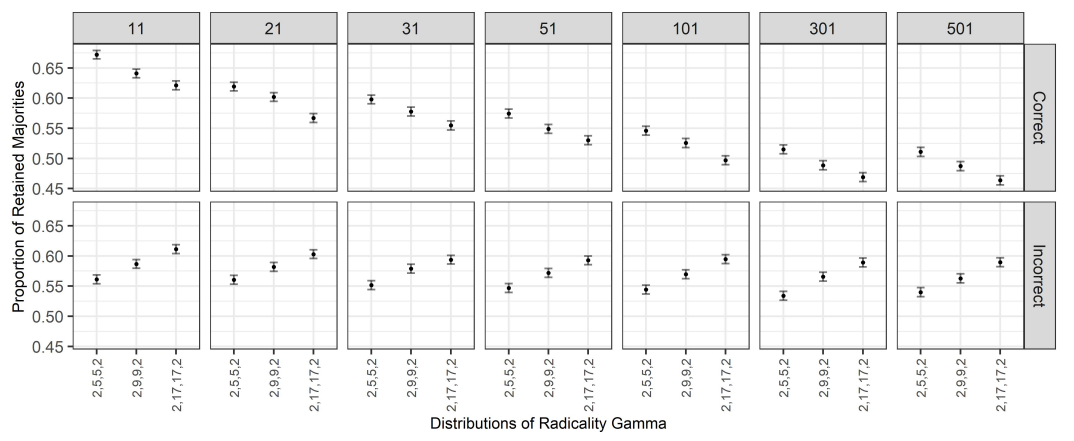
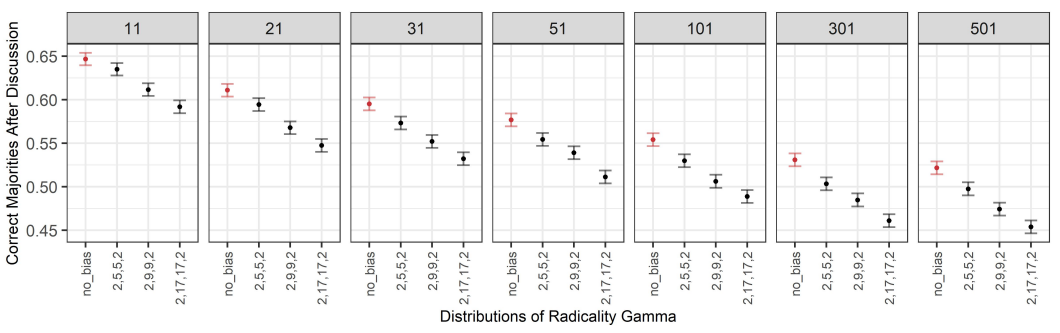
**Figure 20.** The proportion of correct majorities at the start (Correct), and the proportion of incorrect majorities at the start (Incorrect) that are retained at the end of the discussion, for each combination of group size (on top) and pair of $\beta$-distributions for initially correct and initially incorrect agents ($x$-axis), with $99\%$ confidence intervals around the observed value. Values of the proportions are on the y-axis. The mean proportions are averages over $30,000$ repetitions for each combination of majority type (Correct, Incorrect), group size and distribution pairs.

Let us conclude by pointing out how group size again amplifies the undesirable effects of higher radicality among initially incorrect reasoners with respect to deliberative truth-tracking. Indeed, the proportion of correct agents after discussion assumes progressively lower values as group size increases.

Discussion

From the experiments described in the previous section, a clear pattern emerges, highlighting the ways in which myside bias, group size and truth-tracking ability interact in group discussion. Below we discuss the most relevant aspects of our analysis and their implications.

Myside bias and truth

We started our paper by presenting two contrasting views about myside bias. One view supports the idea that myside bias is detrimental to collective wisdom (Hahn et al. 2019; Lorenz et al. 2011); the other view argues that myside bias is a good device for belief formation by preventing deceitful beliefs to spread, thus fostering collective wisdom (Gabriel & O’Connor 2022; Mercier & Sperber 2017).

Our results are located halfway between these two perspectives. Indeed, we found that the question whether myside bias is beneficial or detrimental to the ability of discussants to track truth, significantly depends on how the radicality of the bias is distributed across subgroups of discussants holding different beliefs at the start of the conversation.

As long as the radicality of the bias is distributed in the same way across the agents that are initially correct and those that are not, small groups of biased agents can be better at collectively tracking the truth than non-biased agents. Within our model, this fact happens at the cost of a loss in the effectiveness of communication. Rather than impacting (positively or negatively) on the truth-conduciveness of group discussion, myside bias turns group discussion into a less effective method for agents to adopt beliefs different from their own.

This stands in contrast with the idea that biased agents are more likely to form incorrect beliefs than non-biased agents; in addition, it also contrasts with the idea that groups of biased agents can outperform non-biased ones as a result of virtuous argumentative dynamics triggered by the bias. In this regard, our model retains the core idea of the traditional view that myside bias constitutes a mechanism that reinforces one’s own prior belief (Nickerson 1998; Rabin & Schrag 1999; Stanovich 2021). If agents are homogeneously radical, myside bias tends to produce polarising conversations, where the prior beliefs of the agents are reinforced and become more extreme as a result of argumentation.

This scenario changes when either the discussants that are initially correct are more radically biased than the incorrect ones, or those that are initially incorrect are more radically biased than the correct ones. It is indeed these asymmetries in radicality that can allow myside-biased agents to effectively exchange information and communicate. A truth-conducive exchange of information, then, is conditional on the initially correct discussants being more radically biased, and on the initially incorrect discussants being less radically biased. This way, agents holding the correct belief are not swayed into adopting an incorrect belief. At the same time, agents holding the incorrect belief at the start can correct themselves by updating based on the arguments produced by the initially correct reasoners.

This kind of communicative pattern seems consistent with real-world experiments in which participants are first asked to individually find a solution to a logical or mathematical problem, and then to discuss their solutions to that problem in a group (Mercier 2017; Mercier & Claidière 2022; Navajas et al. 2018; Trouche et al. 2014). Generally, those participants that have found the correct answer are rarely convinced by arguments supporting incorrect answers, while generally being able to convince those that found an incorrect solution.

Of course, discussions over issues that admit a correct and an incorrect answer can be more complex than those about the solution to a logical/mathematical problem. It suffices to think of debates among scientists, or deliberations within the members of a jury. In such scenarios, dynamics are at play that our model does not account for, although we will address some of them in a moment. Nevertheless, we believe that our model highlights the important point that, rather than the myside bias alone, it is its differential strength across subgroups of discussants holding different beliefs that can enhance or harm the truth-conduciveness of the discussion.

Crowd size and truth

The second aspect that emerges from our analyses has to do with the fact that increasing group size is detrimental for truth-tracking. We therefore do not observe a general beneficial wisdom-of-the-crowd effect. Indeed, in our setting, smaller crowds are wiser than larger ones.

As we have pointed out above, this is due to the fact that, in larger groups, agents that are initially incorrect have a higher chance of speaking first. If they do speak first, they are then able to anchor those agents with mild preferences into preferring more strongly the incorrect alternative. Most notably, this effect occurs even if, on average, each group is more competent than not.

This negative phenomenon mirrors findings in network epistemology showing that increasing connectivity in a social network negatively affects the agents’ ability to track the truth. It is indeed well known that an increase in the connectivity of a social network can come with a loss in the agents’ competence (Centola 2022; Hahn et al. 2020; Zollman 2007). This effect generally emerges as a result of the fact that, with increasing connectivity, agents can more easily get locked into supporting false beliefs. In this sense, as far as correct belief formation is concerned, increasing group size and connectivity seem to bear the similarity that they both create communication interfaces where agents can more easily fall prey to incorrect beliefs.

Let us remark, however, that in this paper, we have not concerned ourselves with the effects of different network topologies on the truth-conduciveness of group discussion, and that increasing the size of the group is not the same as increasing the connectivity of a group. Our model has focused only on a single network communication structure where all agents are in a sense connected to all other agents. We leave for future work the development of a detailed analysis of the effects of implementing different network topologies on our model. We have already mentioned above the analysis by Gabriel & O’Connor (2022) about the effects of myside bias on group learning. Surprisingly, they found that the effects of myside bias remain similar across different network topologies. It would be interesting to explore whether this is true also in our model of group discussion.

Still concerning the relation between group size and the ability of groups to track truth, we would like to point out the fact that only a few experimental studies have been conducted on groups of very large size (Mercier & Claidière 2022; Navajas et al. 2018). It is important to note that, even in these studies, participants are only allowed to discuss in small groups during the discussion phase of the experiments. For instance, Navajas et al. (2018) allow participants to discuss in groups of $5$, whereas the total number of participants was extremely extremely large (5180 participants). Similarly, Mercier & Claidière (2022) (33 groups, with sizes ranging from 20 to 208 participants) allow participants to discuss in groups of $8$.

While these studies on large crowds find a beneficial effect of group discussion on collective wisdom, these results might heavily depend on discussion being conducted in small groups. This leaves open the question of how larger discussion platforms affect collective intelligence. This is an important open problem, considering that larger discussion groups are an essential part of many human activities, from the daily interaction on social media to the discussions happening in state parliaments.

Connected to this point is the issue surrounding the above-mentioned debate on whether group discussion is at all beneficial for belief aggregation. In this regard, we found that the chance of having a correct majority after a discussion is almost always lower than the chance of having a correct majority before the discussion. Let us again stress the fact that this is not an effect of the discussants being more or less radically biased. In this regard, our findings are in line with the idea that group discussion is in principle detrimental, and contrasts with the view that group discussion improves the output of belief aggregation.

Limitations and future work

We would like to conclude this discussion section by pointing out several limitations of our model, as well as suggesting potential directions for future work.

Let us start by remarking that our model abstracts away from important dynamics of real-world argumentative contexts that might interact with myside bias in ways that affect group communication patterns and the ability of groups to track truth. We have already mentioned that human communication often takes place in networked environments, where agents interacts with their neighbours. We believe that our model could easily be adapted to capture group discussions in networks in a fashion similar to Gabriel & O’Connor (2022) or Alvim et al. (2021).

Second, the simulation experiments that we performed assume that all agents draw their arguments from a uniform distribution. Note that this a strong assumption on two levels: first, it assumes that all agents have the same competence of argument production, i.e., they all have the same likelihood of producing stronger/weaker arguments; second, it assumes that all arguments, from the weakest to the strongest knock-down argument, have the same likelihood of occurring during a conversation. As we already mentioned above, a consequence of this is that group discussions in our setting tend not to be very long, even if the number of discussants is large. Nevertheless, our model is sufficiently flexible to allow for a relaxation of both these assumptions, by changing the distributions from which the agents draw their arguments. In future work, we would like to explore how relaxing these assumptions impacts the features of the discussion that the agents conduct, as well as its truth-conduciveness, compared to the cases that we have been concerned with in this paper. For instance, one could model situations in which agents differ in their argumentative skills. Furthermore, this framework could be used to model situations in which agents progressively adapt their argumentative skills to a specific conversation, which is an important argumentative dynamic highlighted in Mercier & Sperber (2017).

Moreover, in our model the speakers are selected randomly: at each step, any agent can be picked to be the next one to present an argument. In many contexts this is not the case. For instance, hearings in a court of law or in a parliament chamber are not random, and there is a clear protocol that determines who gets to speak at which time. It would be interesting to implement different communication protocols in our setting and evaluate the truth-tracking abilities of one against the other. For instance, one could test whether agents that communicate with a random communication protocol perform worse than groups in which agents from different sides alternate during the discussion as in Ding & Pivato (2021). In this setting, one could also study how different argument exchanges affect group polarisation, in the fashion of Mäs & Flache (2013), Banisch & Olbrich (2021), Kopecky (2022). More generally, one could enrich our model to test different ways of optimally designing public debates, in the style of Grabisch et al. (2022).

Finally, agents in our model do not strategise. Strategic aspects in opinion dynamics in groups have been extensively studied using many different formal frameworks, see, e.g., Franke & van Rooij (2015), Dykstra et al. (2013), Dykstra et al. (2015). Giving agents the ability to strategize would allow to model situations in which discussants in a group might want to achieve different goals, can perform different actions or want to manipulate the conversation (see Franke & van Rooij 2015 for a strategic extension of the traditional DeGroot’s model (DeGroot 1974)).

Conclusion

In this paper, we proposed a Bayesian model of myside bias that captures relevant empirical facts about the mechanisms of myside bias in the context of argument evaluation. Moreover, we implemented this Bayesian model in an agent-based model of group discussion. In doing so, we investigated the extent to which myside bias and group discussion can be truth-conducive, in terms of improving belief aggregation outcomes.

In this regard, we found that myside bias differently affects truth-tracking depending on how its strength is distributed across groups of discussants supporting different sides of the issue under discussion. When all agents are equally biased, no matter their initial stance, discussion in small groups might slightly improve truth-tracking by inhibiting communication and by preventing agents to change their opinions via discussion. This scenario may change if one group is more biased than the other. In such cases, there may be a positive or negative communication dynamic that can promote or detract from correct belief formation. In the wisdom of crowds tradition, larger groups are generally considered wiser than smaller groups because they are better at tracking the truth. This is true under the condition that agents do not communicate or discuss. Consistent with this view, we found that group discussion negatively affects the group’s ability to track the truth. When agents do communicate, small crowds turn out to be wiser than larger crowds. However, they are wiser in the specific sense that they minimize the overall harm that group discussions appear to cause.

Finally, we would like to point out that our model highlights the importance of contextual aspects in which group discussions may take place, such as the number of discussants or their varying degrees of radicality. Factors such as these appear to play a crucial role in the ability of discussions to foster collective wisdom. We leave it to further experimental and theoretical work to investigate the importance of different contextual aspects for the truth-conduciveness of group discussions.

Acknowledgements

This research was partly funded by the project "Hybrid Intelligence: Augmenting Human Intellect", a 10-year Gravitation programme funded by the Dutch Ministry of Education, Culture and Science through the Netherlands Organisation for Scientific Research, grant number 024.004.022. Zoé Christoff acknowledges support from the project "Social Networks and Democracy" (VENI project number Vl.Veni.201F.032) financed by the Netherlands Organisation for Scientific Research (NWO). Stephan Hartmann’s work on this project was supported by the AHRC-DFG project "Normative vs. Descriptive Accounts in the Philosophy and Psychology of Reasoning and Argumentation: Tension or Productive Interplay?" (HA 3000/20-1) and the project "The Bayesian Approach to Robust Argumentation Machines" (HA 3000/21-1) in the DFG priority program "Robust Argumentation Machines" (SPP1999). He also acknowledges conversations with Ulrike Hahn and Borut Trpin.

Appendix: Proofs

Proof of Proposition 3

Definition 1 implies that

\[ \frac{x'}{x} = \frac{2}{1+ (\bar{b}/b)^\gamma}\textrm{ for $b\geq{1/2}$ }\]

\[(8)\]

and

\[ \frac{x'}{x} = \frac{1+ (\bar{b}/b)^\gamma}{2}\textrm{ for $b<{1/2}$ } .\]

\[(9)\]

Next, we note that $(\overline{b}/b)^\gamma < 1$ for $b > 1/2$, $(\overline{b}/b)^\gamma = 1$ for $b = 1/2$ and $(\overline{b}/b)^\gamma > 1$ for $b < 1/2$. Hence, from Equation (8), $x'/x <1$ if $b > 1/2$, and $x'/x =1$ if $b = 1/2$. Moreover, from Equation (9), $x'/x >1$ if $b < 1/2$. From this, the proposition follows. ◻

Proof of Proposition 4

We differentiate $x'(x,b)$ with respect to $b$ and obtain

\[\frac{\partial x'}{\partial b} = -2\, \gamma \, x \cdot \frac{(b \, \bar{b})^{\gamma -1}}{(b^{\gamma} + \bar{b}^{\gamma})^2} < 0\textrm{ for $b\geq{1/2}$}\]

and

\[\frac{\partial x'}{\partial b} = -\, \frac{\gamma \, x}{2} \cdot \frac{b^{-\gamma-1}\, \bar{b}^{\gamma}}{\bar{b}} < 0\textrm{ for $b<{1/2}$} .\]

Note that these two expressions are the same ($= -2\, \gamma \, x$) when evaluated at $b=1/2$. Hence, $x'(x,b)$ is a strictly monotonically decreasing function of $b$. ◻

Proof of Proposition 5

We denote $P({\rm B})$ by $b_p$ and $Q({\rm B})$ by $b_q$ and obsere that, by assumption, $b_p = \bar{b}_q$. Accordingly, $\bar{b}_p = b_q$. Next, we assume that $b_p\geq{1/2}$ and substitute $\bar{b}_q$ for $b_p$, $b_{q}$ for $\bar{b}_p$, and $1/y$ for $x$ in the following expression from Def. 1:

\[2 \, x \cdot \frac{\bar{b}_p^\gamma}{b_p^\gamma + \bar{b}_p^\gamma}\]

We then obtain:

\[\frac{2}{y} \cdot \frac{b_q^\gamma}{b_q^\gamma + \bar{b}_q^\gamma} = \frac{1}{x'(y,b_q)}.\]

In a similar way, using the second expression in Def. 1, one can prove the case for $b_p<1/2$. ◻

Proof of Proposition 6

It is easy to see from Equations (1) and (3) that (i) $P^{\ast \ast}({\rm B}) > P^{\ast}({\rm B})$ iff $x' < x$, (ii) $P^{\ast \ast}({\rm B}) = P^{\ast}({\rm B})$ iff $x' = x$, and (iii) $P^{\ast \ast}({\rm B}) < P^{\ast}({\rm B})$ iff $x' < x$. Using Proposition 3 then completes the proof. ◻

Proof of Proposition 7

We begin with some notation. We denote the probability of B after first updating on ${\rm A_1}$ by $b'$ and the probability of B after first updating on ${\rm A_2}$ by $c'$. Likewise, we denote the probability that results after first updating on ${\rm A_1}$ and then on ${\rm A_2}$ by $b''$ and the probability that results after first updating on ${\rm A_2}$ and then on ${\rm A_1}$ by $c''$. These are given by

\[ \begin{eqnarray} b' &=& \frac{b}{b + \bar{b} \, x'(x_1, b)} =: \frac{b}{N_1} \\ b'' &=& \frac{b'}{b' + \bar{b'} \, x'(x_2, b')} =: \frac{b'}{N_2} \\ c' &=& \frac{b}{b + \bar{b} \, x'(x_2, b)} =: \frac{b}{N_3} \\ c'' &=& \frac{c'}{c' + \bar{c'} \, x'(x_1, c')} =: \frac{c'}{N_4}. \end{eqnarray} \] Next, we calculate $\Delta := c'' - b''$: \[ \begin{eqnarray} \Delta &=& \frac{1}{N_2 \, N_4} \cdot \left(c'\, (b' + \bar{b'} \, x'(x_2, b')) - b' \, (c' + \bar{c'} \, x'(x_1, c')). \right) \\ &=& \frac{1}{N_2 \, N_4} \cdot \left(c' \, \bar{b'} \, x'(x_2, b')) - b' \, \bar{c'} \, x'(x_1, c')) \right) \\ &=& \frac{b \, \bar{b}}{N_1 \, N_2 \, N_3 \, N_4}\cdot \left(x'(x_1, b) \, x'(x_2, b') - x'(x_2, b) \, x'(x_1, c') \right) \end{eqnarray} \]

We now need to distinguish a number of cases depending on whether $b,b',c'$ are bigger than, equal to, or smaller than $1/2$, in order to know which expressions to plug in for the various $x'$. We start by assuming that $b\geq{1/2}$, and by considering all the cases for $b',c'$ to be greater than, equal to, or smaller than $1/2$. To begin with, consider the case in which $b'\geq{1/2}$ and $c'<1/2$. We note that this holds iff $b'>c'$ iff $x_1<x_2$. We now only need to show that $\Delta<0$ if we substitute the expressions for the various $x'$. After some algebra we obtain that:

\[\Delta = K \cdot \left( \frac{3\left(\overline{b'}c'\right)^\gamma}{\left(c'b'\right)^\gamma+(\overline{c'}{b'})^\gamma+(\overline{c'}{\overline{b'}})^\gamma} -1 \right),\]

\[(10)\]

where $K$ is a positive constant. Note that, since $b'\geq{1/2}$ and $c'<1/2$, we infer that $\Delta<0$. This is so because at the same time, ${\overline{b'}{c'}\leq{c'b'}}$, ${\overline{b'}{c'}<{\overline{c'}{b'}}}$, ${\overline{b'}{c'}<\overline{c'}{\overline{b'}}}$. Thus,

\[ 3\left(\bar{b'} c'\right)^\gamma < \left(c'b'\right)^\gamma+(\bar{c'}b')^\gamma+(\overline{c'b'})^\gamma . \]

This completes the case in which $b,b'\geq{1/2}$ and $c'<1/2$.

In the second case, we assume that $b'<{1/2}$ and $c'\geq1/2$. This obtains iff $b'<c'$ iff $x_1>x_2$. Similarly as the previous case, we now need to show that $\Delta>0$, if we plug in the expressions for the various $x'$. Again, after some algebra one obtains that

\[\Delta = K' \cdot \left( \frac{\left(c'b'\right)^\gamma+(\overline{b'}{c'})^\gamma+(\overline{c'}{\overline{b'}})^\gamma}{3\left(\overline{c'}b'\right)^\gamma} -1 \right),\]

\[(11)\]

where $K'$ is a positive constant. We note that, since $c'\geq{1/2}$ and $b'<1/2$, $\Delta>0$. This follows from the fact that, jointly, ${\overline{c'}{b'}\leq{c'b'}}$, ${\overline{c'}{b'}<{\overline{b'}{c'}}}$, ${\overline{c'}{b'}<\overline{c'}{\overline{b'}}}$. Thus,

\[ 3 \left(\bar{c'} b'\right)^\gamma < \left(c'b'\right)^\gamma+(\bar{b'}c')^\gamma+(\overline{c'b'})^\gamma . \]

This completes the case in which $b,c'\geq{1/2}$ and $b'<1/2$.

Third, if both $b',c'\geq{1/2}$, then, by plugging in the expressions for the various $x'$, one obtains after some algebra that

\[\Delta = K'' \cdot \left( \left(\frac{\overline{b'}\, c'}{b' \, \overline{c'}} \right)^\gamma -1 \right),\]

\[(12)\]

where $K''$ is a positive constant. Hence, $\Delta > 0$ iff $\overline{b'}\, c' > b' \, \overline{c'}$. This holds iff $c' > b'$ which in turn holds iff $x_1 > x_2$. This completes the case in which $b,b',c'\geq{1/2}$.

Fourth, the case in which $b',c'<{1/2}$, is proven similarly as the previous one. By plugging in the expressions for the various $x'$, one obtains that

\[\Delta = K''' \cdot \left( \left(\frac{\overline{b'}\, c'}{b' \, \overline{c'}} \right)^\gamma -1 \right),\]

\[(13)\]

where $K'''$ is a positive constant. Thus, as for the previous case, $\Delta > 0$ iff $x_1 > x_2$.

This completes the proof for all possible cases in which $b\geq1/2$. The cases in which $b<1/2$ are proven similarly as the ones above. ◻

Proof of Proposition 8

We first note that

\[P({\rm B\vert A, E}) = \frac{P({\rm A, B, E})}{P({\rm A, E})}.\]

Next we apply the product rule from the theory of Bayesian networks (see, e.g., Hartmann 2021) and obtain:

\[ \begin{eqnarray} P({\rm B\vert A, E}) &=& \frac{P({\rm B}) \, P({\rm A\vert B}) \, P({\rm E\vert B})}{\sum_{B} P(B) \, P({\rm A}\vert B) \, P({\rm E}\vert B)} \\ &=& \frac{b \,p_1 \,p_2}{b \, p_1\, p_2+\overline{b} \, q_1 \,q_2} \\ &=& \frac{b}{b + \overline{b} \, (q_1/p_1) \, (q_2/p_2)} \end{eqnarray} \]

From this, for both the case in which $b\geq{1/2}$ and the case in which $b<1/2$, the proposition follows. ◻

Notes

We ignore the behavior of initially undecided agents, i.e., agents whose prior belief is exactly $0.5$, given that the number of such agents at the start of conversations was found to be negligible.↩︎
We report here the values of the proportion of correct majorities at the start collected over $180000$ repetitions, for each group size, with their $99\%$ confidence: $11$ agents, $0.84213 \pm 0.00222$; $21$ agents, $0.83869\pm0.00224$; $31$ agents, $0.83651\pm0.00225$; $51$ agents, $0.83448\pm0.00226$; $101$ agents, $0.83338\pm0.00227$; $301$ agents, $0.83317\pm0.00227$; $501$ agents, $0.83336\pm0.00227$. The proportion of correct majorities at the start over the aggregate data is then $0.83596$ ($\pm0.00085$, $99\%$ confidence).↩︎
Due to the fact that we distribute $\gamma$ using a $\beta$-distribution, it is not the case that, for distributions with mean $0.2$, the proportion of agents keeping their initial stance monotonically decreases with dispersion around the mean. This is due to the fact that, for $\beta$-distributions, the exclusion of values higher and lower than the mean does not happen symmetrically around the mean, as dispersion decreases. As a consequence, while for high enough dispersions, the proportion of agents retaining their initial beliefs decreases with a decrease in dispersion, one might see that the proportion of agents that retain their initial beliefs slightly increases for very small variances. Similar considerations apply to the case of distributions with mean $0.8$.↩︎

References

ALVIM, M. S., Amorim, B., Knight, S., Quintero, S., & Valencia, F. (2021). A multi-agent model for polarization under confirmation bias in social networks. In K. Peters & T. A. C. Willemse (Eds.), Formal Techniques for Distributed Objects, Components, and Systems (pp. 22–41). Cham: Springer International Publishing. [doi:10.1007/978-3-030-78089-0_2]

ALVIM, M. S., Knight, S., & Valencia, F. (2019). Toward a formal model for group polarization in social networks. In M. S. ALVIM, K. Chatzikokolakis, C. Olarte, & F. Valencia (Eds.), The Art of Modelling Computational Systems: A Journey From Logic and Concurrency to Security and Privacy: Essays Dedicated to Catuscia Palamidessi on the Occasion of Her 60th Birthday (pp. 419–441). Cham: Springer International Publishing. [doi:10.1007/978-3-030-31175-9_24]

BACCINI, E., & Hartmann, S. (2022). The myside bias in argument evaluation: A Bayesian model. Proceedings of the Annual Meeting of the Cognitive Science Society

BAINS, W., & Petkowski, J. J. (2021). Astrobiologists are rational but not Bayesian. International Journal of Astrobiology, 20(4), 312–318. [doi:10.1017/s1473550421000185]

BALA, V., & Goyal, S. (1998). Learning from neighbours. The Review of Economic Studies, 65(3), 595–621. [doi:10.1111/1467-937x.00059]

BANISCH, S., & Olbrich, E. (2021). An argument communication model of polarization and ideological alignment. Journal of Artificial Societies and Social Simulation, 24(1), 1. [doi:10.18564/jasss.4434]

BANISCH, S., & Shamon, H. (2021). Biased processing and opinion polarisation: Experimental refinement of argument communication theory in the context of the energy debate. arXiv preprint. Available at: https://arxiv.org/abs/2212.10117 [doi:10.2139/ssrn.3895117]

BONJOUR, L. (1985). The Structure of Empirical Knowledge. Cambridge, MA: Harvard University Press.

BOVENS, L., & Hartmann, S. (2003). Bayesian Epistemology. Oxford: Oxford University Press.

BROUSMICHE, K.-L., Kant, J.-D., Sabouret, N., & Prenot-Guinard, F. (2016). From beliefs to attitudes: Polias, a model of attitude dynamics based on cognitive modeling and field data. Journal of Artificial Societies and Social Simulation, 19(4), 2. [doi:10.18564/jasss.3161]

CENTOLA, D. (2022). The network science of collective intelligence. Trends in Cognitive Sciences, 26(11), 923–941. [doi:10.1016/j.tics.2022.08.009]

CHATER, N., & Oaksford, M. (Eds.). (2008). The Probabilistic Mind: Prospects for Bayesian Cognitive Science. Oxford: Oxford University Press.

CLAIDIÈRE, N., Trouche, E., & Mercier, H. (2017). Argumentation and the diffusion of counter-Intuitive beliefs. Journal of Experimental Psychology: General, 146, 1052–1066.

CONDORCET, J.-A.-N. de C. (1785). Essai Sur L’Application De L’Analyse À La Probabilité Des Décisions Rendues À La Pluralité Des Voix. Paris: Imprimerie Royale.

CORNER, A., Whitmarsh, L., & Xenias, D. (2012). Uncertainty, scepticism and attitudes towards climate change: Biased assimilation and attitude polarisation. Climatic Change, 114(3), 463–478. [doi:10.1007/s10584-012-0424-6]

ČAVOJOVÁ, V., Šrol, J., & Adamus, M. (2018). My point is valid, yours is not: Myside bias in reasoning about abortion. Journal of Cognitive Psychology, 30(7), 656–669.

DANDEKAR, P., Goel, A., & Lee, D. T. (2013). Biased assimilation, homophily, and the dynamics of polarization. Proceedings of the National Academy of Sciences, 110(15), 5791–5796. [doi:10.1073/pnas.1217220110]

DEGROOT, M. H. (1974). Reaching a consensus. Journal of the American Statistical Association, 69(345), 118–121. [doi:10.1080/01621459.1974.10480137]

DIETRICH, F. (2008). The premises of Condorcet’s jury theorem are not simultaneously justified. Episteme, 5(1), 56–73.

DIETRICH, F., & Spiekermann, K. (2022). Jury theorems. The Stanford Encyclopedia of Philosophy. Available at: https://plato.stanford.edu/archives/sum2022/entries/jury-theorems/ [doi:10.4324/9781315717937-38]

DING, H., & Pivato, M. (2021). Deliberation and epistemic democracy. Journal of Economic Behavior & Organization, 185, 138–167. [doi:10.1016/j.jebo.2021.02.020]

DOUVEN, I., & Kelp, C. (2011). Truth approximation, social epistemology, and opinion dynamics. Erkenntnis, 75(2), 271. [doi:10.1007/s10670-011-9295-x]

DOUVEN, I., & Meijs, W. (2007). Measuring coherence. Synthese, 156(3), 405–425. [doi:10.1007/s11229-006-9131-z]

DOUVEN, I., & Riegler, A. (2009). Extending the Hegselmann-Krause model I. Logic Journal of the IGPL, 18(2), 323–335. [doi:10.1093/jigpal/jzp059]

DRYZEK, J. S., & List, C. (2003). Social choice theory and deliberative democracy: A reconciliation. British Journal of Political Science, 33(1), 1–28. [doi:10.1017/s0007123403000012]

DYKSTRA, P., Elsenbroich, C., Jager, W., Renardel de Lavalette, G., & Verbrugge, R. (2013). Put your money where your mouth is: DIAL, a dialogical model for opinion dynamics. Journal of Artificial Societies and Social Simulation, 16(3), 4. [doi:10.18564/jasss.2178]

DYKSTRA, P., Jager, W., Elsenbroich, C., Verbrugge, R., & Renardel de Lavalette, G. (2015). An agent-Based dialogical model with fuzzy attitudes. Journal of Artificial Societies and Social Simulation, 18(3), 3. [doi:10.18564/jasss.2813]

EDWARDS, K., & Smith, E. E. (1996). A disconfirmation bias in the evaluation of arguments. Journal of Personality and Social Psychology, 71, 5–24. [doi:10.1037/0022-3514.71.1.5]

EVANS, J. S. (1989). Bias in Human Reasoning: Causes and Consequences. Hillsdale, NJ: Lawrence Erlbaum Associates.

EVANS, J. S. (2002). The influence of prior belief on scientific thinking. In P. Carruthers, S. Stich, & M. Siegal (Eds.), The Cognitive Basis of Science. Cambridge: Cambridge University Press.

EVANS, J. S. (2007). Hypothetical Thinking: Dual Processes in Reasoning and Judgement. New York, NY: Psychology Press.

EVANS, J. S., Newstead, S. E., & Byrne, R. M. J. (1993). Human Reasoning: The Psychology of Deduction. Hillsdale, NJ: Lawrence Erlbaum Associates.

EVANS, J. S., & Over, D. E. (1996). Rationality and Reasoning. Oxford, UK: Psychology/Erlbaum (UK) Taylor & Francis.

FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2. [doi:10.18564/jasss.3521]

FRANKE, M., & van Rooij, R. (2015). Strategies of persuasion, manipulation and propaganda: Psychological and social aspects. In J. van Benthem, S. Ghosh, & R. Verbrugge (Eds.), Models of Strategic Reasoning: Logics, Games, and Communities (pp. 255–291). Berlin, Heidelberg: Springer. [doi:10.1007/978-3-662-48540-8_8]

FRENCH Jr, J. R. (1956). A formal theory of social power. Psychological Review, 63(3), 181.

GABRIEL, N., & O’Connor, C. (2022). Can confirmation bias improve group learning? PhilSci-Archive

GRABISCH, M., Mandel, A., & Rusinowska, A. (2022). On the design of public debate in social networks. Operations Research, 71(2). [doi:10.1287/opre.2022.2356]

HAHN, U. (2022). Collectives and epistemic rationality. Topics in Cognitive Science, 14(3), 602–620. [doi:10.1111/tops.12610]

HAHN, U., Hansen, J. U., & Olsson, E. J. (2020). Truth tracking performance of social networks: How connectivity and clustering can make groups less competent. Synthese, 197(4), 1511–1541. [doi:10.1007/s11229-018-01936-6]

HAHN, U., von Sydow, M., & Merdes, C. (2019). How communication can make voters choose less well. Topics in Cognitive Science, 11(1), 194–206. [doi:10.1111/tops.12401]

HARTMANN, S. (2021). Bayes nets and rationality. In M. Knauff & W. Spohn (Eds.), The Handbook of Rationality (pp. 253–264). Cambridge, MA: MIT Press. [doi:10.7551/mitpress/11252.003.0025]

HARTMANN, S., & Rafiee Rad, S. (2018). Voting, deliberation and truth. Synthese, 195(3), 1273–1293. [doi:10.1007/s11229-016-1268-9]

HARTMANN, S., & Rafiee Rad, S. (2020). Anchoring in deliberations. Erkenntnis, 85, 1041–1069. [doi:10.1007/s10670-018-0064-y]

HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2.

HEGSELMANN, R., & Krause, U. (2006). Truth and cognitive division of labour: First steps towards a computer aided social epistemology. Journal of Artificial Societies and Social Simulation, 9(3), 10.

HEGSELMANN, R., & Krause, U. (2015). Opinion dynamics under the influence of radical groups, charismatic leaders, and other constant signals: A simple unifying model. Networks and Heterogeneous Media, 10(3), 477–509. [doi:10.3934/nhm.2015.10.477]

HORNIKX, J., & Hahn, U. (2012). Reasoning and argumentation: Towards an integrated psychology of argumentation. Thinking & Reasoning, 18, 225–243. [doi:10.1080/13546783.2012.674715]

HUNTER, J. E., Danes, J. E., & Cohen, S. H. (1984). Mathematical Models of Attitude Change: Change in Single Attitudes and Cognitive Structure. New York, NY: Academic Press. [doi:10.1515/9783112470084-007]

KOPECKY, F. (2022). Arguments as drivers of issue polarisation in debates among artificial agents. Journal of Artificial Societies and Social Simulation, 25(1), 4. [doi:10.18564/jasss.4767]

KUHN, D. (1991). The Skills of Argument. Cambridge: Cambridge University Press.

KURAHASHI-NAKAMURA, T., Mäs, M., & Lorenz, J. (2016). Robust clustering in generalized bounded confidence models. Journal of Artificial Societies and Social Simulation, 19(4), 7. [doi:10.18564/jasss.3220]

LANDEMORE, H. (2012). Democratic Reason. Princeton, NJ: Princeton University Press.

LEHRER, K., & Wagner, C. (1981). Rational Consensus in Science and Society: A Philosophical and Mathematical Study. Berlin Heidelberg: Springer.

LIU, C. H., Lee, H. W., Huang, P. S., Chen, H. C., & Sommers, S. (2015). Do incompatible arguments cause extensive processing in the evaluation of arguments? The role of congruence between argument compatibility and argument quality. British Journal of Psychology, 107(1), 179–198. [doi:10.1111/bjop.12133]

LORD, C. G., Ross, L. D., & Lepper, M. R. (1979). Biased assimilation and attitude polarization: The effects of prior theories on subsequently considered evidence. Journal of Personality and Social Psychology, 37(11), 2098–2109. [doi:10.1037/0022-3514.37.11.2098]

LORENZ, J., Neumann, M., & Navarro Schröder, T. (2021). Individual attitude change and societal dynamics: Computational experiments with psychological theories. Psychological Review, 128(4), 623–642. [doi:10.1037/rev0000291]

LORENZ, J., Rauhut, H., Schweitzer, F., & Helbing, D. (2011). How social influence can undermine the wisdom of crowd effect. Proceedings of the National Academy of Sciences, 108(22), 9020–9025. [doi:10.1073/pnas.1008636108]

MÄS, M., & Flache, A. (2013). Differentiation without distancing. Explaining bi-Polarization of opinions without negative influence. PLoS One, 8(e74516), 1–17.

MCKENZIE, C. R. M. (2004). Hypothesis testing and evaluation. In D. J. Koehler & N. Harvey (Eds.), Blackwell Handbook of Judgment and Decision Making (pp. 200–2019). Oxford: Blackwell Publishing. [doi:10.1002/9780470752937.ch10]

MERCIER, H. (2016). The argumentative theory: Predictions and empirical evidence. Trends in Cognitive Sciences, 20(9), 689–700. [doi:10.1016/j.tics.2016.07.001]

MERCIER, H. (2017). Confirmation bias - Myside bias. In R. F. Pohl (Ed.), Cognitive Illusions: Intriguing Phenomena in Thinking, Judgment and Memory. New York, NY: Routledge. [doi:10.4324/9781003154730-7]

MERCIER, H. (2018). A related proposal: An interactionist perspective on reason. Behavioral and Brain Sciences, 41, e53. [doi:10.1017/s0140525x17000772]

MERCIER, H. (2020). Not Born Yesterday. Princeton, NJ: Princeton University Press.

MERCIER, H., & Claidière, N. (2022). Does discussion make crowds any wiser? Cognition, 222, 104912. [doi:10.1016/j.cognition.2021.104912]

MERCIER, H., & Heintz, C. (2014). Scientists’ argumentative reasoning. Topoi, 33, 513–524. [doi:10.1007/s11245-013-9217-4]

MERCIER, H., & Landemore, H. (2012). Reasoning is for arguing: Understanding the successes and failures of deliberation. Political Psychology, 33(2), 243–258. [doi:10.1111/j.1467-9221.2012.00873.x]

MERCIER, H., & Sperber, D. (2011). Why do humans reason? Arguments for an argumentative theory. Behavioral and Brain Sciences, 34(2), 57–74. [doi:10.1017/s0140525x10000968]

MERCIER, H., & Sperber, D. (2017). The Enigma of Reason: A New Theory of Human Understanding. Cambridge, MA: Harvard University Press.

NAVAJAS, J., Niella, T., Garbulsky, G., Bahrami, B., & Sigman, M. (2018). Aggregated knowledge from a small number of debates outperforms the wisdom of large crowds. Nature Human Behaviour, 2(2), 126–132. [doi:10.1038/s41562-017-0273-4]

NEAPOLITAN, R. E. (2003). Learning Bayesian Networks. Upper Saddle River, NJ: Prentice Hall.

NEWMAN, T. P., Nisbet, E. C., & Nisbet, M. C. (2018). Climate change, cultural cognition, and media effects: Worldviews drive news selectivity, biased processing, and polarized attitudes. Public Understanding of Science, 27(8), 985–1002. [doi:10.1177/0963662518801170]

NICKERSON, R. S. (1998). Confirmation bias: A ubiquitous phenomenon in many guises. Review of General Psychology, 2, 175–220. [doi:10.1037/1089-2680.2.2.175]

NISHI, R., & Masuda, N. (2013). Collective opinion formation model under Bayesian updating and confirmation bias. Physical Review E, 87(6), 062123. [doi:10.1103/physreve.87.062123]

OAKSFORD, M., & Chater, N. (2020). New paradigms in the psychology of reasoning. Annual Review of Psychology, 71(1), 305–330. [doi:10.1146/annurev-psych-010419-051132]

OLSSON, E. J. (2022). Coherentism. Cambridge: Cambridge University Press.

OWEN, G., Grofman, B., & Feld, S. L. (1989). Proving a distribution-free generalization of the Condorcet jury theorem. Mathematical Social Sciences, 17(1), 1–16. [doi:10.1016/0165-4896(89)90012-7]

PERKINS, D. N. (1985). Postprimary education has little impact on informal reasoning. Journal of Educational Psychology, 77, 562–571. [doi:10.1037/0022-0663.77.5.562]

PETERS, U. (2020). What is the function of confirmation bias? Erkenntnis, 87(4), 1–26.

RABIN, M., & Schrag, J. L. (1999). First impressions matter: A model of confirmatory bias. The Quarterly Journal of Economics, 114(1), 37–82. [doi:10.1162/003355399555945]

RODRIGUEZ, J. A. A., Nathaniel AND Bollen. (2016). Collective dynamics of belief evolution under cognitive coherence and social conformity. PLOS ONE, 11(11), 1–15. https://doi.org/10.1371/journal.pone.0165910 [doi:10.1371/journal.pone.0165910]

SCHWEIGHOFER, S., Schweitzer, F., & Garcia, D. (2020). A weighted balance model of opinion hyperpolarization. Journal of Artificial Societies and Social Simulation, 23(3), 5. [doi:10.18564/jasss.4306]

SHAMON, H., Schumann, D., Fischer, W., Vögele, S., Heinrichs, H. U., & Kuckshinrichs, W. (2019). Changing attitudes and conflicting arguments: Reviewing stakeholder communication on electricity technologies in Germany. Energy Research & Social Science, 55, 106–121. [doi:10.1016/j.erss.2019.04.012]

SPERBER, D., Ement, F., Heintz, C., Mascaro, O., Mercier, H., Origgi, G., & Wilson, D. (2010). Epistemic vigilance. Mind & Language, 25, 359–393. [doi:10.1111/j.1468-0017.2010.01394.x]

SPRENGER, J., & Hartmann, S. (2019). Bayesian Philosophy of Science. Oxford: Oxford University Press. https://doi.org/10.1093/oso/9780199672110.001.0001 [doi:10.1093/oso/9780199672110.001.0001]

STANOVICH, K. E. (2021). The Bias That Divides Us: The Science and Politics of Myside Thinking. Cambridge, MA: MIT Press. [doi:10.7551/mitpress/13367.001.0001]

STANOVICH, K. E., & West, R. F. (2007). Natural myside bias is independent of cognitive ability. Thinking & Reasoning, 13(3), 225–247. [doi:10.1080/13546780600780796]

STANOVICH, K. E., & West, R. F. (2008). On the failure of cognitive ability to predict myside and one-sided thinking biases. Thinking & Reasoning, 14, 129–167. [doi:10.1080/13546780701679764]

STANOVICH, K. E., & West, R. F. (2008). On the relative independence of thinking biases and cognitive ability. Journal of Personality and Social Psychology, 94(4), 672–695. [doi:10.1037/0022-3514.94.4.672]

STANOVICH, K. E., West, R. F., & Toplak, M. E. (2013). Myside bias, rational thinking, and intelligence. Current Directions in Psychological Science, 22, 259–264. [doi:10.1177/0963721413480174]

SUROWIECKI, J. (2005). The Wisdom of Crowds. New York, NY: Anchor Books.

TABER, C. S., Cann, D., & Kucsova, S. (2009). The motivated processing of political arguments. Political Behavior, 31(2), 137–155. [doi:10.1007/s11109-008-9075-8]

TABER, C. S., & Lodge, M. (2006). Motivated skepticism in the evaluation of political beliefs. American Journal of Political Science, 50, 755–769. [doi:10.1111/j.1540-5907.2006.00214.x]

THAGARD, P. (2006). Hot Thought: Mechanisms and Applications of Emotional Cognition. Cambridge MA: Bradford Book/MIT Press. https://doi.org/10.7551/mitpress/3566.001.0001 [doi:10.7551/mitpress/3566.001.0001]

TOPLAK, M. E., & Stanovich, K. E. (2003). Associations between myside bias on an informal reasoning task and amount of post-secondary education. Applied Cognitive Psychology, 17, 851–860. [doi:10.1002/acp.915]

TROUCHE, E., Sander, E., & Mercier, H. (2014). Arguments, more than confidence, explain the good performance of reasoning groups. Journal of Experimental Psychology: General, 143, 1958–1971. [doi:10.1037/a0037099]

URBIG, D., Lorenz, J., & Herzberg, H. (2008). Opinion dynamics: The effect of the number of peers met at once. Journal of Artificial Societies and Social Simulation, 11(2), 4.

WILENSKY, U. (1999). NetLogo. Northwestern University, Evanston, IL. Available at: http://ccl.northwestern.edu/netlogo/

WOLF, I., Schröder, T., Neumann, J., & de Haan, G. (2015). Changing minds about electric cars: An empirically grounded agent-based modeling approach. Technological Forecasting and Social Change, 94, 269–285. https://doi.org/https://doi.org/10.1016/j.techfore.2014.10.010 [doi:10.1016/j.techfore.2014.10.010]

WOLFE, C. R., & Britt, M. A. (2008). The locus of the myside bias in written argumentation. Thinking & Reasoning, 14(1), 1–27. [doi:10.1080/13546780701527674]

WOOD, W., Rhodes, N., & Biek, M. (1995). Working knowledge and attitude strength: An information-processing analysis. In R. E. Petty & J. A. Krosnick (Eds.), Attitude Strength: Antecedents and Consequences (pp. 283–313). Hillsdale, NJ: Lawrence Erlbaum Associates.

ZENKER, F. (Ed.). (2013). Bayesian Argumentation: The Practical Side of Probability. Berlin Heidelberg: Springer.

ZOLLMAN, K. J. S. (2010). The epistemic benefit of transient diversity. Erkenntnis, 72(1), 17–35. [doi:10.1007/s10670-009-9194-6]

ZOLLMAN, K. J. S. (2007). The communication structure of epistemic communities. Philosophy of Science, 74(5), 574–587. [doi:10.1086/525605]