Modelling Adaptive and Anticipatory Human Decision-Making in Complex Human-Environment Systems

Introduction

It is critical to understand the social and cognitive elements that drive human behaviour to effectively manage human-environment systems – especially in an Anthropocene world increasingly shaped by humans (Schill et al. 2019). For example, in fisheries management, a familiar adage is that managing fisheries is about managing fishers (Jentoft 1997), which is entirely appropriate. After all, while regulations, available biomass, and market forces provide constraints and incentives, it is ultimately fishers who decide how to behave in the environment: what to target, where to fish, how much effort they spend, and so forth. To anticipate and understand impact of interventions, it is vital to understand how fishers adapt to environmental changes such as biological changes (e.g., stock depletion), competitive changes (e.g., inclusion of new trade markets), or policy changes (e.g., setting new quotas).

A recent paper highlights this point for fishing behaviour and calls for social-ecological behavioural models that account for human behavioural diversity and social and ecological complexity (Wijermans et al. 2020). In their review, they describe recent behavioural models and whether they capture four dimensions of behaviour: motivation, ability, livelihood, and social interaction. Wijermans and colleagues review recent behavioural models, showing that some describe motivation (Bastardie et al. 2014; Brede & deVries 2010; Libre et al. 2015), some livelihood (Manning et al. 2018), some ability (Merino et al. 2007; Pelletier et al. 2009; Siguroardóttir et al. 2014), while some describe social interactions (Wilson et al. 2007).

This paper presents a formal behavioural model that includes these dimensions as well as a memory function. As such, the proposed model fulfils a need identified in the literature, with a view to develop the next generation of behavioural models for ecological problems.

We review general behavioural models used for managing complex human-environment systems. Specifically, we explore behavioural models in fishing management. We identify key aspects of behaviour and discuss benefits and limitations of models that rely on historical data, that dynamically adapt to changes, and that assume perfect rationality (and sometimes perfect information). Having identified limitations of current model frameworks and the main functions needed in a fisher behaviour model, we put forth a new modelling framework for adaptive and anticipatory human behaviour in complex human-environment systems.¹ We show how the framework addresses limitations identified in the review and allows for subjective learning, competing preferences, information sharing, and other key functions that facilitate human adaptation.

The architecture of the decision-making model concerns how (fisher) agents learn and form preferences.² Learning can be direct (own experience), indirect (based on knowledge about experience of other agents) or inferential (based on characteristics of unknown fishing water). Preferences are competing and involve financial, cultural, reputational, and legal concerns. In our case learning and preference elements of the model are grounded in a general literature review and field work from Indonesia (Madsen et al. 2023). This work interviewed 93 fishers in Indonesia to get a sense of the concerns that fishers integrate, and we believe these components capture the main issues fishers consider when evaluating what to do on a given day. Learning and preference formation differ from one situation to another. Fisher agents in Indonesia are to some extent unique and differ from fishers in for example the USA, as the weight of social norms may differ in decision-making. Figure 1 gives an illustrative overview of the flow of decision-making (see later for discussion of how each step is resolved).

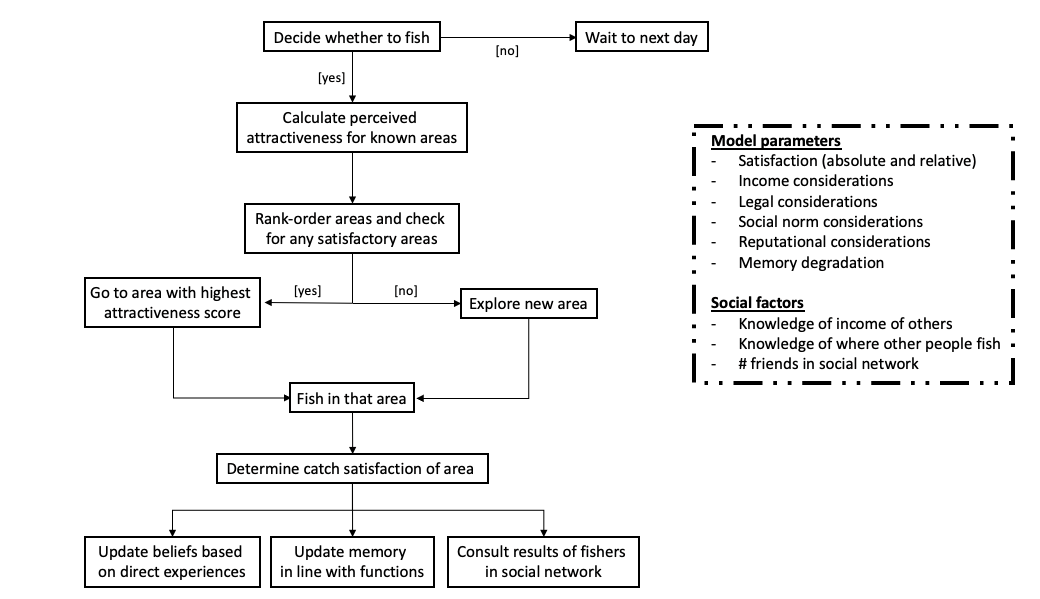
However, while the model discusses how fishers behave, it describes general concerns that are relevant for describing how people behave in natural environments, including farming choices, poaching, and other areas related to sustainability and ecosystems. We believe this has relevance for the JASSS readership in two ways. First, it proposes an anticipatory behavioural model that may be of interest to readers who aim to integrate psychological findings and assumptions in models. Second, it proposes methods for describing anticipatory rather than reactive behaviour that include individual (e.g., financial) and collective (e.g., social norms) pressures on behaviour. This will be of interest to readers who are interested in the psychology of behaviour and how to translate these assumptions into Agent-Based Models (ABMs).

The proposed behavioural model provides formally expressed rules that generate concrete and testable predictions. As these rules are goal-oriented and make use of the information available to each fisher, the model is inherently adaptive (as the fisher will change behaviour upon changing conditions). Given its computational and adaptive nature, it can be implemented in agent-based models.

While we exemplify how the model can be implemented in a fisheries context, the proposed model architecture is general and should be adaptable to other complex human-environment systems such as farming and poaching (e.g., Neil et al. 2020). For example, decisions in farming may rely on considerations that are similar to the functions in the model: a farmer may learn where, what, and how to plant via direct experiences and indirect learning from others; a farmer may consider reputational risks and social norms when considering where, what, and how to plant; a farmer may have access to more or less information about the earnings of neighbours to drive their own decision-making. Of course, future research should determine whether the architecture can be applied to other human-environment systems, but we argue that it has potential for doing so. We hope this will be of interest to JASSS readers, as the model is designed to reach beyond fisheries in this way. Finally, we discuss the adaptive implications of the framework and how it can be used to generate policies to manage fisheries.

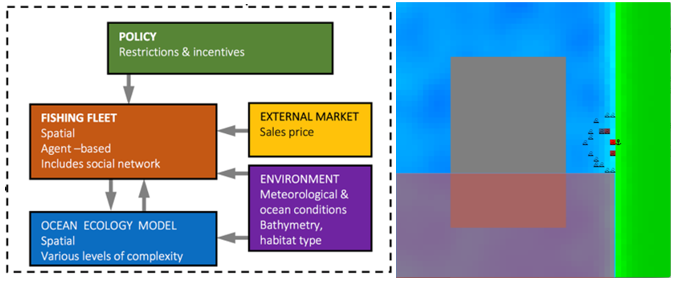
The model is designed as a component of the POSEIDON model (Bailey et al. 2019)³. POSEIDON is a coupled agent-based and ecosystem model, which predicts vessel behaviour and anticipates the resulting changes from policy decisions and other market and environmental factors. It enables implementation of decision-making models (for a discussion of ABMs in fisheries management, see Burgess et al. 2020). The purpose of POSEIDON is to evaluate possible interventions aiming at regulating fishing behaviour. The full model assumes that behaviour depends on external market conditions (e.g., fuel prices, prices of catch), the ocean environment (e.g., type and amount of fish), ocean ecology, policies, and the fishing fleet (number and size of boats and, critically, fisher behaviour) (see Figure 2 for an overview of the model). The ‘fishing fleet’ represents the collective of fishing agents (individual boats) within the model. The proposed model provides the cognitive framework for each fishing agent (fisher).

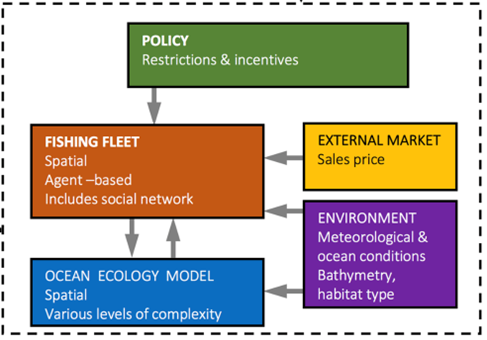
The robustness of POSEIDON as a model has been demonstrated in different ways. Initial simulations in Bailey et al. (2019) used pattern-oriented modelling (Jakoby et al. 2014) to show that interventions (such as placing a Marine-Protected Area) yield expected behaviours (e.g., agents learning to ‘fish the line’ of a Marine-Protected Area). The robustness of policy parameters used Automated Non-linear Testing (Miller 1998) to ‘define the degree to which parameters must be changed to force the model in to ’incorrect’ behaviour’ (Bailey et al. 2019 p. 6). Finally, calibration and validation have been used to test the appropriateness of behavioural assumptions in specific contexts – concretely, the West Coast of the USA (Carrella et al. 2019; Carrella et al. 2020a). Here, available data was compared with synthetically generated data to calculate the distance between model outputs and observations on a number of parameters.

While these checks are foundational to the appropriateness of the POSEIDON framework in general, the behavioural assumptions concerning fisher behaviour are the topic of this article, since we model the social and cognitive elements that drive fisher behaviour. Behavioural and psychological assumptions are critical in POSEIDON, as they directly impact what policies and interventions are proposed by the model (reverse-engineering) and whether these are implementable in real life. Despite the importance of these assumptions, POSEIDON has hitherto relied on more simplified frameworks such as Explore-Exploit-Imitate (EEI) models (Bailey et al. 2019), perfect rational models (Carrella et al. 2020b), and reason-based choice models (Madsen et al. 2020). The paper directly advances the ‘fishing fleet’ component of POSEIDON and thus represents a novel attempt to incorporate into larger models how fishers learn from and make decisions in natural environments.

Fishery Case: Behavioural Assumptions and Their Limitations

A common starting point is for behavioural assumptions to be rooted in neoclassical economics terms (Homo Economucis assumptions, HE), where fishers are perfectly informed rational profit-maximizers (see e.g., Clark 2010; Anderson 2015). Here, fishers have perfect knowledge of the profits they will make in each area before making a trip (see e.g., Toft et al. 2011; Kaplan et al. 2014; Ono et al. 2017). Perfect knowledge and profit-maximisation provides a straightforward abstraction of decision-making. However, both assumptions may be queried

First, some fishers consider non-economic preferences when choosing how to act. This includes deference to in-group fairness (Polania-Reyes & Echeverry Perez 2015), conservation concerns (Holland 2008 p. 339), neighbourliness (Klein et al. 2017), and compliance with social norms (Cardenas et al. 2000; Hatcher et al. 2000). This is in line with behavioural psychological literature that suggests social norms may impact decision-making (e.g., Buckholtz 2015). In line with this, social forces can be important drivers of management success or failure (Gutiérrez et al. 2011). These findings suggest decision-making goes beyond revenue, and that competing preferences may be critical to describe how some fishing communities behave. For example, behaviours that decrease a fisher’s communal standing can have drastic consequences for social cohesion, access to information networks, and other key functions. Thus, a fisher may forego profitable behaviours to comply with social norms.

Second, perfect information is in some cases assumed. For example, Haynie & Layton (2010) use a discrete-choice model where fishers use correctly specified catch expectation functions when choosing which area to target, Baerenklau & Provencher (2005) assume recreational fishers know the average catch they will make before starting their trip, and Hicks & Schnier (2006) assume fishers can perfectly predict catches in every area as well as simulate catch evolution over time. These are excellent models that can capture past observations.

While perfect information reduces computational complexity (see e.g., Clark & Mangel 2000; Dowling et al. 2012), one cannot assume that in reality fishers know the location or quantity of biomass in all possible areas available to them. One of the fundamental challenges for fishers is to learn features such as the spatial location of target species, and how best to catch or avoid them. In Wilson’s (1990) words, perfect information “assumes away the problem of finding fish”.

Finding a successful fishing location can be likened to the well-studied ‘bandit problem’, which describes a person faced with \(K\) slot machines who needs to make strategic decisions to maximise their pay-out (or ‘utility’) (Bubeck & Cesa-Bianchi 2012; Kuleshov & Precup 2014; Vermorel & Mohri 2005). Bandit problems involve a trade-off between exploration of new slot machines and exploitation of ones previously visited (Berger-Tal et al. 2014; He et al. 2018). For fishers, the problem of maximizing utility is more difficult, as biomass can be depleted (and can re-grow), can move, and can be removed by competitors. Thus, finding a bountiful location does not guarantee success upon return (Besbes et al. 2014).

Fishers use their knowledge of the world to choose where to go, what to target, and the time spent fishing. Assuming perfect information risks generating unrealistic adaptive patterns, as fishers would target the area with the highest utility function. For example, if a Marine Protected Area (MPA) is introduced on areas that fishers have targeted in the past, perfectly informed fishers would immediately and perfectly locate a new and satisfactory area without the need to explore or learn. Inefficiencies associated with gathering new information may be an important part of the response of the fishery to any such change in regulation.

Van Putten et al. (2012) classify decision-making in models of fisheries in three ways: dynamic optimization, random utility models and rule-based models. Dynamic optimization (DO) assumes a perfectly rational agent planning the future sequence of actions (locations to visit, gears to use, length of trips, etc.) by solving the optimal control of a dynamic state variable model (Dowling et al. 2015). DOs can be trained on historical data, which may require considerable data to be fully instantiated.

Random utility models (RUMs) are utility functions that can be fit to observed data (Wilen et al. 2002). They can reconstruct the full utility function (including non-monetary factors) from observed behaviour. This makes them particularly useful in cases where logbook data are available. Utilities can be incorporated within DO problems (Hicks & Schnier 2006) but this can make the problem computationally infeasible. While some RUMs assume fishers with perfect knowledge (Haynie & Layton 2010), others allow for incomplete information. For example, Abbott & Wilen (2011) model information sharing between fishers while Hutniczak & Münch (2018) use individual Gaussian catch expectations that are updated as fishers explore and catch fish.

By training the models on historically observed data, DOs and RUMs are able to replicate past behaviour accurately. However, this capacity for replication points to the inherent limitation of historically trained models: the risk of over-reliance on the past. If the external boundary conditions change in the real World, we may expect significant changes in effort (and catch effort), spatial placement of the fleet, and gear selection. If utility functions are trained on past area selection, simulated actors in a fishery may be less able to correctly adapt to changes in the environment, as they contain no specified directions for adopting novel strategies or choosing alternate locations.

Rule-based models (RBMs) can simulate how fishers decide where to fish, what to fish, and for how long they fish (Carrella et al. 2019). Further, adding exploratory behaviour to models may allow them to generate more realistic patterns under changing conditions. Rules can also determine how fishers explore. For example, RBMs can have fixed exploration rates (Kunz 2011), SOFTMAX exploration (Roberts & Goldstone 2006), and optimised exploration-exploitation trade-offs (Berger-Tal et al. 2014; He et al. 2018). Modelled fishers in Dorn (2001) use fixed thresholds to decide whether to fish or search, while Little & McDonald (2007) model agents which always exploit the most promising area. Bastardie et al. (2014) expand on the threshold-based approach to multiple dimensions by using decision trees. These heuristics are unlikely to find a globally optimal solution for profit maximisation, but they are computable and adaptive.

Behavioural assumptions determine the style and speed of fisher adaptation to environment changes. How fishers adapt to changes in the environment influences how the fishery should be managed through interventions. If we misunderstand how fishers behave, our models risk suggesting interventions that will have significant unintended consequences in real life.

Learning About Environment

One of the fundamental challenges for fishers is to learn about the environment. Fishers can gain information in two ways. First, they learn about the biomass of that area through personal experience when visiting a fishing ground. Second, they can get information through their social network. Here, we discuss how the model learns about the environment.⁴ The main model elements are grounded partly in the general literature review and partly in field work from Indonesia (Madsen et al. 2023). The latter interviewed 93 fishers in Indonesia to get a sense of the concerns that fishers integrate when evaluating what to do on a given day. This forms the basis of the proposed model.

Direct learning. For fishers, learning the location, catchability, and quantity of biomass is based on incomplete information and their personal experiences. Even if they are successful in one area, they cannot be certain it will be so next trip. The biomass may have moved, they may have depleted the biomass on the first trip, predators may have intervened, or other fishers may have targeted that area. Given this uncertainty, probabilistic approaches to learning lend themselves naturally to descriptions of fisher agents.

When fishers target a fishing area, they get numerical information on the mass of their catch. The ability for fishers to construct a representation of the distribution of biomass is intrinsically linked to the fisher’s personal experiences. To achieve this, the model compiles catch information as \(\hat{\mu}\) for each area, where:

\[ \hat{\mu} = \frac{1}{\sum_{i = 1}^{N} F(t_{i})}\sum_{i = 1}^{N} F(t_{i})O_{i}\]

\[(1)\]

Here, \(i\) is the index over \(N\) best values, ranked by how much fish they caught in each area, \(O_{i}\) represents the \(i^{th}\) observation, and \(F(t_{i})\) represents time passed since observing the catch in that area (see below). The index allows the agent to represent only the most relevant catches (as the fisher builds an internal model of available biomass, this represents the \(N\) areas with the highest expected catch) while the time function allows for more recent catches to be weighted more than past catches. This generates an index of values for each area, which the fisher can use to compare expected catch at different locations. Critically, the index is based on each fisher’s personal experiences, meaning that each fisher will build personal indices. This engenders endogenous heterogeneity between fishers, as two fishers will have different maps if they have different experiences. Further, computing expected biomass enables the fisher to be sensitive to fluctuations that influence profit (e.g., price changes).

Further, time influences the value of information. Yesterday’s observation is more relevant than information from six months ago⁵. To capture this, the time function, \(F(t_{i})\), weighs recent information more than old information. In Equation 1, the index function, \(i\), represents memory limitations. While future research should integrate more sophisticated memory models, we here propose three simple candidate models for \(F(t_{i})\):

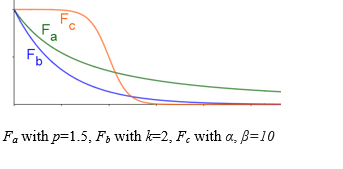
Equation 2a is an inverse power, 2b is an exponential function where \(k\) is a constant determining the decay rate. Finally, 2c is a logistic function where \(\alpha\) and \(\beta\) are constants (\(\alpha\) controls how long before the dip and \(\beta\) controls the steepness of the dip). These are candidate models for weighting of evidence and memory limitations, which should be tested empirically to determine the most plausible (including seasonality).

Indirect learning. While some fishers never share information about the location, abundance, and catchability of biomass, information dissemination is a crucial part of communal fishing in other fisheries. For this reason, the proposed framework allows for information sharing.

As described, each fisher generates an index of expected biomass for each area. The index contains numerical expectations (catch) as well as a rank order of these. This index allows for two types of information sharing. First, the fisher may transmit absolute information by disclosing their experienced catch for a particular location. The receiving fisher then integrates this information in the same way as they would, had they personally experienced the catch (though the use of Equation 1).

Second, fishers can share relative catch information. That is, rather than sharing an absolute number, they share the \(n^{th}\) best location in their index (e.g., if they want to communicate the best spot they have experienced, they share the coordinates of the top-ranked spot in their index). The recipient fisher interprets this in comparison with their personal experiences. Critically, this represents sharing of index placement, not the actual numerical information. For example, Fisher A may communicate the location of their best catch (which happens to be 50kg) to fisher B. However, fisher B has been more successful and has experienced a catch of 83kg elsewhere. For fisher B, ‘best’ means 83kg while ‘best’ means 50kg for fishers A. Thus, given different experiences, fishers in this framework can (unintentionally) miscommunicate if one transmits something which they believe is highly successful, but which the recipient perceives as poor if they act on the advice. Both absolute and relative information transmission can be dated so that the memory function can determine the weight of the evidence.

Absolute and relative information sharing enables different communication strategies. For example, a fisher may share all experienced catch in absolute quantities. This is the most open communication form, as there is no room for misunderstanding. The framework allows for any computationally expressed strategy (e.g., do not share the top-10% of areas, only share five areas, deliberately share median or average areas, etc.). Future work should test the impact of different communication strategies as well as the impact of misinformation and deception.

Inferential learning. In addition to direct and indirect learning, fishers may make inferences about areas they have not yet visited. For example, if the depth of an area is recorded along the numerical catch, fishers may learn that the species they target is more abundant in shallow waters. Given this, they should explore other shallow areas before venturing into deeper waters. Alternatively, the fisher may explore geographically close areas to see if the biomass extends to nearby areas. In other words, fishers may use geographical similarity and proximity to guide their exploration.

To capture this, we amend the function for generating expected biomass at a location (Equation 1) by appropriately weighting catches observed at other explored areas by geographical resemblance and proximity:

\[ \hat{\mu}^{X} = \frac{1}{\sum_{i = 1}^{N}F(t_{i})R_{i}\epsilon_{i}}\sum_{i = 1}^{N}F(t_{i})R_{i}\epsilon_{i}O_{i}\]

\[(3)\]

where \(\hat{\mu}^{X}\) is the inferred biomass at location \(X\), \(R_{i}\) represents the geographical resemblance between the location of observation \(i\) and location \(X\) from 0-1, where 1 represents areas that are identical and 0 represents areas with no similarity. \(\epsilon_{i}\) is a noise parameter between 0 and 1 that moderates the signals from other locations. For any observation \(i\) at location \(X\), \(\epsilon_{i} = 1\). Thus, we may weight information learned from other locations lower than information learned at location \(X\). If \(\epsilon_{i} = 0\), information from other areas is ignored and nothing is learnt. Comparatively, if \(\epsilon_{i} = 1\), fishers treat catches from similar areas exactly as they would in location \(X\).

To capture inferences over proximate areas, we can amend the function further:

\[ \hat{\mu}^{X} = \frac{1}{\sum_{i = 1}^{N}F(t_{i})R_{i}\epsilon_{i}(1 - P_{i})}\sum_{i = 1}^{N}F(t_{i})R_{i}\epsilon_{i}(1 - P_{i})O_{i}\]

\[(4)\]

where \(P_{i}\), from 0 to 1, represents the geographical proximity from area \(X\) to the location of observation \(i\). 1 is defined as the maximum geographic distance which can fit in the fishery in question (e.g., small-scale fisheries may consider areas within 3-4 km while large-scale industrial fisheries may consider areas within 30-40km). By normalising the proximity, the function can fit different types of fisheries. Each fisher applies the above learning mechanisms to every location after every trip. Via direct and indirect learning mechanisms, the fisher forms an impression of the location and bountifulness of the available biomass. This impression can be used to calculate expected income for different areas by multiplying expected catch by catch price and subtracting fixed and variable costs associated with each area. However, this only forms the basis for economic considerations. In the following, we discuss how fishers can use competing preferences to guide their behaviour.

Building Competing Preferences

The suggested learning mechanisms allow fishers to build personal maps of the location of biomass. However, perceived economic satisfaction may influence whether fishers return to a location or explore a new location. We discuss this in the following.

Economic satisfaction is a key driver in fishing, as unsatisfactory catch should lead fishers to explore new areas while a satisfactory catch should lead the fishers to exploit areas they have previously visited. In order to determine if a trip has been economically satisfactory, fishers have to evaluate their earnings from that trip. As people may evaluate their achievements by comparing them with others in similar socio-economic circumstances (Diener & Lucas 2000; Parducci 1995; Smith et al. 1989), economic satisfaction can be described in at least two ways: absolute and relative. For an area to be considered satisfactory, it needs to exceed the absolute and relative thresholds.

Absolute satisfaction refers to the numerical profit obtained from a trip. This can be compared against minimal profit threshold requirements, represented by \(\Phi\) (e.g., if \(\Phi = \$500\), a trip yielding $234 is unsatisfactory). The minimal threshold does not merely equate to operational and fixed costs, but may include income needed for livelihood, family expenditures, and savings.

Relative satisfaction refers to profit compared with other fishers they know. When fishers evaluate their income against other fishers with similar vessels, they may consider a trip to be unsatisfactory if they have a higher income for the same amount of effort. The relative satisfaction threshold, \(\delta\), denotes the place in the social network that would satisfy the fisher. If \(\delta = 1\), the fisher is only satisfied if they are the highest earner in the social network against which they compare their earnings. Comparatively, a \(\delta = 0.5\) fisher wants to be in the top-50% of earners. Finally, a \(\delta = 0\) fisher does not compare their earnings with anyone. This is direct social comparison.

The thresholds enable the inclusion of socio-cultural differences. By changing the thresholds, the model can represent fundamentally different types of fisheries. For example, high \(\delta\)-values represent highly competitive fisheries while low \(\delta\)-values do not engender the same amount of competition. In addition, fishers within a fishery may differ. Some fishers may be highly competitive while others are not. The thresholds can capture heterogeneity within a fishery by implementing thresholds for each fisher. These can be set conceptually (e.g., for one fishery, \(\delta\)-values may be \(\mu = 0.5\), \(\sigma = 25\)) or empirically if data is available (e.g., through survey data).

To understand area selectivity, it is imperative to understand what makes an area attractive to fishers. As discussed, in addition to economic aspects they may consider non-economic aspects, including in-group fairness, sustainability and social norms. The above reviewed literature suggests fishers may consider four broad categories when evaluating the attractiveness of a particular area: ‘Income,’ ‘legality,’ ‘communal norms,’ and ‘personal reputation’ (see Figure 3). As discussed later, fishers may give these concerns different weights (suggesting their relative importance to that fisher), which enables different fishing styles (Boonstra & Hentati-Sundberg 2016).

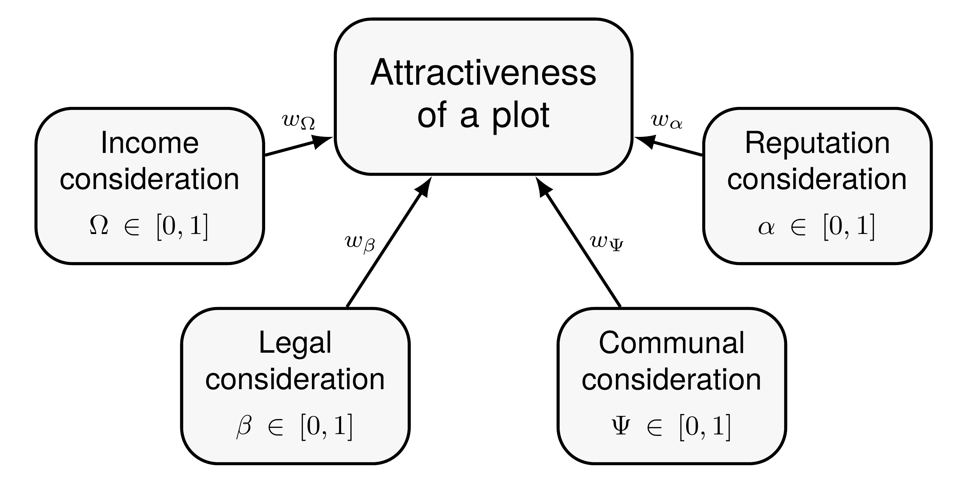
The preferences converge onto a single question: how attractive is a given fishing location (plot) given knowledge about the competing preferences? ‘Income’, \(\Omega\), refers to the expected revenue for the area. To calculate income, fishers consult the index of expected catch they have constructed via direct or indirect learning, using the functions described above. The income potential for an area equals expected catch of that area with the price of fish minus the costs linked with that area. This includes fixed costs (license fees, yearly upkeep, loan repayments, etc.), operational costs (fuel, bait, ice, salaries, etc.), and possible legal costs (fines for breaking the law). Table 1 provides an example of this.

Table 1: Comparing income of three hypothetical areas.

	Area 1	Area 2	Area 3
Expected gain	\(\mu^{1}\) = 47kg	\(\mu^{1}\) = 52kg	\(\mu^{1}\) = 42kg
	Price: $23/kg	Price: $23/kg	Price: $23/kg
	Expected gain: $1081	Expected gain: $1196	Expected gain: $736
Fixed costs	$200	$200	$200
Operational costs	Fuel ($8/L): $168	Fuel ($8/L): $136	Fuel ($8/L): $16
	Bait: $85	Bait: $85	Bait: $85
	Ice: $45	Ice: $45	Ice: $45
	Salaries: $350	Salaries: $350	Salaries: $350
Legal costs	0	0	$25
Total expected costs	$848	$816	$721
Expected income	$233	$380	$245

Any income below either satisfaction threshold is considered unsatisfactory and is not visited. For example, if \(\Phi = 240\), area 1 is not considered a viable option. The relative satisfaction value may fluctuate as a result of the endeavours of other fishers in the social network.

The model updates the estimates, as the fisher learns about the environment. For example, if they (reasonably) target area 2, they might learn that the fish stock has been depleted. In which case, the fisher updates \(\mu^{2}\), which may make the area less attractive for future trips. Further, the model consults the areas in the index and calculates income for each before leaving port. As such, given economic changes, the model adapts in an anticipatory manner. For example, if Area 2 becomes a Marine Protected Area (MPA) and carries a $200 fine, the model updates expected income (in this case to $180), making area 3 more economically attractive. This holds true for all economic changes including the price of the target fish, fixed and operational costs, and legal costs.

Critically, we include legal costs in economic concerns, as fines can be seen as a cost of fishing in that area. For example, if an MPA carries a $50 fine, but yields an additional $200 catch, it may be financially attractive to a fisher who is not concerned about the legality per se, but only considers income (see ‘legality’ preference). To manage such a person requires increase in fine or greater surveillance rather than merely the introduction of new legislation.

The ‘Legality’ preference, \(\beta\), refers to the desire to follow local laws regardless of economic penalties. Some fishers follow the law even if they are neither under surveillance, caught, nor penalised, but simply because it is part of the social contract. The economic consequences of breaking the law are integrated in the \(\Omega\)-variable, as this can be computed as fishing costs. This separates economic from moral and legal considerations. This is paramount, as legal interventions, with no or small fines and little surveillance, work in communities with high \(\beta\)-values. Comparatively, in communities with low \(\beta\)-values, the size of fines is key, as the moral dimension does not carry much weight.

The ‘communal norm’ preference, \(\Psi\), refers to the desire to adhere to norms that are communal and cultural rather than legal. Some fishers live in communities where cultural norms significantly influence their behaviour. For example, a community may entertain religious beliefs that encourage or discourage behaviour (e.g., some Indonesian fishers avoid fishing during the Ramadan despite the fact that they would be able to make money by fishing). Cultural norms may influence behaviour in non-economic ways, as a fisher may forgo a profitable area due to cultural pressures.

Finally, ‘personal reputation’, \(\alpha\), refers to the desire to be seen as a respected person by peers and members of the fisher’s social network. This differs from communal norms, as these refer to broader cultural norms that may be internalised (e.g., breaking a religious taboo). Comparatively, personal reputation refers to acts that influence inter-personal relationships. For example, targeting other fishers’ usual fishing areas, wilfully providing bad information (i.e., lying) when sharing information, or helping someone else in the community (as discussed later, preferences can be positive and negative).

In the current framework, fishers know if a particular area is damaging or helpful to their personal reputation, if it is illegal to fish there, and if fishing there adheres with communal norms. Figure 4 presents aspects that may impact the overall preferences.

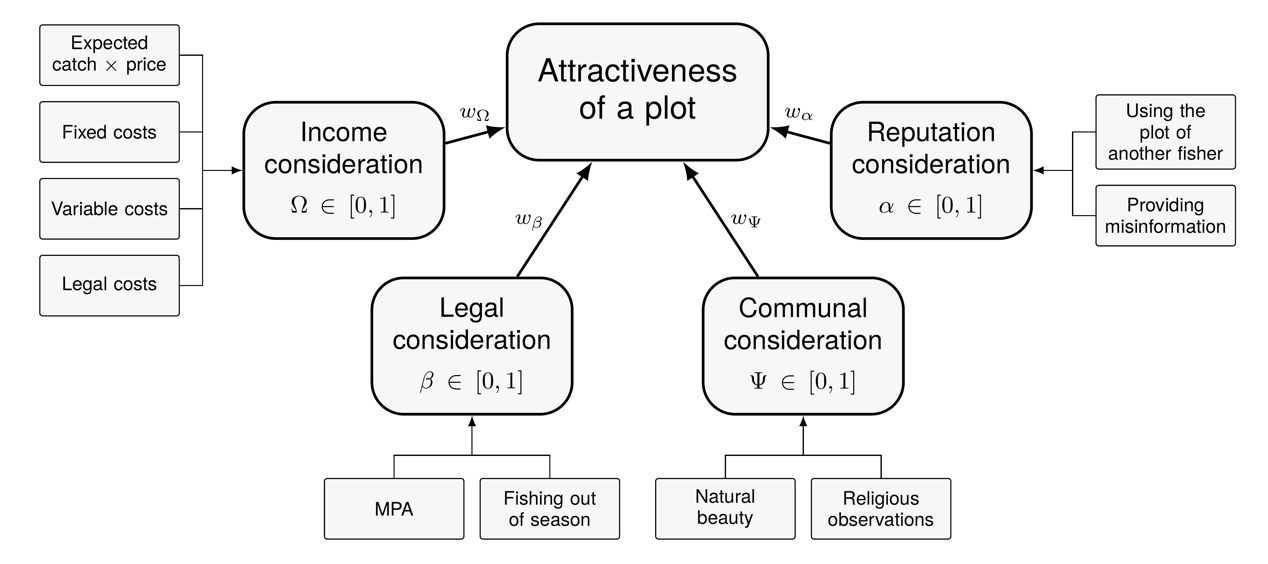
Weights are assigned to each preference. As in the above, this enables the inclusion of socio-cultural differences between fisheries and heterogeneity within a fishery. To compare income expectations with other preferences, \(\Omega\) is calculated as a relative value. We define \(\Omega\) between 0 and 1 as \(\frac{\Omega_{HERE}}{\Omega_{BEST}}\) where \(\Omega_{HERE}\) refers to the area in consideration and \(\Omega_{BEST}\) refers to the area with the highest expected income.

Non-economic considerations can be positive or negative. For example, a cultural norm can be punitive (i.e., overstepping the norm is negative), neutral (i.e., there is no cultural norm associated with the act), or encouraged (i.e., adhering to a cultural norm is a positive). As such, an area can be valued between -1 (making the area less attractive) and 1 (making the area more attractive) for each non-economic consideration. The economic consideration is between 0 and 1, as the satisfaction thresholds ensure only economically satisfactory areas are taken into consideration. In all, the perceived attractiveness for each fishing area, \(\lambda\), is calculated as:

\[ \lambda_{i} = w_{\Omega} \Omega_{i} + w_{\Psi} \Psi_{i} + w_{\alpha} \alpha_{i}\]

\[(5)\]

The model consults the areas in the index and removes all areas that are deemed to be economically unsatisfactory (notably, this may change from day to day if prices, costs, and fines change). The expected income is then normalised as described in the above to yield a value between 0 and 1. Of the remaining areas, the fisher consults information pertaining to legality, communal norms, and personal reputation and scores each area to calculate the \(\lambda\)-value for each area and targets the one with the highest \(\lambda\)-value.

Exploration. If no area is economically satisfactory, the fisher explores new areas. Thus, exploration emerges naturally from dissatisfaction with current fishing grounds. However, even if fishers are content with a selection of areas, they may wish to explore other areas. As with the memory component, future research should explore adequate exploration functions. We suggest the following candidate exploration model:

\[ P(exploration) = \frac{1}{n^{k_{E}}}\]

\[(6)\]

where \(n\) is the number of exploratory trips (since the last exploitation phase) that yielded lower profit than the best area so far and \(k\) is a constant determining the degradation rate.

For example, if \(k_{E}=1\), if a fisher has explored 8 areas, which all yield a worse catch than the best so far, \(p(exploration) = 1/8\) (or 12.5%). When exploration yields a new best spot, \(n\) is reset to 1, as exploration has yielded a positive result, which encourages more exploration. The above is a proposed candidate model. As other exploration models are possible (e.g., greedy multi-armed bandits), future work should test the appropriateness of formal representations of exploration in fisheries. Table 2 summarises the main parameters and factors that can be used to generate different fisher archetypes.

Table 2: Model parameters and factors.

Model parameters (driving behaviour)	Model factors (constraining behaviour)
Satisfaction parameters	Social factors
\(\Phi\): Satisfaction – absolute minimal target (\(1-\infty\))	1. Friends in information sharing network (\(0-\infty\))
\(\delta\): Satisfaction – relative social target (\(0-1\))	2. Knowledge of income of others (yes/no)
	3. Knowledge of where others fish (yes/no)
Preferences parameters	Preference factors
\(w_{\Omega}\): Income consideration (\(0-1\))	1. Causes that reduce/increase personal reputation (e.g., imitation)
\(w_{\beta}\): Legal consideration (\(0-1\))	2. Causes that are culturally frowned upon or encouraged (e.g., flaunting religious tenets)
\(w_{\Psi}\): Communal/cultural consideration (\(0-1\))
\(w_{\alpha}\): Personal reputation consideration (\(0-1\))
\(F\): Memory time scalar function (Eq. 2 a-c)	Operational costs

Simulating Emergent Rule Breaking

To illustrate how the model responds to changes in relevant conditions, we implement it within the POSEIDON model (Figure 5 a-b). To exemplify how the model enables individual and collective behaviours to change over time, we show how fishers with a strong desire to uphold cultural and legal frameworks can end up breaking the rules under some circumstances. That is, \(\Omega = 1\), \(\beta = .95\), \(\Psi = 1\), and \(\alpha = 1\).

In the simulation there are three non-economic factors: ‘cultural taboo’, ‘personal fishing grounds’, and an MPA. The cultural taboo (represented in red in Figure 5 b) denotes an area that the community, for whatever reason, wants to avoid fishing for the first 6 months of every year. Fishing in this area would contravene communal norms. As such, that area becomes less attractive for those 6 months (for communal considerations, \(\Psi\), the area is negatively valued, -1), but is not taboo for the remaining 6 months (for communal considerations, \(\Psi\), the area is like any other ocean area, 0). Second, personal fishing grounds refer to the locations on which fishers are currently fishing. In the model, fishing where others are fishing is damaging to personal reputation. Finally, the MPA (represented in grey in Figure 5 b) denotes a spatial enclosure where fishers are legally not allowed to fish. Notably, we impose no fine for fishing in the MPA (which would provide an economic incentive to avoid the area). Rather, we are interested in whether fishers with a strong desire to adhere to the legal framework (\(\beta\) = .95) can end up breaking the regulations due to economic pressures. As such, the MPA scores -1 for the entire year.

Figure 6 illustrates the evolution of the simulated fishing pressure over a four-year period. In year 1, while the cultural taboo is in effect (days 0-180), fishers avoid the south-most area where the taboo is placed. Rather than randomly exploring the space, they mainly target areas close to the port due to fuel costs and cluster around the port in between the coast and the MPA. However, as fishers desire to avoid areas where other fishers work due to personal reputation, a few fishers target areas North-East and directly West of the MPA. As the cultural taboo lifts (day 181-365), some fishers enter the South-Eastern waters. However, as biomass near the port is still bountiful, most fishers are economically satisfied and do not explore the new area. Thus, only a few explore areas in the South-Eastern ocean (note that exploration in the cultural area in year 1 tends to be as close to the port as possible to save fuel).

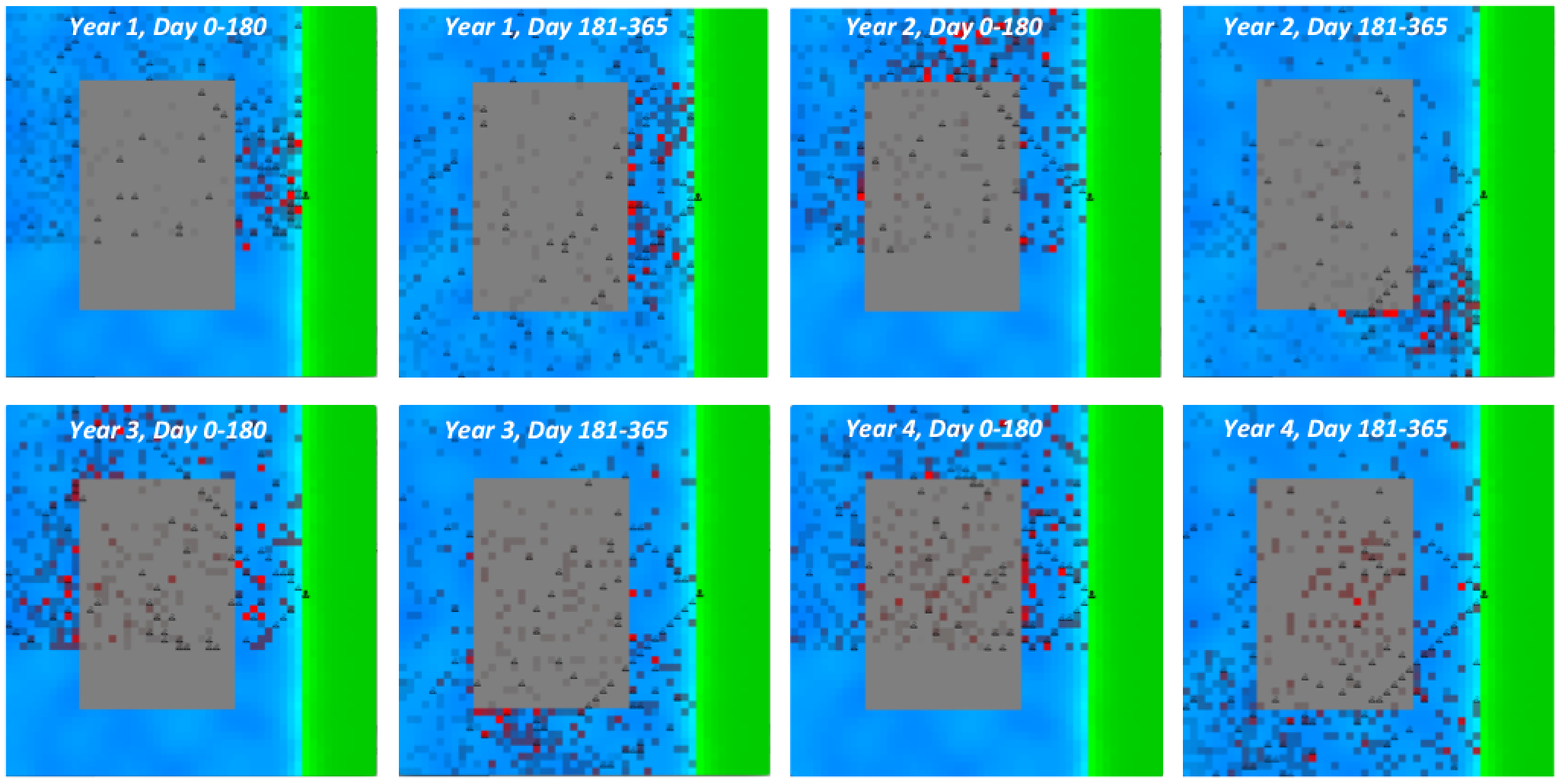
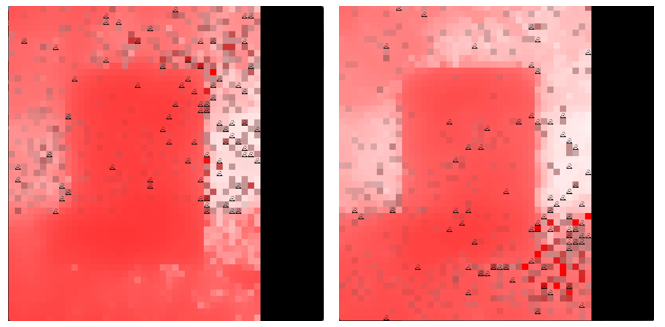
The cultural taboo comes back in effect at the beginning of year 2 (day 0-180). However, as fishers have targeted areas around the port in year 1, biomass has begun to decline precipitously in that area (see Figure 7). Consequently, more fishers are dissatisfied with their catch in those areas and explore other areas. As a consequence, more fishers target areas North-East as well as directly North and West of the MPA (on the Western boundary, it is worth noting that fishers learn to fish the line, as this is the most cost-effective place to go West of the MPA due to biomass emerging from the MPA and reduced fuel cost compared with areas further West). While most fishers in year 1 did not explore the cultural area when it opened due to satisfactory catch elsewhere, most fishers in year 2 explore the cultural area when it re-opens (days 181-365). Interestingly, the fishers almost exclusively explore the South-Eastern part of this area, as they consider fuel costs for exploration (see Figures 6 d and 7 b for illustrations of this).

As year 3 begins, the cultural area closes, and fishers are pushed to explore areas further away from port due to depleting biomass. Concurrently, some fishers now decide to fish within the MPA (a practice which has occurred only sparsely in years 1-2). As fishers run out of viable options for a satisfactory catch, no legal area remains. In the selection process described in section 4, this means no viable places exist for these fishers. Yet, as the desire to adhere to the legal framework \(= .95\), it is not impossible for the fishers to consider areas that are illegal. Thus, as they are unable to locate any remaining attractive areas that are legal, some fishers begin to explore illegal areas within the MPA. This has two effects. First, these fishers are likely to return to the MPA, as the biomass within the MPA has not been overfished. Second, they transmit this information to fishers in the social network in two ways: one, by transmitting information with regards to biomass (as described in the information exchange) and two, by communicating their earnings. The latter may cause fishers in their network to become dissatisfied with their income due to relative satisfaction (that is, a fisher might catch enough to satisfy their absolute demand, but may become dissatisfied when they learn that other fishers are earning more when they fish within the MPA). Due to transmission of biological and economic information as well as the continued depletion of biomass outside the MPA, more fishers eventually begin to fish within the MPA in year 4.

While the simulation is a proof of principle that implements the model in a highly simplified world with regards to biomass, regulatory frameworks, and markets, it shows that the cognitive model responds to cultural, biological, and socio-economic aspects when deciding where to fish – this eventually means that fishers with a strong desire to adhere to the regulatory end up breaking the rules, as they have no satisfactory alternative options left.

Compared with the explore-exploit-imitate approach (or, more generally, bandit approaches), this has several advantages. First, EEI exploration is random. In the current framework, exploration is semi-random, as fishers use costs and inferences to guide exploration. As costs are included in expected income, fishers will choose areas closer to port unless they have reasons to avoid these (e.g., cultural considerations). Further, inferences mean that fishers can estimate catch at hitherto unexplored areas.

Second, EII agents may need to be hard-coded to avoid illegal areas such as MPAs or culturally closed areas (e.g., if there are no consequences for their utility calculation), as their exploration mechanism otherwise does not discriminate (this is the case for MPAs with no fines, as EEI agents would learn to avoid areas with fines). The proposed model provides explicit a priori reasons to avoid (or not) such areas. As such, the current framework enables model simulations that test under which conditions (and how) fishers end up breaking the regulatory framework. For example, in the above simulation, biomass depletion yielded regulatory breakdown. The current model further enables the disentangling of fiscally punitive measures (increased fines or more surveillance) from moral reasons to adhere to the regulatory framework.

Finally, while EEI is reactive, the current framework is anticipatory. That is, EEI agents will return to a previously satisfactory area even if conditions such as fuel or catch prices, fines, and so forth have changed in between trips (because they need to experience ‘bad outcomes’ to learn from them). Comparatively, the current model updates expectations, as the fisher gains information. For example, if prices, costs, and fines change, the model re-computes expected income for all indexed areas. However, as expected catch is updated when the fisher gains direct or indirect information, they need to experience (or hear from others in their network) that the biomass has depleted in order to revise their beliefs and avoid that area in the future. In other words, fishers can behave in an anticipatory manner with information that is socially available (e.g., regulations, pricing, fines, etc.), but will be reactive to information that is not within the socio-economic context (e.g., biomass has depleted unbeknownst to the fisher).

The fisher can behave in anticipatory ways when boundary economic conditions change (price, fuel cost, fine structure, etc.). Equally, the fisher can plan their actions when non-economic boundary conditions change. In the above simulation, the fisher stays away from an area that is considered taboo for 6 months of the year. While the simulation implements where fishing is a considered negative, the opposite would be the case for areas that culturally encourage fishing (or, similarly, where fishing would increase personal reputation rather than damage it). As such, the model can behave in an anticipatory manner with regards to economic and non-economic (positive and negative) considerations. To illustrate how the current framework differs from behavioural models such as EEI and Homo Economicus, we ask the reader to consider three scenarios and how the models would respond to these.

Table 3: Scenarios and behavioural adaptations.

Scenario	EEI Response	Homo Economicus (HE)	Current Model
1. There is a sudden rise in fuel prices due to a market shock. Prices increase five- fold overnight. A week later, the market restores normality and prices drop to pre- shock level.	The agent is a stimuli-response engine that must suffer the consequences of a bad decision to rectify this going forward. The agent would therefore visit the far-away area. We believe this response is unrealistic, as people would not need to experience the economic shock to avoid far-away distances. Further, we believe people would return to far-away distances when prices drop again. Neither is expected by an EEl agent who must experience (rather than anticipate) pain to avoid and who stores pain after the shock has subsided.	The HE agent would be able to calculate perfect expected revenue for any area of the map and would simply move to the place with most profit. While this avoids the economic shock of the EEI, this is most likely to effective compared with people in real life (see Carrella et al., 2020 who show that HE agents are too good compared with actual people.	The agent would calculate expected gain and loss by including expected biomass, fuel expenditures, and so forth. If fuel expenditures are onerous, the agent would forego the far-away area when prices increase and instead fish closer to port. Once prices go down again, the fisher has memory of available biomass in the far-away area and returns immediately if profits are expected to be higher than closer to port. That is, the agent anticipates and avoids the far- away area when prices explore (and thus does not suffer financial harm) and returns when prices normalise.
2. A boat capsizes and the crew drowns. As consequence, the area where they drowned has become a cultural taboo despite significant amount of biomass in the area.	As cultural norms are usually not computed within EEl models, the agent would most likely ignore the event if it would make more money fishing where the boat capsized. However, if social norms are rated as deterrents in the model, the EEI would go and suffer social damage akin to scenario 1 & As cultural norms are usually not computed within HE models, the agent would most likely ignore the event if it would make more money fishing where the boat capsized.	As cultural norms are usually not computed within HE models, the agent would most likely ignore the event if it would make more money fishing where the boat capsized.	Agents who weigh cultural norms highly would avoid the area out of respect for the lost sailors unless the expected financial was so significant compared with alternative areas that the overall attractiveness rating of that area would surpass competing suggestions. This allows for responses to emergent and sudden cultural shifts.
An industrial oil spill contaminates an area that fishers normally visit.	Assuming the area will be hard-coded as unavailable (which raises similar challenges for EEI as Marine Protected Areas), the EEI agent would abandon the oil spilled area and seek new fishing grounds. As exploration is random, it would have to find new grounds via brute force. As such the EEI agents adapts and finds the new space too slowly.	The agent would be able to calculate perfect expected revenue for any area of the map and would simply move to the place with most profit. As with scenario 1, this is probably too good, as it removes the problem of finding the fish given perfect information. As such, the HE agent adapts and finds the new space too quickly.	As the agent can use geographical similarities to estimate other areas with similar biomass and knowledge of costs to estimate the potential profit, the agent would abandon the oily area and engage in non-random exploration. Once a satisfactory new area has been located, the agent will fish there going forward. If the oil spill is cleaned, the agent may return to the original area due to memory of past catches there to see if biomass has returned after the clean-up.

In comparison with EEI and HE models, we thus believe that the current model og adaptive and anticipatory human decision-making in complex human-environment exhibits better and more realistic evaluations of fisher behaviour and thus increases the value of the full ABM.

Discussion and Applicability Beyond the Fisheries Case

Decision-making models in fisheries should capture how fishers adapt to changes in the environment. Typically, this problem has been addressed with simple rule-of-thumb models, statistical fits, or optimisation rules. As argued, simple rule-of-thumb models like exploration-exploitation do not adequately cover fishing behaviour, as they are reactive rather than anticipatory. Explore-exploit models may eventually find appropriate solutions to environmental changes, but take some finite time to find the solution, which may be unrealistic in some contexts, as they have no clear motivated exploration technique. That is, they eventually stumble on an appropriate solution rather than finding the solution through motivated behaviour. Statistical models only extrapolate past data to fit with previously observed patterns. As such, they risk over-reliance on the data. In other words, they risk over-fitting to past actions. As such, these types of models might not be able to predict how fishers will respond to significant changes in the legislative, biological, economic, or competitive environment. Finally, optimisation rules risk being too effective compared with human beings and thus risk being too good at anticipating and changing their behaviour.

In contrast, this paper provides a framework that describes how fishers may use their subjective beliefs and preferences to make decisions. It provides a learning mechanism: fishers can learn directly through personal sampling of the environment and indirectly through information from other fishers. Additionally, the fishers may use the information to estimate the biomass distribution of areas hitherto unexplored. Indirect information transmission can be absolute (another fisher informs of their catch at an area) or relative (another fisher informs how good they find an area). This enables the framework to test sophisticated communication strategies.

Further, the framework operationalizes two modes of economic satisfaction. The first is concerned with absolute catch. This denotes the minimal amount of revenue that the fisher must accrue during a trip for it to be economically viable and satisfactory. The second is concerned with the fisher’s relative income position within their social network of fishers with similar gear and boats. This denotes the relative place at which the fisher considers to be satisfactory – for example, the fisher may deem a trip unsuccessful if their revenue is below the communal average. By conceptualising economic satisfaction along these lines, the framework allows for satisficing, soft maximisation, and complete maximisation.

Finally, the framework provides competing and weighted preferences: income, legality, communal norms, and personal reputation. This enables the fisher to make decisions that are economically unsound, but which may nonetheless reflect real and reasonable decisions (e.g., forgoing fishing due to religious commitments). As preferences are weighted, they can reflect socio-cultural differences between fisheries.

The framework allows for heterogeneity and socio-cultural differences. The weight of preferences, the size of the social network, the information strategy, and the economic satisfaction parameters can be used to represent different fisher archetypes and capture fishing styles (see e.g., Boonstra & Hentati-Sundberg 2016). For example, fishers in small villages may be as concerned about social or reputational aspects as with income. If they break cultural taboos or suffer social reprisals, it may significantly impact their lives outside of fishing. As such, they may forego additional income to adhere to communal norms or to avoid losing social face. Additionally, small-scale fishers may share information about the best fishing grounds with each other. Such a fisher is pro-social and socio-culturally oriented. The framework can represent such a fisher by setting the weights of communal norms and personal reputation as high as income and by setting the communication strategy to reporting all absolute highest catch with all fishers in their network.

Comparatively, some fishers are entirely focussed on income and may disregard consequences to their personal reputation in favour of increased profit. The model can equally represent such a profit-focused fisher by setting social and communal (and possibly legal) preferences low while income preference is high. Additionally, the relative satisfaction parameter is likely to be high, as the fisher is akin to a profit maximiser.

Thus, the same framework can represent fundamentally different types of fishers by setting weights, satisfaction, and information parameters. The parameter setting has direct implications for the management of the fishery. In pro-social communities, it may be possible to manage the fishery through the construction of communal norms while fisheries that disregard legal concerns may only be managed through the size of fines and the frequency of observation or policing.

The simulations show the model makes fishers respond in qualitatively reasonable ways. In these, the fishers are anticipatory rather than reactive and they are not tethered to past behaviour, but use their information about the world to make choices concerning the next fishing locations. The framework naturally allows for heterogeneity within a fishery (e.g., a Gaussian distribution of relative satisfaction) and captures socio-cultural differences between fisheries. In all, it provides a simple, yet computationally specific framework for decision-making in natural environments where resources can be depleted, where social factors influence decision-making, and where information is driven by personal experience or information from others.

As the framework is computationally specified, it can be implemented in any computational fishery model such as the above POSEIDON model (Bailey et al. 2019) to test the impact of environmental changes and to find policy solutions for management problems. Implementing it within such a framework, it can be used to explore questions that have become increasingly prevalent in fisheries management concerning social equity, cohesion, public trust, and cooperation (see e.g., Jentoft 1997; Chan et al. 2012; Gelcich et al. 2010, 2014; Klein et al. 2015) as well as questions on the sensitivity to economic incentives such as operating costs (e.g., Venables et al. 2009), expected revenue (Andersen & Christensen 2006; Hutton et al. 2004; Vermand et al. 2008), and prior knowledge of resource habitat (Begossi 2001; Tidd 2013).

While the current framework offers a psychologically motivated advancement to current fisher decision-making frameworks, the model framework is faced with significant limitations. First, decision-making literature has identified well-known biases and heuristics such as loss aversion and risk aversion (Holland 2008; see Kahneman 2011). Second, it is likely fishers change the relative importance of preferences such as adherence to communal norms if they risk starvation. That is, preference weight should be endogenous rather than exogenous. In other words, social interaction/environmental perturbations may lead to value changes (e.g., a change in value prioritisation). Third, the framework does not specify why fishers choose to enter or exit fisheries. Finally, the framework does not provide a function for planning multiple locations (the travelling salesman problem). These functions should be addressed in future developments.

Fishers are not stimuli-response organisms, but are able to use their knowledge of the world to behave in an anticipatory and planned manner. However, they are also not all-knowing organisms that adapt to changes optimally and instantaneously. Rather, we use our limited personal knowledge to reconfigure and adapt to the new environment over time. As the environment changes, so does behaviour. To capture this adequately, adaptation must lie between ant-like stimuli-response and omniscient, perfect rationality.

Beyond limitations to the model framework itself, there are other important limitations. First, the proposed model is a theoretical proposal that should be tested against extent data, case studies, and through simulated experimentation. Following prior validation exercises of behavioural models using the POSEIDON model (e.g., Carrella et al. 2020b), future work should test the model against extent data to calibrate and validate model assumptions. This is in line with the intention to use interdisciplinary methods "\(\dots\) to check internal consistency and observe the resulting states at the aggregate level, apply cross-methodological experimental methods to validate the hypotheses against real-world data, update data-mining methods, models \(\dots\)" (Conte & Paolucci 2014 p. 8). This would be an important step to apply the model to real-world problems (Filatova et al. 2013), such as the Indonesian case that, in conjunction with the general literature review, inspired the main components (Madsen et al. 2023).

Secondly, the paper provides a conceptual framework grounded in literature review and empirical work. Future work should test model thoroughly including case studies where model parameters are calibrated and validated against extent data (e.g., like Carrella et al. 2020a) as well as sensitivity tested against scenarios that manipulate sensitivity of model parameters, implement the model in differing scenarios such as varying biomass, economic and cultural conditions, and differing reputational consequences of behaviour. As this involves multiple cases, the calibration, validation, and sensitivity-testing is beyond the scope of this paper.

Finally, while we have posited learning and decision-making architecture in the paper, competing approaches should be tested. For example, the learning algorithm at present is frequentist. However, multiple studies in cognitive psychology advocates a Bayesian approach to reasoning (see Oaksford & Chater 2007 for an introduction to this). Moreover, Socio-Economic Status, cultural differences, and psychometrics such as Social Dominance Orientation may impact how people respond to social norm and reputational pressures. The literature on decision-making is too broad to unfold here (see An 2012 for an excellent review of competing methods for understanding human behaviour in complex human-environment systems). Yet, the present model represents a step toward building psychologically informed, anticipatory, and adaptive agents in natural environments.

Conclusion

This paper provides a computationally specified framework for anticipatory and adaptive decision-making in natural environments. Learning is probabilistic from direct, indirect, and inferential reasoning. Exploration and exploitation follow naturally from what is known and what is satisfactory to the individual fisher. The model can represent different fisher types (e.g., collaborative, socially oriented fishers or competitive, individual-oriented fishers).

While it might be possible to generate bespoke behavioural models for a given fishery, it is often impractical due to time constraints or difficult due to lack of available data. Here, we propose a general model framework that allows for human-like adaptation when external factors such as biological, legal, and competitive conditions change. The model can be applied to different types of fisheries, from small-scale developing communal fisheries to large-scale industrial profit-oriented fisheries. The application of the model can be done in (at least) three ways. First, parameters can be set hypothetically to explore principled behavioural patterns. Second, surveys of local fishers, qualitative interviews, and field experiments may be used to set the parameters of the main functions (e.g., the relative weights of income, legal, reputational, and social norm considerations) for a specific fishery. This would take data from the field and use it to apply the model (see e.g., Madsen et al. 2023). Finally, given available data from a fishery, calibration and validation exercises can be used retroactively to estimate the parameters of main functions (e.g., Carrella et al. 2020a).

To our knowledge, the paper provides the first cognitively general framework for describing and predicting fishing behaviour and adaptation. It offers mechanisms for natural learning (information integration), memory limits, and social comparisons that can be parameterised to radically different socio-cultural contexts. The model is quantifiable and therefore falsifiable rather than bespoke or post-hoc. Finally, it is computationally expressed, which enables it to be placed within numerical models such as POSEIDON (Bailey et al. 2019). We illustrate this possibility directly in the case study of rule breaking (Section 4).

While we have exemplified how the model can be implemented in a fisheries context, the functional parameters are general and can be implemented in other complex human-environment systems such as farming and poaching. In principle, any natural system with depletable resources, where humans form subjective beliefs about their environment (and may communicate these to others), and where economic as well as non-economic factors may influence decision-making, the model may be appropriate.

References

ABBOTT, J. K., & Wilen, J. E. (2011). Dissecting the tragedy: A spatial model of behavior in the commons. Journal of Environmental Economic Management, 62(3), 386–401.

AN, L. (2012). Modeling human decisions in coupled human and natural systems: Review of agent-based models. Ecological Modelling, 229, 25–36.

ANDERSEN, B. S., & Christensen, A. S. (2006). Modelling short-term choice behaviour of Danish fishermen in a mixed fishery. Proceedings of the 2005 North American Association of Fisheries Economists Forum

ANDERSON, L. G. (2015). The application of basic economic principles to real-world fisheries management and regulation. Marine Resource Economics, 30, 235–249.

BAERENKLAU, K. A., & Provencher, B. (2005). Static modeling of dynamic recreation behavior: Implications for prediction and welfare estimation. Journal of Environmental Economics and Management, 50(3), 617–636.

BAILEY, R. M., Carrella, E., Axtell, R., Burgess, M. G., Cabral, R. B., Drexler, M., Dorsett, C., Madsen, J. K., Merkl, A., & Saul, S. (2019). A computational approach to managing coupled human-environmental systems: The POSEIDON model of ocean fisheries. Sustainability Science, 14, 259–275.

BASTARDIE, F., Nielsen, J. R., & Miethe, T. (2014). DISPLACE: A dynamic, individual-based model for spatial fishing planning and effort dis-placement - Integrating underlying fish population models. Canadian Journal of Fisheries and Aquatic Sciences, 71(3), 366–386.

BEGOSSI, A. (2001). Mapping spots: Fishing areas or territories among islanders of the Atlantic Forest (Brazil). Regional Environmental Change, 2, 1–12.

BERGER-TAL, O., Nathan, J., Meron, E., & Saltz, D. (2014). The exploration-exploitation dilemma: A multidisciplinary framework. PLoS One, 9(4), e95693.

BESBES, O., Gur, Y., & Zeevi, A. (2014). Stochastic multi-armed-bandit with non-stationary rewards. Advances in Neural Information Processing Systems, 199-207

BOONSTRA, W. J., & Hentati-Sundberg, J. (2016). Classifying fishers’ behaviour: An invitation to fishing styles. Fish and Fisheries, 17(1), 78–100.

BREDE, M., & deVries, H. J. M. (2010). Harvesting heterogeneous renewable resources: Uncoordinated, selfish, team-, and community-oriented strategies. Environmental Modelling & Software, 25(1), 117–128.

BUBECK, S., & Cesa-Bianchi, N. (2012). Regret analysis of stochastic and nonstochastic multi-armed bandit problems. Trends in Machine Learning, 5(1), 1–122.

BUCKHOLTZ, J. W. (2015). Social norms, self-control, and the value of antisocial behavior. Current Opinion in Behavioral Sciences, 3, 122–129.

BURGESS, M. G., Carrella, E., Drexler, M., Axtell, R. L., Bailey, R. M., Watson, J. R., Cabral, R. B., Clemence, M., Costello, C., Dorsett, C., Gaines, S. D., Klein, E. S., Koralus, P., Leonard, G., & Levin, S. A. a. (2020). Opportunities for agent-based modeling in fisheries social science. Fish & Fisheries, 21(3), 570–587.

CARDENAS, J. C., Stranlund, J., & Willis, C. (2000). Local environmental control and institutional crowding-out. World Development, 28(10), 1719–1733.

CARRELLA, E., Bailey, R. M., & Madsen, J. K. (2019). Repeated discrete choices in geographical agent based models with an application to fisheries. Environmental Software, 111, 204–230.

CARRELLA, E., Bailey, R. M., & Madsen, J. K. (2020). Calibrating agent-Based models with linear regressions. Journal of Artificial Societies and Social Simulation, 23(1), 1–7.

CARRELLA, E., Saul, S., Marshall, K., Burgess, M. G., Cabral, R. B., Bailey, R. M., Dorsett, C., Drexler, M., Madsen, J. K., & Merkl, A. (2020). Simple adaptive rules describe fishing behaviour better than perfect rationality in the US West Coast Groundfish fishery. Ecological Economics, 169, 106449.

CHAN, K. M., Satterfield, T., & Goldstein, J. (2012). Rethinking eco-systems services to better address and navigate cultural values. Ecological Economics, 84, 8–18.

CLARK, C. W. (2010). Mathematical Bioeconomics: The Mathematics of Conservation. Hoboken, NJ: John Wiley & Sons.

CLARK, C. W., & Mangel, M. (2000). Dynamic State Variable Models in Ecology: Methods and Applications. Oxford: Oxford University Press.

CONTE, R., & Paolucci, M. (2014). On agent-based modeling and computational social science. Frontier in Psychology, 5, 1–9.

DIENER, E., & Lucas, R. E. (2000). Explaining differences in societal levels of happiness: Relative standards, need fulfilment, culture, and evaluation theory. Journal of Happiness Studies, 1, 41–78.

DORN, M. W. (2001). Fishing behavior of factory trawlers: A hierarchical model of information processing and decision-making. ICES Journal of Marine Science, 58(1), 238–252.

DOWLING, N. A., Wilcox, C., & Mangel, M. (2015). Risk sensitivity and the behaviour of fishing vessels. Fish & Fisheries, 16(3), 399–425.

DOWLING, N. A., Wilcox, C., Mangel, M., & Pascoe, S. (2012). Assessing opportunity and re-location costs of marine protected areas using a behavioural model of longline fleet dynamics. Fish & Fisheries, 13(2), 139–157.

FILATOVA, T., Verburg, P. H., Parker, D. C., & Stannard, C. A. (2013). Spatial agent-based models for socio-ecological systems: Challenges and prospects. Environmental Modelling & Software, 45, 1–7.

GELCICH, S., Buckley, P., Pinnegar, J. K., Chilvers, J., Lorenzoni, I., Terry, G., Guerrero, M., Castilla, J. C., Valdebenito, A., & Duarte, C. M. (2014). Public awareness, concerns, and priorities about anthropogenic impacts on marine environments. Proceedings of the National Academy of Sciences, 111(42), 15042–15047.

GELCICH, S., Hughes, T. P., Olsson, P., Folke, C., Defeo, O., Fernández, M., Foale, S., Gunderson, L. H., Rodríguez-Sickert, C., Scheffer, M., Steneck, R. S., & Castilla, J. C. (2010). Navigating transformations in governance of Chilean marine coastal resources. Proceedings of the National Academy of Sciences, 107(39), 16794–16799.

GUTIÉRREZ, N. L., Hilborn, R., & Defeo, O. (2011). Leadership, social capital and incentives promote successful fisheries. Nature, 470(7334), 386–389.

HATCHER, A., Jaffry, S., Thébaud, O., & Bennett, E. (2000). Normative and social influences affecting compliance with fishery regulations. Land Economics, 76(3), 448–461.

HAYNIE, A., & F. Layton, D. (2010). An expected profit model for monetizing fishing location choices. Journal of Environmental Economics and Management, 59(2), 165–176.

HE, Z., Luo, C., Tan, C.-H., Wu, H., & Fan, B. (2018). Simulating an agent’s decision-making process in black-box managerial environment: An estimation- and-optimisation approach. Journal of Simulation, 13(2), 111–127.

HICKS, R. L., & Schnier, K. E. (2006). Dynamic random utility modeling: A Monte Carlo analysis. American Journal of Agricultural Economics, 88(4), 816–835.

HOLLAND, D. S. (2008). Are fishers rational? A fishing expedition. Marine Resource Economics, 23, 325–344.

HUTNICZAK, B., & Münch, A. (2018). Fishermen’s location choice under spatio-temporal update of expectations. Journal of Choice Modelling, 28, 124–136.

HUTTON, T., Mardle, S., Pascoe, S., & Clark, R. A. (2004). Modelling fishing location choice within mixed fisheries: English North Sea beam trawlers in 2000 and 2001. ICES Journal of Marine Science, 61, 1443–1452.

JAKOBY, O., Grimm, V., & Frank, K. (2014). Pattern-oriented parameteriza- tion of general models for ecological application: Towards realistic evaluations of management approaches. Ecological Model, 275, 78–88.

JENTOFT, S. (1997). Five truisms of fisheries management. Vilamoura International Meeting on Fisheries - Multiple Objectives and Fisheries Management: Strategies for the Future. Vilamoura, Portugal

KAHNEMAN, D. (2011). Thinking Fast and Slow. London: Penguin Books.

KAPLAN, I. C., Holland, D. S., & Fulton, E. A. (2014). Finding the accelerator and brake in an individual quota fishery: Linking ecology, economics, and fleet dynamics of US West Coast trawl fisheries. ICES Journal of Marine Science, 71(2), 308–319.

KLEIN, C., McKinnon, M. C., Wright, B. T., Possingham, H. P., & Halpern, B. S. (2015). Social equity and the probability of success of biodiversity conservation. Global Environmental Change, 35, 299–306.

KLEIN, E. S., Barbier, M. R., & Watson, J. R. (2017). The dual impact of ecology and management on social incentives in marine common-pool resource systems. Royal Society Open Science, 4, 17074.

KULESHOV, V., & Precup, D. (2014). Algorithms for multi-armed bandit problems. Journal of Machine Learning Research, 1, 1–48.

KUNZ, J. (2011). Group-level exploration and exploitation: A computer simulation-based analysis. Journal of Artificial Societies and Social Simulation, 14(4), 18.

LIBRE, S. V. D., van Voorn, G. A. K., ten Broeke, G. A., Bailey, M., Berentsen, P., & Bush, S. R. (2015). Effects of social factors on fishing effort: The case of the Philippine tuna purse seine fishery. Fisheries Research, 172, 250–260.

LITTLE, L. R. & McDonald, A. D. (2007). Simulations of agents in social networks harvesting a resource. Ecological Modelling, 204(3), 379–386.

MADSEN, J. K., Ekawaty, R., Ananthanarayanan, A., Bailey, R., Carrella, E., Dorsett, C., Drexler, M., Mous, P., Muawanah, U., & Saul, S. (2023). Understanding fisher behavior: The case of snapper fishers in Indonesia. Marine Resource Economics, 38, 1.

MADSEN, J. K., Koralus, P., Bailey, R., & Carrella, E. (2020). From reactive toward anticipatory fishing agents. Journal of Simulation, 15(1–2), 23–37.

MANNING, D. T., Taylor, J. E., & Wilen, J. E. (2018). General equilibrium tragedy of the commons. Environmental and Resource Economics, 69(1), 75–101.

MERINO, G., Maynou, F., & García-Olivares, A. (2007). A new bioeconomic simulation tool for small scale fisheries based on game theory: GAMEFISTO model. Aquatic Living Resources, 20(3), 223–230.

MILLER, J. H. (1998). Active nonlinear tests (ANTs) of complex simulation models. Management Science, 44(6), 820–830.

NEIL, E., Madsen, J. K., Bailey, R., Carrella, E., & Payette, N. (2020). Bridging the gaps: Agent-based modelling for elephant poaching mitigation. Ecological Modelling, 427(10905), 4.

OAKSFORD, M., & Chater, N. (2007). Bayesian Rationality: The Probabilistic Approach to Human Reasoning. Oxford: Oxford University Press.

ONO, K., Haynie, A. C., Hollowed, A. B., Ianelli, J. N., McGilliard, C. R., & Punt, A. E. (2017). Management strategy analysis for multispecies fisheries, including technical interactions and human behavior in modelling management decisions and fishing. Canadian Journal of Fisheries and Aquatic Sciences, 75(8), 1185–1202.

PARDUCCI, A. (1995). Happiness, Pleasure, and Judgment: The Contextual Theory and Its Applications. Mahwah, NJ: Lawrence Erlbaum.

PELLETIER, D., Mahevas, S., Drouineau, H., Vermard, Y., Thébaud, O., Guyader, O., & Poussin, B. (2009). Evaluation of the bioeconomic sustainability of multi-species multi-fleet fisheries under a wide range of policy options using ISIS-Fish. Ecological Modelling, 220(7), 1013–1033.

POLANIA-REYES, S., & Echeverry Perez, D. F. (2015). Identification of other-regarding preferences: Evidence from a common pool resource game in Colombia. SSRN preprint. Available at: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2634244

ROBERTS, M. E., & Goldstone, R. L. (2006). EPICURE: Spatial and knowledge limitations in group foraging. Adaptive Behavior, 14(4), 291–313.

SCHILL, C., Anderies, J. M., Lindahl, T., Folke, C., Polasky, S., Cárdenas, J. C., Crépin, A.-S., Janssen, M. A., Norberg, J., & Schlüter, M. (2019). A more dynamic understanding of human behaviour for the Anthropocene. Nature Sustainability, 2, 1075–1082.

SIGUROARDÓTTIR, S., Johansson, B., Margeirsson, S., & Vioarsson, J. R. (2014). Assessing the impact of policy changes in the Icelandic cod fishery using a hybrid simulation model. The Scientific World Journal, 2014(1), 1–8.

SMITH, R. H., Diener, E., & Wedell, D. H. (1989). Intrapersonal and social comparison determinants of happiness: A range-frequency analysis. Journal Personality and Social Psychology, 56(3), 317–325.

TIDD, A. (2013). Spoilt for choice? Linking individual fishing behaviour with fleet dynamics. PhD Thesis, Imperial College London (division of biology)

TOFT, J. E., Punt, A. E., & Little, L. R. (2011). Modelling the economic and ecological impacts of the transition to individual transferable quotas in the multispecies US west coast groundfish trawl fleet. ICES Journal of Marine Science, 68(7), 1566–1579.

VAN Putten, I. E., Kulmala, S., Thébaud, O., Dowling, N., Hamon, K. G., Hutton, T., & Pascoe, S. (2012). Theories and behavioural drivers underlying fleet dynamics models. Fish & Fisheries, 13(2), 216–235.

VENABLES, W. N., Ellis, N., Punt, A. E., Dichmont, C. M., & Deng, R. A. (2009). A simulation strategy for fleet dynamics in Australia’s northern prawn fishery: Effort allocation at two scales. ICES Journal of Marine Science, 66(4), 631–645.

VERMAND, Y., Marchal, P., Mahévas, S., & Thébaud, O. (2008). A dynamics model of the Bay of Biscay pelagic fleet simulating fishing trip choice: The response to the closure of the European anchovy (Engraulis encrasicolus) fishery in 2005. Canadian Journal of Fisheries and Aquatic Sciences, 65, 2444–2453.

VERMOREL, J., & Mohri, M. (2005). Multi-armed bandit algorithms and empirical evaluation. Machine Learning: ECML 2005

WIJERMANS, N., Wiebren, J. B., Orach, K., Hentati-Sundberg, J., & Schlüter, M. (2020). Behavoiural diversity in fishing - Towards a next generation of fishery models. Fish & Fisheries, 21, 872–890.

WILEN, J. E., Smith, M. D., Lockwood, D., & Botsford, L. W. (2002). Avoiding surprises: Incorporating fisherman behavior into management models. Bulletin of Marine Science, 70(2), 553–575.

WILSON, J. A. (1990). Fishing for knowledge. Land Economics, 66(1), 12–29.

WILSON, J., Yan, L., & WILSON, C. (2007). The precursors of governance in the Maine lobster fishery. Proceedings of the National Academy of Sciences, 104(39), 15212–15217.