The Epistemic Role of Diversity in Juries: An Agent-Based Model

, , , ,
and
aUniversity of Michigan, United States; bUniversity of Pennsylvania, United States; cAI Strategy Center, GA technologies, Tokyo, Japan; dYonsei University, South Korea; eNew York University, United States; fUniversity of Arizona, United States
Journal of Artificial
Societies and Social Simulation 27 (1) 12
<https://www.jasss.org/27/1/12.html>
DOI: 10.18564/jasss.5304
Received: 11-Apr-2023 Accepted: 09-Nov-2023 Published: 31-Jan-2024
Abstract
Many factors contribute to whether juries reach right verdicts. Here we focus on the role of diversity. Direct empirical studies of the effect of altering factors in jury deliberation are severely limited for conceptual, practical, and ethical reasons. Using an agent-based model to avoid these difficulties, we argue that diversity can play at least four importantly different roles in affecting jury verdicts. We show that where different subgroups have access to different information, equal representation can strengthen epistemic jury success, and if one subgroup has access to particularly strong evidence, epistemic success may demand participation by that group. Diversity can also reduce the redundancy of the information on which a jury focuses, which can have a positive impact. Finally, and most surprisingly, we show that limiting communication between diverse groups in juries can favor epistemic success as well.Introduction
Computational simulation of jury decision-making has a venerable history, anticipating major aspects of contemporary agent-based modeling with the work of Penrod and collaborators as a seminal beginning (Hastie et al. 1983; Penrod & Hastie 1980; Stasser & Davis 1981; Tanford & Penrod 1983). These early models use a basic ‘strength-in-numbers’ mechanism for opinion updating, in which individuals’ opinions are swayed by the number of other jurors in each ‘camp,’ although individuals may differ in ‘persuadability.’ Stasser‘s (1988) model for small group decision-making was a significant further step, using items of information with weights and valences, a parameter for advocacy in ’sharing’ items with the group, probabilistic ‘retention,’ and consensus in terms of a decision rule. A major focus of the Stasser model was the failure of groups to find ‘hidden profiles,’ with group decisions that failed to reflect information individually distributed. More recent modeling has emphasized affect dynamics rather than cognitive and epistemic considerations. Heise (2013) builds a small group decision model with application to juries, in terms of affect control theory. Agents carry a more permanent affective role identity (defined by EPA dimensions of evaluation, potency, and activity) and keep track of a transient affective meaning (defined in the same dimensions) determined by recent exchanges. The core mechanism is agents’ attempt to reduce differences in the two affective measures by the choice of partners and behaviors; the agent ‘active’ on each turn is the one with the greatest tension between those measures, choosing an interactive partner and a behavior (itself with an EPA signature) which optimally moves the transient affective meaning of both participants toward their role identities. With specific application to juries, Heise’s attempt to match distributions of behavior types to data on mock juries from the 1950s (Strodtbeck & Hook 1961; Strodtbeck & Mann 1956). Zöller et al. (2021) add hierarchical network structure to the affect control theory model.
With an eye to contemporary modeling in social epistemology (Grim et al. 2013; Hegselmann & Krause 2002; Mohseni et al. 2023; Rosenstock et al. 2016; Singer et al. 2019, 2021; Weatherall et al. 2018; Weisberg & Muldoon 2009; Zollman 2007), ours is a return to the basic epistemic questions of the earlier models. Whereas much of the contemporary work in social epistemology is in philosophy of science, our focus is on juries. What role might different communicative dynamics and cognitive limitations of agents play in the collective decisions and ‘truth-tracking’ success of juries? Here Stasser (1988) is our clearest precursor. Our focus, however, is on a particular factor in the dynamics and outcomes of jury decision-making: the issue of diversity (Grim et al. 2019; Hong & Page 2004; Kuehn 2017; Page 2015, 2018; Singer 2019; Thompson 2014). Our modeling points out four very different and sometimes unexpected roles that diversity can play in the accuracy of jury decisions.
Traditionally, juries are conceived of as finders of fact. In that regard, the question of what makes a good jury is a question of social epistemology. Here we’ll use criminal juries as a paradigmatic example. On the standard characterization, it is the jury’s job to find a criminal defendant guilty if and only if they really are guilty.1 On a more sophisticated characterization, the jury’s job is to find the defendant guilty if and only if the prosecution has successfully shown that the accused is guilty. On either characterization, the jury’s job as a finder of fact is to make a judgement about what’s true, and in that sense, the job of the jury is essentially epistemic. Our attempt is to construct a simple model in which we can track a number of ways in which diversity or the lack of it can either contribute to or hinder the epistemic success of juries.
Models are of particular benefit where direct empirical studies are severely limited or impossible for conceptual, practical, or ethical reasons, all of which apply to understanding the dynamics of jury deliberation (Heise 2013; Macy & Willer 2002; Zöller et al. 2021). It is moreover widely recognized that highly idealized models of social phenomena can contribute to our understanding of social mechanisms even when they are far from descriptively realistic (Batterman & Rice 2014; Eason et al. 2007; Epstein 2006; Page 2018; Weisberg 2013). By idealizing and simplifying parameters of a target system, a simple model can help us explore the role that different factors may play in generating the epistemic outcomes of jury decision-making.
In this context an agent-based model is particularly appropriate with regard to the issue of diversity in juries as finders of fact. In the models that follow, the goal is to capture the heterogeneity and stochasticity of actors who exchange and retain different bodies of information on the basis of information they already have – a heterogeneity and stochasticity for which it would be difficult to conceive traditional equation-based models, but for which agent-based models are perfect. Although we have pursued it in only limited ways in the current work, an agent-based model of this sort also offers the prospect of easy extension to studies of diversity in more complex networks.
The Many Parameters of Jury Decision-Making
It is important to emphasize the limited focus of our modeling within a far broader literature across a range of disciplines. There are many factors besides diversity that affect jury verdict accuracy and that have previously been considered by scholars in the law, in empirical studies, and in some cases with formal modeling. We’ll begin by giving an overview of several of these – jury size, unanimity requirements, standards of proof, and deliberative styles – primarily to contrast them with our focus on diversity here.
Jury size
Despite the familiar 12-member jury in criminal cases, the number 12 was held in Williams v. Florida, 399 U.S. 78 (1970) to be a “historical accident,” although later, Ballew v. Georgia, 35 U.S. 223 (1978) required that juries contain at least 6. The largest contemporary jury size requirement is Scotland’s, which requires juries of 15 (but with only a requirement of a majority vote). On review, Kenny MacAskill, Cabinet Secretary for Justice, concluded that Scotland’s jury requirements were “uniquely right” (The Scotsman 2009).
Saks & Marti (1997) offers a meta-analysis of empirical studies of jury size, indicating that larger juries took longer to deliberate, with more thorough discussion, but with no particular lean toward verdicts in either direction. Of most importance to our work on diversity here is the simple observation in Saks and Marti that larger juries were more likely to contain at least one non-white member. Luppi & Parisi (2013) notes that, contrary to simple probabilistic models, reductions in jury sizes in a number of states since Williams v. Florida have not reduced mistrial rates. They propose an explanation in terms of information cascades. On the basis of an agent-based model, Angere et al. (2016) concludes that “while it is in principle better to have a larger jury,” the value of having more than 12-15 jurors is likely to be minimal. Given assumptions of honest information and with jury deliberation modeled as a random walk, Helland & Raviv (2008) concludes on the basis of cost considerations that the optimal number of jurors is one.
In ways evocative of some of our results here, results from early computational models indicate the epistemic importance of including minority views, with their influence a factor of relative representation rather than the absolute size of the jury (Stasser 1988; Tanford & Penrod 1983).
Unanimity vs. Majority
In Ramos v. Louisiana, 590 __ U.S. (2020), by a 6 to 3 vote, the Supreme Court held that the Sixth Amendment, as incorporated against the States under the Fourteenth Amendment, requires a unanimous verdict in cases of serious crime. An amicus brief in Ramos from ‘Law Professors and Social Scientists’ of the Constitutional Accountability Center claims that the cost of requiring unanimity is small, with benefits of more thorough deliberations, increased consideration of minority viewpoints, and more accurate outcomes as a result.
In empirical work, Hastie et al. (1983) found that juries that were required to be unanimous deliberated longer, discussed key facts to a greater extent, touched on more case facts than two-thirds quorum juries, corrected mistaken assertions by members more often, and elicited the participation of minority-view jurors to a greater extent. Toward a meta-analysis, Devine (2012) reports consistent results from the empirical literature on the jury decision rule: that deliberation in juries under a requirement of unanimity, rather than some smaller majority, take longer and result in more hung juries, though their findings are not systematically related to ‘guilty’ or ‘not guilty’ verdicts.
Tanford & Penrod (1983) offers an early computer model in which use of a majority versus unanimity rule makes no difference to the results. In analytic results, Austen-Smith & Banks (1996) and Feddersen & Pesendorfer (1998) show that unanimity is suboptimal if each juror considers themselves pivotal and conditions the probability of guilt on the remaining jurors believing so (but see also Margolis 2001). In a Bayesian model of jury voting as a game of incomplete information, Duggan & César (2001) demonstrates that the probability of a mistaken judgment goes to zero with increased jury size for every voting rule except unanimity. List (2004) further offers a formula intended to reflect the chance that a suspect is guilty, given a particular percentage of guilty judgements in the jury. That formula indicates that it is only an absolute margin between those favoring ‘guilty’ and those favoring ‘not guilty’ that determines the result, whether that reflects a unanimous jury or not (see also Hawthorne 1996). As Bovens & Hartmann (2003) notes:
There is something very counterintuitive about this result. When 10 out of 10 jurors pass a guilty verdict, we would take this to be strong evidence that the suspect is guilty. When 55 out of 100 jurors pass a guilty verdict, then we would not think much of this narrow proportional margin \(\dots\) on List’s model the additional 10 guilty votes have precisely the same evidential value as 10 guilty votes when there are only 10 voters (Bovens & Hartmann 2003 p. 82).2
On the basis of an agent-based model, Angere et al. (2016) conclude that “no more than a >50% majority should be required for a conviction, even in criminal cases.”
The contrast between conclusions from analytic and computational models on the one hand and some empirical findings and the legal tradition on the other is striking. Part of the contrast may be due to measures of jury success: Angere, Olsson and Genot’s model in particular is more complex than that offered here and includes a major role for hung juries in their gauge of jury success. But it should also be noted that none of the models mentioned consider the role of diversity in the information aggregation of jury decision-making. That is the central topic of our work here.
Standards of legal proof
Criminal juries are charged to convict only if the prosecution has proven their case ‘beyond a reasonable doubt,’ a standard the Supreme Court has held is grounded in “a fundamental value determination of our society that it is far worse to convict the innocent than to let a guilty man go free” (In re Winship, 397 U.S. 358, 90 S. Ct. 1068, 25 L. Ed. 2d 368, 1970).
But what constitutes reasonable doubt? Surveys of judges would seem to equate ‘beyond a reasonable doubt’ with a subjective certainty of 90 percent, though a number of studies indicate that jurors apply a far lower threshold (Dane 1985; Hastie et al. 1983). A wording that has passed muster with the Supreme Court, offered by the Federal Judicial Center in 1987, specifies that evidence ‘beyond a reasonable doubt’ is that which leaves a juror “firmly convinced” of the guilt of the accused (Devine 2012).
Laudan (2008) offers a thorough and biting critique of inconsistent jury instruction regarding standards of proof. Underscoring Laudan’s charge, the small body of relevant empirical work has emphasized the wide variability with which juries interpret those instructions (Horowitz & Kirkpatrick 1996; Koch & Devine 1999). Although there are prospects for creating agent-based models that use a notion of epistemic confidence levels, the legal and empirical background is murky enough that it is not clear how these would connect. In the present study, we model jurors only in terms of belief content (‘guilty’ or ‘not guilty’); while we have a natural measure of the strength of their beliefs, we do not use that to model a particular standard of proof.
Deliberation styles
There is a distinction in the social psychological literature on juries between ‘verdict-driven’ and ‘evidence-driven’ styles of jury deliberation. In verdict-driven dynamics, jurors enter deliberations with an initial opinion regarding guilt or innocence, marshalling evidence and argument in terms of that initial inclination. In ‘evidence-driven’ deliberation, jurors tend to withhold judgment until a full set of evidence and arguments have been reviewed. Several studies indicate that a verdict-driven style of deliberation results in less thorough examination of the evidence and more hung juries (Devine et al. 2007; Hastie et al. 1983). Although room remains for exploration, the deliberation style of the jurors in our model is quite simple, involving merely putting forward random reasons heard by all.
Modeling diversity in juries
The diversity of juries has become a topic of increasing concern in the legal literature (Chopra 2014; Joshi & Kline 2015). Recently, Chief Judge Juan R. Sánchez of the Eastern District of Pennsylvania said that “The public’s engagement and trust in the court system is dependent on jury diversity \(\dots\) Jurors from a cross section of the community bring different life experiences and perspectives to jury deliberations, leading to more informed discussions and greater public confidence in the judicial process” (U. S. Courts 2019). An older statement from Thurgood Marshall in Peters v. Kiff, 407 U.S. 493, 503 (1972) echoes the value of diversity in juries: “When any large and identifiable segment of the community is excluded from jury service, the effect is to remove from the jury room qualities of human nature and varieties of human experience, the range of which is unknown and perhaps unknowable”.
There is a series of models and mathematical results (some contested), which support an important role for cognitive diversity in group epistemic success (Grim et al. 2019; Hong & Page 2004; Kuehn 2017; Page 2007, 2011; Singer 2019; Thoma 2015; Thompson 2014; Weisberg & Muldoon 2009; Zollman 2010a). Here we develop and apply an agent-based model of collective information aggregation to the specific topic of diversity in jury decision-making. As indicated below, some aspects of diversity in group decision-making beyond cognitive diversity per se can also have an epistemic impact.
In section 3 we introduce the basics of the model, which we employ with variations in sections 4 through 7 in order to explore four different contributions diversity can make to epistemic jury success. Section 4 shows that where different subgroups have access to different information, in cases of what we call ‘sided access,’ equal representation among subgroups favors epistemic jury success, measured in terms of percentages of correctly modeled verdicts. Section 5 highlights the important effect of diversity in cases we call ‘sided access to better information,’ where one subgroup has special epistemic access to particularly strong evidence. Section 6 explores the effect of diversity in cases of ‘random differential access,’ where we show that different subgroups having access to any different information at all can help the group by reducing the redundancy of the information on which a jury focuses, a finding with links to Hong & Page (2004) and later literature (Grim et al. 2019; Kuehn 2017; Page 2007, 2011; Singer 2019; Thompson 2014). Section 7 presents the surprising result that in increasing ‘enclave communication,’ limiting communication between diverse groups can favor jury success as well.
The model of jury decision-making we’ll describe is of course not meant to fully capture the complex and sophisticated ways real juries deliberate. Indeed, although we will occasionally refer to the process as ‘deliberation,’ our emphasis is on collective information aggregation and consensus on the basis of diverse individual information introduction, exchange, processing and retrieval. Other aspects of full deliberation – complex argument, for example, challenging the structure of other jurors’ arguments, questioning the credibility of witnesses or the interpretation and relevance of circumstantial evidence – are clearly beyond the simple model offered here. What is of interest is that positive epistemic effects of jury diversity are evident even within this simple and limited model.
Modeling the Sharing and Aggregation of Reasons
We will model the aspects of jury decision-making in which jurors exchange reasons for or against different possible verdicts, individually changing opinions toward a final verdict. We take inspiration from the iconic jury-room scenes from 12 Angry Men (Lumet 1956). There, we see jurors sharing reasons for thinking the eighteen-year-old is guilty or not guilty and responding to each other’s reasons. For example, we can think of the fact that the store sold the peculiar knife that was used in the crime to the defendant as a strong reason for thinking the defendant is guilty. But the fact that the stab wound was made at an awkward angle is a reason to think he’s innocent. Inspired by these examples, we model reasons as propositions that support different verdicts with different strengths. As we argue in previous work (Singer et al. 2019, 2021), this conception of reasons is flexible enough to capture important aspects of collective information aggregation while also being simple enough to allow us to understand the mechanisms that give rise to our results.
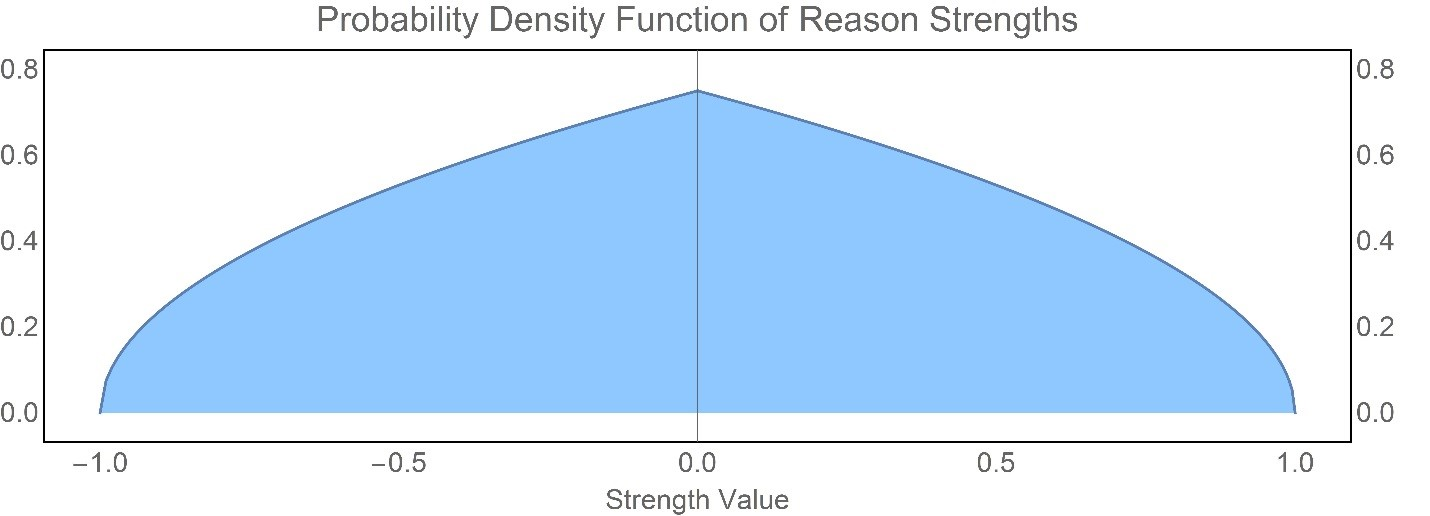
At the beginning of each run of our model, we create a pool of 100 reasons, each of which has both a valence — positive or negative, thought of as indicating whether it’s a reason to think the defendant is guilty or not guilty — and a real-valued strength between 0 and 1. The 100 reasons represent all of the facts relevant to the case. Formally, we create each reason by drawing a strength at random from a beta distribution with \(\alpha = 1\) and \(\beta = 1.5\), then assigning a positive or negative valence uniformly at random (see Figure 1). We use a beta distribution because we want a probability distribution that generates values constrained on the \([-1, 1]\) interval, and we choose these specific values so that weaker reasons are more plentiful than stronger reasons. Exploratory tests show that the qualitative results are invariant to changes in the parameters that roughly preserve the prevalence of weak versus strong reasons.
In each run of the model, there are 12 jurors, each of which starts out with 15 reasons. We’ll say more below about how those reasons are chosen, but for now, let’s think of those reasons as a combination of the juror’s background knowledge and the reasons the juror takes to be salient from the trial. Then, on each step of a run of the model, a random juror is chosen to share a random reason they have. When a reason is shared, all of the other jurors hear it and add it to their bank of reasons (except in the version of the model we discuss in section 7). At any moment, we take the view of a juror to be modelled by the mean of the reasons they hold. So, for example, if a juror has three reasons of strength 0.2 and one reason of strength 0.05 to believe the defendant is guilty, and one reason of strength 0.35 for not guilty, the juror will, all-things-considered, believe the defendant is guilty and will do so with strength \((0.2 + 0.2 + 0.2 + 0.05 - 0.35) = 0.3\). In other work we consider the roles of different ways of sharing reasons and different ways of managing a limited memory in models like this (Singer et al. 2019, 2021). Here, however, we put aside complications of limited memory and complex ways of sharing by idealizing jurors as having unlimited memories and using random sharing in the course of information aggregation and decision-making.
When all the jurors have the same view — guilty or not guilty — a verdict is declared. We also provide results from the same model runs for verdicts declared the first time a simple majority (>50%) and an 80% majority of agents are in agreement, although it turns out that those variations don’t substantively affect our main claims regarding the impact of diversity on jury accuracy. Following Singer et al. (2019), Singer et al. (2021), to measure accuracy of a verdict, we’ll regard the ‘truth’ in a run of the model to be the valence of the sum of the full pool of reasons, i.e. what one would believe if one had access to all of the facts relevant to the case. For ease of exposition, if the sum of the full pool of reasons is positive we’ll think of the defendant as guilty, and if the sum of the full pool of reasons is negative we’ll think of the defendant as not guilty. We can then gauge the epistemic success of the jury under different parameters by looking at what percentage of jury decisions capture the ‘truth’ indicated by the total of all reasons in our original pool of 100. Our standard measure of epistemic success is a percentage of correct verdicts in 10,000 runs of the model. Because our jurors constantly enlarge their held reasons to include all those put forward, the number of hung juries in our data is vanishingly small.3
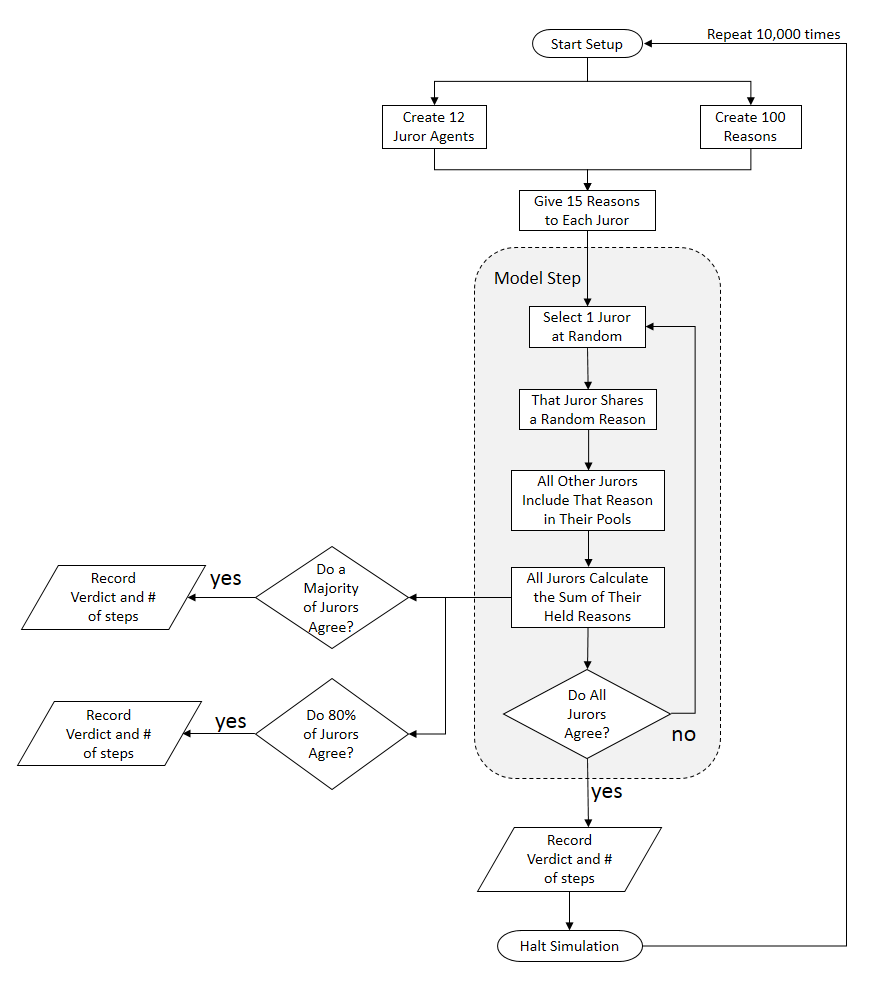
The model is simple by design with a small number of parameters and a clear mechanism. A diagram for the model operation is offered in Figure 2. To further facilitate ease of understanding we also summarize the model details in tables of the parameters and values in Table 1 and our technical terms and meanings in Table 2. We have furthermore made the Netlogo simulation model available on CoMSES (https://www.comses.net/codebases/45ed1706-c1c7-45ad-a9a8-9392e298b947/releases/1.0.0/) for those interested in digging deeper and/or extending the model.
| Parameter | Value(s) |
|---|---|
| Size of full pool of reasons | 100 |
| Reason strengths | [-1, 1] |
| Number of reason types | 2 |
| Number of juror types | 2 |
| Number of jurors | 15 |
| Initial number of reasons per juror | 15 |
| Number of model runs per configuration | 10, 000 |
| Term | Descripton |
|---|---|
| Truth | The valence (+ or -) of the sum of reasons in the full reason pool |
| Agent’s view | The valence of the sum of agent’s reasons |
| Verdict | The valence when enough (\(>50\%, 80\%\) or \(100\%\)) agents have the same view |
| Success | Percentage of verdicts that match the valence of the truth |
| Overlap | The proportion of reasons that are accessible to both types of jurors |
| Correlation | The percentage of A-type reasons that are positive, and B-type that are negative |
Note that positive and negative only need to be thought of as opposed verdicts; the model is entirely symmetrical, so one might alternatively choose to think of a negative value as indicating guilt and a positive mean as indicating innocence.4 Also note that although we’ll talk as though a reason with a positive valence is a reason to see the defendant as guilty and a negative one as a reason against guilt, it’s also possible to adopt a proof-centric conception of the reasons by viewing individual positive reasons as reasons to think that a guilty verdict has been proven by the prosecution and negative reasons as reasons to think the opposite. There is nothing in the formal model which prohibits this alternative (though perhaps more cumbersome) interpretation.
Several admitted artificialities of the model call for specific emphasis: a ‘truth’ reflected in the sum of the initial reasons pool, the random communication of reasons in the course of decision-making, and the unlimited memory of the jurors. Because of the highly idealized and abstract nature of the model, we do not put forward the model as either descriptively realistic of juries in a social psychological sense or as sufficient for normative conclusions regarding jury or other small group deliberations. Of course, considerations beyond the epistemic also bear on the proper construction and conduct of juries. Despite those limitations, however, we take our results to suggest important ways in which certain factors can influence the epistemic success of jury decision-making—in particular, four ways in which jury diversity can influence epistemic success.
Diversity and Sided Information Access
To investigate the role of diversity in jury verdicts, we start by thinking of different subgroups of the population as having differential access or sensitivities to bodies of evidence on different sides of the question of guilt. The idea is that members of different social groups, because of their background information or experience, may be more sensitive to different bodies of evidence (or even straightforwardly biased in favor or against guilt). These are cases of what we’ll call ‘sided access’.
As noted above, in our model, the full pool of reasons consists of 100 reasons with strengths between -1 to 1 (with more reasons closer to 0), where a positive valence can be understood as ‘guilty’ and a negative valence as ‘not guilty’ (or the other way around, because everything is symmetrical). To model sided access, we’ll divide the reasons into two types, designated with letters A and B. Initially, reasons with positive valence are designated A reasons and those with negative valence are designated B reasons. But we also allow for an overlap, a group which contains both A and B reasons (“the AB reasons” or “the reasons in common”). We form the pool of AB reasons by drawing a particular percentage of reasons randomly and equally from the A and B groups.
We also divide the jurors into two types, again designated with letters A and B. Jurors of each type begin deliberations with 15 reasons chosen uniformly at random from reasons matching their type and the reasons in common. That is, A jurors start with 15 reasons from the A \(\cup\) AB reasons, and the same is true mutatis mutandis for B jurors. The model thus includes two subgroups of jurors who may have partially distinct and partially overlapping access to the reasons.
If we fix a specific percentage of reasons that are ‘reasons in common,’ we can track the effect of diversity in modelled decision-making: the representation percentage of each jury type that results in the highest rate of epistemic success – i.e. the percentage of correct verdicts (as outlined, those with valence matching the mean of all reasons). Figure 3 tracks jury success across the percent of jurors that are type B when AB reasons make up 50% of the reasons (for unanimous, 80%, and simple majority verdicts). As throughout, we average results over 10,000 runs using juries of 12.
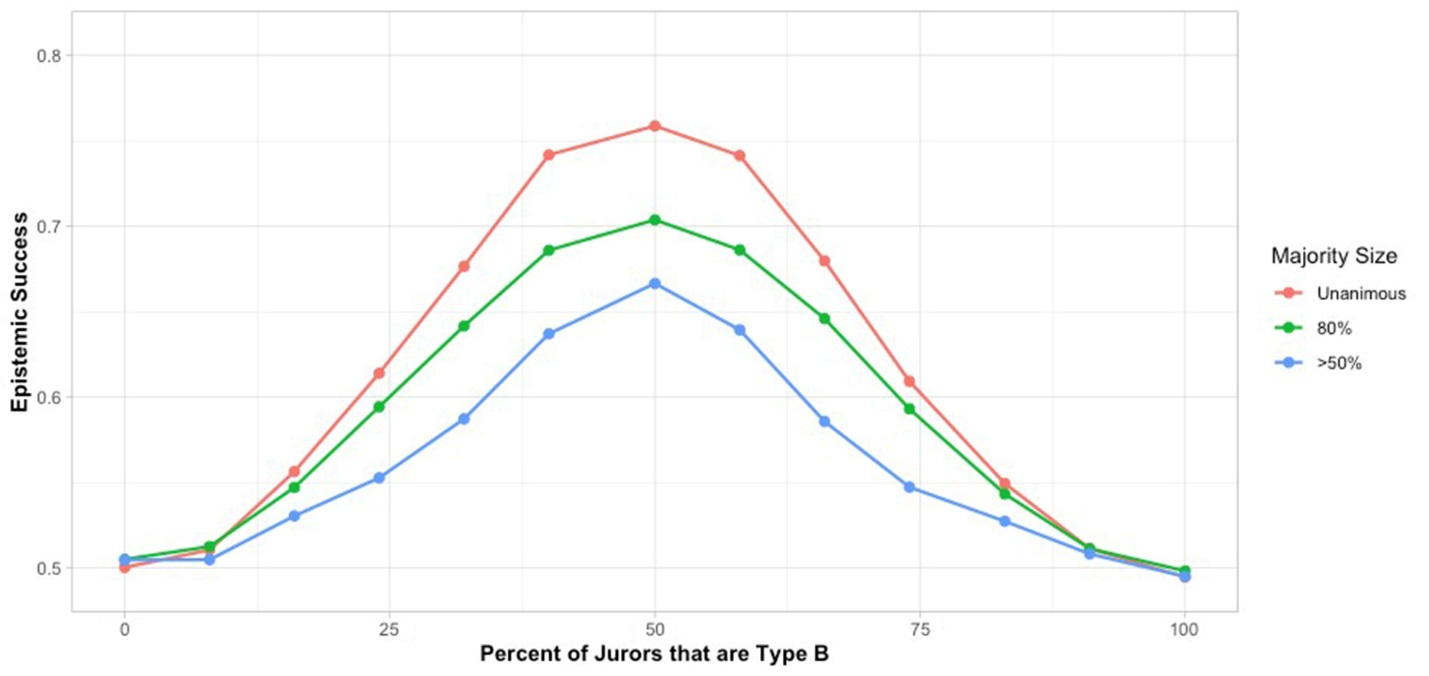
It is clear in this case that unanimous juries do best across all percentages of A and B jurors, but it is also clear that the distance between results in unanimous juries and those with lower majorities is most pronounced when there is equal representation of the two sub-groups. The importance of equal representation is even clearer when there is no overlap along the initial reasons for the two jury sub-groups (Figure 4). Here at least 25% representation of each group is required for anything better than random jury success at any of the majority levels, with the highest rate of success prominent at equal representation.
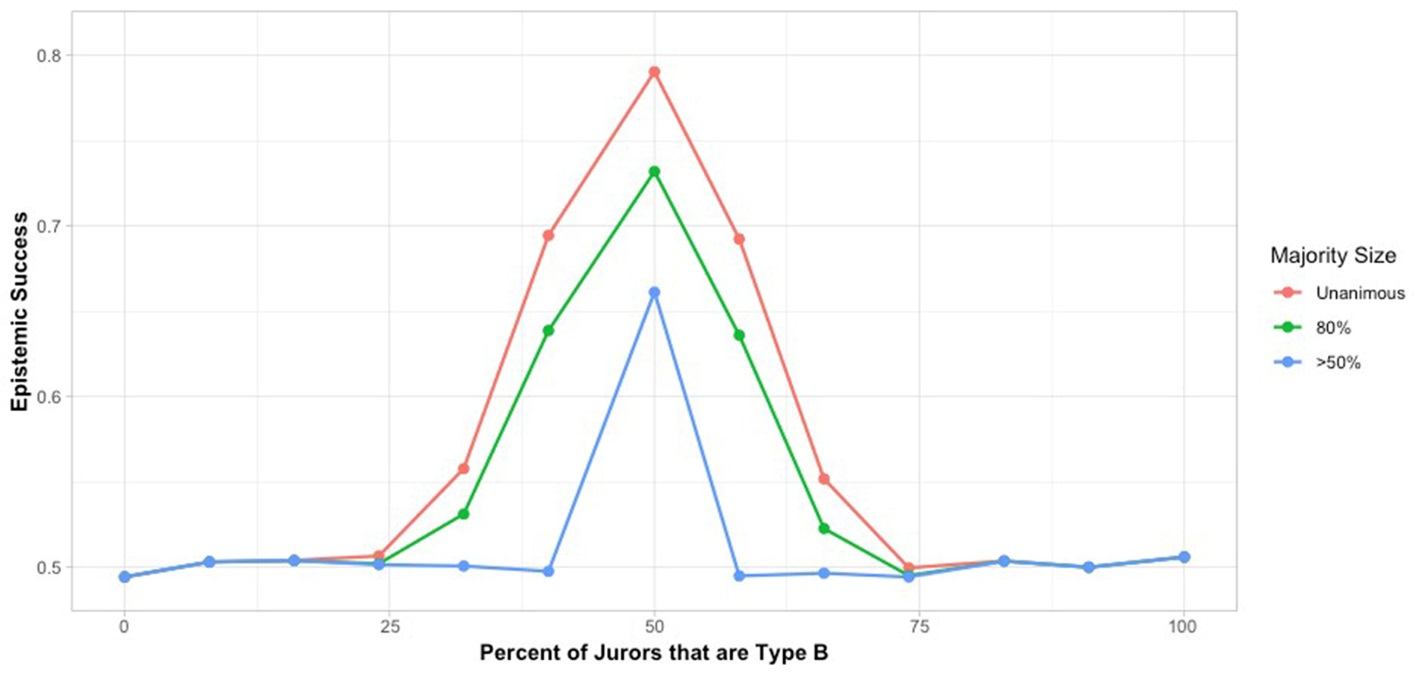
In these first simulations, we have assumed that all A reasons are positive in valence, supporting a guilty verdict, and all B reasons are negative, supporting a verdict of not guilty. But since there is overlap, as in Figure 3, it is still possible for A jurors to draw both negative and positive reasons among their initial 15, since they draw from a pool of reasons in common as well as from ‘pure’ A reasons. Similarly for B jurors.
But we can also relax the assumption that the A reasons that are outside of ‘reasons in common’ (what we might call ‘pure A reasons’) are exclusively positive and that the B reasons that are outside of ‘reasons in common’ (‘pure B reasons’) are exclusively negative. In doing so, we create a new parameter of interest, one that measures the correlation of reason type (A or B) with valence (positive or negative, ‘guilty’ or ‘not guilty’). With 100% correlation between reason type and valence, as assumed in the simulations above, the initial reasons drawn by A jurors outside of reasons in common (the pure A reasons) are all reasons that support a guilty verdict, and the initial reasons drawn by B jurors outside of reasons in common (the pure B reasons) are all reasons that support a verdict of not guilty. With lower correlations, the reasons initially drawn by A jurors beyond reasons in common can be expected to be less exclusively positive, those drawn by B jurors to be less exclusively negative. Figure 5 offers a simple illustration. Correlation is a distinct parameter from overlap because it applies to all A and B reasons, including those initially available exclusively to jurors in virtue of their type.

Figures 6 and 7 show the results of repeating our initial simulations with 50% rather than a full 100% correlation between reason type and valence.
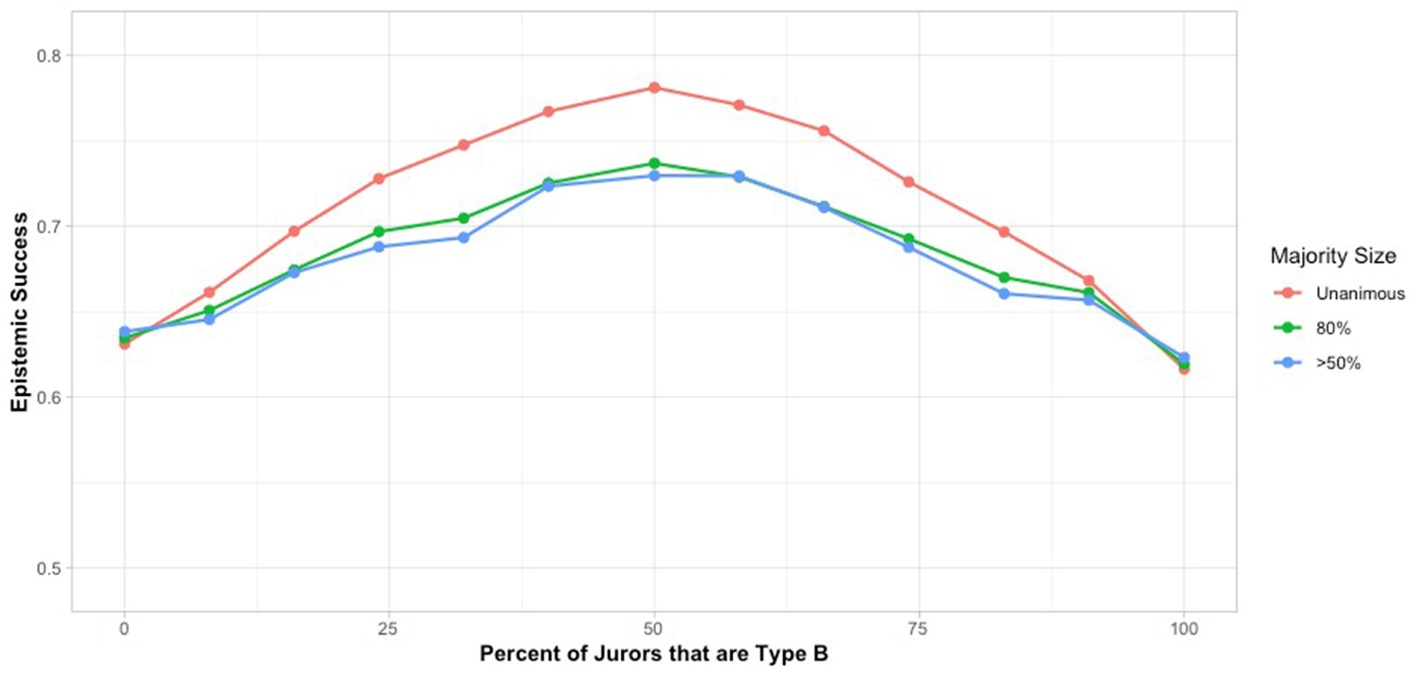
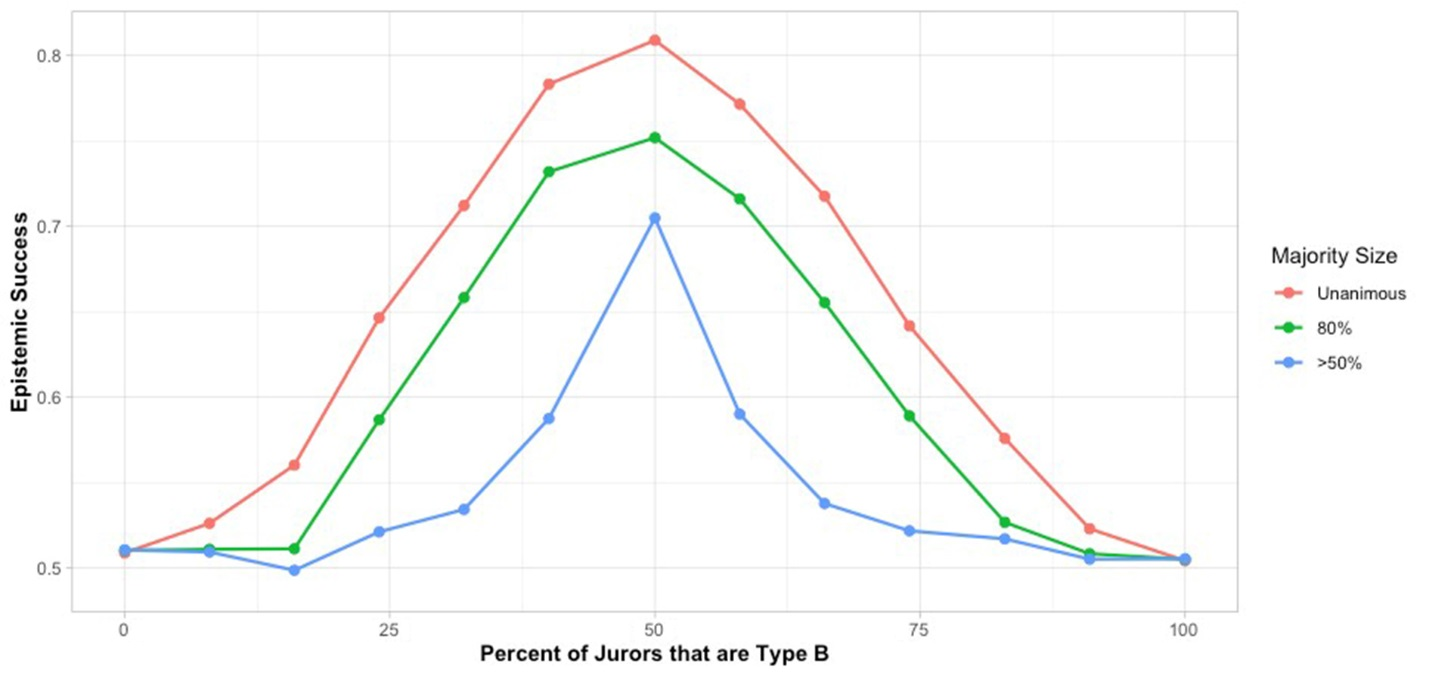
The epistemic superiority of juries with equal representation of subgroups is clear here as well, though the disadvantage of unequal jury representation at the left and right ends is dampened with reduced correlation. The epistemic superiority of requiring unanimous juries is again clear throughout. It is interesting to note that the highest jury success rates in our tests appear with unanimous juries in which subgroups share no initial reasons in common. Here the non-redundancy effect examined in section 6 may play an important role.
What our simulations suggest is the following: if there are juror types that can be expected to have differential access or sensitivity to different bodies of evidence, and where there is a correlation between those bodies of evidence on each side and evidence favoring guilt or innocence, high rates of jury success require genuinely equal representation of the two groups. This holds even when fully half the evidence is ‘evidence in common.’ When those conditions do not hold — when the two groups have little overlap in the evidence they bring to discussion and when the evidence on the two sides correlate strongly with guilt or innocence — a correct verdict essentially demands equal representation of the two groups.
In this section, all of the results are about different distributions of reasons initially brought to the table by jurors. Once information exchange has started in the model, reasons are put forward, heard, and incorporated by all members of the jury, whatever the valence of those reasons or the sub-group from which those reasons are put forward. Results where communication is not fully open in this way are left to section 7.
We should again highlight our modeling assumptions. We have assumed that our two groups have differential access or sensitivities to different bodies of evidence. We take this assumption to be motivated by real world phenomena, such as data showing different perceptions of police bias and profiling between Black and non-Black people (Flexon et al. 2019; Nadal et al. 2017; Nadal & Davidoff 2015). We take this data to suggest that a minority juror may be more alive to real prospects for biased representation and self-protective falsification in police testimony. Our modelling assumption also reflects claims typically put forward in considerations of social diversity and systemic ignorance by proponents of standpoint epistemology (Hartsock 1987; Mills 2007; Wylie 2003).
In setting up the model this way in this section, we have assumed that the type of reason is significantly correlated with whether it’s a reason for or against guilt. That is, we have assumed that not only do members of different groups have access to different individual reasons but also that the reasons different groups have access to are correlated in terms of whether they’re in favor of guilt or innocence. We know of only a few empirical studies that support thinking that familiar forms of social identity diversity work like this. There is some evidence, for example, that female jurors are somewhat more likely to favor conviction in trials involving sexual harm to women or children (Schutte & Horsch 1997). Devine (2012) concludes that the current research is also consistent with a similarity-leniency effect regarding race—jurors differentially favoring defendants of their race. This effect is clearest in capital cases involving a majority of white jurors and an African-American defendant accused of killing a white victim (Lynch & Haney 2011). The data mentioned above regarding Black perceptions of police bias and profiling might also indicate a greater skepticism regarding police-supplied evidence suggesting guilt.
More generally, it’s natural to hypothesize that in societies where the criminal justice system has systemically been used as a tool of oppression, being a member of an oppressed group makes one more likely to be sensitive to the ways those systems are used against members of oppressed groups. If that’s correct, it is one reason to think that sometimes social or demographic diversity may track the kind of sided information access we model here. That said, the equal jury representations that do best in our simulations need not be interpreted as being about social or demographic diversity. What our results most clearly support is the epistemic advantage of equal representation between groups diverse in their sensitivity to evidence supporting a verdict of ‘guilty’ or ‘not guilty,’ which is a kind of cognitive or epistemic diversity, rather than a kind of social or demographic diversity.
When Evidence is Stronger on One Side
In the previous section, we looked at cases of sided access that were symmetric in the sense that they didn’t assume that the evidence for or against guilt was necessarily stronger. Strength values between 0 and 1 were assigned to each of the 100 reasons according to a beta distribution (as discussed above), with positive and negative valences assigned uniformly at random. So, on average, we would expect the strength of reasons that were accessible to the A subgroup and to the B subgroup to be about the same.
In this section, we’ll ask what happens if the evidence is stronger on one side than the other. We call these cases ‘sided access to better information.’ Here we ask, “what if B jurors are not only more sensitive to reasons favoring innocence, for example, but those reasons are also stronger?” In such a case, initial ‘reasons in common’ as well as those accessible to A jurors might indicate a close call between a verdict of guilty and not guilty, but there might still be a significant amount of exculpatory or incriminating evidence that is initially available only to B jurors. With what comparative degree of strength and what proportion of B jurors can we expect correct verdicts in these cases?
To model this, as above, we assume that 50% of our reasons are reasons in common (AB reasons), and we assume B reasons to be fully correlated with innocence and A reasons with guilt. But to look only at cases where the evidence is stronger on one side, we restrict our sample data to cases in which (by chance) the sum of the entire pool of reasons ranges from strongly negative (min value of -10) through lesser degrees of negative strength by unit intervals. Results are shown in Figure 8.
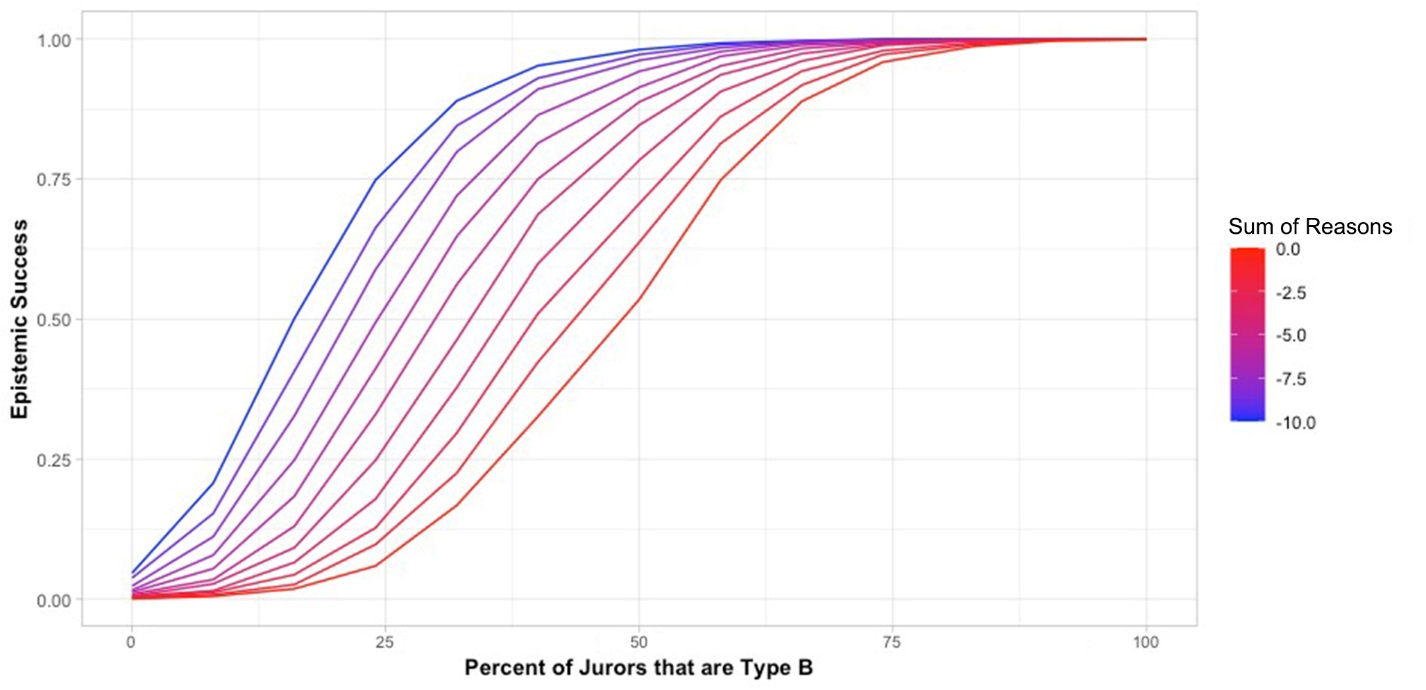
Not surprisingly, the stronger the overall case for innocence (guilt) is, the higher the collective success rate will be given increased representation of a subgroup with heightened sensitivity to evidence on that side. With a strong enough case (sum of reasons between -11 and -10), even 25% representation of that group produces an epistemic success rate comparable to the highest success in earlier simulations. 50% representation produces an epistemic success rate of virtually 100%. Modeling results confirm pre-theoretical expectations: when members of a particular subgroup have more access to (or more sensitivity to) better information, representation by members in that group is essential to jury success, and as the subtlety of the case increases, a greater number of members from the privileged subgroup is required for a high rate of epistemic success.
Diversity and the Reduction in Informational Redundancy
In some of the literature on group cognitive diversity, one source of purported epistemic benefit of diversity is a reduction of redundancy of information and skills in the group. Lu Hong and Scott Page offer a computational model in which agents use ‘heuristics’ to find the highest points on a landscape. Within the constraints of that model, they show a ‘diversity trumps ability’ effect: that groups with randomly diverse heuristics can outperform a group of those individuals with the highest individual performance (Hong & Page 2004; Page 2007, 2011). A mathematical theorem that they offer as an accompaniment to the model has been critiqued, but its legitimate ties to diversity have also been defended (Kuehn 2017; Page 2015; Singer 2019; Thompson 2014). It has been shown that the landscape Hong and Page use in their original model is crucial to their results, undercutting its generality, but that for a range of problems the diversity of heuristics in coordination with other factors can play an important role in group success (Grim et al. 2019).
The informal explanation given for the Hong-Page ‘diversity trumps ability’ effect, where it does hold, is that a group of highest-performing individuals will share the same heuristics. A random group will likely not. Where having multiple heuristics favors the possibility of success, it is the redundancy of the group of highest-performing individuals and the non-redundancy of the random group that explains the greater success of the latter.
In this section, we consider cases where different subgroups randomly have different initial access or sensitivity to different random pieces of information, in contrast to the previous sections where we stipulated that the differential access or sensitivity was (probabilistically likely to be) information on different sides of the question. In these cases of ‘random differential access,’ we see a benefit of diversity in avoiding redundancy in our model that mirrors the Hong-Page result. Since the true verdict in our model corresponds to the sum of all possible reasons, the more reasons that are considered, the greater the chance of a correct verdict. Lack of diversity reduces the number of reasons brought to discussion and thus considered, so the non-redundancy characteristic of diversity can be expected to have a positive epistemic effect.
In the results shown in Figure 9, we have two groups, each with partial initial access to the full pool of reasons. But here there is no correlation between those reasons and positive or negative valences associated with guilt or innocence, nor is the total strength of evidence accessible by one group higher than the other on average. In other words, in these runs the only difference between the subgroups is that they initially have access to different individual pieces of information.
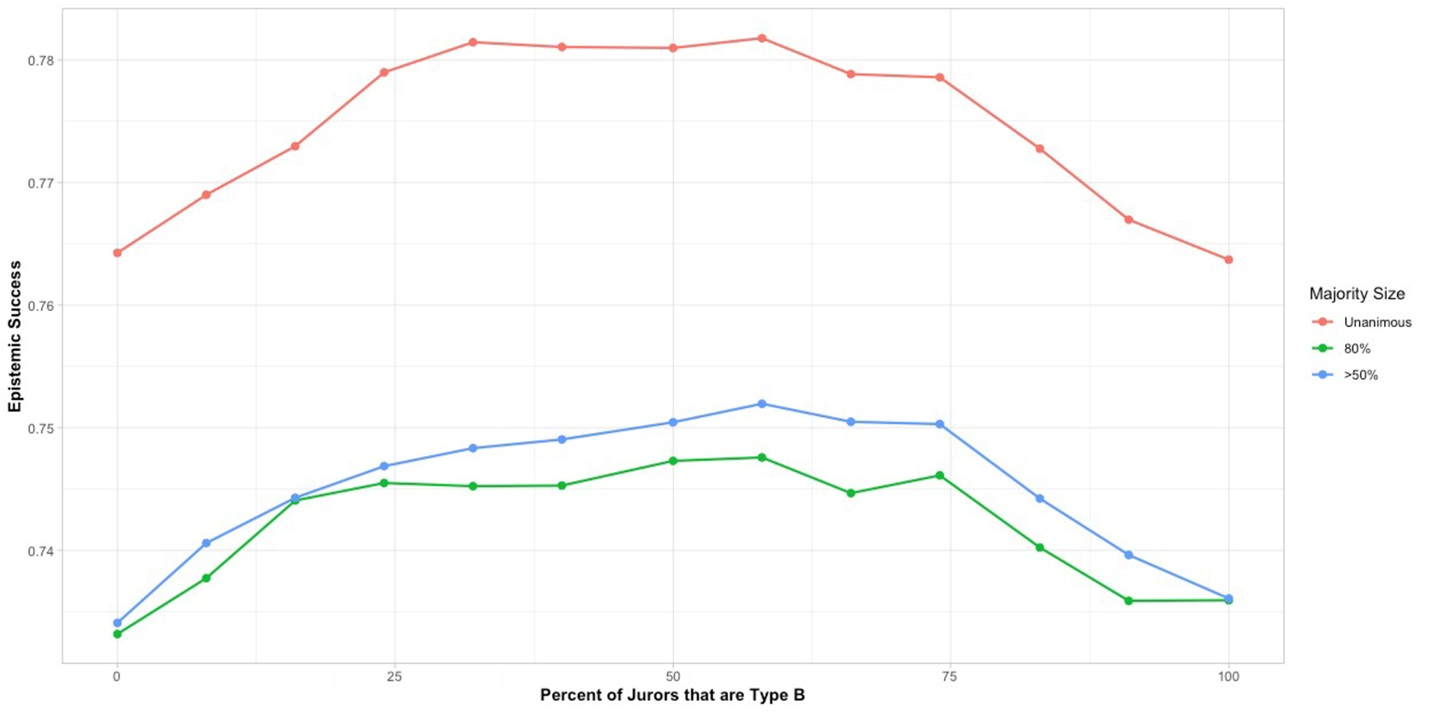
Here jury success is again highest for unanimous juries, with 80% and mere majority decisions performing significantly worse. Success is fairly uniform as long as there is substantial representation of each of the two groups. At the ends of the graph, however, where we approach less diverse juries, jury success falls off slightly. What must explain this result is that the diversity of the jury means that jurors are less likely to bring the same reasons to the discussion. So it must be informational redundancy that explains the weaker results of the less diverse juries.
It should be noted that, in the Hong-Page model, the benefit of diversity is small but consistent. The same is true of our results here, where the non-redundancy benefits of diversity help only minimally.5 But, absent stronger evidence on one side than the other and even absent correlation of the two sides with information favoring ‘guilty’ or ‘not guilty’ respectively, a reduction of information redundancy indicates a small but beneficial role for diversity in jury information aggregation and decision-making.
The Benefits of Limited Communication with Diversity
It is a standard element of liberal belief (perhaps as old as John Stuart Mill) that diversity is to be applauded for its epistemic benefits. This is also a central tenet of the more recent literature on the epistemic benefits of democracy (Anderson 2006; Berger & Sales 2020; Estlund 1993, 2008; Landemore 2012). All of our results so far support this idea.
But another standard element of the liberal picture is that increased communication between social groups also leads to increased benefits (Berry 1999; Grönlund et al. 2015; Iyengar et al. 2019; Mutz 2002; Pettigrew & Tropp 2006). Indeed, it is often lamented that diversity brings with it difficulties of successful communication (Beyer et al. 2015; Jones et al. 2019; Putnam 2007; Rickford & King 2016). In this section, we model the effect of ‘enclaving communication’ on diversity in juries. The results in this section are in tension with the idea that increased ease of communication between groups is always epistemically advantageous. In many cases, in our model, limiting communication between subgroups can actually increase the epistemic success of the full group.
Our results above assumed that there was perfect communication between members of different groups. To examine the effect of enclave communication, we’ll start with the simplest possible version of the model. As above, we have 12 jurors that we divide into two types, A and B. We then model limited communication between the jurors of different types by adding a variable probability that a reason shared by an A juror will be heard by a B juror and vice versa. To focus on the effect of limited communication, we won’t assume (at first) that there is any correlation between the type of a juror and what reasons they start with (i.e. the overlap is 100%) nor will we assume there is any correlation between the type of a reason and its valence (so the correlation is 0). The results in Figure 10 show how likely unanimous juries are to be right when communication between opposite-type jurors is limited in this way.
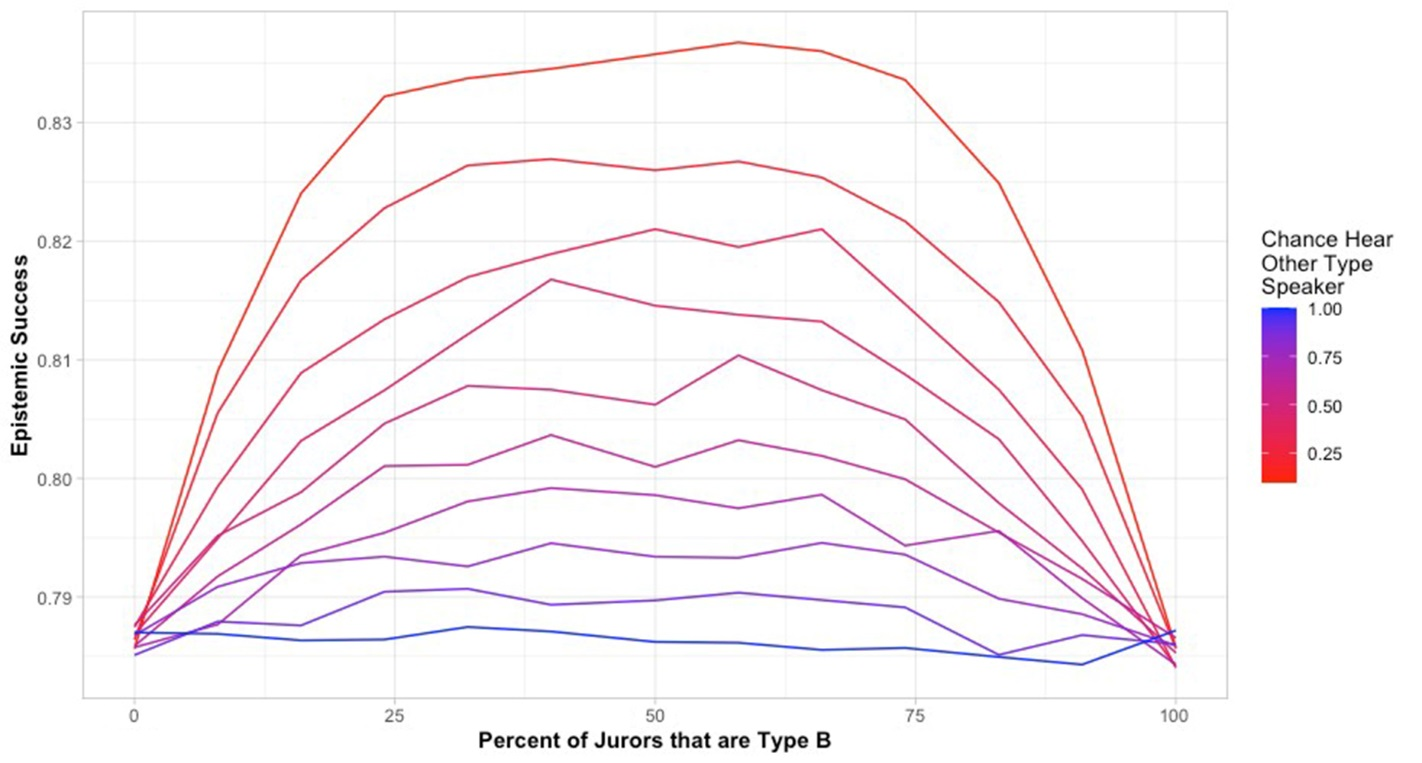
As Figure 10 shows, with each decrease in probability of successful communication between members of the two groups overall jury success increases. The effect is most noticeable with equal representation of our two groups, as before. With full communication, jury success is about 78.6%, whereas with a probability of only 10% of hearing off-type jurors, the success rate of the whole group reaches about 83.5%. In these runs, because we assume there is 100% reason overlap and reason type isn’t correlated with reason valence, there is no difference between members of different groups in terms of what reasons they can access or what the valence of those reasons is likely to be. So, unlike the sections above, there is no sense in which the benefits of diversity we see here could be made sense of in terms of the cognitive diversity of the group. The effect we see here is purely due to members of diverse groups communicating in an enclaved way.
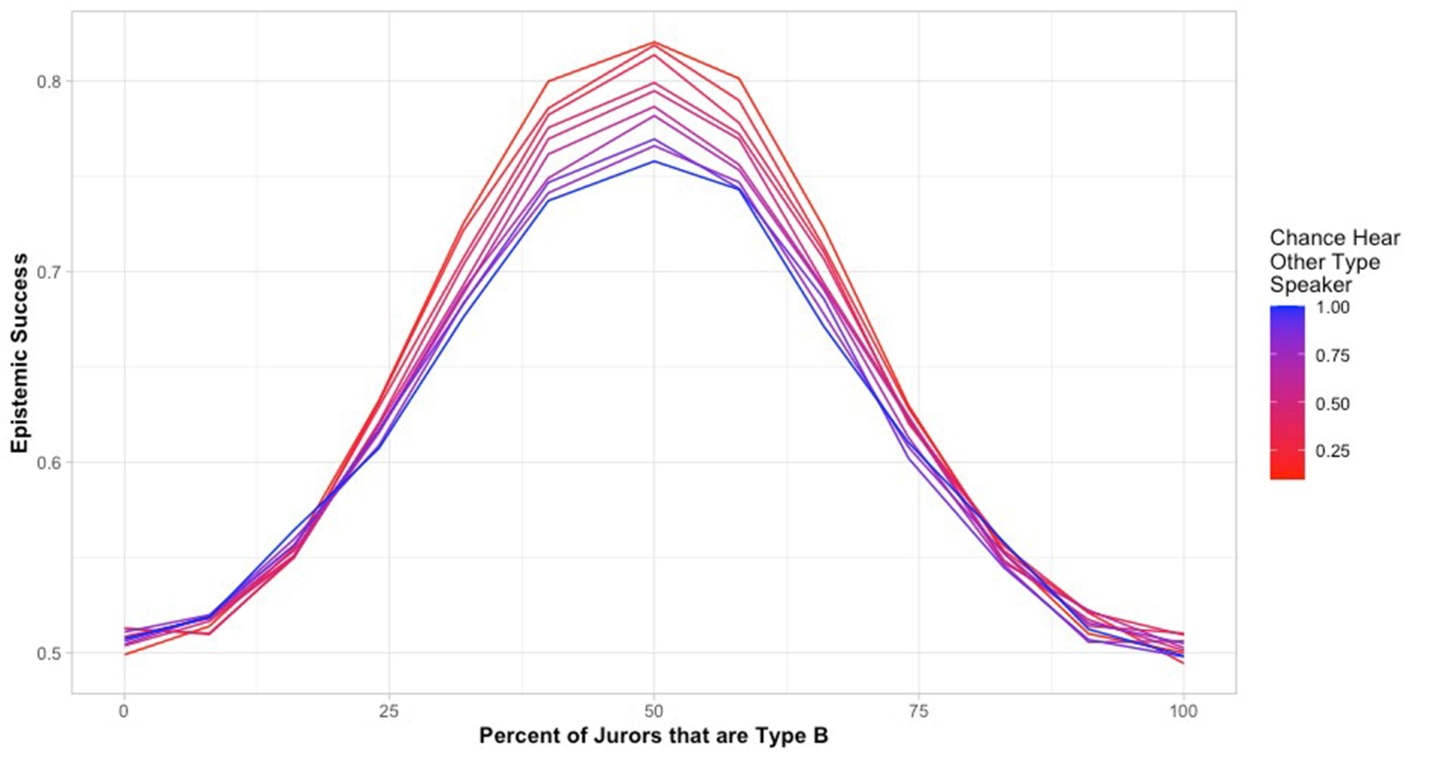
Does the effect remain if groups have access to different information? Figure 11 shows the results of limited communication when there is a perfect correlation between reason type and valence and a 50% overlap of reasons (mimicking the parameters of the model discussed at the beginning of section 4). We see the same effect here. With full communication, jury success is only slightly above 75%. With a communication probability of only 10%, jury success reaches about 82.5%. The effect remains no matter how much we increase correlation between reason type and valence and no matter how much we decrease overlap. The same result also occurs if we limit communication on the basis of whether the reason is the same type as that of the hearer, rather than limiting the speaker type.
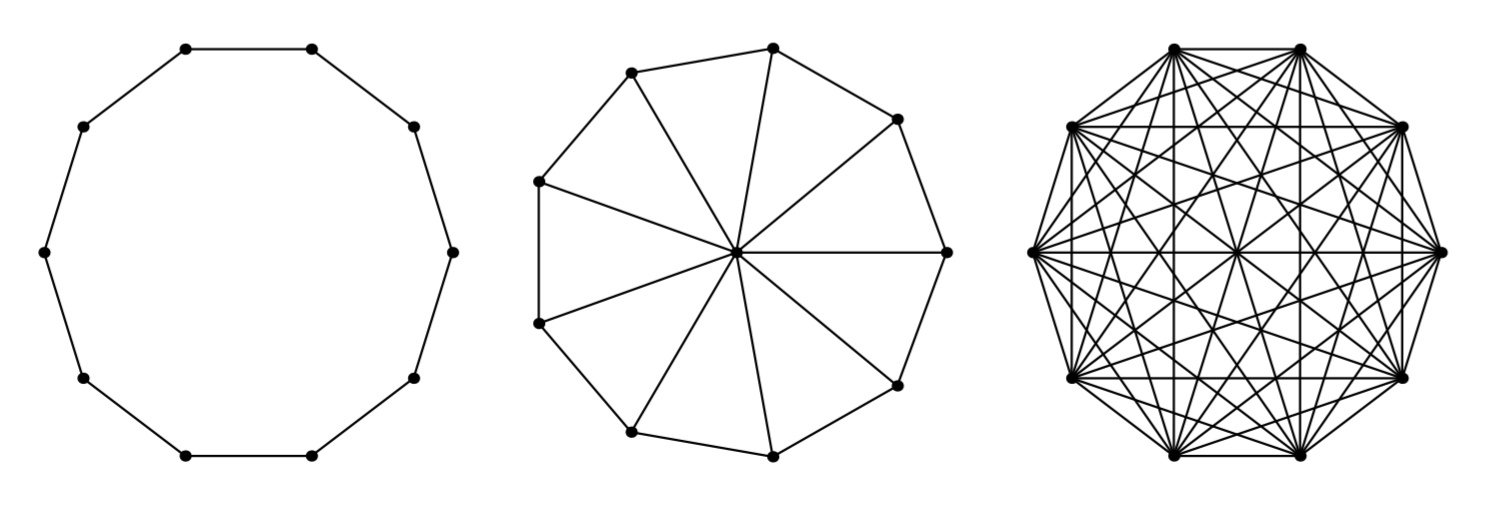
In the previous section we argued that the epistemically positive non-redundancy effects of diversity echoed aspects of the Hong-Page model. The explanation for the epistemically positive effects of enclave communication we see here, we propose, echoes another familiar effect from a model of the social structure of science. In a series of papers, Kevin Zollman (2007, 2010a, 2010b) shows that there is an epistemic benefit from ‘transient diversity.’ In the simplest case, Zollman considers networks in which agents independently explore payoffs from two one-armed bandits (essentially two simple slot-machines that pay off either +1 or 0). The agents also communicate results with linked neighbors in a network (Figure 12). The communication network that performs best is not the fully connected network in which all agents have access to results from all others. Rather, the best network is the least connected one, the maximally distributed ring network. That is also the network that converges to a universally-agreed result most slowly. Related results regarding benefits of restricted communication appear in Grim et al. (2013).
As in our model, information exchange in Zollman’s models ends when the group converges on a shared answer. Convergence happens because evidence sharing eventually gets everyone on the same side. In networks that are less connected, it takes longer for a piece of evidence to move around the network, meaning that some agents who might have changed their mind upon hearing the evidence (potentially resulting in convergence for the group) have more time to explore. In other words, what Zollman saw was that agents in less connected networks generally have more time to explore on their own before the group converges. That extra exploration results in the whole group collectively producing more insight into which bandit is best, thereby increasing the chances the whole group converges on the right answer. So ultimately, the increased success of less connected networks in Zollman’s models is explained by the agents in less connected networks collectively exploring more than agents do in more connected networks.
Our jury model exhibits a similar effect. Limiting communication makes it less likely that members of one subgroup will hear reasons put forward by members of the other subgroup. Like in Zollman’s models, this means that agents who would have been convinced by that reason (potentially resulting in unanimity for the group) are sometimes able to maintain their view when the reason goes unheard. This results in longer times to convergence in models with more limited communication. The longer times to convergence mean that more reasons are shared and a higher average number of reasons end up being held by individual jurors. We see this in the data: when communication is unlimited in an evenly-split jury (with 100% overlap and 0 correlation), the number of reasons held by an agent when a unanimous verdict is reached is 36.4 (averaged over 100,000 runs). That number shoots up to 45.1 when communication between the groups is limited to 10% chance of success. So even though limiting communication limits the chance that a reason will be taken up by an opposite-type juror on any particular occasion of sharing, overall, limiting communication increases the total number of reasons heard by slowing down the time to unanimity. The higher number of reasons held by jurors in these limited runs explains their higher success rates. So like in Zollman’s models, the increased success of juries with limited communication can be explained in terms of the limited groups exploring more before agreeing.
With regards to limitations of the Zollman effect, it should be noted that Zollman’s specific effects rely on extremely close payoffs for chosen alternatives (Rosenstock et al. 2016). Wider differences can cancel out the advantages of limited communication, arguing against easy policy applications or any generalization that limited communication is always better. We take both the general explanatory force of the Zollman point and this reminder of its limitations to be consistent with the results we offer here.
At issue is the standard liberal idea that more communication across diverse groups is always better. The results suggest that limiting communication, effectively insulating subgroups from each other, can be epistemically beneficial in some cases. But, of course, the extent to which limiting communication is helpful is itself limited. It’s easy to see that taking limited communication to the extreme would be extremely detrimental. Were there no communication between subgroups, consensus would often not occur and the epistemic success of the whole would plummet. Moreover, limiting communication has costs in terms of how much time is required to reach consensus. Figure 13 shows the epistemic success of evenly split groups graphed along with the average number of steps it takes for the group to reach consensus (with 0 reason type-valence correlation and 100% overlap).
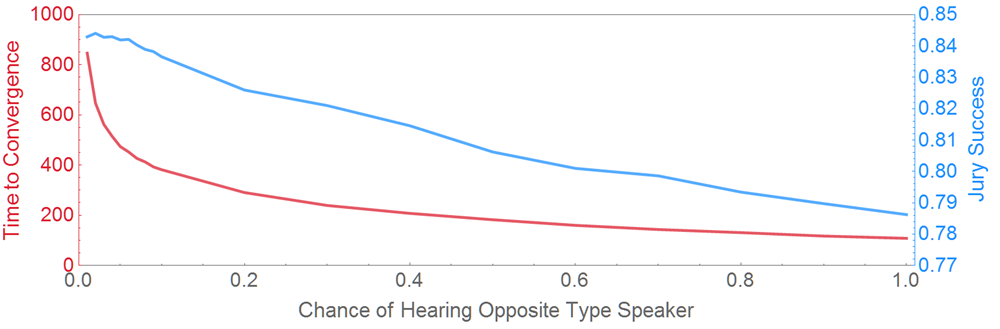
The figure shows a trade-off between group epistemic success and the amount of time that’s required for the group to agree. This too matches the pattern found by Zollman (2007, 2010a, 2010b) and Grim et al. (2013). As the figure also shows, in our model, limiting communication between subgroups improves the epistemic success of the whole group in a generally linear way. But, as communication becomes more limited, the time costs increase exponentially.
Conclusion
Here we’ve used a simple agent-based model to focus on an aspect of jury information aggregation and decision-making that has been overlooked in previous modeling: the role of jury diversity in epistemic success. We find diversity can be an important factor in four different ways. Where different groups are sensitive to different kinds of reasons, and particularly without initial ‘reasons in common’ between the two groups, jury success demands the maximal diversity of equal representation between the two groups (Section 4). Where reasons are particularly strong on one side and the differential sensitivity remains, diversity is of even more importance (Section 5). Even without assumptions regarding correlation and strength of reasons, lack of diversity threatens jury success in ways analogous to Hong and Page’s ‘diversity trumps ability’ result (Section 6). Finally, and somewhat surprisingly, diversity is of value to jury success in limiting communication between the groups—a result evocative of Zollman’s ‘transient diversity’ effect in philosophy of science (Section 7).
As mentioned, we don’t suggest that practical or policy implications can be drawn directly from these results. The proper way to understand these results is as a theoretical insight into what mechanisms might be at play, at a high level, in real world phenomena. We hope that these results might inspire future empirical and theoretical work. The results in sections 4, 5, and 6 all suggest that increasing diversity increases epistemic success of unanimous juries. This concords nicely with recent empirical findings (Anwar et al. 2022). It’s harder to see what the practical import of the benefits of limited communication might be. It’s common to think of jurors as fact-finders and if the goal were truth at any cost, then limiting communication between subgroups at close-to-extreme levels might be beneficial. That said, real jury deliberations need to finish in reasonable amounts of time, and there are probably both moral and morale reasons not to artificially limit communication between jurors. We hope the model results here might inspire further research into alternative mechanisms of capturing some of the benefits that limited communication might bring. Possible mechanisms might include encouraging subgroups of jurors to have private sessions to discuss their views in “breakout sessions” during jury deliberation, permitting subgroups of jurors to privately “backchannel” during the group discussion, or possibly having smaller parts of the jury (“subjuries”) independently deliberate to consensus before joining the other subjuries to deliberate together. Discovering whether and how the theoretical benefits of limited communication between groups can be captured in real jury deliberation will require careful empirical research that goes beyond the scope of what the methodology here can provide.
Finally, as noted in the introduction, other models have shown no positive effect from a requirement of unanimity (Angere et al. 2016; Austen-Smith & Banks 1996; List 2004; Tanford & Penrod 1983). Our results, which incorporate diversity in ways that those models do not, show that unanimous juries do have an importantly higher success rate across all the conditions considered. The suggestion, worthy of further investigation, is that an epistemic justification for demanding a unanimous verdict does not stand alone. It is ultimately tied to fully exploiting the benefits of our diversity.
Author Contribution
Patrick Grim and Daniel Singer contributed equally to this manuscript, and wish to be considered co-first-authors.Notes
- Laudan (2008) terms this ‘material guilt,’ as opposed to ‘probatory guilt’ – a court finding of guilt, correct or incorrect. Laudan also distinguishes a correct verdict from a valid verdict: the first in accord with material guilt, the second in accord with whether evidence at trial meets the applicable standard of proof, which again may or may not accurately indicate material guilt. Our first characterization here is that of material guilt. Whether the prosecution has proven its case is closer to Laudan’s concept of validity, though not an exact match. All that is crucial here and throughout is the fact that the jury’s task is fundamentally epistemic.↩︎
- In response to List’s model, Bowens and Hartmann propose an alternative in which estimated reliability of jurors is moderately keyed to divergence, which does give intuitive results.↩︎
- The number of hung juries in our data is vanishingly small as a result of our jurors having unlimited memory and constantly enlarging their held reasons to include those put forward. The contrast we emphasize here between our results and those of Angere, Olsson and Genot is the fact that our model, unlike theirs, factors in diversity in important ways. But it is also true that memory management is different in their model and that the negative scoring they assign for hung juries plays a major role.↩︎
- As noted, a predecessor to our model is Stasser’s DISCUSS model of group decision making (Stasser 1988). Stasser’s gauge of group success is discovery of hidden profiles. Intriguingly, he also finds a role for something akin to diversity: “…in the presence of a hidden profile, a minority may act as a catalyst facilitating the discovery of the superior decision alternative” (Stasser 1988 p. 416).↩︎
- In Figure 9, results are shown averaging over 100,000 runs, rather than 10,000 as is done in the preceding figures, because the results are slight and the noise in the data makes the effect less visible with less data (although it is subtly visible).↩︎
References
ANDERSON, E. (2006). The epistemology of democracy. Episteme, 3(1–2), 8–22.
ANGERE, S., Olsson, E. J., & Genot, E. J. (2016). Inquiry and deliberation in judicial systems: The problem of jury size. In C. Baskent (Ed.), Perspectives on Interrogative Models of Inquiry: Developments in Inquiry and Questions (pp. 35–56). Berlin Heidelberg: Springer. [doi:10.1007/978-3-319-20762-9_3]
ANWAR, S., Bayer, P., & Hjalmarsson, R. (2022). Unequal jury representation and its consequences. American Economic Review, 4(2), 34–45. [doi:10.1257/aeri.20210149]
AUSTEN-SMITH, D., & Banks, J. S. (1996). Information aggregation, rationality, and the Condorcet jury theorem. American Political Science Review, 90(1), 34–45. [doi:10.2307/2082796]
BATTERMAN, R. W., & Rice, C. C. (2014). Minimal model explanations. Philosophy of Science, 81(3), 349–376. [doi:10.1086/676677]
BERGER, W. J., & Sales, A. (2020). Testing epistemic democracy’s claims for majority rule. Politics, Philosophy & Economics, 19(1), 22–35. [doi:10.1177/1470594x19870260]
BERRY, J. W. (1999). Intercultural relations in plural societies. Canadian Psychology/Psychologie Canadienne, 40(1), 12–21. [doi:10.1037/h0086823]
BEYER, T., Edwards, K. A., & Fuller, C. C. (2015). Misinterpretation of African American English bin by adult speakers of standard American English. Language & Communication, 45, 59–69. [doi:10.1016/j.langcom.2015.09.001]
BOVENS, L., & Hartmann, S. (2003). Bayesian Epistemology. Oxford: Oxford University Press.
CHOPRA, S. (2014). Preserving jury diversity by preventing illegal peremptory challenges: How to make a Batson/Wheeler motion at trial (and why you should). The Trial Lawyer, Summer 2014. Available at: http://www.njp.com/wp-content/uploads/article/article30.pdf
DANE, F. C. (1985). In search of reasonable doubt: A systematic examination of selected quantification approaches. Law and Human Behavior, 9, 141–158. [doi:10.1007/bf01067048]
DEVINE, D. J. (2012). Jury Decision Making: The State of the Science. New York, NY: New York University Press.
DEVINE, D. J., Buddenbaum, J., Houp, S., Stolle, D. P., & Studebaker, N. (2007). Deliberation quality: A preliminary examination in criminal juries. Journal of Empirical Legal Studies, 4(2), 273–303. [doi:10.1111/j.1740-1461.2007.00089.x]
DUGGAN, J., & César, M. (2001). A Bayesian model of voting in juries. Games and Economic Behavior, 37(2), 259–294. [doi:10.1006/game.2001.0843]
EASON, R., Rosenberger, R., Kokalis, T., Selinger, E., & Grim, P. (2007). What kind of science is simulation? Journal of Experimental & Theoretical Artificial Intelligence, 19(1), 19–28. [doi:10.1080/09528130601116154]
EPSTEIN, J. M. (2006). Generative Social Science: Studies in Agent-Based Computational Modeling. Princeton, NJ: Princeton University Press. [doi:10.23943/princeton/9780691158884.003.0003]
ESTLUND, D. (1993). Making truth safe for democracy. In D. Copp, J. Hampton, & J. Roemer (Eds.), The Idea of Democracy. Cambridge: Cambridge University Press.
ESTLUND, D. (2008). Democratic Authority: A Philosophical Framework. Princeton, NJ: Princeton University Press.
FEDDERSEN, T., & Pesendorfer, W. (1998). Convicting the innocent: The inferiority of unanimous jury verdicts under strategic voting. American Political Science Review, 92(1), 23–35. [doi:10.2307/2585926]
FLEXON, J. L., D’Alessio, S. J., Stolzenberg, L., & Greenleaf, R. G. (2019). Interracial encounters with the police: Findings from the NCVS police-public contact survey. Journal of Ethnicity in Criminal Justice, 17(4), 299–320. [doi:10.1080/15377938.2019.1646688]
GRIM, P., Singer, D. J., Fisher, S., Bramson, A., Berger, W. J., Reade, C., Flocken, F., & Sales, A. (2013). Scientific networks on data landscapes: Question difficulty, epistemic success, and convergence. Episteme, 10(4), 441–464. [doi:10.1017/epi.2013.36]
GRIM, P., Singer, D. J., Fisher, S., Bramson, A., Holman, B., McGeehan, S., & Berger, W. J. (2019). Diversity, ability and expertise in epistemic communities. Philosophy of Science, 86(1), 98–123. [doi:10.1086/701070]
GRÖNLUND, K., Herne, K., & Setälä, M. (2015). Does enclave deliberation polarize opinions? Political Behavior, 37, 995–1020.
HARTSOCK, N. (1987). The feminist standpoint: Developing the ground for a specifically feminist historical materialism. In S. Harding & M. B. Hintikka (Eds.), Discovering Reality: Feminist Perspectives on Epistemology, Metaphysics, Methodology and Philosophy of Science (pp. 283–310). Berlin Heidelberg: Springer. [doi:10.1007/0-306-48017-4_15]
HASTIE, R., Penrod, S. D., & Pennington, N. (1983). Inside the Jury. Cambridge, MA: Harvard University Press. [doi:10.4159/harvard.9780674865945]
HAWTHORNE, J. (1996). Voting in search of the public good: The probabilistic logic of majority judgments. Available at: https://www.researchgate.net/publication/228917887_Voting_in_Search_of_the_Public_Good_The_Probabilistic_Logic_of_Majority_Judgements
HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence: Models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2. https://jasss.soc.surrey.ac.uk/5/3/2.html [doi:10.18564/jasss.5257]
HEISE, D. R. (2013). Modeling interactions in small groups. Social Psychology Quarterly, 76(1), 52–72. [doi:10.1177/0190272512467654]
HELLAND, E., & Raviv, Y. (2008). The optimal jury size when jury deliberation follows a random walk. Public Choice, 134, 255–262. [doi:10.1007/s11127-007-9222-5]
HONG, L., & Page, S. E. (2004). Groups of diverse problem solvers can outperform groups of high-ability problem solvers. Proceedings of the National Academy of Sciences, 101(46), 16385–16389. [doi:10.1073/pnas.0403723101]
HOROWITZ, I. A., & Kirkpatrick, L. C. (1996). A concept in search of a definition: The effects of reasonable doubt instructions on certainty of guilt standards and jury verdicts. Law and Human Behavior, 20, 655–670. [doi:10.1007/bf01499236]
IYENGAR, S., Lelkes, Y., Levendusky, M., Malhotra, N., & Westwood, S. J. (2019). The origins and consequences of affective polarization in the United States. Annual Review of Political Science, 22, 129–146. [doi:10.1146/annurev-polisci-051117-073034]
JONES, T., Kalbfeld, J. R., Hancock, R., & Clark, R. (2019). Testifying while black: An experimental study of court reporter accuracy in transcription of African American English. Language, 95(2), e216–e252. [doi:10.1353/lan.2019.0042]
JOSHI, A. S., & Kline, C. T. (2015). Lack of jury diversity: A national problem with individual consequences. American Bar Association, Sept. 01. Available at: https://www.americanbar.org/groups/litigation/committees/diversity-inclusion/articles/2015/lack-of-jury-diversity-national-problem-individual-consequences/
KOCH, C. M., & Devine, D. J. (1999). Effects of reasonable doubt definition and inclusion of a lesser charge on jury verdicts. Law and Human Behavior, 23(6), 653–674. [doi:10.1023/a:1022389305876]
KUEHN, D. (2017). Diversity, ability and democracy: A note on Thompson’s challenge to Hong and Page. Critical Review, 29(1), 72–87. [doi:10.1080/08913811.2017.1288455]
LANDEMORE, H. (2012). Democratic Reason: Politics, Collective Intelligence, and the Rule of the Many. Princeton, NJ: Princeton University Press.
LAUDAN, L. (2008). Truth, Error, and Criminal Law: An Essay in Legal Epistemology. Cambridge: Cambridge University Press.
LIST, C. (2004). On the significance of the absolute margin. British Journal for the Philosophy of Science, 55(3), 521–544. [doi:10.1093/bjps/55.3.521]
LUMET, S. (1956). 12 angry men. United States: United Artists Corporation
LUPPI, B., & Parisi, F. (2013). Jury size and the hung-jury paradox. The Journal of Legal Studies, 42(2), 399–422. [doi:10.1086/670692]
LYNCH, M., & Haney, C. (2011). Mapping the racial bias of the white male capital juror: Jury composition and the “empathic divide”. Law & Society Review, 45(1), 69–102. [doi:10.1111/j.1540-5893.2011.00428.x]
MACY, M. W., & Willer, R. (2002). From factors to actors: Computational sociology and agent-Based modeling. Annual Review of Sociology, 28, 143–166. [doi:10.1146/annurev.soc.28.110601.141117]
MARGOLIS, H. (2001). Game theory and juries: A miraculous result. Journal of Theoretical Politics, 13(4), 425–435. [doi:10.1177/0951692801013004005]
MILLS, C. (2007). White ignorance. In S. Sullivan & N. Tuana (Eds.), Race and Epistemologies of Ignorance (pp. 26–31). New York, NY: State University of New York Press.
MOHSENI, A., O’Connor, C., & Weatherall, J. O. (2023). The best paper you’ll read today: Media bias and the public understanding of science. Philosophical Topics, Forthcoming [doi:10.5840/philtopics202250220]
MUTZ, D. (2002). Cross-cutting social networks: Testing democratic theory in practice. American Political Science Review, 96(1), 111–126. [doi:10.1017/s0003055402004264]
NADAL, K. L., & Davidoff, K. C. (2015). Perceptions of police scale (POPS): Measuring attitudes towards law enforcement and beliefs about police bias. Journal of Psychology and Behavioral Science, 3(2), 1–9. [doi:10.15640/jpbs.v3n2a1]
NADAL, K. L., Davidoff, K. C., Allicock, N., Serpe, C. R., & Erazo, T. (2017). Perceptions of police, racial profiling and psychological outcomes: A mixed methodological study. Journal of Social Issues, 73(4), 808–830. [doi:10.1111/josi.12249]
PAGE, S. E. (2007). The Difference. Princeton, NJ: Princeton University Press.
PAGE, S. E. (2011). Diversity and Complexity. Princeton, NJ: Princeton University Press.
PAGE, S. E. (2015). Diversity trumps ability and the proper use of mathematics. Notices of the American Mathematical Society, 62(1), 9–10.
PAGE, S. E. (2018). The Model Thinker. New York, NY: Basic Books.
PENROD, S. D., & Hastie, R. (1980). A computer simulation of jury decision making. Psychological Review, 87(2), 133–159. [doi:10.1037/0033-295x.87.2.133]
PETTIGREW, T. F., & Tropp, L. R. (2006). A meta-analytic test of intergroup contact theory. Journal of Personality and Social Psychology, 90(5), 751–783. [doi:10.1037/0022-3514.90.5.751]
PUTNAM, R. D. (2007). E pluribus unum: diversity and community in the twenty‐first century the 2006 Johan Skytte Prize lecture. Scandinavian Political Studies, 30(2), 137–174. [doi:10.1111/j.1467-9477.2007.00176.x]
RICKFORD, J. R., & King, S. (2016). Language and linguistics on trial: Hearing Racheal Jeantel (and other vernacular speakers) in the courtroom and beyond. Language, 92(4), 948–988. [doi:10.1353/lan.2016.0078]
ROSENSTOCK, S., O’Connor, C., & Bruner, J. (2016). In epistemic networks is less really more? Philosophy of Science, 84(2), 234–252. [doi:10.1086/690717]
SAKS, M. J., & Marti, M. W. (1997). A meta-Analysis of the effects of jury size. Law and Human Behavior, 2, 451–466. [doi:10.1023/a:1024819605652]
SCHUTTE, J. W., & Horsch, H. M. (1997). Gender differences in sexual assault verdicts: A meta-analysis. Journal of Social Behavior and Personality, 12(3), 759–772.
SINGER, D. J. (2019). Diversity, not randomness trumps ability. Philosophy of Science, 86(1), 178–191. [doi:10.1086/701074]
SINGER, D. J., Bramson, A., Grim, P., Holman, B., Jung, J., Kovaka, K., Ranginani, A., & Berger, W. J. (2019). Rational social and political polarization. Philosophical Studies, 176, 2243–2267. [doi:10.1007/s11098-018-1124-5]
SINGER, D. J., Bramson, A., Grim, P., Holman, B., Kovaka, K., Jung, J., & Berger, W. J. (2021). Don’t forget forgetting: The social epistemic importance of how we forget. Synthese, 198, 5373–5394. [doi:10.1007/s11229-019-02409-0]
STASSER, G. (1988). Computer simulation as a research tool: The DISCUSS model of group decision making. Journal of Experimental Social Psychology, 24(5), 393–422. [doi:10.1016/0022-1031(88)90028-5]
STASSER, G., & Davis, J. H. (1981). Group decision making and social influence: A social interaction sequence model. Psychological Review, 88(6), 523–551. [doi:10.1037/0033-295x.88.6.523]
STRODTBECK, F. L., & Hook, L. H. (1961). The social dimensions of a twelve-man jury table. Sociometry, 24(4), 397–415. [doi:10.2307/2785921]
STRODTBECK, F. L., & Mann, R. D. (1956). Sex role differentiation in jury deliberations. Sociometry, 19(1), 3–11. [doi:10.2307/2786099]
TANFORD, S., & Penrod, S. (1983). Computer modeling of influence in the jury: The role of the consistent juror. Social Psychology Quarterly, 46(3), 200–212. [doi:10.2307/3033791]
THE Scotsman. (2009). Scotland’s unique 15-strong juries will not be abolished. Available at: https://www.scotsman.com/news/politics/scotlands-unique-15-strong-juries-will-not-be-abolished-2443842
THOMA, J. (2015). The epistemic division of labor revisited. Philosophy of Science, 82(3), 454–472. [doi:10.1086/681768]
THOMPSON, A. (2014). Does diversity trump ability? An example of the misuse of mathematics in the social sciences. Notices of the American Mathematical Society, 61(9), 1024–1030. [doi:10.1090/noti1163]
U. S. Courts. (2019). Courts seek to increase jury diversity. Available at: https://www.uscourts.gov/news/2019/05/09/courts-seek-increase-jury-diversity
WEATHERALL, J. O., O’Connor, C., & Bruner, J. (2018). How to beat science and influence people. British Journal for the Philosophy of Science, 71(4), 1157–1186. [doi:10.1093/bjps/axy062]
WEISBERG, M. (2013). Simulation and Similarity: Using Models to Understand the World. Oxford: Oxford University Press.
WEISBERG, M., & Muldoon, R. (2009). Epistemic landscapes and the division of cognitive labor. Philosophy of Science, 76(2), 225–252. [doi:10.1086/644786]
WYLIE, A. (2003). Why standpoint matters. In F. Figueroa & S. Harding (Eds.), Science and Other Cultures: Issues in Philosophies of Science and Technology (pp. 26–48). London: Routledge.
ZOLLMAN, K. (2010a). The epistemic benefit of transient diversity. Erkenntnis, 72(1), 17—35. [doi:10.1007/s10670-009-9194-6]
ZOLLMAN, K. (2007). The communication structure of epistemic communities. Philosophy of Science, 74(5), 574–587. [doi:10.1086/525605]
ZOLLMAN, K. (2010b). Social structure and the effects of conformity. Synthese, 172(3), 317–340. [doi:10.1007/s11229-008-9393-8]
ZÖLLER, N., Morgan, J. H., & Schröder, T. (2021). Modeling interaction in collaborative groups: Affect control within social structure. Journal of Artificial Societies and Social Simulation, 24(4), 6. https://doi.org/10.18564/jasss.4699