Talk Less to Strangers: How Homophily Can Improve Collective Decision-Making in Diverse Teams

,
and
University of Groningen, Netherlands
Journal of Artificial
Societies and Social Simulation 27 (1) 14
<https://www.jasss.org/27/1/14.html>
DOI: 10.18564/jasss.5224
Received: 24-Apr-2023 Accepted: 16-Nov-2023 Published: 31-Jan-2024
Abstract
Identity diversity in teams brings advantages for complex decision-making because it is associated with cognitive diversity among team members. At the same time, homophilous interactions along shared identity dimensions can hinder information exchange among dissimilar individuals and threaten successful exploitation of the team’s cognitive diversity. We present an agent-based model to investigate how homophily impacts decision-making quality in diverse teams. Team members communicate information in a ‘hidden profile’ setting where some pieces of information are known only to single individuals while other pieces of information are known to subgroups with the same identity. While intuition may suggest that homophily impairs collective decision-making, our model reveals how homophilous environments lead to better collective decisions: homophily fosters temporary disagreements between dissimilar team members, which grant teams additional time to uncover crucial information that would not have been shared otherwise. Longer discussion time comes along with improvements in the quality of the final decision, indicating a trade-off between the time needed to deliberate and decision quality.Introduction
A large literature on work teams documents that diverse teams have a greater pool of social, human, and cultural capital translating into a higher potential for team performance (Phillips & O’Reilly 1998). Yet, when diversity activates social identity processes (Tajfel 2010), this potential may not be used. Homophily, the tendency to preferentially interact with those similar to oneself is a strong force in humans (McPherson et al. 2001) and prevents team members from communicating with dissimilar others providing them with information needed to reach higher performance. With an agent-based model, we challenge here the intuition that homophily is detrimental to the performance of diverse teams. We demonstrate that homophily can improve team decision-making, studying agent teams confronted with a hidden profile task (Stasser & Titus 1985) which requires team members to share information not known to others in order to collectively find the best solution to a problem. Our finding contrasts with the conjecture that homophily can hamper the performance of diverse teams (Ertug et al. 2022; Estévez-Mujica et al. 2018; Reagans 2013) and highlights instead the benefits of limiting the flow of information between dissimilar team members.
Structuring collaboration processes and interaction patterns in diverse teams so that they enhance team decision-making has become an increasingly important issue, as a globalized division of labor, rising international migration, and increasingly diverse workforces have led to a ubiquity of heterogenous decision-making groups in organizations (Jackson et al. 1995). Research investigating how this trend shapes collaborative work processes identifies both challenges and benefits (Carter & Phillips 2017; Milliken & Martins 1996; Phillips & O’Reilly 1998). Successful integration of cognitive diversity, referring to the wealth of perspectives, knowledge, and skills present in a team is found to have mostly beneficial outcomes for the quality of a task, especially when tasks are complex because a conjunction of diverse skills and perspectives is expected to enhance team creativity and foster innovative solutions (Page 2019).
At the same time, identity diversity in teams can provide a challenge to the successful integration of cognitive diversity. Identity diversity is sometimes also referred to as ‘surface-level diversity’ or ‘demographic diversity’ (Peters 2021). Including potential demographic or ‘surface-level’ traits, we focus specifically on identities that are easily observable for others, salient during collaborative work, and plausibly correlated with cognitive traits.1 Even without assuming that identity diversity leads to intergroup conflict (Lau & Murnighan 1998) stereotyping and negative outgroup attitudes (Harrison et al. 1998; Northcraft et al. 1995; Phillips 2003), it has been consistently documented that individuals tend to associate themselves with similar others and that similarities are usually recognized along common identities (Brechwald & Prinstein 2011; Ertug et al. 2022; McPherson et al. 2001).
Simulation studies on opinion dynamics (Flache et al. 2017; Hegselmann & Krause 2002) and experimental studies (Bail 2016; Balietti et al. 2021; Mäs & Flache 2013) show that such homophilous preferences are sufficient to drive groups apart and induce polarization. Empirically, identity traits often correlate with cognitive traits (Phillips 2003) and theoretical as well as empirical studies have shown that such correlations tend to amplify polarization tendencies (DellaPosta et al. 2015; Mäs et al. 2013; Stark & Flache 2012). If individuals socially influence each other but tend to interact with similar others, patterns emerge where distinct sets of opinions revolve around similarities in other, seemingly unrelated dimensions.
Models of opinion dynamics highlight how opinion divergence in teams can disable consensus, but they do not clarify how opinion polarization links to the quality of decision-making in a team. In this paper we move beyond modeling the dynamics of opinions alone and develop expectations about how homophilous preferences and social influence affects decision-making quality in a team. Intuitively, one can expect this theoretical extension to show how homophily in diverse teams can negatively affect decision-making quality. For complex tasks where diverse knowledge must be brought together to obtain an optimal decision, a lack of communication between team members with different identities hampers the conjunction of valuable information, leading to failure to realize good solutions. Second, even if some team members find the optimal solution to the task at hand, a lack of consensus endangers the possibility that this solution is adopted by the team. Finally, lacking communication slows down the deliberation process, making decision-making more costly. This expectation aligns with previous experimental and simulation-based research on problem-solving in groups (Estévez-Mujica et al. 2018): especially in those groups where demographic diversity was high, homophilous interactions prevented access to valuable information. This resulted in worse performance on the group level.
Epistemological studies on decision-making in diverse groups, on the other hand, oppose the conjecture that homophily negatively affects group performance in deliberative tasks. Instead, bounded communication between different individuals is beneficial to team decision quality (Zollman 2010) because restrictions on social influence will prevent individuals from prematurely adopting others’ solutions. In other words, boundaries in communication hinder the rapid dissemination of inferior knowledge, ultimately ensuring that individuals explore the full spectrum of possible decisions before exploiting suboptimal knowledge (Frey & Šešelja 2020; Wu & O’Connor 2021; Zollman 2010). Similar to the opinion dynamics literature, these works also suggest that ‘transient diversity’ will lengthen the deliberation process but point out that added discussion time gives room to ensure that knowledge is optimally explored and disseminated.
Studies of transient diversity emphasize possible advantages of boundaries to communication in team decision-making, but they leave us in the dark as to how homophily interacts with diversity in teams. Scholars of this canon are primarily concerned with communication processes in science and argue that skepticism and sparse communication can be induced by adapting macro-level incentive structures such as changing funding policies in research. Yet, we would expect that meso-level social processes such as homophily induced by identity diversity can also bound excessive communication and limit exchange between dissimilar members, even if macro-level structural boundaries are absent. This notion is similar to the ‘value in diversity’ hypothesis (McLeod et al. 1996), arguing that salient markers of diversity can be beneficial to decision-making quality even when they are unrelated to cognitive traits (Levine et al. 2014; Page 2019; Peters 2021; Phillips & Loyd 2006). Easily observable diversity in identities can help groups to apply healthy skepticism, prevent the placement of undue trust, and foster constructive discussion. In sum, it follows from both the transient diversity literature and the value in diversity literature that tendencies to associate with similar over dissimilar individuals improve collective decision-making quality by help groups to examine information critically instead of converging around early, suboptimal consensus.
Research on opinion dynamics in diverse teams and studies of transient diversity lead to competing intuitions: preferential interactions among similar over dissimilar team members are either beneficial or detrimental to a team’s performance. The present paper uses an agent-based model to theorize how homophilous interaction preferences shape decision-making quality in diverse teams. The model combines central aspects that have not been studied in tandem before: first, it evaluates the quality of the decision that is made, which opinion dynamics models have paid little attention to so far. Second, it considers that background traits shape interaction preferences between individuals without having to assume exogenous incentive structures as outlined by the transient diversity literature.
Our model builds on hidden profile tasks, an established paradigm that has been widely used in experimental research to study decision-making in groups (Lu et al. 2012; Schulz-Hardt & Mojzisch 2012; Sohrab et al. 2015; Stasser & Stewart 1992; Stasser & Titus 1985, 2003). In a hidden profile, a team of decision-makers is equipped with a set of information pieces and instructed to deliberate before choosing one of several available decision alternatives, which differ in quality. Individuals are given different pieces of information at the onset of the deliberation task. Pieces of knowledge that point towards inferior options are ‘common information’, i.e., known to everyone in the group. Common information anchors decision-makers to initially prefer inferior options. Anchoring effects, a tendency to share knowledge supporting one’s own views, and social validation from others with similar decision preferences can prevent members from sharing or accepting dissenting information. This makes hidden profiles difficult to solve (Lu et al. 2012), which resonates with the conjecture that diversity has a much greater impact on the outcome of a task when it is complex and challenging (Wittenbaum et al. 2004). Information supporting the optimal option is ‘unique’, in that it is known to not more than one individual. However, a conjunction of multiple pieces of unique information will reveal the optimal option, which captures the well-studied phenomenon of cognitive diversity that bringing together knowledge from different individuals will produce better solutions (Hong & Page 2004). In addition, hidden profiles are a suitable paradigm for the purpose of the present research because they incorporate a number of features that are often hard to observe or hold constant in natural settings: Hidden profiles allow the experimenter to control the distribution of knowledge, as a predefined set of decision options can be perfectly ranked according to their quality, and all communication processes and their outcomes can be observed and subsequently analyzed.
By using the hidden profile paradigm for studying the interplay of identity diversity and homophily in affecting team decision-making quality, we also contribute to the hidden profile literature itself. Identity diversity is a feature that is rarely considered in the literature on hidden profiles and has not received much attention in experimental research using this paradigm (see Phillips et al. 2006 for an exception). Since the impact of identity diversity on decision-making quality is a key aspect of our study, our model extends the traditional hidden profile framework by assigning identity traits to individuals, making them either similar or dissimilar to each other. We capture the aspect that identity is associated with the kind of knowledge individuals possess by distributing a separate set of common information to any group of individuals with a common identity. We further condition interaction preferences on identity traits in such a way that higher homophily levels reflect how much identity-similarity increases the chances of communication between individuals. More precisely, the stronger homophily, the higher are the chances of individuals of identical background to communicate relative to the chances of communication between individuals of different background. Our key interest is in assessing the effects of homophily on decision-making quality. Thus, as further outlined in the ‘setup of simulation experiments’ section, we measure how likely teams were to obtain optimal consensus given different levels of homophily, and how long it took them to reach a decision. In the results section, we show how homophily affects consensus outcomes, uncovering the underlying mechanism and investigating how other discussion features such as deliberation length and belief changes among team members are affected.
Model Description
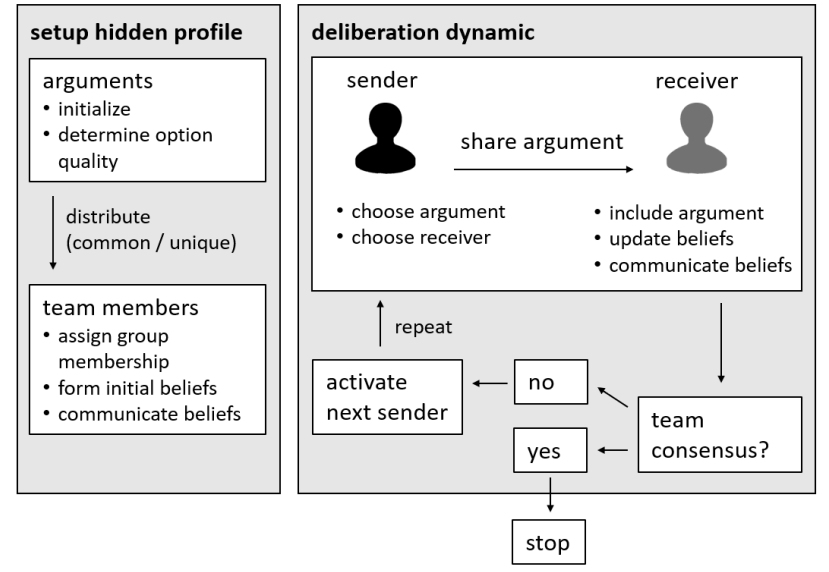
Our model develops a formal representation of a diverse work team facing a decision problem as implemented in the experimental setup of the hidden profile paradigm. Figure 1 illustrates key aspects of the model. We implement a setup where a team seeks to identify the best out of a set of possible decision options. Individuals are equipped with different pieces of information that need to be combined to identify the best option. To this end, we assume a team of \(N\) agents. Each agent belongs to one of \(M\) groups where each group consists of agents who share a common identity. Identities could represent, for example, different branches in an organization, or different academic disciplines in an interdisciplinary project. Our main model assumes that groups are assumed to be of equal group size, although Appendix A, Figure 8 shows that results generalize to unbalanced group contexts. We also abstract from power imbalances between agents or the effects of multiple group memberships.
The virtual teams in our model face a decision problem, in that the best option \(o_{max}\) out of a set of \(J\) discrete options needs to be identified. Every team member forms her own belief about which decision option is best but is open to influence by other team members. Influence is implemented as a sequence of communication events (right side of Figure 1). Agents take turns in sharing an argument with an interaction partner. Every time an argument is emitted, the recipient updates her beliefs and tells her team what option she currently believes to be best. This influence process continues until all agents prefer the same option. This option is the team´s decision. Alternatively, if no consensus is reached after a large number of interaction events (5,000 interactions), the simulation is stopped.
Decision options and arguments
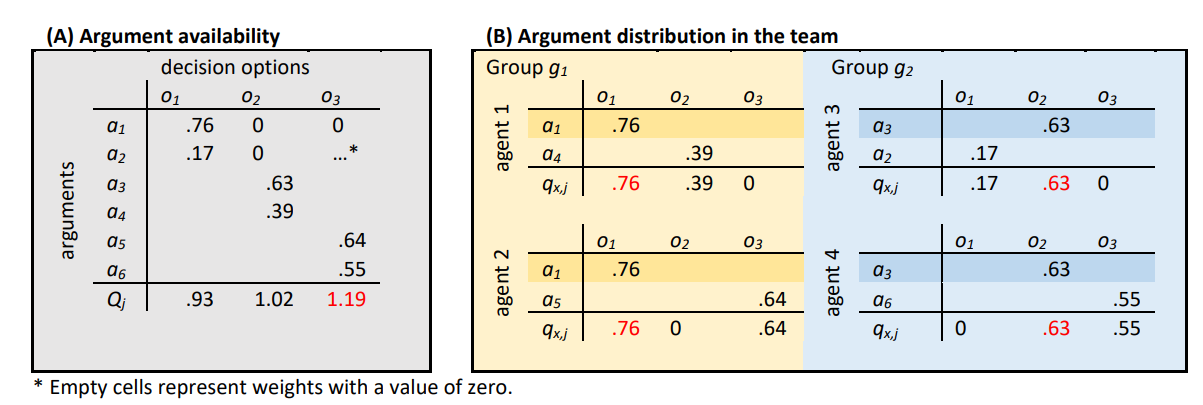
To create a decision problem as implemented in the hidden profile paradigm, we assume that there is a set of \(I\) arguments \(A = \{a_{1}, a_{2}, \dots, a_{i}\}\) pertaining to a predefined set of \(J\) decision options \(O = \{o_{1}, o_{2}, \dots, o_{j}\}\). An example of a set of arguments and decision options is presented in Figure 2A. The set of arguments is fixed, implementing a setting in which agents cannot invent new arguments during the deliberation process. Following common practice in hidden profiles, we define the set of arguments and options prior to the start of the decision process. This excludes the possibility that agents come up with ‘creative’ solutions, which would be hard to design, track, and explain in a simulation. Each argument contains \(J\) weights reflecting the degree to which the argument supports the different decision options, i.e. \(a_{i} = \{w_{i,1}, w_{i,2}, \dots, w_{i,J}\}\). Following the standard assumption of the hidden profile literature, we assume that each argument has a positive weight for only one of the options and a weight of zero for the other options. We further assume that there is an equal number of arguments with a positive weight for each decision option. For a given simulated team, weights are randomly drawn from a uniform distribution so that \(w_{i,j} \in [0, 1]\) The sum of the weights associated with a decision option determines its true quality \(Q_{j} = \sum_{1}^{i}w_{i,j}\), and the decision option \(j\) with the highest quality is the optimal option, \(o_{max}\).
Unique and common arguments
The last ingredient needed to implement a hidden profile task is concerned with the initial distribution of arguments across team members. In hidden profile experiments, participants are provided with so-called ‘common’ and ‘unique’ information. An argument is common when all participants know it already at the outset of the deliberation process. Unique information, in contrast, is provided only to a single participant. This principle is modified for the study of diverse teams: We added that a given piece of common information is provided only to the members of one group (Figure 2B). In this sense, common arguments can reflect certain disciplinary basics that everyone of the same profession was trained with, or specific knowledge shared by everyone working in the same organizational branch. We distribute common arguments in such a way that each agent of group \(g_{m}\) receives the same set of arguments in favor of option \(o_{j}\). Agents in group \(g_{1}\) receive \(C\) arguments favoring option \(o_{1 }\), agents in group \(g_{2}\) receive \(C\) arguments favoring option \(o_{2}\), and so on. Like scientists of one discipline thinking that their approach is superior to others or employees being convinced that the ‘way things are done’ within their organizational branch is best, the distribution of common arguments biases agents of one group to initially favor a specific, but not necessarily optimal option over others. We assume that there are more decision options than groups (\(J > M\)) so that the optimal option can reside outside of those options supported by common arguments, and thus supported initially by all members of one group.
The procedure by which arguments are distributed initially is designed to ensure that teams face a hidden profile task as described above. Once common arguments are assigned to groups, we consider all arguments that remain. These can pertain to any of the decision options. However, because common arguments are distributed already, those arguments that remain unassigned at this stage most often support options other than those favored by common arguments. In the initialization procedure, agents take turns at randomly drawing from the remaining arguments without replacement until all arguments are distributed. By doing so, these arguments represent ‘unique information’ that is held by single agents but not by groups. Whether a task is ‘hidden’ and difficult or ‘manifest’ and easy is determined by whether the optimal option \(o_{max}\) is among those options favored by common arguments. In line with the hidden profile paradigm, we select for our simulation experiments those tasks where only unique arguments favor the optimal option but none of the common arguments in either of the groups do. Hence, to stay within the example of a scientific collaboration, we model a situation in which interdisciplinarity has true advantages because it enables better solutions than those common to either discipline alone. Altogether, our initialization procedure creates the situation of most theoretical interest to this study: distinct sets of common arguments ensure cognitive diversity where groups bring different knowledge to the table, with the different groups initially favoring different alternatives and none of the groups favoring the optimal alternative. Unique arguments provide cognitive diversity at the individual level, but they are dispersed over agents across groups and must be brought together to outweigh common stocks of arguments pointing to inferior solutions.
Argument processing and communication
Similar to how true quality scores \(Q_{j}\) are computed, agents form a perceived quality score for each decision option, \(q_{x,j}\), by summing over the weights of the arguments they possess. Agents always believe the decision option to be best that has the highest perceived quality to them and communicate this belief publicly to everyone at the onset of the simulation.
Over the course of the simulation, agents share arguments and update beliefs, thereby deliberating which option is best. Agents are activated sequentially and according to their identifier, i.e., agent 1 in round 1, agent 2 in round 2, and so forth. Additional analyses included in Appendix A show that results do not depend on a sequential activation of agents but are also obtained when agents are activated at random (see Figure 9). The first task of the active agent is to select an argument she wants to share. Because the agent has limited capacities to communicate information and can only share one argument per round, she carefully needs to consider which argument is most important to communicate. This consideration is represented by a two-step discrete choice procedure. In the first step of the procedure, the agent chooses an option \(o_{j}^{*}\) she wants to support. Psychological research suggests that individuals are most inclined to advocate options they deem most preferable themselves (Wittenbaum et al. 2004). For this reason, we assume that the agent is more likely to choose options with higher perceived quality scores relative to the quality score of other options. The probability to choose option \(j\) at a given moment is formalized by Equation 1.
| \[ p_{o_{j}} = \frac{e^{\beta q_{x,j}}}{\sum_{i = 1}^{J}e^{\beta q_{x,j}}}\] | \[(1)\] |
The parameter \(\beta\) reflects agents’ adherence to choosing an option of higher versus lower perceived quality. When \(\beta \rightarrow \infty\) the probability of choosing the option with highest perceived quality approximates one while probabilities of choosing other options are zero. When \(\beta\) is zero, all options are chosen with equal probability, regardless of their perceived quality.
After an agent has decided which option to support, the second step of the discrete choice procedure determines which argument to communicate. Here, an agent regards all arguments she holds but only considers those weights \(w_{i, j^{*}}\) that contain information on her chosen option \(o_{j^{*}}\). She picks one of her arguments with the probability given by Equation 2:
| \[ p_{a_{i}} = \frac{e^{\beta w_{i, j^{*}}}}{\sum_{i = 1}^{I}e^{\beta w_{i, j^{*}}}}\] | \[(2)\] |
Again, the \(\beta\) parameter determines agents’ adherence to choosing stronger versus weaker arguments pertaining to her chosen option. As long as \(\beta\) does not approach large numbers, the discrete choice equation assigns all arguments a positive probability of being chosen, including those with a weight of zero. For simplicity, we assume that the value of beta in Equation 1 and Equation 2 is the same, representing a general tendency to select arguments that most strongly support the alternative an agent believes to be best, given the information she possesses.
Homophilous interactions
After an agent chose which argument to communicate, she decides whom to share it with. Because we are interested in the effects of homophilous interaction patterns, we assume that agents share arguments in dyadic encounters in which they preferentially interact with those of identical group membership. Interactions are regulated through a homophily parameter \(h\) which ranges from zero to one. The greater \(h\), the more likely agents are to interact with team members from their own group. Choosing an interaction partner is operationalized as follows: whenever a sending agent \(x\) becomes active, we define all remaining team members as potential receiving agents \(Y = \{y_{1}, y_{2}, \dots, y_{N-1}\}\). Each agent \(y_{k}\) is assigned a similarity value \(s_k\), which takes on the value of \(h / 2 + 0.5\) if sending and receiving agent share the same identity and \(1 – (h / 2 + 0.5)\) otherwise. Exactly one of the other members of the team is chosen as recipient, where the probability of choosing agent \(y_{k}\) as the receiving agent is given by Equation 3.
| \[ p_{y_{k}} = \frac{s_{k}}{\sum_{k = 1}^{N - 1}s_{k}}\] | \[(3)\] |
When \(h = 1\), homophily is maximal and the sending agent will always choose a member of her own group. When \(h = 0\), no homophily is present and all agents are chosen with equal probability. Once the receiving agent has been determined, the sending agent shares the argument she picked before, and the receiving agent updates her set of arguments and beliefs. If the new argument changed the receiving agent’s belief about which option is best, she communicates this change immediately with the team. Receiving agents do not forget arguments or value them differently according to recency, frequency of receival, or group membership and beliefs of the sender. The process of activating an agent, sharing an argument, and updating beliefs of the receiver represents one iteration \(t\) and is repeated until the team obtains consensus and all agents agree on which option is best. If no consensus is reached, we stop simulations after a large number of iterations (\(t = 5000\)) and record the belief distribution at the stop moment. We note that if the argument exchange within teams continued even after a consensus is reached, all teams would eventually find optimal consensus. Specifically, because at each iteration, arguments accessible to the sending agent and any potential receiving agent are considered with nonzero probabilities, all members in a simulated team will have access to all arguments and agree on the best option if a simulation runs long enough. However, as we will show, it almost never occurs that all team members learn all arguments because consensus obtains (on any of the options, optimal or suboptimal) before saturation is reached. In that sense, our results show how homophily affects consensus outcomes without every team member having access to all arguments.
Setup of Simulation Experiments
To investigate how homophily affects decision-making quality, we vary homophily while holding all other parameters constant. For each homophily level, we simulate \(5000\) teams and observe how often they obtain optimal consensus and how long it takes them to reach consensus. Homophily is varied from \(h = 0\) to \(0.9\) in steps of \(0.1\). Between \(h = 0.9\) and \(0.98\) we vary homophily in steps of \(0.02\) because at such high levels of homophily we found particularly strong effects on discussion time. We do not consider teams in which no arguments are exchanged across groups at all (\(h = 1\)) because they would represent two separate discussions instead of one.
The results section presents the outcomes of simulation experiments designed to assess six main questions. Based on competing expectations derived from the opinion dynamics and the transient diversity literature, our first and foremost question is whether homophily improves or hampers optimal decision-making. To this end, we study how often simulated teams reach consensus on the optimal, second-best or worst decision option given different homophily levels. Teams in which no consensus obtained in the time-horizon of our simulations were very rare (between 0.1% and 1% of all simulation runs with a given homophily level) and are excluded from analysis. To gain better insights into the dynamics of the deliberation process, our second question concerns how homophily affects belief changes that occur among team members. Hence, we compare for different homophily levels how often agents change their beliefs about which option is best, and which option they preferred before and after a change. Our third question is whether our model is consistent with previous claims that bounded interactions increase discussion time (Frey & Šešelja 2020; Wu & O’Connor 2021; Zollman 2010). Hence, we track the number of iterations needed until a team reaches consensus and compare iteration numbers for different levels of homophily.
Our fourth result concerns the possible reasons behind homophily affecting optimal consensus making. One possibility is that homophily prevents teams from finding the optimal option because they cannot combine crucial arguments across groups. But it is also possible that homophily improves outcomes because it helps groups to find the optimal option on their own, without this process being distorted by influence from another group. To shed more light on the underlying driving effects of homophily, we compare the effect of homophilous interactions on optimal consensus-making for teams in which at least one group can infer the optimal option by themselves versus teams in which arguments from both groups have to be combined to infer the optimal option. The fifth question asks if our model aligns with existing works arguing that homophily matters more for tasks that are challenging (Harrison et al. 1998; Phillips et al. 2006). For different homophily levels, we thus compare decision outcomes in teams where the quality of different options was hard to disentangle (high difficulty) with those where clear differences between options were easy to recognize (low difficulty). Finally, our last result relates to the question of how homophily affects consensus-making within groups, before a decision is made on a team level. To elucidate this question, we present the fraction of both groups and teams with high versus no homophily that have reached optimal consensus after different (maximum) numbers of interactions.
To investigate each of the six questions outlined above, we simulate teams with the properties presented in Table 1. Our teams have \(N = 6\) members, which is a common size among decision-making teams in real-world contexts and hidden profile experiments alike. They are split into \(M = 2\) groups, reflecting a setting where relevant identities proxy a binary. In robustness analyses reported in Appendix A, we also present findings for multigroup settings (\(M > 2\)). A total of \(J = 3\) decision options is chosen and, given the distribution of common arguments, each group initially supports one of the two inferior options. The optimal option, on the other hand, is only supported by unique arguments. Because real-world decision-making often involves numerous possible decision alternatives, Appendix A includes robustness analyses of the effects of homophily on decision quality for \(J > 3\). A total of \(I = 18\) arguments is available in a team (i.e., six arguments per decision option given \(J = 3\)) and each group starts off with \(C = 3\) common arguments. There are thus 18 arguments − 2 groups \(\times\) 3 common arguments = 12 unique arguments, which are distributed across the six agents. Hence, each agent initially holds three common and two unique arguments. This distribution of arguments implies a hidden profile: Common arguments point towards inferior options and agents initially believe such options to be optimal. Throughout the main analyses, we examine teams where agents probabilistically select preferred decision options and arguments according to adherence values of \(\beta = 3.5\). This was found to be a reasonable value for agents to select strong arguments supporting options with higher levels of perceived quality while still allowing for small probabilities of stochastic deviation. Apart from the two, additional analyses mentioned above – homophily in multigroup settings and with many options, respectively – Appendix A materials report on extensive robustness analyses in which we vary the number of \(I\) arguments, \(C\) common arguments, \(N\) team members, and adherence values \(\beta\).
As a further check of our results, we also apply our model to a situation where optimal solutions are not ‘hidden’ to all team members from the start. Hidden profiles are difficult because arguments pointing towards the optimal option are not commonly known to team members. However, not all real-world decision-making tasks are hidden profiles. Tasks can also be ‘manifest’ where agents of at least one group have common information pointing towards the optimal alternative. We expect homophily to be less consequential for decision quality in such situations: homophily will slow down (but is unlikely to fully prevent) the team-wide dissemination of common arguments supporting the optimal alternative. Second, the suggested positive effect that homophily helps to uncover crucial hidden arguments becomes obsolete: arguments pointing to the optimal option are common arguments and do not need to be uncovered.
| Parameter | Description | Simulation values |
|---|---|---|
| \(N\) | Number of team members | 6 |
| \(M\) | Number of groups | 2 |
| \(I\) | Number of arguments | 18 |
| \(J\) | Number of decision options | 3 |
| \(C\) | Number of common arguments per group | 3 |
| \(\beta\) | Adherence to selecting stronger arguments and better options (perceived) | 3.5 |
| \(h\) | Homophily | 0 – 0.98 |
Results
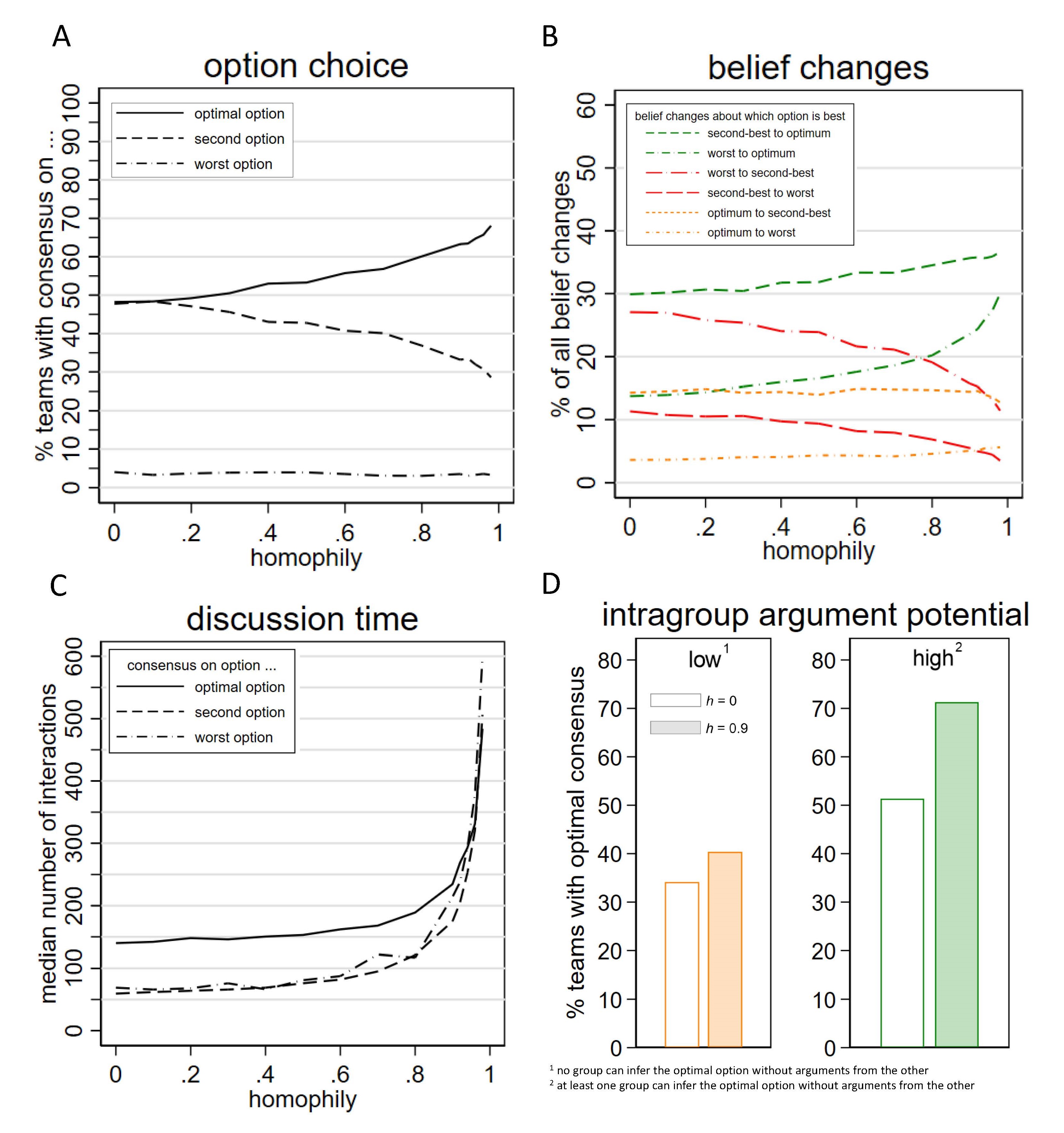
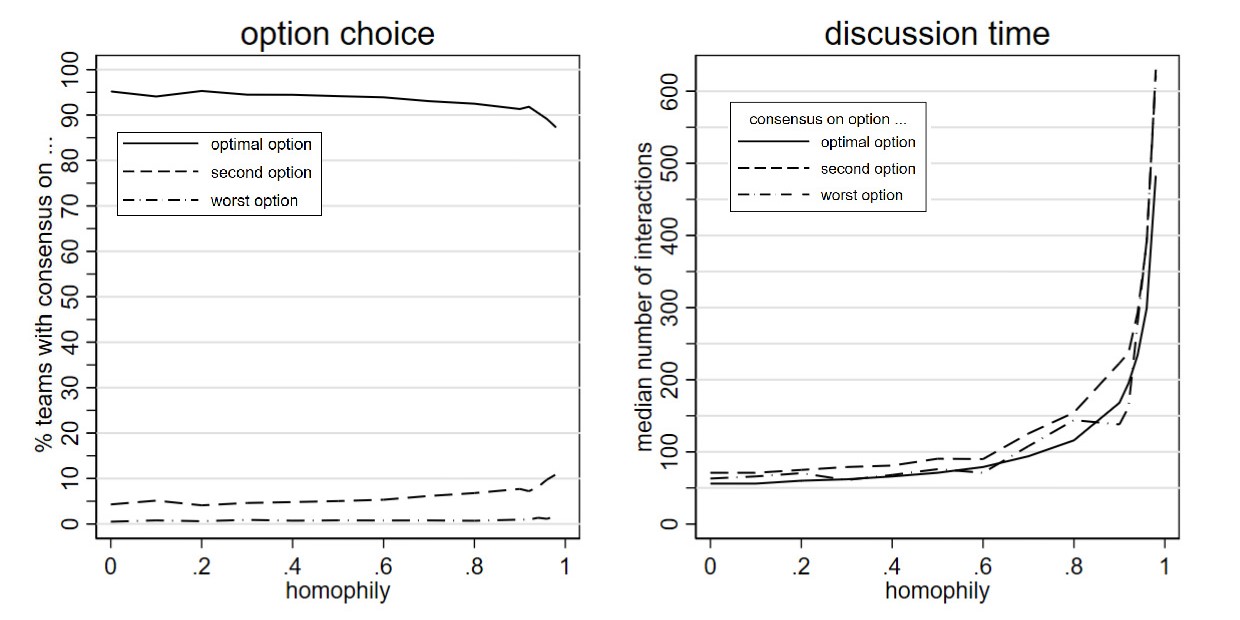
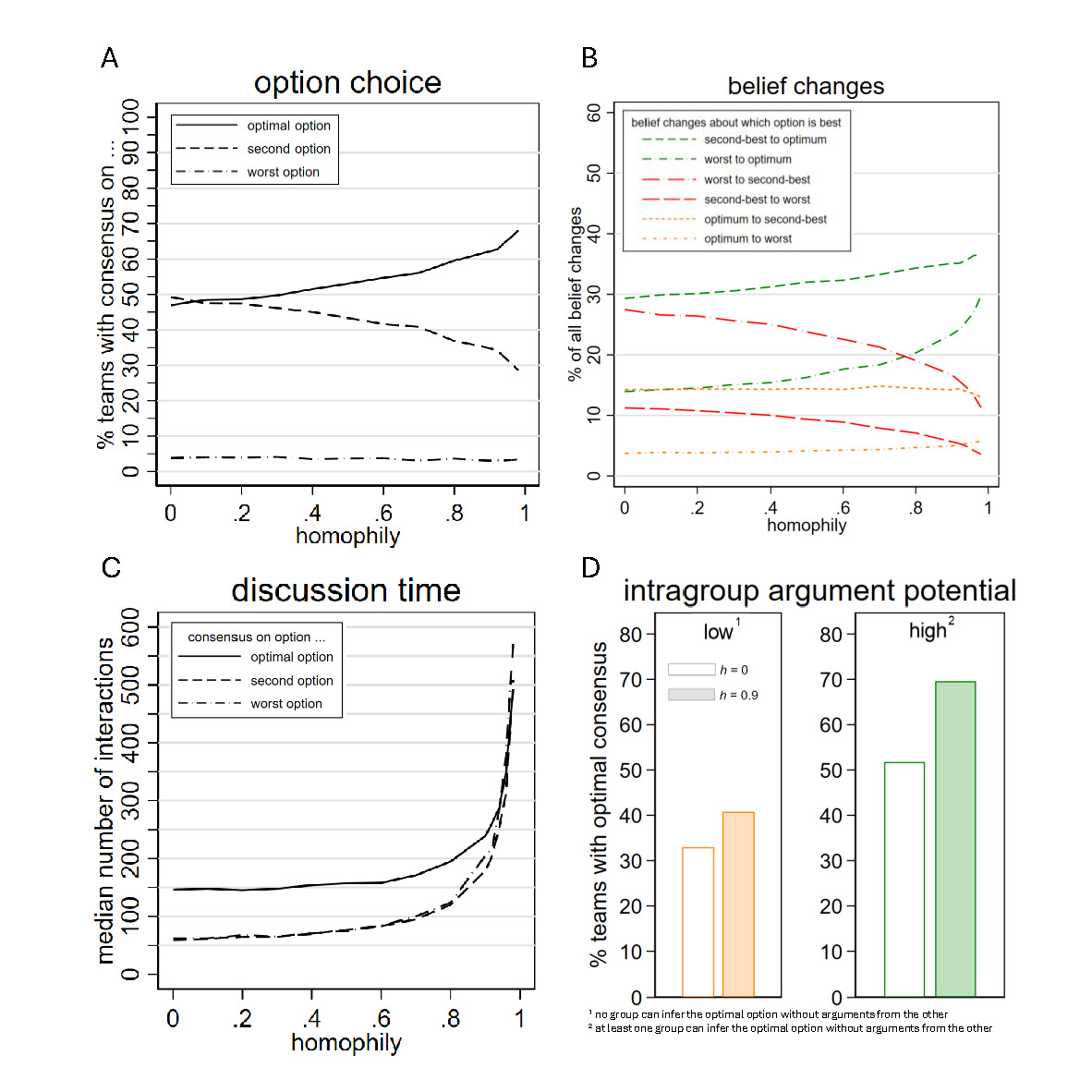
We start off by comparing how often simulated teams reach consensus on each of the three decision options of different quality, given different homophily levels. As Figure 3A shows, more teams form consensus on the optimal option as homophily levels increase and agents tend to interact less with team members with a different identity. The percentage of teams reaching consensus on the second-best option, on the other hand, sinks symmetrically with rising fractions of teams reaching optimal consensus. The share of teams which form consensus on the worst decision option is always below 5 percent, irrespective of the level of homophily. Considering this, and the fact that one group initially favors the second-best and the other group favors the worst option, we conclude that suboptimal consensus is most often made when one group convinces the other of the second-best option. To prevent suboptimal consensus on the second-best option, higher homophily levels could thus be helpful against the diffusion of arguments favoring this alternative from one group to the other.
The explanation provided here implies that as homophily increases and interactions between members of different groups become less likely, fewer agents should change their belief towards finding the second-best option optimal. Figure 3B supports this conjecture, showing how the overall proportion of belief changes from the worst option to the second-best option decreases from 28% to 12% between \(h = 0\) and \(h = 0.98\). Similarly, since homophily limits communication between groups both ways, fewer arguments supporting the worst option are being passed over to the group favoring the second-best option, and fewer belief changes towards the worst option occur. Conversely, belief changes from both the second-best and the worst option towards the optimal option become increasingly frequent in higher homophily levels. While changes towards this option are obviously necessary to obtain optimal consensus, they are not easily explained. If homophily hinders the exchange of arguments across groups, including those that point towards the optimal option, why do more team members change their belief towards the optimal option?
Longer deliberation uncovers optimal arguments
An explanation to this is that because homophily limits argument exchange between groups, disagreement in beliefs across groups is preserved, and neither group can convince the other of their initially preferred option. Hence, discussion continues. Figure 3C illustrates this, showing how higher homophily levels result in higher median discussion time. Prolonged discussions, in turn, enable arguments favoring the optimal option (called ‘optimal arguments’ hereafter) to be revealed and spread within a respective group. This is so because optimal arguments are unique arguments, which need more time than common arguments to be selected. In comparison to common arguments, unique arguments face a sampling disadvantage and are initially disfavored by agents’ argument selection procedure. But because this procedure is stochastic, small probabilities of choosing optimal arguments remain. When exchange between groups is limited and premature consensus kept at bay, optimal arguments are selected and spread within a group, and agents’ perceived quality of the optimal option rises. Once all members in one of the groups realized what the optimal option is, they are unlikely to be swayed: optimal arguments tend to have the highest weights and are difficult to surpass by other arguments. Hence, as soon as one group has discovered the optimal option, the danger of a suboptimal consensus is minute, which gives this group ample time to still convince the other group.
This explanation implies that homophily has a much more powerful effect when at least one of the groups has sufficiently strong optimal arguments to identify the best option by themselves and without the help of the other group. Figure 3D supports this conjecture, showing how homophily increases the share of teams with optimal consensus to a great extent (i.e., from 51% with \(h = 0\) to 71% with \(h = 0.9\)) when the arguments initially provided to one group are sufficient to infer the optimal option. However, when neither group can infer the optimal option without the other, homophilous interactions still increase the chances of making optimal consensus, but only slightly (34% to 40%). The smaller effect is explained by the fact that homophily still prolongs discussion time, making it more likely that optimal unique arguments spread within groups by chance. Altogether, it follows that homophily improves consensus quality mostly because it grants one group with the time to uncover unique arguments and arrive at the optimal option. At the same time, it hinders another group from quickly convincing the team to prefer a suboptimal option through the dissemination of inferior arguments.
Homophily is crucial when tasks are especially difficult
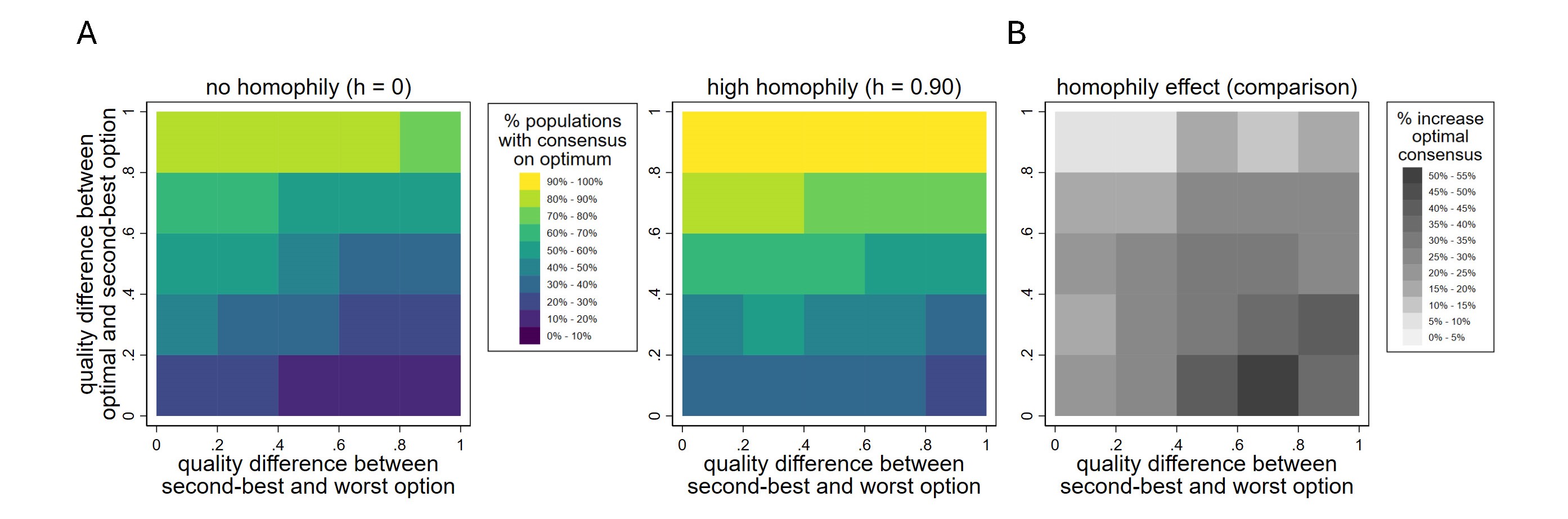
In Figure 3, we have shown that homophily improves decision-making quality because it prevents teams from prematurely adopting a second-best decision option. To further test this proposition, we investigate if optimal consensus is less likely when the second-best and the optimal option are close to each other in quality, and therefore hard to distinguish, and if the worst option has much lower quality than the second-best option and is therefore likely to be neglected quickly. For each simulation run, we compute a distance score reflecting the difference in quality between the optimal and the second-best option, and the second-best and the worst option. If the mechanism works as we have suggested, a smaller quality difference between the second-best and the optimal option should make it easier for the group initially supporting the worst option to get persuaded into the second-best option, thus reducing the chances of reaching optimal consensus. Similarly, a large difference in quality between the second-best and the worst option should make it easier for the second-best group to convince the worst group of the second-best option. In both cases, homophily should have a bigger effect because it is needed more to prevent suboptimal consensus on the second-best option.
In Figure 4A, we present the percentage of homophilous versus non-homophilous teams with optimal consensus by their differences in quality between the optimal and the second-best option, and the differences between the worst and the second-best option. As suspected, a smaller difference between the optimal and the second-best option increases the chances of finding optimal consensus. Greater differences between the second-best and the worst option, on the other hand, lead to lower proportions of optimal consensus. Comparing the fraction of populations with optimal consensus under high homophily versus no homophily, the previous finding persists that higher homophily levels render more populations with optimal consensus. This supports our explanation and shows that the positive effects of homophily we observe generalize to a wide set of different combinations of option quality.
However, Figure 4 B also indicates that the positive effect of homophily varies among problems with different quality combinations across options. In line with our proposed mechanism, homophily appears to matter especially for those problems where chances to obtain optimal consensus are low to begin with. Here, homophily provides the crucial barrier to the team-wide adoption of second-best arguments that are dangerous precisely because they are either almost as strong as arguments supporting the optimal option, or because arguments pertaining to the worst option are weak in comparison. As becomes evident from the figure, the increase in teams obtaining optimal consensus under high homophily levels is largest when differences between the second-best and the optimal option are small, and differences between the worst and the second-best option are large.
Homophily facilitates optimal intragroup consensus
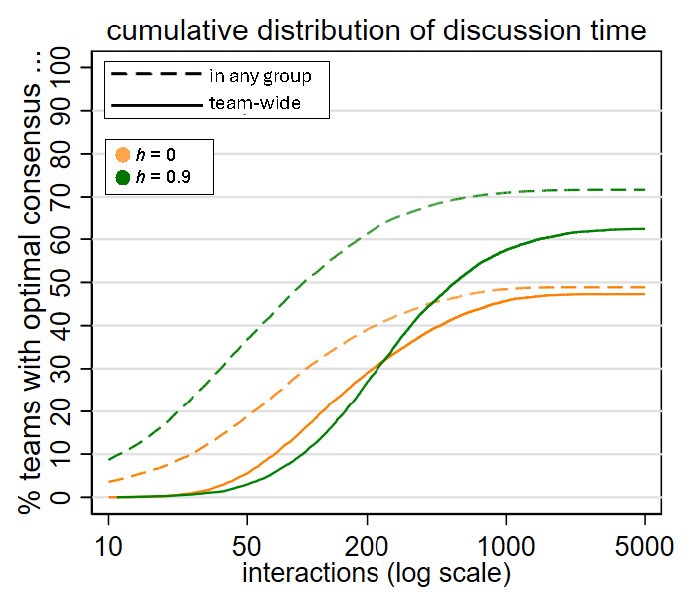
The results from Figure 3 suggest that homophily fosters optimal consensus by granting one of the groups the crucial time to exchange their optimal arguments and, in a subsequent step, convince the rest of the team. To further elucidate this mechanism, Figure 5 shows the fraction of teams with high versus no homophily that have reached optimal consensus across the whole team after a given number of interactions, and the first occurrence of optimal consensus within any of the two groups. If the mechanism works as described, we should find that optimal consensus within either group is more frequent, and occurs sooner under high homophily than in teams with no homophily.
A comparison of teams with and without homophily reveals that at any discussion length, more teams will have reached consensus on the optimal option in either group when homophily is high (dashed lines in Figure 5). This finding aligns with previous results that homophily facilitates optimal consensus within a group without influence from the other group (compare Figure 3D). However, teams with high homophily also need more time from the first occurrence of optimal consensus within a group until team-wide optimal consensus is established. The reason behind this is that homophily also slows down the sharing of arguments from the group with consensus on the optimal option to the other group. This contributes to increased discussion time under homophily.
For both teams with high homophily and no homophily, most teams that reach optimal consensus in a group also establish optimal consensus on a team level. Some teams, however, fail to achieve optimal consensus despite having reached optimal consensus in a group before. This becomes apparent from the fact that also at \(t = 5000\) interactions – a cutoff point at which more than 99% of teams have established any consensus – there remains a vertical difference between the dashed and the solid lines. Suboptimal team consensus despite previous optimal intragroup consensus can materialize because unless all optimal arguments have been uncovered already, belief changes within team members from the optimal to a suboptimal option can still occur. Surprisingly, this happens more frequently in teams with high homophily. The explanation behind this is that while one group may have found the optimal option, homophily tends to tighten intragroup consensus in the other group, enabling them to establish a strong belief that another (suboptimal) option is best. As discussions go on, the group with optimal consensus fails to receive additional optimal arguments from the other group that would be needed to strengthen their belief. Receiving other arguments instead, group members revoke their belief and suboptimal consensus is made. In sum, however, this tendency is insufficient to offset the mechanisms that optimal consensus in a group predates and fosters optimal consensus in the team, both of which occurring more often under homophily.
Homophily and decision quality in manifest profiles
In the above analysis, we have shown that homophily is especially important when a hidden profile task is difficult to solve. However, in real-world decision tasks it is rarely clear if a hidden profile is at hand in the first place. Common arguments do not necessarily need to support inferior options, they can also point towards the optimal option. In this case, multiple team members start off with optimal beliefs and a ‘manifest profile’ is present. Given that homophily only has strong positive effects when the task is difficult, can we still assume homophily to foster optimal consensus-making when a task is an easy manifest profile?
Intuitively, because optimal arguments are common arguments in one group and therefore likely to be shared early in the discussion, homophily hinders the communication of optimal arguments across groups. Hence, we expect that optimal consensus obtains less frequently. Figure 6A shows that this is indeed the case, albeit only to a small degree. The fraction of teams making optimal consensus decreases only slightly from 95 percent to 88 percent over the full range of the homophily parameter. This can be attributed to ceiling effects – when problems are very easy to solve, homophily will only delay the deliberation process but cannot thwart optimal decision-making. Just like in hidden profiles, homophily leads to longer discussion time. However, simulation runs ending in optimal consensus need slightly less time than those with suboptimal consensus (Figure 6B). This is because arguments pointing towards suboptimal options may be present only in the form of unique arguments, which comes along with more time necessary to uncover and share them.
Discussion
Our model identifies homophilous interactions in diverse teams as a key factor to the quality of a team consensus in difficult decision-making tasks. Preferential interaction with similar others prevented team members from being convinced by inferior solutions proposed by those with identities different than their own. As discussions continued, this gave room for communicating crucial arguments that would not have been shared otherwise. This finding resonates with the notion of ‘transient diversity’ (Zollman 2010). Simultaneously, our investigation extends this notion to the new realm of hidden profile problems and revealed a mechanism that had not been considered by the transient diversity literature before. While transient diversity models find that unbounded communication leads to the insufficient generation of diverse information, our hidden profile task showed that even when all information had been created prior to the task, its distribution could lead to unfavorable situations in which non-homophilous interactions resulted in suboptimal decisions. Extensive robustness analyses reported in the appendix reveal that this finding extends to different team sizes, argument distributions, and multigroup settings.
Our results thus run contrary to expectations suggested by the opinion dynamics literature – namely, that homophily will undermine team functioning. Regardless, our simulations feature two central commonalities with prominent opinion dynamics models (Flache et al. 2017; Hegselmann & Krause 2002; Mäs et al. 2013): homophilous interactions prolong discussion time, and they produce disagreement. Different from opinion dynamics research, however, disagreements had a transitionary character that eventually enabled better decisions. Many opinion dynamics models produce irresolvable and lasting intergroup dissent because they have different behavioral assumptions: agents do not search for optimal solutions but strive to maintain consensus with ingroup members and differentiate themselves from outgroup members. In consequence, emerging factions increasingly distance themselves from each other to such an extent that the odds of interaction between them become zero. Integrating assumptions of differentiation from those with different opinions, a possible opportunity for ‘model docking’ with opinion dynamics models (Axtell et al. 1996) and extension to this model is to condition homophilous encounters on endogenously changing interaction preferences based on beliefs. While this may result in unresolvable disagreements, the necessity to study alternative means for making decisions arises. A common approach in real-world teams is to rely on voting procedures and other aggregation rules when failure to obtain consensus is immanent (Levy 2007). Hence, studying decision quality while assuming voting procedures within the context of this model, or an adapted version thereof, provides a promising avenue for future research. Our results also run contrary to those of Estévez-Mujica et al. (2018) who found homophily to limit problem-solving potential in diverse groups. We attribute this divergence to the fact that their task resembled a manifest profile more than a hidden profile: because optimal pieces of information were relatively easy to recognize by agents but needed to be disseminated across groups, homophily hampered performance.
Considering that in our model, individuals truthfully communicate the information they consider most valuable and process information in an unbiased manner, the question arises how homophily also improves team decision-making when individuals are less rational. Previous works on hidden profiles identify anchoring heuristics, recency biases, and needs for social validation that can lead individuals to report and process information less accurately (Stasser & Stewart 1992; Stasser & Titus 2003). While such biases are not considered by our model, it is unlikely that fully accounting for them would fundamentally change the mechanism by which homophily improves decision-making. Due to the setup of the hidden profile and in line with empirical research, behavioral heuristics make it less likely that unique information is shared and accepted (Lu et al. 2012; Wittenbaum et al. 2004). Making the task at hand more difficult, accounting for them would likely amplify the effect that homophily has. In a similar vein, future research may consider status distinctions or different group sizes that would introduce inequality in the influence that one group has over another. Here, homophilous interactions could again provide a crucial mechanism to improve deliberation tasks that would otherwise have been dominated by the group with the greatest influence. This notion is supported by robustness analysis included in Appendix A, showing that homophily is especially important when the group initially supporting the second-best option is larger in size.
A feature that is inherent to hidden profiles is that individuals ultimately share the same goal and are likely to agree on one option to be best when faced with complete evidence. While this is applicable to many real-world situations, it abstracts from the possibility that team members of different identities may have group-based interests that make them attach different values to decision options, or even attach value to maintain disagreement with other groups. Such a case would make it necessary to redefine what an ‘optimal’ solution is and poses interesting distributive and ethical questions. While outside the scope of this paper, an extension of this model could be used as a starting point to investigate whether homophily is helpful in reaching decisions that maximize welfare for the team as a whole versus solutions that optimize payoffs for some groups of team members at the expense of reduced team performance.
For the purpose of this paper, probabilistic encounters between team members represented homophilous interaction preferences. However, the same encounters can also be seen as a manifestation of underlying social foci that structure team deliberation (Feld 1981). Translating the insights of this paper to such a perspective implies that better decisions will be made in settings where team members are structurally guided to interact with similar over dissimilar others more frequently. This resonates with suggestions made by the transient diversity literature (Zollman 2010). Simultaneously, studying the effects of interactions in structurally embedded environments calls for a possible extension of our model in which encounters are not probabilistic but occur along a network that specifies who exchanges information with whom. If the mechanism proposed here holds, networks in which members of different groups are increasingly kept apart should also feature better decisions.
In a more general sense, the model presented here can also be seen as an example of a larger class of phenomena exhibiting puzzling and often unexpected social change. Similar to how information transmission in networks is highly sensitive to ‘percolation thresholds’ (Newman & Watts 1999), residential segregation can emerge from minor preference shifts (Schelling 1971), and spread of new attitudes critically depends on the way supporters of new beliefs are spatially located (Nowak & Vallacher 2019), our model exhibits phase transitions where unlikely sharing of optimal information can determine failure or success to obtain optimal consensus.
While the simulation results reported here convincingly show how homophily fosters the quality of the team decision, it is important to note that homophilous interactions may have other, unintended consequences. Limiting interactions between members of different identities may amplify social identity processes that can lead to negative outgroup attitudes, lower levels of trust, and less cooperative behavior in general (Carter & Phillips 2017; Lau & Murnighan 1998). This raises the question whether improved decision-making can be reached through alternative means. Within the context of our model, such means could involve increased skepticism towards information coming from dissimilar members. However, this would involve that spillover effects from increased skepticism resulting in negative outgroup attitudes had to be tempered all the same. Similar to the extension suggested in the paragraph above and in line with simulation research suggesting that the timing of outgroup contacts matters crucially for multigroup discussions (Flache & Mäs 2008), an alternative to achieve improved consensus while minimizing negative affective consequences is to structurally embed conversations. For example, deliberation could be broken up into phases where groups are first kept apart and given enough time to uncover crucial information without influence from other groups, and only then brought together to find a consensual solution. In addition to future computational experiments, the effectiveness of such an intervention could easily be tested in an empirical setting where teams with a structurally embedded deliberation procedure likely made better decisions than those without.
Lastly, the finding that keeping groups apart has positive effects on decision quality relies to some degree on at least one of the groups having sufficient information to infer an optimal solution by themselves. This provides a scope condition for the mechanism found by this paper, but also raises the important question whether homophily can be helpful in cases where only a specific conjunction of arguments from different groups can reveal the best solution. While exceeding the scope of this paper, this calls for a promising model extension in which this is addressed more explicitly – namely, a model where a complex underlying function enables certain argument combinations to have nonlinear impacts on team members’ beliefs.
In conclusion, the work presented here provides a novel insight on how to better shape interactions in diverse teams with regards to their decision-making abilities. When tasks are difficult, unbounded communication among team members can cause cognitive diversity to pose a liability. In such cases, homophilous interactions improve decision quality because they keep individuals from convincing dissimilar others with their suboptimal responses too quickly. Pointing to a trade-off between decision quality and efficiency, homophily also resulted in increased discussion time. This is an important finding to consider when finite resources have to be weighed against convex returns to optimal over inferior solutions.
Data Availability
The model is written and built in NetLogo. The full NetLogo code is stored on the CoMSES Computational Model Library under the following URL: https://www.comses.net/codebases/e2d16fa2-38f0-48cb-829f-e8feef6f15c0/releases/1.0.0/ The data was analyzed using Stata. The data and Stata syntax can be found on the Open Science Framework (OSF) via the following URL:https://osf.io/76hfm/.
Competing Interests
The authors declare no competing interests.
Funding
This study is part of the research program Sustainable Cooperation – Roadmaps to Resilient Societies (SCOOP). The authors are grateful to the Netherlands Organization for Scientific Research (NWO) and the Dutch Ministry of Education, Culture and Science (OCW) for generously funding this research in the context of its 2017 Gravitation Program (grant number 024.003.025).
Acknowledgments
We are grateful to have received helpful suggestions from two anonymous reviewers and would like to thank the Editor of JASSS, Flaminio Squazzoni. We are indebted to Michael Mäs, Jan-Willem Romeijn, Hendrik Siebe, and the Norms and Networks Cluster of the Department of Sociology at the University of Groningen for inspiring remarks, constructive discussions, and useful feedback.
Appendix
Robustness of findings
In our main results, analyses pertained to small teams with no more than two groups, three decision options, and a limited number of arguments. Here we investigate if the positive effect of homophilous interactions on decision quality also persists under different parameter settings. In each of the panels of Figure 7, we measure discussion time and the fraction of teams obtaining optimal consensus under high (\(h = 0.9\)), medium (\(h = 0.5\)) and no homphily (\(h = 0\)), and vary one of the default parameters described in the section ‘Setup of simulation experiments’. Finally, we vary one component not originally covered by the variable parameters in the model: the proportion of the group initially supporting the second-best option relative to the size of the whole team. All analyses are conducted to investigate if our findings hold in more generalized ecological environments. The finding that homophily improves discussion quality turns out to be remarkably robust across all analyses.
Figure 7, Panel A shows that regardless of the number of total available arguments \(I\), homophily improves decision quality. This is because the mechanism by which homophily operates – enabling one group to find the optimal decision while limiting influence from the other – stays the same, regardless of the number of arguments. However, as visible from the decreasing fractions of teams with optimal consensus, a greater number of available arguments also makes problems more difficult to solve correctly. As more arguments pertain to each option and weights pertaining to arguments are drawn randomly, the law of great numbers makes the true quality scores of the different options more similar and therefore harder to differentiate. More arguments also increase discussion time because there are more possible argument sets team members can hold to form beliefs: in turn, longer deliberation is needed to align everyone’s beliefs.
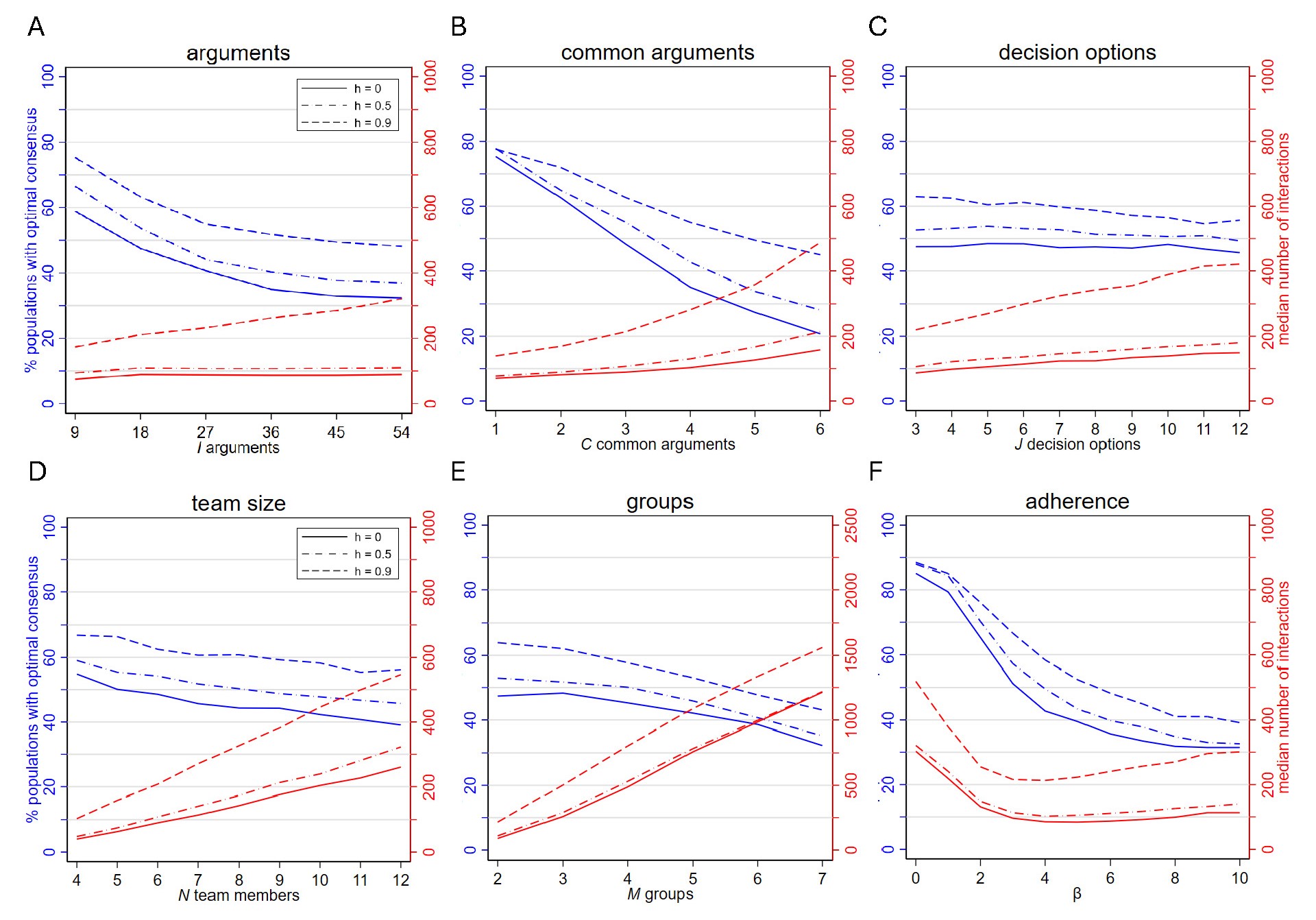
From Figure 7, Panel B it becomes evident that a greater number of common arguments per group leads to decreasing fractions of teams with optimal consensus but amplifies the effect of homophily. This is because an increasing number of suboptimal common arguments will lead to their increased circulation and hence, chances rise that one group will be able to convince the other of a suboptimal option. This makes homophilous interactions even more important, providing the necessary barrier to the diffusion of inferior arguments across groups.
In Figure 7, Panel C we show that the positive effect of homophilous interactions on decision quality persists under a rising number of available decision options \(J\). To ensure that each decision option had a constant number of available arguments pertaining to it, we increased the number of total available arguments by six in each additional option (hence, \(I = J \times 6\)). As \(J\) rose, the effect of homophily on optimal consensus-making decreased slightly but remained positive. We attribute this to the fact a greater number of options diversifies team members’ sets of unique arguments and weakens the correlation between initial beliefs and group membership. This weakens the effect of keeping groups separate. Additionally, greater \(J\) increased discussion time, which is intuitive because an increasing number of options makes it increasingly difficult to align all team members’ beliefs about which option is best.
Figure 7, Panel D confirms that homophily improves decision quality irrespective of the number of team members. As team size increases, the fraction of teams with optimal consensus sinks while the positive effect of homophilous interactions becomes larger. An explanation to this is that as \(N\) rises while the number of available arguments \(J\) and common arguments per group \(C\) are kept constant, each agent holds fewer unique arguments relative to their common arguments. Similar to the effects found in Figure 6B, this leads to an increase in common arguments that are circulating, which in turn makes homophily even more important to prevent suboptimal consensus. In addition to the fact that it takes longer to align everyone’s beliefs when the team is larger, the increase in (redundant) common information that circulates prolongs discussion time.
Figure 7, Panel E shows that homophilous interactions increase the fraction of teams with optimal consensus also when more than \(M = 2\) groups are present. To ensure that each group featured sufficiently many members, we increased team size in steps of three with each group added. Because each group needs to hold common information different from those of other groups, we added one additional decision option with each group, and six arguments with each option (hence, \(N = M \times 3\); \(J = M + 1\) and \(I = J \times 6\)). As the number of groups and decision options rose, chances decreased that one group alone had the arguments necessary to infer the optimal option without information from others and hence, the effect of homophily was smaller when the number of groups was large. Given that additional groups, arguments, and options also increased the overall complexity of the deliberation process, discussion time increased greatly.
Figure 7, Panel F reveals robust homophily effects under varying levels of the adherence parameter \(\beta\) by which agents select a decision option to support and an argument favoring this option. The homophily effect is smaller at low levels of \(\beta\), which is due to a ceiling effect. Most teams reach optimal consensus also in the absence of homophily. The high fraction of teams with optimal consensus results from the fact that lower \(\beta\) values result in an increasingly random selection of arguments. This helps optimal unique arguments to be uncovered. High \(\beta\) values, on the other hand, cause quasi-deterministic sharing of arguments that support agents initial yet inferior beliefs. Discussion time is maximal when \(\beta\) is lowest because randomly selected arguments allow for greater diversity in beliefs, which prevents consensus and delays the deliberation process. Discussion time slightly increases again at high \(\beta\) because increasingly deterministic argument sharing leads to greater redundancy in argument sharing, which is insufficient to convince one group of another group’s preferred option. This leads to lack of consensus, especially when interactions are homophilous.
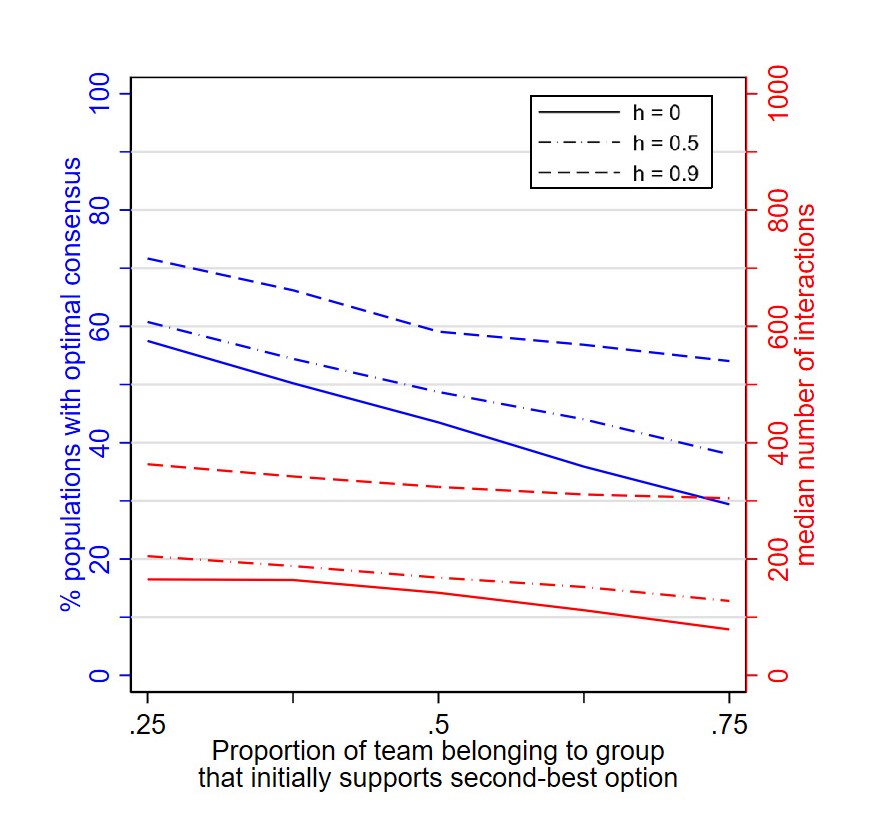
Figure 8 presents the effect of homophily for teams of unbalanced group sizes. All simulated teams have eight members and the size of the group initially supporting the second-best option ranges between two and six members. All other parameters have the default values reported in the main paper. As becomes evident from the figure, homophily makes optimal consensus-making more likely throughout the imbalance levels tested. Optimal consensus is least frequent and homophily effects strongest when the fraction group of members initially supporting the second-best option is large. This is so because creating more team members that prefer the second-best option gives this option additional support, which increases the risk of a second-best consensus. To prevent this, homophily is especially important.
Lastly, Figure 9 presents the main results from Figure 3, but this time using simulated teams where the sending agent is not activated sequentially but randomly. A comparison with Figure 3 reveals that results are virtually identical, leading us to conclude that the model is robust to potential statistical artefacts resulting from a fixed order activation of agents.
Notes
- Identities satisfying these conditions could be, for example, ethnic identities in a team developing a product targeted towards a diverse consumer base or team members’ disciplinary identities in a scientific collaboration.↩︎
References
AXTELL, R., Axelrod, R., Epstein, J. M., & Cohen, M. D. (1996). Aligning simulation models: A case study and results. Computational & Mathematical Organization Theory, 1(2), 123–141. [doi:10.1007/bf01299065]
BAIL, C. A. (2016). Combining natural language processing and network analysis to examine how advocacy organizations stimulate conversation on social media. Proceedings of the National Academy of Sciences, 113(42), 11823–11828. [doi:10.1073/pnas.1607151113]
BALIETTI, S., Getoor, L., Goldstein, D. G., & Watts, D. J. (2021). Reducing opinion polarization: Effects of exposure to similar people with differing political views. Proceedings of the National Academy of Sciences, 118(52), e2112552118. [doi:10.1073/pnas.2112552118]
BRECHWALD, W. A., & Prinstein, M. J. (2011). Beyond homophily: A decade of advances in understanding peer influence processes. Journal of Research on Adolescence, 21(1), 166–179. [doi:10.1111/j.1532-7795.2010.00721.x]
CARTER, A. B., & Phillips, K. W. (2017). The double-edged sword of diversity: Toward a dual pathway model. Social and Personality Psychology Compass, 11(5), e12313. [doi:10.1111/spc3.12313]
DELLAPOSTA, D., Shi, Y., & Macy, M. (2015). Why do liberals drink lattes? American Journal of Sociology, 120(5), 1473–1511. [doi:10.1086/681254]
ERTUG, G., Brennecke, J., Kovács, B., & Zou, T. (2022). What does homophily do? A review of the consequences of homophily. Academy of Management Annals, 16(1), 38–69. [doi:10.5465/annals.2020.0230]
ESTÉVEZ-MUJICA, C. P., Acero, A., Jiménez-Leal, W., & Garc’D’, C. (2018). The influence of homophilous interactions on diversity effects in group problem-Solving. Nonlinear Dynamics, Psychology & Life Sciences, 22, 1.
FELD, S. L. (1981). The focused organization of social ties. American Journal of Sociology, 86(5), 1015–1035. [doi:10.1086/227352]
FLACHE, A., & Mäs, M. (2008). How to get the timing right. A computational model of the effects of the timing of contacts on team cohesion in demographically diverse teams. Computational & Mathematical Organization Theory, 14(1), 23–51. [doi:10.1007/s10588-008-9019-1]
FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2. https://jasss.soc.surrey.ac.uk/20/4/2.html [doi:10.18564/jasss.3521]
FREY, D., & Šešelja, D. (2020). Robustness and idealizations in agent-Based models of scientific interaction. The British Journal for the Philosophy of Science, 71(4), 1411–1437. [doi:10.1093/bjps/axy039]
HARRISON, D. A., Price, K. H., & Bell, M. P. (1998). Beyond relational demography: Time and the effects of surface- and deep-Level diversity on work group cohesion. Academy of Management Journal, 41(1), 96–107. [doi:10.5465/256901]
HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2. https://jasss.soc.surrey.ac.uk/5/3/2.html [doi:10.18564/jasss.5257]
HONG, L., & Page, S. E. (2004). Groups of diverse problem solvers can outperform groups of high-ability problem solvers. Proceedings of the National Academy of Sciences, 101(46), 16385–16389. [doi:10.1073/pnas.0403723101]
JACKSON, S. E., May, K. E., Whitney, K., Guzzo, R. A., & Salas, E. (1995). Understanding the dynamics of diversity in decision-making teams. Team Effectiveness and decision-making in Organizations, 204, 261.
LAU, D. C., & Murnighan, J. K. (1998). Demographic diversity and faultlines: The compositional dynamics of organizational groups. Academy of Management Review, 23(2), 325–340. [doi:10.5465/amr.1998.533229]
LEVINE, S. S., Apfelbaum, E. P., Bernard, M., Bartelt, V. L., Zajac, E. J., & Stark, D. (2014). Ethnic diversity deflates price bubbles. Proceedings of the National Academy of Sciences, 111(52), 18524–18529. [doi:10.1073/pnas.1407301111]
LEVY, G. (2007). decision-making in committees: Transparency, reputation, and voting rules. American Economic Review, 97(1), 150–168. [doi:10.1257/aer.97.1.150]
LU, L., Yuan, Y. C., & McLeod, P. L. (2012). Twenty-Five years of hidden profiles in group decision-making: A meta-Analysis. Personality and Social Psychology Review, 16(1), 54–75. [doi:10.1177/1088868311417243]
MÄS, M., & Flache, A. (2013). Differentiation without distancing. Explaining bi-polarization of opinions without negative influence. PLoS One, 8(11), e74516.
MÄS, M., Flache, A., Takács, K., & Jehn, K. A. (2013). In the short term we divide, in the long term we unite: Demographic crisscrossing and the effects of faultlines on subgroup polarization. Organization Science, 24(3), 716–736.
MCLEOD, P. L., Lobel, S. A., & Cox, T. H. (1996). Ethnic diversity and creativity in small groups. Small Group Research, 27(2), 248–264. [doi:10.1177/1046496496272003]
MCPHERSON, M., Smith-Lovin, L., & Cook, J. M. (2001). Birds of a feather: Homophily in social networks. Annual Review of Sociology, 27(1), 415–444. [doi:10.1146/annurev.soc.27.1.415]
MILLIKEN, F. J., & Martins, L. L. (1996). Searching for common threads: Understanding the multiple effects of diversity in organizational groups. Academy of Management Review, 21(2), 402–433. [doi:10.5465/amr.1996.9605060217]
NEWMAN, M. E. J., & Watts, D. J. (1999). Scaling and percolation in the small-world network model. Physical Review E, 60(6), 7332–7342. [doi:10.1103/physreve.60.7332]
NORTHCRAFT, G. B., Polzer, J. T., Neale, M. A., & Kramer, R. M. (1995). Diversity, social identity, and performance: Emergent social dynamics in cross-functional teams. In S. E. Jackson & M. N. Ruderman (Eds.), Diversity in Work Teams: Research Paradigms for a Changing Workplace (pp. 69–96). Washington, DC: American Psychological Association. [doi:10.1037/10189-003]
NOWAK, A., & Vallacher, R. R. (2019). Nonlinear societal change: The perspective of dynamical systems. British Journal of Social Psychology, 58(1), 105–128. [doi:10.1111/bjso.12271]
PAGE, S. (2019). The Diversity Bonus: How Great Teams Pay Off in the Knowledge Economy. Princeton, NJ: Princeton University Press. [doi:10.2307/j.ctvc77fcq]
PETERS, U. (2021). Hidden figures: Epistemic costs and benefits of detecting (invisible) diversity in science. European Journal for Philosophy of Science, 11(1), 33. [doi:10.1007/s13194-021-00349-6]
PHILLIPS, K. W. (2003). The effects of categorically based expectations on minority influence: The importance of congruence. Personality and Social Psychology Bulletin, 29(1), 3–13. [doi:10.1177/0146167202238367]
PHILLIPS, K. W., & Loyd, D. L. (2006). When surface and deep-level diversity collide: The effects on dissenting group members. Organizational Behavior and Human Decision Processes, 99(2), 143–160. [doi:10.1016/j.obhdp.2005.12.001]
PHILLIPS, K. W., Northcraft, G. B., & Neale, M. A. (2006). Surface-Level diversity and decision-Making in groups: When does deep-Level similarity help? Group Processes & Intergroup Relations, 9(4), 467–482. [doi:10.1177/1368430206067557]
PHILLIPS, K. W., & O’Reilly, C. (1998). Demography and diversity in organizations: A review of 40 years of research. Research in Organizational Behavior, 20, 77–140.
REAGANS, R. (2013). Demographic diversity as network connections: Homophily and the diversity-performance debate. The Oxford Handbook of Diversity and Work, 192–206. [doi:10.1093/oxfordhb/9780199736355.013.0011]
SCHELLING, T. C. (1971). Dynamic models of segregation. The Journal of Mathematical Sociology, 1(2), 143–186.
SCHULZ-HARDT, S., & Mojzisch, A. (2012). How to achieve synergy in group decision-making: Lessons to be learned from the hidden profile paradigm. European Review of Social Psychology, 23(1), 305–343. [doi:10.1080/10463283.2012.744440]
SOHRAB, S. G., Waller, M. J., & Kaplan, S. (2015). Exploring the hidden profile paradigm: A literature review and analysis. Small Group Research, 46(5), 489–535. [doi:10.1177/1046496415599068]
STARK, T. H., & Flache, A. (2012). The double edge of common interest: Ethnic segregation as an unintended byproduct of opinion homophily. Sociology of Education, 85(2), 179–199. [doi:10.1177/0038040711427314]
STASSER, G., & Stewart, D. (1992). Discovery of hidden profiles by decision-making groups: Solving a problem versus making a judgment. Journal of Personality and Social Psychology, 63, 426–434. [doi:10.1037/0022-3514.63.3.426]
STASSER, G., & Titus, W. (1985). Pooling of unshared information in group decision-making: Biased information sampling during discussion. Journal of Personality and Social Psychology, 48, 1467–1478. [doi:10.1037/0022-3514.48.6.1467]
STASSER, G., & Titus, W. (2003). Hidden profiles: A brief history. Psychological Inquiry, 14(3–4), 304–313. [doi:10.1080/1047840x.2003.9682897]
TAJFEL, H. (2010). Social Identity and Intergroup Relations. Cambridge: Cambridge University Press.
WITTENBAUM, G. M., Hollingshead, A. B., & Botero, I. C. (2004). From cooperative to motivated information sharing in groups: Moving beyond the hidden profile paradigm. Communication Monographs, 71(3), 286–310. [doi:10.1080/0363452042000299894]
WU, J., & O’Connor, C. (2021). How should we promote transient diversity in science? Preprint. Available at: http://philsci-archive.pitt.edu/19428/
ZOLLMAN, K. J. (2010). The epistemic benefit of transient diversity. Erkenntnis, 72(1), 17–35. [doi:10.1007/s10670-009-9194-6]