The Role of Values in Pandemic Management: An Agent-Based Model

,
and
aBoston University, United States; bCenter for Mind and Culture, Boston, United States; cUniversity of Agder, Norway
Journal of Artificial
Societies and Social Simulation 27 (1) 19
<https://www.jasss.org/27/1/19.html>
DOI: 10.18564/jasss.5350
Received: 21-Jan-2023 Accepted: 19-Jan-2024 Published: 31-Jan-2024
Abstract
The SARS-CoV-2 pandemic has made abundantly evident that human behavior is a critical factor in determining whether interventions intended to manage infection spread are effective. Human behavior is driven by decision processes about whether to comply with advice from public-health experts and instructions from officials charged with managing pandemic response within organizations and governmental regions. And guiding those decisions are personal values, often shared with others, which are understudied features of pandemic management. Here, we demonstrate the role of values in a pandemic simulation using The Artificial Organization (TAO), an existing, strongly validated, agent-based, decision-support tool for pandemic management. We enhance TAO by adding human values to create TAO-V, focusing particularly on values related to political ideology, the spread of those values, and the way political values and compliance decisions have interacted in the United States of America (and other nations, usually to a lesser extent). TAO-V confirms that human values are influential factors in a pandemic simulation, which invites testing against real-world data from pandemic-management efforts (we pursue this in a subsequent paper). Even before real-world testing, the results of this study suggest that public-health messaging might be more effective if it were to engage values rather than only stress compliance with public-health recommendations.Introduction
At the time of writing, confirmed COVID-19 infections globally are 770 million, COVID-19 deaths are almost seven million, and there is an indeterminate number of people struggling with chronic long-COVID symptoms (WHO 2023). To make matters worse, there is reason to think that there has been extensive undercounting of deaths, based on analysis of reporting patterns and deaths in excess of expectations (Centers for Disease Control and Prevention 2023).
Some nations managed the pandemic far better than others. Pandemic resilience analyses have ranked nations, prioritizing few deaths, high vaccination rates, low economic disruption, and high quality of life (e.g., Bloomberg (2022)). Geographic isolation helps, with island nations and nations having long sea borders tending to do better. But that is only part of the story. Emotions and values matter, too, because they drive compliance decisions within the population. Trusting both scientific experts and government public-health officials goes a long way to inspiring compliance with pandemic management recommendations.
This paper demonstrates the degree to which human values matter in pandemic management, in principle. We employ an existing, well-validated agent-based model, expand it to include human values, and evaluate the impact of having those factors activated versus deactivated. This approach begs for real-world application, demonstrating the importance of human values not only in theory but also in the practice of pandemic management; we pursue that in another paper. This paper makes the case in principle, and supplies quantitative indicators to suggest that taking account of human values may well prove to be a critically important consideration in real-world pandemic management.
Literature Review
Early models (e.g., Ferguson et al. 2020) were built using differential equations and focused on the biological dimensions of susceptibility, exposure, infection, and recovery or death. These longstanding epidemiological tools for understanding the spread of infectious diseases are useful for estimating likely surges of infections. They are thereby useful for anticipating associated shortages in resources such as personal protective equipment, ventilators, and hospital beds. But these traditional epidemiological models not only suffered from a lack of calibration and validation; they also failed to take account of the vital role within pandemic management of human behaviors and beliefs, which influence the effectiveness of non-pharmaceutical interventions (NPIs). Recognizing this, the USA’s Centers for Disease Control announced a $26M program in Advanced Outbreak Forecasting and Analytics (Centers for Disease Control and Prevention 2021).
Human decisions are inflected by emotions such as fear and lack of trust, by tendencies to cognitive error that enliven mis/disinformation and conspiracy theories, and (particularly in the United States) by political polarization of every aspect of human life including pandemic management strategies. Traditional epidemiological models don’t do much to take account of such human factors.
By contrast, human simulation builds human factors into computational simulations. Human simulation is an extension of the established domain of computational social simulation that focuses on building agent-based models with psychologically plausible and behaviorally believable AI agents (Diallo et al. 2019; Shults & Wildman 2020b). As the importance of human factors in pandemic management became clear, several groups endeavored to move beyond traditional epidemiological models to agent-based simulations that take account of human factors to various degrees. These models vary greatly in the scale modeled, consideration of human factors, and the use of real-world data for validation. Examples of agent-based models include the following:
- "An agent-based model to evaluate the COVID-19 transmission risks in facilities" (Cuevas 2020)
- "Covasim" (Kerr et al. 2020) from Institute for Disease Modeling, University of Copenhagen, Burnet Institute, GitHub, and Microsoft
- "High-Resolution Agent-Based Modeling of COVID-19 Spreading in a Small Town" (Truszkowska et al. 2021)
- "CityCOVID" by Argonne, built on top of chiSIM (Argonne National Laboratory 2021)
- "An Agent-Based Model to assess COVID-19 spread and health systems burden in Telangana state, India" (Narassima et al. 2020)
- "COVID-ABS: An agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions" (Petrônio et al. 2020)
- "An Agent-Based Modeling of COVID-19: Validation, Analysis, and Recommendations" (Shamil et al. 2021)
- "An Agent-Based Model of the Local Spread of SARS-CoV-2: Modeling Study" (Staffini et al. 2021)
- "An agent-based model for simulating COVID-19 transmissions on university campus and its implications on mitigation interventions: a case study" (Zhou et al. 2021)
- "A stochastic agent-based model of the SARS-CoV-2 epidemic in France" (Hoertel et al. 2020)
- "The Artificial University: Decision Support for Universities in the COVID-19 Era" (Wildman et al. (2020), with the associated dashboard at: https://mindandculture.org/projects/past-projects/vivid-dashboard/)
- "Agent-Based Social Simulation for the COVID-19 Crisis" (Dignum 2021)
- The Artificial Organization: "The TAO of University Pandemic Forensics: How Good are COVID Simulations?" (Wildman et al. Under review).
(E), (H) and (J) take the largest view and each model a full country or region. (E) and (J) each have millions of agents, while (H) scales down a country to 1,000 agents. (B), (C), (D), (F), (G), and (L) each model a single city or town, although (L) also parameterizes according to country. (A), (I), (K), and (M) take the smallest view, each modeling only a single facility or organization. In most of these models, the agents strictly adhere to public-health restrictions placed on them, but (B), (H), (K), and (M) have a notion of agent compliance. Agents in these models have some chance of disobeying restrictions (e.g., ignoring mask-wearing or lockdown requirements). Several of the models also used real-world data during the modeling process. (C), (D), (G), and (J) used real-world data as an input to the simulation. (E), (K), and (M) used synthetic data based on real-world data to initialize the simulation. (B) went a step further and used a machine-learning algorithm to adjust inputs in light of real-world data, back-validating the model against data from Seattle and then making projections. To our knowledge, the (B) team has not yet attempted a follow-up study to evaluate the accuracy of those predictions. (K) went further than other models in including human factors and (M) went further still.
Each model supplied decision makers in different contexts with information needed to maximize the health, safety, productivity, and happiness of the people in their communities. But none of these simulations has been used to analyze the role of human values in pandemic management, which is what we attempt in this paper (Ghorbani et al. (2021) did consider the influence of culture on pandemic management, which is a good start). We extend the (M) model, The Artificial Organization, by incorporating values directly relevant to compliance, yielding TAO-V.
Incorporating values in computational simulations is not new, even if it is new in pandemic-management simulations. However, most early social-simulation and game-theoretic models approached the simulation of values somewhat abstractly, modeling phenomena such as “cooperation” in ways that presupposed humans are “rational actors,” calculating what is “best” for themselves given a specific goal (e.g., Axelrod & Hamilton 1981). As evidenced in this special issue of JASSS, however, computational social scientists are increasingly interested in modeling the role of human values, norms, or moral tendencies in ways that more concretely account for contemporary psychological understandings of motivated cognition. This interest can be seen in the wave of methodological proposals and computational models in the last decade striving to simulate the role of psychological and cultural values in human cognition and behavior (Antosz et al. 2022; Conte et al. 2014; Diallo et al. 2021; Dignum & Dignum 2014; Elsenbroich & Gilbert 2014; Mahmoud et al. 2014; Merdes 2017).
One important reason for more psychologically realistic cognitive architectures and behavioral rules for simulated agents is primarily scientific. Today, the expert consensus is that human reason is inextricably linked to emotion and moral evaluation. In other words, “rational” acting is always and already morally or emotionally “motivated” acting. Thus, simulating values more concretely within agent-based models takes seriously research in a wide range of disciplines. These related lines of research show that shows how human behavior can only be adequately understood in light of the evolved moral equipment with which we are all born and the ways cultures and subcultures shape and deploy those in-built moral dispositions. Increasingly complex cognitive and emotional architectures have been employed to express this psychologically more accurate way of conceiving human behavior and decisions, including models of terror management theory (Shults, Lane, et al. 2018), identity fusion theory and social identity theory (Shults, Gore, et al. 2018), and prosociality (Galen et al. 2021). From a scientific point of view, adequate simulation of humans will require accounting for “values,” at least for many research questions and purposes.
A second and interrelated motivation concerns linking social simulation to ethical concerns, both practically and philosophically (Diallo et al. 2021; Shults & Wildman 2019; Mascaro 2010; Shults & Wildman 2020a). Grim (2003) treats modeling as a philosophical methodology, and applies this to the phenomenon of polarization (Grim et al. 2012). An important implication of these publications is that the journey from simulation architecture to ethics is clarified and rendered less arbitrary when ethically relevant values are included in the simulation design.
A third motivation is more pragmatic and focused on social policy. Previous ABMs have attempted to incorporate values into simulations oriented toward the analysis or evaluation of policies related to topics such as public smoking (Dechesne et al. 2013) or the integration of refugees into Dutch society (Boshuijzen-van Burken et al. 2020). We believe this approach holds great promise for addressing a wide variety of challenges related to social sustainability both locally and globally (Shults & Wildman 2020a). The “Agent-Based Social Simulation for the COVID-19 Crisis” platform ((L) above) is, to our knowledge, the most developed policy-oriented modeling platform that rigorously includes human values. There agent values are linked to the well-known Schwartz value scale, and simulation runs can be parameterized according to the Hofstede Dimensions of various countries (Dignum 2021). As explained below TAO-V incorporates values into its agent architecture differently, focusing on the tendency to conform and the role of political ideology and affiliation.
TAO-V: Model Description
Origin
TAO, The Artificial Organization, which is model (M) in the list above, is described in detail elsewhere (Wildman et al. Under review). TAO itself borrowed some if its design from the precursor to TAO, The Artificial University (TAU; model (K), above), which specifically explored COVID-19 transmission in universities, taking account of several NPIs and several types of compliance (see Wildman et al. (2020), including the associated dashboard built with the help of the Virginia Modeling, Analysis, and Simulation Center at Old Dominion University, and the open-source model). TAO extends TAU to more general organizations – particularly organizations that have clear structures and schedules, including large corporations, military bases, cruise ships, etc.
TAO is a strongly validated COVID model, able to generate forensic insight by reproducing the daily or weekly infectivity rates of three universities that published detailed testing data. TAO-V incorporates values into TAO. Why is this important? Philosophers and scientists often distinguish between facts and values. Facts refer to states of affairs in the world that are publicly verifiable and thus subject to scientific description and analysis. Values refer to attitudes toward facts, and may be wholly private. Yet values are critical contributors to behavior in our species, and they are known to spread, particularly among people whose private values partially align. Thus, the computational simulation of any process involving human decisions and behaviors must have a good reason to set aside consideration of values. In modeling pandemic management, including values promises an improvement in insight and forecasting reliability.
Model design
TAO-V is made up of people agents, place agents, and a central agent. The people agents go to places, at which infected individuals may spread the infection to other individuals. The central agent dictates interventions such as contact tracing and testing.
At initialization, people agents are assigned a schedule of places to which they go over a two-week period, and this two-week schedule repeats itself for the duration of the simulation. There is one time step per day in the analyses below.
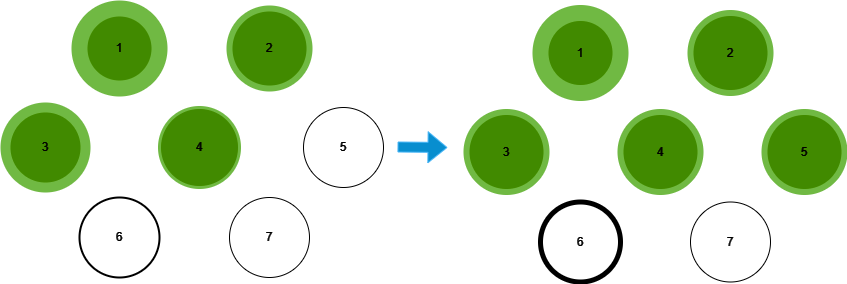
People agents are subtyped into Students, Faculty, and Staff. Students can be Freshman, Sophomore, Junior, Senior, and Graduate. Person type affects scheduling and agent characteristics. Undergraduate and Graduate students go to classes and attend more campus events than Faculty and Staff. Most Undergraduate students have on-campus housing, and most Graduate students have off-campus housing. On-campus housing is grouped by undergraduate year. Faculty and Graduate students instruct classes. Staff go to their offices, and some Staff have student-facing roles. Faculty, Staff, and Students each have different age and compliance distributions, and those compliance patterns are related to agent values in a way that is described below. Figure 1 depicts the initialization process for agents.
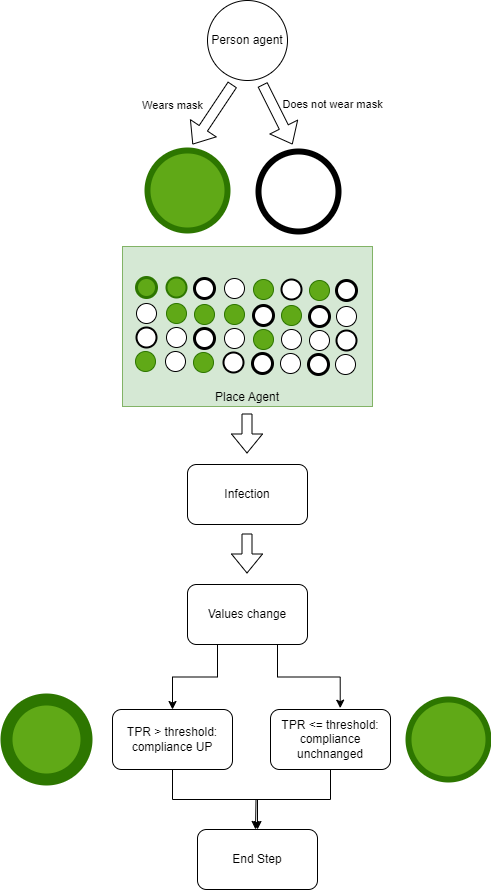
At the beginning of each time step, each agent consults the schedule and goes to the designated place. Agents decide for each place whether to wear a mask, stochastically determined using each agent’s individual compliance value. Then they observe the behavior of the other agents in that place and may change their masking and distancing decisions (Figure 2).
Once all agents have gone to the designated places and made final decisions about masking and distancing, each place agent observes the agents present, noting which are infectious and the precautions each agent has taken (e.g., wearing masks, distancing). The place agent will then spread infection by choosing a set of contacted agents whom each infected agent contacted, and stochastically determining if transmission occurred using a probability tied to a base infectivity likelihood and agent precautions. Mask wearing and physical distancing of agents reduces the likelihood of a contact resulting in a transmission. When a transmission does occur, the contacted agents are messaged by the place agent, and they become exposed. At exposure, the agent calculates an infection trajectory stochastically using a distribution set by the model. This determines the duration of the exposure period and severity of symptoms. A person’s infection may be asymptomatic, symptomatic-non-severe, and severe. When experiencing severe symptoms, a person has a probability of death, based on age.
After transmissions are complete, the central agent performs randomized testing. Test samples are collected by a randomly selected group of people, and test results are available after a delay period. Test samples are stochastically selected to be true negative, true positive, false negative, or false positive based on model input parameters.
While the original TAO model included more features such as contract tracing and quarantining, some features were removed in TAO-V to simplify the model and focus on value-related dynamics.
Agent values
Several features of the model express valuational aspects of agent behavior and interactions. The values selected for implementation in TAO-V focus on our shared pandemic experience, in which political ideology appeared to have a powerful influence on people’s trust in public-health officials and their subsequent willingness to comply with public-health recommendations. The way political-ideology values are implemented corresponds to what has been learned about polarization and ideological distribution within social psychology (e.g., Haidt 2013; Kalimeri et al. 2019; Stewart & Morris 2021).
Conformity Score: Each agent has a conformity score. Each time the agent goes somewhere, the agent draws between 0 and 1. If the value is less than or equal to their conformity score, the agent will adjust their mask wearing to the majority behavior in the room and will adjust their distancing compliance to the average in the room. This change only affects the agent’s behavior in the room, not their overall compliance values.
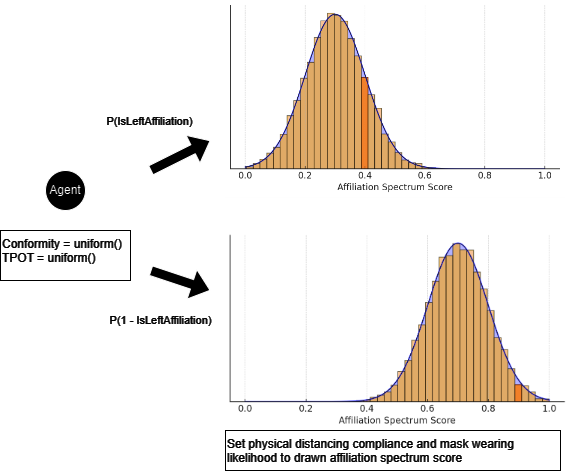
Affiliation Spectrum: Agents are assigned both a binary low/high ideological affiliation and an ideological spectrum score between 0 and 1. Low and high ideological affiliations correspond roughly to tendencies to support low and high levels of compliance with public-health recommendations, respectively. We use low and high throughout rather than more familiar ideological designations. Ideological spectrum scores have truncated normal distributions: the distribution of spectrum scores for agents having the "low" ideological affiliation has mean of 0.3 and standard deviation of 0.1, and the distribution of spectrum scores for agents having the “high” ideological affiliation has mean of 0.7 and standard deviation of 0.1. This ideological spectrum value can override mask wearing and physical distancing compliance (enabled by global parameter). It is possible for an agent with a “low” ideological affiliation to have an ideological spectrum value above many agents with a "high" ideological affiliation, which is important for expressing the way political ideology operates in real life. Thus, while it is not the norm, it is possible for a person with mostly "low" ideological views to self-identify with people having “high” ideological affiliations. An agent’s low/high ideological affiliation doesn’t affect the simulation after initialization. During model runs, only the ideological spectrum value matters.
Values propagation: At each place, an agent has a values interaction with other agents (a global parameter switches this interaction on and off). Based on a global likelihood, this interaction may lead to a values exchange. If a values exchange occurs, the agents flip a coin to see who "wins", and the winner’s affiliation spectrum value overwrites the loser’s. This affects compliance depending on whether global parameters tie compliance to spectrum value. It is possible though unlikely for agents to have multiple value interactions per step. In this situation, the average of the “winning” spectrums is adopted by the agent.
Test positivity observance: Randomized testing occurs every day. Test results are received on a two-day delay. The positivity rate is reported to all agents. Agents are initialized with a positivity rate threshold, and if the positivity rate exceeds this threshold, the agent will increase compliance until the positivity rate goes back below their threshold. Specifically, the agent will halve their distance from 100% compliance. Figure 3 depicts the various elements of each timestep.
Technical architecture
The model is written using the Simudyne SDK in Java and compiled into an executable JAR file that runs on a server accepting model parameters via a REST API. The sever was run on a high-powered machine (100 GByte RAM, dual X5675 chips @ 3.07GHz, Linux OS) via a Python script, which reads model parameters from a csv file and sends the parameters to the model server via Simudyne’s REST API. The model runs produce custom csv and parquet outputs (Apache Parquet 2023).
Methodology
The goal of the study was to demonstrate in principle that including human values in pandemic models can dramatically alter simulation projections, and we also aim to give some quantitative indication of the extent to which including human values matters. While the base TAO model had heterogenous agent compliance values with physical distancing and mask wearing, it did not have agent values informing those compliance values. TAO-V compares the base model (TAO) outputs to model outputs after human values are introduced. The outputs of interest are cumulative infections, peak number of concurrent infections, and day of peak number of concurrent infections; cumulative infections is a general measure of infection spread, while the latter two metrics are important when considering the load on healthcare systems. The model was run with 4,000 agents for 60 days.
We ran the model under several different parameter variations, laid out in Table 1. For affiliation, we set the agent population to be majority high or low ideology spectrum (75/25) or 50/50, or we disabled ideological affiliation altogether and simply set agent compliances to be uniformly distributed between 0.3 and 0.7. The distribution of agent conformity scores was uniform, with bounds being 0-0.25, 0-0.5, 0.5-1, or 0.75-1. For values propagation, the likelihood of values exchange was varied among 0.05, 0.1, 0.25, and 0.5. For test positivity observation, agent thresholds were uniformly distributed with bounds being 0-0.03 or 0-0.1, and tests per day were varied among 100, 500, and 1,000. Note that all parameter variations involved Affiliation and exactly one of Conformity, Values Propagation, and Test Positivity Observation. We did not further combine value settings.
| Affiliation | Majority High, Equal High/Low, Majority Low, No Affiliation |
|---|---|
| Conformity | 0-0.25, 0-0.5, 0.5-1, 0.75-1 |
| Values Propagation | 0.05, 0.1, 0.25, 0.5 |
| Test Positivity Observation | Threshold: 0-0.03, 0-0.1; Tests Per Day: 100, 500, 1000 |
Each parameter variation was run 30 times. One, two, or three-way ANOVAs were run on the parameter settings as applicable to determine significant effects. We used Plotting and Tukey Post-Hoc analyses to explore significant effects.
Results
For each of the human values Affiliation, Conformity, Values Propagation, and Test Positivity Observation, we have separate results.
Affiliation
The model has two affiliations: high compliance, and low compliance. The high compliance affiliation has a truncated normal distribution with mean 0.7 and standard deviation 0.1. The low compliance affiliation has a truncated normal distribution with mean 0.3 and standard deviation 0.1. We ran the model with four settings: majority (75%) high affiliation and minority (25%) low affiliation, 50/50 high-low affiliation, minority (25%) high affiliation and minority (25%) low affiliation, and no affiliation with compliance simply uniformly distributed between 0.3 and 0.7.
Multiple one-way ANOVAs were run to determine if the outputs of cumulative infections, peak number infected, and day of peak infections differ significantly at varying affiliation settings. All mean differences were found to be significant (\(p < 0.001\)). Descriptive statistics are shown in Table 2.
| Affiliation | \(M_{c}\) | \(SD_{c}\) | \(M_{p}\) | \(SD_{p}\) | \(M_{d}\) | \(SD_{d}\) |
|---|---|---|---|---|---|---|
| Majority Low | 2872 | 39.34 | 1168 | 37.32 | 23.27 | 1.70 |
| 50/50 | 2284 | 45.51 | 809 | 33.01 | 28.20 | 2.71 |
| Majority High | 1423 | 80.20 | 403 | 26.43 | 36.00 | 4.70 |
| NoAff | 2156 | 54.21 | 658 | 31.01 | 32.73 | 2.83 |
Conformity
Each agent in the model is assigned a conformity score. At every place an agent goes, the agent draws from a uniform distribution between 0 and 1, and if the draw is less than the agent’s conformity score, the agent will change its mask wearing to match the majority behavior and its physical distancing to match the average behavior. We ran the model with four conformity settings, making the distribution of conformity scores uniform at 0-0.25, 0-0.5, 0.5-1, and 0.75-1. We also varied affiliation settings.
Multiple two-way ANOVAs were run to determine if the outputs of cumulative infections, peak number of infections, and day of peak infections differ at varying compliance distribution settings and affiliation settings. For all outputs, affiliation significantly differentiated mean differences (\(p < 0.001\)). For cumulative infections, conformity distribution significantly differentiated mean differences (\(p < 0.02\)). For peak number of infections, conformity distribution significantly differentiated mean differences (\(p < 0.03\)). For day of peak number of infections, conformity distribution did not significantly differentiate mean differences. The interaction between conformity distribution and affiliation was not found to be significant in any models.
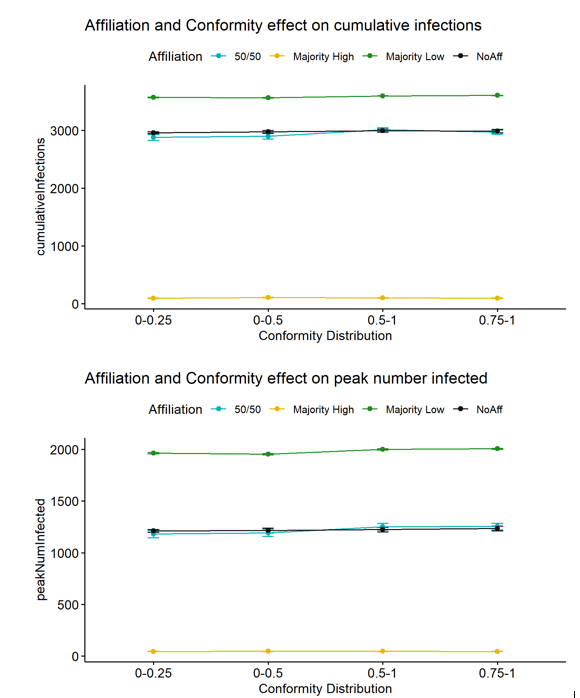
In Figure 4, cumulative infections and peak number of infections are plotted as a function of conformity distribution. The ideological Affiliation setting has a large effect on outputs, indicated in the spread among the lines. The effect of the Conformity distribution is relatively small (the left-to-right rise in the individual lines), though still significant. The effect of Affiliation is further explored below.
Values propagation
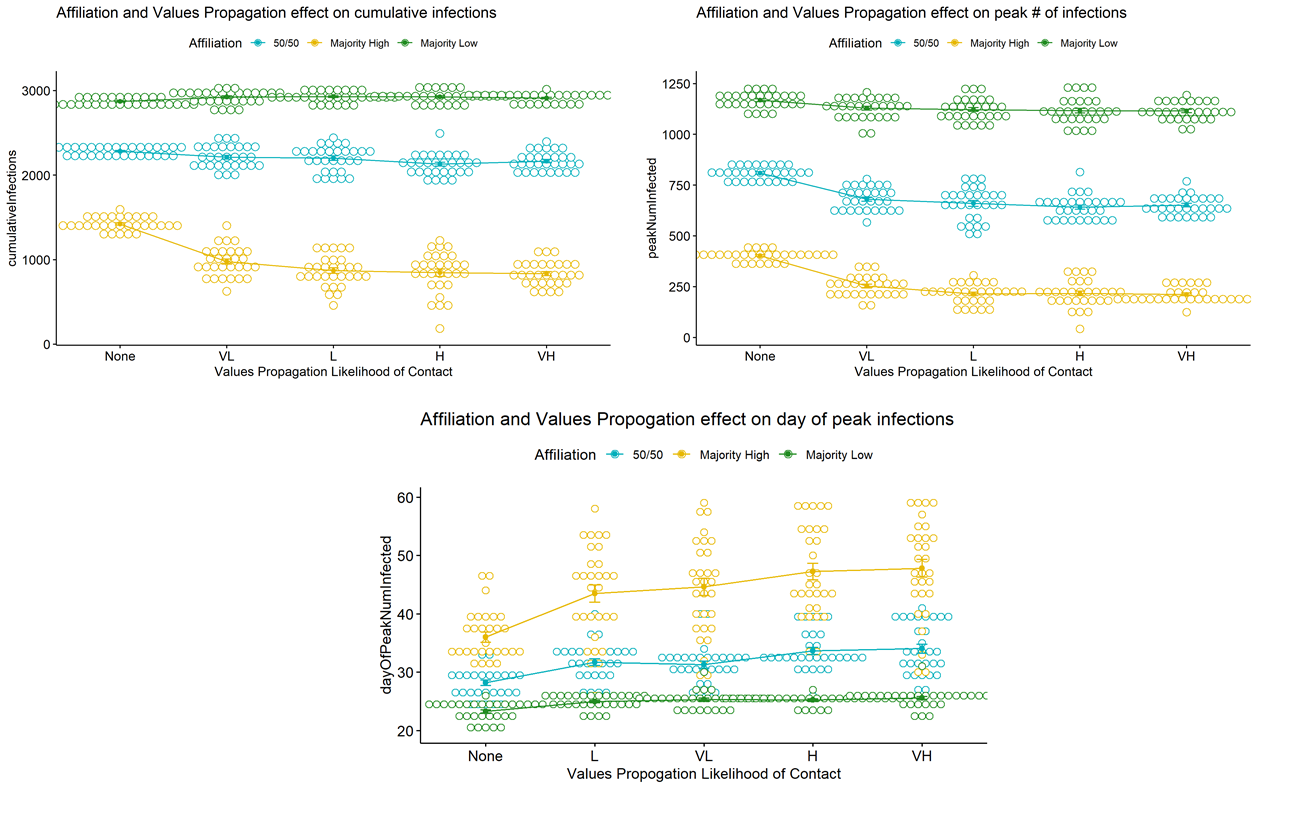
At each place an agent goes, it may make up to six values contacts with other agents. At each values contact, a value is drawn between 0 and 1, and if that value is less than a global values propagation likelihood parameter, one of the agents (chosen randomly) overwrites the other agent’s affiliation score with their own. We varied the likelihood of contacts resulting in values propagation at None (0%), Very Low (5%), Low (10%), High (25%), and Very High (50%). We also varied affiliation to Majority High, 50/50, and Majority Low. Note that we do not consider the No-Affiliation setting since values propagation is not well defined without affiliation.
Multiple two-way ANOVAs were run to determine if the outputs of cumulative infections, peak number infected, and day of peak infections differ at varied values for Values-Propagation Likelihood and ideological Affiliation. For both ideological Affiliation and Values-Propagation Likelihood, all mean differences were significant (\(p < 0.001\)). Interaction between Affiliation and Values-Propagation Likelihood was also significant (\(p < 0.001\)) for all three outputs. Figure 5 shows the differences in outputs over Values-Propagation Likelihood and ideological Affiliation. Ideological Affiliation causes the largest differences. Values propagation produces secondary differences, the starkest being between None (no values propagation) and all other settings, particularly for the Majority High Affiliation setting. This interaction shows that values matter: when the majority of affiliations support a positive effect on health outcomes, the spreading of values amplifies those positive health outcomes.
Test positivity observance
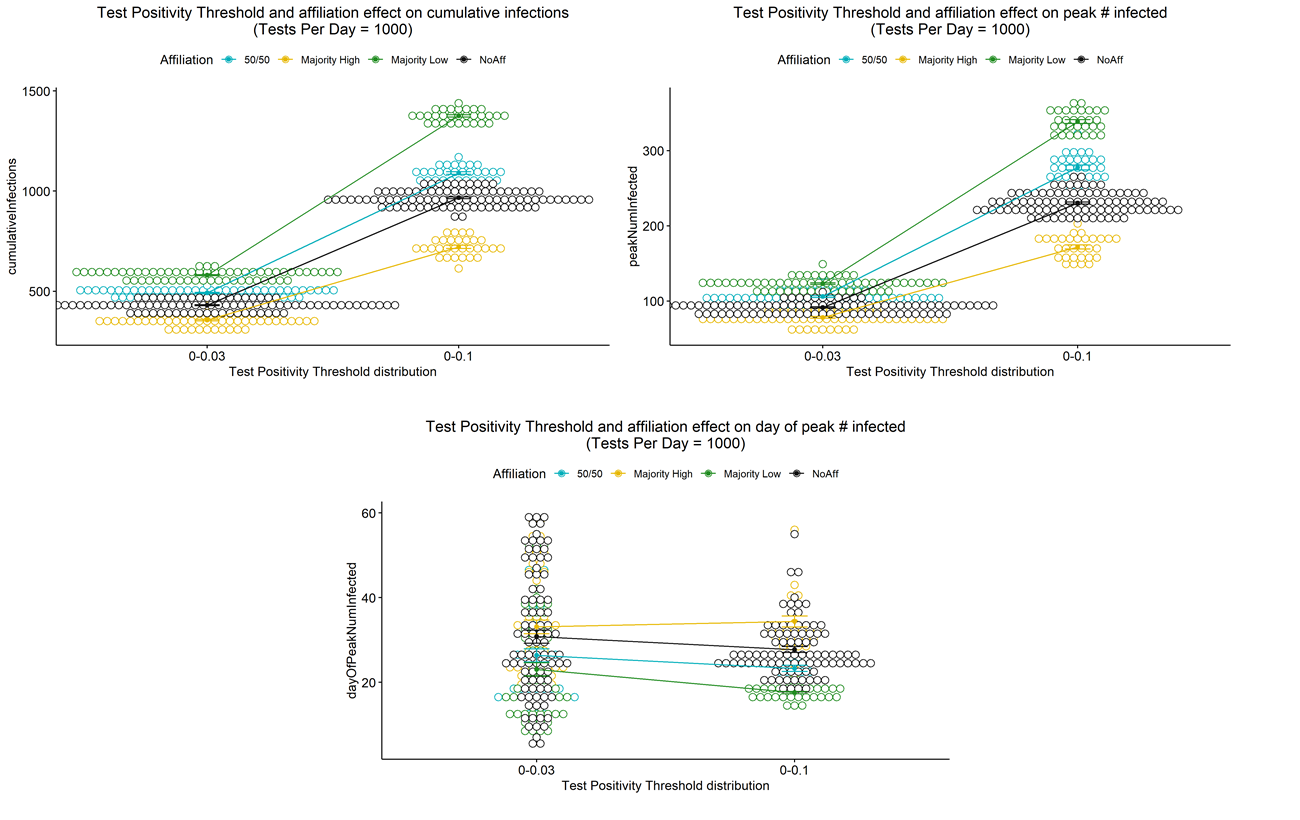
Each agent is initialized with a test positivity threshold. The percentage of positive test results is published globally each day, and if the percentage of positive test results exceeds an agent’s threshold, that agent will increase their compliance until the percentage is below their threshold again. We varied threshold distributions between 0-0.3 and 0-0.1. We varied the number of tests per day among 100, 500, and 1000. We also varied Affiliation among majority (75%) high affiliation and minority (25%) low affiliation, 50/50 high-low affiliation, minority (25%) high affiliation and minority (25%) low affiliation, and no affiliation with compliance simply uniformly distributed between 0.3 and 0.7.
Multiple three-way ANOVAs were run to determine if the outputs of cumulative infections, peak number infected, and day of peak infections differ at varying tests per day, test positivity threshold distribution settings, and affiliation settings. For affiliation, tests per day, and test positivity threshold distribution settings, all mean differences were found to be significant (\(p < 0.001\)). All interactions between affiliation, tests per day, and tests positivity threshold distribution settings were found to be significant (\(p < 0.001\)).
To explore the effect of the test positivity threshold distribution further, we focused on simulation runs with 1,000 tests per day. In Figure 6, the outputs are plotted with respect to Affiliation and Test Positivity Threshold Distribution. The interaction effects between Affiliation and Test Positivity Threshold Distribution are evident in the varied slopes of the lines.
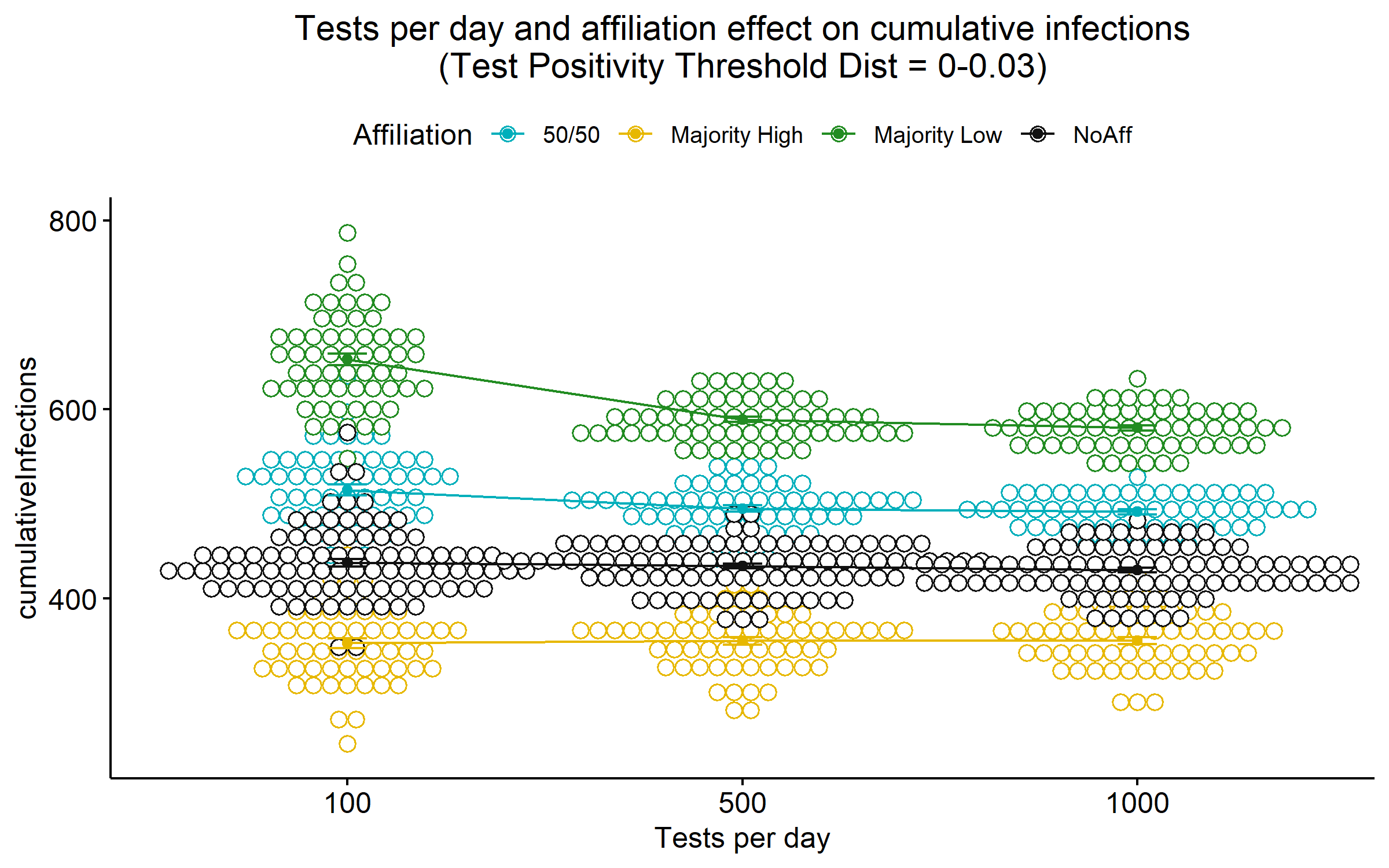
To explore the effect of tests per day further, we considered one setting of the Test Positivity Threshold Distribution at a time. When setting the Test Positivity Threshold Distribution to 0-0.03, we still see a significant effect of tests per day (\(p < 0.001\)) on cumulative infections. However, in Tukey Post Hoc analysis, we see that 100 tests per day has significantly more cumulative infections than 500 (\(p < 0.001\)) and 1,000 (\(p < 0.001\)) tests per day, but no significant difference between 500 and 1,000 tests per day (\(p = 0.28\)). This is shown graphically in Figure 7. When setting the test positivity threshold distribution to the narrower range of 0-0.1, tests per day does not have a significant effect on cumulative infections (not graphed).
Discussion
These results demonstrate several ways in which values matter for health outcomes in a pandemic simulation.
The dominant effect is the way ideological orientation (Affiliation) impacts willingness to comply with public-health recommendations. Politicization of pandemic-related public health recommendations has a direct negative effect on public health.
One secondary effect is an interaction between ideological orientation and the distribution of Conformity (Figure 4). Generally, a relatively high conformity distribution improves health outcomes, but this effect is strongest in the presence of a 50-50 split on ideological orientation and almost disappears when ideological orientation is not activated.
Another secondary effect is an interaction between ideological orientation and the intensity of values propagation (Figure 5). Enabling the propagation of values amplifies whatever effect was in place due to ideological orientation (Affiliation): the largest positive health effect occurs when the majority of people adopt an ideological orientation that supports high compliance, and enabling values propagation amplifies that positive effect. Likewise, the largest negative health effect occurs when the majority of people adopt an ideological orientation that supports low compliance, and enabling values propagation amplifies that negative effect.
Yet another interaction effect relates the capacity of agents to respond to information about test positivity rates in their local region. High test positivity rates inspire increases in compliance for people with lower Test-Positivity Thresholds. The line slopes in Figure 6 indicate that less nervousness about test positivity data has a dramatically negative effect on public health outcomes, but that this dangerous effect is weakest when the majority of agents adopt an ideological orientation that promotes high compliance, and strongest when the majority of agents adopt an ideological orientation that promotes low compliance.
Finally, there is a complex interaction involving testing frequency (Figure 7). According to the simulation, the most effective way to combat infections in a region dominated by an ideological posture inspiring low compliance with public health recommendations is to test often, so that people who pay attention to testing results improve their compliance.
Conclusion
The overall message of this study, using TAO-V, is clear: human values play a critical role in pandemic outcomes in a virtual environment. It follows that taking account of values in simulation-based decision-support systems promises relevant guidance for pandemic management. For example, TAO-V suggests a way to adapt testing frequency in order to improve health outcomes in regions where ideological orientations tend to inspire low compliance with public-health recommendations. Our hope is that computational social simulation will strive to incorporate human values in both pandemic management and other public-health applications.
One of the limitations of this research is that we don’t know for sure whether the marked effects of incorporating human values in a computational simulation carry over to real-world pandemic management. To investigate that, a natural method is to perform a forensic analysis of pandemic management strategies to predict known infectivity rates. This would be the most rigorous form of validation of a pandemic simulation to date. While doing that lies beyond the scope of this paper, this work is occurring (see Wildman et al. 2024). In the meantime, we have every reason to think that, from a theoretical point of view, taking account of human values in pandemic simulations ought to improve the fidelity of pandemic management.
Acknowledgements
We are grateful to Justin Lyon and other experts at Simudyne for use of, and guidance on, the Simudyne simulation development platform.
Model Documentation
Supplemental materials, including code for the model and instructions for running it, are available at: https://github.com/centerformindandculture/TAOPlusV.
References
ANTOSZ, P., Puga-Gonzalez, I., Shults, F. L., Lane, J. E., & Normann, R. (2022). Documenting data use in a model of pandemic "emotional contagion" using the rigour and transparency reporting standard. In M. Czupryna & B. Kaminski (Eds.), Advances in Social Simulation. Berlin Heidelberg: Springer. [doi:10.1007/978-3-030-92843-8_33]
APACHE Parquet. (2023). Apache Parquet. Available at: https://parquet.apache.org/
ARGONNE National Laboratory. (2021). CityCOVID. Available at: https://www.anl.gov/dis/citycovid-about-the-model
AXELROD, R., & Hamilton, R. (1981). The evolution of cooperation. Science, 211(27), 1390–1396. [doi:10.1126/science.7466396]
BLOOMBERG. (2022). The Covid resilience ranking. Available at: https://www.bloomberg.com/graphics/covid-resilience-ranking/
BOSHUIJZEN-VAN Burken, C., Gore, R. J., Dignum, F., Royakkers, L., Wozny, P., & Shults, F. L. (2020). Agent-based modelling of values: The case of value sensitive design for refugee logistics. Journal of Artificial Societies and Social Simulation, 23(4), 6. https://jasss.soc.surrey.ac.uk/23/4/6.html [doi:10.18564/jasss.4411]
CENTERS for Disease Control and Prevention. (2021). CDC to invest $26 million in advanced outbreak forecasting and analytics. Available at: https://www.cdc.gov/media/releases/2021/p-1026-mill-funding.html
CENTERS for Disease Control and Prevention. (2023). Excess deaths associated with COVID-19. Available at: https://www.cdc.gov/nchs/nvss/vsrr/covid19/excess_deaths.htm
CONTE, R., Andrighetto, G., & Campennì, M. (2014). Minding Norms: Mechanisms and Dynamics of Social Order in Agent Societies. Oxford: Oxford University Press. [doi:10.1093/acprof:oso/9780199812677.003.0001]
CUEVAS, E. (2020). An agent-based model to evaluate the COVID-19 transmission risks in facilities. Computers in Biology and Medicine, 121(10382), 7. [doi:10.1016/j.compbiomed.2020.103827]
DECHESNE, F., Di Tosto, G., Dignum, V., & Dignum, F. (2013). No smoking here: Values, norms and culture in multi-agent systems. Artificial Intelligence and Law, 21(1), 79–107. [doi:10.1007/s10506-012-9128-5]
DIALLO, S. Y., Shults, F. L., & Wildman, W. J. (2021). Minding morality: Ethical artificial societies for public policy modeling. AI & Society, 36(1), 49–57. [doi:10.1007/s00146-020-01028-5]
DIALLO, S. Y., Wildman, W. J., Shults, F. L., & Tolk, A. (2019). Human Simulation: Perspectives, Insights, and Applications, New Approaches to the Scientific Study of Religion Series. Cham: Springer.
DIGNUM, F. (Ed.). (2021). Social Simulation for a Crisis: Results and Lessons From Simulating the COVID-19 Crisis. Cham: Springer.
DIGNUM, V., & DIGNUM, F. (2014). Perspectives on Culture and Agent-Based Simulations: Integrating Cultures. Berlin Heidelberg: Springer.
ELSENBROICH, C., & Gilbert, N. (2014). Modelling Norms. Springer.
FERGUSON, N. M., Laydon, D., Nedjati-Gilani, G., Imai, N., Ainslie, K., Baguelin, M., Bhatia, S., Boonyasiri, A., Cucunubá, A., Cuomo-Dannenburg, G., Dighe, A., Dorigatti, I., Fu, H., Gaythorpe, K., Green, W., Hamlet, A., Hinsley, W., Okell, L. C., van Elsland, S., Thompson, H., Verity, R., Volz, E., Wang, H., Wang, Y., Walker, P. G. T., Walters, C., Winskill, P., Whittaker, C., Donnelly, C. A., Riley, S. & Ghani, A. C. (2020). Impact of nonpharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Available at: https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-NPI-modelling-16-03-2020.pdf [doi:10.1101/2020.03.09.20033357]
GALEN, L., Gore, R., & Shults, F. L. (2021). Modeling the effects of religious belief and affiliation on prosociality. Secularism and Nonreligion, 10(1). [doi:10.5334/snr.128]
GHORBANI, A., de Bruin, B., & Kreulen, K. (2021). Studying the influence of culture on the effective management of the COVID-19 crisis. In F. Dignum (Ed.), Social Simulation for a Crisis: Results and Lessons From Simulating the COVID-19 Crisis (pp. 189–230). Cham: Springer. [doi:10.1007/978-3-030-76397-8_8]
GRIM, P. (2003). Computational modeling as a philosophical methodology. In L. Floridi (Ed.), The Blackwell Guide to the Philosophy of Computing and Information (pp. 337–349). London: Blackwell. [doi:10.1002/9780470757017.ch26]
GRIM, P., Bramson, A., Singer, D. J., Fisher, S., Flocken, C., & Berger, W. (2012). Philosophical analysis in modeling polarization: Notes from a work in progress. APA Newsletters, 12(1), 7. [doi:10.1201/b16877-4]
HAIDT, J. (2013). The Righteous Mind. New York, NY: Penguin Books.
HOERTEL, N., Blachier, M., Blanco, C., Olfson, M., Massetti, M., Rico, M. S., Limosin, F., & Leleu, H. A. (2020). Stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nature Medicine, 26, 1417–1421. [doi:10.1038/s41591-020-1001-6]
KALIMERI, K., Beiró, M. G., Delfino, M., Raleigh, R., & Cattuto, C. (2019). Predicting demographics, moral foundations and human values from digital behaviours. Computers in Human Behavior, 92, 428–445. [doi:10.1016/j.chb.2018.11.024]
KERR, C. C., Stuart, R. M., Mistry, D., Abeysuriya, R. G., Rosenfeld, K., Hart, G. R., Núñez, R. C., Cohen, J. A., Selvaraj, P., Hagedorn, B., George, L., Jastrz˛ebski, M., Izzo, A., Fowler, G., Palmer, A., Delport, D., Scott, N., Kelly, S., Bennette, C. S., Wagner, B. G., Chang, S. T., Oron, A. P., Wenger, E. A., Panovska-Griffiths, J., Famulare, M. & Klein, D. J. (2020). Covasim: An agent-based model of COVID-19 dynamics and interventions. PLoS Computational Biology, 17(7), e1009149. [doi:10.1101/2020.05.10.20097469]
MAHMOUD, M. A., Ahmad, M. S., Yusoff, M., & Mustapha, A. (2014). A review of norms and normative multiagent systems. Scientific World Journal, 2014(68458), 7. [doi:10.1155/2014/684587]
MASCARO, S. (2010). Evolving Ethics: The New Science of Good and Evil. Devon: Imprint Academic.
MERDES, C. (2017). Growing unpopular norms. Journal of Artificial Societies and Social Simulation, 20(3), 5. https://jasss.soc.surrey.ac.uk/20/3/5.html [doi:10.18564/jasss.3374]
NARASSIMA, M. S., Jammy, G. R., Sankarshana, A., Pant, R., Anbuudayasankar, S. P., Choudhury, L., Yeldandi, V., Singh, S., & John, D. (2020). An agent-based model to assess COVID-19 spread and health systems burden in Telangana state, India. MedRxiv, 2020.10.03.20206177 [doi:10.1101/2020.06.04.20121848]
PETRÔNIO, C. L. S., Batista, P. V. C., Lima, H. S., Alves, M. A., Guimarães, F. G., & Silva, R. C. P. (2020). COVID-ABS: An agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions. Chaos, Solitons & Fractals, 139(11008), 8. [doi:10.1016/j.chaos.2020.110088]
SHAMIL, M. S., Farheen, F., Ibtehaz, N., Khan, I. M., & Rahman, M. S. (2021). An agent-Based modeling of COVID-19: Validation, analysis, and recommendations. Cognitive Computation, 2021, 1–12. [doi:10.1007/s12559-020-09801-w]
SHULTS, F. L., Gore, R., Wildman, W. J., Lynch, C., Lane, J. E., & Toft, M. (2018). A generative model of the mutual escalation of anxiety between religious groups. Journal of Artificial Societies and Social Simulation, 21(4), 7. https://jasss.soc.surrey.ac.uk/21/4/7.html [doi:10.18564/jasss.3840]
SHULTS, F. L., Lane, J. E., Diallo, S., Lynch, C., Wildman, W. J., & Gore, R. (2018). Modeling terror management theory: Computer simulations of the impact of mortality salience on religiosity. Religion, Brain & Behavior, 8(1), 77–100. [doi:10.1080/2153599x.2016.1238846]
Shults, F., & Wildman, W. J. (2019). Ethics, computer simulation, and the future of humanity. In S. Y. Diallo, W. J. Wildman, F. L. Shults, & A. Tolk (Eds.), Human Simulation: Perspectives, Insights and Applications (pp. 21–40). Berlin Heidelberg: Springer. [doi:10.1007/978-3-030-17090-5_2]
SHULTS, F. L., & Wildman, W. J. (2020a). Artificial social ethics: Simulating culture, conflict, and cooperation. Proceedings of the SpringSim 2020 Conference
SHULTS, F. L., & Wildman, W. J. (2020b). Human simulation and sustainability: Ontological, epistemological, and ethical reflections. Sustainability, 12(23), 10039. [doi:10.3390/su122310039]
STAFFINI, A., Svensson, A., Chung, U., & Svensson, T. (2021). An agent-Based model of the local spread of SARS-CoV-2: Modeling study. JMIR Medical Informatics, 9(4), e24192. [doi:10.2196/24192]
STEWART, B. D., & Morris, D. S. M. (2021). Moving morality beyond the in-group: Liberals and conservatives show differences on group-framed moral foundations and these differences mediate the relationships to perceived bias and threat. Frontiers in Psychology, 12, 2021. [doi:10.3389/fpsyg.2021.579908]
TRUSZKOWSKA, A., Behring, B., Hasanyan, J., Zino, L., Butail, S., Caroppo, E., Jiang, Z.-P., Rizzo, A., & Porfiri, M. (2021). High-resolution agent-Based modeling of COVID-19 spreading in a small town. Advanced Theory and Simulations, 4(3), 2000277. [doi:10.1002/adts.202000277]
WHO. (2023). World Health organizations Coronavirus Dashboard. Available at: https://covid19.who.int/. Accessed: Sep 1, 2023
WILDMAN, W. J., Diallo, S. Y., Hodulik, G., Page, A., Tolk, A., & Gondal, N. (2020). The artificial university: Decision support for universities in the COVID-19 era. Complexity, 2020, 5910209. [doi:10.1155/2020/5910209]
WILDMAN, W. J., Hodulik, G., Maayan, G., Lane, M., & Powell Jr., G. E. (Under review). The TAO of university pandemic forensics: How good are COVID simulations? Journal of Simulation
ZHOU, Y., Li, L., Ghasemi, Y., Kallagudde, R., Goyal, K., & Thakur, D. (2021). An agent-based model for simulating COVID-19 transmissions on university campus and its implications on mitigation interventions: A case study. Information Discovery and Delivery, 49(3), 216–224. [doi:10.1108/idd-12-2020-0154]