An Agent-Based Model of Transhumant Decision-Making Processes in Senegal

Introduction

Transhumance is a seasonal, socio-economic, and environmental mobility pattern widely practiced in the Sahel. Transhumance aims to make the best possible use of environmental resources to both feed herds and satisfy the needs of the transhumants. According to certain pastoralists, the mobility of herds is planned to prevent environmental degradation, given the perpetual dependence of these herds on their environment (Dia & Duponnois 2013b; Gonin 2018). Thus, the herds move on extensive territories guided by specific strategies. These strategies are based on both quantifiable factors (such as vegetation or water availability, markets etc.) and social factors such as relationships with farmers (Corniaux et al. 2018; Kiema et al. 2015). However, on a global scale it is estimated that the livestock sector contributes to \(14.5\%\) of anthropogenic greenhouse gas emissions (FAO 2016). The livestock sector in Sub-Saharan Africa is the third largest emitter of greenhouse gases (FAO 2016). This greenhouse gas balance for Sub-Saharan Africa and other regions of the world has been estimated using indicators based on industrial livestock production systems.

In the industrial farming system, animals are not very mobile and interact minimally with their environment, in contrast to Sahelian animals. This difference between industrial and Sahelian livestock systems led Assouma et al. (2019) to assess the carbon footprint of Sahelian transhumant herds. This method considered the herds in their pastoral ecosystems and a study area with a radius of around \(15\) kilometres. The study area was established with a neutral carbon balance, sometimes negative whereever there are few herds. This is due to the interactions of herds with vegetation, soils and water sources such as vegetation and soils sequester large quantities of greenhouse gases (GHGs). However, soils around waterholes, transhumance routes, and cattle parks have a positive carbon balance. This is because of the high numbers of animals defecating or ruminating in these spaces. Determining the space used by herds on a Sahel scale will allow us to distribute herds throughout broader spaces, sometimes even those they do not currently use. Determining the amount of space used by the herd could potentially reduce the number of spaces with a positive carbon balance.

Implementing Assouma et al. (2019) method on a broader scale raises the challenge of modelling. Indeed, in order to determine the spaces used by herds, we first need to model the dynamics of vegetation and surface water outlets. Next, it is necessary to formalize and simulate the decision-making processes employed by transhumants when deciding on herd movements. These processes are influenced by factors such as the availability of vegetation, water, veterinary centres, markets and the social network of the transhumants. Despite the decision-making processes of transhumants in different Sahelian countries being quite similar, this article, for the sake of brevity, will focus specifically on transhumance in Senegal.

In this article, we assume that the behaviour of transhumants is rational¹ and seek to determine the space used by herds. We formalized (conceptualized) and simulated the rational decision-making processes of Sahelian transhumants through the analysis of the movement strategies they create to move their herds. This formalization is based on a multi-objective optimization problem and algorithms. The constrained multi-objective optimization problem considers the majority of environmental and socio-economic factors impacting transhumants and their herds. The algorithms formalize the evolution of vegetation and water points (ponds). The optimization problem and the algorithms are integrated into an agent-based model (named MSTRANS) whose simulation provides an artificial reproduction of transhumance.

MSTRANS, designed using computational and mathematical methodologies, aims to emulate the intricacies of real transhumance with a high degree of accuracy. The agent-based framework supports simulations across various spatial and temporal scales and takes into account the rationality and adaptability of transhumants. These faculties find representation through spatial diffusion processes and in the multi-objective optimization problem, using parameters, constraints, or equations (for instance Equations 11, 12, 17). Mathematical approaches, such as the implemented algorithms and optimization problem, contribute to the reliable reproducibility of MSTRANS in other Sahelian countries. The purpose of MSTRANS is to determine the space used by transhumant herds based on vegetation and water spatial distribution, veterinary centres, markets and the location of cattle rustlers. MSTRANS could be used by: (1) researchers to estimate greenhouse gas emissions at different spatiotemporal scales while considering a maximum of conditions or exogenous constraints impacting transhumants; (2) decision-makers to determine where to install boreholes, veterinary centres and markets; (3) veterinarians or traders to plan their activities better.

Background: Sahelian Transhumance and Agent-Based modelling

This section presents Sahelian transhumance and emphasize the importance of its modelling through an integrated agent-based model.

Empirical and theoretical background on Sahelian transhumance

In the Sahel, there are primarily transhumant herds of small ruminants (goats and sheep), cattle and camels. When we refer to herds of small ruminants, it should be understood that the herd may also include cattle, but it is predominantly composed of small ruminants. The same applies to other types of herds. In Senegal, we have transhumant herds of small ruminants (goats and sheep) and cattle. Transhumance is carried out from a terroir of origin to one or several host terroir through movement strategies. These strategies depend on the selection of locations (see Figure 1). Each transhumant selects these locations by considering the socio-economic factors (markets, social relations), avoidance of troublemakers (bandits, thieves), conflicts with farmers, availability of vegetation, and water outlets. When a herd spends several nights at a location, this can be considered a host terroir for it.

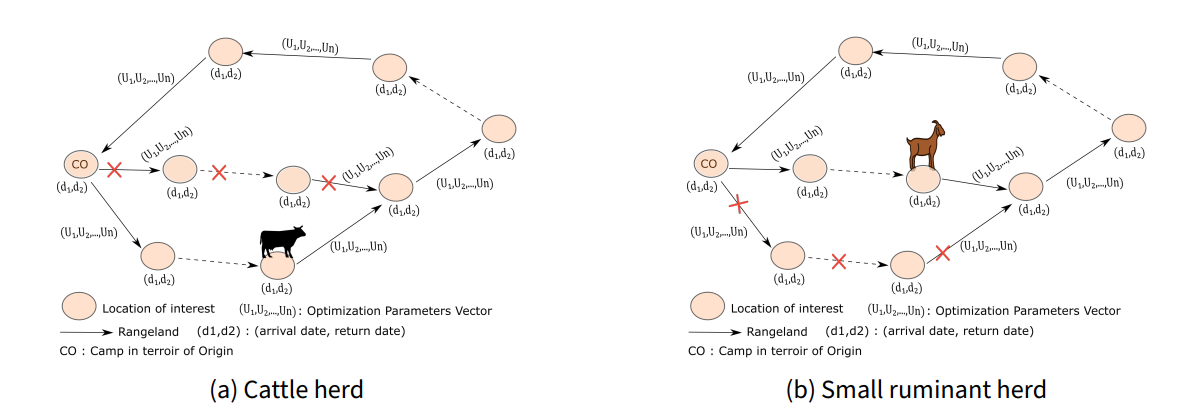
Socio-economic needs and the avoidance of conflictual movements are both impacted by the social relationships that the herder or shepherds maintain with other people (Dia & Duponnois 2013b; Thebaud 2017). These people constitute the social network of transhumant herders. The social network is a structuring element of transhumance, enabling the transhumant to avoid conflicts with local populations or thieves (Dia & Duponnois 2013b; Thebaud 2017). In addition, the social network helps transhumants to purchase water at a reduced cost for themselves and their herd, to sell animals at a higher price, and to stay easily in locations where veterinarians are present (Ancey et al. 2008; Kiema et al. 2015). For example, in Figure 1a, transhumants with a cattle herd choose the lower path where their social network gives them low-cost access to water. However, in Figure 1b, a transhumant with a small ruminant herd chooses the upper path to avoid animal thieves.

Transhumants earn money by selling animals from their herds to cover their expenses. Transhumants’ expenses are mainly related to livelihoods, livestock care, or taxes to be paid in markets or at borders for cross-border transhumance (Corniaux et al. 2012, 2018). Livestock sales occur on the transhumance paths or in markets close to their paths. Livestock buyers are in contact with transhumants through their social network or by telephone (Waters-Bayer 2023). Commonly, they sell animals for their own livelihood, and when they do not have enough money for their own expenses. The transhumants sell many animals at the approach of Muslim celebrations such as Tabaski (Aïd el-Kebir). For such sales, they convoy part of their herds to livestock markets (Apolloni et al. 2019; Corniaux et al. 2012). So to select locations of interest, transhumants reach out to their social network and consider a pastoral calendar (see Figure 2 and Figure 1) (Bah et al. 2006; Dia & Duponnois 2013b). Within this network, they exchange information about: (1) the condition of pastures, water outlets and livestock markets, (2) the schedule of social events such as weddings or baptisms, and (3) any areas marked by conflict or danger. The seasons of the pastoral calendar illustrate significant variations in pastures and water outlets levels.

A transhumant herd walks an average daily distance of \(12 -35\ km\) (Adriansen & Nielsen 2005; Assouma 2016). This average daily distance is \(12-15\ km\) when pastoral resources are abundant on their paths and they are moving towards a host terroir. This average daily distance is \(15-20\ km\) when there are limited pastoral resources on their paths and they are moving towards a host terroir. This average daily distance exceeds \(20\ km\) – sometimes approximately \(35\ km\) – when they are returning to their terroir of origin.

During their movements, the herds interact with the environment by grazing, trampling grasses and shrubs, defecating, and urinating (Assouma et al. 2019; Hiernaux et al. 2018). During the dry season, transhumant herds of cattle, sheep, and goats eat no more than a third of the available herbaceous biomass and less than \(5\%\) of the leaves of trees and shrubs in a pastoral territory of no more than \(20 \ km\) radius (Assouma et al. 2019; Diawara et al. 2018; Traore et al. 2023). The rest of the vegetation is degraded by the absence of rain (in the dry season), by human and microfauna impacts, etc..

During a drought year, livestock populations can increase because herds migrate to where there are pastoral resources, after going to their usual host terroir (Ellis 1988; Sall 1978). Conversely, during multi-year droughts there is a significant reduction in livestock population (Ellis 1988; Gonin 2018). This reduction in livestock population is causing food and economic difficulties for transhumants (herders and shepherds) (Ellis 1988; Rangé 2020). There is feedback from the herd to the herder and from the environment to the herder through the herd (see Figure 3).

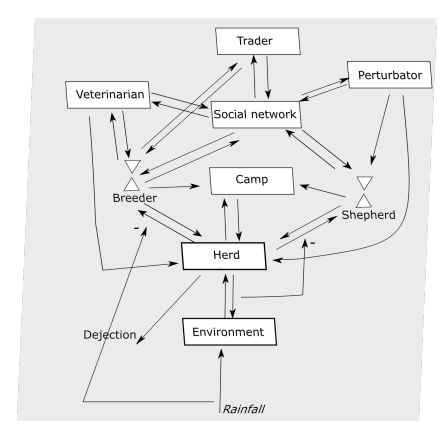
The movement of transhumant herds is a complex adaptive system. Indeed, transhumants and their herds interact in the pastoral ecosystem with other agents (see Figure 3). Adaptation enables transhumance to be resilient to ecosystem and environmental shocks such as drought. These shocks hurt the quantity and quality of pastoral resources (vegetation, water), herd population size and the livelihood of pastoral households. Thus, these shocks modify the movement strategies of pastoralists and their herds. The actions of one agent (transhumant, veterinarian, trader, etc.) influence the actions of others. For example, when a veterinarian changes location, transhumants wishing to care for their herd at veterinarians must move to the changed location. Such adaptive strategies suggest a rationality in the decision-making processes of Sahelian transhumants.

Models that consider the behaviour of pastoralists either use rational actor theory or explore pastoralist adaptation scenarios in the face of environmental or climatic shocks. Pastoral mobility can be modelled using difference equations, machine or deep learning, and agent-based modelling (Belkhiria et al. 2019; Mendy et al. 2023; Moritz et al. 2023). According to Moritz et al. (2023), the number of agent-based modelling studies of pastoral systems has increased steadily over the last 20 years. This trend can be attributed to the fact that agent-based models are capable of integrating mathematical or algorithmic formalizations.

Related works

Agent-based modelling of complex socio-economic and environmental systems

Agent-Based modelling (ABM) serves as a framework for encapsulating the behaviours of individual or group entities and facilitating the simulation of intricate interactions among these entities or with their surrounding milieu across various spatiotemporal dimensions (Hailegiorgis et al. 2018; Lugan 2009; Treuil et al. 2008). ABM enables the emulation of diverse societal activities on multiple spatiotemporal scales, including the decision-making processes of human agents within their respective environments. Furthermore, an agent-based model can integrate algorithms along with mathematical or computational formalizations to enhance its analytical capabilities.

Agent-based model design requires two or three phases². ABM design begins with a systemic analysis of agent behaviour and the constraints to which these agents are subject. The modeller deduces the social concepts or theories related to the agents’ behaviour.

The second phase is formalization. At this phase, the modeller formalizes the agents’ behaviour, more precisely, the processes that induce this behaviour. This formalization can be constructed through ‘if-else’ structures, mathematical or algorithmic approaches (Durand 2017; Kelly et al. 2013). When the model includes human agents, the formalization may require sociology theories such as rational choice theory. Many modellers prefer ‘if-else’ structures or preconceived computer architectures such as finite state machines (Kelly et al. 2013; Lobry 2003). ‘If-else’ structures or preconceived computer architectures require few mathematical prerequisites, theoretical computer science or sociology theories. Such formalizations are not very abstract and ensure neither reproducibility nor reusability of the model. In contrast, mathematical or algorithmic formalizations are more abstract. In these formalizations, the invariants of agent behaviour are described in abstract terms by mathematical laws, differential equations, or algorithms (Bousquet & Le Page 2004; Traore et al. 2024). Such abstract formalizations allow: (1) to consider agent behaviour with maximum complexity and at different spatiotemporal scales; (2) the reproducibility of the model and reduce the risks of subjective interpretations that can occur; (3) to reduce the costs of designing a model of the same complex system due to the non-reproducibility of a previously designed model. For example, a model of transhumant herd movements in Senegal with no abstract formalization will require a long redesign process before applying in Burkina Faso, whereas a model with an abstract formalization will not. In the latter case, the modeller would quickly know where to intervene to implement the model in Burkina Faso. Despite the advantages of abstract formalization in modelling complex systems of environmental and socio-economic mobility, mathematical and algorithmic formalizations are mitigated by many authors (Bousquet & Le Page 2004; Kelly et al. 2013).

The final phase is computer simulation. This phase allows us to observe the evolution of the social system through interactions between agents by testing scenarios. In these scenarios, the modeller simulates the interactions between the agents through their behaviours according to specific objectives.

This article simulates Sahelian transhumance as an artificial society, using an agent-based model. The agent-based model integrates formalizations of the decision-making processes of Sahelian transhumants through mathematical formalisms and algorithms containing equations. As a prerequisite for our model, the following section presents some previous models on the movements of transhumant herds.

Agent-based modelling and transhumance

Agent-based modelling is well suited for complex environmental and socio-economic mobility systems such as transhumance (Bousquet & Le Page 2004; Kelly et al. 2013). ABMs are widely used to simulate the pastoral system at various spatiotemporal scales and consider one or more elements of this system. Models of pastoral mobility are generally concerned with herd demography, pastoral resource management and health dynamics. Few models have addressed the behaviour of pastoralists or the social aspects of pastoral mobility (Moritz et al. 2023). These models present transhumants as rational actors. In addition, they are reductionist because they represent a limited number of actors or interactions involved in transhumance.

For example, Rouchier et al. (2001) model the behaviour of transhumant herders securing their access to rangelands using an ABM. In the model, pastoralists are rational actors. The rationality of pastoralists is formalized mathematically by a simplified optimization process. They highlighted two central elements: regularity of meetings and flexibility in the face of problems. Simulation experiments tested two logics: choices based on the notion of payoffs or the herders’ consideration of meeting history. The simulations successfully showed regular dynamics and considerable differences were observed depending on the rationality used. The authors conclude on the importance of the rationality described through optimization processes.

Dressler et al. (2019) use an ABM based on simplified rational behavioural and decision-making processes of herders to assess the resilience of pastoralism. The rationality of pastoralists is based on a variable. The value of this variable value depends on several factors, including the size of the herd, the quantity of available forage, and the herders’ perceptions of social norms. The authors aim to enhance the understanding of whether and how human decision-making influences the long-term development of livestock numbers, pasture conditions and livelihoods of herder households in a semi-arid pastoral system. They are interested in the impact of behavioural changes on the resilience of pastoralism. More specifically, to determine how a behavioural shift in household decision-making can lead the pastoral system into a degraded state or could counteract such a development. The authors conclude their article by arguing that an analysis of Pastoral Systems and their resilience should pay greater attention to the impact of human decision-making. In particular, through less simplified formalizations that consider many aspects of pastoralism as the social context.

Traore et al. (2024) analyze the movement strategies of Sahelian transhumant herds. The authors present a reductionist agent-based model that simulates herd movements based on a single movement factor. This model uses algorithms to formalize transhumant behavioural adaptability by representing the dynamics of pastoral resources and transhumance social aspects. The authors conclude that herd movements are based on strategies that simultaneously consider several environmental and socio-economic factors. However, there is no agreement on the influence of each factor in these movements. This study contributes to the ongoing discussion about the social aspect of transhumance and how to manage pastoral space.

Differentiating between elements associated with rationality and those about the adaptability of pastoralists results in the formulation of reductionist models. These models, however, may not fully include the complex dynamics of the pastoral ecosystem or the behaviours of other agents. Simultaneously, the pastoralists’ behaviour, which is both complex and adaptive, requires detailed formalization and simulation. It is better to minimize oversimplifications. These formalizations should be holistic, aiming for a comprehensive understanding of the agents’ behaviour and interactions. Therefore, a detailed formalization of the multi-agent model is necessary. This formalization should employ methodologies based on mathematics, algorithmic principles, and sociology theories. An approach of this kind allows to capture the complexity of the pastoralists’ behaviour and their interactions within the ecosystem.

In this article, we design an agent-based model to represent the decision-making processes of Sahelian transhumants. This model takes into account their rationality and adaptability in decision-making processes. This modelling integrates through two main components: (1) the implementation of algorithms and equations that simulate the progression of vegetation and the volume of water in surface water points; (2) the application of multi-objective optimization processes that depict the rational and adaptive decision-making processes of transhumants. Indeed, Simon (1955) demonstrated that we can represent agent rationality through optimization processes. It is well known that all humans have limitations in their reasoning capabilities and, consequently, in their rationality. Acknowledging this, we have formalized the behaviour of transhumants using optimization processes. The aim is to explore the possibility of transcending these inherent limitations. Specifically, we seek to identify the spaces used by some herds.

Material and methods

This section presents the study area and describes MSTRANS by using ODD+D protocol (Müller et al. 2013). This protocol allows the description of agent-based models focused on decision-making processes.

Study area

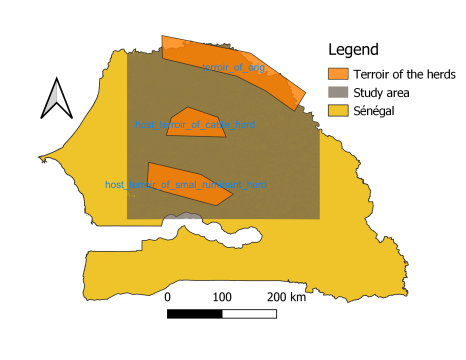
The study area (see Figure 4) is a part of Senegal that extends from the Ferlo (the North) to the groundnut basin (the centre). The study area is crossed from North to South by the \(300\ mm\) and \(500\ mm\) annual rainfall isohyets. The study area has a dry season from October to mid May and a rainy season from mid May to September. In addition, this area is characterized by vegetation consisting of an annual herbaceous stratum and a sparse shrub stratum.

Model (MSTRANS) overview

This section provides a comprehensive overview of the integrated agent-based model, its associated algorithm and the optimization process. The model’s design process, initiated in 2020, actively involved transhumants from the outset. The validity of the model will be ensured using data collected from GPS collars worn by animals in these herds. This data collection process was complemented by conducting interviews with the transhumants, which include both herders and shepherd. Additionally, we spent a portion of the transhumance period accompanying a herd. These immersive experiences, coupled with the interviews, granted us a profound understanding of the intricacies of transhumance.

From 2020 to 2023, we maintained consistent telephonic communication with all the transhumants. This period also saw us undertake multiple missions with two primary objectives: to retrieve the data accumulated in the collars and to ensure the maintenance of these GPS collars. Importantly, these missions served as opportunities for the transhumants to validate the model, thereby enhancing its credibility and relevance.

Purpose

This model determines the space used by transhumant herds based on transhumant decision-making processes, the spatial distribution of vegetation, water outlets, veterinary centres and markets. Thus, it formalizes and simulates the decision-making processes used by transhumants to move their herds. This model could be used by: (1) researchers to estimate greenhouse gas emissions at different spatiotemporal scales while considering a maximum of conditions or exogenous constraints impacting transhumants; (2) decision-makers to determine where to install boreholes, veterinary centres and markets; (3) veterinarians or traders to better plan their movements.

Entities, state variables and scales

The environmental and socioeconomic entities of the model are grouped in the Transhumant_herd, Environment and Socioeconomic_infrastructure modules. These modules and their relationships are represented in Figure 5 through a UML (Unified modelling Language) class diagram.

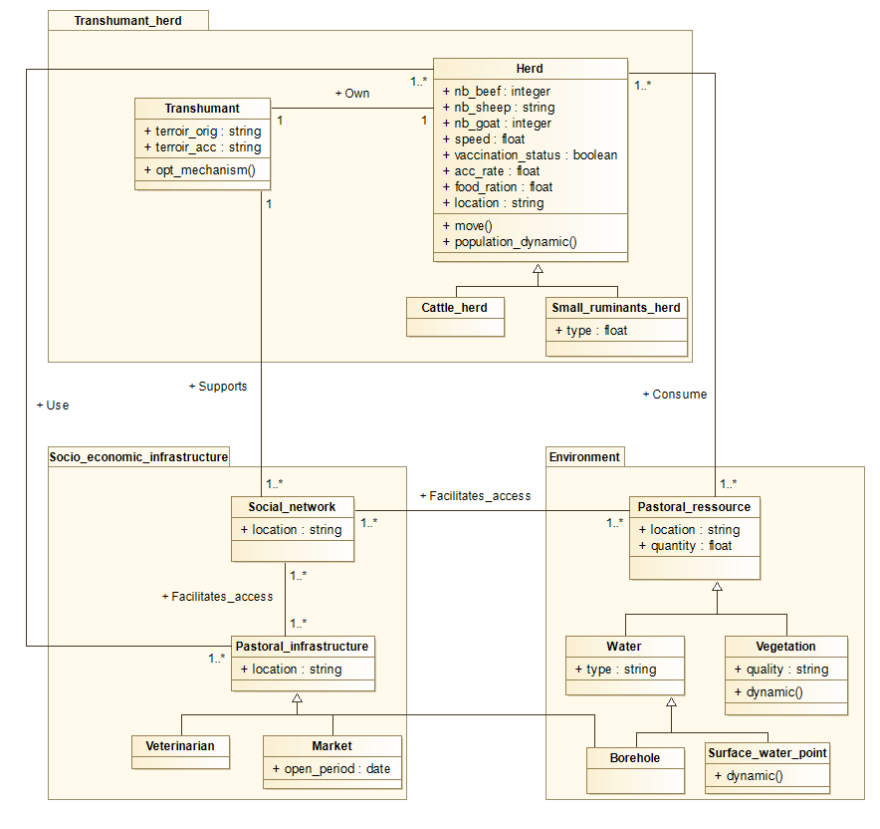
The Transhumant_herd module contains the Transhumant and Herd entities. The Transhumant entity represents the transhumant, who can be the herder or the shepherds. The transhumant makes all decisions concerning the herd. In this model, transhumants are always with their herds. The Herd entity represents the transhumant herd composed of herbivores – cattle, sheep and goat –. The Herd entity generalizes the Cattle_herd and Small_ruminants_herd entities. The attributes of the entity Herd are the vaccination status, the speed of movement, the number of animals, the rate of growth, the food ration, and the parameters of the sub-model \(6\).

The Environment module contains the Pastoral_ressource entity. This entity represents the pastoral resources and generalizes the Water and Vegetation entities. The Water entity represents the water points with a single type attribute. This entity generalizes the Borehole and Surface_water_point entities. The entity Borehole represents the boreholes that are permanent and paying. The Surface_water_point entity represents surface water outlets – ponds, lakes, etc., – which are non-permanent and free. The presence or not of water in the surface water outlets computed by Algorithm 2. The Vegetation entity represents vegetation. The attributes of the vegetation entity are its quality represented by the palatability and its quantity evolving according to Algorithm 3.

The Socio_economic_infrastructure module contains the Social_network and Pastoral_infrastructure entities. The Social_network entity represents the individuals who constitute the social network of the transhumant. The transhumant has a social or economic link with these individuals. The social network facilitates access to pastoral resources and infrastructures to herd. The Pastoral_infrastructure entity generalizes the Veterinarian, Market and Borehole entities. Veterinarians and Markets are places where the transhumant treat and sell some of the herbivores.

The model considers exogenous parameters such as annual rainfall and the average quantity of vegetation available at the end of the rainy season.

The model is designed and simulated at the scale of the study area (see Figure 4). The space is discretized into grid cells. Each cell is a square of \(d_g \times d_g\ km^2 \text{ where } d_g=3k,\ k\in\{1,\dots,12\}\) with Moore topology.

The model runs on a \(10\) month time horizon and a daily time step. The time horizon depends on various environmental and socioeconomic factors that vary from year to year (Dia & Duponnois 2013a; Kiema et al. 2015). The time step is daily in order not to consider infra-daily mobilities that have not been studied.

Process overview and scheduling

The transhumant herd moves in the cells of the discretized space, from its camp in the terroir of origin to its camp in the host terroir and conversely. The movements of the herd consider areas of influence of boreholes, markets, veterinarians and places where there is vegetation in quality and quantity (see Figure 6).

At the first time step (only) is executed in the following order:

1. Sub-model 5 by Borehole, Market and Veterinarian entities;
2. Creation of ten elements of Social network entity by Herd entity. This number allows the herd to have social network elements distant by about \(15\ km\).

Then, at each time step, the processes below are scheduled in the following order:

1. Sub-model 3: vegetation dynamics by each grid cell to determine vegetation availability;
2. Sub-model 2: surface water outlet dynamics by the Surface_water_point entity to determine water availability;
3. Sub-model 6: decision-making processes by the Herd entity to determine the cell to which the herd will be moved;
4. Sub-model 7: operationalization of the herd movement by Herd entity;
5. Sub-model 1: herd population dynamics by Herd entity;
6. Sub-model 4: beginning of rainy season by each grid cell entity.

Design concepts

This section presents some empirical and theoretical background on transhumance and the conceptual design of integrated decision-making model of Sahelian transhumant in Senegal.

Empirical and theoretical concepts

In agent-based modelling of Sahelian pastoral systems, Moritz et al. (2012) uses GPS (Global Positioning System) collars to monitor the trajectories of herds. He argues that the trajectories of a herd can be traced by following the path of a herd’s animal. This animal is outfitted with a GPS collar. Sané et al. (2017) link the modelling objectives with the formalism chosen to represent the environment in which the animals move, the distinction between the different agents that constitute the herd, their capabilities, and the rules that guide the movements of animals. They conclude that if the objective is to study the spatial behaviour of herds at a large spatial scale, the environment can be represented by a grid, and the animals and their herders can be represented by a single herd agent.

Individual decision-making

Sub-model 6 formalizes the transhumant decision-making processes through a constrained multi-objective optimization problem. In order to move his herd, the transhumant determines a target and optimal location at most one day’s walk between his position and his target camp – in the host or origin terroir. So, each transhumant moves his herd considering his social network to:

• Minimize the costs of purchasing water, feed supplements, vaccinations and ensure access to good quality vegetation for the herd;
• to maximize the selling price of herbivores;
• Minimize the risk of disaster – disease, injury – or theft of herbivores.

Individual sensing

The transhumant herd is sensitive to the presence of surface water outlets, the quality of vegetation, the price of water and the sale of herbivores within a day’s walking distance (Ancey et al. 2008; Wane et al. 2010). The closer a transhumant is to a market or borehole, the more advantageous will be the price of buying water and selling his herbivores be (see Equations 14 and 11). The sensitivities to accessing water outlets and selling herbivores are primarily due to the social norms that transhumants share with their social network elements. These norms only exist in spaces under the influence of each transhumant’s social network. Therefore, these sensitivities to accessing water outlets and selling herbivores are spatialized in the grid cells. In addition, an unvaccinated herd is sensitive to veterinarians for its movements. The more a herd is close to the veterinarian, the more this leads to the veterinarian.

Each grid cell’s vegetation quantity is sensitive to the presence of herds and other factors such as microfauna (see Algorithm 3). The availability of water in the surface water outlets depends on their geographical position and the current month (see Algorithm 2).

Interaction

The herds interact with each other through indirect competition for access to vegetation. The herds also interact with boreholes, markets and the social network through the latter’s zones of influence (Ancey et al. 2008; Corniaux et al. 2018; McCabe 2004). Each transhumant has their own social network whose elements cannot belong to any others. In their zone of influence, social network elements reduce the price of buying water from boreholes and increase the price of selling herbivores in markets (Equations 12 and 16).

Heterogeneity

The transhumant herds differ in type – cattle or small ruminants – and in vaccination status. A cattle herd is characterized by a high number of cattle relative to small ruminants, whereas a small ruminant herd is characterized by a high number of small ruminants relative to cattle. Grid cells differ in the quality and quantity of vegetation they contain.

Collectives

All herds have the Ferlo (top polygon in Figure 4) as their terroir of origin and the same pastoral calendar in Figure 2. The cattle herd host terroir is the middle polygon in Figure 4 and the small ruminant herd host terroir is the bottom polygon.

Stochasticity

A transhumant herd has a \(70\%\) probability of being a cattle herd otherwise it is a small ruminant herd. A herd has a probability of \(70\%\) of being vaccinated (Thebaud 2017). The number of ruminants in a herd follows Poisson distributions (see Table 2). The speed of movement of the herd during the outward and return phases follows normal distributions (see Table 1). The herd camps in the origin and host terroir are created at random locations.

The costs of buying water, food supplements and health care for the herd are random (see Table 3). It is the same for the sale price of herbivores. The elements of the social network are created randomly in cells located on the one hand at the intersection of the zones of influence of water points, markets and quality vegetation. On the other hand, they are located between the camps of the herd in the terroir of origin and the host terroir. According to our own observations and Thebaud (2017), we estimate that the transhumant herd has a \(43\%\) probability to have a social network element in its host terroir.

The start date of transhumance for each herd is randomly determined between October \(15\) and November \(15\) (see Figure 2). The end date of transhumance for each herd is between May \(15\) and July \(1^{st}\). The rainy season begins on a random date after May \(15\).

Observation

We observe the paths of a set of transhumant herds. These paths permit us to represent the space used by transhumant herds at different spatio-temporal scales and for given scenarios. The space used by the herds emerges mainly from the spatial resolution \((d_g)\), the speed of movement of the herds, the spatial distribution of water points and vegetation – quality and quantity.

Details

This section details the input data, implementation, initialization and sub-models of MSTRANS.

Implementation details

MSTRANS is implemented in Gama simulator. The transhumant and his herd are always together in the model we implement only the Herd entity (Moritz et al. 2012; Sané et al. 2017). Except for sub-models 6 and 7, which need to be implemented one after the other, the implementation order of the other sub-models does not matter. In this environment, the transhumant is unaware of the order of the daily evolution of resources. Gama data processing is performed in Python. Model data and code are available on CoMSES (https://www.comses.net/codebase-release/2218ccfb-c814-4a8b-993d-3a44365dc6f3/).

Input data

The model takes geographic information systems as input (see Figure 6b). The locations of boreholes, veterinarians and markets are georeferenced as points in shapefiles. Surface water outlets are georeferenced as lines in a shapefile. The vegetation quality layer and the built-up areas are georeferenced as polygons in a shapefile. The vegetation quantity layer is a raster image obtained by processing in Google Earth Engine. The processing of this layer used NDVI (Normalized Difference Vegetation Index) rasters from MODIS (MODerate resolution Imaging Spectroradiometer) captured on October \(7, 2020\).

Initialisation

MSTRANS is initialized at October \(15\) by using Algorithm 1, Table 1 and Table 2. In all tables below \(\mathcal{N}\) represent the normal distribution and \(\mathcal{P}\) represent the Poisson distribution.

Table 1: Initialization parameters

Description	Value	Reference
outward phase speed	\(\mathcal{N}(15.5,2) km.day^{-1}\)	Empirical
Return phase speed	\(\mathcal{N}(17.5,2 ) km.day^{-1}\)	Empirical
Cattle growth rate	\(1.1\%\)	ANSD (2020)
Sheep growth rate	\(3.2\%\)	ANSD (2020)
Goat growth rate	\(2.8\%\)	ANSD (2020)
Cattle daily food ration	\(4.5\ kg\)	Assouma (2016)
Small ruminant daily food ration	\(1.5\ kg\)	Assouma (2016)

Table 2: Number of herbivores in transhumant herds

Herd type	Cattle numbers	Sheep numbers	Goat numbers
Cattle	\(\mathcal{P}(110)\)	\(\mathcal{P}(30)\)	\(\mathcal{P}(20)\)
Small ruminant	\(\mathcal{P}(8)\)	\(\mathcal{P}(150)\)	\(\mathcal{P}(80)\)

Sub-models

This section describes the processes of MSTRANS entities by using equations, algorithms or a constrained multi-objective optimization problem.

Sub-model 1- herd population dynamics Every three months, the herbivore population \(E_i\) of species \(i\) in the herd evolves according to Equation 1. This time step considers the slow evolution of herbivore populations and animal attributes, especially of newborns. A calf starts to eat grass at three weeks of age and can eat plants and ruminate at three months old (Talib & Morosetti 1995). A lamb or a goat will completely eat green plants between \(3-4\) months of age, but starts to eat a little grass from 3 weeks (Talib & Morosetti 1995).

\[ \displaystyle E_i(t+\Delta t)= E_i(t) + \displaystyle\frac{a_i}{4}.E_i(t).\Delta t\ , \ t\ge 0 \qquad \]

(Traore et al. 2023)

\[(1)\]

where \(E_i\): population of herbivores of species \(i\); \(a_i\): annual growth rate of the herbivore population of species \(i\).

Sub-model 2- surface water outlets dynamics Water outlet (pond, lake, etc.) can be full or dry, water availability is based on Algorithm 2. Algorithm 2 considers the isohyets of the study area. These isohyets are represented by the points \(X_1(x_1,y_1),\ X_2(x_2,y_2)\). The surface water outlets located above the \(300\ mm\) isohyet have an ordinate \(y_w\le y_1\). These water outlets dry up on November \(31\) and fill up on August \(1^{st}\). The surface water outlets located above the \(500\ mm\) isohyet (and below the \(300\ mm\) isohyet) have an ordinate \(y_1\le y_w\le y_2\). These water outlets dry up on January \(31\) and fill up on July \(1^{st}\). Surface water outlets located below the \(500\ mm\) isohyet have an ordinate \(y_2\le y_w\). These water outlets dry up on April \(1^{st}\) and fill up on June \(1^{st}\).

Sub-model 3- vegetation dynamics The vegetation of each grid cell evolves according to Algorithm 3. The quantity of vegetation \(r(t)\) of each cell is initialized by Boudet equation (Boudet 1985). Then evolves daily according to equation \((**)\) depending on the presence of herds and other ecosystem factors (Diawara et al. 2018).

Let \(r\) be the vegetation quantity in kilogram (kg) of dry matter per hectare (ha) (Boudet 1985); \(r(t_0)\): initial vegetation quantity. \((\alpha .P + \beta).a\): Boudet equation with \(\alpha=4.1,\beta=-515\) in the Ferlo (Bah et al. 2006); \(P\): average annual rainfall in \(mm\) and \(a\): area of the grid cell; \(\gamma(t)\): daily quantity of vegetation ingested by all herbivores in the herd; \(\delta(t)\): daily vegetation degradation in the absence of herbivores (Diawara et al. 2018).

Sub-model 4- rainy season Algorithm 4 simulates daily rainfall in each grid cell. Rainfall is considered in the submodels \(3\) and \(7\).

Sub-model 5- zones of influence Algorithm 5 presents the diffusion processes of drillings, markets, and veterinarians that create the zones of influence of these elements. The zones of influence of the boreholes, markets, and veterinarians extend respectively over a radius of \(16\ km\), \(8\ km\), and \(4\ km\) around the borehole, market, and veterinarian (Ancey et al. 2008; Tracey-White 1997). Diffusion processes are considered in the submodel \(6\). Figure 6a shows the result of Algorithm 5 in the borehole case.

Sub-model 6- decision-making processes The objective of the transhumant is to choose an "efficient" location – between the current location of the herd and its target camp – at a distance \(d\). We denote by: \(\mathscr{D}\) the grid cells located at most a distance \(d\) between the transhumant herd’s position and its target camp; \(n\) the number of locations – grid cells – where the herd can go and \(\mathscr{S}\) the zone of influence of a social network element.

Let \(E\) be a set, the indicator function \(\displaystyle{1\!\!1_E}\) on \(E\) is such that:

\[ \begin{array}{rcl} \displaystyle{1\!\!1_E} : E & \rightarrow & \{0,1\}\\ x & \mapsto & \left\{\begin{array}{cl} 1 &\text{ if } x\in E\\ 0 & \text{else.} \end{array}\right. \end{array}\]

\[(2)\]

In the rest of this section, we construct a constrained multi-objective optimization problem based on empirical and theoretical background on transhumance. This problem formalizes the decision-making processes of the transhumant through variables and utility functions. Table 3 shows the initialization parameters of sub-model \(6\).

Table 3: Initialization parameters of the sub-model \(6\)

Symbol	Designation	Value	Reference
\(x_{i_1}\)	Cost of access to surface water	1
\(x_{i_2}\)	Cost of access to boreholes	\(\mathcal{N}(3,250; 1,000)\)	Ancey et al. (2008)
\(x_{i_3}\)	Cost of access to pastures	1
\(x_{i_4}\)	Health cost	\(\mathcal{N}(89,000; 1,000)\)	Thebaud (2017)
\(x_{i_5}\)	Cost of food supplement	\(150\) F CFA per kg	Magnani (2020)
\(z_{i_j}\)	Cost of selling herbivore	\(\mathcal{N}(50,000; 5,000)\)	Thebaud (2017)
\(h_i\)	Cost of theft or injury	\(\mathcal{N}(10,000; 1,000)\)	Thebaud (2017)

Minimizing costs of access to pastoral resources and veterinarians. The transhumant seeks out locations where the costs of accessing pastoral resources (vegetation, water outlets, boreholes) are lower and where there are veterinarians to vaccinate the herd’s herbivores. Let \(\alpha_{i_1}\) be the availability of surface water outlets at location \(i\).

\[\alpha_{i_1} = \left\{ \begin{array}{cl} 1 & \text{if there are surface water outlets at location $i$}\\ 100 & \text{else.} \end{array} \right.\]

\[(3)\]

To \(\alpha_{i_1}\) let us associate \(\beta_{i_1}\) representing the risk of the herd being infected by a disease at a surface water outlet at location \(i\).

\[\beta_{i_1} = \left\{ \begin{array}{cl} 1 & \text{if the surface water outlet is not a risk of disease}\\ 100 & \text{else.} \end{array} \right.\]

\[(4)\]

Let \(\alpha_{i_2}\) be the borehole availability for the herd at location \(i\).

\[\alpha_{i_2} = \left\{ \begin{array}{cl} 0 & \text{if there are boreholes at location $i$ and }\alpha_{i_1}=1\\ 1 & \text{if there are boreholes at location $i$ and }\alpha_{i_1}=100\\ 100 & \text{else.} \end{array} \right.\]

\[(5)\]

\(\alpha_{i_2}=0\text{ if }\alpha_{i_1}=1\) because if it is at least one surface water outlet is available at location \(i\), the herd will be moved to that outlet (which is not paying).
To \(\alpha_{i_2}\) we associate \(\beta_{i_2}\) representing the risk for the herd to be infected by a disease at a location \(i\) of a borehole.

\[\beta_{i_2} = \left\{ \begin{array}{cl} 1 & \text{if the borehole is not a risk of disease}\\ 100 & \text{else.} \end{array} \right.\]

\[(6)\]

Let \(\alpha_{i_3}\) be an indicator of the quantity of vegetation at location \(i\). \(\alpha_{i_3}\) allows the transhumant to predict if there will be enough forage for his herd at time \(t+\Delta t\). At location \(i\), vegetation is available for the herd if the vegetation quantity \(r(t)\) exceeds the daily food ratio of the herd \(\gamma(t)\). The daily food ratio of a herd \(\gamma(t)\) is the sum of the daily biomass consumed by its herbivores (Table 1). Consequently, \(\gamma(t)\) allows to consider the variation in herd size. We have \(\alpha_{i_3}=1\) for a sufficient quantity of vegetation for the herd and \(\alpha_{i_3}<\gamma(t)\) for an insufficient quantity of vegetation.

\[\alpha_{i_3}=\left\{ \begin{array}{cl} 1 & \text{if } r(t+\Delta t) > \gamma(t+\Delta t)\\ \displaystyle\frac{\gamma(t+ \Delta t)}{10+ r(t+\Delta t). \displaystyle{1\!\!1_{\{r(t+\Delta t)\neq 0\}}} } & \text{else} \end{array}\right.\]

\[(7)\]

where \(r(t)\) is defined in Algorithm 3.

To \(\alpha_{i_3}\) we associate \(\beta_{i_3}\) representing the quality of vegetation at location \(i\).

\[\beta_{i_3} = \left\{ \begin{array}{cl} -100 & \text{if there is good-quality vegetation}\\ 1& \text{if there is medium-quality vegetation}\\ 100 & \text{else.} \end{array} \right.\]

\[(8)\]

Let \(\alpha_{i_4}\) represent the presence of a veterinarian at location \(i\).

\[\alpha_{i_4} = \left\{ \begin{array}{cl} 0 & \text{if there is no veterinarian}\\ -100 & \text{else.} \end{array} \right.\]

\[(9)\]

To \(\alpha_{i_4}\) we associate \(\beta_{i_4}\) representing the decision to move the herd to the veterinarian.

\[ \beta_{i_4} = \left\{ \begin{array}{cl} 0 & \text{if the herd does not have to go to a veterinarian}\\ 1 & \text{else.} \end{array} \right.\]

\[(10)\]

Let \(\alpha_{i_5}\) be the quantity of food supplement to be purchased at location \(i\).

Let \(x_{i_l}, \forall l \in \{1,\dots, 5\}\) be the average cost to be paid by the transhumant to have the resource \(\alpha_{i_l}\) at location \(i\).

\[ x_{i_2}=x_{i_2}+d_e.x_{i_2} \quad \text{with } d_e\le 1.1\]

\[(11)\]

where \(d_e\) represents the value of the diffusion process marking the influence of the borehole at location \(i\).

Taking into account the zones of influence of the elements of the transhumant’s social network, the purchase price of water becomes:

\[ \displaystyle x_{i_2}= x_{i_2}- \frac{x_{i_2}}{2}.\displaystyle{1\!\!1_{\{self.location\ \in\ \mathscr{S}\}}}.\]

\[(12)\]

Let \(f_i: \mathbb{R}^5 \rightarrow \mathbb{R}\) be the function minimizing the objectives representing the costs of access to vegetation (grazing or supplement), water outlets, and vaccination for the herd at location \(i\).

\[ (\mathcal{O}_1):\left\{ \begin{array}{l} \displaystyle f_i(x_{i_1},\dots,x_{i_5}) =\min_{i\in \mathscr{D}}\left\{ \beta_{i_1}\alpha_{i_1}x_{i_1} +\beta_{i_2}\alpha_{i_2}x_{i_2} + \beta_{i_3}\alpha_{i_3}x_{i_3} + \beta_{i_4}\alpha_{i_4}x_{i_4} + \alpha_{i_5}x_{i_5} \right\} \\ \forall l\in \{2,\dots,5\},\quad x_{i_l}\ge 1, \quad x_{i_1}=1. \end{array} \right.\]

\[(13)\]

For any step, \(i\), the objective function of \((\mathcal{O}_1)\) is convex, with bounded constraints set. Therefore for any step \(i\), \((\mathcal{O}_1)\) admits at least one solution (Boyd & Vandenberghe 2004).

Maximization of the cost of selling herbivores. During the transhumance, the transhumant sells herbivores to obtain money with maximum pay-off. Let \(p\) be the number of species in the herd and \(e_j, j \in \{1,\dots,p\}\) the number of herbivores of species \(j\). Let \(\gamma_{i_j}^M\), \(\gamma_{i_j}^F\) be the number of males and females of herbivore species \(j\) that can be sold at location \(i\), respectively. Let \(x_{i_j}^M\) and \(x_{i_j}^F\) be the average costs of male and female herbivore species \(j\) at location \(i\), respectively.

\[ \left\{\begin{array}{rl} x_{i_j}^M = & x_{i_j}^M+ d_m.x_{i_j}^M \\ x_{i_j}^F = & x_{i_j}^F+ d_m.x_{i_j}^F\\ d_m\le & 1.1 \end{array}\right.\]

\[(14)\]

where \(d_m\) is the value of the diffusion process marking the influence of a market at location \(i\).

Let \(z_{i_j}\) be the average price of a herbivore of species \(j\) at location \(i\).

\[z_{i_j}=\displaystyle\frac{\displaystyle\sum_{j=1}^{p}(x_{i_j}^M + x_{i_j}^F)}{\gamma_{i_j}^M+\gamma_{i_j}^F}\ .\]

\[(15)\]

Taking into account the areas of influence of the social network elements, the average selling price of a herbivore becomes:

\[ z_{i_j}=z_{i_j} + z_{i_j}.\displaystyle{1\!\!1_{\{self.location\ \in\ \mathscr{S}\}}} \ , \forall j\in \{1,\dots,p\}\ .\]

\[(16)\]

Let \(g_i: \mathbb{R}^{2p} \rightarrow \mathbb{R}\) be the function maximizing the costs of selling herbivores in location \(i\).

\[ (\mathcal{O}_2): \left\{ \begin{array}{l} g_i(x_{i_1}^M,\dots,x_{i_p}^M,x_{i_1}^F,\dots,x_{i_p}^F)=\displaystyle \max_{i\in \mathscr{D}}\left\{ \sum_{j=1}^{p} z_{i_j} \right\}\\ \forall j\in \{1,\dots,p\},\ \gamma_{i_j}^M \ge 0, \gamma_{i_j}^F \ge 0, x_{i_j}^M\ge 0, x_{i_j}^F\ge 0, z_{i_j} \ge 0 \ . \end{array}\right.\]

\[(17)\]

Equation 17 allows us to consider the temporal fluctuations in male or female sales. As Tabaski approaches, many males are sold. Furthermore, this formalization offers a greater possibility of coupling the model with a differential equation model of ruminant population dynamics or estimating (fairly precisely) the income of herders at the household level.

For any step, \(i\), the objective function of \((\mathcal{O}_2)\) is convex, with bounded constraints set. Therefore, for any step \(i\), \((\mathcal{O}_2)\) admits at least one solution (Boyd & Vandenberghe 2004).

Minimization of loss due to misfortune. In transhumance, the herbivores could be injured or stolen and the transhumant could be robbed. The transhumant minimizes the loss of money by avoiding locations where misfortune could occur. Let \(\lambda_{i_j}^b\), \(\lambda_{i_j}^v\) be the number of herbivores of species \(j\) that can respectively be injured and robbed at location \(i\). Let \(y_{i_j}\) be the average cost to treat a herbivore of species \(j\). Let \(z_{i_j}\) be the average price of one herbivore of species \(j\). When a transhumant loses a herbivore of species \(j\) at location \(i\), he loses the amount \(z_{i_j}\). Let \(x_{i}\) be the amount of money that could be stolen from the transhumant at location \(i\).

Let \(h_i: \mathbb{R}^{2p+1} \rightarrow \mathbb{R}\) be the function minimizing the possible loss of the transhumant at location \(i\).

\[ (\mathcal{O}_3):\left\{ \begin{array}{l} h_i(x_i,y_{i_1},\dots,y_{i_p},z_{i_1},\dots,z_{i_p})=\displaystyle\min_{i\in \mathscr{D}}\left\{ x_i + \sum_{j=1}^{p} ( \lambda_{i_j}^b.y_{i_j}+\lambda_{i_j}^v.z_{i_j})\right\} \\ \forall j\in \{1,\dots,p\}, 0\le \lambda_{i_j}^b \le e_j, 0\le \lambda_{i_j}^v \le e_j , x_i\ge 0,\ y_{i_j} \ge 0, z_{i_j} \ge 0 \ . \end{array}\right.\]

\[(18)\]

For any step, \(i\), the objective function of \((\mathcal{O}_3)\) is convex, with bounded constraints set. Therefore, for any step \(i\), \((\mathcal{O}_3)\) admits at least one solution (Boyd & Vandenberghe 2004).

Choice of optimal location. After evaluating his movement objectives, the transhumant will determine the optimal location for his herd through Equation 21.

Let \(target_i\) be the linear combination of the minimizations and maximizations performed above.

\[ \left. \begin{array}{lccl} target_i: &\mathbb{R}^5\times\mathbb{R}^{2p}\times\mathbb{R}^{2p+1}& \rightarrow& \mathbb{R} \\ & (f_i,g_i,h_i) & \mapsto & f_i(x_{i_1},\dots,x_{i_5}) - a.g_i(-x_{i_1},\dots,-x_{i_{2p}}) + h_i(x_i,y_1,\dots,y_p,z_1,\dots,z_p) \end{array} \right.\]

\[(19)\]

where \(a\) denotes the desire of the transhumant to sell herbivores. This parameter is an aggregation (a simplification) of the transhumant’s decision to sell herbivores. A model of the decision to sell animals would consider the composition and number of herbivore species in the herd and the characteristics reflecting the well being of household members (average income, number of family members, etc.) (Boone et al. 2011; Mace & Houston 1989). However, this is outside the scope of this model. The parameter \(a\) is such that:

\[a=\left\{ \begin{array}{ll} 1 & \text{if the transhumant desires to sell herbivores}\\ 0 & \text{else.} \end{array} \right.\]

\[(20)\]

The optimal location is determined by solving the problem \((\mathcal{P})\) such that:

\[ \displaystyle (\mathcal{P}): \quad \min_{i\in \mathscr{D}} \{target_i\} .\]

\[(21)\]

Existence of solutions for the problems \((\mathcal{O}_i)_{1\le i \le 3}\) ensures the existence of solutions of problem \((\mathcal{P})\).

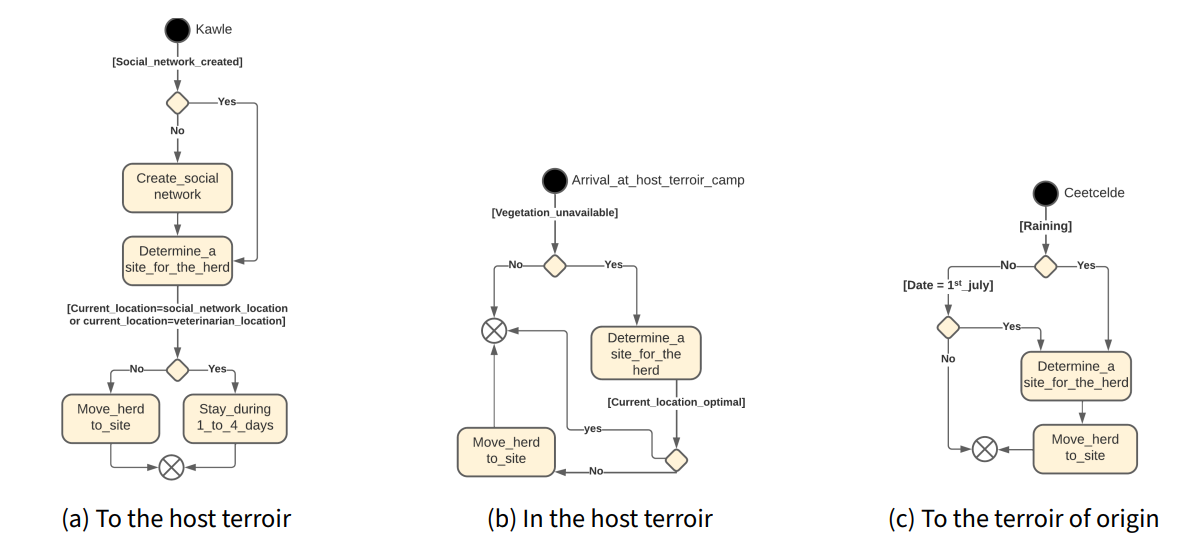
Submodel 7- operationalization of the movement. Once the target location is determined, the herd is moved to that location. Movements depend on the target terroir (see Figure 7).

Movements to the host terroir start in Kawle – from October \(15\) to November \(15\) – (see Figure 7a). For each movement, the transhumant determines an efficient cell where the herd will be moved. During the move, if the herd is in a grid cell containing a social network element or a veterinarian, then it will stay in that cell for \(1\) to \(4\) days. This phase ends when the herd reaches its camp in the host terroir. If transhumants have several host terroir, they will repeat this process when they leave the host terroir where they stayed and until their herd is in the last host terroir.

Once in the host terroir, the movements of the herd follow the processes of Figure 7b. When vegetation is unavailable in the cell where the herd is located, an efficient cell where to move the herd is determined. In order to move the herd to this cell, this cell must have a more optimal value after the sub-model \(6\) evaluation. In addition, this cell must also contain sufficient vegetation to feed the herd for at least one day.

The phase of moving the herd to the terroir of origin starts in Ceetcelde – May \(15\) to June \(30\) – and the day after a rainfall in the herd cell (see Figure 7c). The latest date for this phase is July \(1^{st}\). During this phase the herd does not stay more than one night neither with one of its social network element, nor with a veterinarian. This phase ends when the herd reaches its camp in the terroir of origin.

Results

In this section, MSTRANS is validated and explored. This section used GPS data collected in nine transhumant cattle herds in Senegal during the \(2020-2021\) transhumance. Every \(30\) minutes, each collar recorded the geographic coordinates of the animal wearing it. The geographical coordinates are then linked to trace the path of the herd. Each path is projected into the simulation space of the model to determine the spaces (grid cells) used by the herd considered.

Validation

To validate MSTRANS, the herd paths coming from the GPS collar data are subdivided into three consecutive periods \(t_1,t_2,t_3\), the sum of which is the complete transhumance. The validation of the model is based on Algorithm 6. This algorithm assumes that the paths coming from the GPS collars are rational. In addition, Algorithm 6 determines the proportion of common cells touched by the path of a herd of the model and by the path of its GPS collar. Then returns the average proportion of common cells touched (accuracy).

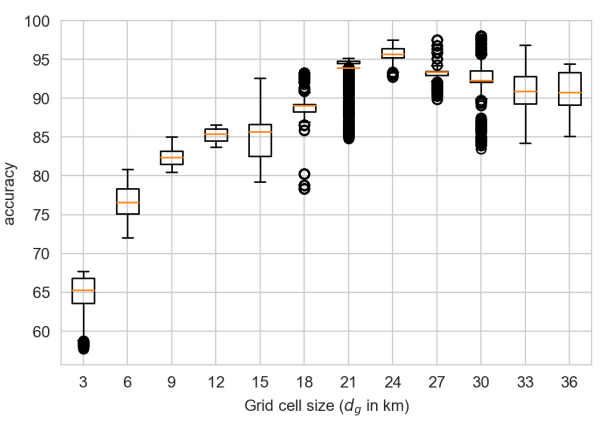
The results may be impacted by the size of the grid cells and the speed of the herds. The influence of these parameters are studied to validate MSTRANS (see Figure 8).

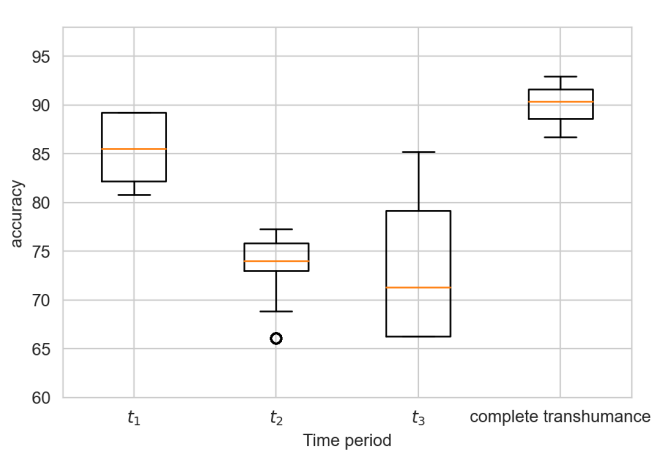
Figure 8 shows satisfactory results. Indeed, the accuracy values establish that the grid cells touched by the herds in the model are similar to the cells touched by the paths from GPS collars. The results for the periods \(t_2\) and \(t_3\) can be explained by the impact of the very frequent daily mobilities during these periods.

Exploration

This section is based on Table 4 scenarios simulated for complete transhumance and \(3\ km \times 3\ km\) grid cells. This cell size is the smallest of the model and then in which there is the most fluctuation in the results of the different replications. This section is organized into two paragraphs. The first paragraph determines the impact of a variation in the speed of herd movement on the results of MSTRANS. The last paragraph examines the spatial behaviour of a transhumant herd when the quantity of vegetation or the number of water outlets is reduced.

Table 4: Exploration scenarios

Symbol	Scenario	Values
\(S_a\)	Variation in the speed of the herd during the outward phase (\(km.day^{-1}\))	min: \(12\) max: \(22\) step: \(3\)
\(S_r\)	Variation in the speed of the herd during the return phase (\(km.day^{-1}\))	min: \(15\) max: \(30\) step: \(3\)
\(\lambda_1\)	Reduction of vegetation quantity	\(\lambda_1 \in \{0.25,0.5,0.75\}\)
\(\lambda_2\)	Reduction in the number of water outlet (surface water outlets \((\lambda_2)\), boreholes \((\frac{\lambda_2}{2})\))	\(\lambda_2 \in~\{0.25,0.5,0.75\}\)

Variation of movement speeds in the outward and return phase

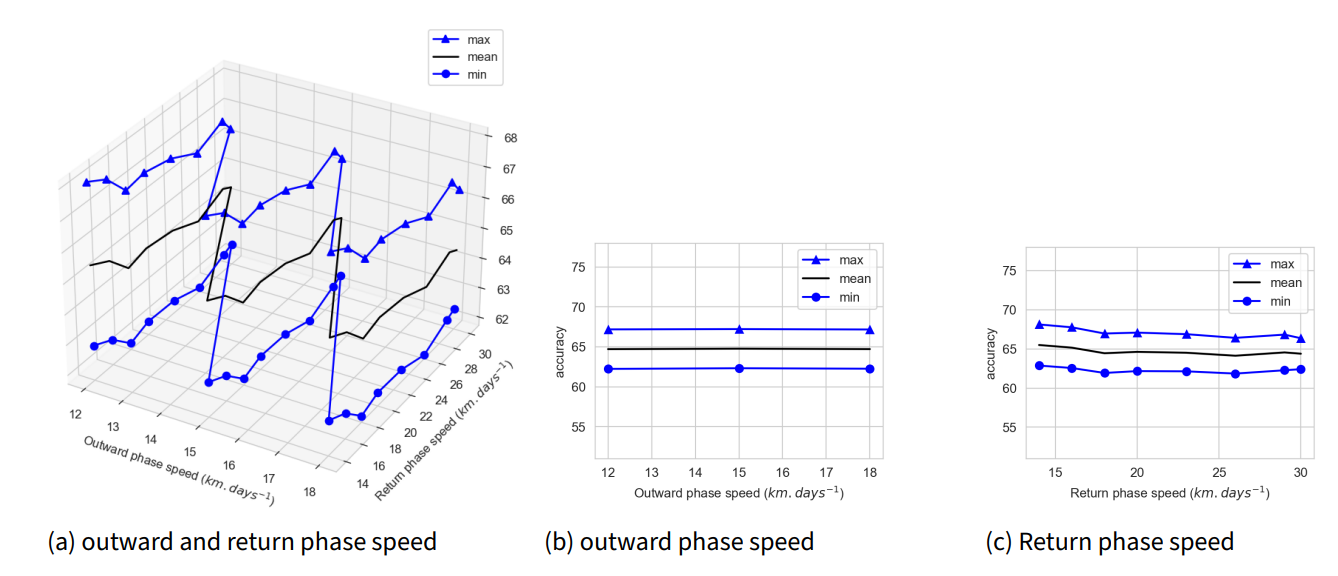
The impact of variations in the speeds of movements of transhumant herds is illustrated in Figure 9. The variation in movement speed has a weak influence on the choice of transhumance path, as transhumants tend not to change their paths.

Impact of pastoral resource reduction

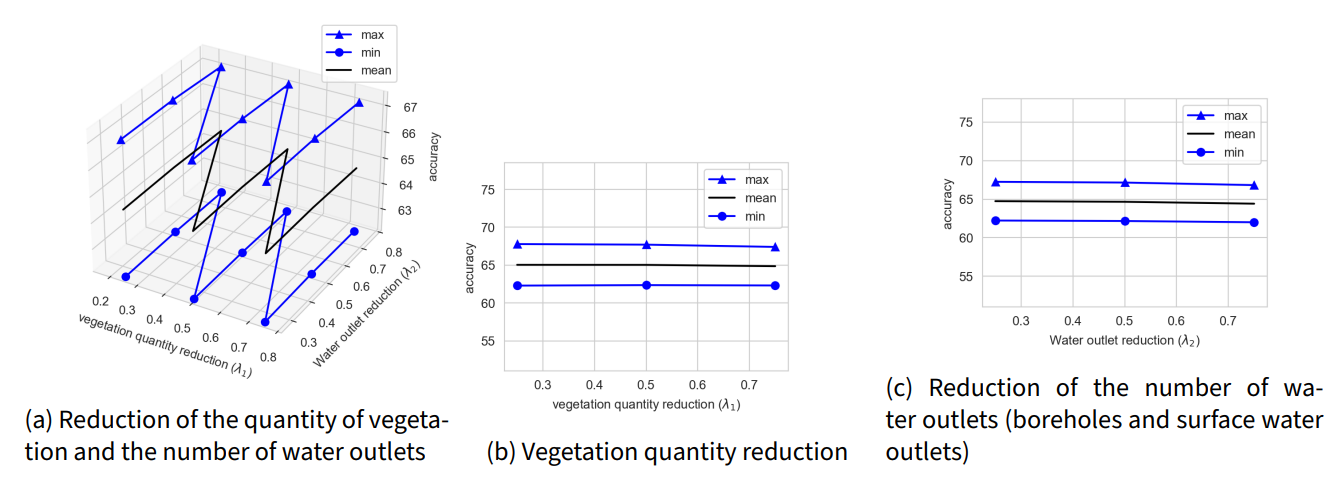
Figure 10 shows a weak impact of reductions in pastoral resources on the choice of transhumance paths. For a reduction in the quantity of vegetation - drought, pests, etc. - Figure 10 and Figure 10a show that transhumants tend not to change their paths. These results are consistent with the movement of transhumant herds first to their usual locations, then to other terroir during drought years. The non-significant decrease for \(\lambda_2 \ge 0.5\) in the accuracy of the results in Figure 10c would illustrate movements of herds to other water outlets located near the ones they usually use but inaccessible.

Robustness of results and example of space used

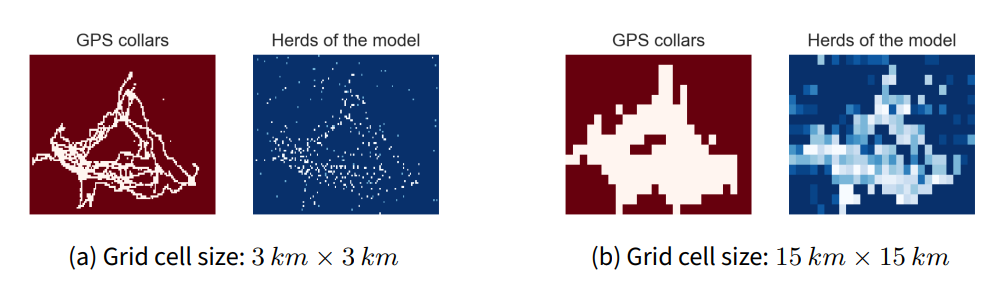
By varying all parameters of Table 4, Figure 11 shows insignificant variations of accuracy within each box of this figure but also with the box of Figure 8 for cells of \(18\ km \times 18\ km\). This establishes the robustness of MSTRANS and that modelling transhumant herd movements by an integrated model based on an agent-based model and constrained multi-objective optimization is efficient. We are satisfied with the results of this section. For each box, the difference in accuracy between the minimum value and the maximum value is less than 20, despite the change in spatial scale and all other exploration parameters considered. For example, Figure 12 illustrates, for different cell sizes, the space used by the GPS collar herds and the MSTRANS herds.

Discussion

This article determines the spaces used by transhumant herds using an integrated mathematical and agent-based model. MSTRANS integrates an agent-based model, a constrained multi-objective optimization, and algorithms to consider the socio-economic and environmental factors involved in transhumance. Associated socio-economic and environmental factors allow a holistic study of transhumant herd movements based on the rationality of transhumants in the ecosystem. Furthermore, the multi-objective optimization and algorithms used in the conceptualization of MSTRANS allow the reproducibility and reuse of this model and remarkable progress in the ecosystemic modelling of pastoral mobilities. This is not the case for most pastoral mobility models (Bah et al. 2006; Leclerc & Sy 2011; Liao 2018).

The results of MSTRANS, in agreement with empirical observations, showed the relative validity of the design of an integrated model (computer and mathematical) of transhumant herd movements. The model’s scenarios are somehow reductionist in terms of pastoral resources on herd movements. Our modelling objective aimed to provide a reusable tool for monitoring herd movement in other Sahelian regions. We therefore tested the model designed on empirical and theoretically proven premises.

Theoretical and empirical backgrounds of transhumance, based on environmental and socio-economic factors, categorize transhumance as both adaptive and rational mobility. The adaptability aspect is related to how a transhumant modifies its decisions to align with the fluctuating environmental and socio-economic conditions. The rationality aspect is related to how herds move efficiently in considering resource management and compliance with social norms, which steer the transhumants’ movements. Transhumants are regarded as rational actors, as their decision-making processes aim to achieve an optimal outcome for their herd or themselves. Some economists, notably Herbert Simon, have contributed to representing rational decision-making processes through optimization problems (Rubinstein 1998; Simon 1955). Optimization problems allow the study and understanding of transhumance, in the whole complexity of the pastoral ecosystem, through more abstract mathematical tools than previously.

Determining the space used by transhumant herds without having to monitor their movements provides decision-makers with a reusable decision-support tool. Decision-makers are better equipped to make environmental and socioeconomic management decisions for pastoral areas. Decision-makers can use MSTRANS to determine where to focus efforts to treat herd effluent and where to install boreholes and markets.

This said, MSTRANS has also two significant limitations. The model focuses on transhumance in Senegal and does not consider factors such as salt cures that are important to transhumants in other Sahelian regions. If such factors are of interest to transhumant herders, the modeller will need to incorporate these factors into the optimal location selection process. Another limitation of this model is that it does not formalize changes in the behaviour of the transhumant. It restricts transhumance paths geographically and does not allow us to model pluriannual transhumance. Future versions of the model could aim to be more geographically inclusive and consider the dynamic nature of transhumant behaviour.

To the agent-based and optimization approaches implemented in MSTRANS, we could implement mathematical image processing approaches such as the Hough transform (Sere et al. 2021; Traoré & Séré 2022). Sere et al. (2021) use the Hough transform and GPS data collected in real-time on moving entities. The real-time processing of collected data by the rectangular Hough transform indicates saturated locations, i.e., where there is a crowd. Knowing that it is common for a transhumant (a shepherd) to have a cell phone, one could thus perform real-time tracking of transhumant herds. Integrating the Hough transform into MSTRANS would allow, in addition to real-time tracking, the prediction of likely herd paths. Potential herd paths could be encoded by a code similar to Freeman’s code, allowing the segmentation of these paths into chunks (Freeman 1974). These chunks could be detected (numerically) by the Hough transform and ranked from most to least optimal according to specific objectives (Barbosa & Vieira 2019; Ouedraogo et al. 2022). The location of the herds at various times and spatial scales will be perfectly known. A model integrating these approaches would allow (1) decision-makers to save money on herd location surveys; (2) veterinarians to track herds with disease; (3) pastoralists to avoid areas with diseased herds; (4) traders to know where to find livestock, and (5) environmental officers to better monitor protected areas and plan agro-ecological activities.

The validity of a model does not always guarantee its operational use in real word. To ensure that the model could be used in the real world, at the end of the modelling process we carried out a validation of the model by transhumants. They approved our modelling approach and our idea of designing a computer application for transhumance. The transhumants even made recommendations for the design of the transhumance application that we had not thought of. For example, the transhumants asked us not to release the application in an open-access store because this could compromise their security. Thieves could use the application to find out where the transhumants were to rob them.

Conclusion

Transhumance, as described, unveils the strategic movements of herds aimed at the proficient stewardship of pastoral resources and adherence to societal norms. This positions transhumance as a logical form of mobility within the ecosystem, with the transhumant emerging as a rational participant whose decision-making processes are optimized for the benefit of his herd or himself. Given the rational nature of individual transhumants’ decision-making processes, this article has chosen to employ model integration for their representation. This approach facilitates the amalgamation of multiple modelling methodologies into a single, comprehensive model.

Within the realm of transhumance, the utilization of model integration has given rise to MSTRANS. This groundbreaking model seamlessly blends a constrained multi-objective optimization problem and algorithms into an agent-based model, offering a comprehensive perspective on the decision-making process of the transhumant.

By coupling these methodologies, we guarantee a superior level of abstraction, while also taking into account the diverse socio-economic and environmental factors intrinsic to transhumance. This elevated level of abstraction paves the way for the replication of MSTRANS across other pastoral regions in the Sahel.

The rigorous validation and exploration of MSTRANS solidify its role as a valuable tool for researchers in pastoralism and policymakers alike, aiding in their dialogues, spatial management projects, and monitoring of herd movements. Indeed, this model encapsulates the decision-making outcomes of transhumants, intertwining complex and evolving socio-environmental factors. However, it is important to note that MSTRANS does come with two primary constraints: its application is currently limited to Senegal, and its lack of pluriannual consideration prevents it from accounting for changes in transhumant behaviour over time.

MSTRANS effectively determines the space used by transhumant herds, implementing a sophisticated model integration that combines mathematical and agent-based models. These models are meticulously crafted on an annual time scale, taking into account the complex interplay of socio-economic and environmental factors that drive the decision-making processes of transhumants. This integration of mathematical and agent-based models is fundamentally grounded in sociological theory. It acknowledges the social structures and interactions that influence individual and group behaviours, providing a more holistic and nuanced understanding of transhumant dynamics. By incorporating sociological theory into the modelling process, we can more accurately represent and predict the complex socio-environmental dynamics at play. Given the non-perennial nature of Sahelian vegetation, environmental factors are assessed annually. However, socio-economic factors can span multiple years, reflecting the dynamic evolution of agents’ behaviours over time.

In perspective, we hope to formalize the changes in transhumant behaviour to model multi-year transhumance. Moreover, we wish to integrate the Hough transform, a mathematical image-processing approach, into MSTRANS. That would allow, with little financial means, real-time monitoring of the movement of the herds and the implementation of early warning systems to avoid the spread of epidemics.

References

ADRIANSEN, H. K., & Nielsen, T. T. (2005). The geography of pastoral mobility: A spatio-Temporal analysis of GPS data from Sahelian Senegal. GeoJournal, 64(3), 177–188.

ANCEY, V., Wane, A., Müller, A., André, D., & Leclerc, G. (2008). Payer l’eau au Ferlo Stratégies pastorales de gestion communautaire de l’eau. Autrepart, 46(2), 51–66.

ANSD. (2020). Situation économique et sociale du Senegal 2017-2018. Agence Nationale de la Statistique et de la Démographie (ANSD), Senegal. Available at: https://www.ansd.sn/ressources/publications/11-SES-2017-2018_Elevage.pdf.

APOLLONI, A., Corniaux, C., Coste, C., Lancelot, R., & Touré, I. (2019). Livestock mobility in West Africa and Sahel and transboundary animal diseases. In M. Kardjadj, A. Diallo, & R. Lancelot (Eds.), Transboundary Animal Diseases in Sahelian Africa and Connected Regions (pp. 31–52). Cham: Springer International Publishing.

ASSOUMA, M. H. (2016). Approche écosystémique du bilan des gaz á effet de serre d’un territoire sylvo-pastoral sahélien: Contribution de l’élevage. Available at: https://agritrop.cirad.fr/593394/.

ASSOUMA, M. H., Lecomte, P., Corniaux, C., Hiernaux, P., Ickowicz, A., & Vayssiéres, J. (2019). Pastoral landscapes in the Sahel: A carbon balance with unexpected potential for climate change mitigation. Available at: https://agritrop.cirad.fr/594230/1/Perspective52_Assouma_ENG.pdf.

BAH, A., Touré, I., Le Page, C., Ickowicz, A., & Diop, A. T. (2006). An agent-based model to understand the multiple uses of land and resources around drillings in Sahel. Mathematical and Computer Modelling, 44(5), 513–534.

BARBOSA, W. O., & Vieira, A. W. (2019). On the improvement of multiple circles detection from images using Hough transform. TEMA, 20, 331–342.

BELKHIRIA, J., Lo, M. M., Sow, F., Martinez-Lopez, B., & Chevalier, V. (2019). Application of exponential random graph models to determine nomadic herders? Movements in Senegal. Transboundary and Emerging Diseases, 66(4), 1642–1652.

BOONE, R. B., Galvin, K. A., BurnSilver, S. B., Thornton, P. K., Ojima, D. S., & Jawson, J. R. (2011). Using coupled simulation models to link pastoral decision making and ecosystem services. Ecology and Society, 16(2).

BOUDET, G. (1985). Manuel sur les páturages tropicaux et les cultures fourragéres. Available at: https://horizon.documentation.ird.fr/exl-doc/pleins_textes/divers18-07/07798.pdf.

BOUSQUET, F., & Le Page, C. (2004). Multi-agent simulations and ecosystem management: A review. Ecological Modelling, 176(3), 313–332.

BOYD, S. P., & Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.

CONLISK, J. (1996). Why bounded rationality? Journal of Economic Literature, 34(2), 669–700.

CORNIAUX, C., Thébaud, B., & Gautier, D. (2012). La mobilité commerciale du bétail entre le Sahel et les pays côtiers: L’avenir du convoyage á pied. Nomadic Peoples, 16, 6–25.

CORNIAUX, C., Thébaud, B., Powell, A., Apolloni, A., & Touré, I. (2018). Cross-Border livestock mobility: Challenge for West Africa. Available at: https://agritrop.cirad.fr/588455/1/FAO-Betail_Corniaux%20ANGLAIS%20HD.pdf.

DIA, A., & Duponnois, R. (2013a). Désertification et élevage pastoral sahélien. In A. Dia & R. Duponnois (Eds.), La Grande Muraille Verte: Capitalisation des Recherches et Valorisation des Savoirs Locaux (pp. 32–43). IRD Éditions.

DIA, A., & Duponnois, R. (2013b). Le pastoralisme en Afrique subsaharienne. In La Grande Muraille Vertes: Capitalisation des recherches et valorisation des savoirs locaux (pp. 12–31). Marseille: IRD Editions.

DIAWARA, M. O., Hiernaux, P., Mougin, E., Grippa, M., Delon, C., & Diakité, H. S. (2018). Effets de la pâture sur la dynamique de la végétation herbacúe au Sahel (Gourma, Mali): Une approche par modélisation. Cahiers Agricultures, 27(1), 15010.

DRESSLER, G., Groeneveld, J., Buchmann, C. M., Guo, C., Hase, N., Thober, J., Frank, K., & Müller, B. (2019). Implications of behavioral change for the resilience of pastoral systems? Lessons from an agent-based model. Ecological Complexity, 40, 100710.

DURAND, D. (2017). La systémique. Paris: Presses Universitaires de France.

ELLIS, J. E. (1988). Stability of African pastoral ecosystems: Alternate paradigms and implications for development. Journal of Range Management, 41, 450–459.

FAO. (2016). L’action de la FAO face au changement climatique: Élevage & changements climatiques. Available at: http://www.fao.org/publications/card/en/c/c2dfa0f8-40d9-48c2-a6bb-3f2bb2722c46/.

FREEMAN, H. (1974). Computer processing of line-drawing images. In Computing Surveys, 6(1).

GONIN, A. (2018). Pastoral land tenure in Sahel: Jeopardized mobilities. Bulletin de l’Association de Géographes Français, 95(2), 175–186.

HAILEGIORGIS, A., Crooks, A., & Cioffi-Revilla, C. (2018). An agent-Based model of rural households’ adaptation to climate change. Journal of Artificial Societies and Social Simulation, 21(4), 4.

HIERNAUX, P., Diawara, M. O., & Assouma, M. H. (2018). Au Sahel, maintenir l’élevage pastoral pour s’adapter au changement climatique. Available at: https://agritrop.cirad.fr/593560/.

KELLY, R. A., Jakeman, A. J., Barreteau, O., Borsuk, M. E., ElSawah, S., Hamilton, S. H., Henriksen, H. J., Kuikka, S., Maier, H. R., Rizzoli, A. E., van Delden, H., & Voinov, A. A. (2013). Selecting among five common modelling approaches for integrated environmental assessment and management. Environmental Modelling & Software, 47, 159–181.

KIEMA, A., Tontibomma, G. B., & Zampaligré, N. (2015). Transhumance et gestion des ressources naturelles au Sahel: Contraintes et perspectives face aux mutations des systémes de productions pastorales. VertigO - La Revue Électronique En Sciences de l’Environnement, 14(3), 16.

LECLERC, G., & Sy, O. (2011). Des indicateurs spatialisés des transhumances pastorales au Ferlo. Cybergeo: European Journal of Geography, 24.

LIAO, C. (2018). Modeling herding decision making in the extensive grazing system in southern Ethiopia. Annals of the American Association of Geographers, 108(1), 260–276.

LOBRY, C. (2003). Modéles mathématiques et modéles informatiques. Annales Des Ponts et Chaussées, 2003(107–108), 10–18.

LUGAN, J.-C. (2009). La Systémique Sociale. Paris: Presses Universitaires de France.

MACE, R., & Houston, A. (1989). Pastoralist strategies for survival in unpredictable environments: A model of herd composition that maximises household viability. Agricultural Systems, 31(2), 185–204.

MAGNANI, S. (2020). Améliorer l’accés des éleveurs a une alimentation du bétail de qualité pour augmenter la production laitiére dans les pays sahéliens d’Afrique de l’Ouest. Oxfam.

MCCABE, J. (2004). Cattle Bring Us to Our Enemies: Turkana Ecology, Politics, and Raiding in a Disequilibrium System. Ann Arbor, MI: University of Michigan Press.

MENDY, A., Yatat-Djeumen, I. V., Lam, M., & Tewa, J. J. (2023). Optimal strategy in a two resources two consumers grazing model. Differential Equations and Dynamical Systems, 2023.

MORITZ, M., Cross, B., & Hunter, C. E. (2023). Artificial pastoral systems: A review of agent-based modelling studies of pastoral systems. Pastoralism, 13(1), 31.

MORITZ, M., Galehouse, Z., Hao, Q., & Garabed, R. B. (2012). Can one animal represent an entire herd? Modeling pastoral mobility using GPS/GIS technology. Human Ecology, 40(4), 623–630.

MÜLLER, B., Bohn, F., Dreßler, G., Groeneveld, J., Klassert, C., Martin, R., Schlüter, M., Schulze, J., Weise, H., & Schwarz, N. (2013). Describing human decisions in agent-based models - ODD + D, an extension of the ODD protocol. Environmental Modelling & Software, 48, 37–48.

OUEDRAOGO, M., Sere, A., Some, B. M. J., & Traore, C. A. D. G. (2022). Straight-Line recognition using a triangular grid. In K. Arai (Ed.), Advances in Information and Communication (pp. 628–644). Cham: Springer International Publishing.

RANGÉ, C. (2020). Jeunes pasteurs en ville: Réseaux et trajectoires migratoires des jeunes d’origine pastorale - Tchad, Burkina Faso. FAO. Available at: http://www.fao.org/documents/card/fr/c/ca7213fr/.

ROUCHIER, J., Bousquet, F., Requier-Desjardins, M., & Antona, M. (2001). A multi-agent model for describing transhumance in North Cameroon: Comparison of different rationality to develop a routine. Journal of Economic Dynamics and Control, 25(3–4), 527–559.

RUBINSTEIN, A. (1998). Modeling Bounded Rationality. Cambridge, MA: MIT Press.

SALL, A. (1978). Quel aménagement pastoral pour le Sahel? Revue Tiers Monde, 19(73), 161–169.

SANÉ, M., Vayssiéres, J., Grillot, M., Bah, A., & Ickowicz, A. (2017). État de l’art de l’approche multi-agents pour modéliser le comportement spatial des troupeaux en systémes d’élevage extensif. Available at: https://agris.fao.org/agris-search/search.do?recordID=FR2018102218.

SERE, A., Traore, C. A. D. G., Traore, Y., & Sie, O. (2021). Towards traffic saturation detection based on the Hough transform method. In K. Arai, S. Kapoor, & R. Bhatia (Eds.), Proceedings of the Future Technologies Conference (FTC) 2020, Volume 2 (pp. 263–270). Cham: Springer International Publishing.

SIMON, H. A. (1955). A Behavioral Model of Rational Choice. The Quarterly Journal of Economics, 69(1), 99.

TALIB, M. A., & Morosetti, G. (1995). Manuel Pour Les Agents Vétérinaires Communautaires. Rome: FAO.

THEBAUD, B. (2017). Résiliences pastorales et agropastorales au Sahel: Portraits de la transhumance 2014-2015 et 2015-2016. Senegal, Mauritanie, Mali, Burkina Faso, Niger) - Inter-réseaux. Available at: https://www.inter-reseaux.org/ressource/resiliences-pastorales-et-agropastorales-au-sahel-portraits-de-la-transhumance-2014-2015-et-2015-2016-senegal-mauritanie-mali-burkina-faso-niger/.

TRACEY-WHITE, J. D. (1997). Manuel de planification des marchés de vente au détail. FAO, Rome.

TRAORÉ, C. A. D. G., Delay, E., Bah, A., & Diop, D. (2023). Agent-Based modeling of the spatio-temporal distribution of Sahelian transhumant herds. In K. Arai (Ed.), Intelligent Systems and Applications (pp. 630–645). Cham: Springer International Publishing.

TRAORÉ, C. A. D. G., Delay, E., Diop, D., & Bah, A. (2024). Agent-Based model for analyzing the impact of movement factors of Sahelian transhumant herds. Human-Centric Intelligent Systems, 2024.

TRAORÉ, C. A. D. G., & Séré, A. (2022). Straight-Line detection with the Hough transform method based on a rectangular grid. In A. Joshi, M. Mahmud, R. G. Ragel, & N. V. Thakur (Eds.), Information and Communication Technology for Competitive Strategies (ICTCS 2020) (pp. 599–610). Singapore: Springer Singapore.

TREUIL, J.-P., Drogoul, A., & Zucker, J.-D. (2008). Modélisation et Simulation á Base d’Agents: Exemples Commentés, Outils Informatiques et Questions Théoriques. Paris: Dunod: IRD.

WANE, A., Ancey, V., & Touré, I. (2010). Pastoralisme et recours aux marchés: Cas du Sahel Sénégalais (Ferlo). Cahiers Agricultures, 19(1), 14–20.

WATERS-BAYER, A. (2023). Book review of media culture in nomadic communities by Allison Hahn. Pastoralism, 13(1), 3.