Triadic Transitions of Opinion Dynamics in a Bounded Confidence Model

Introduction

Analyzing social networks helps improve our understanding of human interactions, social dynamics, and information dissemination (Boyd & Ellison 2007; Freeman 2004; Wasserman & Faust 1994). Social networks are commonly defined as representations of social relationships and interactions between individuals. These networks can be analyzed using various network analysis techniques to uncover important properties such as centrality, community structure, and information flow (Borgatti et al. 2009). Social networks provide insights into the connections between individuals and the structure of relationships, but often fail to reveal the true influence that one person has over another. Although individuals may be connected to others without being significantly influenced by them, there are cases where certain individuals wield considerable influence over many without reciprocating the same level of influence. Thus, social networks may capture connections, but they do not always accurately reflect the dynamics of influence within those connections.

In recent years, there has been a growing interest in studying influence networks, which formalizes "the social process of attitude changes that unfold in a network of interpersonal influence" (Friedkin & Johnsen 2011). Despite their similarities with social networks in terms of network representation, influence networks differ substantially in their underlying assumptions and implications: the question is not to highlight only social connections between individuals but also to highlight who influences whom. Although many of the social networks studied are not directed, an influence network can be represented by a directed graph (Easley & Kleinberg 2010). Because opinions of people evolve in a complex environment in which a network of interpersonal influences is a subset of the social network, both networks (influence and social network) enter into the processes of group emergence and opinion dynamics.

Opinion dynamics (Castellano et al. 2009; Flache et al. 2017; Xia et al. 2011) have been studied in various domains, especially from the perspective of modeling approaches such as the voter model (Castellano et al. 2003; Holley & Liggett 1975), the culture dissemination model (Axelrod 1997) or the bounded confidence (BC) model (Deffuant et al. 2000; Hegselmann & Krause 2002). In the BC model, opinion dynamics have been especially analyzed in the context of extremism and the influence of extremist minorities (Deffuant et al. 2000; Galam 2002) having extreme opinions that never change. In fact, the way minority opinions spread within a population (Galam 2002) may explain the emergence of new opinions and groups in different areas (for example, spreading a reform proposal) (Moscovici et al. 1969). In the BC model, extremist and moderate individuals are characterized by the uncertainty around their own opinion. Individuals are then influenced by people with an opinion sufficiently close to their own opinion, namely when the opinion difference is within their uncertainty. This uncertainty reflects the propensity to be influenced by others, from which we can extract an influence network and its network dynamics can then be analyzed.

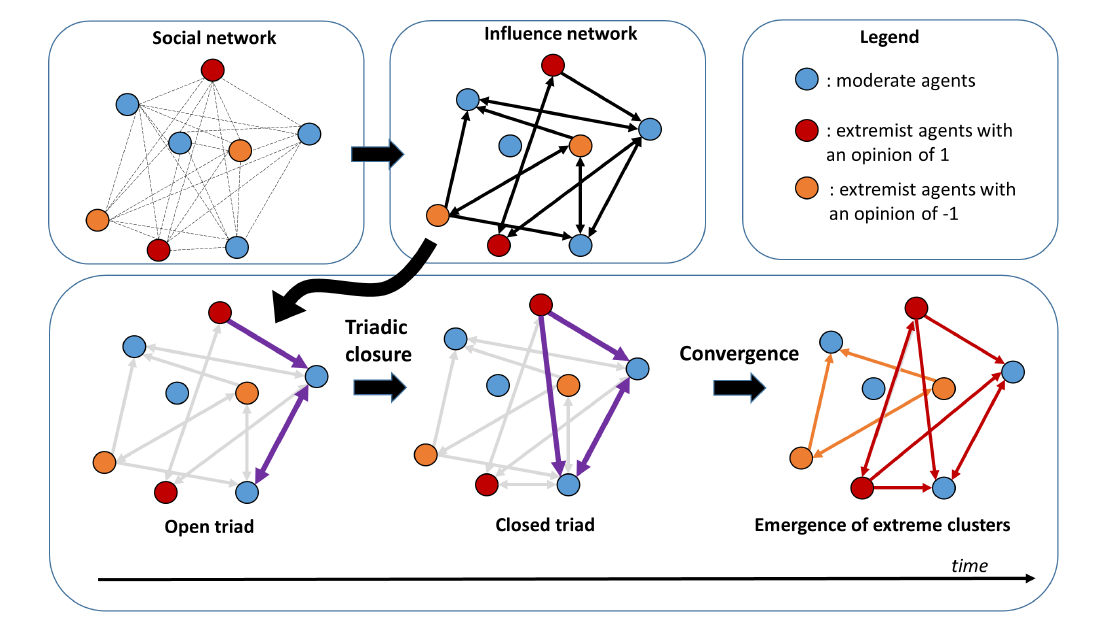
We explore this question in the context of opinion dynamics with the use of triads (Siltaloppi & Vargo 2017). A triad is a group of three people and is represented by a three-node subgraph in which the nodes may be connected by asymmetric (directional) or mutual (bidirectional) edges. The triadic structure was used to analyze the emergence of groups in some social networks (Holland & Leinhardt 1971; Wasserman & Faust 1994). The group emergence can be analyzed by the dynamics of open and closed triads. A closed triad has three edges, which means that the three people of the triad are connected to each other. An important issue is to analyze how open triads become closed over time. The issue of triadic closure has previously been analyzed in social networks to highlight how people can choose new relationships that are friends of my friends (Holland & Leinhardt 1971) and has been analyzed through the lens of social media such as Twitter (Huang et al. 2015). As it has been used for analyzing social media, our approach is to propose a similar analysis to study the influence network in opinion dynamics through a modeling approach. Figure 1 represents the question of the triadic cluster we address here. The moderate and extremist agents interact according to an existing social network, yielding a closure of some open triads. The closure of these triads may then affect the opinion dynamics.

Therefore, the purpose of our study is to highlight the presence of transitory triads in opinion dynamics, which contribute to different convergence type. As explained above, the issue of triadic closure has been previously analyzed in social networks (Holland & Leinhardt 1971; Huang et al. 2015) and seems appealing to mobilize it in the context of opinion dynamics, through the use of the BC model that is first recalled in the next section. Then, even without any simulation, we analyze the BC model through the lens of triadic structure, from a theoretical perspective. The purpose is to highlight why some triads are possible (or not) because of the bounded confidence mechanisms. Finally, we explore the dynamics of triads through typical convergence patterns of the BC model, enabling a better understanding of emerging convergence patterns.

The Bounded Confidence (BC) Model and its Convergence Patterns

Using computer simulations may provide some insight into the emergence of extremism. It enables us to test different parameters and characteristics of individuals within a population and to analyze the corresponding collective behavior. Several models have been developed to study the propagation of extreme opinions or minority influence (Axelrod 1997; Castellano et al. 2009; Flache et al. 2017; Galam & Moscovici 1991; Huet & Mathias 2018). The rationale of these models is that an agent may or may not change their opinion, depending on their local neighborhood (in the opinion space) that determines if the agent is under influence of another agent. Among the different models of opinion dynamics, we consider the bounded confidence (BC) model (Deffuant et al. 2000; Hegselmann & Krause 2002) which is grounded in the theory of social comparison (Festinger 1954) and in the theory of social judgment (Sherif & Hovland 1961). In the BC model, an individual exhibits a personal opinion, normalized between \(-1\) and \(1\), with a constant uncertainty around this opinion. Agents influence each other by slightly moving their opinions towards each other, if the distance between their opinions is less than their uncertainty. This uncertainty reflects the propensity to be influenced by other individuals.

In terms of agent-based modeling (Deffuant et al. 2006), we consider a population of \(N\) agents composed of moderate and extremist agents. Moderate agents exhibit the same uncertainty \(u\), whereas extremists exhibit a very small value of their uncertainty \(u_e\) compared to \(u\) (extremist opinions can be considered quasi-static). For the sake of simplicity, we will consider \(u_e=0\), which means that extremist opinions never change over time. The community is modeled as closed, meaning no new agents are introduced, and no existing agents leave during the simulation. The initial opinions of the moderate agents are uniformly distributed along an opinion axis between -1 and +1. An extremist agent exhibits the two following features: i) it expresses an extreme opinion; ii) it has a high certainty about its opinions. The proportion of extremists in the population is denoted \(p_{e}\): half of them initialize with opinion +1 and the other half with opinion \(-1\). In what follows, we consider that each individual can meet any individual in the population, meaning that we consider a social network in which everyone is connected to everyone. Each agent is paired once in one period: \(N/2\) random pairs interact at each time step. When an agent \(i\) (with opinion \(x_i\) and uncertainty \(u_i\)) meets an agent \(j\) (with opinion \(x_j\) and uncertainty \(u_j\)), opinion \(i\) is modified as follows:

\[ x_i(t+1)=x_i(t) + \mu (x_j(t)-x_i(t))I\left(|x_i(t) - x_j(t)|<u_i\right)\]

\[(1)\]

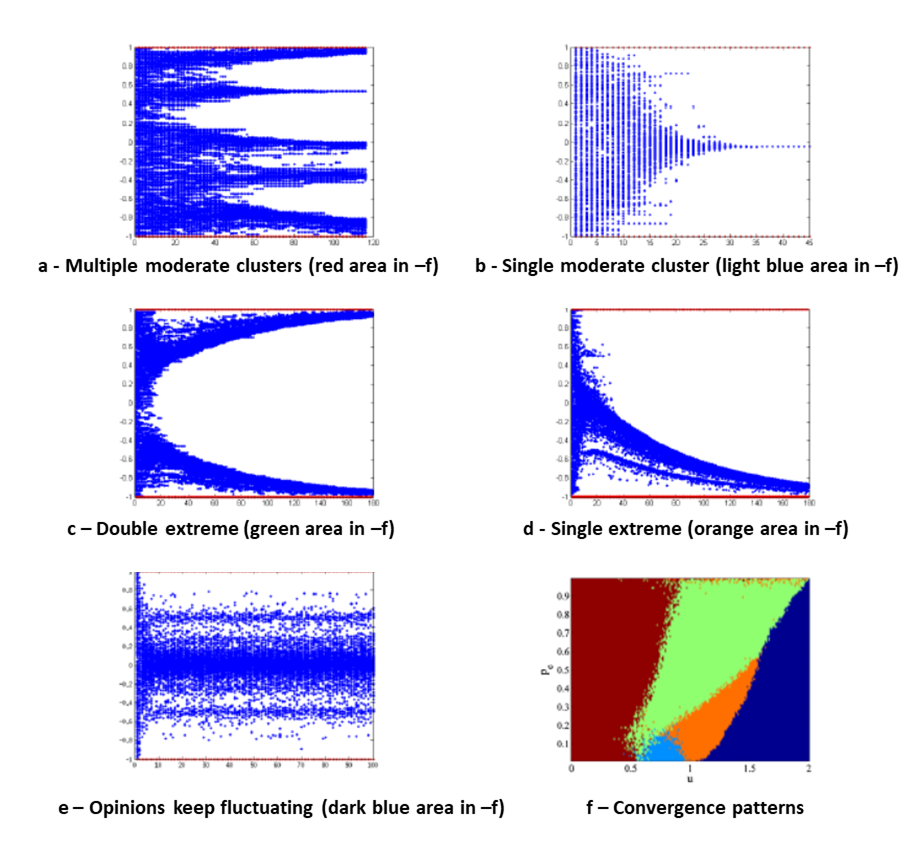
The opinion \(j\) is modified in the same way (by switching \(i\) and \(j\) in Equation 1). \(I(\cdot)=1\) if \((\cdot)\) is true and 0 otherwise: an agent is influenced by another agent only if the opinion of the latter is within his uncertainty. The parameter \(\mu\) models the intensity of the interaction (generally \(0 < \mu \leq 0.5\)). In what follows, we set \(\mu\) to 0.5. Population is composed of 200 agents (\(N=200\)) and the default time horizon for simulations is 200. All individuals’ opinions are updated simultaneously at each time step, yielding a simultaneous updating of the opinions. The code is available in Appendix A. From this agent-based model, Mathias et al. (2016) identify five main convergence patterns (Figure 2):

• The "multiple moderate clusters" convergence pattern (Figure 2a and the red area in Figure 2f) emerges for low uncertainty values \(u\). Moderate people are quite certain about their opinion and they are influenced only by people with very close opinion. Therefore, a large share of the population is not influenced by extremists;
• The "single moderate cluster"convergence pattern (Figure 2b and light blue on Figure 2f) emerge for values of uncertainty \(u\) between 0.5 and 1. There is consensus among the moderates towards a neutral opinion;
• The "double extreme" convergence pattern (Figure 2c and green area on Figure 2f) corresponds to the case where population is split into two extreme subpopulations. It is driven by the proportions of extremists within the population and the uncertainty of moderates;
• The "single extreme" convergence pattern (Figure 2d and orange area on Figure 2f) corresponds to the case where the moderates tips towards one extreme (-1) or the other (1). This tipping toward single extreme corresponds to an instability of the system (see Mathias et al. 2017 for more details);
• When the uncertainty is sufficiently great (high values of \(u\)), the opinions do not stabilize (Figure 2e and dark blue area on Figure 2f). Even if we increase the number of time steps, the moderate opinions keep fluctuating and do not cluster (Mathias et al. 2016;2017).

Triadic Structure of the Influence Network in Opinion Dynamics

How agents’ opinions influence one another can be viewed as a network: a node is an agent; an asymmetric edge from agent \(i\) to agent \(j\) indicates that agent \(j\)’s opinion is influenced by agent \(i\)’s opinion; and a mutual edge between two agents indicates that they influence each other’s opinion. Once viewed as a network, an arsenal of network analysis and concepts can be applied to the influence network to extract unique insights that cannot be obtained – and therefore complement – those from other non-network approaches.

But which network approach? Recent network studies warned that basic network properties alone (e.g. density, centrality, clustering, etc.) provide an inadequate picture for the system under consideration and emphasized the importance of higher-order properties (e.g., Battiston et al. 2021; Lotito et al. 2022). Here, we focus on the triadic structure (see, e.g., Milo et al. 2004; Faust 2010) of the influence network. In network analysis, a triad refers to a group of three nodes (or vertices) and the relationships (edges) between them within a larger network or graph. While being one of the higher-order network properties, triads are simple enough to lend themselves to intuitive interpretation, which is particularly instructive in the context of the influence network (Figure 3).

To be sure, triadic structure has been studied for a wide variety of complex networks, including some social networks (e.g., Milo et al. 2004; Oh et al. 2024 as a few examples; Pham et al. 2022; Shutters & Muneepeerakul 2012); however, this has not been done for the influence network and opinion dynamics. These local network structures can play an important role in driving an opinion within a population and warrant deeper investigation.

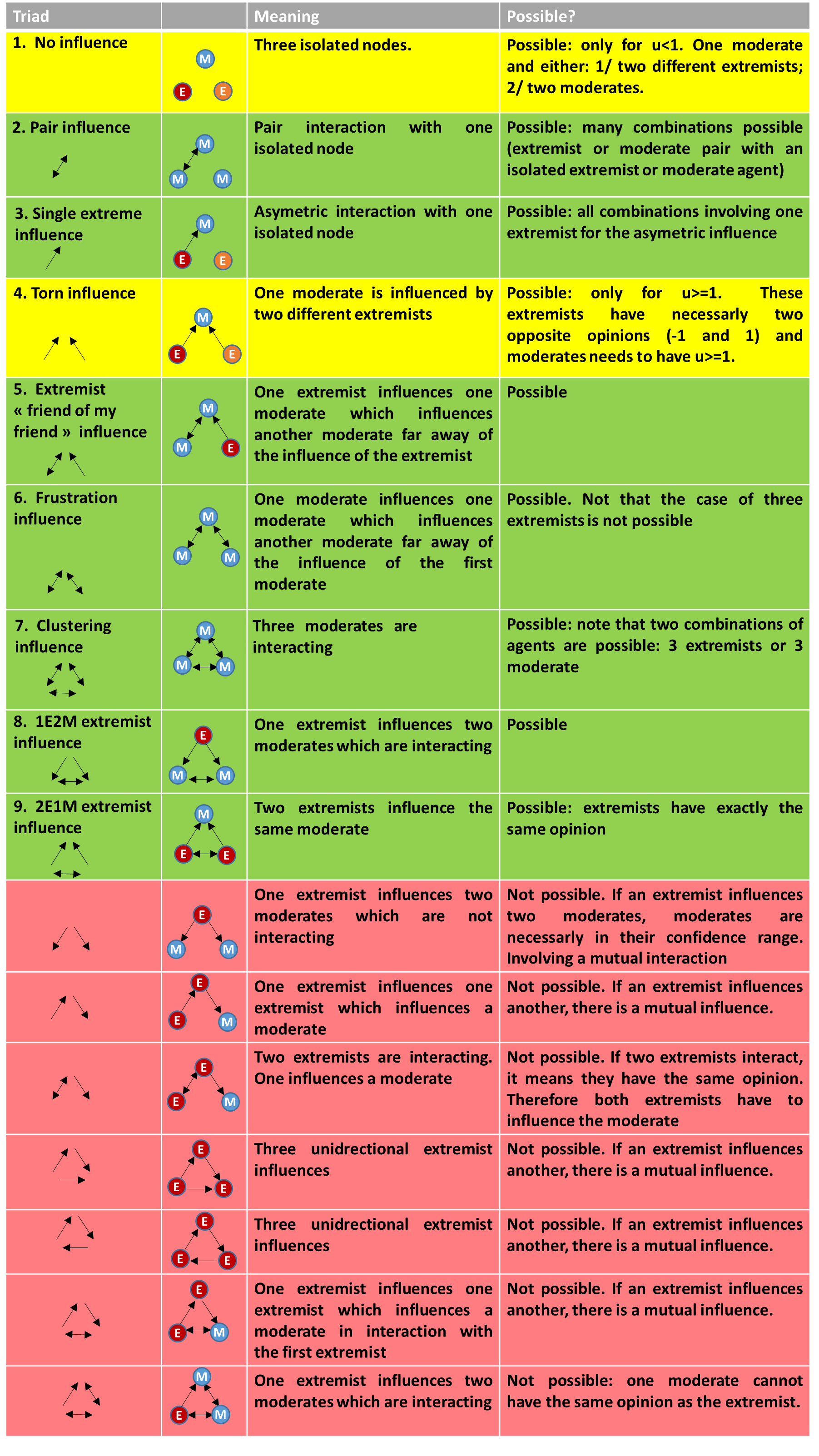
Before proceeding further, let us now introduce the triads in the context of the influence network in the BC model. Theoretically, there are sixteen possible triad types. However, in the context of opinion dynamics resulting from the BC model, not all these sixteen triads are possible. Here, triads must adhere to the dynamics of Equation 1 and have the following properties that are straightforward:

• Property 1. We consider an influence of agent \(i\) on agent \(j\) if \(|x_i(t) - x_j(t)|\leq u_j\), leading to a directional edge in the triad. It means that two extremists can have either no influence (different opinions) or a mutual influence (same opinion), and therefore no unidirectional influence exist between extremists;
• Property 2. A unidirectional influence only represents the influence of one extremist on a moderate;
• Property 3. Bidirectional influences are only possible between two moderates or two extremists. In fact, a bidirectional influence between an extremist and a moderate is not possible because it would mean that moderate and extremist agents have the same extreme opinion (extremist uncertainty \(u_e\)=0). This is not possible because the opinion of a moderate agent may converge to the opinion of the extremist without reaching it (the opinion difference is continuously divided by 2), always resulting in a difference between them.

From the above properties, we analyze the potential existence of triads in Figure 3. In this Figure, moderate agents are represented in blue whereas extremists are represented in red and orange (orange extremists have the opposite opinion of red extremists). Note that illustrations are only for pedagogical purposes, and additional combinations are reported in the last column. The following insights follow (Figure 3):

• Some triads cannot exist because of the specific rules involved in opinion dynamics (red rows). It is mainly due to Property 3 described above;
• Some triads (yellow rows, such as triads 1 and 4) are possible for specific values of the moderate uncertainty \(u\). For instance, the “no influence” triad (triad 1) can exist only for a moderate uncertainty lower than 1 (\(u<1\)). If \(u \geq 1\), a moderate agent cannot be isolated (and this triad necessarily implies a moderate agent). The rationale is similar for the torn triads (triad 4);
• We have one triad without edges (Figure 3, triad 1), two triads with one edge (Figure 3, triads 2-3), three triads with two edges (Figure 3, triads 4-6) and only three triads with three edges (Figure 3, triads 7-9). It shows the importance of open triads in our case;
• Five out of nine triads (3, 4, 5, 8, 9) are composed of unidirectional edge and necessarily involve an extremist, highlighting the importance of extremists in triplet interactions in the BC model.

Results and Discussion

Triad dynamics and bounded confidence convergence patterns

In what follows, we analyze the dynamics and compositions of these triads under five convergence patterns typically emerging in the BC model (see the previous section). For each convergence pattern discussed below, the following results are reported: location of its parameters in the "moderate uncertainty \(u\)- proportion of extremists \(p_e\)" parameter space, an example of the opinion dynamics, time series of the triad counts for all 100 simulations, and the mean densities of the triads averaged across all 100 simulations. As shown by results reported in Appendix B, 100 simulations are enough to achieve representative dynamics of triads. The main insights are summarized in Table 1; the details are discussed in the following subsections. Note that in all convergence patterns, triad 7 is present at the end of the simulation (a proxy of clusters), and triad 6 is present during the transitory dynamics. We now describe the transition dynamics of the triadic structure in more detail.

Table 1: Main triads involved in the convergence patterns identified in the BC model. Triad 7 is present in all convergence patterns at the end of the simulation (a proxy of clusters), while triad 6 is present during the transitory dynamics of all convergence patterns.

	Triads at the quasi-stationary state	Triads during transient dynamics	Main comments
Multiple moderate clusters	Mainly: triads 1, 2, 3 and 7	Triad 6	Triad 1 shows the existence of isolated clusters
Single moderate cluster	Mainly: triads 2 and 7	Mainly: triad 6; Other triads:1, 3, 8, 5	Triads are mainly composed of triad 7, showing clustering effect
Single extreme	Mainly: triads 2, 7 and 8	Mainly: triads 6, 5 and 3	Triad 5 drives the instability causing the tipping towards one extreme
Double extreme	Mainly: triads 2, 3, 7, 9 and 8	Mainly: triads 6, 5 and 1	This convergence pattern results from the interaction of five triads
Opinions keep fluctuating	Mainly: triads 7 and 8; Other triad: 4	Mainly: triads 6, 5 and 4	Triads 4, 5 and 6 only exist in this case at the quasi-stationary state: they may maintain fluctuations

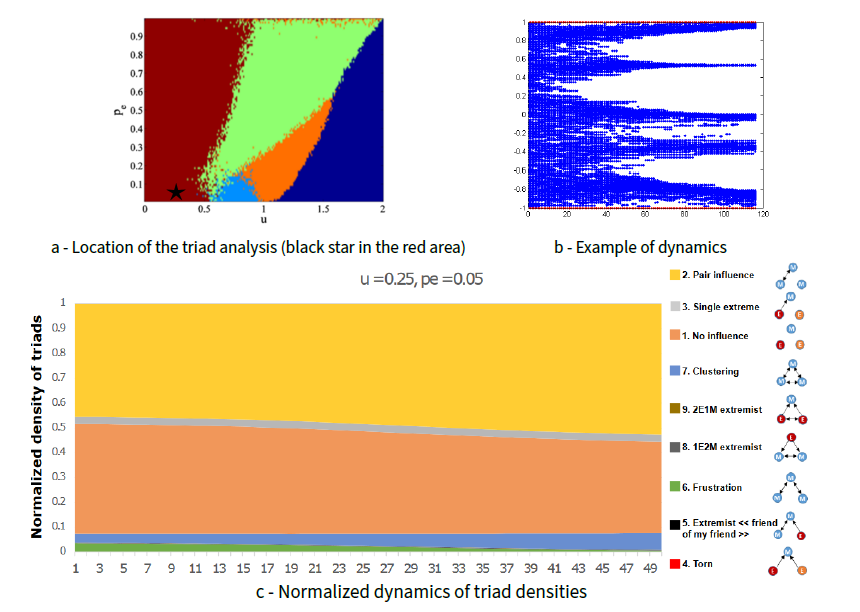
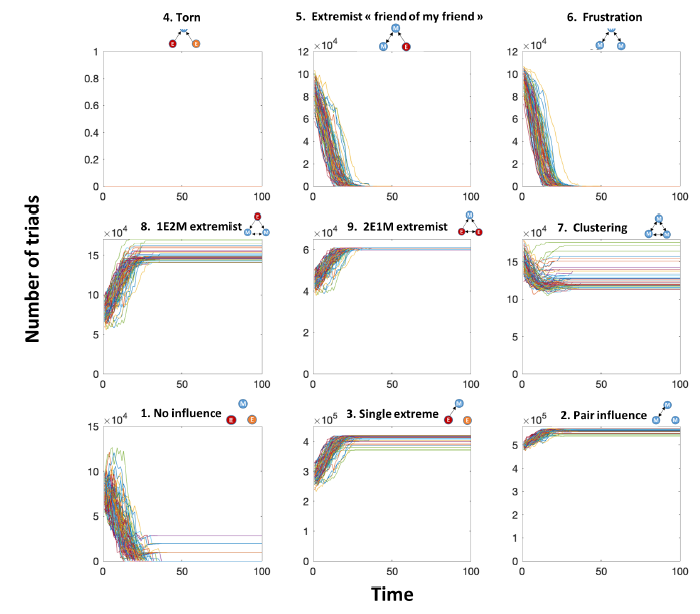
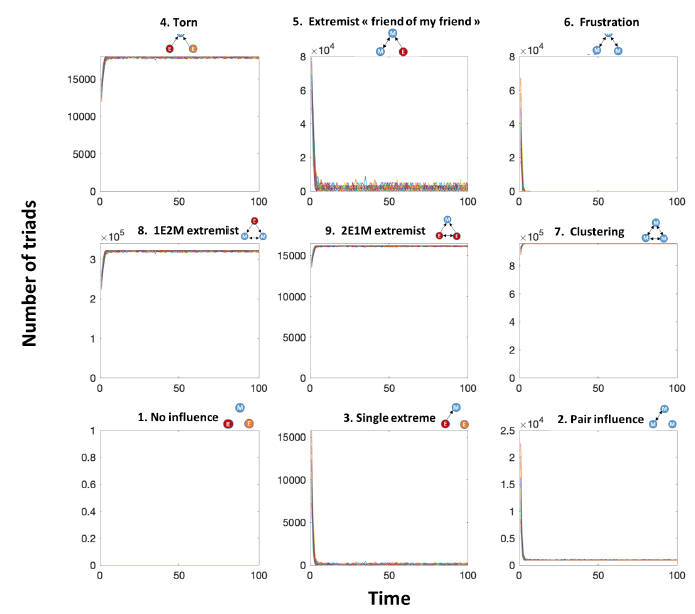
Multiple moderate clusters convergence pattern (moderate uncertainty \(u=0.25\), proportion of extremists \(p_e=0.05\), Figure 4): Triad 2 is significant throughout the dynamics. It corresponds to open triads with a mutual edge and one isolated node: it means that a high proportion of agents are isolated pairs in the opinion space. This corresponds to two agents in the same cluster who do not interact with other agents in other clusters. Triad 1 is also significant throughout the dynamics and corresponds to “no influence” triads (three isolated nodes): it means that a high proportion of agents are isolated in the opinion space in different opinion clusters. More specifically, it represents the lack of interaction among three agents from three different clusters. Triad 7 (clustering triad) represents mutual interactions of three agents within the same cluster (either three moderate agents or three extremist agents). Note that the presence of triads 7 increases over time showing the convergence towards clusters whereas triads 6 disappear—closing of triads. Indeed, this latter corresponds to transitory dynamics where opinions indirectly spreads within moderates: after convergence to cluster, this triad type no longer exists. Finally, recall that "torn" triads 4 do not exist for a moderate uncertainty lower than 1 (\(u<1\)).

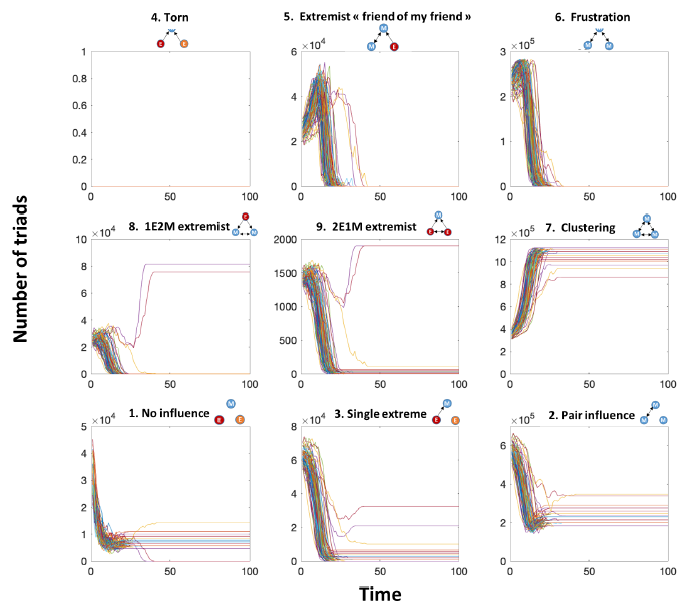
Single moderate cluster convergence pattern (moderate uncertainty \(u=0.75\), proportion of extremists \(p_e=0.05\), Figure 5): Triad 7 (clustering triad) represents mutual interactions of three agents within the same cluster (either three moderate agents or three extremist agents). In this case, triad 7 increases over time, corresponding to the convergence towards the single cluster, whereas triads 6 decreases over time as they are being closed, characteristic of the transitory dynamics where opinions indirectly spread within moderates. Another triad that exists at the end of the simulations is triad 2 because of the presence of extremists who do not influence moderate agents. Note that there is a peak of triads 5 and 6 during the transitory dynamics. Both triads spread opinion in an indirect way – influence of two agents through a third agent.

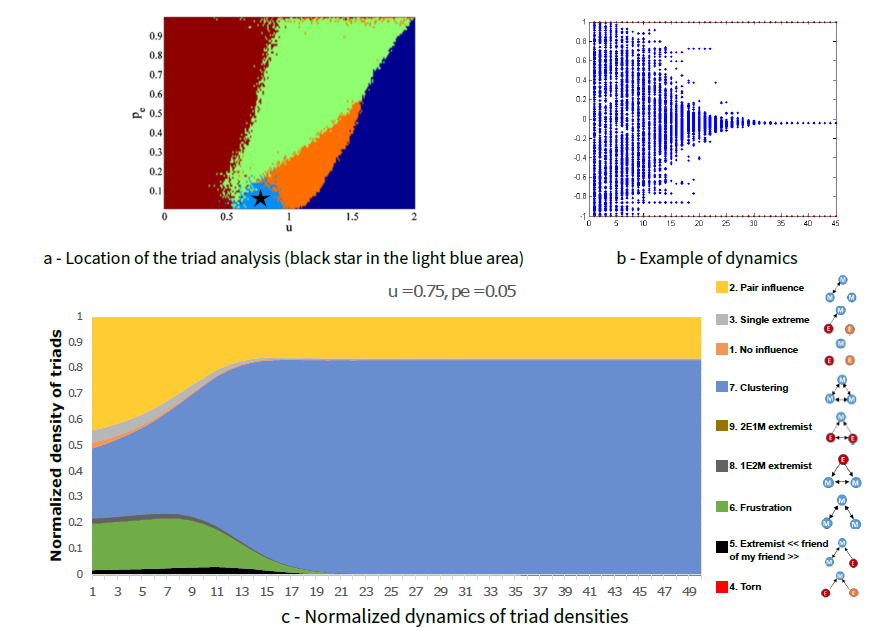
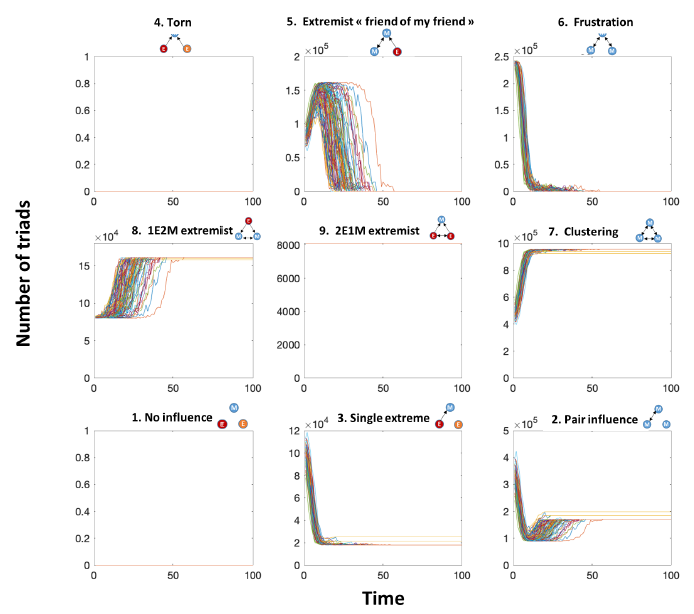
Single extreme cluster convergence pattern (moderate uncertainty \(u=1\), proportion of extremists \(p_e=0.1\), Figure 6): the triad dynamics of the "single extreme" convergence pattern are quite similar to that of a single moderate cluster: triads 7 and 2 are significant, showing the convergence to a low number of clusters (one in the previous case). The main difference lies in the dynamics of triads 8, which correspond to the influence of an extremist on two moderate agents. Note that this triad will not disappear even in the long term. Indeed, we may expect that triads 8 will become type 7 in the long term. However, this is a limit case; indeed, in this particular implementation, moderate opinions will never be exactly equal to the extremist opinions: we divided the distance between opinions by 2, always leading to some residual opinion difference between moderates and extremists.

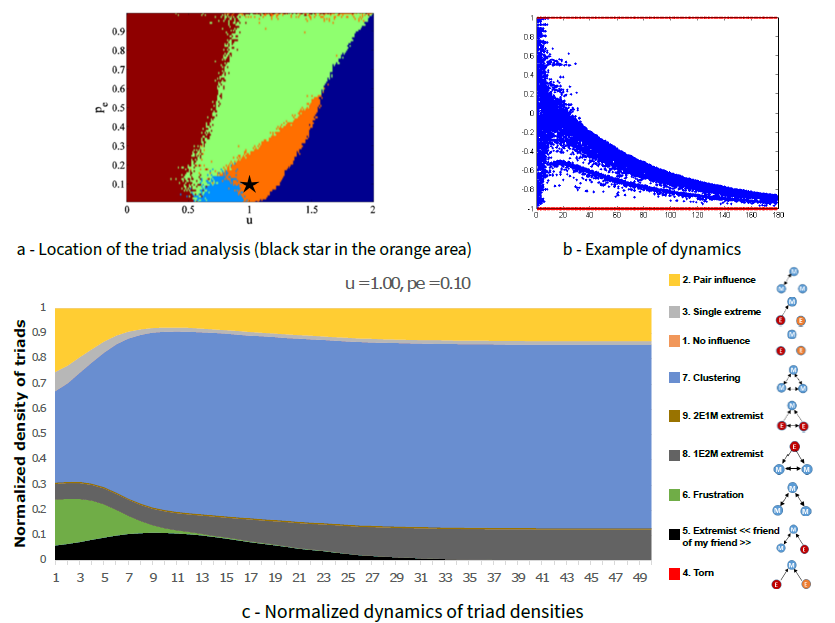
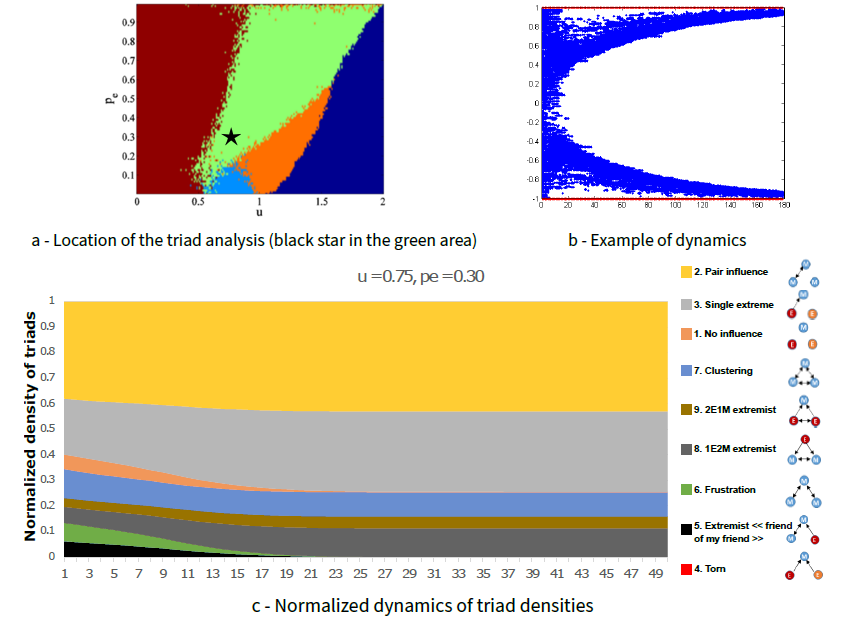
Double extreme clusters convergence pattern (moderate uncertainty \(u=0.75\), proportion of extremists \(p_e=0.3\), Figure 7): triad dynamics of the "double extreme" convergence pattern are more complex than the previous cases. We have five significant triads at the end of the simulations. The clustering (triad 7) and "pair influence" (triad 2) triads are significant, showing the convergence to a low number of clusters for the moderates (two clusters here). Unlike the "single extreme" convergence pattern, triad 2 is more significant than triad 7 because of the existence of two clusters instead of one. "Single extreme" triads 3 show the influence of extremists on moderates in the case of a divided population caused by the "double extreme" convergence pattern (leading to an isolated agent in a triad 3). Triads 9 are also more significant in this case because all extremists influence some moderates; in the single extreme case above, half of the extremists do not influence any moderates as all the moderates converge to the other extreme. As in the single extreme, the dynamics of triads 8 correspond to the influence of extremists on close moderate agents.

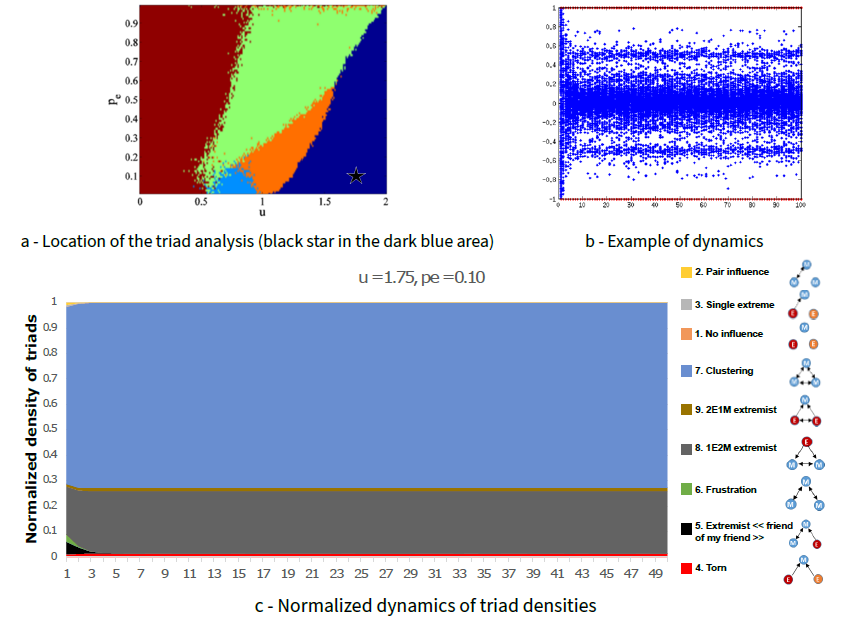
Opinions keep fluctuating convergence pattern (moderate uncertainty \(u=1.75\), proportion of extremists \(p_e=0.1\), Figure 8): dynamics are mainly driven by two triads: triad 7 and triad 8. Triads 7 shows the presence of three-moderate interactions, whereas triad 8 shows the influence of extremists like the "double and single extreme" convergence patterns. Torn triads 4 exist at the end of the simulation, unlike previous cases. This triad 4 enables opinions to keep fluctuating: many moderate agents are under the influence of the two extremes.

Effects of the moderate uncertainty \(u\) and the proportion of extremists \(p_e\) on the triad composition

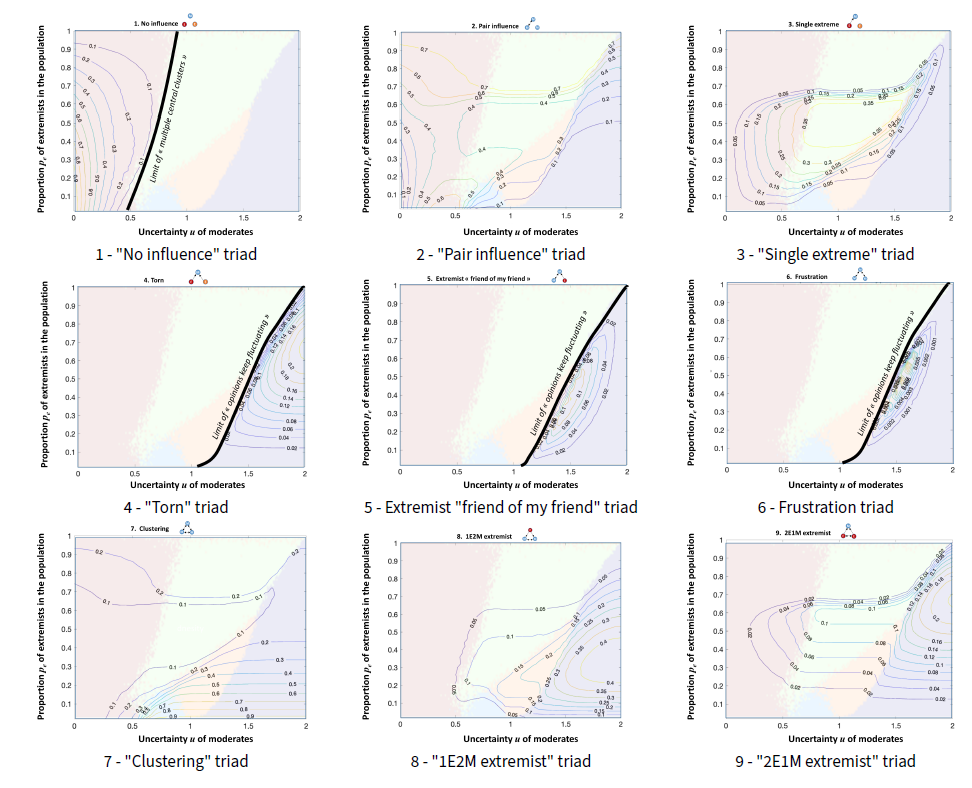
In the previous section, we analyzed the dynamics of triads during the opinion dynamics for a given situation, specified by a particular combination of the moderate uncertainty \(u\) and the proportion of extremists \(p_e\). In this section, we explore the composition and density of triads at the end of the simulation (when a quasi-stationary state is reached) across a wide range of moderate uncertainty \(u\) and the proportion of extremists \(p_e\) (Figure 9), corresponding to a wide variety of system outcomes/scenarios discussed above. We find that:

• The high density of triad 1 is a distinct characteristic of the multiple moderate clusters. This triad highlights the fact that there are isolated agents in the population which can only appear in the case of multiple moderate clusters. A low value of moderate uncertainty \(u\) is required for this isolation. This means that, beyond a certain threshold, all agents are connected to at least one agent, making the completely open triads 1 (without edge) impossible (Figure 9a).
• The density of triad 2 – pair influence – increases with the proportion \(p_e\) of extremists: an extremist increasingly plays the role of the isolated agent in this triad type, while the pair could be 2 extremists or 2 moderates.
• Triad 3 contours show the density of unidirectional extremist influence on a moderate along with an isolated extremist of the opposite opinion. The density depends on the interplay between the moderate uncertainty \(u\) and the proportion \(p_e\) of extremists: if \(p_e\) is too high, most of the population are pair-connected through triads 2 or triads 7. Triads 3 are found the most in the “double extreme” convergence pattern where, by definition, there are many extremists of opposite opinions – an ingredient of triad 3.
• Triads 4, 5 and 6 only exist in the case of “opinion keep fluctuating” convergence pattern. These triads are suspected to maintain fluctuations at the quasi-stationary state even if there are few of them. Indeed triad 4 highlights that a part of the population is always under influence of both extremes, leading to push and pull between opposite extremes, slowing down the closing of triads.
• The density of clustering triad 7 is influenced by the proportion \(p_e\) of extremists in controlling the amount of triplet consensus. When the proportion \(p_e\) of extremits is low, there are many moderates in the population who are sufficiently close in their opinions to form many “clustering” triads. Conversely, when the proportion \(p_e\) of extremists is high, the population is mainly composed of two clusters of extremists (one cluster with an opinion of 1 and the other one with an opinion of -1) forming many ’"clustering" (extremist) triads.
• Triads 8 and 9 (1E2M and 2E1M extremist triads) increase with the moderate uncertainty \(u\): higher \(u\) means more moderates are within influential reach of extremists.

Discussion

Our results highlighted the presence of transitory triads in opinion dynamics, which play a significant role in shaping their convergence patterns by impacting interactions and adjustments among connected individuals. These transient structures often act as intermediaries, driving the alignment of opinions within the network over time. As explained above, the issue of triadic closure has been extensively analyzed in social networks (Holland & Leinhardt 1971; Huang et al. 2015). This phenomenon is critical in fostering clustering and stability within groups, but its interplay with the transitory nature of triads highlights the dynamic and evolving nature of social interactions. Understanding such effects offers deeper insights into how opinions propagate within a population. For example, open triad 6 ("frustration") has been reported to have a high probability of forming a closed triad in social media (Huang et al. 2015), showing its transitory existence in dynamical networks: closing triad 6 and turning it into triad 7 is the common friend ultimately influencing her two friends’ opinions sufficiently to the point that they can influence each other, thereby resolving their frustration (Brito-Montes et al. 2022). Similarly, open triad 6 is also present in many convergence patterns during the transitory phase observed in our simulations but not at the stationary stage. Indeed, open triad 6 is either closed and transition into triad 7 (“clustering” triad with three mutual influence, either three extremists or three moderates) or open and transition into open triads 2 (“pair influence”) or 1 (three isolated individuals). For instance, in the case of “multiple moderate clusters” convergence pattern, open triads 6 disappear as they transition into one of these 3 triads. However, triads 6 are all closed in the case of the “single cluster” convergence pattern because of the convergence of all population towards the same opinion. The “single extreme clusters” convergence pattern highlights similar triadic closure caused by the extreme cluster with closed moderate triads and closed triads with one extremists. The existence of the open triad 4 at the quasi-stationary state is only observable in the case where opinions keep fluctuating. This open triad, showing the influence of opposite extremists on the population, leads to back-and-forth of individuals between both extremes, thereby preventing the population from converging to a cluster.

Conclusions and Avenues for Further Development

Triadic transitions provide useful information for understanding the convergence of opinions within a population. The use of triads may explain some opinion dynamics as the closing of triad 6 or the existence of the open triad 4 when opinions keep fluctuating (see discussion in the previous section). However, the use of triads for analyzing social networks, while insightful, has notable limitations. Triads simplify complex social structures to three-node interactions, which may overlook the nuances of higher-order network dynamics. Their interpretation often depends on contextual factors like cultural norms or algorithm of social platform, limiting the generalizability of findings. In large networks, analyzing numerous overlapping triads can become computationally intensive and less informative. Finally, an overemphasis on triadic closure may neglect other critical phenomena, such as bridging roles and non-transitive relationships, which are also key to understanding broader network behavior.

This triad-based approach to bounded confidence may be developed and generalized to test hypotheses on opinion dynamics within a population. Indeed, beyond application to social media, using triads for analyzing results from opinion dynamics models may inform the theoretical processes involved in social networks. Using such a model may help us understand mechanisms involved in such social media and inform us about the hidden social interactions between individuals. For instance, in Twitter, open triad 6 is expected to be closed (Huang et al. 2015) as it has been observed in our results. In the case of Wikipedia, open triad 4 has been observed as the main triad (Doran 2014). This latter triad has been highlighted in our study only in the case of opinion keep fluctuating, suggesting a significant presence of individuals with fluctuating opinions in this social media. On the other hand, triads 2 and 6 were highlighted in the case of Facebook (Doran 2014), which may correspond to multiple moderate clusters in our case, suggesting the presence of many independent groups in this social media. While the comparison of our results to existing networks is inherently limited and serves merely as circumstantial evidence, it underscores the potential for testing hypotheses regarding individual interactions to enhance our understanding of established social networks. Hence, conducting numerical experiments to test hypotheses about social interactions within models of opinion dynamics (Castellano et al. 2009; Xia et al. 2011) and subsequently comparing the results with data extracted from social networks may help understand dynamics of opinions in social media platforms, which are the windows into the opinion dynamics of the population at large.

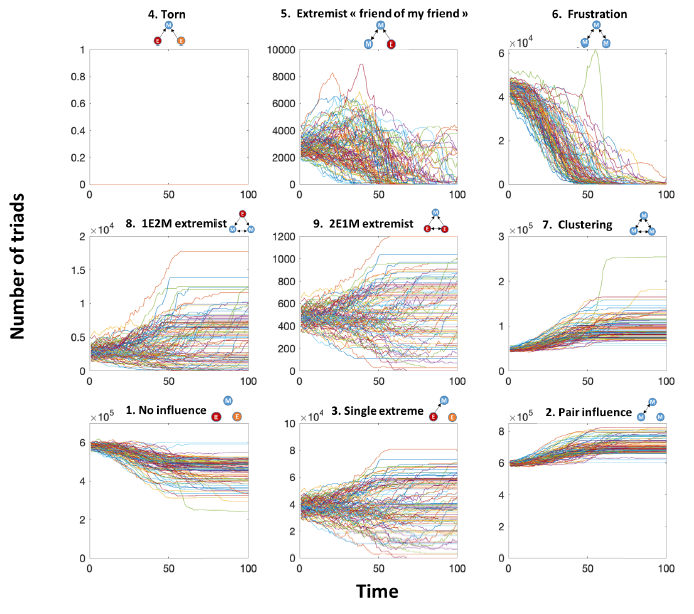
References

AXELROD, R. (1997). The dissemination of culture: A model with local convergence and global polarization. Journal of Conflict Resolution, 41(2), 203–226. [doi:10.1177/0022002797041002001]

BATTISTON, F., Amico, E., Barrat, A., Bianconi, G., Ferraz de Arruda, G., Franceschiello, B., Iacopini, I., Kéfi, S., Latora, V., Moreno, Y., Murray, M. M., Peixoto, T. P., Vaccarino, F., & Petri, G. (2021). The physics of higher-order interactions in complex systems. Nature Physics, 17(10), 1093–1098. [doi:10.1038/s41567-021-01371-4]

BORGATTI, S. P., Mehra, A., Brass, D. J., & Labianca, G. (2009). Network analysis in the social sciences. Science, 323(5916), 892–895. [doi:10.1126/science.1165821]

BOYD, D. M., & Ellison, N. B. (2007). Social network sites: Definition, history, and scholarship. Journal of Computer-Mediated Communication, 13(1), 210–230. [doi:10.1111/j.1083-6101.2007.00393.x]

BRITO-MONTES, J., Canto-Lugo, E., & Huerta-Quintanilla, R. (2022). Modularity, balance, and frustration in student social networks: The role of negative relationships in communities. PLoS One, 17(12), e0278647. [doi:10.1371/journal.pone.0278647]

CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2), 591. [doi:10.1103/revmodphys.81.591]

CASTELLANO, C., Vilone, D., & Vespignani, A. (2003). Incomplete ordering of the voter model on small-world networks. Europhysics Letters, 63(1), 153. [doi:10.1209/epl/i2003-00490-0]

DEFFUANT, G., Moss, S., & Jager, W. (2006). Dialogues concerning a (possibly) new science. Journal of Artificial Societies and Social Simulation, 9(1).

DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(01n04), 87–98. [doi:10.1142/s0219525900000078]

DORAN, D. (2014). Triad-based role discovery for large social systems. International Conference on Social Informatics.

EASLEY, D., & Kleinberg, J. (2010). Networks, crowds, and markets: Reasoning about a Highly Connected World. Cambridge: Cambridge University Press. [doi:10.1017/cbo9780511761942]

FAUST, K. (2010). A puzzle concerning triads in social networks: Graph constraints and the triad census. Social Networks, 32(3), 221–233. [doi:10.1016/j.socnet.2010.03.004]

FESTINGER, L. (1954). A theory of social comparison processes. Human Relations, 7(2), 117–140. [doi:10.1177/001872675400700202]

FLACHE, A., Maes, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., & Huet, S. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2. [doi:10.18564/jasss.3521]

FREEMAN, L. (2004). The Development of Social Network Analysis: A Study in the Sociology of Science. New York, NY: Empirical Press.

FRIEDKIN, N. E., & Johnsen, E. C. (2011). Social Influence Network Theory: A Sociological Examination of Small Group Dynamics. Cambridge: Cambridge University Press. [doi:10.1017/cbo9780511976735]

GALAM, S. (2002). Minority opinion spreading in random geometry. The European Physical Journal B, 25(4), 403–406. [doi:10.1140/epjb/e20020045]

GALAM, S., & Moscovici, S. (1991). Towards a theory of collective phenomena: Consensus and attitude changes in groups. European Journal of Social Psychology, 21(1), 49–74. [doi:10.1002/ejsp.2420210105]

HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence: Models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2.

HOLLAND, P. W., & Leinhardt, S. (1971). Transitivity in structural models of small groups. Comparative Group Studies, 2(2), 107–124. [doi:10.1177/104649647100200201]

HOLLEY, R. A., & Liggett, T. M. (1975). Ergodic theorems for weakly interacting infinite systems and the voter model. The Annals of Probability, 3(4), 643–663. [doi:10.1214/aop/1176996306]

HUANG, H., Tang, J., Liu, L., Luo, J., & Fu, X. (2015). Triadic closure pattern analysis and prediction in social networks. IEEE Transactions on Knowledge and Data Engineering, 27(12), 3374–3389. [doi:10.1109/tkde.2015.2453956]

HUET, S., & Mathias, J.-D. (2018). Few self-involved agents among bounded confidence agents can change norms. Advances in Complex Systems, 21(06n07), 1850007. [doi:10.1142/s0219525918500078]

LOTITO, Q. F., Musciotto, F., Montresor, A., & Battiston, F. (2022). Higher-order motif analysis in hypergraphs. Communications Physics, 5(1), 1–8. [doi:10.1038/s42005-022-00858-7]

MATHIAS, J.-D., Huet, S., & Deffuant, G. (2016). Bounded confidence model with fixed uncertainties and extremists: The opinions can keep fluctuating indefinitely. Journal of Artificial Societies and Social Simulation, 19(1), 6. [doi:10.18564/jasss.2967]

MATHIAS, J.-D., Huet, S., & Deffuant, G. (2017). An energy-like indicator to assess opinion resilience. Physica A: Statistical Mechanics and Its Applications, 473, 501–510. [doi:10.1016/j.physa.2016.12.035]

MILO, R., Itzkovitz, S., Kashtan, N., Levitt, R., Shen-Orr, S., Ayzenshtat, I., Sheffer, M., & Alon, U. (2004). Superfamilies of evolved and designed networks. Science, 303(5663), 1538–1542. [doi:10.1126/science.1089167]

MOSCOVICI, S., Lage, E., & Naffrechoux, M. (1969). Influence of a consistent minority on the responses of a majority in a color perception task. Sociometry, 32(4), 365–380. [doi:10.2307/2786541]

OH, W. S., Muneepeerakul, R., Rubenstein, D., & Levin, S. (2024). Emergent network patterns of internal displacement in Somalia driven by natural disasters and conflicts. Global Environmental Change, 84, 102793. [doi:10.1016/j.gloenvcha.2023.102793]

PHAM, T. M., Korbel, J., Hanel, R., & Thurner, S. (2022). Empirical social triad statistics can be explained with dyadic homophylic interactions. Proceedings of the National Academy of Sciences, 119(6), e2121103119. [doi:10.1073/pnas.2121103119]

SHERIF, M., & Hovland, C. I. (1961). Social Judgment: Assimilation and Contrast Effects in Communication and Attitude Change. New Haven, CT: Yale Univerity Press.

SHUTTERS, S. T., & Muneepeerakul, R. (2012). Agricultural trade networks and patterns of economic development. PLoS One, 7(7), e39756. [doi:10.1371/journal.pone.0039756]

SILTALOPPI, J., & Vargo, S. L. (2017). Triads: A review and analytical framework. Marketing Theory, 17(4), 395–414. [doi:10.1177/1470593117705694]

WASSERMAN, S., & Faust, K. (1994). Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press.

XIA, H., Wang, H., & Xuan, Z. (2011). Opinion dynamics: A multidisciplinary review and perspective on future research. International Journal of Knowledge and Systems Science, 2(4), 72–91. [doi:10.4018/jkss.2011100106]