An Agent-Based Model of Issue Alignment and Polarization Based on the Menu-Independent and Menu-Dependent Influences Model

Introduction

Political opinions are often represented as points in the two-dimensional space depicted in Figure 1. In this representation, opinions are reduced to two values: a social (or sociocultural) attitude and an economic attitude. The social attitude summarizes positions on issues such as individual liberties, law enforcement methods, and the separation of church and state. The economic attitude summarizes positions on fiscal policy, social welfare, market regulation, and so on (Feldman & Johnston 2014; Knight 1999; Swedlow 2008; Treier & Hillygus 2009).¹ Each quadrant of the opinion space corresponds to a broad ideology: libertarianism, conservatism, communitarianism, and liberalism (Janda et al. 2020; Swedlow & Wyckoff 2009).²

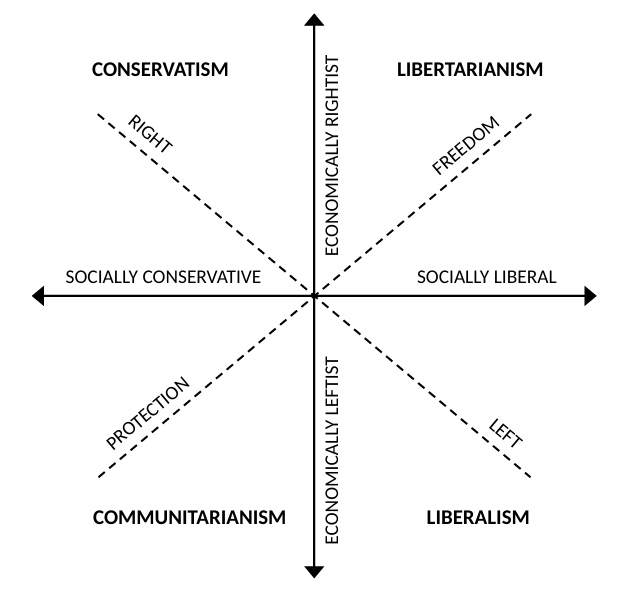
The MIDI model (Malka & Soto 2015) posits that three interacting variables shape the political opinions of ordinary citizens:

• Need for security and certainty (NSC). The internal motivation to avoid risk and maintain stability, coupled with a preference for unambiguous and definitive ideas, as opposed to embracing uncertainty, change, ambiguity, and doubt (Malka et al. 2014).
• Political discourse. The ongoing discussion of political issues in a society. A society’s political discourse validates a limited menu of ideologies put together by political, intellectual, and economic elites. These ideological menus reach the masses through the media and spread through social networks (Converse 1964; Malka et al. 2014).
• Political engagement. The degree to which a citizen pays attention to discourse and participates in politics, whether by following the news, voting, talking to others, or engaging in activism (Converse 1964).

According to the MIDI model, ordinary citizens form their political opinions in two steps

• Step 1. Individuals adopt congruent ideologies. High-NSC individuals value order, stability, and protection, so they adopt socially conservative and economically leftist attitudes — they become communitarians. Low-NSC individuals value autonomy over security, so they adopt socially liberal and economically rightist attitudes — they become libertarians.
• Step 2. When exposed to an ideological menu limited to conservatism and liberalism, politically engaged individuals experience cognitive dissonance. They resolve it by reversing their economic attitudes: Communitarians shift right and become conservatives; libertarians shift left and become liberals. However, in countries where communitarianism and libertarianism are on the menu, politically engaged individuals maintain their original attitudes.

The two-step process makes the following predictions about issue alignments in mass publics

1. In countries where the ideological menu includes only conservatism and liberalism, highly engaged citizens will be conservatives if high in NSC and liberals if low in NSC. Conversely, the least politically engaged citizens will be communitarians or libertarians.
2. In countries where the menu includes communitarianism and libertarianism, all citizens (regardless of their level of engagement) will be communitarians or libertarians.

Table 1 summarizes the predictions of the two-step process.

Table 1: Predictions of the MIDI model given different ideological menus

	Conservatism & liberalism only		Communitarianism & libertarianism included
	High engagement	Low engagement	High engagement	Low engagement
High NSC	Conservative	Communitarian	Communitarian	Communitarian
Low NSC	Liberal	Libertarian	Libertarian	Libertarian

The MIDI model is supported by cross-country survey data. In all countries, high levels of NSC reliably predict socially conservative attitudes, but the association between NSC and economic attitudes is inconsistent. Generally, the association is weak or negative, with specific exceptions: In countries where discourse strongly associates social conservatism with economic rightism, high levels of NSC predict rightist economic attitudes — but only among highly politically engaged citizens. Typically, these countries are developed, with strong democratic institutions, and culturally progressive (Costello et al. 2023; Malka et al. 2014, 2019).

We formalize and extend the MIDI model by embedding its assumptions in an opinion dynamics ABM. The ABM addresses two limitations of the MIDI model. One limitation is theoretical: The MIDI model does not specify how political information spreads from person to person. Instead, the model assumes that ordinary citizens know and choose among the four broad ideologies. The other limitation is empirical: The MIDI model does not account for bipolarization — the hollowing out of the political center coupled with the dominance of extreme views (Carothers & O’Donohue 2019; Schweighofer, Schweitzer, et al. 2020; Somer & McCoy 2018).³

The agent population represents a mass public. Agents vary in their level of NSC, which is normally distributed. Positive values represent high NSC; negative values represent low NSC. In addition, agents hold mutable opinions in the two-dimensional space of Figure 1. An opinion consists of a social attitude and an economic attitude, each having a real value. In the social dimension, positive values are liberal and negative values are conservative, with higher values indicating more liberal and lower values indicating more conservative attitudes, respectively. In the economic dimension, positive values are rightist and negative values are leftist, with higher values indicating more rightist and lower values indicating more leftist attitudes, respectively.

Agents “feel” attitudes as having degrees of congruence. Congruence quantifies the correspondence between an agent’s NSC level and the attitude’s value. For agents with high NSC, congruence increases as social attitudes become more conservative and economic attitudes become more leftist. For agents with low NSC, congruence increases as social attitudes become more liberal and economic attitudes become more rightist.

Each period consists of three stages:

• Biased peer influence. Represents step 1 of the MIDI model. Agents form random pairs (there is neither homophily nor barriers to interaction). Within each pair, agents influence each other’s opinions, causing their attitudes to move closer together in the opinion space (there is no repulsive influence). Each agent updates its social and economic attitudes independently, with more NSC-congruent attitudes exerting greater attraction. A parameter uniform for all agents controls the strength of this congruence bias.
• Discursive influence. Represents step 2 of the MIDI model. The political discourse validates two ideologies as “internally consistent”: conservatism and liberalism. Agents respond by shifting their economic attitudes. Socially conservative agents move rightward, and socially liberal agents move leftward. A parameter uniform for all agents controls the strength of this discursive influence.
• Autonomous thinking. Agents’ attitudes are modified by random shocks that represent individual reasoning and intuition.

The discursive influence mechanism excludes the cases where the menu includes communitarianism and libertarianism because these cases are less interesting. In such cases, both congruence bias and discursive influence push agents toward communitarian and libertarian attitudes, which essentially amounts to deactivating discursive influence and proportionally increasing congruence bias.

Simulations yield two main results. First, the relative strengths of congruence bias and political engagement determine the emergent issue alignment (the sign of the correlation between attitudes). When congruence bias is stronger, the alignment is protection-freedom (positive correlation). When political engagement is stronger, the alignment is right-left (negative correlation). Second, bipolarization emerges if and only if congruence bias exceeds a threshold. While discursive influence does not cause bipolarization, it moderates the polarization threshold and the magnitude of opinion extremeness (the intermodal distance).

The paper proceeds as follows. Section 2 situates the ABM within the family of opinion dynamics models. Section 3 formally presents the ABM. Section 4 reports and analyzes the results. Section 5 explains how the biased peer influence mechanism can be used to model other theories in political psychology. Section 6 concludes.

Opinion Dynamics Models of Polarization and Hyperpolarization

The fundamental mechanism of all opinion dynamics models is assimilative influence: When agents interact, their opinions or beliefs converge. Acting alone, assimilative influence invariably leads a population to consensus, contradicting evidence (Abelson 1964; Berger 1981; DeGroot 1974).

Most opinion dynamics models test mechanisms that could lead to opinion clustering or polarization along a single dimension. The mechanisms that recur most often are homophily and repulsive influence. Homophily can take several forms: Agents converge only when their opinions are already close, or are more likely to interact with similar others, or are more influenced by similar others. This behavior creates a self-reinforcing dynamic in which similar agents become increasingly similar, while differences between groups persist or increase. In models with repulsive influence, agents with distant opinions move further apart rather than closer together. Repulsion increases opinion variance, which is needed for clustering and polarization (Flache et al. 2017; Liu et al. 2023).

Multidimensional models extend the analysis to cases in which individuals hold attitudes or beliefs on multiple issues. Researchers use these models to study opinion clustering, polarization, and the emergence of issue constraints and issue alignments. Issue constraint is the organization of attitudes or beliefs into packages, such as political ideologies or religions. Issue alignment is the statistical relationship among attitudes and beliefs regarding different issues — for example, abortion, guns, and taxes (Baldassarri & Gelman 2008). Of particular interest to modelers is hyperpolarization: the coincidence of issue alignment and polarization along two or more dimensions (Schweighofer, Schweitzer, et al. 2020).

Below we review representative multidimensional models that produce clustering, polarization, issue constraints, and/or issue alignments, depending on their parameterization. The review focuses on the proposed mechanisms rather than the models’ results.

Huet et al. (2008) build on theories of social judgment, balance, and self-categorization to model dissonance when individuals agree on one issue while disagreeing on another. Agents converge when their opinions are close on both dimensions and ignore each other when they are distant on both. When opinions are close on one dimension but distant on the other, agents resolve dissonance by diverging on their dimension of agreement. In a related model, Huet & Deffuant (2010) introduce a dimensional hierarchy: Agents who strongly disagree on the primary dimension diverge on the secondary dimension.

Flache & Mäs (2008) formalize group faultline theory. Agents have fixed demographic attributes and mutable opinions. They form a network and update their links’ valence based on their demographic and opinion similarity. These links mediate social influence: Positive links lead to assimilation, negative links to differentiation. Opinion dynamics and link updating reinforce each other, strengthening the alignment between opinions and demographic attributes.

Flache & Macy (2011) explore opinion dynamics in small-world networks. Agents develop positive or negative links with their neighbors based on opinion similarity. Link valence determines assimilation or differentiation. Long-range ties dampen opinion differentiation in models with only neutral and positive links, but amplify differentiation when negative links are possible.

Schweighofer, Garcia, et al. (2020) draw on cognitive and structural balance theories. They introduce an affective involvement parameter that controls agents’ resistance to influence and varies across agents. In the model’s most complex variant, agents measure angles between opinion vectors to decide whether others are “on the same side of issues”. Small angles lead to angular convergence, large angles to angular divergence. When affective involvement levels are high and vary widely, agents tend to align their opinions in space and polarize along that line.

Schweighofer, Schweitzer, et al. (2020) introduce the weight balance theory (WBT), extending Heider’s cognitive balance theory. Each agent observes a peer and forms positive or negative attitudes toward its peer based on opinion similarity. Agents’ attitudes are reinforced by an “evaluative extremeness” function, which represents the tendency to see the world in black and white. Agents move toward or away from their peers to increase the cognitive balance between attitudes and opinions (moving away to increase balance provides a novel psychological basis for the repulsion mechanism). The feedback between attitude formation and opinion updating, amplified by evaluative extremeness, can lead to polarization and issue alignment without built-in issue constraints. In a later paper, Schweighofer & Garcia (2024) refine the WBT model by including a continuous equanimity parameter that varies across agents. Its value modulates the agent’s responses to political agreement and disagreement.

Friedkin et al. (2016) extend belief updating models by incorporating cognitive consistency constraints. Each agent in a network holds a vector of mutable beliefs and a constraint matrix that specifies logical connections between beliefs. The constraint matrix can be uniform across the population or vary across subgroups. In the influence process, agents update their beliefs by weighing their neighbors’ beliefs against their own susceptibility to influence. After updating, each agent recalibrates its belief system to maintain logical consistency.

Baumann et al. (2021) observe that the same argument can support beliefs about multiple issues. They represent argument overlap using a non-orthogonal opinion space. Drawing on group polarization theory, they assume homophily and radicalization: When in relative agreement, agents adopt more extreme positions. Influence spills over from one issue to related issues in inverse proportion to the angle between dimensions. Results include global consensus, multipolarization, and bipolarization.

All the above multidimensional models, as well as our ABM, build on Converse’s (1964) theory of belief systems. Converse defined a belief system as a “configuration of ideas and attitudes in which the elements are bound together by some form of constraint or functional interdependence.” He identified three sources of constraint: logical, psychological, and social.

Logical sources of constraint force a set of beliefs to be internally consistent (logical constraints are rare and more prevalent among educated elites). Psychological constraints glue together unrelated or contradictory ideas through quasi-logical arguments, usually appealing to higher values (e.g., social justice or natural law). Friedkin et al.’s (2016) constraint matrix and Baumann et al.’s (2021) argument overlap are psychological sources of constraint. The biased peer influence mechanism we propose also creates a psychological constraint: Each agent is drawn to social and economic attitudes of the same sign because they satisfy the same need, not because they are intrinsically connected.

Converse distinguished between primary and secondary social sources of constraint. He noted that “certain postures tend to co-occur and that this co-occurrence has obvious roots in the configuration of interests and information that characterize particular niches in the social structure.” All multidimensional models of opinion dynamics, including our ABM, capture some aspect of the primary social source: from assimilative influence to complex social structures. The secondary social source of constraint is the menu of “internally consistent” ideologies created and disseminated by elites. To our knowledge, our ABM is the first to incorporate the secondary social source.

Political psychologists have proposed that the observed alignment between social and economic attitudes is a spurious correlation caused by a latent trait: the need for security and certainty (Malka & Soto 2015), also known as need to manage uncertainty and threats (Jost et al. 2007) or psychological rigidity (Tetlock 1983). The exact composition of NSC is unknown, but possible ingredients include rigid thinking styles, motivational rigidity, cognitive inflexibility, and dogmatism (Costello et al. 2023). Two prominent theories in this field are the MIDI model (Malka & Soto 2015) and the rigidity of the right hypothesis (Azevedo et al. 2019; Tetlock 1983).

Our ABM embeds this latent trait effect in the peer influence mechanism. The mechanism is biased but purely assimilative: Agents are attracted to both NSC-congruent and NSC-incongruent attitudes, although more congruent attitudes exert a stronger attraction. In addition, the ABM introduces a second source of constraint: discursive influence, which promotes a right-left correlation between social and economic attitudes. Like this ABM, previous models have assumed underlying links between different issues, notably Friedkin et al. (2016) and Baumann et al. (2021).

A useful characteristic of this ABM is that it excludes the following mechanisms: homophily, repulsion, radicalization, argumentation, network structures, and cognitive biases, except for congruence bias and the dissonance of holding “internally inconsistent” ideologies. This allows us to establish that biased peer influence and discursive influence alone cause the ABM’s main result: hyperpolarization in a two-dimensional opinion space.

The Agent-Based Model

Agents

Agents represent a mass public and are indexed by \(i = 1, 2, 3, \ldots, n\). Agent \(i\)’s NSC level, denoted by \(nsc_i\), remains constant throughout a simulation and follows a normal distribution with mean zero and standard deviation \(\sigma > 0\). Agents with \(nsc > 0\) (high NSC) represent people who prefer predictability, stability, and security, while agents with \(nsc < 0\) (low NSC) represent people who prefer novelty, change, and freedom. The value \(|nsc_i|\) measures the intensity of the agent’s NSC.

Agent \(i\)’s opinion at the beginning of period \(t\) is denoted by \(\mathbf{o}_{it} = (s_{it}, e_{it})\), where \(s_{it}\) represents the agent’s social attitude and \(e_{it}\) represents the agent’s economic attitude. If \(s_{it} > 0\), agent \(i\) is socially liberal; if \(s_{it} < 0\), it is socially conservative. Likewise, if \(e_{it} > 0\), agent \(i\) is economically rightist; if \(e_{it} < 0\), it is economically leftist. In the rare case that \(s_{it}\) or \(e_{it}\) is zero, the agent is centrist in that dimension.

Opinions change from period to period through three mechanisms: biased peer influence, discursive influence, and autonomous thinking. The peer influence mechanism corresponds to step 1 of the MIDI model’s two-step process, in which individuals adopt NSC-congruent attitudes. The discursive influence mechanism corresponds to step 2, in which individuals align their economic attitudes with an “internally consistent” ideology (conservative or liberal) while maintaining their social attitudes. The autonomous thinking mechanism represents non-social factors (such as intuition or reasoning) that can change a person’s political opinions.

Variables of interest

We focus on two macroscopic variables: issue correlation and opinion extremeness. Issue correlation is the Pearson correlation coefficient between agents’ social and economic attitudes. Opinion extremeness depends on the modality of the opinion distribution. For unimodal distributions, extremeness is zero; for bimodal distributions, extremeness is the intermodal distance. Other cases are irrelevant, as simulations consistently yield unimodal or bimodal steady-state distributions.

Congruence

An agent can “feel” an attitude as congruent or incongruent. The following function quantifies an agent’s feelings of congruence, given its NSC level:

\[\begin{aligned} C(nsc, z) = -nsc\,z \end{aligned}\]

\[(1)\]

where \(nsc\) is an NSC level and \(z\) is a social or economic attitude. A positive value of \(C(nsc,z)\) indicates congruence; a negative value indicates incongruence; a value of zero indicates neutrality.

The congruence function captures the link between NSC and political attitudes described in the MIDI model. High NSC levels (\(nsc > 0\)) are congruent with socially conservative (\(s < 0\)) and economically leftist (\(e < 0\)) attitudes, while low NSC levels (\(nsc < 0\)) are congruent with socially liberal (\(s > 0\)) and economically rightist (\(e > 0\)) attitudes. The strength of these “feelings of congruence” depends on NSC intensity and attitude extremeness. Agents with intense NSC (high \(|nsc|\)) experience stronger feelings of congruence than those with mild NSC (low \(|nsc|\)). Similarly, extreme attitudes (high \(|z|\)) evoke stronger feelings of congruence than moderate ones (low \(|z|\)) for a given NSC level.

Biased peer influence mechanism

Agents are randomly paired and communicate with each other. Let \((i, j)\) denote a pair of agents. Agent \(i\) updates its attitudes using the following peer influence rules:

\[ s'_{it} = s_{it} + A(nsc_i, s_{it}, s_{jt})\,(s_{jt} - s_{it}) \]	(2)
\[ e'_{it} = e_{it} + A(nsc_i, e_{it}, e_{jt})\,(e_{jt} - e_{it}) \]	(3)

where \(s_{it}\) and \(e_{it}\) are the agents’ current attitudes and \(s'_{it}\) and \(e'_{it}\) are its attitudes after peer influence. The attraction function \(A(nsc,x,y)\) measures the attractiveness of the alternative attitude \(y\) relative to the agent’s attitude \(x\), given the agent’s NSC level. In general, the attraction function takes different values in the Equations 2 and 3. Consequently, agents change their two attitudes to different extents.

Let \(x\) be an agent’s attitude and \(y\) its partner’s attitude, both of the same type (social or economic). The attraction function is

\[\begin{aligned} A(nsc,x,y)= \frac{2^{-1}\exp(B(x)\,C(nsc,y))}{\exp(B(x)\,C(nsc,x)) + \exp(B(x)\,C(nsc,y))} \end{aligned}\]

\[(4)\]

Here \(C(nsc,x)\) and \(C(nsc,y)\) are the attitudes’ congruence values, and \(B\) is the congruence bias function. By construction, function \(A\) takes values in the interval \((0,1/2)\).

The congruence bias function is defined as follows:

\[\begin{aligned} B(x)= \beta\,|x|^{-1} \end{aligned}\]

\[(5)\]

where \(\beta \geq 0\) is a parameter equal for all agents and \(|x|\) measures the extremeness of the agent’s current attitude. Random variations ensure that \(|x|\) never equals zero, guaranteeing that \(B\) is well defined. By construction, function \(A\) takes values in the open interval \((0,1/2)\). Increasing \(\beta\) increases the congruence bias for all values of \(x \neq 0\) (see Equation 5). Conversely, increasing \(|x|\) reduces the bias for all values of \(\beta > 0\). Economists would call this property “diminishing marginal returns to extremism.” At the limit where \(|x|\) tends to infinity, peer influence becomes unbiased.

The influence rules in Equations 2 and 3 can be expressed concisely as

\[\begin{aligned} x' = (1 - A)\,x + A\,y \end{aligned}\]

\[(6)\]

where \(x\) and \(x'\) are the agent’s current and updated attitudes, \(y\) is its partner’s current attitude, and \(A\) is the attractiveness of \(y\) (the three attitudes are of the same type). The equation shows that the updated attitude is a weighted average of the agent’s current attitude and its partner’s current attitude. The term \(1 - A\) represents the agent’s attraction to its current attitude. Since \(A < 1/2\) by construction, the agent’s updated attitude will always be closer to its current attitude than to its partner’s current attitude. Since \(A > 0\), there is no repulsion.

Consider the limiting case where \(\beta = 0\). Substituting \(\beta = 0\) into Equation 5 yields \(B(x) = 0\) for all \(x\). In turn, substituting \(B(x) = 0\) into Equation 4 yields \(A(nsc,x,y) = 1/4\) for all \(nsc\), \(x\), and \(y\). Therefore, when \(\beta = 0\), all alternative attitudes are equally attractive. In other words, peer influence is unbiased.

In the non-trivial case where \(\beta > 0\), agents respond coherently to changes in congruence values and congruence bias. To see how, we rewrite the attraction function in terms of these quantities:

\[\begin{aligned} A(c_x,c_y,b) = \frac{2^{-1}\exp(b\, c_y)}{\exp(b\,c_x) + \exp(b\, c_y)} \end{aligned}\]

\[(7)\]

where \(c_x\) and \(c_y\) are the congruence values of the agent’s attitude and its partner’s attitude, and \(b\) is the agent’s congruence bias. It is straightforward that the attractiveness of \(y\) increases with \(c_y\) and decreases with \(c_x\). The effect of the bias on attractiveness, however, can be positive or negative. Taking the derivative of \(A\) with respect to \(b\), we get

\[\begin{aligned} \frac{\partial{A}}{\partial{b}} = (c_y - c_x)\,A\,(1 - 2A) \end{aligned}\]

\[(8)\]

This derivative is positive if \(y\) is the most congruent attitude (\(c_y > c_x\)) and negative if \(y\) is the least congruent attitude (\(c_y < c_x\)). It follows that a higher congruence bias makes the most congruent of the two attitudes more attractive.

An essential property of an attraction function is unit invariance: The attraction value must be independent of the units in which attitudes are measured. Unit invariance is essential for model realism because political attitudes are measured on ordinal scales (typically from strongly disagree to strongly agree) that are unrelated to objective physical properties. Thus, changing attitude units should not affect agent behavior.

To prove unit invariance, we substitute the congruence function (Equation 1) and the bias function (Equation 5) into the definition of the attraction function (Equation 4) and rearrange terms:

\[\begin{aligned} A(nsc,x,y)= \frac{2^{-1}}{1 + \exp(\beta\, nsc \, \mathrm{sign}(x)(y/x - 1))} \end{aligned}\]

\[(9)\]

Dividing \(y\) by \(x\) cancels their units, so the function’s value is independent of the units used to measure attitudes.

Discursive influence mechanism

After communicating, agents are influenced by political discourse: an exogenous force that instructs agents to align with the ideal right-left axis defined by \(e = -s\) (depicted in Figure 1). Agents respond to this instruction by adjusting their economic attitudes while maintaining their social attitudes.

Agent \(i\) follows these rules:

\[ s''_{it} = s'_{it} \]	(10)
\[ e''_{it} = e'_{it} + \frac{\delta}{2}\, (-s'_{it} - e'_{it}) \]	(11)

where \(s'_{it}\) and \(e'_{it}\) are the agent’s attitudes after peer influence, \(s''_{it}\) and \(e''_{it}\) are its attitudes after discursive influence, and \(\delta \in [0, 1]\) is a parameter equal for all agents. This parameter represents the average political engagement of a mass public. In Equation 11, \(\delta\) is halved to equalize the scales of discursive and peer influences, since attraction values are all less than \(1/2\) (see Equation 4).

Autonomous thinking

We model autonomous thinking as random shocks or ‘innovations.’ These affect attitudes as follows:

\[ s'''_{it} = s''_{it} + u_{it} \]	(12)
\[ e'''_{it} = e''_{it} + v_{it} \]	(13)

where \(s'''_{it}\) and \(e'''_{it}\) are the updated attitudes, and \(u_{it}\) and \(v_{it}\) are normally distributed innovations with mean zero and standard deviation \(\tau > 0\).

Innovations serve three functions. First, innovations kick-start the model by creating opinion variance. Second, their constant influx counteracts the assimilative pull of peer influence, which would otherwise collapse all agents’ opinions into a single point. Third, innovations introduce “new ideas” that evolve through the peer and discursive influence mechanisms. These mechanisms shape the opinion distribution into emergent patterns.

In the autonomous thinking rules, innovations are additive and thus share the units of attitudes (see Equations 12 and 13). Changing the value of \(\tau\) is the same as changing these units: It rescales the opinion distribution without deforming it. Extremeness changes proportionally with \(\tau\), while issue correlation remains constant.

Recentering

When agents update their opinions, the center of the distribution moves slightly. To offset this movement, agents’ opinions are recentered:

\[ s_{i(t+1)} = s'''_{it} - \mathrm{mean}(s'''_{it}) \]	(14)
\[ e_{i(t+1)} = e'''_{it} - \mathrm{mean}(e'''_{it}) \]	(15)

Results

Convergence detection

Simulations run for an unspecified number of periods. To detect convergence, we use Gelman and Shirley’s heuristic (Gelman & Shirley 2011). For each parameter combination, we run three concurrent simulations with different initial configurations: One simulation starts with all agents at the origin of the opinion space. Two simulations start with agents’ attitudes drawn independently from \(\mathrm{N}(0,10\tau)\), where \(\tau\) is the standard deviation of innovations. After a 3000-period burn-in, we monitor three statistics over a rolling time window: issue correlation and opinion extremeness (the variables of interest), and the standardized generalized variance of the opinion distribution. Together, these statistics provide a coarse-grained description of the shape of the opinion distribution: Issue correlation indicates orientation, standardized generalized variance measures dispersion, and opinion extremeness provides the intermodal distance (zero if the distribution is unimodal). As the simulation progresses, the window expands to cover from the midpoint to the most recent period. The simulations terminate when the potential scale reduction factor for the three variables reaches \(1.01\).

To estimate the steady-state values of both variables of interest, we use data from the combined second halves of the three simulations. For issue correlation, we take the mean across all observations. For opinion extremeness, we use the median — a better estimate of central tendency when variables are non-negative and can have significant mass at zero.

Steady-state equilibria

Figure 2 shows snapshots of the final state of several simulations. Each simulation was run with a unique combination of congruence bias (\(\beta\)) and political engagement (\(\delta\)). For \(\beta\), we used 0 (no bias), 0.5 (low bias), 1 (medium bias), and 1.5 (high bias). For \(\delta\), we used 0 (no engagement), 0.33 (low engagement), 0.67 (high engagement), and 1 (full engagement). The simulations reveal five types of steady-state equilibria:

• Type 0 No issue alignment or polarization occurs when bias is zero and agents are politically disengaged (panel 1A).
• Type 1 A protection-freedom alignment without polarization emerges when bias is low and agents are politically disengaged (panel 1B).
• Type 2 Bipolarization emerges with a protection-freedom alignment when bias is medium or high and agents are politically disengaged (panels 1C-1D).
• Type 3 A right-left alignment emerges without polarization when bias ranges from zero to medium and agents are politically engaged (panels 2A-2C, 3A-3C, 4A-4C).
• Type 4 Bipolarization emerges with a right-left alignment when bias is high and agents are politically engaged (panels 2D, 3D, 4D).

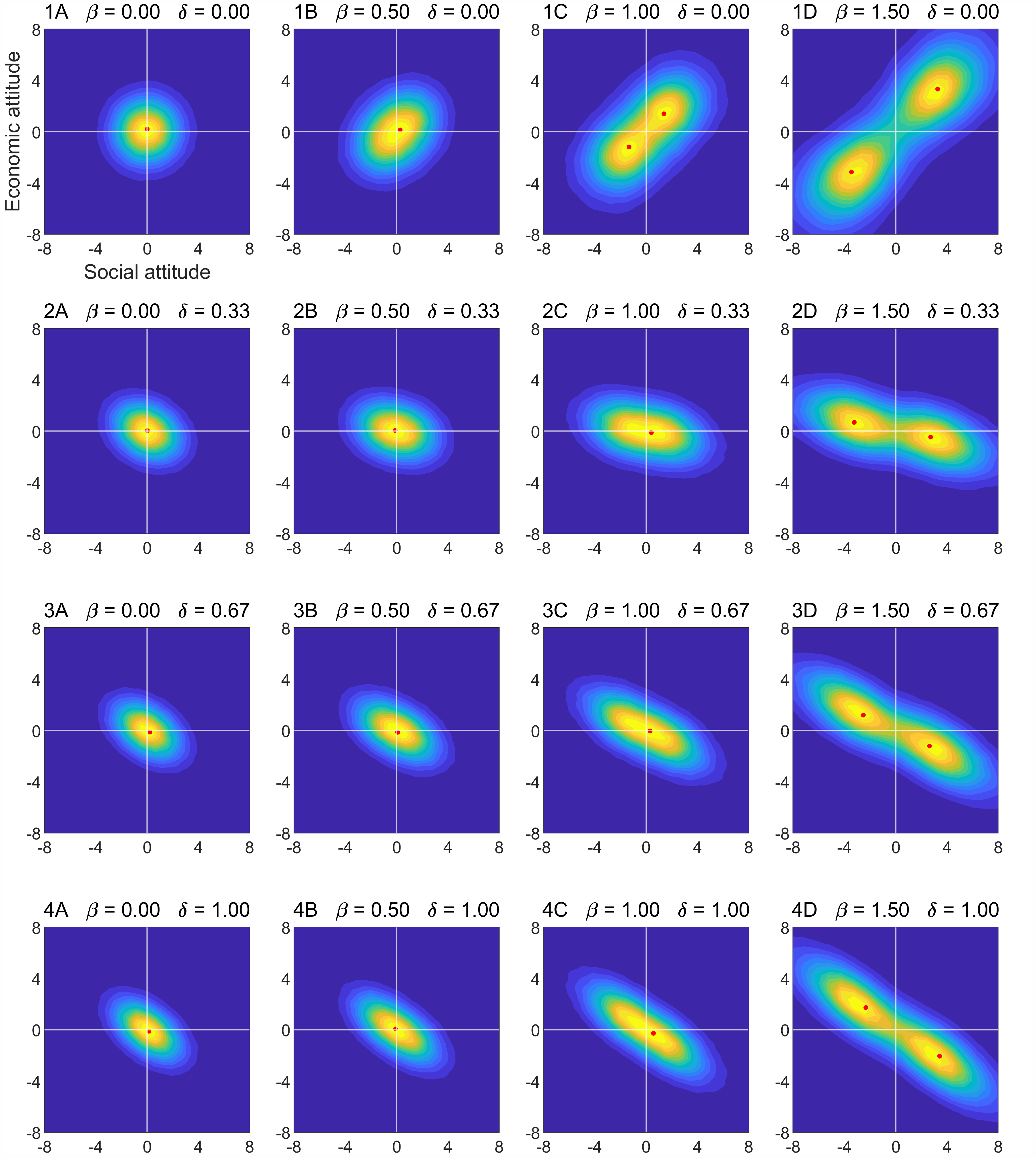
The analysis identifies three effects of the model’s main parameters. First, increasing political engagement rotates the alignment from protection-freedom to right-left. Second, opinions polarize at medium or high levels of congruence bias, whether agents are politically engaged or not. Third, opinion extremeness (the intermodal distance) increases with congruence bias.

Sensitivity analysis

Figure 3 details how congruence bias and political engagement determine the system’s emergent properties. Panels A and B present sensitivity analyses for issue correlation and opinion extremeness, while Panel C maps equilibrium types across the parameter space.

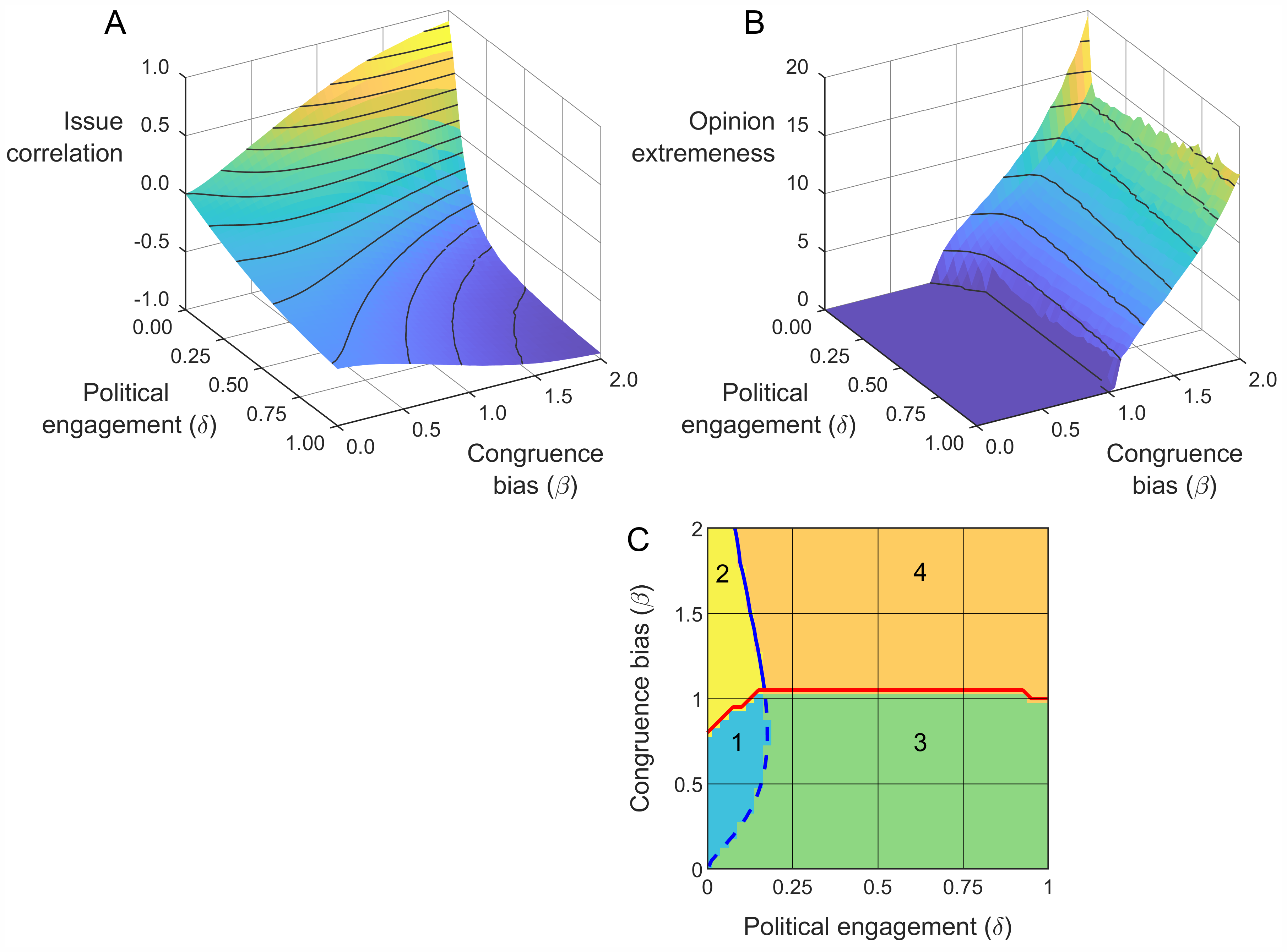
The biased peer influence mechanism and the discursive influence mechanism work in opposition. Increasing congruence bias (\(\beta\)) drives issue correlation toward positive values, while increasing political engagement (\(\delta\)) drives issue correlation toward negative values. When \(\beta\) is high relative to \(\delta\), peer influence dominates and the resulting alignment is protection-freedom. Otherwise, discursive influence dominates and the alignment is right-left.

Biased peer influence alone causes bipolarization: Opinion extremeness appears when \(\beta\) exceeds a threshold. Discursive influence affects this thresholdthe threshold first increases with political engagement \(\delta\) and then plateaus. When \(\beta\) exceeds the threshold, increasing \(\beta\) steadily increases opinion extremeness. Political engagement moderates this effectincreasing \(\delta\) reduces extremeness when \(\delta\) is low.

The mechanics of bipolarization

To understand how bipolarization emerges in this ABM, it is helpful to disentangle peer influence from discursive influence. The results show that peer influence alone causes bipolarization, so studying both influences simultaneously would complicate the analysis unnecessarily. Given that social attitudes (unlike economic attitudes) are not affected by discourse, we will focus on the social dimension of the opinion space.

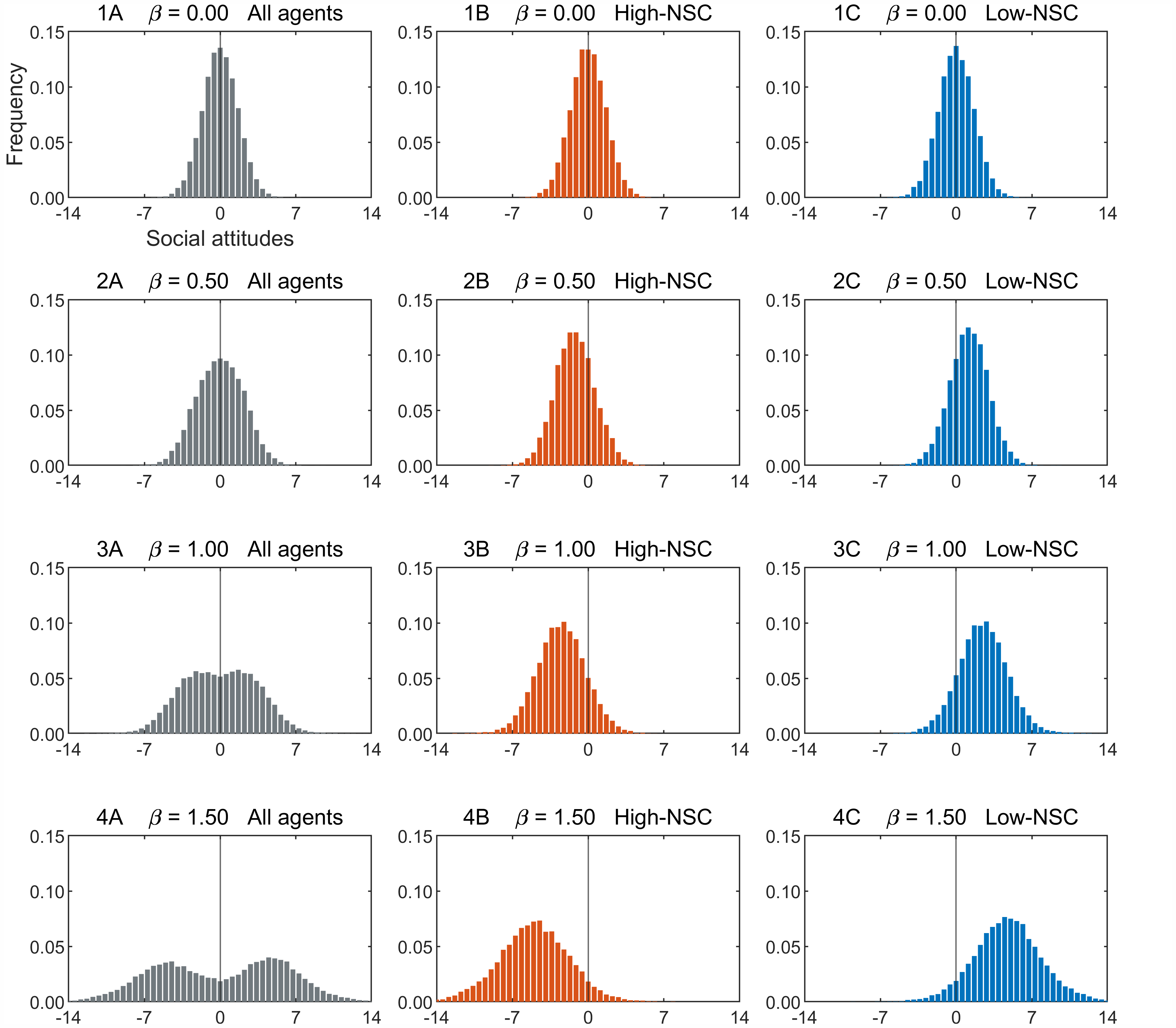
Figure 4 shows the steady-state distribution of social attitudes in simulations with increasing levels of congruence bias (column A). The figure also shows the attitude distributions of two subgroups: high-NSC agents (column B) and low-NSC agents (column C). Both distributions are unimodal, regardless of the level of bias. When peer influence is unbiased (\(\beta = 0\)), high-NSC and low-NSC agents have identical attitude distributions, resulting in a unimodal population distribution. No polarization occurs in this case. As bias increases, the distributions separate: High-NSC agents shift toward the conservative side, low-NSC agents shift toward the liberal side. At low bias levels (\(\beta = 0.5\)), the distributions remain close enough to maintain significant overlap, keeping the population distribution unimodal. Again, no polarization occurs. But at medium or high bias levels (\(\beta = 1, 1.5\)), the two distributions move far apart, so they have little overlap. The population distribution becomes bimodal, and bipolarization emerges.

System dynamics and steady state

The opinion distribution converges to the same stable shape regardless of the agents’ initial opinions. The specific shape — unimodal or bimodal, with positive or negative issue correlationdepends on the agents’ congruence bias (\(\beta\)) and political engagement (\(\delta\)), as shown in Figure 2. The system never diverges, nor does it exhibit path dependencies, or become trapped in unstable equilibria. Several properties of this ABM contribute to its predictable dynamics:

• Markovian property. All mechanisms governing agent behavior — biased peer influence, discursive influence, autonomous thinking, and recentering — are independent of time. This means that agents lack memory: Their behavior depends only on their current situation, not on their history.
• Irreducibility. Agents can traverse the entire opinion space. Normally distributed innovations keep agents moving in all directions. The other three mechanisms make some trajectories more likely, but do not create barriers in the space.
• Aperiodicity. Since agents are constantly shaken by normally distributed innovations, their movement never locks into cycles.
• Non-evanescence. Agents may venture far from the origin, but three forces quickly pull them back: recentering, assimilative influence, and diminishing returns to extremeness (congruence bias tends to zero as attitudes become more extreme).

In summary, the ABM is a continuous state Markov process that is irreducible, aperiodic, and non-evanescent. It follows that the process has a unique steady state. Although agents never stop moving, the opinion distribution maintains its shape (except for small fluctuations) as their movements cancel each other outlike molecules in a gas maintaining stable macroscopic properties. The ABM is also ergodic: Any long simulation equally represents the system’s behavior, and its time averages equal its ensemble averages.⁴ This heuristic proof of the ABM’s properties is supported by numerous simulations. For a formal treatment of Markov processes with continuous state spaces, see Brémaud (2020).

Other Applications of the Biased Peer Influence Mechanism

The MIDI model is not the only theory that posits that the alignment between social and economic attitudes is a spurious correlation caused by a latent trait. Two other theories share this premise: the rigidity of the right hypothesis (RRH) and the conflict of visions hypothesis (COVH). The RRH, like the MIDI model, identifies NSC as the latent trait. The COVH posits a different latent trait: a vision of human nature as tragic or utopian. The biased peer influence mechanism can be used to model both theories.

Like the MIDI model, the RRH predicts a positive association between high NSC and social conservatism, but the theories make opposite predictions about economic attitudes. According to the RRH, people with high NSC are economically rightist because they justify established social hierarchies and see risks in tinkering with capitalist institutions. People with low NSC, by contrast, are economically leftist, as they value equality and see caution as an obstacle to progress.

According to the COVH, individuals with a tragic vision tend to be socially conservative. They view traditional institutions as time-tested safeguards against human moral failings. They also gravitate toward economic rightism, convinced that the invisible hand can harness greed for the benefit of society. By contrast, those with a utopian vision are socially liberal, as they are confident that inherent human goodness will ensure social harmony. Utopians are drawn to economic leftism because they think the state can maximize wealth and distribute it equitably.

Unlike the MIDI model, both the RRH and the COVH predict that individuals are naturally conservative or liberal, not communitarian or libertarian. Nevertheless, the biased peer influence mechanism can be adapted to model both theories. Let \(l\) represent a latent trait, which can be NSC or a vision of human nature, depending on the hypothesis. Agents with \(l > 0\) have a tragic vision or score high on NSC, and thus feel socially conservative and economically rightist attitudes as congruent. Conversely, agents with \(l < 0\) have a utopian vision or score low on NSC, and thus feel socially liberal and economically leftist attitudes as congruent. These tendencies can be represented by changing one sign in the congruence function:

\[ \begin{align} C(l, z) = \left\{ \begin{aligned} & l\,z && \text{if $z$ is a social attitude} \\ & -l\,z && \text{if $z$ is an economic attitude} \end{aligned} \right. \end{align} \]

\[(16)\]

The other components of the peer influence mechanism do not require modification: Random pairing, the peer influence rules (Equations 2 and 3), and the congruence bias function (Equation 5) stay as defined.

Conclusion

This ABM introduces two novel mechanisms to the opinion dynamics modeling toolkit: biased peer influence and discursive influence. The biased peer influence mechanism formalizes how latent traits predispose individuals to adopt particular attitudes on seemingly unrelated issues. In this ABM, this latent trait represents the need for security and certainty, and the unrelated issues are society and the economy. The discursive influence mechanism captures the tension between individual tendencies, socially acquired beliefs, and indoctrination. In this ABM, discourse prompts agents to align their economic attitudes’ signs with their social attitudes.

This ABM achieves both issue alignment and bipolarization without relying on previously studied mechanisms such as homophily, repulsion, radicalization, network structures, and cognitive biases, except for congruence bias and the dissonance of holding “internally inconsistent” ideologies. No explicit polarizing forces are built into the model: Bipolarization emerges under purely assimilative influence. Issue alignment arises from the competition between the biased peer influence mechanism and the discursive influence mechanism.

The list of political issues debated in a society at any given time is vast (Heywood 2021), while this ABM reduces the dimensions of opinion to society and the economy. This dimensional reduction allows us to focus on the causal links between individual differences and the enduring themes that make concepts like ‘right’ and ‘left’ meaningful throughout history. But when we zoom in on the four broad ideologies, complexities become apparent.

Some issues remain perennially divisive (capital punishment, price controls). Disruptive technologies enter the political debate (the contraceptive pill, mechanized looms). Practical issues become ideological (vaccination, nuclear power). Consensus is reached on non-negotiable policies (women’s suffrage, occupational safety standards). Hot-button issues become obsolete (the telegraph monopoly, the horse manure crisis of the late 19th century). And some attitudes keep switching sides (nationalism, protectionism). A highly abstract and ergodic ABM like this one is not designed to account for such events. Other models, drawing on different psychological theories, can address the historical trajectories of ideologies (see Section 2).

One limitation of this ABM is that it treats political discourse as an exogenous force. The model could be extended to endogenize discourse. In the extended model, the population of agents is divided into an elite and a mass public. Peer influence occurs exclusively within each social group, while the two groups exert discursive influence on each other. Plausibly, the elite discourse is more influential than the public discourse. Suppose a divisive opinion shock affects the agents representing the public (the shock simulates, for example, a minor change in school curricula). This shock increases public opinion variance without causing bipolarization. But a feedback loop of discursive influence between the mass public and the elite could amplify the effects of the shock, ultimately leading to bipolarization in both social groups.

Finally, this ABM confirms the value of modeling social dynamics for political psychology theories. Simulations activate a web of causal pathways that non-computational theories inevitably miss. The results of this ABM are a case in point: When embedded in an otherwise standard ABM, the MIDI model predicts both issue alignments and bipolarization.

References

ABELSON, R. P. (1964). Mathematical models of the distribution of attitudes under controversy. In N. Fredericksen & H. Gulliksen (Eds.), Contributions to Mathematical Psychology (pp. 141–160). New York, NY: Holt, Rinehart & Winston.

AZEVEDO, F., Jost, J. T., Rothmund, T., & Sterling, J. (2019). Neoliberal ideology and the justification of inequality in capitalist societies: Why social and economic dimensions of ideology are intertwined. Journal of Social Issues, 75(1), 49–88. [doi:10.1111/josi.12310]

BALDASSARRI, D., & Gelman, A. (2008). Partisans without constraint: Political polarization and trends in american public opinion. American Journal of Sociology, 114(2), 408–446. [doi:10.1086/590649]

BAUMANN, F., Lorenz-Spreen, P., Sokolov, I. M., & Starnini, M. (2021). Emergence of polarized ideological opinions in multidimensional topic spaces. Physical Review X, 11(1), 011012. [doi:10.1103/physrevx.11.011012]

BERGER, R. L. (1981). A necessary and sufficient condition for reaching a consensus using DeGroot’s method. Journal of the American Statistical Association, 76(374), 415–418. [doi:10.1080/01621459.1981.10477662]

BOTEV, Z. I., Grotowski, J. F., & Kroese, D. P. (2010). Kernel density estimation via diffusion. The Annals of Statistics, 38(5), 2916–2957. [doi:10.1214/10-aos799]

BRAMSON, A., Grim, P., Singer, D. J., Berger, W. J., Sack, G., Fisher, S., Flocken, C., & Holman, B. (2017). Understanding polarization: Meanings, measures, and model evaluation. Philosophy of Science, 84(1), 115–159. [doi:10.1086/688938]

BRÉMAUD, P. (2020). Markov chains: Gibbs fields, Monte Carlo simulation and queues. Cham: Springer.

CAROTHERS, T., & O’Donohue, A. (2019). Democracies Divided: The Global Challenge of Political Polarization. Washington, D.C.: Brookings Institution Press.

CONVERSE, P. E. (1964). The nature of belief systems in mass publics. Critical Review, 18(1-3), 1–74. [doi:10.1080/08913810608443650]

COSTELLO, T. H., Bowes, S. M., Baldwin, M. W., Malka, A., & Tasimi, A. (2023). Revisiting the rigidity-of-the-right hypothesis: A meta-analytic review. Journal of Personality and Social Psychology, 124(5), 1025–1052. [doi:10.1037/pspp0000446]

DEGROOT, M. H. (1974). Reaching a consensus. Journal of the American Statistical Association, 69(345), 118–121. [doi:10.1080/01621459.1974.10480137]

FELDMAN, S., & Johnston, C. (2014). Understanding the determinants of political ideology: Implications of structural complexity. Political Psychology, 35(3), 337–358. [doi:10.1111/pops.12055]

FLACHE, A., & Macy, M. W. (2011). Small worlds and cultural polarization. The Journal of Mathematical Sociology, 35(1–3), 146–176. [doi:10.1080/0022250x.2010.532261]

FLACHE, A., & Mäs, M. (2008). Why do faultlines matter? A computational model of how strong demographic faultlines undermine team cohesion. Simulation Modelling Practice and Theory, 16(2), 175–191. [doi:10.1016/j.simpat.2007.11.020]

FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2. [doi:10.18564/jasss.3521]

FRIEDKIN, N. E., Proskurnikov, A. V., Tempo, R., & Parsegov, S. E. (2016). Network science on belief system dynamics under logic constraints. Science, 354(6310), 321–326. [doi:10.1126/science.aag2624]

GELMAN, A., & Shirley, K. (2011). Inference from simulations and monitoring convergence. In S. Brooks, A. Gelman, G. Jones, & X.-L. Meng (Eds.), Handbook of Markov Chain Monte Carlo (pp. 163–174). New York, NY: Chapman; Hall/CRC. [doi:10.1201/b10905-7]

HEYWOOD, A. (2021). Political Ideologies: An Introduction. London: Red Globe Press.

HUET, S., & Deffuant, G. (2010). Openness leads to opinion stability and narrowness to volatility. Advances in Complex Systems, 13(3), 405–423. [doi:10.1142/s0219525910002633]

HUET, S., Deffuant, G., & Jager, W. (2008). A rejection mechanism in 2D bounded confidence provides more conformity. Advances in Complex Systems, 11(4), 529–549. [doi:10.1142/s0219525908001799]

JANDA, K., Berry, J. M., Goldman, J., Deborah, D., & Manna, P. (2020). The Challenge of Democracy: American Government in Global Politics. Boston, MA: Cengage Learning.

JOST, J. T., Napier, J. L., Thorisdottir, H., Gosling, S. D., Palfai, T. P., & Ostafin, B. (2007). Are needs to manage uncertainty and threat associated with political conservatism or ideological extremity? Personality and Social Psychology Bulletin, 33(7), 989–1007. [doi:10.1177/0146167207301028]

KNIGHT, K. (1999). Liberalism and conservatism. In J. P. Robinson, P. R. Shaver, & L. S. Wrightsman (Eds.), Measures of Political Attitudes (pp. 59–158). San Diego, CA: Academic Press.

LIU, S., Mäs, M., Xia, H., & Flache, A. (2023). Job done? future modeling challenges after 20 years of work on bounded-Confidence models. Journal of Artificial Societies and Social Simulation, 26(4), 8. [doi:10.18564/jasss.5137]

MALKA, A., Lelkes, Y., & Soto, C. J. (2019). Are cultural and economic conservatism positively correlated? A large-scale cross-national test. British Journal of Political Science, 49(3), 1045–1069. [doi:10.1017/s0007123417000072]

MALKA, A., & Soto, C. J. (2015). Rigidity of the economic right? Menu-independent and menu-dependent influences of psychological dispositions on political attitudes. Current Directions in Psychological Science, 24(2), 137–142. [doi:10.1177/0963721414556340]

MALKA, A., Soto, C. J., Inzlicht, M., & Lelkes, Y. (2014). Do needs for security and certainty predict cultural and economic conservatism? a cross-national analysis. Journal of Personality and Social Psychology, 106(6), 1031–1051. [doi:10.1037/a0036170]

SCHWEIGHOFER, S., & Garcia, D. (2024). Raising the spectrum of polarization: Generating issue alignment with a weighted balance opinion dynamics model. Journal of Artificial Societies and Social Simulation, 27(1), 15. [doi:10.18564/jasss.5323]

SCHWEIGHOFER, S., Garcia, D., & Schweitzer, F. (2020). An agent-based model of multi-dimensional opinion dynamics and opinion alignment. Chaos, 30(9), 093139. [doi:10.31235/osf.io/mr6we]

SCHWEIGHOFER, S., Schweitzer, F., & Garcia, D. (2020). A weighted balance model of opinion hyperpolarization. Journal of Artificial Societies and Social Simulation, 23(3), 5. [doi:10.18564/jasss.4306]

SOMER, M., & McCoy, J. (2018). Déjà vu? Polarization and endangered democracies in the 21st century. American Behavioral Scientist, 62(1), 3–15. [doi:10.1177/0002764218760371]

SWEDLOW, B. (2008). Beyond liberal and conservative: Two-dimensional conceptions of ideology and the structure of political attitudes and values. Journal of Political Ideologies, 13(2), 157–180. [doi:10.1080/13569310802075969]

SWEDLOW, B., & Wyckoff, M. L. (2009). Value preferences and ideological structuring of attitudes in American public opinion. American Politics Research, 37(6), 1048–1087. [doi:10.1177/1532673x09333959]

TETLOCK, P. E. (1983). Cognitive style and political ideology. Journal of Personality and Social Psychology, 45(1), 118–126. [doi:10.1037//0022-3514.45.1.118]

TREIER, S., & Hillygus, D. S. (2009). The nature of political ideology in the contemporary electorate. Public Opinion Quarterly, 73(4), 679–703. [doi:10.1093/poq/nfp067]