Exploring the Influence of Open-Mindedness and Social Identity on Opinion Polarization in a Modified Hegselmann-Krause Model

, ,
and
aCenter for Advanced Preparedness and Threat Response Simulation, United States; bUniversity of West Bohemia, Czech Republic; cMichigan State University, United States; dThe Ohio State University, United States
*These authors contributed equally to this work
Journal of Artificial
Societies and Social Simulation 28 (3) 3
<https://www.jasss.org/28/3/3.html>
DOI: 10.18564/jasss.5661
Received: 09-May-2024 Accepted: 14-Apr-2025 Published: 30-Jun-2025
Abstract
In this article we further develop agent-based simulations on an extended Hegselmann-Krause (HK) model with social identity dynamics. In Kalvas et al. (2023) we introduced a model of opinion dynamics where agents were bounded in communication based on differences in opinion and identity, the latter of which was modeled as dynamic group assignments dependent on the state of the opinion space at any given time and the observer's sensitivity to opinion clustering. We had also previously presented regression results to demonstrate the effectiveness of identity as a polarizing factor. In this article we present an in-depth analysis of the macro-behavior of our model, specifically the effect on polarization of key variables such as open-mindedness (traditionally known as ε or uncertainty in the HK literature), and the granularity of social identity groups. We also examine the effect of the parameters of naturalistic distributions of these agent variables. We expand upon some known results in opinion dynamics such as the consensus-driving tendency of heterogeneity in ε, and also present results on how identity influences the relationship between openness and polarization.Introduction
Agent-Based Models (ABM’s) of opinion dynamics have typically assumed that social influence works only on an interpersonal basis. Even in models where agents take multiple other agents’ point of view into account at a given time, these views are treated independently of one another. Groups are usually treated as emerging from such independent interactions between pairs, but the effect of grouping itself is rarely if ever assumed to reciprocally influence an effect on opinion dynamics. In a way, the following quote from John C. Turner and colleagues (Turner et al. 1987 p. 24) on the dominant views among social psychologists of the mid-to-late 20th century also parallels the contemporary status quo of opinion dynamics models:
"\(\dots\)interdependence within a group has been studied as a relationship between\(\dots\) isolated persons, and intragroup relations have been assumed to be no different in kind from interpersonal relations, i.e., no theoretical distinction tends to be made between social relations conditioned by the unique individual characteristics of the interactors (which is what is meant here by ‘interpersonal’) and those based on their shared group memberships."
However, a key insight from social psychology developed over the past 50 years is that social influence cannot fully be explained from interpersonal interactions, and that the concepts of group membership, group identification, and in-group favoritism have strong explanatory power (Hornsey 2008; Turner et al. 1987). Groups are not merely categorizations made for semantic or cognitive convenience – rather, identification with a group can influence one’s behavior in a manner not fully explainable by interpersonal interactions or shared interests. The very act of self-categorization into a group can exert strong behavioral changes, primarily in the form of group-based discrimination.
In this modeling study, we propose that identification with political groups, which is a special case of social group identification, is an important but under-explored factor in opinion dynamics. We restrict our model to social identity groups formed on the basis of opinions - thus identity is dynamic and intertwined with the opinion formation process and updated at every step of the simulation similarly to opinions. While there are other conceptions of identity which emphasize the role of more static characteristics that contribute to identity such as ethnicity and mother tongue, political opinion is an interesting case of a relatively dynamic variable that can drive identity group formation, which can reciprocally influence opinion dynamics and drive political polarization (Smith et al. 2024).
In this article, we further analyze an opinion dynamics model we had previously developed and discussed in Kalvas et al. (2023), which was a modified Hegselmann-Krause (HK) model (Hegselmann & Krause 2002) that allowed for dynamic emergence of identity groups as per the Social Identity Approach (Hornsey 2008). In Kalvas et al. (2023) we presented regression results that broadly suggested that higher average open-mindedness alleviates polarization and that identity modulates this relationship. In this article we present a detailed examination of the macro-behavior of our model, with a focus on open-mindedness and identity dynamics, and how these influence political polarization. Along the way, we hope to contextualize our model in the social simulation literature by presenting a review of the underlying social theories, related empirical findings, and some of the existing studies that use Agent-Based Models (ABM’s) of opinion dynamics in the presence of social identity; along with a discussion about how our model incorporates specific theoretical features of the Social Identity Approach, particularly of Self-Categorization Theory.
This study is a part of a larger project with an overarching goal of understanding the influence of different communication landscapes on opinion dynamics using ABM’s. We plan to incrementally build towards a dynamic conceptual model characterized by a positive feedback loop between media use and media-influenced behavior, known as the Reinforcing Spirals Model (RSM; Slater 2007). The strength of this feedback loop in RSM is moderated by openness of the system or subsystem the individual is situated in. We interpret openness in our opinion dynamics model as referring to the open-mindedness (\(\varepsilon\)) variable of the HK model, which can be allowed to vary across agents (Fu & Zhang 2014; Lorenz 2007). In our operationalization, the openness of the whole system refers to the distribution mean of \(\varepsilon\). RSM also conceptualizes the role of social identity as an exacerbating factor for the spiral that can drive societies towards inter-group conflict.
The rest of this article is structured as follows: the remainder of this section covers relevant literature from different fields - here we discuss some aspects of polarization, social identity and self-categorization, and related Agent-Based Models in the literature. In the Methods Section we present a description of our model, along with the rationale for our modeling choices and an overview of the simulation procedure. We discuss our observations in Results, and interpret our findings in the context of existing and planned work in the Discussion Section.
Background
Opinion Polarization and Polarization in Agent-Based Models
Polarization as a social phenomenon has been studied in a variety of contexts and using a variety of study methods. We define polarization as individuals being grouped into clusters based on one or more similar attitudes and beliefs (Esteban & Ray 1994). It is increasingly understood that polarization may jeopardize the political process in the United States (Heltzel & Laurin 2020) and the European Union (Apergis & Pinar 2023) for example, which is encouraging scholars from a variety of disciplines to consider issues related to polarization. Therefore, there are numerous literatures that address issues of polarization including Political Science (Levin et al. 2021), Communication (Bolsen & Shapiro 2017), Sociology (Downey 2022), Economics (Montalvo & Reynal-Querol 2003) and other areas.
Polarization may create an “epistemic threat” to democracy by creating a context in which individuals divided into different subgroups have less access to information and may experience increasing division (Benson 2024). Once these divisions have been developed, it evidence suggests that polarization may extend to new, previously undiscussed topics, reinforcing the process (Carpentras et al. 2023). Polarization has been well studied both empirically and in ABM and other simulation studies. There are many reasons to be concerned about polarization. Empirical evidence suggests that polarization may lead to less satisfaction with the democratic process while simultaneously creating difficulty compromising when there are a few key issues that the public is focused on (Hoerner & Hobolt 2021). Not only can polarization lead to dissatisfaction, but also declining trust in the political process (Jones 2015). Lack of trust and other factors may lead to erosion of the democratic process (Casal Bértoa & Rama 2021; McCoy et al. 2018).
The process by which polarization may impact democracy has been modeled by a number of previous researchers. In a modeling study based on RSM, Song & Boomgaarden (2017) consider the impact of reinforcing spirals and selective exposure on the development of polarization. Coscia & Rossi (2022) focus on the impact of minimizing conflict, which can be viewed as a component of the Spiral of Silence (Noelle-Neumann 1974). Others focus on the impact that emotions have on polarization, they are able to create polarization modeling affective states and the impact of simple, discrete emotions (Schweitzer et al. 2020a). In this model, affective congruence and interaction impact agreement explicitly, whereas in our model, these variables would be included in congruence. Generally, our model differs from these models both in the application of the HK model and in the integration of identity into a model of polarization. Other work focuses on polarization in a socially mediated context (Lu et al. 2021), which is a potential area of application for future work with the model presented in this article.
Though there is some conceptual consensus, there is no single widely accepted method to define polarization operationally, partially due to the diversity of researchers and disciplinary approaches existing in this space. This is true even in the ABM literature. Most measures of polarization typically measure one or more of the following three characteristics of the opinion distribution: (a) the spread of the opinion distribution (Biondi et al. 2023); (b) the distribution of extremists, typically simplified as a ratio or difference (Li & Xiao 2017); (c) the clustering characteristics of the opinion distribution (Schweitzer et al. 2020b). Some studies define polarization as the distance of opinion between pre-determined factions of agents (Diep et al. 2023).
As we wished to adopt a more nuanced measure of polarization that accounts for multiple characteristics of the opinion distribution we chose to adapt the Equal-Size Binary Grouping (ESBG) algorithm (Tang et al. 2022) as our primary polarization metric. The ESBG algorithm can be applied to a continuous opinion space, and outputs a polarization metric in [0, 1], where 0 indicates perfect consensus and 1 indicates perfect polarization (two perfectly tight clusters of equal size that together contain all agents in the population, at maximum possible distance from each other). As intermediate values of this polarization metric are harder to interpret, we also supplement ESBG with more traditional spread-based measures of polarization.
Agent-based models of social influence
Many models of opinion dynamics assume that conformity to socially-derived consensus is one of the central mechanisms behind the shaping of public opinion. This has its empirical roots in the early studies of social conformity, which established that people can be made to doubt their judgement on ambiguous as well as unambiguous situations when they are faced with a dissenting majority (Asch 1955; Sherif 1936). For review see Flache et al. (2017). Besides the assumption of social influence, many contemporary models of opinion dynamics typically also assume two more dynamic principles – (a) homophily, i.e., similar agents are more likely to influence one another; and (b) when an agent is influenced by another, the magnitude of influence scales with the magnitude of dissimilarity between the agents (Flache 2018).
The HK model is a case of Bounded-Confidence models, which form a class of models that emerge from the formalization of theories of social influence. In such models, agents have a (usually homogeneous and stable) tolerance for opinion dissimilarity which is used to filter out prospective influencers. In the HK literature, this variable is typically denoted as \(\varepsilon\), and is variably referred to as "confidence level", "uncertainty", "boundary", or "open-mindedness". While more is known about the behavior of HK models where all the agents share the same \(\varepsilon\) parameter due to them being more analytically tractable (Su et al. 2017), some studies have also looked at HK models with heterogenous \(\varepsilon\) (Han et al. 2019; Kou et al. 2012; Lorenz 2009). Typically models with heterogenous \(\varepsilon\) assume that the \(\varepsilon\) value of agents is drawn from a small pre-determined set. The dearth of models that assume more naturalistic distributions of \(\varepsilon\) is particularly noteworthy when viewed through the lens of the social judgment theory of attitude change (Sherif & Hovland 1961), which assumes that individuals have a range of attitudes that are unacceptable to them in a given time and context, and that this range is variable across individuals (Sherif et al. 1973).
Social identity, self-categorization theory, and the principle of meta-contrast
The term ‘Social Identity Approach’ is conventionally used to refer to the broader theoretical framework comprising two closely related theories in social psychology - Social Identity Theory and the subsequent Self-Categorization Theory (Hornsey 2008). Social Identity Theory was based on experiments where inter-group discrimination effects such as in-group favoritism were observed even when the groups were externally formed by the experimenter on completely arbitrary criteria, and group members were not allowed to interact with one another (Billig & Tajfel 1973; Tajfel et al. 1971). These ‘minimal group paradigm’ experiments helped establish that group phenomena such as partisanship and mob violence cannot be entirely explained as being emergent from interpersonal dynamics in the context of shared (or conflicting) interests between members of the same (different) groups or from competition for resources. Rather, it is the very act of being categorized into a group that can cause individuals to discriminate between in-group and out-group members (Billig & Tajfel 1973). Thus self-identification with the group is the critical variable for inter-group discrimination.
Crucially, the Social Identity Approach purports that individuals are driven to favor their groups not merely because they rationally view participation in group politics as favorable to them in securing their personal goals (‘realistic conflict’), but also because identification with a social group can satisfy one’s deeper psychological needs for a positive self-concept in relation to others (Turner 1975). Furthermore, it proposes that group identification can influence behavior in important ways in a manner that cannot be entirely explained by interpersonal relationships between its constituent members, their shared motives, or shared situations or environments. In the other words, the group is not merely a superfluous construct, but is ‘real’ – in the sense that the act of identifying with the group in itself exerts an influence on behavior. This view of the group is encapsulated in the Social Identity Theory (Tajfel et al. 1979), which comprises a broader set of ideas on how group identification is closely linked with the members’ self-concepts, and how the need for a positive self-concept can cause group members to strive for collective change, thus driving group-level behavior and potentially inter-group conflict.
A deeper analysis of the psychological basis of social identity is presented in the Self-Categorization Theory (SCT; Turner et al. 1987; Turner & Reynolds 2011). SCT can be thought of a dynamic conceptual model of the psychological and contextual factors that lead to the activation of different possible social identities and the corresponding identity-congruent behaviors. At its core, SCT proposes that social group formation results from an application of the cognitive process of stimulus categorization to one’s self-concept in a social environment. Categories of people are assumed to be perceived based on similar mechanisms as other kinds of categories, such as of objects and concepts. Specifically, SCT assumes that a principle of meta-contrast can be applied to self-categorization – that is to say, the process of self-categorization depends on the ratio of within-group similarity to between-group similarity, where similarity is defined in terms of a circumstantially salient feature.
Importantly, SCT assumes that the self-concept is dynamic, and situations and stimuli can determine the specific features of one’s self-concept at a given point. Therefore, one’s social identity also tends to be dynamic and context-dependent, albeit adhering to certain rules. According to SCT, a single individual can identify with one of several hierarchically related groups, defined at different levels of abstraction. The highest and most abstract of these possible groups is the group of all humans, while the lowest and least abstract is the individual themself. There typically are several levels of abstraction in between these two levels. Therefore a single individual could identify as a human, an Italian, a Sicilian, a female, a botanist, or an individual with a specific name and personality, at different points in time. However, one’s self-concept (and therefore, their behaviors) associated with each possible identity group are not experienced all at once – rather, social context at any given time makes one or more identities of an individual more salient than their other possible identities. SCT proposes that a person’s expressed social group identification at any given time exists in a ‘functional antagonism’ with their other possible social identities.
SCT also proposes that social identity plays a central role in the social influence process (Turner & Reynolds 2011). In fact, the idea that categorizing oneself as being similar to an influencer may be a pre-condition for social influence to occur was suggested by Solomon Asch (Asch 1965). Empirical evidence supports the claim that shared identity is a potential mediating factor in social influence (David & Turner 2001; Turner & Reynolds 2011). For example Catapano et al. (2019) observed that cuing towards shared values can promote social influence in the face of disagreements, and in a study of US senator positions across thirty years Liu & Srivastava (2015) observed that congruence in political identity determined whether interaction between pairs of senators caused voting behaviors to converge or diverge.
Our key takeaways from SCT (and from the broader Social Identity Approach) that form the theoretical foundation of our extension to the HK model are as follows: (a) social identity groups are meaningful – the act of categorizing oneself among a social identity group can influence behavior, including the social influence process; (b) categorization is a perceptual process driven by meta-contrast along a salient feature; (c) categorization can occur at multiple levels of abstraction – where higher levels of abstraction contain more inclusive categories; (d) social categories tend to be perceived based on similarities and differences along a circumstantially relevant set of features.
The last of these takeaways enable us to apply SCT principles to opinion dynamics. As self-categorization and group identification are driven by the salience of the defining features of the categories, augmenting an opinion dynamics model with a self-categorization process implicitly assumes that opinions can be a salient feature that determines self-categorization and identity group formation. One can imagine this to be the case especially during high periods of polarization along opinion dimensions, such as just before an election.
There are some important ways in which our model as yet does not attempt to capture the entire conceptual breadth of SCT, as we will discuss in more detail in the Discussion Section. For instance, although we model a variable that controls the level of abstraction or inclusiveness of identity groups, but our model assumes that individuals always belong to a single dynamic identity group. Similarly we do not model the environment or salience of identities. Modeling the complexities of social identity at multiple levels of abstraction, and their activation in response to a dynamic environment would constitute an additional layer of dynamism we would hope to build towards in future explorations with the model.
Social identity in political communication
Group-level dynamics play an important role in political cognition. Although cognitive biases such as motivated reasoning is commonly observed in politically relevant judgements (Druckman & Bolsen 2011), political identities can further strongly bias beliefs in favor of partisan in-groups (for review, see Leeper & Slothuus 2014). For example, people’s judgements of policies are strongly biased by the position of their favored political party without their conscious awareness (Cohen 2003). Similarly, support for conspiratorial rhetoric by political leaders is moderated by political identity (Dow et al. 2023). These partisan biases are more likely a consequence of motivated effortful reasoning than blind conformity to party positions (Petersen et al. 2013), and are sensitive to the salience of partisan identities (Bolsen et al. 2014). Strikingly, people can vote against their personal interest in favor of their identity group even in minimal group settings with randomized group assignments (Bassi et al. 2011).
Studies in cognitive science and neuroscience have shed some light into the processing of political identity. Studies with Implicit Attitude Tests show an automatic preference for policy proposals from in-group members (Smith et al. 2012). Judgement of visually observed stimuli can be biased by one’s political identity (Kahan et al. 2012). Neuroimaging data suggests that individual brains have a representation of "in-groupness" that is common across multiple group identification criteria. A classifier trained to decode in-groupness in experimental minimal group settings from neural data could also predict in-groupness of real political stimuli in relation to the subject (Cikara et al. 2017). Neural responses to in-groupness in minimal group experimental settings (where the minimal group is salient) are similar to the responses to racial in-groups in neuroimaging studies of racial membership representations (where race is salient, Van Bavel et al. 2008).
Of additional interest to us is the existence of social identities that are purely based on political opinion – as opposed to other identity-relevant variables such as ethnicity, gender, or socio-economic status. While much of the social identity literature treats political and non-political social identity similarly - reflecting the broad applicability of the theory – some authors have explicitly referred to opinion-based identities. Bliuc et al. (2007) draws a clear distinction between identity groups centered on opinions, and those constructed around other features, and found that opinion-based group membership can act over and above the opinions themselves in predicting political action. Smith et al. (2015) proposed that the formation of novel collective action groups – that were not perfectly aligned to pre-existing societal fault lines – can be explained by individual agents communicating their grievances to others and renegotiating preferred norms.
The key takeaways for us is that opinion-based social identities exist, and can be thought of as a dynamical component that operates over and above interpersonal dynamics. These theoretical considerations prompted us to model identity as a dynamic feedback process of its own that both depends on one’s opinion, and influences the evolution of future opinions.
Agent-based models of social identity
Simulations of identity have also provided insights of a nature that are difficult to obtain from empirical studies. For example, in a simulation study Dickson & Scheve (2006) found that identity-based signalling can lead to polarization on policy issues even when the policy dimension is uncorrelated with identity. A recent modeling work by Törnberg et al. (2021) assumed that identities are formed and shared through social contact rather than conformity or political discourse, and showed that identity dynamics can be sufficient for polarization. Thus in the study of phenomena such as social identity that are challenging to observe and measure naturalistically, proposing such computational arguments is a promising approach.
On the other hand, it is challenging to build towards scholarly consensus in the model-based understanding of a highly dynamic phenomenon such as social identity which can be formalized in multiple possible ways (Wijermans et al. 2023). Therefore while a number of modeling studies have formalized and incorporated aspects of the Social Identity Approach, including simulation studies in opinion dynamics (for review see Scholz et al. 2023), authors have taken a variety of approaches to modeling social identity. Moreover, owing to the wide conceptual coverage of the Social Identity Approach it is often feasible to only model a subset of the dynamic features of social identity and assume some variables to be either constant or implicit. An important modeling choice in the process of modeling social identity is whether group-membership is static or changes dynamically. In this section we briefly review some multi-agent models of social identity with a focus on models where identity is dynamic in the course of a simulation.
Salzarulo (2006) developed a dynamic model of social identity based on the principle of meta-contrast of SCT that explicitly models the prototypical position of an identity group, which exert their influences on individuals via in-group and out-group interactions. Interestingly, this implementation assumes negative influence in identity dynamics – an agent can be repelled by another agent on account of being in different identity groups. Smaldino et al. (2012) modeled the effect of assuming that agents can dynamically assign themselves to identity groups based on Optimal Distinctiveness Theory, which assumes competing psychological forces arising from individuals seeking safety in numbers while trying to preserve their individuality. The comprehensive Dynamic Identity Model for Agents (DIMA; Dimas & Prada 2014; Lobo et al. 2023) also models social identity groups as an emergent phenomena arising from psychological forces within individuals. In DIMA, individuals have a personal as well as a social identity, and the behavioral output is moderated by social context and identity salience.
Our model combines features from these different studies in a manner suitable for our goals. We assume that behavior can arise due to individual characteristics, interpersonal interactions, as well as social identity. We also include a variable very similar in principle to a group size preference – which we term as "Salience of Proximity in Identity-Relevant Opinions" or SPIRO – which we assume is a stable trait of an individual. In addition to these features, our model also includes an openness variable (\(\varepsilon\)), which is of high importance to communications research, and is a core functional component of bounded-confidence models of opinion dynamics. Finally, while some ABM’s of social identity have directly operationalized the meta-contrast principle of self-categorization to the study of opinion dynamics (Salzarulo 2006; Weimer et al. 2022), these models have assumed that the groups emerging from meta-contrast will also exert repulsion or negative influence between each other. In our model, meta-contrast does not lead to negative influence between detected identity groups.
Methods
Rationale - Integrating social identity with opinion dynamics
Our model was built with a few objectives in mind: firstly we wanted to capture the effect of identity as a component distinct from interpersonal dynamics – meaning we wanted to take an existing model of opinion dynamics based on interpersonal interaction and extend its updating rule with identity dynamics. Secondly, while social identity can arise in a number of contexts, we are specifically interested in one’s political identity, which we assume is a function of one’s opinion in relation to the opinions held by others – in other words we apply the principle of meta-contrast to the dynamic opinion space to derive dynamic identity assignments. Thirdly, we assume that perceived social identities are dependent on the observer – some people may see more identity groups than others. Fourthly we assume that the effect of identity on communication between any two individuals is similar to an all-or-nothing filter – a perceived identity mismatch between the listener and the speaker leads to the listener ignoring the speaker’s opinion entirely. Finally, we have tried to keep the model as general as possible within the scope of our research questions, by allowing heterogeneity in several agent properties.
We built five variants of the HK bounded-confidence model (Hegselmann & Krause 2002), two of which contain identity dynamics, to enable comparison of the influence of different dynamical processes on polarization. The basic HK model assumes that individuals update their opinion by moving towards the average opinion of all other agents who meet a selection criteria. Typically a speaking agent’s opinion is taken into consideration as long as it is within a dissimilarity limit of the listener’s opinion, denoted commonly as \(\varepsilon\). All our models exhibited this basic behavior, but differed in whether identity effects were present and whether there was heterogeneity in agent variables.
We integrated identity dynamics into the HK model by keeping the effect of identity mismatches qualitatively similar to the effect of opinion mismatches in the classical model. At every time step agents classify themselves and others into identity groups based on the distribution of opinions at that time via the Louvain Community Detection algorithm (Blondel et al. 2008) applied to a network-based representation of the opinion space where more similar opinions are represented by larger weights,1 followed by k-means clustering for stabilization. After an agent assigns all agents to some identity group, they filter out incoming opinions from agents that are not perceived to be in the same identity group as themself. Therefore, the listener is selective of incoming information not only based on its content, but also based on the social identity of the speaker.
An important parametrization for Louvain Community Detection is the resolution of the communities found, since the original algorithm is biased to some sizes relative to the network size (Jones et al. 2016). We resolve this by defining a parameter we term as the Salience of Proximity in Identity-Relevant Opinions (SPIRO). SPIRO determines how sensitive an observer is to the tightness of possible identity clusters in the opinion space. We interpret SPIRO as a socially relevant variable that is allowed to vary across observing individuals. Thus, it is possible that two agents observing the same opinion landscape may differ in their judgment as to how many identity groups exist and which agent falls into which group.
With our long-term goals in mind, we also took a more naturalistic approach to our modeling and interpretation. We use approximate Gaussian distributions for key variables such as openness, conformity, and SPIRO, in the model variants for which these variables were heterogeneous. We also explicitly interpret \(\varepsilon\) as openness or open-mindedness to differences in opinion, which is an interpretation present in the HK literature (Fu & Zhang 2014; Lorenz 2009).
Model components
We developed and studied five hierarchically related models with the idea of understanding the influence of different dynamic components with polarization. These five variants were built incrementally, each subsequent model building on top of the components of the previous. Thus the first of these models is closest to the classical HK model with its minimal features, while last of these models is the richest and has several variables related to identity. In this section we will describe the different model components and relevant experimental variables, and then highlight which dynamic components are present in each model.
The model broadly has two interacting dynamic components: the HK bounded confidence rule for updating opinions and the implementation of social identity as an additional barrier to communication. The application of social identity itself is a two-step process – first an agent must assign every agent including itself to an identity group based on the distribution of the opinion space, and its own sensitivity to opinion clustering. Then the agent must take action based on the identity assignments – in our model, this translates to ignoring agents belonging to different identity groups. We break down these components below:
Conformity-modified HK
An agent’s opinion is a real number between \(-1\) and \(+1\) that is updated according to the conformity-modified HK rule, where an agent’s future opinion is their current opinion shifted towards the neighborhood average opinion. The magnitude of opinion shift of an agent i towards its neighborhood average opinion is obtained by weighting the difference of opinion between the agent and its neighborhood average by the conformity parameter, \(\alpha_{i}\). The updating rule for this component is given by:
| \[o_{i}(t) = o_{i}(t - 1) + \alpha_{i}\Bigg[\frac{1}{|N_{i}(t)|}\sum_{j \in N_{i}(t)}o_{j}(t - 1)-o_{i}(t - 1)\Bigg]\] | \[(1)\] |
| \[N_{i}(t) = \Bigg\{ j : \frac{|o_{j}(t - 1) - o_{i}(t - 1)|}{2} <= \varepsilon_{i}\Bigg\}\] | \[(2)\] |
Neighborhood of the agent \(N_{i}(t)\) in models with identity is given by:
| \[N_{i}(t) = \Bigg\{ j : \frac{|o_{j}(t - 1) - o_{i}(t - 1)|}{2} <= \varepsilon_{i}\Bigg\} \cap \{ j : Id_{j}(t) = Id_{i}(t)\}\] | \[(3)\] |
Social identity
For the variants of the model that have identity, identity groups are implemented as discrete tags associated with every agent (see Equation 3) that are updated at every time step. An agent is only influenced by other agents that are in its own identity group.
We conceive of identity group assignment as a perceptual process every agent is engaging in, emulating in principle identity categorization by meta-contrast. The process of assigning agents to identity groups has the following steps:
- Conversion to Proximity Network: The opinion space is converted to an equivalent Proximity Network where agents are nodes and those with similar opinions have stronger ties.2
- SPIRO-filtering: The observing agent filters this Proximity Network based on their own sensitivity to grouping (the ‘SPIRO’ variable, discussed below), retaining only those nodes and links associated with agents that have strong ties with at least two other agents – where ‘strong’ is defined in relation to the observer’s SPIRO value.
- Core Community Detection: The Louvain algorithm for community detection (Blondel et al. 2008) is applied on the sub-network resulting from the SPIRO-filtering.
- Stabilization: We get stabilized identity group assignments for every agent in the opinion space by repeatedly until convergence applying k-means clustering on the entire opinion space using the number of clusters (communities) detected in Step 3 and their corresponding opinion centroids (i.e. centroids of opinions corresponding to the nodes of each detected community) as initial conditions. Agents that were excluded due to SPIRO filtering are assigned to the cluster corresponding to their nearest opinion centroid.
This process of identity group detection is parametrized with the variable we call SPIRO - the Salience of Proximity in Identity-Relevant Opinions. The SPIRO value of the observing agent acts as a threshold for tie detection in the Proximity Network in the SPIRO-filtering step - the filtered sub-network contains only nodes with at least two edges of value greater or equal to the observing agent’s SPIRO value, and only such edges. In practice, the value of SPIRO controls the number and granularity of the discovered identity groups. Higher values of SPIRO lead to detection of more number of more tightly clustered identity groups. In our most advanced model variant, agents with different SPIRO values run community detection independently, and thus can perceive the same third agent to be a member of different identity groups.
We argue that the combination of thresholding group-forming ties in the Proximity Network, detecting core communities from among the filtered sub-network using the Louvain algorithm, and then constructing full and stable identity groups by clustering constitute an implementation of meta-contrast on the opinion space. Both community detection and clustering have the effect of resulting in group assignments that aim to maximize inter-group similarity in relation to intra-group similarity, aligning in principle with meta-contrast. The community detection step can be thought of as identifying the core of each group, while the clustering step outputs stable entire groups.
While we were interested in studying the influence of diversity in perception of identity groups, having every agent perform Louvain Community Detection on the entire opinion space at every time step would be computationally very expensive. We therefore constrained the possible values of SPIRO to a fixed set of \(8\) values. In the model variant where we allow SPIRO to vary across agents, at the beginning of the simulation each agent is assigned one of the eight possible SPIRO values. In this way we could study the influence of diverse perceptions of identity in the same simulation while keeping the number of Louvain Community Detection passes low.
Model variants
We studied the influence of identity in the presence of other important variables by incrementally building towards the richest variant of the model which has variable identity perception. A description of the models is as follows:
- Deterministic Start HK Model (DHK). Initial distribution of opinions is evenly spaced. All agents have the same openness \(\varepsilon\) and conformity \(\alpha\). No identity dynamics.
- Randomized Start HK Model (RHK). Initial distribution of opinions is uniformly distributed. All agents have the same openness \(\varepsilon\) and conformity \(\alpha\). No identity dynamics.
- Heterogeneous Boundary Model (VB). Initial distribution of opinions is done as in DHK in a half of simulations and as in RHK in the other half. Agents have individual values for openness (\(\varepsilon_i\)) and conformity (\(\alpha_i\)), parameterized at the population level with clipped normal distribution3 parameters \(\mu_\varepsilon\), \(\mu_\alpha\) (mean) and \(\sigma_\varepsilon\), \(\sigma_\alpha\) (standard deviation). No identity dynamics.
- Heterogeneous Boundary with Identity (VBI). Initial distribution of opinions is done as in DHK in a half of simulations and as in RHK in the other half. Agents have individual values for openness (\(\varepsilon_i\)) and conformity (\(\alpha_i\)), parameterized at the population level with clipped normal distribution parameters \(\mu_\varepsilon\), \(\mu_\alpha\) (mean) and \(\sigma_\varepsilon\), \(\sigma_\alpha\) (standard deviation). Identity dynamics are present but homogeneous, i.e. all agents have a common SPIRO.
- Heterogeneous Boundary with Heterogeneous Identity (VBVI). Initial distribution of opinions is done as in DHK in a half of simulations and as RHK in the other half. Agents have individual values for openness (\(\varepsilon_i\)) and conformity (\(\alpha_i\)), parameterized at the population level with clipped normal distribution parameters \(\mu_\varepsilon\), \(\mu_\alpha\) (mean) and \(\sigma_\varepsilon\), \(\sigma_\alpha\) (standard deviation). Identity dynamics are present and heterogeneous - agents have variable SPIRO, parameterized at the population level with \(\mu_{SPIRO}\) (mean) and \(\sigma_{SPIRO}\) (standard deviation).4
Simulations
The pseudocode for the simulation logic can be seen in Algorithm 1 for the models without identity and Algorithm 2 for the models with identity. In all we ran 2,504,964 simulations in NetLogo across the five model variants and different combinations of experimental variables (Table 3). We analyzed our simulations in two ways – firstly by examining the behavior of our dependent measures (see below) in different regions of the parameter space, and secondly by expanding upon the multiple regression reported in Kalvas et al. (2023) with step-wise regressions in this article to help understand the relative explanatory power of our independent variables. Our IV’s and DV’s are listed below.


Independent variables
We had 8 IV’s in all: \(\mu_\alpha\), \(\sigma_\alpha\), \(\mu_\varepsilon\), \(\sigma_\varepsilon\), \(\mu_{SPIRO}\), \(\sigma_{SPIRO}\), Evenness of population size, Randomness of initial opinion distribution. For all models except DHK we used 60 random seeds for each IV combination. Not all IV’s are applicable to all models, although all of them are applicable to the VBVI Model - Table 1 lists the independent variables and their range of values. Table 3 in Appendix A contains the IV’s used for each model.
| Independent Variable | Description | Possible Values |
|---|---|---|
| \(\mu_\alpha\) | Mean conformity | {0.2, 0.8} |
| \(\sigma_\alpha\) | Standard deviation of conformity | {0, 0.1} |
| \(\mu_\varepsilon\) | Mean openness | {0.1, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18, 0.19, 0.2, 0.21, 0.22, 0.23, 0.24, 0.25, 0.26, 0.27, 0.28, 0.29, 0.3} |
| \(\sigma_\varepsilon\) | Standard deviation of openness | {0, 0.05, 0.1, 0.15} |
| \(\mu_{SPIRO}\) | Mean SPIRO | {0.37, 0.49, 0.61, 0.73, 0.85} |
| \(\sigma_{SPIRO}\) | Standard deviation of SPIRO | {0, 0.05, 0.1, 0.15} |
| Even_Pop? | Whether the population size is 100 (Even/True) or 101 (Odd/False) | {True, False} |
| Random_Start? | Whether the initial opinion distribution was random, i.e. uniformly drawn from [-1, 1] (True), or evenly spaced in [-1, 1] (False) | {True, False} |
We used three measures to get aggregate characterizations of the opinion space after each simulation - the degree of polarization, extremeness, and diversity. Each combination of experimental variables were subjected to 60 random initializations, allowing us to compute a mean and a variance for each measure. In our analyses we treated the means and variances of the following measures for each parameter combination as dependent measures:
- Equal-Size Binary Grouping (ESBG) Polarization: We adapted the the ESBG algorithm by Tang et al. (2022) which provides a computational logic for measuring polarization in a real-valued opinion space. The value of ESBG polarization is 1 when there are exactly two perfectly tight equally-sized clusters of agents in the opinion space that are as far away from each other in opinion as possible, and zero when there is perfect consensus among all agents anywhere in the opinion space. Details of implementation in our simulation can be found in Kalvas et al. (2023). In brief, the ESBG algorithm applied to the opinion space splits the population into two clusters of equal size while minimizing within-cluster heterogeneity with a modified k-means clustering procedure. The calculation of ESBG polarization occurs after clustering as:
where, \(Norm(x) = \frac{x}{\sqrt{4 \times dimensionality}} = \frac{x}{2}\)\[ESBG = \frac{Norm(B)}{1 + Norm(w_1) + Norm(w_2)}\] \[(4)\]
\(B\) = Absolute distance between the two cluster centroids
\(w_i\) = Total mean deviation of agents of cluster \(i\) from its centroid
Given that ESBG is non-linearly related to some other measures of consensus - for example, diversity - we conduct our analyses after decomposing our experimental variables into categorical factors to avoid problems with assumptions about monotonicity. - Extremeness: Extremeness is the summed magnitudes of all opinions from the centre of the opinion space.
- Diversity: Diversity is the overall standard deviation of the opinions, i.e. the square-root of mean squared distances from the mean opinion.
Results
Identity worsens polarization, but heterogeneity keeps it in check
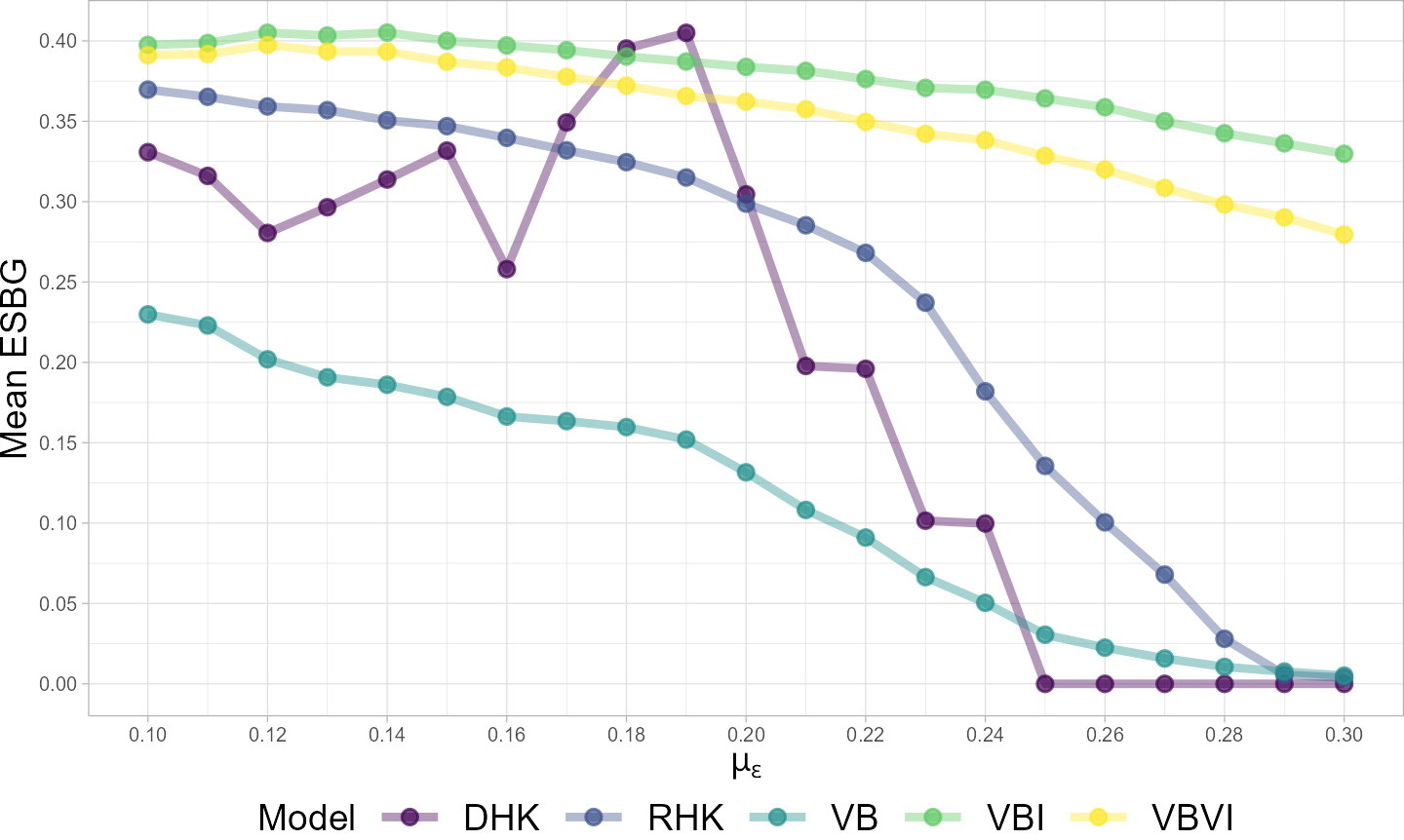
A negative relationship between average agent openness and ESBG polarization was expected, and is consistently found across all our models (Figure 3), as reported in Kalvas et al. (2023). HK models with homogenous \(\varepsilon\) of greater than approximately 0.2 tend towards consensus (Lorenz 2007), which corresponds to an ESBG polarization value of 0. Our models showed the same trend, but the strength of the relationship varies across the models. Our basic model with randomized initial opinions (RHK) maintains higher polarization on average in comparison to the model with heterogenous openness (VB). This is consistent with prior work that suggested a strong consensus-driving effect of variance in open-mindedness (Lorenz 2009).
As reported in Kalvas et al. (2023), both models with identity (VBI and VBVI) maintain significantly higher polarization levels for higher average openness than VB, indicating towards a polarizing role of identity. Taking grand averages across all simulations conducted for each model, we observe that mean polarization across models varies as \(VB < DHK < RHK < VBVI < VBI\) (Table 3). This is consistent with our general conclusion that identity drives polarization, but heterogeneity in openness has a mitigating effect.
In Kalvas et al. (2023) we performed a multiple regression to study the relationship between our different experimental variables and ESBG polarization. Here we take our analysis further by performing a step-wise regression to help identify the relative importance of our experimental variables in our richest dynamical model, VBVI (Table 2)5. We coded our independent variables as categorical variables to avoid making assumptions about monotonicity. We observe that polarization has a negative relationship with all levels of \(\mu_\varepsilon\), and \(\sigma_\varepsilon\), and a positive relationship with all levels of \(\mu_{SPIRO}\). We will discuss in more detail our interpretation of the influence of these variables in the coming sections. We also report weak or absent effects of our other experimental variables - \(\sigma_{SPIRO}\), \(\mu_{\alpha}\), \(\sigma_{\alpha}\), evenness of population size, and non-randomness of the initial opinion distribution.
The step-wise regression helped us understand the explanatory power of our experimental variables. Considering only main effects, we found that including \(\mu_\varepsilon\), \(\sigma_\varepsilon\), \(\mu_{SPIRO}\). \(\sigma_{SPIRO}\), \(\mu_{\alpha}\), \(\sigma_{\alpha}\), evenness of population size, and non-randomness of the initial opinion distribution in the regression model in total explained about 22.4% of the variance in ESBG polarization at the end of each simulation. Including only \(\mu_{\alpha}\), \(\sigma_{\alpha}\), evenness of population size, and non-randomness of the initial opinion distribution as independent variables in the regression explained just 0.4% of the variance but adding \(\mu_\varepsilon\) raised the explained variance to 4.9%. Adding \(\sigma_\varepsilon\) to this model gives us the largest increase in \(R^{2}\) in our step-wise regression model, while further adding \(\mu_{SPIRO}\) gives us the second largest jump in \(R^{2}\), corresponding to explained variance of about 16.3% and 22% respectively. Adding \(\sigma_{SPIRO}\) to this model weakly raises the explained variance to 22.4% in the full regression model with only main effects.
| ESBG | |||||
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | |
| σSPIRO = 0.05 | −0.015*** (0.001) | ||||
| σSPIRO = 0.1 | −0.027*** (0.001) | ||||
| σSPIRO = 0.15 | −0.036*** (0.001) | ||||
| μSPIRO = 0.37 | 0.057*** (0.001) | 0.057*** (0.001) | |||
| μSPIRO = 0.49 | 0.110*** (0.001) | 0.110*** (0.001) | |||
| μSPIRO = 0.61 | 0.150*** (0.001) | 0.150*** (0.001) | |||
| μSPIRO = 0.73 | 0.076*** (0.001) | 0.076*** (0.001) | |||
| μSPIRO = 0.85 | 0.091*** (0.001) | 0.091*** (0.001) | |||
| σε = 0.05 | −0.021*** (0.001) | −0.021*** (0.001) | −0.021*** (0.001) | ||
| σε = 0.1 | −0.129*** (0.001) | −0.129*** (0.001) | −0.129*** (0.001) | ||
| σε = 0.15 | −0.151*** (0.001) | −0.151*** (0.001) | −0.151*** (0.001) | ||
| με = 0.15 | −0.004*** (0.001) | −0.004*** (0.001) | −0.004*** (0.001) | −0.004*** (0.001) | |
| με = 0.2 | −0.029*** (0.001) | −0.029*** (0.001) | −0.029*** (0.001) | −0.029*** (0.001) | |
| με = 0.25 | −0.063*** (0.001) | −0.063*** (0.001) | −0.063*** (0.001) | −0.063*** (0.001) | |
| με = 0.3 | −0.112*** (0.001) | −0.112*** (0.001) | −0.112*** (0.001) | −0.112*** (0.001) | |
| Random_Start? = False | 0.022*** (0.001) | 0.022*** (0.001) | 0.022*** (0.001) | 0.022*** (0.001) | 0.022*** (0.001) |
| Even_Pop = False | −0.008*** (0.001) | −0.008*** (0.001) | −0.008*** (0.001) | −0.008*** (0.001) | −0.008*** (0.001) |
| σα = 0.1 | −0.001 (0.001) | −0.001 (0.001) | −0.001 (0.001) | −0.001 (0.001) | −0.001 (0.001) |
| μα = 0.8 | −0.005*** (0.001) | −0.005*** (0.001) | −0.005*** (0.001) | −0.005*** (0.001) | −0.005*** (0.001) |
| R2 | 0.004 | 0.049 | 0.163 | 0.220 | 0.224 |
| Note: *p<0.1; **p<0.05; ***p<0.01 | |||||
Heterogeneous perceptions of identity have only weak effects on the dynamics
We introduced variability in perception of social identity in our model, which follows from Self-Categorization Theory. While we found a weak relationship between \(\sigma_{SPIRO}\) and polarization in our multiple regression (Table 2), the computational cost of introducing multiple runs of community detection in every time-step would make heterogeneity in SPIRO an unreasonably expensive inclusion to our model unless it strongly influenced dynamics in some way. The weak effects of \(\sigma_{SPIRO}\) on the dynamics of our model are also apparent from observing that the effects of \(\mu_{\varepsilon}\) and \({\mu_{SPIRO}}\) on ESBG (Figure 3) are qualitatively similar in VBI and VBVI.
SPIRO modulates the influence of open-mindedness on polarization
Open-mindedness naturally promotes consensus and mitigates polarization, as is consistently observed in our data. However, our implementation of social identity assumes an additional layer of closure as a consequence of opinion-dependent identity perceptions. In model VBI this translates to the population being divided at any time into mutually closed identity groups that do not communicate with one another irrespective of how open-minded the constituent agents are. The corresponding dynamics in VBVI are slightly more complicated because an agent can perceive itself to be in the same identity group as another agent that perceives the former agent to be in a different group. However, in both models we expected SPIRO to play a modulatory role in the relationship between \(\varepsilon\) and ESBG because of the additional communication barriers introduced by having more identity groups.
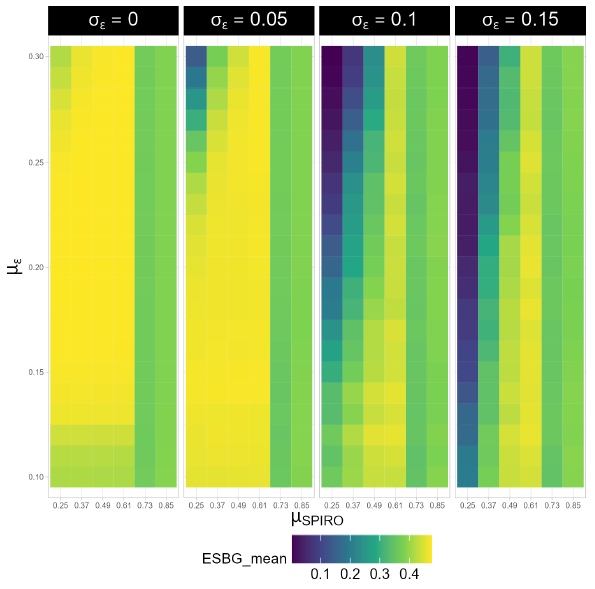
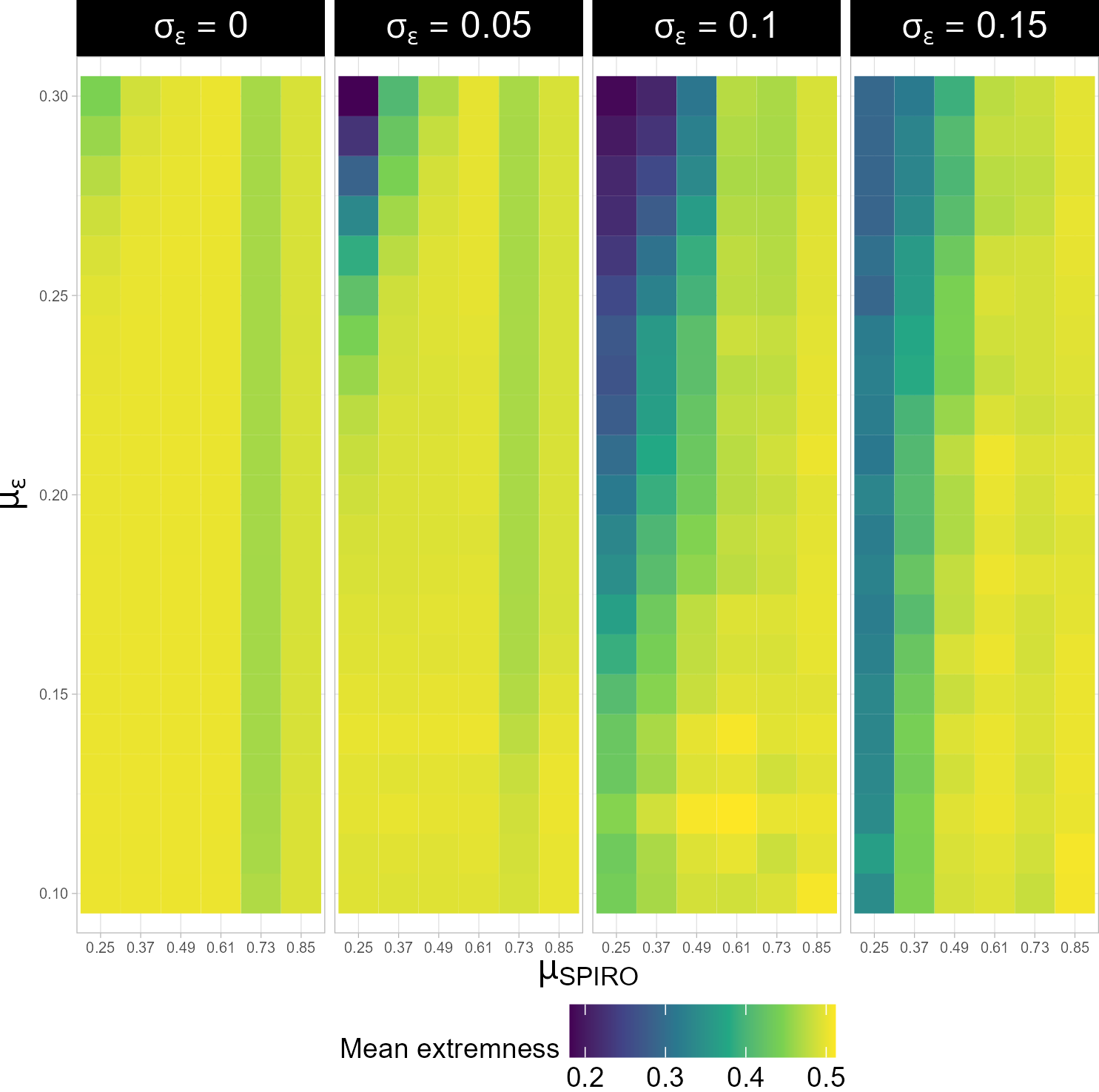
We observe that in the parameter region studied, the dependency of ESBG on \(\varepsilon\) is weakest for the highest values of \(\mu_{SPIRO}\) (Figure 1). The system is likely to be fractured at the end of the simulation in this parameter region, with many tight opinion clusters that arise because of the emergence of many small identity groups. Thus as one increases \(\mu_{SPIRO}\), the system dynamics can be thought of as transitioning from opinion-driven to identity-driven.
Polarization, consensus, fracturing, and transition regions
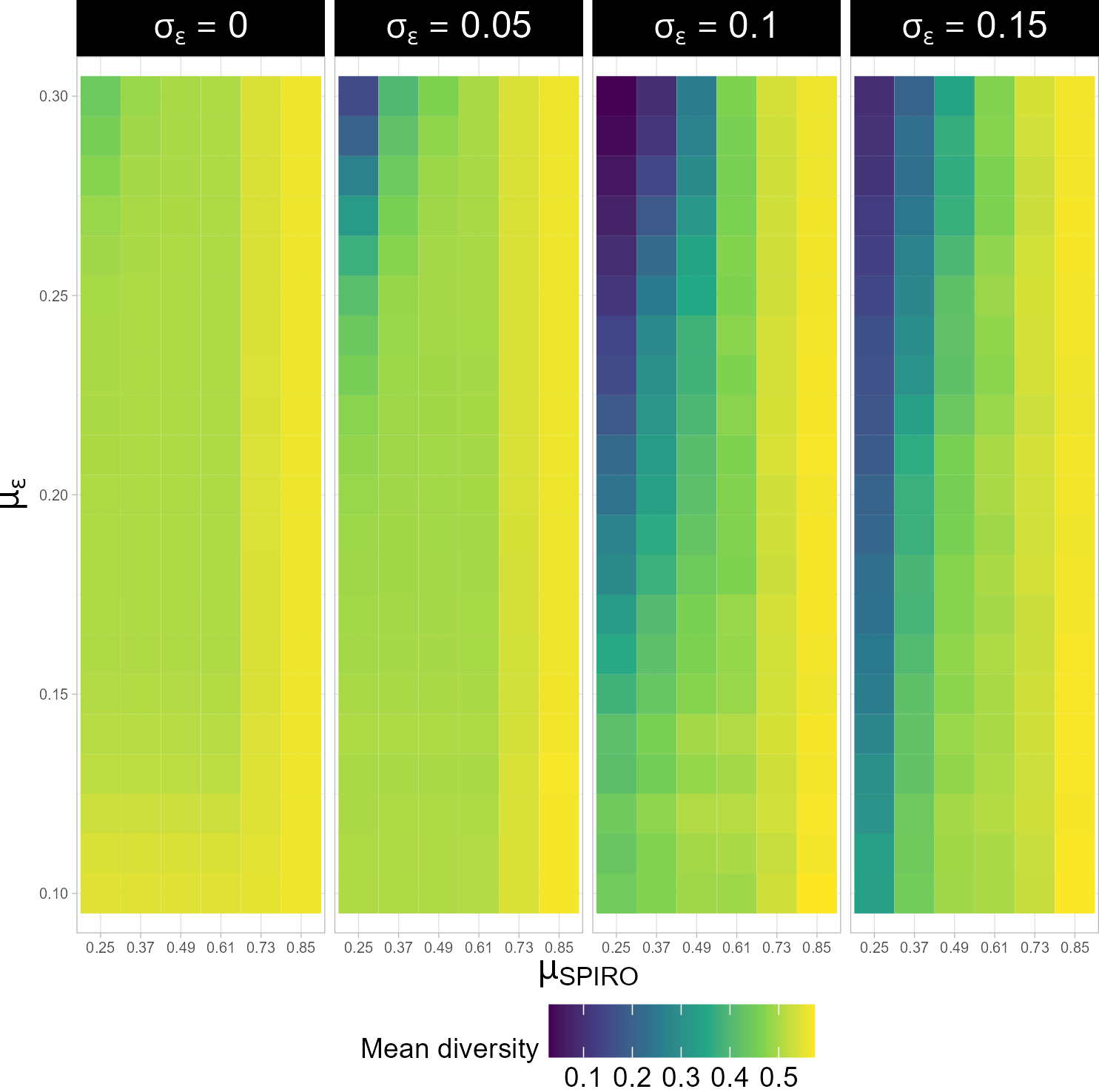
The opinion space at the end of the simulation tended to be in consensus, polarization, or in a fractured state with several tight opinion clusters. Figure 1 shows the variation of average ESBG at the end of VBI simulation runs with \(\mu_{SPIRO}\), \(\mu_\varepsilon\), and \(\sigma_\varepsilon\). A consistent finding in both our models with identity is that polarization is related in a non-linear fashion with \(\mu_{SPIRO}\) – polarization initially increases with \(\mu_{SPIRO}\) and peaks for simulations with \(\mu_{SPIRO}\) at 0.61, but decreases and saturates for the highest SPIRO values. This is to be expected as higher SPIRO values would lead to more number of tighter identity clusters that are closed to other groups. Moderate SPIRO values thus are most likely to support a bi-polarized opinion space, while the highest values would fracture the opinion space into many clusters. This is also supported by the observations that simulations run in the highest SPIRO values were the least sensitive to \(\mu_\varepsilon\) and \(\sigma_\varepsilon\) (Figure 1), and that unlike ESBG, neither extremeness nor diversity – measures which do not privilege bi-polarized states over fractured states – decreased at the highest values (Figures 4 and 5).
The consensus-driving effect of higher \(\sigma_\varepsilon\) values can be seen in Figure 1. Despite the consensus region expanding with higher \(\sigma_\varepsilon\), the system is robustly fractured at the highest two \(\mu_{SPIRO}\) values. Higher \(\sigma_\varepsilon\) values also appear to weaken the dependency of polarization (and diversity and extremeness; Figures 4, 5) on \(\mu_\varepsilon\). For the highest \(\sigma_\varepsilon\) value of 0.15, the state of the system appears much more strongly driven by \(\mu_{SPIRO}\) than by \(\mu_\varepsilon\).
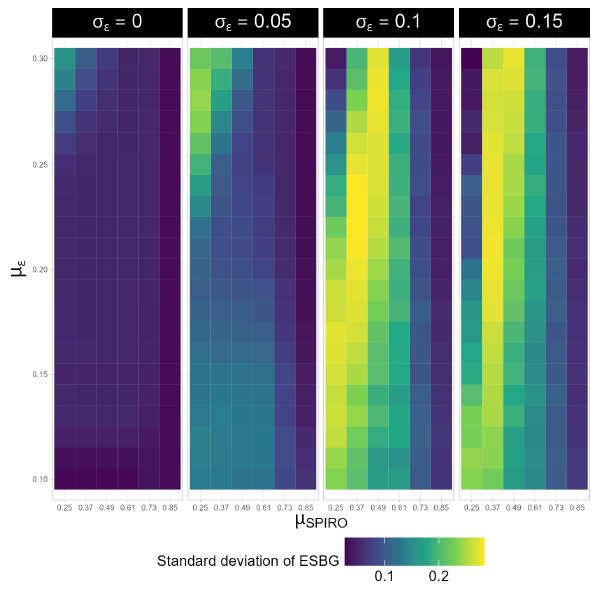
Observing the variance in ESBG at the end of the simulation across different initial conditions reveals that system dynamics are more predictable in some regions of the parameter space than in others (Figure 2). The high variance regions typically occur at intermediate parameter values between high and low polarization causing regions (Figures 1 and 2). For example when \(\mu_{SPIRO} = \sigma_\varepsilon = 0\), the higher variance region (Figure 2) occurs at a \(\mu_{\varepsilon}\) of about 0.23, which is where the ESBG mean indicates a shift to consensus (Figure 1). These can be thought of as transition regions where system behavior sensitive to initial conditions because of shifting dynamics as one moves through the parameter space. Figure 2 suggests a widening in the transition region along the \(\sigma_{\varepsilon}\) axis in the parameter region being studied. Interestingly, we do not observe transition regions close to the highest \(\mu_{SPIRO}\) values as the system dynamics changes from polarized to fractured, suggesting that the system changes sharply as one goes from moderate to high SPIRO values.
Discussion
To our knowledge our work extending the HK model to include social identity group effects is the first study to integrate the Social Identity Approach with a bounded-confidence model of opinion dynamics. In Kalvas et al. (2023) we provided a technical description of the model and covered some basic results on how our experimental variables influence polarization. In this article we placed our model in the context of the social psychology literature on social identity, and discuss the results of our model in detail, and help lay the foundation of future work which aims to test ideas from social science and communication sciences via our extended HK model.
We analyzed our HK model with emergent identity dynamics by examining the effect of our experimental variables on the final state of the system. Specifically, we studied how different parametrizations of open-mindedness, identity detection, and conformity led to different opinion distributions characterized by their ESBG polarization – a metric that emphasizes bi-polarized and distant opinion clusters.
Our key findings can be summarized as follows: firstly we find that including identity dynamics in the model dramatically increases polarization. Secondly, SPIRO, which is our operationalization for an agent’s sensitivity to opinion clustering while assigning identity groups, modulates the influence of open-mindedness on polarization. In simulations where agents were highly sensitive and perceived many identity clusters, open-mindedness did not mitigate polarization as much as in those where agents were less sensitive to clustering. Finally, among all our experimental variables polarization was most strongly predicted by the heterogeneity in open-mindedness.
These findings are a non-trivial contribution to the utilization of agent-based modeling. Though group identity is modeled in other contexts, it has not been integrated into the broadly used HK model. The additional impact of group identity and clustering is an important component of our understanding of real-world social behavior. This reinforces the notion that group identity itself has explanatory power (Hornsey 2008; Turner et al. 1987).
Our results add to a body of work that demonstrate that it is possible for bi-polarization to emerge even without repulsion between dissimilar individuals (Flache et al. 2017; Kurahashi-Nakamura et al. 2016; Mäs & Flache 2013). The implementation of the meta-contrast principle of Self-Categorization Theory in our model took into account dissimilarity only while assigning group identities, but did not assume that these assignments manifest as repulsion or negative influence. The additional communication barriers introduced due to social identity are sufficient to drive polarization as well as formation of multiple clusters or a "fracturing" of the opinion space.
We also looked at how varying our identity parameter SPIRO influences polarization. From our color plots it is evident that SPIRO modulates the influence of \(\varepsilon\), which is the main parameter of the HK model, on the system dynamics. Since higher SPIRO values lead to a larger number of identity groups being detected, the highest SPIRO values fracture the opinion space beyond bi-polarization independently of the average \(\varepsilon\).
This effect of higher SPIRO values driving the system to behave more in accordance with identity dynamics can be seen as paralleling the sociological phenomenon of deindividuation (Reicher et al. 1995) in the context of social identity, but with the key difference that the extent of deindividuation is not modulated by social context. With this in mind, we recognize that future iterations of our model ought to include elements representing social context, so that the balance between interpersonal and identity-driven dynamics is more realistically mediated by the environment.
We also find it interesting that modeling social identity as an observer-dependent phenomenon did not exert as much influence on the dynamics as we had expected. This can be seen from both our regression results and the aggregate behavior of our models (Figure 3) which suggests qualitatively similar model behavior between VBI and VBVI. While our step-wise regression revealed a significant effect of \(\sigma_{SPIRO}\), the magnitude of this effect is far weaker than our expectation. This is particularly noteworthy in recognition of the fact that letting different agents use different criteria to determine co-members is computationally very expensive. However, we also recognize the need for caution with this inference as there may be subtle effects of letting social identity memberships to vary across observers that our macro analysis may not capture.
Despite the presence of identity dynamics which clearly drive polarization, the strongest predictor of polarization in our full model is the heterogeneity in open-mindedness. The strong consensus-driving effect of variance in \(\varepsilon\) has previously been studied by Lorenz (2009). It was very interesting to us to observe that the strength of this effect was even higher than that of our identity variables.
The effect of heterogeneity on alleviating polarization can be understood through at least two computational possibilities. Firstly, having high variance in naturalistic distributions of openness such as in our model means that in any given simulation there will likely be some outlier agents with high open-mindedness that can act as ‘bridging agents’. Essentially open-minded agents may more strongly influence dynamics than close-minded agents, and thus exert a disproportionate consensus-driving effect. This speculated mechanism is also consistent with the observation that moderately high heterogeneity makes the system behave more sensitively to its initial conditions (Figure 2). Specifically, in any given simulation the initial opinion positions and corresponding sampled \(\varepsilon\) values would determine the effectiveness of bridging agents. This effect also predicts that increasing heterogeneity even further ought to collapse the transition region since having more outliers should make it more likely that there are enough bridging agents to promote consensus.
A distinct and more intriguing effect of heterogeneity however was detected in Jan Lorenz’s work (Lorenz 2009), which effectively showed that heterogeneity can promote consensus even in the absence of extraordinarily open-minded agents. This effect is emergent from the complex temporal dynamics driven by the interplay between agents with different \(\varepsilon\) values. Put perhaps a little simplistically, open- and close-minded agents appear to play distinct roles in promoting consensus, and thus having the presence of both types of agents can drastically drive consensus even in comparison to scenarios with only open-minded agents. We adopted a more naturalistic distribution of openness as opposed to the few pre-determined values used by Lorenz, and observe a similarly subtle and complex interplay between the influence of agents with different \(\varepsilon\) values which may go further in explaining the strong effect of heterogeneity in our model (Appendix D).
Model characteristics
Our richest model VBVI captures the dynamics of social identity in the context of opinion formation and dissemination mediated by social influence. We take a classical HK model and include emergent opinion-dependant social identity dynamics between agents such that agents are only influenced by others that satisfy an opinion-based criteria as well as an identity-based criteria. The opinion-based criteria refers to the classical HK rule that thresholds opinion distances, while the identity criteria requires the speaking agent to be perceived as being in the same identity group as the listener. Moreover we assume naturalistic distributions for agent variables such as conformity, openness, and SPIRO.
In contrast with some of the existing ABM formulations of social identity in literature, we make simplified assumptions about the origin of social identity by choosing not to model all of the complex psychological processes that give rise to social identification such as social context, normative fit, accessibility, and the interplay of personal as opposed to social identity (some of these ideas are expanded upon below; for review see Wijermans et al. 2023). Instead, we assume that identification can occur on the basis of opinions alone, and via a mechanism that conceptually parallels the idea of comparative fit, specifically the principle of meta-contrast. This was an appropriate modeling choice for our purposes, since the main variables in our model are also the main variables of interest to us, namely openness, social identity, and the associated distribution parameters. That is of course not to say that these aforementioned features of the Social Identity Approach that our model ignores or takes for granted are not important. Through simulations we were also able to establish some of our other model parameters – mean and variance of conformity, and the variance of SPIRO – did not have a strong influence on dynamics, which allows us to focus our efforts on studying our aforementioned variables of interest.
While most ABM’s of social identity in the context of opinion dynamics assume static and often a priori identity assignments (Scholz et al. 2023), the dynamic social identity component in our identity models operates by assigning identity group tags to agents based on clustering patterns in the opinion space at every time step. Moreover, we assumed observer-dependent identity group assignments, consistent with the theoretical formulation of SCT which has always implied that group membership is perceived from the perspective of an individual: ‘\(\dots\) any collection of stimuli is more likely to be categorized as an entity\(\dots\) to the degree that the differences between those stimuli on relevant dimensions\(\dots\) are perceived as less than the differences between that collection and other stimuli’ (Turner et al. 1987).
Model limitations
Here we discuss some aspects of social identity and self-categorization that are either not explicitly modeled or not fully captured by our models.
Multiple social identities and salience
According to SCT, individuals can identify with multiple identity groups which can have conflicting influences on one’s behavior. An important construct in the Social Identity Approach is salience - which determines which of the multiple possible identities associated with an individual influence their behavior most strongly at a given time. Salience is dependent on social and psychological context at any given time, such that the most salient identity can rapidly change for an individual, leading to shifts in behavior mirroring the shift in their currently most salient social identity.
Although SPIRO is conceptually related to salience, it is a distinct concept. An agent with a higher SPIRO is likely to perceive a smaller, more fine-grained identity group and behave according to that characterization of the opinion space, analogous as per SCT to how an individual can be influenced most by one of their least populous, most immediate identity group when this identity becomes salient. The "Proximity" in the name "Salience of Proximity in Identity Relevant Opinions" refers to proximity in the opinion space. While our formulation of SPIRO hinged on our assumption that identity groups are formed based on opinion alone, conceptually SPIRO is generalizable to identity group assignments on the basis of any other continuous agent characteristic. In this study we modeled SPIRO as a static characteristic for an individual, and looked at the effect of varying SPIRO across different agents. One possibility for future work is to integrate our implementation of SPIRO with an explicit model of identity salience, by modeling a dynamic social environment that cause SPIRO values to vary within an individual agent.
Prototypicality and prototypical behaviors
According to the Social Identity Approach, one way through which social identity groups exert their influence on social dynamics is through prototypical behaviors or norms that characterize the group. Since a core theoretical feature of Self-Categorization Theory is that social identity influences cognition and behavior through a dynamic self-concept held by an individual, a more comprehensive formalization of the theory could account for identity-driven changes in agent behavior beyond disregarding out-group information. Further, according to the theory, group norms not only influence behavior of people identifying with the group at a given time, they also play a role in the process of categorization as observers use stereotypes as aids for categorization – a concept known as ‘normative fit’.
One way to operationalize the influence exerted by the prototypical features of a social identity group is to define a prototypical group characteristic – such as an average opinion – which is explicitly computed and adopted by identity group members. In our identity models we do not explicitly model prototypical opinions of an identity group – rather identity groups have aggregate characteristics that are dynamic but do not exert an influence of their own. Moreover as our identity group assignments are based on opinions, their aggregate characteristics are also limited to the space of opinions. A richer model is conceivable where identity groups are not only assigned dynamically, but also exert their influence on the opinion space through explicitly defined prototypical opinions, or by having other prototypical identity group characteristics – or norms – such as a prototypical openness value. Similarly, while our model operationalizes the categorization process as purely based on comparative fit, it would be possible to account for the template-matching effects expected if a normative fit mechanism were also in play if an observer had access to prototypical opinions of different identity groups.
Future directions
As mentioned in the first section, we are aiming to build towards theories in communication research that can expand our understanding of polarization in the context of modern technology. such as the Reinforcing Spirals Model (RSM; Slater 2007). We are also interested in building models that can also produce system dynamics expected from more classical communication theories such as the Spiral of Silence (Noelle-Neumann 1974). Simulating the behaviors expected to be observed by these theories would require us to build a more rich model of the environment the agents are embedded in. While we have currently assumed a complete network, as is common in simulation studies with bounded-confidence models, we will in the future incorporate geographical constraints, differential broadcasting power, and traditional and social media agents into our model.
RSM also defines characteristic norms, especially with regards to openness and closedness of identity groups. Although we define the distribution of the openness of the population, the average openness of identity groups is an endogenous, emergent variable. In our model openness is a stable attribute of individuals that are not influenced by the average openness of their social groups. However, there are at least two possible directions future work can take to study the openness of identity groups. Firstly, an effective openness can be computed for any agent sub-population which can be taken as the ratio of average number of communication partners in the sub-population to expected number of communication partners. Secondly, while we don’t explicitly impose constraints on the openness of agents in specific identity groups, it is still possible that the emergent groups may differ in their openness because of the dynamics of the model.
Song & Boomgaarden (2017) modeled the dynamic positive feedback between media selectivity and attitude polarization with attention to several variables of interest including prior attitudes, political context, counterattitudinal media exposure, and impact of exposure. A key finding in their study is that allowing media influence to be modulated by attitude-confirming signals from interpersonal communication partners strengthens the polarizing influence of media selectivity. A next natural step to their study is to model two more critical variables in RSM – identity and openness. Our development of a continuous HK model with identity dynamics allows us to integrate the media and context variables with a flexible agent model that has naturalistic distributions of innate agent characteristics.
Our simulation work presented in this article aims to bring us closer to operationalizing the conceptual models from communications research into computational models. Formalizng and simulating these conceptual models can deepen their understanding since we may encounter unexpected behaviors and emergent phenomena that would have been hard to predict without simulations.
Code and Data
All codes and data related to this study are available at: https://github.com/frantisek901/Spirals under the folder "/IdentityPaper/".Notes
- Although it may be mathematically more intuitive to assign agents to opinion-based groups using a clustering technique such as DBScan (Campello et al. 2013), we chose to convert to a network-based representation and back as it better reflected our conceptualization of the process of opinion-based identity group formation, which is fundamentally a grouping mechanism emerging out of interpersonal ties based on opinions. However, we would expect to get qualitatively similar outcomes from simply detecting clusters in the opinion space.↩︎
- The weight of an edge between nodes representing agents \(i\) and \(j\) in the proximity network can be given by: \(w_{i, j} = 1 - \frac{|o_{i}(t) - o_{j}(t)|}{2}\)↩︎
- Values drawn from beyond the variable’s range are resampled.↩︎
- To reduce the number of Louvain Community Detection passes per time step, the drawn sample is replaced by its closest value from a set of \(8\) possible values of \(\{0.15, 0.25, 0.35, 0.45, 0.55, 0.65, 0.75, 0.85\}\).↩︎
- For this analysis we reduced the parameter space along \({\mu_\varepsilon}\) to have 5 values evenly distributed between the minimum and maximum \({\mu_\varepsilon}\) instead of the 21 possible values used in the simulations.↩︎
Appendix A: High-Level Model Characteristics
| Model | N | Independent Variables | Min | Max | IQR | Median | Mean | SD | SE | CI |
|---|---|---|---|---|---|---|---|---|---|---|
| DHK | 84 | ε, α, Even_Pop? | 0 | 0.419 | 0.361 | 0.282 | 0.199 | 0.177 | 0.019 | 0.038 |
| RHK | 5040 | ε, α, Even_Pop? | 0 | 0.534 | 0.371 | 0.304 | 0.242 | 0.167 | 0.002 | 0.005 |
| VB | 80640 | με, σε, μα, σα, Even_Pop? | 0 | 0.872 | 0.251 | 0.026 | 0.114 | 0.157 | 0.001 | 0.001 |
| VBI | 483840 | με, σε, μα, σα, SPIRO, Even_Pop? | 0 | 0.937 | 0.154 | 0.408 | 0.378 | 0.177 | 0.000 | 0.000 |
| VBVI | 1935360 | με, σε, μα, σα, μSPIRO, σSPIRO, Even_Pop? | 0 | 0.940 | 0.208 | 0.405 | 0.354 | 0.195 | 0.000 | 0.000 |
Appendix B: Average Polarization as a Function of Average Openness
Appendix C: Other Dependent Measures - Diversity and Extremeness
Appendix D: Analyzing the Effects of Heterogeneity and Identity in Individual Simulations
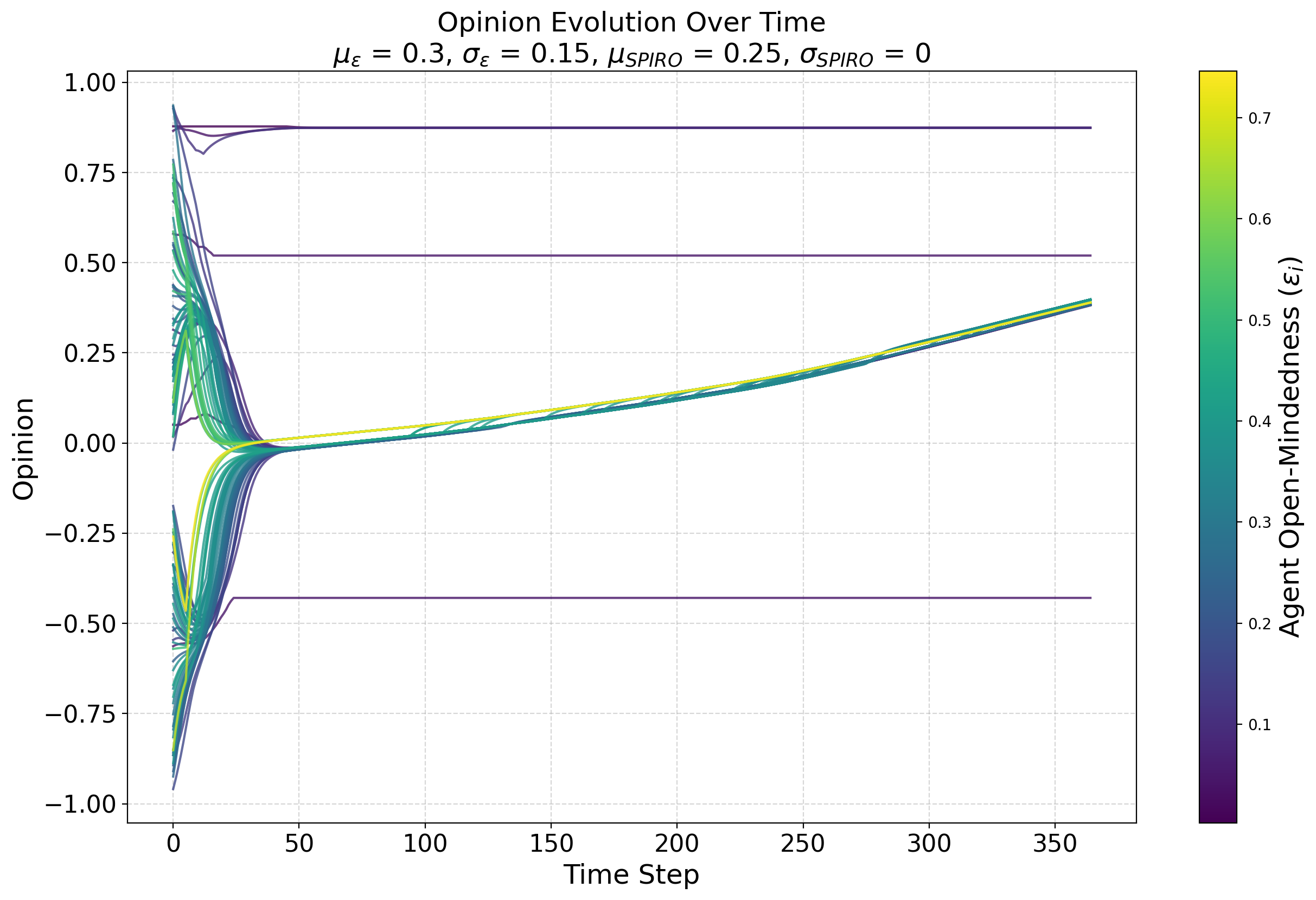
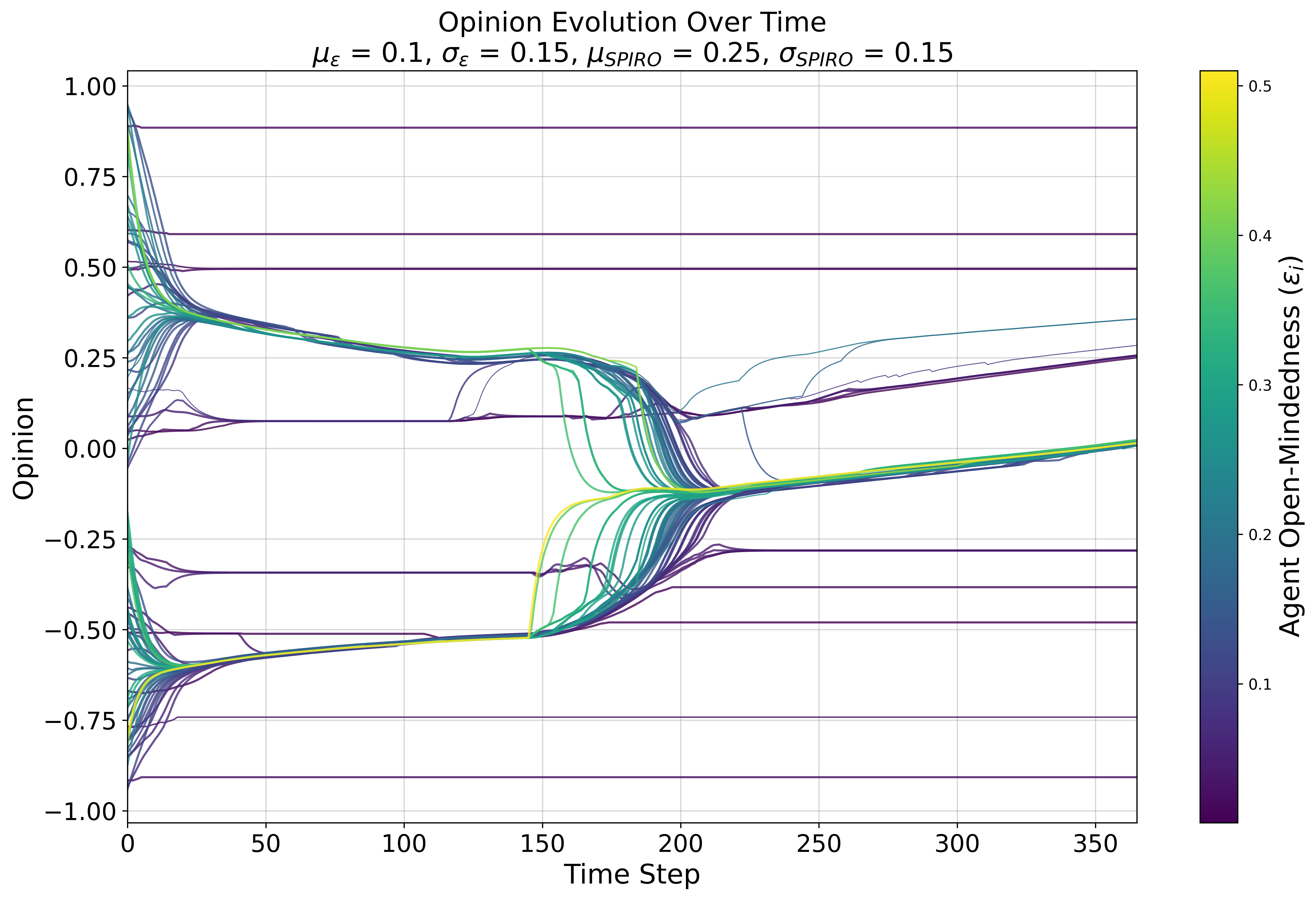
Although a detailed fine-grained analysis of individual agent behavior in our model is beyond the scope of the current article, in this section we present some observations from visualizing the evolution of opinions in individual simulations that can help understand the macro-behavior of our model. For example, the role of open-minded agents can be understood to involve the integration of information from a wide range of agents in the opinion space and prediction of the consensus position – in Figure 6 the most open minded agent arrives quickly at a position that approximates the eventual position of compromise for the two clusters formed around time step 20. One can also infer that it is the open-minded agents that likely drive the upwards drifting of the large consensus group formed after time step 100. On the other hand, the distribution of close-minded agents over the opinion space shapes the dynamics of the system with their stability – the likelihood of consensus and point of convergence is dependent on how they are distributed. Close-minded agents at the extremities can pull large convergence groups towards themselves as long as there are enough open-minded agents within the convergence group (Figure 7). Such analysis also sheds some light on how identity and heterogeneous identity perceptions shape model behavior. Figure 8 shows the convergence of two large identity groups, possibly facilitated by agents with more inclusive perceptions of identity (thicker lines correspond to lower SPIRO values).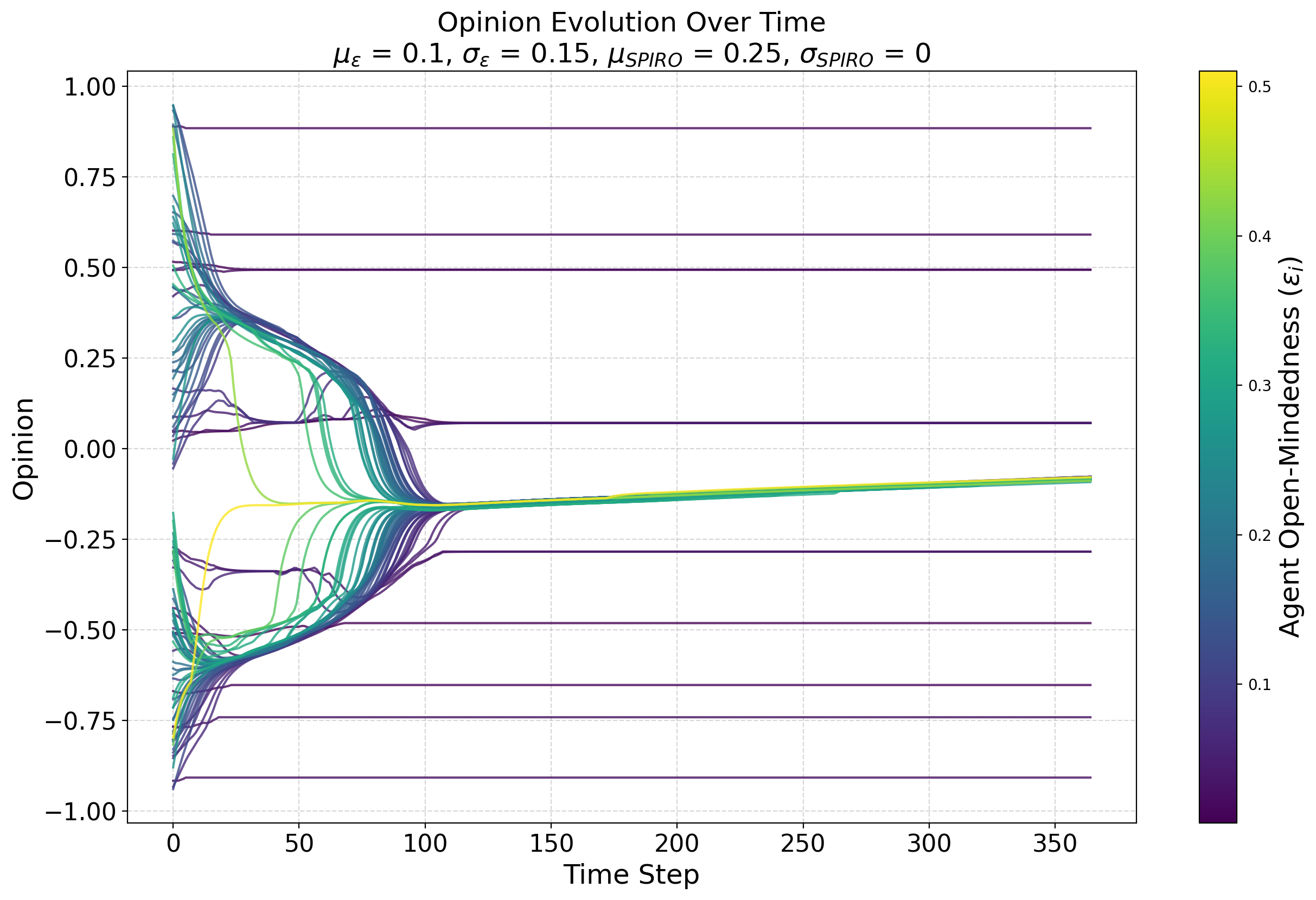
References
APERGIS, N., & Pinar, M. (2023). Corruption and partisan polarization: Evidence from the European Union. Empirical Economics, 64(1), 277–301. [doi:10.1007/s00181-022-02247-z]
ASCH, S. E. (1955). Opinions and social pressure. Scientific American, 193(5), 31–35. [doi:10.1038/scientificamerican1155-31]
ASCH, S. E. (1965). Social Psychology. New York, NY: Prentice-Hall.
BASSI, A., Morton, R. B., & Williams, K. C. (2011). The effects of identities, incentives, and information on voting. The Journal of Politics, 73(2), 558–571. [doi:10.1017/s0022381611000284]
BENSON, J. (2024). Democracy and the epistemic problems of political polarization. American Political Science Review, 118(4), 1719–1732. [doi:10.1017/s0003055423001089]
BILLIG, M., & Tajfel, H. (1973). Social categorization and similarity in intergroup behaviour. European Journal of Social Psychology, 3(1), 27–52. [doi:10.1002/ejsp.2420030103]
BIONDI, E., Boldrini, C., Passarella, A., & Conti, M. (2023). Dynamics of opinion polarization. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 53(9), 5381–5392. [doi:10.1109/tsmc.2023.3268758]
BLIUC, A.-M., McGarty, C., Reynolds, K., & Muntele, D. (2007). Opinion-based group membership as a predictor of commitment to political action. European Journal of Social Psychology, 37(1), 19–32. [doi:10.1002/ejsp.334]
BLONDEL, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of Statistical Mechanics, 2008(10), P10008. [doi:10.1088/1742-5468/2008/10/p10008]
BOLSEN, T., Druckman, J. N., & Cook, F. L. (2014). The influence of partisan motivated reasoning on public opinion. Political Behavior, 36(2), 235–262. [doi:10.1007/s11109-013-9238-0]
BOLSEN, T., & Shapiro, M. (2017). The US news media, polarization on climate change, and pathways to effective communication. Environmental Communication, 12, 1–15. [doi:10.1080/17524032.2017.1397039]
CAMPELLO, R. J., Moulavi, D., & Sander, J. (2013). Density-based clustering based on hierarchical density estimates. Pacific-Asia Conference on Knowledge Discovery and Data Mining. [doi:10.1007/978-3-642-37456-2_14]
CARPENTRAS, D., Lueders, A., Maher, P. J., O’Reilly, C., & Quayle, M. (2023). How polarization extends to new topics: An agent-Based model derived from experimental data. Journal of Artificial Societies and Social Simulation, 26(3), 2. [doi:10.18564/jasss.5105]
CASAL Bértoa, F., & Rama, J. (2021). Polarization: What do we know and what can we do about it? Frontiers in Political Science, 3, 687695. [doi:10.3389/fpos.2021.687695]
CATAPANO, R., Tormala, Z. L., & Rucker, D. D. (2019). Perspective taking and self-Persuasion: Why “putting yourself in their shoes” reduces openness to attitude change. Psychological Science, 30(3), 424–435. [doi:10.1177/0956797618822697]
CIKARA, M., Van Bavel, J. J., Ingbretsen, Z. A., & Lau, T. (2017). Decoding “us” and “them”: Neural representations of generalized group concepts. Journal of Experimental Psychology, 146(5), 621–631. [doi:10.1037/xge0000287]
COHEN, G. L. (2003). Party over policy: The dominating impact of group influence on political beliefs. Journal of Personality and Social Psychology, 85(5), 808–822. [doi:10.1037/0022-3514.85.5.808]
COSCIA, M., & Rossi, L. (2022). How minimizing conflicts could lead to polarization on social media: An agent-based model investigation. PLoS One, 17(1), e0263184. [doi:10.1371/journal.pone.0263184]
DAVID, B., & Turner, J. C. (2001). Majority and minority influence: A single process self-categorization analysis. Group Consensus and Minority Influence: Implications for Innovation, 324, 91–121.
DICKSON, E. S., & Scheve, K. (2006). Social identity, political speech, and electoral competition. Journal of Theoretical Politics, 18(1), 5–39. [doi:10.1177/0951629806059594]
DIEP, H. T., Kaufman, M., & Kaufman, S. (2023). An agent-Based statistical physics model for political polarization: A monte carlo study. Entropy, 25(7). [doi:10.3390/e25070981]
DIMAS, J., & Prada, R. (2014). Dynamic identity model for agents. Multi-Agent-Based Simulation XIV: International Workshop, MABS 2013, Saint Paul, MN, USA, May 6-7, 2013, Revised Selected Papers. [doi:10.1007/978-3-642-54783-6_3]
DOW, B. J., Wang, C. S., & Whitson, J. A. (2023). Support for leaders who use conspiratorial rhetoric: The role of personal control and political identity. Journal of Experimental Social Psychology, 104, 104403. [doi:10.1016/j.jesp.2022.104403]
DOWNEY, D. J. (2022). Polarization and persuasion: Engaging sociology in the moral universe of a divided democracy. Sociological Perspectives, 65(6), 1029–1051. [doi:10.1177/07311214221124443]
DRUCKMAN, J. N., & Bolsen, T. (2011). Framing, motivated reasoning, and opinions about emergent technologies. Journal of Communication, 61(4), 659–688. [doi:10.1111/j.1460-2466.2011.01562.x]
ESTEBAN, J. M., & Ray, D. (1994). On the measurement of polarization. Econometrica, 62(4), 819–851. [doi:10.2307/2951734]
FLACHE, A. (2018). Between monoculture and cultural polarization: Agent-based models of the interplay of social influence and cultural diversity. Journal of Archaeological Method and Theory, 25(4), 996–1023. [doi:10.1007/s10816-018-9391-1]
FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2. [doi:10.18564/jasss.3521]
FU, G., & Zhang, W. (2014). Opinion dynamics of modified Hegselmann-Krause model with group-based bounded confidence. IFAC Proceedings Volumes, 47(3), 9870–9874. [doi:10.3182/20140824-6-za-1003.02770]
HAN, W., Huang, C., & Yang, J. (2019). Opinion clusters in a modified Hegselmann-Krause model with heterogeneous bounded confidences and stubbornness. Physica A: Statistical Mechanics and Its Applications, 531, 121791. [doi:10.1016/j.physa.2019.121791]
HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2.
HELTZEL, G., & Laurin, K. (2020). Polarization in America: Two possible futures. Current Opinion in Behavioral Sciences, 34, 179–184. [doi:10.1016/j.cobeha.2020.03.008]
HOERNER, J. M., & Hobolt, S. B. (2021). Unity in diversity? Polarization, issue diversity and satisfaction with democracy. In S. Hobolt & T. Rodon (Eds.), Domestic Contestation of the European Union (pp. 169–188). London: Routledge. [doi:10.4324/9781003168539-10]
HORNSEY, M. J. (2008). Social identity theory and self-categorization theory: A historical review. Social and Personality Psychology Compass, 2(1), 204–222. [doi:10.1111/j.1751-9004.2007.00066.x]
JONES, D. R. (2015). Declining trust in congress: Effects of polarization and consequences for democracy. The Forum, 13, 375–394. [doi:10.1515/for-2015-0027]
JONES, I., Wang, R., Han, J., & Liu, H. (2016). Community cores: Removing size bias from community detection. Proceedings of the International AAAI Conference on Web and Social Media, 10(1), 603–606. [doi:10.1609/icwsm.v10i1.14780]
KAHAN, D. M., Hoffman, D. A., Braman, D., Evans, D., & Rachlinski, J. J. (2012). “They saw a protest”: Cognitive illiberalism and the speechconduct distinction. Stanford Law Review, 64(4), 851–906.
KALVAS, F., Ramaswamy, A., & Slater, M. (2023). Identity drives polarization: Advancing the Hegselmann-Krause model by identity groups. In F. Squazzoni (Ed.), Advances in Social Simulation. ESSA 2022 (pp. 249–262). Cham: Springer. [doi:10.1007/978-3-031-34920-1_20]
KOU, G., Zhao, Y., Peng, Y., & Shi, Y. (2012). Multi-level opinion dynamics under bounded confidence. PLoS One, 7(9), e43507. [doi:10.1371/journal.pone.0043507]
KURAHASHI-NAKAMURA, T., Mäs, M., & Lorenz, J. (2016). Robust clustering in generalized bounded confidence models. Journal of Artificial Societies and Social Simulation, 19(4), 7. [doi:10.18564/jasss.3220]
LEEPER, T. J., & Slothuus, R. (2014). Political parties, motivated reasoning, and public opinion formation. Political Psychology, 35, 129–156. [doi:10.1111/pops.12164]
LEVIN, S. A., Milner, H. V., & Perrings, C. (2021). The dynamics of political polarization. Proceedings of the National Academy of Sciences, 118(50), e2116950118. [doi:10.1073/pnas.2116950118]
LI, J., & Xiao, R. (2017). Agent-Based modelling approach for multidimensional opinion polarization in collective behaviour. Journal of Artificial Societies and Social Simulation, 20(2), 4. [doi:10.18564/jasss.3385]
LIU, C. C., & Srivastava, S. B. (2015). Pulling closer and moving apart: Interaction, identity, and influence in the US Senate, 1973 to 2009. American Sociological Review, 80(1), 192–217. [doi:10.1177/0003122414564182]
LOBO, I., Dimas, J., Mascarenhas, S. M., Rato, D., & Prada, R. (2023). When "I" becomes "We": Modelling dynamic identity on autonomous agents. Journal of Artificial Societies and Social Simulation, 26(3), 9. [doi:10.18564/jasss.5146]
LORENZ, J. (2007). Continuous opinion dynamics under bounded confidence: A survey. International Journal of Modern Physics C, 18, 1819–1838. [doi:10.1142/s0129183107011789]
LORENZ, J. (2009). Heterogeneous bounds of confidence: Meet, discuss and find consensus! Complexity. [doi:10.1002/cplx.20295]
LU, P., Zhang, Z., & Li, M. (2021). Big data-drive agent-based modeling of online polarized opinions. Complex & Intelligent Systems, 7(6), 3259–3276. [doi:10.1007/s40747-021-00532-5]
MÄS, M., & Flache, A. (2013). Differentiation without distancing. Explaining bi-Polarization of opinions without negative influence. PLoS ONE, 8(11), e74516.
MCCOY, J., Rahman, T., & Somer, M. (2018). Polarization and the global crisis of democracy: Common patterns, dynamics, and pernicious consequences for democratic polities. American Behavioral Scientist, 62(1), 16–42. [doi:10.1177/0002764218759576]
MONTALVO, J. G., & Reynal-Querol, M. (2003). Religious polarization and economic development. Economics Letters, 80(2), 201–210. [doi:10.1016/s0165-1765(03)00080-6]
NOELLE-NEUMANN, E. (1974). The spiral of silence a theory of public opinion. Journal of Communication, 24(2), 43–51. [doi:10.1111/j.1460-2466.1974.tb00367.x]
PETERSEN, M. B., Skov, M., Serritzlew, S., & Ramsøy, T. (2013). Motivated reasoning and political parties: Evidence for increased processing in the face of party cues. Political Behavior, 35(4), 831–854. [doi:10.1007/s11109-012-9213-1]
REICHER, S. D., Spears, R., & Postmes, T. (1995). A social identity model of deindividuation phenomena. European Review of Social Psychology, 6(1), 161–198. [doi:10.1080/14792779443000049]
SALZARULO, L. (2006). A continuous opinion dynamics model based on the principle of Meta-Contrast. Journal of Artificial Societies and Social Simulation, 9(1), 13.
SCHOLZ, G., Wijermans, N., Paolillo, R., Neumann, M., Masson, T., Chappin, E., Templeton, A., & Kocheril, G. (2023). Social agents? A systematic review of social identity formalizations. Journal of Artificial Societies and Social Simulation, 26(2), 6. [doi:10.18564/jasss.5066]
SCHWEITZER, F., Krivachy, T., & Garcia, D. (2020a). An agent-Based model of opinion polarization driven by emotions. Complexity, 2020(1), 5282035. [doi:10.1155/2020/5282035]
SCHWEITZER, F., Krivachy, T., & Garcia, D. (2020b). An agent-Based model of opinion polarization driven by emotions. Complexity, 2020, 5282035. [doi:10.1155/2020/5282035]
SHERIF, C. W., Kelly, M., Rodgers Jr., H. L., Sarup, G., & Tittler, B. I. (1973). Personal involvement, social judgment, and action. Journal of Personality and Social Psychology, 27(3), 311–328. [doi:10.1037/h0034948]
SHERIF, M. (1936). The Psychology of Social Norms. Harper Collins.
SHERIF, M., & Hovland, C. I. (1961). Social Judgment: Assimilation and Contrast Effects in Communication and Attitude Change. Yale Univerity Press.
SLATER, M. D. (2007). Reinforcing spirals: The mutual influence of media selectivity and media effects and their impact on individual behavior and social identity. Communication Theory, 17(3), 281–303. [doi:10.1111/j.1468-2885.2007.00296.x]
SMALDINO, P., Pickett, C., Sherman, J., & Schank, J. (2012). An agent-based model of social identity dynamics. Journal of Artificial Societies and Social Simulation, 15(4), 7. [doi:10.18564/jasss.2030]
SMITH, C. T., Ratliff, K. A., & Nosek, B. A. (2012). Rapid assimilation: Automatically integrating new information with existing beliefs. Social Cognition, 30(2), 199–219. [doi:10.1521/soco.2012.30.2.199]
SMITH, L. G. E., Thomas, E. F., Bliuc, A.-M., & McGarty, C. (2024). Polarization is the psychological foundation of collective engagement. Communications Psychology, 2(1), 41. [doi:10.1038/s44271-024-00089-2]
SMITH, L. G. E., Thomas, E. F., & McGarty, C. (2015). “We Must Be the Change We Want to See in the World”: Integrating norms and identities through social interaction. Political Psychology, 36(5), 543–557. [doi:10.1111/pops.12180]
SONG, H., & Boomgaarden, H. G. (2017). Dynamic spirals put to test: An agent-based model of reinforcing spirals between selective exposure, interpersonal networks, and attitude polarization. Journal of Communication, 67(2), 256–281. [doi:10.1111/jcom.12288]
SU, W., Gu, Y., Wang, S., & Yu, Y. (2017). Partial convergence of heterogeneous Hegselmann-Krause opinion dynamics. Science China Technological Sciences, 60(9), 1433–1438. [doi:10.1007/s11431-016-0615-x]
TAJFEL, H., Billig, M. G., Bundy, R. P., & Flament, C. (1971). Social categorization and intergroup behaviour. Eur. J. Soc. Psychol., 1(2), 149–178. [doi:10.1002/ejsp.2420010202]
TAJFEL, H., Turner, J. C., Austin, W. G., & Worchel, S. (1979). An integrative theory of intergroup conflict. Organizational Identity: A Reader, 56(65), 9780203505984–9780203505916. [doi:10.1093/oso/9780199269464.003.0005]
TANG, T., Ghorbani, A., Squazzoni, F., & Chorus, C. G. (2022). Together alone: A group-based polarization measurement. Quality & Quantity, 56(5), 3587–3619. [doi:10.1007/s11135-021-01271-y]
TÖRNBERG, P., Andersson, C., Lindgren, K., & Banisch, S. (2021). Modeling the emergence of affective polarization in the social media society. PLoS One, 16(10), e0258259.
TURNER, J. C. (1975). Social comparison and social identity: Some prospects for intergroup behaviour. European Journal of Social Psychology, 5(1), 1–34. [doi:10.1002/ejsp.2420050102]
TURNER, J. C., Hogg, M. A., Oakes, P. J., Reicher, S. D., & Wetherell, M. S. (1987). Rediscovering the Social Group: A Self-Categorization Theory. Cambridge, MA: Basil Blackwell.
TURNER, J. C., & Reynolds, K. J. (2011). Self-categorization theory. Handbook of Theories in Social Psychology, 2(1), 399–417. [doi:10.4135/9781446249222.n46]
VAN Bavel, J. J., Packer, D. J., & Cunningham, W. A. (2008). The neural substrates of in-group bias: A functional magnetic resonance imaging investigation. Psychological Science, 19(11), 1131–1139. [doi:10.1111/j.1467-9280.2008.02214.x]
WEIMER, C. W., Miller, J. O., Hill, R. R., & Hodson, D. D. (2022). An opinion dynamics model of meta-contrast with continuous social influence forces. Physica A: Statistical Mechanics and Its Applications, 589, 126617. [doi:10.1016/j.physa.2021.126617]
WIJERMANS, N., Scholz, G., Neumann, M., Paolillo, R., Templeton, A., Netshandama, V., & Neuberger, D. (2023). Editorial: Social identity modelling. Journal of Artificial Societies and Social Simulation, 26(3), 15. [doi:10.18564/jasss.5188]