A Theoretical Analysis of How Multiple Leadership and Flattened Status Structures Affect Cooperation in Task Groups

Introduction

Status inequality and group cooperation are topics each receiving longstanding attention in sociology (Correll & Ridgeway 2006; Hechter 1987; Kollock 1998; Sauder et al. 2012; Whitmeyer 2007). Social hierarchy and status inequality are widely regarded as causes of social and health problems (Burns et al. 2014; Hemingway et al. 1997). Given the negative consequences of status inequality, it is a puzzle of why it is prevalent and persistent in human societies. Recently, some sociologists provided an explanation to the puzzle, contending that hierarchy may benefit the emergence of cooperation in groups against defection (Mark 2018; Simpson & Willer 2015). Indeed, fieldwork and experimental studies have shown that people tend to behave more cooperatively with leaders than without (Bolsen et al. 2014; Grossman & Baldassarri 2012; Hamman et al. 2011; Luo et al. 2007; Olken 2010). At the theoretical end, scholars show mathematically that status behavior can ensure the survival of cooperators against the ‘invasion’ of defectors in the social-dilemma setting (Mark 2018). Status hierarchies are a fundamental feature of task groups, with a single individual often emerging as the highest-status leader while others hold varying levels of status beneath them. However, in rare cases, multiple high-status individuals may share leadership, creating a more ambiguous structure that influences cooperation in distinct ways.

To deepen our understanding of how status inequality shapes cooperation, we turn attention to a rare but theoretically revealing configuration: the multiple-leader status structure. This study presents a theoretical analysis of how multiple leadership, flattened status structures, and deviations from traditional hierarchy impact cooperation in task groups. Using an evolutionary game-theoretic approach, we investigate how cooperation emerges and persists in these uncommon structures and compare their effectiveness to single-leader hierarchies. Despite significant progress, it remains unclear how alternative hierarchical structures influence the emergence of cooperation in task groups. Specifically, if a status hierarchy is defined by the presence of a single leader with the remaining members as followers, what happens when there are multiple leaders? To what extent might multi-leadership dampen the emergence of cooperation? In this paper, we present an evolutionary model to address these questions. Our findings demonstrate that while multi-leadership structures can sustain cooperation, they do so less effectively than single-leader hierarchies. This result helps to explain why task-oriented groups rarely feature multiple leaders.

While existing theoretical accounts predominantly favor the eventual emergence of single-leadership structures, anecdotal reports seem to suggest that multiple leaders may sometimes coexist within a group. This observation raises an important question: Is cooperation possible in such environments and, if so, how? We focus on cohesive, task-oriented groups where leadership roles emerge organically rather than being pre-assigned or formally structured. A useful analogy can be drawn from collaborative research teams, where leadership roles often emerge organically across different domains of expertise, such as theoretical development, methodological design, and data analysis. In such groups, individuals may assume leadership roles in specific areas while still contributing to a shared objective. However, this distributed leadership structure can create ambiguity in hierarchical clarity, potentially influencing how much individuals are willing to contribute to the collective goal. This scenario reflects the type of multi-leadership dynamics our model aims to capture.

Motivation

In what follows, we present an evolutionary model to formally support the argument above. Evolutionary game theory (EVG) is a tool widely used by both biologists and social scientists to formalize explanations for the emergence of human behavior and social institutions (Lee et al. 2018; Nowak & Sigmund 2004; Weibull 1997). In particular, EVG aims to identify the conditions under which the behavior of interest, represented by a strategy in a game, spreads within a specific population or social context and remains resilient against displacement by alternative behaviors over time. The emergence of the target behavior is measured by its evolutionary fitness, in the sense that the more benefits accrued to the behavior, the more likely it would be adopted by an actor, or by more actors. As far as cooperation is concerned, scientists have used the EVG framework to pin down an array of mechanisms by which the free-riding problem can be mitigated in cooperation dilemmas (Nowak 2006b). Below, we present an evolutionary model to investigate the effect of single-leadership and multi-leadership on the emergence of cooperation.

Status hierarchies are typically characterized by a single leader overseeing multiple followers. However, the existence of multiple leaders within a group may be theoretically plausible for the following reasons. First, organizational sociology argues that there could be multiple leaders in a group when the audiences are different. When a group is composed of members with heterogeneous preferences and expectations, it is natural to see that leaders are ranked differently. Take academic units for example. Kovács and Liu (Kovács & Liu 2016) show that in multi-disciplinary departments, such as management in business school, faculty rank academic journals differently in accordance with their background and training. Although each journal can be ranked by citation impacts – global status, scholars tend to emphasize the journals’ status in their fields – local status, when evaluating their academic performance.

Secondly, a group may have multiple leaders, at least in the short run, because of the plurality of subcultures. As noted by sociologist Gary Fine, “Participants engage in multiple scenes, simultaneously and sequentially, and in the process become aware of the scenes that serve as models or as points of differentiation.” (Fine 2010) (p. 371), different subcultures could generate local leaders in the group. It is noteworthy that as actors may participate in multiple subgroups and shift their affiliations from time to time, the boundaries of these subgroups are far from clear-cut. As a consequence, the best representation of interaction with the group, as would be demonstrated in the paper, is a web of networks (Fine 2012).

If, in theory, multiple leaders can exist within a group, why are they rarely observed in practice? One possible explanation is that multi-leadership facilitates cooperation less effectively than single leadership. Cooperation is essential for the functioning – and even survival – of a group, particularly in situations of intergroup conflict (Bornstein 2003; Choi & Bowles 2007; De Dreu et al. 2010). The degree of cooperation achieved within a group reflects the strength of its underlying structure. Thus, if single leadership fosters greater cooperation than multi-leadership, this difference would help explain the prevalence of single-leader hierarchies over multi-leader structures. This raises an important question: if multiple leaders can emerge within a group, why do we predominantly observe single-leader structures? One possible explanation is that multi-leadership represents an early, transient phase of hierarchy formation rather than a stable equilibrium. Groups initially characterized by competing leadership signals may eventually consolidate into clearer hierarchical structures, enabling stronger coordination and cooperation.

In what follows, we present an evolutionary model to formally support the argument above. Evolutionary game theory is a tool widely used by both biologists and social scientists to formalize explanations for the emergence of human behavior and social institutions (Bendor & Swistak 2001; Bergstrom 2002; Nowak 2006a).In particular, EVG aims to identify the conditions under which the behavior of interest, represented by a strategy in a game, comes into being and remains stable against alternative behaviors in a given social context–a set of game settings. The emergence of the target behavior is measured by its evolutionary fitness, in the sense that the more benefits accrued to the behavior, the more (likely) it would be adopted by an actor, or by more actors. As far as cooperation is concerned, scientists have used the EVG framework to pin down an array of mechanisms by which the free-riding problem can be mitigated in cooperation dilemmas (Nowak 2006b). In the sections that follow, we introduce an evolutionary model to contrast the effects of multi-leadership and single leadership on the emergence of cooperation.

Model Formulation

Mark (Mark 2018) introduces a model where groups form hierarchies through preplay signaling, with status cooperators signaling either high or low confidence to establish a single recognized leader. Once a leader is identified, status cooperators imitate the leader’s cooperative behavior, ensuring mutual cooperation within the group. This single-leader hierarchy maximizes coordination and minimizes exploitation by defectors, making status cooperation (SC) an evolutionarily viable strategy under conditions where cooperation might otherwise fail.

In our model, we extend this framework by allowing for multi-leadership, reflecting the diversity of real-world group structures. Multi-leadership emerges during the signaling phase, where each individual signals high status with a probability inversely proportional to group size. Unlike Mark’s model, which forces convergence to a single leader, our approach retains the multi-leader structure when multiple individuals signal high status simultaneously. This modification captures scenarios where leadership roles are distributed among several individuals, often due to shared expertise, diverse audience expectations, or the absence of clear hierarchical distinctions. Also unlike Mark’s SC strategy, which assumes unconditional cooperation once a single leader is established, our strategy relies on conditional cooperation tied to hierarchy clarity. This approach reflects scenarios where ambiguity in leadership structures can reduce the willingness to cooperate. However, in situations where all group members are SCs and leadership clarity is guaranteed, Mark’s strategy may ensure higher evolutionary viability by fostering unconditional cooperation. Our model assumes a trade-off: conditional cooperation is beneficial in ambiguous or transitional contexts but may underperform in environments where hierarchical clarity and assortativity are strong. This distinction highlights the situational adaptability of the conditional cooperation strategy we propose.

The model assumes that as the number of leaders increases, hierarchical clarity diminishes, reducing the capacity to facilitate cooperation effectively. This trade-off reflects the challenges inherent in multi-leader hierarchies, where coordination may suffer despite potential benefits from distributed leadership. By incorporating probabilistic signaling and its implications for cooperation dynamics, our model generalizes Mark’s framework to accommodate a broader range of group structures, bridging the gap between strictly hierarchical and more egalitarian (or contestedly hierarchical) systems.

Given the similarity, we adapted the four-phase EVG of Mark’s paper (Mark 2018) to build our model. First, the group size is fixed at \(n\), among which some are cooperators (\(C\)) and others defectors (\(D\)). Second, in pursuing leadership, cooperators collectively determine the hierarchical structure by nominating themselves as leaders at the top level, while defectors always remain as passive followers at the bottom, alongside cooperators who do not seek leadership. Here, Mark requires the resultant group structure to be either single- or zero-leader, whereas we allow multi-leadership. See the next paragraph for the modification. Third, once leaders are selected out of cooperators, and a structure is formed, all cooperators decide whether to contribute to a common resource pool depending on the structure’s hierarchicalness, while defectors never contribute. All individuals receive their payoffs in this prisoner’s dilemma accordingly. Fourth and finally, the relative fitness of current cooperators and defectors determines the composition of the next generations of players. The whole game then iterates until only one type of individual remains.

We extended Mark’s model to include multi-leader hierarchies. As in Mark’s model, every status cooperator signals the willingness to be a leader with probability \(\frac{1}{n}\). If no player expresses such interest, no cooperator or defector at the bottom level will later contribute to the shared resource pool. In Mark’s model, status cooperators always contribute when a leader is chosen. If multiple leaders are nominated, the structure formation resets until a clear single-leader hierarchy emerges. By contrast, we took into account that leadership is often shared by many and “unclear” in reality (Case & Maner 2014; Eslen-Ziya & Erhart 2015; Selznick 2011). Examples of multi-leadership are not only easy to spot in task-oriented groups and everyday organizations; the emergence and consequences of multi-leadership are also gaining attention among scholars (Badura et al. 2021; Paunova 2015). Accordingly, if multiple cooperators are signaling high (interest in leadership; using Mark’s term) versus low, we retained such an emerging multi-leader structure instead of keeping pruning it and forcing cooperators to decide whether to contribute under such an unclear hierarchy.

In our model, multi-leadership emerges when multiple cooperators signal high confidence (i.e., high status). Unlike Mark’s model, where signaling continues until a single leader is identified, we allow groups to settle into states with multiple leaders. Specifically, when more than one conditional cooperator signals high, the group adopts a multi-leader structure, and all cooperators at the top level are considered leaders. We use the term “conditional cooperator" instead of Mark’s”status cooperator" to emphasize that cooperation depends on contextual factors such as the clarity of the hierarchy and the number of leaders. This terminology better aligns with our model’s focus on the probabilistic and conditional nature of cooperation in less-defined hierarchical settings. This approach reflects real-world scenarios where leadership is shared, such as in research collaborations or executive teams. In these cases, the hierarchy becomes less clear, reducing cooperators’ likelihood of contributing to the common good.

Specifically, cooperators decide whether to contribute, facing multi-leaders, with a likelihood (not) to do so. This likelihood represents the hesitation to cooperate under obscure leadership. With this allowance, the two situations in (Mark 2018), where the group is either clearly hierarchical with one leader or clearly flat with no leader, were covered in our model as special cases. Shortly, our modification depicts the entire spectrum between Mark’s two and only structures by considering groups that are multi-leader and indecisively hierarchical or flat.

Mark’s two scenarios represent the extremes of group hierarchy: full cooperation in a clear hierarchy and no cooperation in the absence of leadership, that is, with a probability of 1 or 0, respectively. By contrast, cooperators in our newly added, less clear hierarchical structures contribute with an intermediate probability. Once a player decides whether to contribute, the same one-shot common-good dilemma is played as in Mark’s EVG. Consequently, our model specifies that a cooperator has a probability \(p_c\) of contributing benefit \(b\) to the common pool and a probability \(1-p_c\) of not contributing and keeping \(c\) for themself. If the individual is a defector, they will never contribute, keeping \(c\) as non-cooperating cooperators. Payoffs in our model are determined by the likelihood of cooperation \(p_c\), which depends on the hierarchical score \(H_n(x)\). A cooperator contributes a benefit \(b\) to the group with probability \(p_c\) and retains \(c\) otherwise. Defectors never contribute and always retain \(c\). The total contributions are pooled and evenly distributed among all group members. To ensure that the cooperation dilemma is maintained, we assume that the benefit of cooperation \(b\) is greater than the individual cost of contributing \(c\), i.e., \(b>c\). This assumption ensures that cooperation remains a viable strategy while still posing a dilemma in strategic decision-making. For example, if we set \(b=4\) and \(c=2\), then the cost-to-benefit ratio is \(c/b=0.5\), which aligns with the feasible cooperation region observed in our simulations. This implies that cooperators who contribute receive a payoff advantage as long as the overall structure supports cooperation. For instance, if two cooperators contribute in a group of size \(n = 5\), each member receives \((2 \cdot b)/5\). This structure ensures that both cooperators and defectors derive benefits based on group composition and contribution levels. Finally, the total contribution in the common pool is split among everyone. Equally, the population composition changes following the same linear replicator as in Mark’s EVG. Together, our model gives

\[ \begin{split} P(C_{t+1}) & = \frac{P(C_{t}) \cdot W(C_t)}{P(C_{t}) \cdot W(C_t) + P(D_{t}) \cdot W(D_t)}, \\ P(D_{t+1}) & = \frac{P(D_{t}) \cdot W(D_t)}{P(C_{t}) \cdot W(C_t) + P(D_{t}) \cdot W(D_t)}, \end{split}\]

\[(1)\]

where \(P(C_{t})\) is the proportion of conditional cooperators in the group at time \(t\), \(P(D_{t})\) the proportion of defectors, \(W(C)\) the expected payoff for a conditional cooperator, and \(W(D)\) the expected payoff for a defector.

Hierarchical score and the cooperation probability \(H_{n}(x)\)

Having described the general setup of our EVG, below, we turn to the specific measure of group hierarchicalness and how it informs about cooperators’ probability to contribute. Conceptually, we assumed having multiple leaders in a group obscures group hierarchy and attenuates leaders’ capability to motivate cooperation. Supporting this assumption, empirical studies have shown that members of multi-leader teams need more resources (e.g., time) to communicate and achieve consensus on a shared goal (Rice 2006). This need subsequently increases the risk of failing to achieve such a consensus under which group members, especially subordinates, can cooperate with one another. Similarly, even if the group can settle with multiple leaders and their distinct goals, this situation opens the possibility that the leaders may get in each other’s way, competing for limited common, material, or human resources in the group (Friedrich et al. 2009). Overall, it seems plausible to use the hierarchicalness of a group as the proxy for the likelihood that conditional cooperators can coordinate and then collaborate: the more clearly hierarchical a group, the more its cooperative members will cooperate.

Practically, we adopted the hierarchicalness measure of Mones et al. (2012), as it would range from 0 to 1 between Mark’s two clear group structures respectively, and can subsequently be used as cooperator’s probability to contribute to the group. Particularly, since this measure is defined for any arbitrary complete network, we restricted it to a system with two layers of players. That is, given an unweighted directed graph \(G = (V, E)\) containing a vertex set \(V\) with \(n = |V|\) number of vertices and an edge set \(E\) with \(M = |E|\) number of edges, the local reaching centrality \(c_{R}(i)\) of node \(i\) was defined as the ratio of the number of reachable nodes of \(i\) through its out-edges, to the total number of nodes that a node could potentially reach (assuming no self-loop). From here, then

\[c_{R}(i) = \frac{|S_{i}|}{n-1},\]

\[(2)\]

where \(S_{i} = \{j \in V | 0< d^{out}(i,j) < \infty\}\) is the set of nodes that have nonzero but finite out-distances from node \(i\), and the general reaching centrality \(GRC(G)\) of graph \(G\) is the normalized sum of all nodes’ local reaching centrality by the maximum local reaching centrality:

\[ GRC(G) = \frac{1}{n-1} \sum_{i \in V} \big[ c^{max}_{R} - c_{R}(i)\big],\]

\[(3)\]

where \(c^{max}_{R}\) denotes the largest local reaching centrality in the network. In other words, when \(GRC = 1\) and the structure is the most hierarchical, the graph would have only one node – the leader – with nonzero local reaching centrality to all others when others have no out-edge at all. Therefore, the structure of the case with only one leader at the top level represents the (clear) hierarchy with the highest possible hierarchical score.

To keep generalizing the GRC to two-level groups of nodes, we considered that the players at the top, however many, have control over others at the bottom and, therefore, each with an out-edge toward every other at the bottom. We then defined the hierarchicalness \(H_{n}(x)\) of this two-level cooperation structure with group size \(n\) and \(x\) players at the top level using the GRC of network \(G\). That is,

\[ H_{n}(x) = \begin{cases} \frac{(n-x) \cdot \frac{n-x}{n-1}}{n-1} = \big( \frac{n-x}{n-1} \big)^2 & \text{if } 0 < x \leqslant n\\ 0 & \text{if } x = 0. \end{cases}\]

\[(4)\]

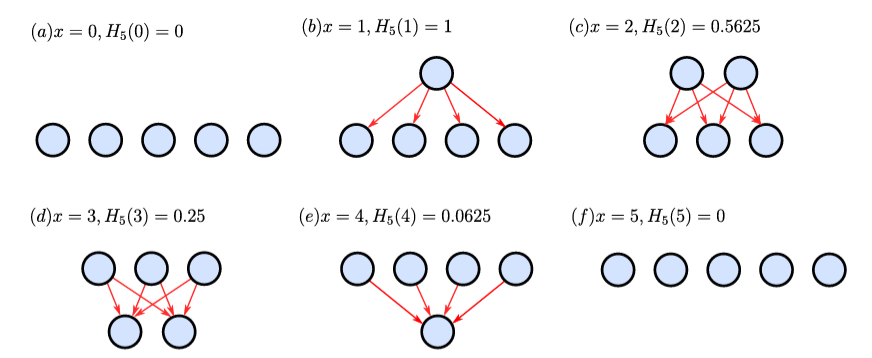
Notice here that, when \(0 < x \leqslant n\), Equation (4) applies Equation (3) to a two-level network with \(x\) players at the top level. In this case, \(c^{max}_{R} = \frac{n-x}{n-1}\) because players at the top show maximum reachability to \(n-x\) nodes/players at the bottom, who do not have this reachability. Moreover, when \(x = 0\) and everyone is at the bottom, we set \(H_{n}(0) = 0\) to represent a lack of leadership, making \(H_{n}(x)\) always takes the value between 0 and 1. For demonstration, Figure 1 shows all group structures and the corresponding \(H\) values that a group with size \(n = 5\) can have. Specifically, in the two cases in the figure where all players are at the same, bottom or top level, \(H = 0\), representing zero hierarchicalness in the network. Further, when \(x = 1\), \(H\) becomes 1, the highest among all scenarios. Finally and critically, except for the special case of \(x = 0\), for which we stipulate \(H = 0\), \(H_{n}(x)\) is a decreasing function of \(x\). This trend fits with our need that, with more leaders at the top, the less clearly hierarchical the commanding system should become.

Given its useful mathematical properties, \(H_{n}(x)\) was then used as the proxy to the probability \(p_c\) that a conditional cooperator would contribute \(b\) to the group and not keep \(c\) to themself. So, if only one player signals their interest in higher status and, thus, rises to the top, all conditional cooperators will contribute, with a probability \(H_{n}(1) = 1\). If there is no player at the top level, no conditional cooperators will contribute, i.e. \(H_{n}(0) = 0\). Lastly and importantly, if there are more than one player at the top level, the larger their number, the less hierarchicalness the group, and the closer to 0 the values of \(H_{n}(x)\). As a result, cooperators will be less likely to contribute as the number of leaders increases.

Analytical methods

Random mixing

Under random mixing, individuals are equally likely to interact with any other group member, regardless of role. This creates a uniform probability distribution of meeting cooperators and defectors, making it challenging for cooperation to evolve without a clear hierarchy. In contrast, assortative mixing introduces a bias: individuals preferentially interact with others of the same role. As the assortativity parameter \(\tau\) increases, cooperators are more likely to form groups, enabling them to organize cooperation more effectively, even under multi-leader structures.

When \(n = 2\), the expressions of the expected payoffs for the conditional cooperators and defectors are shown in Equations (5) and (6), respectively. With the probability for our focal agent, the conditional cooperator, to meet another cooperator being \(f_{c}\) and to meet a defector being \(1- f_{c}\), in Equation (5), the first and the second line are the expected payoff for a conditional cooperator meeting another cooperator and a defector, respectively. Particularly, there are three terms in the first line of Equation (5); they in turn represent the situations where the focal cooperator meets another cooperator while there are 2, 0, or 1 player at the top level. As a result, when all players (i.e., 2) or no player is a leader, no conditional cooperator contributes, and each of them takes \(c\) back. By contrast, when there is 1 and only leader in the group – the special case of \(H_{n}(1)\) – every conditional cooperator contributes equally and receives \(b\) equally. Moreover, the two terms of the second line, in turn, represent the case wherein the conditional cooperator meets a defector, does not go to the top level, and hence does not contribute, and the case wherein the cooperator goes to the top and contributes. Notice that in the latter scenario, the contribution \(b\) will be shared by the two players in the group since the defector does not contribute.

\[\begin{aligned} W(C) &= f_{c} \cdot \bigg\{ {2 \choose 2} \bigg( \frac{1}{2}\bigg)^{2} \bigg( \frac{2-1}{2}\bigg)^{0} \cdot c + {2 \choose 0} \bigg( \frac{1}{2}\bigg)^{0} \bigg( \frac{2-1}{2}\bigg)^{2} \cdot c + {2 \choose 1} \bigg( \frac{1}{2}\bigg)^{1} \bigg( \frac{2-1}{2}\bigg)^{1} \cdot b \bigg \} \\ & + (1-f_{c}) \cdot \bigg\{{1 \choose 0} \bigg( \frac{1}{2}\bigg)^{0} \bigg( \frac{2-1}{2}\bigg)^{1} \cdot c + {1 \choose 1} \bigg( \frac{1}{2}\bigg)^{1} \bigg( \frac{2-1}{2}\bigg)^{0} \cdot \frac{b}{2} \bigg \} \end{aligned}\]

\[(5)\]

Turning to the expected payoff for the defector, here we express it in Equation (6) in that, whether the defector meets a conditional cooperator or another defector, he always keeps his cost \(c\) – the first term in the equation. Therefore we only need to focus on whether they can get additional shares of \(b\). In the current case of \(n = 2\), the defector would only obtain the benefit \(b\) when meeting a cooperator who goes to the top level (therefore contributes). This is the second term in the line.

\[\begin{aligned} W(D) = c + f_{c} \cdot \bigg\{ {1 \choose 1} \bigg( \frac{1}{2}\bigg)^{1} \bigg( \frac{2-1}{2}\bigg)^{0} \cdot \frac{b}{2} \bigg\} \end{aligned}\]

\[(6)\]

Now, generalizing the equations, the hierarchicalness function \(H_{n}(x)\) joins in to form the payoffs for a larger group size \(n\). Notice that \(x = 1\) is always a special case. Here, the status hierarchy is clear and all cooperators contribute. The other special case is that all conditional cooperators are at the same level, either at the top or the bottom. In this case, no cooperator contributes. Accordingly, below are the expected payoffs for the cooperator and the defector when \(n = 3\), in Equations (7) and ( 8), respectively.

\[\begin{aligned} W(C) & = (1-f_{c})^{2} \cdot \bigg( \frac{2}{3} \bigg)\cdot c\\ & + {2 \choose 1} f_{c} (1-f_{c}) \cdot \bigg \{ \bigg( \frac{2}{3} \bigg)^2 + \bigg( \frac{1}{3} \bigg)^2 (1-H_{3}(2))\bigg\} \cdot c\\ & + (f_{c})^2 \cdot \bigg \{ \bigg( \frac{2}{3} \bigg)^3 + {3 \choose 2} \bigg( \frac{1}{3} \bigg)^2 \bigg( \frac{2}{3} \bigg)^2 (1-H_{3}(2)) + \bigg( \frac{1}{3} \bigg)^3 \bigg\} \cdot c\\ & + (1-f_{c})^{2} \cdot \bigg( \frac{1}{3} \bigg) \bigg( \frac{1}{3} \bigg) \cdot b \\ & + {2 \choose 1} f_{c} (1-f_{c}) \cdot \bigg \{ {2 \choose 1} \bigg( \frac{1}{3} \bigg) \bigg( \frac{2}{3} \bigg) \bigg( \frac{2}{3} \bigg) \\ & + {2 \choose 2} \bigg( \frac{1}{3} \bigg)^2 \cdot \bigg[ {2 \choose 1}(H_{3}(2))(1-H_{3}(2))\bigg( \frac{1}{3} \bigg) + {2 \choose 2}(H_{3}(2))^{2}\bigg( \frac{2}{3} \bigg) \bigg] \bigg\} \cdot b \\ & + (f_{c})^2 \cdot \bigg\{ {3 \choose 1} \bigg( \frac{1}{3} \bigg) \bigg( \frac{2}{3} \bigg)^2 + {3 \choose 2} \bigg( \frac{1}{3} \bigg)^2 \bigg( \frac{2}{3} \bigg)^1\\ & \cdot \bigg[ {3 \choose 1} (H_{3}(2))(1-H_{3}(2))^2 \bigg( \frac{1}{3} \bigg) + {3 \choose 2} (H_{3}(2))^2(1-H_{3}(2))^1 \bigg( \frac{2}{3} \bigg) + (H_{3}(2))^3 \bigg] \bigg\} \cdot b \end{aligned}\]

\[(7)\]

\[\begin{aligned} W(D) &= c + 2f_{c}(1-f_{c}) \cdot \bigg\{ \bigg( \frac{1}{3}\bigg) (H_{3}(1)) \bigg( \frac{1}{3}\bigg) \bigg\} \cdot b \\ & + f^{2}_{c} \bigg\{ {2 \choose 1} \bigg( \frac{1}{3}\bigg) \bigg( \frac{2}{3}\bigg) \bigg( \frac{2}{3} \bigg) + \bigg( \frac{1}{3}\bigg)^{2} \bigg[ {2 \choose 1} (H_{3}(2)) (1-H_{3}(2)) \bigg( \frac{1}{3}\bigg)+ (H_{3}(2))^{2} \bigg( \frac{2}{3}\bigg) \bigg] \bigg\} \cdot b \end{aligned}\]

\[(8)\]

The first three lines in Equation (7) represent the situation in which a conditional cooperator doesn’t contribute and takes back its cost \(c\), lines 4 to 8 represent the situation in which the cooperator can earn the benefit \(b\). In each scenario, we need to consider the focal conditional cooperator that meets two defectors (with probability \((1-f_{c})^2\)), one cooperator and one defector (with probability \({2 \choose 1}f_{c}(1-f_{c})\)), and two cooperators (with probability \(f^2_{c}\)). Here, we focus on explaining the last two lines, where the conditional cooperator meets two cooperators as the rest is obtained following the same calculation. The conditional cooperator can always take back \(b\) if there is one cooperator at the top level. Assuming there are two cooperators at the top level (i.e., \(x = 2\)), though a cooperator to start, this player acts as a defector in the end, given the probability \(1- H_{3}(2)\) "not" to follow the lead. Here, one needs to consider two different scenarios: If the focal cooperation does not contribute, they can keep \(c\) and obtain extra portions of \(b\) depending on the number of players who contribute. Consequently, the focal player can take \(\frac{k}{3}\) shares of \(b\) if there are \(k\) cooperators who end up contributing.

On the other hand, Equation (8) is the expected payoff for the defector when \(n = 3\). Note that, again, a defector can always take back \(c\). They then obtain additional fractions of \(b\) if they meet one conditional cooperator – with probability \(2f_{c}(1-f_{c})\) (the second term in the first line) and two cooperators – with probability \(f^{2}_{c}\) (the last line). Specifically, the first term inside the part following \(f^{2}_{c}\) represents that exactly one conditional cooperator becomes the leader, so both conditional cooperators contribute. The second term in line 2 represents the scenario where both conditional cooperators become leaders, and therefore, each of them has a probability \(H_{3}(2)\) to contribute. In this case, the first term in the square bracket expresses that one cooperator contributes and the other does not, and the second term shows both of them do. As a result, the focal defector obtains \(\frac{b}{3}\) and \(\frac{2b}{3}\) of benefits, respectively. The last line then follows the same rationale as in the prior analysis.

Finally, the expected payoffs for a conditional cooperator and a defector in a general case of arbitrary \(n\) are identified in Equations (9) and (10), respectively. To construct the equations, we aggregated the payoff that a focal player obtains based on three quantities: (i) the number of conditional cooperators in the group, (ii) the number of conditional cooperators who become leaders, and (iii) the number of conditional cooperators who end up contributing to the group. Together, the expected payoff of the player can be expressed with a triple summation of the three quantities, denoted with dummy variables \(i\), \(j\), and \(k\), corresponding to the quantities of (i), (ii), and (iii). Here, it might be worth noting that (ii) depends on (i) and (iii) depends on them both. Consequently, the first two lines of Equation (9) describe the scenarios in which the focal conditional cooperator does not contribute and takes back \(c\), whereas the last two lines describe the scenarios in which they take portions of \(b\) depending on quantities (i), (ii), and (iii). On the other hand, Equation (10) indicates that the defector always keeps \(c\) with extra shares of \(b\) similarly depending on (i), (ii), and (iii).

\[\begin{aligned} \begin{split} W(C) &= \sum^{n-1}_{i=0} {n-1 \choose i} (f_{c})^{i} (1-f_{c})^{n-1-i} \cdot \bigg[ \sum^{i+1}_{j = 0} {i+1 \choose j} \bigg(\frac{1}{n} \bigg)^{j} \bigg( \frac{n-1}{n}\bigg)^{i+1-j} \big(1- H_{n}(j)\big) \bigg] \cdot c\\ &+ \sum^{n-1}_{i =0} {n-1 \choose i} (f_{c})^{i} (1-f_{c})^{n-1-i} \cdot \bigg \{ \sum^{i+1}_{j = 0} {i+1 \choose j} \bigg(\frac{1}{n} \bigg)^{j} \bigg( \frac{n-1}{n}\bigg)^{i+1-j} \\ & \cdot \bigg[ \sum^{i+1}_{k = 0} {i+1 \choose k}\big( H_{n}(j)\big)^{k} \big(1- H_{n}(j)\big)^{i+1-k} \bigg( \frac{k}{n}\bigg) \bigg] \bigg\} \cdot b \end{split}\end{aligned}\]

\[(9)\]

\[\begin{aligned} W(D) &= c +\sum^{n-1}_{i =0} {n-1 \choose i} (f_{c})^{i} (1-f_{c})^{n-1-i} \\ & \cdot \bigg\{ \sum^{i}_{j = 0} {i \choose j} \bigg(\frac{1}{n} \bigg)^{j} \bigg( \frac{n-1}{n}\bigg)^{i-j} \cdot \bigg[ \sum^{i}_{k = 0} {i \choose k}\big( H_{n}(j)\big)^{k} \big(1- H_{n}(j)\big)^{i-k} \bigg( \frac{k}{n}\bigg) \bigg] \bigg\} \cdot b \end{aligned}\]

\[(10)\]

Assortative mixing

To construct the analytical solutions in the assortative mixing model, the only change to make lay in the rate of meeting a cooperator \(f_{c}\). We thus derived the expected payoffs for a conditional cooperator and a defector in a multi-leader model with assortative mixing in Equations (11) and (12) as follows. A detailed derivation of these formulas can be found in Supplementary Information.

\[\begin{aligned} W(C) &= \sum^{n-1}_{i=0} \Bigg\{ \bigg(\frac{i+1}{n} \bigg) \bigg\{ \bigg(\frac{1}{i+1} \bigg) {n-1 \choose i} \big[\tau + (1-\tau)f_{c}\big]^{i} \big[(1-\tau)(1-f_{c})\big]^{n-i-1}\\ &+\bigg(\frac{i}{i+1}\bigg) f_{c} {n-1 \choose i} \big[\tau+(1-\tau)f_{c}\big]^{i-1} \big[(1-\tau)(1-f_{c})\big]^{n-i-1}\bigg\} \\ &+ \bigg(\frac{n-i-1}{n}\bigg) \bigg\{ (1-f_{c}) {n-1 \choose i} \big[(1-\tau)f_{c}\big]^{i} \big[\tau + (1-\tau)(1-f_{c})\big]^{n-i-2} \bigg\} \Bigg\}\\ & \cdot \bigg[ \sum^{i+1}_{j = 0} {i+1 \choose j} \bigg(\frac{1}{n} \bigg)^{j} \bigg( \frac{n-1}{n}\bigg)^{i+1-j} \big(1- H_{n}(j)\big) \bigg] \cdot c\\ &+ \sum^{n-1}_{i=0} \Bigg\{ \bigg(\frac{i+1}{n} \bigg) \bigg\{ \bigg(\frac{1}{i+1} \bigg) {n-1 \choose i} \big[\tau + (1-\tau)f_{c}\big]^{i} \big[(1-\tau)(1-f_{c})\big]^{n-i-1}\\ &+\bigg(\frac{i}{i+1}\bigg) f_{c} {n-1 \choose i} \big[\tau+(1-\tau)f_{c}\big]^{i-1} \big[(1-\tau)(1-f_{c})\big]^{n-i-1}\bigg\} \\ &+ \bigg(\frac{n-i-1}{n}\bigg) \bigg\{ (1-f_{c}) {n-1 \choose i} \big[(1-\tau)f_{c}\big]^{i} \big[\tau + (1-\tau)(1-f_{c})\big]^{n-i-2} \bigg\} \Bigg\}\\ & \cdot \bigg \{ \sum^{i+1}_{j = 0} {i+1 \choose j} \bigg(\frac{1}{n} \bigg)^{j} \bigg( \frac{n-1}{n}\bigg)^{i+1-j} \\ & \cdot \bigg[ \sum^{i+1}_{k = 0} {i+1 \choose k}\big( H_{n}(j)\big)^{k} \big(1- H_{n}(j)\big)^{i+1-k} \bigg( \frac{k}{n}\bigg) \bigg] \bigg\} \cdot b \end{aligned}\]

\[(11)\]

\[\begin{aligned} W(D) &= c + \sum^{n-1}_{i=0} \Bigg\{ \bigg(\frac{i}{n} \bigg) \bigg\{ f_{c} {n-1 \choose i} \big[\tau + (1-\tau)f_{c}\big]^{i-1} \big[(1-\tau)(1-f_{c})\big]^{n-i-1}\bigg\} \\ &+\bigg(\frac{n-i}{n}\bigg) \bigg\{ \bigg(\frac{1}{n-i} \bigg) {n-1 \choose i} \big[(1-\tau)f_{c}\big]^{i} \big[\tau + (1-\tau)(1-f_{c})\big]^{n-i-1} \\ &+ \bigg(\frac{n-i-1}{n-i}\bigg) (1-f_{c}) {n-1 \choose i} \big[(1-\tau)f_{c}\big]^{i} \big[\tau + (1-\tau)(1-f_{c})\big]^{n-i-2} \bigg\}\Bigg\} \\ &\cdot \bigg\{ \sum^{i}_{j = 0} {i \choose j} \bigg(\frac{1}{n} \bigg)^{j} \bigg( \frac{n-1}{n}\bigg)^{i-j} \cdot \bigg[ \sum^{i}_{k = 0} {i \choose k}\big( H_{n}(j)\big)^{k} \big(1- H_{n}(j)\big)^{i-k} \bigg( \frac{k}{n}\bigg) \bigg] \bigg\} \cdot b \end{aligned}\]

\[(12)\]

Results

Random mixing

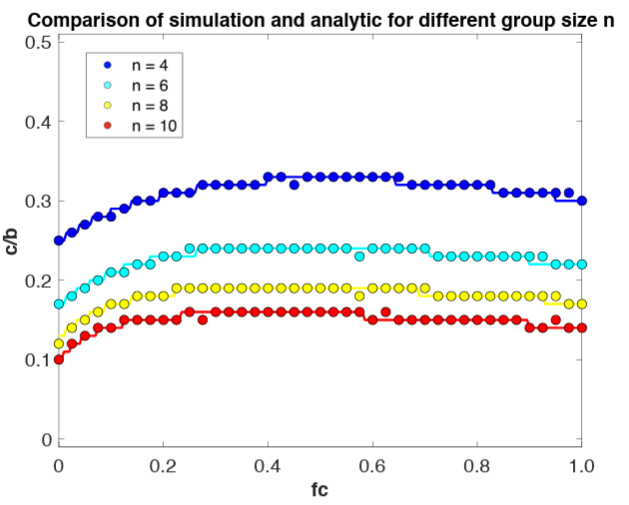
As alluded to, we first produced the analytical approximation and an agent-based simulation of our EVG under the assumption of random mixing; that is, individuals have the same opportunity to meet each other regardless of roles (i.e., leaders, cooperators, or defectors; see the Methods Section). Figure 2 compares the analytical and the simulated results of the internal equilibrium, i.e., the cost-to-benefit ratio of cooperation \(c/b\) that makes \(W(C) = W(D)\), against the proportion of conditional cooperators \(f_{c}\) in groups of different sizes \(n\). The equations that are based on these equilibrium lines in the figure – Equations ( 9) and ( 10) – yielded almost perfect matches with the simulations, bolstering the modeling’s validity.

Theoretically, the depicted equilibria quantify the maximum cost-to-benefit ratio (\(c/b\)) under which cooperation remains viable, reflecting the relative strength of cooperation in the system. When \(W(D) > W(C)\) (above the lines), defectors achieve higher payoffs, causing cooperators to decline until \(P(C) = 0\). Conversely, when \(W(D) < W(C)\) (below the lines), cooperation is advantageous, leading to an increase in cooperators until \(P(C) = 1\). Numerical resolution of \(W(C) = W(D)\) reveals that the equilibrium threshold decreases as the group size (\(n\)) increases, making cooperation less sustainable in larger groups. This finding aligns with the Olson conjecture (Olson 2009), which posits that coordination and cooperation face greater challenges in larger populations. These results highlight the inherent trade-offs in group size, where larger groups dilute the cooperative advantage of hierarchical structures.

An intriguing finding in Figure 2 is the non-linear effect of the proportion of conditional cooperators (\(f_{c}\)) on the strength of cooperation, as measured by the maximum \(c/b\) ratio. Contrary to intuition, higher proportions of cooperators do not always enhance cooperation. While increasing \(f_{c}\) initially strengthens hierarchical structures, excessively high proportions lead to the emergence of multi-leader hierarchies that diminish clarity and compromise cooperators’ willingness to contribute. In such cases, cooperators effectively act as partial defectors, destabilizing group dynamics (see Chrobot-Mason et al. 2009). This highlights the counterintuitive risk of over-cooperation in certain contexts. Compared to the single-leader model of Mark (2018), our findings suggest that cooperative behavior’s evolutionary advantages depend on a delicate balance between hierarchy and cooperator proportions.

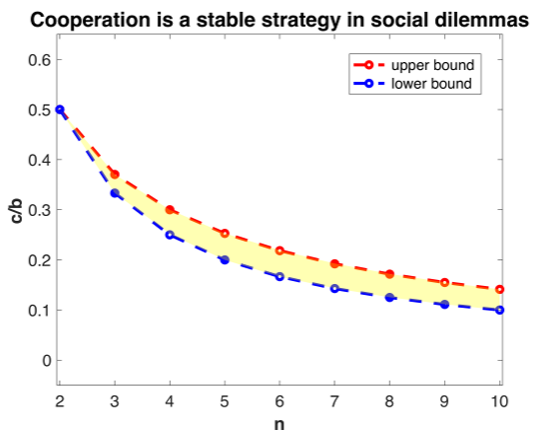
Now, we present the analysis of the cost-to-benefit range wherein status cooperation is a stable evolutionary strategy in social dilemmas. Following Mark, the lower bound of the range is the threshold below which interactions are no longer dilemmas. The upper bound is the threshold above which defectors can invade cooperators. Accordingly, if the cost-to-benefit ratio is smaller than \(\frac{1}{n}\), \(b\) becomes large enough relative to \(c\) that the game is no longer a dilemma: one’s cooperation will always outperform defection whether others cooperate. \(\frac{1}{n}\) is hence the lower bound. For the upper bound, if the expected payoff for cooperators in a homogeneous, all-cooperator group is larger than that for an invading defector, cooperation is deemed a strong and stable strategy against defection. Mathematically, this means, if a conditional cooperator’s payoff under \(f_{c} = 1\) is larger than a defector’s payoff under \(f_{c} = \frac{n-1}{n}\), then cooperation is stable. Following the logic, we plugged these conditions into Equations (9) and (10) to find the boundary of \(c/b\). Together, the stability range of the cost-to-benefit ratio was derived and shown in Figure 3. Again, although there is a greater chance of forming a hierarchical structure when more cooperators and, thus, potential leaders are in a group with multiple leaders, it is less likely that cooperators will contribute to the group. This makes it easier for defectors to invade the group, making the stability range first widens but later seemingly narrow along with group size. We analytically examined the possibility as \(n\) goes to infinity, observing the upper bound approaches 0 and eliminating the stability region. In Supplementary Information, we also compared the region for cooperators to survive in the multiple-leader status-cooperation model and the single-leader status-cooperation model.

Assortative mixing

Having studied random mixing, we generalized our model to assortative mixing; that is, individuals are limited to playing with same-role others at different degrees. Here, Mark found cooperators may reversely invade the group of defectors in single-leader games under enough assortativity because it unequally protects and favors cooperation over defection. Following Mark, the bias parameter \(\tau \in [0, 1]\) in our EVG decides the degree of assortativity in a group, denoting the proportion of required non-randomly mixed, same-role pairs in interactions, leaving the remaining \(1 - \tau\) pairs choosing interaction partners following random mixing. As a result, when \(\tau = 1\), the group will be all cooperators if the first selected individual is a cooperator; the group will be all defectors if the first selected one is a defector.

As before, we built an agent-based simulation to validate Equations (11) and (12). (see Methods for the codes); Figure 4 shows the almost perfectly matched analytical and simulated results of cost-to-benefit ratio \(c/b\) against the fraction of cooperators \(f_{c}\) at internal equilibrium. Here, different from the random-mixing analysis above, we fixed group size \(n = 10\), instead manipulating and color-coding \(\tau\).

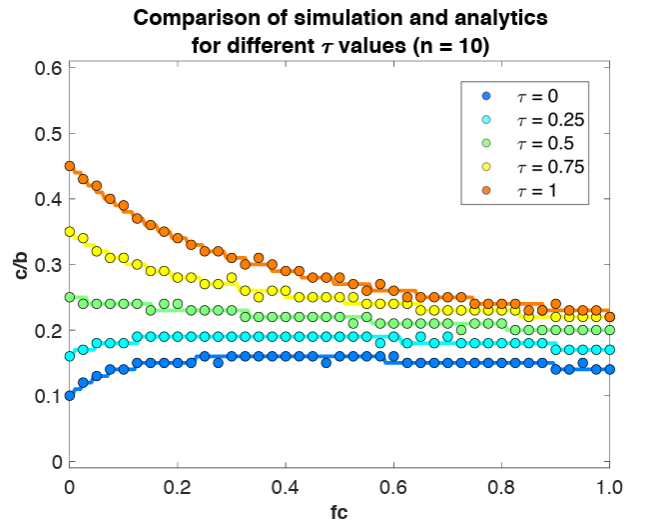
Figure 4 illustrates how assortativity consistently strengthens cooperation across all proportions of conditional cooperators, affirming its protective role against defection, as previously observed in network-based cooperation dilemmas (Wang et al. 2012). This effect is particularly pronounced at low \(f_{c}\), where assortativity creates favorable conditions for cooperation to emerge and persist. However, as \(f_{c}\) increases, the influence of assortativity diminishes, even reversing its benefit at very high \(f_{c}\). In highly assortative groups with excessive cooperator proportions, multi-leader hierarchies become prevalent, attenuating cooperators’ willingness to contribute and destabilizing cooperative dynamics. These findings emphasize assortativity’s dual role: while it enhances cooperation at low \(f_{c}\), it cannot fully mitigate the challenges posed by high cooperator proportions.

Examining the effect of \(f_{c}\) at varying levels of assortativity (\(\tau\)), we observe a distinct shift in the curves of \(W(C) = W(D)\) from concave down to concave up as \(\tau\) increases. At lower \(\tau\), increasing \(f_{c}\) initially enhances cooperation but later diminishes it due to the emergence of multi-leader hierarchies. However, at higher \(\tau\), assortativity reshapes this relationship, enabling cooperators to mitigate the negative effects of multi-leadership, particularly at moderate \(f_{c}\). This shift underscores the interplay between assortativity and cooperator proportion, where assortativity moderates the destabilizing effects of high \(f_{c}\). Nevertheless, the attenuated willingness to contribute in highly cooperative, multi-leader settings persists, highlighting the nuanced trade-offs inherent in hierarchical dynamics.

Together, the present paper reports that the relative size of cooperators to defectors and the assortativity between the two roles do not add to the evolution of cooperation independently in multi-leader groups. First, unlike in single-leader groups, the proportion of cooperators in multi-leader groups, though mostly beneficial, may jeopardize the strength of cooperation against defection when it is too high. Second, even though assortativity helps with cooperation at any proportion of cooperators in the group, when it is too high, it neutralizes and even reverses the generally positive effect on cooperation, making it simply that the more cooperators, the weaker the cooperation is an evolutionary strategy. The two factors interact with one another, giving one interwoven but not two independent relationships with the evolution of cooperation.

Discussion

We have examined the empirically uncommon but theoretically important case of multiple leadership in task groups. Our findings suggest that multi-leadership may often represent a transient stage in the evolution of group hierarchies. In real-world group dynamics, leadership roles are rarely fixed from the outset. Instead, groups often begin with multiple individuals signaling leadership potential, creating an initial phase of leadership competition and coordination ambiguity. This aligns with sociological and organizational perspectives on group formation, where leadership must emerge organically rather than being assigned top-down. Over time, competitive dynamics, clarity-seeking behavior, and evolutionary pressures may consolidate leadership into a more stable single-leader structure, as described in Mark’s (2018) model. This perspective suggests that while multi-leadership can sustain cooperation, its inherent instability may explain why single-leader hierarchies are the predominant form of structured cooperation.

With both analytical and numerical examinations–all computer codes publicized in online repositories–we present a two-layer multi-leader model of the relationship between leadership hierarchy and the evolution of the cooperation facilitated by leaders and the pursuit of status. The work shows that status cooperation could be stable in evolution. Status hierarchy could thus be thought of as organizing cooperation in the long run. While status hierarchies can facilitate cooperation, they do not guarantee full cooperation in all contexts. Cooperation levels depend on additional factors such as group composition, external incentives, and intra-group competition (Bendersky & Hays 2012). This is in contrast with the observation that hierarchy might be detrimental to cooperation (Cronin et al. 2015), but consistent with the fact that hierarchy may arise in initially egalitarian entities and still keep significant cooperation in them (Lozano et al. 2020). Here, the main difference between our model and the one in (Cronin et al. 2015) is that, in the latter, model agents were arranged to interact only in pairs in some unstructured hierarchy. By contrast, we show that the region for cooperation stays evolutionarily stable in the multi-leader hierarchy. This happens when elected leaders receive no extra incentive than non-selected conditional cooperators. The result thus echoes with existing research (Antonioni et al. 2018) that a status hierarchy formed based on performance does not reduce cooperation in groups. The conditional nature of our conditional cooperation strategy introduces important implications for evolutionary viability. While it is well-suited to scenarios with unclear hierarchies, this feature limits its effectiveness in groups where all members are conditional cooperators and hierarchical clarity is established. In such cases, Mark’s SC strategy may outperform ours by promoting unconditional cooperation. Future work could extend this comparison by exploring hybrid strategies that incorporate conditional cooperation for ambiguous settings and unconditional cooperation when group composition ensures trust. This line of inquiry would provide a deeper understanding of how different conditional cooperation strategies interact across a spectrum of social and environmental conditions, including varying degrees of assortativity and hierarchy clarity.

In addition, we assumed that the more group members, the less they would want to be the leader. This follows from the established bystander effect in social psychology, such as that shown in Darley and Latané’s (Darley & Latané 1968) research. Darley and Latané demonstrated that study participants were less likely to speak up and report potential emergencies – fire in the laboratory, for example – when more participants were in the lab. Even if presumably everyone wanted to escape the fire, few would emerge to lead the rest when the group was large. By contrast, people could easily “lead” themselves and simply leave the room.

Group size also significantly impacts the viability of cooperation. While larger groups may benefit from increased synergy and resource pooling, they often face challenges in maintaining cooperation due to coordination difficulties and the diffusion of responsibility (Lee et al. 2023). Our findings align with this observation, as we show that cooperation becomes increasingly difficult to sustain as group size grows. This result reflects a trade-off between the potential benefits of larger group synergy and the structural challenges of maintaining cooperation, reinforcing the importance of clear hierarchies or robust mechanisms for cooperation in larger groups.

Finally, corresponding to the great theoretical accounts on hierarchy is the significant body of literature on the methodology of measuring hierarchicalness. It is nonetheless important to note, even if some other measure is logically applicable to our present investigation – take Krackhardt’s (1994) index – while the measure shares a similar idea with the method developed by Mones et al. (2012) and adopted by the present paper, only the latter distinguishes the hierarchicalness of a structure. That is to say, one that has one leader and \(n-1\) subordinates – from the hierarchicalness of the structure’s reverse form – one that has \(n-1\) leaders and one subordinate. Kackhardt’s method would treat the two structures as equally hierarchical, which is against Mark’s original theorizing and clearly counter-intuitive. Overall, then, future investigations would want to be open yet at the same time mindful of both theory and methodology, as well as their agreement. An intriguing extension of this work would involve a direct comparison between the conditional cooperation strategy presented here and Mark’s status cooperation model under different group mixing scenarios. Based on theoretical expectations, our conditional cooperation strategy, which thrives on conditional cooperation, may perform better in random mixing environments where hierarchical clarity is more challenging to establish. In contrast, Mark’s model, relying on single-leader hierarchies, may excel under strong assortativity, where hierarchical roles are more distinct. Testing these hypotheses analytically or through simulations could provide valuable insights into the evolutionary viability and contextual suitability of each strategy. This line of inquiry would also deepen our understanding of how environmental structures, such as assortativity, interact with social cooperation mechanisms.

Future work could also examine the relationship between multi-leadership and phenomena such as polarization or information overload. Environments marked by competing viewpoints and information ambiguity might amplify the challenges of sustaining cooperation in multi-leader structures, potentially leading to reduced group performance or fragmented cooperation dynamics. Investigating these scenarios could provide valuable insights into the robustness of multi-leadership hierarchies in complex social settings.

One major limitation of our model is that we consider a two-level hierarchy structure, but social hierarchy in real life takes various other forms. Intuitively, for instance, the most hierarchical structure is the linear system, wherein the top actor outranks the second, who in turn outranks the third, and so on and so forth until the bottom position; this system can easily have more than two levels. Further, however, prevalent linear systems are in the dominant structure of social animals (Shizuka & McDonald 2012), but they still do not characterize all human status structures. For one, in many contests such as those of sports, while high-ranked contestants by definition win more in a tournament, they may still lose to low-ranked others from time to time. In ethology, researchers have also found cases (e.g., gorillas) where dominance relations in the group are non-transitive in the sense that actor A dominates B and B dominates C, but C somehow turns back to dominate A, thus forming a cycle structure in the group. Together, future work may continue to contribute to the literature by investigating the extent to which these diverse hierarchical structures ameliorate or deteriorate the evolution of group cooperation and, importantly, how the structures affect cooperation.

References

ANTONIONI, A., Pereda, M., Cronin, K. A., Tomassini, M., & Sánchez, A. (2018). Collaborative hierarchy maintains cooperation in asymmetric games. Scientific Reports, 8(1), 1–9.

BADURA, K. L., Galvin, B. M., & Lee, M. Y. (2021). Leadership emergence: An integrative review. Journal of Applied Psychology, 107(11), 2069–2100.

BENDERSKY, C., & Hays, N. A. (2012). Status conflict in groups. Organization Science, 23(2), 323–340.

BENDOR, J., & Swistak, P. (2001). The evolution of norms. American Journal of Sociology, 106(6), 1493–1545.

BERGSTROM, T. C. (2002). Evolution of social behavior: Individual and group selection. Journal of Economic Perspectives, 16(2), 67–88.

BOLSEN, T., Ferraro, P. J., & Miranda, J. J. (2014). Are voters more likely to contribute to other public goods? Evidence from a large-scale randomized policy experiment. American Journal of Political Science, 58(1), 17–30.

BORNSTEIN, G. (2003). Intergroup conflict: Individual, group, and collective interests. Personality and Social Psychology Review, 7(2), 129–145.

BURNS, J. K., Tomita, A., & Kapadia, A. S. (2014). Income inequality and schizophrenia: Increased schizophrenia incidence in countries with high levels of income inequality. International Journal of Social Psychiatry, 60(2), 185–196.

CASE, C. R., & Maner, J. K. (2014). Divide and conquer: When and why leaders undermine the cohesive fabric of their group. Journal of Personality and Social Psychology, 107(6), 1033.

CHOI, J.-K., & Bowles, S. (2007). The coevolution of parochial altruism and war. Science, 318(5850), 636–640.

CHROBOT-MASON, D., Ruderman, M. N., Weber, T. J., & Ernst, C. (2009). The challenge of leading on unstable ground: Triggers that activate social identity faultlines. Human Relations, 62(11), 1763–1794.

CORRELL, S. J., & Ridgeway, C. L. (2006). Expectation states theory. In J. DeLamater & A. Ward (Eds.), Handbook of Social Psychology (pp. 29–51). Berlin Heidelberg: Springer.

CRONIN, K. A., Acheson, D. J., Hernández, P., & Sánchez, A. (2015). Hierarchy is detrimental for human cooperation. Scientific Reports, 5(1), 1–9.

DARLEY, J. M., & Latané, B. (1968). Bystander intervention in emergencies: Diffusion of responsibility. Journal of Personality and Social Psychology, 8(4p1), 377.

DE Dreu, C. K., Greer, L. L., Handgraaf, M. J., Shalvi, S., Van Kleef, G. A., Baas, M., Ten Velden, F. S., Van Dijk, E., & Feith, S. W. (2010). The neuropeptide oxytocin regulates parochial altruism in intergroup conflict among humans. Science, 328(5984), 1408–1411.

ESLEN-ZIYA, H., & Erhart, I. (2015). Toward postheroic leadership: A case study of Gezi’s collaborating multiple leaders. Leadership, 11(4), 471–488.

FINE, G. A. (2010). The sociology of the local: Action and its publics. Sociological Theory, 28(4), 355–376.

FINE, G. A. (2012). Group culture and the interaction order: Local sociology on the meso-level. Annual Review of Sociology, 38(1), 159–179.

FRIEDRICH, T. L., Vessey, W. B., Schuelke, M. J., Ruark, G. A., & Mumford, M. D. (2009). A framework for understanding collective leadership: The selective utilization of leader and team expertise within networks. The Leadership Quarterly, 20(6), 933–958.

GROSSMAN, G., & Baldassarri, D. (2012). The impact of elections on cooperation: Evidence from a lab-in-the-field experiment in Uganda. American Journal of Political Science, 56(4), 964–985.

HAMMAN, J. R., Weber, R. A., & Woon, J. (2011). An experimental investigation of electoral delegation and the provision of public goods. American Journal of Political Science, 55(4), 738–752.

HECHTER, M. (1987). Principles of Group Solidarity. Berkeley, CA: University of California Press.

HEMINGWAY, H., Nicholson, A., Stafford, M., Roberts, R., & Marmot, M. (1997). The impact of socioeconomic status on health functioning as assessed by the SF-36 questionnaire: The Whitehall II Study. American Journal of Public Health, 87(9), 1484–1490.

KOLLOCK, P. (1998). Social dilemmas: The anatomy of cooperation. Annual Review of Sociology, 24(1), 183–214.

KOVÁCS, B., & Liu, C. (2016). Audience structure and status multiplicity. Social Networks, 44, 36–49.

KRACKHARDT, D. (1994). Graph theoretical dimensions of informal organizations. In K. Carley & M. Prietula (Eds.), Computational Organizational Theory (pp. 89–111). Hillsdale, NJ: Lawrence Erlbaum Associaties Inc.

LEE, H.-W., Cleveland, C., & Szolnoki, A. (2023). Group-size dependent synergy in heterogeneous populations. Chaos, Solitons & Fractals, 167, 113055.

LEE, H.-W., Malik, N., & Mucha, P. J. (2018). Evolutionary prisoner’s dilemma games coevolving on adaptive networks. Journal of Complex Networks, 6(1), 1–23.

LOZANO, P., Gavrilets, S., & Sánchez, A. (2020). Cooperation, social norm internalization, and hierarchical societies. Scientific Reports, 10(1), 1–12.

LUO, R., Zhang, L., Huang, J., & Rozelle, S. (2007). Elections, fiscal reform and public goods provision in rural china. Journal of Comparative Economics, 35(3), 583–611.

MARK, N. P. (2018). Status organizes cooperation: An evolutionary theory of status and social order. American Journal of Sociology, 123(6), 1601–1634.

MONES, E., Vicsek, L., & Vicsek, T. (2012). Hierarchy measure for complex networks. PLoS One, 7(3), e33799.

NOWAK, M. A. (2006a). Evolutionary dynamics: Exploring the equations of life. Cambridge, MA: Harvard University Press.

NOWAK, M. A. (2006b). Five rules for the evolution of cooperation. Science, 314(5805), 1560–1563.

NOWAK, M. A., & Sigmund, K. (2004). Evolutionary dynamics of biological games. Science, 303(5659), 793–799.

OLKEN, B. A. (2010). Direct democracy and local public goods: Evidence from a field experiment in indonesia. American Political Science Review, 104(2), 243–267.

OLSON, M. (2009). The logic of collective action. Cambridge, MA: Harvard University Press.

PAUNOVA, M. (2015). The emergence of individual and collective leadership in task groups: A matter of achievement and ascription. The Leadership Quarterly, 26(6), 935–957.

RICE, N. (2006). Opportunities lost, possibilities found: Shared leadership and inclusion in an urban high school. Journal of Disability Policy Studies, 17(2), 88–100.

SAUDER, M., Lynn, F., & Podolny, J. M. (2012). Status: Insights from organizational sociology. Annual Review of Sociology, 38, 267–283.

SELZNICK, P. (2011). Leadership in Administration: A Sociological Interpretation. New Orleans, LA: Quid Pro Books.

SHIZUKA, D., & McDonald, D. B. (2012). A social network perspective on measurements of dominance hierarchies. Animal Behaviour, 83(4), 925–934.

SIMPSON, B., & Willer, R. (2015). Beyond altruism: Sociological foundations of cooperation and prosocial behavior. Annual Review of Sociology, 41, 43–63.

WANG, J., Suri, S., & Watts, D. J. (2012). Cooperation and assortativity with dynamic partner updating. Proceedings of the National Academy of Sciences, 109(36), 14363–14368.

WEIBULL, J. W. (1997). Evolutionary Game Theory. Cambridge, MA: MIT Press.

WHITMEYER, J. M. (2007). Prestige from the provision of collective goods. Social Forces, 85(4), 1765–1786.