Partner Selection and Evolution of Out-Group Avoidance

Introduction

In-group favoritism is a robustly observed human tendency. Despite the critical importance and pervasiveness of cooperation in human societies (Rand & Nowak 2013), cooperation is often dependent on group affiliation. People distinguish between in- and out-groups and cooperate at different levels with them (Balliet et al. 2014). In fact, preferential treatment of in-group members has been observed in artificial groups constructed in labs (Dunham 2018; Tajfel & Tajfel 1970), as well as in natural groups, such as ethnic (Whitt & Wilson 2007) or religious groups (Enos & Gidron 2016), and political parties (Hahm et al. 2024). In-group favoritism is also observed in other contexts, such as in the positive trait evaluation of in-group members (Dunham 2018).

Evolutionary game theory provides insights into the evolution of pervasive in-group favoritism (Masuda & Fu 2015). In particular, in-group favoritism has been investigated using models of social dilemmas (Riolo et al. 2001). Models on the evolution of cooperation (Nowak 2006; Sigmund 2010) therefore have contributed to our understanding of the evolution of in-group favoritism, and previous studies have identified the conditions that can result in a higher propensity to cooperate with members of in-groups than of out-groups. Repeated interactions support an evolution of cooperation (Axelrod & Hamilton 1981; Rossetti & Hilbe 2024), but this mechanism (direct reciprocity) combined with stable relationships with in-group members can lead to the emergence of in-group favoritism (Rand & Nowak 2013). Models of indirect reciprocity indicate that reputation supports cooperation (Nowak & Sigmund 2005; Takács et al. 2021), but intermediate levels of reputation about cooperativeness can foster in-group favoritism (Masuda & Ohtsuki 2007). Further, in-group interactions can hinder large-scale cooperation sustained by indirect reciprocity (Schnell & Muthukrishna 2024a). Interactions within networks sustain cooperation (Perc et al. 2017; Szabó & Fáth 2007) but also support in-group favoritism when introducing tags differentiating groups (Hochberg et al. 2003; Jensen et al. 2019; Kim & Hanneman 2014). Cooperation can serve as a costly signal for preferred traits (Gintis et al. 2001), but group-dependent costly signaling and in-group favoritism can co-evolve (Macanovic et al. 2024).

The present study examines the emergence of selective interaction with in-group members. In social dilemmas, in-group favoritism indicated a behavioral rule to select cooperation for in-group members and defection for out-group members.¹ The above studies identified the mechanisms that foster selective cooperation with in-group members. This means that individuals participate in interactions in social dilemmas whether or not a partner belongs to the same group. This study considers the possibility that individuals avoid interactions with out-group members. They might avoid the interaction itself without even observing the partner’s cooperativeness. Instead, they might base their decision solely on the partner’s membership in the out-group. We called this behavioral tendency out-group avoidance, and examined its possible emergence in evolutionary agent-based simulations.

Partner selection is a valuable framework because deciding who to interact with and who to avoid is a crucial point in this research. Partner selection is an extensively studied mechanism to support cooperation. Evolutionary games generally assume random matching or interactions on fixed networks and that players cannot choose interaction partners. In contrast, partner selection models emphasize the importance of selecting interaction partners for the evolution of cooperation (Barclay 2016).² We considered partner selection by allowing a leave option in the repeated prisoner’s dilemma game (PDG) (Izquierdo et al. 2014, 2010; Vanberg & Congleton 1992; Wubs et al. 2016).³ In this framework, agents participate in repeated PDG with randomly matched agents; however, they can stop interactions by selecting the leave option after observing the partner’s behavior. Selecting the leave option thus allows the selective continuation of current relationships, namely partner selection. In addition to partner control through the tit-for-tat strategy (Axelrod & Hamilton 1981), this option allows for the out-for-tat strategy (Yamagishi et al. 1994). In out-for-tat, agents respond to cooperation with cooperation but respond to non-cooperation by leaving, namely ending interactions and searching for a new partner. Previous simulation studies have shown that strategies selecting the leave option conditional on the partner’s defection can outperform classic strategies such as tit-for-tat (Izquierdo et al. 2014, 2010; Vanberg & Congleton 1992) and punishment on defection (Wubs et al. 2016). In this study, individuals may determine their actions not only based on the past behavior of their partner but also on the group they belong to. In repeated PDG, out-group avoidance corresponds to the tendency to select the leave option for out-group members solely based on membership to a different group, without observing the partner’s actions. The partner selection framework, including out-for-tat in repeated games, stresses its importance in supporting cooperation, but we focus on the possibility that it is not always true when considering intergroup relations.

To consider group-dependent partner selection, we assumed a higher continuation probability in repeated games for in-group pairs. Specifically, when modeling the group structure, we assumed that exogenous shocks that dissolve pair relationships are more likely for pairs consisting of members of different groups. In other words, we modeled the group structure by presuming different values for an exogenous parameter, namely the continuation probability. A previous study suggested that this assumption fosters the emergence of in-group favoritism in repeated interactions (Rand & Nowak 2013). We examined how this assumption affects selective interaction (and cooperation) with in-group members. Previous research also expressed group boundaries through differences in exogenous parameters. For instance, studies differentiate groups using different payoff values (Macanovic et al. 2024), the presence and absence of interaction opportunities (Schnell & Muthukrishna 2024a), and different interaction probabilities (Gross et al. 2023). We followed a similar strategy for group differentiation. Herein, the crucial exogenous parameter was the continuation probability, and the groups in our model were two populations distinguished by the continuation probability. Therefore, notably, our model depends crucially on the assumptions regarding this parameter.

This assumption on the continuation probability is based on various factors. First, the community structure, i.e., the group structure, is widely observed across social networks. Individuals are located within tightly connected groups, with scarce links across them (Girvan & Newman 2002). This network structure results in frequent and stable relationships among in-group members, which may support the assumption regarding continuation probability (Masuda & Fu 2015). This logic justifies the modeling strategy previously adopted to differentiate groups by the exogenous parameter concerning different interaction structures between groups (Schnell & Muthukrishna 2024b). In addition, some empirical studies reported observations consistent with this assumption, namely, that intergroup relationships are less stable. For instance, sociological and psychological research indicated that cross-group relationships are less stable and less durable than homophilic relationships (Aboud et al. 2003; Bigler et al. 2016; Jugert et al. 2013; Oczlon et al. 2023; Rude & Herda 2010; Schneider et al. 2007), although this relationship may not be statistically significant after controlling for some (possibly intermediate) variables (McDonald et al. 2013; Neray et al. 2023). Previous studies have not directly examined the continuation probability of inter-group interactions within social dilemmas, but they provide relevant insights. Therefore, although it is logically possible to assume that the continuation probability may be higher for interactions with out-group members and that such an assumption can lead to different conclusions, our alternative assumption provides a more empirically grounded basis for deriving meaningful implications. Accordingly, the model, which essentially categorizes groups based on differing continuation probabilities, is relevant for existing discussions of in-group favoritism.

Our evolutionary agent-based simulations demonstrated the emergence of out-group avoidance. In the simulations, we allowed agents to adopt different behavioral rules toward in- and out-group partners. When paired with an in-group member, the agents adopted conditional cooperative strategies such as tit-for-tat and out-for-tat. In contrast, agents did not initiate interactions with an out-group partner. Strategies for out-group interactions tend to select the leave option at the first round of pair interactions so that pairs dissolve before the games effectively start. In other words, individuals dissolve a partnership without observing the behavior when the partner belongs to a different group. This out-group avoidance arises even with a high continuation probability with out-group agents; cooperation can evolve when these values are applied to an entire population and the effective group distinction is removed. These outcomes imply that a default strategy in interaction with out-group members can be avoidance from the outset. Stable relationships with in-group members, as assured by the group structure, can decrease the need to interact with out-group members and foster out-group avoidance.

Model

We considered a population of agents belonging to one of two groups and participating in repeated PDG (Table 1 summarizes relevant symbols in the model). The entire population consists of \(N\) agents (\(N\) is even). Each agent belongs to one of two groups of equal size (i.e., \(N / 2\)). Group affiliation is fixed throughout the simulation run. In other words, agents belong to the same group during each generation and do not copy the group of other agents in the payoff-based strategy evolution. When presenting results for groups of different sizes, we clearly specify this information.

Agents participate in repeated PDG with a leave option (\(L\)) (Szabó & Hauert 2002), as well as the options cooperation (\(C\)) and defection (\(D\)). The payoff for mutual cooperation (defection) is \(b-1 (0)\), whereas unilateral cooperation (defection) leads to a payoff of \(-1 (b)\). Here, the parameter \(b\) represents the benefit of interacting with a cooperator. If at least one of the two paired agents chooses the leave option, both agents gain a payoff of \(\sigma\). Accordingly, the game in each round can be represented using the following payoff matrix:

\[\begin{array}{c} C\\ D\\ L\\ \end{array} \begin{pmatrix} b-1 & -1 & \sigma \\ b & 0 & \sigma \\ \sigma & \sigma & \sigma \\ \end{pmatrix}.\]

\[(1)\]

Basically, the value of \(b\) was set to 3 while that of \(\sigma\) was 0.

Table 1: Symbols and their Meanings

Symbol	Meaning
\(N\)	Population size (2.1)
\(C\)	Cooperation (2.2)
\(D\)	Defection (2.2)
\(L\)	Leave option (2.2)
\(b\)	Benefit from interacting with a cooperator (2.2)
\(\sigma\)	Payoff for the leave option (2.2)
\(T\)	Number of rounds per generation (2.3)
\(w_{\mathrm{in}}\)	Continuation probability for pairs within the same group (2.3)
\(w_{\mathrm{out}}\)	Continuation probability for pairs from different groups (2.3)
\(X\)	A symbol used to refer to multiple strategies, such as \(CCC\_LXX\) (2.4)
\(CCC\_LXX\), \(CCD\_LXX\), \(CCL\_LXX\)	Strategies for out-group avoidance (2.5)
\(CCX\_CCX\)	Strategies for impartial cooperation (2.5)
\(\beta\)	Selection intensity (2.7)
\(\Pi_i\)	Payoffs accumulated by agent \(i\) over \(T\) rounds (2.7)
\(\mu\)	Mutation probability (2.7)
\(p\)	Proportion of agents in the small group (3.8)
Note: The numbers in parentheses refer to the relevant paragraphs where the symbol appears.

The following events occur sequentially in each round. The process repeats for \(T\) rounds across one generation (Figure 1 schematically presents the sequence of events in each round). (i) Pair formation: pairs are constructed randomly from single agents. Group affiliation and strategy are not considered in pair formation. The pool of single agents dynamically changes each round because some agents may return to the pool after pair dissolution in events (iii) or (iv). At the outset of each generation, all agents are single. (ii) PDG: paired agents participate in the PDG with the leave option and acquire payoffs. Agents acquire payoffs exclusively through participation in the game. No other activities contribute to their payoffs. (iii) Endogenous pair dissolution: if at least one paired agent chooses \(L\) in the game (i.e., when agents received \(\sigma\) in event (ii)), the pair dissolves. In this case, the two agents return to the pool of single agents. (iv) Exogenous pair dissolution: pairs may dissolve probabilistically when endogenous dissolution does not occur, and the agents return to the pool of single agents (this process has no consequence in case of endogenous pair dissolution). The probability that a pair continues to the next round, known as the continuation probability, varies depending on the group membership of the agents. The continuation probability for pairs consisting of in-group members is \(w_{\mathrm{in}}\), whereas that for pairs consisting of members of different groups is \(w_{\mathrm{out}}\). In other words, pairs may dissolve with a probability of \(1 - w_{\mathrm{in}}\) (\(1 - w_{\mathrm{out}}\)) when the pair consists of members of the same (different) groups. We assume that \(w_{\mathrm{in}}\geq w_{\mathrm{out}}\), meaning that exogenous pair dissolution is less likely to occur when agents interact with members of the same group. Processes from (i) to (iv) constitute one round. Agents who dissolved the pair and returned to the pool of single agents in event (iii) or (iv) get paired with a randomly selected single agent at next round’s (i). Through this repeated process, all agents participate in \(T\) games (i.e., one game per round) and accumulate payoffs that affect reproduction.

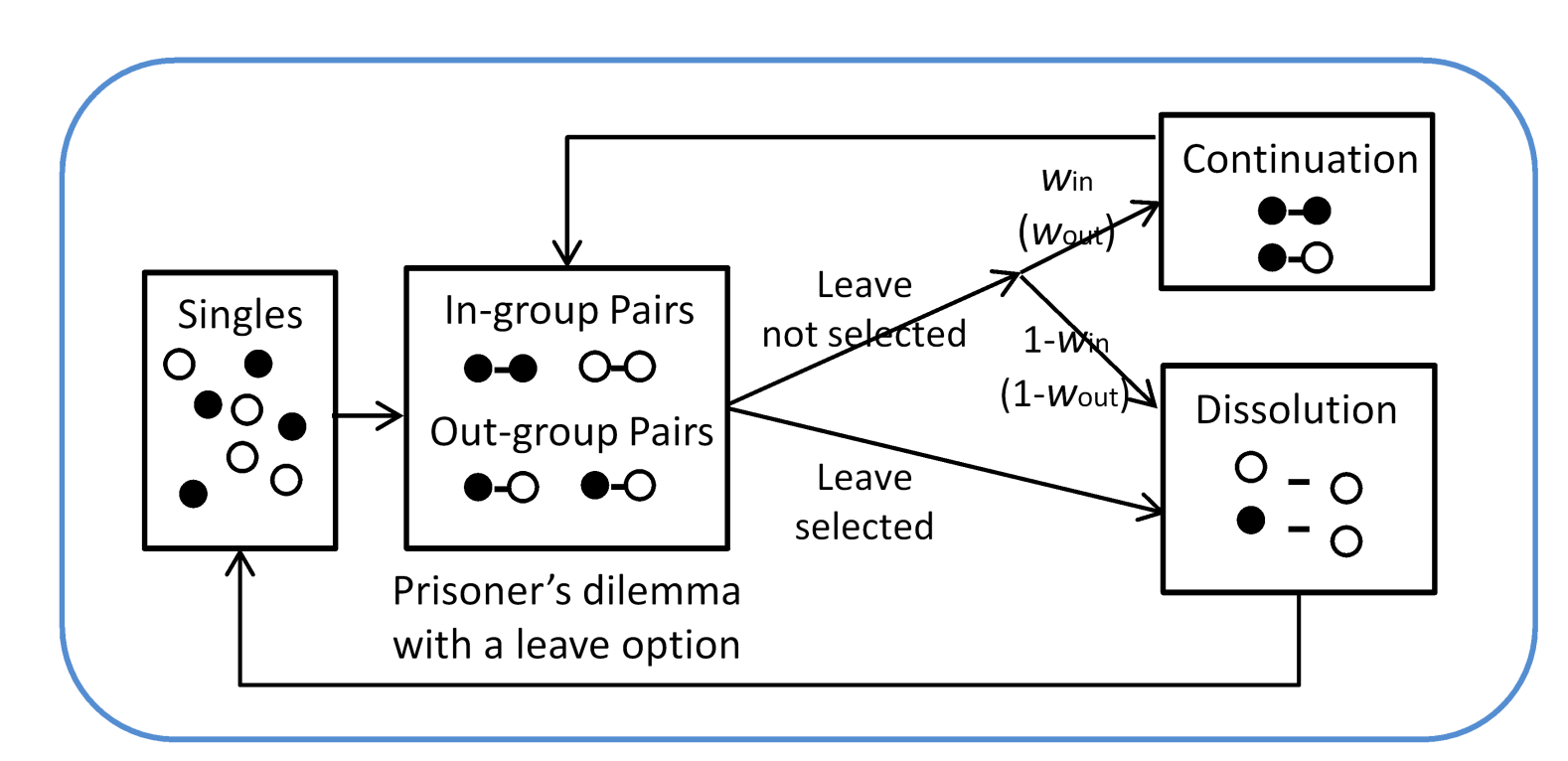
For repeated PDG, we considered strategies to determine actions conditional on group affiliation and the partner’s actions in the previous round. These strategies affect payoffs in the PDG with the leave option and the occurrence of endogenous pair dissolution, as explained above. Strategies comprise six elements; each element can take \(C\), \(D\), or \(L\). The first element specifies the action selected in the first round for pairing with an in-group member. The second and third elements specify actions after observing an in-group partner selecting \(C\) and \(D\) in the previous round, respectively. Similarly, the remaining three elements specify actions toward an out-group partner. Since we specified the strategy in this way, we considered only a subset of the possible strategies in a repeated game. For instance, agents cannot exploit the partner by selecting defection in the final round; this implies that agents do not know the number of games per generation. We explain the specification of the strategy with some examples. For instance, the strategy \(CCD\_DDD\), means that agents adopt tit-for-tat toward an in-group partner but always select \(D\) when interacting with an out-group partner. We adopted the letter \(X\) when referring to multiple strategies. For instance, \(CCL\_LXX\) includes all strategies specifying the out-for-tat toward an in-group partner and selects \(L\) in the first round when paired with an out-group member. The last two elements in this example do not have behavioral consequences because pairs dissolve in the first round regardless of the action of the out-group partner.

Strategies such as \(CCC\_LXX\), \(CCD\_LXX\), \(CCL\_LXX\) are typical examples of out-group avoidance. These strategies specify the leave option in the first round of the interaction with an out-group partner while adopting cooperative behavior among in-group members. Agents adopting these strategies stop pair relationships without observing the behavior of the out-group partner; the selection of the leave option is determined solely by affiliation to a different group. Both agents gain the \(\sigma\) payoff and out-group interactions end in one round. In contrast, the strategies included in \(CCX\_CCX\) can be called impartial cooperation. Agents exhibit cooperative behavior toward both in- and out-group members, namely, impartial cooperation. These strategies may not be unconditional as some strategies respond to partners’ actions. However, group information is not used for decision-making.

An artificial example, presenting the first five rounds of a specific generation from the perspective of agent \(i\), can clarify the process (Table 2). In the first two rounds, agent \(i\) is paired with an in-group member (agent 5) and receives the payoff for mutual cooperation twice because both agents adopt tit-for-tat for in-group members (in this example, the payoff for mutual cooperation is set to 2). In round 3, agent \(i\) participates in the PDG with a new partner (agent 39) because the exogenous dissolution terminated the interaction with agent 5 in the second round. The new partner selects \(L\) for an out-group member in the first round, as specified in the fourth element of the strategy. This is an example of out-group avoidance because this strategy terminates the relationship without observing \(i\)’s behavior. Consequently, agent \(i\) (and agent 39) acquires the payoff for the leave option (\(\sigma = 0.3\) in the example), and the relationship ends. Thereafter, the interaction with the new out-group partner (agent 17) continues for two rounds. Agent \(i\) adopts an out-for-tat for out-group members. Since the partner selected \(D\) in the first interaction, agent \(i\) selected the leave option in round 5, as specified by the sixth element of the strategy.

Table 2: Example of the Sequence of Events

Round	1	2	3	4	5	…
Partner's ID	5	5	39	17	17	…
Same Group	Yes	Yes	No	No	No	…
Partner's Strategy	CCD_CCD	CCD_CCD	CCL_LDD	CDD_DDD	CDD_DDD	…
Agent i's Strategy	CCD_CCL	CCD_CCL	CCD_CCL	CCD_CCL	CCD_CCL	…
Exogenous Dissolution	No	Yes	-	No	-	…
Payoff	2	2	0.3	-1	0.3	…
Accumulated Payoff	2	4	4.3	3.3	3.6	…
Note: The partner's ID is arbitrarily determined by random matching. The row named "Same Group" indicates whether the partner belongs to the same group as agent i, which affects behavior selection. The double lines below the strategy represent the behavior adopted in each round. The three pair relationships continue for two, one, and two rounds, and the causes of dissolution are exogenous, endogenous, and endogenous, respectively. In this example, b and σ values are set to 3 and 0.3.

Reproduction occurs after the PDG with the leave option is repeated for \(T\) rounds. Each agent copies the strategy (but not the group) of an agent selected with a probability proportional to transformed payoffs (Lipowski & Lipowska 2012). In other words, we adopt roulette-wheel selection where the pocket size is the transformed payoff for each agent.⁴ The transformed payoff for agent \(i\) is \(\exp (\beta \Pi_i / T)\), where \(\Pi_i\) is the payoff accumulated in the \(T\) game interactions, and \(\beta\) is selection intensity. In the simulation reported below, the pool of copied agents corresponds to the entire population. However, the basic patterns were not changed when the pool of copied agents was restricted to in-group members. In particular, we confirmed that out-group avoidance evolves with intermediate \(w_{\mathrm{out}}\) values, and impartial cooperation emerges (to some extent) with sufficiently large \(w_{\mathrm{out}}\). Mutation can occur after payoff-based reproduction. With a probability of \(\mu\), each of the six elements of the strategy may independently become one of three options: \(C\), \(D\), or \(L\). It is possible that only some elements mutate. In the initial state, each element of the strategies is randomly assigned, and selection and mutation affect the distribution of the strategies.

To enhance statistical accuracy, the simulation first lasted at least \(10^4\) generations; thereafter, we recorded the strategy frequencies for at least \(10^5\) generations. The long-run strategy frequencies were calculated based on the longer-term sampling period that followed the initial strategy evolution. In addition, we conducted at least five simulations for each combination of parameters and calculated the average strategy frequency. In the analysis below, we used fixed parameter values, as certain parameter values have clearly negative impacts on cooperation. For instance, a small \(T\) impedes cooperation, as agents cannot exploit possible long-term relationships and there is no room for reciprocity. The simulations show that \(T\) values such as 5 nearly impede cooperation with the parameter values adopted in the Results section. Once this value exceeds 30, cooperation emerges and strategy frequencies exhibit stable results. Alternatively, a parameter can only affect the amount of noise. For instance, small population sizes (\(N\)) lead to noisy outcomes where the strategies that disappear in a large population survive. From these observations, we fixed the values of these parameters and analyzed cases in which cooperation evolves to some extent, focusing on the presence and absence of differences between behaviors toward in- and out-group members. The simulation code will be made available via the Open Science Framework at: https://osf.io/qr6nu/.

Results

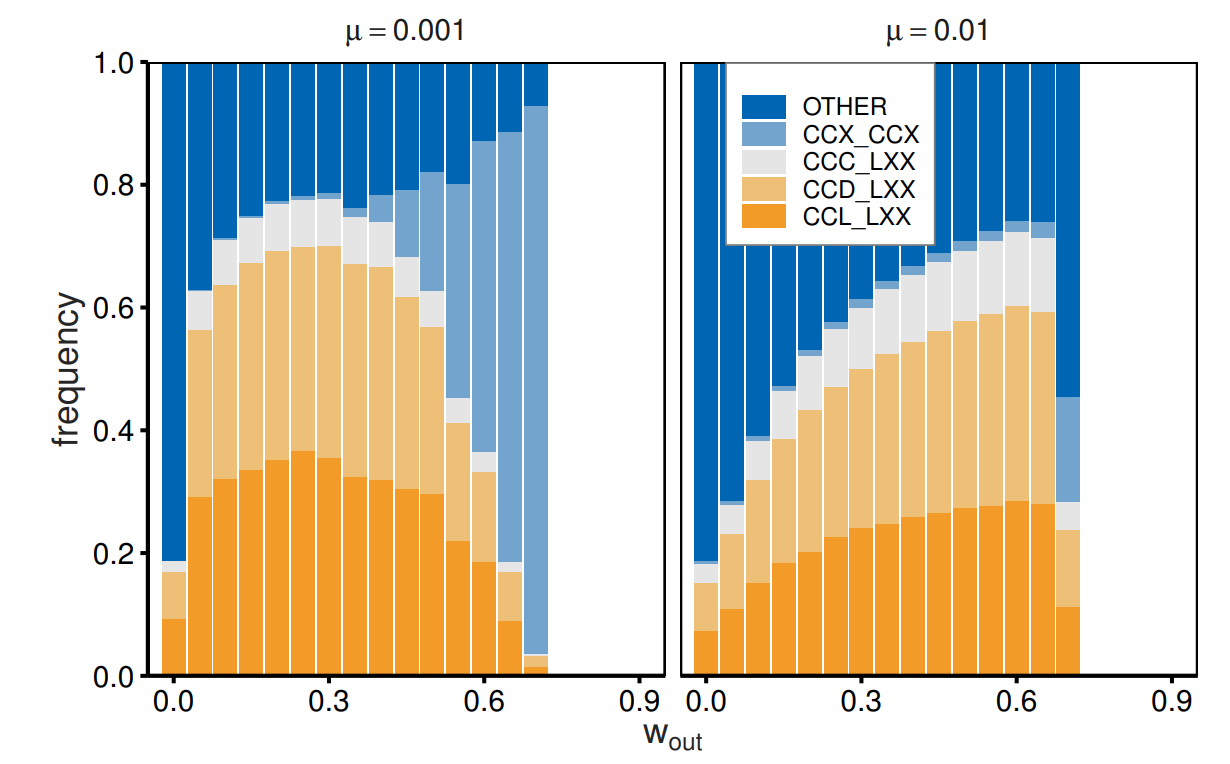
Here, we report how different continuation probability values with out-group partners foster or do not foster cooperation. We focused on four types of strategies. The first three types (out-group avoidance: \(CCC\_LXX\), \(CCD\_LXX\), and \(CCL\_LXX\)) represent cooperative behavior toward in-group members and avoid interactions with out-group members from the outset. The fourth type (\(CCX\_CCX\)) specifies cooperation regardless of group affiliation, unless the partner chooses defection. This type corresponds to impartial cooperation. Figure 2 reports the frequencies of the strategies as a function of \(w_{\mathrm{out}}\) when \(w_{\mathrm{in}}= 0.9\). The strategy of selective cooperation with in-group members and out-group avoidance prevails for small \(w_{\mathrm{out}}\). Agents frequently adopt tit-for-tat (\(CCD\)) or out-for-tat (\(CCL\)) strategies toward in-group partners but select \(L\) immediately following pair formation when paired with an out-group partner. Impartial cooperation (\(CCX\_CCX\)) evolves as the value of \(w_{\mathrm{out}}\) approaches that of \(w_{\mathrm{in}}\). This transition is steeper when there is a high mutation rate (0.01).

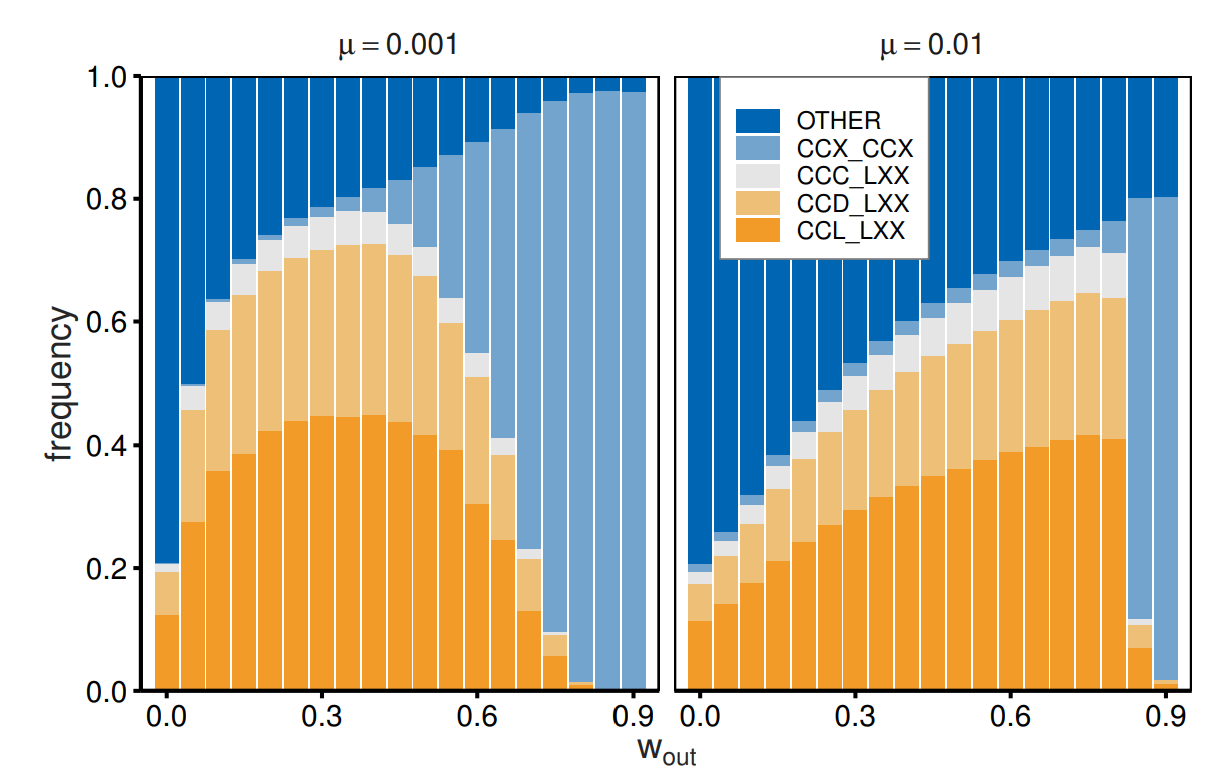
Some notes may be required for cases of small \(w_{\mathrm{out}}\). Figure 2 shows that out-group avoidance is not prominent for small \(w_{\mathrm{out}}\). This is because strategies toward out-group agents have a small impact on payoffs due to their frequent exogenous dissolution. Strategic dissolution plays a minor role since exogenous dissolution frequently terminates interactions. Nonetheless, the behavior toward out-groups is not completely random, as the strategy affects the payoff for the first round, even for \(w_{\mathrm{out}}= 0\). The sums of \(XXX\_DXX\) and \(XXX\_LXX\) frequencies are 0.99 (0.96) when \(\mu = 0.001 (0.01)\).

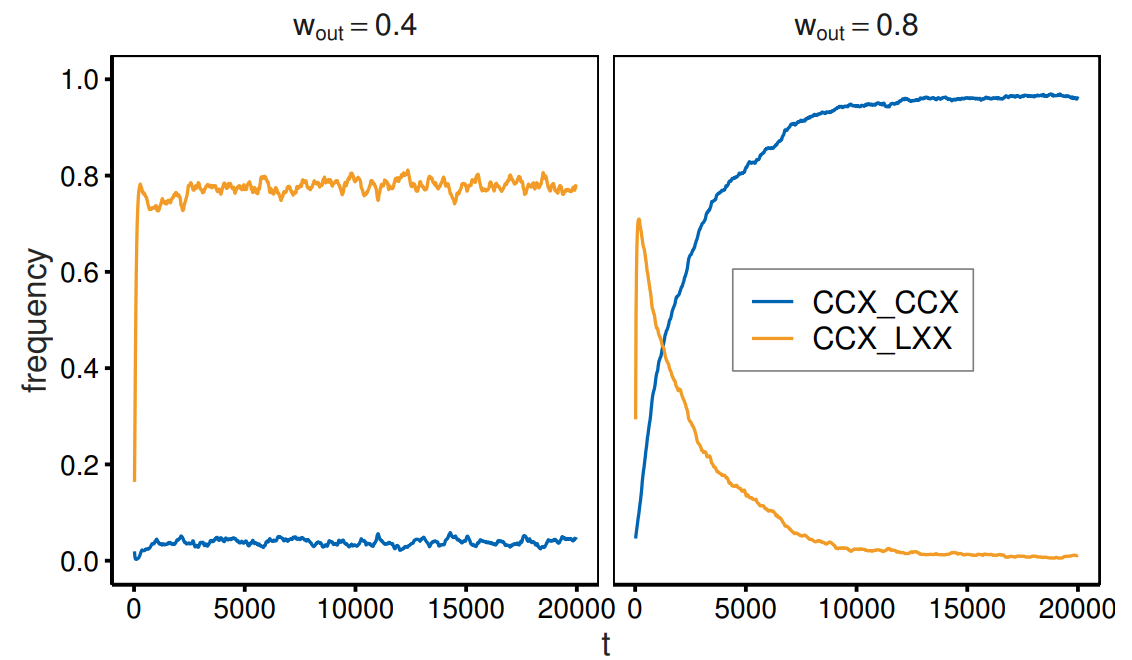
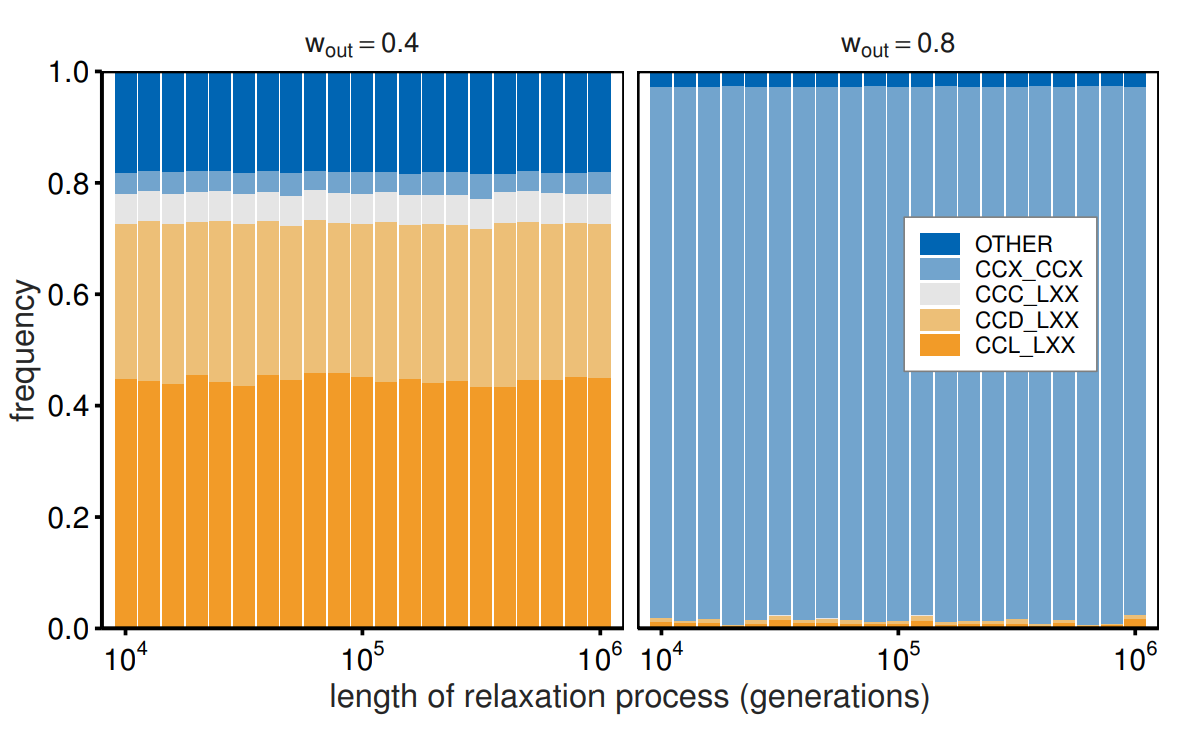
To better understand the dynamics, Figure 3 shows the time evolution of the strategy frequencies. We calculated the average strategy frequencies for each generation by conducting 500 simulation runs. The left panel indicates that the average strategy frequencies reach stable values at an early stage, with proliferating out-group avoidance for \(w_{\mathrm{out}}= 0.4\). The frequencies of \(CCX\_LXX\) increase to approximately 0.75 by the 200th generation. In contrast, the right panel indicates that \(CCX\_CCX\) requires a long time to proliferate for \(w_{\mathrm{out}}= 0.8\). Following the initial increase in the frequency of \(CCX\_LXX\), \(CCX\_CCX\) slowly replaces out-group avoidance. The frequencies of \(CCX\_CCX\) require more than \(10^4\) generations to reach 0.95 and will eventually stabilize at approximately 0.96. A comparison of the two lines on the right panel indicates that out-group cooperation (and impartial cooperation) requires more generations to emerge than that required by in-group cooperation. We sampled strategy frequencies after the initial changes had settled, allowing us to report long-term outcomes. To confirm this point, we also report the strategy frequencies as a function of the length of the relaxation process, namely, periods not included in the frequency calculation to eliminate the influence of initial values (Figure 4). To reduce the effects of the longer sampled generations, we set the sampled generation length to \(10^4\) (rather than \(10^5\)) while that of the relaxation process ranged from \(10^4\) to \(10^6\) generations. Figure 4 shows that the strategy frequencies are stable regardless of the length of the relaxation process.

A basic pattern of strategy frequencies can be observed with different \(w_{\mathrm{in}}\) values. Figure 5 reports the same quantities for \(w_{\mathrm{in}}= 0.7\), for which some differences can be observed. For example, a smaller continuation probability (\(w_{\mathrm{in}}= w_{\mathrm{out}}= 0.7\)) is not sufficiently large to allow the evolution of impartial cooperation for \(\mu = 0.01\). Here, we still observe out-group avoidance (along with other strategies). In addition, in-group avoidance, which falls under the category of other strategies, is also observed with almost the same frequency as out-group avoidance.⁵ As the group structure is removed when \(w_{\mathrm{in}}= w_{\mathrm{out}}\), symmetric strategies appear with the same frequency in the long run. A variety of strategies emerge, particularly because of the high mutation rate (\(\mu = 0.01\)). Despite this difference, a small continuation probability with out-group members fosters cooperation toward in-group members and avoidance of out-group members.

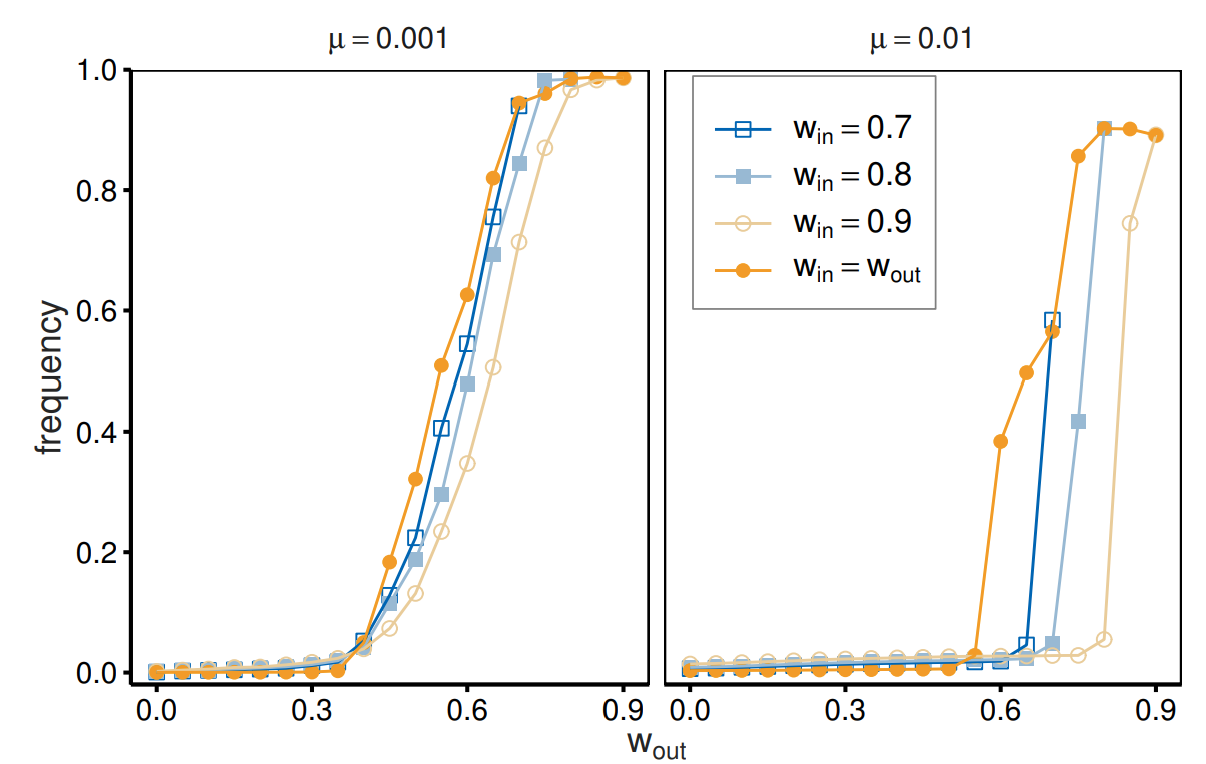
To understand the role of different continuation probabilities, we conducted additional simulations with equal continuation probability for in- and out-group members (\(w_{\mathrm{in}}= w_{\mathrm{out}}\)), which imitates a population without a group structure while preserving the basic simulation settings. We compared this simulation with the main simulation which assumes different continuation probabilities. Although artificial, this simulation is useful for understanding the role of different continuation probabilities.

Figure 6 suggests that the avoidance of out-group members can be attributed to the availability of more stable and, hence, more profitable relationships with in-group members. We present the frequencies of agents who adopt cooperative strategies toward out-group members (\(XXX\_CCX\)). Note that the frequency of \(CCX\_CCX\) does not allow a fair comparison, as a large \(w_{\mathrm{in}}\) enhances in-group cooperation and increases the \(CCX\_CCX\) frequency for \(w_{\mathrm{in}}> w_{\mathrm{out}}\). The evolution of cooperation toward out-group agents requires larger \(w_{\mathrm{out}}\) for \(w_{\mathrm{in}}> w_{\mathrm{out}}\) than for \(w_{\mathrm{in}}= w_{\mathrm{out}}\), as shown in the figure. For \(w_{\mathrm{in}}= w_{\mathrm{out}}\), the frequencies of \(XXX\_CCX\) monotonically increase, as expected from the role of continuation probability. In contrast, for \(w_{\mathrm{in}}> w_{\mathrm{out}}\), out-group cooperation does not evolve even with a large enough \(w_{\mathrm{out}}(= w_{\mathrm{in}})\) that supports cooperation when applied to the entire population (i.e., the two groups). This tendency is more prominent for larger \(w_{\mathrm{in}}\); the evolution of out-group cooperation is most inhibited for \(w_{\mathrm{in}}= 0.9\). A higher continuation probability suggests a conducive setting for cooperation. However, cooperation within in-group members can hinder cooperation with out-group members.

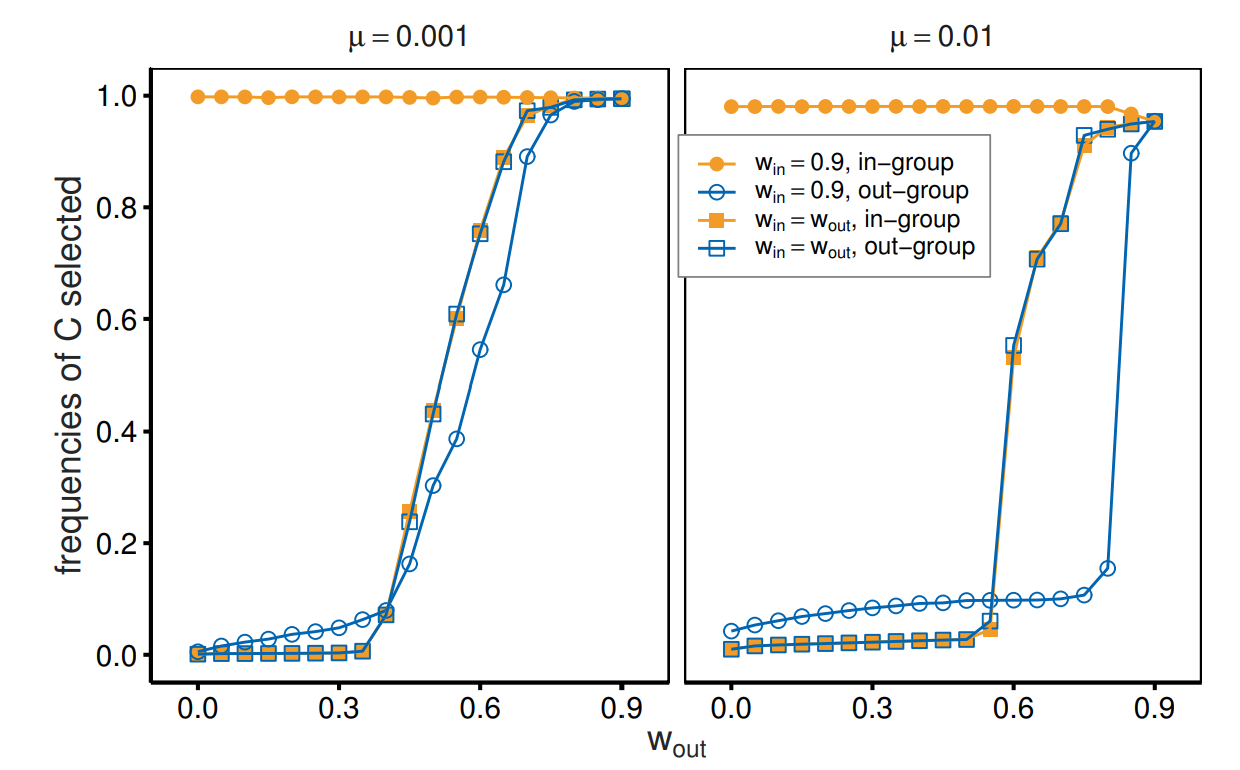
Another way to examine the effects of the two different continuation probabilities is to examine the frequency with which cooperation is selected. This quantity directly shows the outcomes of the realized interactions. By matching the analysis in Figure 6, we compare the cases of \(w_{\mathrm{in}}= w_{\mathrm{out}}\) with those of \(w_{\mathrm{in}}> w_{\mathrm{out}}\). The reported values are also distinguished by interactions with the in- and out-group members. Figure 7 indicates that higher continuation probabilities hinder out-group cooperation. For \(w_{\mathrm{out}}< w_{\mathrm{in}}(= 0.9)\), the frequencies of cooperation that are selected in out-group interactions stagnate compared to \(w_{\mathrm{out}}= w_{\mathrm{in}}\). Drastic effects are observed for \(\mu = 0.01\). When the value of \(w_{\mathrm{out}}(= w_{\mathrm{in}})\) exceeds 0.6, the cooperation frequencies in out-group interactions are greater than 0.5. In addition, when \(w_{\mathrm{out}}\) is greater than 0.75, the cooperation frequencies in out-group interactions exceed 0.9. However, these values drop to just over 0.1 when a different continuation probability (\(w_{\mathrm{in}}> w_{\mathrm{out}})\) is introduced because in-group interactions can almost certainly achieve cooperation. This analysis indicates that cooperation with out-group members may be impeded, despite their potential to foster collaborative relationships, if interactions with in-group members guarantee more stable cooperation.

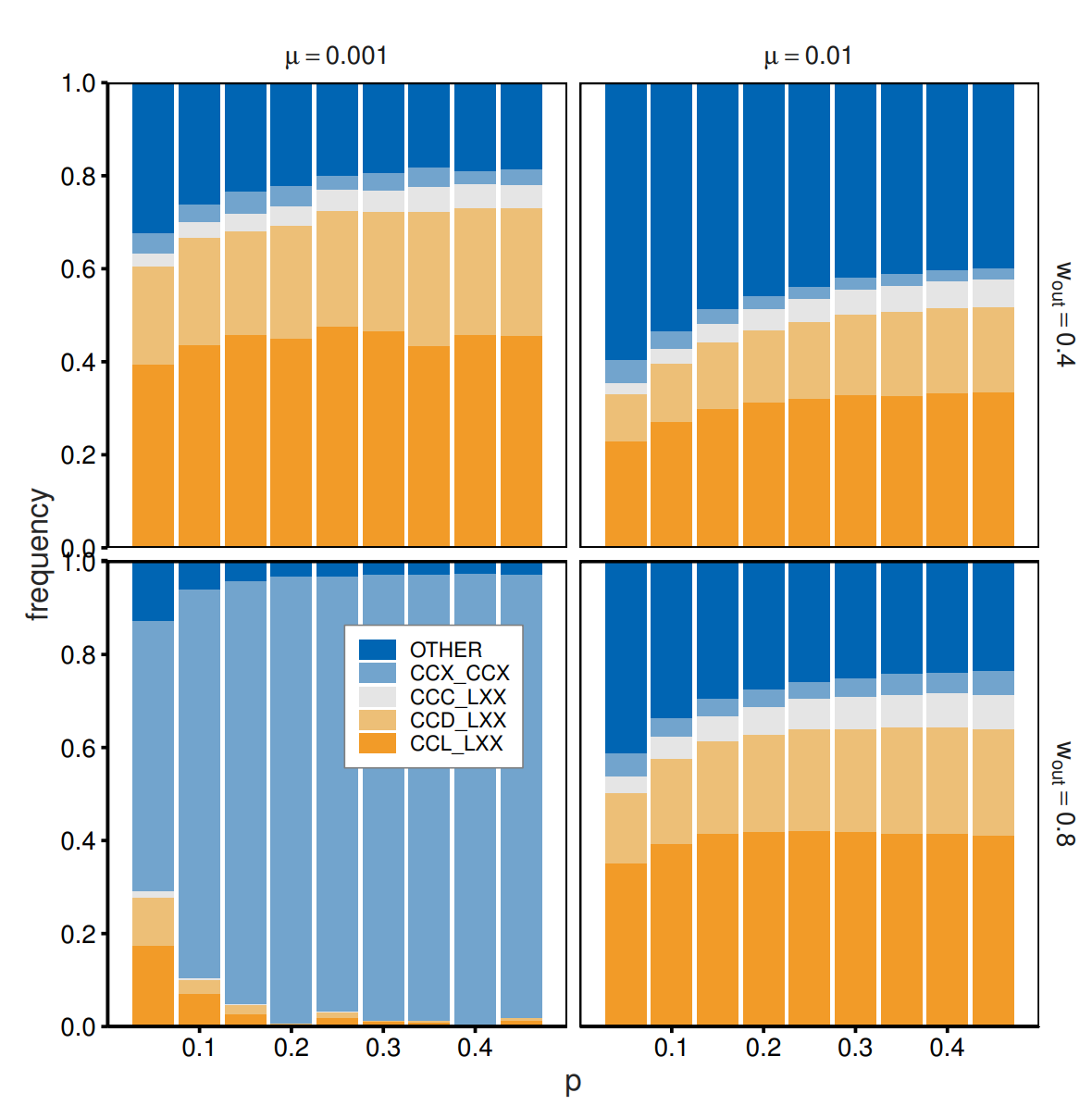
The simulation results reported so far indicate the possible emergence of out-group avoidance and that different continuation probabilities amplify behavioral differences toward different groups. In this section, we explain how altering certain parameters alters the outcomes. First, we relax the assumption that the two populations have the same size by varying the proportion of agents belonging to the smaller group, denoted as \(p\) (\(p < 0.5\)). This means that \(Np\) agents belong to the smaller group, whereas \(N(1-p)\) agents belong to the larger group. Since the two groups reached almost identical strategy frequencies, we report the weighted average frequency for the two groups. Figure 8 shows that \(p\) plays a relatively minor role. Small \(p\) values produce noisier outcomes, as the strategies populated with large \(p\) reduce their frequencies. However, these effects are not qualitative, and the basic patterns remain constant.

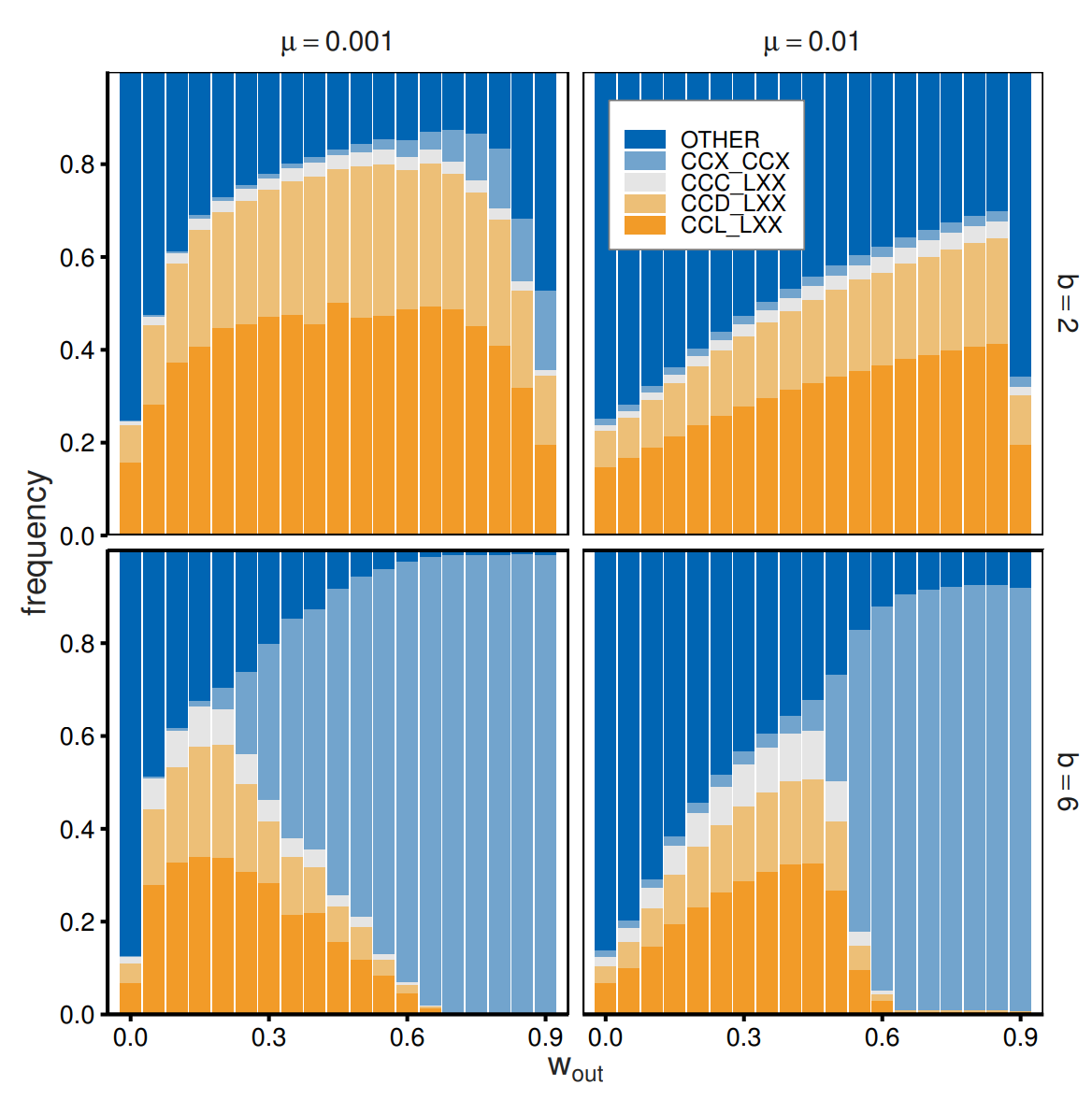
Next, we explored the role of the benefit of cooperation (\(b\)) in the evolution of out-group avoidance. Figure 9 illustrates the evolutionary outcomes obtained for \(b = 2\) and \(b = 6\). Impartial cooperation (\(CCX\_CCX\)) produces large frequencies for a large benefit of cooperation, whereas in-group favoritism and out-group avoidance abound for a small benefit of cooperation. Avoiding out-groups is counterproductive when cooperation offers high benefits. More importantly, however, the qualitative patterns of the effects of \(w_{\mathrm{out}}\) remain constant.

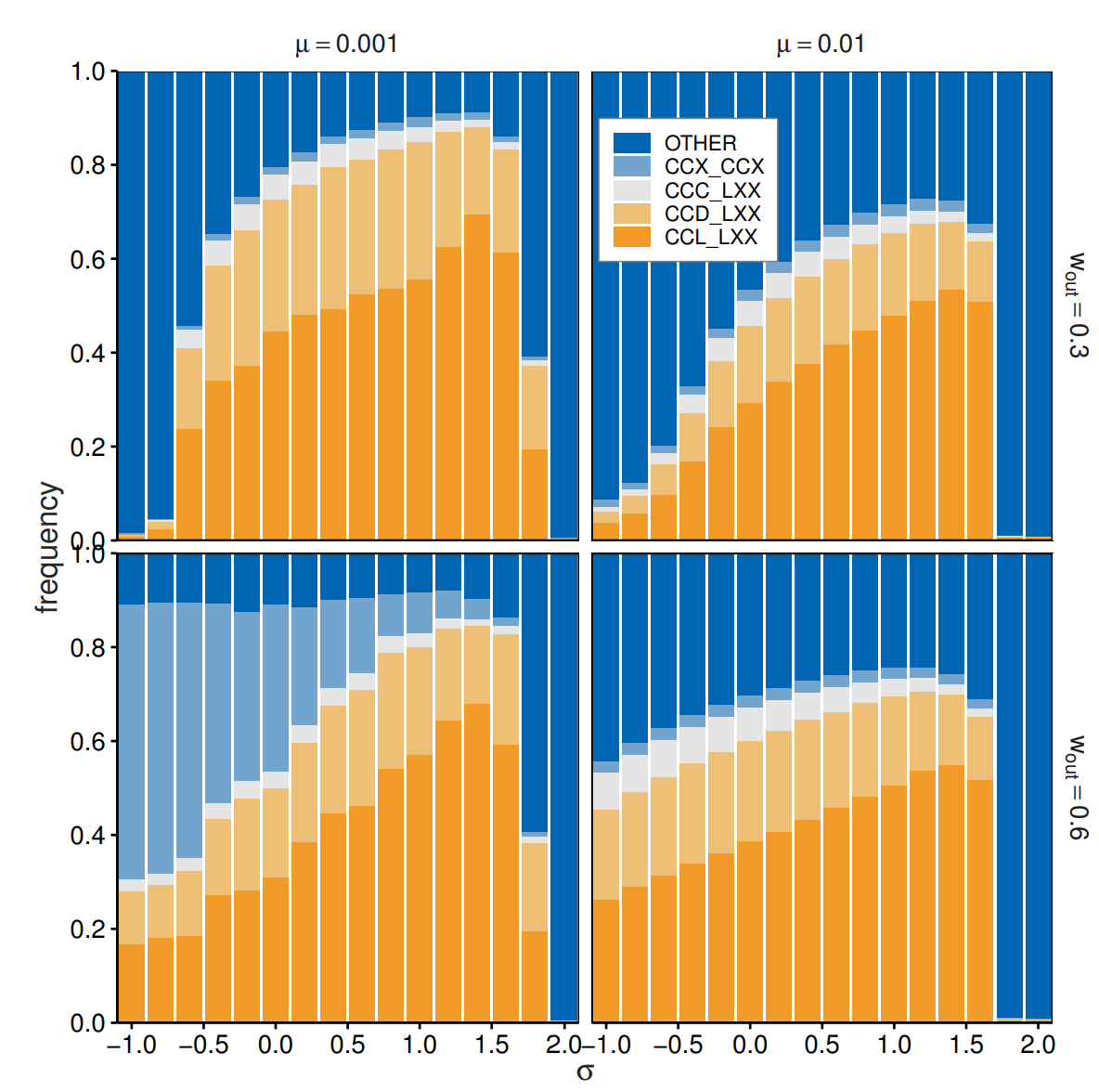
Finally, we investigated the effects of different payoff values for the leave option (\(\sigma\)). This parameter may have a positive value where agents save the cost of participating in the game; however, its value may be negative, considering the expense entailed in searching for new partners. Considering these additional costs, we examined what happens for \(\sigma \neq 0\). Figure 10 reports strategy frequencies as a function of \(\sigma\). Out-group avoidance was observed for moderate \(\sigma\) values indicating the robustness of the reported outcomes. For a large \(\sigma\), out-group avoidance is replaced by unconditional leaving. In the reported case, the \(\sigma = 2\) indicates that the leave option results in payoffs equal to mutual cooperation, removing the social dilemma. In such cases, the frequencies of \(LXX\_LXX\) are larger than 0.9 (0.8) for \(\mu = 0.001 (0.01)\). The opposite extreme, where the leave option realizes payoffs equal to unilateral cooperation (\(-1\)), also decreases the frequencies of out-group avoidance. Significant losses associated with the leave option reduce the advantages of out-group avoidance. Lower frequencies of the leave option result in heightened impartial cooperation or defection, contingent on the parameter values. We observed similar patterns for combinations of \(p =\) 0.2 and 0.5 and \(w_{\mathrm{in}}=\) 0.7, 0.8, and 0.9.

Discussion

People show preferential treatment of in-group members in social dilemmas. In-group favoritism in cooperation has been observed in empirical studies (Balliet et al. 2014), and theoretical models have been proposed to explain this tendency (Masuda & Fu 2015). Although this study is motivated by the literature on in-group favoritism, it focuses on slightly different outcomes – avoidance of members of out-groups as interaction partners.

The direct implication of this study is the potential importance of out-group avoidance. Studies on in-group favoritism in social dilemmas have examined situations where interaction is supposed to occur and participation in games is not optional (Balliet et al. 2014; Masuda & Fu 2015). In contrast, this study focuses on the avoidance of interactions with out-group members. The logic of this study is straightforward: interactions with out-group members are avoided since in-group members offer more stable relationships. Despite this simplicity, the literature has paid scant attention to the possibility that out-groups are excluded as potential interaction partners from the outset. This study contributes to the literature by deriving new empirical implications via consideration of alternative behavioral possibilities. It may be necessary to ask whether the interaction would occur in the first place where the expected payoffs in out-group interactions were small. Moreover, outside the context of the evolution of cooperation, sociological and psychological research has documented homophily and segregation between groups (???. Avoidance of members of the out-groups is a robustly observed phenomenon. Furthermore, a recent laboratory experiment demonstrated the co-evolution of cooperation and homophily in dynamic networks (Melamed et al. 2020). In other words, participants located in networks cooperate with similar people while cutting links with people who do not share identity. This line of research demonstrates that the avoidance of dissimilar people should not be overlooked in analyzing intergroup relations. Our study advances the research on homophily by focusing on the evolution of cooperation and argues that the avoidance of out-groups may require further attention.

In the context of evolutionary games, the consideration of out-group avoidance suggests that careful attention is required regarding the role of partner choice in the evolution of cooperation. Partner choice is widely studied in theoretical and experimental literature as a critical mechanism that supports the evolution of cooperation (Barclay 2016). In repeated games, partner selection can be applied in combination with the leave option, which has also been studied as a mechanism sustaining cooperation (Szolnoki et al. 2014). The leave option allows partner selection by ending interactions with free-riders. The out-for-tat strategy that permits partner selection often outperforms other strategies such as tit-for-tat and punishment in sustaining cooperation (Izquierdo et al. 2014, 2010; Vanberg & Congleton 1992; Wubs et al. 2016). Simply avoiding noncooperative partners robustly supports cooperation. The results of this study suggest that the role of partner selection becomes equivocal when considering the interaction between multiple groups. Partner selection can disrupt interactions between the members of different groups. While considering the evolution of cooperation in intergroup situations, it might be necessary to consider the negative effects of partner selection (and the leave option).

The simulation results may also reflect the emotions observed in intergroup situations. In-group favoritism may not necessarily accompany out-group hate, and discrimination can occur in the absence of aggression toward out-groups (Brewer 1999; Mifune et al. 2017).⁶ In the context of cooperation in social dilemmas, there is no difference between the levels of cooperation with out-group members and those with strangers with an unknown group affiliation (i.e., unidentified strangers) (Balliet et al. 2014); in-group favoritism can be observed in the absence of out-group derogation. In our simulations, agents prefer interactions with in-group members because these relationships tend to be more stable and profitable. Consequently, in-group favoritism can emerge without a hostile intention toward out-groups; out-group members are simply avoided. In addition, agents often avoided out-group members even when the continuation probability was sufficiently high to support cooperation. Here, only interactions with the most profitable candidates, i.e., in-group members, were considered, and all other agents were ignored. This may explain the relative lack of attention paid to the distinction between out-group members and unidentified strangers observed in the experiments. Our simulations demonstrating the possible importance of avoidance also suggest that emotions related to avoidance, rather than hostility, might arise in intergroup relations, as evolutionary psychology suggests that the function of emotions is to trigger adaptive behavior (Cottrell & Neuberg 2005). Indeed, anxiety, which functions to avoid or deter threatening experiences, fosters the avoidance of contact with out-group members (Paolini et al. 2018; Stephan 2014). Our results imply that emotions that prompt avoidance, including anxiety, may trigger selective interactions with in-group members in social dilemmas as well.

There are several limitations to this research and possible future extensions. First, this study only considered direct reciprocity, whereas indirect reciprocity, which stresses the importance of reputation, was not considered. The bounded generalized reciprocity model is an influential theory that explains in-group favoritism by incorporating the framework of indirect reciprocity (Yamagishi & Kiyonari 2000; Yamagishi & Mifune 2008). This theory argues that prosocial behavior enhances fitness only when targeted at in-group members. Prosocial behavior toward out-group members is not repaid because the reputation of being prosocial only holds within the group. We argue that partner selection and the bounded generalized theory can be combined because reputation can be exploited not only to determine whether to cooperate but also to choose an interaction partner (Roberts et al. 2021). For instance, the two frameworks can be combined by considering the different probabilities of obtaining reputation information between the in- and out-groups. A higher propensity to gain reputation for the cooperativeness of potential partners in in-group interactions might make in-group members preferred when choosing interaction partners. A high probability of obtaining a reputation can enhance cooperation arising through indirect reciprocity (Ghang & Nowak 2015), and this finding can be applied to situations in which multiple groups exist. Second, this study assumed the same payoff values for in- and out-group interactions. This assumption implies that avoiding out-group members does not lead to welfare loss in each interaction. However, preference for in-group partners often results in the loss of risky but profitable opportunities with out-groups (Greif 1989; McConnell et al. 2018; Takesue 2020). Considering different payoffs from a single interaction, especially the more profitable out-group interactions, can contribute to understanding the welfare implications of out-group avoidance.

Conclusion

This study examined the emergence of out-group avoidance in a repeated PDG with the leave option using agent-based modeling. We considered a situation in which the continuation probability is higher in interactions with in-group members than in those with out-group members. The simulations demonstrated that cooperation with in-group members was established; however, agents decided to avoid interaction with out-group members even without observing the first move. Cooperation with out-group members did not evolve, even when the continuation probability for pairs consisting of the members of different groups was sufficiently large for cooperation to evolve in a population without effective group distinction. The prospect of maintaining long-term cooperation with out-group members does not necessarily ensure cooperation when a more stable relationship with in-group members is possible. These observations imply the importance of the avoidance of the members of out-groups as an interaction partner in potentially cooperative situations.

References

ABOUD, F. E., Mendelson, M. J., & Purdy, K. T. (2003). Cross-race peer relations and friendship quality. International Journal of Behavioral Development, 27(2), 165–173.

AKTIPIS, C. A. (2004). Know when to walk away: Contingent movement and the evolution of cooperation. Journal of Theoretical Biology, 231(2), 249–260.

ANDRÉ, J.-B., & Baumard, N. (2011). The evolution of fairness in a biological market. Evolution, 65(5), 1447–1456.

AXELROD, R., & Hamilton, W. D. (1981). The evolution of cooperation. Science, 211(4489), 1390–1396.

BALLIET, D., Wu, J., & De Dreu, C. K. W. (2014). Ingroup favoritism in cooperation: A meta-analysis. Psychological Bulletin, 140(6), 1556–1581.

BARCLAY, P. (2016). Biological markets and the effects of partner choice on cooperation and friendship. Current Opinion in Psychology, 7, 33–38.

BETTENCOURT, L., Dixon, J., & Castro, P. (2019). Understanding how and why spatial segregation endures: A systematic review of recent research on intergroup relations at a micro-Ecological scale. Social Psychological Bulletin, 14(2), 1–24.

BIGLER, R. S., Rohrbach, J. M., & Sanchez, K. L. (2016). Children’s intergroup relations and attitudes. In S. S. Horn, M. D. Ruck, & L. S. Liben (Eds.), Advances in Child Development and Behavior (Vol. 51, pp. 131–169). Boston, MA: Academic Press.

BREWER, M. B. (1999). The psychology of prejudice: Ingroup love or outgroup hate? Journal of Social Issues, 55(3), 429–444.

CARDINOT, M., O’Riordan, C., Griffith, J., & Szolnoki, A. (2019). Mobility restores the mechanism which supports cooperation in the voluntary prisoner’s dilemma game. New Journal of Physics, 21(7), 073038.

CHIANG, Y.-S. (2008). A path toward fairness: Preferential association and the evolution of strategies in the ultimatum game. Rationality and Society, 20(2), 173–201.

COTTRELL, C. A., & Neuberg, S. L. (2005). Different emotional reactions to different groups: A sociofunctional threat-based approach to "prejudice". Journal of Personality and Social Psychology, 88(5), 770–789.

DEBOVE, S., Baumard, N., & André, J.-B. (2017). On the evolutionary origins of equity. PLoS One, 12(3), e0173636.

DE Dreu, C. K. W., Gross, J., Fariña, A., & Ma, Y. (2020). Group cooperation, carrying-capacity stress, and intergroup conflict. Trends in Cognitive Sciences, 24(9), 760–776.

DUNHAM, Y. (2018). Mere membership. Trends in Cognitive Sciences, 22(9), 780–793.

ENOS, R. D., & Gidron, N. (2016). Intergroup behavioral strategies as contextually determined: Experimental evidence from Israel. Journal of Politics, 78(3), 851–867.

FU, F., Hauert, C., Nowak, M. A., & Wang, L. (2008). Reputation-based partner choice promotes cooperation in social networks. Physical Review E, 78(2), 026117.

FU, F., Tarnita, C. E., Christakis, N. A., Wang, L., Rand, D. G., & Nowak, M. A. (2012). Evolution of in-group favoritism. Scientific Reports, 2, 460.

GHANG, W., & Nowak, M. A. (2015). Indirect reciprocity with optional interactions. Journal of Theoretical Biology, 365, 1–11.

GINTIS, H., Smith, E. A., & Bowles, S. (2001). Costly signaling and cooperation. Journal of Theoretical Biology, 213(1), 103–119.

GIRVAN, M., & Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 99(12), 7821–7826.

GREIF, A. (1989). Reputation and coalitions in medieval trade: Evidence on the Maghribi traders. The Journal of Economic History, 49(4), 857–882.

GROSS, J., Méder, Z. Z., De Dreu, C. K. W., Romano, A., Molenmaker, W. E., & Hoenig, L. C. (2023). The evolution of universal cooperation. Science Advances, 9, eadd8289.

HAHM, H., Hilpert, D., & König, T. (2024). Divided we unite: The nature of partyism and the role of coalition partnership in Europe. American Political Science Review, 118(1), 69–87.

HELBING, D., & Yu, W. (2009). The outbreak of cooperation among success-driven individuals under noisy conditions. Proceedings of the National Academy of Sciences, 106(10), 3680–3685.

HOCHBERG, M. E., Sinervo, B., & Brown, S. P. (2003). Socially mediated speciation. Evolution, 57(1), 154–158.

IZQUIERDO, L. R., IZQUIERDO, S. S., & Vega-Redondo, F. (2014). Leave and let leave: A sufficient condition to explain the evolutionary emergence of cooperation. Journal of Economic Dynamics and Control, 46, 91–113.

IZQUIERDO, S. S., IZQUIERDO, L. R., & Vega-Redondo, F. (2010). The option to leave: Conditional dissociation in the evolution of cooperation. Journal of Theoretical Biology, 267(1), 76–84.

JENSEN, G. G., Tischel, F., & Bornholdt, S. (2019). Discrimination emerging through spontaneous symmetry breaking in a spatial prisoner’s dilemma model with multiple labels. Physical Review E, 100(6), 062302.

JUGERT, P., Noack, P., & Rutland, A. (2013). Children’s cross-ethnic friendships: Why are they less stable than same-ethnic friendships? European Journal of Developmental Psychology, 10(6), 649–662.

KIM, J.-W., & Hanneman, R. A. (2014). Coevolutionary dynamics of cultural markers, parochial cooperation, and networks. Journal of Conflict Resolution, 58(2), 226–253.

LIPOWSKI, A., & Lipowska, D. (2012). Roulette-wheel selection via stochastic acceptance. Physica A: Statistical Mechanics and Its Applications, 391(6), 2193–2196.

MACANOVIC, A., Tsvetkova, M., Przepiorka, W., & Buskens, V. (2024). Signals of belonging: Emergence of signalling norms as facilitators of trust and parochial cooperation. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 379(1897), 20230029.

MASUDA, N., & Fu, F. (2015). Evolutionary models of in-group favoritism. F1000Prime Reports, 7, 27.

MASUDA, N., & Ohtsuki, H. (2007). Tag-based indirect reciprocity by incomplete social information. Proceedings of the Royal Society B: Biological Sciences, 274(1610), 689–695.

MCCONNELL, C., Margalit, Y., Malhotra, N., & Levendusky, M. (2018). The economic consequences of partisanship in a polarized era. American Journal of Political Science, 62(1), 5–18.

MCDONALD, K. L., Dashiell-Aje, E., Menzer, M. M., Rubin, K. H., Oh, W., & Bowker, J. C. (2013). Contributions of racial and sociobehavioral homophily to friendship stability and quality among same-Race and cross-Race friends. Journal of Early Adolescence, 33(7), 897–919.

MELAMED, D., Simpson, B., Harrell, A., Munn, C. W., Abernathy, J. Z., & Sweitzer, M. (2020). Homophily and segregation in cooperative networks. American Journal of Sociology, 125(4), 1084–1127.

MIFUNE, N., Simunovic, D., & Yamagishi, T. (2017). Intergroup biases in fear-induced aggression. Frontiers in Psychology, 8, 49.

NERAY, B., Copeland, M., & Moody, J. (2023). Our friends keep us together: The stability of adolescents’ cross-Race friendships. Social Forces, 102(1), 202–222.

NOWAK, M. A. (2006). Five rules for the evolution of cooperation. Science, 314(5805), 1560–1563.

NOWAK, M. A., & Sigmund, K. (2005). Evolution of indirect reciprocity. Nature, 437(7063), 1291–1298.

OCZLON, S., Boda, Z., Schwab, S., Bardach, L., Lehofer, M., & Lüftenegger, M. (2023). Ethnic in-and out-group friendships going into early adolescence: Prevalence, quality, stability, and the role of the network structure. Journal of Early Adolescence, 43(7), 867–907.

PACHECO, J. M., Traulsen, A., & Nowak, M. A. (2006). Active linking in evolutionary games. Journal of Theoretical Biology, 243(3), 437–443.

PAOLINI, S., Harwood, J., Hewstone, M., & Neumann, D. L. (2018). Seeking and avoiding intergroup contact: Future frontiers of research on building social integration. Social and Personality Psychology Compass, 12, 12422.

PERC, M., Jordan, J. J., Rand, D. G., Wang, Z., Boccaletti, S., & Szolnoki, A. (2017). Statistical physics of human cooperation. Physics Reports, 687, 1–51.

PERC, M., & Szolnoki, A. (2010). Coevolutionary games—A mini review. Biosystems, 99(2), 109–125.

RAND, D. G., & Nowak, M. A. (2013). Human cooperation. Trends in Cognitive Sciences, 17(8), 413–425.

RIOLO, R. L., Cohen, M. D., & Axelrod, R. (2001). Evolution of cooperation without reciprocity. Nature, 414(6862), 441–443.

ROBERTS, G., Raihani, N., Bshary, R., Manrique, H. M., Farina, A., Samu, F., & Barclay, P. (2021). The benefits of being seen to help others: Indirect reciprocity and reputation-based partner choice. Philosophical Transactions of the Royal Society B: Biological Sciences, 376, 20200290.

ROSSETTI, C. S. L., & Hilbe, C. (2024). Direct reciprocity among humans. Ethology, 130(4), e13407.

RUDE, J., & Herda, D. (2010). Best friends forever? Race and the stability of adolescent friendships. Social Forces, 89(2), 585–607.

SCHNEIDER, B. H., Dixon, K., & Udvari, S. (2007). Closeness and competition in the inter-ethnic and co-ethnic friendships of early adolescents in Toronto and Montreal. Journal of Early Adolescence, 27(1), 115–138.

SCHNELL, E., & Muthukrishna, M. (2024a). Indirect reciprocity undermines indirect reciprocity destabilizing large-scale cooperation. Proceedings of the National Academy of Sciences, 121(19), e2322072121.

SCHNELL, E., & Muthukrishna, M. (2024b). Reply to Gross et al.: Indirect reciprocity undermines large-scale cooperation under realistic conditions. Proceedings of the National Academy of Sciences, 121(27), e2410085121.

SIGMUND, K. (2010). The Calculus of Selfishness. Princeton, NJ: Princeton University Press.

STEPHAN, W. G. (2014). Intergroup anxiety: Theory, research, and practice. Personality and Social Psychology Review, 18(3), 239–255.

SZABÓ, G., & Fáth, G. (2007). Evolutionary games on graphs. Physics Reports, 446(4–6), 97–216.

SZABÓ, G., & Hauert, C. (2002). Phase transitions and volunteering in spatial public goods games. Physical Review Letters, 89(11), 118101.

SZOLNOKI, A., Mobilia, M., Jiang, L.-L., Szczesny, B., Rucklidge, A. M., & Perc, M. (2014). Cyclic dominance in evolutionary games: A review. Journal of the Royal Society Interface, 11(100), 20140735.

TAJFEL, M., & TAJFEL, H. (1970). Experiments in intergroup discrimination. Scientific American, 223(5), 96–102.

TAKÁCS, K., Gross, J., Testori, M., Letina, S., Kenny, A. R., Power, E. A., & Wittek, R. P. M. (2021). Networks of reliable reputations and cooperation: A review. Philosophical Transactions of the Royal Society B: Biological Sciences, 376, 20200297.

TAKESUE, H. (2020). From defection to ingroup favoritism to cooperation: Simulation analysis of the social dilemma in dynamic networks. Journal of Computational Social Science, 3(1), 189–207.

TAKESUE, H., Ozawa, A., & Morikawa, S. (2017). Evolution of favoritism and group fairness in a co-evolving three-person ultimatum game. EPL (Europhysics Letters), 118(4), 48002.

THOMSON, R., Yuki, M., Talhelm, T., Schug, J., Kito, M., Ayanian, A. H., Becker, J. C., Becker, M., Chiu, C.-y., Choi, H.-S., Ferreira, C. M., Fülöp, M., Gul, P., Houghton-Illera, A. M., Joasoo, M., Jong, J., Kavanagh, C. M., Khutkyy, D., Manzi, C., … Visserman, M. L. (2018). Relational mobility predicts social behaviors in 39 countries and is tied to historical farming and threat. Proceedings of the National Academy of Sciences, 115(29), 7521–7526.

VANBERG, V. J., & Congleton, R. D. (1992). Rationality, morality, and exit. American Political Science Review, 86(2), 418–431.

WHITT, S., & Wilson, R. K. (2007). The dictator game, fairness and ethnicity in postwar Bosnia. American Journal of Political Science, 51(3), 655–668.

WUBS, M., Bshary, R., & Lehmann, L. (2016). Coevolution between positive reciprocity, punishment, and partner switching in repeated interactions. Proceedings of the Royal Societ B: Biological Sciences, 283(1832), 20160488.

XIA, C., Wang, J., Perc, M., & Wang, Z. (2023). Reputation and reciprocity. Physics of Life Reviews, 46, 8–45.

YAMAGISHI, T., Hayashi, N., & Jin, N. (1994). Prisoner’s dilemma networks: Selection strategy versus action strategy. In U. Schulz, W. Albers, & U. Mueller (Eds.), Social Dilemmas and Cooperation (pp. 233–250). Berlin Heidelberg: Springer.

YAMAGISHI, T., & Kiyonari, T. (2000). The group as the container of generalized reciprocity. Social Psychology Quarterly, 63(2), 116–132.

YAMAGISHI, T., & Mifune, N. (2008). Does shared group membership promote altruism? Fear, greed, and reputation. Rationality and Society, 20(1), 5–30.

ZIMMERMANN, M. G., Eguíluz, V. M., & San Miguel, M. (2004). Coevolution of dynamical states and interactions in dynamic networks. Physical Review E, 69(6), 065102.