Empirically Estimating an Agent-Based Model of School Choice on Household-Level Register Data

Introduction

Research in the field of (social) complexity has highlighted how interactions between components and the entanglement of a system as a whole can cause unintended and unanticipated consequences at the macro-level due to choices individuals make (Boudon 1977; Conte et al. 2012). Agent-based models (ABMs) are considered a very suitable tool to model such dynamics and interactions (Bonabeau 2002). They are algorithmic models consisting of many, typically heterogeneous agents that interact (spatially, temporally, in social networks) and can respond to their environment as they pursue a certain objective (An et al. 2021). They allow for modelling of complex social interactions explicitly and can systematically link behaviour on the micro-level to their consequences on the macro-level (Bruch & Atwell 2015).

A recurring finding in school choice and school segregation research is that interactions within and between the components of the system are vitally important (Dignum et al. 2023; Perry et al. 2022). For example, households tend to attend schools with larger shares of their own group and avoid schools that have substantial fractions of other groups (Bellei et al. 2018; Billingham & Hunt 2016). This interaction creates a link on at least two levels. Firstly, it connects the micro-level household behaviour to the meso-level of school compositions and the macro-level outcome of school segregation. The decision to (not) attend a school due to a certain composition is both a response to that composition and a result of an action that changes this composition itself (Bruch & Atwell 2015). Second, it creates a dependency on a temporal scale between the current state of the school system and future states, where current school choices might influence future ones. For social systems, Schelling (Schelling 1971) and Sakoda (Sakoda 1971) and a large follow-up literature (Ubarevičienė et al. 2024) showed that this interdependent behaviour implies feedback loops that can lead to non-linearity and path dependence that are difficult to anticipate and control (Bruch & Atwell 2015).

Often used methodologies in school segregation studies, such as interviews, surveys, regression analyses, and macro-level correlations, fail to account for such interactions or their consequences (Dignum et al. 2023). While households might state in interviews/surveys that they interact with others, it is hard to quantify the consequences of these interactions on the macro-level, whereas methods such as regression analysis do provide quantitative estimates but often assume observations are identically and independently distributed. Hence, existing methods might not be able to accurately infer the full mechanisms behind school choice, their consequences for school segregation, and/or policies that try to affect it. This lack of scientific understanding may contribute to the fact that in many educational systems there are still substantial levels of school segregation along various lines, such as race (Reardon & Owens 2014), ethnicity (Boterman 2019), income levels (Gutiérrez et al. 2020), educational attainment (Boterman et al. 2019) and ability (van de Werfhorst & Mijs 2010), widely acknowledged to reproduce and even exacerbate inequalities and result in unequal outcomes (Echenique et al. 2006).

Consequently, ABMs have also been proposed as a very suitable methodology to tackle the complexity of school choice dynamics (Dignum et al. 2023). However, the few ABMs developed in this specific field have not used household data directly. This is a significant gap compared to previously mentioned methodologies, such as regression analysis (e.g., discrete choice models), which are highly data-driven. Estimating ABMs directly on micro-level data would make them more suitable for conducting inference on real systems and performing policy analysis. Unfortunately, in ABM, the estimation of model parameters from data (empirical estimation) is much less straightforward than in traditional but more limited techniques of modelling data, such as regression. For most ABMs, the likelihood of a parameter vector given the data cannot be formulated explicitly nor sampled from, ruling out commonly used techniques such as maximum likelihood estimation (MLE) and Markov chain Monte Carlo (MCMC) sampling.

Existing estimation attempts have circumvented this by first estimating households’ preferences/constraints using separate methodologies and then feeding these estimates into an ABM or by simulating many different preference structures. For example, Mutgan (2021) uses discrete choice models for this purpose. However, estimating preferences through such regression analysis still excludes the effect of interactions in the estimation process, potentially introducing bias by ignoring (non-)linear interaction terms. Moreover, Ukanwa et al. (2022) conducted a hypothetical school choice experiment to obtain estimates, but this experiment may not reflect realistic options, and stated versus revealed preferences can be an issue. Furthermore, Dignum et al. (2024) do not use empirically observed school choices, which makes it difficult to reason what household school choice behaviour results in the observed macro-level patterns. Thus, it still remains an open question what parameter estimation of an ABM directly on household-level school choice data can mean for our understanding of school choices and their macro-level implications.

To estimate the parameters of an ABM directly, likelihood-free methods from the field of simulation-based inference (SBI), such as approximate Bayesian computation (ABC) (Platt 2020), and more recently, techniques using neural networks, have already been successfully applied in small ABMs. Neural posterior estimation (NPE) and its variant neural ratio estimation (NRE) in particular, have shown promising results for ABMs of socio-economic systems with a limited simulation budget (Dyer et al. 2022, 2024). However, it is unclear whether these methods are still accurate in larger ABMs, with substantially more components to simulate and parameters to estimate.

Therefore, this study extends one of the few empirically grounded ABMs of school choice dynamics (Dignum et al. 2024) and estimates it directly on household school choice attendance data from Amsterdam and Almere primary schools using NRE (Hermans et al. 2020). The results demonstrate that, in our ABM that exhibits a substantial number of components and heterogeneity, NRE is able to recover the true parameter values for different choice processes accurately, providing validation for the estimation method. With the actual empirical data, several plausible school choice processes based on distance and school composition are fitted. We find that heuristic-based choice processes are a better fit than a more “rational” distance/composition trade-off approach (e.g., discrete choice models). The latter is similar to how parental preferences/constraints are often estimated in discrete choice models. This implies that the assumptions underlying discrete choice models for school choice studies may not reflect the real choice processes of households. However, the estimation also highlights that important components and/or heterogeneity might still be missing from the ABM, as parts of the empirical data are not fitted closely.

In our view, this results in at least two additions to the existing literature. Firstly, this is the first full city-scale ABM of school choice directly estimated on household register data, taking an important step towards more empirically realistic ABMs in this field and advancing our understanding of school choice dynamics. Secondly, it provides a methodology for incorporating arbitrary choice processes and estimating them within large-scale ABMs on individual-level empirical data, not only for the field of school choice but for ABMs of social systems in general, paving the way for more realistic and validated ABMs in other fields.

Background

This section is separated into two parts. Firstly, existing school choice ABM studies are described, and secondly, a brief overview of empirical estimation methods applied to ABM is given, focusing on NRE specifically.

Table 1: Abbreviations and their full form.

Abbreviation	Full form
ABM	Agent-based model or agent-based modelling
SBI	Simulation-based inference
NPE	Neural posterior estimation
NRE	Neural ratio estimation
PPC	Posterior predictive check
CBS	Central bureau of statistics or statistics Netherlands
VOC-MB	Vocationally educated with migration background
VOC-NMB	Vocationally educated with no migration background
UNI-MB	University educated with migration background
UNI-NMB	University educated with no migration background
MAD	Mean absolute deviation
MRD	Mean relative deviation
TDGP	True data generating process

ABMs of school choice

ABMs are increasingly being used in social science research as a way to model bidirectional links and feedback loops between and within the micro- and macro-level of systems (Bruch & Atwell 2015). They are algorithmic models composed of individual agents that are autonomous entities that interact with each other and their environment. Agents are endowed with rules to describe their behaviour, and each agent can represent individuals, organisations, or even entire populations. They are useful for studying the emergence of collective behaviour from individual behaviour, understanding the effects of policy interventions (Bonabeau 2002) and exploring the effects of uncertainty, randomness, and feedback loops in complex systems (Flache et al. 2022). Rules determine how agents interact with each other and their environment, which can include factors such as geography, resources, and social networks. This is particularly useful for studying social systems, including the dynamics of school choice and school segregation, where the behaviour of individuals is interconnected and often highly dependent on the context in which they are embedded (Bruch & Atwell 2015).

For school choice research, the use of ABMs has been limited and can be divided into two branches. On the one hand there is a branch that uses highly stylised ABM, to analyse how theoretical rules (inspired by empirical research) result in different levels of school segregation (Sage & Flache 2021; Stoica & Flache 2014). These are primarily used to build new theories or extend existing ones, but have limited applicability to reality. The second line of research has focused more on using empirical estimates of the school choice processes in ABM and analysing the impact of specific policies.

For example, Mutgan (2021) uses conditional logit models (i.e., discrete choice) to estimate parental preferences for various school characteristics for eight different types of households. Incorporating these estimates in an ABM and conducting policy simulations, they find that most of the ethnic school segregation in Stockholm is due to ethnic residential segregation. The reasoning behind this is that in their assumed two-step school choice procedure, households first construct a feasible school choice set. Schools further than a certain distance threshold are filtered out, which already results in ethnically very similar schools being the only “feasible” choices.

Ukanwa et al. (2022) base their parental preference estimates on a survey conducted on American households combined with a hierarchical Bayesian model. Presenting hypothetical schools to households, which differ substantially (on purpose) on several school characteristics, they estimate the preferences of Black and White households for commute times, their own group, school quality, teacher experience, and the share of low-income students. One of the findings is that households have preferences for more of their own group in a school. However, even excluding these composition preferences in the ABM (i.e., no explicit own-group preferences), the system nevertheless ends up with substantial school segregation because preferences for other school characteristics differ considerably. It should be noted, as the authors do as well, that it is possible that households were reluctant to reveal their true preferences regarding school racial compositions (i.e., sensitivity) and stated different preferences than in real-life school decisions.

Lastly, Dignum et al. (2024) use aggregated data to estimate residential locations of high- and low-income households in Amsterdam. Treating these residential locations as fixed, primary school choices are simulated under a wide range of distance and composition preferences. The main result reiterates the theoretical findings that even with relatively tolerant households that value mixed schools over homogeneous ones, the system segregates substantially. This is in part attributed to the fact that the average household has many schools nearby in Amsterdam, giving distance preferences less opportunity to limit school segregation. In other words, there are enough close proximity schools without large distance differences. This is substantiated by an experiment restricting school choice to the 1, 2, 4 or 8 closest primary schools. In this policy experiment, going from one to two choices leads to a substantial increase in school segregation, with 4 and 8 even reaching higher levels. This implies that more school choice leads to higher levels of school segregation in this model, which is a consistent finding in empirical school choice research as well (Wilson & Bridge 2019).

However, all these attempts still do not estimate their ABM directly on household-level data, but either use a different methodology to estimate preferences/constraints or use aggregate statistics and approximations. Dignum et al. (2024) use approximations to the real system, but without actual school choice data. Discrete choice models, as used in Mutgan (2021), cannot take feedback loops into account, which can lead to biased estimates. In addition, the hypothetical experiment of Ukanwa et al. (2022) measures the stated rather than revealed preferences. Hence, it remains unclear what the use of actual school choices in ABM can add to our understanding of school choice behaviour. However, to use school choice data for ABM estimation, one has to resort to simulation-based inference (SBI) in absence of a tractable likelihood function (Cranmer et al. 2020).

Simulation-based inference for ABM

ABMs often involve a lot of computation, analyses and are hard to estimate and validate. Previous studies have partially circumvented this by using other methodologies to estimate the parameters of ABMs. This often excludes the effect of interdependencies in the estimation process, missing potentially important feedback loops, non-linearity and path-dependency which are reasons ABMs are employed to begin with and which could introduce biases in the estimates. However, for direct estimation of the ABM, common techniques require a specification of the likelihood function, which is very hard or impossible to write down for ABMs. Note that the literature on estimation of ABMs is vast and, for reasons stated in the following, this study focusses on NRE. For brevity, other techniques are not described here, but for a more elaborate discussion the reader is referred to Platt (2020) and Dyer et al. (2024) for ABM estimation, and Cranmer et al. (2020) for an overview of SBI methods.

NRE has demonstrated improved performance with a smaller or equal simulation budget for parameter inference of a small ABM compared to other techniques (Durkan et al. 2020; Dyer et al. 2022, 2024). This is important as ABMs, especially of large scale, can be computationally expensive to simulate. Additionally, neural networks can better capture complex relationships between the parameters and the observations, which are often found in ABM (Bruch & Atwell 2015). However, it remains an open question how well this technique will scale to more parameters and elaborate summary statistics (i.e., higher dimensionality), such as in this study. Although neural networks are criticised as being “black-box” techniques, here this is less of a concern as they are simply used to obtain parameter estimates for the ABM that can be interpreted. We focus on NRE, as NPE is argued to scale less well to higher dimensions (i.e., the number of model parameters). This is because NRE transforms the estimation procedure into a classification problem, which is a supervised and intuitively an easier task, while NPE tries to estimate the functional form of the joint posterior distribution directly. An advantage of targeting the posterior directly is that one can sample it for further inference without simulating the potentially expensive simulator again or having to use MCMC.

For accurate inference, these methods require a large number of evaluations of the ABM (i.e., model runs or simulations) and adequate summary statistics. First, many (random) values for \(\boldsymbol{\theta}_m \in \{1, ..., M\}\) are sampled from a prior distribution. Here, the vector \(\boldsymbol{\theta}_m\) contains a value for all the parameters of the model. For each sampled value of \(\boldsymbol{\theta}_m\) the ABM is simulated, resulting in an output \(\boldsymbol{x}_m\), also called the summary statistics. Hence, the \(M\) model runs create a dataset of input values and simulated outputs (\((\boldsymbol{\theta}_m, \boldsymbol{x}_m) \in \{1, ..., M\}\)). If, for example, one chooses the level of school segregation as a summary statistic, the technique tries to learn what values of the parameter vector \((\boldsymbol{\theta})\) lead to which levels of school segregation. Note that in this example \(\boldsymbol{x}_m\) is a scalar value, but for the eventual estimation, more elaborate summary statistics are used, as this can considerably improve inference (Cranmer et al. 2020). These values can then be compared with actual empirical observations. However, the choice of summary statistics has proven important for performance in previous studies (Dyer et al. 2024) and should contain sufficient and useful information to estimate the parameters.

An Agent-Based Model of School Choice

The ABM used in this study is based on that of Dignum et al. (2024), but for completeness, the model will be described in detail in this section. The purpose of the ABM is to model households’ school choice in the Amsterdam and Almere contexts, and estimate their preferences from empirical data. Note that the terms households, agents, parents, and children are used as synonyms throughout this section, as well as city and environment. To ground the model in the empirical context, research on primary school segregation in Amsterdam is described first (household-level studies on Almere are very scarce), followed by the technical details of the ABM.

Primary school segregation in Amsterdam and Almere

Most studies on school choice in The Netherlands make use of register data from the Central Bureau of Statistics (CBS). Consistent with the group classifications of CBS¹ and the existing literature, the groups are constructed along educational and ethnic lines. Children are considered to have a migration background (MB) if at least one of their parents is born in a country that is not the Netherlands and have no MB (NMB) otherwise. For educational attainment, households are classified as university (UNI) educated if at least one of the parents has attained a university (of applied sciences) diploma and vocational (VOC) otherwise. This results in four mutually exclusive groups used in this study: VOC-MB, VOC-NMB, UNI-MB and UNI-NMB, their detailed construction can be found in the appendix.

The reason for not using income categories is that these categories correlate substantially with educational attainment, using both groups might then lead to identification problems. Furthermore, educational groups are naturally categorical, which avoids substantiating cut-offs for income levels. Additionally, the literature often uses the four largest ethnic groups: Surinamese, Moroccan, Turkish, and Dutch as subgroups, but here a binary classification is made: NMB and MB. Together with the educational groups, this results in four distinct groups. There are at least two reasons for using a binary ethnic classification. Four instead of eight different groups halves the amount of parameters to estimate, which means a drastic reduction in the number of samples (i.e., ABM runs) needed. Second, some groups would become very small relative to others, possibly leading to identification problems.

Although factors in school segregation are context-specific, different educational systems exhibit similarities through which the dynamics of school segregation operate similarly (Dignum et al. 2023). Distance is found to be an important determinant of (primary) school choice in Amsterdam and Almere (Boterman 2013; Boterman 2019). This is because households prefer a school close to home or are constrained in their ability to travel far. This results in residential segregation projecting itself in schools simply due to these distance mechanisms. Furthermore, these preferences/constraints are also found to vary between groups (Clark et al. 1992; Denessen et al. 2001; Vedder 2006), for example, highly educated households have been found to travel further compared to their lower educated counterparts (Karsten et al. 2003).

In some educational systems, households might be assigned a neighbourhood school and can only opt-out. However, in the Netherlands this is not the case, making school choice relatively free (Boterman et al. 2019). Amsterdam, however, does grant you priority at your eight closest primary schools. Although this might induce certain households to move into neighbourhoods with favourable school characteristics, most households choose schools given their current residential location (Boterman 2021). These eight primary schools are within a fairly small radius for most households and more than 86% attend such a priority school in practice (Breed Bestuurlijk Overleg 2021). Tables 2 and 3 show that all but one household group attend a school within a radius of 1000 metres on average. In Almere, households travel slightly further than in Amsterdam, with the UNI-NMB group attending schools the furthest on average in Almere (1077m), while in Amsterdam they only travel 880m.

Table 2: Descriptive statistics for the Amsterdam case.

Amsterdam (191 schools)
Group	Count	Avg. school%	Q90 school%	Municipality%	Avg. distance (m)	%Religious	%Pedagogical
UNI-MB	11417	22%	31%	24%	955	37%	13%
UNI-NMB	16162	28%	63%	33%	880	29%	16%
VOC-MB	15893	38%	75%	33%	793	47%	3.9%
VOC-NMB	5069	11%	21%	10%	975	45%	7.5%

Table 3: Descriptive statistics for the Almere case.

Almere (72 schools)
Group	Count	Avg. school%	Q90 school%	Municipality%	Avg. distance (m)	%Religious	%Pedagogical
UNI-MB	3094	18%	27%	19%	972	43%	3.9%
UNI-NMB	4169	22%	41%	26%	1077	45%	7.1%
VOC-MB	4534	33%	57%	28%	883	39%	1.1%
VOC-NMB	4275	28%	40%	27%	911	46%	3.2%

Moreover, research highlights that households tend to prefer schools with more of their own group and avoid schools with large shares of others (Clark et al. 1992). Interestingly, parents in Amsterdam also state that they want their children to attend a diverse school (Boterman 2013). However, whether composition preferences are only due to choice homophily, an actual preference for more of your own group, or whether this is due to other mechanisms such as the link between residential segregation and distance, is harder to disentangle. Additionally, households also associate certain compositions with lower quality education and want their children to attend a school that performs well, thus avoiding schools with particular compositions (Vedder 2006). The Dutch constitution also allows schools to have a specific religion or pedagogy (e.g., Catholic, Montessori). Certain profiles might only attract specific households, resulting in a higher share of those groups in these schools. For example, higher educated parents consider social education and creative development very important (Denessen et al. 2001), and Turkish/Moroccan parents mention that they would send their children to an Islamic school if the opportunity arises (Clark et al. 1992). Our data confirms this on an aggregate level. In both cities, the UNI groups attend a pedagogical school more often than the VOC groups, but children with NMB even more than those with a MB. For religious schools, it is the opposite (29% versus 37%). Within the VOC group, both MB and NMB attend religious schools substantially more often than their UNI counterparts, but VOC-NMB attend pedagogical schools almost twice as much as MB, but substantially less than the UNI group.

On an aggregate level, Boterman (2019) notes that levels of school segregation along ethnic and socioeconomic lines are lower in Almere than in Amsterdam, but both are substantial. This is confirmed by the data used here: the multi-group Dissimilarity index for Amsterdam is 0.38 and for Almere it is 0.22. The average fraction of VOC-MB in schools is 38% in Amsterdam, while its share in the municipality is 33%. For Almere, this is 33% versus 28%. This may indicate that this group is more segregated from the rest. However, note that this descriptive finding could be due to the preference of the own group or the preferences of other groups, but also due to the spatial distribution of specific schools and (distance) constraints combined with residential segregation.

Hence, the factors households use in choice of school, or by which they are constrained, interact with each other on multiple levels. Moreover, the local context determines what factors are important and for which specific groups of households (heterogeneity). This is what makes it hard to disentangle the mechanisms behind the school choices and their (non-linear) effects on school segregation and policy. It might also explain why parents state that they want their children to attend a diverse school (Boterman 2013), but end up choosing schools that are less diverse because the system is already in a (too) segregated state. Schools that have a composition close to that of the municipality might be rare, or the other schools have too large shares of others (i.e., segregation). These are all reasons why ABMs could be an important addition to our understanding of school segregation, especially when estimated and validated using empirical data (Bruch & Atwell 2015). In the next sections, the technical details of the ABM are described.

Households

Consistent with the literature described in Section 3.1, it is assumed that household school choices are driven by school compositions and distance preferences/constraints. However, the vast majority of existing studies, including contexts outside of the Netherlands, use discrete choice models. Here, it is often assumed that distance and composition affect the propensity to choose a school linearly. For example, a school that is 500m away is twice as likely to be chosen over one that is 1000m away (all else being equal). While we implement this mechanism in the ABM, two other choice mechanisms are also implemented to study which type of mechanism is most consistent with the data. More in line with the bounded rationality of humans when making decisions in social contexts (Bruch & Feinberg 2017) and contrary to discrete choice models in school choice research, heuristics are employed for composition and distance preferences.

For all three implementations, households are assumed to first apply a distance filter: they only consider schools within a certain radius (\(\theta_{rad}\)). \(D_{is}\) is the Euclidean distance in kilometres from household \(i\) to school \(s\). Other accessibility metrics, such as travel time, are not available. Additional preferences are described in the following three subsections. Note that every group has their own set of parameters, hence preferences are allowed to differ between groups and that are to be estimated from the data.

Thresholds

In this choice process, households are assumed to at least want a minimum share of their own group in a school (homophily) or using a different interpretation: they are repelled by large shares of other groups. They receive a composition utility of 1 if the share of their own group exceeds a certain threshold (\(\theta_{comp}\)) and 0 otherwise. For distance utility, households receive 1 if the school falls within the specific radius \(\theta_{rad}\) and 0 if not. Thus, a household is fully satisfied if a school has a fraction higher than (\(\theta_{comp}\)) and is within a certain radius, however, it could happen that only one of the thresholds or none is satisfied.

\[U_{ist} = U^{comp}_{ist} + U^{dist}_{ist} \]

\[(1)\]

\[U^{comp}_{ist} = \begin{cases} 1 & \text{if } C_{ist} > \theta_{comp} \\ 0 & \text{if } C_{ist} \leq \theta_{comp} \end{cases} \]

\[(2)\]

\[U^{dist}_{ist} = \begin{cases} 1 & \text{if } D_{is} \leq \theta_{rad} \\ 0 & \text{if } D_{is} > \theta_{rad} \end{cases} \]

\[(3)\]

Discrete choice

This implementation is very close to a discrete choice model, where households are assumed to weigh their own group composition in a school (more is better) and distance (closer is better). Note that these distance preferences are in addition to the strict radius preferences. The weight parameter \(\theta_{comp}\) is between [0,1] and \(\theta_{comp} > 0.5\) would indicate that the composition is more important than the distance for that specific group.

\[U_{ist} = \begin{cases} \theta_{comp} C_{ist} + (1-\theta_{comp})(1-\frac{D_{ist}}{\theta_{rad}}) & \text{if } D_{ist} \leq \theta_{rad} \\ 0 & \text{if } D_{is} > \theta_{rad} \end{cases} \]

\[(4)\]

Linear composition

The last choice process assumes that households have a preference for more of their own group in a school but only up to a certain point, after which it no longer matters. Utility increases linearly from 0 to 1 up until \(\theta_{comp}\) and is equal to 1 onwards. The distance utility is as previously described in Equation 3. This excludes the possibility that the utility can also decline if there are “too many” of the own group. Although this is also stated by parents in Amsterdam (Boterman 2013), preliminary estimations with such a choice process did not seem to make much difference in model fit.

\[U^{comp}_{ist} = \begin{cases} C_{ist} & \text{if } \frac{C_{ist}}{\theta_{comp}} \leq \theta_{comp} \\ 1 & \text{if } C_{ist} > \theta_{comp} \end{cases} \]

\[(5)\]

Schools

Schools are assumed to be passive entities that only have a distance to all households, and their compositions vary as the result of households’ choices. However, there is a minimum capacity of 50 to avoid unrealistically small schools and no maximum size. It should be noted, that there is evidence that certain schools are more active in the educational system than is modelled here. For example, through organising school visits, partnering with specific preschools, propagating certain identities/values (e.g., through websites) or advising particular households other schools. Note that these observed activities can affect school choices, but they are assumed to be less important than the ones that are modelled here, and this kind of data is simply hard to acquire.

Environment

The environment consists of primary schools and households. Although primary school locations are known and freely available (Dienst Uitvoering Onderwijs 2023), this does not contain sensitive school and household student information, which CBS does not allow to be published. Specifically, this means that no statistics on households or schools that contain less than 10 individual data points are allowed, which reflects itself in the aggregate numbers presented in this study. Figure 1 gives a visual representation of the ABM environment for two hypothetical groups (red/blue) and the actual locations of primary schools in Amsterdam (Dienst Uitvoering Onderwijs 2023). Note that this model is simplified by assuming that the residential locations of the households are fixed. Although this is a strong assumption, this is more plausible for educational systems where there are no catchment areas, such as the Netherlands.

Simulation

Below, one run of the ABM (i.e., simulation) is described in detail:

1. Select 90% of the actual households for the simulation. This reduces computations by 10% and introduces randomness which can reduce overfitting.
2. To avoid giving every household within a group exactly the same parameter values, a normally distributed shock (zero mean, standard deviation of 0.02) is added to the group-specific parameters. This within-group heterogeneity allows for the fact that not every group member will have exactly the same parameter values. In future studies, this standard deviation could also be estimated from the data.
3. Allocate every household to one of their three closest schools to start the simulation. This reflects reality better compared to a random start, since households in 2019 already observed a segregated system and based their choices on that.
4. Calculate utilities for every school and household combination
5. Select a fraction (\(f=0.05\)) that is allowed to switch schools this time step. Every household, in random order, does the following:
   • Rank schools according to their utility
   • Switch to your top-ranked school. If your current school has a population below the minimum capacity, you are not allowed to switch.
6. Repeat steps 4 and 5 until the average and standard deviation of all utilities stabilises or the maximum number of time steps is reached. The model is considered converged if the average and standard deviation of all household utilities have a mean absolute deviation (MAD) smaller than 0.02 for the last 20 time steps. Note that this means that at least 20 steps are executed. The maximum amount of steps is set to 300; visual inspection of model runs shows that almost all converge within this time frame.

Every time step \(t\), all households have full information on all school characteristics in the environment. However, only after all agents have actually made their decisions, the household utilities are updated. This means that the last household that considers switching still uses the school compositions that were calculated at the end of step \(t-1\). One exception is the school minimum capacity, which is updated in real-time to avoid schools ending up below their minimum allowed size.

Methodology

Empirical estimation is concerned with finding which configurations of our ABM are (most) consistent with the empirical data. As outlined in the introduction, for ABM one often needs to turn to techniques from SBI, as the likelihood is unavailable or impossible to sample from. For this study, NRE is employed to estimate the posterior distributions of the parameter vector \(\boldsymbol{\theta}\). This vector contains, for every group, the parameters of Equations 2-5.

In summary, the inference process works as follows. Samples are drawn from the specified priors, where each sample consists of random values for all model parameters that are to be estimated. For every sample, the ABM is initialised with these specific values and simulated until it converges or has reached the maximum number of steps. At the end of the simulation, the summary statistics (high-level descriptions of the ABM behaviour) are calculated. Parameter values and their associated summary statistics construct input-output combinations. This data set serves as training data for NRE which tries to learn the probabilistic relationship between the parameters and the summary statistics, i.e., which values of the model parameters are likely to lead to what values of the summary statistics.

NRE is chosen because it is argued to be more (simulation) efficient than for example more commonly used techniques such as approximate Bayesian computation (ABC) and possibly scales better to higher dimensions than NPE, which is more important for large-scale ABMs. NRE does not discard simulated samples such as ABC, does not require choosing a distance metric, and estimates the true posterior instead of an approximation (Dyer et al. 2024). However, selecting an appropriate neural network architecture (i.e., hyperparameter settings) and proper summary statistics are still important for NRE. Even though NRE does involve a more computationally costly MCMC-step than NPE, the argued improvement of NRE over NPE in higher dimensions is given priority. As the ABM is already described in the previous section, the next sections will describe the remaining two ingredients for the estimation: NRE and the summary statistics.

Neural ratio estimation

NRE requires prior knowledge or constraints on the parameters which is modelled through the prior: \(P(\boldsymbol{\theta})\). Furthermore, it needs the ABM to generate simulated data (\(\boldsymbol{x}^{sim}\)) and observational data (\(\boldsymbol{x}^{obs}\)) of the real system. For the latter two, it is common to use high-level descriptions of the ABM output instead of raw data, or also called summary statistics. The method then proceeds as follows:

1. Generate \(M\) samples from the priors: \(\boldsymbol{\theta}_m \in \{1, ..., M\}\)
2. Run the ABM for every \(\boldsymbol{\theta}_m\) and save the summary statistics, \(\boldsymbol{x_m}^{sim}\). This results in a training dataset of input-output combinations \((\boldsymbol{\theta}_m, \boldsymbol{x_m}^{sim}) \in \{1, ..., M\}\).
3. Use the training data to learn the relationship between the summary statistics of the simulated data and the underlying parameter vector \(\boldsymbol{\theta}\) of the ABM using NRE.
4. Condition the posteriors on the empirically observed data (\(\boldsymbol{x}^{obs}\)), to obtain inference for the specific data under study. Note that this implies that the simulated summary statistics should be the same measures as those of the observational data (\(\boldsymbol{x}^{obs}\)). High posterior probability is assigned to parameters which are consistent with both the data and the prior, and low probability to inconsistent ones.
5. This process can be repeated, also called sequential NRE (SNRE), focusing the next steps around the empirical observation of interest (\(\boldsymbol{x}^{obs}\)). Apart from the first round, where the proposal values are sampled from the specified prior distributions, subsequent rounds draw new proposals from the estimated posterior of the previous round. This means that the ABM has to be simulated for these newly proposed values by constructing a new input-output dataset. This focuses the attention on the posteriors conditional on a specific observation, increasing efficiency of the samples used, but losing amortisation. Hence, posterior inference is only valid for the specific empirical data used.

NRE transforms the posterior estimation problem into a classification task. The simplest implementation randomly shuffles the training data pairs coming from the ABM output \((\boldsymbol{\theta}_m, \boldsymbol{x}_m^{sim}) \in \{1, \ldots, M\}\). The non-shuffled part gets the label \(y=1\), while the shuffled part gets the label \(y=0\). It then leverages a neural network as a classifier to discern between the two types of data points: those that come from the ABM (i.e., the joint posterior, \(y=1\)) and those that are independent (\(y=0\)). This shuffling destroys the inherent dependencies, associating \(\boldsymbol{x}_j^{sim}\) with a randomly selected \(\boldsymbol{\theta}_j\). Consequently, the likelihood-to-evidence ratio signifies the probability that a given pair belongs to the dependent dataset. Miller et al. (2022) have extended this to a multi-class classification problem, increasing performance, which is the variant employed in this study.

A slightly adapted version of the standard implementation of NRE from the SBI Python package (Tejero-Cantero et al. 2020) is used. The network consists of 200 hidden features, has a learning rate of 0.0005, uses a validation fraction of 0.1 and is considered converged if the validation loss stabilises for the last 20 epochs. Both the inputs (\(\boldsymbol{\theta}\)) and the simulated outputs (\(\boldsymbol{x}^{sim}\)) are z-scored on the entire batch of simulations, as the dimensions depend on each other. Because of computational constraints and irrespective of the number of parameters to estimate, each case and choice process combination is given two rounds of inference, 50,000 simulations each. Thus, the neural networks obtain a dataset of 50,000 combinations to train on. For MCMC sampling, 20 chains start with a thinning factor of 5 and a warm-up of 1000 steps each. Note that these hyperparameters can all be varied and that the type of density estimator (resnet) can be changed. However, this is left for future work.

As very little initial information is assumed, a uniform prior is specified for every parameter in Equations 2- 5. Fractions or weights are bounded between 0 and 1, and hence \(P(\theta_{comp}) \sim \mathcal{U}(0, 1)\). However, for the threshold choice processes it is insensible to run simulations with a large threshold while the group fraction is small. For example, a threshold of 0.9 while the group fraction is 0.1. Hence, for the threshold mechanisms, the upper bound of the prior is set to the 90% percentile of school fractions found per group in the actual municipality (see Tables 2 and 3). Although distances are truncated to five kilometres in the pre-processing step, households are unlikely to have a very large radius, as this would contain a substantial number of schools, hence \(P(\theta_{rad}) \sim \mathcal{U}(0, 3)\). However, for the discrete choice process, this could impact the distance/composition trade-off and hence in this case \(P(\theta_{rad}) \sim \mathcal{U}(0, 5)\).

Summary statistics

An essential ingredient for SBI methods is the use of summary statistics or high-level descriptions of the simulation model used for inference. To build some intuition as to why this is important, let us consider two extreme cases. If one takes the scalar value of school segregation as a summary statistic, then this is likely to have lost critical information. This can lead to very broad or multimodal posterior distributions, as numerous combinations of parameter values could result in the same level of school segregation. On the other end, one can provide very elaborate data. For example, for every household their eventual school choice, distance travelled to school, and the share of each group in each school, but the estimation methods might have a hard time identifying the complicated relationships in this data.

Although neural networks are theoretically able to distinguish very complex relationships in the data, this is conditional on the sample size of the training dataset and the values of the hyperparameters. In this study, a very standard implementation of the neural network is employed, and computational constraints do not allow for simulating the ABM millions of times, hence the sample size is also restricted. These constraints would likely lead to the estimation methods not being able to infer the posteriors in the case of very elaborate summary statistics. Importantly, these statistics should also be meaningful for the processes studied, i.e., school choice and school segregation. Analysing which summary statistics the eventual empirically estimated ABM is able to fit accurately and which not can lead to interesting insights into the models’ shortcomings.

For this study, two sets of summary statistics are used that ideally lead to the same posterior distributions. The first set uses statistics at the group level, while the second uses school-level statistics. For every group, the average and standard deviation of the fraction in each school, the average and standard deviation travelled to schools, and the percentage attending religious and pedagogical schools are used as summary statistics. This results in 24 values in total and six statistics per group. These statistics are insightful, one can see which are over or under predicted, they are also very easy to calculate given the data, and for some educational systems even publicly available such as in London (Greater London Authority 2024). Intuitively, this should provide NRE with substantial information for estimation purposes, but it is possible that different school choice mechanisms lead to the same summary statistics (i.e., identification problems). However, the prior bounds for the distance and composition parameters and common sense should mitigate the problem to a certain extent.

As a robustness check, parameter estimates using a second set of summary statistics are also reported. For every school, the average distance travelled to that school and the contribution to Theil’s measure of segregation (Theil & Finizza 1971) are calculated. The latter is an indication of how much the school contributes to the level of segregation. Unfortunately, as privacy regulations also hold for individual schools, the actual empirical observation of the summary statistics cannot be shown here. However, the empirical summary statistics at the group level in Tables 2- 3 give some insight into the different school choice behaviours.

Performance assessment

To assess how well the empirically estimated ABMs perform, various predictive checks are conducted based on the mean absolute deviation (MAD) and mean relative deviation (MRD) of the simulated summary statistics and the empirically observed versions. Firstly, 5,000 samples are drawn from the approximated joint posterior distribution. With these samples, the ABM is simulated again, leading to 5,000 simulated summary statistics (the ABM output). These simulated outputs are then compared with the empirical summary statistics. This is also called a posterior predictive check (PPC). In case of a summary statistic of length \(S\) and \(K\) newly generated values, the MAD and MRD can be calculated as follows:

\[ MAD = \frac{1}{S \cdot K} \sum_{s=1}^{S} \sum_{k=1}^{K} |x^{obs}_s - x^{new}_{sk}|\]

\[(6)\]

\[ MRD = \frac{1}{S \cdot K} \sum_{s=1}^{S} \sum_{k=1}^{K} \frac{|x^{obs}_s - x^{new}_{sk}|}{|x^{obs}_s| + |x^{new}_{sk}|}\]

\[(7)\]

Adequate posterior estimation would have most empirical summary statistics fall within the support of the distributions of those generated in the PPC. If this is the case, one can conclude that the estimated ABM is capable of reproducing the observed data of the real system with substantial accuracy. Therefore, we report the fraction of empirical summary statistics that do not fall within the PPC limits and the fraction that does not fall within the 95% credible interval (CI). Note that this is a necessary but not a sufficient condition for correct posterior inference (Dyer et al. 2024). This procedure is repeated for the geometric median estimate, i.e., the ABM is simulated 5,000 times with the median (point) estimate as input, resulting in the median MAD and median MRD. Ideally, all empirically observed summary statistics fall within the support of the distribution of simulated summary statistics corresponding to the PPC.

Additionally, if the PPC and median performance metrics are very similar, it suggests something about the sensitivity of the summary statistics to the parameter values in this region of the parameter space. In general, the posteriors are wider than the median estimates (point estimate versus distribution). If the performance metrics are close to each other, it indicates that perturbations of the input parameters do not change the summary statistics substantially, which increases the validity of the estimation.

Results

First, the posterior estimates for all combinations of cases and choice processes, along with performance metrics are presented. The second part reports on a validation check of the estimation procedure. This check assumes that the empirical estimates of the first section are the true values (i.e., the ground truth is known) and that the ABM is the true data-generating process. Given these assumptions, the estimation method should be able to retrieve the true parameter values with reasonable accuracy.

Posterior estimates

For each case, the median estimates are reported in the tables. Reason for reporting median point estimates is that some posteriors are multi-modal, which impacts the mean more than the median. Visual inspection of the approximated posteriors would immediately reveal this, but due to space limitations, only posterior plots of the best performing models are presented.

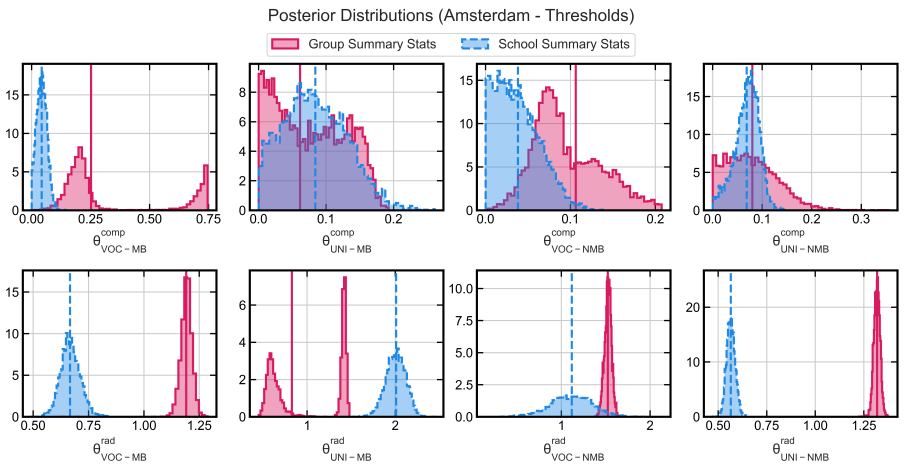
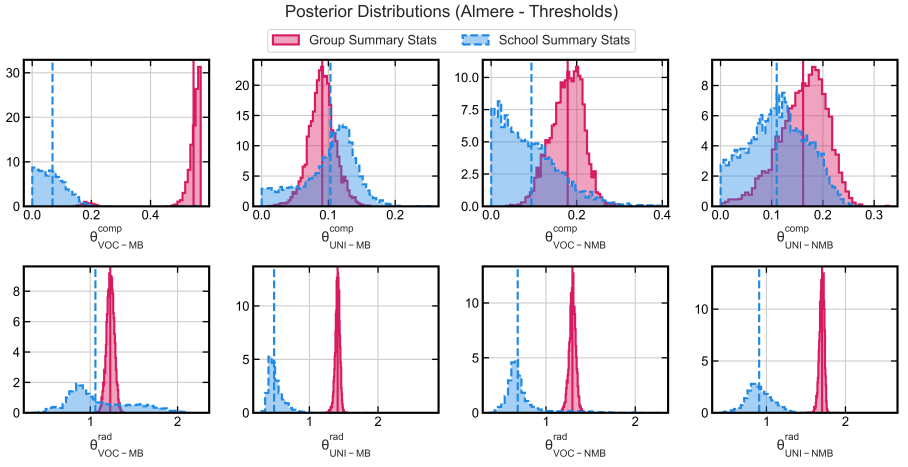
Table 4 shows that the best performing model, using summary statistics at the group level for the Amsterdam case, is the threshold choice process in terms of almost all performance metrics. Only the percentage of summary statistics that fall outside the 95% CI of the posterior support is higher than both the discrete choice and the linear composition process. This implies that for 33% of the empirically observed summary statistics, the estimated threshold model is not that likely to reproduce them. For Almere, the threshold choice process also outperforms the rest in terms of MAD/MRD and has a high percentage of \(\boldsymbol{x}^{obs}\) falling outside of 95% CI. The discrete choice implementation performs substantially worse than the other two choice mechanisms and is therefore deemed less plausible to have generated these empirically observed summary statistics given this ABM configuration.

However, if these choice processes are close to the true choice processes of these household groups, then a second, but different set of summary statistics should lead to similar estimates. Unfortunately, the median estimates for all choice processes are substantially different from the first set of summary statistics (Figure 2). Admittedly, this is not an entirely fair comparison, in the Amsterdam case the second set of summary statistics consists of 382 values and the first only has 24. Using the same computational budget and neural network architecture, this could be an important factor in the accuracy/feasibility of the estimation. However, for the Almere case (142 versus 24 values), this potential computational limitation is less severe, and indeed the relative differences between the median estimates seem less stark, but are still substantial (Figure 3). Thus, although the next sections will describe interpretations of the estimated posteriors, this should be read with the aforementioned in mind.

Table 4: Posterior estimates and predictive performance in terms of MAD/MRD for the Amsterdam case.

Amsterdam
Summary statistics		Thresholds		Discrete choice		Lin. Composition		Municipal avg.
		Group	School	Group	School	Group	School
VOC-MB	\(\theta_{comp}\)	0.25	0.04	0.44	0.22	0.17	0.13	0.33
	\(\theta_{rad}\)	1.19	0.67	3.94	1.23	1.22	0.71	0.79
UNI-MB	\(\theta_{comp}\)	0.06	0.08	0.45	0.49	0.85	0.06	0.24
	\(\theta_{rad}\)	0.83	2.01	3.92	4.52	1.36	2.42	0.96
VOC-NMB	\(\theta_{comp}\)	0.11	0.04	0.37	0.56	0.52	0.09	0.10
	\(\theta_{rad}\)	1.52	1.12	4.46	0.64	0.44	1.11	0.98
UNI-NMB	\(\theta_{comp}\)	0.08	0.07	0.49	0.20	0.54	0.26	0.33
	\(\theta_{rad}\)	1.32	0.56	4.32	1.58	1.26	0.69	0.88
PPC	MAD	0.11*	0.15	0.11*	0.66	0.20	0.20
	MRD	0.10*	0.26	0.17	0.48	0.16	0.29
	Outside bounds	0.08	0.06	0.21	0.02*	0.12	0.01
	Outside 95% CI	0.33	0.38	0.29	0.20	0.21	0.15*
Median	MAD	0.04*	0.15	0.11	0.54	0.07	0.19
	MRD	0.07*	0.26	0.17	0.45	0.12	0.30

For both cases, the threshold choice process performs best in terms of MAD and MRD metrics, thus we will proceed with interpreting those estimates first. For the Amsterdam case, the composition estimates of all groups are close to 0 and estimates of both sets of summary statistics are relatively aligned, implying that there is no substantial preference for a greater share of your own group in schools. However, theoretical models have shown that even small preferences for the own group can lead to non-linear effects in terms of (school) segregation (Dignum et al. 2022; Sage & Flache 2021; Schelling 1971; Stoica & Flache 2014). This is exacerbated when the groups are small in relative size, as shown in Dignum et al. (2024). For example, requiring 10% of your own group in a school can lead to substantial segregation, especially when this group is already under-represented in the neighbourhood. Moreover, despite evidence suggesting that Amsterdam parents prefer some diversity (Boterman 2013), we do not model this. Incorporating a specific penalty for homogeneity (schools with only one group attending) as in Dignum et al. (2022), Dignum et al. (2024) did not lead to meaningfully different results, and therefore this choice process is not incorporated. The second peak from the posterior distribution for the VOC-MB composition parameter is deemed less plausible, as this would imply this group requires 75% of their own group in a school to be satisfied from a composition perspective, while they only have 33% in the municipality as a whole (Table 2). Note that another way of dealing with less plausible parts of the parameter space is through the prior. One could have assumed a prior that assigns more probability close to the shares in the municipality for example. The radius estimate for the UNI-MB group and group summary statistics shows bimodality. The first peak is around 0.5, i.e. 500 metres, and the second around 1.3 kilometres. Table 2 shows that this group has an average travel distance of almost a kilometre to their school, while the standard deviation is also around a kilometre (Figure 5), hence there might be considerable within-group heterogeneity unaccounted for, which could explain the bimodality. Although the other radius estimates are unimodal, the 0.56 (UNI-NMB) and 0.67 (VOC-MB) estimates using school summary statistics are very low and the different sets of summary statistics lead to very different results. Again, the standard deviation of the distance travelled to school is close to one kilometre for these groups (Figure 5). Subdividing these groups in a meaningful way can potentially solve this.

Table 5: Posterior estimates and predictive performance in terms of MAD/MRD for the Almere case.

Almere
Summary statistics		Thresholds		Discrete choice		Lin. Composition		Municipal avg.
		Group	School	Group	School	Group	School
VOC-MB	\(\theta_{comp}\)	0.55	0.07	0.08	0.03	0.09	0.07	0.28
	\(\theta_{rad}\)	1.23	1.06	0.73	0.75	0.70	1.01	0.88
UNI-MB	\(\theta_{comp}\)	0.09	0.10	0.47	0.05	0.20	0.06	0.19
	\(\theta_{rad}\)	1.41	0.49	3.60	1.23	1.46	1.63	0.97
VOC-NMB	\(\theta_{comp}\)	0.18	0.09	0.48	0.04	0.15	0.06	0.27
	\(\theta_{rad}\)	1.30	0.68	1.12	1.11	1.28	0.60	0.91
UNI-NMB	\(\theta_{comp}\)	0.16	0.11	0.45	0.03	0.60	0.04	0.26
	\(\theta_{rad}\)	1.70	0.91	4.20	0.70	0.83	0.99	1.08
PPC	MAD	0.13*	0.19	0.22	0.42	0.13*	0.21
	MRD	0.15*	0.29	0.26	0.41	0.19	0.31
	Outside bounds	0.04	0.01*	0.17	0.06	0.21	0.01*
	Outside 95% CI	0.38	0.15*	0.25	0.36	0.38	0.16
Median	MAD	0.09*	0.18	0.22	0.37	0.12	0.20
	MRD	0.11*	0.29	0.27	0.36	0.16	0.30

The posteriors for the threshold process in the Almere case only show unimodal posterior distributions. Moreover, the radius estimates show a different trend from that in the Amsterdam case. Here, both UNI groups have larger radius estimates than their vocational counterparts and the estimates for the composition parameters of the NMB groups are also larger (i.e., they want more of their own group in schools) than in Amsterdam. Almere has substantially lower values of residential segregation (Boterman 2019), which could induce UNI groups, who are often considered more active choosers, to look further for schools with a higher share of their own group. Interestingly, Almere has larger estimates for composition preferences (around 0.2) for the NMB groups, but has lower empirical school segregation than Amsterdam (Boterman 2019). This can be explained by the following reasoning. Almere has a more equal distribution of the four groups (Tables 2-3) and lower residential segregation, this may mean that the composition preference can be more easily satisfied without the need to travel further for schools and possibly induce feedback effects.

The results for both cities imply that the main component of primary school choices is distance and hence for school segregation: residential patterns. This is reinforced by the composition preference estimates for the linear composition model (in both cities) and the discrete choice (in Almere). The discrete choice estimates in Amsterdam imply that UNI-MB and VOC-NMB weigh distance and composition almost equally. It should be noted that the MAD/MRD in this case are also the highest among all metrics and are hence unlikely to represent the true choice processes of households. However, it should be reiterated that even though composition preference are small, this can still lead to substantial levels of school segregation, especially when there is existing residential segregation and few schools within feasible distance (Dignum et al. 2024).

Unfortunately, we can only report the group-level summary statistics, as the school-level is considered sensitive data by CBS regulations. Visually inspecting the summary statistics of the threshold implementation in Figures 5- 6 show that the standard deviation of the distances seems furthest away from their empirical values. This can be a sign of important within-group heterogeneity (a part of the group travels further than others). Moreover, the percentages attending religious and pedagogical schools are very close to their values, without explicitly modelling them. However, the UNI-NMB group seems to attend pedagogical schools more often than one would expect based on this model, which is in line with the existing literature (Denessen et al. 2001). Caution should be taken with concluding that these factors are not important for the other groups in Amsterdam, because these profiles can correlate substantially with composition preferences, meaning that the composition estimates are actually due to preferences for a certain profile. Adding these factors into the model could shed more light on this, but also would increase the computational burden substantially, and this is left for future studies.

Estimation with known ground truth

NRE does not guarantee that the posterior inference is correct or accurate. To increase credibility of the estimation process, an experiment with a hypothetical ground-truth is conducted:

• Assume the ABM is the true data generating process (TDGP)
• Use median point estimates from the empirical estimation of Section 5.1 as the true values
• Create artificial “empirical” summary statistics (based on the geometric median of the PPC) that will serve as the equivalent of the empirical summary statistics used in the actual estimation.
• Use the same priors and inference pipeline as in Section 5.1
• Confirm that the true values can be retrieved with the MAD/MRD performance metrics

To illustrate that NRE is able to retrieve the correct parameter estimates when the ABM is the TDGP, the median estimates from all models in the Almere case are treated as the true values. The Almere case is substantially smaller than the Amsterdam case and thus less computationally costly. Although the number of parameters to estimate and the training of the neural networks are equal for both cases, the dynamics within the model can be different. However, the assumption is that by presenting a successful estimation for the Almere case, the same will hold for the Amsterdam case when the ABM is the TDGP.

The results in Table 6 and Figure 4 confirm that the true values can be retrieved for all parameters, which validates the estimation method. Most of the posterior mass is concentrated around the true values (vertical lines in Figure 4), but the composition and radius estimates for the VOC-MB group in the threshold process have some probability mass in regions different from the true values. For the former, this is also seen in the actual estimate of the composition parameter of this group (Figure 3) and thus is expected. The UNI-NMB composition posterior for the linear composition process and two radius posteriors for the discrete choice process (UNI-MB and UNI-NMB) are very broad, implying that these values lead to similar values of the summary statistics. This highlights that choosing summary statistics is important for accuracy or even identifiability in other cases. For example, with another set of summary statistics, accuracy could have been higher or in different estimation problems, some summary statistics might not provide sufficient information to estimate the parameters (i.e., structural identifiability).

Table 6: Posterior estimates and predictive performance in terms of MAD/MRD for the Almere case when the ground truth is known.

Almere (true values known)
		Thresholds	\(\theta_{true}\)	Discrete choice	\(\theta_{true}\)	Lin. Composition	\(\theta_{true}\)
VOC-MB	\(\theta_{comp}\)	0.52	0.55	0.11	0.08	0.08	0.09
	\(\theta_{rad}\)	1.25	1.23	0.72	0.73	0.70	0.70
UNI-MB	\(\theta_{comp}\)	0.08	0.09	0.48	0.47	0.17	0.20
	\(\theta_{rad}\)	1.41	1.41	3.55	3.60	1.47	1.46
VOC-NMB	\(\theta_{comp}\)	0.17	0.18	0.50	0.48	0.16	0.15
	\(\theta_{rad}\)	1.30	1.30	1.13	1.12	1.29	1.28
UNI-NMB	\(\theta_{comp}\)	0.16	0.16	0.43	0.45	0.58	0.60
	\(\theta_{rad}\)	1.70	1.70	4.12	4.20	0.82	0.83
PPC	MAD	0.04		0.07		0.03
	MRD	0.07		0.11		0.08
	Outside bounds	0.00		0.00		0.00
	Outside 95% CI	0.00		0.00		0.00
Median	MAD	0.04		0.05		0.03
	MRD	0.06		0.10		0.07

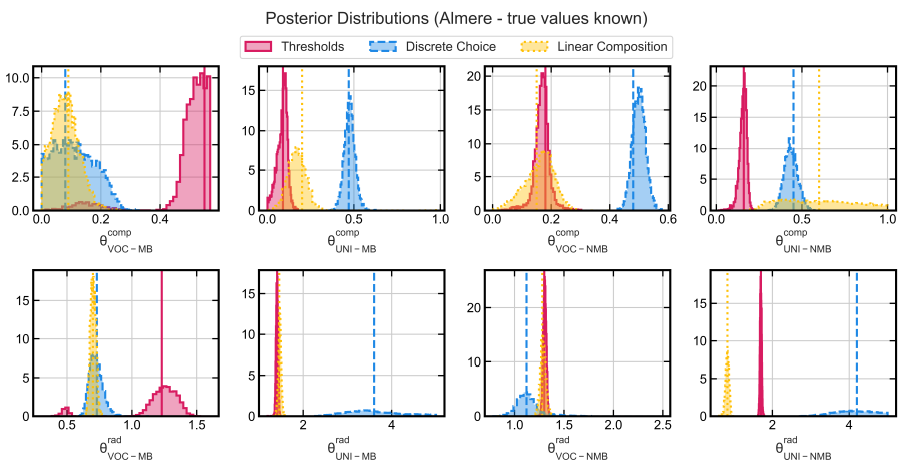
Compared to the actual empirical estimates, two things stand out. First, none of the summary statistics falls outside the posterior bounds or outside the 95% CI. This means that the artificial “empirical” summary statistics are well within the posterior support and that the model is able to accurately recreate the summary statistics, as expected. However, in the actual estimation, the fraction of summary statistics outside of the 95% CI is considerably greater than 0. This implies that there is something left to explain in the choice processes of households. Additionally, the MAD/MRD values are very close but not equal to zero. This can be due to the fact that not entire posterior distributions are compared but point estimates, combined with the fact that the model contains some degree of stochasticity. Note that the estimated posterior distributions of the actual empirical estimation could have been compared with the posteriors of this experiment. However, the reported MAD/MRD values and the fraction of summary statistics outside of the PPC bounds can now serve as a benchmark of what one could expect if the true process is not known. Importantly, the MAD/MRD metrics in the Almere case with the group-level summary statistics for the actual estimation are slightly larger than in this experiment, suggesting some unexplained errors.

Conclusion

ABMs are increasingly being used to model interactions and dynamics within social systems (Bruch & Atwell 2015). Consequently, they are also considered to be a very suitable tool for studying the dynamics of school choice and school segregation. However, empirically estimated ABMs have received limited attention, due to computational challenges, a lack of data, and shortcomings in the methodologies for estimation. Although empirical data has been used in ABMs specifically designed for school choice (Dignum et al. 2024; Mutgan 2021; Ukanwa et al. 2022), this has either been through the use of another methodology to estimate household parameters (e.g., hypothetical experiments, discrete choice modelling) or by employing aggregate data.

Therefore, large-scale individual-level data has not been used directly to estimate ABMs of school choice and extract household school choice behaviour. Previously mentioned methodologies might contain biases in their estimation process, such as stated-versus revealed preferences in hypothetical experiments or not accounting for interactions and non-linearity in discrete choice estimates. Hence, it remains an open question what direct estimation of an ABM on household-level data can mean for our understanding of school choice. However, estimating ABMs directly on large-scale individual-level data in general is very difficult, as the likelihood is often intractable or impossible to sample from, but it would make ABM more suitable to represent real systems and to perform policy analysis.

This study extended the school choice ABM of Dignum et al. (2024) and estimated it on household-level primary school choice register data. Using neural ratio estimation (NRE) and high-level descriptions of the register data as summary statistics, three plausible school choice mechanisms based on distance and composition are estimated on the data. This is done for four different ethnic-educational groups in two specific cities in the Netherlands: Amsterdam and Almere and two sets of summary statistics.

Although the implemented choice processes contain only distance and composition heuristics for four groups, the results show that, in most cases, the heuristic choice processes fit the data better in both cities. The discrete choice implementation, where households take a weighted sum of composition and distance preferences, performs substantially worse. This could be important for more commonly used methodologies in this field that often assume perfectly rational households that have complete information about the system, such as discrete-choice models. Although these assumptions have been questioned extensively for many systems and numerous types of choices (Bruch & Feinberg 2017), this study provides a methodology to actually put avoiding these assumptions into practice for modelling the dynamics of school choice in the Netherlands. This is an important step towards more empirically realistic ABMs in this field and possibly other application areas.

However, the actual empirical estimates are more difficult to trust. One would expect that if actual mechanisms of school choice are discovered that the estimated ABM can reproduce empirical summary statistics on various (spatial) scales. For the two sets of summary statistics used in this study, this is not the case. Group-level statistics lead to very different results than more granular school-level statistics. Admittedly, it could be the increase in dimensionality of the summary statistics while keeping the training set and computational budget fixed. However, it is left for future studies to shed light on that or potential other issues.

To strengthen our confidence in the estimation methodology as no guarantees on accurate posterior inference can be given, a hypothetical experiment was conducted that treats ABM as the true data-generating process. Using the posterior estimates from the empirical estimation, this experiment shows that NRE is able to recover the true values with reasonable accuracy. Even though the ABM is tailored to a specific context, many features such as heterogeneity, feedback loops and non-linearity apply to ABMs of other systems, demonstrating feasibility for larger and more heterogeneous systems than in previous studies employing NRE (Dyer et al. 2024; Miller et al. 2022). However, future work could replicate this experiment in larger parts of the parameter space and different ABMs, to check if these results hold or when the estimation fails to accurately infer the true values.

Discussion

The true process of household school choice can obviously not be captured by only two factors. There is evidence that other factors, such as the religious and pedagogical profile of schools, matter. For example, university-educated households value special pedagogical profiles more than their vocationally educated counterparts, which is not modelled in this study. However, it should also be noted that the group percentages attending a religious and pedagogical school are already close to their empirical values without specifically modelling a preference for such schools. The existing literature also highlights that within the migration background group there could be considerable heterogeneity. Households with different ethnic backgrounds and the same educational group may choose schools differently, but are modelled as one group in this study. Hence, the ABM might have missed important dynamics and heterogeneity within the system of school choice. Therefore, future studies could incorporate more factors in school choice and/or more groups that are influential for the context at hand. This could improve the fit of the ABM on the empirical data and reduce the discrepancy between the results of the two sets of summary statistics.

Additionally, it is not only extra factors or more groups, there are numerous other combinations of using distance and composition in the school choice process that are not explored. Moreover, not all groups necessarily have the same choice mechanism, which is assumed in this study. One way to implement this is to use more general choice processes that nest more simple ones. Although most choice processes can be interpreted as a heuristic way of choosing schools, the actual implementation is still based on utility maximisation principles and having full information. While this is an improvement in light of empirical evidence on decision-making in social contexts (Bruch & Feinberg 2017), future implementations could also use different paradigms.

These aspects touch upon a more general question: how much complexity and empirical data should one add in order to obtain a valid representation of the system under study? By assuming that people belong and identify with only a few large overarching groups and have “simple” choice mechanisms, one is likely to obtain more tractability and interpretability. Even though already complex dynamics can evolve in those cases, it becomes even more complicated the more real world complexity one adds.

In addition, for the actual estimation method, several robustness and predictive checks are performed. However, there is much to validate and potentially improve. The summary statistics are a crucial aspect of SBI methods in general, and although accurate posterior inference is proven by simulation when the ground truth is known, it is unclear what this means when the true process is not fully known. Other studies could help determine “optimal” summary statistics, which are important for the dynamics of the system under study, to improve posterior inference compared to hand-crafted summary statistics. One option is to learn the summary statistics, as demonstrated by Dyer et al. (2024).

A further challenge for the choice of appropriate summary statistics is that a model can generate different equilibrium outcomes all of which are similar in terms of certain macro-level characteristics such as the overall level of segregation, but different in terms of the underlying micro-patterns. For example, for a given parameter combination the typical outcome could be that the four groups are mixed 50-20-20-10 in a certain school, while in another run (with different parameter values) we would have the same mix in the same school but different individuals of the same groups. All else being equal, the summary statistics would be exactly the same. This may be another reason why the estimation on school-level statistics was less successful in our study, since reality represents “only one run”, to which then only a fraction of the simulated runs can be fitted well. Future work needs to explore summary statistics at school level which capture crucial characteristics of the distribution of groups across schools, while being robust against variation in the specific way that distribution is realised.

Also of interest would be the comparison with other estimation methods and the difference in performance, changing the neural network architectures or learning the summary statistics instead of handcrafting them (Dyer et al. 2024). Moreover, from a validation perspective, the ABM is shown to reproduce the empirical summary statistics up to a reasonable level. However, these are only two sets of summary statistics, and estimations lead to different interpretations of household school choice behaviour. Ideally, the behaviour of the households within the model and statistics at higher aggregate levels would also be comparable with the empirical data. This more extensive validation could give the model more credibility and provide additional insight into where the model can improve. A validated model can also be used to assess the impact of policies such as changing the number of priority schools, opening new schools, and closing too small schools. For the latter, the model currently caps schools at a minimum of 50 pupils, but in reality such schools might be closed.

Lastly, while the validation experiment demonstrates the method’s ability to recover the true parameter values under a known model structure, an important limitation remains: In empirical settings, researchers often face uncertainty not only about parameter values, but also about the choice process itself. A key question is how the method performs when the assumed functional form is incorrect, i.e., structural misspecification. For example, estimating a threshold-based model when the true process follows a discrete-choice framework. In addition, the model likely has omitted variables. If an important factor, such as school quality, is excluded from the estimated model, how does this affect the accuracy of the remaining parameter estimates? Although these questions are important to study, we leave these for future research. However, there is still value in understanding the values of the parameters under an assumed choice process and validating if the estimation method works under these assumptions.

References

AN, L., Grimm, V., Sullivan, A., Turner II, B., Malleson, N., Heppenstall, A., Vincenot, C., Robinson, D., Ye, X., Liu, J., Lindkvist, E., & Tang, W. (2021). Challenges, tasks, and opportunities in modeling agent-based complex systems. Ecological Modelling, 457, 109685. [doi:10.1016/j.ecolmodel.2021.109685]

BELLEI, C., Contreras, M., Canales, M., & Orellana, V. (2018). The production of socio-economic segregation in Chilean education: School choice, social class and market dynamics. In X. Bonal & C. Bellei (Eds.), Understanding School Segregation: Patterns, Causes and Consequences of Spatial Inequalities in Education (pp. 221–242). London: Bloomsbury Publishing. [doi:10.5040/9781350033542.ch-011]

BILLINGHAM, C. M., & Hunt, M. O. (2016). School racial composition and parental choice: New evidence on the preferences of white parents in the United States. Sociology of Education, 89(2), 99–117. [doi:10.1177/0038040716635718]

BONABEAU, E. (2002). Agent-based modeling: Methods and techniques for simulating human systems. Proceedings of the National Academy of Sciences, 99(3), 7280–7287. [doi:10.1073/pnas.082080899]

BOTERMAN, W. R., Musterd, S., Pacchi, C., & Ranci, C. (2019). School segregation in contemporary cities: Socio-spatial dynamics, institutional context and urban outcomes. Urban Studies, 56(15), 3055–3073. [doi:10.1177/0042098019868377]

BOTERMAN, W. R. (2013). Dealing with diversity: Middle-class family households and the issue of “black” and “white” schools in Amsterdam. Urban Studies, 50(6), 1130–1147. [doi:10.1177/0042098012461673]

BOTERMAN, W. R. (2019). The role of geography in school segregation in the free parental choice context of Dutch cities. Urban Studies, 56(15), 3074–3094. [doi:10.1177/0042098019832201]

BOTERMAN, W. R. (2021). Socio-spatial strategies of school selection in a free parental choice context. Transactions of the Institute of British Geographers, 46(4), 882–899. [doi:10.1111/tran.12454]

BOUDON, R. (1977). The Unintended Consequences of Social Action. Berlin Heidelberg: Springer.

BREED Bestuurlijk Overleg. (2021). Placement of children in Amsterdam primary schools 2020-2021. Available at: https://bboamsterdam.nl/wat-we-doen/toelatingsbeleid/uitvoering-van-stedelijk-toelatingsbeleid-in-cijfers/

BRUCH, E., & Atwell, J. (2015). Agent-based models in empirical social research. Sociological Methods & Research, 44(2), 186–221. [doi:10.1177/0049124113506405]

BRUCH, E., & Feinberg, F. (2017). Decision-making processes in social contexts. Annual Review of Sociology, 43, 207–227. [doi:10.1146/annurev-soc-060116-053622]

CBS. (2023). Microdata statistics Netherlands. Available at: https://www.cbs.nl/en-gb/our-services/customised-services-microdata/microdata-conducting-your-own-research/microdata-files/microdata-catalogue

CLARK, W., Dieleman, F., & De Klerk, L. (1992). School segregation: Managed integration or free choice? Environment and Planning C: Government and Policy, 10(1), 91–103. [doi:10.1068/c100091]

CONTE, R., Gilbert, N., Bonelli, G., Cioffi-Revilla, C., Deffuant, G., Kertesz, J., Loreto, V., Moat, S., Nadal, J.-P., Sanchez, A., Nowak, A., Flache, A., San Miguel, M., & Helbing, D. (2012). Manifesto of computational social science. The European Physical Journal Special Topics, 214(1), 325–346. [doi:10.1140/epjst/e2012-01697-8]

CRANMER, K., Brehmer, J., & Louppe, G. (2020). The frontier of simulation-based inference. Proceedings of the National Academy of Sciences, 117(48), 30055–30062. [doi:10.1073/pnas.1912789117]

DENESSEN, E., Sleegers, P., & Smit, F. (2001). Reasons for school choice in the Netherlands and in Finland. National Center for the Study of Privatization in Education Occasional Paper.

DIENST Uitvoering Onderwijs. (2023). Primary school addresses. Available at: https://duo.nl/open_onderwijsdata/primair-onderwijs/scholen-en-adressen/

DIGNUM, E., Athieniti, E., Boterman, W., Flache, A., & Lees, M. (2022). Mechanisms for increased school segregation relative to residential segregation: A model-based analysis. Computers, Environment and Urban Systems, 93, 101772. [doi:10.1016/j.compenvurbsys.2022.101772]

DIGNUM, E., Boterman, W., Flache, A., & Lees, M. (2023). Modeling mechanisms of school segregation and policy interventions: A complexity perspective. Springer Lecture Notes in Computer Science (LNCS). [doi:10.1007/978-3-031-36024-4_6]

DIGNUM, E., Boterman, W., Flache, A., & Lees, M. (2024). A data-driven agent-based model of primary school segregation in Amsterdam. The Journal of Mathematical Sociology, 48(3), 1–31. [doi:10.1080/0022250x.2024.2340136]

DURKAN, C., Murray, I., & Papamakarios, G. (2020). On contrastive learning for likelihood-free inference. International Conference on Machine Learning.

DYER, J., Cannon, P., Farmer, J. D., & Schmon, S. M. (2022). Calibrating agent-based models to microdata with graph neural networks. arXiv preprint. arXiv:2206.07570.

DYER, J., Cannon, P., Farmer, J. D., & Schmon, S. M. (2024). Black-box Bayesian inference for agent-based models. Journal of Economic Dynamics and Control, 161, 104827. [doi:10.1016/j.jedc.2024.104827]

ECHENIQUE, F., Fryer Jr, R. G., & Kaufman, A. (2006). Is school segregation good or bad? American Economic Review, 96(2), 265–269. [doi:10.1257/000282806777212198]

FLACHE, A., Mäs, M., & Keijzer, M. A. (2022). Computational approaches in rigorous sociology: Agent-based computational modeling and computational social science. In K. Gërxhani, N. D. de Graaf, & W. Raub (Eds.), Handbook of Sociological Science (pp. 57–72). Cheltenham: Edward Elgar Publishing. [doi:10.4337/9781789909432.00011]

GREATER London Authority. (2024). London datastore. Available at: https://data.london.gov.uk/dataset?q=&topics=2c4d2275-67a6-401b-89ca-4ed62556b901

GUTIÉRREZ, G., Jerrim, J., & Torres, R. (2020). School segregation across the world: Has any progress been made in reducing the separation of the rich from the poor? The Journal of Economic Inequality, 18(2), 157–179.

HERMANS, J., Begy, V., & Louppe, G. (2020). Likelihood-free MCMC with amortized approximate ratio estimators. International Conference on Machine Learning.

KARSTEN, S., Ledoux, G., Roeleveld, J., Felix, C., & Elshof, D. (2003). School choice and ethnic segregation. Educational Policy, 17(4), 452–477. [doi:10.1177/0895904803254963]

MILLER, B. K., Weniger, C., & Forré, P. (2022). Contrastive neural ratio estimation. Advances in Neural Information Processing Systems, 35, 3262–3278.

MUTGAN, S. (2021). Free to choose? Studies of opportunity constraints and the dynamics of school segregation. PhD Thesis, Linköping University Electronic Press. [doi:10.3384/9789179291020]

PERRY, L. B., Rowe, E., & Lubienski, C. (2022). School segregation: Theoretical insights and future directions. In Comparative Education (Nos. 1; Vol. 58, pp. 1–15). [doi:10.1080/03050068.2021.2021066]

PLATT, D. (2020). A comparison of economic agent-based model calibration methods. Journal of Economic Dynamics and Control, 113, 103859. [doi:10.1016/j.jedc.2020.103859]

REARDON, S. F., & Owens, A. (2014). 60 years after Brown: Trends and consequences of school segregation. Annual Review of Sociology, 40(1), 199–218. [doi:10.1146/annurev-soc-071913-043152]

SAGE, L., & Flache, A. (2021). Can ethnic tolerance curb self-Reinforcing school segregation? A theoretical agent based model. Journal of Artificial Societies and Social Simulation, 24(2), 2. [doi:10.18564/jasss.4544]

SAKODA, J. M. (1971). The checkerboard model of social interaction. The Journal of Mathematical Sociology, 1(1), 119–132. [doi:10.1080/0022250x.1971.9989791]

SCHELLING, T. C. (1971). Dynamic models of segregation. Journal of Mathematical Sociology, 1(2), 143–186.

STOICA, V. I., & Flache, A. (2014). From Schelling to schools: A comparison of a model of residential segregation with a model of school segregation. Journal of Artificial Societies and Social Simulation, 17(1), 5. [doi:10.18564/jasss.2342]

TEJERO-CANTERO, A., Boelts, J., Deistler, M., Lueckmann, J.-M., Durkan, C., Gonçalves, P. J., Greenberg, D. S., & Macke, J. H. (2020). SBI - A toolkit for simulation-based inference. arXiv preprint. arXiv:2007.09114 [doi:10.21105/joss.02505]

THEIL, H., & Finizza, A. J. (1971). A note on the measurement of racial integration of schools by means of informational concepts. The Journal of Mathematical Sociology, 1(2), 187–193. [doi:10.1080/0022250x.1971.9989795]

UBAREVIČIENĖ, R., van Ham, M., & Tammaru, T. (2024). Fifty years after the Schelling’s models of segregation: Bibliometric analysis of the legacy of Schelling and the future directions of segregation research. Cities, 147, 104838.

UKANWA, K., Jones, A. C., & Turner Jr, B. L. (2022). School choice increases racial segregation even when parents do not care about race. Proceedings of the National Academy of Sciences, 119(35), e2117979119. [doi:10.1073/pnas.2117979119]

VAN de Werfhorst, H. G., & Mijs, J. J. (2010). Achievement inequality and the institutional structure of educational systems: A comparative perspective. Annual Review of Sociology, 36, 407–428. [doi:10.1146/annurev.soc.012809.102538]

VEDDER, P. (2006). Black and white schools in the Netherlands. European Education, 38(2), 36–49. [doi:10.2753/eue1056-4934380203]

WILSON, D., & Bridge, G. (2019). School choice and the city: Geographies of allocation and segregation. Urban Studies, 56(15), 3198–3215. [doi:10.1177/0042098019843481]