David Hales (1998)

Journal of Artificial Societies and Social Simulation vol. 1, no. 4, <https://www.jasss.org/1/4/2.html>

Abstract

Using the "meme" conception (Dawkins 1976) of cultural transmission and computer simulations, an exploration is made of the relationship between agents, their beliefs about their environment, communication of those beliefs, and the global behaviours that emerge in a simple artificial society. This paper builds on previous work using the Minimeme model (Bura 1994). The model is extended to incorporate open-mindedness meta-memes (memes about memes). In the scenarios presented such meta-memes have dramatic effects, increasing the optimality of population distribution and the accuracy of existing beliefs. It is argued that artifical society experimentation offers a potentially fruitful response to the inherent problems of building new meme theory.

Keywords:

Artificial Societies, Computer Simulation, Memetics, Meta-memes

Introduction

1.1

If ideas are seen as replicating, mutating entities (replicating through people's minds via communication) then they can be viewed as "viruses of the mind" (Dawkins 1993). The analogy is that ideas spread through a population by "infecting" brains in a similar way to the spread of a virus. It is argued that memes are often successful because they induce their hosts to replicate them. Since Dawkins' seminal work, several other writers have used the meme concept to explain various cultural and social phenomena (Bonner 1980; Dennett 1995; Gabora 1997).

1.2

In order to investigate the implications of this conception of belief spread I have constructed a computational simulation of a simple artificial society. Several experiments have been conducted and some interesting and counter-intuitive results have been observed.

1.3

Various computational models of cultural transmission have been advanced (e.g. Axelrod 1995; Epstein and Axtell 1996; Reynolds 1994; Gabora 1995). "Cultural Algorithms" introduced by Reynolds (1994) augment standard Genetic Algorithm techniques with a belief structure of hierarchically organised beliefs and their generalisations. In the simulations he presents, group level fitness values are used to update the belief structure. The belief structure is then used to bias the selection of chromosomes for reproduction into the next generation. The model shows how cognitive abilities (generalisation in this case) and intergenerational cultural knowledge (the belief structure) can be used to improve the performance of GAs when applied to tricky group co-operation scenarios. It is a high-level model which assumes the existence of shared cultural knowledge and group level selection. The model was not designed to address issues such as the spatial aspects of cultural transmission or the emergence of stable shared cultural characteristics from micro-level asynchronous cultural transmission and innovation. It is this latter aspect that memetic models attempt to address.

1.4

The Sugarscape (Epstein and Axtell 1996) model uses strings of binary flags to represent cultural transmission units. Each agent randomly propagates flags to local neighbours. A function is then applied to the string in order to ascribe cultural identity ^[1]. The spread of such identities (or "tribes") can then be monitored and behaviours can be influenced by them (e.g. combat).

1.5

It would seem that individuals in real societies are much more active in their selection of ideas, practices and beliefs. They often reject or "repel" new ideas and beliefs, particularly if they are currently strongly attached to contradictory ones. Attachment or confidence in a particular belief may grow if many others with whom the individual has come into contact also share such a belief (a form of "reinforcement" or "frequency dependant bias" (Boyd & Richerson 1985).

1.6

A multiple agent model of meme spread which attempts to address these issues has been proposed by Bura (1994). This model is extended to incorporate meta-memes (ideas about ideas). A comparison is then made between three simulation scenarios with and without a particular meta-meme.

1.7

Gabora's ( 1995) "Meme and Variation" Model is a more fine grained model which utilises neural networks to capture a form of meme evaluation. In contrast, the Minimeme model described in tis paper is a higher-level model. It does not make assumptions concerning agents' cognitive functioning, specifically, agents do not evaluate memes. In this sense the agents presented here are more passive than those presented by Gabora. However, evaluation mechanisms should be seen as meta-memes. The Minimeme model can accommodate evaluation mechanisms but these would be implemented as meta-memes within the system. The argument is that evaluative functioning can be "boot-strapped" from a simpler meme model without building in such functions initially. However, this is not a dogmatic statement: in general artificial societies are constructed to answer specific questions and explore particular phenomena and as such different architectures are dictated by the requirements at hand.

The Minimeme Model

2.1

The model is composed of two parts: (a) the environment and agents, (b) the meme level (or noosphere ^[2]). The environments and agents differ from simulation to simulation, but the rules governing the noosphere do not.

The Noosphere

2.2

According to Dawkins (1993) any idea capable of transmitting itself from one person to another (replicating itself) is a meme. In Minimeme only memes that define behaviour are considered. Such memes can be "executed" by their hosts to produce an effect (e.g. movement, fighting, socialising etc.). In order to be successful and continue to exist, a meme must satisfy three conditions:

1. it must find at least one host (an agent that stores it in its memory);
2. the "execution" of the meme must not endanger the host's life (at least not before the meme has been able to reproduce itself);
3. the meme must be able to resist the attack of opposing memes (termed "concurrent" memes) in the meantime.

2.3

The sum of the memories of all the agents in the environment constitutes a space called the noosphere. Memes inhabit the noosphere in the same way that agents inhabit the simulated environment.

How Memes Evolve And Spread

2.4

To simulate the ability of the memes to conquer a part of the noosphere two parameters are associated with each meme : "change", which is a measure of the meme's propensity to mutate or to succumb to attacks by other memes and "aggression", which is a measure of the meme's propensity to try to reproduce itself. These parameters take real values in the range [0..1]. It is important to note that these parameters do not take into account the ability of the meme to keep its agent host alive.

2.5

Memes evolve and spread in three stages:

1. Satisfaction test: update change and aggression values;
2. Mutation: mutate the meme in some way;
3. Replication: attempt to spread the meme to other agents.

2.6

First a satisfaction function is evaluated for each host. This function is simulation dependent. It may involve an estimation of the correct accomplishment of a task or the inspection of state variables in the host (e.g. is it hungry, ill etc.). The function should return an all-or-nothing result. Either the host is or is not satisfied. If the host is satisfied, it increases the aggression of each of its memes by 25 per cent and decreases their change by 25 per cent. Conversely, if the host is not satisfied, it decreases its memes' aggression and increases their change.

2.7

After this stage the memes may mutate and reproduce. A mutation occurs when a random draw in the range [0..1] gives a number lower than the meme's change. The actual nature of the mutation is simulation dependent.

2.8

If a meme was not mutated and if another random draw in range [0..1] is lower than its aggression, replication may take place. A random number of individuals are chosen among the host's neighbours (i.e. the ones it can communicate with) and the meme is proposed to each of them. If any of the neighbours are hosts to concurrent memes then a random draw in the range [0..1] is made. If this is lower than the attacked meme's change the meme is overwritten by the attacking meme (replicated) otherwise it stays in the host's memory (repelling the attacking meme). If a meme tries to infect a host that already possesses the same meme it is reinforced (its change is decreased and its aggression is increased).

2.9

It is important to note that hosts can learn new memes only by interacting with each other. Memes can not be coded into the environment or learned by experience.

2.10

These mechanisms are the same for all the simulations using the model. The characteristics to be defined for a given simulation are: (a) The satisfaction function for the hosts; (b) The nature of the mutations each meme can undergo; (c) The range of communication between hosts (i.e. how to find the "neighbours" of a given host).

The World Of The Grazers

3.1

"Grazers" are very simple agents who live in a very simple environment. They can move, feed (accumulate energy), die and communicate with others in their territory. The environment they inhabit consists of just four territories. Each territory can feed a fixed number of grazers during each cycle (a "carrying capacity"). Any number of agents can occupy a territory. Grazers have one decision to make in each cycle: whether to move to a new territory ^[3] or "stay put". Grazers try to maximise their energy (if it falls below a minimum, they die). The desirability of a territory is a function of its carrying capacity and the number of grazers that already occupy it. The grazers do not have knowledge of the carrying capacities of the territories, but they do have knowledge of the distribution of the population in each territory and as "grazers" they have a natural propensity to herd. They determine the desirability of each territory based on the number of grazers already occupying it. A grazer makes a decision with reference to a meme which tells it the ideal number of grazers that should occupy a territory. It makes a rational decision using its current meme ^[4]. This "herding" meme is represented by a single integer in the range 1 to 10. If a grazer possessed a '1' meme it would look for an empty territory (or the most empty if none were empty). Grazers mutate their memes by increasing or decreasing them by one.

Accumulating And Consuming Energy

3.2

Movement from one territory to another costs a grazer one energy point. If a grazer can not feed during the system cycle it loses an energy point. If a grazer can feed it gains an energy point (up to a maximum of 5 energy points). If there are more grazers in a territory than the specified carrying capacity, the grazers that will go hungry are selected at random. When the energy level of a grazer falls below 1 it dies instantly ^[5]. Newly born grazers start with a maximum energy level of 5 and take their memes from a random neighbour or generate them randomly if no neighbour exists. At the start of a simulation, the locations and memes of grazers are generated randomly. All energy levels are set to the maximum.

The System Cycle

3.3

One pass through the following phases constitutes a single system cycle ^[6]:

• Action Phase: Each grazer gets a chance to move to a new territory.
• Environment Phase: Predators attack any vulnerable grazers (see below).
• Feeding Phase: Each grazer tries to eat from its current location.
• Meme Phase: Each grazer tests its satisfaction and then updates, mutates or spreads its memes (see above).

Three Simulation Scenarios

4.1

The following grazer simulation scenarios were implemented:

A

"Just Enough Food": The carrying capacities of all territories are set to 3. This means that there is one optimal distribution of agents: a 3-3-3-3 population distribution (three grazers in each territory). Such a distribution is optimal since it allows each grazer to harvest enough energy to stay alive. Intuitively one would assume that a noosphere dominated by the "3" meme would produce such an optimal solution. On reflection though, it can be seen that any noosphere totally populated with memes less than "4" should be optimal.

B

"Too Much Food": The carrying capacities of all territories are set to 4. An environmental constraint has been relaxed. This means that there are many possible optimal distributions. One might expect that such a scenario would give the grazers a better chance of finding an optimal distribution.

C

"Too Much Food With Predators": The carrying capacities are as scenario B but any territory which is occupied by less than 4 grazers is "attacked" by "predators" during the environment phase. Practically this means that all the grazers within such a territory have 2 energy points deducted. There are four possible optimal distributions (4-4-4-0, 4-4-0-4, 4-0-4-4 and 0-4-4-4). Intuitively such a scenario seems to place heavy constraints on the possible composition of the noosphere. For example, if agents were distributed in one of these optimal arrangements it would not be stable if any one of the agents held a meme greater than "4" or less than "3". An agent holding a lower meme would move to the empty territory. An agent holding a higher meme would move to a territory holding four agents.

Experimental Methods And Presentation

5.1

For the purposes of analysis, the model is iteratively executed until a stable noosphere is attained (termed equilibrium). A stable state is one in which the composition of the noosphere stays constant over time ^[7]. In such a situation "deviant" memes (those which destabilise the noosphere) will tend to be repelled and replaced by non-deviant memes through the process of replication. Such a state has parallels to the concept of an evolutionary stable strategy (Dawkins 1982). The noosphere defines the social behaviour of every agent. Any stable state could be said to be a viable social organisation (or "culture") since it persists over time even though agents may die and be replaced. Noosphere stability does not indicate the stability of other properties of the population such as death rates or the population distribution (which could be stable, seemingly random or periodic).

5.2

For each of the three scenarios, two experiments were performed, one without meta-memes and one with meta-memes (described below). Each experiment consisted of 100 simulation runs. The summary presented below (see Table 2) is therefore a synthesis of 600 individual simulation runs.

5.3

Results are presented for each experiment in the form of general observations based on a synthesis of 100 individual simulation runs. This synthesis is presented in the form of a surface contour map plotting x, y, and z as, respectively, maximum density of agents in a single territory, most dominant meme in the noosphere and total number of such couples (i.e. maximum density / dominant meme) accumulated over all simulations. Each simulation represents a point on the x, y plane. The cumulative distribution of these points is used to give a z component. This gives a contour map of the relative frequencies of stable noosphere compositions (based on the dominant meme) against an optimality measure (maximum density)^[8]. The contour maps are shown in Figures 1, 3, 4, 5, 9 and 10. In order to illustrate the dynamics of individual runs, graphs are given showing the changing composition of the noosphere and the movement of agents between locations over time (Figures 2, 6, 7 and8 ).

Experiments Without Meta-Memes

6.1

Each of the grazer simulation scenarios were initially executed without meta-memes.

Experiment 1a - "Just Enough Food"

6.2

By the 1,000th cycle 76 per cent of the simulation runs had reached equilibrium. By the 3,000th cycle 97 per cent had done so. Most of the runs (94%) did not result in an optimal population distribution but the results are more optimal than would be expected from a totally random distribution (see Figure 1). The "self-catalytic" ^{[ 9]} process is strongly evident.

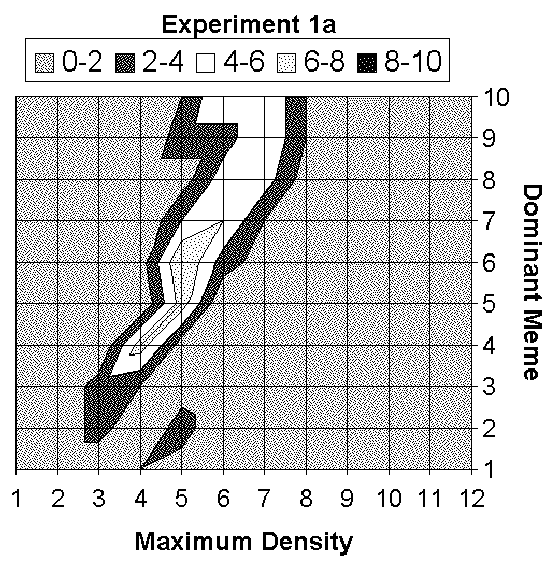Figure 1. Dominant meme / Maximum density synthesis

6.3

Figure 2 shows the evolution of the noosphere in a typical run. There is a speedy domination of the noosphere by the "9" meme. This takes place via the self-catalytic process in a single overpopulated territory. Notice that the single "5" meme (cycle 15 to cycle 115) lasts for about 100 cycles before succumbing to the "4" meme (which becomes dominant within another territory). The death rate is high before and after equilibrium.

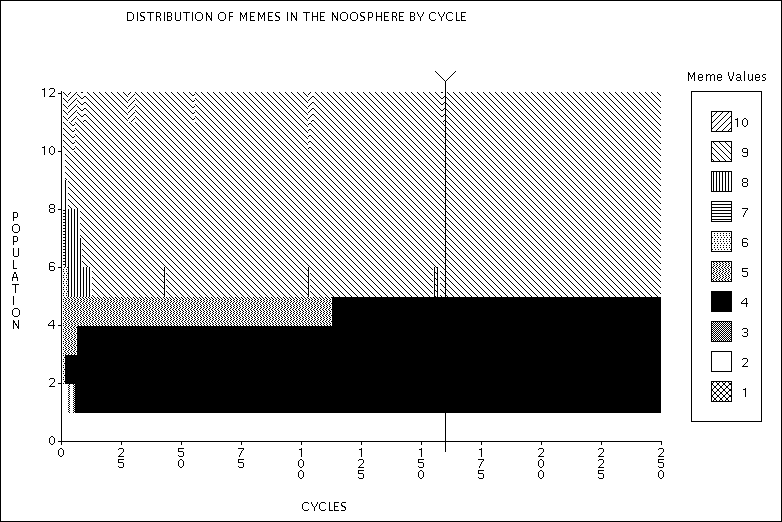Figure 2. Distribution of memes in the noosphere. Experiment 1a - Just enough food.

Equilibrium is reached at cycle 160. The single black line through the graph indicates this point (just after the elimination of the single "10" meme). At the start of the run the "9" meme quickly takes over the whole of a territory. The "5" meme manages to hold out for over 100 cycles before it is replaced by the "4" meme (dominant in its territory).

Experiment 1b - "Too Much Food"

6.4

By the 300th cycle 92 per cent of the simulation runs had found an equilibrium. By the 800th cycle all (100%) had reached equilibrium. As illustrated in Figure 3, most of these are far from optimal. Relaxation of the environment constraint significantly speeds up the self-catalytic process due to the reduced death rate.

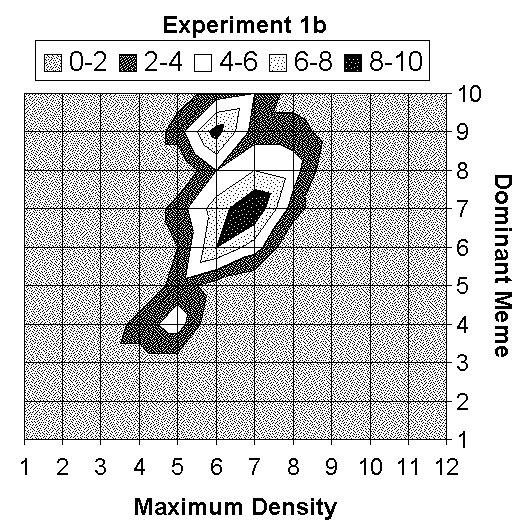Figure 3. Dominant meme / Maximum density synthesis

Experiment 1c - "Too Much Food With Predators"

6.5

By the 300th cycle 67 per cent of the simulation runs had found an equilibrium. By the 1000th cycle it was 92 per cent. Only 2 per cent of the simulation runs resulted in optimal population distributions (see Figure 4). The attacks of predators increased the effects of the self-catalytic process by forcing grazers into overpopulated territories. They also increased the time taken to attain equilibrium due to the increased death rate.

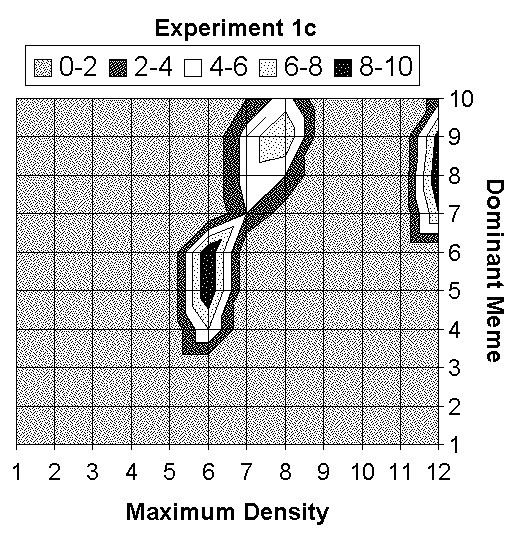Figure 4. Dominant meme / Maximum density synthesis

6.6

Notice the far right grouping in Figure 4, indicating that in a significant number (32%) of simulation runs, high value memes formed an equilibrium even when all grazers were in the same territory. Consequently the average optimality of the population distribution is low (see the CAE measure given in Table 2).

Observations from the experiments

6.7

Consideration of the experiments without meta-memes leads to the following observations:

Many stable noosphere states

Many distributions of memes produce a stable noosphere. The model therefore, produces many viable "cultures" given the same conditions. One consequence of this is that misbelief is high (in the sense of the mismatch between actual carrying capacities and the memes which predominate in the noosphere).

Optimal distributions in the minority

Most of the simulation runs produce non-optimal stabilities. This means that the death rate can be high and constant but the noosphere stays stable. This indicates that a viable "culture" is not based on the optimality of the population as a whole. In this sense memes do not need to keep agents alive to prosper.

Dynamic equilibria of population distribution

A stable noosphere does not necessarily indicate a stable population distribution. Oscillations or seemingly random movements are sometimes observed. This is interesting since it suggests that certain stable noosphere compositions accommodate complex dynamical behaviours of populations.

Killing memes can prosper

The "self-catalytic" effect of the production of aggressive "killing memes" is well described by Bura and easy enough to understand. Abstracting the observation from the specifics of the simulation we might say that: any meme that can influence an agent's behaviour in so as to reinforce and spread itself can continue to exist regardless of its side-effects. It may become dominant even if this is dysfunctional to agents individually or as a population. In the context of the model this works by mutual reinforcement. In the context of the specifics of the grazer simulations this involves getting lots of agents into one territory. This experimental evidence throws doubt on Bonner's(1980) statement concerning the possibility of successful "killing memes":

The instinct for survival is important to culture because a meme, in order to be invented or acquired must pass a severe test: If it in any way endangers the lives of the animals concerned, it will automatically be rejected. (Bonner 1980, p197)

6.8

Without some perfect evaluation function to "screen-out" killing memes, how can an animal avoid the traps that these agents have fallen into? Could meta-memes help to dampen such a process?

The Introduction Of Meta-Memes Into The Model

7.1

In the grazer simulations a simple unit of behaviour (herding) is represented by a meme. The meme takes the form of different varieties of herding. These memes are simply varieties of the same behaviour. We can say they are part of the same "meme family" (Bura 1994). Of course it is quite possible to have memes which influence different sorts of agent behaviour. In the context of the grazer simulations the agents are simple, they move, feed and communicate memes. In the simulations so far, movement was determined by the herding memes held by the agents. But the grazers' handling of memes is a behaviour that can itself be mediated by memes. This is what meta-memes are. They are a subset of all possible memes which directly effect an agent's meme handling abilities. In a sense they are ideas about ideas^[10].

7.2

In human society the "meme" concept is itself a meta-meme. The "scientific method" could be considered to be a high-level meta-meme (its primary function to filter other ideas, theories, beliefs etc.). But statements such as: "Do not believe what agent B believes" can also be viewed as meta-memes.

7.3

Meta-memes require high-level cognitive and communication behaviours such as language. It is hard to imagine how meta-memes could replicate via simple imitation (apart from indirectly through some side-effect of an imitated behaviour ^[11]). In these experiments meta-memes have been introduced to the model. They do not "emerge" from the model.

7.4

Meta-memes effectively allow a constraint to be turned into a variable and adapted differentially across individual agents. In the previous experiments it was found that the noosphere tends to stabilise with a variety of different memes. It is very rare for the whole noosphere to be dominated by a single meme. The introduction of meta-memes should therefore increase diversity of behaviour, specifically, behaviour related to the way agents handle memes. The population as a whole might therefore be more flexible.

7.5

The potential interaction of memes, meta-memes, agents and environment could be very complex. In order to take a step back from this complexity, analysis is best kept to population level indicators. The introduction of meta-memes could increase or decrease: (a) stability in the noosphere; (b) the death rate ^{[ 12]}; and (c) the optimality of population distribution.

Meta-Memes And The Model

7.6

In order to implement meta-memes the memory capacity of the agents is increased so they can hold one standard herding meme and one meta-meme. Standard memes and meta-memes do not compete with each other directly (i.e. a standard meme can not replace or repel a meta-meme). The standard meme is "executed" during the action phase of the system cycle whereas the meta-meme is "executed" during the meme phase. For each agent the meme phase is carried out once for the standard meme and once for the meta-meme. The size of the noosphere is therefore doubled but partitioned. One half of the noosphere is occupied by meta-memes, the other by standard memes.

The "Open-Mindedness" Meta-Meme

7.7

Intuitively one can envisage certain kinds of meta-memes that might completely "kill" noosphere dynamics. Consider a meta-meme that stops agents attempting to replicate memes or allows them to repel all memes from other agents. Such meta-memes would appear to have the potential to halt noosphere evolution. The self-referential nature of meta-memes seems to indicate that self-catalytic phenomena at a meta-level could be swifter and more disastrous to the population than those already observed.

7.8

In the context of the experiments this intuition is put to the test. An "open-mindedness" meta-meme was selected for the simulations. It has the capacity to increase an agent's probability of repelling or accepting attempted meme infections from other agents.

7.9

The "open-mindedness" meta-meme refers to a family of memes represented by the integers 1 to 10. The higher the meta-meme, the more "open-minded" the grazer possessing the meme becomes. A high value predisposes a grazer to accept memes from other grazers during an attempted infection. A low value predisposes a grazer to repel memes. A grazer with an open-mindedness meme of "6" will behave identically to a grazer without meta-memes.

7.10

In Minimeme each copy of each meme has two values associated with it: aggression and change. The change value [0..1] determines the probability that the meme will succumb to infection and be replaced by a different meme. The open-mindedness meta-meme is added to the change value (see Table 1) for the purposes of deciding if infection takes place. The value of the meta-meme can therefore be seen as a bias which is added to the change values of all memes held by the agent during an attempted infection from another agent ^[13]. In this way the probability of infection or repelling is modified by the meta-meme value. A grazer that posses a low value meta-meme reduces the change value of all its memes ^[14]. Conversely a grazer with a high value meta-meme increases the change value of all its memes ^[15].

Table 1. Meta-meme values and biases
Meta-meme	1	2	3	4	5	6	7	8	9	10
Bias value	-1.0	-0.8	-0.6	-0.4	-0.2	0.0	+0.2	+0.4	+0.6	+0.8
Each meta-meme value is shown along with the bias it produces. This value is added to the change parameter of each meme held by the agent when an attempted infection is taking place. Note that meta-meme value "6" has a zero bias. This means that a grazer possessing a "6" meta-meme will behave in exactly the same way as a grazer with no meta-meme at all.

7.11

For a simulation with meta-memes we have two noosphere graphs (one for standard memes and one for meta-memes). The two together represent the entire noosphere. We can analyse them separately because the meta-memes and standard memes do not compete for space in the noosphere ^[16].

7.12

Since the noosphere is now twice the size, we might expect it to take longer to settle down to an equilibrium. We also might expect low value (closed-minded) meta-memes to take over the noosphere because they are self-reinforcing, whereas higher value meta-memes are self-destroying ^[17].

Experiments With Meta-Memes

8.1

The three previous experiments were performed again but with the open-mindedness meta-meme turned on.

Experiment 2a - "Just Enough Food" With Meta-Memes

8.2

By the 1,000th cycle 76 per cent (same as experiment 1a) of the simulation runs had found an equilibrium. By the 2,000th cycle it was 99 per cent (2 per cent more than experiment 1a -- an insignificant difference given the inherent randomness in the simulations). Most of the runs (87%) did not result in an optimal population distribution at equilibrium (this is only slightly better than experiment 1a). However, the non-optimal equilibria obtained were substantially more optimal (on average) than those obtained for experiment 1a (compare Figures 1 and 5). An optimality measure which takes account of dynamic population distributions can be obtained by calculating the average total cumulative deaths after equilibrium has been attained. For each of the 100 simulation runs, the number of agent deaths is measured during the last 100 cycles (during which the noosphere does not change). This value is then averaged (divided by 100). For experiment 1a this value was 18, and for experiment 2a it was 2 (see Table 2). The introduction of meta-memes has therefore increased average optimality while keeping stability about the same (i.e. time taken to attain noosphere equilibrium).

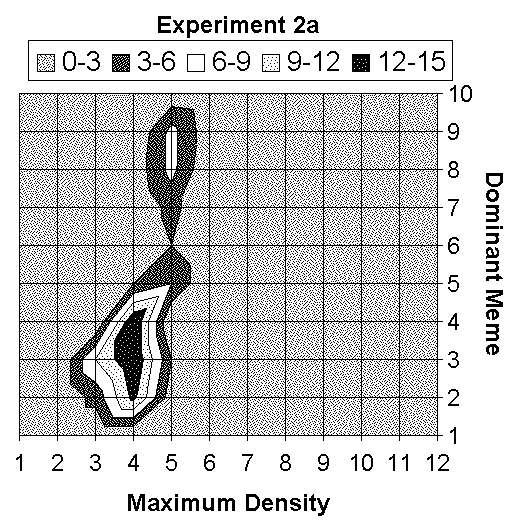Figure 5. Dominant meme / Maximum density synthesis

8.3

Figures 6, 7 and 8 show the results of a typical simulation run. At the start of the simulation Figure 6 shows an overpopulated territory (location 3) occupied by 6 grazers. Within a few cycles this increases to 7 grazers. Figure 7 shows the self-catalytic process occurring in this territory (the high meme values). This is as observed for experiment 1a. With the introduction of meta-memes however this process is less stable and breaks-down completely around cycle 150. During the self-catalytic process the death rate is high. Notice the oscillations of high and low meta-meme values (Figure 8) up to cycle 160. These oscillations correspond to the period during which the self-catalytic process is occurring. Between cycles 30 and 50 there is an increase of low value meta-memes. By about cycle 60 however, higher value meta-memes have begun to dominate. After about cycle 100 low value meta-memes make a come back reaching a plateau around cycle 150. This meta-meme oscillation process appears to destabilises the part of the noosphere containing the standard memes. The oscillations appear to correlate with periods of high death rates. High death rates are a natural consequence of overpopulated territories and it is the self-catalytic process that forces territories to become overpopulated. The meta-meme noosphere is stable between about cycle 140 and cycle 160. In this period movement occurs (Figure 6) and the death rate is low.

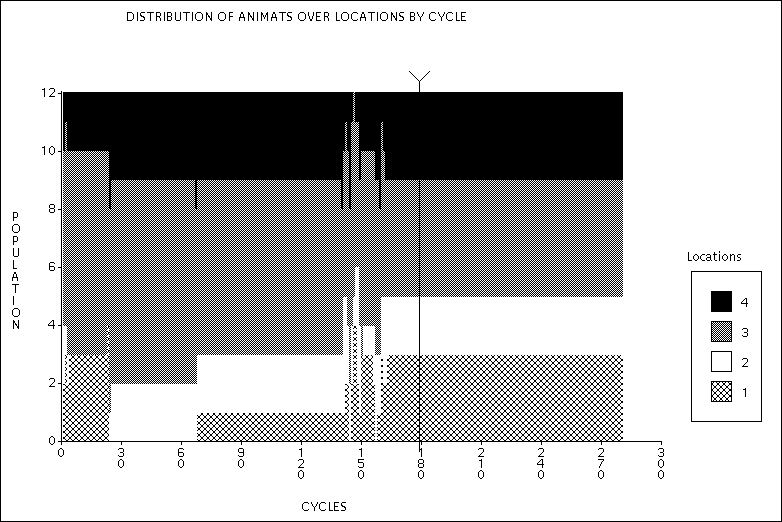Figure 6. Distribution of the population over the four territories. Experiment 2a - Just enough food.

Notice the redistribution of the population between cycles 140 and 160.

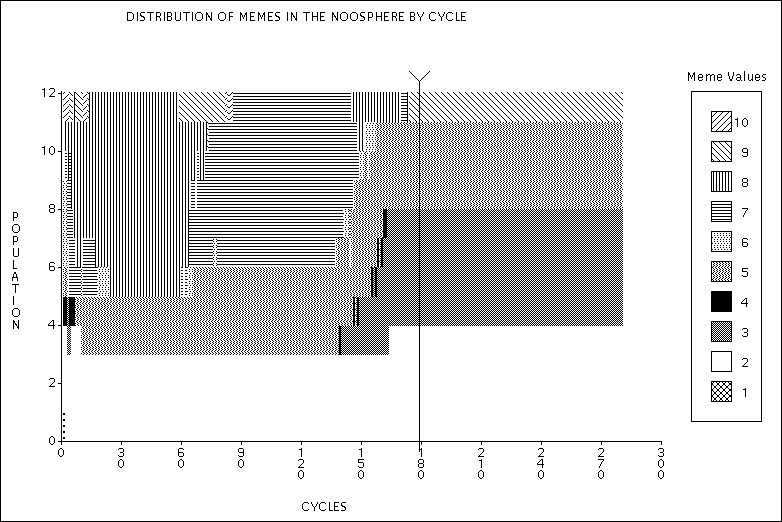Figure 7. Distribution of memes in the noosphere. Experiment 2a - Just enough food.

Notice the self-catalytic process and when it breaks down.

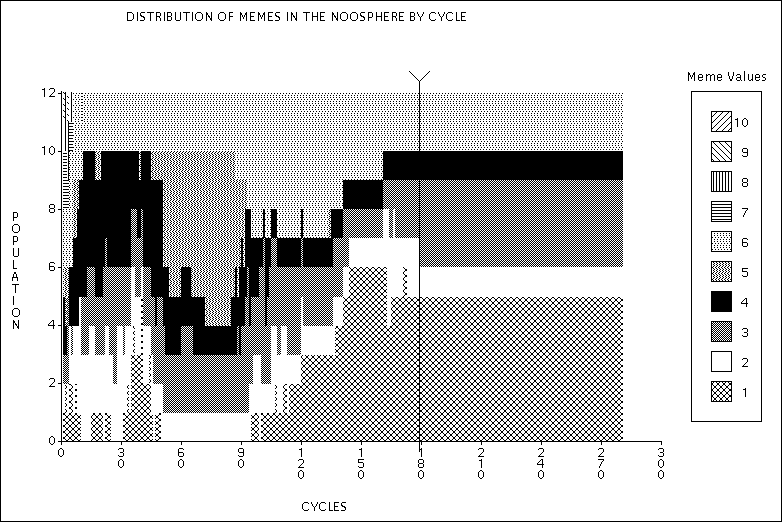Figure 8. Distribution of memes in the noosphere. Experiment 2a - Just enough food.

Notice the oscillations and then the minor stability between cycles 140 and 160.

Experiment 2b - "Too Much Food" With Meta-Memes

8.4

By the 300th cycle 62 per cent (30 per cent less than experiment 1b) of the simulation runs had found an equilibrium. By the 1000th cycle it was 97 per cent (3 per cent less than experiment 1b). The equilibria obtained were substantially more optimal than those obtained for experiment 1b (compare Figures 3 and 9). The average total cumulative deaths after equilibrium was 2 compared to 9 for experiment 1b. The introduction of meta-memes has substantially increased the time taken to attain equilibrium but increased the optimality of those equilibria.

Figure 9. Dominant meme / Maximum density synthesis

Experiment 2c - "Too Much Food With Predators" With Meta-Memes

8.5

By the 300th cycle 19 per cent (47 per cent less than experiment 1c) of the simulation runs had found an equilibrium. By 5,000 it was 95 per cent. Only 3 per cent of the simulation runs found a noosphere equilibrium with an optimal population distribution compared to 2 per cent for experiment 1c. The population distributions were more optimal than experiment 1c (compare Figs. 4 and 10). Notice that the far right grouping (in Figure 4) has been totally removed. This is a result of the meta-memes breaking down the most extreme manifestation of the self-catalytic process (when all grazers occupy a single territory). The mechanisms by which this process occurs are discussed in detail later but note that in such a situation (all grazers in one territory) the death rate will be very high and as such will de-stabilise the meta-meme noosphere.

Figure 10. Dominant meme / Maximum density synthesis

8.6

The introduction of meta-memes has substantially increased the time taken to attain equilibrium but increased the optimality of those equilibria significantly.

Observations and Findings

9.1

Table 2 gives a summary of the results of all the experiments. Taking averages across all three experiments, the introduction of the open-mindedness meta-meme resulted in the following (compared to experiments 1a, 1b and 1c) ^[18]:

• A decrease in the stability of the noosphere (i.e. equilibrium is reached more slowly).
• A slight increase in the number of agent deaths before equilibrium ^[19].
• An increase in the optimality of the equilbriums found.
• An increase in the "accuracy" of the dominant meme (more closely reflects the actual carrying capacities of the territories, see Figures 11a, 11b and 11c).

Table 2. A summary of results
Simulation Description	0.3	1	3	5	10	CBE	CAE
......Experiments without meta-memes
1a) Just enough food	49	76	97	100	100	296	18
1b) Too much food	92	100	100	100	100	22	9
1c) Too much food & predators	67	92	100	100	100	349	41
Averages	69	89	99	100	100	222	23
......Experiments with meta-memes
2a) Just enough food	26	76	99	99	100	173	2
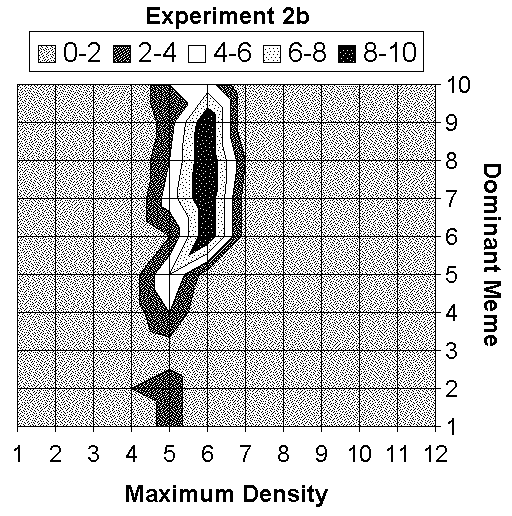
2b) Too much food	62	97	100	100	100	32	2
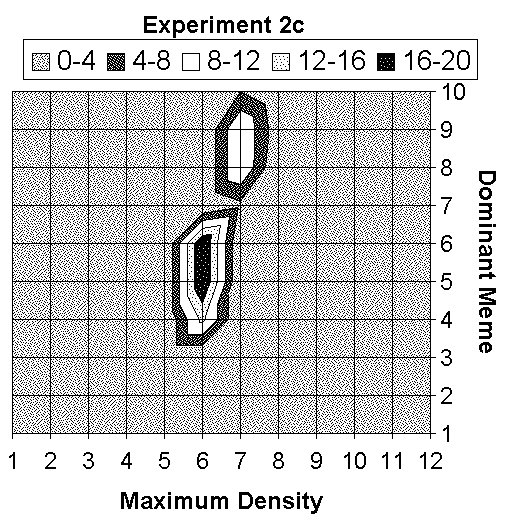
2c) Too much food & predators	19	49	85	95	100	690	7
Averages	33	73	95	98	100	298	4
The numbered columns represent cycles (in thousands). The numbers in those columns represent the percentage of simulation runs that had reached an equilibrium by the given number of cycles. The CBE column shows the average Cumulative deaths Before Equilibrium. The CAE column shows the average Cumulative deaths After Equilibrium. After each set of three experiments the average of the columns is given.

9.2

Table 2 shows the optimality in terms of average "Cumulative deaths After Equilibrium" in the "CAE" column. The CAE value is the number of agents that died for the 100 cycles at the end of each run (during which the noosphere is stable) averaged over the 100 runs. Notice that experiment 2c (too much food with predators) has a much lower CAE at the expense of a much higher "CBE" (average Cumulative deaths Before Equilibrium). The CBE value is the number of agents that died up to the point that equilibrium was attained averaged over the 100 runs. Comparison of Figures 4 and 10 show that the removal of the far right grouping, where all grazers stay in one territory, is responsible for the bulk of this reduction in the CAE.

What's Going On In The Meta-Noosphere?

9.3

An explanation for all the above effects which is consistent with the experimental results can be summarised as: Two opposing processes create oscillations in the meta-meme noosphere during periods of high death rates. This causes instability and population migrations. The self-catalytic process in which killing memes prosper in overpopulated territories is generally broken after a few hundred cycles.

9.4

The meta-meme noosphere tends to oscillate ^[21] during periods with a high death rate. This will occur whenever there is a self-catalytic process (overpopulation of a territory with high standard memes dominating it). This oscillation in the meta-meme noosphere has two effects. Firstly, a noosphere stability is prevented. This stops an equilibrium from being achieved at a point which is highly non-optimal. Secondly, the standard meme noosphere is affected when the oscillations become extreme. If the meta-meme noosphere becomes dominated by either extreme of meta-meme (highly open-minded or highly closed minded) the standard meme noosphere becomes unstable and vulnerable to dramatic changes based on mutation. This tends to push the population out of a territory where a self-catalytic process is occurring.

9.5

Oscillations in the meta-meme noosphere are caused by the interaction of two opposing processes. There are two ways in which meta-memes can increase stability in the noosphere:

1. High value meta-memes predominate producing increased "homogenisation". If a population in a given territory are strongly open-minded (high meta-meme values) then any new grazer entering the territory has a high probability of being infected with a high value meta-meme thus "converting" a potentially closed-minded grazer into an open-minded one. Such a newly converted open-minded grazer subsequently has a high probability of infection by the dominant standard meme within the territory. A deviant mutated standard meme generated from within the territory is easily suppressed due to the already open-minded nature of the grazer. The grazer tends to get quickly re-infected with the dominant standard meme for the given territory. However, if a closed-minded grazer manages to infect another host in the territory before being infected itself the territory can quickly become closed-minded.

2. Low value meta-memes predominate producing a closed-minded population. If low value meta-memes predominate in a given territory then all attempted infections are strongly resisted. Such a territory is however vulnerable because any new arrival into the territory (or mutation) has a high probability of being infected by a low value meta-meme making a potentially deviant standard meme resistant against infection.

9.6

Mutation is high when the death rate of a territory is high. During times of high mutation it is more likely that the vulnerabilities (outlined above) of the two stability producing processes will be exploited. When this occurs the meta-meme noosphere tends to oscillate between the two. In effect, the open-mindedness meta-meme can stabilise the noosphere in either of the above ways but will tend to oscillate between the two when the death rate is high. This oscillation prevents equilibrium and tends to produce instability in the standard meme noosphere.

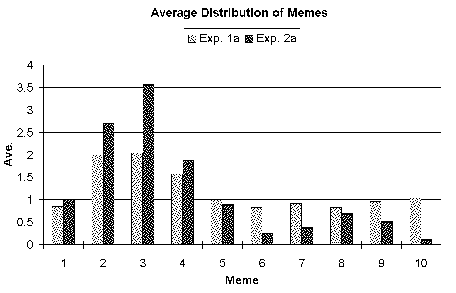Figure 11a. Distribution of memes averaged over all the simulation runs for scenario A: "Just enough food".

The darker bars show the results of the meta-meme experiments. After the introduction of meta-memes, meme "3" representing the actual carrying capacity is favoured. Consequently the average accuracy of the memes is improved.

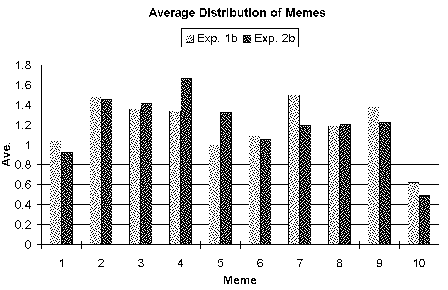Figure 11b. Distribution of memes averaged over all the simulation runs for scenario B: "Too much food".

The darker bars show the results of the meta-meme experiments. After the introduction of meta-memes, meme "4" representing the actual carrying capacity is favoured. Consequently the average accuracy of the memes is improved.

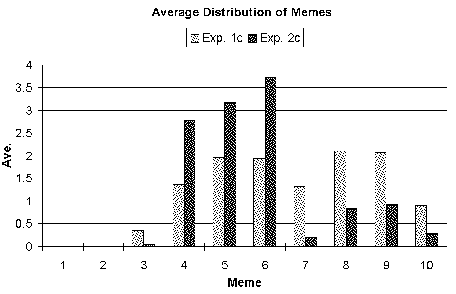Figure 11c. Distribution of memes averaged over all the simulation runs for scenario C: "Too much food with predators".

The darker bars show the results of the meta-meme experiments. After the introduction of meta-memes, lower value memes are favoured. Consequently the average accuracy of the memes is improved.

9.7

The open-mindedness meta-meme will therefore increase the stability of the population when the death rate is low and decrease it when the death rate is high. This extra instability is functional since it produces population instabilities (movement) which generally change the death rate. If this new death rate is low enough then an equilibrium may be achieved otherwise the whole cycle will repeat. The system therefore lurches quite blindly but tends over time to increase stability and lower the death rate.

9.8

Experiment 2c (too much food with predators) has a substantially higher CBE and takes longer to find an equilibrium than did 1c. This result is due to the high death rates that such a scenario produces. This results in a constantly oscillating meta-meme noosphere which causes constant population shifts. It is therefore more difficult for the system to achieve an equilibrium. When equilibrium is attained however, it is much more optimal (the CAE drops from 41 to 7).

9.9

It was previously speculated that closed-minded (i.e. low value) meta-memes would prosper since they are self-selecting because any host that carries them is less likely to change memes through infection. Indeed the meta-meme noosphere quickly reduces to low values. However results show the "1" meta-meme is no more successful than the "2", "3" or "4" meta-memes.

Conclusions

10.1

Starting from a set of assumptions which specified a co-ordination problem based on resource harvesting and agents which individually satisfice, a memetic process was investigated. The process involved the replication, reinforcement and repelling of memes held by agents. The memes held by an agent determined its behaviour. They were exchanged via social contact between agents located within the same territory.

10.2

The original results found by Bura (1994) were reproduced indicating that memes which lead to rapid agent death can prosper by causing agents to participate in a "self-catalytic" process in which they gathered in a single territory exhausting its resources and reinforcing the very meme which brought them there. This result is at odds with Bonner's (1980) intuition.

10.3

With the addition of an open-mindedness / closed-mindedness meta-meme to the same scenario the "self-catalytic" process was destabilised resulting in less agent deaths. More optimal population distributions were found. Also the intuition that complete closed-mindedness would predominate is shown to be incorrect. These results are determined by the complex interplay of several feedback processes involving agents, resources and memes.

10.4

Much human social phenomena results from consciously planned and co-ordinated interactions. Conversely, there is much which, it is claimed, is not. It is this latter class of phenomena (which challenges rational action theory) that can benefit from a memetic treatment. The "self-catalytic" process demonstrates that human and artificial societies which consist of agents who practice "boundedly rational" and "socially docile" strategies suggested by Simon (1990) can become trapped into highly non-optimal behaviours without any knowledge of what is occurring. Also the results here demonstrate that (at least some) such traps can be avoided without necessarily requiring agents to have a high level of social knowledge and planned co-ordination.

10.5

One major result that emerged was the vast diversity of meme distributions that produced optimal stabilities and hence the easy coexistence of different views (memes) of reality. The co-evolution of several "incorrect" memes can produce fairly optimal behaviour patterns: each meme tied together through mutual correction based on incorrect views of reality. This finding can be compared to the conception of functional misbelief (Doran 1994, Doran 1998).

10.6

Why produce computational models of meme spread? In many areas of anthropology and sociology theories are constructed and described using natural language. However, the complexity of the phenomena to be explained (namely social reality) poses two fundamental problems. Firstly, natural language is often ambiguous and theories may "gloss over" important areas. Secondly, it may be impossible to test or falsify such theories because it is very difficult to collect "clean" data from real societies. This is of particular relevance to the memetics community since the hypothesised objects of interest (memes) are difficult to track or measure. If a computational artificial society is constructed then this forces the explicit statement of assumptions in the form of a computer program. The society can then be studied (conducting experiments and collecting clean data) which hopefully can feedback or at least inform theory construction for the real social world. Experimentation in the artificial realm is neither purely inductive or deductive but involves both (Axelrod 1997). I use the term "ceduction" (Computer Experimental Induction/Deduction) to describe this mode of investigation (Hales 1998a, Hales 1998d). This kind of speculative ceductive mode of enquiry using artificial societies is a growing area and has been embraced by sociologists, philosophers, psychologists, economists, political scientists and computer scientists in order to test and build new social theory (Conte et al, Conte & Gilbert 1995, Doran & Gilbert 1994). However, existing disciplines possess their own traditions resulting in cultural inertia and consequently slow up-take of new methodological tools. Memetics as a young and (for the most part) computationally aware discipline can utilise these factors to its benefit if it embraces this new methodology as a testing ground for new theory construction and testing. On-going work using memetic simulations to investigate altruism, group formation and stereotyping are detailed in Hales (1998b) and Hales (1998c).

10.7

Memetic models do not automatically provide any new understanding. What they do provide is a fresh perspective on an old debate and a flexible experimental and objective method to test assumptions and intuitions. Of course, the assumptions we start with are based on our own ideas of social reality. It is notoriously difficult to get hard facts or principles concerning real social systems. The social sciences are dominated by many different views of social reality. This should come as no surprise. As the meme simulations presented in this paper suggest, social reality is constructed from competing ideas which do more than just coexist, they have often co-evolved to produce global actions which are functional even though the memes (beliefs) that predominate may be objectively incorrect.

Acknowledgements

This work would not have been possible without the help, discussions and suggestions of Prof. Jim Doran, Department of Computer Science, University of Essex, Colchester, UK, and Stephane Bura, 4 Place Jussieu 75252 Paris cedex 05, France. Thanks also go to the JASSS reviewers and editors for comments and corrections and Jan Neil for lucid questioning which helped to keep me (at least partially) within the real (as opposed to the artificial) world. This work was supported by an EPSRC research studentship award. A significant proportion of this paper is based on an earlier paper (Hales 1997).

Notes

¹

In the context of Sugarscape this involves counting the number of "1" digits in the string.

²

This is an apt word to use. It was first introduced in an essay written in 1949 by Teilhard de Chardin. It is used to signify the realm in which mind is exercised. Teilhard's contention was that in the ordinary course of the evolution of living things the biosphere is being supplanted by the noosphere (Bullock 1988).

³

A grazer can move into any territory from any other.

⁴

If more than one territory is equally desirable then one is chosen at random.

⁵

Within the scenario of the grazer simulations, "birth control" is applied. In such a scheme the population is kept at a fixed size (12 in this case). A new grazer is "born" every time an old grazer dies. The new born grazer is placed within the same territory. This maintains a fixed size noosphere for the purposes of analysis.

⁶

The order in which agents take turns in the Action, Feeding and Meme phases of the system cycle has been randomised. This is a modification of the original Minimeme model as presented by Bura. This change was made to avoid any artefacts that might result from synchronous turn-taking (Hagselmann 1996).

⁷

A stable noosphere is defined as one in which no change has occurred in the last 100 cycles. Experiments have shown that after such a state is reached the noosphere generally resists attacks from mutant memes and does not evolve anymore.

⁸

It is important to note that such a map does not show the full picture. It deals only with the dominant meme and the territory with the maximum density. It does however, give a general picture of the major trends across all simulation runs in a digestible form.

⁹

This is the term used by Bura to describe the following: If a grazer holds a high value meme it will move to an overpopulated territory. By definition, the grazers in this territory will also hold high value memes. When a large enough group is formed mutual reinforcement of this meme will continue although deaths may be high if the carrying capacity of the territory is exceeded.

¹⁰

The words "idea", "belief" and "meme" are used interchangeably throughout this paper.

¹¹

For example: A preference for a certain location could isolate an agent from exposure to memes from agents who have a preference for a different location. But this is a side-effect of the meme. A true meta-meme operates directly on the meme process.

¹²

There are two death rates: the initial death rate which is the number of deaths up to the point at which equilibrium is attained (these will usually be sporadic and unpredictable); and the generally constant death rate after equilibrium. Each death rate is considered separately.

¹³

If the result of this addition is greater than 1 or less than 0 then the result is taken to be 1 or 0 respectively.

¹⁴

This includes the open-mindedness meta-meme itself.

¹⁵

This modification process is only performed when deciding if infection should occur in the meme phase of the system cycle. The open-mindedness meta-meme has no effect on the change value during other phases (i.e. mutation). The bias values given in Table 1 are the result of applying the following formula to the meta-meme value (m):

bias = (m - 6) * 0.2

This formula was used because it delivers uniform increments, a neutral bias (meta-meme "6" = zero bias) and a fully closed minded meta-meme (meta-meme "1" = -1 bias).

¹⁶

This is a simulation specific constraint, since a grazer can not hold two standard memes or two meta-memes because they are "concurrent". Other scenarios might not have such a constraint.

¹⁷

Any low value meta-meme will make the grazer less likely to accept an attempted replication over any of its memes and this includes the meta-meme itself. A low value meta-meme (once taken by an agent) will therefore be very resistant to being replaced by replication.

¹⁸

These observations are also consistent with the results of additional experiments using a scenario based on a 2-2-2-2 carrying capacity (not enough food). Interestingly, the CAE values for these experiments were roughly equivalent to experiments 1b and 2b. The harsh environment seemed to improve the accuracy of the standard memes which compensated for the lower level of resources available.

¹⁹

This is almost entirely due to the results of experiment 2c (too much food with predators). Indeed experiment 2a (just enough food) resulted in a substantial reduction of the CBE figure.

²⁰

All of the experiments were reproduced using a different pseudo random number generation algorithm to avoid artefacts. All the conclusions drawn are consistent with both sets of results. For these additional results see Hales (1995). For a discussion of random number generators see Mathews (1995) and Press et al. (1992).

²¹

Oscillations tend to take place within the lower half of the meta-meme range ("1" to "5"). In this sense the system does select closed-minded grazer behaviour. Interestingly it does not favour the "1" meta-meme above all others.

References

AXELROD, R. (1995). The Convergence and Stability of Cultures: Local Convergence and Global Polarization. Working Paper 95-03-028. Santa Fe, N.M.: Santa Fe Institute.

AXELROD, R. (1997). Advancing the Art of Simulation in the Social Sciences. In Conte, R., Hegselmann, R. & Terna P. (Eds.) Simulating Social Phenomena. Berlin: Springer.

BONNER, J.T. (1980). The Evolution of Culture in Animals. New Jersey: Princeton University Press.

BOYD, R. & Richerson P. (1985). Culture and the Evolutionary Process. Chicago: University of Chicago Press.

BULLOCK, A. (ed.) (1988). Fontana Dictionary of Modern Thought. London: Fontana Press.

BURA, S. (1994). Minimeme: Of Life and Death in the Noosphere. In J. Mayer & S. Wilson (eds.) From Animals to Animats 3: Proceedings of the 3rd International Conference on the Simulation of Adaptive Behaviour (SAB94). London: MIT Press.

CONTE, R. & Gilbert, N. (1995). Introduction: Computer Simulation for Social Theory. In Gilbert, N. & Conte, R. (Eds.) Artificial Societes: the Computer Simulation of Social Life. London: UCL Press.

CONTE, R. et al (1997). Social Simulation - A New Disciplinary Synthesis. In Conte, R., Hegselmann, R. & Terna P. (Eds.) Simulating Social Phenomena. Berlin: Springer.

DAWKINS, R. (1976). The Selfish Gene. New York: Oxford University Press.

DAWKINS, R. (1982). The Extended Phenotype. Oxford: Freeman. pp97 - 117.

DAWKINS, R. (1993). Viruses of the Mind. In B. Dahlbom. (ed.) Dennett and His Critics. Cambridge: Blackwell.

DENNETT, D. (1995). Darwin's Dangerous Idea. New York: Simon & Schuster.

DORAN, J. (1994), Modelling Collective Belief and Misbelief. In M. Keane, P. Cunningham, M. Brady, & R. Byrne, (eds.) Proceedings of the Seventh Annual Conference on AI and Cognitive Science (AICS94). Dublin: Dublin University Press.

DORAN, J. (1998), Simulating Collective Belief and Misbelief. In the Journal of Artificial Societes and Social Simulation vol. 1, no.1, https://www.jasss.org/1/1/3.html

DORAN, J. & Gilbert, N. (1994), Simulating Societies: an Introduction In Gilbert, N. & Doran, J. (Eds.) Simulating Societes: The Computer Simulation of Social Phenomena. London: UCL Press.

EPSTEIN, J.M. and Axtell, R. (1996). Growing Artificial Societies: Social Science From The Bottom Up. London: MIT Press.

GABORA, L.M. (1995) Meme and Variation: A Computational Model of Cultural Evolution. In Nadel, L. & Stein, D. (Eds.) 1993 Lectures in Complex Systems. New York: Addison-Wessley.

GABORA, L.M. (1997) The Origin and Evolution of Culture and Creativity. In Journal of Memetics - Evolutionary Models of Information Transmmission vol.1, no.1, http://www.cpm.mmu.ac.uk/jom-emit/1997/vol1/gabora_l.html

HALES, D. (1995). Modelling Meta-Memes. Unpublished MSc Dissertation. Department Of Computer Science, University Of Essex, UK.

HALES, D. (1997). Modelling Meta-Memes. In Conte, R., Hegselmann, R. & Terna P. (Eds.) Simulating Social Phenomena. Berlin: Springer.

HALES, D. (1998a). Artificial Societies, Theory Building and "Ceduction". Unpublished paper, Presented at the CRESS workshop "The Potential of Computer Simulation in the Social Sciences", January 1988, University of Surrey, UK.

HALES, D. (1998b). Selfish Memes and Selfless Agents: Altruism in the Swap Shop. In The Proceedings of ICMAS 1998 (ICMAS'98). California: IEEE Computer Society.

HALES, D. (1998c). Stereotyping, Groups and Cultural Evolution. In Proceedings of the Multi-Agent Based Simulation Workshop 1998 (MABS'98) To be published by Springer in the LNAI series late 1998.

HALES, D. (1998d). Artificial Societies, Theory Building and Memetics. In Proceedings of the 15th International Congress on Cybernetics. Namur: Int. Association for Cybernetics.

HEGSELMANN, R. (1996). Cellular Automata in the Social Sciences: Perspectives, Restrictions and Artefacts. In R. Hegselmann, U. Mueller & K.G. Troitzsch (eds.) Modelling and simulation in the social sciences from a philosophy of science point of view [Theory and Decision Library]. Dordrecht: Kluver.

MATHEWS, R. (1995). It's a Lottery. New Scientist 1987, 38-42.

PRESS, H., Flannery, B., Teukolsky, S., Vetterling, W. (1992). Numerical Recipes in C : The Art Of Scientific Computing. Cambridge: Cambridge University Press.

REYNOLDS, R. (1994). Learning to Co-operate using Cultural Algorithms. In Gilbert, N. & Doran, J. (Eds.) Simulating Societies: The Computer Simulation of Social Phenomena. London: UCL Press.

SIMON, H. (1990). A Mechanism for Social Selection and Successful Altruism. Science 250: 1665-1668

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, 1998