The Empirical Semantics Approach to Communication Structure Learning and Usage: Individualistic Vs. Systemic Views
Journal of Artificial Societies and Social Simulation
vol. 10, no. 1
<https://www.jasss.org/10/1/5.html>
For information about citing this article, click here
Received: 20-Jan-2006 Accepted: 05-Aug-2006 Published: 31-Jan-2007
 Abstract
AbstractNote: This article is accompanied by a glossary of the most important technical terms used in the context of our approach and Distributed Artificial Intelligence in general. The glossary is available by clicking on the underlined red terms.
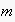 to event
to event
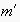 is thought to reflect the probability that
is thought to reflect the probability that
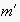 follows
follows
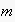 from the observer's point of view.
from the observer's point of view.

|
Table 1. A grammar for event nodes of ENs, generating the language
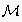 (the language of concrete actions, starting with
(the language of concrete actions, starting with
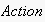 ). ).
|
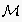 to define the events used for labeling nodes in expectation networks. Its
syntax is given by the grammar in table 1.
Agent actions observed in the system can be either "physical"
`(non-symbolic) actions of the format
to define the events used for labeling nodes in expectation networks. Its
syntax is given by the grammar in table 1.
Agent actions observed in the system can be either "physical"
`(non-symbolic) actions of the format
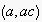 where
where
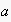 is the executing agent, and
is the executing agent, and
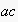 is an domain-dependent symbol used for a physical action, or symbolic
elementary communication act
is an domain-dependent symbol used for a physical action, or symbolic
elementary communication act
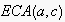 sent from
sent from
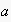 with content
with content
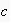 .
We do not talk about "utterances" or "messages" here, because a single
utterance might need to be decomposed into multiple ECAs. The symbols used in
the
.
We do not talk about "utterances" or "messages" here, because a single
utterance might need to be decomposed into multiple ECAs. The symbols used in
the
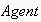 and
and
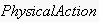 rules might be domain-dependent symbols the existence of which we take for
granted. For convenience,
rules might be domain-dependent symbols the existence of which we take for
granted. For convenience,
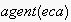 shall retrieve the acting agent of an ECA eca.
shall retrieve the acting agent of an ECA eca.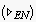 to denote the root node of an specific EN.
The
content
to denote the root node of an specific EN.
The
content
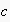 of a non-physical action is given by type
of a non-physical action is given by type
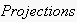 .
The meaning of
.
The meaning of
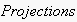 will be described later.
will be described later.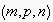 where
where
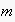 and
and
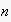 are actions, and
are actions, and
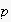 ,
,
![$p \in [0;1]$](5/graphics/jasssdraft5__31.gif) is a transition probability (expectability) from
is a transition probability (expectability) from
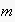 to
to
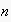 .
.
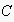 is the set of all edges,
is the set of all edges,
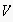 the set of all nodes in the EN. We use functions
the set of all nodes in the EN. We use functions
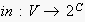 ,
,
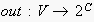 ,
,
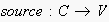 and
and
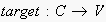 which return the ingoing and outgoing edges of a node and the source and
target node of an edge, respectively.
which return the ingoing and outgoing edges of a node and the source and
target node of an edge, respectively.
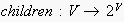 returns the set of children of a node, with
returns the set of children of a node, with
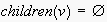 in case
in case
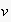 is a leaf.
Edges denote correlations in observed communication sequences. Each edge is
associated with an expectability (returned by
is a leaf.
Edges denote correlations in observed communication sequences. Each edge is
associated with an expectability (returned by
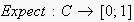 )
which reflects the probability of
)
which reflects the probability of
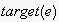 occurring after
occurring after
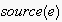 in the same communicative context (i.e. in spatial proximity, between the same
agents, etc.).
in the same communicative context (i.e. in spatial proximity, between the same
agents, etc.).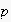 in an EN leading from
in an EN leading from
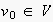 to
to
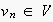 as concatenations of message labels (corresponding to ECAs)
as concatenations of message labels (corresponding to ECAs)
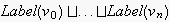 .
The
.
The
 symbols are sometimes omitted for brevity and we denote the length of a sequence by
symbols are sometimes omitted for brevity and we denote the length of a sequence by
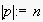 .
.
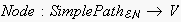 results in the last node of a certain path given as a string of labels. Nodes
or corresponding messages along a path
results in the last node of a certain path given as a string of labels. Nodes
or corresponding messages along a path
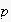 will be denoted as
will be denoted as
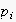 .
.
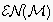 is the set of all possible expectation networks over
is the set of all possible expectation networks over
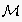 .
.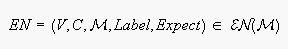 where
where
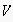 with
with
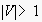 is the set of nodes,
is the set of nodes,
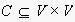 are the edges of
are the edges of
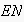 .
.
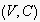 is a tree called expectation tree.
is a tree called expectation tree.
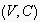 shall have a unique root node called
shall have a unique root node called
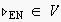 which corresponds to the first ever observed
action. The following
condition should hold:
which corresponds to the first ever observed
action. The following
condition should hold:
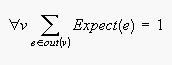
 is the action language. As defined in table 1, actions can be
symbolic
(
is the action language. As defined in table 1, actions can be
symbolic
( )
or physical actions
(
)
or physical actions
(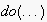 ).
While we take the existence and the meaning of the latter in terms of
resulting observer expectations for granted and assume it is domain-dependent,
the former will be described in detail later. Physical actions could be
assigned an empirical semantics also (being their expected consequences in
terms of subsequent events).
).
While we take the existence and the meaning of the latter in terms of
resulting observer expectations for granted and assume it is domain-dependent,
the former will be described in detail later. Physical actions could be
assigned an empirical semantics also (being their expected consequences in
terms of subsequent events).
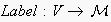 is the action label function for nodes, with
is the action label function for nodes, with
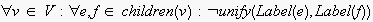
(where
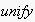 shall be
shall be
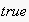 iff its arguments are syntactically unifiable. (Cf.
Nickles et al 2005 for the use of variables in ENs),
iff its arguments are syntactically unifiable. (Cf.
Nickles et al 2005 for the use of variables in ENs),
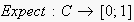 returns the edges' expectabilities. For convenience, we define
returns the edges' expectabilities. For convenience, we define
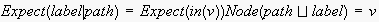 .
.
Paths starting with
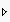 are called states (of the communication
process)[3].
are called states (of the communication
process)[3].
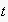 is a structure
is a structure
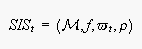 where
where
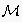 is the formal language used for agent actions (according to table 1),
is the formal language used for agent actions (according to table 1),
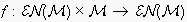 is the expectations update function that transforms any expectation
network
is the expectations update function that transforms any expectation
network
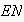 to a new network upon experience of an action
to a new network upon experience of an action
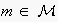 .
.
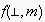 returns the so-called initial EN, transformed by the observation of
returns the so-called initial EN, transformed by the observation of
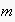 .
This initial EN can be used for the pre-structuring of the social system using
given e.g. social norms or other a priori knowledge which can not be
learned using
.
This initial EN can be used for the pre-structuring of the social system using
given e.g. social norms or other a priori knowledge which can not be
learned using
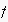 .
Any ENs resulting from an application of
.
Any ENs resulting from an application of
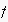 are called Social Interaction Structures.
are called Social Interaction Structures.
As a non-incremental
variant we define
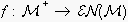 to be
to be
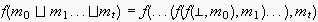 ,
,
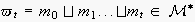 is the list of all actions observed until time t. The subindices of the
is the list of all actions observed until time t. The subindices of the
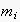 impose a linear order on the actions corresponding to the times they have been
observed[5],
impose a linear order on the actions corresponding to the times they have been
observed[5],
 is a duration greater of equal to the expected life span of the SIS. We
require this to calculate the so-called spheres of communication (see
below). If the life time is unknown, we set
is a duration greater of equal to the expected life span of the SIS. We
require this to calculate the so-called spheres of communication (see
below). If the life time is unknown, we set
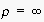 .
Although a sphere of communication denotes the ultimate boundaries of
trustability for a single communication, even with
.
Although a sphere of communication denotes the ultimate boundaries of
trustability for a single communication, even with
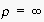 initially certain limits of trustability and sincerity become visible in
empirical semantics by means of the extrapolation of interaction sequences.
Suppose, e.g., a certain agent
initially certain limits of trustability and sincerity become visible in
empirical semantics by means of the extrapolation of interaction sequences.
Suppose, e.g., a certain agent
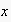 takes opinion
takes opinion
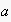 in discourses with agent
in discourses with agent
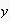 ,
but opinion
,
but opinion
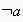 in all interactions with agent
in all interactions with agent
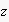 .
Since this "opinion switching" shows regularities, our algorithm will reveal it.
.
Since this "opinion switching" shows regularities, our algorithm will reveal it.
We refer to events and EN nodes as past, current or
future depending on their timely position (or the timely position of
their corresponding node, respectively) before, at or after
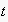 .
We refer to
.
We refer to
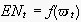 as the current EN from the semantics observer's point of view, if the
semantics observer has observed exactly the sequence
as the current EN from the semantics observer's point of view, if the
semantics observer has observed exactly the sequence
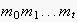 of events so far.
of events so far.
The intuition behind our definition of
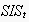 is that a social interaction system can be characterised by how it would
update an existing expectation network upon newly observed actions
is that a social interaction system can be characterised by how it would
update an existing expectation network upon newly observed actions
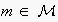 .
The EN within
.
The EN within
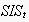 can thus be computed through the sequential application of the structures
update function
can thus be computed through the sequential application of the structures
update function
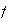 for each action within
for each action within
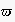 ,
starting with a given expectation network which models the observers' a
priori knowledge.
,
starting with a given expectation network which models the observers' a
priori knowledge.
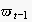 is called the context (or precondition) of the action
observed at time
is called the context (or precondition) of the action
observed at time
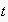 .
.
To simplify the following formalism, we demand that an EN ought to be
implicitly complete, i.e., to contain all possible paths,
representing all possible event sequences (thus the EN within an interaction
system is always infinite and represents all possible world states, even
extremely unlikely ones). If the semantics observer has no a priori
knowledge about a certain branch, we assume this branch to represent uniform
distribution and thus a very low probability for every future decision
alternative
(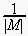 ),
if the action language is not trivially small.
),
if the action language is not trivially small.
Note that any part of an EN
of an SIS does describe exactly one time period, i.e., each node within the
respective EN corresponds to exactly one moment on the time scale in the past
or the future of observation or prediction, respectively, whereas this is not
necessarily true of ENs in general. For simplicity, and to express the
definiteness of the past, we will define the update function
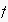 such that the a posteriori expectabilities of past events (i.e.,
observations) become 1 (admittedly leading to problems if the past is unknown
or contested, or we would like to allow contested assertive ECAs
about the past). There shall be exactly one path
such that the a posteriori expectabilities of past events (i.e.,
observations) become 1 (admittedly leading to problems if the past is unknown
or contested, or we would like to allow contested assertive ECAs
about the past). There shall be exactly one path
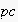 in the current EN leading from start node
in the current EN leading from start node
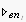 leading to a node
leading to a node
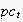 such that
such that
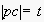 and
and
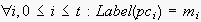 .
The node
.
The node
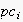 and the ECA
and the ECA
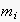 are said to correspond to each other.
are said to correspond to each other.
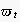 (respectively, the empirical semantic of the message
(respectively, the empirical semantic of the message
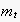 within a context of preceeding events
within a context of preceeding events
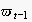 )
is formally defined as the probability distribution
)
is formally defined as the probability distribution
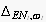 represented by the EN sub-tree starting with the node within
represented by the EN sub-tree starting with the node within
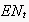 that corresponds to
that corresponds to
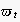 :
:
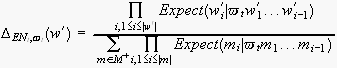
for all
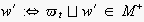 .
The
.
The
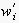 denote single event labels along
denote single event labels along
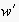 ,
i.e.,
,
i.e.,
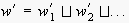 (for
(for
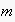 analogously).
analogously).
 ,
or starting at nodes after the node which corresponds to the ECA. The end
nodes of all matches in the EN are called the condition nodes of the ECA
projections. So, if the node list is empty, the only condition node is the
node corresponding to the ECA. Path matching is always successful, since in
our model, an EN implicitly contains all possible paths, although with a
probability close to zero for most of them.
,
or starting at nodes after the node which corresponds to the ECA. The end
nodes of all matches in the EN are called the condition nodes of the ECA
projections. So, if the node list is empty, the only condition node is the
node corresponding to the ECA. Path matching is always successful, since in
our model, an EN implicitly contains all possible paths, although with a
probability close to zero for most of them.
GoalStates chooses, using an EN path (without expectabilities), the (possibly infinite) set of states of the expectation network the uttering agent is expected to strive for. The uttered GoalStates path must match with a set of paths within the EN such that the last node of each match is a node of an EN branch that has a condition node from Conditions as its root. Both in Conditions and GoalStates paths, wildcards "?" for single actions are allowed.
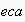 is simply
is simply
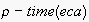 ,
where the first operand is the expected time of the last observed utterance
within the SIS, and the second is the utterance time of the projecting ECA.
Independent of this value, the actual spheres of communication are implicitly
evolving during communication.
,
where the first operand is the expected time of the last observed utterance
within the SIS, and the second is the utterance time of the projecting ECA.
Independent of this value, the actual spheres of communication are implicitly
evolving during communication.
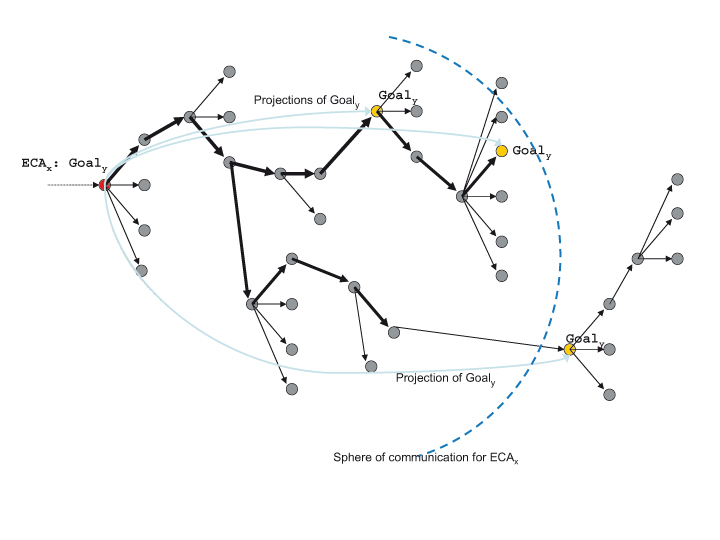
|
| Figure 1. An EN with projections and a sphere of communication |
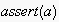 would be inconsistent with the attitude of
would be inconsistent with the attitude of
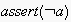 ,
and is thus very unlikely given overlapping spheres of communication
(but of course it is not so unlikely a self-interested agent utters
inconsistent ECAs in different contexts, e.g. facing different communication
partners).
,
and is thus very unlikely given overlapping spheres of communication
(but of course it is not so unlikely a self-interested agent utters
inconsistent ECAs in different contexts, e.g. facing different communication
partners).
Capturing these intentions, and given the set of projections for each ECA
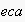 `uttered by an agent
`uttered by an agent
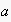 ,
we calculate the semantics of ECAs using the following two principles.
,
we calculate the semantics of ECAs using the following two principles.
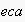 ,
an agent
,
an agent
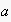 is expected to choose an action policy such that, within the respective
sphere of communication, his actions maximise the probability of the
projected state(s). Again, it is important to see that this expectable
rational behaviour does not need to reflect the "true", hidden intentions of
the observed agents, but is an external ascription made by the observer
instead. Let
is expected to choose an action policy such that, within the respective
sphere of communication, his actions maximise the probability of the
projected state(s). Again, it is important to see that this expectable
rational behaviour does not need to reflect the "true", hidden intentions of
the observed agents, but is an external ascription made by the observer
instead. Let
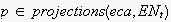 be a projection. Then, considering that
be a projection. Then, considering that
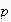 would be a useful state for the uttering agent to be in, the rule of rational
choice proposes that for every node
would be a useful state for the uttering agent to be in, the rule of rational
choice proposes that for every node
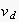 with
with
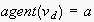 along the path
along the path
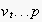 leading from the current node
leading from the current node
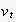 to
to
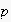 ,
,
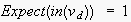 for the incoming edge of
for the incoming edge of
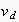 ,
and that the expectabilities of the remaining outgoing edges of the
predecessor of
,
and that the expectabilities of the remaining outgoing edges of the
predecessor of
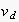 are reduced to 0 appropriately (if no other goals have to be considered).
are reduced to 0 appropriately (if no other goals have to be considered).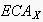 is an utterance which encodes
is an utterance which encodes
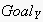 .
This goal itself stands for several (seemingly) desirable states of the EN
(yellow nodes). Since within the sphere of communication of
.
This goal itself stands for several (seemingly) desirable states of the EN
(yellow nodes). Since within the sphere of communication of
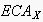 it is expected that the uttering person rationally strives for
these states, certain EN paths leading to these states become more likely
(bold edges) because the actions along these EN paths are followed more
likely than others by subsequent communications. Such paths need to be (more or less)
rational in terms
of their expected "utility" (e.g., in comparison with competing goal states),
and they need to reflect experiences from analogous behaviour in the
past. Not much
could be said about the "true utilities" the agents assign internally to EN states, nevertheless.
it is expected that the uttering person rationally strives for
these states, certain EN paths leading to these states become more likely
(bold edges) because the actions along these EN paths are followed more
likely than others by subsequent communications. Such paths need to be (more or less)
rational in terms
of their expected "utility" (e.g., in comparison with competing goal states),
and they need to reflect experiences from analogous behaviour in the
past. Not much
could be said about the "true utilities" the agents assign internally to EN states, nevertheless.
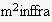 of an instance of abstract InFFrA that is based on empirical semantics and
uses a combination of hierarchical reinforcement learning
(Barto and Mahadevan 2003), case-based reasoning
(Kolodner 1993) and cluster validation techniques. Since
both the abstract architecture (Rovatsos et al 2002) and the
concrete computational model
(Fischer and Rovatsos 2004; Rovatsos et al 2004; Fischer et al 2005) have been described in
previous accounts[10] we will
only provide a brief description here which only covers those aspects that are
necessary to understand how InFFrA re-interprets the empirical semantics
approach from an agent-centric, individualistic perspective.
of an instance of abstract InFFrA that is based on empirical semantics and
uses a combination of hierarchical reinforcement learning
(Barto and Mahadevan 2003), case-based reasoning
(Kolodner 1993) and cluster validation techniques. Since
both the abstract architecture (Rovatsos et al 2002) and the
concrete computational model
(Fischer and Rovatsos 2004; Rovatsos et al 2004; Fischer et al 2005) have been described in
previous accounts[10] we will
only provide a brief description here which only covers those aspects that are
necessary to understand how InFFrA re-interprets the empirical semantics
approach from an agent-centric, individualistic perspective.
roles held by the interacting parties and relationships between them,
trajectories that describe the observable surface structure of the interaction, and
context and belief conditions that need to be fulfilled for the respective frame to be enacted.
Interpreting the current interaction situation in terms of a perceived frame and matching it against the normative model of the active frame which determines what the interaction should look like.
Assessing the current active frame (based on whether its conditions are currently met, whether its surface structure resembles the perceived interaction sequence, and whether it serves the agent's own goals).
Deciding on whether to retain the current active frame or whether to re-frame (i.e. to retrieve a more suitable frame from one's frame repository or to adjust an existing frame model to match the current interaction situation and the agent's current needs) on the grounds of the previous assessment phase.
Using the active frame to determine one's next (communicative/social) action, i.e. apply the active frame as a prescriptive model of social behaviour in the current interaction encounter.
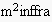 model has been proposed as one possible concrete instance of the general
framework that can be readily (and has been) implemented and includes learning
and generalisation capabilities as well as methods for boundadly rational
decision making in interaction situations.
model has been proposed as one possible concrete instance of the general
framework that can be readily (and has been) implemented and includes learning
and generalisation capabilities as well as methods for boundadly rational
decision making in interaction situations.
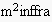 can be seen as the result of imposing a number of constraints on general SISs
to yield a simple, computationally lightweight representation of expectation
structures which allows for an application of learning and decision-making
algorithms that are appropriate for implementation in reasonably complex
socially intelligent agents. Using the EN/SIS terminology, these restrictions
can be described as follows:
can be seen as the result of imposing a number of constraints on general SISs
to yield a simple, computationally lightweight representation of expectation
structures which allows for an application of learning and decision-making
algorithms that are appropriate for implementation in reasonably complex
socially intelligent agents. Using the EN/SIS terminology, these restrictions
can be described as follows:
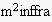 only considers two-party turn-taking interaction episodes called
encounters which have clear start and termination conditions. In
other words, agents interact by initiating a "conversation" with a single
other agent, exchanging a number of messages in a strictly turn-taking
fashion, and can unambiguously determine when this conversation is finished.
only considers two-party turn-taking interaction episodes called
encounters which have clear start and termination conditions. In
other words, agents interact by initiating a "conversation" with a single
other agent, exchanging a number of messages in a strictly turn-taking
fashion, and can unambiguously determine when this conversation is finished.
All social reasoning activity is conducted within the horizon of the current encounter. This implies that subsequent agent dialogues are not related to each other, which is equivalent to limiting the EN that would result from constructing an expectation structure from interaction experience to a certain depth.
ECAs are equivalent to elementary utterances, i.e. each utterance is considered an independent and self-contained communicative action (there are no composite ECAs) that is taken as a primitive in forming expectations.
The trajectory of every
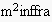 frame is a sequence of message patterns (i.e. speech-act like messages which
may contain variables for sender, receiver and (parts of their) content) that
describes the surface structure of a particular class of interaction
encounters. Thus, an individual frame trajectory corresponds to a path on an
EN, and while the whole set of frames (or frame repository) an agent
may dispose of is equivalent to a tree, whenever the agent activates a single
frame he disregards all other possible paths of execution and reasons only
about the degrees of freedom provided by a single frame (at least until the
next re-framing process). This helps to greatly reduce the complexity of the
expectation structure reasoned about at least as long as the currently active
frame can be upheld (e.g. it is not applicable/desirable anymore).
frame is a sequence of message patterns (i.e. speech-act like messages which
may contain variables for sender, receiver and (parts of their) content) that
describes the surface structure of a particular class of interaction
encounters. Thus, an individual frame trajectory corresponds to a path on an
EN, and while the whole set of frames (or frame repository) an agent
may dispose of is equivalent to a tree, whenever the agent activates a single
frame he disregards all other possible paths of execution and reasons only
about the degrees of freedom provided by a single frame (at least until the
next re-framing process). This helps to greatly reduce the complexity of the
expectation structure reasoned about at least as long as the currently active
frame can be upheld (e.g. it is not applicable/desirable anymore).
In addition to its trajectory model, each frame keeps track of the number of encounters that matched (prefixes of) that trajectory (which is the simplest possible method to derive transition probabilities in the EN view), and lists of corresponding variable substitutions/logical conditions to record the values variables had in previous enactments of the frame and the conditions that held true at the time of enactment.
Agents maintain a set of these frames instead of an EN but the size of this frame repository is implicitly bounded because agents apply generalisation techniques (which make use of heuristics from the area of cluster validation) to represent similar encounters by a single, (by virtue of replacing instance values by variables) more abstract frame whenever this seems appropriate (Fischer 2003). What this means is that agents are not allowed to grow arbitrarily large ENs and are instead forced to coerce their experience into a frame repository of manageable size.
The SIS initialisation and update mechanism is fairly simple. Agents start out with a frame repository specified a priori by the human designer, and simply add every new encounter they experience to this repository in the form of a new frame unless it can be subsumed under an existing frame as a new substitution/condition pair or the generalisation methods mentioned above suggest abstracting from some existing frame conception to accommodate the new observation (in which case it also simply becomes a substitution/condition pair in the newly created, more abstract frame). While it is possible in theory to observe third-party encounters in which one is not directly involved as a participant this method is not used at present.
We assume that each agent can assess the usefulness of any sequence of messages and physical action (i.e. ground instance of any frame trajectory) using a real-valued utility function. This facilitates the application of decision-theoretic principles (note, however, that this utility estimate need not be equivalent to the rewards received from the environment and is just thought to provide the agent with hints as to which possible future interaction sequences to prefer).
The agent's decision-making process is modelled as a two-level Markov Decision Process (MDP) (Puterman 1994). At the frame selection level, agents pick the most appropriate frame according to its long-term utility and the current state. For this purpose, we apply the options framework (Precup 2000) for hierarchical reinforcement learning to interpret encounter sequences as macro-actions in the MDP sense and to approximate the value of each frame in each state through experience. We assume that the rewards received from the environment after an interaction encounter depend only on the physical (i.e. environment-manipulating) actions that were performed during that encounter (however, non-physical actions are assigned a small negative utility to prevent endless conversations that do not result in physical action). At the "lower" action selection level, the agent seeks to optimise her choices given the degrees of freedom that the current frame still offers. These are defined by the variables contained (and still unbound by the encounter so far) in the remaining steps of the trajectory model of the active defined. Here, using a (domain-dependent) similarity measure over messages and considering past cases as stored in the substitution/condition lists of the active frame, we are able to derive probabilities for the possible outcomes of the frame (and for the moves the other party might make within it). Together with the utility estimates for each of these predictions, agents can then choose the action that maximises the expected utility of the encounter to be performed in the next step.
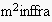 model more concrete, we go through a simple example:
model more concrete, we go through a simple example:
This frame reflects the following interaction experience:
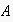 asked
asked
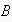 five times to perform (physical) action
five times to perform (physical) action
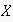 ,
out of which
,
out of which
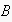 actually did so in three instances. In two of successful instances, it was
actually did so in three instances. In two of successful instances, it was
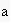 who asked and
who asked and
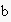 who headed the request, and the action was to pay $100. In both cases,
who headed the request, and the action was to pay $100. In both cases,
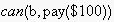 held true. In the third case, roles were swapped between
held true. In the third case, roles were swapped between
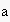 and
and
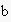 and the amount
and the amount
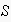 remains unspecified (which does not mean that it did not have a concrete
value, but that this was abstracted away in the frame). Note that in such
frames it is neither required that the reasoning agent is either of
remains unspecified (which does not mean that it did not have a concrete
value, but that this was abstracted away in the frame). Note that in such
frames it is neither required that the reasoning agent is either of
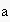 or
or
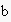 ,
nor that all the trajectory variables are substituted by concrete values.
Also, trajectories may be specified at different levels of abstraction.
Finally, any frame will only give evidence of successful completions of the
trajectory, i.e. information about the three requests that were unsuccessful
have to be stored in a different frame.
,
nor that all the trajectory variables are substituted by concrete values.
Also, trajectories may be specified at different levels of abstraction.
Finally, any frame will only give evidence of successful completions of the
trajectory, i.e. information about the three requests that were unsuccessful
have to be stored in a different frame.
In the
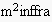 reasoning cycle, the reasoning agent
reasoning cycle, the reasoning agent
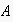 enters the framing loop whenever sub-social (e.g. BDI) reasoning processes
generate a goal that requires actions to be taken that
enters the framing loop whenever sub-social (e.g. BDI) reasoning processes
generate a goal that requires actions to be taken that
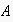 cannot perform herself. (If
cannot perform herself. (If
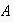 is already engaged in an ongoing conversation, this step is skipped.) From all
those frames contained in her frame repository
is already engaged in an ongoing conversation, this step is skipped.) From all
those frames contained in her frame repository
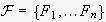 she then picks the frame that (1) achieves the
goal[11], (2) is executable
in the current state of affairs and (3) has proven reliable and utile in the
past (this is done using the reinforcement learning methods described above).
Let us assume that frame is the example frame
she then picks the frame that (1) achieves the
goal[11], (2) is executable
in the current state of affairs and (3) has proven reliable and utile in the
past (this is done using the reinforcement learning methods described above).
Let us assume that frame is the example frame
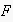 used above. In a decision-making step that does not mark the initiation of a
new encounter (i.e. if the interaction has already started),
used above. In a decision-making step that does not mark the initiation of a
new encounter (i.e. if the interaction has already started),
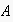 would also have to ensure that the frames considered for selection match the
current "encounter prefix", i.e. the initial sequence of messages already
uttered.
would also have to ensure that the frames considered for selection match the
current "encounter prefix", i.e. the initial sequence of messages already
uttered.
Once the frame has been selected,
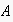 has to make an optimal choice regarding the specific choices for variables the
frame may contain. In the case of
has to make an optimal choice regarding the specific choices for variables the
frame may contain. In the case of
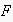 this is trivial, because if
this is trivial, because if
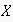 is already instantiated with the action
is already instantiated with the action
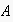 wants
wants
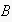 to perform, then the frame leaves no further degrees of freedom. However, if,
for example, the frame contained additional steps and/or variables(e.g. an
exchange of arguments before
to perform, then the frame leaves no further degrees of freedom. However, if,
for example, the frame contained additional steps and/or variables(e.g. an
exchange of arguments before
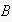 actually agrees to perform
actually agrees to perform
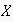 ),
),
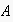 would compute probabilities and utility estimates for each ground instance of
the "encounter postfix" (the steps still to be executed along the current
frame trajectory) to be able to chose that next action to perform which
maximises the expected "utility-to-go" of the encounter.
would compute probabilities and utility estimates for each ground instance of
the "encounter postfix" (the steps still to be executed along the current
frame trajectory) to be able to chose that next action to perform which
maximises the expected "utility-to-go" of the encounter.
The process of reasoning about specific action choices within the bounds of a single frame of course involves reasoning about the actions the other party will perform, i.e. it has to be borne in mind that some of the variables in the postfix sequence message patterns will be "selected" by the opponent.
As the encounter unfolds, either of the two parties (or both) may find that the current active frame is not appropriate anymore, and that there is a need to re-frame. Three different reasons may lead to re-framing which spawns a process that is similar to frame selection at the start of an encounter:
The other party has made an utterance that does not match the message pattern that was expected according to the active frame.
At least one of the physical actions along the postfix sequence is not executable anymore because some of its pre-conditions are not fulfilled (and not expected to become true until they are needed).
No ground instance of the remaining trajectory steps seems desirable utility-wise.
While the first two cases are straightforward in the sense that they clearly necessitate looking for an alternative frame, the last step largely depends on the "social attitude" of the agent, and is closely related to issues of social order as discussed in section 2. Obviously, if agents were only to select frames that provide some positive profit to them, cooperation would be quite unlikely, and also they would also be prone to missing opportunities for cooperation because they do not "try out" frames to see how profitable they are in practice.
To balance social expectations as captured by the current set of frames with the agent's private needs, we have developed an entropy-based heuristics for trading off framing utility against framing reliability (Rovatsos et al 2003). Using this heuristics, the agent will occasionally consider frames that do not yield an immediate profit, if this is considered useful to increase mutual trust in existing expectations.
Finally, agents terminate the encounter when the last message on the trajectory of the active frame has been executed (unless the other party sends another message, in which we have to re-frame again). Whenever no suitable frame can be found in the trajectory that matches the perceived message sequence, this sequence is stored as a new frame, i.e. agents are capable of learning frames that are new altogether.
 architecture has been successfully implemented and validated in complex
argumentation-based negotiation scenarios. It can be seen as a
realisation of the empirical semantics approach for agent-level social
reasoning architectures thus illustrating its wide applicability.
architecture has been successfully implemented and validated in complex
argumentation-based negotiation scenarios. It can be seen as a
realisation of the empirical semantics approach for agent-level social
reasoning architectures thus illustrating its wide applicability.
Note that in these simulations, agents have the possibility to reject any proposal, so in principle they can avoid any undesirable agreement. However, this does not imply that they will adhere to the frames, because they might be insincere and not execute actions they have committed themselves because their private desirability considerations suggest different utility values from those expected when the agreement was reached (or simply because they calculated that lying is more profitable than keeping one's promises).
Add link from agent1's site to agent2's site with weight w
--> do(addLink(agent1, agent2, w))
Remove link from agent1's site to agent2's site
--> do(deleteLink(agent1, agent2))
Modify the weight of an existing link
--> do(modifyRating(agent1, agent2, w))
agent1 asks agent2 to perform act(...)
--> project(agent1, agent2, do(act(...))
agent1 agrees to perform act(...)
--> project(agent1, agent1, act(...))
I.e., "accept" means to project the fulfilment of a previously requested action (a request
of agent1 to do something by herself, so to say). This can also be done
implicitely by performing the requested action.
agent1 rejects a request or proposal
--> project(agent1, agent2, not act(...))
agent1 proposes to perform by herself act(...)
--> project(agent1, agent2, do(act(...))
request(agent1, agent2,addLink(agent2,agent1,3))
reject(agent2,agent1, addLink(agent2,agent1,3))
request(agent2, agent1, addLink(agent1,agent2,4))
addLink(agent1,agent2,4)
request(agent1, agent2, addLink(agent2,agent1,3))
addLink(agent2,agent1,3)
request(agent1, agent2, addLink(agent2,agent1,3))
addLink(agent2,agent1,3)
In order to estimate the performance of the EN-based prediction algorithm applied to action sequences like this, we performed several experiments. ENs of both types were retrieved from prefixes of the whole protocol as empirical evidence, and then parts of the rest of the protocols (i.e., the actual continuations of the conversation) were compared with paths within the ENs to yield an estimation for the prediction achievement. The comparisons were performed automatically, since the resulting ENs were mostly to complex to evaluate them manually.
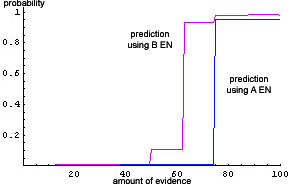
|
| Figure 2. Prediction of communication sequences (example 1) |
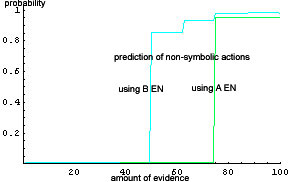
|
| Figure 3. Prediction of non-symbolic actions (example 1) |
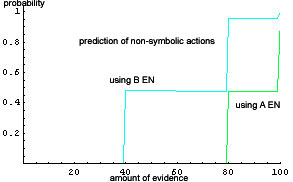
|
| Figure 4. Prediction of communication sequences (example 2) |

|
| Figure 5. Prediction of non-symbolic actions (example 2) |
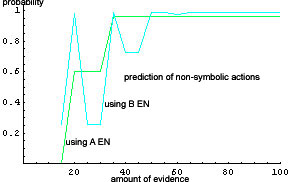
|
| Figure 6. Prediction of non-symbolic actions (example 3) |
request(agent1, agent2,addLink(agent2,agent1,3)) by accepting the counter proposal (request(agent2, agent1, addLink(agent1,agent2,4))) .
addLink(agent2,agent1,3) within this EN, the maximum expectation is taken and plotted on the y-axis. This is done both purely-empirically (green curve) and empirically-rational (cyan curve). Figure 3 thus shows the overall probability of fulfilling agent 1's request. This yields roughly the same result as above (Figure 2), but is for technical reasons much easier to compute in case the predicted sequence (the 20% at the end of the example sequence here) is very long. Figure 4 and 5 show such a case (rather extreme, for clearness), obtained from a protocol of 236 LIESON actions. Here, Figure 5 shows a good predictability, whereas Figure 4 predicts the protocol remainder only if at least 80% of the protocol is given as evidence, i.e., if the predicted sequence and the evidence overlap.
2 Of course, the (expectation of) triggered behaviour can trigger (the expectation of) other agent's behaviour and so on.
3 Actually, two different paths can have the same semantics in terms of their expected continuations, a fact which could be used to reduce the size of the EN by making them directed graphs with more than one path leading to a node instead of trees as in this work.
4 To be precise, a single utterance might be split into several so-called elementary communication acts, each corresponding to a dedicated EN node.
5We assume a discrete time scale with 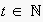 , and that no pair of actions is performed at the same time (quasi-parallel events achieved through a highly fine grained time scale), and that the expected action time corresponds with the depth of the respective node within in the EN.
, and that no pair of actions is performed at the same time (quasi-parallel events achieved through a highly fine grained time scale), and that the expected action time corresponds with the depth of the respective node within in the EN.
6A future version of our framework might allow the utterance of whole ENs as projections, in order to freely project new expectabilities or even introduce novel event types not found in the current EN.
7This time span of projection trustability can be very short though — think of joke questions.
8This probability distribution must also cover projected events and assign them a (however low) probability even if these events are beyond the spheres of communication, because otherwise it would be impossible to calculate the rational hull.
9We regard the identification of the necessity of combining these two (admittedly closely related) theories to be able to produce adequate computational models of reasoning about interaction as one of the major insights of our research that sociologists can benefit from. This nicely illustrates the bi-directional benefits of transdisciplinary collaboration in the Socionics research programme.
10In particular, Rovatsos et al (2004) describes both models and their theoretical foundations in detail and includes an account of an extensive experimental validation of the approach.
11In an AI planning sense, agents will also activate frames that achieve sub-goals towards some more complex goal, but we ignore this case here for simplicity.
BARTO A G and Mahadevan S (2003) Recent advances in hierarchical reinforcement learning. Discrete Event Dynamic Systems , 13(4):41–77, 2003.
COHEN P R and Levesque H J (1990) Performatives in a Rationally Based Speech Act Theory. In Proceedings of the 28th Annual Meeting of the ACL, 1990.
COHEN P R, Levesque H J (1995) Communicative Actions for Artificial Agents. In Proceedings of ICMAS-95, 1995.
FISCHER F and Nickles M (2006) Computational Opinions. Proceedings of the 17th European Conference on Artificial Intelligence (ECAI-2006), IOS press. To appear.
FISCHER F and Rovatsos M (2004) Reasoning about Communication: A Practical Approach based on Empirical Semantics. Proceedings of the 8th International Workshop on Cooperative Information Agents (CIA-2004), Erfurt, Germany, Sep 27-29, LNCS 3191, Springer-Verlag, Berlin, 2004.
FISCHER F (2003) Frame-based learning and generalisation for multiagent communication. Diploma Thesis. Department of Informatics, Technical University of Munich, 2003.
FISCHER F, Rovatsos M and Weiss G (2005) Acquiring and Adapting Probabilistic Models of Agent Conversation. In Proceedings of the 4th International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS), Utrecht, The Netherlands, 2005.
GAUDOU B, Herzig A, Longin D, and Nickles M (2006) A New Semantics for the FIPA Agent Communication Language based on Social Attitudes. Proceedings of the 17th European Conference on Artificial Intelligence (ECAI-2006), IOS press. To appear.
GOFFMAN E (1974) Frame Analysis: An Essay on the Organisation of Experience. Harper and Row, New York, NY, 1974.
GRICE H. P. (1968) Utterer's Meaning, Sentence Meaning, and Word-Meaning. Foundations of Language, 4: 225-42, 1968.
GUERIN F and Pitt J (2001) Denotational Semantics for Agent Communication Languages. In Proceedings of Agents'01, ACM Press, 2001.
KOLODNER J L (1993) Case-Based Reasoning . Morgan Kaufmann, San Francisco, CA, 1993.
LABROU Y and Finin T (1997) Semantics and Conversations for an Agent Communication Language. In Proceedings of IJCAI-97, 1997.
LORENTZEN K F and Nickles M (2002) Ordnung aus Chaos — Prolegomena zu einer Luhmann'schen Modellierung deentropisierender Strukturbildung in Multiagentensystemen. In T. Kron, editor, Luhmann modelliert. Ans‰tze zur Simulation von Kommunikationssystemen. Leske & Budrich, 2002.
LUHMANN N (1995) Social Systems. Stanford University Press, Palo Alto, CA, 1995.
MATURANA H R (1970) Biology of Cognition. Biological Computer Laboratory Research Report BCL 9.0. Urbana, Illinois: University of Illinois, 1970.
MEAD G H (1934) Mind, Self, and Society. University of Chicago Press, Chicago, IL, 1934.
MÜLLER H J , Malsch Th and Schulz-Schaeffer I (1998) SOCIONICS: Introduction and Potential. Journal of Artificial Societies and Social Simulation vol. 1, no. 3, https://www.jasss.org/1/3/5.html
NICKLES M and Weiss G (2003) Empirical Semantics of Agent Communication in Open Systems. Proceedings of the Second International Workshop on Challenges in Open Agent Environments. 2003
NICKLES M, Rovatsos M and Weiss G (2004a) Empirical-Rational Semantics of Agent Communication. Proceedings of the Third International Joint Conference on Autonomous Agents and Multi-Agent Systems (AAMAS'04), New York City, 2004.
NICKLES M, Rovatsos M, Brauer W and Weiss G (2004b) Towards a Unified Model of Sociality in Multiagent Systems. International Journal of Computer and Information Science (IJCIS), Vol. 5, No. 1, 2004.
NICKLES M, Froehner T and Weiss G (2004c) Social Annotation of Semantically Heterogeneous Knowledge. Notes of the Fourth International Workshop on Knowledge Markup and Semantic Annotation (SemAnnot-2004), Hiroshima, Japan, 2004.
NICKLES M and Weiss G (2005) Multiagent Systems without Agents: Mirror-Holons for the Compilation and Enactment of Communication Structures. In Fischer K, Florian M and Malsch Th. (Eds.): Socionics: Its Contributions to the Scalability of Complex Social Systems. Springer LNAI, 2005.
NICKLES M, Rovatsos R and Weiss G (2005a) Expectation-Oriented Modeling. In International Journal on Engineering Applications of Artificial Intelligence (EAAI) Vol. 18. Elsevier, 2005.
NICKLES M, Fischer F and Weiss G (2005b) Communication Attitudes: A Formal Approach to Ostensible Intentions, and Individual and Group Opinions. In Proceedings of the Third International Workshop on Logic and Multi-Agent Systems (LCMAS), 2005.
NICKLES M, Fischer F and Weiss G (2005c) Formulating Agent Communication Semantics and Pragmatics as Behavioral Expectations. In Frank Dignum, Rogier van Eijk, Marc-Philippe Huget (eds.): Agent Communication Languages II, Springer Lecture Notes in Artificial Intelligence (LNAI), 2005.
PARSONS T (1951) The Social System. Glencoe, Illinois: The Free Press, 1951.
PITT J and Mamdani A (1999) A Protocol-based Semantics for an Agent Communication Language. In Proceedings of IJCAI-99, 1999.
PRECUP D (2000) Temporal Abstraction in Reinforcement Learning. PhD thesis, Department of Computer Science, University of Massachusetts, Amherst, 2000.
PUTERMAN M L (1994) Markov Decision Processes . John Wiley & Sons, New York, NY, 1994.
RON D, Singer Y and Tishby N (1996) The Power of Amnesia - Learning Probabilistic Automata with Variable Memory Length. In Machine Learning Vol. 25, p. 117–149, 1996
ROVATSOS M, Weiss G and Wolf M (2002) An Approach to the Analysis and Design of Multiagent Systems based on Interaction Frames. In Proceedings of the First International Joint Conference on Autonomous Agents and Multi-Agent Systems (AAMAS'02), Bologna, Italy, 2002.
ROVATSOS M, Nickles M and Weiss G (2003) Interaction is Meaning: A New Model for Communication in Open Systems. In Proceedings of the Second International Joint Conference on Autonomous Agents and Multi-Agent Systems (AAMAS'03), Melbourne, Australia, 2003.
ROVATSOS M, Fischer F and Weiss G (2004a) Hierarchical Reinforcement Learning for Communicating Agents. Proceedings of the 2nd European Workshop on Multiagent Systems (EUMAS), Barcelona, Spain, 2004.
ROVATSOS M, Nickles M and Weiss G (2004b) An Empirical Model of Communication in Multiagent Systems. In Dignum F (Ed.), Agent Communication Languages. Lecture Notes in Computer Science, Vol. 2922, 2004.
ROVATSOS M (2004) Computational Interaction Frames. Doctoral thesis, Department of Informatics, Technical University of Munich, 2004.
SINGH M P (2000) A Social Semantics for Agent Communication Languages. In Proceedings of the IJCAI Workshop on Agent Communication Languages, 2000.
SINGH M P (1993) A Semantics for Speech Acts. Annals of Mathematics and Artificial Intelligence, 8(1–2):47–71, 1993.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]