Thorsten Chmura and Thomas Pitz (2007)
An Extended Reinforcement Algorithm for Estimation of Human Behaviour in Experimental Congestion Games
Journal of Artificial Societies and Social Simulation
vol. 10, no. 2
<https://www.jasss.org/10/2/1.html>
For information about citing this article, click here
Received: 19-Jun-2006 Accepted: 20-Nov-2006 Published: 31-Mar-2007
 Abstract
Abstract
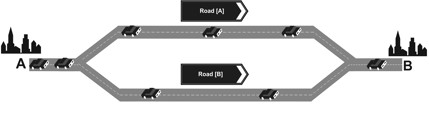 |
| Figure 1. Participants had to choose between a road [A] and a road [B] |
| tA = 1, tB = 0, ⇔ nA < nB |
| tB = 1, tA = 0, ⇔ nA > nB |
The period payoff was tA if A was chosen and tB if B was chosen. There are no pure equilibria in this game. The pareto-optimum can be reached by 4 players on one and 5 players at the other place.
| tA = 6 + 2n and tB = 12 + 3 nB |
In the route choice scenario A represents a main road and B a side road. A is faster if A and B are chosen by the same number of people (Selten et al 2003).
| nA = 11 and nB = 7 |
| 18λ, λ =2,…, 5, |
where
| pA = 40 λ = [6 λ + 2 nA] |
| pB = 40 λ = [12 λ + 3nB] |
| Table 1: Pure equilibria in CII. The equilibria depend on the number of participating agents | ||
| Number of Players | Equilibrium | |
| A | B | |
| 18 | 12 | 6 |
| 36 | 24 | 12 |
| 54 | 36 | 18 |
| 72 | 48 | 24 |
| 90 | 60 | 30 |
 |
| Figure 2. Reinforcement algorithm |
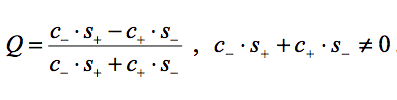
|
The Yule coefficient has a range from -1 to +1. In the rare cases that a subject never (in each period) changes his last choice, we defined Q = 0 because the decision of such a subject does not depend on the last period payoff. A subject with Yule coefficients below -.5 could be understood to be classified as direct and subjects above +.5 as contrarian.
| Place A: | This strategy consists in taking A. |
| Place B: | This strategy consists in taking B. |
| After the first period in each of the two games (CI) and (CII) the two extended strategies direct and contrarian are available: | |
| (CI) direct: | If the payoff of a player is 1, then the player stays on the same place last chosen. If his payoff is 0, the players changes (from A to B or from B to A). |
| (CI) contrarian: | If the payoff of a player is 1, then the player changes (from A to B or from B to A). If his payoff is 0, the players will stay on the same place. |
| (CII) direct: | This strategy corresponds to the direct response mode. The payoff of a player is compared to his median payoff among his payoffs for all periods up to now. If the present payoff is lower then this median payoff, then the place is changed. If the payoff is greater than this median payoff, the player stays on the same place as before. It may also happen that the current payoff is equal to the median payoff. In this case, the place is changed if the number of previous payoffs above the median is greater than the number of previous payoffs below the median. In the opposite case, the place is not changed. In the rare cases where both numbers are equal, the place is changed with probability ½. |
| (CII) contrarian: | A player who takes this strategy stays on the last chosen place if his current payoff is smaller then the median payoff among this payoffs for all previous periods, and he changes the place in the opposite case. If the current payoff is equal to this median payoff, then he changes the place if the number of previous payoff below the median payoff is greater then the number above the median payoff. If the numbers of previous payoff below and above the median payoff are equal, the place is changed with probability ½. |
 |
| Figure 3. Initial Propensities |
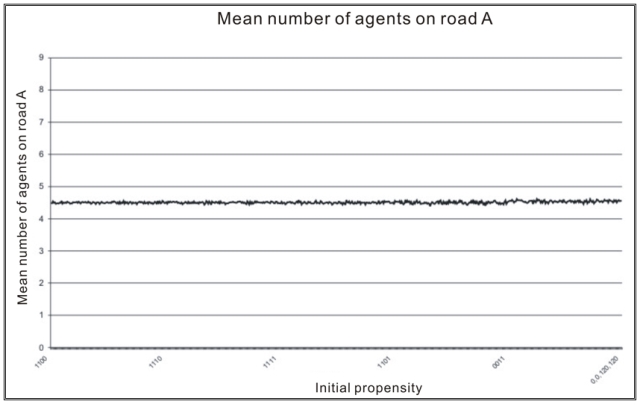 |
| Figure 4. Number of players on A |
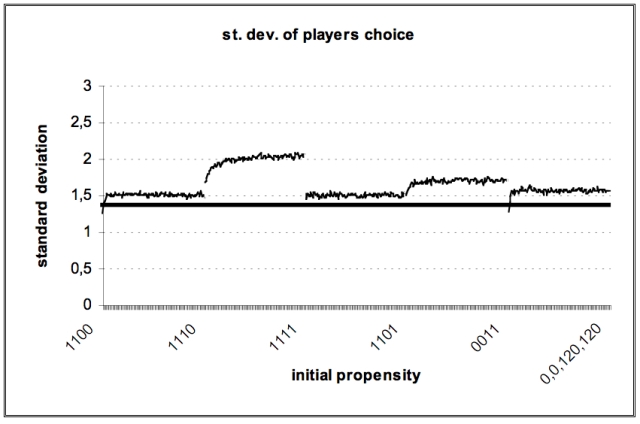 |
| Figure 5. Standard deviation of number of players on A |
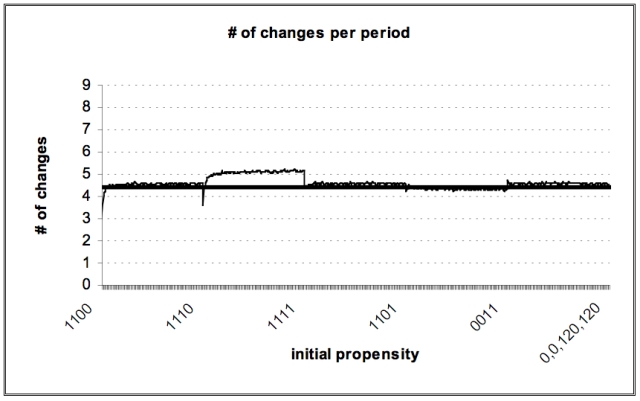 |
| Figure 6. Number of changes per period |
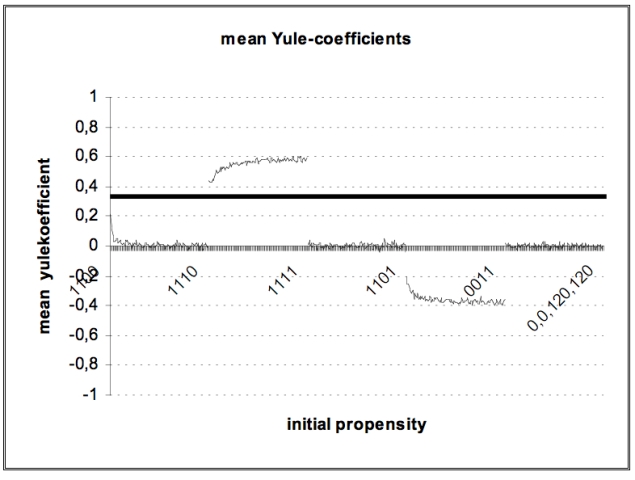 |
| Figure 7. Mean Yule-coefficients |
Similar results could be obtained by investigations of the initial propensities for simulations of CII.
| Table 2: CI — 9 Players - Experimental minima & maxima vs. simulation means | |||||
| CI | Experiment | Simulations | Experiment | ||
| Minimum | {1,1,2,1} | {2,2,1,1} | {3,3,4,2} | Maximum | |
| Player on A [mean] | 4,19 | 4.48 | 4.50 | 4.54 | 4.74 |
| Player on A [standard deviation] | 0.67 | 1.45 | 1.48 | 1.50 | 1.50 |
| Changes [mean] | 0.59 | 4.32 | 4.18 | 4.51 | 5.17 |
| Period of last Change | 54.44 | 96.11 | 97.67 | 97.44 | 98.11 |
| Yule Q [mean] | -0.01 | 0.10 | 0.04 | 0.14 | 0.87 |
| Yule Q [standard deviation] | 0.33 | 0.50 | 0.40 | 0.35 | 0.76 |
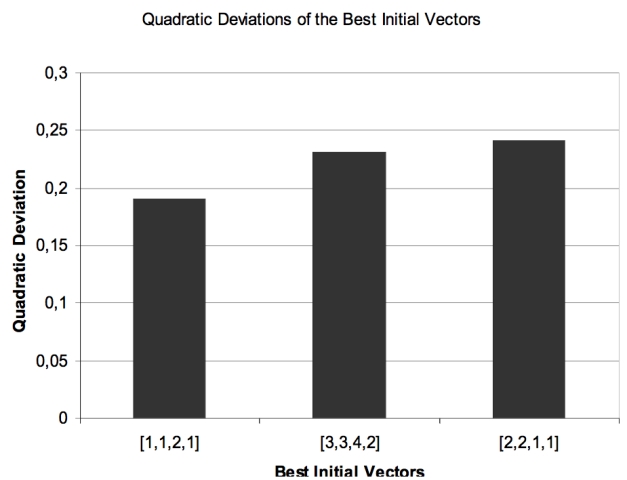 |
| Figure 8. Quadratic deviations of the best initial vectors from the average experimental data |
| Table 3: CII — 18 Players: experimental minima & maxima vs. simulation means | |||
| CII | Experiment | Simulations | Experiment |
| Minimum | {4,3,3,2} | Minimum | |
| Player on B [mean] | 5,85 | 5,95 | 6,17 |
| Player on B [standard deviation] | 1,59 | 1,65 | 1,99 |
| Changes [mean] | 4,62 | 5,17 | 5,38 |
| Period of last Change | 64,78 | 83,73 | 90,39 |
| Yule Q [mean] | 0,11 | 0,14 | 0,39 |
| Yule Q [standard deviation] | 0,53 | 0,61 | 0,75 |
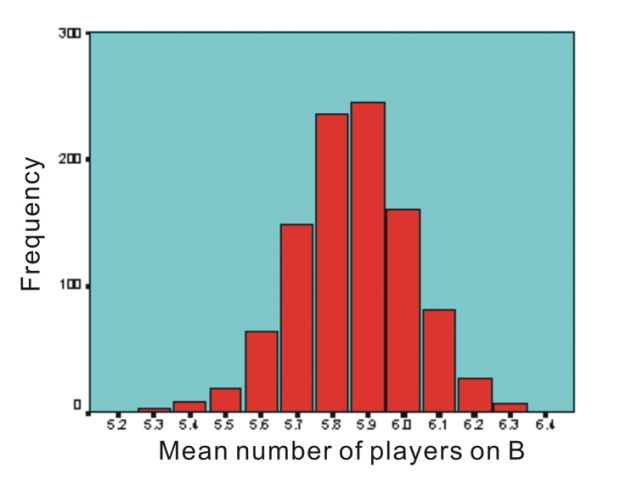 |
| Figure 9. Distribution of the mean number of players on B for the simulated vector (4,3,3,2) in 1000 simulations |
| Table 4: CII — Experimental means (E) vs. Simulation means (S) | ||||||
| Statistical Data CII | Data Source | Number of Players | ||||
| 18 | 36 | 54 | 72 | 90 | ||
| Mean (# players on B) | E | 5.98 | 12.21 | 17.98 | 24.2 | 30.02 |
| S | 5.95 | 11.91 | 17.9 | 23.83 | 29.02 | |
| st. Dev. (# players on B) | E | 1.78 | 2.64 | 3.24 | 4.54 | 5.02 |
| S | 1.65 | 2.39 | 3.04 | 3.78 | 4.58 | |
| Mean (# of place changes) | E | 4.82 | 11.35 | 15.57 | 22.76 | 26.02 |
| S | 5.17 | 10.07 | 15.98 | 21.32 | 23.04 | |
| Mean (last place change | E | 81 | 82 | 86 | 89 | 88 |
| S | 84 | 89 | 84 | 88 | 90 | |
| Mean (Yule-coefficient) | E | 0.28 | 0.14 | 0.22 | 0.2 | 0.24 |
| S | 0.14 | 0.16 | 0.15 | 0.15 | 0.16 | |
| st. Dev. (Yule-coefficient) | E | 0.58 | 0.58 | 0.58 | 0.57 | 0.6 |
| S | 0.61 | 0.54 | 0.54 | 0.52 | 0.56 | |
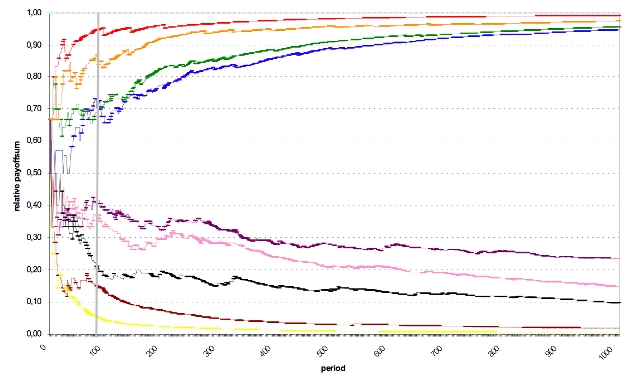 |
| Figure 10. Example simulation shows the relative payoff-sum for each of the 9 players over 1000 periods |
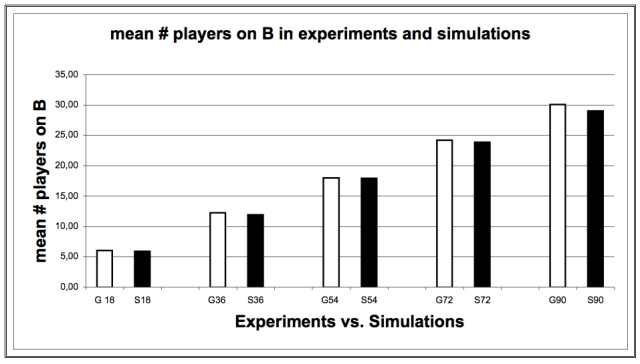 |
| Figure 11. Mean Number of Players on B in Experiments and Simulations |
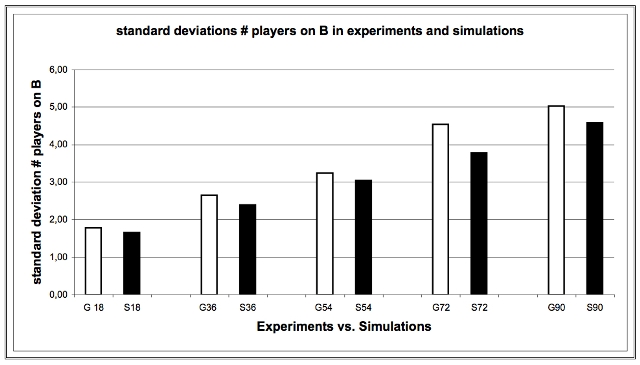 |
| Figure 12. Standard Deviation number of Players on B in Experiments and Simulations |
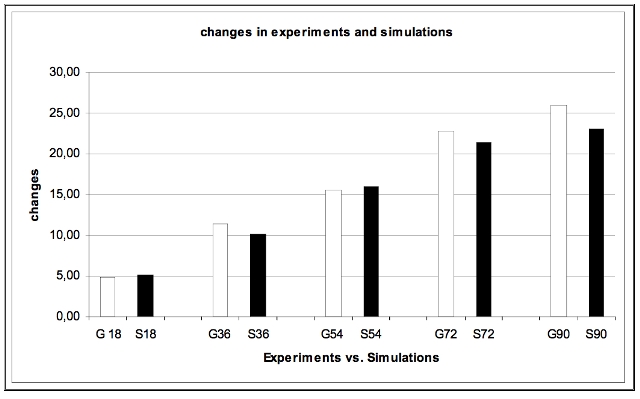 |
| Figure 13. Number of Changes in Experiments and Simulations |
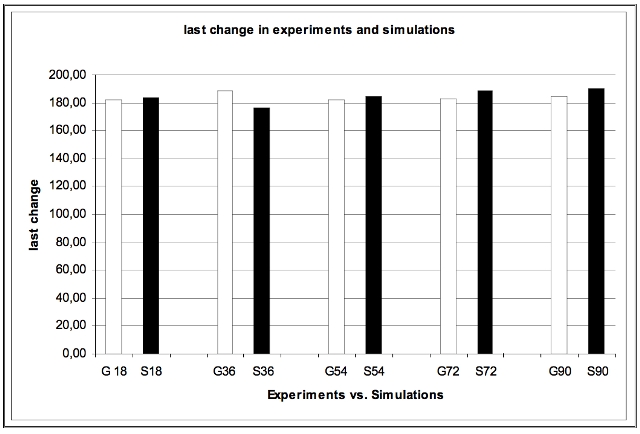 |
| Figure 14. Last change in experiments and simulations |
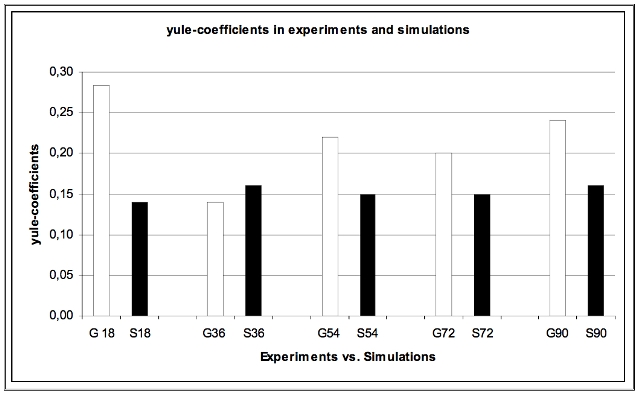 |
| Figure 15. Mean Yule-coefficients in experiments and simulations |
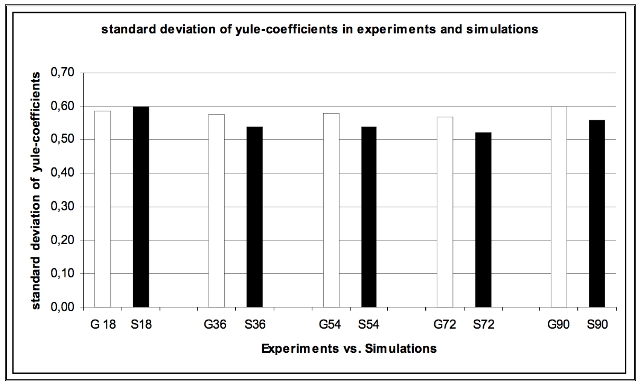 |
| Figure 16. Standard Deviation of Yule-coefficients in Experiments and Simulations |
CHALLET, D., Zhang, Y.-C., (1997) Emergence of cooperation and organization in an evolutionary game. Physica A 246, 407-418.
CHALLET , D., Zhang, Y.-C., (1998) On the minority game: Analytical and numerical studies. Physica A 256, 514-532.
CHMURA, T.., Pitz, T., (2006) Successful Strategies in Repeated Minority Games. Physica A 363, 477-480.
HARLEY, C. B. (1981) Learning in Evolutionary Stable Strategies, J. Theoretical Biology 89, 611-633.
HELBING, D., Schönhof, M., Kern, D. (2002) Volatile decision dynamics: Experiments, stochastic description, intermittency control, and traffic optimization. New Journal of Physics 4, 33.1-33.16.
HELBING, D. (2004) Dynamic decision behavior and optimal guidance through information services: Models and experiments in: M. Schreckenberg and R. Selten (eds.) Human Behaviour and Traffic Networks (Springer, Berlin) Pages 47-95.
JOHNSON, N. F., S. Jarvis, R. Jonson, P. Cheung, Y. R. Kwong, and P. M. Hui (1998) Volatility and agent adaptability in a self-organizing market. Physica A 258, 230-236.
LASLIER , F, Walliser, B., (2005) Reinforcement Learning Process in Extensive Form Games Game Theory, 33, 219-227.
ROTH, A.E., Erev, I. (1995), Learning in extensive form games: Experimental data and simple dynamic models in the intermediate term, Games and Economic Behavior 8, 164-212.
SELTEN, R., Schreckenberg, M., Pitz, T., Chmura, T., Kube, S. (2003) Experiments and Simulations on Day-to-Day Route Choice Behaviour, CESIFO Working Paper No. 900, Munich.
SELTEN, R., Chmura, T., Pitz, T., Kube, S., Schreckenberg, M. (2007) Commuters Route Choice Behaviour, Games and Economic Behaviour 58, 394-406.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]