Sergi Lozano and Alexandre Arenas (2007)
A Model to Test How Diversity Affects Resilience in Regional Innovation Networks
Journal of Artificial Societies and Social Simulation
vol. 10, no. 4 8
<https://www.jasss.org/10/4/8.html>
For information about citing this article, click here
Received: 02-Mar-2007 Accepted: 24-Jun-2007 Published: 31-Oct-2007
 Abstract
Abstract|
ai → ai + Δ |
(1) |
where Δi is a random variable with mean λ.
| ai – aj ≥ C ⇒ aj = ai | (2) |
where C is a constant, for simplicity
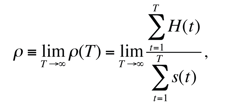
|
(3) |
where H(t) is the total technological advance induced by a technological avalanche (the sum of all increases on the a level achieved by agents in the system) and s(t) corresponds to the avalanche size (the total number of agents 'affected' by it).
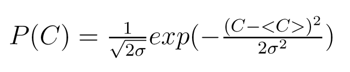
|
(4) |
Where <C> is the average value of resistance to change in the system, and σ is the standard deviation that determines the degree of heterogeneity of individual behaviours.
|
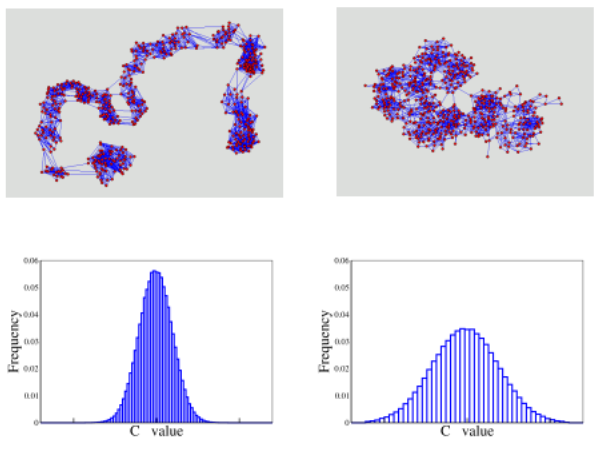
| Figure 1. Characteristics of the synthetic models proposed for Boston Route 128 (left) and Silicon Valley (right). Top: structures obtained using the model described in the text for high (left) and low (right) homophile for N=500 agents. Bottom: resistance to change profiles used in both respective scenarios |
|
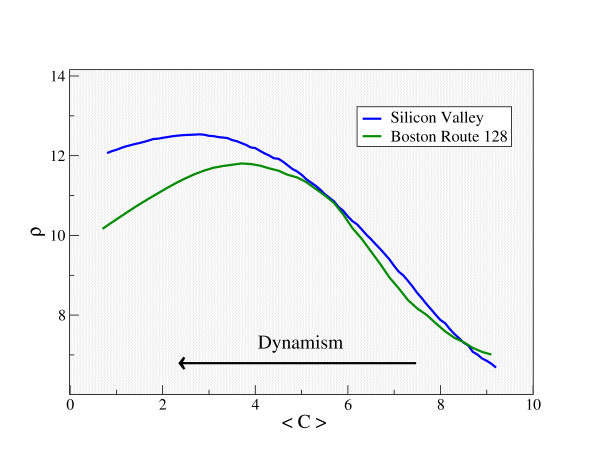
| Figure 2. Evolution of the performance of each simulated industrial pole in terms of the mean rate of advance, as a function of the dynamism of the environment (calculated as the opposite of the average resistance value). These results have been obtained by averaging 100 independent realizations, each one consisting on 5000 iterations of the three-step dynamics presented above |
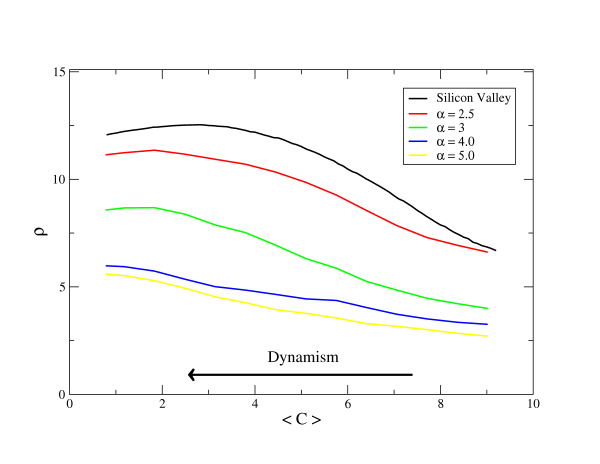
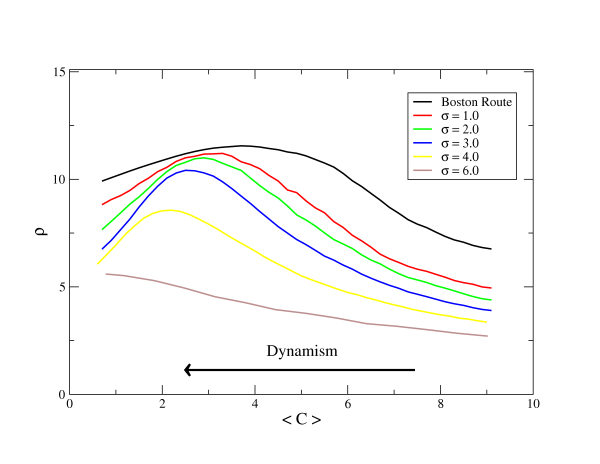
| Table 1: Maximum fitness value (ρ max.) and its position (<C>) for nine different system configurations, determined by their homophile ( α ) and deviation of change profile ( σ ). Cases corresponding to Silicon Valley (SV) and Boston Route (BR) are indicated as a reference to the eye. Though both parametres of the model influence the position and value of the maximum fitness, the dependence of the fitness value on α seem to be stronger (see text) | ||||
| σ | ||||
| 0.8 | 2 | 6 | ||
| α | 2.9 | ρ max.: 13.74 <C>: 5.00 | ρ max.: 13.10 <C>: 4.00 | (SV) ρ max.: 12.54 <C>: 2.80 |
| 5 | (BR) ρ max.: 11.80 <C>: 3.70 | ρ max.: 10.99 <C>: 2.90 | ρ max.: 10.63 <C>: 1.83 | |
| 7 | ρ max.: 9.35 <C>: 2.85 | ρ max.: 7.15 <C>: 1.75 | ρ max.: 5.49 <C>: 0.75 | |
| |
| |
| Figure 3a (top) & Figure 3b (bottom). Effect of modifying the original configurations by increasing the homophily (controlled by the homophile α) and the width of the resistance profile (controlled by the deviation σ), respectively. As in figure 2, these plots are the result of averaging 100 realizations of 5000 steps of our model dynamics | |
N: integer; -- Number of agents composing the population
type agent {
Id: integer; -- Agent's identification number
a: float; -- Real value describing, for instance, the technological level
C: float; -- Resistance to change value
caract: float; -- Numerical value of the social trait, needed to calculate the social distance
}
type tagents is array (0..N-1) of agent;
type System {
agents: tagents; -- Population of agents
scale: float; -- Scale of the social attribute, known as 'b'
-- in Boguñá et al (2004).
homo: float; -- Homophile value of the social attribute, known as α in the text
}
procedure Crea_sistema (C_ave, C_dev: in float) { -- Procedure that builds the system
-- Agent initialization
for each agent in agents {
agent.a:= 0.0; -- Initial value of 'a' is 0 for
-- all the elements in the population.
agent.C:= dist_norm(C_ave, C_dev); -- The resistance to change value is
-- determined by a gaussian distribution
-- defined by C_ave and C_dev
agent.caract:=dist_uni(Float(N)/10.0));
-- Value of the social trait is defined by a
-- uniformly distributed random variable
-- with an average depending on the
-- system size.
}
-- Determination of links between agents
for each agent i in agents {
for each agent j in agents that (j.Id > i.Id) {
-- Calculation of the linkage probability
-- as defined in Boguñá et al. (2004)
prob := (1.0/(1.0+(((1.0/scale)*abs(i.caract - j.caract) ^ (homo));
-- Creation of the link in function of the probability
if (dist_uni(0.5) ≤ prob) then agents i and j become neighbours;
}
}
}
function Intro_innovation (){ --Introduces an innovation in the system (1st step of diffusion dynamics).
first_agent := dist_uni (N / 2); -- The agent who starts the avalanche is chosen
-- randomly with equal probability.
first_agent.a : = fist_agent.a + incr; -- Here 'a' is upgraded by a random 'incr' value
return (first_agent);
}
procedure Update_neighbours (principal: in agent) { -- Implements the innovation avalanche (2nd and 3rd steps of diffusion dynamics)
candidates_list := Check_neighbours(principal); -- All neighbours of agent principal that want
-- to upgrade their 'a' level are listed in
-- candidates_list.
while candidates_list is not empty {
next := chosen randomly from candidates_list; -- One neighbour in candidates_list is chosen
-- randomly...
next.a := pos.a; -- ... to upgrade her 'a' level.
Update_neighbours (next); -- As agent next has upgraded her level, her
-- neighborhood also notice the innovation
-- avalanche. This process is implemented
-- by calling recursively the procedure
-- Update_neighbours.
candidates_list := Check_neighbours(pos);
}
}
procedure Genera_jocs () { -- Generates the diffusion dynamics
for num_real independent realizations of the experiment {
for each agent in agents {
agent.a:= 0.0; -- The value of 'a' is reset to 0
agent.C:= dist_norm(C_ave, C_dev); -- The resistance to change value is determined
-- by a gaussian distribution with an average
-- and standard deviation
}
for num_steps time steps {
initial := Intro_innovation(); -- A new innovation is introduced in the
-- system. Variable 'initial' receives the Id of
-- the agent that has upgraded her 'a' value
-- (first step of the dynamics).
Update_neighbours(initial); -- Innovation avalanche (second and third steps of the dynamics)
s := Number of agents in the avalanche; -- Data about the extension and magnitude of
H := Total increment on 'a' values; -- the avalanche is stored.
}
rho := rho + (H/s); -- The value of ρ (mean rate of advance) is
-- calculated for each independent realization.
}
rho := rho / Float(num_real); -- The final value of Rho is calculated as an
-- average of the values obtained at each
-- independent realization.
}
Procedure Main() {
Num_real : Number of independent realizations
num_steps : Number of time steps
C_ave: Average value of the resistance to change (related to environment dynamism)
C_dev: Standard deviation of the resistance to change (related to indidual initiative);
Crea_sistema (C_ave, C_dev); -- The system is created
for each Cave value from Cmin to Cmax { -- ρ is calculated for diferent values of C_ave
-- (for different values of the dynamism of the
-- socio-economical environment).
Genera_jocs(C_ave, C_dev, );
}
}
ABRAHAMSON, E., and L. ROSENKOPF. (1997). Social network effects on the extent of innovation diffusion: a computer simulation. Organization Science, 8, 289-309.
ALBERT, R., JEONG, H., BARABSI, A.-L. (2000). Error and attack tolerance of complex networks. Nature, 406, 378-382.
BERKES, F., COLDING, J. and FOLKE, C. (editors) (2003) Navigating Social-Ecological Systems: Building Resilience for Complexity and Change. Cambridge, UK: Cambridge University Press.
BURT, R.S. (1981) Innovation as Structural Interest: Rethinking the Impact of Network Position on Innovation Adoption. Social Networks, 2, 327-355.
BURT, R.S. (1987) Social Contagion and Innovation, Cohesion versus Structural Equivalence. American Journal of Sociology, 92, 1287-1335.
BODIN, Ö. A network perspective on ecosystems, societies and natural resource management. PhD thesis. Available at: http://www.diva-portal.org/su/abstract.xsql?lang=en&dbid=844
BOGUÑÁ, M, PASTOR-SATORRAS, R, DÍAZ-GUILERA, A and ARENAS, A (2004) Models of social networks based on social distance attachment. Phys. Rev. E, 70 (056122).
CRUCITTI, P., LATORA, V. and MARCHIORI, M. (2004) A model for cascading failures in complex networks. Phys. Rev. E 69, 045104(R).
DAVIES, S. (1979). The diffusion of process innovations. Cambridge, UK: Cambridge University Press.
FONTOURA COSTA, L. (2004). Reinforcing the Resilience of Complex Networks. Phys. Rev. E, 69, (066127).
FREEMAN, C. (1995). The National System of innovation in historical perspective. Cambridge Journal of Economics, 19 (1), 5-24.
GERSTLBERGER, W. (2004). Regional innovation systems and sustainability - selected examples of international discussion. Technovation, 24 (9).
GRANOVETTER, M. (1985). Economic Action and Social Structure: The Problem of Embeddedness. American Journal of Sociology, 91, 481-510.
GUARDIOLA, X, DÍAZ-GUILERA, A, PÉREZ, C.J., ARENAS, A, and LLAS, M, (2002) Modelling diffusion of innovation in a social network. Phys. Rev. E, 66 (026121).
GUNDERSON, L.H. (2000) Ecological resilience-in theory and application. Annual Review of Ecology and Systematics, 31, 425-439.
HOLLING, C.S. (1973) Resilience and Stability of Ecological Systems. Annual Review of Ecology and Systematics 4, 1-23.
ISDR (2006) International Strategy for Disaster Reduction - United Nations. http://www.unisdr.org/eng/library/lib-terminology-eng%20home.htm.
JAIN, S. and KRISHNA, S. (2002). Crashes, recoveries, and "core shifts" in a model of evolving networks. Phys. Rev. E, 65 (026103).
MANSFIELD, E. (1961). Technical Change and the Rate of imitation. Econometrica, 61, 741-766.
MEYER, J. and ROWAN, B. (1977). Institutionalized Organizations: Formal Structure as Myth and Ceremony. American Journal of Sociology, 83, 340-363.
MORENO, Y., PASTOR-SATORRAS, R., VÁZQUEZ, A. and VESPIGNANI, A. (2003) Critical load and congestion instabilities in scale-free networks. Europhys. Lett., 62 (2), 292-298.
MOTTER, A.E. and LAI, Y.C. (2002). Cascade-based attacks on complex networks. Phys. Rev. E, 66, 065102(R).
NEWMAN, M.E.J, (2003) The structure and function of complex networks. SIAM Review, 45, 167-256.
PETERSON, G., ALLEN, C.R. and HOLLING, C.S. (1998) Ecological Resilience, Biodiversity and Scale. Ecosystems, 1 (1): 6-18.
PIORE, M. and SABEL, C. (1984) The second industrial divide: Possibilities for prosperity. New York: Basic Books.
RA (2006) Resilience Alliance. http://www.resalliance.org/
ROGERS, E. M. (2003) Diffusion of innovations. New York, USA: The Free Press.
SAXENIAN, A. (1994) Regional Advantage: Culture and Competition in Silicon Valley and Route 128. Cambridge, MA, USA: Harvard University Press.
SCOTT, A. and PAUL, A. (1990). Collective order and economic coordination in industrial agglomerations: The technopoles of Southern California. Environment and Planning C: Government and Policy, 8, 179-193.
STABER, U. and SYDOW, J. (2002). Organizational Adaptive Capacity: A Structuration Perspective. Journal of Management Inquiry, 11, 408-424.
VALENTE, T. W. (1995) Network models of the diffusion of innovations. Cresskill, NJ, USA: Hampton Press.
VALENTE, T. W. and DAVIS, R. L. (1999). Accelerating the diffusion of innovations using opinion leaders. The Annals of the American Academy of the Political and Social Sciences, 566, 55-67.
VALENTE, T. W. (2005). Models and methods for innovation diffusion. In Carrington, P. J., Scott, J. and Wasserman, S. (Eds.) Models and Methods in Social Network Analysis. Cambridge, UK: Cambridge University Press.
WESTMAN, W.E. (1978) Measuring the inertia and resilience of ecosystems. BioScience, 28 (11), 705-710.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]