Oliver Will and Rainer Hegselmann (2008)
A Replication That Failed: On the Computational Model in 'Michael W. Macy and Yoshimichi Sato: Trust, Cooperation and Market Formation in the U.S. and Japan. Proceedings of the National Academy of Sciences, May 2002'
Journal of Artificial Societies and Social Simulation
vol. 11, no. 3 3
<https://www.jasss.org/11/3/3.html>
For information about citing this article, click here
Received: 30-Aug-2007 Accepted: 29-Apr-2008 Published: 30-Jun-2008
 Abstract
AbstractCompared with the U.S., Japan is believed to have a collectivist culture that nurtures high trust. Results from laboratory and survey research, however, show that Americans are more likely to trust strangers than are Japanese. Why would trust be lower in a collectivist culture? We use an agent-based computational model to explore the evolutionary origin of this puzzling empirical finding. Computer simulations suggest that higher social mobility[1] in the U.S. may be the explanation. With low mobility, agents rarely encounter strangers and thus remain highly parochial, trusting only their neighbors and avoiding open-market transactions with outsiders. With moderate mobility, agents learn to read telltale signs of character so that they can take advantage of better opportunities outside the neighborhood. However, if mobility is too great, there is too little trustworthiness to make the effort to discriminate worthwhile. This finding suggests that higher mobility in the U.S. may explain why Americans are more trusting than Japanese, but if mobility becomes too high, the self-reinforcing high-trust equilibrium could collapse. (Macy and Sato 2002, p.7214).
In particular, the nonmonotonic effects of mobility raise a warning flag for the U.S. Although American society enjoys relatively high trust and participation in global markets, there is no guarantee that this will continue indefinitely. Rapid advances in telecommunications could undermine the embeddedness of social relationships needed to make trust and trustworthiness self-reinforcing. (Macy and Sato 2002, p.7220)A lot is at stake: namely, modern western social life. And it is an agent-based computational model that bears the burden of proof for the threatening cultural diagnosis.
The Japanese
… tend to believe that trustworthy behavior occurs only when it is prudent, as when transactions are embedded in tight social networks where malfeasance is discouraged by the need to maintain a good reputation in a set of dense social interactions (Macy and Sato 2002, p.7214[4]).The Americans
… are more likely to believe in character that produces trustworthy behavior even when someone could cheat with impunity. Trustworthy individuals learn to send and receive reliable signals that allow them to avoid miscreants. Thus, Americans focus not on social or physical proximity but on a Calvinist concern for telltale signs of character. Strangers can be trusted if they display appropriate emotional, cultural, and social cues that cannot be easily faked. This strategy allows them to participate in unembedded exchanges in the open market in relative safety (Macy and Sato 2002, p.7214[4]).
We hypothesize that embedded relations are not just a provincial alternative to participation in the open market but are the classroom where the skills are developed for navigating outside the neighborhood. (Macy and Sato 2002, p.7214[5])Obviously the Macy-Sato-model is meant to answer a fundamental question about societal life: Why, when and how is it possible to build trust with distant people? By contrast, it is not that difficult to understand why cooperation normally works in small family or tribal groups. But trusting of strangers? A riddle!
| Figure 1: Payoff matrix of the Macy and Sato's trust game | |||||||
| player 2 | |||||||
| cooperates | defects | exits | |||||
| player 1 | cooperates | 0.7 - O | 0.7 - O | -0.5 | 1.0 - O | ||
| defects | 1.0 - O | -0.5 | -0.2 | -0.2 | |||
| exits | -0.2 | -0.2 | |||||
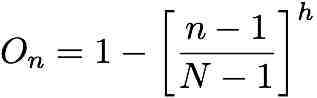
|
(1) |
There is not much to say about the implementation of transaction costs right now. What seems to be unambiguous is that transaction costs are not implemented as easy as opportunity costs. They "depend on the level of trustworthiness, which is endogenous to the model" (Macy and Sato 2002, p.7215[9]). This topic is discussed in detail in section 3.2.4.
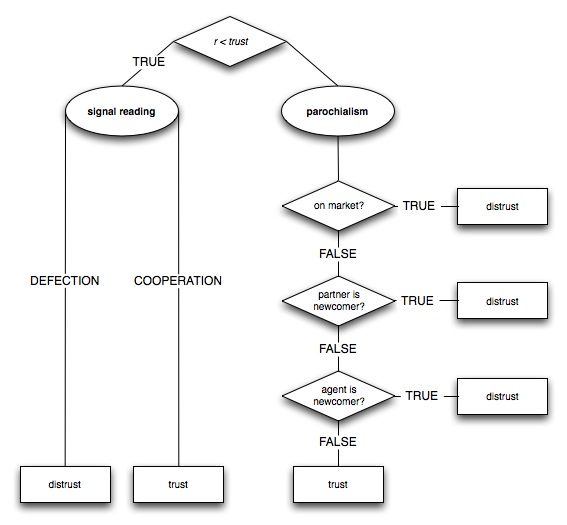
|
| Figure 2. How agents are assumed to decide on trusting |
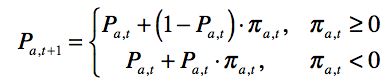
|
(2) |
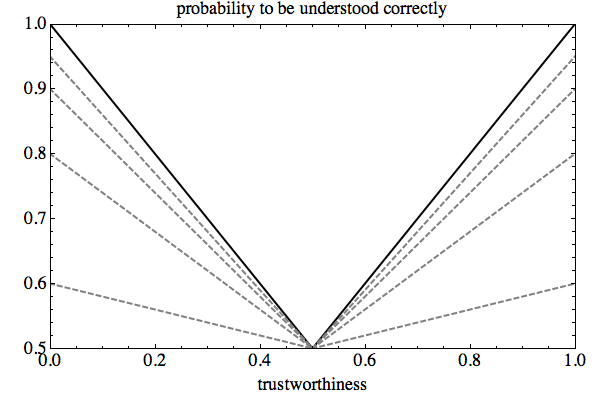
Trustworthy agents have an interest in signaling in a way that is difficult for cheaters to mimic, but we assume that these are imperfect. The reliability of the signal depends on the agents level of trustworthiness. The stronger the agents commitment to honest (or dishonest) behavior, the less likely their signal will be misleading. Signals from ambivalent agents are highly unreliable (no better than a coin toss) (Macy and Sato 2002, p.7216[3]).As trustworthy agents are described to be "imperfect" in "signaling in a way that is difficult for cheaters to mimic", one could conclude that agents that intend to defect are in some way able to mimic cooperative agents. But is this true? If we take a look at the passage that describes the actions committed by all agents in each iteration, we learn that they "decide whether to cooperate" and "give the appropriate signal" (Macy and Sato 2002, p.7217[1]). It is not clear, what "appropriate" means in this context. A signal of defection may be 'appropriate' for an agent that intends to defect in the sense that it is the correct signal. On the other hand, from the agent's point of view a signal of cooperation is perfectly 'appropriate' for it to maximize her payoff if she intends to defect. Though the passage on signalling is ambiguous, we are fairly sure that agents are not able to mimic signals. The hint is in the conclusion, where Macy and Sato discuss opportunities of further research and mention the possibility to "allow agents to learn how to fake signals of trustworthiness" (Macy and Sato 2002, p.7220[3]). This sentence would not make sense if agents in this study were able to mimic certain signals. We therefore assume that agents always send a correct signal.
|
| Figure 3. Imperfect signalling |
|
|
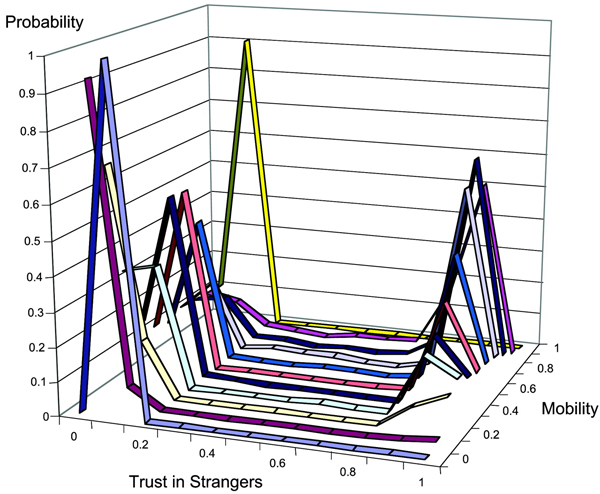
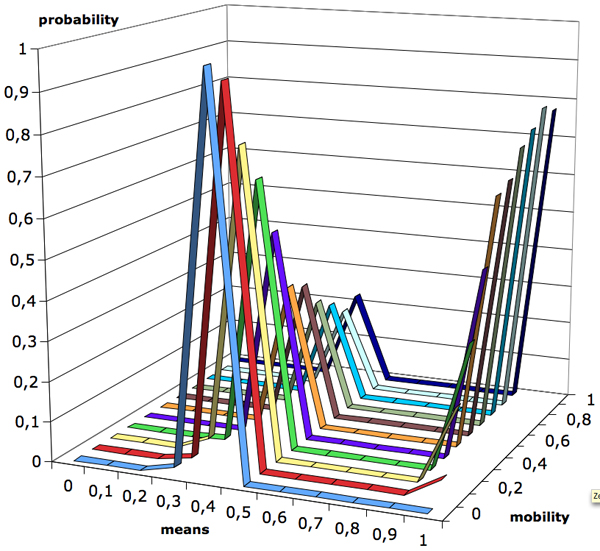
| Figure 4. Distribution of trust in strangers by mobility rate in the original (top) and the replicated model (bottom), with N = 1,000, n = {10..100}, X = P, h = 1) |
|
|
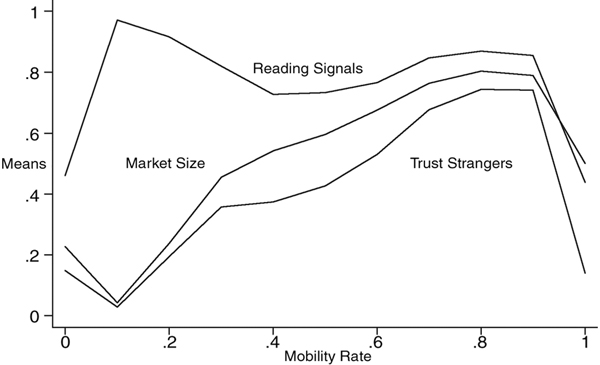
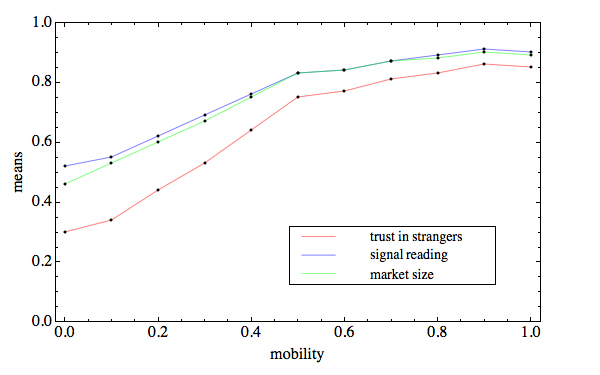
| Figure 5. Expected value of three indicators of market interaction in original (top) and replicated model (bottom), based on 200 observations at each level of mobility, with N = 1,000, n = {10..100}, X = P, h =1 |
|
|
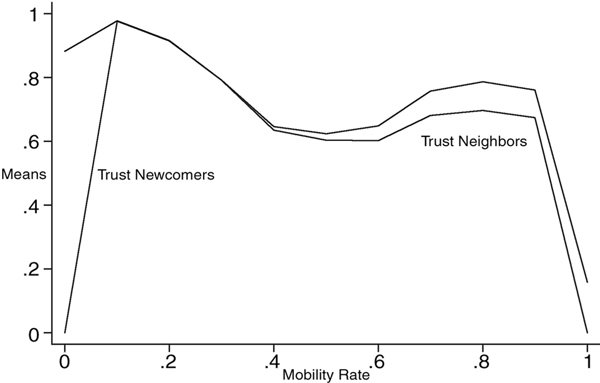
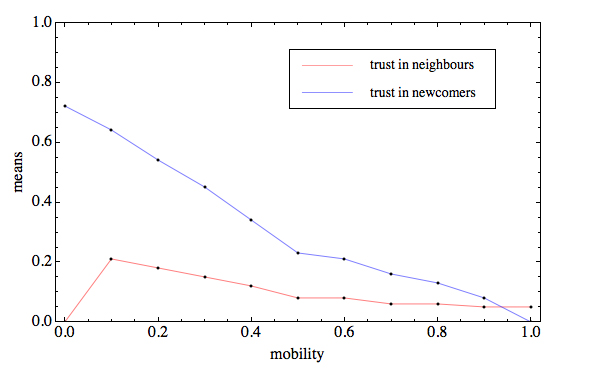
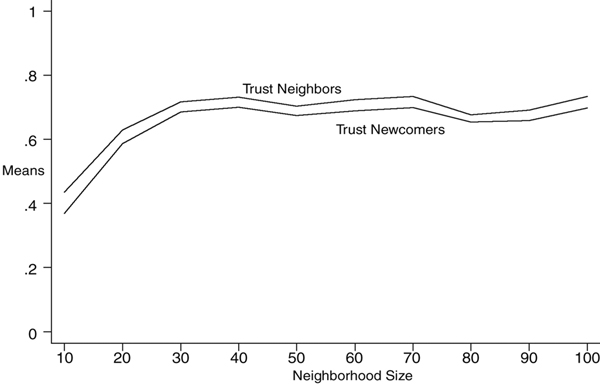
| Figure 6. Expected value of three indicators of local interaction in original (top) and replicated model (bottom), based on 200 observations at each level of mobility, with N = 1,000, n = {10..100}, X = P, h = 1 |
|
|
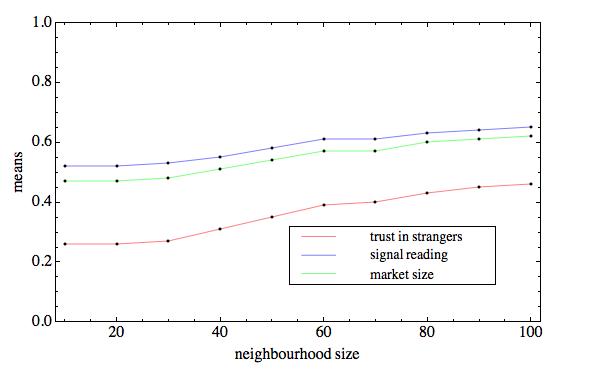
| Figure 7. Expected value of three indicators of market interaction in original (top) and replicated model (bottom), based on 220 observations at each level of mobility, with N = 1,000, n = {10..100}, X = P, h = 1 |
|
|
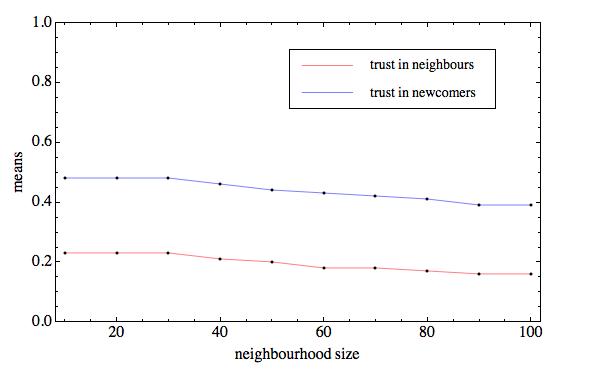
| Figure 8. Expected value of three indicators of market interaction in original (top) and replicated model (bottom), based on 200 observations at each level of mobility, with N = 1,000, n = {10..100}, X = P, h = 1 |
|
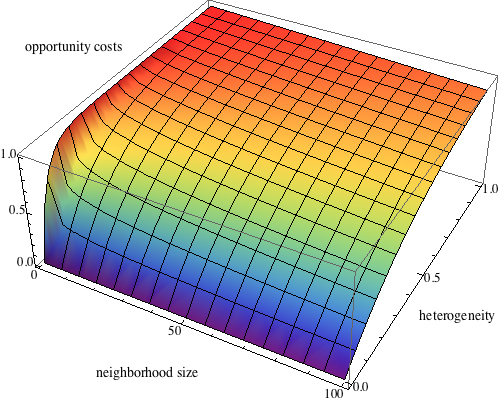
|
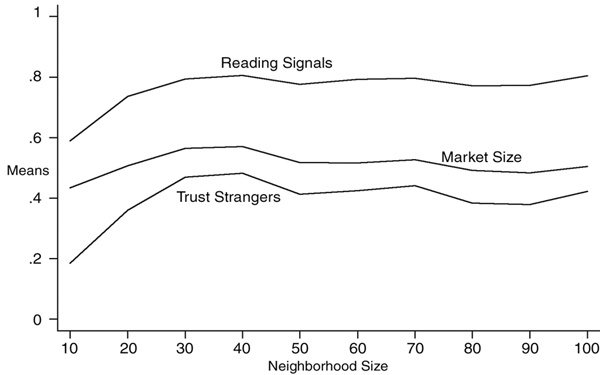
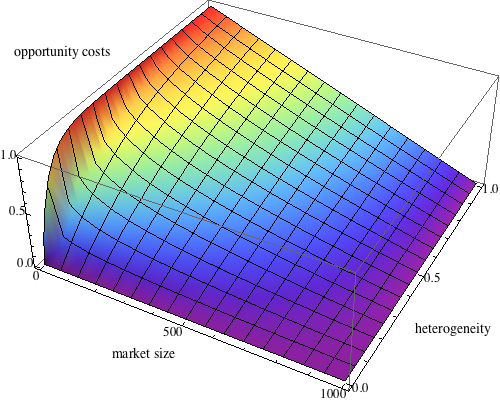
| Figure 9. Opportunity costs in dependency on neighbourhood (top) and market size (bottom) |
2 For Hume's contemporary and friend Adam Smith the empirical findings that motivated the Macy-Sato-model would probably not have come as a big surprise. Already in 1763 he stated important differences between the Dutch, the English and the Scots in his lecture The Influence of Commerce on Manners (Smith 1964). According to Smith's observations, the Dutch are the most faithful. “The English are more so than the Scotch, but much inferior to the Dutch.” The important point here is the explanation he gives. He explicitly rejects to impute the observed effects to different national characters. Instead he stresses that the Dutch are the “most commercial”, involved in lots of market exchanges — and under such circumstances learn that cheating does not pay off.
3 It might be better to speak of “partition” because the “neighbourhoods” do not have a location themselves, i.e. we cannot say that a neighbourhood one is next to another neighbourhood. We keep Macy and Sato's jargon but this should be kept in mind.
4 The effect of undiscounted payoffs of the first 1000 steps on the last 1000 steps would be avoided by a discount factor of 0.999
AXTELL R L, Axelrod R M, Epstein J M and Cohen M D (1996) Aligning Simulation Models: A Case Study and Results. Computational and Mathematical Organization Theory, 1 (2), pp. 123-141
CASSON M (1991) The economics of business culture : game theory, transaction costs, and economic performance. Oxford: Clarendon Press.
DORE R P (1987) Taking Japan seriously : a Confucian perspective on leading economic issues. Stanford, CA: Stanford University Press.
HAGEN JM and Choe S (1998) Institutional sanctions matter trust in japanese interfirm relations. Academy of Management Review, 23(3), pp. 589-600. 1998.
HUME D (1975a) A Treatise of Human Nature. Oxford: Clarendon Press.
HUME D (1975b) Enquiry concerning the Principles of Morals. Oxford: Clarendon Press.
MACY M and Sato Y (2002) Trust, cooperation and market formation in the US and Japan. Proceedings of the National Academy of Sciences, 99, pp. 7214-7220.
OUCHI W G (1981) Theory Z : how American business can meet the Japanese challenge. Reading, MA: Addison-Wesley Publishing Company, Inc..
PLATO (1961) "Protagoras". In Hamilton E and Huntington C (Eds.) The collected Dialogues of Plato. Princeton: Princeton University Press
SINGER P (1981) The Expanding Circle: Ethics and Sociobiology. New York: Farrar, Straus and Giroux.
SMITH A (1964) Lectures on Justice, Police, Revenue, and Arms. New York: August M. Kelley Publishers
YAMAGISHI T (1988) The provision of a sanctioning system in the united states and japan. Social Psychology Quarterly, 51, pp. 265-271.
YAMAGISHI T and Yamagishi M . (1994) Trust and commitment in the United States and Japan. Motivation and Emotion, 18, pp. 129-166.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]