Thomas Grebel and Esther Merey (2009)
Industrial Dynamics and Financial Markets
Journal of Artificial Societies and Social Simulation
vol. 12, no. 1 12
<https://www.jasss.org/12/1/12.html>
For information about citing this article, click here
Received: 16-Jun-2008 Accepted: 19-Aug-2008 Published: 31-Jan-2009
 Abstract
Abstract
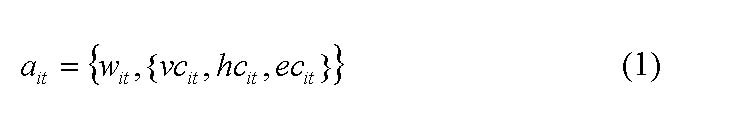
|
The additional component wit of an actor ait is dichotomous and takes values 1 or 0, saying whether the individual either has absorbed the new knowledge or not[2]. In case the actor understands the diffusing knowledge about a new technology, he is activated to possibly found a firm[3]. The diffusion of knowledge is a time-consuming process which has a crucial influence on the endogenous evolution of an industry: the faster the diffusion of knowledge, that is, the better actors understand a new technology, the higher expectations may be in terms of economic prospects; the foundation of the first firms at an early stage may induce a bandwagon effect triggering a surge of follow-up foundations. With a slow rate of knowledge diffusion, firms will be formed gradually step by step without the possibility of bandwagon effects occurring, since too few actors understand how to apply a new technology, a swarm of firm foundations will not occur: the percolation threshold of knowledge diffusion will not be reached and thus the shakeout phase will be less prominent over time. The diffusion of new technological knowledge is induced by the interaction of individuals, so that knowledge is eventually transmitted through society. The rate of diffusion is thereby determined by the actors' absorptive capacities.
|
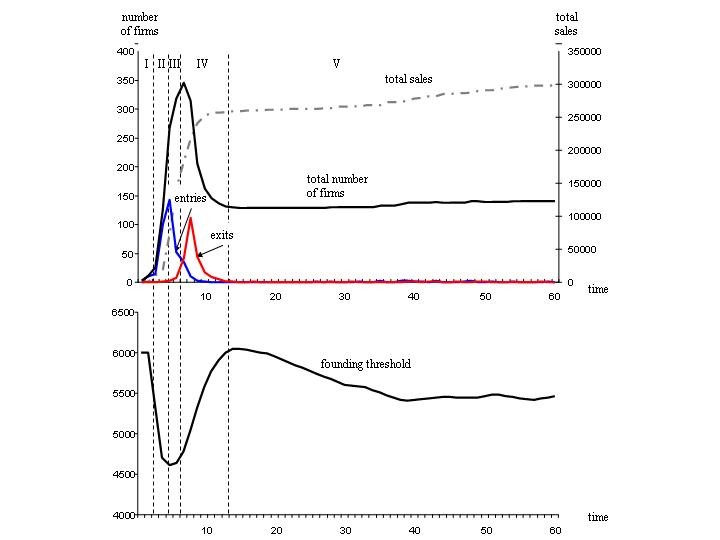
| Figure 1. Simulation results of the endogenous evolution of an industry with a high rate of knowledge diffusion |
|
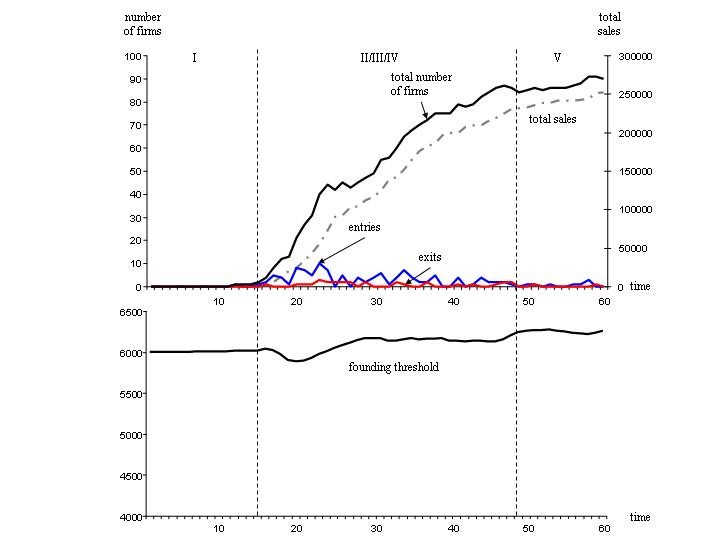
| Figure 2. Simulation results of the endogenous evolution of an industry with a low rate of knowledge diffusion. |
|
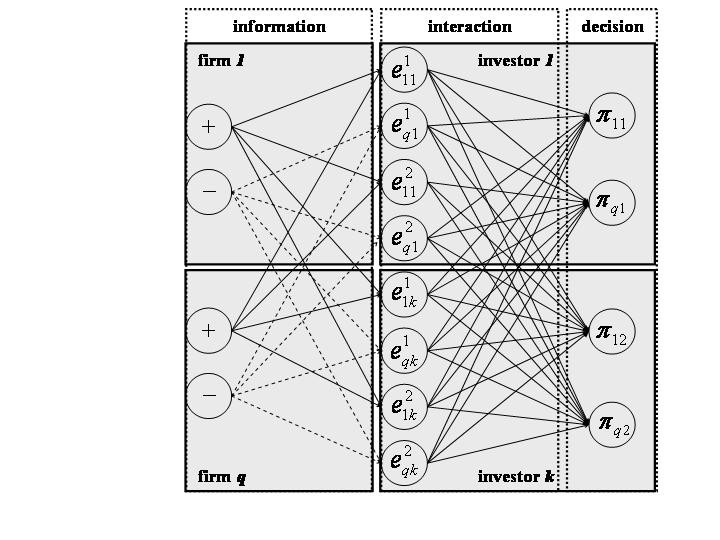
| Figure 3. Investors as a Multilayer Perceptron |
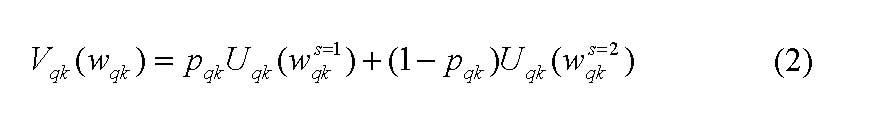
|
The maximization problem concerning share q takes the following form:
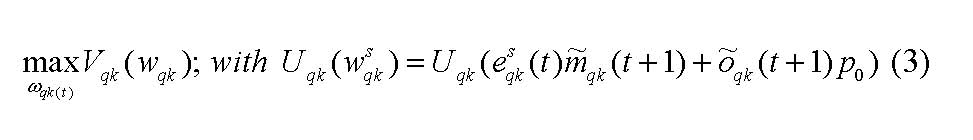
|
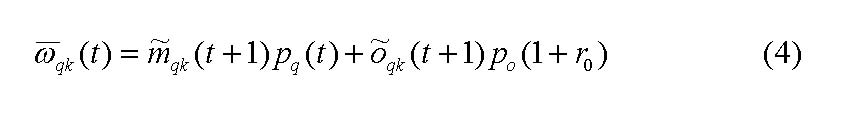
|
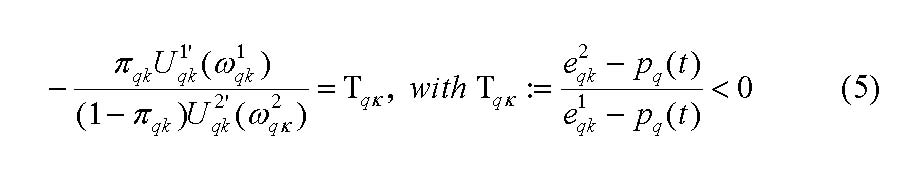
|
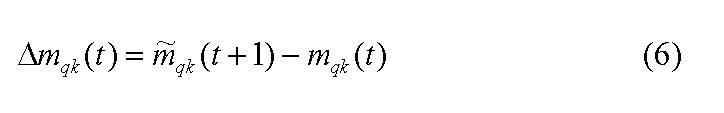
|
which derives from the difference in the stock of shares the investor wants to hold in two subsequent periods. The desired stock of shares the investor intends to hold at time t + 1 is calculated in the following:
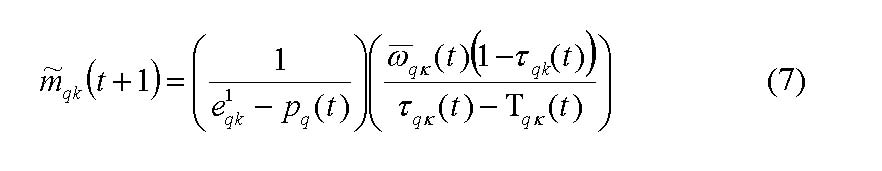
|
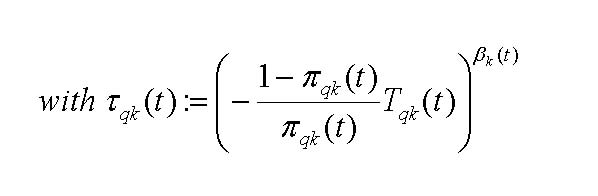
|
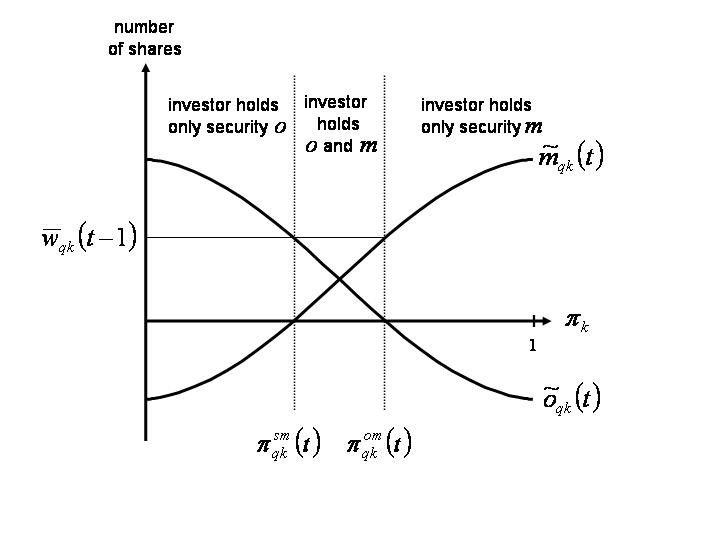
|
| Figure 4. Demand for shares and secure bonds dependent on πk |
Figure 4 graphs the resulting demand (supply) of investor k for share q, mqk(t), and the demand (supply) for the secure bond o, oqk(t)[17] subject to πk. If πk increases, since the subjective evaluation of the investor is gradually reinforced by other investors, he will want to redeploy its wealth from holding only secure bonds oqk, to holding both shares and bonds, to holding only shares mqk .
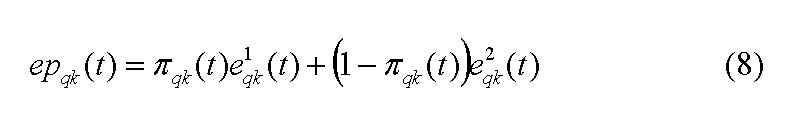
|
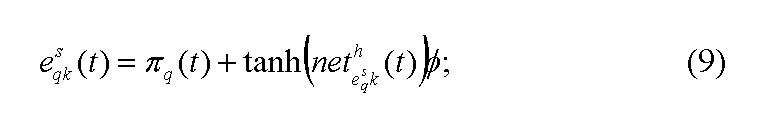
|
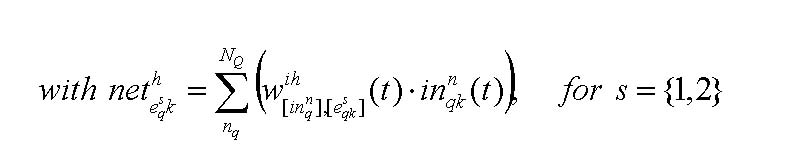
|
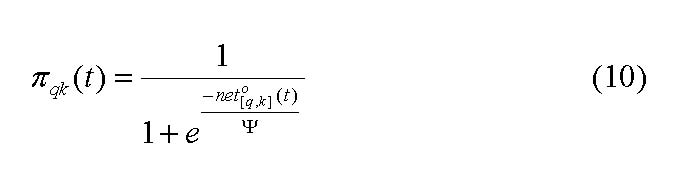
|
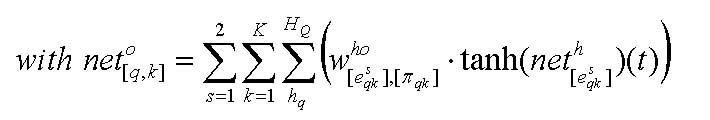
|
Parameter ψ indicates the sensitivity investors react to the market sentiment represented by the remaining investors' opinion to the investment opportunities.
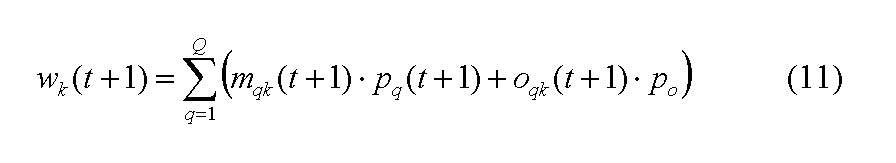
|
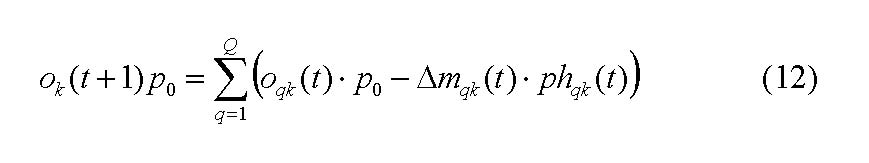
|
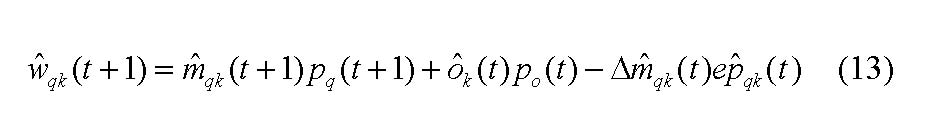
|
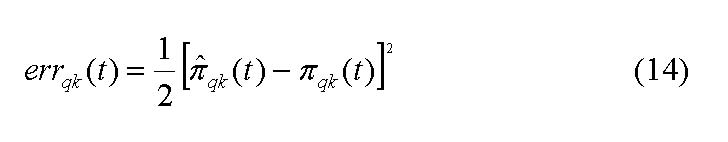
|
The adjustment of the weights between the hidden and the output layer, that is, the extent investors take account of other investors opinion looks as in the following[20]:
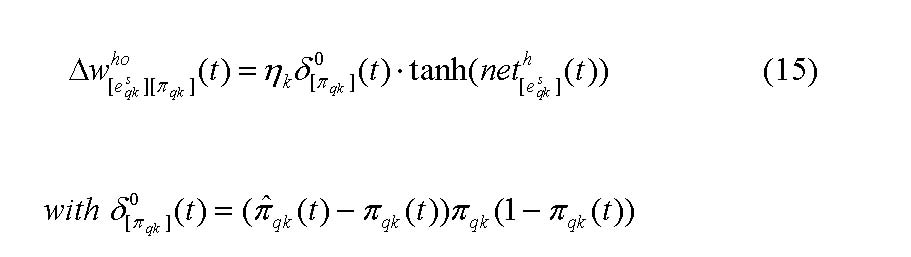
|
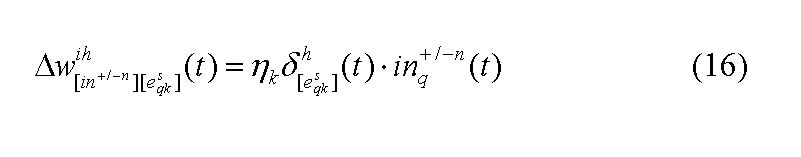
|
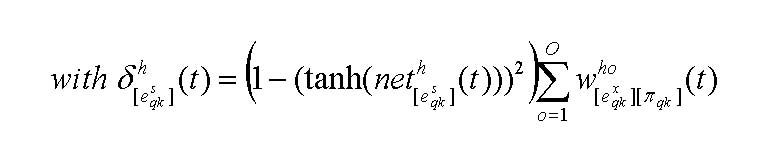
|
|
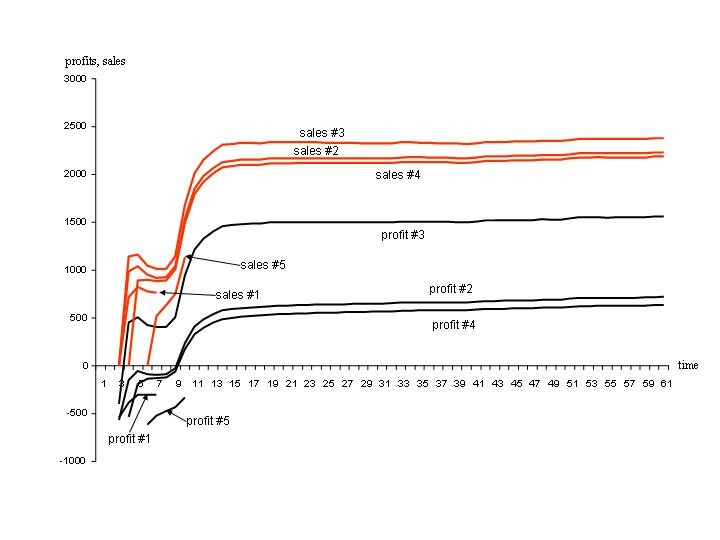
| Figure 5. Stylized profits and sales of four selected firms |
|
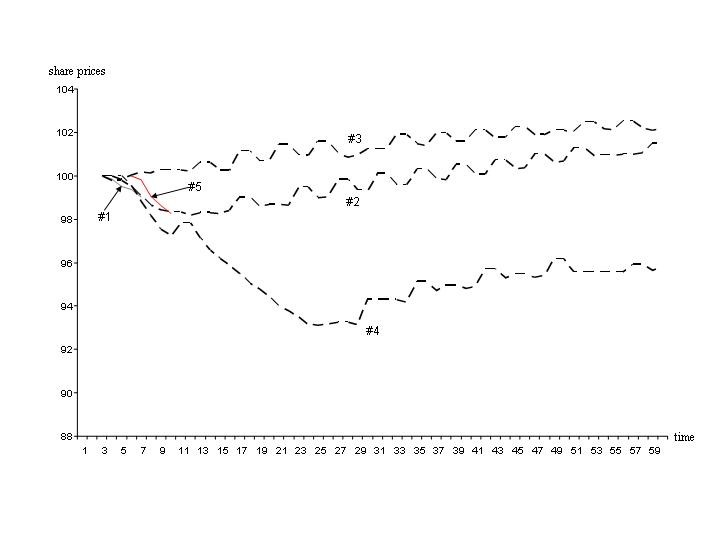
| Figure 6. Corresponding share prices of the four firms selected |
|
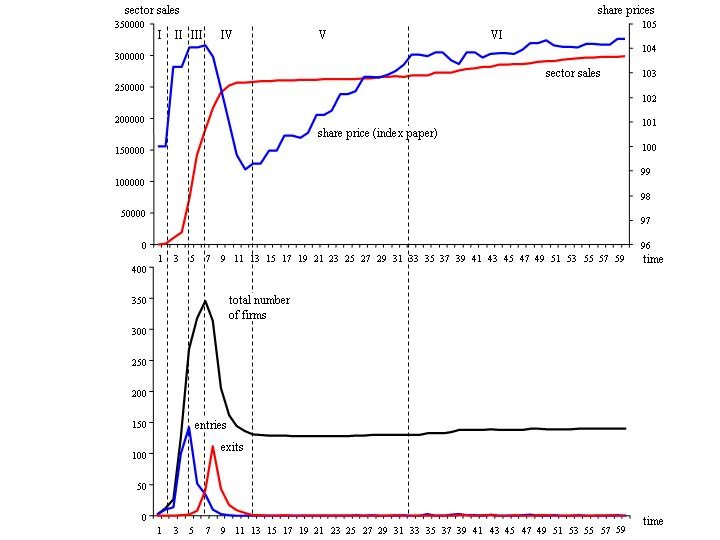
| Figure 7. Capital market and industry life cycle of a fictitious economic sector (high rate of knowledge diffusion) |
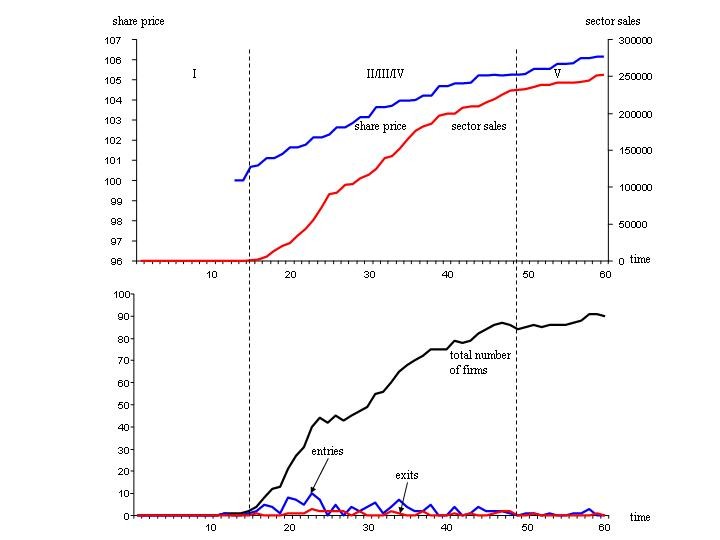
|
| Figure 8. Capital market and industry life cycle of a fictitious economic sector (low rate of knowledge diffusion) |
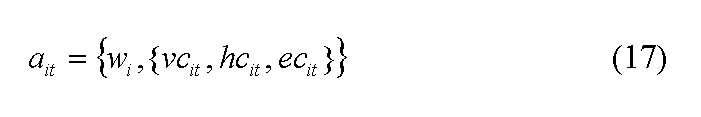
|
where ati := actor i at time t, i∈{1,…,n}. Since entrepreneurial behaviour is about innovative behaviour, actors first have to get to know a new technology in order to be able to innovate on it. The diffusion of new knowledge is a time-consuming process, whereby the rate of knowledge diffusion also has an influence on entrepreneurial behaviour seen from a macro perspective. To model this, wit is introduced which indicates an actor's stock of new knowledge. In case the actor has absorbed the new knowledge, wit =1, if not, wit remains 0. The diffusion process itself is modelled using a von-Neumann cellular automaton[24].

|
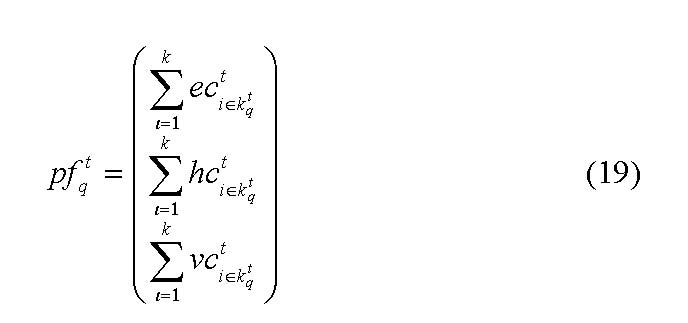
|
so that the set of potential firms at time t is
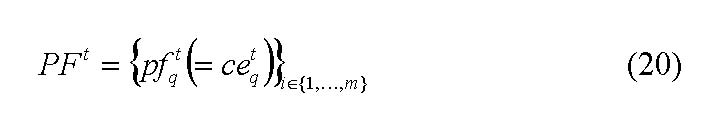
|
where q∈{1,…,m} denotes the specific potential firm and m the number of potential firms, i.e. the number of temporarily formed k -groups q in period t. Each group of actors has to evaluate if their comprehensive endowment ![]() , which for simplicity is equal to
, which for simplicity is equal to ![]() , is adequate. Yet, the actors' mere perception of their common resources, attitudes and motivation is not the only determinant for founding a firm. The actors involved are also influenced by their environment and the respective mood within the population. For modeling reasons, the so-called founding or entry threshold ψt is introduced, a "meso-macroeconomic signal" which endogenously depends negatively on the growth rate of the sector's sales wt. The growth rate of the sector's sales decreases the threshold in return. Furthermore, the threshold depends negatively on the return on sales rut and positively on the rate of exits dt and positively on time t:
, is adequate. Yet, the actors' mere perception of their common resources, attitudes and motivation is not the only determinant for founding a firm. The actors involved are also influenced by their environment and the respective mood within the population. For modeling reasons, the so-called founding or entry threshold ψt is introduced, a "meso-macroeconomic signal" which endogenously depends negatively on the growth rate of the sector's sales wt. The growth rate of the sector's sales decreases the threshold in return. Furthermore, the threshold depends negatively on the return on sales rut and positively on the rate of exits dt and positively on time t:
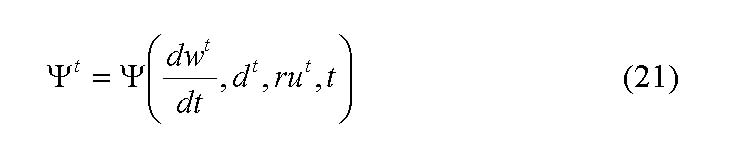
|
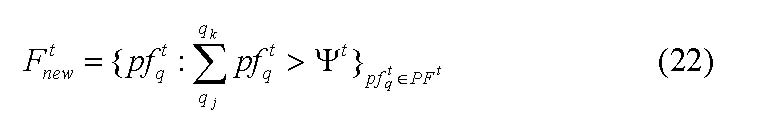
|
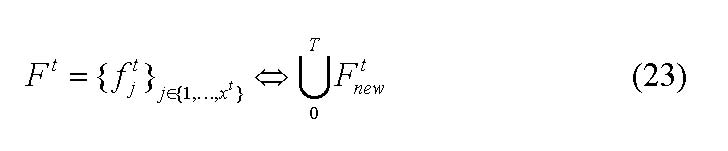
|
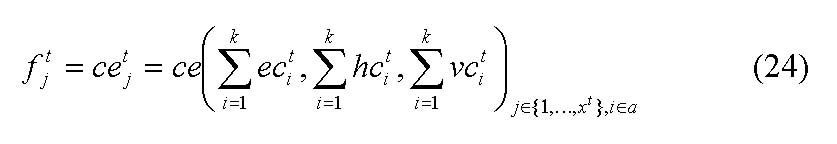
|

|
x t := number of firms in the industry at time t.
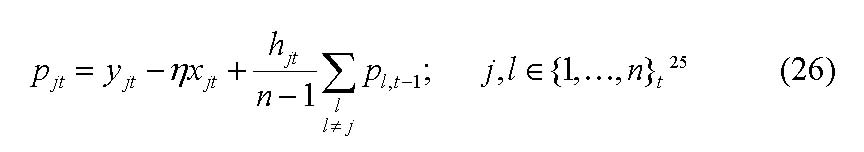
|
2Differences in absorptive capacities among actors can easily be taken into account as shown in Grebel (2004).
3As an example one may think of someone who becomes acquainted with new information and communication technologies (ICT) and thinks of forming an e-commerce business.
4As an empirical fact, there is more than just one individual involved in a firm-founding process.
5See Grebel (2004) and Grebel, Pyka and Hanusch (2003) for more details.
6The founding threshold is a concept developed on the grounds of social psychology and mental models. See Grebel (2004) for more details.
7For simplicity reasons, each firm that emerges in the real economy is assumed to be listed at the stock exchange from the very beginning of its existence.
9Neural networks provide an ideal modeling framework for complex economic systems, which are able to handle high-dimensional problems along with a high degree of nonlinearity . Besides the learning from data, neural networks allow for the integration of the decision behavior of individual economic agents into a market model. The decision-making scheme of an agent is thereby modeled by a single neuron. That process consists of three stages: information filtering, market evaluation and acting based on the rated information (Haykin 1999).
10As long as we consider a single share such as Sommer (1997) and let the investor decide whether to invest in a risk-bearing share or in a secure bond, there exists a unique solution of the investor's optimization problem. This is what the state-preference approach by Arrow states. If we increase the number of shares, although we might still have a pure bond, as Arrow calls it, there exists in general no unique optimal portfolio. Using budgets for each investment decision, we circumvent this problem which has definitely to be tackled in future research.
11Introducing a positive interest rate changes investment behavior. This can easily be implemented into the model, but to keep it simple, the interest rate shall be i=0.
12We assume risk-averse investors with
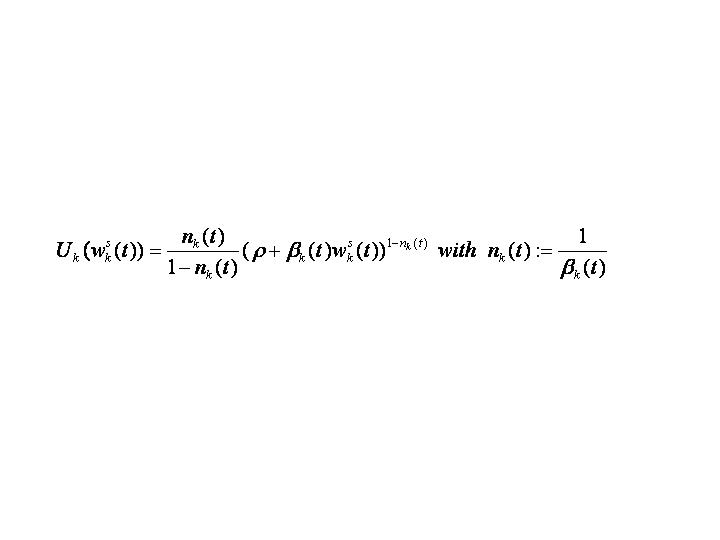
|
This is a standard assumption as discussed in Sommer (1999).
13The tilde over any parameter stands for the expected value.
14Since the existence of a unique optimal portfolio is at random, we need to presume a routinized behavior of investors. Therefore, we assume that investors partition their portfolio among all existing shares, so that for each share he has a fixed budget x which he decides how much of it should be invested into the share considered.
15The price of the secure bond functions as a numeraire. The prices for shares are determined using a double auction system as used in practice. Compare e.g. Garman (1976).
16Second-order conditions are fulfilled, since we deal with a convex optimization problem.
17As already stated, we assume that investors divide their budget into partial budgets per investment decision q. In each single investment decision the investor decides how much of the partial budget will be invested into investment mqk(t) and consequently, how much of the partial budget will be invested in secure bonds oqk(t)
18See Garman (1976, p. 267) for further details.
19Compare e.g. Rummelhart and McClelland (1987).
21The simulation runs with all firms generated by the real economy module would last for decades with the computational capacity available to us.
22Further details on the industry life cycle theory is neglected, since we intent to show how to connect a real economic model with a capital market model.
23The information investors have are categorized into positive and negative information. Exemplarily, we chose the growth rate of sales and profits as positive information whereas losses and exits are considered negative information. These data we picked as an example in order to show the functioning of the model. At the same time, this cancels out excessive speculative aspects, which would cause the share price to fluctuate even more. This aspect we leave for future research.
24For brevity this aspect is not outlaid any further here. For a detailed description of the knowledge diffusion process and how it is implemented into this model see Grebel (2004) or email the author.
25pjt := product price of firm j at time t; yjt :=price limit of firm j at time t; ∑ :=price elasticity of demand; xjt :=output of firm j at time t; hjt := oligopolistic interdependence of firm j at time t; nt :=number of firms at time t.
ABERNATHY W and Townsend P (1985) Technology, productivity and process change. Technological Forecasting and Social Change 8(4), pp. 379-396.
ANG A, M Piazzesi, and MWei. (2006) What does the yield curve tell us about GDP growth? Journal of Econometrics 131(1-2) pp. 359-403
ARROW K (1964) The role of securities in the optimal allocation of risk bearing. Review of Economic Studies, 31, pp. 91-96.
BECKENBACH F. Briegel R and Daskalakis M (2007) Behavioural foundation and agent-based simulation of regional innovation, Papers on agent-based economics. University of Kassel, No3.
CAMPBELL J and Shiller R (1988) The dividend-price ratio and expectations of future dividends and discount factors. Review of Financial Studies 14, pp. 195-228.
COCHRANE J H (1991) Production-based asset pricing and the link between stock returns and economic fluctuations. Journal of Finance 46(1), pp. 209-237.
COCHRANE J H (2005) Financial markets and the real economy, Working Paper NBER (11193).
DAY R H and Chen P (1993) Nonlinear Dynamics and Evolutionary Economics. Oxford University Press, Oxford.
FAMA E F and French K R (1989) Business conditions and expected returns on stocks and bonds. Journal of Financial Economics, 25, pp. 23-49.
GARMAN M B (1976) Market microstructure. Journal of Financial Economics, 3, pp. 257-275.
GILBERT N (2006) When does Social Simulation Need Cognitive Models? In: Cognition and Multi-Agent Interaction. Sun, R. (Ed.), Cambridge University Press.
GORT M and Klepper S (1982) Time paths in the diffusion of product innovations. Economic Journal. 92, pp. 630-653.
GREBEL T and Pyka A (2006) Agent-Based Modelling - A Methodology for the Analysis of Qualitative Development Processes, in: Francesco C. Billari, Thomas Fent, Alexia Prskawetz, Jürgen Scheffran (Eds.), Agent-Based Computational Modelling - Applications in Demography, Social, Economic and Environmental Sciences. Physica-Verlag, Heidelberg, 17-36.
GREBEL T Krafft J and Saviotti P-P (2006) On the life cycle of knowledge intensive sectors, Revue de l'OFCE, No. 97 , pp. 63-85.
GREBEL T (2004) Entrepreneurship - A New Perspective, Routledge.
GREBEL T Hanusch H and Merey E (2004) Schumpeterian dynamics and financial market anomalies. University of Augsburg working paper. Nº 264.
GREBEL T Pyka A and Hanusch H (2003) An evolutionary approach to the theory of entrepreneurship. Industry and Innovation, 20(4), pp. 493-514.
HAYKIN S (1999) Neural Networks: A Comprehensive Foundation, Prentice Hall.
JOVANOVIC B (1982) Selection and the evolution of industry, Econometrica, 50(3), pp. 649-670.
JOVANOVIC B and MacDonald G (1994) The life-cycle of a competitive industry. Journal of Political Economy, 102(2), pp. 322-347.
KIRZNER I (1999) Creativity and/or Alertness: A Reconsideration of the Schumpeterian Entrepreneur. Review of Austrian Economics, 11, pp. 5-17.
KLEPPER S and Graddy E (1990) The evolution of new industries and the determinants of market structure. RAND Journal of Economics, 21(1), pp. 27-44.
LETTAU M and Ludvigson S (2001) Consumption, aggregate wealth, and expected stock returns. Journal of Finance, 56, pp. 815-849.
MAZZUCATO M and Semmler W (1999) Market share instability and stock price volatility during the industry life-cycle: the US automobile industry. Journal of Evolutionary Economics, 9(1), pp. 67-96.
MEYER B Vogt C and Voβkamp R (1996) Schumpeterian competition in heterogeneous oligopolies, Journal of Evolutionary Economics, 6, pp. 411-423.
PASTOR L and Veronesi P (2005) Rational IPO waves. Journal of Finance, 60(4), pp. 1713-1757.
PAJARES J López A and Hernández C (2003) Industry as an Organization of Agents: Innovation and R&D Management. Journal of Artificial Societies and Social Simulation, 6(2)7 https://www.jasss.org/6/2/7.html.
PORTER M E (1980) Competitive Strategy: Techniques for Analyzing Industries and Competitors, Free Press, New York.
POSADA M Hernández C and López-Paredes A (2006) Strategic Behaviour in Continuous Double Auction. In: Advances in Artificial Economics. The Economy as a Complex Dynamic System. Bruun C. (Ed.), Springer Verlag, Lecture notes in Economics and Mathematical Systems. Nº 584.
PYKA A (1999) Der kollektive Innovationsprozeß. Eine theoretische Analyse informeller Netzwerke und absorptiver Fähigkeiten, Special Issue, Duncker & Humblot, Berlin.
RUMMELHART D E and McClelland J L (1987) Parallel Distributed Processing, MIT Press, Cambridge, MA.
SHILLER R (1989) Market Volatility, MIT Press, Cambridge, MA.
SMITH V L (1989) Theory, Experiment and Economics. The Journal of Economic Perspectives, 3(1), pp. 151-169.
SOMMER J (1997) An artificial stock market: Asset pricing and endogenous expectations using neural networks, Volkswirtschaftliche Diskussionsreihe (168).
SOMMER J (1999) Künstliche neuronale Netze zur Beschreibung des Anlegerverhaltens auf spekulativen Märkten: Eine theoretisch-experimentelle Analyse, Tenea, Berlin.
UTTERBACK J M and Abernathy W J (1975) A dynamic model of product and process innovation, Omega, 3(6), pp. 639-56.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2009]