| Number of possible states: | 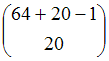 |
In 1986 Axelrod (1986) wrote a pioneering and influential paper about the emergence and collapse of norms to cooperate in social dilemmas. In his original model Axelrod considers a game with 20 players. Each player has two variables (boldness and vengefulness) that determine its strategic behaviour. The possible values for each of these two variables are the integers between 0 and 7, codified as 3-bit strings. Thus, there are 64 possible strategies that a player may have.
Axelrod was interested in exploring the type of strategies that would emerge in an evolutionary context. To do that, he simulated a population of players subjected to evolutionary pressures: the most successful players would tend to have more offspring –with the same strategy as their parent– than those with lower payoffs.
To be precise, at the beginning of every generation the players' payoffs are set to zero; then they all play the game four times and, after computing all the payoffs, two evolutionary forces (natural selection and mutation) come into play to replace the old generation with a brand new one:
The state of this system can be defined as the number of players that are following each specific strategy at any given time. With this definition [1], the number of possible states is:
| Number of possible states: | 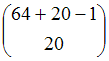 |
And the induced Markov chain satisfies sufficient condition (i) for irreducibility and aperiodicity pointed out in Proposition 4 of our paper:
The demonstration of this statement is simple when one realises that the mutation operator guarantees that it is possible to go from any state to any other state in one single step. Consequently the model is an irreducible and aperiodic THMC, also called ergodic.
As we have seen in the paper, in these processes the probability of finding the system in each of its states in the long run is strictly positive and independent of the initial conditions, and the limiting distribution π coincides with the occupancy distribution π*. Although calculating such probabilities from the transition matrix is rather impractical, we can approximate them as much as we want by running just one simulation for long enough.
It is also important to notice that if the mutation probability were zero, then the system would not be ergodic. There would be several absorbing states (in particular, any state in which every player is following the same strategy would be an absorbing state of the system), and hence the long-run dynamics of the system would not be independent of the initial conditions.
AXELROD R M (1986) An Evolutionary Approach to Norms. American Political Science Review, 80(4), pp. 1095-1111
GALAN J M and Izquierdo L R (2005) Appearances Can Be Deceiving: Lessons Learned Re-Implementing Axelrod's 'Evolutionary Approach to Norms'. Journal of Artificial Societies and Social Simulation, 8(3)2. https://www.jasss.org/8/3/2.html.
1 The definition of the state of the system is never unique. For instance, Galan and Izquierdo (2005) define the state of the system as a certain particularisation of every player's strategy, so the number of possible states is then 6420 (corresponding to the 64 strategies that each of the 20 players may have). In general, which definition is more appropriate depends not only on the model itself but also on the purpose of our analysis. If we are only interested in studying the prevalence of each strategy in the population of players, then the definition provided in this appendix (which implies a lower number of states) is sufficient. With this definition, all the players with the same strategy would be completely equivalent in our analysis. If, on the other hand, some personal trait of each player beyond its strategy is relevant for our analysis, then we could use the definition of the state of the system given by Galan and Izquierdo (2005). This latter definition has the potential drawback that it implies a greater number of states.