Jose Manuel Galan and Luis R. Izquierdo (2005)
Appearances Can Be Deceiving: Lessons Learned Re-Implementing Axelrod's 'Evolutionary Approach to Norms'
Journal of Artificial Societies and Social Simulation
vol. 8, no. 3
<https://www.jasss.org/8/3/2.html>
For information about citing this article, click here
Received: 18-Nov-2004 Accepted: 30-Mar-2005 Published: 30-Jun-2005
 Abstract
Abstract
|
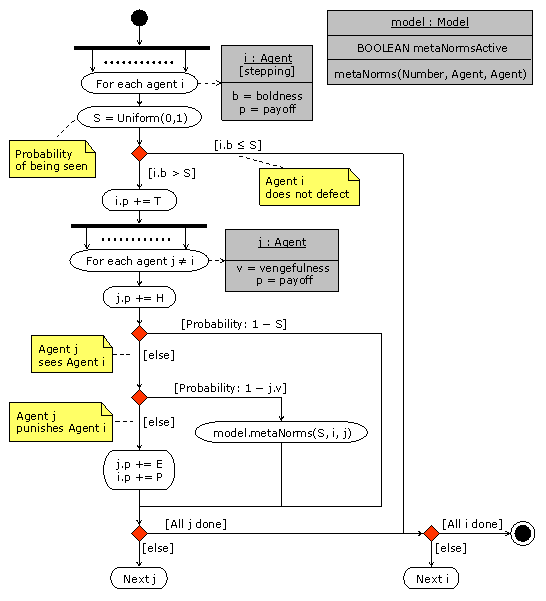
| Figure 1. UML Activity diagram of one round in Axelrod's models[3]. The UML diagram of method metaNorms(Number, Agent, Agent), which does nothing in the Norms model, is provided in figure 2. |
|
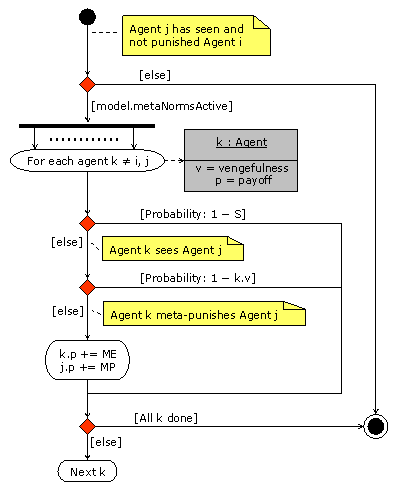
| Figure 2. UML activity diagram of the method metaNorms(Number, Agent, Agent) of the object model. This method is called in the UML activity diagram shown in figure 1. The condition metaNormsActive is false in the Norms model and true in the Metanorms model. |
| Table 1: Summary of Parameter Values Used by Axelrod | |
| PARAMETER | AXELROD'S VALUE |
| Number of Agents | 20 |
| Number of Rounds per Generation | 4 |
| Mutation Rate | MutationRate = 0.01 |
| Temptation payoff | T = 3 |
| Hurt payoff | H = -1 |
| Enforcement payoff | E = -2 |
| Punishment payoff | P = -9 |
| Meta-Enforcement payoff | ME = -2 |
| Meta-Punishment payoff | MP = -9 |
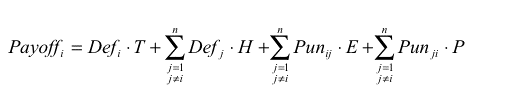
|
(1) |
where
T, H, E, P are the payoffs mentioned in the description of the model,
n is the number of agents, and

|
Thus the expected payoff of agent i in one round is:
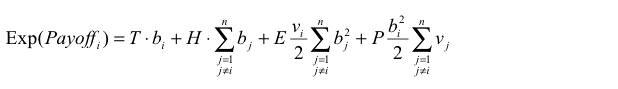
|
(2) |
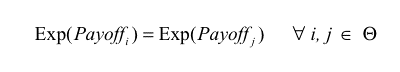
|
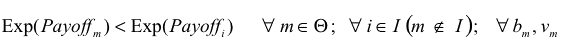
|
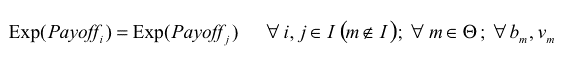
|
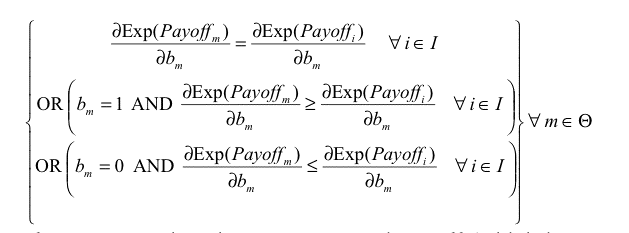
|
(3) |
If every agent has the same expected payoff (which is a necessary condition for ESS) and eq. (3) does not hold for some m, i, the potential mutant m could get a differential advantage over incumbent agent i by changing its Boldness bm , meaning that the state under study would not be evolutionary stable. As an example, if we find some m, i such that
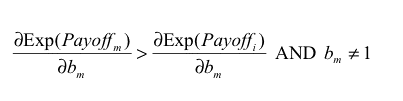 |
then agent m could get a higher payoff than agent i by increasing its boldness bm , and condition b) in the definition of ESS would not apply. Similarly, we obtain another necessary condition substituting vm for bm in eq. (3).
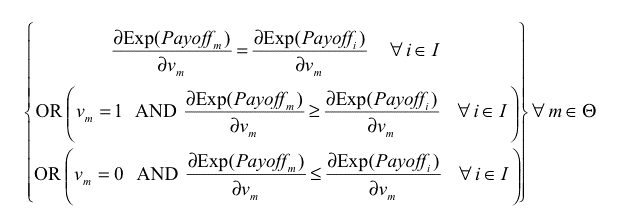
|
(4) |
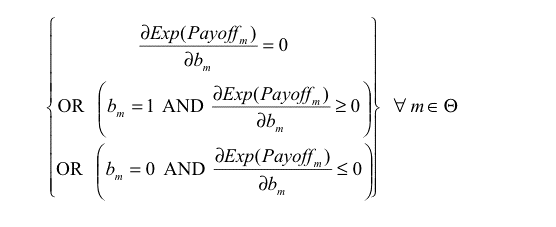
|
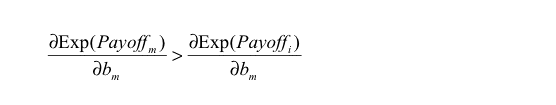
|
and negative otherwise. The vertical component is worked out in a similar way but using eq. (4) instead. Only vertical lines, horizontal lines, and the four main diagonals are considered. If both equations (3) and (4) are true then a red point is drawn.
|
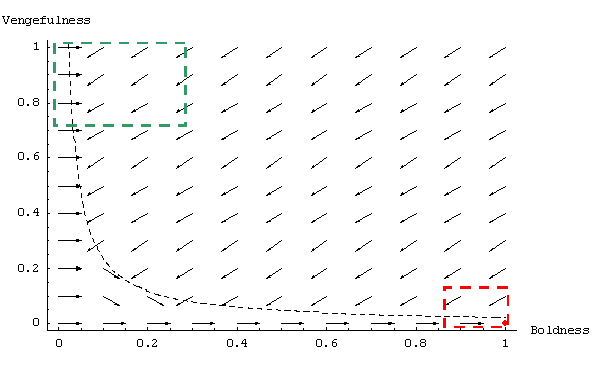
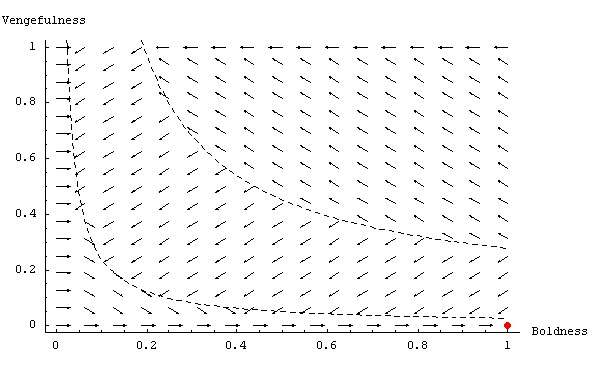
| Figure 3. Graph showing the expected dynamics in the Norms model, using Axelrod's parameter values, and assuming continuity and homogeneity of agents' properties. The procedure used to create this graph is explained in the text. The dashed squares represent the states of norm establishment (green, top-left) and norm collapse (red, bottom-right) as defined in the text below. The red point is the only ESS. The black dashed line is the boundary that separates the region of left-pointing arrows and the region of right-pointing arrows. |
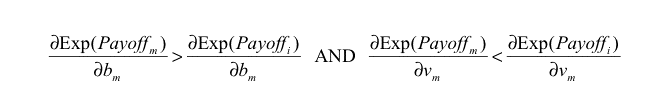
|
We would then draw a diagonal arrow pointing towards greater Boldness and less Vengefulness, since a mutant with greater Boldness and less Vengefulness than the (homogeneous) population could invade it (e.g. B = 0.1, V = 0.1).
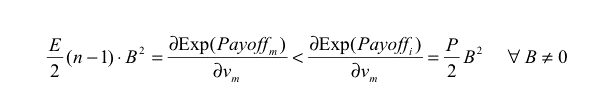
|
(5) |
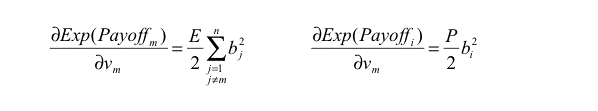
|
(6) |
|
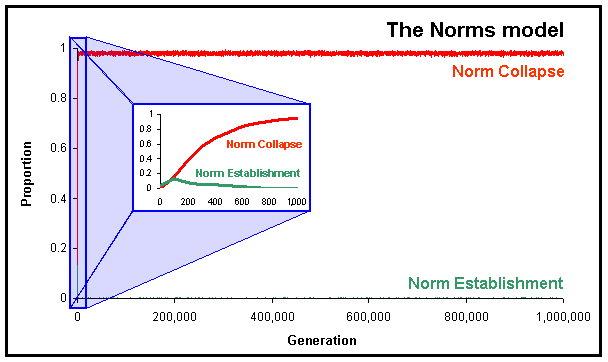
| Figure 4. Proportion of runs where the norm has been established and where the norm has collapsed in the Norms model, calculated over 1,000 runs up to 106 generations using Axelrod's Parameter values. The little figure in the middle of the graph represents the first 1,000 generations zoomed. |
As predicted in the previous analysis, the norm collapses almost always, as Axelrod concluded; only now the argument has been corroborated with more convincing evidence. We can also notice looking at the zoomed graph in figure 4 that it is not surprising that Axelrod found three completely different possible outcomes after having run the simulation 5 times for 100 generations.
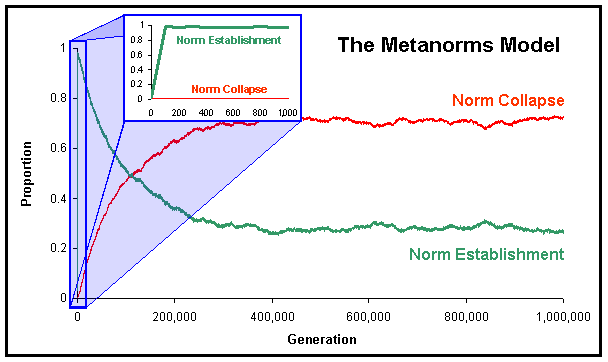
|
| Figure 5. Proportion of runs where the norm has been established and where the norm has collapsed in the Metanorms model, calculated over 1,000 runs up to 106 generations using Axelrod's Parameter values. The little figure in the middle of the graph represents the first 1,000 generations zoomed. |
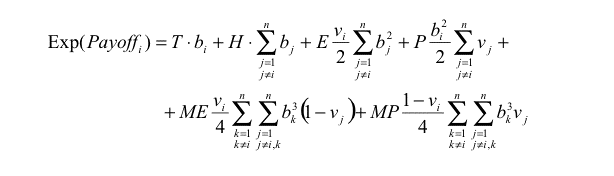
|
(7) |
|
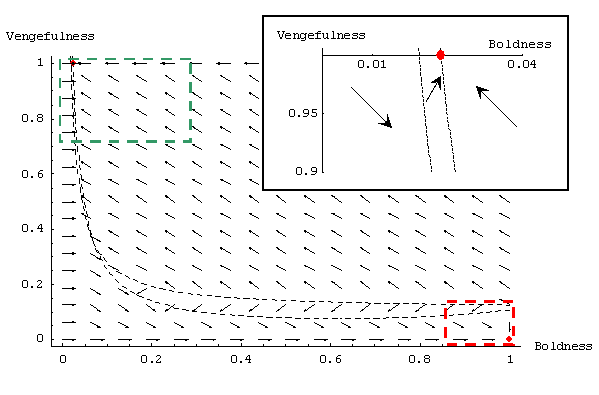
| Figure 6. Graph showing the expected dynamics in the Metanorms model, using Axelrod's parameter values, and assuming continuity and homogeneity of agents' properties. Red points are ESS. The dashed black lines are boundaries between regions where every arrow is pointing in the same direction. This figure has been drawn following the same procedure as in figure 3. |
|
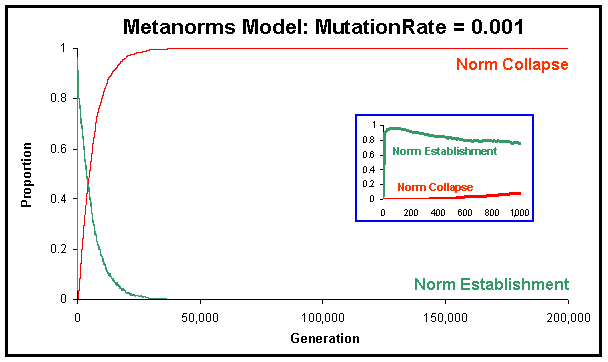
| Figure 7. Proportion of runs where the norm has been established and where the norm has collapsed in the Metanorms model, calculated over 1,000 runs up to 2·105 generations, with MutationRate equal to 0.001 and the rest of the parameter values equal to Axelrod's. |
|
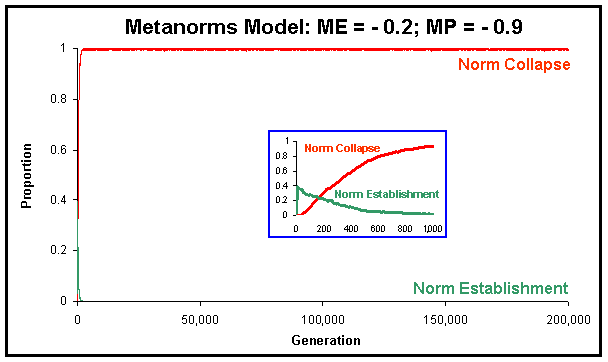
| Figure 8. Graph showing the expected dynamics in the Metanorms model, with ME = -0.2; MP = -0.9 (the rest of parameter values equal to Axelrod's), and assuming continuity and homogeneity of agents' properties. The dashed black lines are boundaries between regions where every arrow is pointing in the same direction. |
|
| Figure 9. Proportion of runs where the norm has been established and where the norm has collapsed in the Metanorms model, calculated over 1,000 runs up to 2 ·105 generations, with ME = -0.2, and MP = -0.9 (the rest of parameter values equal to Axelrod's). |
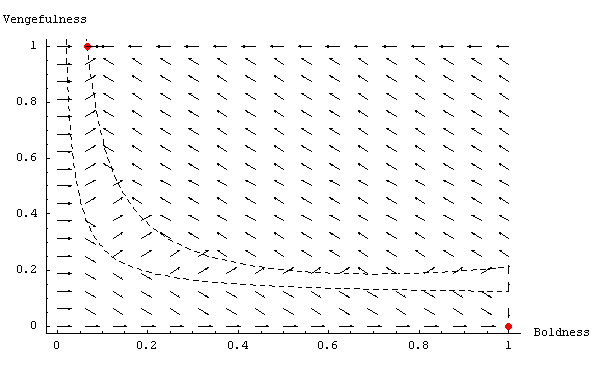
|
| Figure 10. Graph showing the expected dynamics in the Metanorms model, with T = 10 (the rest of parameter values equal to Axelrod's) and assuming continuity and homogeneity of agents' properties. The dashed black lines are boundaries between regions where every arrow is pointing in the same direction. |
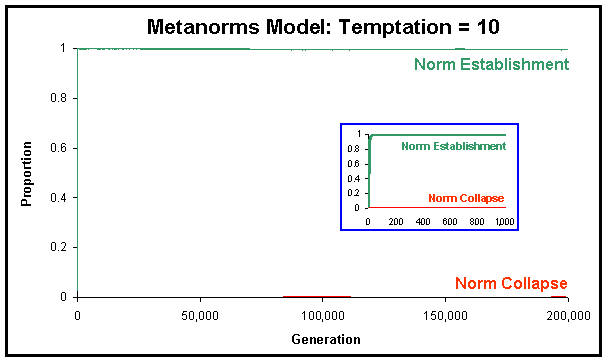
|
| Figure 11. Proportion of runs where the norm has been established and where the norm has collapsed in the Metanorms model, calculated over 1,000 runs up to 2·105 generations, with T = 10 (the rest of parameter values equal to Axelrod's). |
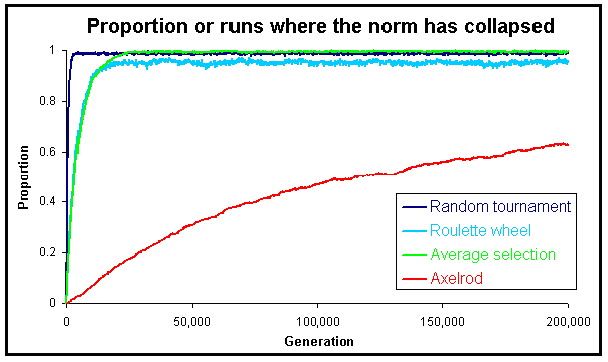
|
| Figure 12. Proportion of runs where the norm has collapsed in the Metanorms model, calculated over 1,000 runs up to 2·105 generations, for different selection mechanisms and using Axelrod's parameter values. |
Replication is one of the hallmarks of cumulative science. It is needed to confirm whether the claimed results of a given simulation are reliable in the sense that they can be reproduced by someone starting from scratch. Without this confirmation, it is possible that some published results are simply mistaken due to programming errors, misrepresentation of what was actually simulated, or errors in analysing or reporting the results. Replication can also be useful for testing the robustness of inferences from models. (Axelrod 1997b)
2An equilibrium is deficient if there exists another outcome which is preferred by every player.
3Arrows with solid lines represent flow of program control from the start (black circle) to the end (black circle with concentric white ring). Immediately below the top-most arrow there is a thick horizontal line, which denotes a concurring process. The dotted horizontal line between two vertical arrows departing from the same concurrent process (thick) line indicates many objects (in this case, agents) engaged in the same activity (Polhill, Izquierdo, and Gotts 2005a). Arrows with dashed lines are object flows, indicating the involvement of an object in a particular action. Objects are represented in grey boxes divided into possibly three sections. The top-most section shows the name of the object (e.g. i) and the class it belongs to (e.g. Agent), underlined and separated by a colon, with the state optionally in square brackets underneath (e.g. [stepping]). The second section in a grey box shows certain instance variables of the object; and the bottom-most section, which appears optionally, shows methods to which the object can respond (e.g. metanorms(Number, Agent, Agent)). The type of each of the arguments of a method is written between brackets after the name of the method. Comments are indicated in yellow boxes with a folded down corner, and connected by a dashed line without an arrowhead to the item with which they are associated. Red diamonds represent decision points, with one out-flowing arrow labelled with text in square brackets indicating the condition under which that branch is used, and the other out-flowing arrow indicating the 'else' branch. When the condition is of the form [Probability: x], the associated branch is followed with probability x.
4This description of the selection algorithm is ambiguous when every agent in a generation happens to obtain the same payoff. In that case, in our particular re-implementation of the model, every agent is replicated twice, and then half of the newly created agents are randomly eliminated to keep the number of agents constant. Proceeding in a different way when every agent has the same payoff can alter the long-term results significantly.
5The term 'state' denotes here a certain particularisation of every agent's strategy.
6Yamagishi and Takahashi (1994) use a model similar to Axelrod's, but propose a linkage between cooperation (not being bold) and vengefulness.
7The demonstration of this statement is simple when one realises that the mutation operator guarantees that it is possible to go from any state to any other state in one single step.
8This is also the long-run fraction of the time that the system spends in each of its states.
9By 'one single mutation', we refer to any change in one single agent's strategy, not a single flip of a bit.
10This is true for the selection mechanism used by Axelrod, and also for three other selection mechanisms that we explore in a later section.
11In other words, if every agent is following the same strategy in an Evolutionary Stable State as defined above, we can confirm that such strategy is evolutionary stable as understood in the literature (a strategy with the property that if most members of the population adopt it, no mutant strategy can invade the population by natural selection (Maynard Smith and Price 1973)).
12Since every agent is following the same strategy in this state, we can guarantee that this ESS is resistant to one single mutation in terms of expected payoffs.
13This ESS is not a Nash equilibrium.
14Remember that agents defect if and only if their boldness is higher than the probability of being seen.
15Interestingly enough, recent research suggests that people genuinely enjoy punishing others who have done something wrong (de Quervain et al. 2004).
16A lower Punishment yields very similar results, and the reasoning is the same.
17A similar approach is followed by Takadama et al. (2003), Kluver and Stoica (2003), and by Edmonds and Hales (2003a). Takadama et al. (2003) propose a cross-element validation method to validate computational models by investigating whether several models can produce the same results after changing an element in the agent architecture. Specifically they study the effect of different learning mechanisms in the bargaining game model. Similarly, Klüver and Stoica (2003) compare different adaptive algorithms over one single domain. Edmonds and Hales (2003a) compare three different evolutionary selection mechanisms, just as we have done here.
18If all agents happen to have the same payoff then random tournament is applied.
AXELROD R M (1986) An Evolutionary Approach to Norms. American Political Science Review, 80 (4), pp. 1095-1111
AXELROD R M (1997a) The complexity of cooperation. Agent-based models of competition and collaboration. Princeton, N.J: Princeton University Press.
AXELROD R M (1997b) Advancing the Art of Simulation in the Social Sciences. In Conte R, Hegselmann R, Terna P, editors. Simulating Social Phenomena (Lecture Notes in Economics and Mathematical Systems 456). Berlin: Springer-Verlag.
AXTELL R L (2000) Why Agents? On the Varied Motivations for Agents in the Social Sciences. In Macah C M, Sallach D, editors. Proceedings of the Workshop on Agent Simulation: Applications, Models, and Tools. Argonne, Illinois.: Argonne National Laboratory.
AXTELL R L, Axelrod R M, Epstein J M and Cohen M D (1996) Aligning Simulation Models: A Case Study and Results. Computational and Mathematical Organization Theory, 1 (2), pp. 123-141
BENDOR J and Swistak P (1997) The evolutionary stability of cooperation. American Political Science Review, 91 (2), pp. 290-307
BENDOR J and Swistak P (1998) Evolutionary equilibria: Characterization theorems and their implications. Theory and Decision, 45 (2), pp. 99-159
BINMORE K (1998) Review of the book: The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration, by Axelrod, R., Princeton, New Jersey: Princeton University Press, 1997. Journal of Artificial Societies and Social Simulation, 1 (1) https://www.jasss.org/1/1/review1.html.
BONABEAU E (2002) Agent-based modeling: Methods and techniques for simulating human systems. Proceedings of the National Academy of Sciences of the United States of America, 99 (2), pp. 7280-7287
BOUSQUET F and Le Page C (2004) Multi-agent simulations and ecosystem management: a review. Ecological Modelling, 176, pp. 313-332
BOYD R and Richerson P J (1992) Punishment Allows the Evolution of Cooperation (or Anything Else) in Sizable Groups. Ethology and Sociobiology, 13, pp. 171-195
BROWN D G, Page S E, Riolo R L and Rand W (2004) Agent-based and analytical modeling to evaluate the effectiveness of greenbelts. Environmental Modelling and Software, 19 (12), pp. 1097-1109
CASTELLANO C, Marsili M and Vespignani A (2000) Nonequilibrium phase transition in a model for social influence. Physical Review Letters, 85 (16), pp. 3536-3539
CIOFFI-REVILLA C (2002) Invariance and universality in social agent-based simulations. Proceedings of the National Academy of Sciences of the United States of America, 99 (3), pp. 7314-7316
COLLIER N (2003) RePast: An Extensible Framework for Agent Simulation. http://repast.sourceforge.net/
COLMAN A M (1995) Game Theory and its Applications in the Social and Biological Sciences, 2nd edition ed. Oxford, UK.: Butterworth-Heinemann.
CONTE R, Hegselmann R and Terna P (1997) Simulating Social Phenomena (Lecture Notes in Economics and Mathematical Systems 456). Berlin: Springer-Verlag.
DAWES R M (1980) Social Dilemmas. Annual Review of Psychology, 31, pp. 161-193
de QUERVAIN D J F, Fischbacher U, Treyer V, Schellhammer M, Schnyder U, Buck A, Fehr E (2004) The Neural Basis of Altruistic Punishment. Science, 305, pp. 1254-1258
DEGUCHI H (2004) Mathematical foundation for agent based social systems sciences: Reformulation of norm game by social learning dynamics. Sociological Theory and Methods, 19 (1), pp. 67-86
EDMONDS B (2001) The Use of Models - making MABS actually work. In Moss S, Davidsson P, editors. Multi-Agent-Based Simulation, Lecture Notes in Artificial Intelligence 1979. Berlin: Springer-Verlag.
EDMONDS B and Hales D (2003a) Computational Simulation as Theoretical Experiment. Centre for Policy Modelling Report, No.: 03-106 http://cfpm.org/cpmrep106.html.
EDMONDS B and Hales D (2003b) Replication, replication and replication: Some hard lessons from model alignment. Journal of Artificial Societies and Social Simulation, 6 (4) https://www.jasss.org/6/4/11.html.
EDWARDS M, Huet S, Goreaud F and Deffuant G (2003) Comparing an individual-based model of behaviour diffusion with its mean field aggregate approximation. Journal of Artificial Societies and Social Simulation, 6 (4) https://www.jasss.org/6/4/9.html.
EPSTEIN J M (1999) Agent-based computational models and generative social science. Complexity, 4 (5), pp. 41-60
GILBERT N and Conte R (1995) Artificial Societies: the Computer Simulation of Social Life. London: UCL Press.
GILBERT N and Troitzsch K (1999) Simulation for the social scientist. Buckingham: Open University Press.
GOTTS N M, Polhill J G and Adam W J (2003). Simulation and Analysis in Agent-Based Modelling of Land Use Change. Online Proceedings of the First Conference of the European Social Simulation Association, Groningen, The Netherlands, 18-21 September 2003. http://www.uni-koblenz.de/~kgt/ESSA/ESSA1/proceedings.htm
GOTTS N M, Polhill J G and Law A N R (2003) Agent-based simulation in the study of social dilemmas. Artificial Intelligence Review, 19 (1), pp. 3-92
HALES D, Rouchier J and Edmonds B (2003) Model-to-model analysis. Journal of Artificial Societies and Social Simulation, 6 (4) https://www.jasss.org/6/4/5.html.
HARE M and Deadman P (2004) Further towards a taxonomy of agent-based simulation models in environmental management. Mathematics and Computers in Simulation, 64, pp. 25-40
JANSSEN M (2002) Complexity and ecosystem management. The theory and practice of multi-agent systems. Chelteham, UK: Edward Elgar Pub.
KIM Y G (1994) Evolutionarily Stable Strategies in the Repeated Prisoners-Dilemma. Mathematical Social Sciences, 28 (3), pp. 167-197
KLEMM K, Eguiluz V M, Toral R and San Miguel M (2003) Nonequilibrium transitions in complex networks: A model of social interaction. Physical Review E, 67 (2)
KLEMM K, Eguiluz V M, Toral R and San Miguel M (2005) Globalization, polarization and cultural drift. Journal of Economic Dynamics & Control, 29 (1-2), pp. 321-334
KLUVER J and Stoica C (2003) Simulations of group dynamics with different models. Journal of Artificial Societies and Social Simulation, 6 (4) https://www.jasss.org/6/4/8.html.
KOHLER T and Gumerman G J (2000) Dynamics in human and primate societies: Agent-based modeling of social and spatial processes. New York: Oxford University Press and Santa Fe Institute.
KULKARNI V G (1995) Modelling and Analysis of Stochastic Systems. Boca Raton, Florida: Chapman & Hall/CRC.
LANSING J S (2003) Complex Adaptive Systems. Annual Review of Anthropology, 32, pp. 183-204
MAYNARD SMITH J and Price G (1973) The Logic of Animal Conflict. Nature, 246 (2), pp. 15-18
MOSS S, Edmonds B and Wallis S (1997) Validation and Verification of Computational Models with Multiple Cognitive Agents. Centre for Policy Modelling Report, No.: 97-25 http://cfpm.org/cpmrep25.html.
POLHILL J G, Izquierdo L R and Gotts N M (2005a) The ghost in the model (and other effects of floating point arithmetic). Journal of Artificial Societies and Social Simulation, 8 (1) https://www.jasss.org/8/1/5.html.
POLHILL J G, Izquierdo L R and Gotts N M. (2005b) What every agent-based modeller should know about floating point arithmetic. Environmental Modelling & Software. In Press.
RESNICK M (1995) Turtles, Termites, and Traffic Jams: Explorations in Massively Parallel Microworlds (Complex Adaptive Systems). Cambridge, US: MIT Press.
ROUCHIER J (2003) Re-implementation of a multi-agent model aimed at sustaining experimental economic research: The case of simulations with emerging speculation. Journal of Artificial Societies and Social Simulation, 6 (4) https://www.jasss.org/6/4/7.html.
SULEIMAN R, Troitzsch K G and Gilbert N (2000) Tools and Techniques for Social Science Simulation. Heidelberg, New York: Physica-Verlag.
TAKADAMA K, Suematsu Y L, Sugimoto N, Nawa N E and Shimohara K (2003) Cross-element validation in multiagent-based simulation: Switching learning mechanisms in agents. Journal of Artificial Societies and Social Simulation, 6 (4) https://www.jasss.org/6/4/6.html.
TESFATSION L (2002) Agent-based computational economics: Growing economies from the bottom up. Artificial Life, 8 (1), pp. 55-82
VILONE D, Vespignani A and Castellano C (2002) Ordering phase transition in the one-dimensional Axelrod model. European Physical Journal B, 30 (3), pp. 399-406
WEIBULL J W (1995) Evolutionary Game Theory. Cambridge, MA: MIT Press.
YAMAGISHI T and Takahashi N (1994) Evolution of Norms without Metanorms. In Schulz U, Albers W, Mueller U, editors. Social Dilemmas and Cooperation. Berlin: Springer-Verlag.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]