| Number of possible states: | 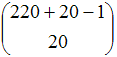 |
In 2000 Takahashi (2000) developed two ingenious agent-based models to explain the emergence of generalised exchange among multiple agents under the hypothesis of selective altruism based on fairness. In his article Takahashi shows that his results are valid not only in artificial societies where information is shared among all agents (i.e. global information) but also in artificial societies where agents only know about their immediate neighbours (i.e. local information).
The results obtained under the assumption of global information have been corroborated by Edmonds and Hales (2005) even in more general conditions. Edmonds and Hales (2005) also replicate Takahashi's (spatial) model of local information and point out that the results obtained with this spatial model contribute to the significant body of work supporting the idea that artificial agents tend to deal better with Prisoner's dilemma type of games in spatial contexts (Doebeli and Hauert 2005; Fort and Pérez 2005; Nowak and May 1992; Nowak and Sigmund 1998). The literature suggests that context preservation in general tends to promote cooperation in the Prisoner's dilemma (Cohen, Riolo and Axelrod 1999; Gotts, Polhill and Law 2003) –a conclusion that has been confirmed in other games (Németh and Takács 2007) but does not necessarily extend to all other social dilemmas (see e.g. Doebeli et al. 2005; Hauert and Doebeli 2004)–.
We start by analysing the model with global information. In Takahashi's (2000) original model there are 20 agents who interact over some number of generations. Each generation consists of a set of "trials". In each trial every agent receives 10 units of resource and is given the option to donate as many units as he wants to another agent. Thus, agents must decide how many units to give and to whom. This decision is determined by the agent's genetic code, which is divided into two parts:
The giving agent donates GG units of resource, but the recipient obtains GG·RV units. Thus, when RV > 1 the receiver obtains a greater benefit than the cost incurred by the giver, so the strategic situation becomes a social dilemma (Dawes 1980).
At the end of each generation those agents who have obtained more units of resource are replicated comparatively more frequently in the next generation. The selection mechanism implemented in the evolutionary process is a truncation method (De Jong 2006) similar to the mechanism used by Axelrod (1986) in the metanorm games (which is also analysed in this appendix): at the end of each generation two evolutionary forces (natural selection and mutation) come into play to replace the old generation with a brand new one:
This model can be represented as a time homogeneous Markov chain by defining the state of the system as the number of agents having a certain genetic code at the beginning of each generation. The number of different genetic codes is 11·20 = 220 (10 units of resource an agent can give plus the option of not giving, times 20 different values for the tolerance gene). Thus the number of possible states of the system is:
| Number of possible states: | 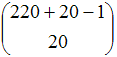 |
The mutation operator of this model guarantees that the induced THMC is irreducible and aperiodic.
If both genes can change at the same time, the induced Markov chain satisfies sufficient condition (i) for irreducibility and aperiodicity pointed out in Proposition 4 of our paper:
If only one gene can change at a time, then we can use sufficient condition (iii) for irreducibility and aperiodicity:
In this model it is possible to go from any state i to state j in three steps. The demonstration of this statement is simple when one realises that one can go from any state i to a state i* where all agents have tolerance gene as in state i and giving gene GG = 0. In that intermediate state i* every agent obtains the same units of resources so every agent is replicated once. From state i* it is possible to go to state j*, where every agent has its tolerance gene as in state j and its giving gene GG still equal to 0. Again, every agent is replicated once. Finally, from state j* it is possible to go to state j.
Consequently, regardless of the precise way in which the mutation operator works, the model is an irreducible and aperiodic THMC, also called ergodic.
As we have seen in the paper, in these processes the probability of finding the system in each of its states in the long run is strictly positive and independent of the initial conditions, and the limiting distribution π coincides with the occupancy distribution π*. Although calculating such probabilities from the transition matrix is rather impractical, we can approximate them as much as we want by running just one simulation for long enough.
Both Takahashi (2000) in his original paper and Edmonds and Hales (2005) in their reimplementation conduct two experiments with this model: in one experiment the agents' genetic code is initialised randomly and in the other experiment every agent starts with giving gene GG = 0. Both experiments consist of 50 replications of 1000 generations each. The two groups of researchers observe that the results obtained in both experiments are very similar. Having proved that the long-run dynamics of the model are independent of the initial conditions, the empirical results obtained by Takahashi (2000) and by Edmonds and Hales (2005) suggest –but do not prove– that 50 replications of 1000 generations seem to be sufficient to approximate the long-run dynamics of the model.
As we explain in section 9.2.1 of the paper, since the limiting and the occupancy distribution coincide, another method to approximate the limiting distribution would be to run just one simulation for long enough. We recommend running various simulation runs starting from widely different initial conditions to increase our confidence that the conducted simulations are long enough to accurately approximate the limiting distribution.
In the second model proposed by Takahashi (i.e. the spatial model with local information only) there are 100 agents located on a square [1] grid of 10×10 cells. Each agent only interacts with his local neighbours (Moore neighbourhood of radius 1). The selection mechanism is different from that in the non-spatial model: at the end of each generation, if an agent has any neighbour with more units of resource than himself, then he adopts the genetic code of the most successful agent in his neighbourhood. Updating of genetic codes takes place synchronously.
Again, the state space in this second model can be defined as the set of different genetic codes that an agent may have. With this definition, the model has 220100 different states! Assuming that the model includes a probability of mutation for every agent's genetic code in each generation, we can state –for the same reasons discussed above– that the local information model is also ergodic.
AXELROD R M (1986) An Evolutionary Approach to Norms. American Political Science Review, 80(4), pp. 1095-1111
COHEN M D, Riolo R L, and Axelrod R M (1999) The Emergence of Social Organization in the Prisoner's Dilemma: How Context-Preservation and Other Factors Promote Cooperation. Santa Fe Institute Working Paper, 99-01-002,
DAWES R M (1980) Social Dilemmas. Annual Review of Psychology, 31, pp. 161-193
DE JONG K A (2006) Evolutionary computation. A unified approach. Cambridge, Mass: MIT Press.
DOEBELI M and Hauert C (2005) Models of cooperation based on the Prisoner's Dilemma and the Snowdrift game. Ecology Letters, 8(7), pp. 748-766
EDMONDS B and Hales D (2005) Computational Simulation as Theoretical Experiment. Journal of Mathematical Sociology, 29(3), pp. 209-232.
FORT H and Pérez N (2005) The Fate of Spatial Dilemmas with Different Fuzzy Measures of Success. Journal of Artificial Societies and Social Simulation, 8(3)1. https://www.jasss.org/8/3/1.html.
GOTTS N M, Polhill J G, and Law A N R (2003) Agent-based simulation in the study of social dilemmas. Artificial Intelligence Review, 19(1), pp. 3-92
HAUERT C and Doebeli M (2004) Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature, 428(6983), pp. 643-646
NÉMETH A and Takács K (2007) The Evolution of Altruism in Spatially Structured Populations. Journal of Artificial Societies and Social Simulation, 10(3)4. https://www.jasss.org/10/3/4.html.
NOWAK M A and May R M (1992) Evolutionary Games and Spatial Chaos. Nature, 359(6398), pp. 826-829
NOWAK M A and Sigmund K (1998) Evolution of indirect reciprocity by image scoring. Nature, 393(6685), pp. 573-577
TAKAHASHI N (2000) The emergence of generalized exchange. American Journal of Sociology, 10(4), pp. 1105-1134
1 The lattice is not a torus; agents on the edges and agents at the corners have fewer neighbours than agents in central positions.