Hugo Fort and Nicolás Pérez (2005)
The Fate of Spatial Dilemmas with Different Fuzzy Measures of Success
Journal of Artificial Societies and Social Simulation
vol. 8, no. 3
<https://www.jasss.org/8/3/1.html>
For information about citing this article, click here
Received: 26-Jul-2004 Accepted: 16-Mar-2005 Published: 30-Jun-2005
 Abstract
Abstract| T > R > P > S | (1a) |
| 2R > S + T | (1b) |
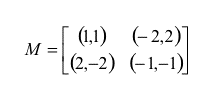
|
i.e. R =1, S = -2, T = 2 and P = -1. Since the four payoffs sum to zero, if all players would update their behavioural variable at random they would get, on average, a null score. The state of players are updated cell by cell so we have an asynchronous cellular automata (ACA)[4]. The initial state at t=0 is taken as C and D chosen at random for each cell i.e. the fraction of cooperators c is equal to 0.5 (we checked that the equilibrium states are independent from the initial configurations. The number of agents in our simulations varied from N=2500 (a 50 × 50 grid) to N = 1,000,000 (a 1000 × 1000 grid). The typical number of lattice sweeps is Ns=400 (i.e. from 1,000,000 to 400,000,000 time steps). The results we present here do not change appreciably with the size of the grid.
μIU(T) = 1
μIU(R) = 2/3
μIU(P) = 1/3
μIU(S) = 0.
μ(X) = 1 if (Wmax + <w>)/2 < X
μ(X) = 2/3 if <w> < X d (Wmax + <w>)/2
μ(X) = 1/3 if (Wmin + <w>)/2 < X ≤ <w>
μ(X) = 0 if X ≤ (Wmin + <w>)/2
where X ≡ W(x,y) (X ≡ WN ) for measures of success ICL and ICG (for measure of success NW) and <w> ≡ WavN (<w> ≡ Wav) for measure of success ICL (ICG and NW).
| JCD = 1/3 c2 + c(1-c). | (2) |
| JDC = 2/3 (1-c)2. | (3) |
| 4ceq2+ -7ceq+2 = 0. (MS IU ) | (4) |
|
|
| Figure 1. The fraction of C agents for different measure of success MSs. Thin lines, from below to above: ICL, IU, ICG and NW. Thick upper line corresponds to the discriminating or two-level strategy. The lowest ceq corresponds to ICL. |
| Ueq E U(ceq) = (R-S-T+P) ceq2 +(S+T-2P) ceq +P = 2 ceq -1. | (5) |
Hence, Ueq is greater (smaller) than zero if ceq is greater (smaller) than 1/2. We found that for MS IU and ICL we get respectively Ueq ≅ -0.28 and Ueq ≅ -0.4 in complete agreement with equation (4). On the other hand, for measures ICG and NW, Ueq ≅ 0 in consonance with the fact that ceq ≅ 0.5 for both. Let us denote by ¢ the normalised temporal average of the number of times a player played C. In Figure 2 histograms of ¢and W are depicted for the von Neumann neighbourhood. For measures ICL and ICG both are multi-peaked. The ¢ histograms exhibit two peaks: One centred around c=0.5 and the other at c=0 (indicated by an arrow), which is large for ICL (Figure 2c) and very small in the case of ICG (Figure 2e ), which corresponds to D-agents. The peaks of the respective W histograms can be explained in terms of different local spatial patterns for c. For instance, the right peak at W=400 (large in Figure 2d and small indicated by an arrow in Figure 2f) corresponds to a D player surrounded by four players with c=0.5. This configuration gives to the central player average utilities U=(T+P)/2=1/2 per game. On average each agent plays two times per lattice sweep (one for sure plus another one with each of his z neighbours with probability 1/z). Therefore the average capital accumulated during Ns lattice sweeps is given by U × 2 × Ns = Ns = 400, in accordance with Figure 2. In an analogous way all the peaks can be explained[6].
|
|
| Figure 2. Histograms for temporal average ¢ (right column) and average capital (left column). (a) & (b) IU , (c) & (d) ICL, (e) & (f) ICG and (g) & (h) NW. The ¢ and W histograms for measures ICL and ICG are multi-peaked. The cooperation histograms exhibit two peaks, one of them at ¢=0 -large (very small) for ICL (ICG) (see arrows in Figure 2c and 2e)-, corresponding to D-agents, and the other centred around ¢=0.5. The peaks of the respective capital histograms can be explained in terms of different local spatial patterns for c (see text). |
|
|
| Figure 3. Asymptotic capital maps for different MSs (50 × 50 subsets of 500 × 500 lattices): (a) IU, (b) ICL, (c) ICG and (d) NW. IC measures, produce spatial patterns that are in consonance with their multi-modal histograms, whilst measures IU and NW produce random spatial structure. |
| Table 1: Summary of equilibrium properties for the 4 elementary measures of success (von Neumann's neighbourhood) | ||||||
| MS | ceq | Ueq | W Histogram | C Histogram | W fluctuations | W Spatial patterns |
| IU | ≅0.36 | ≅-0.28 | Gaussian like | Gaussian like | ξ = 0.5 | Random |
| ICL | ≅0.3 | ≅-0.4 | 6 peaks histogram | 2 peaks histogram | ξ ≅ 2 | "Chess board" patches |
| ICG | 0.5- | 0- | 3 peaks histogram | 2 peaks histogram | ξ ≅ 1 | "Flowers" |
| NW | 0.5+ | 0+ | Gaussian like | Gaussian like | ξ = 0.5 | Random |
μCU(2R)=1
μCU(0)=1/2
μCU(2P)=0.
This strategy gives rise to a more cooperative (and more efficient) society with a ceq higher than all the straightforward applications of the 4 elementary MSs (see Figure 1). It turns out that the interesting "segregation" patterns depicted in Figure 4 emerge: "islands" of rich C-agents (red) and of poor D-agents (yellow) in a sea of medium class (blue).
|
|
| Figure 4. Asymptotic capital map for the two level strategy (50 × 50 subset of 500 × 500 lattices). (a): von Neumann's neighbourhood; (b): Moore's neighbourhood. A segregation pattern with "islands" of rich C-agents (red) and "islands" of poor D-agents (yellow) in a sea of medium class (blue) is clear. |
2In what follows we will call these steady states by the usual terminology of "equilibrium" states, however one should bear in mind that indeed are dynamical equilibriums (i.e on average the fraction of C's agents is fixed but, there are C agents that transform into D and vice versa).
3We checked that for sufficiently large lattices the results are independent of the boundary conditions.
4We also considered the synchronous dynamics in which all the agents update their states simultaneously at the end of each lattice sweep (that correspond to ordinary CA) to check the robustness of results.
5Indeed, the determination of the global minimum and maximum of W is not a trivial matter for players and the informational assumptions involved in using Wmax and Wmin are rather implausible. However, we checked that changing Wmax and Wmin whith rough estimates doesn't change results qualitatively.
6This identification of peaks of the histogram of capital with local patterns of c works also for z=2 and z=8 neighbours.
BARÁBASI, A. L. (2002) Linked: The New Science of Networks, Cambridge: Perseus.
BINMORE, Ken and Samuelson, L. (1991), Evolutionary Stability in Repeated Games Played By Finite Automata, Journal of Economic Theory 57, 278-305 (1991).
DOMJAN, M. and Burkhard, B. (1986) "Chapter 5: Instrumental conditioning: Foundations", The principles of learning and behavior, (2nd Edition). Monterey, CA: Brooks/ Cole Publishing Company 1986.
EPSTEIN, J. (1998), Zones of Cooperation in Demographic Prisoner's Dilemma, Complexity Vol. 4, Number 2, November-December 1998.
FLOOD, M. (1952), Some Experimental Games, Research Memorandum, RM-789-(1952).
FRIEDMAN, D (1998) "On economic applications of evolutionary game theory", Journal of Evolutionary Economics 8, 15-43 (1998).
FORT, H. (2003a), Cooperation with random interactions and without memory or "tags", Journal of Artificial Societies and Social Simulation 6, 2, https://www.jasss.org/6/2/4.html.
FORT, H. (2003b), Cooperation and Self-Regulation in a Model of Agents Playing different Games, Phys. Rev. E 68, 026118.
HELLIWELL, John F. and Putnam Robert D. (1995) "Economic Growth and Social Capital in Italy", Eastern Economic Journal 21(3), 295-308.
KRAINES, D. and Kraines, V. (1988) "Pavlov and the Prisoner's Dilemma" Theory Decision 26, 47-79.
MAYNARD-SMITH, J. and Price, G. (1973), The Logic of Animal Conflict, Nature (London) 146, 15.
MAYNARD-SMITH, J. (1982), Evolution and the Theory of Games, Cambridge University Press.
MAYNARD-SMITH, J. and Szathmary, E. (1995), The Major Transitions in Evolution, Oxford University Press.
NOWAK, M. and May, R. 1992 Nature 359, 826-828.
NOWAK, M. and Sigmund, K. (1993), "Win-stay, lose-shift outperforms tit-for-tat." Nature 364, 56-58.
POSCH M. , Pischler A. and Sigmund K. (1999), "The efficiency of adapting aspiration levels", Proc. R. Soc. Lond. B 266, 1427-1435.
PUTNAM R. D. (1993), Making democracy work. Civic traditions in modern Italy. Princeton: Princeton University Press.
RAPOPORT A. and Chammah A. M., (1965) Prisoner's Dilemma: A Study in Conflict and Cooperation. The University of Michigan Press.
SAMUELSON, L. (1997). Evolutionary Games and Equilibrium Selection. Cambridge, Massachusetts: MIT Press.
SKYRMS, B. (2004), The Stag Hunt and the Evolution of Social Structure, Cambridge University Press.
WATTS, D. (1999) Small Worlds: The Dynamics of Networks between Order and Randomness, Princeton University Press.
WEDEKIND, C. And Milinski, M. (1996) "Human cooperation in the simultaneous and the alternating Prisoner's Dilemma: Pavlov versus Generous Tit-for-Tat." Proc. Natl. Acad. Sci. 93, 2686-2689.
WEIBULL, J. W. (1995) Evolutionary Game Theory, The MIT Press, Cambridge, Massachusetts.
WOLFRAM, S. (1984), "Universality and complexity in cellular automata" Physica D 10, 1-35.
ZADEH, L. (1965), "Fuzzy Sets," Information and Control 8, 338.
ZADEH, L. (1975), "The Calculus of Fuzzy Restrictions", in Fuzzy Sets and Applications to Cognitive and Decision Making Processes, edited by L. A. Zadeh et. al., Academic Press, New York, pages 1-39.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]