Lynne Hamill and Nigel Gilbert (2009)
Social Circles: A Simple Structure for Agent-Based Social Network Models
Journal of Artificial Societies and Social Simulation
vol. 12, no. 2 3
<https://www.jasss.org/12/2/3.html>
For information about citing this article, click here
Received: 20-Nov-2008 Accepted: 03-Mar-2009 Published: 31-Mar-2009
 Abstract
Abstract| Box 1: Network jargon used in this paper |
|
A network is comprised of nodes and links, which combine to create paths. The basic characteristics of a node are its degree and clustering coefficient:
The basic characteristics of a network are size, path length and density:
|
|
|
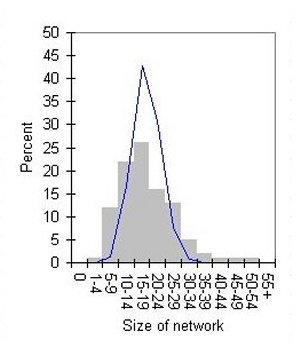
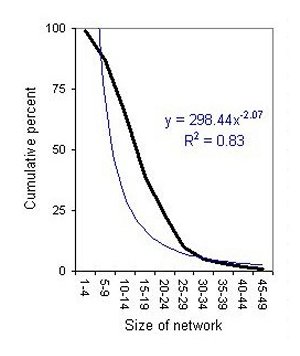
| Compared to a Poisson distribution with the same mean (thin line) | Cumulative, fitted to a power distribution (thin line) |
| Figure 1. Fischer's distribution of personal networks | |
|
|
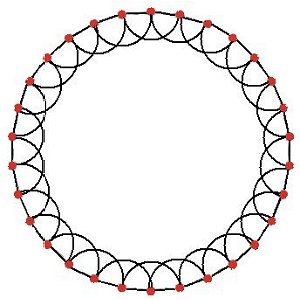
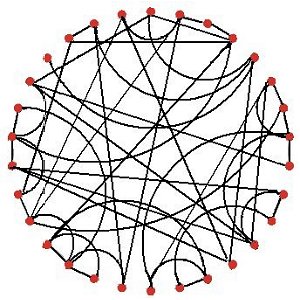
| (a) Regular lattice: each node is linked to its four immediate neighbours | (b) Random network: most nodes have three or four links. |
|
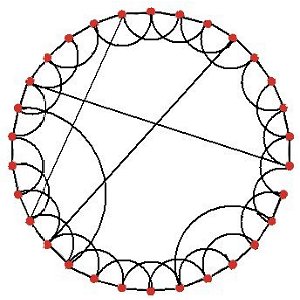
|
| (c) Small world network: most nodes are linked only to their immediate neighbours. | (d) Preferential attachment (scale-free) network: a few nodes have many links. |
| Figure 2. Examples of four basic models of networks: all with 30 nodes | |
despite the random placement of links…most nodes will have approximately the same number of links..Indeed, in a random network, the nodes follow a Poisson distribution with a bell shape and it is extremely rare to find nodes that have a significantly more or fewer links than the average.Not surprisingly, the assortativity index of a random graph can be shown analytically to be zero (Newman 2002). Although such models display the short paths of social networks (Dorogovtsev & Mendes 2003: 105), it is hardly surprising that random networks fail to replicate other key features of social networks because we know that social networks are not in general created by making random links, although Aiello et al's (2001) recent analysis of phone call data suggested that, at the very large scale, random patterns may appear. So random networks are not good models of social networks either.
| Table 1: Summary of characteristics of the four basic network models | ||||
| Characteristic | Regular | Random | Small-world | Preferential attachment |
| Low density | √ | √ | √ | √ |
| Personal network size limited | √ | √ | √ | × |
| Variation in size of personal network | × | Limited | Limited | √ |
| Fat-tail | × | × | × | √ |
| Assortative | × | × | × | × |
| High clustering | √ | × | √ | × |
| Communities | × | × | × | √ |
| Short path lengths | × | √ | √ | × |
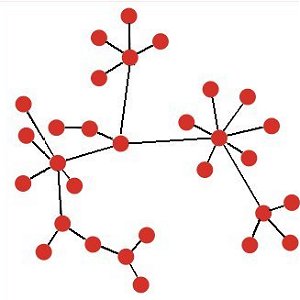
|
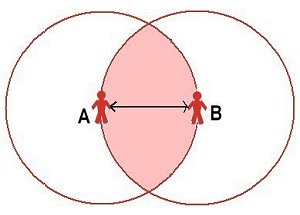
|
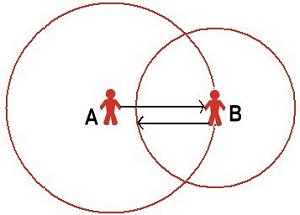
| (a) No reciprocity: different social reaches: A knows B but B does not know A | (b) Reciprocity with the same social reach |
| Figure 3. Reciprocity and social reach | |
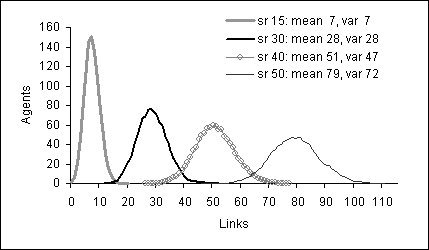
|
| Figure 4. Degree of connectivity by social reach (sr) |

|

|
| Social reach = 15 | Social reach = 30 |
| Figure 5. Examples of how networks vary with the size of the social reach. (Red nodes, grey links.) | |
| Box 2: Mathematics of circles | |
 | 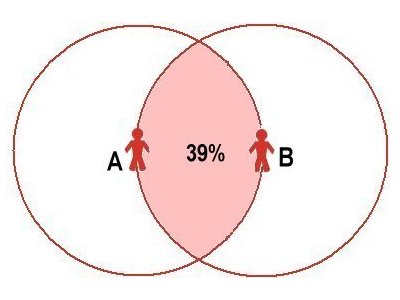 |
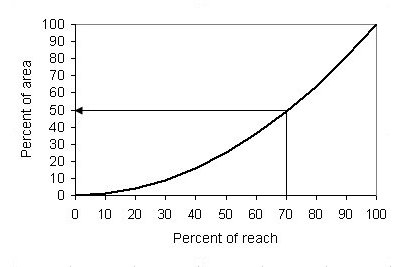 | |
 | |
|
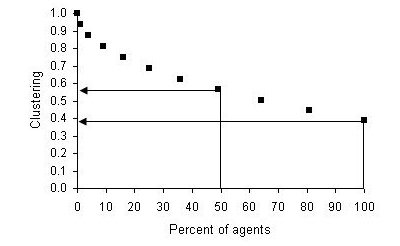
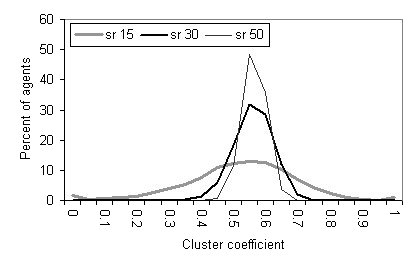
| Figure 6. Cluster coefficient for the single-reach model with the social reach (sr) set at 15, 30 and 50 |
| Box 3: Calculating the cluster coefficient: example and pseudo-code | ||||
| ||||
|
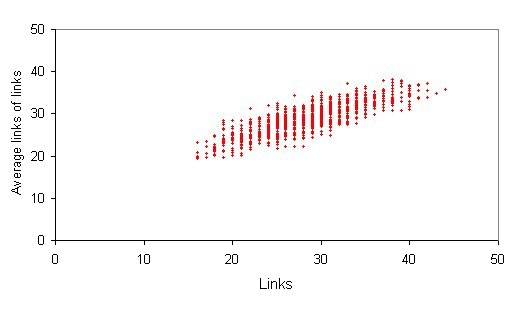
| Figure 7. Assortativity of degree: typical example of correlation between degrees of connectivity: social reach of 30 |
|
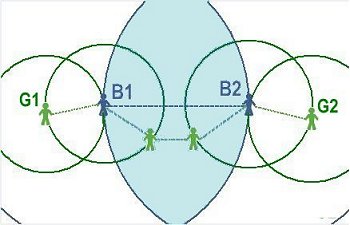
|
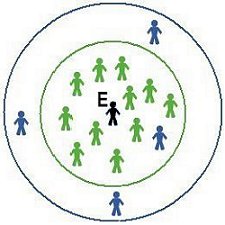
| If E is a Green, then E links with everyone in the smaller (green) circle. If E is a Blue, then E also links to the three Blues within the larger (blue) circle | A link between Blues B1 and B2 creates a short-cut and, for Blues, reduces clustering. The shaded area indicates overlap between the Blues' circles. |
| Figure 8. Two-reach model | |
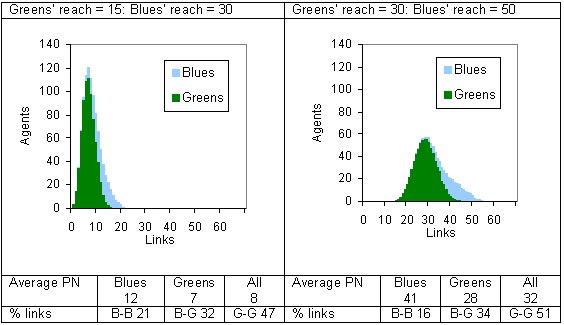
|
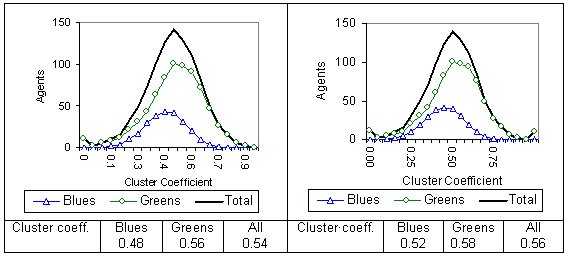
|
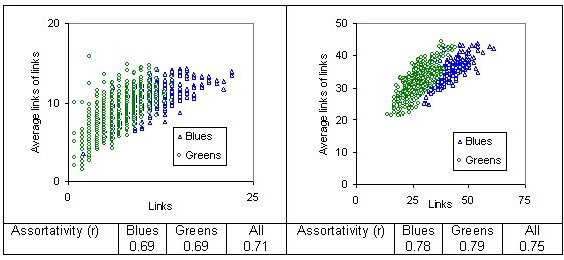
|
| Figure 9. Examples of two-reach models: Blues 25 percent. (PN = personal network) |
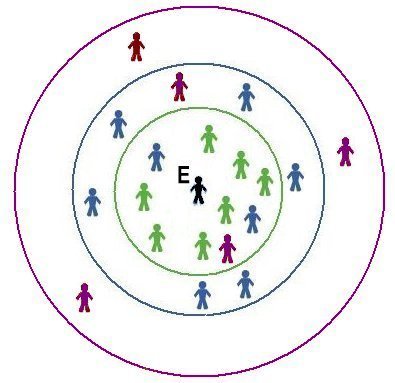
|
| Figure 10. A three-reach model |
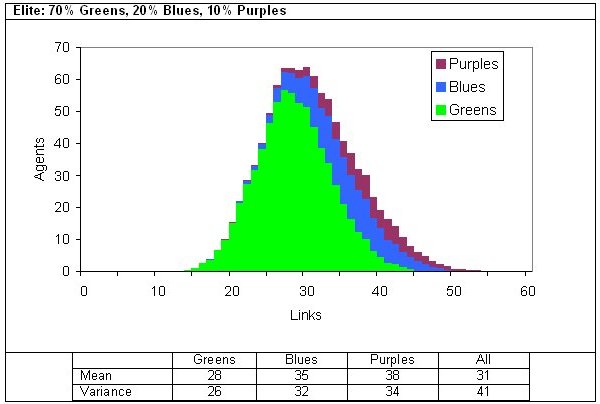
|
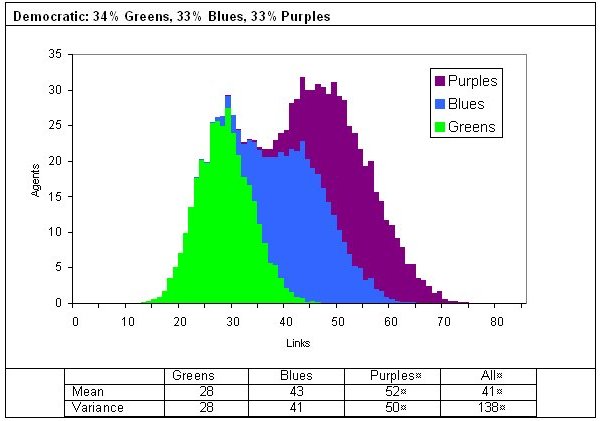
|
| Figure 11. Two examples of degrees of connectivity in a three-reach model |
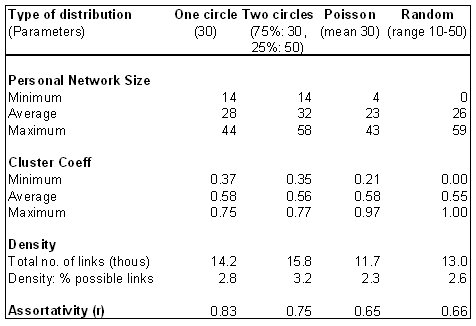
|
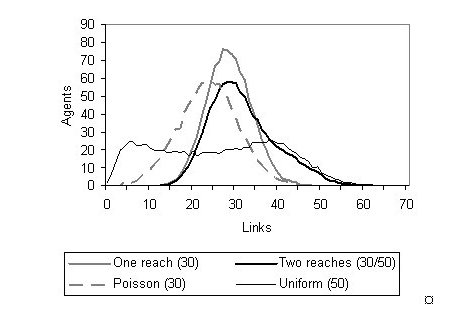
|
| Figure 12. Comparison of various ways of producing an average personal network of around 30 |
|
| Figure 13. The parallelogram problem |
AMARAL, L. A. N., Scala, A. Barthélemy M., & Stanley H. E. (2000) Classes of small-world networks. PNAS. Vol. 97. No. 21 pp.11149-11152.
ARISTOTLE (c300BC/1996) The Nicomachean Ethics. Ware. Wordsworth.
BARABSI A-L. & Albert, R. (1999) Emergence of Scaling in Random Networks. Science, New Series, Vol. 286, No. 5439., pp. 509-512.
BARABSI A-L, & Bonabeau, E. (2003) Scale-Free Networks. Scientific American (May) pp.52-59.
BARTHÉLEMY, M. (2003) Crossover from scale-free to spatial networks. Europhysics Letters. 63 pp.915-912.
BOISSEVAIN, J. (1974/78) Friends of Friends: Networks, Manipulators & Coalitions. Oxford. Basil Blackwell.
BRUGGEMAN, J. (2008) Social Networks. London. Routledge.
CALDERELLI, G. (2007) Scale-Free Networks: Complex Webs in Natural, Technological and Social Sciences. Oxford. Oxford University Press.
COULTHARD, M., Walker, A. & Morgan, A. (2002). People's perceptions of their neighbourhood and community involvement: Results from the social capital module of the General Household Survey 2000. London. National Statistics. The Stationery Office.
CROSSLEY, N. (2008) Small-world networks, complex systems and sociology. Sociology. Vol 42, No. 2, pp.261-277.
DODDS, P.S., Muhammad, R. & Watts, D.J. (2003) An Experimental Study of Search in Global Social Networks. Science, 8 August pp. 827-829.
DOROGOVTSEV, S. & Mendes, J. (2003) Evolution of Networks: From biological nets to the Internet and WWW. OUP.
EDMONDS, B. (2006) How are physical and social spaces related? In Billari, F.C., Fent, T.; Prskawetz, A. & Scheffran, J. (eds.) Agent-Based Computational Modelling Springer. (Downloaded on 10 March 08 from cfpm.org/cpmrep127.html).
FISCHER, C.S. (1982) To Dwell Among Friends. Chicago. University of Chicago Press.
GILBERT, N. (2006) Putting the Social into Social Simulation. Keynote address to the First World Social Simulation Conference, Kyoto.
HEIDER, F. (1958) The Psychology of Interpersonal Relations. New York. Wiley.
HERMANN, C. Bathélemy, M. & Provero, P. (2003) Connectivity distribution of spatial networks. Physical Review E 68 026128.
HOFF, P. D., Raftery, A. E. & Handcock M. S. (2002) Latent Space Approaches to Social Network Analysis . Journal of the American Statistical Association, Vol 97, No 460, 1090-1098
LILJEROS, F., Edling, C., Amaral, L., Stanley, H.E., & Aberg, Y. (2001/2006) The web of human sexual contacts. Nature. Vol 411, 21 June. 907-8.
MARSDEN, P.V. (1987) Core discussion networks of Americans. American Sociological Review. Vol 52. No.1. pp.122-131.
MCFARLAND, D.D. & Brown, D.J. (1973) Social Distance as a Metric: A systematic Introduction to Smallest Space Analysis. In Laumann, E.O. Bonds of Pluralism: The Form and Substance of Urban Social Networks. New York. Wiley.
MCPHERSON, M., Smith-Lovin, L. & Cook, J.M (2001) Birds of a Feather: Homophily in Social Networks. Annual Review of Sociology. 27. pp.415-444.
MERTON, R.K. (1968) The Matthew Effect in Science. Science, New Series, Vol. 159, No. 3810 (Jan. 5, 1968), pp. 56-63.
NEWMAN, M. (2002) Assortative mixing in networks. Physical Review Letters. Vol 89. No.20. 208701.
NEWMAN, M. (2003) Mixing patterns in networks. Physical Review E. 026126.
NEWMAN, M., Barabasi, A-L. & Watts, D.J. (2006) The Structure and Dynamics of Networks. Princeton University Press.
NEWMAN, M. & Park, J. (2003) Why social networks are different from other types of networks. Physical Review E. Vol 68, 036122
POOL, I.S. & Kochen, M. (1978) Contacts and Influence. Social Networks. 1. pp.5-51.
PUJOL, J. M., Flache, A., Delgado, J. & Sanguesa, R. (2005) How Can Social Networks Ever Become Complex? Modelling the Emergence of Complex Networks from Local Social Exchanges. Journal of Artificial Societies and Social Simulation 8(4)12 https://www.jasss.org/8/4/12.html.
SCOTT, J. (1991) Social Network Analysis: A Handbook. London. Sage.
SCOTT, J. (2009 forthcoming) Handbook of Social Networks.
SIMMEL, G. (1902) The Number of Members as Determining the Sociological Form of the Group.I. American Journal of Sociology. Vol 8, No.1. pp1-46.
SOROKIN, P.M (1927/1959) Social and Cultural Mobility. London. Collier-Macmillan.
THIRIOT , S. & Kant, J-D. (2008) Generate country-scale networks of interaction from scattered statistics. Presented at ESSA 08, Brescia, Italy.
TRAVERS, J. & Milgram, S. (1969) An Experimental Study of the Small World Problem. Sociometry. Vol (32) 4. pp 425-443.
WASSERMAN, S. & Faust, K. (1994) Social Network Analysis. Cambridge University Press.
WATTS, D.J. (2004) Six Degrees: The Science of a Connected Age. London. Vintage. Watts, D.J., Dodds, P.S., & Newman, M. (2002) Identity and search in social networks. Science. Vol 296. 17 May.pp.1302-1305
WATTS, D.J. Dodds, P.S., & Newman, M. (2002) Identity and search in social networks. Science. Vol 296. 17 May. pp 1302-1305.
WATTS, D. J. &. Strogatz, S. H. (1998) Collective dynamics of 'small-world' networks. Nature. Vol 393 4 June.
WEISSTEIN, E. (1998) CRC Concise Encyclopedia of Mathematics. Boca Raton. CRC Press.
WELLMAN, B. (1988) Structural analysis: from method and metaphor to theory and substance. In Wellman, B. & Berkowitz, S.D. (eds) Social Structures: A Network Approach. Cambridge. Cambridge University Press. Pp 19-61.
WETHERELL, C. (1998) Historical Social Network Analysis. International Review of Social History. Vol. 43. Supplmement 125-144
WILENSKY, U. (1999) NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
WONG, L.H., Pattison, P. & Robins. G. (2006) A spatial model for social networks. Physica A. 360, pp. 99-120.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2009]