Cooperation in the Prisoner's Dilemma Game Based on the Second-Best Decision

©Copyright JASSS

Tetsushi Ohdaira and Takao Terano (2009)

Journal of Artificial Societies and Social Simulation 12 (4) 7
<https://www.jasss.org/12/4/7.html>

For information about citing this article, click here

Received: 31-Jan-2008 Accepted: 19-Jul-2009 Published: 31-Oct-2009

Abstract

: In the research addressing the prisoner's dilemma game, the effectiveness and accountableness of the method allowing for the emergence of cooperation is generally discussed. The most well-known solutions for this question are memory based iteration, the tag used to distinguish between defector and cooperator, the spatial structure of the game and the either direct or indirect reciprocity. We have also challenged to approach the topic from a different point of view namely that temperate acquisitiveness in decision making could be possible to achieve cooperation. It was already shown in our previous research that the exclusion of the best decision had a remarkable effect on the emergence of an almost cooperative state. In this paper, we advance the decision of our former research to become more explainable by introducing the second-best decision. If that decision is adopted, players also reach an extremely high level cooperative state in the prisoner's dilemma game and also in that of extended strategy expression. The cooperation of this extended game is facilitated only if the product of two parameters is under the criticality. In addition, the applicability of our model to the problem in the real world is discussed.
Keywords:: Cooperation, Altruism, Agent-Based Simulation, Evolutionary Game Theory

Introduction

1.1: The prisoner's dilemma game and its repeated form, the iterated prisoner's dilemma game are very popular and often used for studies that researches how cooperation arises when all people pursue their own benefit. An eminent work of the iterated prisoner's dilemma game is the Robert Axelrod's tournament that was held twice about 25 years ago (Axelrod 1984). In the study, he found the toughness of the Tit-for-Tat (TFT) strategy and the factor for the development of mutual cooperation. Recently applications of the prisoner's dilemma game have been widely spread in various areas: spatial extension (Nowak 1992; Cao 1999; Ahmed 2002; Kim 2002; Hauert 2004; Nowak 2004; Ohtsuki 2006; Ohdaira 2006; Fort 2007) that uses square lattice or graph/network theory, n-person extension (Yao 1994; Seo 2000), experiment for researching the cooperation of animal (Stephens 2002; Bshary 2006; Warneken 2007; Rutte 2007), biological study about the interaction of phages (Turner 1999; Turner 2003), bacteria (Griffin 2004; Fiegna 2006) and yeast (Craig MacLean 2006), and behavioral study of humans regarding altruism (altruistic punishment) (Fehr 2002; Fehr 2003a; Fehr 2003b; Fowler 2005; Bernhard 2006; Kurzban 2007; Andres Guzman 2007; Dawes 2007).
1.2: In the study of the prisoner's dilemma game, there are two important topics. First, what method is effective for the emergence of cooperation. Second, once cooperation emerges, how stable it is. These topics have been discussed for a long period of time, but they are still inconclusive. There have been some methods challenging this question. It is thought that the most successful one at present is indirect reciprocity (Nowak 1998a; Nowak 1998b; Panchanathan 2003; Panchanathan 2004; Nowak 2005; Rockenbach 2006). In this model, game players intend to increase their social reputation, and free riders (players who receive social property without any costs) can not prevail because they have no chance to raise their status.
1.3: We think there is a possibility that another method which differs from previously proposed ideas realizes cooperation in the prisoner's dilemma game. Please imagine a negotiation with many conflicts of interest. Generally, all participants can not fully satisfy their desire. They somewhat need to compromise in order to reach agreement. Besides, we often discard the best choice and select the second-best one if we want to keep a good relationship. This kind of action is seemingly like cooperative behavior and has not been dealt with by any previous research.
1.4: Here, from this point of view, we study the property of cooperation based on some compromise by using the model of agent based simulation. When every group composed of some agents makes its second-best decision, cooperation at a high level is observed. It is also revealed that cooperation does not develop in all cases. One condition like criticality regarding the relationship between two parameters is essential for that growth. We also discuss the applicability of our model to social phenomenon observed in the real world.

Model

Prisoner's Dilemma Game

2.1

At first, we introduce the basics of the prisoner's dilemma game before the description of the model. In the prisoner's dilemma game, the following scenario is commonly used. First, there are two players and they can choose their strategies (Defection or Cooperation). Second, they are separated from each other, so that each of them can not know the strategy of the opponent. After choosing strategies, payoff of each player is decided by the payoff matrix (Table 1). In the table, the meaning of every capitalized bold letter is as follows; T - Temptation to defect, R - Reward for mutual cooperation, P - Punishment, S - Sucker's payoff. In the prisoner's dilemma game, the condition T>R>P>S is necessary, and for the iterated prisoner's dilemma game, the additional condition 2R>T+S should be satisfied. The payoff matrix meets both conditions.

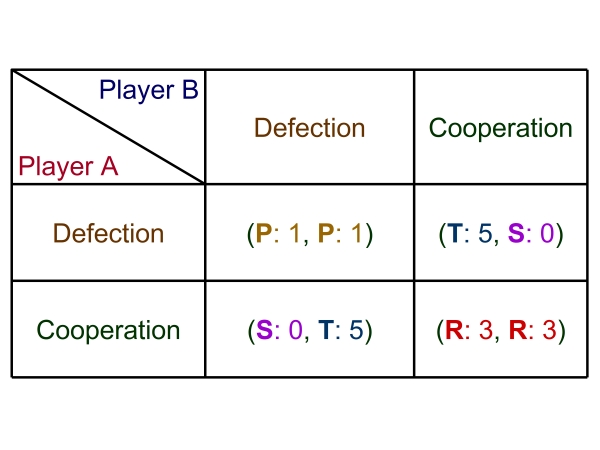
Table 1. Payoff matrix of the prisoner's dilemma game

2.2

Looking at the payoff matrix, if you choose the strategy of Cooperation, you can get the reward as long as your opponent cooperates. But if your opponent defects, you will have no payoff. On the other hand, in the case that your strategy is Defection, you have the opportunity to get the highest or at least minimum payoff. Therefore the strategy of Defection is the most appropriate in the prisoner's dilemma game. However, if you and your opponent think in the same way (take the strategy of defection), your payoff becomes smaller than in the case of mutual cooperation. That is the reason this game is referred to as the prisoner's 'dilemma' game. However, if the game is repeated infinitely, defection is not always the best strategy. If you can not know the number of iteration, mutual cooperation becomes one option to get more payoff. This repeatedly played game is referred to as the iterated prisoner's dilemma game. The effectiveness of strategy depends on the strategy of the opponent. Research of the iterated prisoner's dilemma game generally discusses what types of strategy get the most payoff (what the successful strategy is). The 'successful' strategy will be used by many agents and become the majority.

2.3

As noted before, the most remarkable work of the iterated prisoner's dilemma game is the Axelrod's tournament with computer simulation. This study reveals the essential factor for the emergence of cooperation as follows (Maynard Smith 1982; Axelrod 1984). Players with the TFT strategy must cooperate at the first iteration. They should remember the previous strategy of the opponent (memory) and give profits to each other, i.e., they have to take the same action as the past moves of the opponents (reciprocity). Because players do not know how long the game lasts, they tend to make allowances for their opponents (the effect of the 'shadow of the future'). If a player wishes to keep a good (cooperative) relationship with the other, he/she should not be prepossessed with the temptation of near future benefits by utilizing the strategy of defection.

Sequential Prisoner's Dilemma Game

2.4

In most research regarding the prisoner's dilemma game (and also the iterated version), the flaw exists that the variation of strategy is fixed and does not change during a simulation. Axelrod has previously used genetic algorithms and succeeded in producing strategies which are similar to the TFT strategy (Axelrod 1997). However, there are some prerequisite conditions in this research; for example, agents play the game with a pre-prepared repertoire of eight types of strategies. The TFT-like strategy does not evolve from the repeated matching with each other. In addition, it uses a particular environment where the ratio of eight representative strategies is definite.

2.5

To resolve this problem, we make the strategy of the prisoner's dilemma game more diverse and also evolvable. In this research, we use the prisoner's dilemma game with the strategy of extended form, which is named as the 'sequential' prisoner's dilemma game derived from the expression of strategy (Ohdaira 2006; Ohdaira 2007). In this game, the player's strategy is expressed as an array of length Ls that describes actions (Defection or Cooperation) in finite rounds. 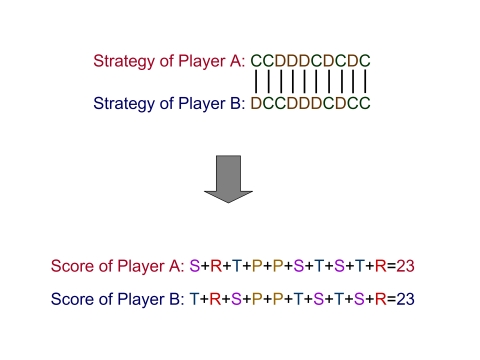The practice of the sequential prisoner's dilemma game is illustrated in Figure 1. You may know a game that is similar to the sequential prisoner's dilemma game, which is usually referred to as the centipede game (McNamara 2004). In the centipede game, the main aim of the game is to see how long every player cooperates from the beginning of the game. The game will continue until players defect once with each other. On the other hand, the sequential prisoner's dilemma game concentrates on the frequency of cooperation (or defection) in finite rounds.

Figure 1. Illustration of the sequential prisoner's dilemma game

2.6

We describe the distinction between the sequential prisoner's dilemma game and the (iterated) prisoner's dilemma game. Basically, the sequential prisoner's dilemma game is like the prisoner's dilemma game because players have no chance to refer to the past moves of their opponents once the game starts. However, if carefully compared, you can see that there is a substantial difference in the diversity of strategies (2 vs. 2^Lspatterns). The distinction between the iterated prisoner's dilemma game and the sequential prisoner's dilemma game is the structure of strategy. The strategy of the iterated prisoner's dilemma game is defined as a reactive motion to the past choice of the opponent. On the other hand, in the sequential prisoner's dilemma game, there is no reference to the past move of his/her opponent. The action of the game player in every round of the prisoner's dilemma game is already regulated by his/her strategy at the beginning of the game. Furthermore, each strategy can be updated by the use of evolutionary computation described below. Hence, the expression of strategy is fundamentally different between the iterated and the sequential forms of the game.

2.7

Using a mathematical equation, the strategy of player u is designated as a sequential array whose length is Ls (1). Each character represents a move of one round (D: Defection, C: Cooperation). Precisely, D or C means the component vector, which is expressed as (0, 1) or (1, 0). The former represents that the selection in one round is defection, the latter shows the player chooses cooperation.

(1)

Details of the Model

2.8

The focus of our research is not only modeling a specific phenomenon but also offering some novel knowledge about the research of the prisoner's dilemma game, especially in the evolvability of strategy. To achieve this purpose, the framework of the match is simplified. One agent will play the game against the agent of the same ID in the opponent group. The reason why the game is played between two agents of the same ID is because we follow the basis of simple spatial game where an opponent player does not change. We would like to apply the model to a spatial game smoothly in future work. On the other hand, the strategy of an agent has evolvability in comparison with other research, and also evolves based on the decision of each assigned group. Every group has a finite number (Na) of agents respectively. Agents of both groups have an ID (from 1 to Na) and a strategy of the sequential prisoner's dilemma game (that will be simply noted as a strategy). Each strategy is randomly initialized (the configuration of every strategy is a random sequence of cooperation and defection). 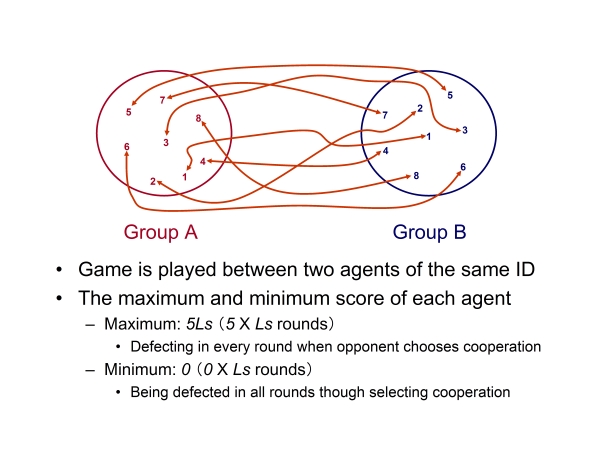An outline of the model is illustrated in Figure 2.

Figure 2. Outline of the model

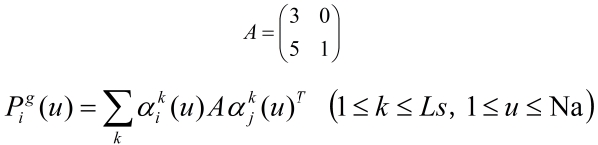
2.9

The payoff of each agent in the group at generation g is numerically expressed in the following equation (2). If the group i whose opponent group has the ID j is focused, the agent u in the group i gets his/her payoff P_i^g(u) respectively. A designates the payoff matrix, and where α_i^k(u) and α_j^k(u) means the element of strategy (1).

(2)

2.10

After all agents of both groups finish their sequential prisoner's dilemma game, the decision of each group will be made separately. 'Decision' in this case means the selection of the representative strategy of the group. Every group has initiative in the choice. If the representative strategy is decided, then the process of the evolution of strategy starts. The process is composed of the following two steps. First, two parts of the representative strategy are copied to other strategies in turn (duplication). The length of fraction randomly changes in every duplication. Second, each character of the newly created strategies is reversed according to the uniform rate (Rm) (mutation). The mutation, which is conducted after the creation of all new strategies, may be regarded as a mistake by humans in decision making. The method controlling the evolution of strategy is similar to the crossover in common genetic algorithm (GA). However, in fact, the process in this research is achieved by segmental duplication, which is different from the procedure of GA (in which individuals of the next generation are created by the crossover of some candidates). You can consider that the evolution of strategy is the partial adoption of the representative strategy by each agent. 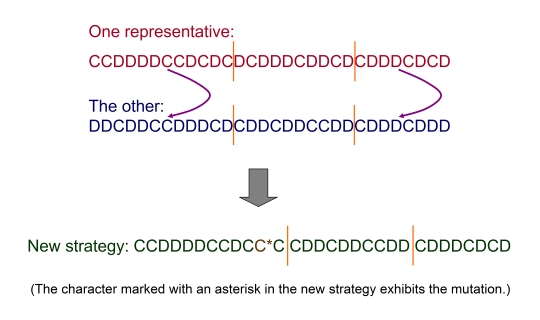Figure 3 also illustrates the process.

Figure 3. Illustration of the evolutionary process

2.11

The above process is executed independently in both groups. The representative strategy itself does not change except for mutation. This mechanism of selecting a representative and updating other strategies is called the 'evolutionary process'. Through this process, every strategy is updated and ready for the following match. This procedure from the match of the sequential prisoner's dilemma game to the evolutionary process is defined as one generation, and to investigate the fluctuation over a long period, one simulation runs until the number of generations reaches to 5,000. All results described later depict the average of 30 simulation runs.

Introduction of the Second-best Decision

2.12

In the context of the prisoner's dilemma game, as we noted before, if all players take the rational strategy, it is thought that mutual cooperation would not develop without additional constraints that control either the range of interaction or the decision of each player. Our model with the optimal response (rational decision) also reaches a state where all players defect against another in every round even if alternate procedures of crossover are used. This situation is called 'Nash equilibrium' in game theory, and is not desirable for game players because they have the chance to get higher payoff through mutual cooperation.

2.13

Constraints often mentioned before are the 'tag' (Riolo 1997; Hales 2001; Riolo 2001), the 'spatial structure' (Nowak 1992; Cao 1999; Ahmed 2002; Kim 2002; Hauert 2004; Nowak 2004; Ohtsuki 2006; Fort 2007) and 'indirect reciprocity' (Nowak 1998a; Nowak 1998b; Panchanathan 2003; Panchanathan 2004; Nowak 2005; Rockenbach 2006). The first one means that game players can distinguish each other by the use of their identifier. A player can refer to the tag of another player and know whether he/she is cooperative or not. The second is introduced to define neighborhood connection around agents. In the spatial game, agents interact only with those who are directly connected. Even if simple Markovian or one step conditional strategies (like TFT or Pavlov) are used, a system with the spatial structure can escape from Nash equilibrium (Fort 2007). Those strategies can be deterministic or binary. The third is advanced study of tag based solution. In the model of indirect reciprocity, cooperation can arise even though recipients do not have the opportunity to return profits to their donors. This mechanism is generally based on the system that everyone who helps others can raise his/her reputation and it brings him/her the chance that he/she is helped by others. Indirect reciprocity is also achieved by less sophisticated agents, without depending on reputation, when the agents can compare themselves with their opponents or detect whether their payoffs are under the threshold which is necessary to survive (Fort 2003).

2.14

In this research, as a new candidate to establish cooperation, we introduce the 'second-best decision' that means every group adopts the second-best strategy as his/her representative strategy. In former research, we have studied cooperation based on the decision that all groups do not desire to get more payoffs (Ohdaira 2006; Ohdaira 2007). The second-best decision is more improved and practical than the one used in those previous studies (elimination of the best strategy, which was named as the perfectly altruistic decision). If one group adopts the second-best decision, the representative strategy of the group becomes the strategy of 'second grade' regarding payoff. If all strategies become first grade, one strategy is randomly chosen from them. In recent research about brain science (Tankersley 2007; Krueger 2007), it has been revealed that people are naturally moderate altruist. These studies also remark that both the choice of altruistic behavior and the construction of cooperation are pleasant to humans. Those findings support our proposition that there is a case where cooperation is facilitated by the action of sacrifice like the second-best decision.

Results

Basic Sets of Variables

3.1

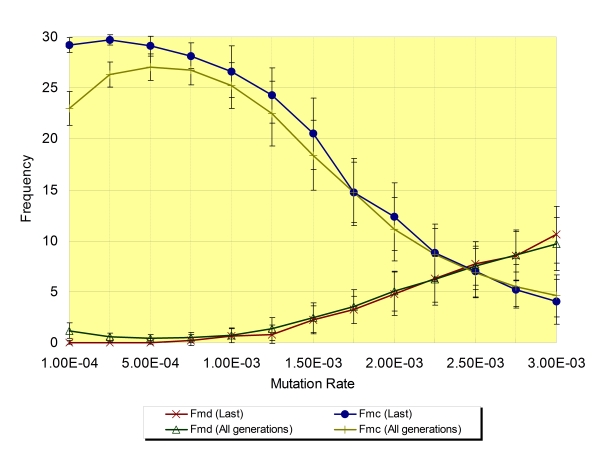
Before researching various parameters, the effect of mutation rate (Rm) is examined. The middle value in this research (Na=8, Ls=30) is used, and the finite range of Rm (from 1.0E-04 to 3.0E-03) is tested. The result is shown in Figure 4. In the figure, the average frequency of mutual cooperation (Fmc) regarding all generations becomes highest when Rm is equal to 5.0E-04. The average frequency of mutual defection (Fmd) regarding all generations also has its lowest peak with that value. The value is applied to all examinations because in this research we focus on both the Fmd and the Fmc for all generations rather than the last generation. Further examination reveals that Fmc/Ls of both the last and all generations takes a value above 0.80 when Rm is in the range of 1.5E-04 (minimum) to 1.1E-03 (maximum). If Rm exceeds the maximum, Fmc gradually decreases for both results. On the other hand, when Rm drops under the minimum, Fmc is still high up at Rm=7.5E-04 except regarding the result of all generations.

3.2

In the following, we show the results of basic sets of variables, which means that pairs of parameters are simple, that is, either very low Na or Ls changes (Figure 5 and 6). Please note that the rate of mutual defection (Rmd) and cooperation (Rmc) show how often each agent mutually defects (or cooperates) in the sequential prisoner's dilemma game. Each value can be found as follows; Rmd=Fmd/Ls and Rmc=Fmc/Ls. As is commonly seen in all the results of this research, the standard deviation (SD) for either Fmc or Rmc is comparatively large at the average of all generations. On the other hand, at the average of the last generation, the SD for each value is small. This phenomenon is derived from the variation between each run in the process of evolution. When Rmc is larger than 0.80 at the average of the last generation, the SD for Rmc is quite small. In that case, it is permissible to remark that a high level cooperative state is eventually realized by evolution based on the second-best decision.

3.3

Figure 5 is the simple case of two agents in both groups. From this result, you can see that Rmc regarding the last generation does not change too much even though the length of strategy (Ls) in each group increases. It indicates that agents finally cooperate regardless of the strategy length. Figure 6 exhibits the result of Ls=1 with changes in the number of agents. In this case, the game is regarded as the simple prisoner's dilemma game. Our model with the second-best decision shows its high effectiveness for the emergence of mutual cooperation. Especially regarding the result of all generations, Fmc steadily increases although the number of agents grows.

Figure 4. The dependence of the frequency of mutual defection (Fmd) and mutual cooperation (Fmc) on mutation rate (Rm) regarding the average of the last generation and all generations (Na=8, Ls=30, ±SD)

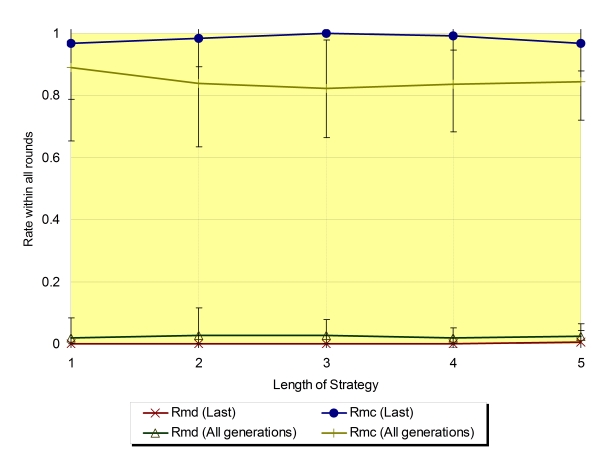
Figure 5. The rate of mutual defection (Rmd) and mutual cooperation (Rmc) (Na=2, Ls=1 to 5, ±SD) regarding the average of the last generation and all generations

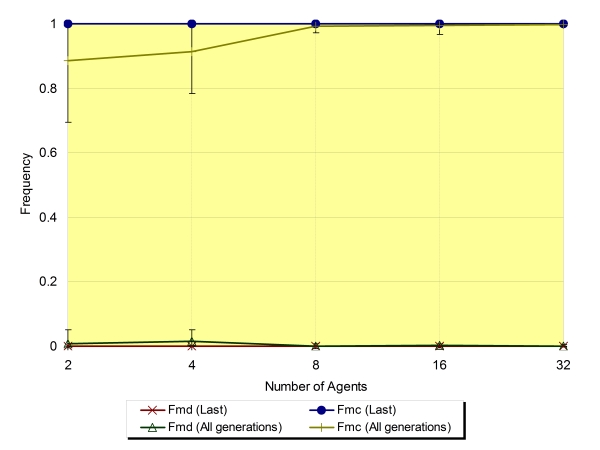
Figure 6. This figure show the dependence of the frequency of mutual defection (Fmd) and mutual cooperation (Fmc) on Na (Na=2 to 32, Ls=1, ±SD). In this case, the game takes the form of the simple prisoner's dilemma game

Various Sets of Variables

3.4

In the previous section, it is revealed that the second-best decision has an effect on the development of mutual cooperation in the sequential prisoner's dilemma game with simple situations. Next we show the results of various parameters, altering Na and Ls in a wider range. The traits of the second-best decision are probed from many viewpoints.

3.5

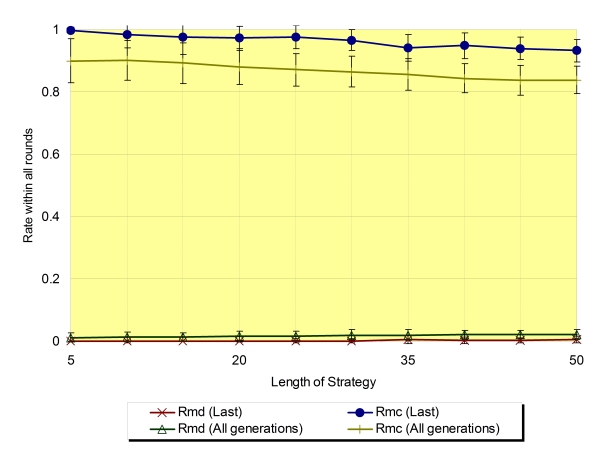
Figures 7, 8, 9 and 10 exhibit the dependence of Rmc and Rmd on Ls in cases of Na=4, 8, 16 and 32. In the results of Na=4 and 8 (Figure 7, 8), general characteristics of Rmd and Rmc do not differ greatly. Rmc slightly decreases when Ls grows. Nevertheless, its value is still high (around 0.80) in the case of Ls=50. On the other hand, the increase of Rmd is considerably suppressed at each Ls. These results show that the second-best decision works well for the emergence of cooperation. Figure 9 (at the case of Na=16) demonstrates another property. Rmc decreases rapidly when Ls exceeds 40. Moreover, for the case of Na=32 (Figure 10), Rmc is high only when Ls ≤ 20. These results do not change any more if the number of generations is doubled (from 5,000 to 10,000). Therefore, Rmd and Rmcare fully stable within 5,000 generations.

3.6

It is considered from these results that at high Na, Rmc decreases when Ls lengthens. This situation is caused by the diversity of initial strategies derived from the increase of Ls (and also Na). In that case, mutual cooperation can not easily settle among players. It is supposed from the results that the second-best decision is valid at every Na in the case that Ls is approximately under the critical value. The evidence of this supposition is described in the discussion section.

Figure 7. The rate of mutual defection (Rmd) and mutual cooperation (Rmc) regarding the average of the last generation and all generations (Na=4,±SD)

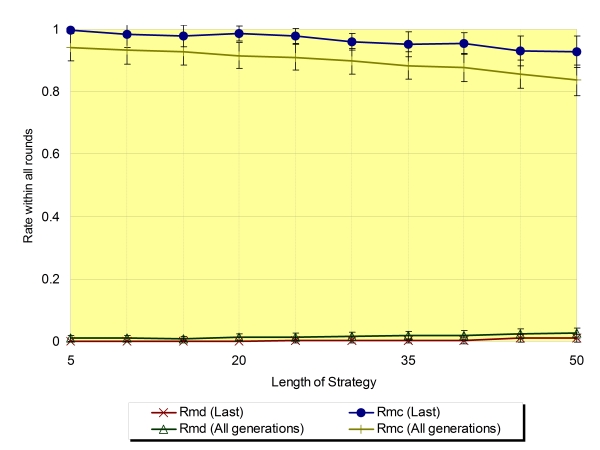
Figure 8. Rmd and Rmc regarding the average of the last generation and all generations (Na=8,±SD)

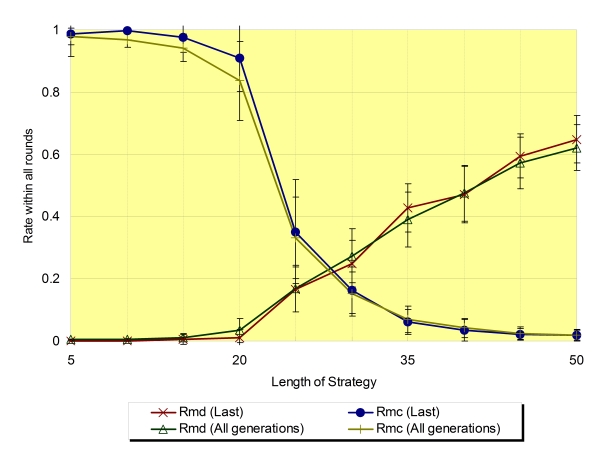
Figure 9. Rmd and Rmc regarding the average of the last generation and all generations (Na=16,±SD)

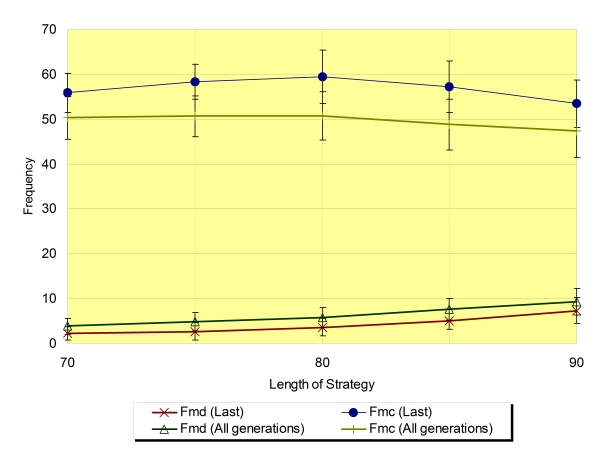
Figure 10. Rmd and Rmc regarding the average of the last generation and all generations (Na=32,±SD)

Discussion

Evaluation of the Critical Value

4.1

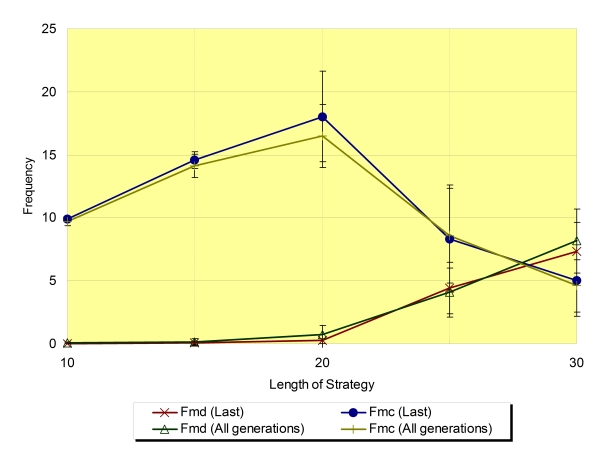
From the examination of various sets of Na and Ls, a criticality is found where Fmc no longer increases even if Ls lengthens. The critical length of strategy in each Na is studied and the results are also designated in Figures 11 to 13. If Na equals 8 (Figure 11), the critical length Lsc is approximately 80 (NaLsc≅6.4E+02). In the case of Na=16 (Figure 12), Lsc is nearly 35 (NaLsc≅5.6E+02). When Na has the value of 32 (Figure 13), Lsc roughly has the value of 20 (NaLsc≅6.4E+02). When mutual cooperation is at a high level, the range of Ls is necessarily under the value of Lsc in each case of Na.

Figure 11. The frequency of mutual defection (Fmd) and mutual cooperation (Fmc) around the critical value of Ls regarding the average of the last generation and all generations (Na=8,±SD)

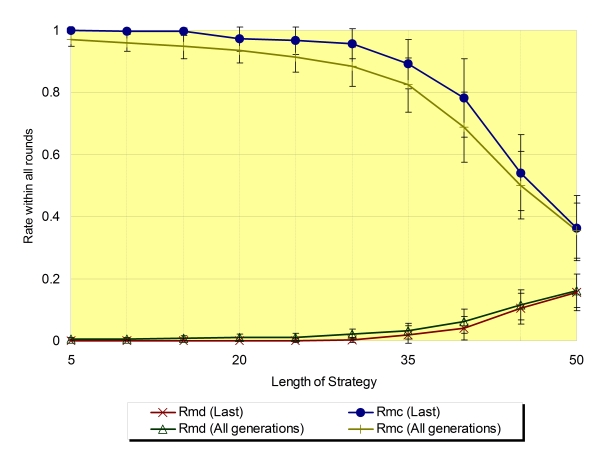
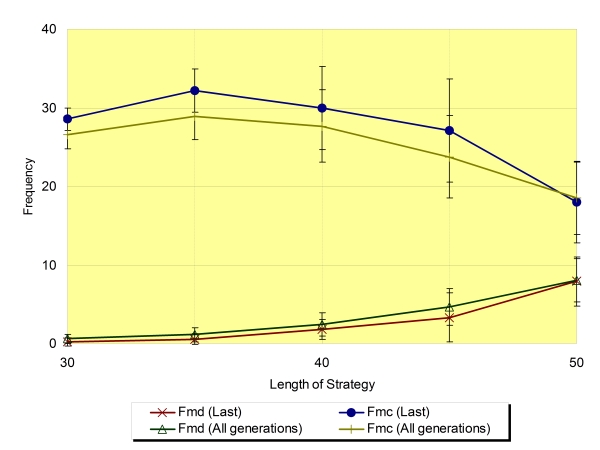
Figure 12. Fmd and Fmc around the critical value of Ls regarding the average of the last generation and all generations (Na=16,±SD)

Figure 13. Fmd and Fmc around the critical value of Ls regarding the average of the last generation and all generations (Na=32,±SD)

Applicability of our Model to Problems in the Real World

4.2

As we noted before, our model does not precisely express specific social phenomenon. However, the second-best decision in the model, which is the pursuit of moderate payoff and not maximum profit is similar to the mindset of collusive bidding. This bid-rigging scandal has become a significant social problem in Japan.

4.3

If you contemplate the strategy of the prisoner's dilemma game, you can see that outwitting the opponent in a bid can be regarded as defection and proposing the same price is also considered to be cooperation. Therefore, the strategy of our research corresponds to price bidding for each object at one time (Figure 14). The scenario of this model, which is that some matches are played between two groups at once, seems to be unrealistic because it correlates to the proposal of simultaneous price bidding. However, if you regard that context as the following method, the setting of this model becomes fully practical. First, bids are continuously made in some rounds (=Na=8 in this model). Second, the second-best decision is made based on the result of finite rounds. Third, subsequent proposals for continuous bids are prepared through decision (evolutionary process). You may think that the match between agents of the same ID seems to hinder evolution in the model. Nevertheless, that framework will become natural if an ID is recognized at the time of bidding (round 1, round 2,…; please refer to Figure 15).

4.4

Some methods have been proposed for the research of collusive bidding; for example, using the system based on the auction theory (Graham 1987; McAfee 1992), or trying to approach the question from the realm of experimental economics (Saijo 1996). Despite the limit of players (only two), our notion described here is novel and also significant because there has been no former research which has dealt with a case where spontaneously bidding players sacrifice their own payoff to some extent. As noted before, when the value of NaLs is over the criticality, cooperation is not facilitated even if each group adopts the second-best decision. From the result, it is expected that the increase of either the variety of proposals for bids (=Na) or the number of bidding objects in one bid (=Ls) makes it difficult to collude with each other.

Figure 14. Introduction of specific manner bidding

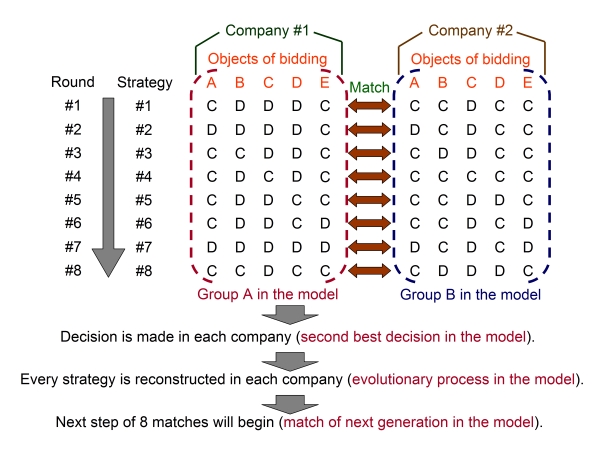
Figure 15. Correspondence between the particular bidding and the model

Conclusion

5.1: We have introduced a new method for mutual cooperation in the prisoner's dilemma game. It is referred to as the 'second-best decision' in this research, and works effectively when the product of NaLs is under the criticality. Our model challenges to offer other aspects of research to the prisoner's dilemma game, especially regarding strategy. In previous research, strategies have been limited in number or in pattern. Therefore, we improved strategy to become much more diverse and evolvable. The main feature of our model is summarized by the following two points. The first one is the variation derived from the structure of strategy. As strategy lengthens, it will become more varied. The second one is the evolvability of strategy. Through the evolutionary process, every strategy is consistently overwritten by the representative strategy. Patterns of strategy are quite large.
5.2: As we described in section 3, the second-best decision loses its effect on the development of mutual cooperation in the case of large Na (or Ls). The reason why that phenomenon occurs is that the diversity of strategy types is expanded. The result is understandable when it is compared to the situation of practical negotiation where there are many strategies (in other words, many opinions). In that situation, it is quite difficult to reach an agreement. That phenomenon did not occur in our previous research which treated perfectly altruistic decision. This is the fact that the second-best decision is not an expression of pure altruism, but has a selfish nature to some extent and also shows its practicality. It is significant for the applicability of the model that there is a case where cooperation is not facilitated even if each group acts somewhat altruistically. As described before, cooperative groups are similar to the minds of collusive companies. By further research, we can find more detailed conditions that interfere with cooperation, which is beneficial to the construction of rules for the prevention of collusive bidding.
5.3: At the present time, it is no doubt that the combination of the second-best decision and the evolutionary process has an effect on the emergence of cooperation. On the other hand, each strategy becomes uniform quite rapidly by that mechanism. We can not consequently remark from these results which method is the best scheme to facilitate cooperation. Either the rapid homogenization or the conservation of diversity at the initial generation. Our task in the future is to resolve this question through the use of another system in place of the procedure utilized in this research.

Appendix 1: results of two cases (either no duplication or no mutation)

A.1

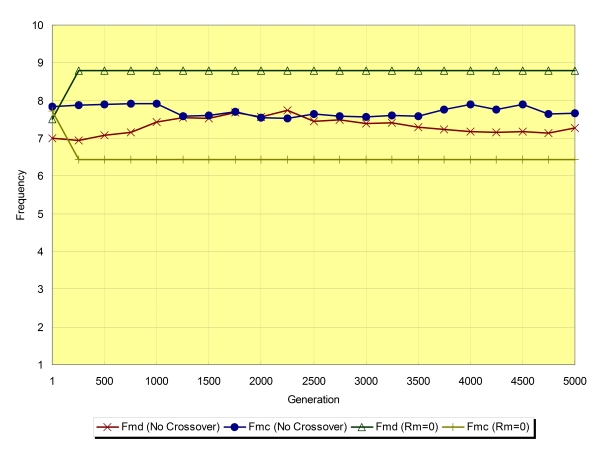
As shown in figure 16 below (Na=8, Ls=30, with the second-best decision), those cases do not achieve a highly cooperative state. In the case of no duplication, Fmd and Fmc fluctuate little (approximate 7.5) through the effect of mutation. On the other hand, when the mutation rate Rm is equal to 0 (no mutation), Fmd increases and Fmc decreases slightly at initial generation, but does not change any more for the rest of the generation. As a result, it is concluded that the collaboration of duplication and mutation (and also the second-best decision) facilitates mutual cooperation.

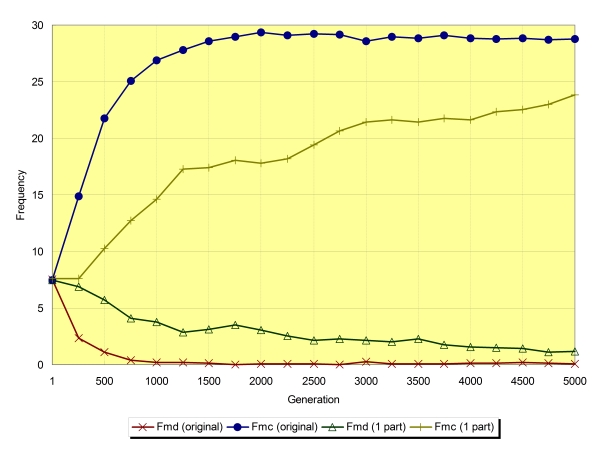
Figure 16.

Appendix 2: comparison between two methods (original vs 1 part duplication)

A.2

This research uses the method of 2 part duplication as the original method in the evolutionary process, because it performed much better than 1 part duplication, i.e., the convergence to the mutual cooperative state is faster (the following Figure 17, Na=8, Ls=30, with the second-best decision). The values of standard deviation (SD) regarding the Fmc in the last generation are quite different. In the case of 1 part duplication, the SD roughly equals 3.13, on the other hand, the SD in the original method is nearly 0.82. Now we plan to investigate differences between other methods in future work.

Figure 17.

Appendix 3: pseudo code regarding main routine


Function Main:
Start:
// The number of groups equals two in this research.
  for number_of_generations (<= from 1,000 to 5,000):
    for group_id (<= number_of_groups):
      Play_Match (group_id):
      Update_Strategy (group_id):
    end for:
  end for:
End:

Function Play_Match (Group_ID):
Start:
  // The sequential prisoner's dilemma game is played between the agents
  // of the same id.
  // The number of total game is equal to the number of opponent groups.
  // The number of opponent groups equals one in this research.
  for opponent_group_id (<= number_of_opponent_groups):
    for agent_id (<= number_of_agents, Na):
      for rounds (<= length_of_strategy, Ls):
        if Strategy[Group_ID][agent_id][rounds] == D and
        Strategy[opponent_group_id][agent_id][rounds] == C then:
          Score[Group_ID][agent_id]
          = Score[Group_ID][agent_id] + 5:
        end if:
        else if Strategy[Group_ID][agent_id][rounds] == C and
        Strategy[opponent_group_id][agent_id][rounds] == C then:
          Score[Group_ID][agent_id]
          = Score[Group_ID][agent_id] + 3:
        end else if:
        else if Strategy[Group_ID][agent_id][rounds] == D and
        Strategy[opponent_group_id][agent_id][rounds] == D then:
          Score[Group_ID][agent_id]
          = Score[Group_ID][agent_id] + 1:
        end else if:
        else:
          Score[Group_ID][agent_id]
          = Score[Group_ID][agent_id] + 0:
        end else:
      end for:
    end for:
  end for:
  // Final score about the strategy of agent is the average of all Sequential PDGs.
  for agent_id (<= Na):
    Score[Group_ID][agent_id]
    = Score[Group_ID][agent_id] / number_of_opponent_groups:
  end for:
End:

Function Update_Strategy (Group_ID):
Start:
  // All strategies of agents about the group are graded by their score.
  Grade_Strategy:
  // The strategy of the second grade in the group is selected as the representative
  // strategy. The representative agent ID (=strategy ID) is decided.
  representative_agent_id = agent_id (with the second grade strategy):
  // Note. Both values of the length_of_fraction_1 (Lf1) and the
  // length_of_fraction_2 (Lf2) are randomly changes in every step.
  // The Lf1 and the Lf2 are less than Ls. The Lf1 is smaller than the Lf2.
  // The representative strategy is partly duplicated to every strategy as follows.
  for agent_id (<= Na, not equal to the representative agent ID):
    for rounds_1 (<= Lf1):
      Strategy[Group_ID][agent_id][rounds_1] =
      Strategy[Group_ID][representative_agent_id][rounds_1]:
    end for:
    for rounds_2 (Lf2 <= rounds_2 <= Ls):
      Strategy[Group_ID][agent_id][rounds_2] =
      Strategy[Group_ID][representative_agent_id][rounds_2]:
    end for:
  end for:
  // The process of mutation is executed for every strategy of agent.
  for agent_id (<= Na):
    for rounds (<= Ls):
      if (a value randomly generated is over the threshold) then:
        if Strategy[Group_ID][agent_id][rounds] == C then:
          Strategy[Group_ID][agent_id][rounds] = D:
        end if:
        else:
          Strategy[Group_ID][agent_id][rounds] = C:
        end else:
      end if:
    end for:
  end for:
End:

Acknowledgements

: We greatly appreciate fruitful discussions with laboratory members and helpful comments from them for the improvement of our research.

References

AHMED, E, Hegazi, A S and Elgazzar, A S (2002) On spatial asymmetric games. Advances in Complex Systems, 5, pp. 433-443.

ANDRES GUZMAN, R, Rodriguez-Sickert, C and Rowthorn, R (2007) When in Rome, do as the Romans do: the coevolution of altruistic punishment, conformist learning, and cooperation. Evolution and Human Behavior, 28, pp. 112-117.

AXELROD, R (1984) The Evolution of Cooperation. Basic Books, New York.

AXELROD, R (1997) The Complexity of Cooperation. Princeton University Press, Princeton.

BERNHARD, H, Fischbacher, U and Fehr, E (2006) Parochial altruism in humans. Nature, 442, pp. 912-915.

BSHARY, R and Grutter, A S (2006) Image scoring and cooperation in a cleaner fish mutualism. Nature, 441, pp. 975-978.

CAO, Z and Hwa, R C (1999) Phase transition in evolutionary games. Int. Jour. of Mod. Phys. A, 14, pp. 1551-1560.

CRAIG MACLEAN, R and Gudelj, I (2006) Resource competition and social conflict in experimental populations of yeast. Nature, 441, pp. 498-501.

DAWES, C T, Fowler, J H, Johnson, T, McElreath, R and Smirnov, O (2007) Egalitarian motives in humans. Nature, 446, pp. 794-796.

FEHR, E and Gachter, S (2002) Altruistic punishment in humans. Nature, 415, pp. 137-140.

FEHR, E and Rockenbach, B (2003a) Detrimental effects of sanctions on human altruism. Nature, 422, pp. 137-140.

FEHR, E and Fischbacher, U (2003b) The nature of human altruism. Nature, 425, pp. 785-791.

FIEGNA, F, Yu, Yuen-Tsu N, Kadam, S V and Velicer, G J (2006) Evolution of an obligate social cheater to a superior cooperator. Nature, 441, pp. 310-314.

FORT, H (2003) Cooperation with random interaction and without memory or "tags". Journal of Artificial Societies and Social Simulation 6 (2) 4 https://www.jasss.org/6/2/4.html.

FORT, H and Sicardi, E (2007) Evolutionary Markovian strategies in 2×2 spatial games. Physica A, 375, pp. 323-335.

FOWLER, J H (2005) Altruistic punishment and the origin of cooperation. Proc. Natl. Acad. Sci. USA, 102, pp. 7047-7049.

GRAHAM, D and Marshall, R (1987) Collusive behavior at single-object second-price and English auctions, Journal of Political Economy, 95, pp. 1217-1239.

GRIFFIN, A S, West, S A and Buckling, A (2004) Cooperation and competition in pathogenic bacteria. Nature, 430, pp. 1024-1027.

HALES, D (2001) Tags produce cooperation in the prisoner's dilemma. Simulating Society V workshop: "The frontiers of social science simulation", Kazimierz Dolny, Poland.

HAUERT, C and Doebeli, M (2004) Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature, 428, pp. 643-646.

KIM, B J et al. (2002) Dynamic instabilities induced by asymmetric influence: prisoner's dilemma game on small-world networks. Phys. Rev. E, 66, 021907.

KRUEGER, F et al. (2007) The Neural Correlates of Trust. Proc. Natl. Acad. Sci. USA, 104, pp. 20084-20089.

KURZBAN, R, DeScioli, P and O'Brien, E (2007) Audience effects on moralistic punishment. Evolution and Human Behavior, 28, pp. 75-84.

MAYNARD SMITH, J (1982) Evolution and the Theory of Games. Cambridge University Press, Cambridge.

MCAFEE, P and McMillan, J (1992) Bidding rings, American Economic Review, 82, pp. 579-599.

MCNAMARA, J M, Barta, Z and Houston, A I (2004) Variation in behaviour promotes cooperation in the Prisoner's Dilemma game. Nature, 428, pp. 745-748.

NOWAK, M A and May, R M (1992) Evolutionary games and spatial chaos. Nature, 359, pp. 826-829.

NOWAK, M A and Sigmund, K (1998a) The dynamics of indirect reciprocity. J. Theor. Biol., 194, pp. 561-574.

NOWAK, M A and Sigmund, K (1998b) Evolution of indirect reciprocity by image scoring. Nature, 393, pp. 573-577.

NOWAK, M A, Sasaki, A, Taylor, C and Fudenberg, D (2004) Emergence of cooperation and evolutionary stability in finite populations. Nature, 428, pp. 646-650.

NOWAK, M A and Sigmund, K (2005) Evolution of indirect reciprocity. Nature, 437, pp. 1291-1298.

OHDAIRA, T, Ohashi, H, Chen, Y and Hashimoto, Y (2006) Partiality causes unhappiness: randomness of network induces difficulty in establishing cooperative relationship. The First World Congress on Social Simulation (WCSS06), Kyoto, Japan.

OHDAIRA, T and Ohashi, H (2007) The effect of occasional rational decision on the cooperative relationship between groups. The Twelfth International Symposium on Artificial Life and Robotics (AROB 12th '07), Beppu, Oita, Japan.

OHTSUKI, H, Hauert, C, Lieberman, E and Nowak, M A (2006) A simple rule for the evolution of cooperation on graphs and social networks. Nature, 441, pp. 502-505.

PANCHANATHAN, K and Boyd, R (2003) A tale of two defectors: the importance of standing for the evolution of reciprocity. J. Theor. Biol., 224, pp. 115-126.

PANCHANATHAN, K and Boyd, R (2004) Indirect reciprocity can stabilize cooperation without the second-order free rider problem. Nature, 432, pp. 499-502.

RIOLO, R L (1997) The effects and evolution of tag-mediated selection of partners in populations playing the iterated prisoner's dilemma. Proc. of the 7th Int. Conf. on Genetic Algorithms (ICGA97), Morgan Kaufmann, San Francisco, pp. 378-385.

RIOLO, R L, Cohen, M D C and Axelrod, R (2001) Evolution of cooperation without reciprocity. Nature, 414, pp. 441-443.

ROCKENBACH, B and Milinski, M (2006) The efficient interaction of indirect reciprocity and costly punishment. Nature, 444, pp. 718-723.

RUTTE, C and Taborsky, M (2007) Generalized reciprocity in rats. PLoS Biol. 5(7): e196 doi:10.1371/journal.pbio.0050196.

SAIJO, T, Une, M and Yamaguchi, T (1996) Dango experiments, Journal of Japanese and International Economics, 10, pp. 1-11.

SEO, Y G, Cho, S B and Yao, X (2000) The impact of payoff function and local interaction on the n-player iterated prisoner's dilemma. Knowledge and Information Systems, 2, pp. 461-478.

STEPHENS, D W, McLinn, C M and Stevens, J R (2002) Discounting and reciprocity in an iterated prisoner's dilemma. Science, 298, pp. 2216-2218.

TANKERSLEY, D, Jill Stowe, C and Huettel, S A (2007) Altruism is associated with an increased neural response to agency. Nature Neuroscience, 10, pp. 150-151.

TURNER, P E and Chao, L (1999) Prisoner's dilemma in an RNA virus. Nature, 398, pp. 441-443.

TURNER, P E and Chao, L (2003) Escape from prisoner's dilemma in RNA phage Φ6. The American Naturalist, 161, pp. 497-505.

WARNEKEN, F, Hare, B, Melis, A P, Hanus, D and Tomasello, M (2007) Spontaneous altruism by chimpanzees and young children. PLoS Biol. 5(7): e184 doi:10.1371/journal.pbio.0050184.

YAO, X and Darwen, P J (1994) An experimental study of n-person iterated prisoner's dilemma games. Informatica, 18, pp. 435-450.

Button Return to Contents of this issue