Abstract

Now that complex Agent-Based Models and computer simulations spread over economics and social sciences - as in most sciences of complex systems -, epistemological puzzles (re)emerge. We introduce new epistemological concepts so as to show to what extent authors are right when they focus on some empirical, instrumental or conceptual significance of their model or simulation. By distinguishing between models and simulations, between types of models, between types of computer simulations and between types of empiricity obtained through a simulation, section 2 gives the possibility to understand more precisely - and then to justify - the diversity of the epistemological positions presented in section 1. Our final claim is that careful attention to the multiplicity of the denotational powers of symbols at stake in complex models and computer simulations is necessary to determine, in each case, their proper epistemic status and credibility.

Keywords:

Agent-Based Models and Simulations, Epistemology, Economics, Social Sciences, Conceptual Exploration, Model World, Credible World, Experiment, Denotational Hierarchy

Introduction: Methodical Observation versus Conceptual Analysis

1.1

Models and empirical enquiries have often been opposed. Such an opposition between observational experiment and reasoning has led to classical oppositions: empirical sciences are seen as based on methodic observation (inquiry, experiment) whereas theoretical and modeling approaches are thought of as founded on a conceptual or hypothetico-deductive approach.

1.2

Interestingly, even if simulation is still often defined with reference to modeling (e.g. as a “dynamical model … that imitates a process by another process”, Hartmann, 1996), it has been more systematically compared to a kind of experiment or to an intermediary method between theory and experiment (Peck, 2004, Varenne 2001). In agent-based simulation, Tesfatsion (2006) talked about “computational laboratory” as a way “to study complex system behaviors by means of controlled and replicable experiments”, and Axelrod (1997/2006) claimed that simulation in social sciences is “a third way for doing science”, between induction and deduction.

1.3

The first aim of this paper is to review, discuss and extend these rather converging positions on simulations in the case of agent-based models of simulation in economics and social sciences, based on MAS (multi-agent systems) software technology (Ferber, 1999, 2007). In this case, as underlined by Axelrod (1997/2006), simulation begins with model building activity, even if analytical exploration of the model is often impracticable. Recently, authors have proposed to distinguish between ontology design and model implementation in this initial step of model engineering (Bommel, Müller 2007, Livet et al. 2008). As model building is an unavoidable phase of agent-based simulation, the first section is a review of the main epistemologies of models, with a special interest for economics models, taking the paradigmatic Schelling models of segregation as an example. It stresses some recent claims about the empirical nature of models in economics and social sciences. More and more authors say that models and simulations in social sciences - specifically as far as multi-agent models are concerned - present a shift from a kind of “conceptual exploration” to a new way of doing “experiments”. Section two recalls some of the recent puzzles about the empiricity (i.e. the empirical aspect) of such practices. It proposes to adapt and use the two notions of sub-symbolization (Smolensky, 1998) and denotational hierarchy (Goodman, 1981) to explain further crucial differences, (1) between models and simulations, (2) between models and simulations of models and (3) between kinds of simulations. Those concepts enable us to explain why multi-agent modeling and simulation produce new kinds of empiricity, not far from the epistemic power of ordinary experiments. They enable us to understand why some authors are right to disagree on the epistemic status of models and simulations, especially when they do not agree on the denotational level of the systems of symbols they implement.

Modeling and experiment (1) Epistemological conceptions on scientific models

2.1

Since the beginning of the 20th century, the term “model” has spread in the descriptions of scientific practices, particularly in the descriptions of the practices of formalization.

2.2

Having founded their first expansion in a movement of emancipation toward monolithic theories in physics (such as mechanics), scientific models have first been explained by epistemologists through systematic comparisons to theories. Consequently, in the first neo-positivist epistemology, models were viewed not as autonomous objects, but as theoretically driven derivative instruments. Following the modelistic turn in mathematical logic, the semantic epistemological conception of scientific models persisted to emphasize on theory. For such a view, a model is a structure of objects and relations (more or less abstract) that is one of the possible interpretations of a given theory. But this view stresses also the different layers of formal structures, hence their discontinuity and heterogeneity.

2.3

More recently, models have been compared to experimental practices (Fischer, 1996; Franklin, 1986; Galison, 1997; Hacking, 1983; Morrison, 1998). For a rather similar pragmatic point of view (Morgan, 1999), models are “autonomous mediators” between theories, practices and experimental data. They are built in a singular socio-technical context and in order to solve a specific and explicit problem emerging from this context.

Modeling and experiment (2) An open and pragmatic view: the model as a questionable construct

3.1

Without going further in the debate between semantic and pragmatic views in epistemology of models, it is possible to get some insight on the weak relations between scientific models and theories through the general and pragmatic characterization of a model by Minsky (1965): “To an observer B, an object A* is a model of an object A to the extent that B can use A* to answer questions that interest him about A”.

3.2

Minsky minimally sees a model as a questionable construct. As a construct, the model is an abstraction of an “object domain” formalized by means of an unambiguous language. Such a characterization assumes that the model A* is sufficient to answer the question asked by B (see Amblard et al. 2007).

3.3

Note that this loose characterization does not imply that the model is based on a relevant theory of the empirical phenomenon of the considered domain. It is enough to say that such a questionable construct exemplifies some definite “constraints on some specific operations” (Livet, 2007). Therefore, in general, a scientific model is not an interpretation of a pre-existing theory, but a way to explore some properties in the virtual world of the model. In particular, according to Solow (1997), it can serve to evaluate the explanatory power of some hypothesis (constructed by abduction) isolated by abstraction: “the idea is to focus on one or two causal or conditioning factors, exclude everything else, and hope to understand how just these aspects of reality work and interact” (p. 43). Due to this characteristic, some authors have compared the model to real experiment. Let us further clarify some of the points that models share with experiment.

Modeling and experiment (3) The “isolative analogy” between models and experiments

4.1

Economists usually distinguish the abstract worlds of the models from the “real world” of the empirical phenomenon. This neither means that they are pure formalists nor that talking about a “real world” implies a metaphysical realistic commitment. This is just to underline the recognition of a problematic relationship between the abstract world of the models and the concrete empirical reality.

4.2

For Mäki, abstractions in models are similar to abstractions in experiments as they both can be interpreted as a kind of isolation. Accordingly, model building can be viewed as a quasi-experimental activity or as the “economist’s laboratory” (Mäki, 1992, 2002, 2005). This analogy between models and experiments is called “isolative analogy” by Guala (2008). From Mäki’s standpoint, a model can be said to be experimented in its explanatory dimension: the finality of such a model is to explore the explanatory power of some causal mechanism taken in isolation. Significantly, Guala is less optimistic than Mäki. He refuses to overlook the remaining differences between a model and an experiment:

“In a simulation, one reproduces the behavior of a certain entity or system by means of a mechanism and/or material that is radically different in kind from that of a simulated entity (…) In this sense, models simulate whereas experimental systems do not. Theoretical models are conceptual entities, whereas experiments are made of the same ‘stuff’ as the target entity they are exploring and aiming at understanding” (Guala 2008, p.14).

It is often by using the mediating and rather paradoxical notion of “stylized facts” that authors give themselves the possibility to overlook this difference in “stuff”, when comparing models and experiments.

4.3

Sugden (2002) suggests a slightly different approach in which the two worlds are to be distinguished. The abstract “world of the model” is a way to evaluate through virtual experiments the explanatory power of some empirically selected assumptions. The problematic relationship between this abstract world and the real one can be summarized by two questions. To what extent can such a virtual world have some link with the “real world”? What kind of (weak) realism is at stake here?

Modeling and experiment (4) The scope and meaning of Schelling’s conjecture according to Sugden (2002)

5.1

A model (in a broad meaning) can be seen as an abstract object. As such, it is based on a principle of parsimony. It is a conceptual simplification which stresses one or more conjecture(s) concerning the empirical reality. Moreover, it is built to answer a specific question which can have an empirical origin. In this specific case, one talks about empirically oriented conceptualization.

5.2

Sugden (2002) takes Schelling’s model of segregation (Schelling, 1978) as an example. According to Solow (1997), there is a first empirical question in every process of modeling: a regularity (or “stylized fact”) is previously observed in phenomenological material from empirical reality. In the Schelling case, it is the persistence of racial segregation in housing. Then a conjecture is proposed. In this case, Schelling’s conjecture says that this phenomenon (persistent racial segregation in housing) could be explained by a limited set of causal factors (parsimony).

5.3

According to this conjecture, a simplified model is constructed where agents interact only locally with their 8 direct neighbors (within a Moore neighborhood). No global representation about the residential structure is available to agents. The only rule specifies that each agent would stay in a neighborhood with up to 62% of people with another color. Finally, the simulation of the model shows that a slight perturbation is sufficient to induce local chain reactions and emergence of segregationist patterns. In other words, “segregation” (clusters) is observed as an emergent property of the model.

5.4

This does not mean that these explanatory factors are the only possible ones, nor that they are effectively the main causal factors for the empirical observed phenomenon. This empirical observation of the model only gives the right to claim that these factors are possible explanatory candidates. What is tested with this approach is nothing but “conditions of possibilities” and not directly the genuine presence of these conjectured factors in the empirical reality.

5.5

In the Schelling case, (1) he observes a regularity R in the phenomenological data observed from the “real world” (here it is that persistent racial segregation in housing); (2) he conjectures that this regularity can be explained by a limited set (parsimony) of causal factors F (here it is the simple local preferences about neighborhood).

5.6

Hence, according to Sugden (2002), Schelling’s approach relies on three claims:

(1) R occurs (or often occurs)

(2) F operates (or often operates)

(3) F causes R (or tends to cause it)

Schelling doesn’t present explicitly these claims as testable hypotheses. But claims (1) and (2) get informal evidence from selected case studies.

5.7

The unresolved question concerning the problematic relationship between the conjectural and abstract “world of the model” and the “real world” remains. Sugden (2002) discusses different strategies to answer this question. He rejects first the instrumentalist view (Friedman, 1953) which represents models as (testable) instruments with predicting power. For Sugden, the goal of Schelling clearly is an explanatory one. Contrary to the instrumentalists’ view, Schelling does not construct “any explicit and testable hypothesis about the real world” (Sugden, 2002, p.118). Sugden discusses also the notions of models as conceptual explorations, thought experiments and explaining metaphors. According to Hausman (1992), all these approaches are incomplete, because the persistent gap between the “world of the model” and the “real world” is not filled. Sugden suggests filling the gap by an inductive inference: the credible world argument.

5.8

In the suggested interpretation, Schelling connects first in abstracto real causes (segregationist preferences) to real effects (segregationist cluster emergence). Afterwards, instead of “testing” empirical predictions from the models, he tries to convince us of the credibility of the corresponding assumptions. Schelling’s unrealistic model is “supposed to give support to these claims about real tendencies”. For Sugden, this method “is not instrumentalism: it is some form of realism” (Sugden, 2002,  p.118). Before going deeper in this question of “realist” credible world (section 7), let us discuss first the strategy of “conceptual exploration”.

Modeling and experiment (5) Conceptual exploration and “internal validity”

6.1

Following Hausman (1992), we speak of the use of a model as a “conceptual exploration” when we put the emphasis on the internal properties of the model itself, without taking into account the question of the relationship between the “model world” and the “real world”. The study of the model’s properties is the ultimate aim of this approach. The relevant methods used to explore and evaluate “internally” the properties of the model depend on its type, and not on its relationship with the corresponding empirical phenomenon.

6.2

Similarly to a test of consistency performed on a set of concepts put together in a form of a closed verbal argument, the properties of the model which are tested here are essentially evaluated in terms of consistency. From this standpoint, the model is viewed as a pure conceptual construct. As Hausman (1992) underlines, conceptual exploration can be valuable because there are numerous examples of unsuspected inconsistencies or unidentified properties in the existing models.

6.3

An extension of this method enables an assessment of the robustness of the results of the model with respect to variations in its hypotheses (as in the studies of sensibility). But it is important to note that when the exploratory method is no more purely analytic, some scholars claim that it becomes a quasi-experimental activity.

6.4

Following Guala (2003) on this point, we can interpret all the means used by this approach of conceptual exploration as different efforts to validate the model in the sense of an internal validity:

 “Whereas internal validity is fundamentally a problem of identifying causal relations, external validity involves an inference to the robustness of a causal relation outside the narrow circumstances in which it was observed and established in the first instance” (Guala 2003, p. 1198-1199).

6.5

Guala sees a huge gap between internal and external validity because, for him, models always simulate with the aid of radically different stuffs from the ones of the real world. But many cases of development of conceptual explorations on models show that there is a more gradual and progressive shift from a “conceptual exploration”, strictly speaking, to a first kind of “external validation”. According to us, that is the reason why some scholars persist to use - with some good reasons - the notion of quasi-experimental activity. So, let us further explore this notion of “credible worlds”.

Modeling and experiment (6) Models as “credible worlds” (Sugden, 2002)

7.1

In this concern, Sugden’s approach is interesting. First, it gives more details on the nature of the conceptual exploration performed through a model. Second, by introducing the notion of “credible world”, he proposes that we treat more directly the link between the model world and the real world.

7.2

According to Sugden, economists “formulate credible (ceteris paribus) and pragmatically convenient generalizations concerning operations related to the appropriate causal variable”. Then, the model analyst uses deductive reasoning to identify what effects these factors will have under these specific hypotheses (i.e. in this particular isolated environment). These analyses of robustness provide reasons to believe that the model is not specific but could be generalized, including the original model as a special case.

7.3

To that extent, the corresponding cognitive process is an inductive inference, i.e. an inference from the cases of already experimented models to more general model cases. But this mode of reasoning concerns scenarios for conceptual exploration which remain within the world of models. From this viewpoint, the test of robustness cannot really be interpreted as being on the adequacy between the world of models and the real world. As Sugden emphasizes, some special links between the two worlds are still required.

7.4

At this point, Sugden introduces the idea that a model has to be thought of as a “credible world”. This argument works as an inductive inference too, but an inference from the model world to the real world. The desirable outcome is the recognition of some “significant similarity” between these two worlds. For Sugden, Schelling constructed “imaginary cities” which are easily understandable because of their explicit generative mechanisms. “Such cities can be viewed as possible cities, together with real cities”. Through Schelling’s argument, we are invited to make the inductive inference that similar causal processes occur in real cities.

7.5

The whole process can be summed up as 3 phases of an abductive process:

(a) The modeler observes that segregation occurs in the real world, and makes the abduction (in a narrow sense) or conjecture that segregation (S) is caused by Individual Preferences over Neighborhood Structure (IPoNS).
(b) The modeler experiments and deduces that in the model world, S is caused by IPoNS.
(c) The modeler infers that there are some good reasons to believe that IPoNS also operates in the real world, even if it is not the only possible cause of S.

That is, IPoNS is a credible candidate to explain S and then the “world of model” is a “possible reality” or a “parallel reality”. Sugden (2002) specifies this kind of “realism”: “Here, the model is realistic in the same sense as a novel can be called realistic […] the characters and locations are imaginary, but the author has to convince us that they are credible” (p.131).

7.6

Clearly, such an assessment of the “model world” is not strictly about its empirical testability, but more about its argumentative power. Anyway, the notions of “similar causal processes” and “parallel reality” can play a role in an empiricist epistemology of simulation. But Sugden does not give us much precision on these notions of “similarity” and “parallelism”. The notions of “significant similarity” and “constraint on the operations” of Livet (2007) also could help us to go further into the evaluation of the empirical roles of models and simulations.

7.7

Section 2 aims to introduce conceptual tools (such as relative iconicity) so as to give a more detailed account of what determines the epistemic status of models and computer simulations and what determines their credibility.

Models, Simulations and Kinds of Empiricity

8.1

An epistemic means is a means that is used in the construction of knowledge (such as observations, field enquiries, data collections, experiments, hypotheses, drawings, graphics, diagrams, mnemotechnic means, informal or formal laws, theories, models, simulations, …). From this viewpoint, models - and even more simulations - are quite often said to be empirical epistemic means. What is less often noticed is that such claims are rarely founded on the same reasons.

8.2

 

Following (Nadeau 1999), who defines empiricity as “the characteristic of what is empirical”, let’s call empiricity the property of an epistemic means to lead to any empirical knowledge. A given knowledge is said to be empirical as it is elaborated through a certain process of experience, this last term being taken in its broad meaning, ranging from a passive observation to an active inquiry and/or experimentation.

8.3

 

If, as we assume it, this is not always for the same and unique reason that models and/or simulations are sometimes viewed as empirical means, there must be different kinds of empiricity. Accordingly, the aim of this section is to introduce concepts which enable to distinguish and characterize these different kinds of empiricity. In this concern, what we need first, is to clarify again the notions of model, of simulation, of model of simulation and of experiment on a model.

 

Models, Simulations and Kinds of Empiricity (1) Models and computer simulations: some more definitions and characterizations

9.1

First of all, although they seem to remain constantly linked in practice - even in simulations based on multi-models and multi-formalisms (Nadeau 1999) -, it is necessary to conceptually distinguish models from simulations and to characterize the practice of computer simulation (CS) apart from a central reference to a unique model. Roughly speaking, a model can still be defined as a formal construct possessing a kind of unity, formal homogeneity and simplicity, which are chosen so as to satisfy a specific request (prediction, explanation, communication, decision, etc.). But, concerning simulation, current definitions need to be modified and somewhat generalized. Scholars, especially in physics and engineering sciences, often used to say that “a simulation is a model in time”. For instance, according to Hartmann (1996):

“Simulations are closely related to dynamic models” [i.e. models with assumptions about the time-evolution of the system] ... More concretely, a simulation results when the equations of the underlying dynamic model are solved. This model is designed to imitate the time evolution of a real system. To put it another way, a simulation imitates a process by another process” (Hartmann, 1996, p. 82).

9.2

Humphreys (2004) follows Hartmann (1996) on the “dynamic process”. For Parker (forthcoming work quoted by Winsberg 2009), a simulation is:

“A time-ordered sequence of states that serves as a representation of some other time-ordered sequence of states ; at each point in the former sequence, the simulating system’s having certain properties represents the target system’s having certain properties.”

It is true that a simulation takes time as a step by step operation. It is also true that a modeled system interests us in particular in its temporal aspect. But it is not always true that the dynamic aspect of the simulation imitates the temporal aspect of the target system. Some CS can be said to be mimetic in their results but non-mimetic in their trajectory (Varenne 2007).

9.3

A partially similar distinction is evoked by Winsberg (2009). In fact, we have to distinguish simulations of which the trajectory tends to be temporally mimetic from other simulations that are tricks of numerical calculus. These tricks enable us to attain the result without following a trajectory similar to the one either of the real system, or of the apparent temporal (historical) aspect of the resulting pattern of the simulation. For instance, it is possible to simulate the growth of a botanical plant sequentially and branch by branch (through a non-mimetic trajectory) and not through a realistic parallelism, i.e. burgeon by burgeon (through a mimetic trajectory), and to obtain the same resulting and imitating image (Varenne 2007). Thereafter, the resulting static image can be interpreted by the observer as a pattern which has an evident temporal (because historical) aspect, clearly visible from the arrangement of its branching structure. But, this observer has no way to know whether this imitated historical aspect has been obtained through a really mimetic temporal approach or not. But both of them are simulation processes.

9.4

The same remark holds for Social Sciences. If we distinguish between “historical genesis” and “logical genesis, the processes are not the same. The logical genesis progresses along an abstract / a-historic succession of steps, with no intrinsic temporality.

9.5

So, depending on its kind, a simulation does not always have to be founded on the direct imitation of the temporal aspect of the target system. It depends on what is first simulated, or imitated. It is a bit problematic to see that the temporal aspect is itself dependent on the persistent - but vague - notion of imitation. Surely, it remains most of the time correct and useful to see a CS as an imitating temporal process originally founded on a mathematical model. It is a convenient definition because the notion of similitude is only alluded to. This definition remains correct when it suffices to analyze the relations between a classical implementation of a unique model and its computational instantiation on a computer (“simulation of model”).

9.6

However, it becomes very restrictive - and sometimes false - when we consider the variety of contemporary CS strategies. Today, there exist various kinds of CS of the same model or of different systems of submodels. As a result, in order to characterize a CS, are we condemned to rehabilitate the old notion of similitude which Goodman (1968), among others, shows to be very problematic due to being relativistic? Are we condemned to the classical puzzle caused - as shown again by Winsberg (2009) - by a dualistic position assuming that there are only two types of similarities at stake in an experiment or a simulation: formal or material (Guala, 2008)?

Models, Simulations and Kinds of Empiricity (2) Subsymbols and denotational hierarchy in simulations

10.1

In fact, following Varenne (2007, 2008), it is possible to give a minimal characterization of a CS (not a definition) referring neither to an absolute similitude (formal or material) nor to a dynamical model.

10.2

First, let’s say that a simulation is minimally characterized by a strategy of symbolization taking the form of at least one step by step treatment. This step by step treatment proceeds at least in two major phases:

- 1^st phase (operating phase): a certain amount of operations running on symbolic entities (taken as such) which are supposed to denote either real or fictional entities, reified rules, global phenomena, etc.

- 2^nd phase (observational phase): an observation or a measure or any mathematical or computational re-use (e.g., in CSs, the simulated “data” taken as data for a model or another simulation, etc.) of the result of this amount of operations taken as given through a visualizing display or a statistical treatment or any kind of external or internal evaluations.

10.3

In analog simulations, for instance, some material properties are taken as symbolically denoting other material properties. In this characterization, the external entities are said “external” as they are external to the systems of symbols specified for the simulations, whether these external entities are directly observable in empirical reality or whether they are fictional or holistic constructs (such as “rate of suicide”).

10.4

Because of these two distinct and major phases in any simulations, the symbolic entities denoting the external entities can be said to be used in a classical symbolic way (as in any calculus), but also in a subsymbolic way. Smolensky (1988) coined the term “subsymbol” to designate those empirical entities processing in a connectionist network at a lower level and which aggregation can be called a symbol at an upper level. They are constituents of symbols: “they participate in numerical – not symbolic – computation” (p.3). Berkeley (2008) has recently shown that Smolensky’s notion has to be interpreted in regard to a larger scale and from an internal relativistic point of view. This relativity of symbolic power is what we want to express through our relativistic use of the term.

10.5

In a simulation, the symbolic entities are denoting (sometimes through complex routes of reference). They are symbols as such. But, it is some global result of their interactions which is of interest, during the second phase. During this evaluation phase, they are treated at another level than the one at which they first operated. They were first treated as symbols, each one denoting at a certain level and through a precise route of reference. But they finally are treated as relative subsymbols.

10.6

Simulation is a process, but it is more characteristically a way of partially using entities taken as symbols in a less convention-oriented fashion and with less combinatorial power Berkeley (2000), i.e. with more “independence to any individual language” (Fischer, 1996), comparatively to other levels of systems of symbols. So, we define here a sub-symbolization as a strategy to use symbols for a partial “iconic modeling” (Frey, 1961). Contrary to what could be said in 1961 (in Frey, 1961), not all simulations are iconic modeling in the sense of the iconicity images can have. However, they present at least some level of relative iconicity. Fischer (1996) defines “iconicity” as “a natural resemblance or analogy between a form of a sign [...] and the object or concept it refers to in the world or rather in our perception of the world”. She insists on the fact that not all iconicities are imagic and that an iconic relation is relative to the standpoint of the observer-interpreter. What is the most important is this property of an iconic relation to be - relatively to a given language or vision of the world - less dependent of this language.

10.7

Let us say now that a CS is a simulation for which we delegate (at least) the first phase (the operating one) of the step by step treatment of symbolization to a digital and programmable computer. Usually, with the progress in power, in programming facilities and in visualizing displays, computers are used for the second phase two. At any rate, all kinds of CS make use of, at least, one kind of subsymbolization. Note that the symmetrical relations of subsymbolization and relative iconicity entail a representation of the mutual relations between levels of signs in a CS which is similar to the denotational hierarchy presented by Goodman (1981). For Goodman, “reference” is a general term “covering all sorts of symbolization, all cases of standing for”. Denotation is a kind of reference: it is the “application of a word or a picture or other label to one or many things”.

10.8

There is a hierarchy of denotations: “At the bottom level are nonlabels like tables and null labels as ‘unicorn’ that denote nothing. A label like ‘red’ or ‘unicorn-description’ or a family portrait, denoting something at the bottom level is at the next level up; and every label for a label is usually one level higher than the labeled level” (Goodman, 1981, p. 127). For Goodman, a ‘unicorn-description’ is a ‘description-of-a-unicorn’ and not a description of a unicorn, because it is a particular denoting symbol that does not denote anything existing.

10.9

There are many kinds of denotation. Goodman (1968) subsumes mathematical modeling and computational treatment in a kind called “notation”. Contrary to what happens in a system of pictorial denotation, in notations, symbols are “unambiguous and both syntactically and semantically distinct”. Notation must meet the requirements of “work-identity in every chain of correct steps from score to performance and performance to score”. For instance, the western system for writing music tends to be a notation. Many authors who assume that a kind of formal analogy - and nothing else - must be at stake in a CS (which they often reduce to a calculus of a uniform model) do implicitly agree with this reduction of CS to a system of notation. But, in fact, many simulations present a variety of notations. No unique notation governs them. Moreover, many CS have symbols operating without having been given any clear semantic differentiation (for instance, those CS which are computational tricks to solve a model manipulate discrete finite elements which have no meaning or no corresponding entities in the target system) nor stable (absolute) semantic during the process itself (e.g. in some multileveled complex simulations).

10.10

Following Goodman (1968) on symbols, but reversing his specific analyses on computational models, we can say that, in a numerical simulation of a fluid mechanics’ model, e.g., each operating subsymbol is a denotation-of-an-element-of-the-fluid but not a denotation of an element of the fluid. During the course of a computation, the same level of symbol (from the implementer point of view) can be taken either as iconic or as symbolic, depending on the level at which the event or operation considers the actual elements.

10.11

It is not possible to show here in details the various routes of reference that are used in various CS. It suffices to say that, whether a simulation or an experiment finally is successful or not, simulationists and experimenters first ought to have a representation of the denotational hierarchy and then of the remoteness of the references of the symbols they will use or will let use (by the computer).

 

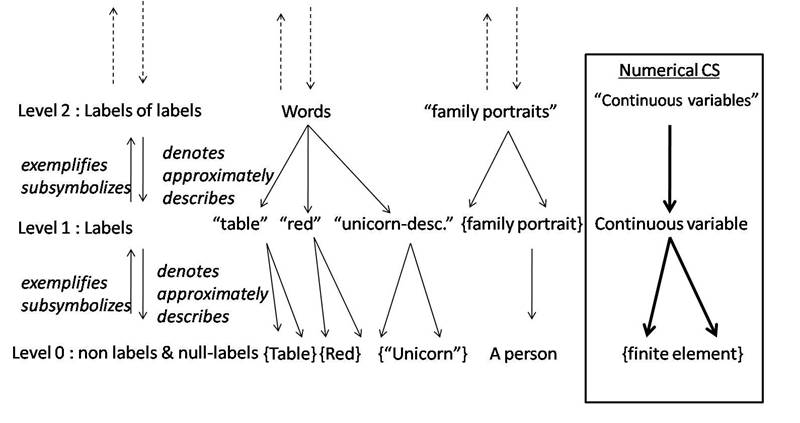
Figure 1 - The denotational hierarchy and its relative subsymbols

10.12

Figures 1 & 2 can help to follow instances of such routes by following successive arrows between levels of symbols. Figure 1 represents 1^st the levels, 2^nd some of Goodman’s examples, 3^rd the first kind of CS we propose to insert in this hierarchical interpretation and 4^th the types of semiotic relations between things and/or symbols across levels.

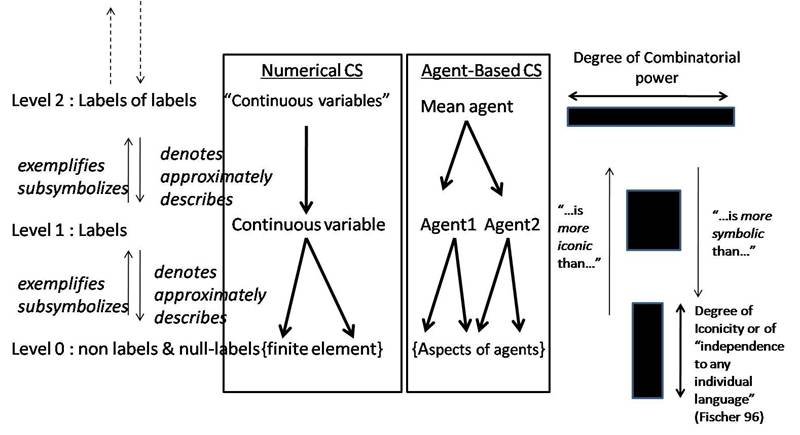
Figure 2 - Degree of combinatorial power and degree of iconicity

10.13

Figure 2 shows the insertion of Agent-Based CS. The analysis surely can be refined. For instance, the place of such a CS can be expanded or changed in the hierarchy, but not the kinds of local relations between levels of symbols at stake. What is important is that the relative position between symbols is preserved. Accordingly, figure 2 shows the correlation between the degrees of combinatorial power and iconicity across levels. We image it through a deforming black quadrilateral (which tends to possess a constant surface): the greater the iconic aspect of the symbol, the smaller its combinatorial power. Here, the combinatorial power measures the variety (number of different types) of combinations and operations on symbols which are available at a given level. And the degree of iconicity measures the degree of independency of the denotational power of a level of symbols from the combinatorial rules of another given level of symbols.

10.14

With this new way of representing the referential relations between symbols in CS and between things (or facts, etc.) and symbols, we can see that Winsberg (2009) is perfectly right when he says that the dualistic approach (material analogy Vs formal analogy) is too simple and puzzling. But he is too rapid when he returns to an epistemology of deference instead of trying a careful and differentiating epistemology of reference. Contemporary epistemology of deference remains a restrictive philosophy of knowledge because it persists to see any symbolic construct produced by sciences - and their instruments - as analogue to human knowledge: i.e. as propositional, such as a belief (“S believes that p”). So, its ability to offer any new differentiating focuses on CS, especially between models and simulations and - what seems so crucial today - between kinds of simulations, sounds very uncertain. The puzzle concerning the empirical or conceptual status of CS largely stems from this large and simplistic reduction of any CS to a notation and, through that, to a formal language always instantiating some “propositions” analogous to “musical sentences” performed through a unique system of notation.

10.15

Our characterization gives the possibility to stay at the level of the symbols at stake, and not to jump prematurely to propositions, this without going back to a naïve vision of an absolute iconicity of simulations. Iconicity does not entail absolute similitude nor materiality; it is a relativistic term. For instance, in cognitive economics (Walliser, 2004, 2008), agent-based simulations can be said to operate on some iconic signs because they denote directly – term to term, so with a weak dependence on linguistic conventions - some credible rule of reasoning.

Models, Simulations and Kinds of Empiricity (3) Three kinds of Computer Simulations

11.1

Following this characterization, it is possible to distinguish at least three kinds of CS depending on the kinds of subsymbolization at stake:

1. a CS is model-driven (or numerical) when it proceeds from a subsymbolization of a given model. That is: the model is treated through a discrete system which still can be seen as a system of notation. Note that the term “model” possesses here its neutral and broadest meaning in that it denotes only any kind of formal construct. This construct can be considered as a genuine “theory” by the domain specialists or, more strictly as a “model” of a theory. Accordingly, the domain specialist can say that such a CS is “theory-driven”. Let’s recall that sociology has produced theories without suggesting clear models of them, as this is the case for some theories of social action: a CS of such a theory can more properly be said “theory-driven” by domain specialists. And it could seem a mistake to call them “model-driven” CS, strictly speaking. But, in this paragraph, we do not put at the forefront the degree of ontological commitment of the formalism on which the CS is founded, but only the internal denotational relation between the formalism and the CS of it.
2. a CS is rule-driven (or algorithmic) when it does not proceed from the subsymbolization of a previous mathematical model. Rules are now constitutive. The rules of the algorithm are subsymbolic regarding some hypothetical algebraic or analytical mathematical model and they are iconic regarding (relatively to) the formal hypotheses implemented (e.g. “stylized facts”). Hence, from the point of view of the user, an iconic aspect still appears in such a simulation. And this iconicity serves as another argument to speak about experiment in another sense. As underlined by Sugden it is precisely the case of Schelling’s model: causal mechanisms are denoted through partial and relative iconic symbols. Those elementary mechanisms - which are elementarily denoted in the CS - are what is “empirically” assessed here. It is empirical to the extent that there is no theory of the mass-behavior of such distributed mechanisms. So, the symbols denoting this mechanism operate in a poor symbolic manner: they have a weak combinatorial power, and a weak ability to be directly condensed and abridged in a symbolic manner. Experience (passive strategy of observation) is invoked there, rather than experiment (an interactive strategy of selection, preparation, instrumentation, control, interrogation and observation).
3. a CS is object-driven (or software-based) when it first proceeds not from a given uniform formalism (either mathematical or logical) but from various kinds and levels of denoting symbols which symbolicity and iconicity are internally relative and depend on internal relations between these kinds and levels. Most of the time (but not necessarily), such simulations are based on multi-agents systems implemented by agent- / object-oriented programming so as to enable the representation of various degrees of relative reifications - or, conversely, relative formalizations - of objects and relations.

11.2

Concerning the first kind, the focus is on the model. Then scholars are willing to say that they are computing the model, or, at most, that they are experimenting on the model. We have seen that a symbol-denoting-an-element-of-the-fluid is not necessarily a symbol denoting anything. It can be a null-label which nevertheless possesses some residual (weak) combinatorial power which can be worked upon once placed in the conditions of some machine delegated computational iterations (CS).

11.3

In the case of algorithmic CS, scholars often say that their list of rules is a “model of simulation” and that they make with it a “simulation experiment”. They say that because the iconicity of the operating subsymbols is put at the forefront: these subsymbols are supposed to denote directly some (credible) real rules or relations existing in the target system. That is:  they denote them with a weak dependence on linguistic conventions (such as in the case of computational cognitive economics).

11.4

The recent emergence of complex multidisciplinary and/or multi-levelled CS has given rise to mixed CS: some of their operations are considered as calculus of models, whereas some others are algorithmic and not far from being iconic to some extent, while others are only exploitations of digitalizations of scenes (such as CS coupled to Geographic Information Systems). From this standpoint, as noted by Varenne (2007, 2008, 2009), a software-based simulation of a complex system is often a simulation of interacting pluri-formalized models. The technical usefulness of such a CS is new. It no longer relies on the practical calculability of one intractable model but on the co-calculability of heterogeneous - from an axiomatic point of view – models, e.g.: CS in artificial life, CS in computational ecology, CS in post-genomic developmental biology, CS of interrelated process in multi-models, multi-perspective CS and so forth.

Models, Simulations and Kinds of Empiricity (4) Types of empiricity for Computer Simulations

12.1

Varenne (2007) has shown that 4 criteria of empiricity, at least, can be used for a CS according to this characterization.
 

1. when focusing on a partial or global result of the CS to see some kind of similarity of this result (this similarity being interpreted in terms of relative iconicity, formal analogy, exemplification or identity of features), and when the result is found to denote some target system, we can speak of an empiricity of the CS regarding the effects. The focus relies here on the second phase of the simulation. Once seen from the global results, the elementary symbols - which first operated - are overlooked and treated as subsymbols. In his epistemological study of the Monte Carlo simulations of neutron diffusion (at Los Alamos), (Galison 1996, 1997) characterizes this approach of simulations as the “epistemic” or “pragmatic” one:

   “All of the forms of assimilation of Monte Carlo to experimentations that I have presented so far (stability, error tracking, variance reduction, replicability, and so on) have been fundamentally epistemic. That is, they are all means by which the researchers car argue toward the validity and robustness of their conclusions” (Galison, 1997, p. 738).

   The argument lies here: as both the simulator and the experimentalist use the same techniques of getting knowledge (i.e. techniques of error tracking or variance reduction) from the results (or effects) of the CS or of the real experiment, they tend to identify. Note that this is more between the processes of planning and analyzing the “experiment” (be it a real experiment or a CS) that lies the similarity than between any direct observations. This approach still relies on a kind of similarity: a similarity between the pragmatic aspects of the construction of knowledge in both contexts. Galison chose to emphasize on the variable attitudes of researchers. But this assimilation of simulation to “a kind of experimentation” can be interpreted as unraveling some possible empirical aspect of a CS: from our viewpoint, it is a specific kind of empiricity. This kind of empiricity is specific in that it is more relative to the process of experiencing itself than to the experienced “data” themselves. It is based on the similarity of the processes of analysis of the effects of both the CS and the real experiment. Let’s remind that empiricity is the property of an epistemic means to lead to a given knowledge which is said to be empirical as it is elaborated through a certain process of experience. In this case, the emphasis is on the process.
    

2. when focusing on the partial iconic aspects of some of the various types of elementary symbols operating in the computation, we can speak of some empiricity of the CS regarding the causes. The focus relies here on the first phase of the CS and on the supposed realism or credibility of these elements with respects to the target system.
   
   This kind of empiricity has been characterized in subjective terms by Galison too. It is what he calls a “stochasticism” or “the metaphysical case for the validity of Monte Carlos as a form of natural philosophical inquiry” (Galison, 1997, pp. 738-739). Galison quotes numerous researchers who claimed that discrete and stochastic simulations of diffusion-reaction processes of neutrons in nuclear bombs are more valid than integro-differential approaches in that these simulations much more correctly imitate the reality at stake: i.e. numerous and discrete elements interacting in a stochastic manner. This kind of empiricity is radically different from the first one. It is an essentialist or a metaphysical one as it is assumed to rely on the similarity between some real elements and the elements which are at the beginning of the process of computation, i.e. which are some of its causes. This kind of empiricity relies on the similarity not between technical processes but “directly” between data or considerations of data.

12.2

These first two kinds  of empiricity have been evoked by Galison (1997) in the case of numerical simulations, but not the two others to come (for which simulation is not only numerical). Both consider the external validity of the simulation in the sense of Guala.
 

3. When focusing on the intrication of levels of denotations operating in a complex pluriformalized CS, it is possible to decide that there is an intellectual opacity different in nature from the one coming from a classical intractability (as it still was the case for the solution of using Monte Carlo simulations in the diffusion-reaction equations). We can speak then of an empiricity regarding the intrication of the referential routes. Such an empiricity (as the 4th) does not come from the existence of a rather passively experienced level of symbols as in (1) or (2). But it comes from an uncontrollability of the different and numerous iterative intrications of levels of symbol, be they controlled (semantically or instrumentally) or uncontrolled factors in this virtual experiment. Note that even the pragmatic approach of CS - when, for instance, applying the statistical techniques of analysis of variance - tends to uniformize the factors intervening in the CS. In this case, the formal heterogeneity of symbols and the heterogeneity of their denotational power are not respected. On the contrary, the kind of empiricity based on the intrication of the referential routes is due to the fact that the CS seems to us like a “thing” in quite the same meaning as (Durkheim; 1982) told us to “treat social facts as things”. In fact, such a CS is not similar to a real (material) thing. It is not the opacity of a material and external thing which is imitated through it. But such a CS possesses a kind of empiricity as the thing it creates can not be known by our intelligence only through a kind of reflection or by introspection. But, moreover, and contrary to most of the social facts as they were studied by Durkheim, its opacity cannot be unraveled only by statistic instruments, because of the uniformization they impose on levels of symbols at stake. So, this opacity, again, is more to be compared to the complex heterogeneous functioning of the brain, mixing simulations, symbolizations, denotations with proprioceptive, computational and modeling processes (Jeannerod 2006), than to well multi-dimensioned (factor dependant) social facts. There is an empiricity in this case in that some thing is given to us. But it differs from the two first empiricities in the kind of things given.
    
4. when focusing on the intrication of the resulting epistemic status of such a complex CS with levels of models and then levels of denotational systems, a 4th kind of empiricity comes to view. It is a problem because not only each of its level has its own form, that is, its own alphabet and rules of (weak or strong) combination, but each one has a different denotational level or position in the hierarchy too. So, each one can entail for itself a different route back to reference. Each one can have a different epistemic status in that it belongs to a different “world” (Goodman, 1987) the one being fictional, the other descriptive, the other explanative. We can speak here of an empiricity regarding the defect of any a priori epistemic status. That is: the CS has to be treated - first and a minima - as an experiment because we do not know a priori if it is an experiment for any of the 3 other reasons, or a theoretical argument, or only a conceptual exploration. Moreover, it is probable that there exists no general composition law of epistemic statuses for some of such complex CS and that they demand a case-by-case epistemological investigation, with the help of careful denotational analyses. In this case, the empiricity still is due to the intrication of levels of symbols. But, moreoever, it is also due to the intrication of the epistemic statuses. The thing simulated is not only opaque but its epistemic status remains itself opaque.

12.3

Note that these kinds of empiricity do not (as such) entail the complete substitutability of the CS in view to a real experiment. Such empiricities do not borrow their characteristic from a complete substitutability of the CS to an experiment, but only from a partial substitutability (criteria 1 and 2) or even not from any substitutability at all, but from the opacity of the intrication of symbols (criteria 3 and 4). As such, they are always partially intrinsic empiricities, and never completely borrowed ones.

Models, Simulations and Kinds of Empiricity (5) Models, simulations and kinds of experiment

13.1

Now that we have gained some conceptual tools, let us accordingly reinterpret some of the different epistemological positions we first put into perspective in section 1.

13.2

How and to what extent models can be seen as some kind of experiment?

• In some cases, like Schelling’s model discussed by Sugden, we can say that a model has an empirical dimension in itself because some causal factors are denoted through symbols of which partial iconicity is patent and can be reasonably recognized as a sufficiently “realistic” conjecture in the argumentative approach of the “credible world”.
• On the contrary, models are seen from an instrumentalist standpoint when the level of iconicity of their symbols is weak (the remoteness of reference is important) and when this is their combinatorial power at a high level in the denotational hierarchy which is requested - see Friedman’s unrealism of assumption argument (Friedman 1953). Retrospectively, such an epistemology can be seen as a contingent rationalization of some limited mono-leveled formalizations (which were the only ones available in the past) in contrast to the current more complex and developed abilities to vary routes of reference through ABM and computer-aided simulations.
• The notion of “stylized fact” is ambiguous in this concern because it can serve to put the emphasis either on the stylization, or on the factuality and then on the eventual iconicity of the used symbolization. The fact is that, independently of an explicit commitment toward a denotational hierarchy, models of “stylized facts” cannot be said a priori to be “conceptual exploration” or “experiments”.

13.3

How and why can a CS be seen as an experiment on a model?

• As a CS entails some kind of subsymbolization, every CS of a model treats a model at a sublevel which tends to make its relation to the model analogous to the naïve dualistic relation between the formal constructs and the concrete reality. Because of this analogy of relations between two levels of different denotational authority (no matter what these levels are), such a CS can be said to be an experiment on the model. But if we focus on some symbolic aspects of used subsymbols, we can speak of such a CS of model as a conceptual exploration.
• It follows that the external validity is a matter of degree and depends on the strength of the alleged iconic aspects. If this iconic aspect is extremely stabilized and characterized, the simulation can even be compared to an exemplification. In this case, external validity is not far from an internal one

13.4

To what extent can a CS be seen as an experiment in itself?

• There are at least 4 criteria to decide whether a simulation is not only an experiment on the model but an experiment in itself. A CS can first lend its empiricity from an experiencing, that is, from a comparison with the target (external validity): and those are (1) the empiricity regarding the causes (of the computation) and (2) the empiricity regarding the effects (of the computation). Second, its empiricity can be decided not from an experiencing of a more or less direct route of reference but from a real experimenting on the interaction between levels of symbols, i.e. with controlled and uncontrolled changing factors: and these are (1) the empiricity regarding the intrication of the referential routes, and (2) the empiricity regarding the defect of any a priori epistemic status. Through this particular experimenting dimension, software-based CS gain a particular kind of empiricity which gives them a similar epistemic power (pace Morgan) to ordinary experiments.

Conclusion

14.1

The coming years will see the expansion of more empirically based computer simulations with agents in social sciences as in all the sciences of complex systems, and of multidisciplinary computer simulations, especially between social sciences and biology or ecology. Due to differences in methodological habits, epistemological misunderstandings between disciplines will increase. This paper has shown that the epistemic status of models and simulations can be analyzed in regard to the concept of denotational hierarchy. It has shown that the denotational power of the different levels of symbols has to be taken into account if we want to assess the status of conceptual exploration - or of empiricity - that a given computer simulation possesses. Specifically, such an epistemological approach shows its fruitfulness in that it enables us to distinguish between 3 types of computer simulations and between 4 types of empiricity in computer simulations. Finally, it has been proposed that careful attention to the multiplicity of standpoints on symbols, on their mutual relations and on the implicit routes of references operated through them by computations will help to discern more precisely the denotational power, hence the epistemic status and credibility of complex models and simulations. In this concern, this paper has presented a first outline of conceptual and applicative developments in the domain of an applied, referentialist but multi-level centered epistemology of agent-based and, more generally, complex models and simulations. Compared to a standpoint using ontologies, this approach is a complimentary one, as it proposes rigorous discriminating tools which can be applied to any complex model or simulation during an analytic phase, whereas ontologies entail a synthetic phase based on the re-organization of levels of symbols that are used in the modeling or simulation process (with the help of an ontological test, for instance).

Acknowledgements

We would like to Acknowledge Alexandra Frenod for his remarks on the first (EPOS) version of this paper, Johnny Hartz Søraker for his useful reading of the revised version and Michel Dubois for his contribution to discussion of Economics and Social Science modelling in sections 4 to 7 from Dubois, Phan (2007). We also thank the two anonymous reviewers and all the participants of the EPOS’08 workshop who - through their questions - have enabled us to enhance it. The authors also acknowledge the program ANR CORPUS of the French National Research Agency (ANR) for financial support through the project COSMAGEMS (Corpus of Ontologies for Multi-Agent Systems in Geography, Economics, Marketing and Sociology). D.P. is CNRS member.

References

ACHINSTEIN, P (1968) Concepts of Science, Baltimore, Johns Hopkins University Press

AMBLARD, F, Bommel P. and Rouchier J.(2007) Assessment and Validation of multi-agents Models. In: Phan, D., Amblard, F. (eds.), pp.93-114.

AXELROD, R. (1997/2006) Advancing the Art of Simulation in the Social Sciences. In: Conte, R., Hegselmann, R., Terna, P. (eds.), Simulating Social Phenomena, Berlin, Springer-Verlag, pp.21-40. Updated version in Rennard, J.P. (ed.), Handbook of Research on Nature Inspired Computing for Economy and Management, Hersey, PA: Idea Group, 2006. [doi:10.1007/978-3-662-03366-1_2]

AXTELL, R. L. (2000) Why agents? On the varied motivations for agent computing in the social sciences. In: Macal, M., Sallach, D. (eds.), Proceedings of the workshop on agent simulation: Applications, models, and tools, Chicago, IL: Argonne National Laboratory, pp.3-24.

BERKELEY, I. (2000) What the ... is a subsymbol? Minds and Machines, 10, pp.1-14. [doi:10.1023/A:1008329513803]

BERKELEY, I. (2008) What the ... is a symbol? Minds and Machines, 18, pp.93-105. [doi:10.1007/s11023-007-9086-y]

BOMMEL, P. and Müller J.P. (2007) An introduction to UML for Modelling in the Human and Social Sciences. In: Phan, D., Amblard, F, pp. 273-294.

DESSALLES, J.L., Müller, J.P. and Phan, D. (2007) Emergence in multi-agent systems: conceptual and methodological issues. In: Phan, D., Amblard, F. (eds.), pp. 327-356.

DUBOIS, M. and Phan, D. (2007) Philosophy of Social Science in a nutshell: from discourse to model and experiment. In: Phan, D., Amblard, F. (eds.), pp 393-431).

DURKHEIM, E. (1982 ) The rules of sociological method , New York, The Free Press, [doi:10.1007/978-1-349-16939-9]

FERBER, J. (1999) Multi-agent Systems: an Introduction to Distributed Artificial Intelligence, Reading, MA: Addison-Wesley Publishing Company.

FERBER, J. (2007) Multi-agent Concepts and Methodologies. In: Phan, D., Amblard, F (eds.), pp.7-34.

FISCHER, O. (1996) “Iconicity : A definition”. In: Fischer, O. (ed), Iconicity in Language and Literature, Academic Website of the University of Amsterdam, maintained since 1996, http://home.hum.uva.nl/iconicity/

FRANKLIN, A. (1986) The Neglect of Experiment, Cambridge, Ma., Cambridge University Press. [doi:10.1017/CBO9780511624896]

FREY, G. (1961) Symbolische und Ikonische Modelle. In: Freudenthal, H. (ed.), The concept and the role of the model in mathematics and natural and social sciences, Dordrecht, Reidel pub., pp.89-97. [doi:10.1007/978-94-010-3667-2_8]

FRIEDMAN, M. (1953) Essays on Positive Economics, Chicago, Il., University of Chicago Press.

GALISON, P. (1987) How Experiments End, Chicago, Il., University of Chicago Press.

GALISON, P. (1996) "Computer Simulations and the Trading Zone", in: P. Galison & D.J. Stump (ed.), The Disunity of Science, Stanford University Press, pp. 118-157.

GALISON, P. (1997) Image and Logic, Chicago, Il., University of Chicago Press

GILBERT, N. and Conte, R. Eds., (1995) Artificial Societies: The Computer Simulation of Social Life. London, UCL Press.

GILBERT, N. and Troitzsch, K. Eds. (1999) Simulation for the Social Scientist. Philadelphia, Open University Press.

GOODMAN N. (1968) Languages of Art: An Approach to a Theory of Symbols, Indianapolis, Bobbs-Merrill.

GOODMAN N. (1981) Routes of reference, Critical Inquiry, 8(1), pp. 121-132. [doi:10.1086/448143]

GOODMAN N.(1987) Ways of Worldmaking, Indianapolis, Hackett Pub.

GUALA, F. (2002) Models, Simulations, and Experiments. In: Magnani, L., Nersessian, N. J. (eds.) Model-Based Reasoning: Science, Technology, Values, NY, Kluwer, pp.59-74. [doi:10.1007/978-1-4615-0605-8_4]

GUALA, F. (2003) Experimental Localism and External Validity, Philosophy of Science, 70, pp.1195-1205. [doi:10.1086/377400]

GUALA, F. (2008) Experimentation in Economics. In: Mäki, U. (ed.) Handbook of the Philosophy of Science, Volume 13: Philosophy of Economics, forthcoming

HACKING, I. (1983) Representing and Intervening, Cambridge Ma, Cambridge University Press. [doi:10.1017/CBO9780511814563]

HALES, D., Edmonds B. and Rouchier, J. (2003) Model to model analysis, Journal of Artificial Societies and Social Simulation, 6(4) https://www.jasss.org/6/4/5.html

HARTMAN, S. (1996) The world as a process, In: Hegselmann, R., Müller, U., Troitzsch, K. (eds.) Modelling and simulation in the social sciences from the philosophy of science point of view, Dordrecht, Kluwer, pp.77-100. [doi:10.1007/978-94-015-8686-3_5]

HAUSMAN, D.M. (1992) The Inexact and Separate Science of Economics, Cambridge Ma, Cambridge University Press. [doi:10.1017/CBO9780511752032]

HUMPHREYS, P. (2004) Extending Ourselves: Computational Science, Empiricism, and Scientific Method, Oxford,  Oxford University Press. [doi:10.1093/0195158709.001.0001]

JEANNEROD, M. (2006) Motor Cognition: What Action tells to the Self, Oxford University Press. [doi:10.1093/acprof:oso/9780198569657.001.0001]

LIVET P. (2007) Towards an Epistemology of Multi-agent Simulations in social Sciences. In Phan, D., Amblard, F (eds.), pp.169-193.

LIVET P., Phan, D. and Sanders, L. (2008) Why do we need ontology for Agent-Based Models? In: Schredelseker, K., Hauser, F. (eds.) Complexity and Artificial Markets. LNEMS, 614, Berlin, Springer, pp. 133-146. [doi:10.1007/978-3-540-70556-7_11]

MÄKI, U. (1992) On the method of isolation in economics. In: Dilworth, C (ed.), special issue of Poznan Studies in the Philosophy of the Sciences and the Humanities, “Idealization IV: Intelligibility in Science”, 26, pp. 319-354; reprinted in Davis, J. B. (ed.), Recent Developments in Economic Methodology, Aldershot, Edward Elgar (2004)

MÄKI, U. (2002) The dismal queen of the social sciences. In: M√§ki, U. (ed.) Fact and Fiction in Economics, Cambridge Ma., Cambridge University Press, pp. 3-34. [doi:10.1017/cbo9780511493317.002]

MÄKI, U. (2005) Models are experiments, experiments are models, Journal of Economic Methodology, 12(2), pp. 303-315. [doi:10.1080/13501780500086255]

MINSKY, M. (1965) Matter, Mind and Models, Proceedings of IFIP Congress, pp.45-49.

MORGAN, M.S. and Morrison, M. (eds.) (1999) Models as Mediators, Cambridge Ma., Cambridge University Press. [doi:10.1017/CBO9780511660108]

MORGAN, M.S. (2005) Experiments versus Models: New Phenomena, Inference and Surprise, Journal of Economic Methodology, 12, pp. 317-329. [doi:10.1080/13501780500086313]

MORRISON, M.C. (1998) Experiment. In: Craig, E. (ed.) The Routledge Encyclopaedia of Philosophy. London, Routledge, pp. 514-518.

NADEAU, R. (1999) Vocabulaire technique et analytique de l'epistemologie, Paris, PUF.

PECK, S.L.  (2004)  Simulation as experiment: a philosophical reassessment for biological modeling, Trends in Ecology & Evolution, 19(10), pp. 530-534. [doi:10.1016/j.tree.2004.07.019]

PHAN, D. and Amblard, F. Eds. (2007) Agent Based Modelling and Simulations in the Human and Social Sciences, Oxford, The Bardwell Press.

PHAN, D., Schmid, A.F. and Varenne, F. (2007) Epistemology in a nutshell: Theory, model, simulation and experiment. In: Phan, D., Amblard, F (eds.), pp. 357-392.

RAMAT, E. (2007) Introduction to Discrete Event Modelling and Simulation. In: Phan, D., Amblard, F (eds.), pp.35-62.

SCHELLING, T.S. (1978) Micromotives and Macrobehaviour, N.Y, Norton and Co.

SMOLENSKY, P. (1988) On the proper treatment of connectionism, The Behavioural and Brain Sciences, 11, pp. 1-74. [doi:10.1017/S0140525X00052432]

SOLOW, R.M. (1997) How did economics get that way and what way did it get? Daedalus, Winter, 126(1), pp. 39-58.

SUGDEN, R. (2002) Credible Worlds: The Status of Theoretical Models in Economics. In: Mäki, U. (ed.) Fact and Fiction in Economics, Cambridge Ma., Cambridge University Press, pp. 107-136. [doi:10.1017/cbo9780511493317.006]

TESFATSION, L. (2002) Agent-Based Computational Economics: Growing Economies from the Bottom Up, Artificial Life, 8(1), March pp.55-82. [doi:10.1162/106454602753694765]

TESFATSION, L. and Judd, K.L. Eds. (2006) Handbook of Computational Economics, Vol. 2: Agent-Based Computational Economics, Amsterdam, Elsevier North-Holland.

VARENNE, F. (2001) What does a computer simulation prove? In: Giambiasi, N., Frydman, C. (eds.) Simulation in industry - ESS 2001, Proc. of the 13th European Simulation Symposium, SCS Europe Bvba, Ghent, pp. 549-554.

VARENNE, F. (2007) Du modele à la simulation informatique. Paris, Vrin.

VARENNE, F. (2008)  Modeles et simulations : pluriformaliser, simuler, remathematiser. In: Kupiec, J.J., Lecointre, G., Silberstein, M., Varenne, F. (eds.) Modeles Simulations Systemes. Paris, Syllepse, pp.153-180.

VARENNE, F. (2009): Models and Simulations in the Historical Emergence of the Science of Complexity. In: M.A. Aziz-Alaoui & C. Bertelle (eds), From System Complexity to Emergent Properties, Berlin, Springer, pp. 3-21. [doi:10.1007/978-3-642-02199-2_1]

WALLISER, B. (2004) Topics of cognitive economics. In: Bourgine, P., Nadal, J.P. (eds.) Cognitive Economics, an interdisciplinary approach, Berlin, Springer, pp. 183-198. [doi:10.1007/978-3-540-24708-1_11]

WALLISER, B. (2008) Les modeles de l’economie cognitive, In: Kupiec, J.J., Lecointre, G., Silberstein, M., Varenne, F. (eds.) Modeles Simulations Systemes. Paris, Syllepse, pp. 183-199.

WINSBERG, E. (1999) Sanctioning models: the epistemology of simulation, Science in Context, 12, pp. 275-292. [doi:10.1017/S0269889700003422]

WINSBERG, E. (2009) A Tale of Two Methods. Synthese, 169 (3), pp. 575-592. [doi:10.1007/s11229-008-9437-0]