Abstract
Abstract
- Is it possible to abstract a formal mechanism originating schisms and governing the size evolution of social conversations? In this work we propose a constructive solution to this problem: an abstract model of a generic N-party turn-taking conversation. The model develops from simple yet realistic assumptions derived from experimental evidence, abstracts from conversation content and semantics while including topological information, and is driven by stochastic dynamics. We find that a single mechanism, namely the dynamics of conversational party's individual fitness as related to conversation size, controls the development of the self-organized schisming phenomenon. Potential generalizations of the model - including individual traits and preferences, memory effects and more elaborated conversational topologies - may find important applications also in other fields of research, where dynamically-interacting and networked agents play a fundamental role.
- Keywords:
- ABM, Complexity, Turn-Taking Dynamics, Schism, Stochastic Dynamics
 Introduction
Introduction
- 1.1
-
Multi-party conversations are prime manifestations of collective socio-cultural
interactions. The Santa Fe Institute's Complex Systems Summer School
2009 was an excellent occasion for the authors to investigate this
statement from an alternative and formal vantage point. During all
meals, groups of up to 20 people comfortably clustered in quasi-circular
ensembles and entered into lively turn-taking conversations. An occasional
observer could easily discern that table conversations were not stable.
Not all participants seated around a specific table took part at all
times in a table-wide conversation. Usually, participants took part
in conversations that involved only a subset of the people seated
around that table. As a result, each table had multiple, separate
sub-conversations going on at the same time. Moreover, people taking
part in one of these parallel chats usually did not remain involved
in the same sub-conversation indefinitely, but tended to leave their
original sub-conversation and join another, possibly neighboring one
going on at their same table. Remarkably, all of this happened independently
of the very topics of conversation - that indeed fluctuated spatially
and temporally.
- 1.2
-
Was this set of behaviors accidental, or was there, on the contrary,
any general underlying mechanism driving the group size evolution
of conversations? This question has been addressed in social sciences
from several perspectives. The general issue of pointing out the sociological
factors that determine the group size of a conversation dates back
to the seminal works of Simmel Simmel (1902). The splitting up of
a single conversation into two or more sub-conversations, referred
to as schism Egbert (1997); Schegloff (1995); Parker (1984); Sacks et al. (1974); Goodwin (1987); Goffman (1963); Goodwin (1984),
was investigated by Goffmann in a qualitative, context-sensitive interpretative
approach Goffman (1963), and by Sacks and collaborators in the context
of discourse analysis Sacks et al. (1974). Several social features and
effects of schisming were also addressed, including schism-induced
turns Egbert (1997), multi-focused gatherings Goffman (1963) and
co-occurrence of turn-taking systems Sacks et al. (1974); Goodwin (1984).
Specific behaviors were documented by concrete experiments, such as
video tape recordings Egbert (1997); Goodwin (1987), everyday experience
Goffman (1963), or hypothesizing and reasoning methodology Simmel (1902).
Significantly less work addressed the analysis of conversations and
schisming processes from an abstract, context-free point of view.
Such an approach was probably difficult to pursue in earlier times,
as most data were empiric and therefore context-related. However,
in recent years it has been possible to circumvent these restrictions
thanks to the social simulation framework Axelrod (1997); Axelrod (2006b); Bandini et al. (2009); Byrne (1998); Miller & Page (2007); Axelrod (2006a).
This was developed to improve the understanding of and to evaluate
strategies, explanatory and predictive schemes of the behavior of
social systems whenever - for e.g. practical or ethical reasons
- gathering direct observations was impossible. Particularly, the
well-established agent-based model (ABM) paradigm Bonabeau (2002); Bandini et al. (2009); Miller & Page (2007)
has proven fruitful to simulate complex collective phenomena in several
domains Axelrod (1997); Byrne (1998); Schweitzer (2003); Miller & Page (2007); Axelrod (2006a).
Works on multi-party interactions were pursued in the context of artificial
intelligence, addressing specific challenges such as e.g. human-robot
interaction Bono et al. (2003) or pattern recognition Aoki et al. (2006); interaction
structure in meetings, among which e.g. co-present meetings
in smart meeting rooms for archival and assistive purposes Stiefekhagen et al. (2002); Ishizaki & Kato (1998),
and remote interaction Vertegaal et al. (2003); and in more general scenarios
Miller & Page (2007); Schweitzer (2003). Closer to our interests, Galley et
al. proposed a remarkable topic segmentation algorithm for multi-party
speech, which is domain-independent but nonetheless content- and knowledge-sensitive
Galley et al. (2003). To our knowledge, no work so far addressed turn-taking
conversation dynamics from a purely-formal perspective, abstracting
from both content and context.
- 1.3
-
In this paper we introduce such an approach by describing the emergence
of conversational schisming as a self-organized complex collective
phenomenon. We present an abstract model, based on simple formal yet
realistic rules and driven by stochastic dynamics, that predicts the
time-evolving size of conversation groups. By embodying the rules
and boundary conditions into an ABM, we analyze how schisming drives
the development of conversations. Since our model is deliberately
abstract and context-free, our conclusions are general and do not
restrict to any particular class of turn-taking conversations. Furthermore,
proposed generalizations of our model may find useful applications
in other research areas, as well.
- 1.4
-
The rest of the paper is organized as follows: in Section 2 we present
the baseline conversational model, defining the basic agent rules.
In Section 3 we implement such model and provide the results of several
simulation runs; particularly, we distinguish between transient dynamics,
like real-life conversations, from stationary dynamics, which is the
(probably unrealistic) asymptotic limit of the dynamics which, nonetheless,
can in some cases be solved analytically in a mean-field approximation.
Finally, we provide a summary of conclusions, as well as a discussion
on the possible model generalizations and further applications of
the work.
 The baseline model: assumptions
The baseline model: assumptions
- 2.1
-
We define our baseline conversation model by instantiating a set of
simplifying yet realistic assumptions:
- Homogeneous initial conditions. At the beginning, all parties (i.e. participants) participate in a unique conversation and are in the same state. The conversation starts with a random participant entitled to speak - she will be called the speaker - while all other participants are listeners. Other initial configurations can of course be imposed; however, the dynamics tends towards attractors whose basins of attraction are global (see Sec. 3): every initial condition will thus tend to the same steady state. Hence, for simplicity and without lack of generality, we adopt a homogeneous initial condition.
- Roundtable topology. The participants are arranged around an ideal roundtable (i.e. a one-dimensional torus with periodic boundary conditions): each participant can speak with any other participant, but she is in intimate (i.e. spatial) contact only with her two nearest neighbors - which define her own topological neighborhood. This time-invariant conversational topology reproduces realistic, spatially embedded conversations that tend to cluster in a circular-like geometry.
- Turn-taking dynamics. In a given conversation, only one person (the speaker) speaks at any given time before another (different) participant (a listener of the same group) is entitled to speak. Within a single conversation, several non-overlapping sub-conversations can nucleate. We assume for simplicity that the speakers of all sub-conversations are appointed concurrently and simultaneously (this synchronous updating rule can be relaxed, if needed). This rule introduces the turn-taking dynamics in the model.
- Abstraction from conversational content. We model the succession of speakers within any given (sub-)conversational group as a stochastic process. In principle, it is possible to use any kind of speaker-dependent or history-dependent probability distribution to determine the choice of the new speaker. However, in this work we wonder whether complex patterns in the schisming dynamics can still develop without resorting to additional and detailed individual information. This approach, consistent with the complexity paradigm Byrne (1998); Miller & Page (2007); Schweitzer (2003), is also coherent with content abstraction: any kind of emergent conversation pattern will eventually appear as consequence of the cooperative behavior mutuated by multi-party interaction, rather than of a mixture of poorly-defined mechanisms. The probability distributions adopted in the baseline model are uniform, i.e. speaker- and history-independent.
- Joining/leaving force balance. Participants in a specific conversation remain in the conversation as long as they feel actively involved in it up to their preferred degree; otherwise, they start to wish to leave the conversation. We model this lively behavior by assigning a degree of happiness to each participant of the conversation. Happiness hereby stands for e.g. attention span, patience, assertiveness, self-esteem, and more: it is the index of the willingness of a participant to remain in a given conversation. The baseline scenario has all participants initially involved in the same table-wide conversation and assigned with the maximum level of the happiness scale, which is set equal to that of anyone else - i.e. we optimistically assume a person is happy to take part in a conversation that is about to start. Again, different initial conditions would evolve towards the same stationary state, as we will see. The individual happiness level is then subjected to dynamic change. It is decreased by one unit for every conversation turn during which the participant is not a speaker, while it is reset back to the initial level when the person gets a new opportunity to speak. As soon as the happiness level drops to the minimum tolerated level (set to zero in the baseline model), the participant becomes latent, i.e. she feels excluded enough to watch out around her for opportunities to enter another or a new conversation. Our parties can thus be considered as finite-states automata with a set (ideally, a continuum) of states between the fully conversation-integrated state (i.e. the conversation's current speaker or newcomers - parties with maximal happiness) and the fully-excluded state (i.e. the latent - parties of minimal happiness). Corollaries: a) a speaker is always fully happy; b) a latent is necessarily a listener.
- Neighborhood-based schism dynamics. When a participant is latent, she will look to her topological neighbors to be eventually engaged in a different conversation. She will first check whether at least one of the neighbors is in turn latent: if this is the case, she will start a new conversation with her/them. This nucleation mechanism is the responsible for the onset of schisming in our model. She will instead join the ongoing conversation of either of her neighbors, if such conversation differs from hers. In both cases, her happiness level will reset to its maximum level. If none of these options are possible, the agent remains latent, waiting for someone to talk to her (and to return active in her previous conversation) or for someone to go latent, or for a different conversation to take place. The use of only local resources to escape from a stagnant conversation is what we define as the conversational principle of least effort.
 The baseline model: analysis and results
The baseline model: analysis and results
- 3.1
-
The baseline model can be thought of as describing a homogenous group
of people leisurely engaged in chat without selection biases due to
accidental geometry, common interests, hierarchies or previous discourse
patterns.
- 3.2
-
Running the ABM with the homogeneous initial condition, it was found
that the initial table-wide conversation group splits over time into
several sub-convsersations of smaller group size. This is akin to
a spatial symmetry-breaking phenomenon: the initial, spatially-homogeneous
system (i.e. lacking boundaries) evolves into one with spatially-defined
boundaries. This splitting process continues - despite temporary increases
of the sizes of conversation groups - until the conversation
groups cannot split any further, that is, until each sub-conversation
reaches the absorbing state. Indeed, as long as there are more than
2 people in a (sub-)conversation, there exists always a non-null probability
that one participant will not speak before her happiness level decreases
to the minimum value, eventually driving her to leave the conversation;
this is true independent of the total number of participants in the
conversation and of their maximum happiness level. In the case of
an even (odd) initial number N
of agents, the asymptotic
configuration presents N/2
sub-conversations of two agents (N/2 - 1
sub-conversations of 2 agents and a single sub-conversation of three
agents). Equivalently said, the optimal though only asymptotic number
of parties in a conversation, according to the baseline model, is
predicted to be essentially 2
.
- 3.3
-
The characteristic time until reaching this steady state (i.e.
the characteristic amount of turn-taking time steps) depends on two
factors, namely 1) the number of agents, and 2) the maximum happiness
level. As expected, if the maximum happiness level is set to infinite,
the steady state will never be reached, while if set to 1, it will
be reached very soon. Numerical simulations indicate that this characteristic
time scales exponentially with the overall maximum happiness level,
and linearly with the number of agents (Figure 1).
The relation between happiness level and number of agents is the single
most important aspect of the model. As a matter of fact, maximum happiness
level and number of agents have opposite effects, since their increase induces
an increase and a decrease, respectively, of the probability of a
single agent to be entitled as speaker. Anyway, it can be expected
that the asymptotic state is hardly reached in real-life conversations,
that typically develop within shorter timescales than the characteristic
time to stationarity.
Figure 1: Semi-logaritmic plots of the characteristic time needed to reach the steady state, for different settings of the maximum happiness level (data averaged over 5 simulation runs). The straight line denotes exponential fitting. 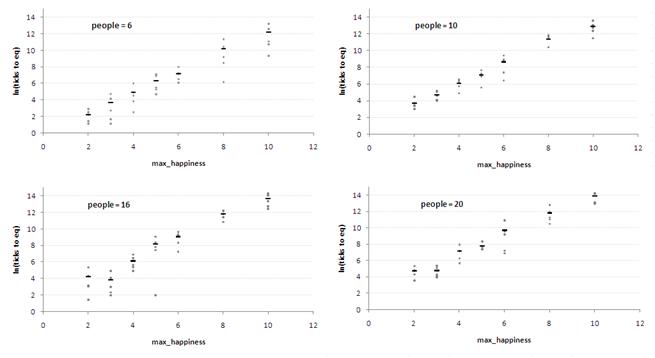
Mean-field approach
- 3.4
-
In a mean-field treatment of the baseline model, we will assume that
the probability pi
of a participant i
in a conversation to
be entitled to speak by the present speaker at time t is: 1) independent
of previous conversation history, and 2) constant in time. In general,
pi = pi(N, i)
where N
is the number of participants, and
the specific dependence of pi
on each participant characterizes
individuality, both intrinsic (e.g. psychological factors)
or extrinsic (e.g. conversation geometry). Let Fi(t)
be the happiness level of participant i
at time t
; for what
said before, Fi(t)
is semipositive definite.
Evolution equation
- 3.5
-
Participant i
at time t + 1
will have probability pi
of
being a speaker - and thus of increasing Fi
to its maximum level
MAXi
, and probability 1 - pi
of being a listener - thus
of decreasing her happiness level by one:
Fi(t) - 1
. Hence we
have the following N-dimensional map
g(Fi(t))
:
Fi(t + 1) = pi . MAXi + (1 - pi)(Fi(t) - 1), ∀i = 1,..., N (1) Fixed point and stability analysis
- 3.6
-
To find the fixed points Fi*
of each of these equations,
we drop the time dependence, i.e.:
from which we get:
Fi* = pi . MAXi + (1 - pi)(Fi* -1), ∀i = 1,..., N (2) Fi* is stable when -1 < dg(Fi*)/dFi* < 1 . We have:Fi* = MAXi +1 - 1/pi, (3) Accordingly, for normalization reasons we conclude that Fi* = MAXi +1 - 1/pi is the stable fixed point of each participant. Now, a participant becomes latent when Fi = 0 . In order for a participant to be active in the steady state, we must have Fi* > 0 . This translates into MAXi > 1/pi - 1 which is a restriction in the waiting time (i.e. patience) of agent i . Note that depending on pi , each agent will have a different critical patience.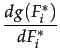 = - pi,
= - pi,
(4) - 3.7
-
As an example, in our baseline model we suppose that every agent has
the same probability of being a speaker. Imposing probability normalization,
we have
pi = 1/N, ∀i = 1,..., N
. In this condition an active
steady state is achieved for
MAXi > N - 1, ∀i = 1,..., N
. That
is, in order for every participant to be active in the same conversation,
their maximal waiting time cannot be less than the number of participants
minus one (the participant herself). If this requirement is fulfilled,
the initial conversation will, on average, be stable - all parties
will remain actively involved as time evolves.
Extinction cascade and sociological interpretation
- 3.8
-
The same analysis as before can be performed iteratively. Suppose
that we start at time t = 0
with N
agents such that:
- pi = 1/N, ∀ agents,
- MAXi > N - 1 for i = 1,..., N - 1 .
- MAXi < N - 1 for i = N .
- 3.9
-
A straightforward conclusion is the following: the number of parties
within a conversation will decrease until everybody feels comfortable
(i.e. until the patience thresholds of everybody are above the critical
values), and from there, it will remain as a stable conversation that
every speaker will profit of. The possible introduction of newcomers
into an ongoing conversation renders a direct analytic approach, even
in this very basic scenario, more difficult and goes beyond the scope
of this work. Furthermore, the analytical developments only provide
insight on the steady state, i.e. for conversations of infinite
duration. However, as commented above, real-time conversations only
develop in finite time. Therefore, to focus on realistic scenarios
it is required to study the conversation dynamics within finite time
windows, as discussed in the following Section.
Transient dynamics
- 3.10
-
The baseline model's assumption of simultaneous turn-taking (2) roughly
defines the characteristic time unit of the model (1 tick = 1 conversation
turn) as well as the empirically-relevant range of the total number
of turns taking place during a reasonable table talk. Now, what is
the correspondence between computational time steps and actual time?
While a time turn can in the real world last even very-few seconds,
here we deliberately obviate very-short time turns, since these short
turns may not have a relevant influence on the agents happiness. Accordingly,
we set a conservative estimation of an average of ten seconds per
time step (we remark that, as for the conceptual aim of the present
work, this actual value is secundary - still it will nonetheless need
to be confirmed with real experiments). A one hour-long conversation
then would allow for about 360 turns, which is hereby defined as the
actual conversation time window. For what said before, this
information may also be used to put a lower bound on the range of
permissible maximum levels of happiness. We found that, for even and
odd numbers of participants larger than 5, avoidance of convergence
to the stationary distribution within the first 360 turns can be achieved
by setting the maximum happiness level larger than about 8 - i.e.
8 is the minimum number of conversation turns which needs to be tolerated
without being a speaker to avoid precocious conversation convergence.
Tables of participants with higher maximum levels of happiness would
be able to maintain large conversation groups for longer periods of
time. As an example, Figure 3 shows the transient dynamics up to 376
ticks and the final stationary distribution of a model run with 15
participants and a maximum happiness level of 8. The geometric location
of, and the very participants involved in a group conversation, tend
to be persistent over time. Conversation groups rarely include people
who are not direct geometric neighbors of other people in the same
conversation. Also, latents can be trapped within a conversation group
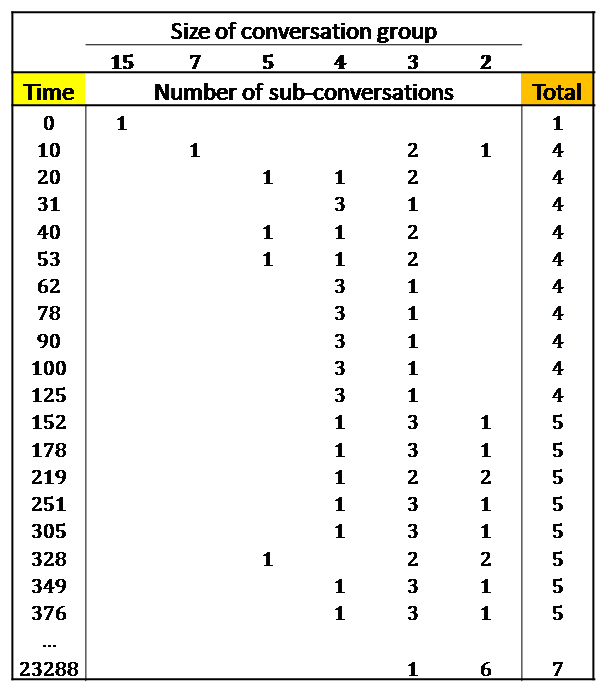
(see e.g. at ticks 10 and 53 in Figure 2).
Finally, the typical size of a conversation group mildly fluctuates
in the transient timescale, assuming a typical value of 4
parties.
Figure 2: Example of transient dynamics for a 15-party conversation with maximum happiness level of 8. Each agent is colored according to his belonging sub-conversation; latents are colored in dark grey. The initial table-wide conversation splits right after the beginning into 4 smaller sub-conversations because the happiness levels of some table members necessarily become simultaneously minimal, and latents can be mutually-close with high probability. After the initial schism (first 10 steps), non-trivial schisming dynamics develops, and agents hop from a sub-conversation to another according to the evolution of their individual happiness status. The 4 sub-conversations persist for 150 ticks before another sub-conversation is started. No other conversation group is formed until 376 ticks, i.e. the end of the table conversation. 
- 3.11
-
All the above findings hold in general and not only in the special
illustrated example. Importantly, in spite of abstracting from conversation
contents and contexts, many of these findings seem to correspond,
at least qualitatively, to phenomena that can be observed in real
table conversations. For example: table-wide conversations involving
a large number of people are unstable, while smaller conversation
groups persist over longer periods of time; people sometimes change
conversation groups, and when this happens they confine themselves
to nearby conversations (the conversational principle of least effort
is the reason why party organizers often pay so much attention to
the initial table population and configuration, if it is supposed
to remain fixed); people within a conversation group change from time
to time, but the conversation group has a tendency to remain in a
specific geometric location, and only a limited number of people around
the table join a specific conversation group; people who have left
a conversation group may eventually return to that same conversation
later; sometimes people would like to leave a conversation, but nonetheless
they may remain in it because they are trapped between two people
eagerly taking turns in that very conversation.
- 3.12
-
The previous analysis support a fundamental conclusion: the nucleation
of sub-conversations may be considered a dynamical mechanism that
take place in conversation dynamics according to abstract and purely-local
rules of happiness evolution, also independently of context- and content-related
arguments.
 A proxy for empirical evidence?
A proxy for empirical evidence?
- 4.1
-
To assess the extent to which our model replicates quantitatively
real-world table conversation dynamics, one should compare the predicted
dynamics to large empirical data sets. While a detailed comparison
with controlled dynamical experiments is left for future investigations,
we inquired into the ABM predictions for optimal transient size of
a conversation group. We performed a preliminary e-mail poll of 105
people (with ages in the range of 20 to 40), asking the pollees to
answer to the following question: In your opinion, what is,
on average, the maximum number of people that can be involved in the
same table conversation before this conversation gets uncomfortable?
Notice that the question does not suggest a pre-determined context-
or content-related conversation, and is free from any cognitive bias
except for the freedom implicitly allowed in the interpretation of
an uncomfortable conversation. Figure 4 shows the
histogram of the answer's frequency. The maximal value for the size
of a stable conversation group (N = 4
) matches the typical upper
bound of conversation group sizes that were reached in our simulations
within the actual duration of conversations (see Sec. 3.2)
While encouraging, this match does not suffice as empirical evidence
for the model; and we could wonder why we should assume that the opinions
of the respondents to the survey provide credible evidence. This is
statistically straightforward: people's opinion is biased on experience,
that is, their opinion is a byproduct of an average over many previous
conversations, in many different situations, scenarios, conversation
topics, conversation group characteristics, and so forth. The opinion
of individuals is therefore a proxy for real behavior. On the one
hand, such massive average over contexts and contents holds up with
our focus on context-independency; on the other hand, one could argue
that each individual is likely to have a different opinion, since
each individual is susceptible to have different experiences. Nevertheless,
if a common underlying mechanism exists, and if the histogram of individual's
opinions has a well defined average, the central limit theorem indicates
that the actual average result will tend to such average in the histogram.
Further empirical data should be obtained in order to confirm these
preliminary results.
Figure 4: Histogram of the maximal number of people for a comfortable conversation according to our e-mail survey. The distribution's mode (N = 4 ) agrees fairly-well with the numerical prediction of the baseline model. 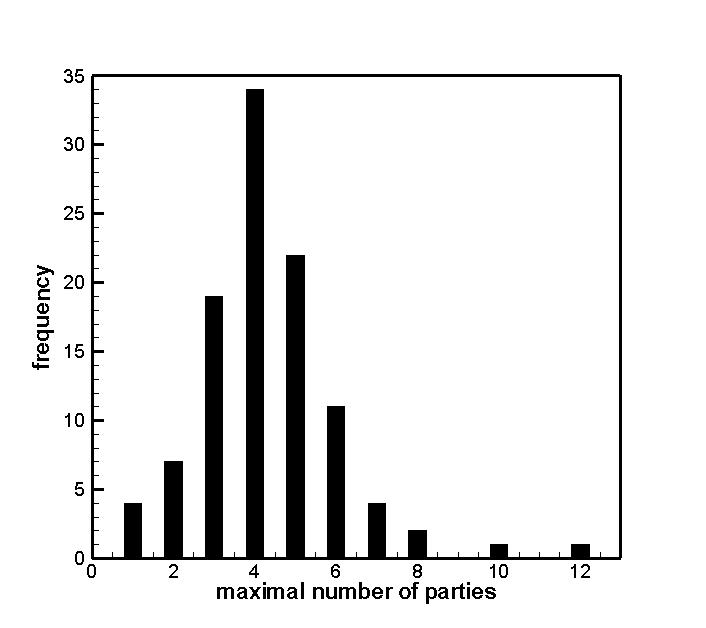
 Summary, discussion and future work
Summary, discussion and future work
- 5.1
-
The proposed, simple and abstract model of conversation dynamics predicts
a familiar behavioral scenario:
- Large conversation groups are unstable. Within a finite and reasonable time window, we may find stable conversations of more than two people. Schisming develops mainly from a balance between local rules (e.g. happiness of parties) and the global characteristics (e.g. number of participants, eventual criteria of target choice) of the conversation.
- The formation of new conversation groups is a relatively-rare event after the initial conversation split: the conversation dynamics mainly consists of people joining and leaving already-existing conversation groups, according to non-trivial spatio-temporal patterns.
- Table conversations rarely involve people who are not geometric nearest neighbors.
- Participants may remain trapped within their present conversation group, in spite of their dissatisfaction.
- 5.2
-
As for the (asymptotic) stationary states, we shall also
note that:
- Dyadic conversation groups are asymptotic absorbing states.
- The characteristic time needed to reach the stationary state scales exponentially with the maximum level of happiness, and linearly with the number of participants.
- 5.3
-
The focus of the present investigation was on the rather-conservative
baseline model of conversation dynamics, that originated as an attempt
to demonstrate a context- and content-free schisming mechanism. Further
progress in this direction will depend on the matching of simulated
and experimental data, which might well entail the refinement of the
model assumptions.
- 5.4
-
Moreover, the actual table conversation setting suggests interesting
generalizations of the model, to be tackled in further research:
- Agents heterogeneity and memory. The baseline model has one control parameter (the happiness degree) that can be used to fit empirical data; also, all agents are homogenous and follow the same time-independent behavioral rules. It seems obvious, though, that the large heterogeneity and variety of human behavior manifests itself also in conversations. For example, some people in a conversation group can actively try to let people speak who have not spoken for a long time; or, on the contrary, speakers might tend to address only people in their conversation group who have contributed recently. As such behaviors are here modeled by the probability distribution that determines the next speaker, it is natural to allow for speaker-dependent and time-dependent probability distributions, as well as for updates of the same distributions to encode memory effects.
- Asynchronous updating. Inclusion of the current speaker in the probability function that determines the speaker of the next turn. This eliminates the table-wide simultaneity of turn taking, and allows a different interpretation of the characteristic time to stationarity of the system. It also removes the stability of 2-people conversations, and makes the stationary states potentially more interesting - if one further assumes that 1-person conversation group cannot socially exist, and lonely people have to join other conversation groups instead.
- Dynamical neighborhood topologies: Modify the conversation geometry so that parties can form conversation groups with more than only two neighbors; any number of neighbors becomes possible (reminding of e.g. the connectivity of brain networks). A dynamic topology might eventually reproduce cocktail party dynamics.
 Acknowledgements
Acknowledgements
- The authors would like to acknowledge the great hospitality and support of the Santa Fe Institute during the Complex Systems Summer School '09, funded by the SFI and the National Science Foundation. Special thanks go to Dan Rockmore and Tom Carter. The authors also thank Jordi Luque and Andrea Firrincieli for fruitful discussions. LL acknowledges financial support from Spanish grant FIS2009-13690. Finally, the authors would like to thank Chuck Brown for being a perpetual source of inspiration and funk.
 Notes
Notes
- All codes as well as their NetLogo
implementations utilized in and derived from this work are freely
available under request.
1 Distributed Intelligent Systems and Algorithms Laboratory (DISAL), Ecole Politechnique Fédérale de Lausanne, Lausanne (CH)
2 Department of Economics, University of Maryland, College Park (USA)
3 Instituto de Fisica Interdisciplinar y Sistemas Complejos (IFISC, CSIC-UIB), Palma de Mallorca (ES)
4 NetLogo is available at: http://ccl.northwestern.edu/netlogo/
 References
References
-
AOKI, P. M., SZYMANSKI, M. H., PLURKOWSKI, L., THORNTON, J. D.,
WOODRUFF, A. & YI, W. (2006).
Where's the "party" in "multi-party"?: analyzing the structure of
small-group sociable talk.
In: Proc. 20th Anniversary Conference on Computer Supported
Cooperative Work.
AXELROD, R. (1997). The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration. Princeton University Press. [doi:10.1515/9781400822300]
AXELROD, R. (2006a). Agent-based modeling as a bridge between disciplines. In: Handbook of Computational Economics, Vol. 2: Agent-based computational economics (TESFATSION, L. & JUDD, K. L., eds.). Elsevier, pp. 1565-1584. [doi:10.1016/S1574-0021(05)02033-2]
AXELROD, R. (2006b). The evolution of cooperation. Basic Books.
BANDINI, S., MANZONI, S. & VIZZARI, G. (2009). Agent based modeling and simulation: An informatics perspective. Journal of Artificial Societies and Social Simulation 12, (4) 4. https://www.jasss.org/12/4/4.html [doi:10.1007/978-0-387-30440-3_12]
BONABEAU, E. (2002). Agent-based modeling: Methods and techniques for simulating human systems. Proceedings of the National Academy of Sciences 14, 7280-7. [doi:10.1073/pnas.082080899]
BONO, M., SUZUKI, N. & KATAGIRI, Y. (2003). An analysis of participation structure in conversation based on interaction corpus of ubiquitous sensor data. In: Proc. INTERACT 2003. IOS Press.
BYRNE, D. (1998). Complexity theory and the social sciences: An introduction. Routledge.
EGBERT, M. (1997). Schisming: the transformation from a single conversation to multiple conversations. Research in Language and Social Interactions 1, 1-51. [doi:10.1207/s15327973rlsi3001_1]
GALLEY, M., MCKEOWN, K., FOSLER-LUSSIER, E. & JING, H. (2003). Discourse segmentation of multi-party conversation. In: Proc. 41st Annual Meeting on Association for Computational Linguistics. [doi:10.3115/1075096.1075167]
GOFFMAN, E. (1963). Behavior in public places. Notes on the social organization of gatherings. Free Press.
GOODWIN, C. (1984). Notes on story structure and the organization of participation. In: Structures of social action (ATKINSON, J. & HERITAGE, J., eds.). Cambridge University Press.
GOODWIN, C. (1987). Forgetfulness as an interactive resource. Social Psychology Quarterly 50, 115-131. [doi:10.2307/2786746]
ISHIZAKI, M. & KATO, T. (1998). Exploring the characteristics of multi-party dialogues. In: Proc. 17th International Conference on Computational Linguistics. [doi:10.3115/980451.980942]
MILLER, J. H. & PAGE, S. E. (2007). Complex adaptive systems: An Introduction to Computational Models of Social Life. Princeton University Press.
PARKER, R. (1984). Conversational grouping and fragmentation: a preliminary investigation. Semiotica 50, 43-68. [doi:10.1515/semi.1984.50.1-2.43]
SACKS, H., SCHEGLOFF, E. A. & JEFFERSON, V. (1974). A simplest systematic for the organization of turn-taking for conversation. Language 50, 696-735. [doi:10.1353/lan.1974.0010]
SCHEGLOFF, E. A. (1995). Parties and talking together: two ways in which numbers are significant for talk-in-interaction. In: Situated order: studies in the social organization of talk and embodied activities (P.TENHAVE & PSATHAS, G., eds.). University Press of America, pp. 31-42.
SCHWEITZER, F. (2003). Browinian agents and active particles. Springer.
SIMMEL, G. (1902). The number of members as determining the sociological form of the group. American Journal of Sociology 8, 1-46. [doi:10.1086/211115]
STIEFEKHAGEN, R., YANG, J. & WAIBEL, A. (2002). Modeling focus of attention for meeting indexing based on multiple cues. IEEE Trans. Neural Networks 13, 928-938.
VERTEGAAL, R., WEEVERS, I., SOHN, C. & CHEUNG, C. (2003). Gaze 2: Conveying eye contact in group video conferencing using eye-controlled camera direction. In: Proc. SIGCHI conference on Human factors in computing systems. [doi:10.1145/642611.642702]