Abstract

An agent-based model to simulate a pedestrian crowd in a corridor is presented. Pedestrian crowd models are valuable tools to gain insight into the behavior of human crowds in both, everyday and crisis situations. The main contribution of this work is the definition of a pedestrian crowd model by applying ideas from the field of the kinetic theory of living systems on the one hand, and ideas from the field of computational agents on the other hand. Such combination supported a quantitative characterization of the performance of our agents, a neglected issue in agent-based models, through well-known kinetic parameters. Fundamental diagrams of flow and activity are presented for both, groups of homogeneous pedestrians, and groups of heterogeneous pedestrians in terms of their willingness to reach their goals.

Keywords:

Agent-Based Modeling, Pedestrian Crowd, Activity Measurement

Introduction

1.1

Understanding collective human motion is a key issue in designing and developing urban spaces and pedestrian facilities. Pedestrian and crowd models are also valuable tools to gain insight into the behavior of human crowds in both, everyday and crisis situations. There is an extensive literature describing pedestrian and crowd models. These models include, for instance, studies of collective motion under both, normal and competitive situations, the identification and analysis of spatial walking patterns, and the influence of the geometry of pedestrian facilities in pedestrian behavior. For detailed surveys of both, the theoretical literature and the empirical aspects of pedestrian dynamics, see the works of Harney (2002), Helbing et al. (2005), Leigh (2009), and Schadschneider et al. (2008).

1.2

It is worth to mention that there is a number of studies interested in contrasting simulation results with experimental results using real pedestrians. See, for instance, the work of Nagai et al. (2005), where experiments using people going on all fours in counterflow are reproduced by a lattice-gas simulation. See also the work of Kretz et al. (2006) that describes bottleneck experiments at different densities. This kind of experiments are, however, beyond the reach of our investigation.

1.3

Two kinds of influences are usually taken into account in pedestrian and crowd models: global and local influences. Global influences represent high-level properties involving the entire problem of pedestrian traffic, such as the average continuous flow or pressure-gradient forces. Local influences represent low-level properties concerning parts of the problem of pedestrian traffic, such as the pedestrian's emotional state or its proper velocity. In the literature, high-level and low-level properties are also referred to as extrinsic and intrinsic properties, respectively (Schadschneider et al. 2008), whereas the macroscopic and microscopic models are also referred to as aggregate and disaggregate models, respectively (Ronald et al. 2007).

1.4

Various taxonomies to classify pedestrian and crowd models have been proposed, such as discrete vs. continuous models, or microscopic vs. macroscopic models. Taxonomies can help researchers to grasp the complexity and multidimensionality of studies about collective motion. However, proposed taxonomies are usually represented as extreme points in a linear dimension. In that sense, we prefer to use a well-known taxonomy and refine it in the light of a more comprehensive coverage, that holds hybrid and sui generis current models. Thus, according to the influences considered in pedestrian models, these can be classified into three categories: macroscopic models, intermediate models, and microscopic models. Macroscopic models describe pedestrian crowd behavior exclusively in terms of global influences, see, for instance, the hydrodynamic model of Henderson (1974). Intermediate models describe pedestrian crowd behavior by taking into account both, global and local influences, see, for instance, agent-based models (Bandini et al. 2004, Dijkstra et al. 2000, Fridman and Kaminka 2009, Ronald et al. 2007) and models based on stochastic cellular automata (Burstedde et al. 2001). Microscopic models describe pedestrian crowd behavior uniquely in terms of local influences, see, for instance, the behavior-based lattice-gas model of Weng et al. (2006), cellular automata based models (Yu and Song 2007; Gipps and Marksj 1985), or the social force model (Helbing and Molnr 1995; Parisi et al. 2009).

1.5

The influences involved in crowd models determine also the granularity of parameters that measure the dynamics of the system. In macroscopic models, for instance, coarse parameters such as the average speed of crowd motion, order/disorder relationships, appearance and structure of spatial patterns, may be recorded and evaluated. Refined parameters, such as the average speed of highlighted pedestrians, or the number of encounters among pedestrians at every simulation step, are rather calculated for pedestrian crowds based on both intermediate and microscopic models. The determination of the abstraction level is involved with the modeling consideration on granularity and generality. A macroscopic model is good enough to reproduce and evaluate generic crowd behavior under different environmental conditions, whereas intermediate and microscopic models can properly reproduce the behavior of heterogeneous pedestrians, their local interactions and preferences. Heterogeneity among individuals seems to be an essential feature in a living crowd that however has been rarely addressed in pedestrian crowd models.

1.6

The flexibility of pedestrians modeled applying intermediate and microscopic models has to come at the cost of acquiring and processing data concerning individual entities. Greater the flexibility, higher the cost. Thus, an important aspect to take into account in pedestrian and crowd models is how to represent the core operating entities of the problem. Pedestrians have been modeled such as, for instance, self-propelled particles, cells of cellular automata, and computational agents. As we are concerned in this work with agent-based pedestrian models, we briefly review the most relevant work on agent-based models for crowd simulation. Existing agent-based crowd models are essentially intermediate models that represent entities as composed (Bandini et al. 2004) or cognitive agents (Dijkstra et al. 2000, Fridman and Kaminka 2009, Ronald et al. 2007). In these models, global influences such as attraction forces in the pedestrian's environment, are combined with local influences concerning individual preferences. Agents in these models depend usually on refined data sets and are also equipped with very specialized capabilities, such as sensors to acquire the state features of their partners. These considerations lead to flexible platforms for simulating crowd motion that however rely on very expensive computational resources. As we are additionally concerned with heterogeneous pedestrians, we also review a work in which two classes of pedestrians are modeled (Burstedde et al. 2001).

1.7

Bandini et al. (2004) combine autonomous agents and cellular automata for pedestrian crowd modeling, in the so-called situated cellular agent approach. Individual aspects of the simulation, such as choice-preferences, are modeled by applying an agent-based approach, whereas physical aspects, such as information transmission, perception and motion, are solved by applying local rules based on cellular automata. Such combination provides a very flexible model that can theoretically be used to analyze forward and backward scenarios. Even though this model relies on simple rules for solving pedestrian motion, it involves complex capabilities for the establishment of agreements among agents, and for joining and leaving groups of agents that have reached agreements. The situated cellular agent approach has been applied to simulate pedestrians visiting a museum (Bandini et al. 2004), as well as pedestrians in an underground station scenario (Bandini et al. 2006). The results of previous works are presented in the form of screenshots of the simulation, the plot of the number of active agents, and records of individual measurements of signals by agents during experiments.

1.8

The work of Dijkstra et al. (2000) is oriented to simulate pedestrian motion within a shopping mall, by combining an agent-based approach and a cellular automata based approach. Thus, pedestrians are agents that move over a cellular automata grid. Agents are represented as very complex autonomous agents that know detailed and differentiated information about the problem. Agents know, among others, the state of the environment that include the state of other agents, their own preferences and choices. Agents know also series of stops that represent attractive shopping sites, or sites to start a conversation with other agents. From that, particular paths between a starting and a goal position in the environment can be defined, such as the shortest path or the most attractive path. The operation of these agents relies on a set of simple rules that capture general situations, such as check-decision-point and check-adjacent-cells, that are related with more specific actions. In this work, the 3D representation as well as the visualization of the environment are considered key aspects of the simulation. For that, the results are presented in the form of snapshots of the simulation.

1.9

Fridman and Kaminka (2009) are interested in the development of a generic agent-based model rooted in ideas of social psychology theory, namely the Social Comparison Theory (SCT). Their agents rely on a simple process that can be summarized in two actions: comparison and imitation. An agent in this model compares specific features of its state, such as orientation, position and sense of flow, with the features of agents perceived within its local field of view, in order to calculate their similarity. After that, each agent selects one of its partners, whose state is bounded by maximum and minimum values of similarity, in order to reduce the distance between the selected partner and itself. Thus, as long as agents become "infected" by this desire of uniformity, they converge gradually towards common goals. Concerning the crowd parameters, pedestrian flow is calculated in low-density occupation of a corridor, as well as the formation of spatial patterns measured from individual pedestrian lane changes using different levels of reaction. Based on these parameters SCT model is compared with a random-choice model, and from that the authors conclude that their agents are more "persistent" when following lanes than random agents. However, the efficiency of pedestrian transport, measured as pedestrian flow, is in both models almost identical (Kaminka and Fridman 2006).

1.10

Ronald et al. (2007) analyse the convenience of modeling pedestrian crowds by applying a BDI agent approach. They are interested in applying this approach for simulating crowd behavior in a stadium, where visit attractions are also available. Pedestrians are autonomous agents that know a lot of information about the environment and about themselves, such as the location of attractive sites, the effect of their actions on their environment, and what to do in case of failures. Agents are also able to communicate to each other directly. In this work, a thorough specification of the goals and actions of the system entities is required in order to enable the execution of feasible schedules, but also in order to cope with infeasible schedules. The work focuses on a qualitative description of the BDI agent framework, and quantitative measurement of the results of applying this model in crowd simulation are not provided.

1.11

Burstedde et al. (2001) propose a two-dimensional cellular automaton model to simulate pedestrian traffic. Cellular automata used in this work are extended with the so-called "floor field", a second grid of cells underlying the grid of cells occupied by the pedestrians. The floor field acts as a spatial collective memory where forces on microscopic levels are recorded. These forces may include the geometry of the building, pedestrian traces, attractive or repulsive regions. The floor field values can both, affect the behavior of pedestrians and be affected by them. Pedestrians can effectively modify their transition probabilities from the floor field values. And reciprocally, the floor field values can be modified according to their occupation. In this work, two classes of pedestrian are simulated which can be distinguished by their fluctuations. "Happy" pedestrians try to move in a "preferred" direction, whereas "unhappy" pedestrians move randomly. Spatial patterns such as lane formation in corridors, and oscillatory flows at bottlenecks in evacuation scenarios are reproduced with this model. The results of this investigation are provided in the form of snapshots of the simulation as well as velocity profiles and plots of mean evacuation time.

1.12

In contrast to existing agent-based models, in this work a model based on a previous microscopic model (Rangel-Huerta and Muñoz-Meléndez 2010) for pedestrian crowd simulation is presented. The work of Kaminka et al. (Kaminka and Fridman 2006, Fridman and Kaminka 2009) is probably the closer agent-based model to our model because the walking process is summarized in a simple cycle and agents rely on local perception. However the cited authors argue that imitation and contagion are the underlying mechanism of collective motion, including pedestrian crowd motion as a particular instance, which seems to be a raw generalization where there is not place for modeling, for instance, heterogeneous pedestrians.

1.13

The main difference with related work is that situated agents proposed in our model are simpler than composed and cognitive agents, in terms of their level of abstraction. In effect, an agent in our model acquires local information about its environment, and knows a priori only few pieces of information, such as its goal and its preferences of turn and step size. In addition to that an agent applies a set of rules, as the ones applied in cellular automata, that trigger actions according to local states. In our case rules are not strictly applied, they are instead modulated by individual profiles of agents. Composed and cognitive agents rely on very complex and specialized structures such as, for instance, processes by which agents might anticipate or guest actions or preferences of other agents, individual records of precedent interactions, to mention a few examples. These features of crowd models involving composed and cognitive agents make difficult the calculation of traditional crowd parameters in a wide range of pedestrian densities, as well as the system characterization from these parameters. In contrast to that, our model results in an entirely decentralized simulation of pedestrian crowd motion, that reproduces properly walking patterns observed in human pedestrians.

1.14

In this work, a homogeneous crowd means a crowd composed by individuals that behave similarly. In contrast, a heterogeneous crowd is composed by individuals that can be differentiated into two or more subgroups that exhibit different behaviors. Note that other features of individuals might be considered when defining heterogeneity, such as physical morphological features, sensors or even the quality of sensors for acquiring information. The definition of heterogeneity in pedestrian crowds from a behavioral perspective is just a starting point in our research. In the current stage of our model it is straightforward to define pedestrian profiles that result in different behaviors. However, other sources of differences among pedestrians will be considered in our work in the future.

1.15

The rest of the paper is organized as follows. Section 2 describes the agent model. Section 3 describes evaluation criteria and results obtained from various experiments. Section 4 compares our models with related work, and discusses important remarks raised by our results. Finally, section 5 closes with conclusions of this work.

Pedestrian Model

Composition and Representation of Agents

2.1

A pedestrian is an autonomous agent consisting of a set of state variables, such as its position, its heading, and its step size. In addition to that, each agent consists of three interconnected modules in charge of its perception, its decision making and its actuation. Figure 1 illustrates the agent composition, and the composition of these modules is described in detailed below.

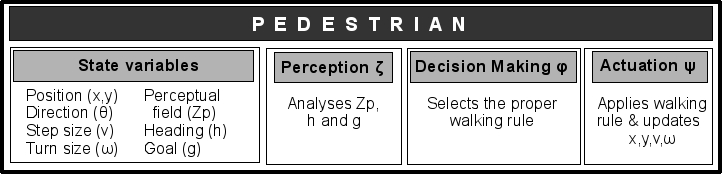
Figure 1. Composition of a pedestrian.

2.2

Regarding representation aspects, the microscopic pedestrian state is defined as the tuple expressed in formula (1).

Pα(t) = (x, v, z; t)α   α = 1, 2, 3, ..., N

(1)

where N is the total number of pedestrians within the corridor. Each pedestrian has information about its location and orientation in the corridor x_α = (x, y, θ)_α . The walking speed is denoted by v_α = (v, ω)_α, where v_α is the step size and ω_α the turn size. The vector of perceptual information, z_α= (Zp,h, g)_α, where Zp_α is the perceptual field, h_α the pedestrian heading, and g_α its goal direction.

2.3

The multiagent system or crowd is represented as the "supertuple" C(t). It represents the entire group of pedestrians, the perception, decision making and actuation modules, ζ, φ and ψ respectively, as indicated in formula (2).

C(t) = ({Pα | α = 1, 2, 3, ..., N}, ζ, φ, ψ ; t)

(2)

2.4

The perception module ζ analyses the information acquired by pedestrians. The decision making module φ represents socially accepted walking rules. The actuation module ψ is in charge of implementing the decisions made by an agent by updating its state variables. These modules are described in detail below.

Perception Module (ζ)

2.5

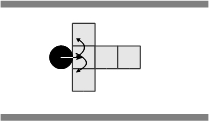
Perception is the agent module in charge of acquiring information about itself and about the environment. A pedestrian is capable of perceiving different nature of information: internal and external. Internal information, such as the agent's heading -its orientation with respect to the walls-, its goal or its step size, is perceived through its proprioception mechanism. External information, such as the conditions of the area surrounding the agent are acquired through the agent's T-perceptual field, consisting of three frontal squares and two lateral squares, as illustrated in Figure 2. Note that a perceptual field is attached to each agent, and that it is symmetrical with respect to the vector representing the walking orientation or the agent's heading.

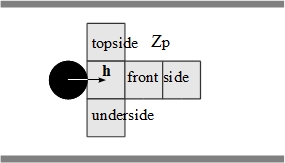
Figure 2. T-perceptual field of a pedestrian.

2.6

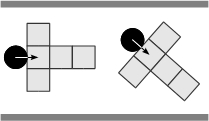
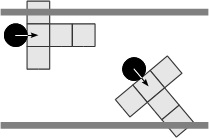
Each agent examines constantly the state of its perceptual field, starting from the nearer frontal square and finishing with lateral squares. The situations that an agent is capable of perceiving from the occupation of its perceptual field are, free path (FP, Figure 3(a)), obstructed path (OP, Figure 3(b)), pedestrian encounters (PE, Figure 3(c)), and combined encounters involving both, obstacles and other pedestrians (CE, Figure 3(d)). In each one of previous situations an agent can be aligned or non-aligned with respect to the borders of the corridor.

(a)	(b)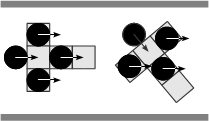
(c)	(d)
Figure 3. Situations perceived by a pedestrian through its perceptual field: (a) Free path, (b) obstructed path, (c) pedestrian encounters, and (d) combined encounters.

2.7

It is worth mentioning that an agent has access uniquely to external information when perceiving a partner, such as its sense of flow, its position within its own perceptual field, or its heading. Internal information, such as the speed of an agent -represented as its step size- or its goal location, are not perceived through this mechanism. This restriction is intended to reproduce realistic mechanisms of perception, that enable effectively the sharing of information among the members of the system, but at same time do not assume that the state of an agent is completely translucent for their partners.

Decision Making Module (φ)

2.8

Once an agent knows its state from the information acquired through its perception module, it makes a decision about the next movement to get closer to its goal. Even though an agent is capable of limited perception in a local area, a wide variety of cases that result from the occupation of the cells of its perceptual field is possible. Various of these cases, that involve direct interaction among agents and of agents with their environment (see Figures 3(c) and 3(d)) are traffic conflicts that must be solved using a set of collision avoidance conventions. Traffic collisions are relevant because they may hinder the achievement of the agent's goal, that is traversing the corridor.

2.9

The decision making module consists of a set of walking rules that are common among agents. Walking rules are generic rules synthesizing a variety of situations that were identified. These rules enable pedestrians to negotiate pedestrian encounters and combined encounters as binary encounters. From that, a pedestrian decides whether or not it has to turn and move, and if so, its angle turn and its step size, as well as the order in which these actions, turn and move, should be executed. The main condition considered by agents in order to know which rule should be applied is their orientation with respect to the corridor. Thus, when an agent is non-aligned, its primary action is to go forward a "permitted step", that is a step of a size permitted by the frontal occupation of its perceptual field, and then turn in order to realign itself with respect to the borders of the corridor.

2.10

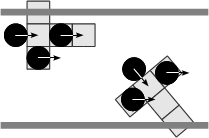
When aligned with respect to the corridor and free path is perceived, an agent performs, from time to time, a comfort turn that lead it to lose temporary its alignment (Figure 4(a)). If obstructed path is perceived, the agent performs a turn to avoid the wall (Figure 4(b)). In both cases the agent moves subsequently a step forward. When aligned to the corridor an agent solves frontal encounters with other pedestrian that is aligned to itself by turning towards its right or its left (Figures 4(c) and 4(d)). Similar encounters between two agents that are not aligned to each other are solved by the agent who perceives the situation by turning towards the very same (Figure 4(e)) or the negative (Figure 4(f)) orientation of its partner. These four basic rules synthesize various combinations of situations that may happen. Figure 5 illustrates, for instance, the situations summarized by the rule expressed in Figure 4(c). In the latter situations, various cases of multiple occupation of the perceptual field of an agent, for both agents and walls, are represented. Note that for these variations, the step size performed by an agent is constrained accordingly with the permitted step previously explained.

(a)	(b)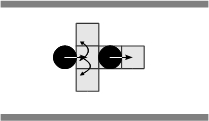
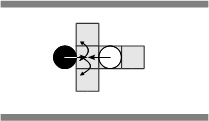
(c)	(d)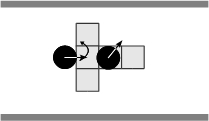
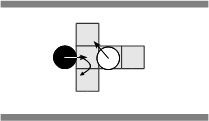
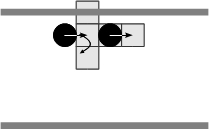
(e)	(f)
Figure 4. Solving situations of pedestrians aligned with respect to the corridor: (a) free path, (b) obstructed path, (c) flow encounter of aligned pedestrians, (d) counter-flow encounter of aligned pedestrians, (e) flow encounter of non-aligned pedestrians, and (f) counter-flow encounter of non-aligned pedestrians.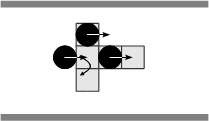

(a)	(b)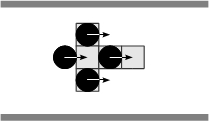
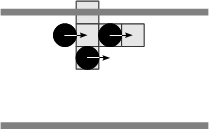
(c)	(d)
Figure 5. Specific pedestrian and combined encounters synthesized as the binary encounter shown in Figure 4(c). The domain of turn angle and step size are constrained as a pedestrian perceives an obstacle or partners within its perceptual field.

2.11

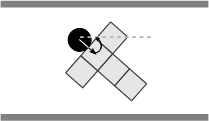
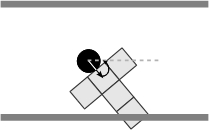
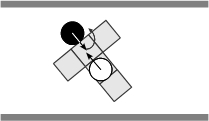
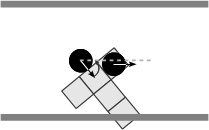
When non-aligned with respect to the corridor, an agent changes its walking sequence by going forward a permitted step first, and then turning in order to align itself with the corridor. Whenever it is possible an agent moves forward without regard to the orientation or the sense of flow of a perceived partner, if any, and then it turns to align itself with respect to the corridor (Figures 6(a)-6(f)). As for the basic rules, note that the latter summarize a variety of situations, Figure 7 illustrates, for instance, the situations summarized by the rule expressed in Figure 6(c).

(a)	(b)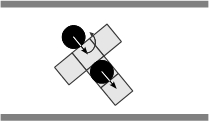
(c)	(d)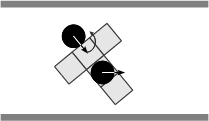
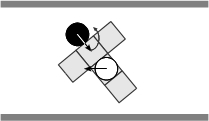
(e)	(f)
Figure 6. Solving situations of non-aligned pedestrians with respect to the corridor: (a) free path, (b) obstructed path, (c) flow encounter of aligned pedestrians, (d) counter-flow encounter of aligned pedestrians, (e) flow encounter of non-aligned pedestrians, and (f) counter-flow encounter of non-aligned pedestrians.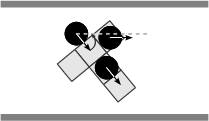

(a)	(b)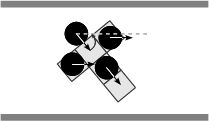
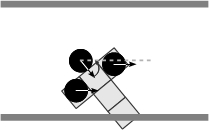
(c)	(d)
Figure 7. Specific pedestrian and combined encounters synthesized as the binary encounter shown in Figure 6(c). The domain of the step size is constrained as a pedestrian perceives an obstacle or partners within its frontal perceptual field.

Actuation Module (ψ)

2.12

Actuation module ψ is in charge of implementing the decisions made by agents by updating their state variables. In this Section, a kinematic model to describe the movement of pedestrians as well as the domains of the position and walking speed of pedestrians are presented.

2.13

The walking speed of pedestrians results from the heading, h_α(t); which has an associated normal unit vector, n_α(t); oriented acording the sign of ^dθ_α /_dt , as expressed in formula (3).

vα(t) = vα(t) hα(t)

(3)

2.14

The acceleration is obtained by the derivative of Equation (3) and represents the kinematics of walking. It has been observed that pedestrians turn mainly for avoiding partners while they maintain their walking speed (Helbing et al. 2005). In this case the acceleration is denoted by:

aα(t) = dvα /dt

(4)

therefore it can be splitted into two terms, step size, v_α(t); and turn size, ω_α(t):

aα(t) = dvα /dt hα(t) + vα(t) | dθα /dt | nα(t)

(5)

where the transverse change of heading satisfy: ^dh_α /_dt = | ^dθ_α /_dt | n_α(t). In the simulation ω_α(t) = | ^dθ_α/_dt | is the turn size.

2.15

After some simplifications, we have obtained the discrete walking process model described by formula (6),

aα(t) = vα(t) | &Deltaθα(t)/&tau | nα(t)

(6)

the new pedestrian walking speed is defined by formula (7),

vα(t + &tau) = vα(t) + vα(t) | &Delta θα(t)/&tau | nα(t) &tau

(7)

and the new pedestrian position is updated by formula (8)

xα(t + &tau) = xα(t) + vα(t + &tau) &tau

(8)

2.16

Thus, actuation module represents the state transition (xⁱ, vⁱ, Zpⁱ; t) _α &rarr (x^j,v^j, Zp^j; t + &tau)_α of pedestrians. The domains of state variables are defined as follows: The range variation of the agent position within the corridor is defined as D_x = {x_α | x_α &isin area of the corridor }. The walking speed domain, D_v = D_v × D_ω, being D_v = {v_α | v_α &isin {0, 1}} and D_ω = { ω_α | ω_α &isin {-&pi/4, 0, +&pi/4 }. These values are normalized with respect to the values of the standard walking speed (Rangel-Huerta and Muñoz-Meléndez 2010).

2.17

The specific values of position and walking speed depend on the local circumstances perceived by an agent during each simulation step. The domains D_x, D_v are available in situations of free walking and some other frontal encounters. The domains of variation are constrained accordingly to the degree of occupation of the perceptual field of an agent. The values (0, 0) correspond, for instance, to a valid update to deal with the total occupation of the perceptual field of the agent.

2.18

Note that while the perception and decision modules are internal information processes for agents, the actuation module concerns the walking process in the simulation. Agents update their positions and their walking speed internally, and then they perform corresponding actions on the external environment through its actuation module.

Walking Process

2.19

The agent modules are interconnected in such a way that during each simulation step, the agent acquires information about the environment and about itself, processes this information, and updates its state accordingly. The walking process is a loop that is constantly executed by the agents, that can be summarized as follows:

1. Perceive: The agent acquires information from its proprioception and from its perceptual field.
2. Decide turn size/step size: The agent determines its walking speed, v^j_α(t + &tau), by applying the general walking rules.
3. Perform decision: The agent applies the transition of states to update its position in the corridor x^j_α(t + &tau) = xⁱ_α(t) + vⁱ_α(t) &tau, and its walking speed vⁱ_α(t) &rarr v^j_α(t + &tau).

2.20

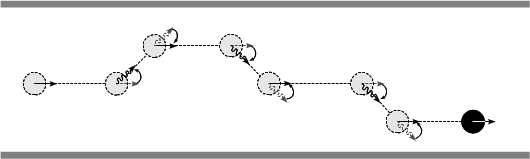
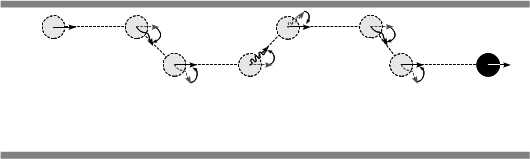
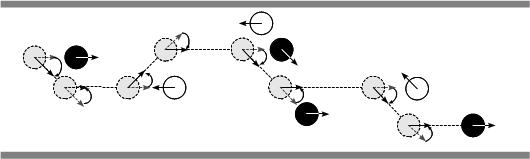
The walking process integrates the different capabilities that must be jointly applied by agents in order to traverse the corridor. This process is based on a functional decomposition of agents oriented to provide them the necessary equipment to deal with a wide variety of situations, from free-path situations to pedestrian encounters, and from pedestrian encounters at low-densities to pedestrian encounters at high densities of occupation of the corridor. Figure 8 illustrates different trajectories of pedestrians dealing with various situations. Figure 8(a) shows the pathway of an agent who always perceived free path, and performed eventually comfort turns, represented as zigzagged arrows. Figure 8(b) shows the pathway of an agent that performed turns to avoid the walls of the corridor, represented as undulating arrows, as well as comfort turns. Finally, Figure 8(c) shows the pathway of an agent that performed turns to avoid other agents, represented as linear arrows. Figure 9 shows some snapshots of the simulation of a pedestrian crowd based on the described model at different densities of occupation of the corridor.

(a)

(b)

(c)

Figure 8. Trajectories of agents during different situations of occupation of the corridor.

(a) 20 pedestrians

(b) 100 pedestrians

(c) 360 pedestrians

(d) 550 pedestrians

(d) 650 pedestrians

Figure 9. Flow patterns observed in the corridor at different densities. (a)-(b), (c), and (d)-(e) correspond, respectively, to a low density region, a critical region, and a high density region plotted in Figures 10 and 11. The size of the corridor is 100 cells wide × 12 cells height. Red pedestrians move left to right, whereas blue pedestrians move right to left.

Simulation Results

3.1

The quantification of multi-agent systems performance is an open issue and a lot of work remains to be done in order to characterize the behavior of multi-agent systems under various circumstances. In this work, a quantification of the pedestrian crowd in terms of kinetic parameters is proposed. Below, a description of these quantitative criteria is given.

Kinetic Parameters

3.2

The kinetic description of pedestrian flow in a corridor is represented as a function of probability of a particle. Let &eta(v,t) = &eta(x, v, u; t), the average number of pedestrians around (x, v), with activity function u at time t. The activity in crowd and swarm simulation usually represents the degree of interaction among the entities of the system. In this work, the activity of pedestrians, u = u(Zp), represents the number of restrained maneuvers for pedestrian mobility from the occupation of their perceptual field. Note that (x, v) represents the influence of the agent over the environment, whereas u represents reciprocally the influence of the environment over the agent. The kinetic equation of the crowd is obtained as indicated by formula (9).

d/dt [&eta(v,t)] =

∑ijk (1 - &eta(vjα,t)) &eta(vkα',t) &gamma(viα,vkα') B(viα,vkα' ; vjα) &delta(v - vjα) - ∑ijk &eta(vjα,t) (1 - &eta(vkα',t)) &gamma(vjα,vkα') B(vjα,vkα' ; viα) &delta(v - vjα)

(9)

3.3

The function &delta considers the actual values of the walking speed. Formula (10) expresses the frequency of pedestrian encounters, a measure of the change in the perceptual field of pedestrian P_α(t) with walking speed vⁱ_α, produced by the presence of a partner P_α' (t) with walking speed v^k_α'. The function B(vⁱ_α,v^k_α' ; v^j_α) represents the probability that P_α changes its walking speed, from vⁱ_α to v^j_α because of an encounter with P_α' with walking speed v^k_α'.

&gamma(viα, vkα') = 1/2 &Delta [(Zpiα(t) + Zpkα' (t))] / &tau &delta(xiα - xkα')

(10)

3.4

Once the density of probabilities &eta(v,t) is known, we evaluate the quantities of interest that describe the macroscopic conditions of the collective behavior such as, the density (formula 11), the rate of flow (formula 12), and the mean activity function or activation (formula 13). The pedestrian crowd performance is expressed in terms of these variables, the kinetic parameters.

< n(t) > = ∫ &eta(v, t) dx dv du

(11)

< v(t) > = ∫ v &eta(v, t) dx dv du

(12)

< u(t) > = ∫ u &eta(v, t) dx dv du

(13)

Average speed and activity

3.5

The main results of the simulation are presented in the form of fundamental diagrams of phase transitions of the average flow and the average activity with respect to the pedestrian density. In Figures 10 and 11, a critical region (Figure 9(c)) can be clearly identified between low (Figures 9(a) and 9(b)) and high values (Figures 9(d) and 9(e)) of density. As we know, in this critical region the different phases of flow and activity coexist with oscillations of great amplitude even under small variations of density. Note that the fundamental diagrams of both, flow (Figure 10) and activity (Figure 11), have a critical zone at the same value of density. These diagrams have symmetrical tendencies, even though the former is produced by an external observer in charge of collecting data of walking speed of pedestrians, while the second is produced from data provided by individual pedestrians concerning the occupation of their perceptual fields.

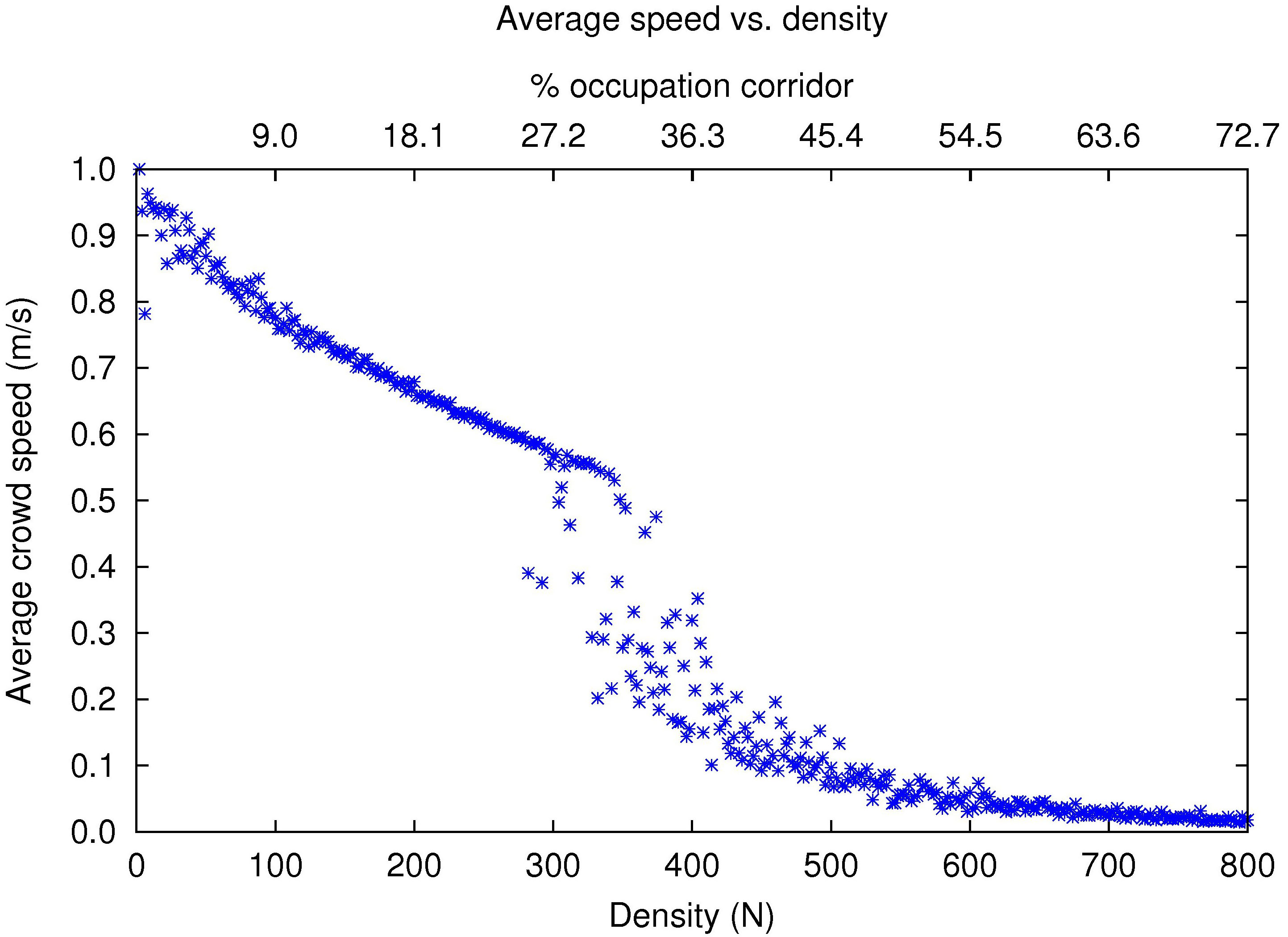
Figure 10. Average velocity by varying the number of pedestrians, from 2-800, during 200 iterations. The X-Axis is labeled in the bottom with the number of pedestrians in the simulation, and it is labeled in the top with the percentage of occupation of the corridor of the corresponding number of pedestrians.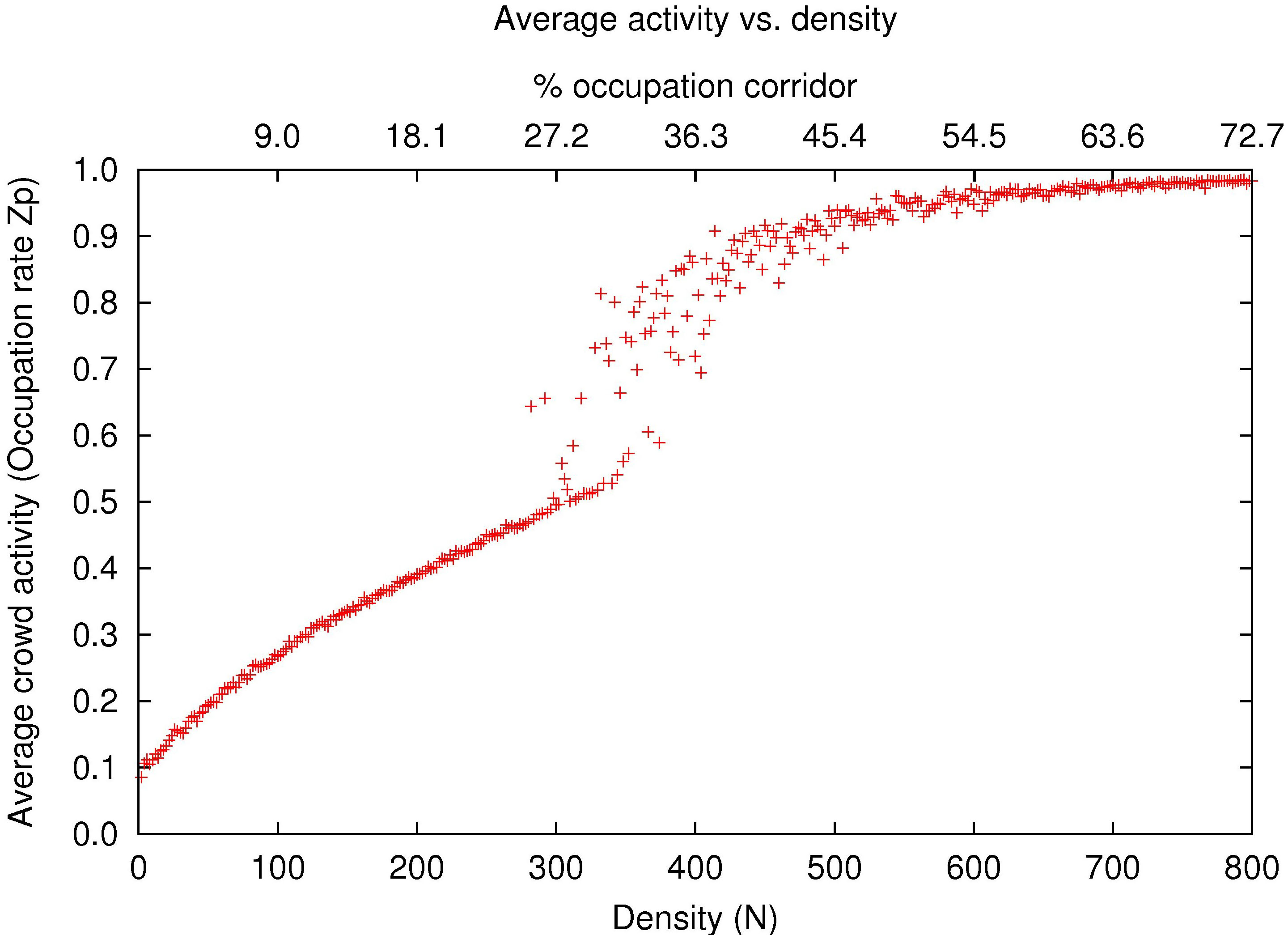

Figure 11. Average activity by varying the number of pedestrians, from 2-800, during 200 iterations. The X-Axis is labeled in the bottom with the number of pedestrians in the simulation, and it is labeled in the top with the percentage of occupation of the corridor of the corresponding number of pedestrians.

Customized agents

3.6

In order to explore the flexibility of our model, we conducted an experiment of specialization of pedestrians in heterogeneous groups according to their walking preferences, namely in terms of the chosen angle turn. Agents are specialized into three profiles: "relaxed", standard and "hurried" pedestrians. Standard pedestrians are in fact the agents introduced in the pedestrian model described in section 2. "Relaxed" pedestrians do not want to reach their goal quickly, thus they perform comfort turns constantly and they prefer to give others the right of way when dealing with pedestrian encounters. In contrast, "hurried" pedestrians want to reach their goal quickly, thus they minimize the frequency of comfort turns and find their ways by turning to deal with pedestrian encounters. Figure 12 shows the different factors of turn preference used by pedestrians of different profiles in order to deal with the situations perceived by them (see Figure 3).

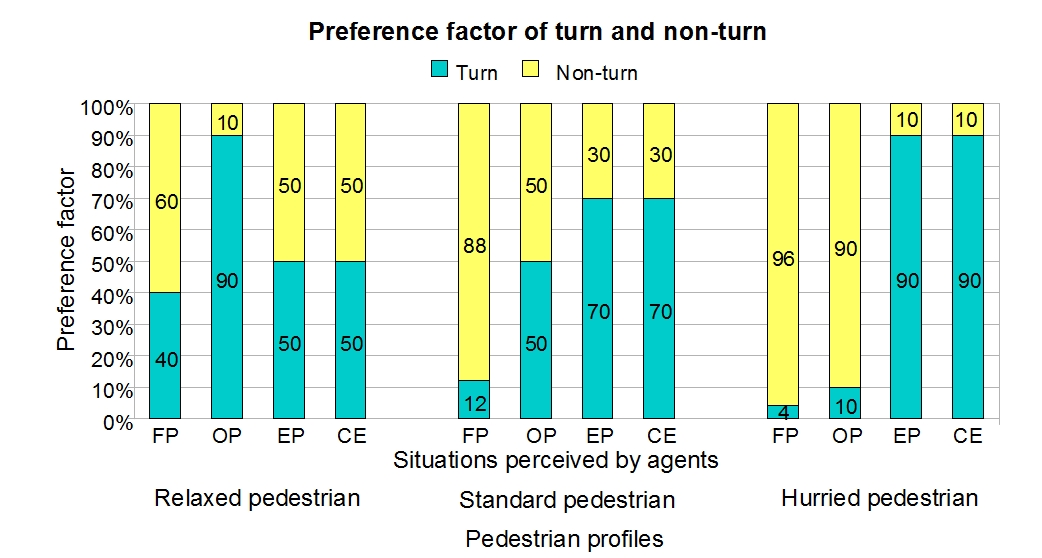
Figure 12. Definition of heterogeneous pedestrians by varying their preferences of turn in order to deal with these situations: FP, free path; OP, obstructed path; PE, pedestrian encounters; and CE, combined encounters.

3.7

Figures 13 and 14 illustrate the fundamental diagrams of average flow and average activity for heterogeneous pedestrians. Note that at low densities, the different pedestrian profiles are clearly distinguished among them. "Relaxed" pedestrians have a worse flow than standard pedestrian, while "hurried" pedestrian have a better flow than standard pedestrians. However in the critical zone, where the phase transition happens, varied oscillations for all pedestrian profiles can be noticed. Finally, at high densities the flow is equivalent whatever the profile of pedestrians measured. The differentiation corresponding to different pedestrian profiles is however unnoticed in the average activity diagram.

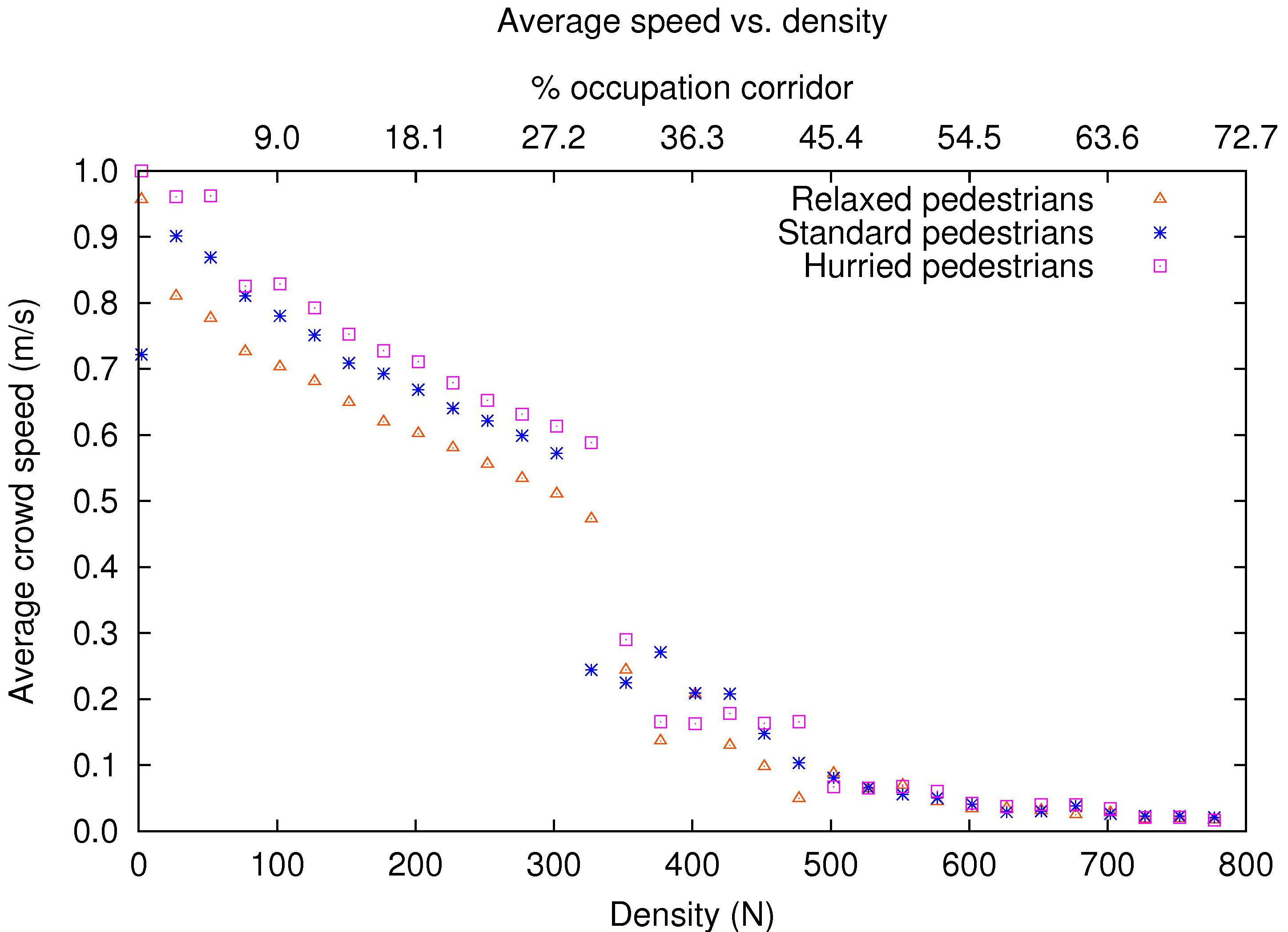
Figure 13. Average velocity of heterogeneous pedestrians by varying the number of pedestrians, from 2-800, during 200 iterations. The X-Axis is labeled in the bottom with the number of pedestrians in the simulation, and it is labeled in the top with the percentage of occupation of the corridor of the corresponding number of pedestrians.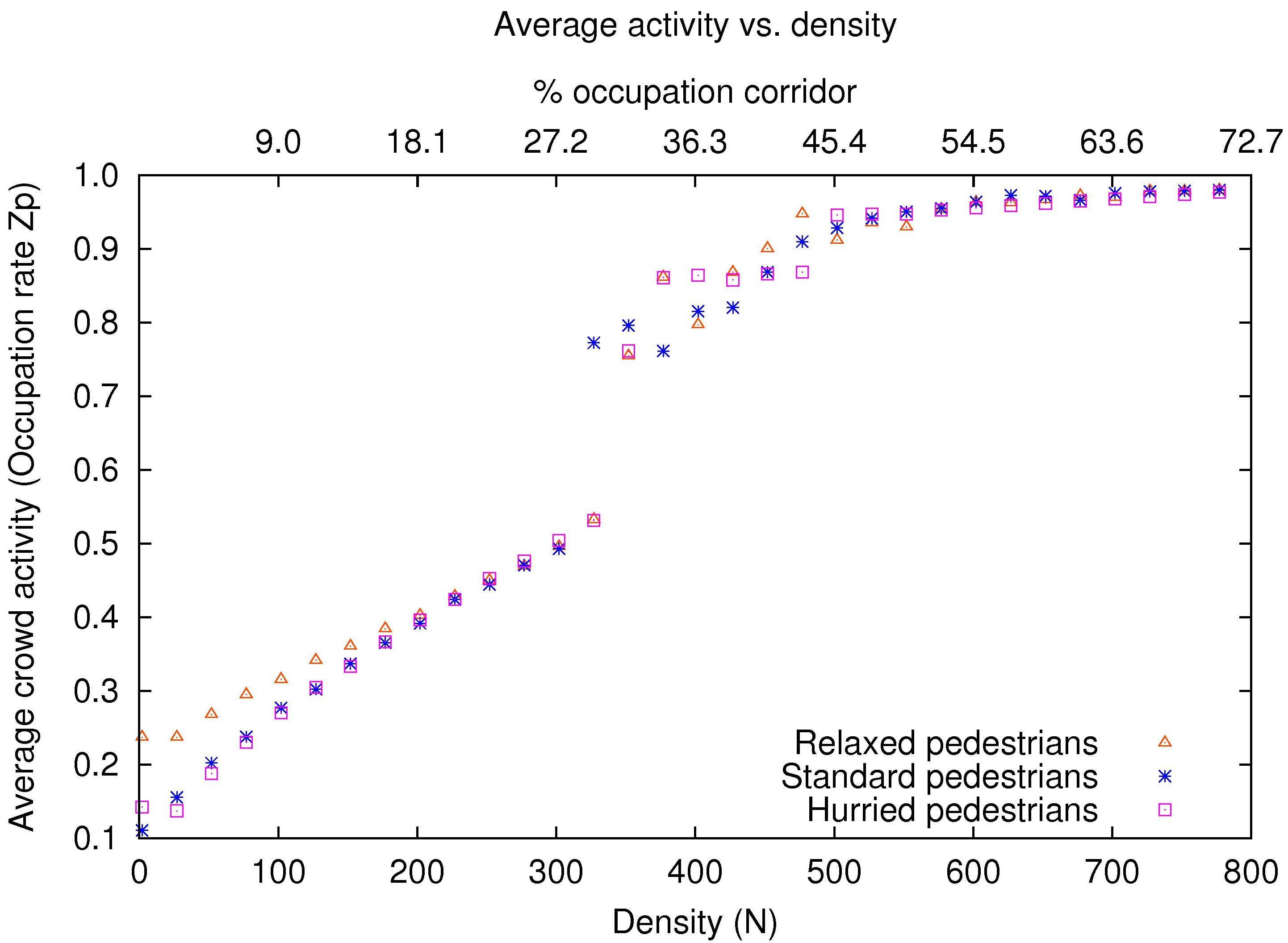

Figure 14. Average activity of heterogeneous pedestrians by varying the number of pedestrians, from 2-800, during 200 iterations. The X-Axis is labeled in the bottom with the number of pedestrians in the simulation, and it is labeled in the top with the percentage of occupation of the corridor of the corresponding number of pedestrians.

Comparison and Discussion

4.1

Establishing a reasonable comparison of different pedestrian crowd models is not easy because of their great diversity. As we mentioned in the Introduction of this article, the granularity of parameters that measure the dynamics of the system is closely related with the kind of model that is applied. Fundamental diagrams of traffic flow, for instance, have largely dominated the representation of pedestrian crowd dynamics in both, macroscopic and microscopic models. However, intermediate agent-based models are not always feasible for large-scale experiments necessary to plot gradually varied flow, because of the expensive processing time of individuals modeled as software agents. In this section we contrast our model (referred to as Ballinas-Hernández et al. 2011) to other pedestrian crowd models at different levels, according to the results reported in the literature.

4.2

Table 1 summarizes three general features of cited intermediate and microscopic pedestrian crowd models, as well as of the current model. Note that the most of models based on conceptual design principles similar to those applied in our work, i.e., agent-based simulation (see Bandini et al. 2004, Dijkstra et al. 2000, Fridman and Kaminka 2009, Ronald et al. 2007) is categorized in the class of intermediate models. The results of such models, focused mainly on refined parameters concerning individual agent states, are not directly comparable to our results. An exception to that is the microscopic model of Rangel-Huerta and Muñoz-Meléndez (2010) that is compared in detail to our model later (see 4.10).

4.3

The model proposed by Burstedde et al. (2001) deserves a special mention for its rare capability to reproduce heterogeneous pedestrians. This work is based on an extended Cellular Automaton that includes an additional grid called the "floor field". The additional grid captures both, global and local influences of the environment that are perceived by pedestrians, modeled as the cells of the base cellular automaton. The authors of this work argue that the "floor field" substitutes individual intelligence of pedestrians, because the information required by them is coded in such a way in this virtual crowd memory. Our model is closely related to the cited work in the sense that, in both models, local dynamic information is considered an essential requirement to accomplish realistic simulations. Local information might be acquired from a floor field, as in the model of Burstedde et al. (2001), or through specific mechanisms of local perception and proprioception as the ones implemented in our agents. To paraphrase the authors, we argue that the availability of reliable local information makes possible individual intelligence of pedestrians.

Table 1: Comparison of Pedestrian Models
Authors	Model category	Kind of pedestrians	Crowd parameters
Henderson (1974)	Macroscopic	Homogeneous	Fundamental diagram of traffic flow
Bandini et al. (2004)	Intermediate	Homogeneous	Plots of active agents, records of individual measure of agent's signals
Burstedde et al. (2001)	Intermediate	Heterogeneous	Velocity profiles, plots of mean evacuation time
Dijkstra et al. (2000)	Intermediate	Homogeneous	None
Fridman and Kaminka (2009)	Intermediate	Homogeneous	Fundamental diagram of traffic flow at low densities
Ronald et al. (2007)	Intermediate	Homogeneous	None
Parisi et al. (2009)	Microscopic	Homogeneous	Fundamental diagram of traffic flow
Rangel-Huerta and Muñoz-Meléndez (2010)	Microscopic	Homogeneous	Fundamental diagram of traffic flow, and a proposed measure of crowd activity
Seyfried et al. (2006)	Microscopic	Homogeneous	Fundamental diagram of traffic flow
Yu and Song (2007)	Microscopic	Homogeneous	Fundamental diagram of traffic flow
Ballinas-Hernández et al. (2011)	Microscopic	Heterogeneous	Fundamental diagram of traffic flow, and a proposed measure of crowd activity.

4.4

A closer comparison of our model is made in terms of quantitative crowd parameters, usually reported in microscopic and microscopic models. We compare our work with related models of the category of microscopic models. Unlike our work, none of the models discussed in the rest of this section involves heterogeneous pedestrians. For that, from now on we compare uniquely the "standard" pedestrians of our model. In order to establish a proper comparison, the compared results concern pedestrian crowds simulated in conditions similar to those considered in our research, i.e., pedestrian counterflow simulations in a corridor.

4.5

Figure 15 compares our model with three microscopic pedestrian models. Two of these models are based on the Social Force Model (Seyfried et al. 2006; Parisi et al. 2009), and the third one is a Cellular Automata based model (Yu and Song 2007). In order to plot the results shown in Figure 15, we recorded the corresponding values reported in the cited works by using a homemade software designed to get actual coordinates of superimposed points in graphical plots. Then we normalized the values of average flow and average density by applying a scale factor using a unique reference. For that we used as reference, the scale reported in the results of the Social Force Model (Seyfried et al. 2006).

4.6

From this comparison we can observe that the walking flow of pedestrians modeled under different microscopic models behaves similarly to each other. That is, three well-defined regions can be identified in the average flow. First, at low densities we can observe how a crowd is capable of moving and flowing along the corridor. Note that at intermediate densities there is usually an abrupt fall in the average flow. And finally, at high densities, the average flow is considerably reduced in the models that report results in this region.

4.7

However, from a closer comparison in similar ranges of density, we can notice interesting differences among the models. In the cited microscopic models (Seyfried et al. 2006; Parisi et al. 2009; Yu and Song 2007), the average flow at low densities is uniform whereas in our model this parameter falls linearly. In other words, pedestrians modeled under both approaches, Social Force and Cellular Automata, have in general a better flow that our pedestrians at low densities. That can be explained by the fact that in prior models pedestrians are subject to a kind of "blindpulling" walking. In contrast, the actions of pedestrians in agent-based models result from their perception and decision making mechanisms, that presumably respond progressively to the increases of density.

4.8

Concerning the phase transition note that the compared models (Seyfried et al. 2006; Parisi et al. 2009; Yu and Song 2007) present well-defined phase transitions whereas a "fuzzy" phase transition can be observed in our model. Moreover, this fuzzy transition might question whether a phase transition exists at critical densities of flow in agent based crowd simulation. Different interpretations of this question have already been advanced, such as the coexistence of different forms of collective walking by Rangel-Huerta and Muñoz-Meléndez (2010). We discuss in more detail the observed "fuzzy" phase transition at the end of this section.

4.9

Finally, at high densities the average flow in all the compared models tends to become saturated, as a result of multiple jams and collisions. Note that in this region only the Cellular Automata based model maintains a constant flow, whereas the average flow decreases as the density increases in the Social Force based models and in our own model. In order to deal with these situations, our model should be extended with the new rules oriented to avoid traffic congestion. For instance a "traffic rule" (Yu and Song 2007b) by which the turns of agents are biased towards one side instead of the other, could solve traffic jams and promote the formation of lanes at different flow densities.

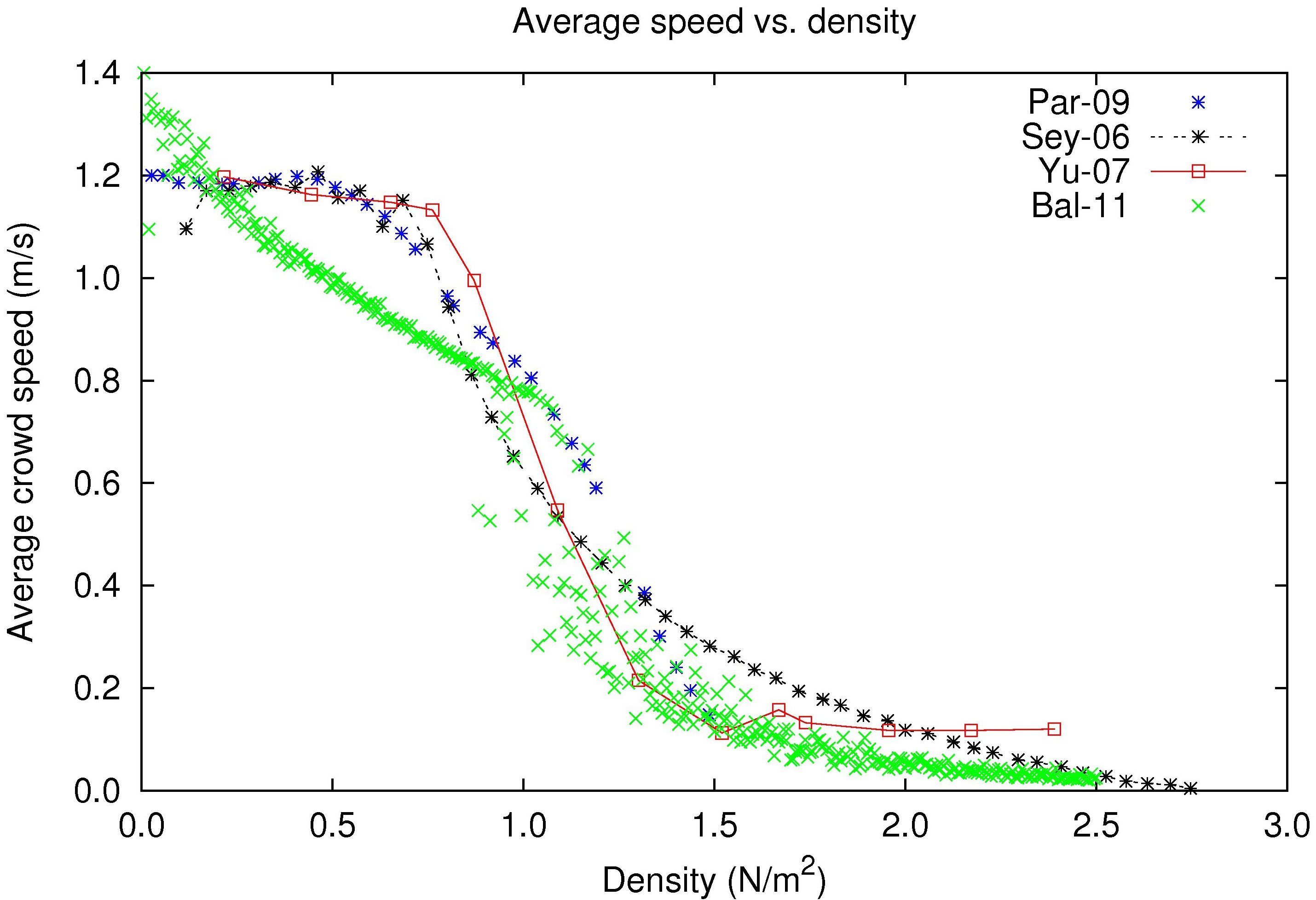
Figure 15. Comparison of models based on the fundamental diagram of flow with our "standard" pedestrians. Data sets were obtained from the reported results of the cited works, and normalize with respect to a uniform scale of reference. Results are normalized in terms of number of pedestrians in the simulation (N) per square meter, represented in the X-Axis, and meter per second, represented in the Y-Axis.

4.10

A direct comparison of pedestrian crowd models can be performed between our model and its predecessor (Rangel-Huerta and Muñoz-Meléndez 2010). Both models are microscopic models based on similar conceptual design ideas, those of agent-based simulation. In addition to that, these are the unique models that report a quantitative measurement of the crowd activity. A normalization of the results similar to the one mentioned in paragraph 4.5 was performed to compare the results of these models.

4.11

Figure 16 illustrates the average speed of multiple experiments comprising from 2 to 800 pedestrians, that represent respectively, 0.18% and 73.0% of occupation of the corridor of our model and the model of Rangel-Huerta and Muñoz-Meléndez (2010). Note that at low densities the flow of our agents is better that the flow of their predecessors. Also, the degradation of the flow appears sooner in the precedent model that in our model. Such difference can be explained by the fact that our agents acquire more information about the environment than their predecessors. This information is available through the lateral cells of the perceptual field of our agents, and is useful to them when they transit the corridor. Finally, note that both models behave similarly at high densities, where an extended perceptual field or differentiated profiles are insufficient elements to solve traffic jams. Both models rely on local information, therefore agents are similarly affected by the lack of information in their surroundings, a typical situation of traffic jams.

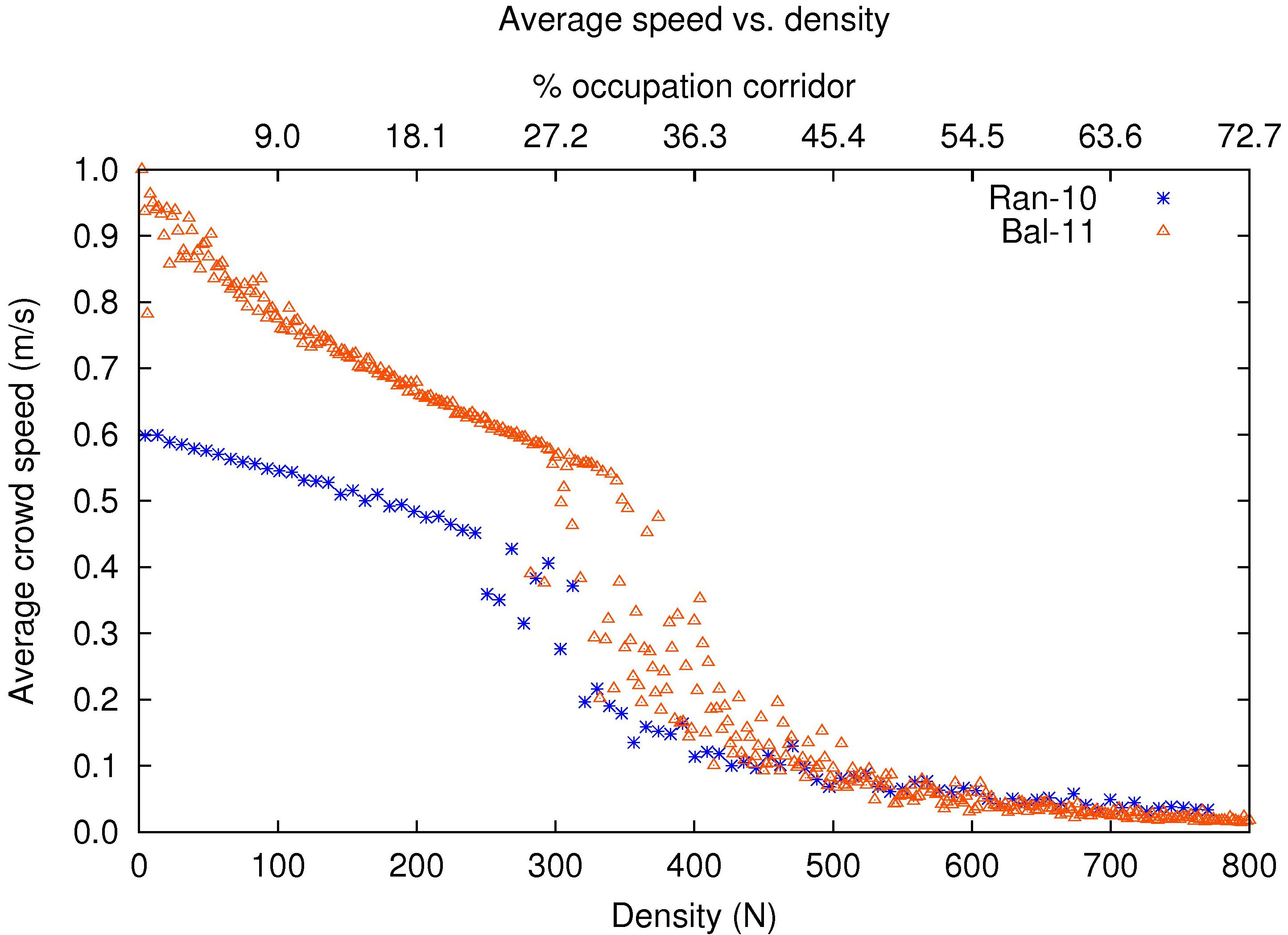
Figure 16. Comparison of two agent-based microscopic models in terms of average velocity.

4.12

Now let's focus our discussion in the quantitative measure of the crowd, the so-called activity. Activity is a measure that captures in such a way the social aspect of the system, a parameter that indicates how active are the system's entities under different circumstances. Activity is also referred to as "activation" in the literature of crowd models, and there is not a standard way to measure it. In agent-based simulations where local perception is at the core of models, the measurement of activity has a major importance because it represents the degree of interaction among pedestrians, and also the interaction of them with their environment.

4.13

The activity is related to the "connectivity" of pedestrians derived from their encounters in our model and its predecessor. Activity is measured as a simple binary value related to the occupation of the perceptual field of pedestrians in the model of Rangel-Huerta and Muñoz-Meléndez (2010). In our model where pedestrians are equipped with an extended perceptual field, activity is measured as the number of allowable maneuvers for pedestrians calculated from the occupation of their perceptual field.

4.14

Figure 17 illustrates the average activity of the experiments plotted in Figure 16. Low activity in both models represent cases where pedestrians have few interactions and few data is processed, whereas high activity means a high degree of connectivity and a large amount of data processing. As it can be seen in the graph both models behave similarly. Note however that at low densities our agents are slightly more active that their predecessors, that is understandable given the number of interactions perceived through their extended perceptual field.

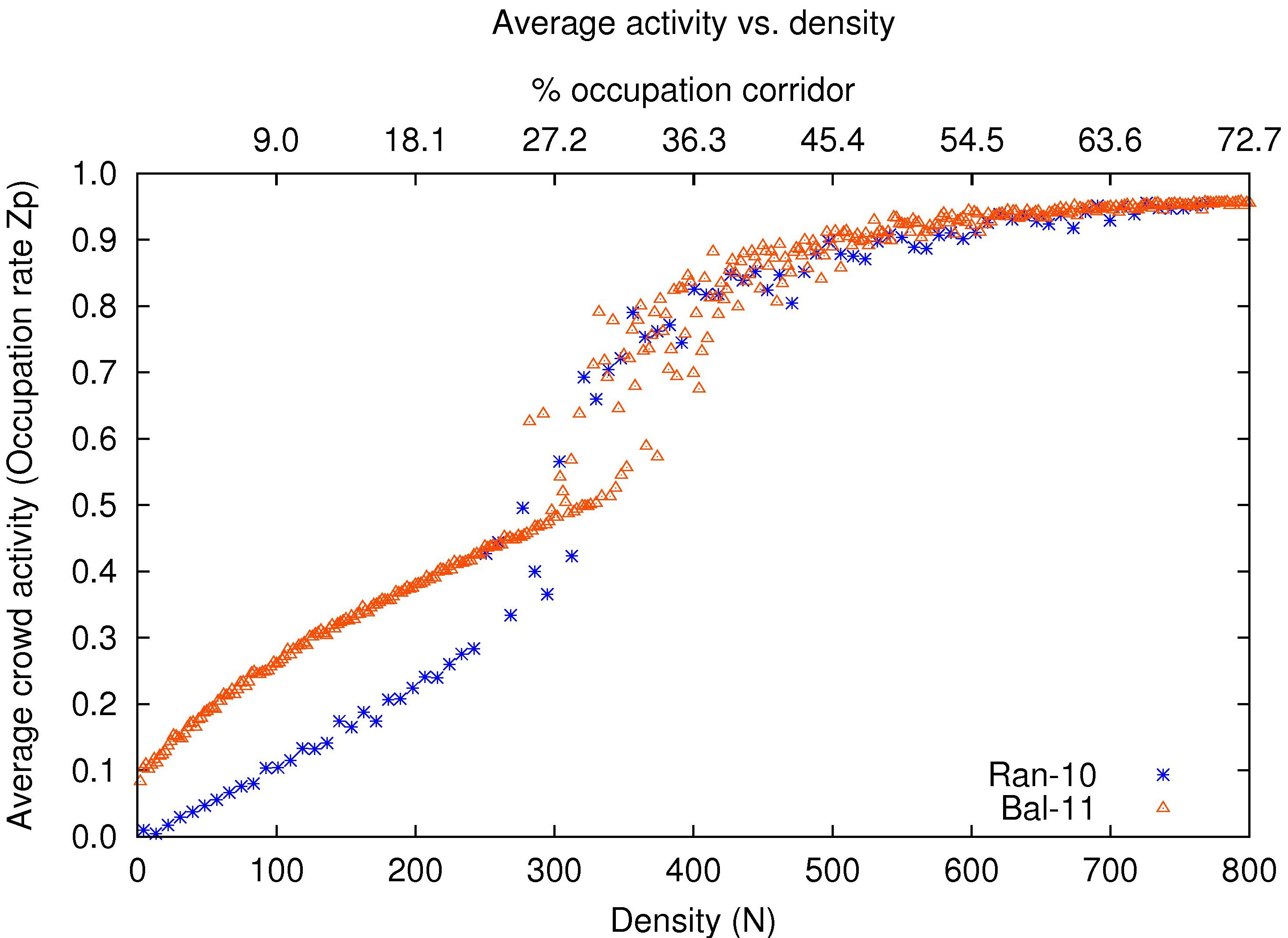
Figure 17. Comparison of two agent-based microscopic models in terms of average activity.

4.15

Finally it is remarkable to state the absence of a sharp phase transition in agent-based crowd models that were compared (the one of Rangel-Huerta and Muñoz-Meléndez 2010 and the present model) in both measures, average flow and average activity. It is also worth to recall that the appearance of phase transitions has been properly observed in macroscopic and microscopic pedestrian crowd models, as it was clearly shown in Figure 15. To the best of our knowledge, there is not evidence that phase transitions take place in experiments involving human pedestrians. "Fuzzy" phase transitions as the ones highlighted in this work might be related to the "mere" essence of the individuals that form an agent-based crowd. Pedestrian modeled as agents are equipped with sets of rules or conventions that enable a gently degradation of the system when possible, e.g., at low densities, that however behave analogously to pedestrians of microscopic models when the system deals with certain conditions, such as a critical increase of the density.

Final Remarks

5.1

An agent-based model to simulate a pedestrian crowd in a corridor is presented. The fundamental principle of this work is that situated agents are appropriate to model realistic crowds, because of their capacity to capture one essential property of human pedestrians: autonomy, the capability of perceiving and making decisions. We can reasonably expect that real pedestrian appeal to these capability under ordinary situations. The motion of pedestrians in our model does not result from the application of "blind pulling" forces. Agents in our model do not move unless they have previously decided such a movement based on their internal state and the information perceived in their surroundings. This scheme does not necessarily implies the design of fully rational and "introspective" agents, but of agents which are "aware" of their state in the environment.

5.2

We have proposed a set of simple walking rules that a group of agents applies to traverse a corridor and solve their collision conflicts. These rules can be applied at both, low and high densities, for walking situations perceived by the agents as mentioned above (see Figure 3). However, at high densities these basic rules do not enable agents to solve traffic jams.

5.3

This work is based on a previous model (Rangel-Huerta and Muñoz-Meléndez 2010) where only a frontal perceptual field is considered. In the actual extension a lateral perception is introduced, resulting in a redefinition of the previous model, namely the walking rules, in order to consider the new pedestrian and obstacle encounters. The extended pedestrians exhibit a better efficiency of flow compared with the previous ones (Rangel-Huerta and Muñoz-Meléndez 2010). However, similar fundamental diagrams of flow and activity are obtained using both models, which suggests that pedestrian crowd based on situated multi-agent systems are similarly degraded, without much regard to the way as agents perceive their environment.

5.4

The main contribution of this work is the definition of a pedestrian crowd model by applying ideas from the field of the kinetic theory of living systems on the one hand, and ideas from the field of computational agents on the other hand. Such combination supported a quantitative characterization of the performance of our agents, a neglected issue in agent-based models, through the fundamental diagram of average flow and average activity by varying the density of occupation of the corridor. A relevant result of this characterization is that intrinsic properties of autonomous agents concerning their perception and decision making, exhibit properties that are regularly observed in models of self-propelled particles based on very different design principles, as it was remarked in a comparison with related microscopic crowd models.

5.5

Finally we consider to investigate, in the near future, to what extent the "fuzzy" phase transitions observed in this work and its predecessor are present in agent-based crowd models. If similar conditions of the degradation of agent-based systems are confirmed, we are probably in face of an innovative way to represent and characterize the dynamics of multi-agent systems.

Code

The Netlogo source code of the program developed for this research and a user's guide are available here.

Acknowledgements

The first author was supported by the Mexican National Council for Science and Technology, under the contract number 266291.

The authors would like to thank the anonymous reviewers for their useful comments and suggestions to improve the quality of this paper.

References

BANDINI, A, Manzoni, S, Vizzari, G (2004) Situated cellular agents: a model to simulate crowding dynamics. IEICE Transactions on Information and Systems, special section on Cellular Automata, E87-D, pp. 669-676.

BANDINI, A, Federici, M L, Manzoni, S, Vizzari, G (2006) Towards a methodology for situated cellullar agent based crowd simulations. Proceedings of the 7th Annual International Workshop Engineering Societies in the Agents World, ESAW, pp. 203-220.

BURSTEDDE, A, Manzoni, S, Vizzari, G (2001) Simulation of pedestrian dynamics using a two-dimensional cellular automaton. Physica A, 295, pp. 507-525. [doi:10.1016/S0378-4371(01)00141-8]

DIJKSTRA, J, Timmermans, H J P, Jessurun, A J (2000) A multi agent cellular automata system for visualising simulated pedestrian activity. Theoretical and practical issues on cellular automata, Proceedings of 4th international Conference on Cellular Automata, pp. 29-36.

FRIDMAN, N, Kaminka, G A (2009) Comparing human and synthetic group behaviors: A model based on social psychology. International Conference on Cognitive Modeling, ICCM2009, Manchester, UK.

GIPPS, P G, Marks J, B (1985) A micro-simulation model for pedestrian flows. Mathematics and Computer Simulation, 27, pp. 95-105. [doi:10.1016/0378-4754(85)90027-8]

HARNEY, D (2002) Pedestrian modelling: Current methods and future directions. Road & Transport Research, December 2002.

HENDERSON, L F (1974) On the fluid mechanics of human crowd motion. Transportation Research, 6, pp. 509-515.

HELBING, D, Molnár, P (1995) Social force model for pedestrian dynamics, Physical Review E 51(5), pp. 4282-4286.

HELBING, D, Buzna, L, Johansson, A, Werner, T (2005) Self-organized pedestrian crowd dynamics: Experiments, simulations, and design solutions. Transportation Science, 39(1), pp. 1-24. [doi:10.1287/trsc.1040.0108]

KAMINKA, G A, Fridman, N (2006) A cognitive model of crowd behavior based on social comparison theory. Proceedings of the AAAI-2006 Workshop on Cognitive Modeling.

KRETZ, T, Grünebohm, A, Schreckenberg, M (2006) Experimental study of pedestrian flow through a bottleneck. Journal of Statistical Mechanics: Theory and Experiment , P10014.

LEIGH, M -consulting editor- (2009) Understanding crowd behaviors: Supporting documentation. Technical report, Emergency Planning College, University of Leeds.

NAGAI, C, Klauck, K, Schadschneider, A, Zittartz, J (2005) Experiment and simulation for counterflow of people going on all fours. Physica A, 358, pp. 516-528. [doi:10.1016/j.physa.2005.04.024]

PARISI, D R, Gilman, M, Moldovan, H (2009) A modification of the social force model can reproduce experimental data of pedestrians flows in normal conditions. Physica A, 388, pp. 3600-3608. [doi:10.1016/j.physa.2009.05.027]

RANGEL-HUERTA, A, Muñoz-Meléndez, A (2010) Kinetic theory of situated agents applied to pedestrian flow in a corridor. Physica A, 389, pp. 1077-1089. [doi:10.1016/j.physa.2009.11.031]

RONALD, N, Sterling, L, Kirley, M (2007) An agent-based approach to modelling pedestrian behaviour. International Journal of Simulation. Systems, Science and Technology, special issue on IT-Modelling in Logistics and Transport, 8(1), pp. 25-38.

SCHADSCHNEIDER, A, Klingsch, W, Klüpfel, H, Kretz, T, Rogsch, C, Seyfried A (2008) Evacuation Dynamics: Empirical Results, Modeling and Applications. Encyclopedia of Complexity and System Science, pp. 3142-3176.

SEYFRIED, A, Steffen, B, Lippert, T (2006) Basics of modelling the pedestrian flow. Physica A, 368, 232-238. [doi:10.1016/j.physa.2005.11.052]

WENG, W G, Shen, S F, Yuan, H Y, Fan, W C (2006) A behavior based model for pedestrian counter flow. Physica A, 375, pp. 668-678.

YU, Y F, Song, W G (2007) Cellular automaton simulation of pedestrian counterflow considering the surrounding environment. Physical Review E, 75 046112, April 2007. [doi:10.1103/PhysRevE.75.046112]

YU, Y F, Song, W G, (2007b) Effect of traffic rule breaking behavior on pedestrian counterflow in a channel with a partition line. Physical Review E, 76 026102, August 2007. [doi:10.1103/PhysRevE.76.026102]