Abstract

This paper makes use of an agent-based framework to extend traditional models of comparative advantage in international trade, illustrating several cases that make theoretical room for industrial policy and the regulation of trade. Using an agent based implementation of the Hecksher-Ohlin trade model; the paper confirms Samuelson's 2004 result demonstrating that the principle of comparative advantage does not ensure that technological progress in one country benefits its trading partners. It goes on to demonstrate that the presence of increasing returns leads to a situation with multiple equilibria, where free market trading policies can not be relied on to deliver an outcome which is efficient or equitable, with first movers in development enjoying permanent advantage over later developing nations. Finally, the paper examines the impact of relaxation of the Ricardian assumption of capital immobility on the principle of comparative advantage. It finds that the dynamics of factor trade are radically different from the dynamics of trade in goods and that factor mobility converts a regime of comparative advantage into a regime of absolute advantage, thus obviating the reassuring equity results that stem from comparative advantage.

Keywords:

Agent-Based Modeling, Agent-Based Computational Economics, International Economics, Comparative Advantage, Increasing Returns, NetLogo

Introduction

1.1

Of the many beautiful results that have emerged from economic theory over its long history, few are as elegant or have been as influential as Ricardo's principle of comparative advantage in international trade. This principle is often taken to prove that all nations, regardless of their level of development or productivity, can only benefit from increased international trade. Indeed, this argument is so counterintuitive on its face, but so convincing on further thought that it has come to dominate the thinking of those concerned with international trade, often leading them to overlook the assumptions on which the argument rests.

1.2

Every model rests on a set of assumptions. When modeling is conducted in the service of policy analysis, it is particularly important that these assumptions be made plain and that the result be recognized as the result of those assumptions. One critical assumption on which the comparative advantage argument depends is that there are constant or decreasing returns to scale in all industries. The relaxation of this assumption complicates analysis somewhat, leading to multiple equilibria and destroying the market's ability to deliver a unique outcome that can be considered to be "optimal" in some objective sense.

1.3

While an agent-based model is not the only way to explore the implications of relaxing this assumption (Krugman 1979; Markusen & Venables 1988; Matsuyama 1991; Costinot 2009), the agent-based approach can be used to build confidence in the insights generated through analysis and to communicate them to policymakers with limited background in economics. In this paper, I will review two models that seek to realign the generalizations from trade theory with their underlying assumptions. I will then proceed to demonstrate how an agent-based model can be used to illustrate these points in a way that clearly shows how the results follow from the assumptions about the behavior of the people and nations involved.

Samuelson's Analysis of Outsourcing

1.4

Paul Samuelson takes contemporary trade theorists to task for over generalizing the benefits of free trade by demonstrating that there are situations where the gains from trade for one nation can be undone by technological developments in a second nation (Samuelson 2004). Because Samuelson sets up his simple analytical model in a way that is compatible with our agent analysis, it serves nicely to validate the agent model that will be presented below. If the model is correctly specified, it should be able to produce results that agree with Samuelson's mathematically rigorous analysis.

1.5

Samuelson uses a fairly standard version of the Hecksher-Ohlin trade model (Jones 1956) to consider two countries designed to look something like the US and China. His stylized US has 100 citizens while his stylized China has ten times that population with 1000 citizens. For the sake of symmetry, he further assumes that the US average productivity is ten times as high as Chinese productivity, thus producing equal amounts of total production in the two countries (though Chinese per capita productivity is only 1/10 ^th that of the US). These productivities are asymmetrically distributed between industries, however, with the US having Ricardian productivity parameters of 2 and 1/2, while China has parameters of 1/20 and 2/10.

1.6

One problem with models of this sort, which represent the economy in barter terms, is that it has traditionally been difficult to compare outcomes in absolute terms. Samuelson overcomes this problem by pointing out that there is a definite relationship between demand and utility functions. He assumes a J. S. Mill style pair of hyperbolic demand functions: D_c = Y/2P_c and D_w = Y/2P_w. These demand functions imply that consumers spend half of their income on each good. He then shows that these are the logical outgrowth of a utility function U = (C*W)^0.5 which takes the geometric mean of the consumption of the two goods as a measure of welfare. This relationship allows us to measure the total utility of each nation. In the absence of money, this utility measure allows us to assess the value of the nation's consumption. It can thus be used as a fair measure of the nation's utility.

1.7

Samuelson refers to this measure as a proxy for GDP, but this is not necessary or entirely correct. Generally, GDP is taken as a proxy for total utility, which is difficult to measure. GDP is, however, a poor proxy for a variety of reasons (Daly 2003). Because we are working with a theoretical system, it is possible for us to work directly with utility rather than resorting to the poor proxy of GDP. In the current specification of the model, we would assume that GDP and utility would be highly correlated but other interesting formulations would weaken this link. To avoid confusing the end (utility) with its means (GDP), we will break from Samuelson's usage and refer to the geometric mean of consumption as utility rather than GDP.

1.8

Using these production and demand functions, Samuelson demonstrates that there are substantial gains to be had when the countries specialize and trade the product in which they are relatively strong for that in which they are relatively weak. In autarky, the US can produce 100 units of cloth and 25 units of wine. This gives a utility of (100*25)^0.5 or 50. China, similarly, can produce 25 units of cloth and 100 units of wine to achieve the same utility level of 50. US utility per capita is therefore 50/100 or 0.5, while China's is 50/1000 or 0.05.

1.9

Samuelson then demonstrates that, under free trade, the US is able to specialize in cloth, producing 200 units of cloth, whereas China is able to specialize in wine, also producing 200 units. Because of the symmetry of the example, each country is able to trade and consume 100 units of each good, thus raising total utility in each country to (100*100)^0.5 or 100 units. Both countries have thus doubled their real utility by specializing and trading.

1.10

Finally, Samuelson demonstrates that not all technological changes need be beneficial for both nations. For the sake of this example, he posits a tremendous technological improvement in China's cloth sector (where the US had previously been stronger) from 0.05 to 0.8. This leaves cloth productivity substantially below the US level of 2, but much higher than it had been. This change serves to equalize the factor prices in both countries (the ratio of the efficiencies in both nations is now 4). This equalization removes all incentive to trade, reducing the problem to calculating the output of each country in autarky.

1.11

The result is a boon for China and a plague for the US. China is now capable of producing 400 units of cloth and 100 units of wine for a total utility of (400*100)^0.5 or 200 (0.2 per capita), while US once again can produce (100*25)^0.5 or 50 (0.5 per capita). Chinese consumption thus expands by a factor of four while US consumption is halved.

1.12

Samuelson uses this model to argue that outsourcing of high technology jobs from the US to India and China is not automatically good for both nations. Indeed the transfer of jobs in a sector where the US was once a leader to countries which did not previously participate heavily in such industries has the potential to make the economies of various nations more alike in their productivity, thus eroding gains from trade to which the US has become accustomed.

Gomory and Baumol's Model of International Trade

1.13

In their book, Global Trade and Conflicting National Interests, Ralph E. Gomory and William J. Baumol offer a logical extension to the Hecksher-Ohlin model by relaxing the assumption of decreasing returns to scale for national industries. This dramatically changes Ricardo's policy conclusions based on comparative advantage (Gomory & Baumol 2000). With the introduction of startup costs and increasing returns, the situation goes from one of always-coincident national interests in favor of openness, to a more nuanced picture where interests sometimes coincide and sometimes conflict.

1.14

A major result of their analysis is to move international trade theory out of the realm of pure efficiency analysis, making way for discussions of equity and the application of policy. In their analysis, it becomes clear that the market cannot be expected to deliver a single, "optimal" pattern of production that allows each country to make the most of what God has given it. Rather, the market can produce myriad stable patterns of production. Some of these patterns are more efficient, some less, some distribute income relatively evenly among nations, some distribute income very unevenly. Gomory and Baumol argue convincingly that which one of these equilibria the market produces depends, to a great degree, on history and therefore on temporary policy measures such as the protection of infant industries.

1.15

Under the traditional assumption of decreasing returns, the market can be expected to produce a unique allocation of production and income based on each country's natural endowments, which are given. This equilibrium is independent of history in that over the long run, the system can be expected to allocate production in the same way regardless of the order in which nations develop. Barring market failures, this also results in global production at the maximum scale that demand and technology allow at any given time.

1.16

If we relax the assumption of decreasing returns and allow some industries to display increasing returns over at least part of their range of production scale, natural endowments come to matter much less and have little to do with the distribution of productive capacity. Those who are first to enter an industry face falling costs as they increase production, making entry difficult even when the entrants have a lower wage bill. This means that it is often the first country - not always the best suited one - which ends up producing a given product.

1.17

In Ricardo's day, the assumption of decreasing returns was a reasonable one. Agriculture made up the largest share of even the most highly developed nation's utility. In many agricultural sectors decreasing returns still dominate: the best land is used first with production increases requiring the use of increasingly marginal lands and more intensive (and expensive) management techniques. Before the industrial revolution, this principle held even in manufactured goods: a hat maker could make only so many hats in a day, and there quickly came a point where supervising more apprentices became uneconomical.

1.18

During the industrial era, however, agriculture and handcrafts became relatively minor economic sectors while large-scale manufacturing and high-skill services became the driving force behind the rapid growth of economic activity. These sectors, however, display a different type of productivity curve. While the first tomato may be the cheapest to grow, the first automobile is far from the least expensive to manufacture. In many modern industries, economical production requires huge scale, and that huge scale requires tremendous investment, a high level of skill, and the reputation required to bring the resulting products to market. Gomory and Baumol refer to industries characterized by high startup costs due to significant economies of scale (like automobile manufacture), as "retainable" industries, because once a nation has developed such an industry and realized the resulting cost reductions it becomes very difficult for another nation - even one with lower labor costs and more plentiful raw materials - to take that industry away through competition.

1.19

Gomory and Baumol's analysis demonstrates that relaxing the standard assumption of constant or decreasing returns to scale to allow for increasing returns to scale in some industries changes the complexion of trade theory dramatically. With constant or decreasing returns, the Hecksher-Ohlin (along with its various Ricardian cousins) indicates that the market will always deliver a better result for each country with trade than it will without. Though the standard model is not dynamic, it also implies that changes in productive capacity will be reflected in the market - as we saw in Samuelson's stylized treatment of the US and China.

1.20

Gomory and Baumol observe, however, that in a world where some industries produce increasing returns to scale, these industries can be "retainable" by a nation that develops them early. First movers in such industries have a huge advantage and there are many situations where the resulting equilibrium is far from optimal. Because costs fall as more units are produced, it may be possible for a nation with a less efficient production function to retain an industry over a later entry that would be able to produce the good more cheaply if only it could attain the required scale of production. A late developing country may, under some circumstances, be able to do better in the long run by temporarily abandoning trade in some industries.

1.21

The recognition of the importance of increasing returns is not entirely new, having been explored by such authors as Kenneth Arrow (1962), Paul Krugman (1979, 1983) and Brian Arthur (1989), among others. It has, however, failed to make a major dent in the mainstream policy discourse concerning trade and development.

Daly's observations on capital mobility

1.22

The third economic phenomenon that will be explored with the agent-based model presented here is Daly's (1996) observation (also mentioned by Samuelson (2004)) that the mechanism of the comparative advantage argument depends on internationally immobile capital.

1.23

This assumption is explicitly stated by Ricardo (1817), but is generally omitted from modern discussions. Given the realities of early 19 ^th century international travel and communication, Ricardo found this assumption reasonable:

Experience, however, shews, that the fancied or real insecurity of capital, when not under the immediate control of its owner, together with the natural disinclination which every man has to quit the country of his birth and connexions, and intrust himself with all his habits fixed, to a strange government and new laws, checks the emigration of capital. These feelings, which I should be sorry to see weakened, induce most men of property to be satisfied with a low rate of profits in their own country, rather than seek a more advantageous employment for their wealth in foreign nations.

1.24

In the early 21^st century, international investment is a much simpler matter and the increasing trend toward globalization continues to make national borders less relevant to investment decisions. Daly points out (following Ricardo closely) that mobile capital shifts the situation from one of comparative advantage - where all nations benefit - to one of absolute advantage. Under absolute advantage total global output can be expected to increase (as capital moves to find its maximum return), but more efficient nations benefit while less efficient nations suffer. In a decreasing returns world, this would lead to equalization of incomes among nations, as capital moved to the places where it was in shortest supply (and thus produced the highest marginal return). In the more complex world that we inhabit, with increasing returns, industrial synergies, critical infrastructure, etc., the effects of relaxing the assumption of international capital immobility are harder to identify with certainty. Thus, in a world with increasing returns and mobile capital (i.e. the world in which we live), the traditional economic prescription of freer trade always being better for everyone is called into real question.

1.25

These three theorists argue that there is a place for trade and industrial policy. With decreasing (or constant) returns and internationally immobile capital, simple economic models were sufficient to show that the best policy was always the least restrictive - while there might be a need to deter other nations from cheating, the economically optimal goal of trade policy was simply to remove as many barriers as possible. In this new world, however, we find ourselves with real decisions to make. Some trading partners are more beneficial than others. Sometimes it is in the national interest to support certain industries - even, as Gomory and Baumol show, industries in other countries. In this case, there is need for models that can begin to grapple with the messiness of real economies and trade relationships. The agent-based model that follows is designed to be a first step in this direction.

Methods

2.1

In an effort to gain insight into the mechanisms involved with international trade and development, we can construct a simple agent-based model of production and trade. This model will follow the basic outline of the classic Hecksher-Ohlin trade model, but will further disaggregate the model, resting it on the behavior of individuals and firms. The model is capable of reproducing Samuelson's results as well as verifying the retainability of industries as described by Gomory and Baumol. It also allows for a preliminary exploration of the comparative vs. absolute advantage argument presented by Daly.

Model Specification

2.2

To explore the ideas presented above and how they fit together, we will construct an agent-based model of national industries and international trade that is designed to be as simple as possible while capturing the desired dynamics. This model is implemented in NetLogo (Wilensky 1999), which handles the randomized agent activation regime (i.e. agents activate in a changing, randomized order) while also facilitating the collection of statistics and the production of graphical output. The model can be downloaded from here.

2.3

We begin by defining the agents. There are two types of agents: citizens and nations. Citizens are each associated with one nation and possess one unit each of labor and capital, which they choose to deploy in one of two national industries depending on which pays the higher wage or higher return to capital (they may choose to work in one industry and invest in the other). They use these wages and returns to demand goods.

2.4

Nations possess national industries (we can follow convention by thinking of them as wine and cloth) that produce goods according to Cobb-Douglass production functions using the labor and capital that the citizen agents provide. They calculate wages and returns to capital along with prices for each of the goods produced. When trade is enabled, they also engage in trade, importing more of a good if its price is lower in the other country and paying for these imports by bartering with goods from the industry where their price is lower.

2.5

More specifically, the citizen agents has two state variables: a job and an investment. It also has a demand function. In each round, each agent does these things:

• Asks the nation for the current price of both wine and cloth.
• Asks the nation for the current wage in the industry where the agent works.
• Asks the nation for the current return on capital in the industry where the agent has invested.
• Calculates its demand for both wine and cloth based on its income (from wages and investments) and the prices of the two goods using the simple hyperbolic demand function D_w = Y/2P_w. This amounts to saying that each agent spends half of its income on each good - buying less and more of the good as the price goes up and down.
• With a small probability, the agent reexamines its job and investment choice, changing jobs or shifting its investment to the industry that provides the higher wage or return to capital. The low rate of turnover in employment and investment insures that the model is able to adjust to each change, thus avoiding stampedes from one industry to another that dramatically overshoot the required correction in the employment or investment level.

2.6

The nation agent has three basic parameters. The structure of the nation's two industries is given by a pair of Cobb-Douglas production functions of the form Q_w = A*L^α _w *K^β _w, where the quantity of wine produced Q_w is the product of an efficiency A, the amount of labor devoted to wine L_w to some exponent α and the amount of capital K_w devoted to wine to some exponent β.

2.7

Because the model relies on barter rather than money, the price of one good (wine) is fixed at 1, while the price of the other good (cloth) adjusts to reflect its relative scarcity. The price of cloth is adjusted upward by a small amount when demand for cloth exceeds its supply and down by a similar amount when supply exceeds demand. Because wages and returns on investment are calculated as shares of current production, Walras' law ensures that if the cloth market clears, the wine market will also clear. The price of cloth is a state variable.

2.8

When trade is opened, the nations barter goods. Cloth flows from the country in which its price (relative to wine) is lower to that where its price is higher, with compensation being made in wine according to the current price of cloth. When the international market is out of equilibrium (i.e. when the price of cloth differs between the two countries) the trade price of cloth is taken to be the average price between the two countries. The amount of cloth exported is increased by a small amount when the nation's partner has a higher relative price for cloth and is decreased by a small amount when the partner has a lower relative price for cloth. This level of trade is the nation's final state variable.

2.9

In each round, each nation does these things:

• Counts the number of citizens working and investing in each industry.
• Determines the quantity of each good which it will produce using each industry's production function and the current level of employment and investment in each industry.
• Determines the wage for each industry by calculating the marginal product of labor in that industry by subtracting the current level of production from the production that would result from the addition of one additional unit of labor.
• Determines the return to capital for each industry by subtracting the wage bill for that industry from the total output of the industry (at current prices) and dividing by the number of investors in the industry.
• Adjusts the price of cloth as described above.
• Adjusts the level of trade to reflect the new price level in both countries as described above.

2.10

These straightforward behavioral rules are adequate to reproduce the primary features of the Hecksher-Ohlin trade model in a dynamic context.

2.11

We allow for exploration of international capital mobility by allowing the agents to invest in any of the four industries - two domestic and two foreign. With capital mobility enabled, each investor examines not only the domestic industries, but also the foreign ones. The agent's investment is then placed with the industry that has the highest return to capital at the given time. As capital flows out of one industry and into another, the return to capital will increase in the first and decrease in the second. This basic principle prevents all investors from flocking into the same industry. We now face the problem of where to count these returns. Should all returns be repatriated and used for consumption in the home nation of the investor, or should the returns be consumed (or reinvested) in the nation of investment? The actual fate of revenues from foreign investment is rather complex and the literature conflicting (Gomory & Baumol 2000). Modeling it well enough to make specific policy recommendations is a non-trivial task. We make a start, however, by providing a slider in the NetLogo interface that allows the user to examine the spectrum of possibilities, ranging from complete repatriation to entirely local consumption.

Results and Analysis

3.1

We will first verify that the agent-based model is capable of reproducing Samuelson's straightforward result. We will then use the model to illustrate the multiple equilibria in the face of increasing returns discussed by Gomory and Baumol. Finally, we will explore the impact of capital mobility in the increasing returns environment.

Verifying the Model Against Samuelson's Analysis

3.2

We can gain some confidence in both the agent model and in the soundness of Samuelson's analysis by verifying that they both produce the same result. Because our modeling approach is compatible with Samuelson's analysis, it is easy to translate his numbers into parameters that can be plugged into the agent model.

3.3

The "US" nation agent begins with 100 citizens. It has two industries specified by these production functions that (following Samuelson) exhibit constant returns to scale:

• Q_c=2*L_c^0.5*K_c^0.5
• Q_w = 0.5*L_w^0.5*K_w^0.5

3.4

The "China" nation agent begins with 1000 citizens. Its industries are similarly specified with these production functions:

• Q_c=0.05*L_c^0.5*K_c^0.5
• Q_w = 0.2*L_w^0.5*K_w^0.5

3.5

The citizen agents of each country are initially randomly assigned a job, an investment and a demand function as described above. This demand function is identical for each agent.

3.6

The model run begins in autarky. After 500 rounds, both nations have established equilibrium production at 50 units of utility. At round 500, trading opens allowing the nations to import a good if its relative price is lower in the other country. This results in a major restructuring of each economy.

3.7

After another 500 rounds, at round 1000, China undergoes its remarkable invention in the cloth industry, raising its productivity there from 1/20 to 8/10. As Samuelson's analysis indicates, Chinese utility jumps to 200, while US utility falls back to its previous autarkic level of 50. After yet another 500 rounds, trade is stopped and the model shows no major difference, thus demonstrating that these productivity levels produce trade terms that are functionally equivalent to autarky.

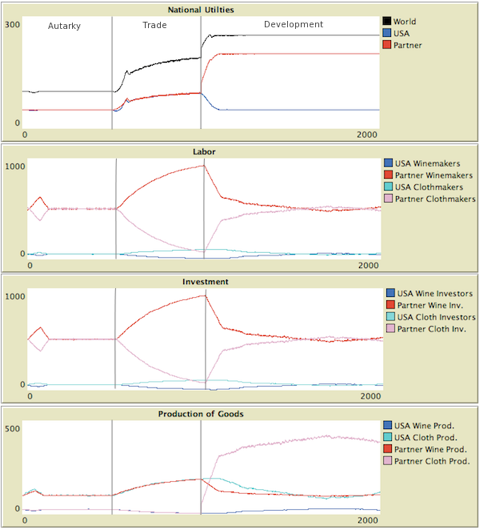
Figure 1. Agent-based Realization of Samuelson Trade Model

Illustrating Gomory and Baumol's Retainable Industries

3.8

Now that we have established the basic functioning of the model, we can use it to explore the more interesting case where we relax the assumption of constant returns to scale, shifting instead to the combination of increasing and decreasing returns examined by Gomory and Baumol.

3.9

We can illustrate the existence of retainability by running our agent-based trade model with an appropriate set of parameters. In this case, we imagine a large (500 citizen), industrialized nation and a smaller (100 citizen) "third world" nation that develops later. Once again we have two industries, but this time they are industries of a specific character. One is a basic agricultural industry that exhibits low productivity and decreasing returns to scale. The other is a high productivity industry - let's generically call it manufactures - that exhibits increasing returns to scale. We will assume that this industry exhibits increasing returns over its whole range of production.

3.10

With the exception of levels of productivity, these production functions are identical in both countries:

• Q_a = A*L_a^0.4*K_a^0.4
• Q_m = B*L_m^0.7*K_m^0.7

3.11

As in Samuelson's case, the nations differ only in their production efficiency in each industry. The developed nation is more efficient in both industries, having an efficiency in agriculture of A=0.5 and an efficiency in manufactures of B=1.0. The developing nation begins with equal efficiency in both industries: A=0.2 and B=0.2. This gives the developing nation a comparative advantage in agriculture and the industrialized nation a comparative advantage in manufactures.

3.12

We run the model forward as we did in the Samuelson case. For the first 500 rounds, both countries produce and consume as best they can in autarky. For the next 500 rounds, the nations trade, both realizing gains because they are able to specialize in the area where they are relatively most efficient.

3.13

As in the Samuelson case, at round 1000, we introduce a substantial exogenous change in productivity in one industry. In this case, the developing country drastically increases its productivity in manufactures from a paltry 0.2 to an impressive 1.5, jumping from 20% of the developed nation's productivity to 150%. At this point, however, we observe a marked contrast to Samuelson's giant increase in productivity: nothing happens.

3.14

Because the developing nation has specialized in agriculture, it has virtually no industry in manufactures. Any attempt to start such an industry is bound to fail because the industrialized country has attained a scale such that it can produce manufactures more cheaply than the developing nation - even given the developing nation's new, superior productivity at any given point on the production function. In each round, the citizens and investors of the developing nation examine the feasibility of moving into manufactures, and in each round they find that they can do better by sticking to agriculture. The industrialized nation is thus able to retain the industry despite the fact that, all else being equal, it is no longer the most efficient producer in either absolute or relative terms.

3.15

In the Samuelson case, we cut off trade at round 1500 and found that there was no impact on utility in either country because their proportional productivities had become similar. If we cut off trade in this case, something even more surprising happens. After an initial plunge in utility, the developing country begins to restructure its economy. Where its manufactures had been unable to compete with cheap, mass produced imports in its domestic market, they are now the only game in town. Workers and investors begin to shift away from agriculture and into manufactures. Initially, this sector is not terribly productive, but with experience and scale, it becomes more and more productive. In time, given the parameters we have chosen, the manufacturing sector becomes so productive that the small nation is actually able to do better in autarky than it previously did through trade!

3.16

In round 2000, we reopen trade. The newly industrialized country is now in a much stronger position to compete on the international market and sees a substantial gain. The larger, more established country actually looses more utility as a result of this trade over autarky. It is forced to restructure its economy to produce the lower productivity agricultural good. Because this good has decreasing rather than increasing returns, its productivity erodes as it becomes more specialized, leading to a long-term decline in income as compared to autarky.

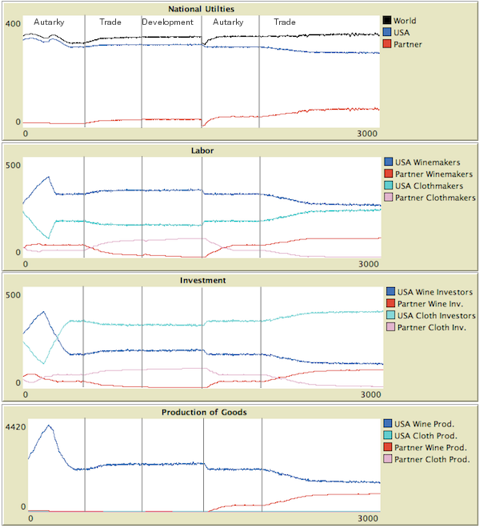
Figure 2. Retainability of Industries with Increasing Returns

Exploring Capital Mobility

3.17

Having demonstrated that the model can reproduce the expected results with both constant and increasing returns, we now examine a case with mobile capital. In Samuelson's pre-development case, where the USA is more productive than China in both industries, but China is relatively more productive in wine and also more populous so as to create equivalent levels of total utility that increase with trade and specialization, capital mobility increases the utility of both nations. With full repatriation of profits, Chinese investors move into US cloth creating lower cloth prices and considerable additional income in China. Both nations move from a utility of 100 to a utility of 120.

3.18

When we eliminate repatriation, assuming that investors consume all of their returns in the country of investment, we see a surprising result: the US is hurt and China benefits further. Keeping income in the country where it is produced drives down prices yet further; this increases global utility slightly and strengthens demand for Chinese wine while simultaneously decreasing demand for US cloth. The result is that the US drops back to 100 utils and China moves up to 150 - this in spite of the fact that significant Chinese capital is generating goods and consumption in the USA.

3.19

In the post-development Samuelson case, where China has suddenly become relatively much more efficient in cloth, the effect of capital mobility is even more dramatic. With trade enabled, the US enjoys 50 utils and China 200 (as stated above). Enabling capital mobility with full repatriation produces a major shift of investment away from China to the US - which is still more efficient in absolute terms. This results in a very small increase in global utility - from 250 to 255 utils, but a huge boon to the US, which jumps from 50 to 95, and a blow to China, which drops from 200 to 160. The elimination of repatriation, in this case, makes only a small difference in utilities. The US falls from 95 to 92 and China grows from 160 to 163. Global utility increases by only about a single unit

3.20

The differential impacts of capital mobility are more pronounced in the face of increasing returns in one industry. In the Gomory-Baumol (US and Ghana) world described above, before Ghana has developed (when it is relatively better in the decreasing returns good), we find that capital mobility drops its the utility from 28 to about 19, while increasing US utility from 300 to 310 as investment shifts to the more productive industry. Eliminating the repatriation of returns to capital offers a further boon to the US, raising its utility to about 320, but yields only about a single point of benefit to Ghana, moving it up to 20 utils.

3.21

The case where Ghana has developed and captured the increasing returns industry is also quite stark. Before allowing for mobile capital, we find US utility stabilizing around 266 units, while Ghana utility has stabilized around 68 units. With full repatriation of returns on investment, mobility has only a minor impact on total world utility (dropping it from 334 to about 330), but a significant impact on each nation. The US gains back some of its capacity in the increasing returns industry, growing to 290 units, while Ghana loses some of its advantage—dropping back to 40 units. This is because Ghana's workforce was not large enough to capture the whole increasing returns industry. The US, though not as efficient as the hyper-developed Ghana, still had a significant wine industry, and when additional capital became available, this industry was able to offer a higher return due to its larger scale. Even though the gains from capital made by Ghanaian investors in the US are fully repatriated to Ghana, Ghana is hurt because reduced investment in Ghana depresses wages there. Eliminating repatriation exacerbates these effects. Now US utility rises to about 305 units, while Ghanaian utility drops further to about 35 units.

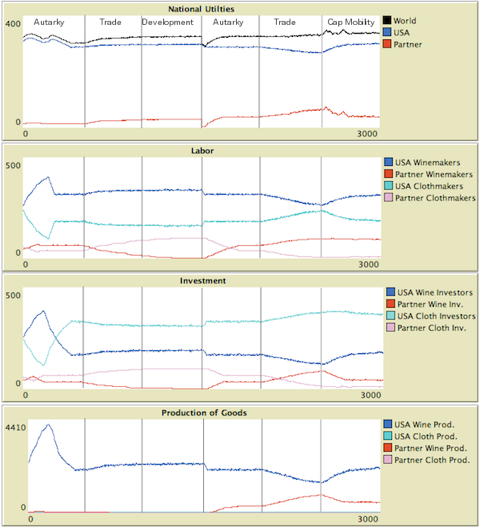
Figure 3. Mobile capital with increasing returns in one industry without repatriation

3.22

One key observation here is that the repatriation of capital gains does not have a major impact on the dynamics. In an industry with increasing returns, the nation with the larger industry will benefit from mobile capital. Under most conditions, global output will increase, but again, there will be winners and losers among nations. The story here is not the story of Ricardian comparative advantage where everyone benefits from greater mobility in goods. When it comes to productive factors, there are times when nations would do well to hold on to as much as they can.

3.23

We also note that free capital mobility makes development via the protection of infant industries impossible under the assumptions of the model. When the developing nation attempts to build its increasing returns industry by shutting off trade, it is unable to attract investors to that industry because its partner nation is still offering better returns to investment because of its scale. Investment in the local industry only takes place if both trade and capital mobility are halted.

Discussion

4.1

This model is admittedly highly stylized; however, it makes sense in terms of development and has important implications for development policy. In the constant or decreasing returns world of neo-classical trade theory, the productivities of nations in different industries determine a unique set of equilibria in trade and utility unless some sort of trade policy intervenes to interfere with trade and lower that utility. A poor country is poor either because it is not very productive, or because it is not making good use of its comparative advantages in productivity through trade.

4.2

The policy prescription that comes out of the neo-classical model is simple. Poor nations should try to improve their productivity in areas where they have a chance to compete - keeping wages low and focusing on low skill sectors such as agriculture (the stereotypical example would be bananas). Furthermore, they should seek to increase trade in every situation. The standard set of assumptions about trade indicate that this is the very best they can hope to do. If such a country is unable to compete in any of the more modern industries which are characterized by increasing returns, that is simply because they as a nation are no good at them. Their best strategy for obtaining these high value added goods, in both the short and long terms, is to grow ever more bananas and look for additional markets in which to trade them.

4.3

The introduction of increasing returns into this picture changes everything. A poor country no longer faces a simple policy prescription, and the invisible hand can no longer be counted on to deliver the industrial structure that will give the country its highest long-run level of consumption. The multiple equilibrium situation introduced by increasing returns leaves the country with difficult choices. In the short run, protecting a domestic industry will almost certainly hurt them. In the long run, however, this protection might allow the protected industry to attain sufficient scale that the country would be better off. Even if the long run autarkic equilibrium utility would be lower than the free trade equilibrium, a period of protection and domestic development might allow the protected industry to develop to the point where it could become a competitive producer on the world market, thus allowing the nation to reopen to substantially improved terms of trade and higher consumption. The Asian "tiger" economies come to mind as nations that achieved tremendous development by following this kind of strategy. (UNIDO 2004)

4.4

As simple as this paper's treatment of capital mobility may be, it makes the point that the rosy picture painted by the comparative advantage argument is suspect. Unless winning nations are prepared to compensate losing nations (which is unlikely), nations would do well to proceed with caution with regard to capital mobility because there is no assurance that each will benefit.

References

ARROW, K. (1962). The economic implications of learning by doing. Review of Economic Studies 29: 155-73. [doi:10.2307/2295952]

ARTHUR, W. B. (1989). Competing technologies, increasing returns and lock in by historical events. Economics Journal 99: 116-31 [doi:10.2307/2234208]

COSTINOT, A. (2009). On the Origins of Comparative Advantage. Journal of International Economics, vol. 77, no. 2, pp. 255-264. [doi:10.1016/j.jinteco.2009.01.007]

DALY, H. (1996). Beyond Growth. Beacon Press, Boston

DALY, H. and Farely J., (2003). Ecological Economics: Principles and Applications. Island Press, Washington, DC.

GOMORY, R. E. and Baumol, W. J. (2000). Global Trade and Conflicting National Interests. Cambridge, Mass.: MIT Press.

GOMORY, R. E. and Baumol, W. J. (2009) Globalization: Country and Company Interests in Conflict. Journal of Policy Modeling 31(4): 540-555. [doi:10.1016/j.jpolmod.2009.05.013]

JONES, R. W. (1956). Factor Proportions and the Heckscher-Ohlin Theorem. The Review of Economic Studies 24, no. 1:1-10. [doi:10.2307/2296232]

KRUGMAN, P. R. (1979). Increasing returns, monopolistic competition and international trade. Journal of International Economics. 9:469-79 [doi:10.1016/0022-1996(79)90017-5]

KRUGMAN, P. R. (1983). Targeted industrial policies: Theory and evidence. Industrial Change and Public Policy. Kansas City, MO: Federal Reserve Bank, pp. 123-55.

MARKUSEN, J. R. and Venables, A. J. (1988). Trade policy with increasing returns and imperfect competition: Contradictory results from competing assumptions. Journal of International Economics, vol. 24, no. 3-4, pp. 299-316. [doi:10.1016/0022-1996(88)90039-6]

MATSUYAMA, K. (1991). Increasing Returns, Industrialization, and Indeterminacy of Equilibrium. The Quarterly Journal of Economics, vol. 106, no. 2, pp. 617 -650. [doi:10.2307/2937949]

RICARDO, D. (1817). Principles of Political Economy and Taxation. G. Bell and Sons, London.

SAMUELSON, P. A. (2004). Where Ricardo and Mill Rebut and Confirm Arguments of Mainstream Economists Against Globalization. Journal of Economic Perspectives. Vol. 18, No. 3. pp 161-180. [doi:10.1257/0895330042162403]

UNIDO. (2004). Industrial Development Report 2004, Vienna: United Nations Industrial Development Organization.

WILENSKY, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.