 Abstract
Abstract
- Recent agent-based computer simulations suggest that ethnocentrism, often thought to rely on complex social cognition and learning, may have arisen through biological evolution. From a random start, ethnocentric strategies dominate other possible strategies (selfish, traitorous, and humanitarian) based on cooperation or non-cooperation with in-group and out-group agents. Here we show that ethnocentrism eventually overcomes its closest competitor, humanitarianism, by exploiting humanitarian cooperation across group boundaries as world population saturates. Selfish and traitorous strategies are self-limiting because such agents do not cooperate with agents sharing the same genes. Traitorous strategies fare even worse than selfish ones because traitors are exploited by ethnocentrics across group boundaries in the same manner as humanitarians are, via unreciprocated cooperation. By tracking evolution across time, we find individual differences between evolving worlds in terms of early humanitarian competition with ethnocentrism, including early stages of humanitarian dominance. Our evidence indicates that such variation, in terms of differences between humanitarian and ethnocentric agents, is normally distributed and due to early, rather than later, stochastic differences in immigrant strategies.
- Keywords:
- Ethnocentrism, Evolution of Cooperation, Evolutionary Game Theory, Minimal Cognition, Prisoner's Dilemma
 Introduction
Introduction
- 1.1
- Ethnocentrism is the tendency to favor one's own group at the expense of other groups. It is implicated in a variety of important phenomena from voting patterns to ethnic discrimination and armed conflict. It is widely believed in social science that ethnocentrism involves extensive social learning and considerable social and cognitive abilities (Hewstone, Rubin, & Willis 2002; LeVine & Campbell 1972; Sherif 1966). However, there is also evidence that ethnocentrism is common throughout a diverse range of animal (Chase 1980) and even plant (Dudley & File 2007; Runyon, Mescher & De Moraes 2006) species. Such evidence suggests that ethnocentrism may be rooted in biological evolution, and that its essential cognitive component is quite simple: the ability to distinguish in- vs. out-group members and select different behaviors based on that distinction. A striking example from red fire ants is that queens without a particular gene are detected and killed at birth by worker ants (Keller & Ross 1998).
- 1.2
- Recent computer simulations with simple abstract agents demonstrate that ethnocentrism can indeed originate through evolutionary processes (Hammond & Axelrod 2006a, 2006b). The agents in these simulations can either defect against, or cooperate with, other in-group or out-group agents, generating four possible strategies: (a) a selfish strategy of constant defection, (b) a traitorous strategy of cooperation with out-group, but not in-group, agents, (c) an ethnocentric strategy of cooperation within one's own group but not with agents from different groups, and (d) a humanitarian strategy of indiscriminate cooperation. From a random starting point, ethnocentrism evolves to become the dominant strategy under some variation in parameter settings, eventually characterizing about 75% of the world population. Our present work attempts to explain the evolutionary fates of each of these four strategies, and thus more fully understand the processes that may lead to ethnocentric dominance. We present two studies that test hypotheses for explaining ethnocentric dominance and two other studies documenting and explaining variation in early humanitarian competitiveness. We start by describing the simulation (Hammond & Axelrod 2006b) on which our work is based. We presented preliminary data on some of these issues in two conference papers (Shultz, Hartshorn & Hammond 2008; Shultz, Hartshorn & Kaznatcheev 2009), but much of the data, analyses, and interpretation presented here is new.
The Original Simulation of Ethnocentric Dominance
- 1.3
- Interacting agents in virtually any social situation can choose to cooperate with each other or not. In the terminology of game theory, defection is the opposite of cooperation. The classic, non-zero-sum game often used to study such interactions is Prisoner's Dilemma (PD). In PD games, two autonomous agents choose, independent of the other's decision, whether to cooperate with or defect against the other. Table 1 displays the payoffs for PD interaction, computed for Player 1 as the benefit b of receiving cooperation minus the cost c of giving it. In relatively abundant environments with some degree of social specialization, the cost is typically less than the benefit. In the simulations discussed here, cost = 0.01 and benefit = 0.03. The payoff is added to Player 1's reproductive potential RP. The best overall outcome occurs when both players cooperate, the worst when both defect. The dilemma arises because of the temptation to defect, which can yield an even higher payoff b for a defector against a cooperator. In this case, the cooperator incurs the cost of c without receiving any benefit.
Table 1: Payoffs in the PD game Player 2 Player 1 Cooperate Defect Cooperate b - c - c Defect b 0 - 1.4
- In these simulations, agents possess four simple traits: a perceivable tag (one of four possible), a strategy towards agents with the same tag (either cooperate or defect), a strategy towards agents with a different tag (again, either cooperate or defect), and an RP initialized to .12. Agents come to populate a 50 x 50 lattice, with each cell containing at most one agent at a time. Agents are stationary, can only interact with agents in the four neighboring cells, and may only reproduce a cloned offspring into an empty neighboring cell. The edges of the lattice wrap around to create a torus shape, thus ensuring that each location has the same number of potential neighbors.
- 1.5
- In Hammond & Axelrod (2006b), each simulation started with an empty lattice and ran for 2000 cycles, as stable patterns generally arise well before this point. Each evolutionary cycle has four phases: immigration, interaction, reproduction, and death. In the immigration phase, a randomly constructed agent is placed in a random empty location. The interaction phase begins by initializing each agent's RP to the default value of .12. Then each agent interacts with each of its neighbors (up to four) in a one-shot PD game by independently deciding whether or not to cooperate based on its own strategy and a comparison between its neighbor's tag and its own. As described earlier, the agent's payoff is added to its RP. At the start of the reproduction phase, a list of all existing agents is sorted into a new random order. This eliminates the advantage that earlier-reproducing agents incur by having more free spaces available to place their offspring. In this random order, each agent is given a chance (its RP) to place a cloned offspring if there is an adjacent empty space. A clone has its parent's traits subject to a small mutation rate (default of .005). Strategy traits can mutate by switching values (cooperate to defect or vice versa). Tags can mutate to any one of the three other tags with equal probability. In the final, death phase each agent has a chance of expiring equal to the death rate (default of .10), which would result in its removal from the lattice.
- 1.6
- The average proportions of the four strategies during the last 100 of 2000 evolutionary cycles were .08 selfish, .02 traitorous, .75 ethnocentric, and .15 humanitarian (Hammond & Axelrod 2006b). Systematic doubling and halving of key parameters (e.g., lattice size, number of cycles, number of tags, cost of cooperation) did not alter this distribution much, suggesting that evolution of ethnocentrism is not a knife-edge phenomenon but is instead quite robust. In fact, (Kaznatcheev 2010a) showed that the model is also robust to changes in the qualitative nature of the game matrix from PD to other competitive games.
- 1.7
- The resilience of ethnocentrism in our model can be contrasted with other tag-based models of cooperation such as those of Traulsen and Nowak (2007) and Antal et al. (2009), in which ethnocentrism only evolves when there are a large number of tags, and under restrictive mutation conditions. Earlier work on tag-based ethnocentrism (Hales 2000; Holland 1993; Riolo 1997) lacks sufficient variation in strategy to make the evolution of ethnocentrism paradoxical. Differences between our model and previous models are reviewed more thoroughly in the general discussion.
Table 2: Glossary of Key Terms Cooperation Providing a benefit to another agent at a cost to oneself. Defection Not cooperating with another agent, thus incurring no cost. Prisoner's Dilemma A symmetric game in which each of two agents independently chooses to cooperate with or defect against the other, with the ordering of payoffs given in Table 1. Tag 1 of 4 perceivable identifiers possessed by each agent. The number 4 is arbitrary and may be increased without qualitatively changing the results. Group Agents with the same perceivable tag regardless of their location. Strain Genetic identity between agents in both strategy and tag. Strategy 1 of 4 genotypes, coded on two binary genes, that specify whether to cooperate or defect depending on the tags of the interacting agents. Selfish A strategy of defecting against all other agents. Traitor A strategy of cooperating with agents of a different tag and defecting against agents of one's own tag. Ethnocentric A strategy of cooperating with agents of one's own tag and defecting against agents with a different tag. Humanitarian A strategy of cooperating with all other agents. Cluster A collection of spatially localized agents, predominantly of one strain. Free-rider A selfish or same-group traitorous agent in, or interacting with, a cluster of agents of the same group. World A toroidal square lattice on which agents immigrate, interact, reproduce, and die, along with an historical record of the evolution of agent genotypes. Neighbor An agent located directly above, below, to the left, or to the right of another agent on the toroidal lattice. Because the world is a torus, each agent has a maximum of four neighbors. Clone An offspring with the same genotype as its parent, subject here to a small mutation rate. Immigration Creating a random agent and placing it in an empty random location in the lattice. Hypotheses for Explaining Ethnocentric Dominance
- 1.8
- In explaining eventual ethnocentric dominance, Hammond and Axelrod (Hammond & Axelrod 2006a, 2006b) focus on the ability of ethnocentrics to out-compete free-riders in neighboring clusters. They defined a free-rider as a selfish agent who benefits from the cooperation of others while defecting and thus incurring no cost to itself. Hammond and Axelrod illustrate the dynamics of ethnocentric dominance over selfish free-riders by imagining a cluster of selfish agents near a differently tagged cluster of ethnocentric agents. These two clusters compete for neighboring free space. Although neither cluster cooperates across group lines, agents within the ethnocentric cluster benefit more from the cooperation of fellow members than do agents within the selfish cluster. Agents from the ethnocentric cluster have higher net RP, and thus are more likely to win the competition for space by placing more offspring in it.
- 1.9
- This ability to out-compete free-riders would presumably be undermined if the ethnocentrics in this example were replaced by humanitarians, because humanitarians cooperate across group boundaries. Indeed, in a simulation consisting of only humanitarian and selfish agents, group distinctions are trivial because they do not affect cooperative behavior; humanitarians cooperate with everyone, and selfish agents cooperate with no one. Thus, unlike ethnocentrics, humanitarians seem to lack a mechanism for defeating free-riders. If ethnocentrics out-compete free-riders better than humanitarians do, this could explain why ethnocentrics eventually dominate over humanitarians. We can term this the mediation hypothesis because it holds that interactions with selfish free-riders mediate the outcome of ethnocentric-humanitarian competition.
- 1.10
- Alternatively, one might focus on the dynamics of direct competition between humanitarian and ethnocentric clusters. As suggested by both previous results (Hammond & Axelrod 2006b) and present results, the chief competitor for ethnocentrism is humanitarianism rather than selfishness. Ethnocentrics of one cluster exploit humanitarians of another cluster, benefiting from the latter's cooperation while donating nothing in return. There are thus two candidate hypotheses to explain eventual ethnocentric dominance: the mediation hypothesis that ethnocentrics out-compete free-riders more effectively than humanitarians do, and the direct hypothesis that ethnocentrics exploit humanitarians across cluster frontiers. We test these two hypotheses in Studies 1 and 2.
- 1.11
- We are also interested in explaining the lack of success of selfish and traitorous strategies, as well as the differences between the two. As noted, Hammond and Axelrod (2006b) reported the mean proportions of selfish and traitorous strategies across the last 100 of 2000 evolutionary cycles as .08 and .02, respectively. Are free-riders defeated by fitter strategies or are they self-limiting? In a viscous environment, with tags that come to correlate with strategy, one might well focus on the likelihood of interacting with in-group v. out-group members, as well as interaction strategy. Lacking any out-group cooperators to exploit, a spatially-clustered strain of selfish free-riders would be self-limiting. Traitorous agents would have the added disadvantage of being exploited in between-cluster interactions with out-group defectors. Study 2 attempts to tease out these dynamics by examining simpler worlds restricted to only some strategies.
- 1.12
- Study 3 examines individual differences between simulated worlds, which concern early competition between humanitarianism and ethnocentrism. Study 4 attempts to explain these individual differences in terms of chance events early in evolution.
 Study 1: Timing of Ethnocentric Dominance and Its Relation to Humanitarian Decline
Study 1: Timing of Ethnocentric Dominance and Its Relation to Humanitarian Decline
- 2.1
- In this study, we examine the possible temporal coincidence between population saturation and the establishment of ethnocentric dominance. Both the mediation and direct hypotheses predict a close temporal coincidence between population saturation and ethnocentric dominance. Both hypotheses also predict that the frequency of humanitarian agents decreases with ethnocentric growth, though the direct hypothesis predicts a direct relation not using the mediating influence of free-riders.
Method
- 2.2
- Our methodology is the same as in the original simulation (Hammond & Axelrod 2006b), except that we record strategy frequencies at every evolutionary cycle in 50 worlds and stop at 1000 cycles because solutions are always stable by then. We record results at every evolutionary cycle to provide a more complete picture of evolutionary processes and insights into the determinants of stable evolutionary outcomes.
- 2.3
- To examine the unique predictions of each hypothesis, we perform a mediation analysis to determine whether the relation between ethnocentric and humanitarian strategies is mediated by suppression of selfish strategies. The direct hypothesis would be uniquely supported by finding an unmediated negative relation between ethnocentrism and humanitarianism, while the mediation hypothesis would be uniquely supported by finding evidence of such mediation through selfish free-riders.
Results
- 2.4
- Mean evolving strategy frequencies over the 50 worlds are plotted in Figure 1. These plots indicate that ethnocentric dominance occurs, on average, at around 300 evolutionary cycles. Until that point, there is strong competition from humanitarians. Both selfish and traitorous strategies increase over the first 300 cycles but then stagnate at such low levels that they never pose much of a threat to either humanitarianism or ethnocentrism. A plot of evolving population sizes in 50 worlds, in Figure 2 left-side Y-axis, indicates that world population saturates at around that same time, 300 cycles. The right-side Y-axis in Figure 2 shows that the proportion of out-group interactions, averaged over 50 worlds in a fresh simulation, increases across the first 300 evolutionary cycles and then stagnates at just under .2. Proportion of out-group interactions is computed as the number of out-group interactions divided by number of total interactions (out-group interactions + in-group interactions). In summary, as the world fills up, out-group interactions reach a maximum and final decisive splits in strategy frequencies emerge. Similar to earlier results (Hammond & Axelrod 2006b), the mean proportions of strategies at 1000 cycles are .08 selfish, .02 traitorous, .73 ethnocentric, and .17 humanitarian.
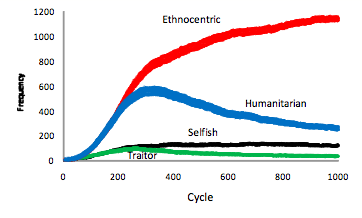
Figure 1. Mean evolving strategy frequencies in 50 worlds ± SE. 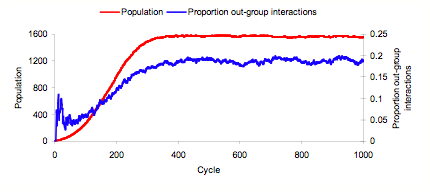
Figure 2. Mean evolving population size and proportion of out-group interactions in 50 worlds. - 2.5
- Mediation analysis indicates a strong, inverse direct relation between ethnocentric and humanitarian frequencies during the last 698 cycles, after population saturation, that is not mediated by selfish free-riders. Mediation analysis employs multiple linear regression to determine whether or not the relation between two variables is mediated by a third variable (MacKinnon, Fairchild & Fritz 2007). The question in our case is whether the negative relation between number of ethnocentrics (variable X) and humanitarians (Y) is direct or mediated by changes in the number of selfish agents (M). Summary results are presented in Figure 3 in terms of standardized regression coefficients.
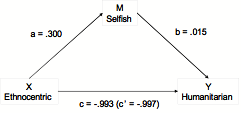
Figure 3. Standardized regression coefficients among mean strategy counts across the last 698 evolutionary cycles. Populations at each evolutionary cycle are averaged across 50 simulated worlds. - 2.6
- The mediation analysis proceeds through four steps (MacKinnon et al. 2007), using three regression equations: a) Regression of Y onto X yields the c coefficient, representing here the total effect of ethnocentrism on humanitarianism, including any causally mediating variables that are influenced by ethnocentrism, such as the hypothesized free-riding by selfish agents. b) Regression of M onto X yields the a coefficient, representing here the effect of ethnocentrism on selfishness. c) Regression of Y onto X and M yields both the b coefficient, representing here the relation between selfishness and humanitarianism and the c' coefficient, representing here the direct relation between ethnocentrism and humanitarianism with selfishness removed. In a mediation analysis, the direct effect ( c') plus the mediated effect ( ab) equals the total effect ( c).
- 2.7
- The proportion of the total effect (X → Y) due to mediation (X → M → Y) is computed as either 1 - c'/c or ab / ab+c', and is found here to be essentially 0. Computation of a Z score for the significance of a mediated effect (Sobel 1982) is not significant, Z = ab / sqrt ( SEab) = 0.11. This Z value would need to reach 1.96 to be significant at p < .05.
- 2.8
- Because correct specification of a causal model is important for mediation analysis, the results reported here reflect a lag of one evolutionary cycle between measures of ethnocentric and selfish populations, and two evolutionary cycles between ethnocentric and humanitarian populations. This ensures that direction of causation between X and M can be only from ethnocentrism (at cycle n) to selfishness (at cycle n +1), and that direction of causation between X plus M and Y can only be from ethnocentrism and selfishness to humanitarianism (at cycle n +2). These time lags are conservatively designed to reflect a pure mediation effect, but virtually identical mediation results are also evident without any time lags.
Discussion
- 2.9
- These results indicate that the decline of humanitarians is due to direct exploitation by ethnocentrics and is not mediated by humanitarian deficiencies in out-competing selfish agents. As the world fills up and clusters of agents collide, ethnocentrism starts to dominate its closest competitor humanitarianism by virtue of ethnocentrics directly exploiting humanitarians across cluster boundaries. Strategies start to separate in frequency, whether ethnocentrics over humanitarians or selfish over traitors, when clusters collide as world population saturates.
 Study 2: Restricted-strategy Simulations
Study 2: Restricted-strategy Simulations
- 3.1
- In this study, we test every possible combination of the four strategies independently. This includes testing all four strategies individually, all six strategy pairs, and all four strategy triples. Rather than focusing on early cycles, our goal here is to see whether certain strategies finish differently in the absence of other strategies. Although this is a significant departure from the full four-strategy simulation, it could provide insight into more subtle dynamics. In earlier work, humanitarians dominated selfish agents in a two-strategy design, under some parameter settings (Hammond & Axelrod 2006a), but here we include all strategy combinations and focus on why humanitarians lose out to ethnocentrics. Although Hammond and Axelrod considered only selfish free-riders in their analysis of this outcome, our analysis also includes traitorous free-riders.
Method
- 3.2
- These simulations are identical to the simulations in Study 1, except that immigration and mutation are altered to restrict allowable agent strategies to the particular strategy subsets of interest. Every evolutionary cycle, a new immigrant is created with random in-group and out-group strategy traits. If these traits result in a strategy that is disallowed, that agent is aborted and a new agent is created with new random strategy traits. This process is repeated until an immigrant with an allowed strategy is created.
- 3.3
- Mutations are treated similarly. Recall that offspring inherit their parent's traits with each trait subject to a mutation rate of .005. If a particular mutation results in an offspring with a disallowed strategy, that mutation is ignored. For each combination of allowed strategies, we compute the mean number of agents possessing each strategy over the last 100 of 2000 cycles, and average that over 10 simulated worlds.
Results
- 3.4
- The mean numbers of agents having each of the allowed strategies in the last 100 cycles are shown in Table 3.
- 3.5
- Underscoring the robustness of the original simulation (Hammond & Axelrod 2006b) and replicating our earlier dataset (Shultz, et al. 2009), we see that when we remove one or two strategies, the relative ordering of frequencies of the remaining strategies remains. That is, the final strategy frequency distribution obeys the familiar, four-strategy ordering (ethnocentric > humanitarian > selfish > traitorous) regardless of which strategies are missing. The lone exception is in the simulation run without ethnocentrism (HST), where traitorous agents actually perform better than selfish agents. This case is interesting, and we discuss it shortly.
Table 3: Mean Agents with Each Strategy Allowed strategies Ethnocentric E Humanitarian H Selfish S Traitorous T EHST 1183 229 123 47 HST 1368 115 150 EHT 1334 247 39 EHS 1183 271 124 EST 1395 139 32 ST 482 247 HT 1479 188 HS 1517 143 ET 1587 34 ES 1414 157 EH 1369 257 E 1615 H 1707 S 659 T 966 - 3.6
- Most interesting for the mediation and direct hypotheses, however, is the extent to which humanitarians thrive in the absence of ethnocentrism. In simulations without ethnocentrism, humanitarianism dominates in a manner similar to ethnocentrism. This is evident in both three- and two-strategy simulations. Figure 4 shows mean strategy frequencies for three-strategy simulations that disallow either humanitarian (EST) or ethnocentric (HST) strategies, across 10 worlds averaged over the last 100 of 1000 cycles. Humanitarians perform similarly to ethnocentrics here, greatly outperforming both traitorous and selfish agents. A much smaller effect is that ethnocentrics out-compete traitors a bit more than humanitarians do, although this does not diminish the numbers of humanitarians relative to ethnocentrics, or the strong superiority of either humanitarians or ethnocentrics over traitors and selfish agents.
- 3.7
- A strategy x other strategy factorial ANOVA revealed a large main effect of strategy, F (2, 54) = 8274, p < .001, reflecting the superiority of both humanitarianism and ethnocentrism, and an interaction of strategy with other strategy, F (2, 54) = 26, p < .001, reflecting that traitors did worse against ethnocentrics than against humanitarians. The main effect of other strategy was not significant, indicating that humanitarians were just as successful as ethnocentrics.
- 3.8
- Figure 5 plots mean strategy frequencies across 10 worlds averaged over the last 100 of 1000 cycles for some key two-strategy simulations that disallow either humanitarian or ethnocentric strategies: HT v. ET (left half) and HS v. ES (right half). The main finding is that either humanitarian or ethnocentric strategies strongly out-compete traitorous and selfish strategies.
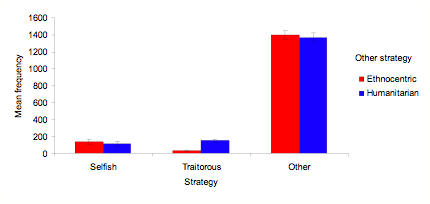
Figure 4. Mean strategy frequencies across 10 worlds averaged over the last 100 of 1000 cycles for three-strategy simulations that disallow either humanitarian or ethnocentric strategies, with SD bars. 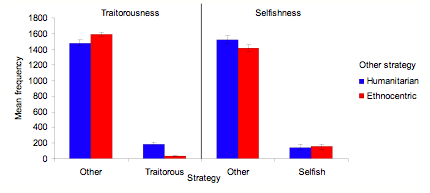
Figure 5. Mean strategy frequencies across 10 worlds averaged over the last 100 of 1000 cycles for two-strategy simulations that disallow either humanitarian or ethnocentric strategies, with SD bars: either traitorous (left half) or selfish (right half) competing with another strategy, either humanitarian or ethnocentric. - 3.9
- In a strategy x other strategy factorial ANOVA of performance against traitorousness, there was a main effect of strategy, F (1, 36) = 12340, p < .001, and an interaction between strategy and other strategy, F (1, 36) = 5783, p < .001. Analogous effects were also present against selfishness, F (1, 36) = 8729, p < .001 for the strategy main effect, and F (1, 36) = 17, p < .001 for the interaction.
- 3.10
- There is the one anomaly in which traitors out-performed selfish agents in the HST simulation. Figure 6 shows that this is part of a more general trend in which traitorous agents fare significantly better whenever ethnocentrics are absent. A factorial ANOVA, with presence v. absence of ethnocentrism and strategy contrasts as factors, yields main effects for presence v. absence, F (1, 54) = 389, p < .001, and strategies, F (2, 54) = 13, p < .001, and an interaction between them, F (2, 54) = 12, p < .001.
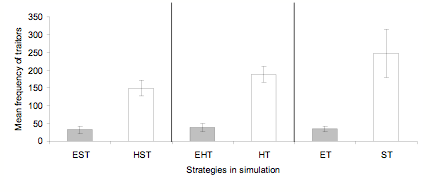
Figure 6. Mean frequencies of traitors in three key pairs of simulations in which ethnocentrism is either present (left of each pair) or absent (right of each pair). Results are based on the last 100 of 1000 cycles averaged over 10 worlds. SD bars are shown. - 3.11
- In isolation, ethnocentrism and humanitarianism both do considerably better than either selfishness or traitorousness (see the last four rows of Table 3). Traitorousness does better than selfishness, and humanitarianism does better than ethnocentrism. A one-way ANOVA yields a main effect of strategy, F (3, 36) = 571, p < .001. Individual comparisons reveal that all four means differ from each other, p < .001.
- 3.12
- We have an additional set of simulations in which mutations creating blocked strategies result in an offspring not being born, without a search for an acceptable substitute. Those results do not differ significantly from the foregoing so we do not present them here.
- 3.13
- Finally, because this was the first time that these strategies were restricted in all possible combinations, we ran additional simulations varying the often important benefit to cost ratio. In three separate simulations, we decreased the standard benefit value of 0.03 to values of 0.025, 0.02, and 0.015. Results are qualitatively similar to those in our standard condition with a benefit of 0.03. In particular, humanitarianism continues to perform well against both selfishness and traitorousness in the absence of ethnocentrism, and traitorousness continues to perform significantly worse whenever ethnocentrism is present. The one difference from our standard simulations is that selfishness begins to perform better when benefit descends to 0.015, but even here selfishness does not dominate when either ethnocentrism or humanitarianism is allowed.
Discussion
- 3.14
- The results of these restricted-strategy simulations contradict the predictions of the mediation hypothesis. In contrast to the notion that humanitarians cannot out-compete free-riders, humanitarians do very well against both selfish and traitorous agents. Selfish and traitorous agents limit growth of their own genotypes by not cooperating with them; although Laird (2011) noted circumstances where across-tag cooperation can sustain traitorous agents. Consistent with the direct hypothesis, the chief problem for humanitarians is ethnocentrism.
- 3.15
- The relatively poorer performance of traitors in the presence of ethnocentric agents can be explained by agent interaction across cluster boundaries. When traitorous agents of one cluster collide with ethnocentric agents of another, the ethnocentric agents earn outcome b, exploiting cooperating traitors by defecting against them. Just as ethnocentrism is poisonous to humanitarians, it is also poisonous to traitors, who incur a cost of c in such interactions.
 Study 3: Early Humanitarian Dominance
Study 3: Early Humanitarian Dominance
- 4.1
- Averaging results across worlds in Study 1 obscures possible individual differences between simulated worlds in evolutionary progressions. In this study, we examine plots of strategy growth in each of the 50 worlds used in Study 1. After each cycle in each world, we tabulate the number of agents with each of the four genotypic strategies, and perform chi-square tests to determine whether any one of the four strategies statistically dominates the others.
Method
- 4.2
- For a strategy to be considered dominant at a given cycle, two chi-square tests have to be significant: a 3- df test indicating that the frequency distribution differs from chance, and another 1- df test of whether the most frequent strategy is significantly more frequent than the next most frequent strategy. Expected values in each cell are computed by dividing the total number of agents by the number of cells being tested. We use a strict level for significance testing, p < .01, rather than the more common .05.
Results
- 4.3
- Whereas all populations, as noted earlier, end up being strongly ethnocentric, there are some interesting individual differences concerning early competition between humanitarian and ethnocentric strategies. This early variation can be described in terms of three different patterns: humanitarian dominance, ethnocentric dominance, and strong competition between these two strategies.
- 4.4
- Figure 7 shows an example with a strong early stage of humanitarian dominance, eventually giving way to ethnocentric dominance. The chi-square tests for this world reveal significant humanitarian dominance between cycles 111 and 350, followed by significant ethnocentric dominance from cycle 425. Sixteen of the 50 worlds showed this general pattern.
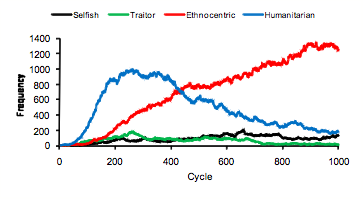
Figure 7. Strategy frequencies in World 3, showing early humanitarian dominance. 
Animation 1. This is a rendering of a world exhibiting humanitarian dominance. Colors indicate group tags and letters indicate strategy. The lattice size has been reduced to 25 by 25 to conserve space. Recall that agents on edges also interact with agents on opposing edges, so all cells have exactly four neighbors. Only the first 800 cycles are animated as population dynamics are more or less stable by this point. - 4.5
- Another common evolutionary pattern, illustrated by the plot in Figure 8, is characterized by early and persistent ethnocentric dominance. This world shows statistically reliable ethnocentric dominance for cycles 14-59, 68-73, 77-128, and from cycle 142 to the end. Sixteen of the 50 worlds show this general pattern.
- 4.6
- Early competition between humanitarianism and ethnocentrism with no clear front-runner is illustrated in Figure 9. In this world, there is a brief period of significant humanitarian dominance between cycles 75-98, but until ethnocentrism pulls away at cycle 235, there are no other statistically reliable differences between these two strategies. Eighteen of the 50 worlds show this general pattern of strong early competition.
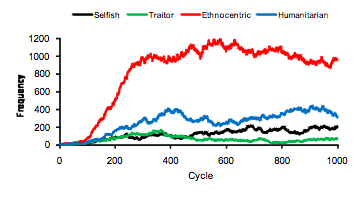
Figure 8. Strategy frequencies in World 18, showing early ethnocentric dominance. 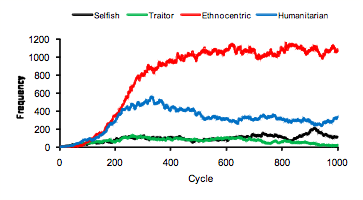
Figure 9. Strategy frequencies in World 4, showing early strong competition between humanitarianism and ethnocentrism. 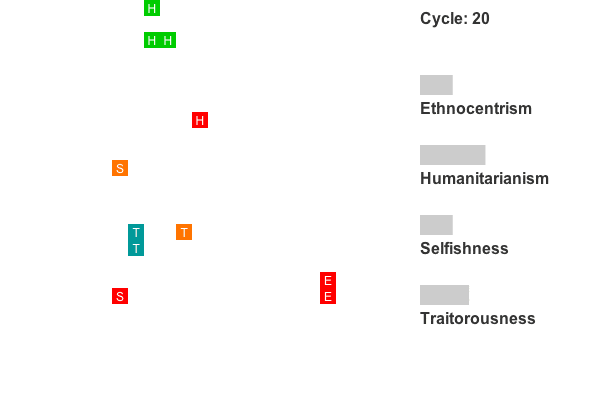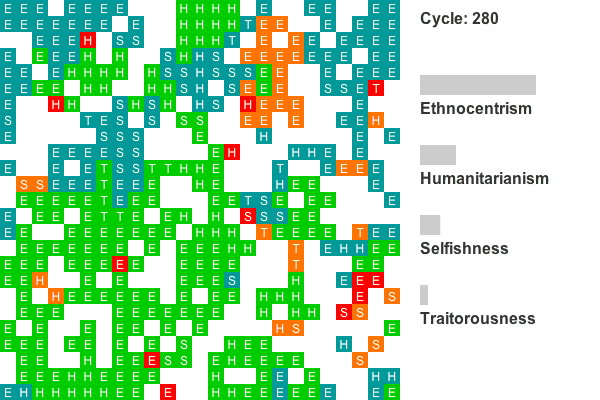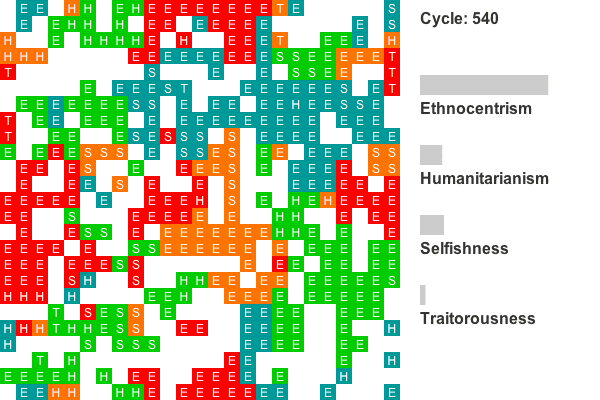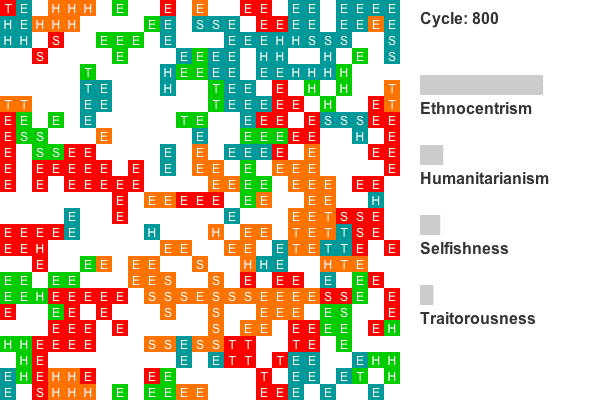
Animation 2. This is a rendering of a world where ethnocentrism dominates from the beginning. Colors indicate group tags and letters indicate strategy. The lattice size has been reduced to 25 by 25 to conserve space. Recall that agents on edges also interact with agents on opposing edges, so all cells have exactly four neighbors. Only the first 800 cycles are animated as population dynamics are more or less stable by this point. - 4.7
- Although these individual differences can be described in terms of types, a closer examination reveals that they actually form a continuous distribution, with a peak around the point of equality in the strength of the two strategies. Figure 10 shows a representative plot, composed by calculating the difference between humanitarian and ethnocentric strategies at each of the first 200 evolutionary cycles and averaging those differences across those cycles. This estimates the average integral between the frequency curves for humanitarianism and ethnocentrism in this critical early period of evolution. Strong positive differences signal humanitarian dominance, while strong negative differences indicate ethnocentric dominance. By the Kolmogorov-Smirnov test with the Lilliefors significance correction, this distribution does not deviate from normal, Z (50) = .089, ns.
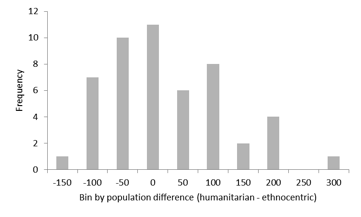
Figure 10. Distribution of mean humanitarian minus ethnocentric counts across the first 200 evolutionary cycles of 50 worlds. Discussion
- 4.8
- We find here that individual differences between evolving worlds are characterized mainly by early competition between the two fittest strategies: ethnocentrism and humanitarianism. Ethnocentrism always pulls away from humanitarianism by around cycle 300 as world population reaches its asymptote, while selfish and traitorous strategies never gain much of a foothold. Examples of extreme cases can be described in terms of two extreme types (Shultz et al. 2008) or three types as we do here, but variation in outcomes of this early competition between humanitarianism and ethnocentrism is actually normally distributed.
- 4.9
- The normal distribution of the differences between the two fittest strategies in early cycles, with a peak at equality (difference of 0) suggests that these variations are due to chance, perhaps in the makeup of early immigrants. So-called founder effects in the early evolution of a species are known to have strong effects on the course of evolution (Mayr 1970; Ramachandran et al. 2005).We test this hypothesis in Study 4.
 Study 4: Explaining Early Humanitarian Stages
Study 4: Explaining Early Humanitarian Stages
- 5.1
- Study 3 suggests the operation of chance factors allowing either humanitarianism or ethnocentrism to gain an early advantage. Instead of trying to measure such immigration randomness, here we systematically manipulate immigration rates for these two strategies, either at the start or a bit later in evolution. We hypothesize, for example, that initial immigration bias in favor of humanitarianism would produce early humanitarian dominance, while the same bias applied a bit later may not. We test this hypothesis by varying the type and timing of immigration bias.
Method
- 5.2
- We run four sets of simulations in which we alter immigration strategy assignment at different points in evolution. As before, the immigration rate is one immigrant per cycle.
- 20 worlds where each immigrant in cycles 1-20 is humanitarian.
- 20 worlds where each immigrant in cycles 1-20 is ethnocentric.
- 20 worlds where each immigrant in cycles 101-120 is humanitarian.
- 20 worlds where each immigrant in cycles 101-120 is ethnocentric.
- 5.3
- In each simulation set, immigration strategy assignment outside the intervention period returns to the standard single random immigrant per cycle. At each cycle in each simulation, we tabulate the number of agents with each strategy and analyze relative humanitarian dominance as in Study 3.
Results
- 5.4
- As in Study 3, we average humanitarian minus ethnocentric scores across the first 200 evolutionary cycles. Here we subject these averages to a factorial ANOVA in which the timing and type of immigration bias are the independent factors. There is a main effect of bias, F (1, 76) = 48, p < .001 and an interaction between timing and bias, F (1, 76) = 29, p < .001. Means and SE bars for this interaction are shown in Figure 11. Early bias has a large effect in the expected direction, while the same degree of bias has a negligible effect after 100 cycles, t (38) = 1.06, ns.
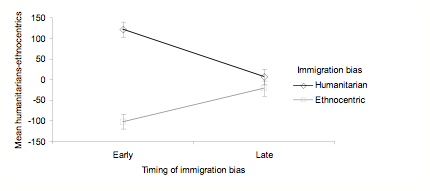
Figure 11. Mean numbers of humanitarians minus ethnocentrics, with SE bars, as a function of the type and timing of immigration bias. - 5.5
- Much the same results are obtained below and above a limit of 200 cycles. With few cycles, though, numbers of agents are small. By 300 cycles, there is evidence of ethnocentrics starting to establish dominance. But in between, centered around 200 cycles, there is an approximate balance between the effects of biasing immigration towards ethnocentrism or humanitarianism. Regardless of these early immigration bias effects, in all four of these simulation sets, ethnocentrism dominates by roughly 300 cycles and maintains this dominance to the end, as in our other studies.
Discussion
- 5.6
- An early immigration bias, whether towards humanitarianism or ethnocentrism, has a large effect on which strategy enjoys early dominance because reproduction with a small mutation rate creates a dynamic system in which offspring tend to resemble their parents across generations (as mutation rate increases this reproductive resemblance degrades towards chance). Such effects are large in a sparsely settled world without much competition from other strains. However, the same bias applied later on, in a slightly fuller world, has much less of an effect on early dominance because other strategies are already in place and are able to compete in this same dynamic fashion.
 General Discussion
General Discussion
- 6.1
- The mediation analysis in Study 1 and the restricted strategy simulations in Study 2 support the direct hypothesis for ethnocentric dominance over humanitarianism. Across ethno-humanitarian cluster borders, humanitarians cooperate while ethnocentrics do not. This provides a reproductive advantage for border-dwelling ethnocentrics, who receive the benefit of humanitarian cooperation while donating nothing across cluster lines. In terms of the payoffs in Table 1, for such interactions, ethnocentrics increase their RPs by b, while humanitarians decrease their RPs by c. Ethnocentric agents are thus more likely to succeed in competition for empty locations along these borders.
- 6.2
- The fact that traitorous and selfish genotypes perform just as badly against humanitarians as they do against ethnocentrics, and the lack of any mediation effect of free-riding contradict the alternative mediation hypothesis that only ethnocentrics out-compete selfish free-riders. Although ethnocentrics can exploit selfish agents in neighboring clusters, the self-limiting properties of defection against the free-riders' own gene pool tend to diminish this advantage. Under many conditions, there are not enough free-riders to allow this potential ethnocentric advantage to be widely used. Notice that the dominance of ethnocentrism over humanitarianism, and the marginalization of selfish and traitorous strategies, can be explained purely via individual selection, without recourse to group-selection mechanisms.
- 6.3
- Unlike selfish free-riders, traitorous agents have the additional problem of being exploited by the very out-groups they cooperate with. This explains why traitorous genotypes typically do even worse than selfish genotypes, despite the traitors' greater capacity for cooperation.
- 6.4
- Our simulations suggest that very early stochastic bias in favor of either humanitarian or ethnocentric immigrants affects early competition between these two main strategies. Before worlds fill up, most interactions are with an agent's own strain. Because the in-group strategy components of humanitarianism and ethnocentrism are identical, there is little in these early cycles to favor one over the other. But chance variation in early immigrant strategies can be important. The more initial immigrants there are with a given strategy, the more offspring they have, and the more offspring those offspring produce, etc. Early in evolution, when the environment is relatively open, this dynamic population growth can allow a lucky strategy to dominate, at least temporarily. Our experimental manipulation of immigration bias shows that identical favoring of an immigrant strategy later in evolution has much less effect because other strains are already around to offer competition.
- 6.5
- The earliest work on tag-based ethnocentrism (Hales 2000; Holland 1993; Riolo 1997) used tags not to adjust strategy, but to control assortment: agents interacted only with those of the same tag. In our model, agents interact with others regardless of tag, but have the potential to cooperate or defect based on the relation between their own tag and the tag of the agent they are interacting with. Riolo, Cohen, and Axelrod (2001) were the first to consider a model where agents interacted with others regardless of tag. However, in their model (and the minimal discrete variant of it proposed by Traulsen and Schuster (2003)) agents could not defect from same-tag partners; they could only adjust the level of cooperation they extended to other tags. In our paradigm, this would be analogous to restricting the simulation only to humanitarian and ethnocentric agents, without the possibility for selfish agents or traitors. Note that without the possibility of selfish agents, the dilemma in PD disappears inside groups, making the evolution of ethnocentric cooperation not paradoxical.
- 6.6
- To restore the dilemma of cooperation, Traulsen and Nowak (2007) and Antal et al. (2009) allow ethnocentric and selfish agents (although no humanitarians or traitors) and build analytic theories for inviscid populations. Unfortunately, their approach relies on a very large number of tags and differential mutation in tag and strategy, while our results hold even for a small number of tags and co-mutation of tag and strategy. One section of Traulsen and Nowak (2007) applies to the linked mutations that we use, but their conditions on the permissible benefit-to-cost ratio for low number of tags are more restrictive than ours. In particular, the spatial structure of our model allows ethnocentric cooperation to emerge in regions where it would be impossible in Traulsen and Nowak's inviscid model. Fu et al. (2012) considered the case with all four possible strategies, but still relied on drastically different probabilities of mutation for tags and strategies, and a large number of possible tags. Also, although Traulsen and Nowak (2007), Antal et al. (2009), and Fu et al. (2012) provide elegant analytic theories for inviscid environments, their approach applies only in the limit of weak selection. Thus, in settings where games have a large effect on the payoff of the agents, and the genome is far from neutral drift as in our simulations, the previous results do not apply.
- 6.7
- An advantage of the PD framework is that it is simple enough to serve as a useful metaphor for cooperation and competition across a wide range of species, yet rich enough to capture the emergence of complex social outcomes such as ethnocentrism (Axelrod & Hamilton 1981; Dawes, McTavish & Shaklee 1977; Halevy, Bornstein & Sagiv 2008).
- 6.8
- Unlike previous simulations (Hammond & Axelrod 2006a, 2006b) that focus on stable evolutionary outcomes, we examine the entire course of evolution. This provides a more complete picture of evolutionary processes, as well as insights into the determinants of stable evolutionary outcomes. Despite eventual ethnocentric dominance under viscous environments and group tags, we found surprisingly strong early competition from humanitarians. In contrast, strategies that fail to cooperate with their own kind (selfish and traitorous) never gained much of a foothold. Examination of the full evolutionary course also helped to test hypotheses about the eventual ethnocentric dominance. To thrive early in evolution, it is useful for population clusters to support their own kind. Later, as the world fills up, it is useful to exploit the cooperation of neighboring clusters.
- 6.9
- In addition to adopting PD as a framework for cooperation, our model makes three other assumptions that merit future study: perceivable group tags, a viscous environment forcing local interactions, and sufficient environmental abundance that the benefit of receiving cooperation is greater than the cost of giving it. The importance of group tags are well documented in species from bacteria (Lenski & Velicer 2000; Velicer 2003) to humans (Barth 1969 ; Greenwald & Banaji 1995; Tajfel, Billig, Bundy & Flament 1971).
- 6.10
- Child-proximity and the lattice structure are important factors in our model (Hammond & Axelrod 2006a; Kaznatcheev & Shultz, 2011). While viscosity is clearly evident in simple animal populations (Gadgil, Joshi, & Gadgjil, 1983; Seppä & Pamilo 1995), it is less obvious in modern humans with access to jet travel and the internet. Many of the environments in which early humans evolved were considerably more viscous than currently (Foley 1995). Moreover, many current human social environments still exhibit a high degree of viscosity in that spatial and cognitive closeness play a large role in social relations (Festinger, Schacter & Back, 1963; Hipp & Perrin 2009; Katz & Hill, 1958; Kubitschek & Hallinan 1998; Nahemow & Lawton 1975). Nonetheless, it could be of considerable interest to study the evolution of ethnocentrism in a range of network structures, of which the lattice is just one (Antal, Ohtsuki, Wakeley, Taylor & Nowak 2009; Kim 2010; Lima, Hadzibeganovic & Stauffer 2009).
- 6.11
- As mentioned earlier, a relatively high benefit/cost ratio is a natural consequence of social specialization in abundant environments. For example, a healthful tip from your doctor or a free tuneup from a mechanic friend cost little to give, but can yield considerable benefit to the recipient. Interestingly, task specialization is not limited to humans, but can be found in a variety of social animal species, and not just the eusocial insects (Anderson & Franks 2001;Gazda, Connor, Edgar & Cox 2005).
- 6.12
- Importantly, our decision to study a one-shot PD framework, where agents have no memory of previous interactions, significantly reduces the cognitive assumptions placed on our agents. A number of simulations have demonstrated how cooperation may emerge in an iterated Prisoner's Dilemma framework, where agents remember the outcomes of previous interactions (Axelrod 1997; Fogel 1993; Sandholm & Crites 1996). We opted for Hammond and Axelrod's (2006) memoryless model because we are interested in ethnocentrism in its most elemental form.
- 6.13
- The high degree of abstraction in the models discussed here ignores many of the complexities of cooperation and social organization. However, these models are useful abstractions that capture some fundamental principles that function in a variety of species and environments. They make few cognitive assumptions about the agents, and remain within the scope of minimal cognition. The most complex of these agents use categorical perception (Beer 2003) to distinguish group tags and choose the appropriate action based on that distinction. The minimal cognition should not be ignored. It can be associated with a fitness cost and its effect on evolutionary outcomes can be studied. (Kaznatcheev 2010, 2010b). The range of complex social phenomena that naturally emerge from such simple components is interesting and impressive. Even so, it will be important to explore the role of additional processes including development, learning, and cultural transmission, particularly in explaining human interactions.
 Acknowledgements
Acknowledgements
- This work was supported by research grants to TRS from the Natural Sciences and Engineering Research Council of Canada (NSERC), the Social Sciences and Humanities Research Council of Canada, and the Dean's Excellence Fund, Faculty of Science, McGill University. AK was partially supported by an NSERC summer research fellowship. Vakar Khan assisted with some data analysis. Valuable comments on the research were contributed by Khan, Kyler Brown, Julian Z. Xue, Vincent Berthiaume, and Ross Hammond.
 References
References
-
ANDERSON, C., & Franks, N. R. (2001). Teams in animal societies. Behavioral Ecology, 12(5), 534-540. [doi:10.1093/beheco/12.5.534]
ANTAL, T., Ohtsuki, H., Wakeley, J., Taylor, P. D., & Nowak, M. A. (2009). Evolution of cooperation by phenotypic similarity. Proceedings National Academy of Sciences U.S.A., 106(21), 8401-8792. [doi:10.1073/pnas.0902528106]
AXELROD, R. (1997). The evolution of strategies in the iterated prisoner's dilemma. In C. Bicchieri, R. Jeffrey & B. Skyrms (Eds.), The dynamics of norms (pp. 1-16). Cambridge: Cambridge University Press.
AXELROD, R., & Hamilton, W. D. (1981). The evolution of cooperation. Science, 211, 1390-1396. [doi:10.1126/science.7466396]
BARTH, F. (Ed.). (1969 ). Ethnic groups and boundaries. Boston: Little Brown.
BEER, R. D. (2003). The dynamics of active categorical perception in an evolved model agent. Adaptive Behavior, 11, 209-243. [doi:10.1177/1059712303114001]
CHASE, I. D. (1980). Cooperative and noncooperative behavior in animals. The American Naturalist, 115, 827-857. [doi:10.1086/283603]
DAWES, R. M., McTavish, J., & Shaklee, H. (1977). Behavior, communication, and assumptions about other people's behavior in a commons dilemma situation. Journal of Personality and Social Psychology, 35(1), 1-11. [doi:10.1037/0022-3514.35.1.1]
DUDLEY, S. A., & File, A. L. (2007). Kin recognition in an annual plant. Biology Letters, 3, 435-438. [doi:10.1098/rsbl.2007.0232]
FESTINGER, L., Schacter, S., & Back, K. W. (1963). Social pressures in informal groups: a study of human factors in housing. Stanford, CA: Stanford University.
FOGEL, D. B. (1993). Evolving behaviors in the iterated prisoner's dilemma. Evolutionary Computation, 1(1), 77-97. [doi:10.1162/evco.1993.1.1.77]
FOLEY, R. (1995). The adaptive legacy of human evolution: A search for the environment of evolutionary adaptedness. Evolutionary Anthropology: Issues, News, and Reviews, 4(6), 194-203. [doi:10.1002/evan.1360040603]
FU, F., Tarnita, C. E., Christakis, N. A., Wang, L., Rand, D. G., & Nowak, M. A. (2012). Evolution of in-group favoritism. Sci Rep 2(460). [doi:10.1038/srep00460]
GADGIL, M., Joshi, N. V., & Gadgjil, S. (1983). On the moulding of population viscosity by natural selection. Journal of Theoretical Biology, 104(1), 21-24. [doi:10.1016/0022-5193(83)90399-5]
GAZDA, S. K., Connor, R. C., Edgar, R. K., & Cox, F. (2005). A division of labour with role specialization in group-hunting bottlenose dolphins (Tursiops truncatus) off Cedar Key, Florida. Proceedings of the Royal Society B, 272, 135-140. [doi:10.1098/rspb.2004.2937]
GREENWALD, A. G., & Banaji, M. R. (1995). Implicit social cognition: Attitudes, self-esteem, and stereotypes. Psychological Review, 102, 4-27. [doi:10.1037/0033-295X.102.1.4]
HALES, D. (2000). Cooperation without space of memory: Tags, groups and the prisoner's dilemma. In S. Moss & P. Davidsson (Eds.), Multi-Agent-Based Simulation, Lecture Notes in Artificial Intelligence (pp. 157-166). Berlin: Springer. [doi:10.1007/3-540-44561-7_12]
HALEVY, N., Bornstein, G., & Sagiv, L. (2008). "In-group love" and "out-group hate" as motives for individual participation in intergroup conflict. Psychological Science, 19(4), 405. [doi:10.1111/j.1467-9280.2008.02100.x]
HAMMOND, R. A., & Axelrod, R. (2006a). Evolution of contingent altruism when cooperation is expensive. Theoretical Population Biology, 69, 333-338. [doi:10.1016/j.tpb.2005.12.002]
HAMMOND, R. A., & Axelrod, R. (2006b). The evolution of ethnocentrism. Journal of Conflict Resolution, 50, 926-936. [doi:10.1177/0022002706293470]
HEWSTONE, M., Rubin, M., & Willis, H. (2002). Intergroup bias. Annual Review of Psychology, 53, 575-604. [doi:10.1146/annurev.psych.53.100901.135109]
HIPP, J. R., & Perrin, A. J. (2009). The simultaneous effect of social distance and physical distance on the formation of neighborhood ties. City & Community, 8(1), 5-12. [doi:10.1111/j.1540-6040.2009.01267.x]
HOLLAND, J. (1993). The effects of (tags) on social interactions.
KATZ, A. M., & Hill, R. (1958). Residential propinquity and marital selection: A review of theory, method, and fact. Marriage and Family Living, 20(1), 27-35. [doi:10.2307/347359]
KAZNATCHEEV, A. (2010). The cognitive cost of ethnocentrism. In S. Ohlsson & R. Catrambone (Eds.), Proceedings of the 32nd annual conference of the Cognitive Science Society (pp. 967-971). Austin, TX: Cognitive Science Society.
KAZNATCHEEV, A. (2010a). Robustness of ethnocentrism to changes in inter-personal interactions. Paper presented at the Complex Adaptive Systems - AAAI Fall Symposium., Arlington, VA.
KAZNATCHEEV, A. (2010b). The cognitive cost of ethnocentrism. Paper presented at the Proceedings of the 32nd annual conference of the Cognitive Science Society, Austin, TX.
KAZNATCHEEV, A., & Shultz, T. R. (2011). Ethnocentrism Maintains Cooperation, but Keeping One's Children Close Fuels It. In L. Carlson, C. Hoelscher & T. F. Shipley (Eds.), Proceedings of the 33rd Annual Meeting of the Cognitive Science Society (pp. 3174-3179). Austin, TX: Cognitive Science Society.
KELLER, L., & Ross, K. G. (1998). Selfish genes: a green beard in the red fire ant. Nature, 394, 573-575. [doi:10.1038/29064]
KIM, J.-W. (2010). A tag-based evolutionary prisoner's dilemma game on networks with different topologies. Journal of Artificial Societies and Social Simulation, 13(3), 2.
KUBITSCHEK, W. N., & Hallinan, M. T. (1998). Tracking and students' friendships. Social Psychology Quarterly, 61(1), 1-15. [doi:10.2307/2787054]
LAIRD, R. A. (2011). Green-beard effect predicts the evolution of traitorousness in the two-tag prisoner's dilemma. Journal of Theoretical Biology, 288, 84-91. [doi:10.1016/j.jtbi.2011.07.023]
LENSKI, R. E., & Velicer, G. J. (2000). Games microbes play. Selection 1, 1-3, 89-95.
LEVINE, R. A., & Campbell, D. T. (1972). Ethnocentrism. New York: Wiley.
LIMA, F. W. S., Hadzibeganovic, T., & Stauffer, D. (2009). Evolution of ethnocentrism on undirected and directed Barabási-Albert networks. Physica A: Statistical Mechanics and its Applications, 338(24), 4999-5004. [doi:10.1016/j.physa.2009.08.029]
MACKINNON, D. P., Fairchild, A. J., & Fritz, M. S. (2007). Mediation analysis. Annual Review of Psychology, 58, 593-614. [doi:10.1146/annurev.psych.58.110405.085542]
MAYR, E. (1970). Populations, species and evolution. Cambridge, MA: Harvard University Press.
NAHEMOW, L., & Lawton, M. P. (1975). Similarity and propinquity in friendship formation. Journal of Personality and Social Psychology, 32(2), 205-213. [doi:10.1037/0022-3514.32.2.205]
RAMACHANDRAN, S., Deshpande, O., Roseman, C. C., Rosenberg, N. A., Feldman, M. W., & Cavalli-Sforza, L. L. (2005). Support from the relationship of genetic and geographic distance in human populations for a serial founder effect originating in Africa. Proceedings National Academy of Sciences U.S.A., 102(44), 15942-15947. [doi:10.1073/pnas.0507611102]
RIOLO, R. (1997). The effects of tag-mediated selection of partners in evolving populations playing the iterated prisoner's dilemma. Santa Fe Institute Working Paper, 97-02-016.
RIOLO, R. L., Cohen, M. D., & Axelrod, R. (2001). Evolution of cooperation without reciprocity. Nature, 414, 441-443. [doi:10.1038/35106555]
RUNYON, J. B., Mescher, M. C., & De Moraes, C. M. (2006). Volatile chemical cues guide host location and host selection by parasitic plants. Science, 313, 1964-1967. [doi:10.1126/science.1131371]
SANDHOLM, T. W., & Crites, R. H. (1996). Multiagent reinforcement learning in the iterated prisoner's dilemma. Biosystems, 37(1-2), 147-166. [doi:10.1016/0303-2647(95)01551-5]
SEPPÄ, P., & Pamilo, P. (1995). Gene flow and population viscosity in Myrmica ants. Heredity, 74 200-209. [doi:10.1038/hdy.1995.28]
SHERIF, M. (1966). Group conflict and co-operation: Their social psychology. London: Routledge & Kegan Paul.
SHULTZ, T. R., Hartshorn, M., & Hammond, R. A. (2008). Stages in the evolution of ethnocentrism. In B. C. Love, K. McRae & V. M. Sloutsky (Eds.), Proceedings of the 30th Annual Conference of the Cognitive Science Society (pp. 1244-1249). Austin, TX: Cognitive Science Society.
SHULTZ, T. R., Hartshorn, M., & Kaznatcheev, A. (2009). Why is ethnocentrism more common than humanitarianism? In N. A. Taatgen & H. v. Rijn (Eds.), Proceedings of the 31st Annual Conference of the Cognitive Science Society (pp. 2100-2105). Austin, TX: Cognitive Science Society.
SOBEL, M. E. (1982). Asymptotic confidence intervals for indirect effects in structural equation models. Sociological Methodology, 13, 290-312. [doi:10.2307/270723]
TAJFEL, H., Billig, M. G., Bundy, R. P., & Flament, C. (1971). Social categorization and intergroup behavior. European Journal of Social Psychology, 1, 149-178. [doi:10.1002/ejsp.2420010202]
TRAULSEN, A., & Nowak, M. A. (2007). Chromodynamics of cooperation in finite populations. PLoS ONE, 2(3), e270. [doi:10.1371/journal.pone.0000270]
TRAULSEN, A., & Schuster, H. G. (2003). Minimal model for tag-based cooperation. Physical Review E, 68. [doi:10.1103/PhysRevE.68.046129]
VELICER, G. J. (2003). Social strife in the microbial world. Trends in Microbiology, 11(7), 330-337. [doi:10.1016/S0966-842X(03)00152-5]