Abstract

In this paper we present an agent-based model of a human population, designed to illustrate the potential synergies between demography and agent-based social simulation. In the modelling process, we take advantage of the perspectives of both disciplines: demography being more focused on matching statistical models to empirical data, and social simulation on explanations of social mechanisms underlying the observed phenomena. This work is based on earlier attempts to introduce agent-based modelling to demography, but extends them into a multi-level and multi-state framework. We illustrate our approach with a proof-of-concept model of partnership formation and changing health status over the life course. In addition to the agent-based component, the model includes empirical elements based on demographic data for the United Kingdom. As such, the model allows analysis of the demographic dynamics at a variety of levels, from the individual, through the household, to the whole population. We bolster this analysis further by using statistical emulation techniques, which allow for in-depth investigation of the interaction of model parameters and of the resulting output uncertainty. We argue that the approach—although not fully predictive per se—has four important advantages. First, the model is capable of studying the linked lives of simulated individuals in a variety of scenarios. Second, the simulations can be readily embedded in the relevant social or physical spaces. Third, the approach allows for overcoming some data-related limitations, augmenting the available statistical information with assumptions on behavioural rules. Fourth, statistical emulators enable exploration of the parameter space of the underlying agent-based models.

Keywords:

Complexity Science, Demography, Health Care, Scenario Generation

Introduction

1.1

The main aim of this paper is to bring together methodological perspectives from two scientific disciplines: demography and social simulation, and to illustrate it using a proof-of-concept model of partnership formation, population change and health. For demography, the current state of the art is multi-level multi-state modelling (Courgeau 2007), while in social simulation these are various forms of agent-based models (Gilbert and Troitzsch 2005). Existing work on agent-based computational demography, which has been pioneered by Billari and Prskawetz (2003), focused largely on partnership and family formation (Todd, Billari and Simão 2005; Billari 2006;Billari et al. 2006, 2007; Hills and Todd 2008; Aparicio-Diaz et al. 2011), but also provided examples of applications to other areas, such as migration (Heiland 2003; Kniveton, Smith and Wood, 2011; Willekens 2012), residential mobility (Benenson, Omer and Hatna 2003) and household dynamics (Geard et al. 2013). However, what has been missing so far is a higher-level synthesis, which would bring together various components of population change within a broader agent-based, multi-level and multi-state framework. This paper aims to contribute to filling this gap, by trying to reconcile the approaches of both disciplines - statistical demography and social simulation.

1.2

Our initial motivation in carrying out this work has been our involvement in the Care Life Cycle project (CLC, http://www.southampton.ac.uk/clc). The CLC is a five-year research programme at the University of Southampton that commenced in October 2010. The project looks at the extent to which we can predict supply and demand for health and social care in the United Kingdom's ageing society, and explain mechanisms of the underlying dynamics. The research team spans a wide range of disciplines, including agent-based modelling, demography, gerontology, operations research, and social statistics, and includes a variety of points of view: from micro-level to macro-level, and from empirical to theoretical. In this paper, we attempt to bring some of these perspectives closer together.

1.3

The paper is structured as follows: in the next section, we begin by discussing agent-based modelling in the context of its demographic applications. We illustrate the discussion by presenting a two-dimensional extension of the 'Wedding Ring' model of partnership formation (Billari et al., 2007). Subsequently, the model architecture is explained in more detail, including further description of the agents, and a discussion of how the model incorporates demographic data and methods. We then offer insights into selected results from various model runs, including plausible scenarios of population development and a sensitivity analysis of selected parameters obtained by using statistical emulators. Finally, we present conclusions and implications for demography and social simulation, alongside suggestions for further extensions and methodological development of the presented framework. In order to present all the relevant technical details, and potentially enable replications of our work, the model has been uploaded to the OpenABM archive and is available at http://www.openabm.org/model/3549.

Agent-based demography revisited

Is there a need for agent-based demography?

2.1

As argued elsewhere (Silverman et al. 2011), modern demography is facing three important challenges in an increasingly complex world. Firstly, in order to describe population phenomena correctly, and to address policy challenges appropriately, the analysis has to operate across a range of levels: from individuals, through households and different geographies, to whole societies (Courgeau 2007). Attempts to address this issue have recently been made by linking multilevel statistical analysis with the event history and micro-simulation approaches (Willekens 2005; Courgeau 2007; Zinn et al. 2009).

2.2

However, having a correct grasp on the issue of aggregation does not guarantee better accuracy of prediction, which is typically the main aim of demographic modelling endeavours. Conversely, the increase in the dimensionality of the problem at hand, as well as of the related ever-expanding data requirements, may boost the predictive uncertainty rather than reduce it. Moreover, for many multidimensional questions, adequate data on all possible transitions between various demographic states are simply unavailable. The second challenge is thus: how do we link statistical data with other useful pieces of information in order to produce meaningful statements about plausible future trajectories of demographic processes?

2.3

Finally, the third challenge, linked with the previous two, is to resolve the question of how complex demographic models should be, and to what extent they should be built exclusively on the foundation of empirical data derived from cross-sectional and longitudinal surveys. Ideally, these models should be able to capture the most important features of population processes (such as that the life histories of people sharing a common family or household are intimately linked), whilst interfacing with all of the available information constraining the model's form - statistical, qualitative, or otherwise.

2.4

In terms of their potential in addressing these challenges, agent-based models (ABMs) differ quite substantially from statistical approaches, as they can address phenomena for which there is no explicit analytical representation. Such models can therefore provide explanatory power in the case of non-linear phenomena or complex interactions, such as social behaviour, and can include difficult-to-formalise elements, such as being embedded in a social context, networks of relationships, and related spatial considerations. Statistical demography may struggle with these elements of the social realm, as even individual-based approaches such as micro-simulation rarely allow for such complexities.

2.5

As regular readers of this journal will no doubt be aware, ABMs have become increasingly popular in the social sciences as the methodology has become more established. Following the early success of Schelling's (1978) residential segregation model, Axelrod's (1984) The Evolution of Cooperation, and later Cederman's (1997) applications in political science, the use of similar models to examine the development and evolution of human society has become increasingly popular. The potential for ABMs to offer explanatory power while reducing the need for expensive and time-consuming primary data collection is understandably appealing to many social scientists.

2.6

In this context, one of the possibilities of social scientific exploration is to treat models as valid tools of theory generation through an approach aptly labelled as 'model-based science', whereby the world is represented and understood indirectly, via the use of simplifying models (Godfrey-Smith 2006). Further, as the new field of social simulation has grown, new uses for ABMs in social science, beyond explanation and prediction, have also been outlined (Epstein 2008). The flexibility of the approach offers a way of developing greater understanding of how micro-level interactions produce macro-level effects - and some recent work in demography has turned to ABMs as a way to push population research forward in this respect. A strong case for model-based studies of populations has been made by Burch (2003a, b), with reference to an earlier statement to that effect by one of the most prominent demographers of the 20 ^th century, Nathan Keyfitz (1971).

Towards agent-based computational demography

2.7

Previous work in social simulation has identified two main approaches to the use of agent-based models in social science: systems sociology and social simulation sensu stricto (Silverman and Bryden 2007). Systems sociology focuses on models with few predefined interactions or structures within associated models, instead focusing on the emergence of recognisable social structures or institutions from low-level interactions (e.g., Schelling 1978; Cederman 1997). In contrast, social simulation models are generally described as displaying greater specificity than systems sociology models, often focusing on a particular class of behaviour at the individual level and using these to understand macro-level patterns. Such models frequently have some relevant link to empirical data (e.g., the reconstruction of the dynamics of the Anasazi population in pre-Columbian America, by Axtell et al. 2002). Models in the social simulation vein are more likely to be of interest in demography, given their closer link to empirical data.

2.8

The volume edited by Francesco Billari and Alexia Prskawetz (2003) is perhaps the most notable example in the recent demographic literature arguing for the incorporation of agent-based modelling techniques into population research, through an approach the authors refer to as 'agent-based computational demography' (ABCD). Agent-based modelling is viewed therein as a paradigm in which "the simulation is used first of all to develop and explore theories rather than to evaluate empirically the consequences of given rates/probabilities" (Billari and Prskawetz 2003: 11).

2.9

Historically, demography as a discipline has been generally more concerned with prediction, whereas agent-based modellers often use these techniques for quite varied purposes (Epstein 2008). Unlike traditional population studies, which are solidly rooted in data-based 'logical empiricism' (Burch 2003b), agent-based models are often used to attempt explanation rather than prediction; in particular, examining the link between micro-level behaviours and macro-level population dynamics. Obviously, these boundaries are somewhat permeable: demographers utilise micro-simulation models, which feed assumptions on mechanisms into the general framework of population dynamics (Gilbert and Troitzsch 2005). Agent-based modellers, on the other hand, increasingly use empirical data to inform their assumptions (see Silverman and Bullock 2004, for discussion, or Grim et al. 2012, and Geard et al. 2013, for some of the latest examples).

2.10

In recent years multi-level micro-simulation models, based on event history analysis, have become increasingly popular in demography, despite problems with their rapidly expanding data requirements due to the 'combinatorial explosion' of the parameter space (Silverman et al. 2011). Nevertheless, these modelling platforms still largely fail to capture the feedback effects of macro-level entities on the micro-level behaviour of the simulated agents (with notable exceptions, such as the SOCSIM model developed at the University of California at Berkeley, available from http://lab.demog.berkeley.edu/socsim). Most of such models also do not capture social interactions, formation of social networks, or other elements that may contribute to the social processes underlying demographic change - here, agent-based models are more suitable (Gilbert and Troitzsch 2005).

2.11

Thus, agent-based models continue to provide a potential platform for demographers, in which the dynamic relationship between the micro- and macro-levels of a simulated population can be more fully represented. Similarly, demographers can contribute expertise in using empirical information to verify the findings of ABMs and align them with the 'real world' wherever possible (for examples, see Todd et al. 2005; Billari et al. 2007; Hills and Todd 2008; Aparicio-Diaz et al. 2011). Given that agent-based models rely on micro-level mechanisms that drive macro-level behaviour, finding means to validate those micro-level assumptions is of some importance; aligning the models more closely with empirical data can be of great benefit in that respect. In that spirit, agent-based computational demography that links these two methodologies can benefit from the advantages of both approaches.

The statistical and simulated individuals

2.12

Statistical and agent-based models describe slightly different types of 'individuals', who are supposed to reflect the properties of actual people - members of the population under study. Thus, models in statistical demography rely on observations (censuses, surveys, registration) in an attempt to describe and predict the behaviour of statistical individuals (Courgeau 2012). In contrast, ABMs deal with simulated individuals - agents - equipped with some rules governing their behaviour, which can hopefully provide plausible explanations of patterns observed at the population level. The latter can be seen as a behavioural extension of the notion of virtual or synthetic individuals suggested by Willekens (2005) in the context of micro-simulation models. As stated before, links between the two approaches are already in existence: some multi-state demographic micro-simulation models use assumptions based on simple behavioural rules (including those governing transition probabilities between states), and agent-based models may utilise empirical information for building assumptions about various parameters of interest.

2.13

Given the already-existing synergies, we argue that by partnering well-established demographic methods with agent-based frameworks, we can produce models which increase our understanding of population change - while ensuring that we base the models on demographic data when suitable. In this context, our contention is that ABMs augmented with statistical knowledge can alleviate the growing hunger for data associated with traditional demographic models. Given that agent-based models rely upon particular parameter settings to generate appropriate results from low-level interactions, altering those parameters allows the modeller to easily generate variations (scenarios) within that parameter space and investigate the impact of those changes on agent behaviour. Furthermore, the modeller as well as the model user can see the impact of these variations on macro-level events, which can help answer some policy-relevant 'what-if' research questions, possibly in an interactive way. A conceptual summary of the methodological focus of both traditions, together with some possible cross-influence and scope for synergies, is offered in Fig. 1.

2.14

As shown in this framework, agent-based models augmented with statistical information allow demographers to investigate scenarios of demographic change over longer time horizons, as opposed to being limited by heavily data-dependent methodologies. Given that a reasonable predictive horizon in demography is thought to be about one generation (e.g., Keyfitz 1981), scenario generation offers an opportunity to explore some of the possible futures further ahead (see e.g., Nico Keilman's contribution to Willekens 1990; Wright and Goodwin 2009; Bijak 2010). Deriving such scenarios from a coherent methodological framework, whereby events at various levels (from micro to macro, with possible feedback effects) are linked with each other, offers demographers a chance to study complex patterns and behaviours in populations which are artificial, yet equipped with some real-world characteristics.

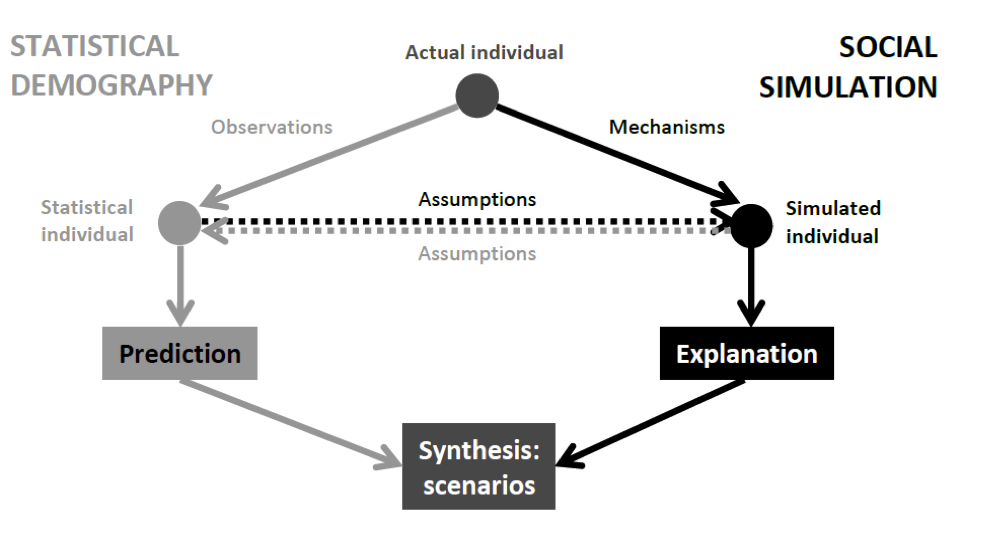
Figure 1. Two approaches to modelling social systems: statistical demography and agent-based social simulation Source: own elaboration, drawing from Willekens (2005) and Courgeau (2012).

2.15

Our inspiration for this work draws on the words of the prominent British demographer John Hajnal, who argued for building models which "involve less computation and more cognition than has generally been applied" (Hajnal 1955: 321). Here, we interpret 'computation' as referring to statistical, data-based inference, and 'cognition' as theory-building. The strength of demographic approaches lies in their predictive capacity and the richness and complexity inherent in the age and other structures of populations, while agent-based models provide strength in theoretical investigation and explanation. When combined within agent-based demography, these two approaches offer a compelling new direction for demographic modelling. We argue then for a shift in focus in the demographic community: from predictions based firmly upon the empirical grounding offered by survey data, to a combined approach incorporating elements of theoretical exploration and scenario generation. In successive sections of this paper we attempt to follow the logic presented above, first by discussing the architecture of a proposed agent-based demographic model, and then by presenting stylised examples of policy-relevant applications of the derived population scenarios.

Extending Computational Demography: Example of the Wedding Ring Model

Wedding Ring: The Basics

3.1

In order to demonstrate the utility of a combined statistical-demography-cum-social-simulation approach, we built a proof-of-concept agent-based model which additionally incorporates more traditional statistical demographic methods. We replicated and expanded upon the Wedding Ring, a model of partnership formation designed by Billari et al. (2007). We have selected this model because given our involvement in the CLC project our ultimate aim is to model demographic processes associated with social care in the context of the ageing population of the United Kingdom (UK). Most social care in the UK is informal and is delivered by family members (Vlachantoni et al. 2011) and thus partnership formation and the family structures that result from it are going to be a key part of our overall modelling efforts.

3.2

The Wedding Ring model seeks to explain the process of partnership formation as a consequence of social pressure, which arises from contact between partnered- and non-partnered agents within a social network. Billari et al. take as inspiration Hernes's (1972) initial investigations into the influence of married peer groups on marriage decisions. Subsequent modelling studies indicate that the Hernes model appears to account for observed patterns of marriage (Diekmann 1989), and empirical studies suggest that the opinions of peers influence marriage timing (Yabiku 2006). Further research in social influence and social learning indicates that peer influence or pressure can have a strong impact on fertility decisions as well (e.g., Bernardi 2003; Bernardi et al. 2007;Bühler and Fratczak 2007).

3.3

The agents in the Wedding Ring live in a one-dimensional ring-like space. They are effectively embedded in a cylindrical space, however, when we consider the dimension of age (Billari et al. 2007). Each agent has a network of 'relevant others' which consists of agents situated both within their neighbourhood in physical space, and within their broad age category in 'age space'. Social pressure varies with the proportion of married agents found within that neighbourhood, and this pressure then influences that agent's marriage decisions (Billari et al. 2007). The level of social pressure, mediated by a piecewise-linear 'age influence' function, determines how far an agent is willing to look to find an available partner. Thus, agents under greater social pressure will widen their search area. The social pressure function within the model is defined as a sigmoid function, the shape of which is governed by two parameters, α and β.

3.4

In essence, marriage in the Wedding Ring is represented as a diffusion process, although even those experiencing a high level of social pressure may still remain unmarried if they are unable to find a suitable partner, which marks a distinct difference from other diffusion processes (Billari et al. 2007). Searches for partnerships are thus mutual: marriage only occurs when both the agent and the suitable partner are within the acceptable age range. Once an agent is able to find a spouse, they can bear children, and those children are added to the population of the Wedding Ring.

3.5

Each agent is classified initially into one of five possible varieties, which determine the age ranges of agents that most influence their behaviour; agents may be influenced similarly by older and younger agents, mostly or only by older agents, or mostly or only by younger agents. The spatial interval around the agents in which relevant others can be found varies according to the size of the initial Ring population, and is symmetric around the agent's spatial location.

Extension of the model: From Wedding Ring to Wedding Doughnut

3.6

In the current application we suggest several extensions to the original Wedding Ring of Billari et al. (2007). This is in keeping with our long-term goal of producing a model of how changing family structures in the UK population may influence the provision of social care. First of all, situating the agents in a one-dimensional ring-shaped world can have unintended effects due to the restrictions on agents' spatial location and their ability to form reasonable networks of relevant others. In order to address this issue, our extension of the model moves therefore from a Wedding Ring to a Wedding Doughnut: the agents are embedded in a two-dimensional space in which the vertical and horizontal edges wrap, meaning that the overall space is toroidal.

3.7

In the current implementation, the whole world is 72 grid squares in length along each edge, and is populated by an initial population of 1,600 agents; test runs indicated that this produced a population density sufficient to yield interesting dynamics, whilst also allowing for reasonable running times. Certain aspects of the simulation had to be changed significantly from the Wedding Ring model once the toroidal surface was implemented. The original model had agents' spatial location recorded as their angular displacement along the ring; this meant that methods used for calculating spatial separation had to be amended. Similarly, default parameter settings for these methods were changed as the original settings were tuned for the one-dimensional case rather than a more diffuse population spread across a torus.

3.8

Secondly, accepting that micro-level interactions drive macro-level population dynamics means that ideally the relevant processes should be represented in the model. Hence, in order to make a stronger case for the utility of agent-based models in exploring the nature of contemporary population processes, we elected to make some significant changes to the formulation of Wedding Doughnut demographics. Mortality is thus no longer restricted to 100-year-old agents, as was the case in the original Wedding Ring; any agent can die at any time, subject to observed and forecasted death rates based on empirical data from the Human Mortality Database (2011). Also fertility patterns follow the empirical and forecasted birth rates for England and Wales obtained from the Office of National Statistics (ONS 1998) for the period 1951-1972, and from Eurostat (2011) thereafter. For future years, the rates were predicted using a variant of a standard bi-linear demographic model by Lee and Carter (1992). The initial population structure by age, sex, and marital status follows that of the 1951 population census for England and Wales, obtained from the Office for National Statistics (ONS).

3.9

The Wedding Doughnut also considers a broader definition of partnership that was present in the original Wedding Ring model - one that is not restricted to legal marriage. In this formulation the agents can be forming any cohabiting partnerships, as births often occur outside the bounds of a marital relationship. In addition, however, some 15.9% of births in the UK in 2011 were to single parents or parents living in separate addresses (ONS 2011); this fact is not currently addressed in this model and is an area for future refinement.

3.10

Given the current focus on the problems facing ageing populations, especially in developed countries, and particularly with respect to ever-increasing social care need, we also included a very simplistic model of health status in the Wedding Doughnut. This simple model allows us to demonstrate the potential utility of a scenario-based approach to policy-relevant problems. Thus, agents have a probability of transitioning into a state of 'ill health' which increases with age. We assume that once agents transition into the state of ill health - limiting long-term illness - they remain therein until they die. The annual transition probabilities for agents aged x years are arbitrarily assumed as:

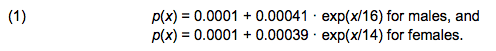
The additional parameters for males and females define a differential scaling of the age of the agents in order to allow for variation in care-need probabilities between the sexes.

Agent behaviour, record-keeping and simulation flow

3.11

The Wedding Doughnut model uses the same agent properties as applied in the Wedding Ring model, which has been discussed above. Additions were made in order to facilitate the placement of agents on the torus and their movement around that space. The agents' spatial locations are recorded as a set of (x,y) coordinates which places each of them on the 72-by-72 grid. Agents may change location if they form a partnership. Once a partnership is formed, the agents entering into this partnership will move together to a new location that lies between their initial positions. The distances between the original and the new locations are inversely proportional to the number of 'relevant others' in each agent's network—in this way, we aim at capturing the 'gravity' effect of their social ties. If the partnership produces children, these children will be placed at a grid location next to the partner agents, and that location is recorded in the agents' records.

3.12

For simplicity, we assume here that partnerships, once formed, cannot be dissolved, and that children can be born only within partnerships (and thus households). Within the model, the agents cannot form partnerships until they reach the age of 16. When an agent enters into a partnership, they establish a new, separately-located household with their partner, who then also 'leaves the parental home'.

3.13

The simulation outputs records of every birth, death, and partnership event in every time-step. These are supplemented with detailed records for members of the population; every agent is assigned a unique ID number at birth, and the simulation records their birth year, year of partnership formation (if they form one), the ID numbers of the partner and children, spatial location, health status, and year of death. These records can be cross-referenced with yearly records of the entire simulation to obtain a complete picture of any agent's life-course.

3.14

The Wedding Doughnut has been implemented in Repast Simphony v. 2.0, which is a Java-based environment for agent-based and simulation modelling. In this implementation, the simulation proceeds in a series of time-steps, each of which is equivalent to one year. Each run continues for 300 time-steps (double the 150 years in the original Wedding Ring model). This length of run allows us to examine longer-term population dynamics, whilst remaining reasonable from the point of view of computing time, even on a simple desktop machine (ca. 2-3 minutes per run on a 2.8 GHz Intel i7 quad-core processor). The first time-step corresponds to the calendar year 1951, and hence the simulation nominally extends to 2250, of which the first 60 years (1951-2011) are of particular interest due to the availability of data for this period.

3.15

During each time-step, a series of procedures are performed as the simulation updates:

1. All agents are aged one year;
2. For agents outside of partnerships:
   • For each agent, relevant others are identified;
   • Social pressure derived from relevant others is calculated;
   • Possible partners are selected, and
   • If a suitable partner is found, a partnership forms.
3. For agents in partnerships:
   • Fertility status is checked - some agents will give birth to their children.
4. For all agents:
   • Health status is checked - agents may transition into a state of ill health;
   • Mortality status is checked - some agents will die according to relevant age-specific probabilities.
5. Deceased agents are removed from the population, and newborn children are added.

3.16

In the course of these procedures, statistics are continually recorded in an overall summary file for the entire population, which records the numbers of yearly birth, death and partnership events in detailed agent logs for both the male and female populations, and in a hazard-rate file. The latter continually calculates the hazard rate of partnership across the population and outputs results every simulated decade with an overall output produced at the end of the simulation.

3.17

Space concerns preclude a complete description of every aspect of the model, but readers interested in replicating our work are directed to the model's OpenABM page mentioned in the Introduction.

Selected Results

The basic scenario of population dynamics

4.1

Starting from the 1951 structure by sex, age and marital status, we have propagated the demographic dynamics forward, obtaining the expected picture of an ageing population. Results presented in this section relate to the base scenario of health transitions, and have been obtained from an average of 250 runs of the simulation, in order to smooth out the randomness in the underlying patterns. The presentation is by necessity very selective, since the number of outcomes obtained from simulations is very high. In this section we present some of the results for the simulation year 2011, which we were able to compare with the most recent data provided by the UK Office for National Statistics. Figure 2 illustrates the overall population structure in the simulation, as well as in the ONS statistics for mid-2010. As expected, there are some structural differences due to not including migration in the simulation, but nevertheless the overall process of population dynamics matches the UK population data quite closely, which is not surprising given that it is based on empirical birth and death rates.

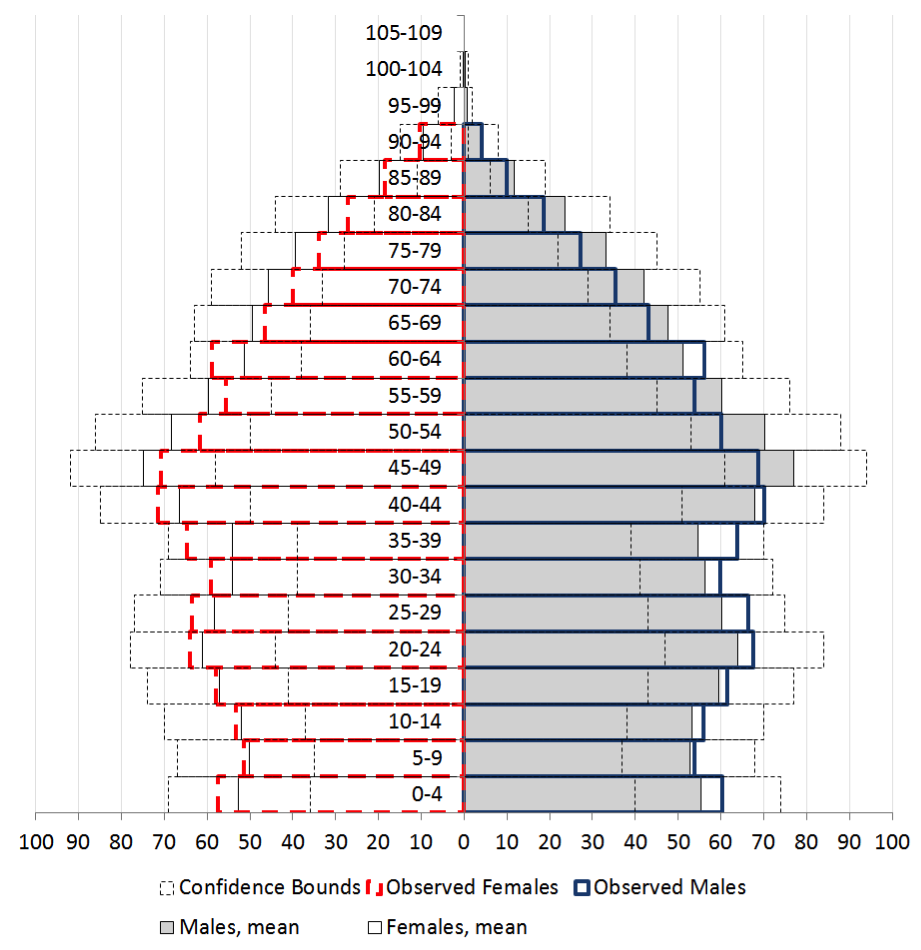
Figure 2. Population pyramid for the simulation year 2011, compared with the UK in mid-2010 Source (observed): Office for National Statistics, data rescaled to match the number of agents shown on the x axis

Descriptive sensitivity analysis: Hazard function for partnership formation

4.2

In terms of the sensitivity analysis, we have followed Billari et al. (2007) in our reimplementation. Figure 3 illustrates four examples of hazard functions for partnership formation obtained under different assumptions concerning the partner search process. These hazard functions were obtained for the whole simulation period, accumulating information for successive cohorts of agents until the simulation year 2250, and averaged for ten simulation runs. The solid line shows the hazard function resulting from our default settings of α = 1.3, β = 2.0, radius for choice of relevant others d = 25 grid units, and initial population of 1,600 agents. The dashed and dotted ones replicate some alternative scenarios from Billari et al. (2007: 72); with constant social pressure, set at a value of 0.2, constant age influence functions, set at 0.9, and with a small spatial distance of 10 units for choice of relevant others (Billari et al. 2007: 72). As compared to the original results, and to the empirical rates for one particular birth cohort (1958), the partnership formation of agents in this model is more concentrated in younger ages, in the Base settings being largely limited to the age group of 20-29-year-olds. This result suggests high sensitivity to parameterisation of the model, which is discussed in more detail below.

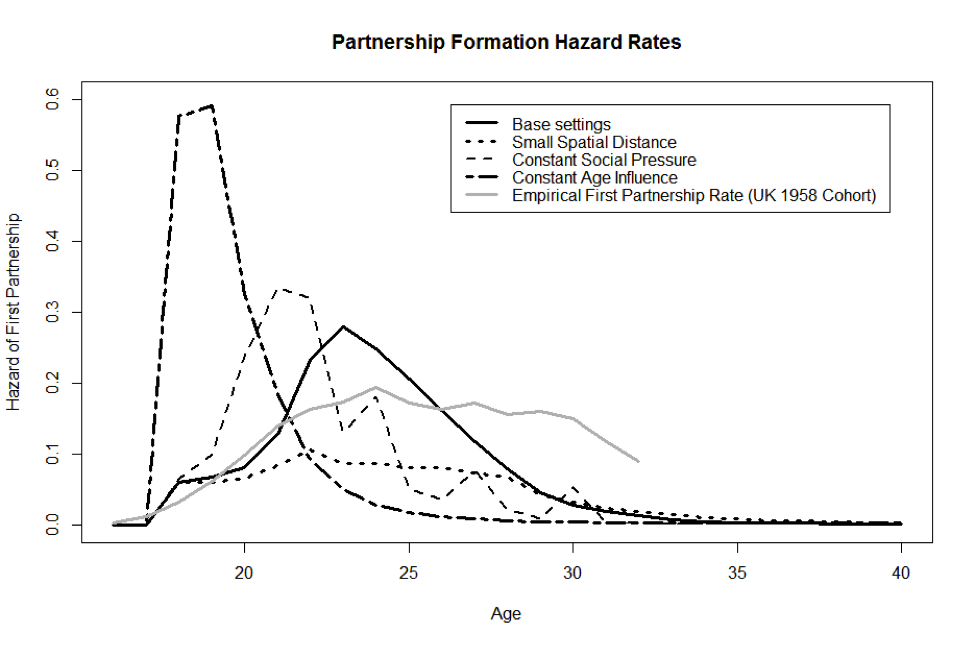
Figure 3. Hazard rates for partnership formation for the whole simulation (various assumptions) Source (empirical rates): Berrington & Diamond (2000)

4.3

The outcome presented above reinforces the view that the space in which the agents operate can influence the demographic patterns observed at the macro level. This notion is further examined in the following two subsections. First, the impact of space, this time on potential provision of care for ill agents, is discussed within a scenario framework. Subsequently, we examine the impact of distance of partner search on two outcomes - the share of ill agents with no healthy partner or children and the share of ever-partnered agents - by using a probabilistic sensitivity analysis, with the aim to locate the base parameter settings in a wider parameter space of our reimplementation of the model.

'What-if' scenario-setting: A stylised example

4.4

The results offered in this subsection illustrate the concept of 'linked lives', i.e., the benefits of working with simulated individuals that have meaningful connections to other specific individuals (see Noble et al. 2012 for discussion). With a few notable exceptions (e.g. Lelièvre et al. 1998), statistical demographic models usually do not capture the linked lives, as the focus is chiefly either on the analysis of population-level statistics, or on individual life-course trajectories. However, in this case the ABM foundations of the Wedding Doughnut model make some investigation of linked lives possible. Such analysis can be very valuable when examining scenarios for detailed policy-relevant research questions, as our example will demonstrate.

4.5

The current results are based on 250 runs of the model for three different health scenarios - one with the base probabilities of transitioning into illness; 'good health' with halved probabilities; and 'bad health' with doubled probabilities. In this stylised example, an overarching policy-relevant question is: how many of the individuals who develop a limiting long-term illness at some stage in their lives, will potentially have recourse to the help of their healthy partners or adult children (aged 16 or above). Hence, we are trying to assess in a joint modelling framework, both the demand for care, as well as the supply of care available from two groups of family members: partners and children, under different 'what-if' assumptions on the health transition probabilities. The gap between the demand and the supply indicates the extent of the care provision which would have to come from other sources - the state or other providers, either in the private or charitable sectors.

4.6

We note that our stylised example here is only concerned with the impact of these possible health scenarios on care availability. We do not seek to draw any causal link between partnership formation and health outcomes - to do so would require a vastly more detailed model of transitions into long-term limiting illness and of the processes which influence these transitions (see e.g. Verbrugge and Jette 1994).

4.7

Figure 4 presents selected average outcomes of a simple analysis of the three health scenarios for the simulation year 2011. The resultant share of ill agents was found ranging from 9% ('good health' scenario), through 16% (base scenario), to 26% ('bad health'). Notably, in the 'bad health' scenario the burden of care placed on the adult children was disproportionately higher than in two other cases, where the proportions of ill agents with an available healthy partner were much higher.

4.8

In addition to the above results, Fig. 5 shows the cumulative fraction of ill agents, by the distance to their nearest available healthy family member (partner or adult child). The figure cuts off at 50 grid units of distance, given that the maximum distance possible on a 72-by-72 torus is 36 x sqrt(2) = 50.91 grid units. One important observation here is that the differences between the three scenarios are much less pronounced when all available potential 'carers' at all distances are considered, rather than just the partners who live together with the ill agents at distance = 0. One possible interpretation can highlight the trade-offs between care provided by partners and children: in healthier populations, ill people are more likely to have healthy partners and do not have to resort to the help of their children. In this way, the 'care potential' of children is underutilised. On the other hand, a higher fraction of ill people implies a need for the 'all hands on deck' care provision.

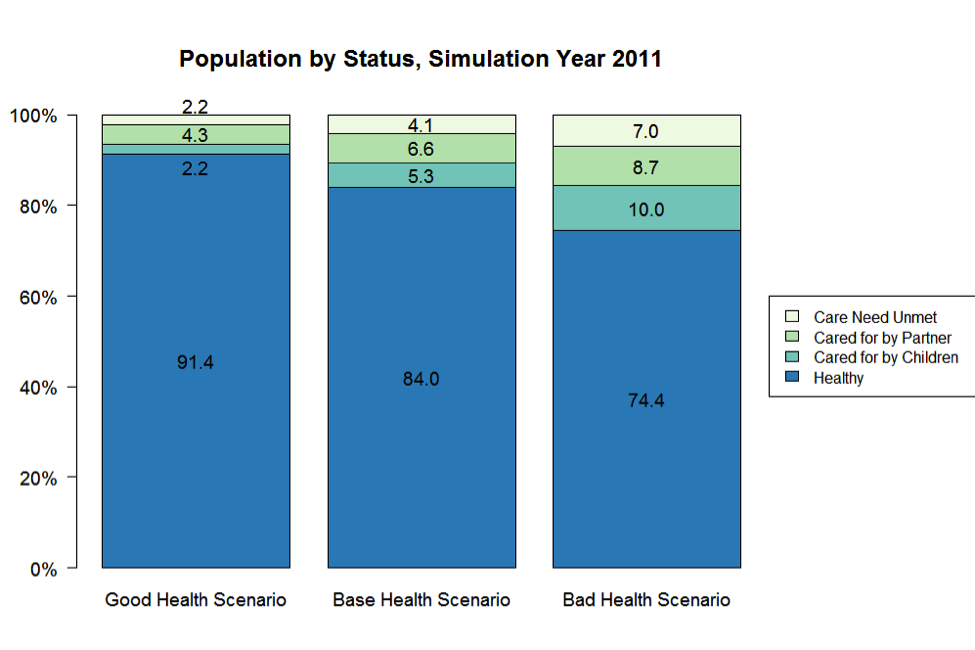
Figure 4. Health outcomes of the agents and their availability of care, simulation year 2011 Note: The percentages may not add up exactly to 100.0% due to rounding.

4.9

An interesting resultant policy problem becomes then, for example, whether and how to help balance the care provision between different generations in low-morbidity societies. This is exactly the type of policy-relevant question that can be explored by decision-makers who can interactively simulate the impacts of the various policy levers available to them. In that respect, it needs to be stressed that in line with the overall aim of this paper, the results of the above modelling exercise are mainly a proof-of-concept illustration of the scenario generation capabilities of the proposed methods, rather than providing any prescriptive policy recommendations. In particular, the scenarios presented in the above illustration are very simplistic, and leave out many aspects of the real processes and phenomena, for the sake of transparency of the presentation.

4.10

In future, more realistic extensions of the model, additional factors may include such aspects as the possibility of the agents' recovery, dissolution of partnerships, multiple states of health (and thus gradation of care needs), differential mortality by health status, willingness of agents to provide care, availability of closely-linked non-family members, etc. Nevertheless, even in such a simplified model as presented in this paper, we have managed to isolate the effects of family links and spatial distance on the interplay between care demand and supply, which differ between the health scenarios studied. Creating coherent micro-macro level scenarios was possible thanks to supplementing a traditional, data-based multi-state model of population dynamics with simple rules governing partnership formation and spatial mobility.

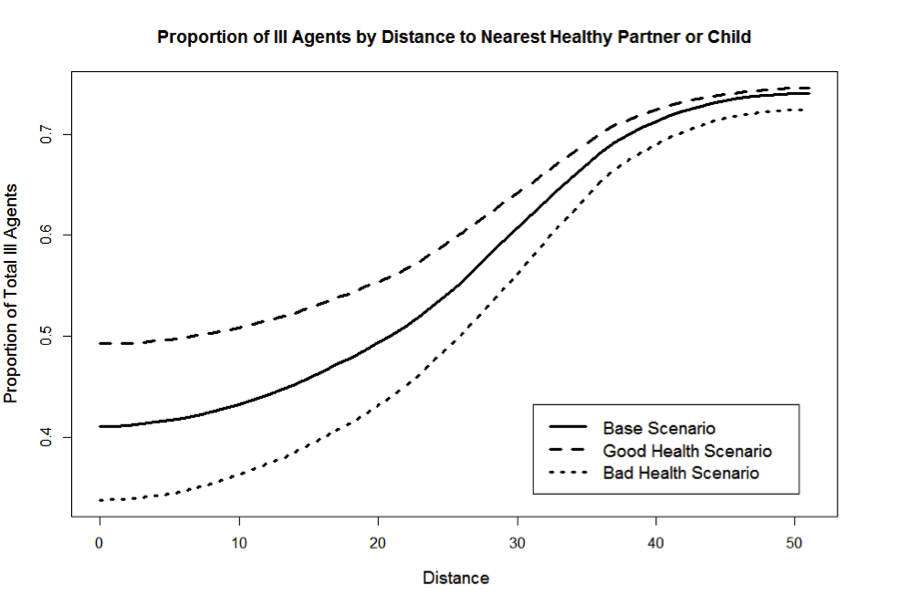
Figure 5. Cumulative availability of care for ill agents by distance, simulation year 2011

Health transition probability: A probabilistic sensitivity analysis

4.11

Analysing the impact of particular parameters in complex models is by no means an easy task. In particular, direct statistical analysis may not be possible due to various feedback effects present in the model. Nevertheless we wanted to illustrate the usefulness of exploring the parameter space of an ABM. Hence, in this paper we follow the ideas of the MUCM project (Managing Uncertainty in Complex Models, http://www.mucm.ac.uk), and build a statistical emulator of the model for a chosen model output and a selection of inputs. We propose that this approach further enhances this modelling framework by allowing for a more in-depth examination of model uncertainty and the impact of key model parameters.

4.12

In general, an emulator is effectively a statistical model (or a statistical approximation) of the base model, the latter also referred to as a simulator (O'Hagan 2006: 1290-1291). One choice of models for emulators are Gaussian processes, briefly summarised below, which are analysed within the Bayesian statistical framework in order to account for various sources of uncertainty in a coherent way. Amongst the main uses of emulators for complex models are uncertainty analysis - evaluation of how much uncertainty of the output is induced by a given set of inputs, as well as sensitivity analysis - analysis of relative importance of various inputs in explaining the variability of the given output (O'Hagan 2006).

4.13

Briefly, let the base model be denoted by a function f, which transforms a vector of n inputs of interest, x ∈ X ⊂ ℜⁿ, into a scalar output, y ∈ Y ⊂ ℜ, so that y = f (x). The Gaussian process emulator is then defined through a multivariate Normal distribution of a vector f of any p realisations of f (x _i), where i = 1, …, p (idem):

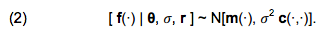
4.14

The elements of the mean vector m (⋅), m (x_i) = h(x_i)^T θ, are linear functions of x_i with regression coefficients θ, c(⋅,⋅) is a correlation matrix with elements c_ij (x_i, x_j) = exp{-(x_i -x_j)^T R (x_i -x_j)}, and R = diag(r ₁, …, r _n) is a diagonal matrix of roughness parameters r _k (Kennedy 2004: 2; see also Kennedy and O'Hagan 2001: 432-433). To complete the statistical specification of (2), the prior distributions for the parameters are assumed to be hardly informative, with p(θ,σ²) ∝ σ^-2. The roughness parameters r _k are here a priori assumed to follow independent exponential distributions with the parameter 0.01 (Kennedy 2004: 2). The parameters of the emulator are subsequently estimated by conditioning (2) on a set of simulation data Δ = {δ₁, …, δ _N } ⊂ X or, more precisely, on the related output data vector D = [f (δ₁), …, f (δ _N)] ^T ∈ ℜ ^N (Kennedy 2004).

4.15

As noted by Kennedy (2004), there may be some variability in the model code itself, and thus runs may yield non-deterministic outcomes. To allow for such instances, an additional variance term (called a nugget) can be included in calculating the posterior distribution of the emulator function f given the simulation data D, which posterior distribution itself has a marginal multivariate Student's t density (Kennedy 2004: 3). A more detailed statistical theory underlying the estimation of Gaussian process emulators is provided by Kennedy and O'Hagan (2001), Oakley and O'Hagan (2002), and Kennedy (2004).

4.16

More in-depth statistical treatment of the sensitivity analysis, in turn, has been offered by Oakley and O'Hagan (2004). In short, their approach, which is also followed in this paper, assumes that the variance of the output variable y can be decomposed into a constant (mean) term, a series of n main effects related to particular inputs x₁, …, x_n, a series of ((n -1)n)/2 two-term interaction effects for all pairs of inputs (x_i, x_j) such that i < j, and so on, up to a single n -term interaction effect for (x₁, …, x_n). These mean effects are denoted by 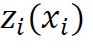, and the respective interaction terms by 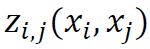, , 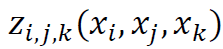…, 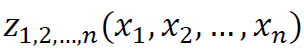(idem: 752-753). Assuming mutual independence of the elements of X, the variance of y can be then decomposed into terms corresponding to the main effects and various interaction effects (idem: 754):

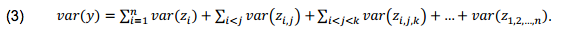
4.17

The probabilistic sensitivity analysis therefore aims to identify, how much of the total variance in the output y can be attributed to particular inputs x_i, as well as to their various interactions.

4.18

In our illustration, the analysis focuses on four model inputs. One of them, the parameter a, regulates the exponential function governing the health transition probability (1). Here, this function is parametrised as p(x) = c + a exp(x/k), constrained to p(x) ≤ 1, where k is a constant age scaling factor, and a is the main component of the transition probability. The baseline constant c has not been specifically considered here, since it anyway becomes very heavily dominated by the exponential component of (1). Similarly, we do not vary the sex-specific age scaling constants k, because preliminary analysis have indicated it had very little bearing on our outcome, and holding it constant allowed us to learn more about the other parameters. In the model, differential values of a for both sexes are implemented as (a +0.00001) and (a -0.00001), respectively for males and females.

4.19

The second and third parameters, α and β, are related to the social pressure function s(r) defined by Billari et al. (2007: 66) as:

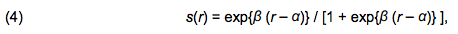
where r is the proportion of agents with partners in a particular agent's group of relevant others. Finally, the fourth parameter denotes spatial distance of partner search, d. In our example, the general formula applied for a Cartesian distance between two points, (x₁,y₁) and (x₂,y₂), on the torus (Doughnut) is as follows:

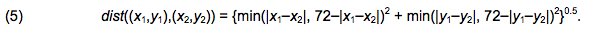
4.20

In terms of the input values of the parameters used to construct the emulator, we have pre-set a Cartesian product C = a′ × α′ × β′ × d′, whereby α′ = [0.0002, 0.0004, 0.0006, 0.0008] ^T, α′ = [0, 0.4375, 0.8750, 1.3125, 1.7500] ^T, β′ = [exp(-1), exp(0.5), exp(2), exp(3.5), exp(5.0)] ^T, and d′ = [10, 231/3, 362/3, 50] ^T.

4.21

The output variable, y, was set to be a logit of the share u of ill agents without a healthy partner or adult children. The logit transformation y = ln(u) / (1-ln(u)) was applied to ensure that the values of u = expit(y) remain bounded by 0 and 1. For the analysis, the outputs were standardised to a form with zero mean and unitary variance. We have assumed a priori that all inputs are normally distributed, and that the mean of the Gaussian process (2) is a linear function of its inputs. In order to account for uncertainty resulting from non-deterministic character of the model, we have also allowed an additional error term (nugget) for the code uncertainty.

4.22

The analysis was executed in a specialised software GEM-SA (Gaussian Emulation Machine for Sensitivity Analysis) version 1.1, written by Marc Kennedy and Anthony O'Hagan (Kennedy, 2004; O'Hagan 2006, and available from http://ctcd.group.shef.ac.uk/gem.html, as of 30 April 2013) A single run of the algorithm took a few minutes in a similar hardware setting to the one discussed in the previous section.

4.23

The uncertainty analysis resulted in a computed emulator mean of y = 0.2167, corresponding to on average u = 55.4% ill agents with no healthy partner or children, with the emulator-related variance calculated as 0.00035. The total output variance in y induced by input uncertainties was very high, being estimated as 1.525. This indicates very high variability of the output variable y across the analysed fragment of the parameter space. The roughness matrix R has been computed as R = diag(12.140, 9.223, 2.469, 0.000). The sensitivity analysis indicates that, out of the four inputs considered, the two components of the social pressure function α and β account for 29.8% and 48.6% of the variability, respectively. Relationship between these two parameters and the emulated mean for y is shown in Fig. 6 for α ∈ [0, 1.75] and β ∈ [exp(-1), exp(5)]. In this case, the spatial distance parameter d and the main component of the transition probability a do not have much impact on the share of ill agents without a healthy partner or adult children.

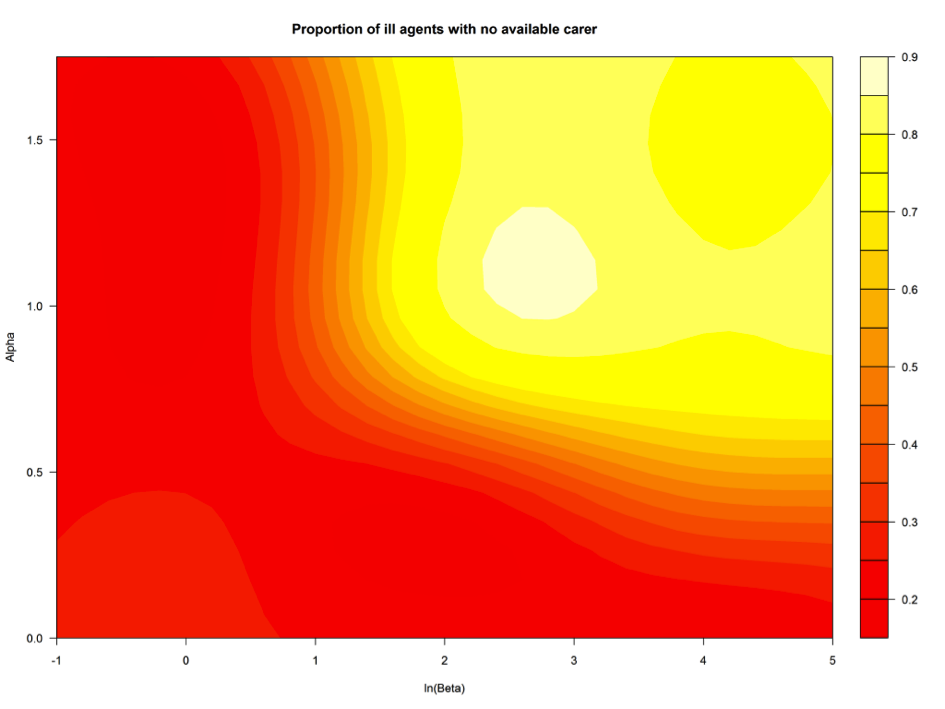
Figure 6. Share of ill agents with no healthy partner or adult children by social pressure parameters, simulation year 2011

4.24

In a similar vein, we have built another emulator for the proportion of agents who have ever had a partner, q, just to see an overlap of the plausible parameter subspace with the outcome shown in Fig. 6, and to explain the hazard functions reported in the previous section. Given that partnership formation does not depend on health, this time we have used a the following design space: C^* = α″ × β″ × d″, where α″= [0, 0.3333, 0.6667, 1, 1.3333, 1.6667, 2] ^T, β″= [exp(-1), exp(0), exp(1), exp(2), exp(3), exp(4), exp(5)] ^T, and d″ = [7, 14, 21, 28, 35, 42, 49] ^T. The output variable, v, was set to be a logit of the share of ever-partnered agents, q. As before, the outputs were standardised, and we have assumed the same types of a priori distributions as in the case of ill agents without potential carers. The outcomes are shown in Fig. 7 providing a clear link, and indicating important trade-offs between the availability of care to ill agents and the general propensity of entering into partnerships in the artificial population studied.

4.25

This time, the uncertainty analysis resulted in a computed emulator mean of v = 0.2102, corresponding to on average q = 55.2% agents over 16 who have ever had a partner, compared to the empirical value of 74.2% calculated from the 2011 census. Again, this substantial difference is not surprising given that we are looking at mean across the parameter space; as we shall see many areas of the space are unrealistic. The emulator-related variance has been estimated as 0.0006, and the total output variance in v again being very high, amounting to 2.3411. Once more, the two components of the social pressure function, α and β, were found most important, accounting for 30.2% and 45.6% of the variability respectively, with their interaction accounting for 17.17% of the remaining variance. The spatial distance parameter contributes here only to 1.26% of the total variability of the output variable v.

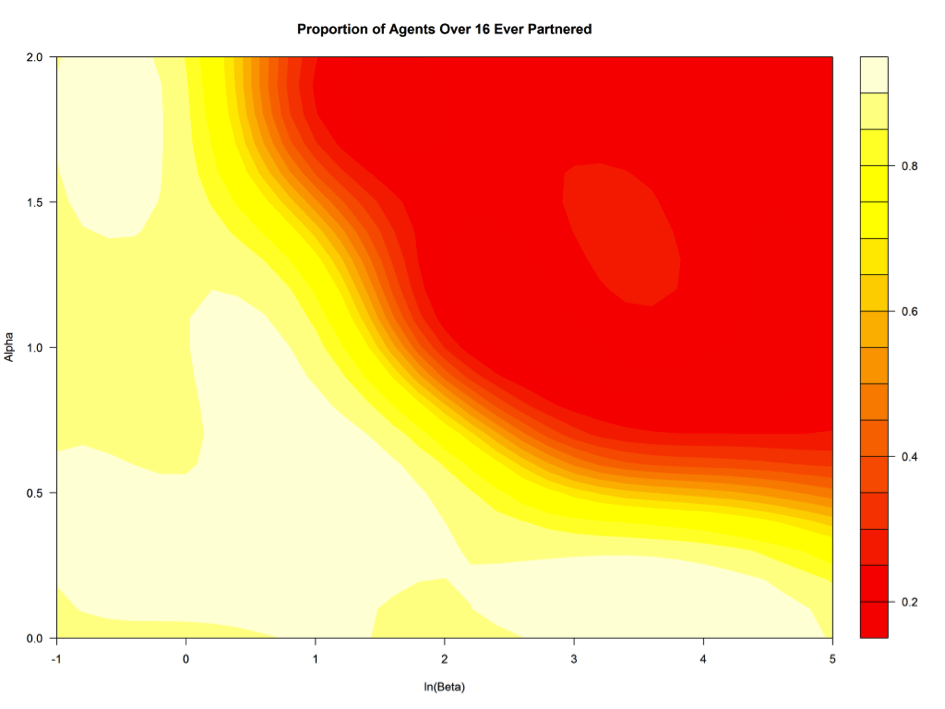
Figure 7. Share of agents 16+ who have ever had a partner by social pressure parameters, simulation year 2011

4.26

The emulator results shown in Figures 6 and 7 illustrate the links between the partnership formation and health care availability in the model, and also enable to position and interpret the parameters used for generation of scenarios reported in the previous section. These scenarios assumed α = 1.3 and β = 2, hence, ln(β) = 0.70. In Fig. 6 this setting corresponds to about 25-30% of ill agents without healthy partners or children, which is consistent with the results reported in Fig. 5, exact to the emulator fit. The same parameter setting is also related to reasonable rates of ever-partnered agents - over 70%, as indicated in Fig. 7, which is directly comparable with the empirical rate of 74.2%, reported by the Office for National Statistics for mid-2011. Figures 6 and 7 indicate clear relationships between the two outputs: high levels of partnership formation correspond to low proportions of ill agents without kin available for providing care, and vice versa. Hence, the default scenarios reported above match the selected empirical outcome variable closely, even though the underlying hazard functions, illustrated in Figure 3, do not match exactly rates for the 1958 birth cohorts.

4.27

In a similar spirit, the statistical emulators discussed in this section allow for a thorough exploration of the model parameter space in the context of various policy goals (e.g. minimising the share of agents without access to informal care) and constraints (e.g. realistic partnership and childbearing patterns). A natural extension of this approach would thus consist of a full, stakeholder-driven decision analysis which, despite being outside of the scope of the current paper, remains high on the agenda of the Care Life Cycle project as a whole.

Conclusion

5.1

The model presented in this paper represents a substantive step toward the integration of statistical demographic methods with agent-based modelling. The use of empirical data and Lee-Carter projections for mortality and fertility has enabled us to produce a more detailed and data-driven agent-based model, while avoiding the problem of data-overdependence that often presents a challenge for demographers. The addition of statistical emulators for sensitivity analysis has allowed us to produce an in-depth examination of possible output scenarios, which has illuminated the effects of key model parameters. We contend that this combination of elements moves us closer to a scenario-based computational demography, which provides a platform for exploratory study of policy-relevant problems.

5.2

This example model and the analyses presented above demonstrate several features of combined agent-based and statistical modelling, which may be potentially appealing to both demographers and to the social simulation community. Firstly, such models enable studying the linked lives of individuals at various levels, in a similar way as do more traditional micro-simulation models, but also including explicit statements about the behavioural assumptions being applied to those individuals, as suggested by Murphy (2003). Secondly, the analysis can be easily embedded in social or physical spaces, which is one of the important contributions of social simulation. Thirdly, the mixed approach allows for overcoming some data-related limitations, augmenting the available statistical information with assumptions on behavioural rules. Fourthly, statistical emulators enable exploration of the parameter space of the underlying agent-based models. These features allow for a greater extensibility of the agent-based model, though at a price of departing from the entirely data-driven paradigm.

5.3

In methodological terms, the findings suggest that demography as a discipline has scope for including more elements of 'model-based science' as a potential tool for conceptual theory building (Burch 2003a; Godfrey-Smith 2006), whilst still remaining empirically-relevant. This would facilitate further incremental progression of demography as a domain of scientific inquiry, through building theory-generating demographic models. Such an eclectic approach would also help overcome one of the main limitations of the current practice - over-reliance on purely statistical information at the expense of theories and mechanisms, and generating very large and increasing requirements for data to feed into large-scale models (Silverman et al. 2011). On the other hand, for the practical applications in the area of social simulation, the potential benefits consist of as much alignment with empirical evidence as practicable.

5.4

Of course, the presented model, itself being an extension of Billari et al. (2007), is far from being comprehensive, as indicated by trade-offs between different values of various outputs that can be seen as reasonable. As such, the model is still well-positioned for a number of possible extensions. As mentioned before, the included model of health status is illustrative and demonstrates patterns we expect to see in real populations, but the model itself is highly simplistic and thus cannot reflect the true complexity of relationships between ageing and health. One possible extension of this aspect would be to incorporate empirical data on long-term limiting illness in the UK. In addition, the model of partnership formation here does not produce ideal hazard rates, and does not allow for same-sex partnerships or the dissolution of partnerships. Finally, while agents have the ability to shift position on the Doughnut, they only do so when a partnership is formed; incorporating more sophisticated agent behaviours would allow us to investigate the effects of within-country migration and similar phenomena. Still, following the ideas of Franck (2002) and Burch (2003a), we believe that models do not need to provide a perfect representation of reality to be useful, as long as they capture the main functions of the systems under study. In our case, we have illustrated some of the mechanisms through which the partnership formation process can translate into provision of informal care, and have identified the most important features (parameters) of this process.

5.5

On the other hand, the current model already provides an example of the power and utility of a combined demography-social simulation approach. We propose that incorporating demographic data and methods into an agent-based framework can produce models which have a stronger link to empirical data and thus to real human society - which is a useful step forward for social simulation. At the same time, such methods can produce useful demographic knowledge without relying on enormous, expensive data-sets - which is a boon for demographers. This combined approach - when coupled with rigorous sensitivity analysis, as provided here by statistical emulation techniques - gives us a robust starting point for agent-based demography.

5.6

The most significant future methodological challenge remains model validation. Given the complexity of the underlying model and the involved non-linearities, this task is non-trivial and extends far beyond the scope of this paper. The use of statistical emulators for exploring the properties of complex computational models is a first step in that direction. Nevertheless, if successful, such an approach would help bring the statistical and simulated individuals (Courgeau 2012) not only closer to each other, but closer also to the actual members of the population under study.

Acknowledgements

This work was supported by the Engineering and Physical Sciences Research Council (EPSRC) grant EP/H021698/1 "Care Life Cycle", funded within the 'Complexity Science in the Real World' theme. Fragments of this paper have been first presented as Silverman et al. (2012), and demographic extensions are offered in Bijak (2013). The authors are grateful to Daniel Courgeau and Frans Willekens for stimulating discussions, which helped shape the methodological exposition, as well as to anonymous reviewers, whose comments were really inspiring and challenging, and helped improve the earlier draft. All the remaining errors and omissions are exclusively ours.

References

APARICIO-DIAZ, B., Fent, T., Prskawetz, A. & Bernardi, L. (2011). Transition to Parenthood: The Role of Social Interaction and Endogenous Networks. Demography, 48(2): 559-579. [doi:10.1007/s13524-011-0023-6]

AXELROD, R. (1984). The Evolution of Cooperation, New York: Basic Books.

AXTELL, R.L., Epstein, J.M., Dean, J.S., Gumerman, G.J., Swedlund, A.C., Harberger, J., Chakravarty, S., Hammond, R., Parker, J. & Parker, M. (2002). Population Growth and Collapse in a Multi-Agent Model of the Kayenta Anasazi in Long House Valley. Proceedings of the National Academy of Sciences, Colloquium 99(3): 7275-7279. [doi:10.1073/pnas.092080799]

BENENSON, I., Omer, I. & Hatna, E. (2003). Agent-Based Modeling of Householders' Migration Behaviour and Its Consequences. In: Billari, F. and Prskawetz, A. (eds.), Agent-Based Computational Demography: Using Simulation to Improve Our Understanding of Demographic Behaviour. Heidelberg: Physica Verlag. (pp. 97-115). [doi:10.1007/978-3-7908-2715-6_6]

BERNARDI, L. (2003). Channels of social influence on reproduction, Population Research and Policy Review, 22(5-6): 527-555. [doi:10.1023/b:popu.0000020892.15221.44]

BERNARDI, L., Keim, S., & von der Lippe, H. (2007). Social Influences on Fertility: A Comparative Mixed Methods Study in Eastern and Western Germany. Journal of Mixed Methods Research, 1: 23-47. [doi:10.1177/2345678906292238]

BERRINGTON, A., & Diamond, I. (2000). Marriage or cohabitation_: a competing risks formation analysis of first-partnership among the 1958 British birth cohort. Journal of the Royal Statistical Society, Series A, 163(2): 127-151. [doi:10.1111/1467-985X.00162]

BIJAK, J. (2010). Forecasting International Migration in Europe: A Bayesian View. Springer Series on Demographic Methods and Population Analysis, vol. 24. Dordrecht: Springer.

BIJAK, J., Hilton, J., Silverman, E. & Cao, V. D. (2013). Reforging the Wedding Ring: Exploring a Semi-Artificial Model of Population for the United Kingdom with Gaussian process emulators. Demographic Research, 29(27): 729-766. http://www.demographic-research.org/volumes/vol29/27/29-27.pdf [doi:10.4054/DemRes.2013.29.27]

BILLARI, F., Aparicio Diaz, B., Fent, T. & Prskawetz A. (2007). The "Wedding-Ring". An agent-based marriage model based on social interaction. Demographic Research, 17(3): 59-82. http://www.demographic-research.org/Volumes/Vol17/3/17-3.pdf [doi:10.4054/demres.2007.17.3]

BILLARI, F., Fent T., Prskawetz A. & Scheffran J. (eds.) (2006). Agent-Based Computational Modelling: Applications in Demography, Social, Economic and Environmental Sciences. [doi:10.1007/3-7908-1721-X]

Heidelberg: Physica Verlag.

BILLARI, F. & Prskawetz, A. (eds.) (2003), Agent-Based Computational Demography: Using Simulation to Improve Our Understanding of Demographic Behaviour. Heidelberg: Physica Verlag. [doi:10.1007/978-3-7908-2715-6]

BILLARI, F.C. (2006). Bridging the gap between micro-demography and macro-demography. In: Caselli, G., Vallin J., and Wunsch, G. (eds.) Demography: analysis and synthesis, Vol 4. New York: Academic Press / Elsevier (pp. 695-707).

BÜHLER, Ch. and Fratczak, E. (2007). Learning from others and receiving support: the impact of personal networks on fertility intentions in Poland. European Societies, 9(3): 359-382. [doi:10.1080/14616690701314101]

BURCH, T. (2003a). Demography in a new key: A theory of population theory. Demographic Research, 9(11): 263-284. http://www.demographic-research.org/Volumes/Vol9/11 [doi:10.4054/DemRes.2003.9.11]

BURCH, T.K. (2003b). Data, Models, Theory and Reality: The Structure of Demographic Knowledge. In: Billari, F. and Prskawetz, A. (eds.), op. cit. (pp. 19-40). [doi:10.1007/978-3-7908-2715-6_2]

CEDERMAN, L.-E. (1997). Emergent Actors in World Politics: How States and Nations Develop and Dissolve. Princeton, NJ: Princeton University Press.

COURGEAU, D. (2007). Multilevel Synthesis: From the Group to the Individual. Springer Series on Demographic Methods and Population Analysis, vol. 18. Dordrecht: Springer.

COURGEAU, D. (2012). Probability and Social Science. Methodological Relationships between the two Approaches. Methodos Series, vol. 10. Dordrecht: Springer. [doi:10.1007/978-94-007-2879-0]

DIEKMANN, A. (1989). Diffusion and survival models for the process of entry into marriage. Journal of Mathematical Sociology, 14(1): 31-44. [doi:10.1080/0022250X.1989.9990042]

EPSTEIN, J. M. (2008). Why model? Journal of Artificial Societies and Social Simulation, 11(4),12 http:// jasss.soc.surrey.ac.uk/11/4/12.html‎.

EUROSTAT (2011). Eurostat Statistics Database; Domain Population and Social Conditions. Retrieved from http://epp.eurostat.ec.europa.eu on 27/10/11

FRANCK, R. (ed.) (2002). The explanatory power of models. Bridging the gap between empirical and theoretical research in the social sciences. Dordrecht: Kluwer Academic Publishers. [doi:10.1007/978-1-4020-4676-6]

GEARD, N., McCaw, J. M., Dorin, A., Korb, K. B. & McVernon, J. (2013) Synthetic Population Dynamics: A Model of Household Demography. Journal of Artificial Societies and Social Simulation, 16(1): 8, https://www.jasss.org/16/1/8.html.

GILBERT, N. & Troitzsch, K.G. (2005). Simulation for the Social Scientist. 2nd ed. Maidenhead: Open University Press.

GODFREY-SMITH, P. (2006). The strategy of model-based science. Biology and Philosophy, 21(5): 725-740. [doi:10.1007/s10539-006-9054-6]

GRIM, P., Thomas, S.B., Fisher, S., Reade, C., Singer, D.J., Garza, M.A., Frye, C.S. & Chatman, J. (2012). Polarization and Belief Dynamics in the Black and White Communities: An Agent-Based Network Model from the Data. In: Artificial Life XIII: Proceedings of the Thirteenth International Conference, MIT Press: Cambridge, MA, USA (pp. 186-193). Retrieved from http://mitpress.mit.edu/books/artificial-life-13 on 14/10/13. [doi:10.7551/978-0-262-31050-5-ch026]

HAJNAL, J. (1955). The prospects for population forecasts. Journal of the American Statistical Association, 50(270): 309-322. [doi:10.1080/01621459.1955.10501267]

HEILAND, F. (2003). The Collapse of the Berlin Wall: Simulating State-Level East to West German Migration Patterns. In: Billari, F. and Prskawetz, A. (eds.), op. cit. (pp. 73-96). [doi:10.1007/978-3-7908-2715-6_5]

HERNES, G. (1972). The Process of Entry into First Marriage. American Sociological Review, 37(2): 173-182. [doi:10.2307/2094025]

HILLS, T. & Todd, P. (2008). Population Heterogeneity and Individual Differences in an Assortative Agent-Based Marriage and Divorce Model (MADAM) Using Search with Relaxing Expectations. Journal of Artificial Societies and Social Simulation, 11(4),5 http:// jasss.soc.surrey.ac.uk/11/4/5.html‎.

HUMAN Mortality Database. (2011). Human Mortality Database. Retrieved from http://www.mortality.org/cgi-bin/hmd on 26/07/11.

KENNEDY, M. (2004). Description of the Gaussian process model used in GEM-SA. Software manual. Retrieved from http://ctcd.group.shef.ac.uk/gem.html on 23/05/12.

KENNEDY, M., O'Hagan, T. (2001). Bayesian Calibration of Computer Models. Journal of the Royal Statistical Society, Series B, 63(3): 425-464. [doi:10.1111/1467-9868.00294]

KEYFITZ, N. (1971). Models. Demography, 8(4): 571-580. [doi:10.2307/2060692]

KEYFITZ, N. (1981). The limits of population forecasting. Population and Development Review, 7(4): 579-593. [doi:10.2307/1972799]

KNIVETON, D., Smith, Ch. & Wood, S. (2011). Agent-based model simulations of future changes in migration flows for Burkina Faso. Global Environmental Change, 21 (Suppl. 1): S34-S40. [doi:10.1016/j.gloenvcha.2011.09.006]

LEE, R. D. & Carter, L. R. (1992). Modeling and Forecasting U.S. Mortality. Journal of the American Statistical Association, 87(419): 659-671. [doi:10.1080/01621459.1992.10475265]

LELIÈVRE, É., Bonvalet C. & Bry X. (1998). Event History Analysis of Groups. Findings of an On-Going Research Project. Population-English edition, 10: 11-38.

MURPHY, M. (2003). Bringing Behavior Back into Micro-Simulation: Feedback Mechanisms in Demographic Models. In: F. Billari and A. Prskawetz (eds.), op. cit. (pp. 159-174). [doi:10.1007/978-3-7908-2715-6_9]

NOBLE, J., Silverman, E., Bijak, J., Rossiter, S., Evandrou, M., Bullock, S., Vlachantoni, A. & Falkingham, J. (2012). Linked lives: the utility of an agent-based approach to modelling partnership and household formation in the context of social care. In Laroque, C., Himmelspach, J., Pasupathy, R., Rose, O. & Uhrmacher, J.M. (Eds.), Proceedings of the 2012 Winter Simulation Conference. IEEE. http://ieeexplore.ieee.org [doi:10.1109/wsc.2012.6465264]

OAKLEY, J. & O'Hagan, A. (2002). Bayesian inference for the uncertainty distribution of computer model outputs. Biometrika, 89(4), 769-784. [doi:10.1093/biomet/89.4.769]

OAKLEY, J. & O'Hagan, A. (2004). Probabilistic sensitivity analysis of complex models: a Bayesian approach. Journal of the Royal Statistical Society, Series B, 66(3), 751-769. [doi:10.1111/j.1467-9868.2004.05304.x]

O'HAGAN, A. (2006). Bayesian analysis of computer code outputs: A tutorial. Reliability Engineering and System Safety, 91(10-11): 1290-1300. [doi:10.1016/j.ress.2005.11.025]

ONS (1998). Birth Statistics. Series FM1 (27), London: Office for National Statistics.

ONS (2011). Characteristics of Mother 1, England and Wales. London: Office for National Statistics. Retrieved from http://www.ons.gov.uk/ons/rel/vsob1/characteristics-of-Mother-1--england-and-wales/2011/index.htmlon 21/03/2013.

SCHELLING, T. (1978). Micromotives and Macrobehavior. Norton, New York, USA.

SILVERMAN, E., Bijak, J. & Noble, J. (2011) Feeding the Beast: Can Computational Demographic Models Free Us from the Tyranny of Data? In: Lenaerts, T., Giacobini, M., Bersini, H., Bourgine, P. , Dorigo, M. and Doursat, R. (eds.) Advances in Artificial Life, ECAL 2011, MIT Press, Cambridge MA, USA (pp. 747-754).

SILVERMAN, E., Bijak, J., Noble, J., Cao, V. & Hilton, J. (2012) Semi-Artificial Models of Population: Connecting Demography with Agent-Based Modelling. Paper for the 4th World Congress on Social Simulation, Taipei, Taiwan, 4-7 September 2012.

SILVERMAN, E. & Bullock, S. (2004). Empiricism in Artificial Life. In Artificial Life IX: Proceedings of the Ninth International Conference, MIT Press: Cambridge, MA, USA (pp. 534-539).

SILVERMAN, E. & Bryden, J. (2007). From artificial societies to new social science theory. In: Almeida e Costa, F., Rocha, L.M., Costa, E., Harvey, I. and Coutinho, A. (eds.) Advances in Artificial Life, 9th European Conference, ECAL 2007 Proceedings. Berlin-Heidelberg: Springer (pp. 645-654). [doi:10.1007/978-3-540-74913-4_57]

TODD, P.M., Billari, F.C. & Simão, J. (2005). Aggregate age-at-marriage patterns from individual mate-search heuristics. Demography, 42(3): 559-574.

VERBRUGGE, L.M., & Jette, A.M. (1994). The disablement process. Social Science and Medicine, 38(1): 1-14. [doi:10.1016/0277-9536(94)90294-1]

VLACHANTONI, A., Shaw, R., Willis, R., Evandrou, M., & Luff, J. F. R. (2011). Measuring unmet need for social care amongst older people. Population Trends 145: 60-76. [doi:10.1057/pt.2011.17]

WILLEKENS, F. (1990). Demographic forecasting; state-of-the-art and research needs. In: Hazeu, C.A. and Frinking, G.A.B. (eds.), Emerging issues in demographic research. Amsterdam: Elsevier (pp. 9-66).

WILLEKENS, F. (2005). Biographic forecasting: bridging the micro-macro gap in population forecasting. New Zealand Population Review, 31(1): 77-124.

WILLEKENS, F. (2012) Migration: A perspective from complexity science. Paper for the Migration workshop of the Complexity Science for the Real World (CSRW) network, Chilworth, UK, 16 February 2012.

WRIGHT, G. & Goodwin, P. (2009). Decision making and planning under low levels of predictability: Enhancing the scenario method. International Journal of Forecasting, 25(4): 813-825. [doi:10.1016/j.ijforecast.2009.05.019]

YABIKU, S. T. (2006). Neighbors and neighborhoods: effects on marriage timing. Population Research and Policy Review, 25(4): 305-327. [doi:10.1007/s11113-006-9006-5]

ZINN, S., Gampe, J., Himmelspach, J. & Uhrmacher, A. M. (2009). MIC-CORE: a tool for microsimulation. In: Rossetti, M.D., Hill, R.R., Johansson, B., Dunkin, A. and Ingalls, R.G. (eds.) Proceedings of the 2009 Winter Simulation Conference. IEEE (pp. 992-1002). http://ieeexplore.ieee.org