Abstract

In this article a multi-agent system is presented which generates melody pitch sequences with a hierarchical structure. The agents have no explicit melodic intelligence and generate the pitches as a result of artificial emotional influence and communication between agents, and the melody's hierarchical structure is a result of the emerging agent social structure. The system is not a mapping from multi-agent interaction onto musical features, but actually utilizes music for the agents to communicate artificial emotions. Each agent in the society learns its own growing tune during the interaction process. Experiments are presented demonstrating that diverse and non-trivial melodies can be generated, as well as a hierarchical musical structure.

Keywords:

Social Networks, Music, Emotion

Introduction

1.1

The generation of novel music is at the heart of many computer-aided composition (CAC) systems. Without some way of generating new material, a CAC will churn out the same material time after time. To avoid this, many systems utilize random numbers. A more recent alternative is the generation of complex structures which are ordered but unpredictable. Popular types of systems that generate structures with such complexity are found in the field of artificial life or A-Life (Brown 2002). A-Life investigates systems related to life, their processes, and evolution; it does this most often through computer simulations and models – for example cellular automata. Many A-life systems have two elements in common with have made them attractive to composers for use in CAC: they generate complex data with order and structure, and they inspire composers by the variety of patterns in the data (Panzarasa & Jennings 2006). So although A-Life systems can generate unexpected behaviour, there is an inherent order – they are not solely random. This is often called emergent behaviour.

1.2

One field which has a large intersection with artificial life is multi-agent systems (MAS), which is one of the 2 key areas utilized in this article. Each agent in an MAS is a digital entity which can interact with other agents to solve problems as a group, though not necessarily in an explicitly co-ordinated way. What often separates agent-based approaches from normal object-oriented or modular systems is their emergent behaviour (Dahlstedt & McBurney 2006). The solution of the problem tackled by the agents is often generated in an unexpected way due to their complex interactional dynamics, though individual agents may not be that complex. As with the application of other A-Life systems in CAC, these social dynamics can be both artistically functional – for example each agent in an ensemble can contribute a motif or play an artificial instrument in a piece of music; or artistically motivational, inspiring an algorithmic composer to produce the music of artificial societies.

1.3

In this article a multi-agent system is presented which generates melody pitch sequences with a hierarchical structure. The agents have no explicit melodic intelligence and generate the pitches as a result of artificial emotional influence and communication between agents, and the music's hierarchical structure is a result of the emerging agent social structure. Another key element is that the system is not a mapping from multi-agent interaction onto musical features, but actually utilizes music for the agents to communicate artificial emotions. Each agent in the society learns its own growing tune during the interaction process.

Related Work

2.1

A number of systems with similarities to the one in this paper are now examined in detail. Before doing that, a brief overview of more general multi-agent music systems is given using Table 1. These are not examined in detail but the table is designed to give quick familiarity with a number of key issues found in musical multi-agent systems. The fields will now be explained. Complexity describes the level of processing in individual agents, how complex are they? Homog / Het indicates whether the agents in the MAS are homogeneous or heterogeneous – i.e. do agents all start out the same, or are some different? Comm indicates whether the agents communicate, and if so do they do it synchronously or asynchronously; i.e. do they take it in turns to communicate and process, or do they do it concurrently? Initial Hierarchy describes whether there is a hierarchy of planning/control for the agents; are some agents dependent on others? Can some agents control others? Tune indicates whether the system generates multiple composition alternatives when it completes processing, or a single composition. Real-time describes whether when the agents are activated, the music generated in real-time. Size gives – where available and relevant – the number, or average number, of agents in the system. Finally Model / Func indicates whether the system is designed solely to model some element of music, or as a computer-aided composition system. Many of the above properties are also key defining features of non-musical MAS.

2.2

The system in this article is a non-realtime system which works with a small to medium number of agents – i.e. not hundreds of agents, it generates multiple tunes in parallel, and it is focused on computer-aided composition not on modelling the composition process or musical culture.

Table 1: Musical Multi-Agent Systems
System	Complexity	Homog / Het	Comm	Tune	Initial Hierarchy	Real time	Size	Model / Func
Swarm Music (Blackwell & Bentley 2002)	Low	Het	No	1	Flat	Y	21	F
Ant Colony Music ((Clair et al. 2008)	Low	Homog	No	1	Flat	Y		F
Swarm Orchestra (Bisig & Neukom 2008)	Low	Homog	No	1	Flat	Y		F
Society of Music Agents (Beyls 2007	Low	Homog	Sync	1	Flat	N		F
MMAS (Wulfhost et al. 2003)	Higher	Het	ASync	1	Flat	Y	8	F
Musical Agents (Fonseka 2000)	Higher	Het	Async	1	Flat	Y		F
Andante (Ueda & Kon 2003)	Higher	Het	Async	1	Flat	Y		F
VirtuaLatin (Murray-Rust et al. 2005)	Higher	Het	Sync	1	Hierarchy	N	1	F
MAMA (Murray-Rust and Smaill 2005)	Higher	Het	ASync	1	Hierarchy	Y		F
Kinetic Engine (Eigenfeldt 2009)	Higher	Het	ASync	1	Hierarchy	Y		F
CinBalada (Sampaio et al. 2008)	Higher	Het	ASync	1	Flat	N		F
AALIVE (Spicer et al. 2003)	Higher	Het	ASync	1	Hierarchy	Y		F

2.3

The systems which are closest to the one in this article (and not listed in Table 1) are now examined in more detail. The Dahlstedt and McBurney (2006) system uses agents which have different explicit goals that represent different parts of the process of music composition. An example is given of an agent whose goal is to reduce sound object density if the population of the system's sound landscape becomes too cluttered; another is given of an agent who does the opposite. Both agents would take into account the musical context while doing this. The researchers explicitly intend to utilise emergence to generate interesting music. This is a similarity with the system in this article, though key differences are: the Dahlstedt and McBurney agents act on a single music composition together, whereas agents in this article each have their own repertoires which can develop in parallel, and do not have explicit and distinct goals.

2.4

Miranda's (2002) system generates musical motifs in a way designed to study the evolution of culture. In this case the agents use a two-way imitation procedure to bond socially. Agents can store a repertoire of tunes and have a basic biological model of an adaptive voice box and auditory system. Agents pick other agents to interact with randomly.

2.5

When two agents A and B interact the following process occurs: if agent A has tunes in its repertoire it picks one randomly and sings it, if not then it sings a random tune. These tunes are three notes long and do not grow in length. Agent B compares the tune from A to its own repertoire and if it finds one similar enough, plays it back to agent B as an attempted imitation. Then agent B makes a judgement about how good the imitation is. If it is satisfied with the imitation it makes a "re-assuring" noise back to agent A, otherwise it does not. Based on the success of the imitation Agents A and B update their repertoires and their voice box settings to try to improve their chances of socially bonding in later interactions – e.g. by deleting or re-enforcing tunes, or making random deviations to their voice box parameters. The aim of the system is to see how the repertoire is generated and affected under such social pressures. As a result of the social bonding interactions a community repertoire was found to emerge.

2.6

Gong et al. (2005) produced a simple music generating system with a similar purpose to Miranda (2002) – investigating the emergence of musical culture. The agents start with a set of random motifs, together with different agents being equipped with distinct but very simple aesthetic evaluation functions (for rhythm, pitch, etc.). An agent plays its tune to another agent and if the second agent finds the tune unpleasant, it modifies it (based on its musical evaluation), and plays it back to the first agent. If the first agent thinks the modified tune is better than its original, it deletes its original and stores the modified version. As agents interact this leads to "more pleasant" motifs emerging. Also, using an interaction-history measure, the social link between first and second agent is strengthened so that they are more likely to interact in the future. However if the first agent does not prefer the modified tune to its own version, it discards it and the link between the two agents is not strengthened. It was found that in the emergent social network the agents tended to cluster according to their aesthetic preference function. This system has a couple of similarities to the one in this article: it utilizes MAS social network/trust techniques (Ramchurn et al. 2004) to decide who interacts with whom, and in each interaction agents vary their repertoire based on their opinion of the other agent's repertoire. The key differences between this system and the one in this article is that agents in this article have no explicit evaluative melodic intelligence, and they can extend the number of notes in their repertoire; and finally the social network in this article is used to generate hierarchical music structure within an agent's repertoire not to experiment with the clustering of agents according to their repertoires.

2.7

The A-Rhythm (Martins & Miranda 2007) system sets out to examine the application of multi-agent systems to algorithmic composition. Current reports focus on, like Miranda and Gong et al., investigating the emergence of social clusters, and are solely based on rhythmic repertoire. A-Rhythm has some similarities to the system in this article: the agents communicate and process one at a time serially, rather than in parallel, and their musical content grows longer. However A-Rhythm focuses on rhythm, i.e. is non-pitched. Also the similarity measures are more directly based on the music, rather than affective content of the music. Finally A-Rhythm uses measures for the popularity of rhythms in an agent's repertoire, but not for the popularity/trust of agents. Agents in this system can transform their repertoires based on interaction – using certain rhythmic transformation rules, rather than the affective-based transformations used in this article. A number of experiments are done based on different interaction approaches, and the resulting population and repertoire dynamics are examined, showing the potential for the emergence of structured rhythmic repertoires.

Multi-agent Affective Social Composition System: MASC

Overview

3.1

The system in this article – the multi-agent affective social composition system (MASC) – is now presented in overview. Agents in MASC are initialized with a tune containing a single note, and over the interaction period each agent builds longer tunes through interaction. Figure 1 shows an overview representation of a collection of agents.

Figure 1. Six MASC agents in a variety of affective states with one agent performing.

3.2

The following are some of the key features of the system. MASC usually consists of a small-medium size – 2 to 16 – collection of agents, but can be more. Each agent can perform monophonic MIDI tunes and learn monophonic tunes from other agents. An agent has an affective state, an artificial emotional state which affects how it performs the music to other agents; e.g. a "happy" agent will perform their music more "happily". An agent's affective state is in turn affected by the affective content of the music performed to it; e.g. if "sad" music is performed to a happy agent, the agent will become a little "more sad". Agents can be made to only learn tunes performed to them if the affective content of the tune is similar enough to their current affective state; learned tunes are added to the end of their current tune. Agents develop opinions/trust of other agents that perform to them, depending on how much the other agents can help their tunes grow. These opinions affect who they interact with in the future.

Affective Models

3.3

Before going in to the data structures within each agent in detail, the issue of affective models will be covered. There is a variety of approaches for affective represenation which can be broadly divided in the Dimensional type and the Category type (Zentner et al. 2008). Category approaches range from basic emotion definitions – which assumes that some emotions are more fundamental than others and attempts to list these; to the more everyday emotion label systems – which do not attempt to categorize based on an emotion hierarchy. A recent category-based approach for emotion is the Geneva Emotion Music Scales (GEMS) approach (Zentner et al. 2008) which attempts to provide categories optimal for musical emotion. This is done by first investigating through psychological tests which sorts of emotion are most commonly expressed to people by music. Although GEMS does get users to score the category with an integer from 1 to 5, the fact it has up to 45 categories puts it more in the realm of categorical than the dimensional systems now discussed.

3.4

The Dimensional approach to specifying emotion utilizes an n-dimensional space made up of emotion "factors". Any emotion can be plotted as some combination of these factors. For example, in this paper, two dimensions are used: Valence and Arousal (Lang 1995). In this model, emotions are plotted on a graph with the first dimension being how positive or negative the emotion is (Valence), and the second dimension being how intense the physical arousal of the emotion is (Arousal). This is shown in Figure 2. Just as category approaches would not claim to list all possible emotions, so dimensional approaches do not claim to be complete. It is not known if emotions can be pinpointed based on unique independent dimensions. Other dimensional approaches include the three dimensional valence/arousal/dominance system (Oehme at al. 2007). In this case Valence and Arousal have the same meaning as in the 2D version. However in the 2D approach Fear and Anger are both low valence, high arousal. In the 3D version, Dominance differentiates emotions such as anger (high dominance) and fear (low dominance); anger can be seen as more of an active emotion, fear as more of a re-active one. There are also examples such as Canazza et al. (2004) where a task-specific mood-space is constructed for expressive performance using experiments and principle component analysis. In that particular case the dimensions are not explicit.

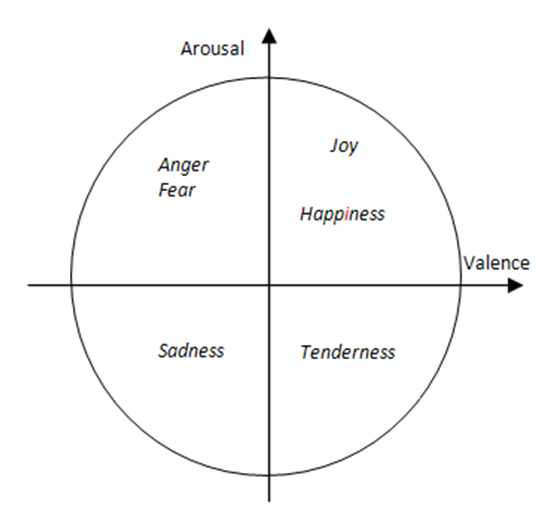
Figure 2. The Valence/Arousal Model of Emotion

Agent Data Structures

3.5

Each agent contains three data structures. The first is an agent tune, a monophonic tune in MIDI format. The second is an agent affective state – a number pair [valence, arousal] representing the artificial affective state of the agent based on the valence/arousal model of affectivity. This is the most common dimensional affective representation in computer music. As has been mentioned Valence refers to the positivity or negativity of an emotion – e.g. a high valence emotion is joy or contentment, a low valence one is sadness or anger. Arousal refers to the arousal level of the emotion – for example joy has a higher arousal than happiness, though both have high valence, and anger a higher arousal than sadness, though both have low valence. A linguistic element needs to be clarified. The use of affective labels such as happy and sad are used to assist clarity in introducing the reader to the concepts of MASC; they are not meant to be taken literally. For example happy refers to a region of high valence and arousal values, and sad refers to a region of low valence and arousal values. The same goes for any words which may seem to imply that agents have any kind of personification, or deeper intentional or biological model. Such language is merely a shorthand for clarifying functionality.

3.6

The third and final agent data structure is an interaction coefficient list, which is a list of interaction coefficients of all the other agents in the collection. These are non-negative floating point numbers which measure how popular the agent finds each of the other agents. The concept of interaction coefficient is used here to attempt to create emergent compositional hierarchies, as will be demonstrated. Another way of thinking of interaction coefficient at this point is to consider an imagined motivation for an agent. The aim of MASC is – starting with each agent having a single note – to build actual melodies. So an agent should want notes. An agent A's interaction coefficient measure of another, say Agent B, is based on the note count and number of performances it has added from B to its own tune.

3.7

An agent also has a number of internal processing functions. The performance output choice function involves an agent choosing who to perform to, based on the agent's interaction coefficient list of other agents. It will only perform to agents it finds useful enough. The performance output transform function involves the agent playing its single stored tune as a performance to another agent, with musical features based on its own current affective state. The performance input estimate function allows the agent to estimate the affective content of a tune performed to it by another agent, and adjust its own internal affective state based on the affective content. An agent's performance input choice function involves it deciding whether to store a performance from another agent, and is based on: (a) the affective content of that performance, and (b) how many notes are in the listening agent's current tune – an agent has a finite tune length memory which can fill up. The performance input interaction coefficient function lets the agent update its interaction coefficient measure of another agent based on that agent's performance. Finally the performance input add function lets the agent store a performance by concatenating it to the end of its current tune. An example interaction cycle is shown in Figure 3. This cycle is repeated until the desired compositional result is reached.

Figure 3. Example Interaction Cycle

Performance Output Transform Function

4.1

The function for performance output transform will now be examined in more detail. Before performing its tune to another agent, an agent will transform its tune in a compositional way.

Compositional Transforms

4.2

Two types of compositional transformations are applied – linear feature transforms and a key mode transform into C major or C minor. The aim of this work was it to investigate the effects of multi-agent emergent effects, rather than the transformations themselves – hence the transformations were kept as simple as possible, forgoing non-linearity and psychophysical accuracy. They can be compared to the simplistic linear rules used in swarm or flocking systems (Reynolds 1987). Clearly such linear rules are an over-simplification of bird/insect biology and psychology. However, what is of interest is that such simple rules can create such complex dynamics. The underlying elements being simplified here are the relationships between music and emotion. This area has been meta-surveyed in Livingstone et al. (2010), which then established a series of rules for transforming music to express emotions. These rules are shown in table 2.

Table 2: Transformation Rules proposed in (Livingstone et al. 2010)
Emotion Label	Valence	Arousal	Features
			Tempo	Loudness	Pitch	Key mode
Happy	Higher	Higher	Increase 10 BPM	Increase 5 db	+4	Major
Angry	Lower	Higher	Increase 10 BPM	Increase 7 db	0	Minor
Sad	Lower	Lower	Decrease 15 BPM	Decrease 5 db	-4	Minor
Tender	Higher	Lower	Decrease 20 BPM	Decrease 7 db	+4	Major

4.3

Equations (1) to (4) show the result of transforming these into simplified linear rules for multi-agent system interaction. The process of this simplification is explained below, after their presentation. When an agent A is about to perform and has a particular level of valence, written valence_A, and arousal, written arousal_A, it will first compositionally transform its stored tune based on the effects of equations (1) to (4). The primed values on the left hand side of the equations are the defining features of the compositionally transformed music, and are used to unambiguously generate a transformed MIDI file. The pre-transformation values IOI_i(A), dur_i(A), loud_i(A), and pitch_i(A) are: the inter-onset interval between note i and the next note i+1, the note duration in seconds, the MIDI loudness, and MIDI pitch of the i-th musical note of Agent A's stored tune. The theta values – θ_onset, θ_loud, and θ_pitch – define the affective sensitivity of the transformation – i.e. how much effect a change in Agent A's valence or arousal will have on the transformation. They are the maximum variation percentage bars around the current feature value.

IOIi(A)' = IOIi(A) ( 1 − θIOIarousalA

(1)

duri(A)' = duri(A) (1 − θIOIarousalA)

(2)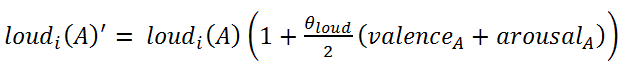

(3)

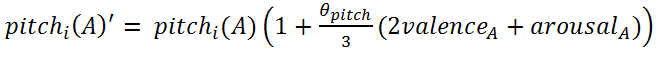
(4)

4.4

For example if θ_IOI is 0.25, then by Equation (1) the onset will vary from 25% below its current value to 25% above its current value when arousal varies from -1 to 1. If a transformation goes above the maximum MIDI value (127) then it is set to 127. Similarly if it goes below 1 it is set to 1. Note that θ_IOI is used both for onsets and duration so that as gaps between notes are increased or decreased, the duration of the same notes is increased and decreased by the same amount.

4.5

The mapping between Table 2 and Equations (1) to (4) is explained as follows. A smaller average inter-onset interval in a piece of music leads to a higher tempo (Dixon 2010), and equation (1) means that a higher arousal will create a smaller inter-onset interval, and thus a higher tempo. This approximately captures the linear dynamics of the tempo column in Table 2 where tempo changes in the same direction as arousal, but is not affected by valence. Duration in (2) is changed proportional to inter-onset interval – so that when notes are closer together (due to a higher tempo) they will be proportionally shorter, as would be expected.

4.6

Equation (3) is a linear simplification of the fact that Table 2 shows how changing valence tends to cause loudness to increase in the same direction, and changing arousal also tends to cause loudness to increase in the same direction. Equation (4) is based on the fact that Table 2 shows pitch to be changed by changes in valence and arousal, but slightly more so by changes in valence.

4.7

Table 2 was not originally a prescription for a linear model, in the sense it says nothing about what happens in between the four states. Even if the valence / arousal model of emotion was complete (which clearly it is not) there would certainly be non-linear behavior between the origin and the four points referenced in this table. This is one reason why no attempt was made in the equations to calculate precise linear correlation coefficients.

4.8

So the equations are not meant to be an accurate linear model of the behavior in Table 2, but the simplest possible linear model of music features and emotion informed by Table 2. The model does not claim that all high pitched music is higher valence, or that all low tempo music is low arousal. Contra-examples can be found for both of these in music: for example high pitched melancholy violins, or slow but grand and inspiring orchestral pieces. There are however no complete models for music and emotion, just as there are no complete models for bird and insect flocking. For example, you can keep adding or removing birds from a flocking model, and the flock will increase or decrease in size in an unlimited way – obviously a contra-example of the flocking model. Hence it is argued that the incompleteness of the above linear model is acceptable for the purposes of the work here presented.

4.9

One music feature which cannot be changed linearly is key mode, so a different – but still simple – approach is used. It is largely based on Table 2 but with one adjustment. For positive emotion a major key is utilized and for negative valence with negative arousal (e.g. sadness), a minor key is utilized. For negative valence and positive arousal – e.g. anger or fear – each note in the tune is transformed to C minor then moved alternately up or down a semitone; this is designed to inject an atonal element to the music. For example the sequence "C Eb D F Eb G C" would become "Db D Eb E E Gb Db". This is based on the idea that fear and anger can be represented by atonality (Chong et al 2013). This will impact the effect of Equation (4) which also raises and lowers pitch due to valence. However the changes in pitch due to valence in (4) – in the experiments detailed later – are of a significantly greater order than one semi-tone. Thus the impact of the atonal transformation is minimal on (4). Also equation (4) is a linear simplification, so there is no claim to it being accurate to within a semi-tone in terms of its valence representation.

4.10

The transform is algorithmic and deterministic – it searches either side of the current notes for a note in the new mode which does not violate a MIDI boundary – i.e. not out of the MIDI 128 parameter range. So suppose an agent A has stored a tune from a happy agent which is a major key. If agent A then performs its tune while sad it will convert all of its tune, including the major part it received from another agent, into the minor mode. The current version in this article has no ability for actual key composition functionality, hence the reason for using only C major and C minor.

Tune Affective Estimation Function

5.1

A linear equation is used to model the listening agent's, say agent B, affective estimate of a performance by agent A – this is shown in equations (5) and (6).

valenceEstB = xpmean(pitchA) + xlmean(loudA) + xkkeyModeA + xIOImean(IOIA) + x0

(5)

arousalEstB = ypmean(pitchA) + ylmean(loudA) + yIOImean(IOIA) + y0

(6)

In these equations pitch_A and loud_A refer to the average MIDI pitch and MIDI loudness of an agent A's performance heard by B. keyMode_A represents the key mode of A's tune estimated using a key profile-based algorithm (Krumhansl & Kessler 1982) defined as having value 2 for a minor key, and 1 for a major key. A key profile is a vector of 12 elements, one for each note in the scale. Each key has its own profile. Pitches which fit well into a scale have a higher weighting in its key profile vector, and those which fit less well have a lower weighting. These weightings were calculated for each key from perceptual experiments in Krumhansl and Kessler (1982). Thus they can be used to find whether a particular set of notes fits best into a major or a minor key.

5.2

The x and y coefficients in the Equations are constants estimated by linear regression. These are estimated in a one-off process as follows. A set of 1920 random MIDI files was generated, of random lengths between 1 and 128 notes. Each MIDI file was transformed for 10 given and equally spaced valence and arousal values between −1 and 1 using transformation equations (1) to (4), and key mode transformations.

5.3

Then a linear regression was run on the resulting transformed MIDI files against the known arousal and valence values – based on equations (5) and (6). The resulting coefficients were tested on a separate set of 1920 transformed random files, and the average percentage errors were 10% for valence and 9% for arousal. These are considered to be sufficiently accurate given that actual human musical emotion recognition error rates can be as high as 23% and other far more complex artificial musical emotion detection systems have rates such as 81% (Legaspi et al. 2007). The actual coefficients for pitch, loudness, keymode and IOI were respectively in equations 5 and 6 for x = [−0.00214, 0.012954, 1.1874, −0.6201] and y = [0.003025, 0.052129, −1.4301, 0.59736]; with the additive constants for x and y respectively of 0.61425 and −4.5185.

5.4

The linear estimator is used in two aspects of the agents – firstly for an agent to decide whether or not to add a performance to its own tune, and secondly for an agent to be influenced by the approximated emotional content of a performance it has heard. Equations (7) and (8) below are used to update the valence and arousal of agent B after a performance from agent A. The γ (gamma) constant – between 0 and 1 – defines how sensitive an agent is to affective state change – i.e. the amount of change to valence and arousal. If it is set to 1 then the new valence and arousal values will be totally changed to the estimated values of the performance the agent has just heard. A value of 0 will lead to no change. Values between 0 and 1 will cause the estimate to have a proportionally greater effect.

valence'B = (1 − γv)valenceB + γvvalenceEstA

(7)

arousal'B = (1 − γa)arousalB + γaarousalEstA

(8)

5.5

Once the agent B has decided whether or not to append the performance from A – and if so, has done so – it will update its valence and arousal based on Equations (7) and (8). In future, when it next performs a tune, it will transform it based on its new valence and arousal state. It is designed so that through this series of updating affective states and the agent tune communication and system, new musical structures will emerge.

5.6

It is worth taking a moment to discuss the above process, in particular the affective communication and estimation elements. An alternative would have been for the system to directly transmit the valence and arousal of agent A to agent B, rather than computing coefficients for Equations (5) and (6) and going through the process of estimating valence and arousal from the music features. The estimating the coefficients for (5) and (6) could be seen as quite a recursive process: first an approximation was made of how valence and arousal can be communicated through music features, and then an approximation was made of how music features communicate valence and arousal. Wouldn't it have been simpler to just communicate the valence and arousal directly; or – if we wanted to observe the musical effects – still perform the compositional transforms, which communicating the valence and arousal of the performing agent directly?

5.7

These simplifications would have removed the artificial life foundation from the formulation. The music would have not been part of the process, but merely influenced by the process. What makes the formalism of interest is that the music is part of the process, and thus any creative results are emergent from the process. Furthermore, had the agents communicated their valence and arousal directly, with say a random communication error, then it would become a less novel multi-agent system. It would have been an MAS in which each agent had two numeric parameters and agents whose numeric parameters were close would then influence each other's parameters more strongly. This is a type of artificial life system that has been studied many times before, and leads to agents tending to cluster into groups of similar parameter values – i.e. similar valence and arousal values. By putting the music at the centre of the parameter communication not only does it create a novel artificial life process but also makes the music emergent to the process. Thus something is learned about the dynamics of a new AL system, and also about how applicable that system might be to algorithmic composition.

5.8

At the heart of the experiments are the questions: can musical communication in multi-agent systems be used as a form of algorithmic composition? Music, in communication terms, is most commonly considered a form of emotional communication (Juslin & Laukka 2004). Past research has most commonly linked musical features to communicated emotion. However this communication is imperfect: people detect emotion in music ambiguously, and communicate in emotion ambiguously. So the system as designed captures many elements of musical communication in a more realistic way that simply communicating valence and arousal with an error. It generates musical features based on the emotion being communicated. The listening agent is then affected by the musical features. This effect is the simplest non-direct method possible based on musical features: a linear model based on the non-invertible equations (1) to (4). This – although significantly less simple – it is the equivalent in the flocking example of agent's movement and their perception of each other's movement. However, unlike movement, the process here is not an immediately visible one; it concerns the agents' emotions which are not so simply observable or communicable. In fact even when human beings attempt to communicate emotions directly, there are limitations; which is one of the reasons that the arts are often considered to be forms of emotional expression, able to communicate in ways that language is not (Juslin & Laukka 2004).

Performance Input Interaction Coefficient Function

6.1

Before an Agent A performs to an Agent B it compares its interaction coefficient measure of Agent B to the average of its interaction coefficient (IC) for other agents:

IC(A,B) > mean[IC(A, all agents)]

(9)

where IC(A,B) is A's interaction coefficient measure of B. If it is not, then it does not perform to Agent B and moves on to the next agent. The increase in Interaction Coefficient is proportional to the length of tune it has added. So the more notes in Agent B's past performances, the greater its interaction coefficient will be viewed by Agent A. If agent A adds a tune from agent B of length N notes then:

IC(A,B) = IC(A,B) + d.N

(10)

6.2

The parameter d is a constant called the interaction coefficient update rate. This can be visualised as an agent's basic resources being tunes – so the more notes in an agent's tune, the greater its potential interaction coefficient to other agents. However the actual reason for including interaction coefficient functionality, and making interaction coefficient proportional to the number of notes in a performing agent's tune is primarily to generate an interaction/social hierarchy amongst the agents which influences the hierarchical structure of the composed music. Bearing in mind that an agent will only perform to other agents with a high enough interaction coefficient, it can be seen that agents which perform more than listen will tend to have lower interaction coefficients. Furthermore agents which mostly listen and store will have longer tunes and higher interaction coefficients; and agents with higher interaction coefficients will tend to be selected as listeners more often

6.3

So the system is designed to turn the agent population into a set of agents who tend to perform and have shorter tunes, and a set of agents who tend to listen and store. The aim is for lower interaction coefficient agents to be focused on providing lower elements – i.e. shorter elements – of the musical hierarchy.

An Example Cycle

6.4

An example cycle will now be shown. In this example a three agent system is examined. Agent 1 is the performer and starts by considering performing to Agent 2; Agent 1's measure of Agent 2's interaction coefficient is very low in this example; Agent 1's measure of Agent 3's interaction coefficient is very high; Agent 1's affective state is high valence and high arousal – i.e. happy; and Agent 3's affective state is low valence and low arousal – i.e. sad.

6.5

As the cycling starts, because Agent 1's interaction coefficient of Agent 2 is very low, Agent 1 does not even perform to Agent 2. It selects the next Agent iteratively. Agent 3 is selected because agents are ordered by numerical label. Agent 1's view of Agent 3's interaction coefficient is very high – so Agent 1 performs its tune T1 adjusting it to make it happier because of its high valence and arousal state, giving a performance P1.

6.6

Agent 3 estimates the affective content of Agent 1's performance P1 and gets a result of high valence and arousal – i.e. it estimates it is a happy performance. Because Agent 3's affective estimate of Agent 1's tune is high valence and arousal but Agent 3's state is low valence and arousal – i.e. very different to happy – Agent 3 discards Agent 1's tune. However Agent 3 still adjusts it owns affective state towards its estimate of the affective content of performance P1 i.e. it becomes a little more happy. Neither Agent makes any adjustment to their interaction coefficient measures since no performances were stored. Next Agent 2 becomes the performer, and the first agent is iteratively chosen to listen – i.e. Agent 1.

Experiments

7.1

The issue of how to evaluate an algorithmic composition is by no means agreed in the research community. Parametric/Example-based investigations are common in investigating algorithmic composition systems (e.g., Beyls 2007; Fonseka 2000; Anders 2007). Such experiments were done analysing how MASC output responded to various parameter changes, giving objective information on MASC's behaviour for a potential user. Such experiments are important because they provide insight into the dynamics of the system. It should be noted that in this system there are a number of parameters which need to be set; it is beyond the scope of this article to describe all of them. Those not mentioned explicitly here were set to default values.

Melody Generation

7.2

A helpful way to indicate that this system can produce non-trivial melodies, in spite of its lack of melodic intelligence, is to explore the output space for some different initial affective states. Usually in a MAS one would want to perform a statistical analysis of behaviour, but it is an unsolved problem in algorithmic composition as to what statistics are musically relevant (Freitas et al. 2012). So instead specific musical results are presented. Figures 4 to 8 show agent 6's final tune, from an 8 agent system run for 10 cycles. The similarity threshold was 1, the interaction coefficient system was switched off, and valence and arousal update rates - gamma in equations (7) and (8) – were 0.001. Agents were initialised each with the single note of middle C, of duration 0.5 seconds. Four initializing states were used with different levels for [Valence, Arousal] pairs. These were: Happy = [0.5, 0.5]; Sad = [−0.5, −0.5]; Angry = [−0.5, 0.5]; Tender = [0.5; −0.5]. The first letters of each state were used to indicate the agent initial states. For example TTTTTTHH is 6 Tender and 2 Happy.

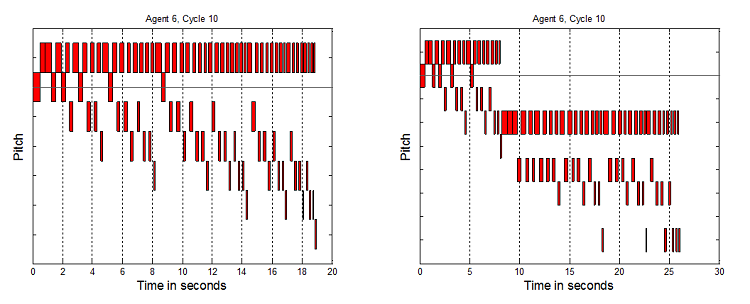
Figure 4. 8 Agents AAAAAAAA, 10 Cycles, and 8 Agents AAAAAASS, 10 Cycles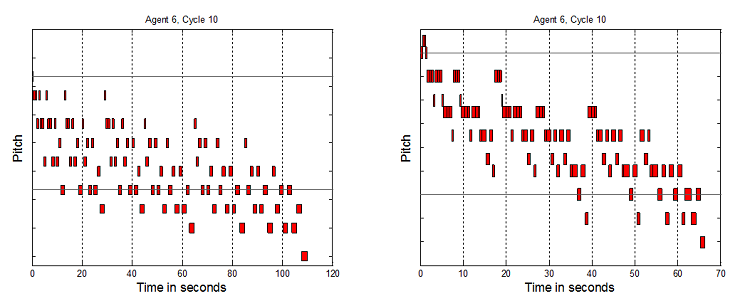

Figure 5. 8 Agents SSSSSSSS, 10 Cycles, and 8 Agents SSSSSSAA, 10 Cycles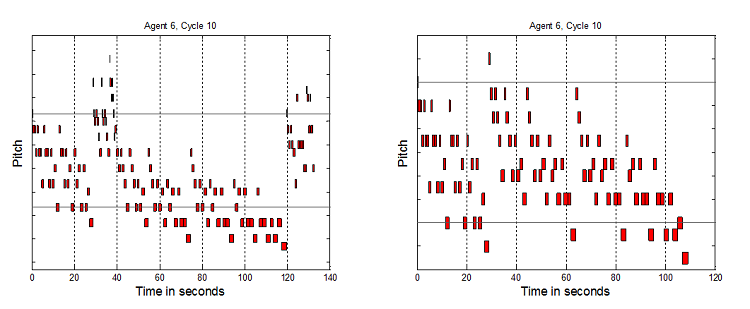

Figure 6. 8 Agents SSSSSSHH, 10 Cycles, and 8 Agents SSSSSSTT, 10 Cycles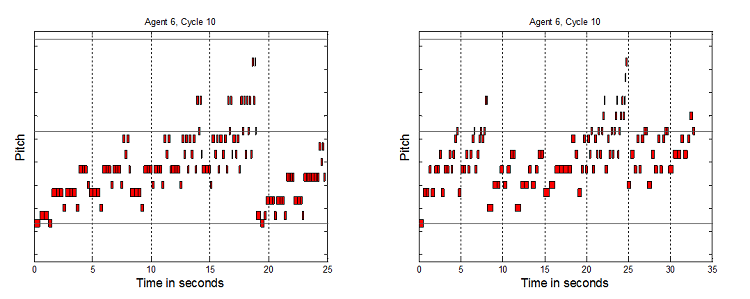

Figure 7. 8 Agents HHHHHHSS, 10 Cycles, and 8 Agents HHHHHHTT, 10 Cycles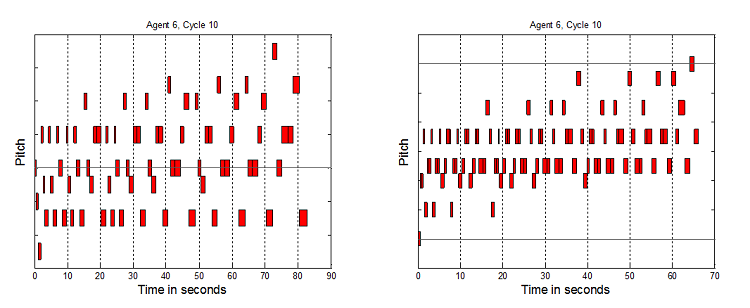

Figure 8. 8 Agents TTTTTTSS, 10 Cycles, and 8 Agents TTTTTTHH, 10 Cycles

7.3

Each vertical tick is a semi-tone. Precise pitch values have been removed from the graphs to aid readability, and because absolute pitch values are not the key element here, but the relative interplay of structures which it will now be argued indicate non-triviality. To clarify why this broad range of tunes is considered non-trivial as melodies, a number of elements are now highlighted. Music has been generated up to and over 50 seconds long. If the tunes were only 3 to 6 notes or a few seconds long, these would be trivial. The melodies are not just simple directional pitch patterns, like single repeated notes, uniformly rising or falling patterns, or repeated "zig-zags". The melodies are not just groups of repeated notes, e.g. 5 notes at one pitch, then 4 notes at another, etc. The pitches vary much more than that. However they do not vary all the time – there are times when notes are repeated 2 or 3 times, as one would expect in melodies. Timing repetition is not too high or too low. Melodies have been generated where the tempo does not stay constant, but also the tempo does not simply seem to vary randomly. It would seem odd if note only raised or lowered by one pitch in all tunes. In music there are sometimes larger jumps. However it would also seem odd if all the pitch changes were large. It has been shown that tunes can be generated which avoid these two extremes. Finally, the melodies contain recognizable note groupings which are repeated and transformed to different pitches and timings. This is expected by western listeners who usually look to identify a motif structure.

7.4

Ideally it would be desired to have some more scientific measure of non-triviality for the melodies, however there is no such agreed measure. There have been some attempts to use measures like entropy but no conclusive results have been obtained (Kirke & Miranda 2007). Another approach might be to use measures of complexity, as it was stated at the start of this paper that such complexity was a major motivation in using artificial life systems for creativity. However there is no conclusive work on artistically informed measures of complexity. So although the above approach is non-scientific, it is fairly detailed and does capture many elements which a composer would consider to be key to non-triviality of music.

7.5

In summary the following example of a full composition can be heard http://cmr.soc.plymouth.ac.uk/alexiskirke/mapc.html

7.6

This composition has been put through a computer system for expressive performance to make it more listenable through a sequencer (Kirke & Miranda 2009).

7.7

It was stated at the beginning of this paper that an aim was that the non-trivial melody pitch structures would be developed by agents without explicit melodic knowledge. Given we have now claimed the production of non-trivial melody structures, we will examine the claim of no explicit melodic knowledge. This does not mean he agents have no musical knowledge. In fact the agents have a significant amount of hand-crafted musical knowledge in the musical transformation and affective estimation formulae. However, this knowledge does not include how to sequentially construct melodies. It includes how to change key modes, timings and pitches, but no musical rules about which musical features should follow which. The basis of melodic structure is which pitches follow and which note timings follow which. This is a significant gap in the agents' explicit knowledge about music which can be reduced by careful hand-crafting of the rules, but not removed without including ordering constraints in the musical equations. Thus the ordering of notes in this system emerges as a result of the social interactions between the agents.

7.8

It would be informative to see how simple the musical rules could have been made before the tunes failed to be non-trivial (with non-triviality formulated based on the process described earlier in this section). This might bring the whole system closer in philosophy to the flocking simulations discussed. However this is beyond the scope of this current work.

Agent Affective Tune and State Adaptation

7.9

It helps to understand the MASC dynamics more clearly by looking in a more general way at how music features are effected by agent initial affective states, as well as how agent affective states are changed as is done in Figures 9 and 10. Note that these experiments involved switching off the similarity threshold as well, so as to focus purely on affective interaction dynamics. These figures examine the result music features after 10 cycles of interation of MASC, for the system of 8 agents above, as well as for a smaller system of 2 agents. The pitch spread is the distance between the highest and lowest MIDI pitch in the final tune averaged across all agents, similarly with the median pitch. The average key is found using a key profiling algorithm (Krumhansl & Kessler 1982). Figures 9 and 10 also have arrows to highlight the progression of features as initial affective states are changed. They furthermore have dashed ellipses to highlight how close together the resulting features of the 2 agent system are to their "equivalent" 8 agent system.

7.10

A key element of MASC which would be new for many composers utilizing it, would be the assigning of initial affective states to the indiviual agents. Thus the more intutitve the results of such assignments the more useful MASC could be. This may at first seem contradictory to what was said initially cautioning the reader earlier on their interpretation of the our uses of the words "Happy" and "Sad" in relation to agents. However this caution was to prevent intepretation that the agents themselves were somehow "Happy" or "Sad". The use of labels such as these as a shorthand for arousal and valence configurations is still valid, and helpful to the composer using this system. Figures 9 and 10 provide insight into the effects of this process. It can be seen that broadly there are understandable patterns/trajectories, in terms of music feature results, when the initial affective states are changed. For example increasing the number of happy agents increases median pitch and reduces pitch spread.

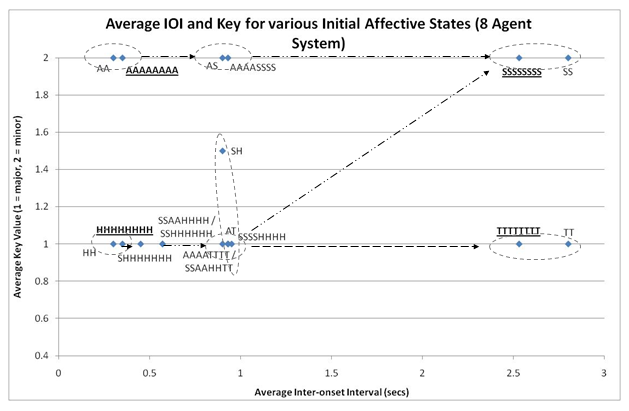
Figure 9. Effects of Initial Affective States in 8 Agent System on average IOI and Key, 8 Cycles Run

7.11

The tunes in Figures 8 and 9 generated by the 8 agent system, together with six more involving further combinations of H, S, A and T, were played to 10 listeners. It was found that when at least 6 of the 8 agents had the same initial valence and arousal, then the listeners had a 71% chance of detecting that same valence in the final tune, and an 82% chance of detecting that same arousal in the tune. Although the small number of participants means that the results are not very significant, they are certainly indicative that – given the support of the remainder of the parametric evaluation – it is worth doing a substantial set of listening tests to evaluate this potential affective pattern. This would further highlight the ability of MASC to be used in a relatively intutive way as a computer-aided composition tool.

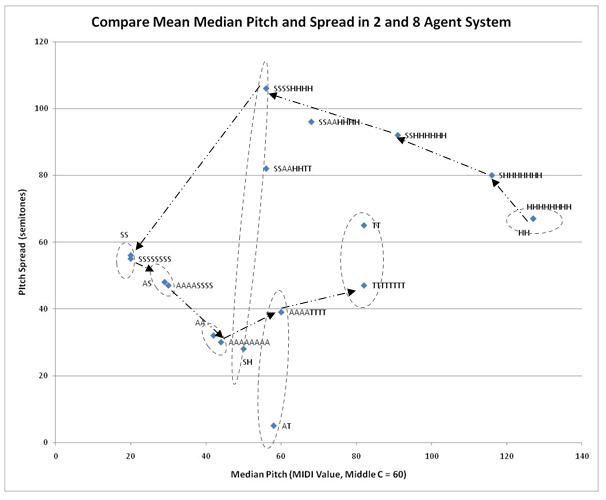
Figure 10. Effects of Initial Affective States in 8 Agent System on Pitch Median / Spread, 8 Cycles Run

Interaction Coefficient and Musical Hierarchy

7.12

As has been mentioned, the interaction coefficient process is designed as an attempt to regulate tune growth in such a way that certain agents will become tune provider agents and some will become tune receiver agents, thus creating a hierarchy in the agent's interaction structure which is hopefully reflected in the hierarchal structure of the melodies. In this experiment, an 8 agent system was used with equally spread agent initial affective states, 300 note memory size, 32 cycles, affective similarity threshold of 1, pitch update rate of 0.1, and IOI and loudness update rates of 0.5; valence and arousal update rates were set to 0.1. The interaction coefficient update rate was set to 0.2; and the interaction coefficient threshold was set to 0.9. Figure 11 shows the evolution of an agent's interaction coefficient averaged across all other agents. So the top graph shows the average view/trust that agents 2 to 8 have of agent 1 by averaging their coefficient values for agent 1.

7.13

After 32 cycles the number of notes that agents 1 to 8 have is respectively: 291, 102, 102, 102, 102, 102, 18, and 5. These tunes can be seen in Figure 12. Looking at Figure 11, it can be seen that this relates to the interaction coefficient – the higher an agent's final interaction coefficient the higher its note count. Table 3 shows in each cycle which agents an agent receives tunes from. So for example in cycle 1, agents 2 to 6 receive tunes from agent 1. In cycle 2 agent 1 receives a tune from agent 2, but no other agents receive tunes.

7.14

In Table 3 it can be seen that the lower interaction coefficient agents tend to give out tunes, while the higher interaction coefficient agents tend to receive tunes. The lower numbered agents have higher interaction coefficient because of the ordering of agent interaction in each cycle. The lower numbered agents will be receivers first, and have a chance to build up the size of their tunes. Then when they become performers – givers – the lower agents will receive large tunes from them and their interaction coefficient will increase as a result.

7.15

To see how this creates the hierarchical structure, consider that by Table 3 Agent 1's final tune could be written as a concatenation of sub-tunes 1₀2₁3₂4₃5₄6₅7₆2₉3₁₀4₁₁5₁₂6₁₃2₁₇3₁₈ where each number indicates the agent who performed, and the subscripts are the cycle numbers; an agent's tune varies over different cycles – e.g. 3₁₈ is not the same 3₂. Because the MAS is a closed system, all tunes in this structure are the result of a transformation on another agent's tune.

7.16

So for example 2₁ = 2₀1₀' and 3₂ = 3₀1₀'' and 7₆ = 7₀1₀'''. Here the primes represent transformations on Agent 1's tune due to Agent 1's affective state at the time. In the next round of tunes being given to Agent 1 this gives 2₉ = 2₁7₇'18₈' = (2₀1₀') 7₇'18₈'

7.17

This expansion can be continued until there is a full description of Agent 1's tunes based on the way in which the tune grows. This description will show the building structure of the tune. It will not necessarily show the perceptual structure of the tune – this is not claimed, but it will show how the tune was built from the motifs and phrases and so forth of other agents. This structure is clearly a function of the agent interaction hierarchy, and as has been seen this hierarchy is strongly influenced by the Interaction Coefficient functionality.

7.18

These diagrams highlight a characteristic of the system – its sequential update rule. Because agents are always updated in the same order, the agents with a lower index number tend to develop much larger tunes and have a high interaction coefficient. An asynchronous system simulation could have been utilized to avoid this – where the next agent to interact is randomly selected. However this would have moved away from the process of algorithmic – i.e. non-random – composition processes which this work was designed to build upon.

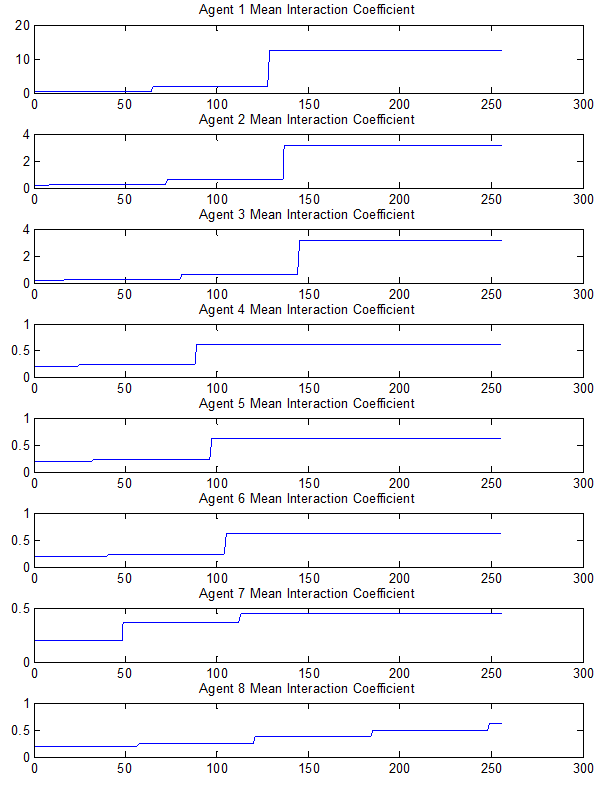
Figure 11. Change in mean Interaction Coefficient (x-axis = number of interactions)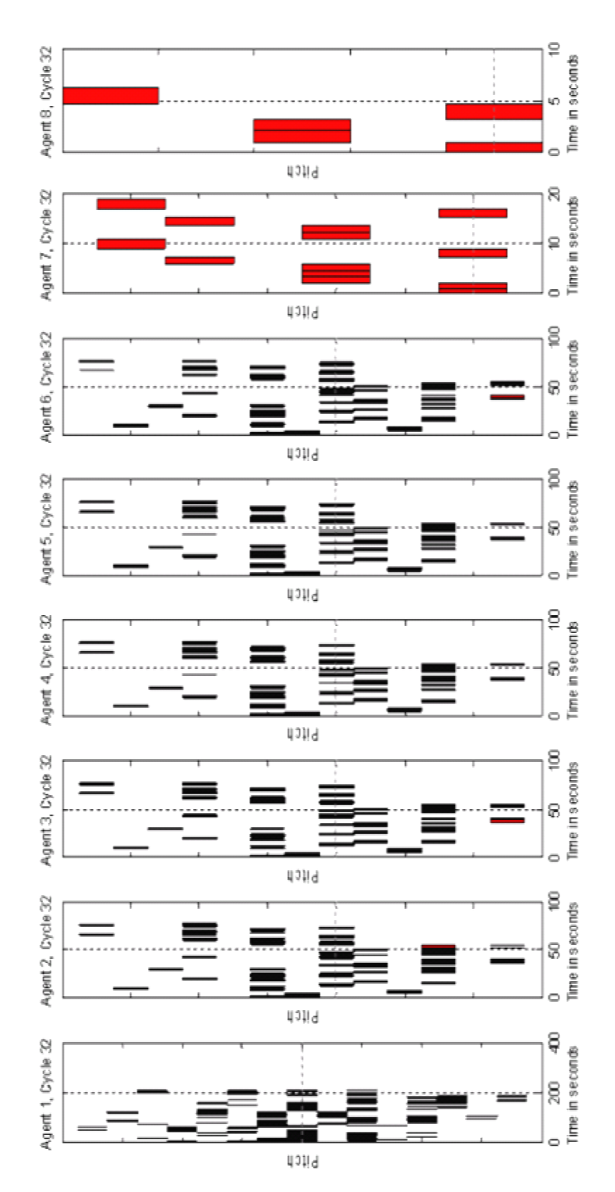

Figure 12. Tunes after 32 cycles

Table 3: Pattern of Interaction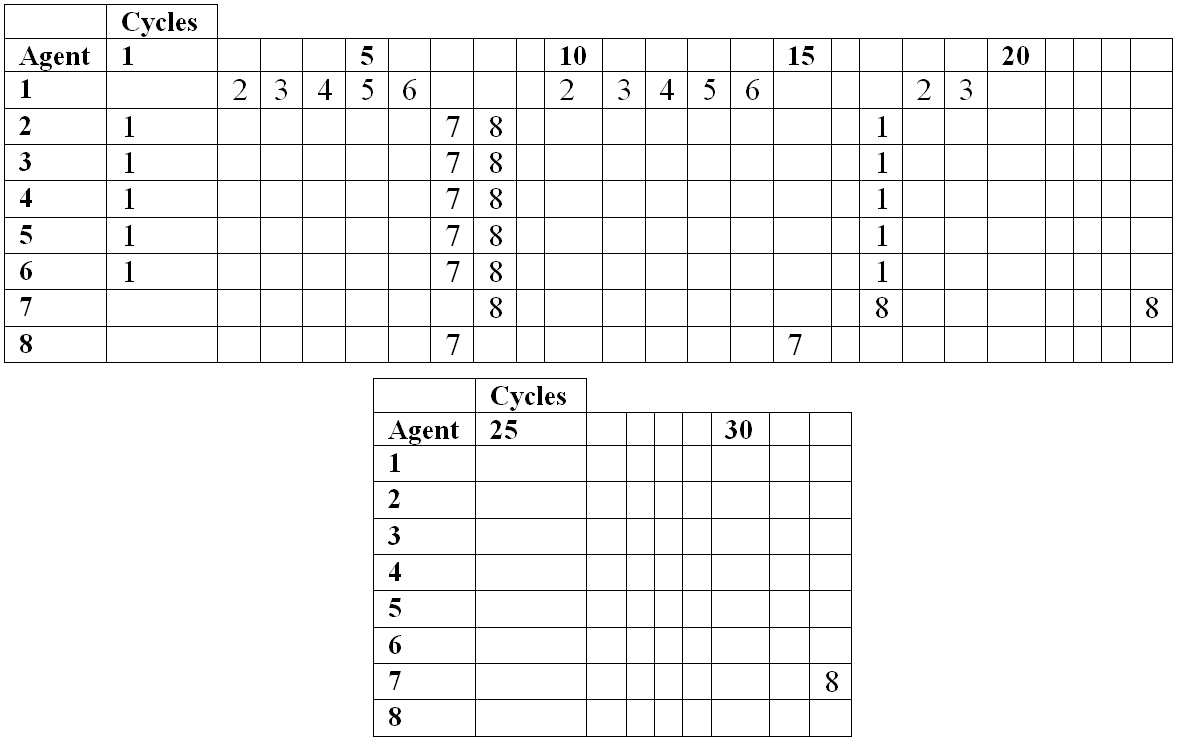

Conclusions and Future Work

8.1

A multi-agent system MASC has been presented which is a proof of concept that a multi-agent system can develop non-trivial melody pitch structures through affective interaction of agents without explicit melodic knowledge. Agents have no explicit knowledge of which notes should follow which, how they should repeat, and so forth. An agent's only compositional knowledge of music is its ability to extract affective data from the whole and impose affective features on the whole. MASC also demonstrates that multi-agent social structures can generate musical structure on thematic and sectional levels as well as on a note or phrase level. There were two demonstrations. It was demonstrated diagrammatically how the interaction structure would relate to the musical structure. Then an example was given showing the musical structure building up and how it related to the agents' social structure. A final contribution of MASC is the linear music-emotion analyzing model which takes as input a monophonic MIDI file and estimates its affective content.

8.2

In terms of future work, the listening tests performed were fairly basic, using a small number of subjects and thus only indicative. More extensive tests are needed to support the ability of MASC to be used in a relatively intutive way as an affective computer-aided composition tool. Such tests could also be used to examine the difference between the generative structure in MASC tunes, and the perceived structure for human listeners. This would help to clarify the effectiveness of the interaction coefficient approach to hierarchical structure generation.

8.3

On the subject of Interaction Coefficient, there are other contexts that could be investigated to influence future agent interactions, besides their past interactions lists. For example an agent could have time varying trajectories set by the composer, which could bias elements like their arousal and valence, or the extent to which their affective state transforms the music they perform. This would provide additional contexts for the composer to use in controlling the MAS output.

8.4

Another element of future work is the addition of indeterminacy. It was desired to examine the multi-agent system as a form of algorithmic composition – hence keeping the whole system deterministic. For example in previous work the authors have utilized semi-random communication errors between agents, contributing to changes in their tunes and transformations (Kirke & Miranda 2011). As has already been mentioned, the use of indeterminacy would also allow for the simulation of asynchronous communication – so that it is not always the same agents who begin the singing cycle.

Acknowledgements

This work was partially financially supported by the EPSRC funded project "Learning the Structure of Music,"grant EPD063612-1.

References

ANDERS, T. (2007). Composing Music by Composing Rules: Design and Usage of a Generic Music Constraint System. Thesis/Dissertation, Queens University, Belfast.

BEYLS, P. (2007). Interaction and Self-organisation in a Society of Musical Agents. Proceedings of ECAL 2007 Workshop on Music and Artificial Life (MusicAL 2007), Lisbon, Portugal.

BLACKWELL, T. & Bentley, P. (2002). Improvised Music with Swarms. Proceedings of the 2002 World Congress on Evolutionary Computation, Honolulu, Hawaii. [doi:10.1109/CEC.2002.1004458]

BISIG, D. & Neukom, N. (2008). Interactive Swarm Orchestra, an Artificial Life Approach to Computer Music. Proceedings of the 11th Generative Art Conference, Milan, Italy.

BROWN, A. (2002). Opportunities for Evolutionary Music Composition. Proceedings of 2002 ACMC, Melbourne, Australia.

CANAZZA, S., De Poli, G., Drioli, C., Rodà, A., & Vidolin, A. (2004). Modeling and control of expressiveness in music performance. The Proceedings of the IEEE 92, 686–701. [doi:10.1109/JPROC.2004.825889]

CHONG, H., Jeong, E. & Kim, S. (2013). Listeners' Perception of Intended Emotions in Music. International Journal of Contents 9(4), 78–85. [doi:10.5392/IJoC.2013.9.4.078]

CLAIR, R., Moncharce, N. & Slimane, M. (2008). Interactions between an artificial colony of musical ants and an impaired human composer: towards accessible generative arts. Proceedings of the 11th Generative Art Conference Milan, Italy.

DAHLSTEDT, P. & McBurney, P. (2006). Musical agents: Toward Computer-Aided Music Composition Using Autonomous Software Agents. Leonardo 39, 469–470 [doi:10.1162/leon.2006.39.5.469]

DIXON, S. (2010). Automatic Extraction of Tempo and Beat From Expressive Performances. Journal of New Music Research 30(1), 39–58. [doi:10.1076/jnmr.30.1.39.7119]

EIGENFELDT, A. (2009). The Evolution of Evolutionary Software: Intelligent Rhythm Generation in Kinetic Engine. Applications of Evolutionary Computing. Springer, Heidelberg, 498-507. [doi:10.1007/978-3-642-01129-0_56]

FONSEKA, J. (2000). Musical Agents. Thesis/Dissertation, Monash University

FREITAS, A., Guimarães, F., and Barbosa, R. (2012). Ideas in Automatic Evaluation Methods for Melodies in Algorithmic Composition. Proceedings of the 2012 Sound and Music Computing Conference, Copenhagen, Denmark.

GONG, T., Zhang, Q., & Wu, H. (2005). Music evolution in a complex system of interacting agents. Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK. [doi:10.1109/CEC.2005.1554815]

JUSLIN, P. & Laukka, P. (2004). Expression, perception, and induction of musical emotion: a review and a questionnaire study of everyday listening. Journal of New Music Research 33, 216–237. [doi:10.1080/0929821042000317813]

KIRKE A. & Miranda, E.R. (2007). Evaluating Mappings for Cellular Automata Music, In Proceedings of ECAL 2007 Workshop on Music and Artificial Life, Lisbon, Portugal.

KIRKE, A. & Miranda, E.R. (2009). A Survey of Computer Systems for Expressive Music Performance. ACM Computing Surveys. 42(1). [doi:10.1145/1592451.1592454]

KIRKE, A. & Miranda, E. (2011). A Biophysically Constrained Multi-agent Systems Approach to Algorithmic Composition with Expressive Performance. In CA-life for Music, Wisconsin: A-R Editions, Inc., 165–195.

KRUMHANSL, C. & Kessler, E. (1982). Tracing the dynamic changes in perceived tonal organization in a spatial representation of musical keys. Psychological Review, 89, 334–368. [doi:10.1037/0033-295X.89.4.334]

LANG, P. (1995). The emotion probe: Studies of motivation and attention. The American Psychologist, 50, 372–385. [doi:10.1037/0003-066X.50.5.372]

LEGASPI, R., Hashimoto, Y., Moriyama, K., Kurihara, S. & Numao, M. (2007). Music Compositional Intelligence with an Affective Flavor. Proceedings of ICIUII, USA. [doi:10.1145/1216295.1216335]

LIVINGSTONE, S. R., Muhlberger, R., Brown, A. R. & Thompson, W. (2010). "Changing Musical Emotion: A Computational Rule System for Modifying Score and Performance." Computer Music Journal, 13(41). [doi:10.1162/comj.2010.34.1.41]

MARTINS, J.M. & Miranda, E.R. (2007). Emergent Rhythmic Phrases in an A-Life Environment. Proceedings of ECAL 2007 Workshop on Music and Artificial Life (MusicAL 2007), Lisbon, Portugal.

MIRANDA, E.R. (2002) Emergent Sound Repertoires in Virtual Societies. Computer Music Journal, 26(2), 77–90. [doi:10.1162/014892602760137194]

MURRAY-RUST, A.& Smaill, A. (2005). Musical Acts and Musical Agents. Proceedings of the 5th Open Workshop of MUSICNETWORK. Vienna, Austria.

MURRAY-RUST, A., Smaill, A. & Maya, M.C. (2005). VirtuaLatin - Towards a Musical Multi-Agent System. Proceedings of Sixth International Conference on Computational Intelligence and Multimedia Applications. Las Vegas, NV, USA.

OEHME, A., Herbon, A., Kupschick, S. & Zentsch, E. (2007). Physiological correlates of emotions, in Proceedings of the 2007 Conference on Artificial Intelligence and Simulation of Behaviour. Newcastle, UK.

PANZARASA, P. & Jennings, N. (2006). Collective cognition and emergence in multi-agent systems. In Cognition and Multi-Agent Interaction, Cambridge: Cambridge University Press, 401–408.

RAMCHURN, S., Huyunh, D., & Jennings, N. (2004). Trust in multi-agent systems. The Knowledge Engineering Review, 19, 1–25. [doi:10.1017/S0269888904000116]

REYNOLDS, C. (1987). Flocks, herds, and schools: A distributed behavioral model. Computer Graphics 21(4), 25–34. [doi:10.1145/37402.37406]

SAMPAIO, P. A., Ramalho, G., & Tedesco, P. (2008). CinBalada: a multiagent rhythm factory. Journal of the Brazilian Computer Society, 14, 31–49. [doi:10.1007/BF03192563]

SPICER, M., Tan, B., & Tan, C. (2003). A Learning Agent Based Interactive Performance System. Proceedings of the 2003 International Computer Music Conference. San Francisco, USA.

UEDA, L. K, & Kon, E. (2003). Andante: A Mobile Musical Agents Infrastructure. Proceedings of the 9th Brazilian Symposium on Computer Music. Campinas, Brazil.

WULFHOST, D., Flores, L.V., Nakayama, L., Flores, C.D., Alvares, O.C., & Vicari, R. M. (2003). An Open Architecture for a Musical Multi-Agent System. Proceedings of the second international joint conference on Autonomous agents and multiagent systems. Melbourne, Australia. [doi:10.1145/860575.860669]

ZENTNER, M., Grandjean, D. & Scherer, K. (2008). Emotions Evoked by the Sound of Music: Characterization, Classification, and Measurement. Emotion, 8(4), 494–521. [doi:10.1037/1528-3542.8.4.494]