Abstract

Providing parents and students a choice to attend schools other than their assigned neighborhood school has been a leading theme in recent education reform. To evaluate the effects of such choice-based programs, researchers have taken advantage of the randomization that occurs in student assignment lotteries put in place to deal with oversubscription to popular schools and pilot programs. In this study, I used an agent-based model of the transition to school choice as platform for examining the sensitivity of school choice treatment effects from lottery-based studies to differences in student preferences and program participation rates across hypothetical study populations. I found that districts with higher participation rates had lower treatment effects, even when there were no differences in the distributions of school quality and student preferences between districts. This is because capacity constraints increasingly limited the amount of students who are able to attend the highest quality schools, causing the magnitude of the treatment effect to fall. I discuss the implications of this finding for interpreting the results of lottery-based studies involving choice schools.

Keywords:

Public Policy, Education, School Choice, Causal Inference

Introduction

1.1

Providing parents and students a choice to attend schools other than their assigned neighborhood school has been a leading theme in recent education reform in many countries (Gill et al. 2007; Berends et al. 2009). Computational models of such school choice programs have been helpful in articulating and testing their underlying market-based logic (Maroulis et al. 2010). In the complex systems literature, the models have taken the form of agent-based simulations that model the emergence of school district-level outcomes from the micro-level behaviors of students and parents (Harland & Heppenstall 2012; Millington et al. 2014; Maroulis et al. 2014).^[1]

1.2

For example, Millington et al. (2014) developed an agent-based simulation where parents differ in their "aspiration" for school achievement and schools differ in their ability to improve student outcomes. They demonstrated that such a model can generate distributions of enrollment, performance, and spatial allocation that match empirically observed patterns, and examined the consequences for parents with different aspirations. Maroulis et al. (2014) modeled the transition from a catchment area to open enrollment system, using data from Chicago Public Schools to initialize their simulation. Analysis of their model revealed how district-level achievement outcomes depend not only on the quantity and quality of new schools, but also on the timing of their entry. Harland and Heppenstall (2012) outlined the usefulness of agent-based simulation for student allocation by creating an agent-based simulation of an educational market in the United Kingdom.

1.3

In this paper, I use computational modeling to make a complementary but different type of contribution. Instead of creating a new model to investigate some not-yet-well-understood aspect of school choice dynamics, I use an existing agent-based model of school choice to gain a better understanding of the advantages and limitations of an approach for estimating the effectiveness of school choice programs that is growing in popularity and influence in the educational policy literature – randomized field trials made possible by student assignment lotteries put in place to deal with oversubscription. The larger motivation for this use of computational modeling is as follows: Despite the usefulness and growing utilization of the complex systems perspective in studying emergence and change in social and economic systems (Maroulis et al. 2010), its ideas and tools have yet to have a widespread impact on traditional management and policy research. An underlying premise of this paper is that in order to have greater impact on management and public policy, complex systems research must attempt to be more tightly integrated with existing the theory, methods, and findings in the substantive area of the phenomenon of interest. In the context of school choice reform, the current methodological state-of-the art is the use of lottery-based experiments to draw causal inference, and consequently the focus of this paper.

1.4

More specifically, I use an agent-based model calibrated to data on Chicago Public Schools to investigate the sensitivity of the treatment effect estimates of lottery-based studies – that is, the difference in educational outcomes between participants and non-participants of such programs that is attributable to the policy intervention – to differences in the underlying student preferences and the program participation rates in a district implementing a choice program. Experimentation with the model reveals that as the student participation rate rises, the magnitude of the treatment effect falls, even when there are no differences in distributions of school quality and student preferences across districts. The primary implication of this finding is that treatment effect estimates across districts cannot be compared without also simultaneously considering the participation rate and capacity of the district. This is a limitation of lottery-based studies that in hindsight is clear but in practice almost always overlooked.

1.5

The paper proceeds in four main sections. The first section briefly reviews the value and use of lottery-based studies in the school choice literature. The second section describes the agent-based model used as the platform for the computational experiments. The third section presents results from computational experiments from hypothetical districts that differ with respect to the emphasis on school achievement students place on their school choice decision, as well as the participation rates of the program. The final section discusses the implications of the computational results for interpreting the results of lottery-based studies involving choice schools.

Randomized Field Experiments in School Choice

2.1

Regardless of whether this idea manifests itself as increased access to non-neighborhood public schools, specialized charter schools, or private schooling, a much-studied aspect of such programs is identifying the treatment effect of "choice" schools on students. Historically, estimates of this effect have come from large observational studies of student performance from different school sectors (e.g., public, private, religious) – studies that have been subject to the long-standing criticism of unobserved selection bias (Alexander & Pallas 1983, Manski 1993). That is, even when controlling for observable differences between those who attend choice schools and those who do not, one cannot eliminate the possibility that unobservable differences, such as student motivation or the value a family places on education, are inflating the observed difference in outcomes between the two groups.

2.2

Student assignment lotteries put in place to deal with oversubscription to popular schools and pilot choice programs (mostly in the United States) have helped overcome this methodological problem. Such lotteries – where after submitting an application to a school or a program, students are randomly selected for admission – have provided researchers excellent opportunities to conduct randomized field experiments. By eliminating the selection bias concerns that have historically caused much debate in observational studies on the achievement effects of non-neighborhood schools (Coleman et al. 1982; Alexander & Pallas 1983; Bryk et al. 1993; Morgan 2001; Altonji et al. 2002), lottery-based studies are forming a base of evidence that can help us assess the achievement effects within and across types of choice schools. Examples include analyses of private school voucher pilots (Greene et al. 1997; Howell et al. 2002), charter schools (Hoxby & Rockoff 2005; Abdulkadiroglu et al. 2009; Gleason et al. 2010), and public choice programs (Cullen et al. 2006).

2.3

However despite their high internal validity, treatment effect estimates from lottery-based studies have been critiqued for not telling us all we need to know about choice as educational policy. The primary critique is that their effect estimates are only able to capture the short-term gains from students sorting into different schools (Goldhaber & Eide 2003). They likely cannot capture the longer-term, systemic effects predicted by the market-based logic of school choice reform, such as gains from increased competition or investment as predicted (Hoxby 2003; Sirer et al. 2015). In the next section, I describe a model that demonstrates an additional, and often overlooked, limitation of lottery-based studies that is independent of these typical critiques.

Model Description

3.1

To conduct the computational experiments, I used an agent-based model of the transition to public school choice recently published in JASSS (Maroulis et al. 2014). The original model highlighted the importance of considering the dynamics, and not just equilibrium characteristics, of the transition to school choice. More specifically, it demonstrated that the equilibrium outcome of transitioning to choice depends not only on the quality and total number of new schools in the system, but also on the timing of the entry of those new entrants. In this section, I provide a brief overview of the model highlighting the features most pertinent to the current study. For additional details, the reader is referred to the original paper. The model itself is publicly available at the ComSES Computational Model Library.^[2] The ComSES upload includes an initialization file of synthetic data resembling the Chicago Public Schools (CPS) data used by the authors of the original study.

3.2

The agents in the model are students and schools who are a placed on a grid of sites that represent the geography of the city of Chicago (Figure 1). Students rank schools by using a preference function based on the mean student achievement and geographic proximity of a school:

$$ U_{ij} (ma_j, proximity_{ij}) = ma_j^{\alpha_i} \ast proximity_{ij}^{(1-\alpha_i)} $$

(1)

\(\alpha_i\) determines the weight given by a student to the mean achievement of the school. In the original model values of \(\alpha_i\) were distributed across students by drawing from a normal distribution with mean \(\alpha\) and a standard deviation of 0.05, a parameterization I keep here.

3.3

Schools augment the achievement of their students using a growth function based on the characteristics of the student and a school-specific quality parameter referred to as the "value-added" of the school. The coefficients of the achievement growth function and the distribution of the school-specific value-added parameter were statistically estimated using data from CPS. More specifically, achievement for student \(i\) attending school \(j\) in any given time period of the model is determined using the following equation (Maroulis et al. 2014, Table 1):

$$ achiev_{2i} = -0.0956 + 0.6794 \ast achiev_{1i} + 0.1567*white_i + 0.1151*male_i- 0.0629 \ast poverty_i + va_j + r_{ij} $$

(2)

\(achiev_1\) is the 8th grade standardize math score of a student. \(white\) and \(male\) are indicator variables for race and gender, respectively. \(poverty\) is the concentration of poverty in the student's home census block. \(achiev_1\), \(white\), \(male\), and \(poverty\) are all student-level variables that come from the initialization file. \(va_j\) is the value-added of school \(j\). \(r_{ij}\) is an error term drawn randomly from a normal distribution with mean zero. The \(va\) for each school and the standard deviation of the distribution of \(r_{ij}\) were estimated from the CPS data.

3.4

At time period zero, all students attend their assigned catchment area school. Starting with time period 1, incoming cohorts of students are allowed to start choosing their school based on the preference function described in Equation (1). The percentage of students who can choose (the "choosers") is determined by the exogenous parameter, \(pc\). In random order, choosers attempt to attend their top ranked school and continue working through their ranked list of schools until they find a placement. Students are guaranteed admission to their assigned catchment area school. For others, placement can be denied only if there are no spaces available at a chosen school. The number of available spaces at a school is a function of its design capacity, which comes from the initialization file of the model.

3.5

Once enrolled in a school, a student remains at the same school for four years and receives an achievement gain determined by Equation (2). Over time, some schools gain students while others lose them. Schools whose enrollments fall below a minimum threshold of enrollment are permanently closed. The original model included a mechanism for the introduction of new schools. I turn this mechanism off for the purposes of the experiments presented below. I also created a new measure, "better available capacity" (\(bac\)), to capture a dimension important to the current study – the amount of "good slack" or "good excess capacity" available to choosers at the beginning of the simulation. \(bac\) was calculated by asking every randomly assigned chooser at the start of the simulation to calculate the number of spaces per school potentially available to them with a higher value-added. It is the mean of this student-level quantity across all choosers.

Figure 1. Model Description (adapted from Maroulis et al. 2014)

Computational Experiments and Analysis

4.1

The primary goal of the computational experiments presented in this section was to understand how district-level achievement outcomes varied depending on a) the relative weight given to mean achievement of the a school by the choosers, \(\alpha\), and b) the percentage of students who are able to take advantage of the ability to choose, \(pc\). Data was generated by systematically running the model for twenty time periods under various combinations of \(\alpha\) and \(pc\). Each run of the model represents a stochastic process. Therefore, each combination of parameters was repeated fifty times to create a distribution of outcomes for a particular set of parameter values.

Outcome 1: Mean Achievement

4.2

Figure 2 plots the mean achievement across all students at the end of twenty time periods. Each point on the figure represents the average of the final mean achievement value across the fifty runs for the hypothetical district characterized by a particular combination of \(\alpha\) and the percent choosers, \(pc\). When comparing the scenarios in Figure 2, there were no surprises: the more that individual students favored achievement relative to geographic proximity (i.e., high \(\alpha\)), the higher the mean achievement. Also, with the exception of the case where students heavily favored geographic proximity (\(\alpha = 0.2\)), the greater fraction of students who participated in the program, the higher the mean achievement of the district. It is interesting to note, however, that the overall change in mean achievement across runs in Figure 2 was rather small. Even in the best-case scenario (\(\alpha =1\)), the difference between the initial mean achievement and the final mean achievement after giving students choice was not greater than 0.05 standard deviations. The reason for this is that for the sample of CPS students used to initialize the achievement growth rule of the model, school effects make a relatively small contribution to a student achievement growth when compared to individual-level factors (Maroulis et al. 2014, Table 1).

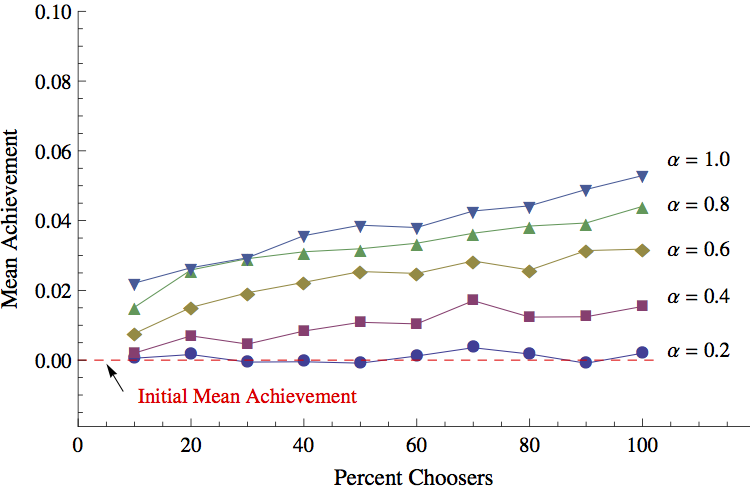
Figure 2. Mean Achievement versus Percent Choosers, by \(\alpha\)

Outcome 2: Treatment Effect

4.3

The treatment effect of a real world lottery-based study is estimated by comparing the outcomes of those given the opportunity to attend a new school to those who were not (e.g., lottery winners vs. non-winners). A conceptually similar measure can be calculated in the simulation by comparing the choosers to the non-choosers. More specifically, the treatment effect for any given run of the model was calculated by taking the difference in mean achievement between choosers and non-choosers at the completion of a run. Since in the simulation we can be certain only the randomly selected choosers could attend a different school and that all of those given the opportunity to choose did indeed do so (e.g., there were no "non-compliers"), no additional adjustments are necessary. Figure 3 plots this treatment effect at the completion of the twenty-time period runs versus \(pc\) for a range of \(\alpha\) values. As in Figure 2, each point represents the average across the fifty runs for the hypothetical district characterized by that particular combination of parameters.

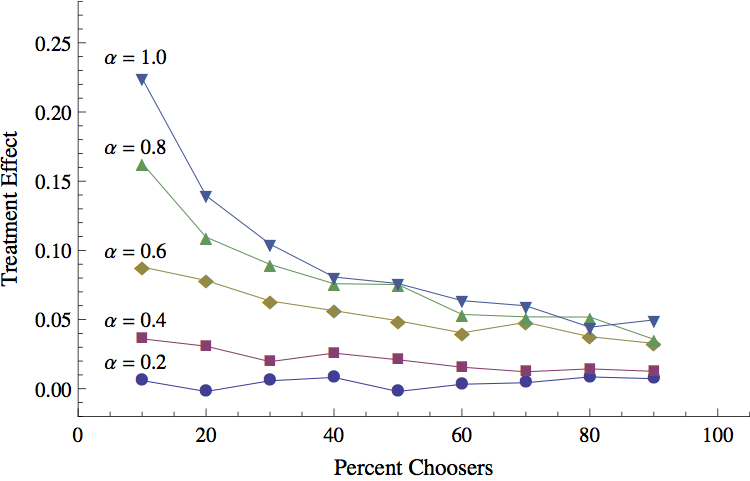
Figure 3. Treatment Effect vs. Percent Choosers, by \(\alpha\)

4.4

As might be expected, treatment effects were for the most part larger for the hypothetical districts where individuals placed a higher value on the achievement of the school (higher \(\alpha\)). However, when comparing the results for hypothetical districts with the same value of \(\alpha\), the treatment effect largely goes down as \(pc\) increases – the exact opposite relationship than what was observed between percent choosers and mean achievement in Figure 2. Stated differently, if one were to use the treatment effects to compare the effectiveness of school choice in high participation district and low participation district – but identical in every other way – one would mistakenly infer that the choice program helped the high participation district less than the low participation district.

4.5

The reason for this highlights the importance of considering the underlying mechanisms of a system when estimating and interpreting causal effects: In cases where there is very low participation, most students looking for a new school are likely to find a spot at one of the highest value-added schools, consequently realizing the largest achievement increases possible in the system. For example, in the extreme case where only one student is given the ability to choose, that student would likely find room in a very high value-added school. When comparing her achievement gain to the non-choosers (i.e., everyone else) it will be high. But what if fifty, or a hundred, or a thousand students participated? While the program participants would still likely to attend schools with higher value-added than the one from which they came, they would also have to start filing into schools with lower value-added. That is, the thousandth chooser would most likely not attend a school with as high a value-added as the first chooser, and therefore receive less benefit from the program than the first. Consequently, as long as capacity constraints exist and schools do not have essentially the same value-added, the mean achievement of choosers in comparison to non-choosers must necessarily decrease as more students take advantage of the opportunity to choose.^[3]

Relationship to Initial District Capacity

4.6

The results depicted in Figure 3 were generated using the same distribution of available capacity across schools for each run, namely, the one inherited in the initialization file of Chicago Public Schools. School districts, of course, can vary in the amount of excess capacity available when a choice program is first implemented. Consequently, one would expect that in addition to the participation rate, the amount of high value-added capacity initially available in the system should impact the treatment effect of an experiment. To verify, I ran the model 200 times, each time randomly assigning the amount of better available capacity at the start of a run.^[4] \(\alpha\) was set to 1 for all runs. Figure 4 presents the treatment effect calculated at the end of each of the 200 runs corresponding to the \(bac\) of the run. As expected, there was a clear relationship between \(bac\) and treatment effect. Higher levels of better available capacity corresponded to larger differences in achievement between choosers and non-choosers. Note again that the hypothetical districts in these runs only differed in \(bac\) and no other way. Students in each district valued academic achievement similarly and the distribution of value-added across schools was the same for each run.

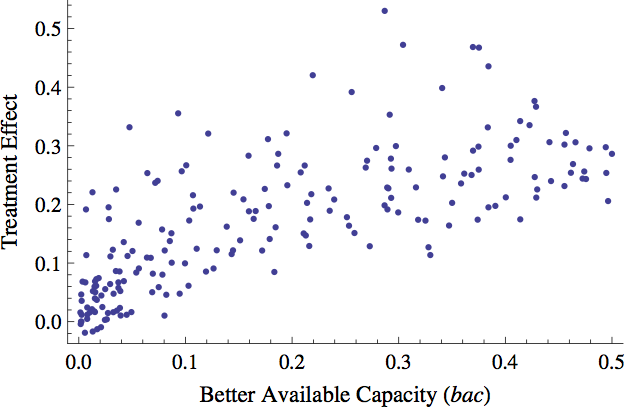
Figure 4. Mean Achievement vs. Better Available Capacity

Discussion and Conclusion

5.1

For research to be useful to policymaking it must be based on valid causal inferences. In the school choice debate, as in many other contexts, a key factor casting doubt on statements of cause has been concern about selection bias: How can we be sure that differences between students who attend choice schools and others are not attributable to unobserved factors that both influence their performance and make them more likely to attend those schools? Lotteries put in place to deal with oversubscription to sought-after programs and schools have provided a way out of this conundrum. By randomizing who is offered the opportunity to participate, lottery-based research designs break the link between treatment assignment and unobserved individual characteristics.

5.2

But as important as it is for researchers to make causal inferences with high internal validity, from a policy perspective it is equally important that we be able to interpret those inferences: Was the estimate due to the manner in which members of the study population chose which schools to attend? Will the effects at scale mirror those from a small program? Indeed, with a reform like school choice that has so many variants and is applied in so many contexts, the space of policy-relevant contingencies is quite large.

5.3

In this paper, I took a step towards the exploration that space through the use of agent-based simulation. More specifically, I conducted computational experiments similar in design and rationale to field experiments that compare the outcomes of randomly assigned lottery winners to non-winners. I kept the experimentation simple. I used an existing model that utilized a minimal set of stylized decision rules for the agents, and conducted experiments that manipulated those rules in straightforward ways. The experimentation led to a finding that in retrospect is necessarily true, but in foresight (and practice) almost always put in the background: Treatment effect estimates from districts with different program participation rates will be different, even if the districts are identical in every other way. This is because capacity constraints increasingly limit the amount of choosers who are able to attend the highest value-added schools, causing the magnitude of the treatment effect to fall.

5.4

One way to interpret this finding is that our model illustrates a violation of the stable unit treatment value assumption (SUTVA) of the "potential outcomes framework" of statistical causal inference (Rubin 1986). SUTVA states that the outcome for one subject does not depend on the treatment assigned to others. One potential SUTVA violation in school choice is already well known – the achievement of one student may depend on the composition of the others in their classroom or school (Zimmer & Toma 2000). This study highlights a less direct, but perhaps equally concerning problem: Even in the absence of classroom- or school-level peer effects, as long as capacity is limited, the expected outcome for any given student is dependent on the number of other students in the district who have similar preferences for schools.

5.5

At a minimum, the findings of this study imply that researchers should consider accounting for the amount of "better" capacity initially available to participants when using treatment effects estimated from existing programs to either a) project the impact of a larger scale program, or b) synthesize effect sizes estimated across programs. The measure developed in this study to characterize the better available capacity of the hypothetical districts in the model, \(bac\), could be applied to program data to aid with both these purposes.

5.6

At a maximum, the findings of this study significantly add to existing concerns about using treatment effects from lottery-based studies to draw policy implications for school choice models. A common critique of short-term social experiments is that they do not adequately capture the general equilibrium consequences of a full-scale program, such as the effects of sustained competitive interaction between schools or investment by new entrants (as in the case of government vouchers that can be used in private schools) (Goldhaber & Eide 2003). A second concern pertains to the representativeness of the schools included in lottery-based studies (Tuttle et al. 2012). This study illustrates that even in the absence of systemic effects and sample representativeness issues, treatment effect estimates from well-executed field experiments can still yield misleading results. Indeed in the computational experiments, treatment effects were the most misleading when one would expect choice programs to be most effective – in cases where a large fraction of students took advantage of the increased access to schools (high \(pc\)), and did so by selecting schools on the basis of school achievement (high \(\alpha\)).

5.7

To be clear, the results of this study do not imply that lottery-based studies do not meaningfully estimate the effects of attending particular groups of schools. In fact, quite the opposite is true when SUTVA holds. But this study suggests that all else being equal, SUTVA is less likely to hold as participation in choice programs grows, even without turning to arguments about competition, investment, and direct peer effects. In this sense, lottery-based studies of school choice share a resemblance to randomized experiments that estimate the extent to which vaccines can protect individuals from becoming infected with disease. The SUTVA violation in vaccine trials has long been recognized as limitation, since vaccination can affect the infection likelihood of both treated and untreated persons. Consequently, to extrapolate from estimates of individual to population-level effectiveness, epidemiologists and public health researchers rely on computational models that treat the estimates of individual effectiveness as a single input in a larger dynamic process (e.g., Woodhouse et al. 1995; Colizza et al. 2007). This study suggests that a similar approach could be used with great benefit in the analysis of school choice programs.

5.8

Several caveats are warranted about the approach and assumptions of this study. First, I reiterate that the goal of this study was not to evaluate the causal effect of introducing any particular choice intervention. Instead, my intent was to generate insight that can aid the interpretation of existing findings, as well as guide the design of future empirical work. Relatedly, the data used to initialize this model come from a district that had already introduced an open enrollment program. As such, the initial state of the model may already reflect changes in student composition or school quality attributable to that program. While for current purposes this does not pose a problem, it does underscore that one should not attempt to draw causal inferences about the effect of the Chicago open enrollment program from any parts of the analysis and modeling in this study.

5.9

Second, though having the virtue of being simple and easy to interpret, the model used for experimentation admittedly uses incomplete rules for student and school behavior. Students used a utility function that evaluated schools on only two factors: mean achievement, whose value was shared by all students; and geographic proximity, whose value was calculated relative to a particular student. Moreover, schools could only impact students by improving their achievement, and that improvement was uniform across all students. An interesting extension of this study would relax these assumptions in a manner that would allow students to pick schools on criteria that "fit" them best. To the extent such matching occurs, one might find that the SUTVA violation observed this study might apply more to the estimation of effects for some student groups over others.

5.10

Third, two important feedback mechanisms associated with choice program improvement are not in the model: within-school improvement and new school entry. Both would likely affect the relative differences across scenarios depicted in Figure 2, and the magnitude of the treatment effects in Figure 3. However, the extent to which either mechanism would mitigate the SUTVA violation highlighted by our computational experiments depends on the extent to which this improvement was associated with adding better available capacity to the district. For example, if new schools (spawned by existing schools or started by new entities) could very quickly provide better available capacity, treatment effect estimates would be less sensitive to participation rates. While neither of these improvement mechanisms was explored in this paper, agent-based modeling is an approach well suited to the investigation of both in future work.

Notes

¹In economics, the models have taken the form of computational general equilibrium models (CGE) that incorporate interrelationships between education and related markets such as housing (for review, see Nechyba 2003).

²The model was developed using the NetLogo Programmable Modeling Environment (Wilensky 1999). The NetLogo code and initialization file can be accessed here: http://www.openabm.org/model/3695

³Note that this discussion assumes a positive correlation between mean achievement and value-added, which is indeed the case in the CPS data used to initialize the model. As a sensitivity analysis, I also ran computational experiments where students rank schools based on the value-added of the school, as opposed to the mean achievement. The decrease in treatment effect size as participation rate increased was even more pronounced when under this condition.

⁴The model does not have a slider specifically for \(bac\). Instead, for each run I randomly assigned the percentage of choosers, and the extent to which schools are allowed to expand beyond their design capacity. Together these two factors determine \(bac\).

References

ABDULKADIROGLU, A., Cohodes, S., Dynarski, S., Fullerton, J., Kane, T. J., & Pathak, P. (2009). Informing the debate: Comparing Boston's charter, pilot and traditional schools (Tech. Rep.). The Boston Foundation.

ALEXANDER, K. L., & Pallas, A. M. (1983). School sector and cognitive performance: When is a little a little? Sociology of Education, 58(2), 115–128. [doi:10.2307/2112251]

ALTONJI, J., Elder, T., & Taber, C. (2002). An evaluation of instrumental variable strategies for estimating the effect of catholic schools (No. 9358). National Bureau of Economic Research. [doi:10.3386/w9358]

BERENDS, M., Springer, M. G., Ballou, D., & Walberg, H. (Eds.). (2009). Handbook of research on school choice. Taylor and Francis.

BRYK, A. S., Lee, V. E., & Holland, P. B. (1993). Catholic schools and the common good. Cambridge: Harvard University Press.

COLEMAN, J. S., Hoffer, T., & Kilgore, S. (1982). High school achievement: Public, catholic, and private schools compared. New York: Basic Books.

COLIZZA, V., Barrat, A., Barthelemy, M., Valleron, A. J., & Vespignani, A. (2007). Modeling the worldwide spread of pandemic influenza: baseline case and containment interventions. PLoS Medicine, 4(1), e13. [doi:10.1371/journal.pmed.0040013]

CULLEN, J. B., Jacob, B. A., & Levitt, S. (2006). The effect of school choice on participants: Evidence from randomized lotteries. Econometrica, 74(5), 1191–1230. [doi:10.1111/j.1468-0262.2006.00702.x]

GILL, B., Timpane, P. M., Ross, K., Brewer, D. J., & Booker, K. (2007). Rhetoric versus reality: What we know and what we need to know about vouchers and charter schools. RAND Corporation.

GLEASON, P., Clark, M., Tuttle, C., & Dwoyer, E. (2010). The evaluation of charter school impacts: Final report (Tech. Rep. No. NCEE 2010-4029). U.S. Department of Education.

GOLDHABER, D. D., & Eide, E. R. (2003). Methodological thoughts on measuring the impact of private sector competition. Educational Evaluation and Policy Analysis, 25(2), 217–232. [doi:10.3102/01623737025002217]

GREENE, J. P., Peterson, P., & Du, J. (1997). Effectiveness of school choice: The milwaukee experiment. Education and Urban Society, 31(2), 190-213 [doi:10.1177/0013124599031002005]

HARLAND, K., & Heppenstall, A. J. (2012). 'Using Agent-Based Models for Education Planning: Is the UK Education System Agent Based?' In Agent-based models of geographical systems (pp. 481–497). Springer Netherland. HOWELL, W., Wolfe, P., Campbell, D., & Peterson, P. (2002). School vouchers and academic performance: Results from three randomized field trials. Journal of Policy Analysis and Management, 21(2), 191–217.

HOXBY, C. M. (2003). School choice and school productivity: Could school choice be a tide that lifts all boats? In C. M. Hoxby (Ed.), The economics of school choice. Chicago: The University of Chicago Press. [doi:10.7208/chicago/9780226355344.003.0009]

HOXBY, C. M., & Rockoff, J. E. (2005). Findings from the city of big shoulders. Education Next, 4, 52–59.

MANSKI, C. F. (1993). Identification of endogenous social effects: The reflection problem. The Review of Economic Studies, 60(3), 531–542. [doi:10.2307/2298123]

MAROULIS, S., Bakshy, E., Gomez, L., & Wilensky, U. (2014). Modeling the Transition to Public School Choice. Journal of Artificial Societies and Social Simulation, 17(2), 3. https://www.jasss.org/17/2/3.html. [doi:10.18564/jasss.2402]

MAROULIS, S., Guimerà, R., Petry, H., Stringer, M.J., Gomez, L.M., Amaral, L.A.N. & Wilensky, U. (2010). Complex Systems View of Educational Policy Research. Science, 330, 38–89. [doi:10.1126/science.1195153]

MILLINGTON, D.A., Butler, T. and Hamnett, C. (2014). Aspiration, Attainment and Success: An agent-based model of distance-based school allocation. Journal of Artificial Societies and Social Simulation, 17(1), 10. https://www.jasss.org/17/1/10.html. [doi:10.18564/jasss.2332]

MORGAN, S. L. (2001). Counterfactuals, causal effect heterogeneity, and the catholic school effect on learning. Sociology of Education, 74, 341–374. [doi:10.2307/2673139]

NECHYBA, T. (2003). What can be (and what has been) learned from general equilibrium simulation models of school finance? National Tax Journal, 56 (2). [doi:10.17310/ntj.2003.2.06]

RUBIN, D. B. (1986). Statistics and causal inference: Comment: Which ifs have causal answers. Journal of the American Statistical Association, 81(396), 961–962. [doi:10.2307/2289065]

SIRER, M.I., Maroulis, S.,Guimera, R., Wilensky, U., & Amaral, L.A.N. (2015). "The Currents Beneath the 'Rising Tide' of School Choice: An Analysis of Student Enrollment Flows in the Chicago Public Schools". Journal of Policy Analysis and Management, 34(2), 354–357. [doi:10.1002/pam.21826]

TUTTLE, C., Gleason, P., & Clark, M. (2012). Using lotteries to evaluate schools of choice: Evidence from a national study of charter schools. Economics of Education Review, 31(2), 237–253. [doi:10.1016/j.econedurev.2011.07.002]

WILENSKY, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.

WOODHOUSE, D.E., Potterat, J.J, Rothenberg, R.B, Darrow, W.W, Klovdahl A.S. & Muth, S.Q. (1995). "Ethical and Legal Issues in Social Network Research: The Real and Ideal." Pp. 131-143 in Social Networks, Drug Abuse and HIV Transmission, edited by Richard H. Needle, Susan L. Coyle, Sander G. Genaer and Robert T. Trotter II. Bethesda, MD: National Institute on Drug Abuse Series, NIDA Research Monograph 151.

ZIMMER, R. W., & Toma, E. F. (2000). Peer effects in private and public schools across countries. Journal of Policy Analysis and Management, 19(1), 75–92. [doi:10.1002/(SICI)1520-6688(200024)19:1<75::AID-PAM5>3.0.CO;2-W]