Bruce Edmonds (1999)

Journal of Artificial Societies and Social Simulation vol. 2, no. 3, <https://www.jasss.org/2/3/2.html>

Abstract

An investigation into the conditions conducive to the emergence of heterogeneity amoung agents is presented. This is done by using a model of creative artificial agents to investigate some of the possibilities. The simulation is based on Brian Arthur's 'El Farol Bar' model but extended so that the agents also learn and communicate. The learning and communication is implemented using an evolutionary process acting upon a population of strategies inside each agent. This evolutionary learning process is based on a Genetic Programming algorithm. This is chosen to make the agents as creative as possible and thus allow the outside edge of the simulation trajectory to be explored. A detailed case study from the simulations show how the agents have differentiated so that by the end of the run they had taken on qualitatively different roles. It provides some evidence that the introduction of a flexible learning process and an expressive internal representation has facilitated the emergence of this heterogeneity.

Keywords:

differentiation, El Farol, evolution, co-evolution, emergence, heterogeneity, society, roles, social structure, genetic programming, SDML, naming, creativity

Introduction - the El Farol Bar

1.1

In 1994, Brian Arthur (1994) introduced the 'El Farol Bar' problem as a paradigm of complex economic systems. In this model each agent in a population has to decide whether to go to the bar each week (i.e. make a binary choice). It is given that all agents will try to take this decision so that they aim to go to the bar when it is not too crowded (which is the case when more that 60% of the agents go). So it is in the interest of each agent to do the opposite of the majority of the other agents. In other words this is a discoordination game [note 1]. This set-up ensures that any model of the problem that is shared by most of the agents will be self-defeating, for if most agents predict that the bar will not be too crowded then they will all go and it will be too crowded, and vice versa.

1.2

Brian Arthur modelled this problem by randomly dealing each agent a fixed menu of potentially suitable models to predict the number who will go given past data (e.g. the same as two weeks ago, the average of the last 3 weeks, 90 minus the number who went last time, or the number indicated by the rational expectations equilibrium). Each week each agent evaluates its menu of models against the past data and chooses the one that was the best predictor. It then uses this to predict the number who will go this time. The agent then decides to go if this prediction is less than 60 and not if it is more than 60.

1.3

As a result the number who, in fact, go to the bar oscillates in an apparently random manner around the critical 60% mark, but this is not due to any single pattern of behaviour - different groups of agents swap their preferred model of the process all the time. Although each agent is applying a different model at any one time chosen from a different menu of models, with varying degrees of success, when viewed globally they all seem pretty indistinguishable, in that they all regularly swap their preferred model and join with different sets of other agents in going or not. None takes up any particular strategy for any length of time or adopts any identifiably characteristic role. Viewed globally they seem to be acting homogeneously.

1.4

The purpose of this paper is to report on the difference in their behaviour when Arthur's model of the problem is extended. In this extension these agents are given suitably powerful learning and communicative mechanisms and the whole system is allowed to co-develop. The key result is that if one does this then the agents seem to spontaneously differentiate, acquiring qualitatively different roles and types of strategy. I will also note the importance of the ability of the agents to distinguish between other agents by name and include aspects of these other's actions as inputs in their strategies.

1.5

The approach taken in this paper is to endow each agent with a creative but bounded rationality in the form of an evolutionary process among a population of competing mental models inside each agent. This is described in next section. I briefly review a paper by Akiyama and Kaneko that illustrates temporal and class differentiation. I describe how this is applied to the El Farol Bar problem in a way which will allow social relations to emerge among the agents. The results are considered in general, and then in more detail with an examination of a single run and a study of the interactions at the end of this run. The heterogeneity which emerges is considered in a concluding discussion.

Modelling Boundedly Rational Agents using the Evolution of Mental Models

2.1

The purpose of the simulation to be described is to investigate how the presence of certain agent abilities (e.g. the ability to distinguish other agents by name) enables or inhibits the emergence of qualitatively different roles among the members of that society (given a particular social structure). I am not claiming in any way that certain conditions make any particular outcomes inevitable, the point is only to examine some of the possibilities.

2.2

In order to get a handle on the outside possibilities inherent in this simulated society I have tried to give the agents a learning and decision ability that is as unconstrained as possible by artificial limitations as to what sort of models they can devise and use, i.e. the agent is allowed an pretty open-ended creativity limited only by some resource bounds. The development of the models/strategies that the agents use is rooted in their evaluation in actual or potential use as a determinant of action. This approach can be broadly characterized as "constructivist" in the sense of Dresher (1991), Reigler (1992), and Vario (1994).

2.3

The approach to such a creative cognition that I will take is based on that presented in (Holland et al. 1985). This takes results and thiniking in cognitive science and philosophy and presents a picture of creative induction within a computational framework. The key features of this picture are that such cognition proceeds by:

• acting upon a population of rules;
• selecting these rules according to how successful they have been (or would have been);
• introducing variation into these rules using a variety of mechanisms;
• allowing feedback with the environment to substantially influence their development.

2.4

The source is not critical to this paper as I am not claiming descriptive accuracy, but rather using a credible model of agent cognition to investigate some of the possibilities inherent in their interaction.

2.5

The Genetic Programming algorithm (Koza, 1992) provides a paradigm which enables this picture of cognition to be implemented in an artificial agent. This paradigm is explained elsewhere in this journal (Edmonds 1999a) - it involves a collection of tree-like expressions which conform to a formal grammar, that are evolved by the operations of random variation, propagation and selection, in response to its interaction with its environment. This algorithm is modified in two main ways in order to make it more suitable: a relatively small population is use for each agent and the variation operator is restricted so that the variation does not sdominate the development of agent strategies. This model has been shown to be descriptively appropriate in at least one case with real subjects (Edmonds, 1999d).

2.6

This model results in agents:

• who incrementally develop models of their environment;
• who develop their models in a parallel manner so that different (and even contrary) models can be brought to bear in different circumstances;
• whose mechanisms of learning dominate those of inference;
• who can develop context sensitive strategies;
• who are able to identify other agents individually and develop models specifically concerned with those agents;
• who have a flexible and expressive internal system of representation, so that they are as little constrained as possible in what model the can develop;
• who are able to develop any connection between their communication and their action that is appropriate;
• who are able to deal with received communication in what-ever way is best for it;

Evolution of Co-operation, Differentiation, Complexity, and Diversity

3.1

The work in this paper can be seen as following that of Akiyama and Kaneko (1996), who investigated the evolution of "Co-operation, Differentiation, Complexity, and Diversity" in a three person game. In this game the players get a payoff if their play (0 or 1) matched one and only one of the other player's plays in that round. Thus there is motivation for the players to evolve strategies with a mixture of co-operation and competition. They distinguish between two types of differentiation:

• Class differentiation - here a sub-group of the players learn to co-ordinate their play so as to exploit the others over a period of time.
• Temporal differentiation - here players 'take turns' at gaining payoff by effectively co-ordinating their plays over time to maximize and share the gains.

3.2

They noticed that when the players could distinguish between the players on their left and right in their representation of strategies a 'bootstrapping' process of increasing diversity and complexity arose. When players had no mechanism for distinguishing between their peers, no temporal differentiation emerged. The model exhibited below can be seen as an extension of Akiyama and Kaneko's study, showing the crucial importance of the open-endedness of the learning and the presence of effective naming of individuals.

The Simulation Set-up

4.1

The agent modelling approach adopted come from the framework described in (Moss and Edmonds 1998) and broadly follows (Edmonds 1999b). Each agent has a population of strategies, which implicitly correspond to alternative models of its world. This population develops in a slow evolutionary manner based on their past successes (or otherwise). The basic agent architecture is illustrated below in figure 1. In this simulation the strategies are restricted to the syntax of formal language (see the appendix). The goals of the agent are to maximise its total score which represents the agent's success in going to the Bar when it is not too crowded.

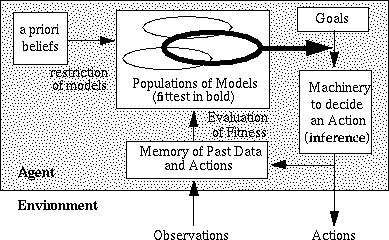
Figure 1: The agent architecture.

4.2

Each notional week, the new population of strategies ls is produced using a genetic programming (GP) algorithm (Koza, 1992). In GP each 'gene' is a tree structure, representing a program or other formal expression of arbitrary complexity. A population of such genes is evolved using a version of crossover that swaps randomly selected sub-trees and propagation which simply caries over trees into the next generation. Selection of genes for crossover and propagation is done probabilistically with a likelihood of selection in proportion to its fitness so that genes that have been more successful are preferentially selected for.

4.3

I have slightly modified this to make this a little more descriptively approapriate than a standard GP algorithm. I have used only a small proportion of tree crossover [note 2], a higher proportion of propagation and set it up so that a few new (randomly genberated) genes are introduced each time. Then the best model is selected and used to determine first its communicative action and subsequently whether to go to El Farol's or not.

4.4

In this extension of the model agents have a chance to communicate with other agents before making their decision whether to go to El Farol's Bar. Each of the agents' models of their environment is composed of a pair of expressions: one to determine the action (whether to go or not) and a one second to determine their communication with other agents. The action can be dependent upon both the content and the source of communications received from other agents. Although the beliefs and goals of other named agents are not explicitly represented, they emerge implicitly in the effects of the agents' models.

4.5

The two parts of each model are expressions from a two-typed language specified (by the programmer) at the start (thus, strictly, this is strongly-typed GP (Montana, 1985)). A simple but real example is shown in Figure 2 below. Translated this example means: that it will say that it will go to El Farol's if the trend predicted over observed number going over the last two weeks is greater than 5/3; but it will only actually go if it said it would go or if agent 3 said it will go.

Figure 2: A simple example model

4.6

The agent gains by going to the El Farol Bar when it is not too crowded. I have set it so that the agents evaluate their success by adding scores allocated to the results of each action. They score 0.4 if they go when it is two crowded, 0.5 if they stay at home and 0.6 if they go when it is not too crowded. Thus each agent is competitively developing its models of what the other agents are going to do.

4.7

In this simulation the agents judge their internal models by the total score they would have gained over the past 5 time periods if they had used that model. Each agent had 40 mental models of average depth of 5 generated from the language of nodes and terminal specified in Figure 3.

Figure 3: Possible nodes and terminals of the tree structured genes

4.8

The formal languages indicated in figure 3 allow for a great variety of possible models, including arithmetic projections, stochastic models, models based on an agents own past actions, or the actions of other agents, logical expressions and simple trend projections. The primitives are briefly explained in figure 4.

Figure 4: A brief explanation of the primitives that can be used to construct strategies

4.9

The whole simulation proceeds in the following way:

Each week each agent does the following in parallel with the other agents:

1. It generates a new population of strategies based on its old population by applying the operations of tree-crossover and propogation with a probability in proporation to their past success. Also a few newly generated strategies are introduced.
2. It the assigns a fitness to all these strategies by evaluating what actions they would have led to if used in the past 5 weeks and adding the scores that would have resulted.
3. It chooses the strategy with the best fitness.
4. It evaluates the "talk" half of the best strategy in the present context to determin what it communicates to the other agents.
5. It remembers what the other agents said.
6. It evalutates the "action" half of the best strategy in the present context (including the communications from set 5) to determin whether it goes to the bar or not.
7. It remembers what each of the other agents did.

A fuller specification of the simulation is given in the appendix.

Some Results

5.1

As a result of the model attendance at the bar fluctuates chaotically about the critical number of agents (see the example plot in figure 5). Although this appears to be stochastic but in fact this an example of complex globally-coupled chaos (for more discussion on this issue see Edmonds 1999b). In any case the attendance does not seem to settle down into any regular pattern.

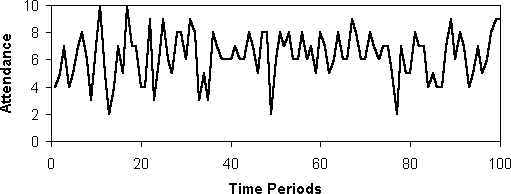
Figure 5: Number of people going to El Farol's each week in a typical run

5.2

This paper is concerned with the emergence of differentiation among the agents. One indication of the emergence of class-based differentiation is whether each agent's population of strategies converges onto strategies that are different from those converged upon by the other agents. Thus an indication of the emergence of differentiation would be that average spread of fitnesses of each agents population of strategies decreased but each agent's average fitness diverged from the other's averages (i.e. they spread apart). In other words the population average of the standard deviation of each agents' model fitnesses should decrease, indicating that each agent was settling on a particular style of strategy, while the population standard deviation of each agent's average model fitness should increase, indicating that the strategy styles that they were settling upon where different from each other in terms of fitness.

5.3

Figure 6 shows the average spread (in standard deviations) of the fitnesses of each agent's population of strategies (averaged over the 11 runs) for the standard set-up as described above over 11 runs of the simulation [note 3] (in each of the following figures the dark line indicates the average value over these runs and the grey lines one standard deviation of the variance over these runs up and down from this). Figure 7 shows the spread of the average fitnesses for each agent's population of strategies. These two graphs clearly indicate that there this simulation results in a class-based differentiation among the agents (at least in terms of the fitnesses of their strategies).

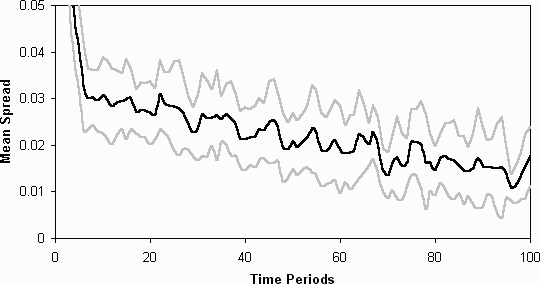
Figure 6: The average spread (in standard deviations) of the fitnesses of each agent's collection of models, (11 runs, black line shows average of these runs and the grey a standard deviation of the variation over the runs up and down)

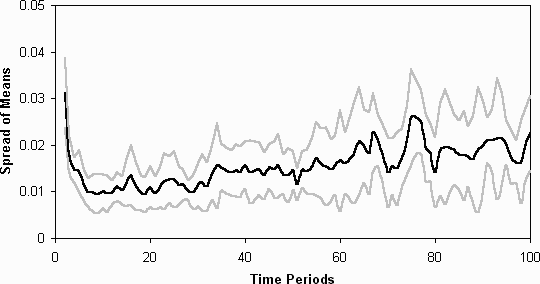
Figure 7: The spread (in standard deviations) of the averages of the fitnesses of the agent's models (11 runs)

5.4

In order to start teasing out the reasons for this differentiation, I ran the simulation again but keeping each agent's menu of strategies fixed (instead of evolving). The agent's would still evaluate all their strategies each time period and pick which was best to determine their action. This would make the simulation similar to Arthur's original simulation, except that there is a richer variety of strategies including one's which allow the imitation of action and the inclusion of utterances as factors in their strategies. Unsurprisingly we do not see any evidence of class-based differentiation (figure 8 and figure 9).

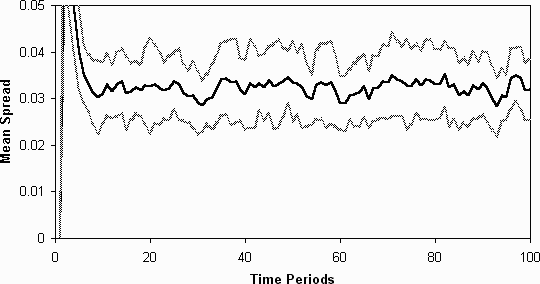
Figure 8: The average spread (in standard deviations) of the fitnesses of each agent's collection of strategies, without learning (averaged over 20 runs)

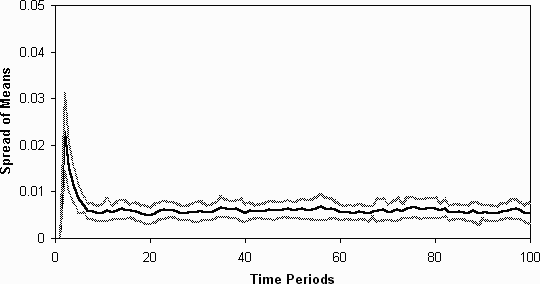
Figure 9: The spread (in standard deviations) of the averages of the fitnesses of the agent's models, without learning (averaged over 20 runs)

5.5

More interesting is the comparison with a simulation where agents lack the ability to use any of the primitives which refer to other agent by name (saidBy, wentLastTime and saidByLast). Thus the agent's are still capable of learning complex strategies based on past attendance patterns but not able to include facts about the actions or utterances of other particular (i.e. named) agents. In this case there was still a tendency towards differentiation but this tendency was now very much less (figure 10 and figure 11) [note 4]. Thus the ability to relate actions directly to those of the other agents has greatly aided the process of differentiation. Only 7 of these runs were done because they took a lot longer than those of the standard set-up described - this seems to be because the agents developed extremely complex strategies which took a lot of computational effort to evaluate. Thus it may be that the tactic of using other agent's strategies as 'proxies' for explicitly modelling the trends using predictive strategies is far more efficient in terms of computational effort.

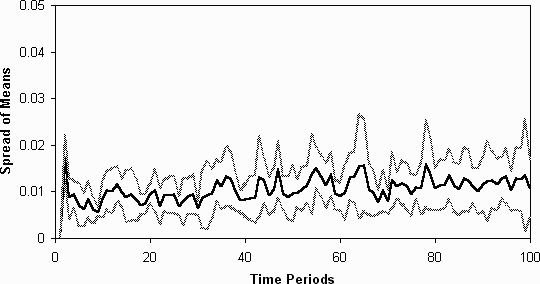
Figure 10: The average spreads of the fitnesses of the agent's models without naming (averaged over 7 runs)

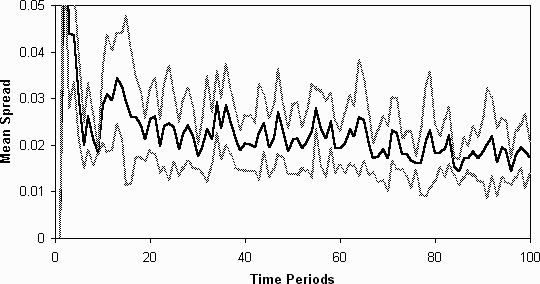
Figure 11: The spread (in standard deviations) of the averages of the fitnesses of the agent's models without naming (averaged over 7 runs)

An Examination of a Single Simulation Run

6.1

The above results are certainly evidence that class-based differentiation emerges as a result of the simulation but it does not tell us much about the kind of differentiation that occurs. To give an insight into this I will examine one simulation run in more detail. This will be one run with the standard set-up.

6.2

Figure 12 shows the pattern of attendance for each agent over the 100 time periods. No obvious pattern is apparent except for the fact that two of the agents settle down to fixed (but opposite) attendance strategies.

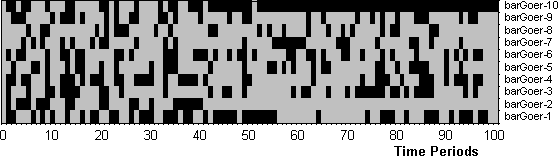
Figure 12: The pattern of attendance (grey=went, black=stayed at home)

6.3

Figure 13 shows the success of the 10 agents over the simulation as measured by the scores the agents use to evaluate the success of their own strategies. This is smoothed so that trends are visible (which is why the first 10 dates are not plotted). Considerable temporal differentiation is apparent - no single agent dominates (or is dominated) for long, but the agents are not visibly converging to the same success rate. In fact the success rates are closer together at the beginning of the simulation than at the end. This confirms the general trend towards a differentiation of fitnesses shown by the figures in theprevious section. The differentiation is not a simple class-based differentiation with straight-out winners and losers but a more dynamic temporal differentiation.

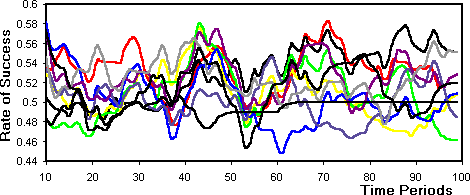
Figure 13: The success of the agents (smoothed so that trends are visible)

6.4

A literal analysis of the causation involved in this simulation is extremely difficult. Not only does the GP learning algorithm tend to result in the development complex 'inhuman' strategies included much apparently useless 'junk' code, but a phenomena of social embedding occurs where the utterances or actions of one agent depend on the previous actions and utterances of agents etc. To get a handle on the development of strategies I have plotted the smoothed rates of attendance (figure 14) and rates of utterances of 'true' (figure 15).

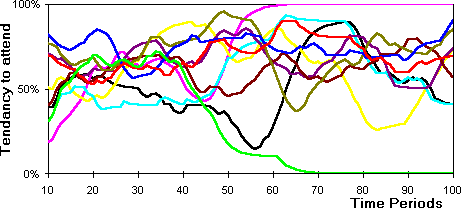
Figure 14: The development of attendance strategies (greatly smoothed so that trends are visible, 100%= always attends)

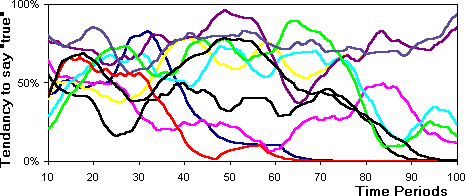
Figure 15: The development of communication strategies
(greatly smoothed so that trends are visible, 100%=always says 'true')

6.5

In figure 14 one sees the two agents that developed fixed attendance strategies, however as you can see from figure 15 they still have active strategies in terms of what they utter to other agents. By the end of the simulation four agents have developed utterance strategies that consist in always uttering 'false'.

6.6

To keep these two different strategic dimensions in mind simultaneously is difficult. Figure 16 is an animation of each of the agents average attendance and average utterance over the simulation. Each frame is drawn by plotting the agent at its average position over each 10 time periods. One can see that while the agents start with fairly central averages in terms of attendance and utterance, over the simulation they differentiate out, spreading out across the average attendance/average utterance strategy space. They do not do this simply but as a result of some sort of 'game', resulting in a sort of dynamic 'jostling for position' with respect for each other.

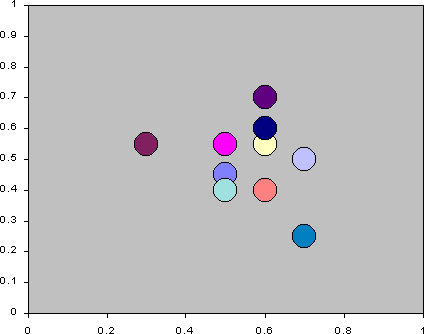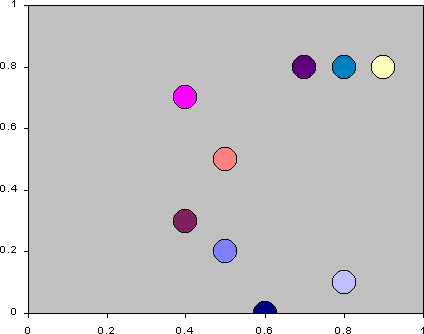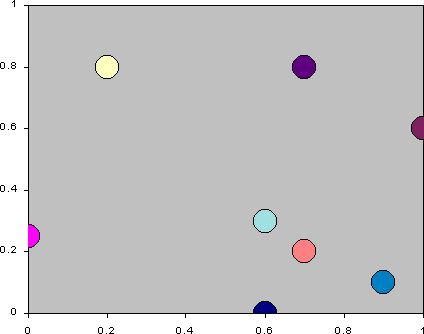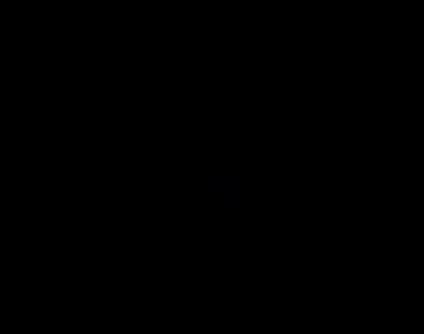
Figure 16: The trajectories of the agents' strategies in terms of average action and utterance

6.7

In this particular run something particular seems to occur around time period 80. Non-social strategies (i.e. those not involving the saidBy, wentLastTime and saidByLast primitives) loose out to social primitives. This is illustrated in figure 17, where the overall proportion of different types of primitives that occur in all the strategies of all the agents is plotted . The society of agents looses the predictive strategies and becomes entirely self defining in terms of actions. I discuss this sort of phenomenon in greater detail elsewhere (Edmonds 1999c).

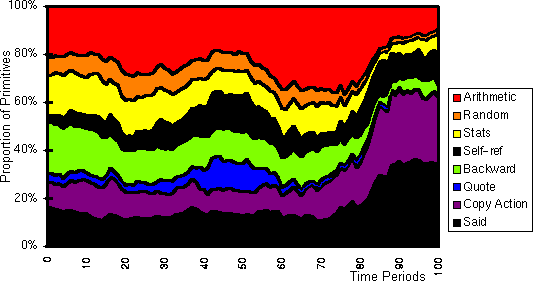
Figure 17: Distribution of the relative proportions of some primitive types in the run.

A More Detailed Look at the End of This Simulation

7.1

To finish with I will briefly analyse the position at the end of the simulation described in section 6 (i.e. at date 100). I will analyse the situation in terms of the causation of the action and utterances at date 100 in terms of previous actions and utterances. I will not display the actual strategies that the agents evolved - the actual genes contain much logically redundant material which may put in an appearance in later populations due to the activity of cross-over in producing later models. Also it must be remembered that other alternative models may well be selected in subsequent weeks, so that the behaviour of each agent may 'flip' between different modes (represented by different models) depending on the context of the other agent's recent behaviour.

7.2

In the figures below I indicate the immediate causes of the agent's actions (figure 18) and utterances (figure 19). In the first diagram (figure 18): if the previous actions or utterances of one agent have effected the action or utterances of another (at time 100), I have connected the two agents with an arrow. If it is the action of the first that has effected the second then I have indicated this with a solid arrow - a dashed arrow indicates that it is the utterance of the first that affected the seconds' action. If the casual effect is negated (e.g. the first agent going to the bar would influence the second not to go) then I have crossed the arrow with a short line. The second diagram uses the same conventions as the first but it indicates the causes of the agents utterances at week 100. If an agent is not shown this is because it was not causally effected by the actions or utterances of the other agents.

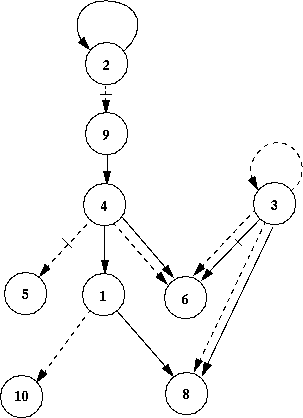
Figure 18: Causation of Actions in week 100

7.3

I will summarize the causation at week 100: agent 2 will go if it went last period (this is not as trivial as it may seem because last time period the agent may have selected a different strategy to determine its action; agent 3 goes if it said it would; agent 9 goes if agent 2 said it would not; agent 4 tends to go if agent 9 went last time; agent 5 goes if agent 4 said it would not; agent 1 tends to go if agent 4 did last time; agent 10 tends to go if agent 1 said it would. The determination of the action of agents 6 and 8 is more complex: agent 6 is more likely to go if agents 4 and 3 said they would go, if agent 4 went last time and agent 3 did not go last time; agent 8 is positively influences by the actions last time of agents 1 and 3 and whether agent 3 said it would go.

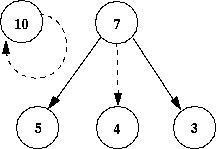
Figure 19: Causation of Utterance for week 100

7.4

The causation of the utterances (figure 19) is less intricate: agent 10 says what it said last time; the action of agent 7 positively effects the utterances of agents 3 and 5 (which would effect the actions of 6 and 8 if the networks remained the same); and the utterance of agent 7 positively affects the utterance of agent 4 (which would go on to effect the actions of other agents as plotted in figure 18.

7.5

As one can see the social structure that results is far from uniform. Some agents have developed strategies to influence other agents; some have developed more complex ways of evaluating the other's past actions and utterances; and the others use a mixture of these approaches. Some strategies are such that they tend to go to the bar; some that mean they tend not to go; and some which use a mixture. Some of the agents develop fairly fixed utterance strategies; some use a mixture of messages. Only agent 10 has completely cut itself off from the social web of cause and effect.

Discussion

7.6

Unlike the Brian Arthur's original El Farol model, this model shows the clear development of different roles. This goes beyond differentiation as a matter of degree, the agents clearly develop qualitatively different social strategies. By the end of the simulation exhibited in greatest detail, the agents had developed a complex coordination mechanism involving a network of causation. Thus although all agents were indistinguishable at the start of the run in terms of their resources and computational structure, they evolved not only different models but also very distinct strategies and roles. We have the emergence of temporal differentiation as a result of the emergence of inter-related but qualitatively different social strategies among the agents.

7.7

Clearly, there are many aspects of this model which are yet unexplored. This is unsurprising given the complexity of the model - one writer (Casti, 1996) characterized the simpler model of Arthur's as the paradigm for complex systems! For example it is clear that the introduction of more cross-over; mutation or new strategies into the evolutionary operators acting on each agent's population of strategies would prevent the (separate) convergence of these populations. It is not surprising that these populations would converge in this set-up given the high rate of fitness-dependent propagation. What is more surprising is that they each converge on very different solutions. However this paper does start to tease out some of the social processes that occur.

7.8

In some other papers I have discussed some other aspects of this model: (Edmonds, 1999c) explores the social embeddedness that occurs; and (Edmonds, 1998) looks at some of the philosophical implications in terms of modelling socially intelligent agents.

Conclusion

8.1

The conclusion of the paper is that if one only allows global communicative mechanisms, and internal models of limited expressiveness then one might well be preventing the emergence of heterogeneity in your model. Or, to put it another way, endowing ones agents with the ability to make real social distinctions and (implicit or explicit) models of each other may allow the emergence of social situated behaviour that might be qualitatively different than a model without this capacity.

8.2

Such a conclusion marries well with other models which enable local and specific communication between its agents (e.g. Moss and Esther-Mirjiam, 1999) and goes some way to addressing the criticisms in (Gaylard, 1996).

Acknowledgements

SDML is developed in VisualWorks 2.5.1. the Smalltalk environment produced by ParcPlace-Digitalk. Free distribution of SDML for use in academic research is made possible by the sponsorship of ParcPlace-Digitalk (UK) Ltd. The research reported here was funded by the Economic and Social Research Council of the United Kingdom under contract number R000236179 and by the Faculty of Management and Business, Manchester Metropolitan University.

---

References

The original description of the 'El Farol Bar' problem and Brian Arthur's model of it can be found in (Arthur, 1994).

Static structure

The model has 10 agents. Each agent has 30 strategies. Each strategy has two components:, the part to determine its utterance and the part to determine its action (i.e. binary decision). Each part is a formal expression (i.e. a tree) taken from a typed grammar.

Dynamic structure

Each simulation has 100 discrete time periods (called 'weeks'). Each week is divided into four stages (called 'days') in which the agents act in parallel (i.e. they can not make use of the results of other agent's action until the next stage) concerned with: strategy development; utterance; action; and accounting. These are described in greater detail immediately below.

Model development

Each agent does the following. (1) Apply the GP algorithm to last weeks set of strategies using last week's fitnesses to guide the probability of selection. The algorithm applies the operators of tree-crossover and propagation evenly, i.e. half of the new set of strategies is produced by one and half the other. (2) The resulting population of strategies is evaluated as to how well the agent would have done if this strategy was consistently applied over the last 5 weeks (and other agents' actions and utterances had remained the same). This uses a score of 0.7 if they go when not crowded, 0.5 if they don't go and 0.4 if they go when crowded [note 5]. (3) Choose the best such strategy according to this evaluation.

Utterance

Recursively interpret and evaluate the 'talk' half of the best strategy with respect to the past history of the simulation to determine the agents utterance. Make this utterance to all other agents (this utterance is only accessible by other agents after this stage).

Action

Recursively interpret and evaluate the 'action' half of the best strategy with respect to the past history of the simulation (including now the utterances in the preceding stage) to determine whether or not to go to the El Farol Bar or not. Post ones action for other agents to see (which, will only be accessible to other agents next week).

Accounting

The total attendance is calculated and posted. Various statistics and reports are generated for the user of the simulation.

Key parameters and options

Their are a lot of settings, which can be altered. Here I list the relevant ones, giving their values in the runs described above in brackets. [note 6]

Standard set-up

• Number of agents (10).
• Number of strategies each agent has (40).
• The initial depth of the strategies (6).
• Time that the simulation runs for (100 'weeks').
• The length of history that the strategies are evaluated over (5 previous weeks).
• Critical crowding proportion (67% of all agents).
• Number of other agents any agent can 'talk' to or 'hear' (9, i.e. everybody else).
• Number of stages of talking each week (1).
• 'Scores' for actions used in evaluating strategies (0.7 go when not crowded; 0.5 not go; 0.4 go when crowded).
• Proportion of tree-crossover used (50%).
• Proportion of propagation used (50%).
• Proportion of brand new strategies introduced (0%).
• Proportion of strategies simply carried over, without fitness selection (0%).
• Maximum depth of the strategies developed (none).
• The language of the 'talk' half of the strategies:
• [AND [boolean] [boolean]] --> boolean
• [OR [boolean] [boolean]] --> boolean
• [NOT [boolean]] --> boolean
• [plus [numeric] [numeric]] --> numeric
• [minus [numeric] [numeric]] --> numeric
• [times [numeric] [numeric]] --> numeric
• [divide [numeric] [numeric]] --> numeric
• [randomIntegerUpTo [numeric]] --> numeric
• [numWentLag [numeric]] --> numeric
• [boundedByPopulation [numeric]] --> numeric
• [trendOverLast [numeric]] --> numeric
• [averageOverLast [averageOverLast]] --> numeric
• [lessThan [numeric] [numeric]] --> boolean
• [greaterThan [numeric] [numeric]] --> boolean
• [wentLastWeek [name]] --> boolean
• [saidByLast [name]] --> boolean | quoted-tree
• [previous [anytype]] --> anytype
• [quote [any]] --> quoted-tree
• [1] --> numeric
• ...
• [10] --> numeric
• [IPredictedLastWeek] --> boolean
• [randomGuess] --> numeric
• [maxPopulation] --> numeric
• [numWentLastTime] --> numeric
• The language of the 'action' half of the strategies:
• [AND [boolean] [boolean]] --> boolean
• [OR [boolean] [boolean]] --> boolean
• [NOT [boolean]] --> boolean
• [previous [anytype]] --> anytype
• [saidBy [name]] --> boolean | quoted-tree
• [wentLastWeek [name]] --> boolean
• [IPredictedLastWeek] --> boolean
• [T] --> boolean
• [F] --> boolean
• [ISaidYesterday] --> boolean | quoted-tree
• [IWentLastWeek] --> boolean
• [randomDecision] --> boolean

Set-up without learning

The same as the standard set-up above, except:

• Proportion of tree-crossover used (0%).
• Proportion of propagation used (0%).
• Proportion of brand new strategies introduced (0%).
• Proportion of strategies simply carried over, without fitness selection (100%).

Set-up without naming

The same as the standard set-up above, except that the saidBy, saidByLast and wentLastWeek primitives are missing from the 'talk' and 'action' strategy languages.

Initialization

Each agents' population of strategies was recursively generated using the above languages to the give maximum depth, by randomly choosing a primitive of the appropriate type dependent on the current type.

To start the simulation off, a bogus history is needed for agents to be able to evaluate their strategies in the first few weeks. There were thus default values of the appropriate terminals that came into play if an agent attempted to evaluate the terminals at a date prior to week 1.

Intended interpretation

That the presence of an open-ended learning mechanism working with an expressive representation of strategies and the ability to distinguish and model other agents can promote the spontaneous differentiation of strategy in competitive discoordination games.

Details necessary for implementation but not thought to be critical to the results

The initialization of the past history before week 1 seemed to have no lasting effect in trials I made. I tried a random past history and various default settings, but the dynamics of the model seemed to dominate very quickly, so that the effect of this 'bogus' history was quickly lost.

The quoting mechanism allows for infinite loops to appear in rare circumstances. For example if agent 1 made the utterance "[saidByLast [barGoer-2]]" and agent 2 made the utterance "[saidByLast [barGoer-1]]" in the previous week, attempting to fully interpret an action strategy that specified [saidByLast [barGoer-1]] would never end. Thus a limit of the number of such recursions due to this mechanism of 3 was introduced. This limit did not seem to have any effect in trial I ran (except in the time the simulation took to run!).

Description of variations

Two other variations of this simulation were run as partial controls:

1. one with no variation in the learning mechanism
2. one without the ability to distinguish the actions of individual agents in their strategies.

Software Environment

The model was implemented in a declarative forward chaining programming language called SDML (a Strictly Declarative Modelling Language) which has been written specifically for agent-based modelling in the fields of business, management, organization theory and economics (Moss et al, 1998). SDML is particularly suited to this model because is provides facilities for the easy programming of multi-layered object-orientated structures (so the populations of genes within a population of agents is easy) with several levels of time (in this case weeks and days).

For more about SDML see http://www.cpm.mmu.ac.uk/sdml

Code

The modules with the code for this simulation is available at URL: http://www.cpm.mmu.ac.uk/~bruce/jasss/code.html

These modules require SDML version 3.4c or later. SDML is freely available for academic use, it can be acquired from URL: http://www.cpm.mmu.ac.uk/sdml/

Raw Results

The complete set of 38 transcripts would be too large to be made available, but the statistics from the runs and the transcript of the single run examined in more detail is available at URL: http://www.cpm.mmu.ac.uk/~bruce/jasss/data.html

Notes

1. This has since been recently renamed as the "minority game". See the URL http://www.unifr.ch/econophysics/principal/minorite.html for more details and several papers about this game.

2. The cross-over operation is not very realistic (in terms of human reasoning) but does as a first approximation. For a critique of cross-over and further discussion of the philosophy of agent design for the purposes of the credible modelling of human agents, see (Edmonds 1999b).

3. The reason for the small number of runs is the time each one takes. In the standard set up each simulation tool about 4 days to run! The reason for this is that some agent evolve extremely large and complex strategies.

4. At this point in a paper one might accompany such comparisons of graphs with some statistics. The usual use of such statistics is to infer there is a real difference in the underlying unknown processes from the data. In this case we know that there is a real difference in behaviour because there are known differences in the code which determines the underlying processes (as described in the section 5 and the appendix). In such a situation given a sufficiently long run it would be utterly astounding if there were not a significant statistical difference (it would be an improbability of trillions to one, odds which could be increased at will merely by extending the run). The appropriate null hypothesis here is that the runs are not the same! Showing they are statistically different using a null hypothesis that they are the same would not tell us anything.

5. The evaluation of quoted strings (e.g. of the form [quote [...]] derived from other agents' utterances was slightly more complex than indicated, to allow sensible results when evaluated with other types. For example [AND [quote [...]] [F]] would evaluate to false and [AND [quote [...]] [F]] would evaluation to [quote [...]].

6. People who download and play with the program will discover that the simulation is structured to allow for many other, more radical, alterations easily. This is because I programmed the simulation so as to be adaptable to a whole variety of configurations which are not relevant here.

References

ARTHUR, B. 1994. Inductive Reasoning and Bounded Rationality. American Economic Association Papers, 84, 406-411. (Also available at http://www.santafe.edu/arthur/Papers/El_Farol.html)

AKIYAMA, E. and Kaneko, K. 1996. Evolution of Co-operation, Differentiation, Complexity, and Diversity in an Iterated Three-person Game, Artificial Life, 2, 293-304. (Also available at http://mitpress.mit.edu/journals/ARTL/Akiyama.pdf)

CASTI, J. L. 1996. What If. New Scientist, 13 July 1996. (Also available at http://www.newscientist.com/nsplus/insight/ai/whatif.html)

EDMONDS, B. 1998. Modelling Socially Intelligent Agents. Applied Artificial Intelligence, 12:677-699. (An earlier version is available at http://www.cpm.mmu.ac.uk/cpmrep26.html)

EDMONDS, B. 1999a. The Uses of Genetic Programming in Social Simulation: A Review of Five Books. Journal of Artificial Societies and Social Simulation, 2(1). (https://www.jasss.org/2/1/review1.html)

EDMONDS, B. 1999b. Modelling Bounded Rationality In Agent-Based Simulations using the Evolution of Mental Models. In Brenner, T. (Ed.), Computational Techniques for Modelling Learning in Economics, Kluwer, forthcoming. (An earlier version is at http://www.cpm.mmu.ac.uk/cpmrep33.html)

EDMONDS, B. 1999c. Capturing Social Embeddedness: a constructivist approach, Adaptive Behavior, 7(3/4). (An earlier version is at http://www.cpm.mmu.ac.uk/cpmrep34.html)

EDMONDS, B. 1999d. Towards a Descriptive Model of Agent Strategy Search. CPM Report 99-54, MMU, Manchester, UK. (http://www.cpm.mmu.ac.uk/cpmrep54.html)

DRESCHER, G. L. (1991). Made-up Minds - A Constructivist Approach to Artificial Intelligence. Cambridge, MA: MIT Press.

GAYLARD, H. A Cognitive Approach to Modelling Structural Change. Workshop on Modelling Structural Change, Manchester Metropolitan University, May, 1996. (Available at http://www.cpm.mmu.ac.uk/cpmrep20.html)

HOLLAND, J. H. et al. (1986). Induction: processes of inference, learning and discovery. Cambridge, MA: MIT Press.

KOZA, J. R. 1992. Genetic Programming: On the Programming of Computers by Means of Natural Selection. Cambridge, MA: MIT Press.

MONTANA, D. J. 1995. Strongly Typed Genetic Programming, Evolutionary Computation, 3, 199-230.

MOSS, S. and Esther-Mirjiam, S. (1999). Boundedly versus Procedurally Rational Expectations. In Hughes-Hallet, A. and McAdam, P. (eds.), Analyses in Macro Modelling, Amsterdam: Kluwer. (An earlier version is available at http://www.cpm.mmu.ac.uk/cpmrep12.html)

MOSS, S. J. and Edmonds, B. 1998. Modelling Economic Learning as Modelling. Systems and Cybernetics, 29, 5-37. (An earlier version is available at http://www.cpm.mmu.ac.uk/cpmrep03.html)

MOSS, S., Gaylard, H., Wallis, S. and Edmonds, B. (1998). SDML: A Multi-Agent Language for Organizational Modelling. Computational and Mathematical Organization Theory, 4, 43-69. (http://www.cpm.mmu.ac.uk/cpmrep16.html)

REIGLER, A. (1992). Constructivist Artificial Life and Beyond. Workshop on Autopoiesis and Perception, Dublin City University, Aug. 1992.

VARIO, J. (1994). Artificial Life as Constructivist AI. Journal of SICE (Society of Instrument and Control Engineers), 33(1):65-714.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, 1999