Comparing Mechanisms of Food Choice in an Agent-Based Model of Milk Consumption and Substitution in the UK

, ,
and
aImperial College London, United Kingdom; bEnergy Planning Program, Universidade Federal do Rio de Janeiro, Brazil
Journal of Artificial
Societies and Social Simulation 24 (3) 9
<https://www.jasss.org/24/3/9.html>
DOI: 10.18564/jasss.4637
Received: 19-Dec-2020 Accepted: 17-Jun-2021 Published: 30-Jun-2021
Abstract
Substitution of food products will be key to realising widespread adoption of sustainable diets. We present an agent-based model of decision-making and influences on food choice, and apply it to historically observed trends of British whole and skimmed (including semi) milk consumption from 1974 to 2005. We aim to give a plausible representation of milk choice substitution, and test different mechanisms of choice consideration. Agents are consumers that perceive information regarding the two milk choices, and hold values that inform their position on the health and environmental impact of those choices. Habit, social influence and post-decision evaluation are modelled. Representative survey data on human values and long-running public concerns empirically inform the model. An experiment was run to compare two model variants by how they perform in reproducing these trends. This was measured by recording mean weekly milk consumption per person. The variants differed in how agents became disposed to consider alternative milk choices. One followed a threshold approach, the other was probability based. All other model aspects remained unchanged. An optimisation exercise via an evolutionary algorithm was used to calibrate the model variants independently to observed data. Following calibration, uncertainty and global variance-based temporal sensitivity analysis were conducted. Both model variants were able to reproduce the general pattern of historical milk consumption, however, the probability-based approach gave a closer fit to the observed data, but over a wider range of uncertainty. This responds to, and further highlights, the need for research that looks at, and compares, different models of human decision-making in agent-based and simulation models. This study is the first to present an agent-based modelling of food choice substitution in the context of British milk consumption. It can serve as a valuable pre-curser to the modelling of dietary shift and sustainable product substitution to plant-based alternatives in Britain.Introduction
A significant dietary shift for much of the Global North is needed to drastically reduce the planetary burden of the current global food system. Much of this burden stems from livestock and animal-sourced foods, with the sector responsible for 14.5% of anthropogenic greenhouse gas emissions (GHGs), mainly through methane production from ruminants and deforestation (Gerber et al. 2013). Within this, the global dairy system generates around 20% of emissions from this sector (Gerber et al. 2013), approximately 1.7 Gt CO2eq in 2015 (GDP 2018). Dairy also places significant stresses on water resources, land use, and ecosystem pollution (Mekonnen & Hoekstra 2012; Poore & Nemecek 2018). Impacts from dairy milk production and consumption are not equally distributed, with variability due to geography and farming methods. However, even taking this into account, evidence suggests that lower animal product diets would deliver sizeable improvements in several measures of sustainability (Poore & Nemecek 2018; Springmann et al. 2016).
However, dietary change and animal-product substitution have not typically been well captured or explicitly treated in most major modelling efforts on climate mitigation (Rogelj et al. 2018). An exploration of heterogeneity, behaviour, and food choice influences are key in understanding how these societal shifts may occur. Food choices are influenced by a multitude of interacting factors, some of which are complex (Chen & Antonelli 2020; Monteleone et al. 2017). These factors include: sensory and physiology (Leng et al. 2017); habit (Riet et al. 2011); social influence (Cruwys et al. 2015; Higgs & Thomas 2016; Pachucki et al. 2011); emotion (Leigh Gibson 2006); and the wider environmental context (Booth et al. 2001; Bucher et al. 2016; Popkin et al. 2005).
There is a challenge to incorporate a more nuanced understanding of these influences and decision-factors into models and analysis of societal adoption of sustainable diets. Further, wholesale societal shifts to substitute food products toward more sustainable food choices has yet to occur, and so real-world data is limited. However, these challenges should not prevent efforts to generate and investigate more representative trajectories of these possible future trends of sustainable diets.
This study contributes to narrowing this gap by developing an agent-based model (ABM) of food choice for United Kingdom (UK) consumers and applying it in the context of historical trends of milk consumption. Simulated outputs are compared against empirical data from the UK’s Family Food survey (DEFRA 2020). This survey contains 32 data points (for each milk type) covering 1974 – 2005 for the average milk consumption per person per week. The Family Food survey is a sub-set of the UK’s Living Costs and Food Survey, which samples 5,000 households annually (via multi-stage stratified random sampling).
Specifically, we ask: can a conceptualisation of food choice decision-making based on cognitive, habit, and social influence give plausible representations of historic UK milk choice substitution? Within this, we ask a secondary question: which model mechanism of choice disposition (i.e. how agents are triggered to consider their options) performs better against empirical survey data, a threshold-based disposition approach, or a probability-based disposition approach? In doing so, this paper looks to contribute to the body of ABMs that compare models of human decision making, answering the call of a grand challenge in the field as set out by the recent JASSS editorial (An et al. 2020).
We choose milk as a base of investigation as, in Britain, consumption has already experienced a clear substitution of whole for skimmed varieties (UK Family Food survey data - DEFRA 2020), and so makes a potentially good candidate to test and explore such a model. Further, plant-based milk alternatives (e.g. oat, soy, almond) are among the most advanced of sustainable substitutes with regards to consumer popularity and market penetration into conventional animal product categories. However, the focus of this study is not to model the adoption of plant-based alternatives, although this is a natural line of future work. Rather, it looks at how an agent-based model of food-choice can give a plausible representation for observed substitution of milk varieties within UK consumers.
Using an agent-based modelling approach, this work aims to integrate scientific theories and evidence from social psychology, consumer behaviour, and food influence, to construct a simulation model of the milk choice among UK consumers. The model is tested against historic macro-level trends of average consumption of whole and skimmed (including semi) milk.
A brief clarification on food choice, and its use in this study. Literature on food choice, its drivers and influences, is extensive and diverse. As a result, food choice presents a complex, nuanced, and debated landscape with no universally accepted set of definitions and factors. Indeed, some have critiqued the use of the word ‘choice’ in the context of food consumer behaviour (Smeaton et al. 2010). Despite the multi-dimensional nature of food choice and its associated evidence base, general categories of influence can be seen, acting at different spatial and temporal scales. These can be conceived as: food specific features (sensory, physiological, social and physical food environment), individual (personal) differences (psychological components, habits, knowledge, values, beliefs, preferences, demographics), and structural features (cultural norms, food system actors, economic drivers, policy and regulation) (Chen & Antonelli 2020).
We use Chen & Antonelli (2020)'s proposed conceptual framework of food choice (developed from review and analysis of existing food choice models that we take to be a reasonable synthesis of extant literature in this space) and focus on factors associated with the individual (i.e. personal differences and a person’s immediate social environment). Specifically, the set of factors influencing milk purchasing decisions are: cognitive perception of the health and environmental effects of milk choice; habit; social influence; and choice evaluation, conceived as value-based cognitive dissonance. The model explores how these influences on individual choices impact the consumption dynamics of a population at large (Bruch & Atwell 2015). The model’s individual decision-making processes are based upon utility maximisation, following a general approach common to agent-based models of innovation diffusion and consumer adoption (Zhang & Vorobeychik 2019).
Background: Agent-Based Modelling of Food Choice
Agent-based models (ABMs) are simulated ‘worlds’ that contain a set of entities (agents) that exist and interact with each other and their environment. They behave according to a set of rules, ‘empowering’ them to make autonomous decisions at an individual level. These decisions, behaviours and interactions lead to emergent outcomes that cannot be understood simply by the constituent components of the simulation. Agent-based approaches are part of a suite of tools and methods that can help provide insight in a world where problems, and their solutions, are rarely simple and, increasingly, complex. Their ability to represent heterogeneity and incorporate diverse empirical data, for example in attitudes, preferences, biases, habits and demographics across populations, makes them a valuable tool in studying social systems in transition, where behaviour change is necessary and populations may not act rationally.
ABMs have been used within behavioural change research that have looked at health, diet, environmental and sustainable behaviours. Some have focused on the food environment as an influence for healthy food choice (Auchincloss et al. 2011), or social influence of healthy eating from peers and marketing campaigns (Zhang et al. 2014). These and other studies are part of a growing number of ABMs focusing on health and diet (see a recent review paper of their use in public health from Tracy et al. 2018). However, there are fewer ABM studies concerned with the non-health impact of diets. One such study looked at meat consumption of UK consumers, focusing on social eating networks and testing responses to marketing strategies or price increases (Scalco et al. 2019). Another constructed a number of consumption profiles (food, energy, transport) of Italian households, and tested how the associated GHGs could change under a number of policy interventions designed to effect food choice (Bravo et al. 2013). A recent study explored consumer behaviour and policy interventions with an ABM of Australian organic wine purchasing (Taghikhah et al. 2020). Further analysis, using the same agent-based model, looked to compare a theory driven vs data-driven modelling approach and the relative merits of each (Taghikhah et al. 2021).
We build on this previous literature of consumer behaviour of (more) sustainable food, and model food choice influence and decision-making in the context of historical UK milk consumption, assessing the performance of two different model approaches.
Model Description – ODD
The model is described using the ODD (Overview, Design concepts, Details) protocol, which is a standard approach to describe, share, and compare agent-based models (Grimm et al. 2006, 2010, 2020).
Overview
Purpose
The overall objective of the model is to reproduce adoption behaviours of milk consumption by the UK public, by replicating individual preferences and decision factors. Specifically, the goal of the model is to explore the influence of perception, habits, social influence and choice evaluation in an individual’s decision-making process of milk choice. The model looks to replicate the substitution of whole milk for skimmed and semi-skimmed milk from the 1970s onwards. The main outcome reported here is the average weekly consumption of each milk type per person. The simulation uses both a theoretical grounding and empirical data to inform the ABM, with calibration performed against observed macro level data.
In particular, the study conducts an experiment to compare the performance of two model variants in reproducing overserved milk consumption trends. These variants present different mechanisms for how agents become disposed to consider their choices, representing a threshold-based, and a probability-based approach.
Agents, state variables, scale
The agents in the model represent adult consumers who occupy a random position in an information environment. Each agent has a disposition to consider alternative milk choices. Two disposition mechanisms are tested in the model, a threshold-based approach, and a probability-based approach. Each agent makes a choice of milk selection based on a function for each alternative, made up of the perceived health and environmental characterises of each choice. These are computed at the initialisation of the simulation and then calculated at each time step. An agent’s milk choice function is modified by habit, social influence, and evaluation of previous choices. Agents ascribe different relative importance to each constituent part of the choice function (health factors and environmental factors). If the disposition requirement has been met, consumption of each milk type is split proportionately by the size of each choice function, modulated by the other influences. If not, agents keep their existing choice.
Agents (\(n=1,000\)) start with an existing choice based on the dominant position of whole milk versus skimmed varieties in 1974 (start year of the data). All agents are part of a social network. Each agent in the network can sense and be influenced by the choice function of each milk alternative for other agents in their network. Links between agents are unidirectional, and influence occurs as a function of interaction probability, with the degree of influence characterised by agent susceptibility. Social norms are globally perceived by agents and impact the weightings of the choice function (see social influence sub-model).
Process overview and scheduling
At the start of each model run a set of agents are created, positioned and linked with other agents in a network (see social influence sub-model) in the information environment. Agents are initialised with a choice, reflecting the milk consumption split between whole and skimmed (including semi) milk in 1974. Agents perceive information about milk choices in their immediate neighbourhood of grid cells and construct a choice function based on the average of values perceived. Agents have a memory and draw on pervious information to inform the new choice functions. Some agents begin with being habitual to reflect the incumbent, long standing milk choice (whole milk). Habit, social influence, and choice evaluation impact the final choice functions. Milk choice for each time-step is determined, proportionally, by the scores of the final milk choice functions. The simulation runs at annual time steps from 1974 to 2005.
Design concepts
Basic principles
Decision-making follows a basic structure of: agent perception of choice characteristics, the triggering, or not, of disposition to consider alternatives, a set of scored choice functions made up of the perceived characteristics and modulated by habit and social influence, and finally, choice evaluation where agents consider the impact of their choices and may adjust their future decisions. Figure 4 in the Appendix represents the model flow schematically. The choice function is made up of two cognitive components: the health and environmental impact of the two milk types.
Other properties that are known to be important in food choice, e.g. price and accessibility, are not explicitly considered here as we assume that whole milk and skimmed (including semi) have similar profiles among these characteristics. The price component of this is supported in Family Food survey data by matching expenditure and consumption for both milk types. Excluding the influence of the first few years of data, as the very low skimmed milk consumption generates high pence/litre volatility, the average skimmed milk price between 1981 and 2005 was 47.8 pence/litre compared with whole milk at 47.9 pence/litre. Across the same price data range, mean absolute percentage error for these two curves was 3.1%. Future work looking to incorporate plant-based alternatives would look to include and model price, accessibility and availability factors given the significant differences here with dairy milks.
The choice function is modulated by habit, social influence (peer effect and norms), and evaluation functions, from which an overall set of options are possible and agents seek to maximise the utility of their choice. These functions are somewhat akin to Epstein (2014) agent formalism of rational, emotional and social components – but differ in the decision-making mechanism. Each of these functions are described in the sub-model section. Table 1 gives the model parameters that operate within these functions. A more detailed description is given in Table 3 in the Appendix.
| Parameter | Group | Dynamic | Range |
|---|---|---|---|
| Memory length | Cognitive perception | No | \([1,10]\) |
| Perception of health component of alternative | Cognitive perception | Yes | \([1,3]\) |
| Perception of environmental component of alternative | Cognitive perception | Yes | \([1,3]\) |
| Habit threshold | Habit | No | \([1,10]\) |
| Initial habit of incumbent | Habit | No | \([0,10]\) |
| Probability of interacting | Social influence | No | \([0,1]\) |
| Social susceptibility | Social influence | No | \([0,1]\) |
| Social conformity | Social influence | No | \([-1,1]\) |
| No. of neighbours | Social influence | No | \([2,10]\) |
| Gradient probability disposition (probability model variant only) | Social influence | No | \([14,16]\) |
| Social blindness | Evaluation | No | \([0,1]\) |
| Post-choice justification | Evaluation | No | \([0,1]\) |
| Cognitive dissonance threshold | Evaluation | No | \([0,1]\) |
Details
Implementation and initialization
The model is implemented in NetLogo 6.0.4 (Wilensky 1999). A copy of the model with supplementary information can be downloaded from the model library of the CoMSES website (www.comses.net). Python code of model analysis is also made available. Agents are initialised with a choice to reflect the average weekly UK milk consumption in 1974.
Input data
At the start of the model, agents are initialised with human values (universalism, security and openness) drawn from UK responses of the basic human value question set of the 2018 European Social Survey. At each time-step, data is read containing the empirically informed (via Ipsos Mori and YouGov long-run surveys) concerns of the UK public regarding health and the environment. We use this to represent the population level observed social norms that agents perceive and seek to align with to a greater or lesser degree. See Table 4 in the Appendix for details of the survey questions.
Sub-models
Disposition
Agent-based models frequently employ mechanisms of transition between different agent states (Zhang & Vorobeychik 2019). Rand et al. (2015) present an ABM of diffusion dynamics where agents are triggered to an ‘aware’ state by imitation of their neighbours in a social network. Another ABM, looking at urban water demand, contains agents whose binary state (environmentalist or non-environmentalist) in part depends on the relative proportion of agent neighbours in each state, with a logistic function governing the probability of transitioning between the two (Galán et al. 2009). The disposition sub-model follows these previous studies and makes use of agent social networks (neighbours) to form the basis of the disposition mechanism. Here, an agent will only consider changing their milk choice if they are in a state of disposition to do so.
Given its significance to how the model operates, we explore different model conceptualisations of how to represent this. The first conceptualisation is a threshold disposition approach. Here, agents each have a threshold (0 to 1) below which they remain indisposed, i.e. remain with their existing choice. Thresholds are not random but rather, are informed by European Social Survey 2018 data on human values of UK respondents. The values component of the survey is based on Schwartz’s theory of basic human values (Schwartz 2012). We operationalise answers to a survey question associated with openness to change (Schwartz 2012) to indicate the level at which an agent would consider alternatives. Agents in the model replicate the distribution of answers from UK respondents on a scale of 0, very low threshold, to 1, very high threshold. Agent disposition is calculated by the proportion of agents that have chosen whole milk or skimmed/semi-skimmed milk. In this mechanism, there is also a small random probability (3%) that agents will become disposed. This is to reflect the sometime spontaneous or impulsive nature of food choice.
The second model variant is a probability-based mechanism, and follows an approach by Wang et al. (2017), adapted and developed for this model. Rather than a discrete threshold, disposition is expressed as a likelihood given by Equation 1:
| \[ p(disposition) = \frac{1}{1+exp(-k (\frac{h}{h_{max}}- 0.5))}\] | \[(1)\] |
| \[ h = - (\frac{f_{whole}}{f_{all}})\log_2 (\frac{f_{whole}}{f_{all}}) + (- (\frac{f_{skim}}{f_{all}})\log_2 (\frac{f_{skim}}{f_{all}}))\] | \[(2)\] |
Cognitive perception
The cognitive perception sub-model represents the processes of how information regarding food choices operates and is perceived by agents. To reduce computation time, information is held directly by agents rather than an environment, with values drawn from a normal distribution of each of the components. The means of these distributions are determined by the health and environmental perception parameters. Values are given relative to the incumbent choice, i.e. whole milk. That is, whole milk has a mean value of 1 for each component and alternative values are set relative to this. At each time-step, the information points are redistributed stochastically. This is to mimic the reality that information perceived by people is often transient in everyday life.
Memory effects are included, with agents able to store a limited amount of averaged information from a set number of previous time-steps. At each new time-step, new information is added to a rolling average of previous time-steps and information is removed beyond a threshold governed by the memory length parameter. The upper and lower memory bounds (1, 10) follow the El Farol NetLogo model by Rand & Wilensky (2007).
The choice function is made up of the memory averaged components, weighted by the importance an agent ascribes to a particular component. This is given by Equation 3:
| \[ f(cog.) = \beta_{1}(health \: score) + \beta_{2}(environment \: score)\] | \[(3)\] |
Habit
Food behaviours are habitual (Riet et al. 2011). We model this as a multiplicative bonus on the milk score that repeatedly outturns as the highest scored choice. I.e. repeat behaviour makes it easier to continue this behaviour. The form of this is adapted from the empirical mathematical function of habit formulation (automaticity) of simple healthy activities from Lally et al. (2010). It is scaled to between 1 to 2, 2 being the upper habit ‘multiplier’ an agent can experience. The value of the upper ‘multiplier’ is a modelling choice to prevent this model component unduly dominating the decision-making process. The value that this takes should be subjected to robustness analysis in future work. This habitual inertia to change resets at each new choice. And so, repeat behaviours get reinforced but can be overcome if the choice function of the other option is sufficiently large. The equations governing habit are given by the following:
| \[ f(habit) = peak \: habit - exp(-0.042(consecutive \: choices - habit \: threshold))\] | \[(4)\] |
| \[ f(cog.)_{habit} = f(cog.)f(habit)\] | \[(5)\] |
Social influence
This sub-model represents the process of how agents interact with each other, and how the influence of social norms is modelled. Each node (agent) on the network has an average number of connections (degree) and strength of connection. The structure used in the model follows a small-world network (Watts & Strogatz 1998). We refer to this network as an agent’s neighbours. They represent social interaction and peer influence in a broad sense for example within households, food shopping, and retail, and do not simply represent real-world physical ‘neighbours’. The process is as follows: each agent has an incumbent choice at model initialisation and a new set of choices based on the latest information, an agent has a probability of sensing the choice functions of the other agents in their network. Influence is modelled as the mean of neighbour choice function values, with the effect on an agent modulated by social susceptibility. The equation governing peer influence is given by the following:
| \[ f(cog.)_{social} = f(cog.)(1- social \: susceptibility) + f(cog.)_{neighbour} social \: susceptibility\] | \[(6)\] |
In addition to social influence through an agent’s network, social norms also play a role in choice. Here, social norms are modelled as the relative weights (\(\beta_{1}\) and \(\beta_{1}\) in Equation 3) between the two components (health, environmental). This is conceptualised as the population level view of how important health and environmental matters are in general. This is a global variable that all agents can perceive. It is informed by empirical data from long running longitudinal surveys on concerns and issues perceived by the UK public (Ipsos Mori and YouGov). Each agent has a degree of conformity (between 0 and 1) to the changing importance of health and the environment. Conformers (i.e. factor of 1), will look to wholly align their individual weightings with the social norms. Non-conforming agents look to do the opposite, and all other agents in between see a proportionate effect. Each time-step the agents can shift their weights by at most 1% to closer reflect the weighting implied by the public concern data.
Evaluation
Agents reflect and evaluate the choices they make. Evaluation offers a mechanism for agents learn from prior experience and use this to inform future decisions. Cognitive dissonance in food choice is one theory of evaluation (see Ong et al. (2017) for a review), and we model this through a conceptualisation of tension between an agent’s human values and their milk choice behaviour. Here we use the theory of basic human values to assign two values (security and universalism) to each agent, reflecting, broadly, their position on health and their position on the environment. High importance for universalism values are associated with a deeper concern and action toward environmental issues (Schultz et al. 2005; Schwartz 2012). Within Schwartz’s theory of basic human values, health is orientated to the security value (Schwartz 2012). The European Social Survey includes questions from Schwartz basic human values. We take UK responses for universalism and security questions and operationalise them to give a distribution of values relating to environmental and health impacts of agent choice (based on data in Table 2).
Each milk choice has an associated health and environmental impact. Note, in the model, agents are free to consume any combination of each type up to the total average consumption, with a minimum consumption of 1 pint (568ml). At each time step, the aggregate impact of the choices is calculated and then compared against the agent’s values on a relative basis. If this relative impact is within a given proximity to their value position, determined by the ‘cognitive dissonance threshold’ parameter, no feedback is sent. However, if the difference is sufficiently large, the agent enters a state of cognitive dissonance whereby their actions are incongruent with the values they hold. Here, agents pursue the least costly path to try and escape this uncomfortable state. They will either reconsider their behaviour (next choice) and become spontaneously disposed, or they will alter their value base slightly to better fit the choices they make. The change of values is fixed at 1% each time step. If the difference between impact and value base is too large, given by the ‘justification’ parameter, agents simply rationalise this dissonance and once again no feedback occurs.
| Milk (per litre) | Sugar (g) | Sat. Fat (g) | Protein (g) | GHG (kgCO2eq) | Land Use (\(m^{2})\) | Water Use (L) |
| Whole | 49.39 | 19.76 | 36.12 | 1.30 | 9.00 | 628.00 |
| Semi/skimmed | 50.6 | 6.61 | 37.03 | 1.07 | 9.00 | 628.00 |
Calibration, Simulation Experiments, and Model Analysis
Calibration and model output verification
Calibration was performed on the whole model across all parameters over the bounded range of values (see Table 1 for ranges). The empirical pattern to be matched by the model was a set of two longitudinal curves of trends in the average weekly consumption of whole milk and skimmed (including semi) per person by the UK public from 1974 to 2005 (DEFRA 2020). The model looked to replicate the observed substitution of one food product with the adoption of an alternative. Therefore, we chose the fitting criteria to be the value of average skimmed milk consumption when the curves crossover (1992 – see Figure 2 for crossover) and the final value of skimmed milk consumption in 2005. The optimisation looked to minimise the difference between the model and observed output at these time steps. The strategy used was a bi-objective evolutionary algorithm (EA) implemented in Python (van Rossum & Drake 2009). The NetLogo model and Python were linked via the NL4PY package (Gunaratne 2018), which allows the remote control, execution, and analysis of the model from within a Python environment (in our case Jupyter). The DEAP Python package was used to execute the EA (Fortin et al. 2012). Specifically, we employed the “Mu Plus Lambda” algorithm, using a simulated binary crossover, polynomial bounded mutation and the NSGA-II selection algorithm. Candidate parameter sets were drawn from a uniform distribution over upper and lower bounds and an initial population of 50 individual sets were created, with the algorithm running over 10 generations. Prior to running the EA, analysis was conducted to narrow the parameter space of \(k\), the gradient of the probability logistic function, given that it is the sole additional parameter in the probability-based model variant, and its possible importance in model performance and comparison. The results of this pre-calibration analysis are given in Figure 5 of the Appendix.
Initial conditions were set at 1,000 agents, with a starting average whole milk consumption of 2,654.81 ml and skimmed (including semi) consumption of 5.29 ml per person per week which ran at yearly intervals from 1974 to 2005.
Post-calibration, uncertainty analysis sampled the optimised parameter sets and ran the full model output against observed data. Given the bi-objective function for the calibration, it is expected that more than one parameter set will be found, i.e. multiple non-dominated candidate sets. Saltelli sampling was used to generate parameters sets to run, with sample size given by the expression \(n(2p +2)\), where \(n\) is the baseline sample size and \(p\) the number of model parameters. Total sample size for each parameter set was fixed at 364 to ensure that each model variant had the same number of runs. This figure represents a compromise between sufficient sampling of the optimised parameter space, and computational resource constraints. The baseline sample size (\(n\)) was reduced in the probability-based approach, given the extra parameter in this model variant.
Sensitivity analysis
A temporal global variance-based sensitivity analysis was performed on the skimmed milk output curve from the best performing parameter sets of each model variant (see Figure 2 c) from the calibration exercise. Samples (\(n = 1,040\)) were drawn from a bounded \(\pm 2\) % range of the central value and the analysis repeated seven times, at 5-year intervals, for each model variant. This constrains the parameter search space to allow a more manageable exploration, given the computational expense in a single model run.
We use Sobol analysis with Saltelli sampling, implemented in Python using the SALib package (Herman & Usher 2017). Sobol analysis is a technique that estimates the relative contribution a parameter makes to a summary statistic (here, average weekly milk consumption) within different parameter sets (Sobol 2001). Saltelli sampling extends Sobel’ analysis and is robust to non-linearity between model inputs and outputs, and can give a quantified assessment of the contribution to overall model uncertainty attributed to the interactions between inputs, as well the individual inputs themselves (Saltelli 2002; Saltelli et al. 2002).
Simulation experiments for model analysis
The aim of this experiment was to compare two different model structures of agent decision making to consider alternative choices. Here we model two modes of agent disposition, a discrete threshold approach and a continuous probability approach. The rest of the model structure remains unchanged, see Figure 4 of the Appendix. Initial conditions were set at 1,000 agents, with a starting average whole milk consumption of 2654.81ml and skimmed (including semi) consumption of 5.29ml per person per week, which ran at yearly intervals from 1974 to 2005. Parameter values and ranges are those given in Table 1. The only difference between the two variant sets is an additional parameter governing the gradient of the logistic function in the probability-based disposition approach. The parameter space of each model is explored via the calibration exercise detailed in Section 4.1.
Results
Calibration
The choice of objective function is key in calibrating model output to observed data, and we considered two approaches here. These were; minimise the root mean square error between the pairs of models and observed curves, and minimise the absolute difference at the point of consumption crossover and final value for the skimmed milk consumption curve. The latter was chosen as it performed better in pre-calibration tests.
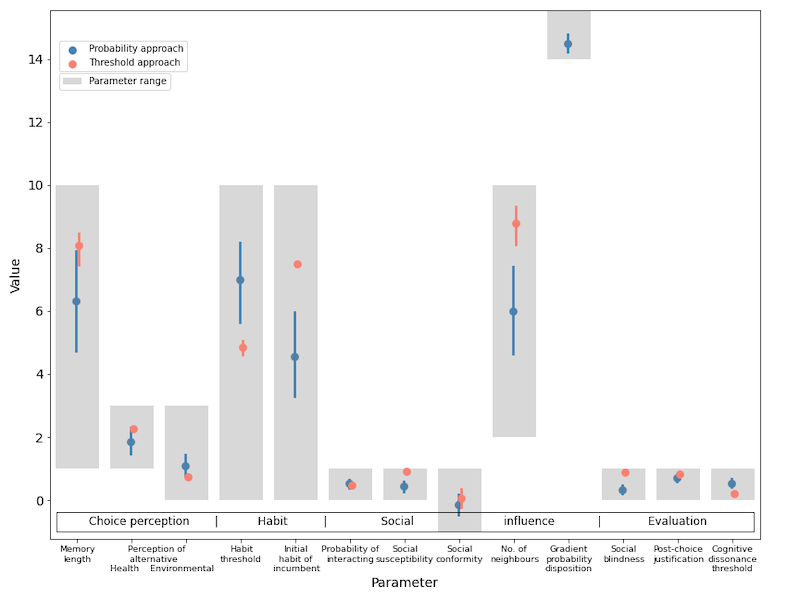
The calibration exercise produced optimisation results of 10 parameter sets for the probability-based model variant, and 11 sets for the threshold-based variant. Figure 1 shows these results, comparing the mean and spread (95% CI) of the parameter values. Blue dots and ranges represent the probability-based variant, pink dots, the threshold model variant. Parameters are grouped under their respective meta-parameters. A change in optimised values of the parameter set occurs with the introduction of a 13th parameter, ‘gradient probability disposition’ in the probability-based approach. It is not certain that this addition was directly responsible for these changes, or if simply re-running the optimisation exercise resulted in a different set of values. We can point to stability (pink dots, no/very little variation) of the threshold-based parameter sets and the wider variation of parameter values under the probability model variant, as evidence of the former.
Simulation experiment
Model comparison and uncertainty analysis
Figure 2 shows the comparison between outputs of the threshold and probability-based disposition models. Calibration was performed on each model variation with candidate parameter sets, n=10 and n=11 respectively, sampled (Saltelli) over a \(\pm 2\)% range of optimised values. Figure 2a and Figure 2b show model output against observed milk data for the threshold and probability-based disposition approaches respectively. Figure 2c combines the ‘best’ set of runs from each approach, defined here as the closest match to observed data by way of smallest error (root mean squared error). Figure 2d shows this error, calculated from Figure 2c. The threshold approach on average has a higher root mean squared error (389 and 440 ml/week) than the probability approach (284 and 309 ml/week), but over a narrower range (interquartile range of 40 and 49 ml/week vs 131 and 133 ml/week).
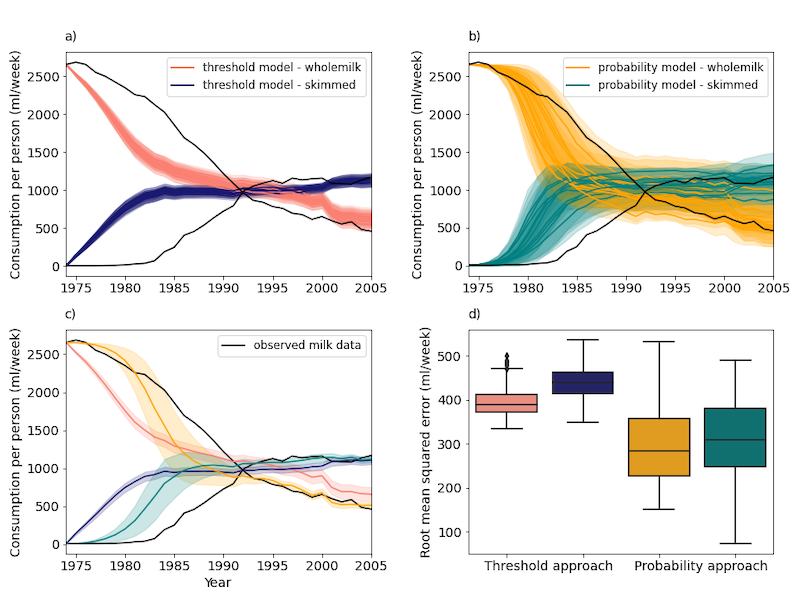
To compare the simulated and empirical survey data - from the UK’s Family Food survey (DEFRA 2020)– the dynamics of the latter are briefly detailed. Very little skimmed (and semi-skimmed) milk consumption occurred until 1983, where began a period of increased consumption for the next 14 years, surpassing whole milk in 1992 and peaking in 1997 at 1.16 litres per person per week before experiencing a plateauing of consumption. The simulated data was in general able to replicate the empirical data, with the probability approach performing better (lower RMSE), however, there are some differences. Focusing on the ‘best’ selected skimmed milk simulated model runs (Figure 2 c), the threshold approach output (blue line) had no period of limited or gradual consumption increase, instead rising rapidly from initialisation (1974). The output for the probability approach (green) more closely resembled the initial period of low consumption, but once again entered a phase of rapid increase several time steps (years) before the empirical curve. The crossover with whole milk, although in good alignment in terms of milk quantity, occurred 5 years earlier (1988) for the probability approach, and 4 year later (1996) for the threshold approach. The probability approach output (green) was able to closely match the peak and plateau dynamics, whereas the output of the probability approach (blue) was consistently less than that of the empirical data.
Sensitivity analysis
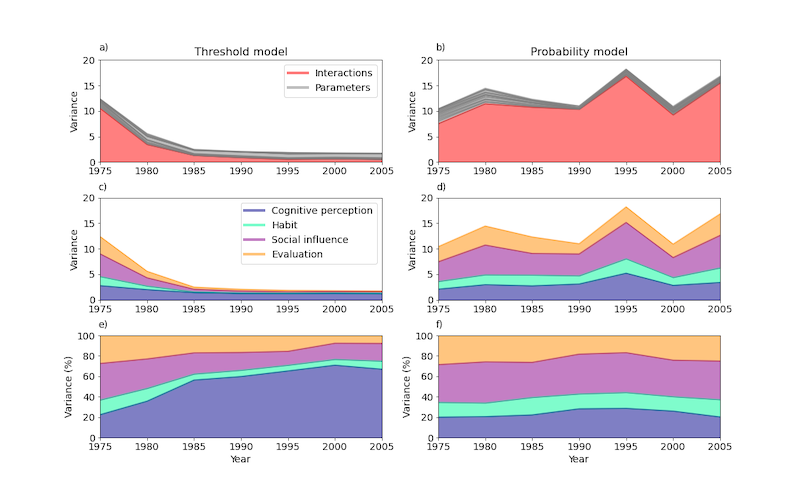
Figure 3 shows temporal (5-year time step) variance-based global sensitivity analysis for each model variant. Left hand figures represent the threshold model and right hand figures the probability model. Overall, ‘Initial perception of environmental component of alternative’ had the highest mean (over the temporal interval) sensitivity (0.98) of parameters in the threshold model, and ‘Initial habit of incumbent’ the lowest (0.19). Sensitivity was overall higher in the probability model, with fairly equal mean parameter sensitivity ranging from 0.85 to 1.14. However, single time-step sensitivity was more variable with ‘Social blindness’ having the highest sensitivity (2.13), and ‘No. of neighbours’ the lowest (0.59).
Figures 3a and 3b show the total variance at each time-step split by parameter variance and the variance due to parameter interactions. In the threshold model (Fig. 3a), the cumulative variance (across the entire time interval) was 36% due to parameters, and 64% due to interactions between parameters. In the probability model (Figure 3b) this split was even more marked at 13% to 87%. Figure 3c and 3d show this same output, but now split by parameter group and their interactions. The threshold disposition model shows a downward trend toward a stable output made up of variance overwhelmingly due to cognitive perception parameters. Output for the probability disposition model does not show this same trend, and does not converge over the analysis time frame. Figure 3e and 3f give the variance composition as a relative measure and show the increasing relative sensitivity dominance of cognitive perception parameters in the threshold model, and a reasonably stable variance attribution to the four parameter groupings in the probability-based approach.
Discussion
This agent-based model aimed to give a plausible representation of historical UK milk consumption trends to explore choice substitution from an incumbent (whole milk) to an alternative (skimmed/semi-skimmed milk). We ground the model in theory from social psychology, behavioural economics and environmental psychology, and use empirical evidence (human values survey data and public concerns data) to generate a richer representation of possible agent food influences and decision-making. UK historical milk consumption was chosen as its trend exhibits a classic substitution and adoption curve between two product choices. Overall, the model succeeded in reproducing the consumption pattern observed during the years 1974-2005.
Comparing models of human decision-making has been described as a grand challenge for ABM’s (An et al. 2020). We compared two model variants, tweaking the agent disposition mechanism, while keeping the rest of the model unchanged, to give a threshold-based approach, and a probability-based approach. The probability-based approach performed better than the threshold variant, characterised by a lower average root mean squared error against observed data. The could stem from the continuous versus discrete nature of each approach in deciding if an agent will become disposed to consider alternative choices, i.e. a less binary choice trigger mechanism could be more reflective of real-world decision-making.
Within global variance-based sensitivity analysis, most studies do not look at temporal dynamics, instead performing a snapshot of the final outcome that does not consider variability in parameter sensitivity influence over time (Ligmann-Zielinska et al. 2020). The temporal global variance-based sensitivity analysis that we conducted indicated that the probability-based approach showed greater output variance than the threshold approach. This is supported by the larger spread of model outputs given in Figure 2. The reason for this could be that a less deterministic agent choice disposition (the threshold approach does still allow for some randomness) feeds through the model structure and results in a larger variance of model outcome. Across parameters, the health perception of alternatives was the dominant source of variance in the threshold model. In this model, the environmental perception parameter had a small contribution to model uncertainty. This could be explained by the stark difference in nutrition (principally saturated fat) of the two milk options, but only the slight difference in environmental impacts (see Table 2). If plant-based alternatives were considered as a third option in an extended model, it is plausible that this component would have a larger effect. No single parameter dominated in the probability approach, with variance instead more evenly distributed.
The model was able to reproduce, with quantified uncertainty, the observed pattern of historical milk consumption. However, the model curves differ from observed data in their rate of change. Model variants produces a pair of more aggressive curves than the real-world data. This could be due to a number of reasons, including the exclusion or inclusion of choice influences, and the effect size of fixed values in the model. The latter point was somewhat explored through analysis of \(k\), the gradient of the probability function, however, more complete and rigorous robustness analysis should be conducted in future model iterations. Second, the modelling choices and structure reflect just one of a great many different model components and possible combinations. Although we explore this through different model variants, it is but one plausible representation of observed phenomena. Indeed, the question of model structure and model discovery is the central line of investigation of an emerging field within the ABM literature known as inverse generative social science (Vu et al. 2019).
Finally, the model did not look to predict agent absolute consumption of milk, rather, it allowed for the relative split under a total average weekly milk consumption, e.g., from 100%/0% whole milk and 0%/100% skimmed (including semi) and every combination in between. The reason for this was that although skimmed and whole milk show a classic substitution curve, it is against a backdrop of declining overall consumption. The model does not aim to account for the factors involved in this decline, only the relative consumption between milk types. Neither did it allow for non-milk consumers in the population (but agents could choose to consume no whole or skimmed milk). We justify this modelling choice based of market research for the Agricultural and Horticultural Development Board that found 98% of UK households purchase liquid milk (AHDB 2019).
The study presented here serves as a foundation to extend the model. In particular, future work could give a forward-looking study of milk consumption with scenario analysis to investigate consumption dynamics under changes to milk choice influences. Future work should also include plant-based alternatives to understand their possible adoption trajectories, and the policy interventions that may influence this.
Conclusion
This paper described an agent-based model of food choice substitution, applied in the context of UK milk consumption. The model was structured around the perception of, and disposition to, consider alternatives, and is modulated by habit, social influence and choice evaluation. The model was informed empirically, and grounded by theories of social psychology, behaviour change, and consumer food acceptance. Simulation experiments were conducted to test the capability of the model to represent observed phenomena, the robustness of which was tested by comparing the performance of two model variants. Both model variants reproduced the general pattern of the observed data, however, the probability-based disposition approach performed better (smaller average error) than the threshold disposition approach.
We employed temporal global variance-based sensitivity analysis, an improvement on final snapshot global sensitivity analysis, to understand how the variance associated with model parameters changed over the simulation. In both model variants, interactions between parameters, rather than parameters themselves were the source of most variance. This is an expected feature of agent-based models, however, temporal analysis showed the threshold approach converged toward a lower variance, whereas the probability-based approach remained at higher and less stable variance.
This study is the first to present an ABM of food choice substitution in the context of UK milk consumption. The model takes a novel approach to the inclusion of basic human values, and, to our knowledge, is the first ABM to incorporate values survey data and use it to inform agent decision-making on food choice. Analytically, this study contributes to widening the limited literature base of ABMs that conduct temporal sensitivity analysis.
Testing different human decision-making models in the context of real-world phenomena is an important area of investigation, that can push the frontiers of agent-based modelling and research. This study contributes, with the exploration of small differences in decisions-making, to this evidence base, and provides a basis for further testing of more detailed decision-making models. Finally, the results of this experimental analysis and simulation provide evidence for modelling choices going forward. Specifically, the probability-based approach performed better in the experiment and this mechanism will inform the design choices for future modelling work that looks to incorporate plant-based milk alternatives.
Model Documentation
The model has been developed in Python. The code is available here: https://www.comses.net/codebase-release/8b2e5a29-ad2d-4b45-9038-67d06d6b7c80/.Appendix
Additional ODD elements
Emergence
The key results of modelled outputs that emerge from the behaviours and interactions of individuals are the macro-level average consumption of milk choice among the simulated population, the crossover point of the consumption of substituted milk types, and the stability of this consumption over time.
Interaction
Individuals interact with other individuals through a social network (small-world structure) where information exchange occurs. The mechanism by which information exchange occurs is not explicitly modelled, rather, this is governed by a probability of interaction and social susceptibility parameter.
Stochasticity
The information of health and environmental impacts of different milk types that agents perceive is randomly drawn from a normal distribution with mean values determined by the ‘Initial perception of health component of alternative’ and ‘Initial perception of environmental component of alternative’ parameters. In the threshold model variant, stochasticity is employed following a 3% random chance that an agent will become spontaneously disposed to consider their alternatives, even if their threshold to do so is not met. In the probability-based model variant, stochasticity is reflected in the logistic function of neighbour milk choice information entropy and probability of an agent becoming disposed to consider their alternatives.
Heterogeneity
Heterogeneity is represented by the assignment of state variables among the agents. Principally, agents have different basic human values assigned according to the distribution of UK results data from the European Social Survey.
Observation (including Emergence)
At each time step, the component choice functions and decision-making function for each choice and each agent is collected.

| Parameter | Group | Description |
|---|---|---|
| Memory length | Cognitive perception | The size of an agent’s memory that it can recall previous information. Cognitive perception is based on averaging values in the memory. |
| Initial perception of health component of alternative | Cognitive perception | The perception of the health impact of skimmed (inc. semi) milk given as a relative score against whole milk. |
| Initial perception of environmental component of alternative | The perception of the health | The perception of the environmental impact of skimmed (inc. semi) milk given as a relative score against whole milk. |
| Habit threshold | Habit | The number of consecutive choices that return the same majority milk type consumption needed before the effects of habit take place. |
| Initial habit of incumbent | Habit | The initial number of consecutive choices that have returned the same majority milk type. |
| Probability of interacting | Social influence | The probability of an agent interacting (exchanging information on milk choice function scores) with other agents in its network. |
| Social susceptibility | Social influence | The susceptibility of an agent to modify its milk choice function scores based on information it receives from neighbours. |
| Social conformity | Social influence | The degree to which an agent will seek to conform its weighting between cognitive milk components (health, environment) to closer reflect the general public concern for each of these issues. |
| No. of neighbours | Social influence | The number of neighbours in an agent’s network. |
| Gradient probability disposition (probability model variant only) |
Social influence | The slope of the function that determines how quickly the probability of being disposed to consider choice of milk as a function of the informational entropy of milk choices in an agent’s neighbour network. |
| Social blindness | Evaluation | The probability that an agent has the ability to perceive the impact of its choice and therefore the option of evaluating it. |
| Post-choice justification | Evaluation | The threshold beyond which an agent will simply justify the discrepancy between its values and behaviour (milk choice impacts), rather than act to resolve it. |
| Cognitive dissonance threshold | Evaluation | The threshold below which any discrepancy between an agent’s values and its behaviour (milk choice impacts) will not trigger a state of cognitive dissonance. |
| Question | Survey | Model use |
|---|---|---|
| She/he strongly believes that people should care for nature. Looking after the environment is important to her/him. | European Social Survey, 2018 | This question relates to the ‘universalism’ value and responses inform the environmental value position of agents used in evaluation sub-model. |
| It is important to him/her to live in secure surroundings. She/he avoids anything that might endanger his safety. | European Social Survey, 2018 | This question relates to the ‘security’ value which contains the health dimension. Note, the expanded 40 item PVQ includes a direct question on health, ‘She/he tries hard to avoid getting sick. Staying healthy is very important to her/him’, but in the absence of this data in the ESS, we opt for the most relevant security value question. |
| She/he likes surprises and is always looking for new things to do. She/he thinks it is important to do lots of different things in life. | European Social Survey, 2018 | This question relates to the ‘stimulation’ value which forms part of Schwartz’s openness to change higher order value dimension. UK responses to this question inform the level at which agents would consider alternative milk choice in the threshold-based model approach. |
| What do you see as the most/other important issues facing Britain today? | Ipsos Mori | Here, the relative change in concerns on health and the environment are used to inform the social norm sub-model. |
| Which do you think are the most important issues facing the country at this time? Please tick up to three. | YouGov | |
The gradient (\(k\)) in Equation 1 governs the rate of change of the logistic function. Physically, \(k\) represents the rate at which the set of agent’s neighbour choices (given by an expression of information entropy) effects the probability that they will become disposed to consider alternatives (Equation 2). To narrow the parameter space for calibration, we explored values of \(k\) from 11 to 18 and averaged the resulting model behaviour over a number (\(n = 520\)) of different runs. Figure 5 shows that an increasing \(k\) flattens the curve pair and delays the point at which curves undergo the rapid rate of increase or decrease. This shows the choice of gradient is significant with the model’s macro behaviour diverging from the desired trend as it tended toward higher values. From this analysis, we bound \(k\) between 14 and 16 as an allowable range for the calibration exercise.
References
AHDB. (2019). The future of milk. Retrieved from: https://ahdb.org.uk/news/consumer-insight-the-future-of-milk#_edn1.
AN, L., Grimm, V., & Turner II, B. L. (2020). Editorial: Meeting grand challenges in agent-based models. Journal of Artificial Societies and Social Simulation, 23(1), 13: https://www.jasss.org/23/1/13.html. [doi:10.18564/jasss.4012]
AUCHINCLOSS, A. H., Riolo, R. L., Brown, D. G., Cook, J., & Roux, A. V. D. (2011). An agent-Based model of income inequalities in diet in the context of residential segregation. American Journal of Preventive Medicine, 40(3), 303–311. [doi:10.1016/j.amepre.2010.10.033]
BOOTH, S. L., Sallis, J. F., Ritenbaugh, C., Hill, J. O., Birch, L. L., Frank, L. D., Glanz, K., Himmelgreen, D. A., Mudd, M., Popkin, B. M., Rickard, K. A., St Jeor, S., & Hays, N. P. (2001). Environmental and societal factors affect food choice and physical activity: Rationale, influences, and leverage points. Nutrition Reviews, 59, 21–36. [doi:10.1111/j.1753-4887.2001.tb06983.x]
BRAVO, G., Vallino, E., Cerutti, A. K., & Pairotti, M. B. (2013). Alternative scenarios of green consumption in Italy: An empirically grounded model. Environmental Modelling & Software, 47, 225–234. [doi:10.1016/j.envsoft.2013.05.015]
BRUCH, E., & Atwell, J. (2015). Agent-based models in empirical social research. Sociological Methods & Research, 44(2), 186–221. [doi:10.1177/0049124113506405]
BUCHER, T., Collins, C., Rollo, M. E., McCaffrey, T. A., De Vlieger, N., van der Bend, D., Truby, H., & Perez-Cueto, F. J. A. (2016). Nudging consumers towards healthier choices: A systematic review of positional influences on food choice. British Journal of Nutrition, 115(12), 2252–2263. [doi:10.1017/s0007114516001653]
CHEN, P. J., & Antonelli, M. (2020). Conceptual models of food choice: Influential factors related to foods, individual differences, and society. Foods, 9(12), 1898. [doi:10.3390/foods9121898]
CLUNE, S., Crossin, E., & Verghese, K. (2017). Systematic review of greenhouse gas emissions for different fresh food categories. Journal of Cleaner Production, 140, 766–783. [doi:10.1016/j.jclepro.2016.04.082]
CRUWYS, T., Bevelander, K. E., & Hermans, R. C. J. (2015). Social modeling of eating: A review of when and why social influence affects food intake and choice. Appetite, 86, 3–18. [doi:10.1016/j.appet.2014.08.035]
DEFRA. (2020). Family food survey. Retrieved May 15, 2021, from: https://www.gov.uk/government/statistical-data-sets/family-food-datasets.
EPSTEIN, J. M. (2014). Agent Zero: Toward Neurocognitive Foundations for Generative Social Science. Princeton University Press.
FORTIN, F. A., De Rainville, F. M., Gardner, M. A., Parizeau, M., & Gagné, C. (2012). DEAP: Evolutionary algorithms made easy. Journal of Machine Learning Research, 13(70), 2171–2175. [doi:10.1145/2330784.2330799]
GALÁN, J. M., López-Paredes, A., & Del Olmo, R. (2009). An agent-based model for domestic water management in Valladolid metropolitan area. Water Resources Research, 45(5), 2009.
GDP, F. &. (2018). Climate change and the global dairy cattle sector – The role of the dairy sector in a low-carbon future. Rome. Available at: http://www.fao.org/publications/.
GERBER, P., Steinfeld, H., Henderson, B., Mottet, A., & Opio, C. (2013). Tackling climate change through livestock: A global assessment of emissions and mitigation opportunities.
GRIMM, V., Berger, U., Bastiansen, F., Eliassen, S., Ginot, V., Giske, J., Goss-Custard, J., Grand, T., Heinz, S. K., Huse, G., Huth, A., Jepsen, J. U., Jørgensen, C., Mooij, W. M., Müller, B., Pe’er, G., Piou, C., Railsback, S. F., Robbins, A. W., … DeAngelis, D. L. (2006). A standard protocol for describing individual-based and agent-based models. Ecological Modelling, 198(1–2), 115–126. [doi:10.1016/j.ecolmodel.2006.04.023]
GRIMM, V., Berger, U., DeAngelis, D. L., Polhill, J. G., Giske, J., & Railsback, S. F. (2010). The ODD protocol: A review and first update. Ecological Modelling, 221(23), 2760–2768. [doi:10.1016/j.ecolmodel.2010.08.019]
GRIMM, V., Railsback, S. F., Vincenot, C. E., Berger, U., Gallagher, C., DeAngelis, D. L., Groeneveld, J., Edmonds, B., Ge, J., Giske, J., Johnston, A. S. A., Milles, A., Nabe-Nielsen, A., Polhill, J. G., Radchuk, V., Rohwäder, M. S., Stillman, R. A. and, Thiele, J. C., & Ayllón, D. (2020). The ODD protocol for describing agent-based and other simulation models: A second update to improve clarity, replication, and structural realism. Journal of Artificial Societies and Social Simulation, 23(3), 7: https://www.jasss.org/23/3/7.html. [doi:10.18564/jasss.4259]
GUNARATNE, C. (2018). NL4Py. Complex Adaptive Systems Lab, University of Central Florida, Orlando, FL. Retrieved from: https://github.com/chathika/NL4Py.
HERMAN, J., & Usher, W. (2017). SALib: An open-source Python library for sensitivity analysis. The Journal of Open Source Software, 2(9), 97. [doi:10.21105/joss.00097]
HIGGS, S., & Thomas, J. (2016). Social influences on eating. Current Opinion in Behavioral Sciences, 9, 1–6.
LALLY, P., van Jaarsveld, C. H. M., Potts, H. W. W., & Wardle, J. (2010). How are habits formed: Modelling habit formation in the real world. European Journal of Social Psychology, 40(6), 998–1009. [doi:10.1002/ejsp.674]
LEIGH Gibson, E. (2006). Emotional influences on food choice: Sensory, physiological and psychological pathways. Physiology and Behavior, 89(1), 53–61. [doi:10.1016/j.physbeh.2006.01.024]
LENG, G., Adan, R. A. H., Belot, M., Brunstrom, J. M., De Graaf, K., Dickson, S. L., Hare, T., Maier, S., Menzies, J., Preissl, H., Reisch, L. A., Rogers, P. J., & Smeets, P. A. M. (2017). The determinants of food choice. Proceedings of the Nutrition Society, 76(3), 316–327. [doi:10.1017/s002966511600286x]
LIGMANN-ZIELINSKA, A., Siebers, P. O., Maglioccia, N., Parker, D., Grimm, V., Du, E. J., Cenek, M., Radchuk, V., Arbab, N. N., Li, S., Berger, U., Paudel, R., Robinson, D. T., Jankowski, P., An, L., & Ye, X. (2020). “One size does not fit all”: A roadmap of purpose-driven mixed-method pathways for sensitivity analysis of agent-based models. Journal of Artificial Societies and Social Simulation, 23(1), 6: https://www.jasss.org/23/1/6.html. [doi:10.18564/jasss.4201]
MEKONNEN, M. M., & Hoekstra, A. Y. (2012). A global assessment of the water footprint of farm animal products. Ecosystems, 15(3), 401–415. [doi:10.1007/s10021-011-9517-8]
MONTELEONE, E., Spinelli, S., Dinnella, C., Endrizzi, I., Laureati, M., Pagliarini, E., Sinesio, F., Gasperi, F., Torri, L., Aprea, E., Bailetti, L. I., Bendini, A., Braghieri, A., Cattaneo, C., Cliceri, D., Condelli, N., Cravero, M. C., Del Caro, A., Di Monaco, R., … Tesini, F. (2017). Exploring influences on food choice in a large population sample: The Italian Taste project. Food Quality and Preference, 59, 123–140. [doi:10.1016/j.foodqual.2017.02.013]
ONG, A. S. J., Frewer, L., & Chan, M. Y. (2017). Cognitive dissonance in food and nutrition – A review. Critical Reviews in Food Science and Nutrition, 57(11), 2330–2342. [doi:10.1080/10408398.2015.1013622]
PACHUCKI, M. A., Jacques, P. F., & Christakis, N. A. (2011). Social network concordance in food choice among spouses, friends, and siblings. American Journal of Public Health, 101(11), 2170–2177. [doi:10.2105/ajph.2011.300282]
POORE, J., & Nemecek, T. (2018). Reducing food’s environmental impacts through producers and consumers. Science, 360(6392), 987–992. [doi:10.1126/science.aaq0216]
POPKIN, B. M., Duffey, K., & Gordon-Larsen, P. (2005). Environmental influences on food choice, physical activity and energy balance. Physiology and Behavior, 86, 603–613. [doi:10.1016/j.physbeh.2005.08.051]
RAND, W., Herrmann, J., Schein, B., & Vodopivec, N. (2015). An agent-based model of urgent diffusion in social media. Journal of Artificial Societies and Social Simulation, 18(2), 1: https://www.jasss.org/18/2/1.html. [doi:10.18564/jasss.2616]
RAND, W., & Wilensky, U. (2007). NetLogo El Farol model. Retrieved May 23, 2021, from: https://ccl.northwestern.edu/netlogo/models/ElFarol.
RIET, J. V., Sijtsema, S. J., Dagevos, H., & De Bruijn, G. J. (2011). The importance of habits in eating behaviour. An overview and recommendations for future research. Appetite, 57(3), 585–596. [doi:10.1016/j.appet.2011.07.010]
ROGELJ, J., Shindell, D., Jiang, K., Fifita, S., Forster, P., Ginzburg, V., Handa, C., Kheshgi, H., Kobayashi, S., Kriegler, E., Mundaca, L., Séférian, R., & Vilariño, M. V. (2018). Mitigation pathways compatible with 1.5°C in the context of sustainable development. Retrieved from: https://www.ipcc.ch/sr15/chapter/chapter-2/.
RÖÖS, E., Garnett, T., Watz, V., & Sjörs, C. (2018). The role of dairy and plant based dairy alternatives in sustainable diets. Swedish University of Agricultural Sciences, The research platform Future Food
SALTELLI, A. (2002). Making best use of model evaluations to compute sensitivity indices. Computer Physics Communications, 145(2), 280–297. [doi:10.1016/s0010-4655(02)00280-1]
SALTELLI, A., Annoni, P., Azzini, I., Campolongo, F., Ratto, M., & Tarantola, S. (2002). Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Computer Physics Communications, 182(2), 259–270. [doi:10.1016/j.cpc.2009.09.018]
SCALCO, A., Macdiarmid, J. I., Craig, T., Whybrow, S., & Horgan, G. W. (2019). An agent-based model to simulate meat consumption behaviour of consumers in Britain. Journal of Artificial Societies and Social Simulation, 22(4), 8_ https://www.jasss.org/22/4/8.html. [doi:10.18564/jasss.4134]
SCHULTZ, P. W., Gouveia, V. V., Cameron, L. D., Tankha, G., Schmuck, P., & Franěk, M. (2005). Values and their relationship to environmental concern and conservation behavior. Journal of Cross-Cultural Psychology, 36(4), 457–475. [doi:10.1177/0022022105275962]
SCHWARTZ, S. H. (2012). An overview of the Schwartz theory of basic values. Online Readings in Psychology and Culture, 2(1), 12–13. [doi:10.9707/2307-0919.1116]
SMEATON, D., Draper, A., Vowden, K., & Durante, L. (2010). Development work for Wave 2 of the Food and You survey. Available at: https://www.food.gov.uk/sites/.
SOBOL, I. M. (2001). Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Mathematics and Computers in Simulation, 55(1–3), 271–280.
SPRINGMANN, M., Godfray, H. C. J., Rayner, M., & Scarborough, P. (2016). Analysis and valuation of the health and climate change cobenefits of dietary change. Proceedings of the National Academy of Sciences, 113(15), 4146–4151. [doi:10.1073/pnas.1523119113]
TAGHIKHAH, F., Filatova, T., & Voinov, A. (2021). Where does theory have it right? A comparison of theory-driven and empirical agent based models. Journal of Artificial Societies and Social Simulation, 24(2), 4: https://www.jasss.org/24/2/4.html. [doi:10.18564/jasss.4573]
TAGHIKHAH, F., Voinov, A., Shukla, N., & Filatova, T. (2020). Exploring consumer behavior and policy options in organic food adoption: Insights from the Australian wine sector. Environmental Science and Policy, 109, 116–124. [doi:10.1016/j.envsci.2020.04.001]
TRACY, M., Cerdá, M., & Keyes, K. M. (2018). Agent-Based modeling in public health: Current applications and future directions. Annual Review of Public Health, 39(1), 77–94. [doi:10.1146/annurev-publhealth-040617-014317]
VANGA, S. K., & Raghavan, V. (2018). How well do plant based alternatives fare nutritionally compared to cow’s milk? Journal of Food Science and Technology, 55, 10–20. [doi:10.1007/s13197-017-2915-y]
VAN Rossum, G., & Drake, F. L. (2009). Python 3 reference manual. Retrieved from: https://dl.acm.org/doi/book/10.5555/1593511.
VU, T. M., Brennan, A., Probst, C., Strong, M., Epstein, J. M., & Purshouse, R. C. (2019). Toward inverse generative social science using multi-objective genetic programming. GECCO 2019 - Proceedings of the 2019 Genetic and Evolutionary Computation Conference. [doi:10.1145/3321707.3321840]
WANG, C., Tan, Z. X., Ye, Y., WANG, L., Cheong, K. H., & Xie, N. G. (2017). A rumor spreading model based on information entropy. Nature Scientific Reports, 7(1), 1–14. [doi:10.1038/s41598-017-09171-8]
WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of “Small-World” networks. Nature, 393(6684), 440–442. [doi:10.1038/30918]
WILENSKY, U. (1999). NetLogo. Evanston, IL: Center for connected learning and computer-based modeling, Northwestern University.
ZHANG, D., Giabbanelli, P. J., Arah, O. A., & Zimmerman, F. J. (2014). Impact of different policies on unhealthy dietary behaviors in an urban adult population: An agent-based simulation model. American Journal of Public Health, 104(7), 1217–1222. [doi:10.2105/ajph.2014.301934]
ZHANG, H., & Vorobeychik, Y. (2019). Empirically grounded agent-Based models of innovation diffusion: A critical review. Artificial Intelligence Review, 52(2017), 707–714. [doi:10.1007/s10462-017-9577-z]