The Role of Mistrust in the Modelling of Opinion Adoption

Introduction

Truth is hard to glean from information that we obtain from interactions. A common method we use to assess the integrity of a new piece of information is to compare the latest information to what we already assume to be true. If the information is consistent with what we already believe, then the new information is deemed more likely to be true. Otherwise, if this latest information contradicts our current understanding, we are more likely to disregard it. Psychology explains this phenomenon by appealing to the notion of cognitive dissonance and confirmation bias.

Cognitive dissonance results from new information conflicting with a person’s beliefs (Festinger 1957), causing psychological stress. People tend to avoid stress and resolve their cognitive dissonances. People use confirmation bias as one way to relieve this stress. Confirmation bias is placing more emphasis or focus on information, or parts of information, which conform to wanted or expected results (Oswald & Grosjean 2004). Confirmation bias naturally results in less cognitive dissonance. As someone focuses more on information conforming to their expectation, which is informed by what they believe, they focus less on anything that contradicts expectation. Confirmation bias describes human action, but it is not a cause, leaving a question as to why people rely on confirmation bias.

Mistrust of a source is a common reason to reject new information, implying that mistrust is a cause of confirmation bias. We often rationalise dismissing information from sources we mistrust, assuming it is likely misinformation, either incidentally or deliberately, and therefore safe to ignore. So if we believe there is no reason to mistrust a source, would we lose our propensity to accept only that information that conforms to our belief? Is it the possibility of deception that allows us to disregard any evidence that contradicts our internal narrative? Would it eliminate confirmation bias?

These are difficult questions to answer, and this paper will attempt to shed some light on a model that inspires these questions. Understanding how individuals come to adopt their beliefs, how they spread those beliefs to the next individual, and how that individual accepts or rejects those beliefs allows for powerful predictions of human behaviour from the scale of individuals to whole societies.

Background

Opinion Dynamics is the field of study interested in modelling opinion dissemination, specifically how opinions spread from person to person and across a social network. Opinion dynamics has a rich history and has received contributions from many different disciplines, ranging from statistical physics (Castellano et al. 2009; Holley & Liggett 1975; Sznajd-Weron & Sznajd 2000), to psychology (Abelson 1967; French Jr 1956), to social network science (Christakis & Fowler 2009). Given the rich history of contribution to this field, there is now interest in coalescing these various models into a unified framework (Coates et al. 2018). This paper will focus more on the modelling area of opinion dynamics, particularly how models have created disagreement in their simulations.

A central concept in opinion dynamics, and the focus of this paper, is polarisation, i.e. when individuals partition themselves in opinion space into two or more distinct opinion clusters. The motivation for studying polarisation is that many important controversial issues polarise individuals. If we understand why polarisation happens, this leads, for instance, to understanding political factions and other social divisions.

There are two classes of models in opinion dynamics differing in how they represent opinions. One class of models represents opinions as discrete values, e.g. selecting candidates in an election, and the other class of models represents opinions as continuous values, e.g. level of support for a candidate or their policies. One of the first opinion dynamics models, investigating continuous opinions (Abelson 1967; French Jr 1956), originated in the social sciences. Later models of discrete opinions, broadly classed as cellular automata models, (Clifford & Sudburry 1973; Sznajd-Weron & Sznajd 2000) originated in statical physics. These early models of both discrete and continuous opinion formed the foundation of opinion dynamics modelling.

The early models (both for discrete and continuous opinions) are structurally limited in creating polarisation. Based on the French model, the first opinion dynamics models focus on finding the individual that had the most influence over the final opinion consensus, a concept called ‘social power’ rather than attempting to induce polarisation (French Jr 1956). Inspired by the behaviour of atoms in a lattice of ferromagnetic materials, statistical physicists constructed cellular automata models of opinion dynamics where individuals or cells in a lattice structure held discrete opinions and obeyed rules defining their interactions (Castellano et al. 2009). Although ferromagnetic materials are broadly analogous to real-world voting populations, voters in the real world are more connected (and more complicated in their connections) with other voters than atoms in a lattice. As a result, cellular automata models always resulted in consensus (Castellano et al. 2003; Sood & Redner 2005).

These models represented a major step in developing the field of opinion dynamics, but they both suffer from the drawback that they produce consensus under realistic conditions. Abelson (1967) first identified what is known as the cleavage problem with respect to the French model by posing the question: if the French model (and its derivatives) mostly predicted consensuses, then why in society is there so much polarisation around contentious issues? While the original cleavage problem statement is directed at the French model, it has broader implications for all opinion dynamics models.

The continuous opinion discrete action (CODA) model addresses the cleavage problem in discrete opinion models (Martins 2008). The CODA model allocates agents latent opinions in an unobservable continuous space, but these opinions are only observable by others in a discrete space. In the model, there are two discrete events, e.g. \(A\) or \(B\), an agent’s latent opinion is their belief in the likelihood of \(A\) or \(B\) occurring. An agent expresses their latent opinion by predicting that either \(A\) or \(B\) will occur. Agents update their latent opinion by a fixed quantity \(\alpha\) based on which event their partner predicted in an interaction. So if agent \(i\) predicted \(A\), then agent \(j\) would increase their opinion that \(A\) occurs by some function of \(\alpha\).

The CODA model addresses the cleavage problem by allowing agents to become extreme in their discrete opinion. The updating mechanism for their latent opinion allows it to reach the extremes of the opinion space, leading to polarisation. Later extensions of the CODA model introduce concepts like trust between agents (Martins 2013), building on the model’s ability to induce polarisation. Specifically, trust naturally introduced contrarianism, where an agent adopts the opposite choice of their interaction partner. Other models have introduced contrarianism explicitly, but CODA derives contrarianism from the trust between agents. The CODA model influenced much of modern opinion dynamics through introducing a latent continuous opinion driving the choice of discrete opinions and has inspired many models (Ceragioli & Frasca 2018; Jiao & Li 2021; Zino et al. 2020).

The bounded confidence model addresses the cleavage problem for continuous opinions taking inspiration from Axelrod (1997), which introduces similarity bias, i.e. individuals will only interact if they are similar to each other. The bounded confidence models (Deffuant et al. 2000; Hegselmann & Krause 2002; Krause 2000; Weisbuch et al. 2002) only allow agents to interact if their opinions are within \(\epsilon\) in the opinion space. The parameter \(\epsilon\) induces polarisation by restricting interactions between agents with divergent opinions. The extent of polarisation depends on \(\epsilon\); small values of \(\epsilon\) yield more opinion clusters, and larger values of \(\epsilon\) yield fewer clusters.

Although \(\epsilon\) creates polarisation in bounded confidence models, it is unclear if or how \(\epsilon\) manifests real-world interactions. As a mathematical concept, \(\epsilon\) is a distance, but the crucial question for interpreting bounded confidence models is how “distance” is measured in real interactions. An extension to bounded confidence (Deffuant et al. 2002) implies that \(\epsilon\) is the confidence of an agent, i.e. the greater \(\epsilon\), the more unsure an agent is of their opinion. Yet this interpretation lacks any guidance on measuring \(\epsilon\) for real people, and it isn’t clear how cognitive processes which guide individuals to accept or reject others’ opinions relate to \(\epsilon\).

The model framework in Martins (2009), later elaborated on in Martins (2012), uses Bayesian inference to establish opinion updating rules. The rules derive from treating an agent’s knowledge as a normally distributed prior and their interaction partner’s knowledge as data to update via Bayes’ Theorem. This framework produces two distinct models: a ‘trivial’ model and a ‘developed’ model. The ‘trivial’ model is similar to the French model and only exhibits consensus. The ‘developed’ model introduces a global trust rate \(p\) into the ‘trivial’ model, and the result is that agents in simulations polarise.

The non-trivial Martins model creates polarisation behaviour similar to the bounded confidence models. The Martins model gives each agent uncertainty in their opinion. In the Martins model, uncertainty is the standard deviation of the density function representing the agent’s opinion. Uncertainty in the Martins model functions similarly to \(\epsilon\) in the bounded confidence models, following the same inversely proportional relationship with the number opinion clusters. It was speculated in Martins (2009) that, if the prior was step-functions instead of a Gaussian distribution in the Martins model, the Martins model would be identical to bounded confidence models, and claimed that the bounded confidence models approximated the Martins model at fixed uncertainty. Since uncertainty as a standard deviation is congruent with how people think of confidence (Stankov et al. 2015), the model framework of Martins (2009) explains why the bounded confidence model work, thereby pointing to insights into the causes of polarisation.

The work (Martins 2009) leaves some gaps not addressed in the modern opinion dynamics literature. First, the model assumes that agents cannot share their uncertainties. This trait leads to agents assuming their interaction partner has the same uncertainty as themselves. We call this the unshared uncertainty assumption. Second, Martins only investigated the trust rate through simulations. A deeper analysis needs to performed on \(p\) since it is the cause of polarisation in the model.

The present paper seeks to address the gaps of Martins (2009) by re-deriving the model without the unshared uncertainty assumption and analytical investigating the impact of the trust rate \(p\). We first summarise the derivation of the model in Martins (2009). Then the unshared uncertainty assumption is relaxed, creating our extended model. Our extended model is thoroughly investigated by simulation studies, comparing the extended model to the original Martins model. We also present a new analytical investigation of the model giving close attention to how \(p\) influences the model outputs, and briefly investigate extremism in a small simulation study. We conclude with a discussion of the extended model, a discussion about the simulation results, and an outline for future directions for the Martins modelling framework.

A Bayesian Inference Model for Opinion Dynamics

This section will first summarise the derivation of the model in Martins (2009) and then re-derive the model by relaxing the shared uncertainty assumption made in the original model, thereby creating an extended model.

The modelling framework

The model developed in Martins (2009) establishes \(\theta\) as a random variable whose value all agents are trying to guess. Agent \(i\)’s opinion, \(x_i\), is their ‘guess’ at \(\theta\). Agent \(i\)’s uncertainty of \(x_i\) is quantified as \(\sigma_i\). Both \(x_i\) and \(\sigma_i\) are part of a normal distribution \(f_i(\theta) = \frac{1}{\sqrt{2\pi}\sigma_i}e^{-(\theta - x_i(t))^2/(2\sigma^2_i)}\), where \(x_i\) is the mean and \(\sigma_i\) is the standard deviation. This normal distribution \(f_i(\theta)\) describes agent \(i\)’s understanding of \(\theta\).

When agents interact, they share information such as their opinion and uncertainty. The unshared uncertainty assumption restricts this interaction so that only opinion is shared. Suppose agent \(i\) and agent \(j\) interact in the model at some time \(t\). Because of the unshared uncertainty assumption, agent \(j\) is only able to share their opinion \(x_j\). Agent \(i\) requires the reliability of \(x_j\) for Bayesian inference to work, and therefore has to assume that \(x_j\) has the same uncertainty as they have \(\sigma_i\). As a consequence, although this makes the derivation of opinion updating easier, it obscures the meaning of a heuristic created in the derivation of the updating equations.

The updating rules in the model of Martins (2009) are derived as follows: Suppose agent \(i\) recently interacted with agent \(j\) and learned their opinion \(x_j\). Under the unshared uncertainty assumption agent \(i\) assumes that agent \(j\) shares agent \(i\)’s uncertainty \(\sigma_i\). With the data \(x_j\) and a measure of variance on the data \(\sigma_i\), a likelihood can be constructed for \(\theta\) with respect to \(x_j\). As outlined in Martins (2009) a true likelihood of \(x_j\) would need to account for the influences on agent \(j\), including agent \(i\)’s influence. This is impractical to implement and furthermore unrealistic. A reasonable and convenient likelihood for \(\theta\) is a normal distribution, with \(\theta\) as the mean and the uncertainty on \(x_j\), \(\sigma_i\), as the standard deviation. Therefore,

\[ x_j|\theta \sim N(\theta,\sigma^2_i) %Write the full gaussian function\]

\[(1)\]

Using both the likelihood \(f_i(x_j|\theta)\) and prior \(f_i(\theta)\) in Bayes’ Theorem creates a posterior \(f_i(\theta|x_j)\). Agent \(i\)’s opinion updates to the mean of the posterior \(f_i(\theta|x_j)\). Similarly, agent \(i\)’s uncertainty updates to the square root of the posterior’s variance.

An important consequence of using (1) in the derivation of agent \(i\)’s new opinion is that, in the application of Bayes’ Theorem, the new opinion at time \(t+1\) will be

\[ x_i(t+1) = \frac{x_i(t) + x_j(t)}{2}\]

\[(2)\]

Thus, no matter the network structure, if (2) is used as the opinion update rule, the model will always lead to consensus.

To create a more compelling model Martins introduces a probability \(p\) that agent \(j\) is sharing erroneous information. This new parameter \(p\) represents the proportion of valid information on \(\theta\) and by extension is the probability that a generic agent \(j\) is not misinforming agent \(i\). This modifies the likelihood to

\[ x_j|\theta \sim p N(\theta,\sigma^2_i) + (1-p)U\]

\[(3)\]

where \(U\) is a function such that \(1=\int_{-\infty}^{\infty}U \mathrm{dx}\) and \(\mathrm{d}U/\mathrm{dx} = 0\) for all \(x\). This creates a posterior with a more dynamic mean, leading to the opinion updating rule for agent \(i\)’s opinion at time \(t+1\) as

\[x_i(t+1) = p^* \frac{x_i(t) + x_j(t)}{2} + (1 - p^*) x_i(t) \]

\[(4)\]

where

\[p^* = \frac{p(1/(2\sqrt{\pi}\sigma_i))e^{-(x_i(t) - x_j(t))^2/(4\sigma^2_i)}}{p(1/(2\sqrt{\pi}\sigma_i))e^{-(x_i(t) - x_j(t))^2/(4\sigma^2_i)} + (1 - p)} \]

\[(5)\]

Whereas the updating rule given by (2) leads inexorably to consensus, the new updating rule (4) addresses the cleavage problem with the parameter \(p^*\), defined by (5), creating the potential for polarisation. In particular \(p^*\) controls whether agent \(i\) will be completely stubborn (\(p^* = 0\)) or completely open minded (\(p^* = 1\)). Martins also derived the uncertainty update at \(t+1\) through calculating the variance of the posterior originating from (3). The result is

\[\sigma_i^2(t + 1) = \sigma_i^2(t)\left(1 - \frac{p^*}{2}\right) + p^* (1 - p^*)\left(\frac{x_i(t) - x_j(t)}{2}\right)^2 \]

\[(6)\]

The introduction of \(p\) into (1) creates the new parameter (5) which allows agents to discriminate against other agents with very different opinions depending on their confidence. As the ratio of opinion difference \(|x_i-x_j|\) to uncertainty \(\sigma_i\) tends to zero, (5) approaches unity, allowing agent \(i\) and \(j\) to share opinions. Otherwise if the ratio tends towards infinity then (5) approaches 0 making agent \(i\) stubborn towards agent \(j\)’s opinion. This is reflected in the modelling of Martins (2009) where models that froze uncertainty updating exhibited polarisation similar to the bounded confidence models. The bounded confidence models were justified by the idea that agents with large disagreement in opinion tend not to compromise. The work (Martins 2009) lends credence to that idea, but also supplies a plausible reason why agents don’t listen to other agents with very different opinions through the introduction of mistrust in the form of \(p\). The model encapsulates the concept: “Based on how much I already know, how likely is this new information false?”

Relaxing the unshared uncertainty assumption

Relaxing the unshared uncertainty assumption allows agent \(j\) to share their uncertainty on their opinion \(x_j\). This eliminates the need for agent \(i\) to make an assumption about the uncertainty on \(x_j\) and use \(\sigma_j\) as the standard deviation in (1). This changes the likelihood (3) to

\[x_j|\theta \sim p N(\theta,\sigma^2_j) + (1-p)U \]

\[(7)\]

The process of re-deriving agent \(i\)’s new opinion and uncertainty without the unshared uncertainty assumption remains the same, although the algebraic manipulation becomes more complicated. Without the unshared uncertainty assumption, agent \(i\) updates their opinion and uncertainty to

\[\begin{aligned} x_i(t+1) = p^* \frac{(x_i/\sigma_i^2) + (x_j/\sigma_j^2)}{(1/\sigma_i^2)+(1/\sigma_j^2)} + (1 - p^*) x_i(t) \end{aligned}\]

\[(8)\]

and

\[\begin{aligned} \sigma_i^2(t + 1) = \sigma_i^2(t) \left(1 - p^*\frac{\sigma_i^2(t)}{\sigma_i^2(t)+\sigma_j^2(t)}\right) + p^* (1 - p^*)\left(\frac{x_i(t) - x_j(t)}{1+(\sigma_j(t)/\sigma_i(t))^2}\right)^2 \end{aligned}\]

\[(9)\]

where

\[\begin{aligned} p^* = \frac{p\phi\left(x_i(t) - x_j(t),\sqrt{\sigma^2_i + \sigma^2_j}\right)}{p\phi\left(x_i(t) - x_j(t),\sqrt{\sigma^2_i + \sigma^2_j}\right) + (1 - p)} \end{aligned}\]

\[(10)\]

and

\[\begin{aligned} \phi\left(x_i(t) - x_j(t),\sqrt{\sigma^2_i + \sigma^2_j}\right) = \left(1/\left(\sqrt{2\pi(\sigma^2_i + \sigma^2_j)}\right)\right)e^{-(x_i(t) - x_j(t))^2/2(\sigma^2_i + \sigma^2_j)}\end{aligned}\]

\[(11)\]

Relaxing the unshared uncertainty assumption has created some new dynamics. The most significant changes are from (4) and (6) to (8) and (9). The update formula (8) now replaces (4) with a weighted average, weighted according to each agents’ uncertainty. The consequence is that agents that are highly confident compared to their interaction partner shift their opinion less, regardless of \(p^*\). Likewise, agents that have less confidence than their interaction partner are more willing to shift their opinion, depending on \(p^*\) as given by (10). This is consistent with the idea that confident individuals have strong arguments for their beliefs and have more inertia when shifting their opinions, and more momentum when changing another individual’s opinion.

The changes in both (8) and (9) result in low uncertainty agents having more influence relative to agents with high uncertainty. The weighted average in (8) results in low uncertainty agents being barely affected by those with high uncertainty, even when they are compatible through high (10). In the uncertainty update (9) high confidence agents are less likely to increase in uncertainty because the second term of (9) controls how much uncertainty increase, which is maximized at \(p^* = 0.5\). A \(p^*=0.5\) places limits on how small \(\sigma_j\) can be along with how big the difference between \(x_i\) and \(x_j\) can be, thus limiting the pool of agents that can convince a highly confident agent to be less confident. Leaving highly confident agents to become more confident on average. Overall this extension mainly gives the original model an additional dimension that reinforces highly confident agents.

More interestingly is the subtle change in \(p^*\). The only change between (5) and (10) is all instances of \(2\sigma_i^2\) are replaced with \(\sigma^2_i + \sigma^2_j\). This does not change the dynamics of \(p^*\) and \(p^*\) will behave similar in both the original and extended models, but the change does reveal the meaning of \(p^*\). In the original model, if \(\sigma_i \neq \sigma_j\), using (5) to generate \(p^*\) would mean an interacting pair of agents, \(i\) and \(j\), would produce different \(p^*\)s. Only when \(\sigma_i = \sigma_j\) would they produce the same \(p^*\). In the extended model however, using (10) to generate \(p^*\) would make agent \(i\) and \(j\) produce \(p^*\)s that are equal regardless of \(\sigma_i\) or \(\sigma_j\). The change of replacing \(2\sigma_i^2\) with \(\sigma^2_i + \sigma^2_j\) has created a \(p^*\) which is symmetrical through agent interaction. This suggests that \(p^*\) is measure of agent compatibility, when \(p^*\) is 1 agents are completely compatible and when \(p^*\) is 0 they are completely incompatible.

Shared Uncertainty Modelling

This section will detail the implementation of the extended martins model, including a comparison between the extended and original models.

The model

The model creates \(n\) agents with an initial state in opinion and uncertainty, and specify an array of time points \(T\), where agent states of the simulation at those time points will be recorded all the states. The model then feeds the agents and \(T\) into Algorithm 1 while pre-initialising Algorithm 2 to have a fixed third input of \(p\) equal to a specific value.

Algorithm 2 can be easily modified to support the models found in Martins (2009) by replacing ( 10) with ( 5), ( 8) with ( 4) and, if uncertainty is evolving for Martins, replacing ( 9) with ( 6); otherwise, when the uncertainty is fixed, the uncertainty updating part of Algorithm 2 is skipped.

Results

Figures 1 and 2 compare the two simulations in Martins (2009) of fixed and evolving uncertainty, with the extend model. The simulations use \(p=0.7\) and had 10 000 agents as in Martins (2009). The simulation ran according to Algorithms 1 and 2, but the Martins simulations replaced (10) with (5), (8) with (4) and, (9) with (6).

Figure 1 shows a substantial difference between the original Martins models and the extended model. The extended model follows the same trend as the two Martins models, but the extended model creates more opinion clusters. Consequently, the critical point in the graph changes when simulations reached a consensus for the different initial \(\sigma\)s of the agents. In the extend model it is at initial \(\sigma = 0.14\), in fixed uncertainty it is at initial \(\sigma = 0.08\) and, for evolving uncertainty it is at initial \(\sigma = 0.12\). The cause for the more opinion cluster in the extended model is likely that agents with high confidence have more power over less confident agents. In the original Martins models, less confident agents ‘bridged the gap’ between high confidence agents, allowing all agents to reach consensus at low initial uncertainty. Less confident agents hold less sway in the extended model and are more likely to be consumed by clusters of highly confident agents.

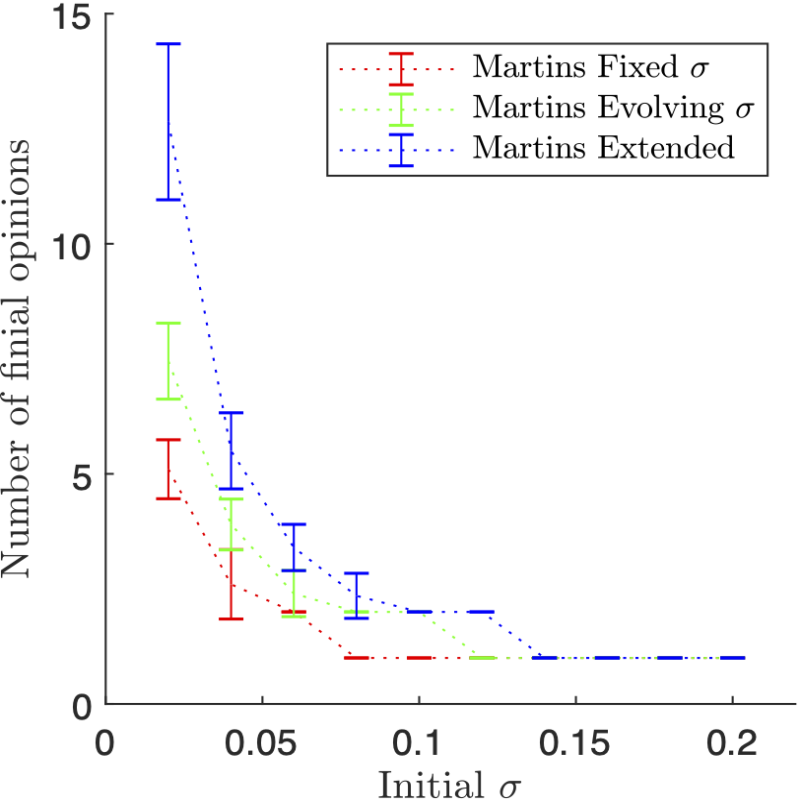
Figure 2 supports the conclusion of Figure 1, but proves more specific detail. The fixed Martins model is exhibiting the expected ‘bounded confidence like’ behaviour from Martins (2009) and the evolving model is showing the expected fragmented behaviour from Martins (2009), which is reminiscent of how fractal shapes behave; where better resolutions on a fractal shape reveal greater complexity of that shape. The extended model differs from Martins evolving by being more ‘clumpy’. Agents in the evolving Martins are more diffuse than in the extended model. An explanation could be that a particular agent is getting highly confident, and because the agent is highly confident, they’re able to convince the lower confidence agents around them to adopt their opinion more readily. Due to the weighted average in (8), the low confidence agents will closely adopt a higher confidence opinion, which creates tighter opinion clusters. The tighter the opinion cluster means that more clusters can form, explaining Figure 1.

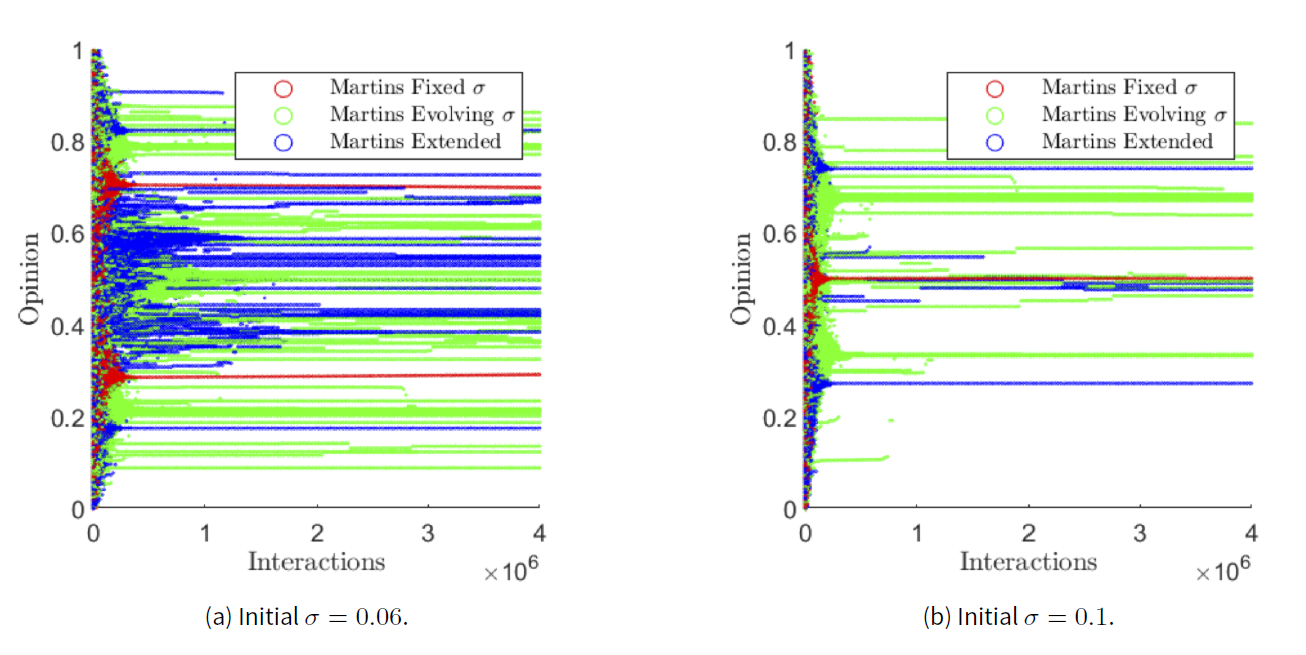
Figures 1 and 2 demonstrate the new model results in more polarisation. Compared to the fixed and evolving Martins, in the extended model, a higher initial uncertainty is required for agents to reach a consensus, likely due to high confidence agents being more influential and low agents being less influential in the extended. Under the extended model, high confidence agents in an opinion cluster can swiftly recruit low confidence agents, themselves quickly becoming highly confident after being recruited. This is radicalisation, and this more effective radicalisation of the extended model is demonstrated in Figure 2. The weighted average in (8) is the cause for the distinct behaviour of the extended model. When interacting with a high confidence opinion, a low confidence agent will shift their opinion closer to the high confidence opinion. The opposite effect will be the case for high confidence agents.

Analysing the Impact of the Trust Rate \(p\)

To further understand the influence of \(p\) on the new model equations (8) and (9) need to reformatted such that change in opinion and uncertainty is explicit, i.e. \(x_i(t+1) = x_i(t) + h(\Delta x, R_\sigma)\) and \(\sigma^2_i(t+1) = \sigma^2_i(t) + k(\Delta x, R_\sigma),\) where \(\Delta x = x_j-x_i\) and \(R_\sigma = \sigma_j/\sigma_i\). When (8) and (9) are organised in this way, the functions \(h\) and \(k\) are

\[\begin{aligned} h(\Delta x, R_\sigma) &= p^* \frac{\Delta x}{1 + R^2_\sigma}, \\ k(\Delta x, R_\sigma) &= p^*\left(\frac{1}{1 + R^2_\sigma}\right) \left( (1-p^*)\frac{(\Delta x)^2}{1 + R^2_\sigma} - \sigma_i^2\right), \end{aligned}\]

\[(12)\]

where

\[p^* = \frac{p\phi\left(\Delta x,\sigma_i\sqrt{1 + R^2_\sigma}\right)}{p\phi\left(\Delta x,\sigma_i\sqrt{1 + R^2_\sigma}\right) + (1 - p)} \]

\[(13)\]

and

\[\phi\left(\Delta x,\sigma_i\sqrt{1 + R^2_\sigma}\right) = \left(1/\left(\sigma_i\sqrt{2\pi(1 + R^2_\sigma)}\right)\right)e^{-(\Delta x)^2/2\sigma^2_i(1 + R^2_\sigma)} \]

\[(14)\]

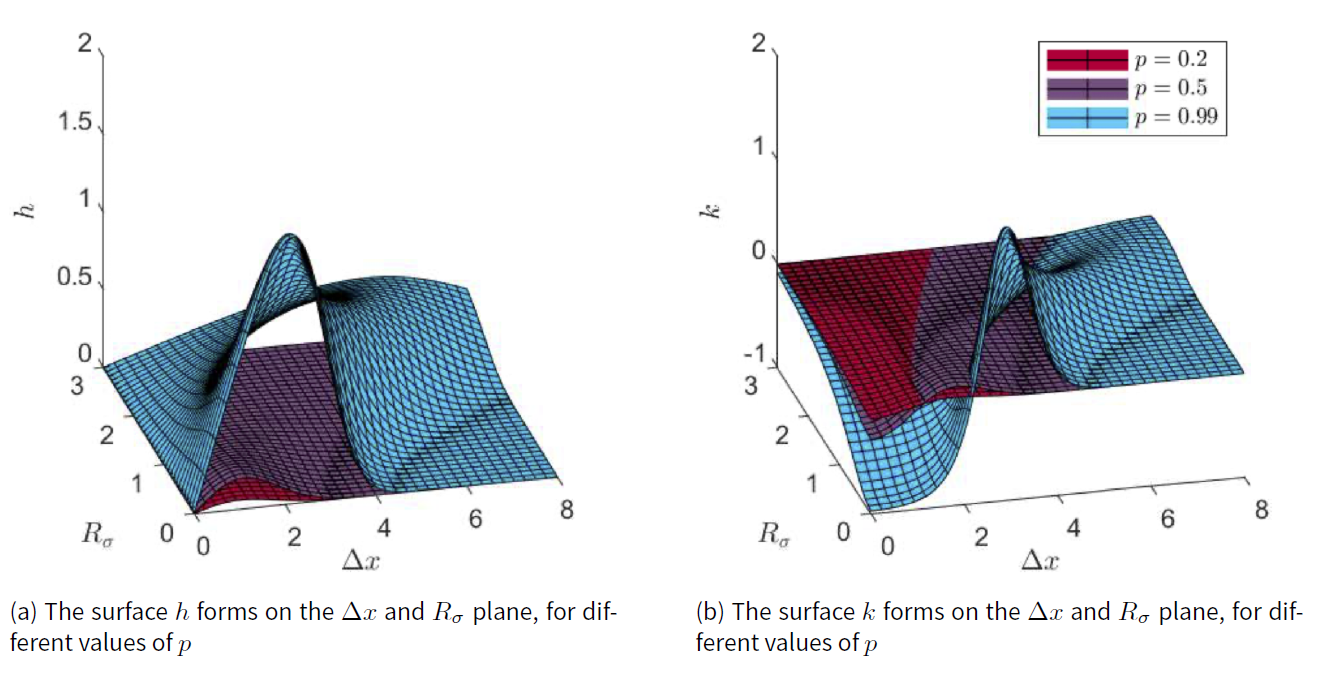
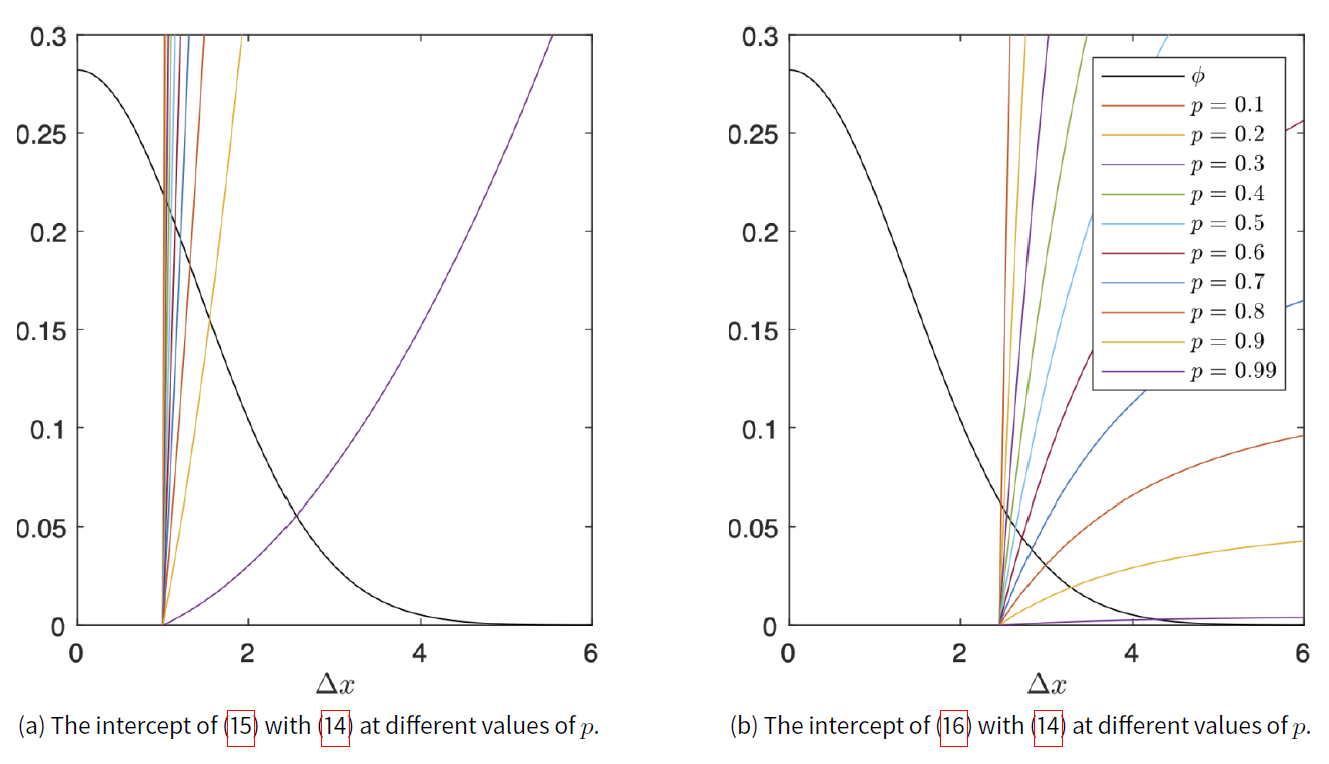
As shown in Figure 3, at lower values of \(p\), (12) and (13) maintain their critical point locations while compressing into the plane. This means that the dynamics of the simulation will remain similar while slowing the speed of the simulation. This is congruent with the analysis in Martins (2009) where \(p\) controlled the speed of consensus or polarisation. At \(p = 0.99\), however, there is a clear shift in critical locations in both (12) and (13), particularly in (13).

Investigating the critical points of both (12) and (13) reveal that their location in \(\Delta x\) space is governed by the intersection of (14) with

\[\begin{aligned} \frac{1-p}{p}\left(\frac{2}{\sigma^2_i(1 + R_\sigma^2)} (\Delta x)^2 - 1 \right). \end{aligned}\]

\[(15)\]

for the critical points of (12) and

\[\begin{aligned} \frac{1-p}{p} \frac{(\Delta x)^2/\sigma^2_i(1 + R_\sigma^2) - 3}{2(\Delta x)^2/\sigma^2_i(1 + R_\sigma^2) + 3}. \end{aligned}\]

\[(16)\]

for the critical points of (13).

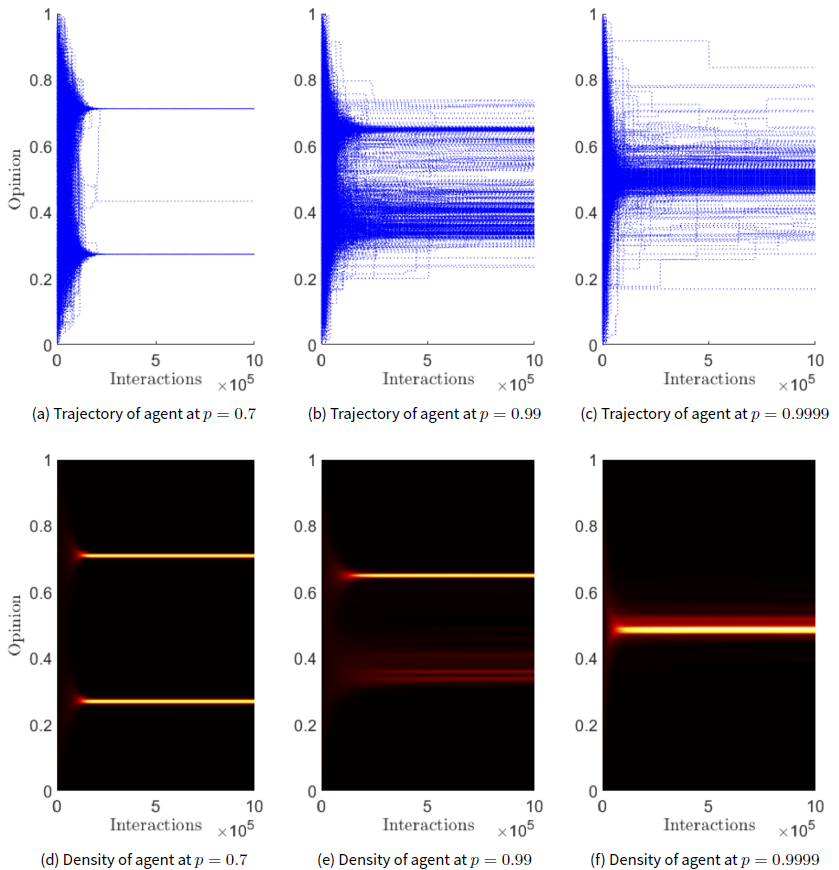
The effect of \(p\) on (12) and (13) is to shift their critical points along the \(\Delta x\) axis. As \(p\rightarrow 1\), both (15) and (16) approach 0. This shifts the intersection with the normal (14) further from 0, carrying the critical points with them. The shift of the critical points of (15) and (16) from 0 allows the agent to interact with more different opinion, essentially making the agent more trusting. It is reasonable that this behaviour is occurring while \(p\rightarrow 1\), because agents are less likely to be lying, allowing agents to trust other ‘outlandish’ opinions. This process of the agents becoming more trusting as \(p\rightarrow 1\) is evidence that (8) reduces to the ‘trivial model’ continuously - the ‘trivial model’ being the model of (2), where \(p\) was not included in the likelihood and thus no misinformation was accounted for. More evidence to support this is the fact that, at \(p=1\), (4) becomes the ‘trivial model’. Figure 4 illustrates the effect on the model as \(p \rightarrow 1\). The final opinions when \(p\) is not close to 1 start to migrate closer to the center and combine to form a consensus as \(p \rightarrow 1\).

Interestingly as \(p\rightarrow 0\) the critical point locations of (12) and (13) converge to specific values. This explains why there was little variation in critical point location for (12) and (13) with low \(p\). Figure 5 shows the relationship of \(p\) with the intersections of (14) with (15) and (16), and illustrates the nature of (16)’s flattening as \(\Delta x\) becomes large. This makes the intersection of (16), and with it the critical point of (13), shift faster away from 0 than for the quadratic governing (12)’s critical point location. This explains why (13)’s critical point shifts more in Figure 3 when \(p = 0.99\).

Mistrust and Extremism

In this section, we investigate the impact of mistrust on polarisation in the presence of extreme agents. We have defined an extreme agent as an agent that begins a simulation with lower initial uncertainty than the average agent’s and holds an initial opinion close to the boundaries of opinion space. Figure 6 is the result of running simulations with different distributions of extreme agents along with varying rates of trust \(p\).

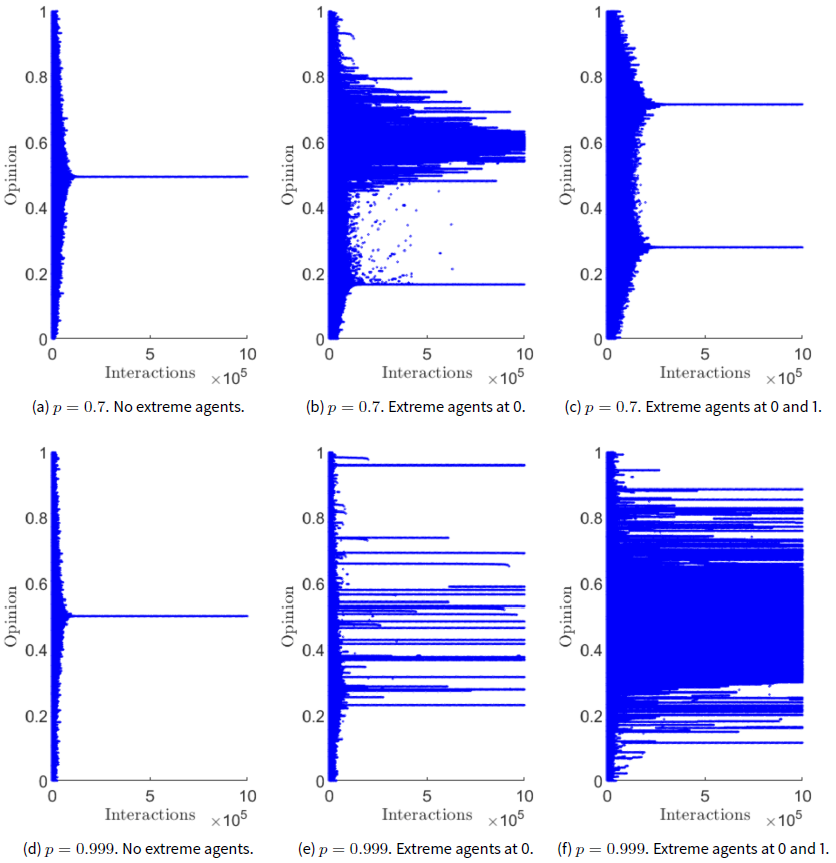
Figure 6 shows interesting impacts of mistrust with extremism on polarisation. The simulations of Figures 6 a and 6 d with no extreme agents and \(p=0.7\) and \(p=0.999\) demonstrate the expected results. With no extreme agents and initial \(\sigma_i = 0.2\:\forall i\) the agents converged to consensus, for both \(p=0.7\) and \(p=0.999\), which follows from Figure 1.

The simulations depicted in Figures 6 b and 6 e had extreme agents with opinions of 0 and \(\sigma_i=0.14\). When \(p=0.7\), shown in Figure 6 b, a dense opinion cluster formed at 0.2. This opinion cluster consists of the original extreme agents. More interestingly, there is a second more diffuse opinion cluster centred at approximately 0.6. The more diffuse cluster contains regular agents who were not persuaded by the extreme agents and thus tend to consensus. The simulation results with extreme agents and \(p=0.999\) shown in Figure 6 e exhibit multiple disparate opinion clusters. Interestingly there seem to be no opinion clusters around 0 and, instead, the bulk of the clusters are between 0.2 to 0.6. More interestingly, there seems to be an opinion cluster at 1, despite the initial extreme agents at 0. This is a very intriguing result that occurs consistently in multiple simulations.

The simulation results shown in Figure 6 c and 6 f had extreme agents at 0 and 1. The simulation results shown in Figure 6 c have a trust rate \(p=0.7\) and exhibit bi-polarisation. There are two opinion clusters one at 0.7 and the other at 0.3 and these cluster contain the extreme agents that began closest to them. In contrast to the simulation results shown in Figure 6 c the simulation results for extreme agents at 0 and 1, and \(p=0.999\) shown in Figure 6 f are diffuse and indistinct. The agents in the simulation appear to be in a state of ‘confusion’ and can’t reach consensus, despite high levels of trust between agents.

Discussion

In this paper we have extended the model in Martins (2009) and investigated a critical part of the models, the global trust rate \(p\).

The extended model produced more closely clustered opinions in simulation as compared to results for the simulations with evolving uncertainty in Martins (2009). The likely cause is that agents who gain confidence early can then easily attract low confidence agents to their opinion. The extended model also introduces symmetry in \(p^*\) i.e. if two agents switch roles in an interaction they produce the same \(p^*\), this suggests that \(p^*\) is a compatibility score between two interacting agents.

In principle, the extended model is more adaptable in representing opinion exchange than the models in Martins (2009). In the Martins model, agents assume other agents had equivalent uncertainty to themselves. Such an assumption is reasonable when you don’t know your interaction partner’s confidence but may not be valid in different contexts. For example, an agent could infer that other agents are less or more confident than themselves. The extended model makes it easier to investigate these different agent’s perceptions of others’ confidence.

Furthermore, in real-world interactions, it is generally clear how confident someone is in their opinion. Whether it is subtle, like body language, or more explicit, like direct declarations of confidence, the extended model can capture these real-world exchanges, whereas the Martins model can not.

The mistrust rate \(p\) of the extended model plays an important role in the emergence of polarisation in simulations. We confirmed what was found in Martins (2009), that \(p\) mostly controls how quickly simulations achieve a steady-state. How simulations from the extended model behave as \(p \rightarrow 1\) seems reasonable; as trust increases, consensus becomes more coherent, as seen in Figures 4 c and 4 b. There is consensus, particularly in Figure 4 c, but variation in opinion still exists. Despite the agents being more trusting, they seem to be less certain of a single consensus. Mathematically the reason this is happening is clear. Global trust is a static variable, whereas uncertainty decays exponentially, according to (9), so uncertainty will quickly reach the point when the amount of mistrust in \(p=0.999\) is important, stopping a strong consensus. What it means in terms of real-world opinion dynamics is less clear. Perhaps it suggests that even a small amount of global mistrust can inhibit strong consensus.

As a consequence of analysing \(p\), we derive an implicit form for the maximum opinion and uncertainty change for an interaction as a function of the distance between the two agents’ opinions. As \(p \rightarrow 1\) the optimum opinion distance between two agents to maximise change in opinion and uncertainty approaches infinity. For \(p \rightarrow 0\) these optimum distances approach fixed values. For change in opinion this optimal value is

\[\begin{aligned} \Delta x&=& \frac{\sqrt{2}}{2}\sigma_i\sqrt{1+R_\sigma^2},\\ &=&\sqrt{\frac{\sigma^2_i+\sigma_j^2}{2}}\end{aligned}\]

\[(17)\]

and for change in uncertainty

\[\begin{aligned} \Delta x &=& \sqrt{3}\sigma_i\sqrt{1+R_\sigma^2}\\ &=&\sqrt{3(\sigma_i^2+\sigma_j^2)}.\end{aligned}\]

\[(18)\]

These values are proportional to the quantity \(\sqrt{\sigma_i^2+\sigma_j^2}\), the standard deviation of \(\phi\). The optimal distance for uncertainty is larger by a factor of \(\sqrt{6}\) than the optimal distance for opinion, meaning that agents which induce the most opinion change do not effect the most uncertainty change, and vice versa. Further, it is useful to note that as \(p\rightarrow 0\) the relationship between the change in uncertainty \(k\) and the opinion distance \(\Delta x\)

\[\begin{aligned} \Delta x<\sqrt{\sigma_i^2+\sigma_j^2},&&k>0\\ \Delta x>\sqrt{\sigma_i^2+\sigma_j^2},&&k<0.\end{aligned}\]

\[(19)\]

In other words, there is an inflection point \(\sqrt{\sigma_i^2+\sigma_j^2},\) for \(\Delta x\) in increasing or decreasing uncertainty. The influence of \(\phi\) in this relationship is not surprising since \(p^*\), which depends on \(\phi\), substantially impacts the magnitude of opinion and uncertainty change. These observations merit further exploration beyond the scope of this work.

Analysing mistrust in the extended model allows empirical investigations into the influences of mistrust on polarisation. Controlling for mistrust as an independent variable in an experimental trial is straightforward. For example, an experiment could give participants an initial opinion and uncertainty; then, participants would receive information about another participant’s opinion, uncertainty, and trustworthiness. Data from the experiment can be used to create an influence map, similar to Moussaïd et al. (2013), and compared to influence maps created by the model in Figure 3. If the model is accurate in how real individuals adopt opinions, then the influence map the model produces should be similar to the one generated from the experiment, thereby validating the model. If the model is valid, this addresses the gap identified in Flache et al. (2017), implying that mistrust is the foundation of polarisation.

The results of the extended model simulations with extremism with mistrust are interesting. Figure 6 f shows that high trust leads to a highly disorganised final state. Compared to the two clear opinion clusters of Figure 6 c, Figure 6 f shows extremely diffuse consensus. As explained previously, this effect is likely from how uncertainty decays exponentially while \(p\) remains fixed. So uncertainty would reach zero quickly, thereby locking agents into a state before reaching clear polarisation or consensus. Figure 6 e is perplexing. Despite there being extreme agents only at 0 when \(p=0.999\), an opinion cluster forms close to 1 while no cluster forms close to 0. The likely explanation is the extreme agents at 0 attracted agents located at 0.8 or closer to 0 while failing to attract agents further away than 0.8. As a result, the agents with opinions above 0.8 form their opinion cluster. In contrast Figure 6 b is easier to understand and explain. The cluster at 0.2 is formed mainly by the original extreme agents shifted slightly from 0 to 0.2. The cluster at 0.6 results from the attraction of regular agents initially closer to 0 to the pole at 0.2 and the remainder of the regular agents, whose initial opinion was closer to 1, forming a more diffuse consensus at 0.6.

This paper shows that the models devised in Martins (2009), and the extended model, are fertile ground for research in opinion dynamics. These models present interesting behaviour with extremism along with novel behaviour without extremism. The extension made to Martins (2009) increased the model’s flexibility and allowed for more realistic agent interaction. Most importantly, these models can address the cleavage problem fundamentally, and if we can empirically verify the models, we will establish a deeper understanding of opinion dynamics.

References

ABELSON, R. P. (1967). Mathematical models in social psychology. Advances in Experimental Social Psychology, 3, 1–54. [doi:10.1016/s0065-2601(08)60341-x]

AXELROD, R. (1997). The dissemination of culture. Journal of Conflict Resolution, 41(2), 203–226.

CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2), 591–646. [doi:10.1103/revmodphys.81.591]

CASTELLANO, C., Vilone, D., & Vespignani, A. (2003). Incomplete ordering of the voter model on small-world networks. EPL (Europhysics Letters), 63(1), 153–158. [doi:10.1209/epl/i2003-00490-0]

CERAGIOLI, F., & Frasca, P. (2018). Consensus and disagreement: The role of quantized behaviors in opinion dynamics. SIAM Journal on Control and Optimization, 56, 1058–1080. [doi:10.1137/16m1083402]

CHRISTAKIS, N. A., & Fowler, J. H. (2009). Connected: The Surprising Power of Our Social Networks and How They Shape Our Lives. New York, NY: Little, Brown and Company.

CLIFFORD, P., & Sudburry, A. (1973). A model for spatial conflict. Biometrika, 60(3), 581–588.

COATES, A., Han, L., & Kleerekoper, A. (2018). A unified framework for opinion dynamics. Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems. International Foundation for Autonomous Agents and Multiagent Systems.

DEFFUANT, G., Amblard, F., Weisbuch, G., & Faure, T. (2002). How can extremism Prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation, 5(4), 1: https://www.jasss.org/5/4/1.html. [doi:10.18564/jasss.2211]

DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3, 87–98. [doi:10.1142/s0219525900000078]

FESTINGER, L. (1957). A Theory of Cognitive Dissonance. Palo Alto, CA: Stanford University Press.

FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2: https://www.jasss.org/20/4/2.html. [doi:10.18564/jasss.3521]

FRENCH Jr, J. R. (1956). A formal theory of social power. Psychological Review, 63(3), 181.

HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence: Models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html.

HOLLEY, R. A., & Liggett, T. M. (1975). Ergodic theorems for weakly interacting infinite systems and the voter model. The Annals of Probability, 3, 643–663. [doi:10.1214/aop/1176996306]

JIAO, Y., & Li, Y. (2021). An active opinion dynamics model: The gap between the voting result and group opinion. Information Fusion, 65, 128–146. [doi:10.1016/j.inffus.2020.08.009]

KRAUSE, U. (2000). A discrete nonlinear and non-Autonomous model of consensus formation. Communications in Difference Equations, 2000, 227–236.

MARTINS, A. C. R. (2008). Continuous opinions and discrete actions in opinion dynamics problems. International Journal of Modern Physics C, 19, 617–624. [doi:10.1142/s0129183108012339]

MARTINS, A. C. R. (2009). Bayesian updating rules in continuous opinion dynamics models. Journal of Statistical Mechanics: Theory and Experiment, 2009(2), P02017. [doi:10.1088/1742-5468/2009/02/p02017]

MARTINS, A. C. R. (2012). Bayesian updating as basis for opinion dynamics models. American Institute of Physics, AIP Conference Proceedings.

MARTINS, A. C. R. (2013). Trust in the CODA model: Opinion dynamics and the reliability of other agents. Physics Letters A, 377(37), 2333–2339. [doi:10.1016/j.physleta.2013.07.007]

MOUSSAÏD, M., Kämmer, J. E., Analytis, P. P., & Neth, H. (2013). Social influence and the collective dynamics of opinion formation. PlOS ONE, 8(11), e78433.

OSWALD, M. E., & Grosjean, S. (2004). 'Confirmation bias.' In R. F. Pohl (Ed.), Cognitive Illusions: A Handbook on Fallacies and Biases in Thinking, Judgement and Memory (pp. 79–96). New York, NY: Psychology Press.

SOOD, V., & Redner, S. (2005). Voter model on heterogeneous graphs. Physical Review Letters, 94(17), 178701. [doi:10.1103/physrevlett.94.178701]

STANKOV, L., Kleitman, S., & Jackson, S. A. (2015). 'Measures of the trait of confidence.' In G. J. Boyle, D. H. Saklofske, & G. Matthews (Eds.), Measures of Personality and Social Psychological Constructs (pp. 158–189). Amsterdam, NL: Elsevier. [doi:10.1016/b978-0-12-386915-9.00007-3]

SZNAJD-WERON, K., & Sznajd, J. (2000). Opinion evolution in closed community. International Journal of Modern Physics C, 11(6), 1157–1165. [doi:10.1142/s0129183100000936]

WEISBUCH, G., Deffuant, G., Amblard, F., & Nadal, J.-P. (2002). Meet, discuss, and segregate! Complexity, 7(3), 55–63. [doi:10.1002/cplx.10031]

ZINO, L., Ye, M., & Cao, M. (2020). A two-layer model for coevolving opinion dynamics and collective decision-making in complex social systems. Chaos: An Interdisciplinary Journal of Nonlinear Science, 30(8), 083107. [doi:10.1063/5.0004787]