A Bad Barrel Spoils a Good Apple: How Uncertainty and Networks Affect Whether Matching Rules Can Foster Cooperation

, ,
and
University of Groningen, Netherlands
Journal of Artificial
Societies and Social Simulation 25 (1) 6
<https://www.jasss.org/25/1/6.html>
DOI: 10.18564/jasss.4754
Received: 16-Jul-2021 Accepted: 21-Dec-2021 Published: 31-Jan-2022
Abstract
Meritocratic matching solves the problem of cooperation by ensuring that only prosocial agents group together while excluding proselfs who are less inclined to cooperate. However, matching is less effective when estimations of individual merit rely on group-level outcomes. Prosocials in uncooperative groups are unable to change the nature of the group and are themselves forced to defect to avoid exploitation. They are then indistinguishable from proselfs, preventing them from accessing cooperative groups. We investigate informal social networks as a potential solution. Interactions in dyadic network relations provide signals of individual cooperativeness which are easier to interpret. Network relations can thus help prosocials to escape from uncooperative groups. To test our intuitions, we develop an ABM modeling cooperative behavior based on a stochastic learning model with adaptive thresholds. We investigate both randomly and homophilously formed networks. We find that homophilous networks create conditions under which meritocratic matching can function as intended. Simulation experiments identify two underlying reasons. First, dyadic network interactions in homophilous networks differentiate more between prosocials and proselfs. Second, homophilous networks create groups of prosocial agents who are aware of each other’s behavior. The stronger this prosociality segregation is, the more easily prosocials cooperate in the group context. Further analyses also highlight a downside of homophilous networks. When prosocials successfully escape from uncooperative groups, non-cooperatives have fewer encounters with prosocials, diminishing their chances to learn to cooperate through those encounters.Introduction
Cooperation is central to human life and difficult to achieve. Students, community members, activists, employees, or scholars, for example, need to join forces with their peers to realize benefits they could never generate alone. Yet, individuals are also tempted to free-ride on others’ efforts. This jeopardizes the successful cooperation they would like to benefit from in the first place (Heckatorn 1996; Olson 1965; Simpson & Willer 2015). Among a range of possible solutions to this “social dilemma” (Dawes 1980; Nowak 2006), matching mechanisms prevent people who are less inclined to cooperate from entering a group that needs cooperation from its members (Chaudhuri 2011; Guido et al. 2019). An example would be a student project group whose members only allow peers with high grades to join because they believe that those peers are hard workers.
Matching mechanisms exploit stable individual differences in individuals’ tendencies to be cooperative, conceptualized for example as prosocial value orientation (Balliet et al. 2009) or as personality traits related to altruism or agreeableness (Thielmann et al. 2020). A successful matching mechanism ensures that only members sufficiently personally disposed to cooperate (hereafter: prosocials) can enter. Matching mechanisms also provide a powerful incentive to behave cooperatively even for those who are only motivated by self-interest (hereafter: proselfs). Game theoretical models of so-called meritocratic matching show theoretically how matching mechanisms foster cooperation (Gunnthorsdottir et al. 2007; Nax et al. 2017a, b; Nax & Rigos 2016). Through meritocratic matching, cooperative group members are selected into cooperative and thus highly profitable groups. Persistently uncooperative individuals are effectively punished by being left to team up with other persistent defectors in poorly performing groups. Yet, defectors who change their behavior will be rewarded for becoming and remaining cooperative by being allowed to enter productive groups. In other words, a well-functioning and meritocratic matching system under ideal conditions fosters cooperation in a population. The matching system protects genuine cooperators from exploitation by free-riders and incentivizes non-cooperative individuals to act cooperatively.
We contribute to the literature about meritocratic matching in two ways. First, we demonstrate and analyze how imperfect information threatens the success of meritocratic matching. We address the largely overlooked problem that “bad barrels can spoil good apples”, referring to situations where imperfect initial matching discourages cooperation among prosocial group members. For example, at the beginning of a course teachers may match students in groups based on alphabetical order or date of enrollment when other information signaling students’ cooperativeness is not available as input for matching. In this case, some prosocial students can end up in project groups comprising many non-cooperative members. This provides a perverse incentive to those prosocials to change their behavior from cooperation to defection, in order to protect themselves against exploitation by their fellow group members. However, “spoiled” prosocials may also have a hard time escaping from unproductive groups because both their (involuntary) non-cooperative behavior and the low performance of the group they reside in makes it difficult for other groups to recognize their cooperative intentions.
The “bad barrels” problem occurs to the extent that actors in other groups lack full and accurate information on the “true” cooperative nature of individuals. Consider the student groups discussed above. Students may prefer members with high grades to join their project group, but these grades can reflect outcomes from earlier group projects in which the final grade was determined on the group-level, not on the level of the individual students. There may be substantial differences in the effort that individual students were willing to invest, but this heterogeneity is not reflected in their grades. It is hard for outside observers to disentangle individual actions from the group context.
To study situations in which imperfect information undermines meritocratic matching as a solution to cooperation problems, we developed an agent-based model (ABM) in which cooperation decisions are based on a learning process. Using this model, we analyze the conditions and mechanisms under which imperfect information about individual cooperation jeopardizes the effectiveness of meritocratic matching. Specifically, we compare different information rules on the degree to which they effectively promote cooperation. To be clear, “rules” do not refer to exogenously imposed institutions but reflect different conditions in which agents have (in)complete information due to individual and contextual constraints. The baseline for this comparison is the standard implementation of meritocratic matching based on full information regarding individual merit. We thereby deviate from the conventional full rationality assumption underlying meritocratic matching. To summarize, we investigate whether and under which information conditions meritocratic matching is meritocratic enough in an uncertain world.
Our second contribution to the literature is our investigation of informal social networks as a possible solution to the “bad barrels” problem. Social networks provide an additional source of information agents can use for matching. Dyadic interactions in informal social networks provide signals of individual cooperativeness which are easier to interpret and more explicit. For example, students matched in project groups often also have academic support relations with peers (Brouwer et al. 2018). In these relations, they can learn more about whether these peers are desirable partners for academic cooperation. Our agent-based model incorporates therefore a mechanism describing how network ties cutting across groups provide additional individual information.
In particular, we use our model to analyze whether homophily in informal social networks, one of the most prominent structural features of social networks, helps to restore the effectiveness of meritocratic matching in a world of imperfect information. Homophily (Lazarsfeld & Merton 1954; McPherson et al. 2001) refers to the tendency to preferentially connect to similar others in a network, driven by shared attributes (gender or educational background) or geographical closeness (neighborhood). Similarity may arise out of sharing a status (gender, educational background) or value attribute (attitudes, behavior). We stress in the next paragraph how value homophily in cooperation may arise as a byproduct of status homophily. We show how homophily conditions the effectiveness of informal social networks as an additional source of information for overcoming the bad barrels problem.
Recent work shows a strong correlation between sociodemographic attributes and cooperation. For example, some suggest that women are more cooperative than men (Höglinger & Wehrli 2017), while economics students are more likely proselfs than other students (Marwell & Ames 1981). In other words, personal predispositions towards certain forms of cooperative behavior are more likely to occur for individuals with similar characteristics or socialized in some similar way. Combining these differences in cooperativeness with the tendency to preferentially connect to sociodemographically similar others, informal social networks are likely to be homophilous also in terms of cooperativeness. The importance of homophily for cooperation is also reflected by the fact that individuals cooperate more willingly with similar others (Melamed et al. 2020). An informal homophilous network link may then help mismatched “good apples” to escape from defective groups by giving them the chance to dyadically show behavior that convinces their network neighbors (and likely members of good groups) of their genuine cooperativeness. We thus argue that homophily improves the chances of spoiled prosocials to be identified as potentially valuable candidates for future groups.
But there is also a downside to homophily in social networks. If prosocial actors are quickly able to escape uncooperative groups by displaying their cooperativeness in informal social networks, proselfs increasingly find themselves stranded in poorly performing uncooperative groups. This undermines the other mechanism through which meritocratic matching works: the provision of incentives for defectors to change their behavior. The more proselfs are concentrated in a group, the more difficult it will become for them to change their ways. Homophily would further exacerbate this problem by restricting their network interactions to other non-cooperative individuals. Thus, our second contribution to the literature is that we use our ABM to clarify the network conditions under which homophily promotes or jeopardizes the effectiveness of meritocratic matching in a world of imperfect information.
In Section 2, we discuss earlier formal models of meritocratic matching and show how we build on and move beyond this work, formulating three intuitions about the implications of the mechanism the ABM implements. Section 3 describes the ABM and Section 4 presents a detailed analysis of the information conditions and network conditions under which meritocratic matching helps solve the conundrum of cooperation.
Theoretical Foundations and New Intuitions
Prior affiliations to groups, organizations, firms, or teams can serve as signals of an individual’s potential merit under uncertainty (Bacharach & Gambetta 2001; Gambetta 2009; Spence 1973). For hiring committees, for example, previous affiliation to a reputable firm is a signal of an employees’ unobservable “true” individual qualities. Similarly, a past affiliation with a fraudulent firm may be interpreted as indicating bad qualities. Signaling theory proposes that the rational use and interpretation of the information conveyed by signals sustain trust and cooperation in an uncertain world (Bacharach & Gambetta 2001). This type of signaling assumes that individuals rationally display and read such signals so that credible signals (e.g., cooperative behavior that is prohibitively costly for proselfs) differentiate between genuinely prosocial and proself types. In our model, cooperative behavior is the only available behavioral cue. A rationality assumption on which signaling theory rests, related to classical rational choice theory, is that individuals have the unlimited cognitive capacity to process signals and information. This rationality assumption is challenged by decades of research, demonstrating that people are boundedly rational, incompletely informed, and cognitively constrained (Wittek et al. 2013). For the analysis of meritocratic matching under uncertainty, this is a particularly relevant concern, as elucidating individual cooperative signals from behavior in groups requires a lot of cognitive capacity and information processing, and even in dyadic interactions in a network, cooperative behavior cannot be separated from the network context. Led by the critique of rationality assumptions, we rely on simple “low rationality” decision heuristics to explore what happens if agents select new group members, and group members rely on similarly simple heuristics to decide whether to cooperate or not in a given group or dyadic context and then to relate observed behavior to infer cooperative traits.
Our work advances earlier ABM literature linking cooperation to matching mechanisms. First, Bowles & Gintis (2004) used an ABM to show how cooperative strategies that ostracize free-riders from groups can thrive and foster cooperation in an evolutionary context. Similar to meritocratic matching, their key mechanism is that ostracized agents are less likely to be accepted into cooperative groups in the future. However, the authors rely on random matching rather than matching based on merit and do not incorporate informal social networks. Second, Duca et al. (2018) studied how meritocratic matching is affected by heterogeneity in endowments. Assuming myopic best response behavior, they show how inequality can strongly hamper the effectiveness of meritocratic matching. Our work introduces inequality likewise, albeit in individual cooperativeness traits rather than endowments. Unlike Duca et al. (2018) we add the assumption that information about individual merit is unreliable but that networks can provide additional information. Third, we build on Nax et al. (2015) who were among the first to show, using simulations of an evolutionary imitation dynamic, how reliance on group merits (group scoring) during matching deteriorates cooperation compared to individual merit-based matching. Interestingly, they find that cooperation still arises even when there is only a 1% chance that individual merits are used instead of group merits. However, their model neglects heterogeneity among individuals as well as network solutions and does thus not allow us to highlight conditions for the bad barrels problem we identify. Unlike Nax et al. (2015) we focus on conditions under which the bad barrels problem arises.
We follow earlier work modeling bounded rationality with learning theory and evolutionary models to explicate how bad barrels can spoil good apples when it comes to cooperation in groups. To be more precise, simulation studies of evolutionary dynamics in cooperation problems highlighted how cooperation can thrive as a successful strategy, but only when combined with (in)direct reciprocity (Axelrod 1984; Nowak & Sigmund 1998). If others defect, then even cooperative recipients are more prone to reciprocate defective behavior. In other words, a good apple can be spoiled by contact with a bad apple. Simulation models based on reinforcement learning lead to a similar conclusion, especially when combined with the assumption that being exposed to others’ defections leads initially cooperative agents over time to lower their expectations and be content with low cooperation as an outcome (Macy & Flache 2002). To be sure, there are differences between explanations of cooperation based on evolutionary dynamics (Nowak 2006) and explanations based on stochastic learning models (Macy & Flache 2002). Stochastic learning stresses that changes in cooperation are not driven by payoff-dependent variation in rates of offspring across different strategies or types of agents – as in evolutionary selection – but by variation in the likelihood that agents choose particular cooperative or defective actions over time. Despite this difference, under both approaches agents increasingly adopt behavior that is associated with better outcomes. In this paper, we choose a model based on stochastic learning, because we believe that success-driven change of behavior within agents better captures the decision-making of human social actors than the assumption that behavioral strategies are fixed and all change comes from mutation and selection (for a reflecting critique on this critique on the use of evolutionary algorithms in ABM, see, e.g., Chattoe-Brown 1998).
Combining and advancing the perspectives of signaling theory, bounded rationality, reinforcement learning, and meritocratic matching under heterogeneity and uncertainty, we develop in what follows a set of theoretical intuitions that serve to guide the design of our ABM and simulation experiments. Earlier work leads to the intuition that prosocials develop a low level of cooperation through reciprocity if mismatched into groups with many non-cooperative members. Thus, when outsiders are incapable of perfectly inferring the qualities of a group member by observing group outcomes and individual contributions, these “good apples” are spoiled. Various strands of literature support the assumption that human decision-makers tend to (falsely) infer individual qualities from group characteristics, as suggested, for example, by research on fundamental attribution error (Ross 1977) and statistical discrimination (Fang & Moro 2011).
Intuition 1. Due to mismatching, prosocial agents cooperate less when matching is based on agents’ prior group performance.
In order to escape the negative reputation of a poorly performing group, innately cooperative individuals need some other channel through which they can show their individual quality. Dyadic interactions in informal networks allow for the development of individual reputations (Buskens & Raub 2002; Raub & Weesie 1990). Once cooperative reputations have been established in such dyadic interactions, agents from other groups can use the network information in addition to information in the group context when determining the matching of agents into new groups. This allows them to eventually achieve higher levels of cooperation.
Intuition 2. The possibility to signal prosociality in dyadic network interactions increases cooperation among prosocials.
In a homophilous network, cooperative types are more likely to cluster together and mainly, but not exclusively, interact with other cooperative types. Homophily thus increases the chances that members of highly cooperative groups interact with mismatched “good apples” from low-performing groups. It thus further improves the possibility of mismatched cooperators being “spotted” as potentially promising new recruits.
Intuition 3. Network clustering and information from dyadic network interactions increase cooperation levels of formerly mismatched prosocials in the group context.
The Agent-Based Model
Agents in our model are either prosocial or proself. Prosocial agents are more cooperative, while proselfs are more egoistic and defection-oriented. Figure 1 depicts the basic interaction structure. The matching procedure places each agent into one group. Each group produces its own local collective good (Figure 1a). Figure 1b shows how the same population of agents is connected by an informal network of dyadic relations that potentially links agents also across group boundaries. Both in their group as well as in dyadic interactions, agents are confronted with cooperation problems. These cooperation problems are modeled as iterated \(n\)-person Prisoner Dilemmas (PD) at the group-level, and iterated 2-person PDs at the dyadic level, respectively. From time to time, agents can decide to leave their current groups and groups need to admit new members (rematching). After rematching, a new iterated PD game is started in all groups. Throughout the entire simulation, agents play bilateral PD games with one of their network partners at randomly selected moments. Thus, sometimes they decide in the same iteration whether to contribute to their group’s collective good and whether to cooperate in the ongoing private interaction with a particular network partner.
In what follows, we describe the various elements of the model. More precisely, we elaborate on the behavioral and learning algorithms for cooperation, the implementation of prosocial and proself agents, the timing of cooperation decisions in groups and network dyads, the network model, and the different matching rules we compare to assess the effectiveness of meritocratic matching under different conditions. We end with the design of our simulation experiments. The pseudocode of a simulation run is visualized in Algorithm 1 (Appendix A1).

Cooperate or not? The decision-making model for cooperation
Cooperation is modelled with a probabilistic threshold model (Macy 1991a, 1991b; Macy & Evtushenko 2020; Mäs & Opp 2016). We apply the model both in the group and in dyadic interactions. Somewhat simplified, agents cooperate if enough others in their group (or network partner) also cooperated in the past, otherwise they defect. How many others is “enough” is defined by an agent-specific threshold. Cooperative types have lower initial thresholds than non-cooperative types. All other things being equal, prosocials are thus more likely to behave cooperatively. Yet, agents’ propensity to cooperate is also affected by others’ behavior. This happens through reinforcement learning. Agents become more likely to repeat a behavior associated with a satisfactory outcome and avoid behavior that resulted in an unsatisfactory outcome. Generally, if cooperation (defection) generates a positive outcome, thresholds decline (increase), making cooperation more (less) likely.
We now explain the model for the cooperation decision in the group. Its application to the network game is explained further below. Figure 2 provides an overview of the decision and learning sequence. First, each agent compares their current threshold (\(\tau_{i,t}\)) to the most recent proportion of cooperation by group mates (\(k_{t}\)). Second, all agents decide probabilistically in a random sequence to cooperate or defect (Equation 1; \(p_{i,t}\)). Third, after all decided (\(c_{i,t}\)), each agent calculates their payoff (Equation 2; \(s_{i,t}\)) and standardized outcome (Equation 3; \(o_{i,t}\)), subsequently applying a learning heuristic to adapt the threshold accordingly for the next iteration (Equation 4).
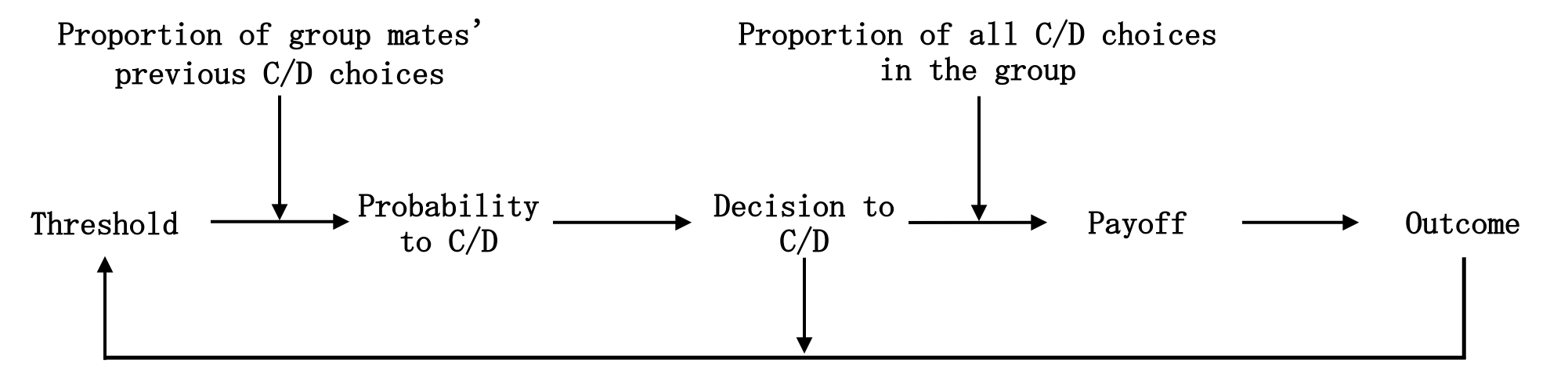
In the first iteration of a game, others’ cooperation is unknown. Initial behavior is governed by agents’ innate characteristics given by the initial threshold (\(\tau_{i}\)) such that the lower \(\tau_{i}\), the higher the probability of initial cooperation, \(p_{i,t}\) (\(c_{i,t} = 1\)) \(= 1-\tau_{i}\) (Mäs & Opp 2016). After the first decision, thresholds and behavior then change based on past outcomes, reflecting adaptive learning within a group or network relation over time. More precisely, the more the current rate of cooperation in a group (\(k_{t}\)) exceeds an agent’s adaptive threshold (\(\tau_{i,t}\)), the higher the probability of cooperation. Equation 1 formalizes the logistic function modeling this link. The slope parameter \(m\) controls the degree of randomness in agents’ decisions. The higher \(m\), the more the cooperation decision is determined by the difference between threshold and past group cooperation rate.
| \[ p_{i,t} (c_{i,t} = 1) = \frac{1}{\{1 + exp[ m (\tau_{i,t}-k_{t})]\}}\] | \[(1)\] |
After all agents decided, each agent calculates its payoff, denoted by \(s_{i,t}\) in Equation 2. The cost of cooperation is 3 (\(h\)), while the benefit of cooperation is 4.5 (\(b\)). These payoffs constitute a PD in which agents are tempted to defect. For cooperators, we multiply \(b\) by the count of cooperative acts in the group (\(v_{c,t}\)) and divide it by group size (\(FS\)) to calculate payoffs, minus the cost of cooperation (\(h\)). Defectors benefit from cooperating others while not paying the cost of cooperation. However, agents receive -0.5 (\(d\)) when all defect. Thus, when all agents defect this is detrimental to both the agent and the group.
| \[ s_{i,t} = \frac{b(v_{c,t})}{FS-h}\] | \[(2)\] |
After calculating payoffs, agents compare their payoff of the current iteration to their payoff in the previous iteration, followed by dividing the difference by three times the maximum payoff possible. This yields a standardized outcome \(o_{i,t}\) specified in Equation 3. Current payoffs weigh more heavily in \(o_{i,t}\) than the payoff in the previous iteration. Essentially, the higher the current payoff, the higher the standardized outcome, and the more likely behavior that led to this satisfactory outcome is reinforced. The rate at which thresholds adapt is controlled by the learning rate (\(l\)). If \(o_{i,t} = 0\), we set \(o_{i,t}\) to \(0.00001\) to ensure that thresholds are updated.
| \[ o_{i,t} = \frac{l [(2s_{i,t}-s_{i, t-1})]}{3\mid s_{max}\mid}\] | \[(3)\] |
Finally, agents update their threshold based on \(c_{i,t}\)and \(o_{i,t}\) (Equation 4). If cooperation is associated with \(o_{i,t} > 0\), thresholds drop, increasing the chances of future cooperation, while outcomes \(o_{i,t} < 0\), increase the threshold following cooperation. The same principle holds following defection. Outcomes \(o_{i,t} > 0\) increase the threshold and thereby the probability of future defection, while a negative outcome reduces both.
| \[ \begin{gathered} \tau_{i,t+1} = \tau_{i,t}-\{o_{i,t} [1-(1-\tau_{i,t})^{(1 / \mid o_{i,t}\mid )}] c_{i,t}\} + \\ \{o_{i,t} [1-(1-\tau_{i,t})^{(1 / \mid o_{it}\mid)}](1-c_{i,t})\} \end{gathered}\] | \[(4)\] |
Prosocial and proself agents
Agents are randomly selected to be either prosocial or proself, based on a given proportion of prosocial agents in the population. We assume that prosocial types need less external motivation to cooperate at first, implemented by the assumption that their initial thresholds (\(\tau_{i} = 0.3\)) are lower than those of proselfs (\(\tau_{i} = 0.7\)). Agents’ first decision after a rematching phase is governed by their initial threshold (\(\tau_{i}\)), reflecting their innate cooperativeness. Thus, agents reset after matching.
Discrete-time steps per iteration
In an iteration of the group game agents decide, in random sequence, to cooperate or defect. An iteration is divided into discrete time steps. Per time step, each agent has the same probability (\(1/n\)) to be selected. Due to asynchronicity, agents may have different values for the perceived proportion of cooperation in the group, depending on prior cooperation and defection decisions in previous discrete-time steps. The iteration ends when all agents decided at least once to cooperate or defect, followed by calculating their payoffs, and then finally by updating their threshold.
A different number of time steps is used for the network 2-person PD, reflecting that interactions with network partners occur in a different context and at a different pace than interactions in the group game. Specifically, in the network context, each dyad has an \(r\) chance (\(r = 0.05\)) to be selected per iteration, this means that each agent has a 10% likelihood to play the game in any given iteration (and 90% chance to not play a network 2-PD in the given iteration). Hence, the chances to play the 2-person PD are slimmer than playing the \(n\)-person PD in each iteration. The value of \(r = 0.05\) is chosen to assure that cooperation is learned slowly enough in network interactions. In this way, behavior in network interactions is not fully determined by an agent’s type but is still a signal of it. Different values for \(r\) were explored in a sensitivity analysis (Appendix A9.4).
Social network
Random spatial graph algorithm
Following earlier ABM studies (Grow et al. 2017b; Keijzer et al. 2018), we adopted a spatial random graph algorithm (Wong et al. 2006) to generate the network structure. We rely on a NetLogo algorithm, freely available in the CoMSES computational model library (Grow et al. 2017a). This algorithm can create networks with structural features resembling real-life social networks, such as a high level of clustering and short average geodesic distances. Its core idea is that agents are assigned random coordinates in a two-dimensional space and that then network ties between agents are created such that geographically close agents are more likely to be linked than geographically distant ones. Details of the algorithm are explained in Appendix A2. Here, we concentrate on how we adapt it to induce homophily.
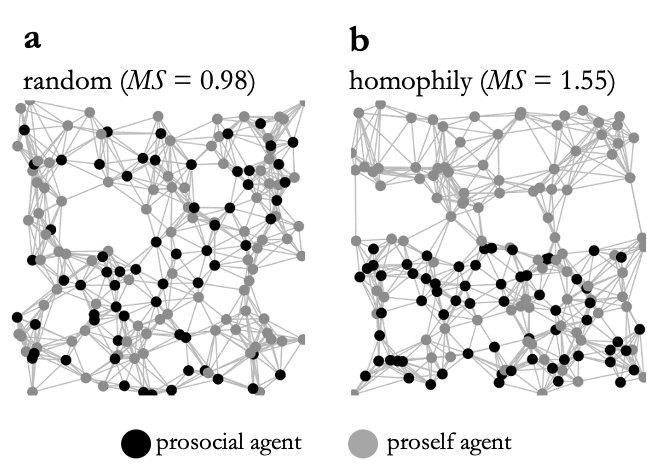
Figure 3 visualizes how structural homophily between prosocial agents is imposed in the spatial random graphs. In random networks (Figure 3a), both the geographic location of prosocial and non-prosocial agents and thus also the probability for a network link between two agents are unrelated to their type. In homophilous networks (Figure 3b) the geographic allocation is such that prosocial agents are locally clustered so that the algorithm more likely links agents of the same type to each other than would be given by random chance. To assess the resulting degree of type-homophily in the network we adopt Moody’s gross-segregation (MS) index (Bianchi et al. 2020; Moody 2001). Intuitively, the interpretation of the measure is that it is MS times as likely for a network link to occur in a dyad of same-type agents than in a dyad of agents of different types. Details of the implementation of MS are given in Appendix A3. As Figure 3 shows, MS is about 1.0 in random networks, while in the networks with homophily same-type agents are linked about 1.5 times as likely than different-type agents.
Reputation formation through interactions in the network
Whenever a dyad in the network is selected to play their 2-person PD game, both players decide whether to cooperate based on the same decision procedure, learning algorithm, and payoff scheme described above for the group game. We add the subscript \(sn\) to indicate network parameters. More specifically, agents make separate decisions per tie, governed by the same threshold for every network partner and taking into account each of their alters’ previous cooperation decision. After the interaction, agents update their outcome and adjust their single threshold for all network partners for future interaction with potentially different alters. This implementation also means that an agent can cooperate in an interaction with alter \(j\) but defect with alter \(k\). Alter refers to a directly connected agent.
Stable cooperation is more likely to emerge in dyads between prosocial players than between proself players. For instance, in prosocial-prosocial interactions in which both previously cooperated, both keep cooperating with a probability of 0.97. After an interaction, thresholds of cooperators tend to lower towards 0. The contrary is true for proself-proself interactions in which both previously defected, then the probability to cooperate is 0.03. In proself dyads, defecting will result in negative outcomes and decrease proself agents’ thresholds, making them more likely to cooperate in the near future. However, they are still less likely to cooperate than players in prosocial-prosocial interactions, quickly earning them a worse reputation.
In addition to homophily in the structure of the network, we implement homophily in dyadic interactions. Only similarly-behaving agents will play the 2-person PD. Practically, this implementation facilitates cooperator-cooperator and defector-defector interactions. If agent \(i\) and \(j\) both cooperated in the previous iterations (or defected) and the dyad is selected, they do play the 2-person PD, otherwise they do not interact. This assumption reflects what in a more detailed elaboration of a backward-looking partner selection process would intuitively be the outcome. Players would be satisfied with mutual cooperation with a network partner and thus repeat that interaction. Players who experience mutual defection or exploitation would abandon their partner and try to find better matches. However, sooner or later defecting proselfs can find only other proselfs to connect with, due to the reputation they acquired. Further assuming that actors prefer mutual defection to not interacting at all in network relations, we therefore assume that both mutual cooperation and mutual defection result in repetition of an interaction with the same partner. Only after defectors change to cooperation, they are available for interactions with cooperators. In Appendix A9.5, we show that although plausible, this assumption of ‘behavioral homophily’ is not crucial for the qualitative results of our analysis. Yet, the differences between conditions in our simulation experiment are highlighted more clearly if behavioral homophily is assumed.
The accumulation of individual cooperative and defective decisions in the network yields a personal reputation score, formalized as \(C_{10,sn}\), capturing the most recent 10 network decisions of an individual. Furthermore, we assume that one’s reputation is known among alters and alters of their alters. For example, agent \(i\) plays the 2-person PD with alter \(j\), but \(i\) knows how \(j\) behaved in all of his last 10 interactions. Personal reputations can be used in the matching phase to assess the cooperative qualities of a potential new group member, as we will explain next.
Meritocratic matching
Leave-stay procedure
Agents decide to leave a group when they are not happy with the average level of cooperation from the last 10 iterations (\(G_{10}\)) in the group. More precisely, we assume that agents stay if past cooperation exceeds their innate threshold, \(\tau_{i} \leq G_{10}\), and leave otherwise (\(\tau_{i} > G_{10}\)). Thus, prosocials accept a lower level of cooperation (\(0.3 \leq G_{10}\)) than proselfs (\(0.7 \leq G_{10}\)) reflecting their innate cooperativeness even when others defect. However, agents still condition their decision to leave or stay on what others do so that also proselfs leave a group when cooperation drops too low. Sensitivity analyses were conducted to test the effects of the leave-stay procedure (Appendix A9.3). Next to \(\tau_{i} > G_{10}\), we test the consequences of leaving if \(1-\tau_{i} > G_{10}\) and \(0.5 > G_{10}\). The leave-stay procedure is activated after 100, 200, and 300 iterations. Agents who decide to leave are put into a pool, followed by matching to a new group. Note that leavers start in the new group with their initial threshold (\(\tau_{i} \rightarrow \tau_{i,t}\)), while stayers maintain their current threshold (\(\tau_{i,t}\)). Resetting is done to model the fact that threshold changes depend on social interactions, and it resembles a reset effect for leavers.
Matching rules
After a leave-stay decision, groups are ranked from high to low based on the group-specific \(G_{10}\). We assume that all leavers prefer a higher-ranked group to a lower-ranked one. Agents, in turn, are ranked based on their perceived merit. In general, the matching procedure assures that groups with higher ranks also receive agents with higher perceived merit. More precisely, the procedure starts by assigning as many agents to the highest-ranked group as there are empty slots, starting with the highest-ranked agents, then takes the remaining highest ranked agent and assigns them to the empty slots in the next highest-ranked group. Note that it is expected that the best functioning groups do not have empty slots to fill because no agent left the group. This procedure repeats until all agents from the pool are matched. What determines merit depends on the exact matching rule and whether reputational information from the networks is available, as will be explained below.
As we set out in the theory section, the severity of the “bad barrels” problem is determined by the extent to which agents lack information about the individual behavior of others. We therefore compare three different matching rules to assess how moving from perfect to imperfect information concerning individual cooperation and the possibility to use network-based reputation for matching decisions moderate the effectiveness of meritocratic matching. Appendix A4 presents some additional rules we explored as the benchmark for comparison with earlier work. Findings for these additional matching rules are reported in Appendix A6. Figure 4 shows three matching rules for agents who left their group.
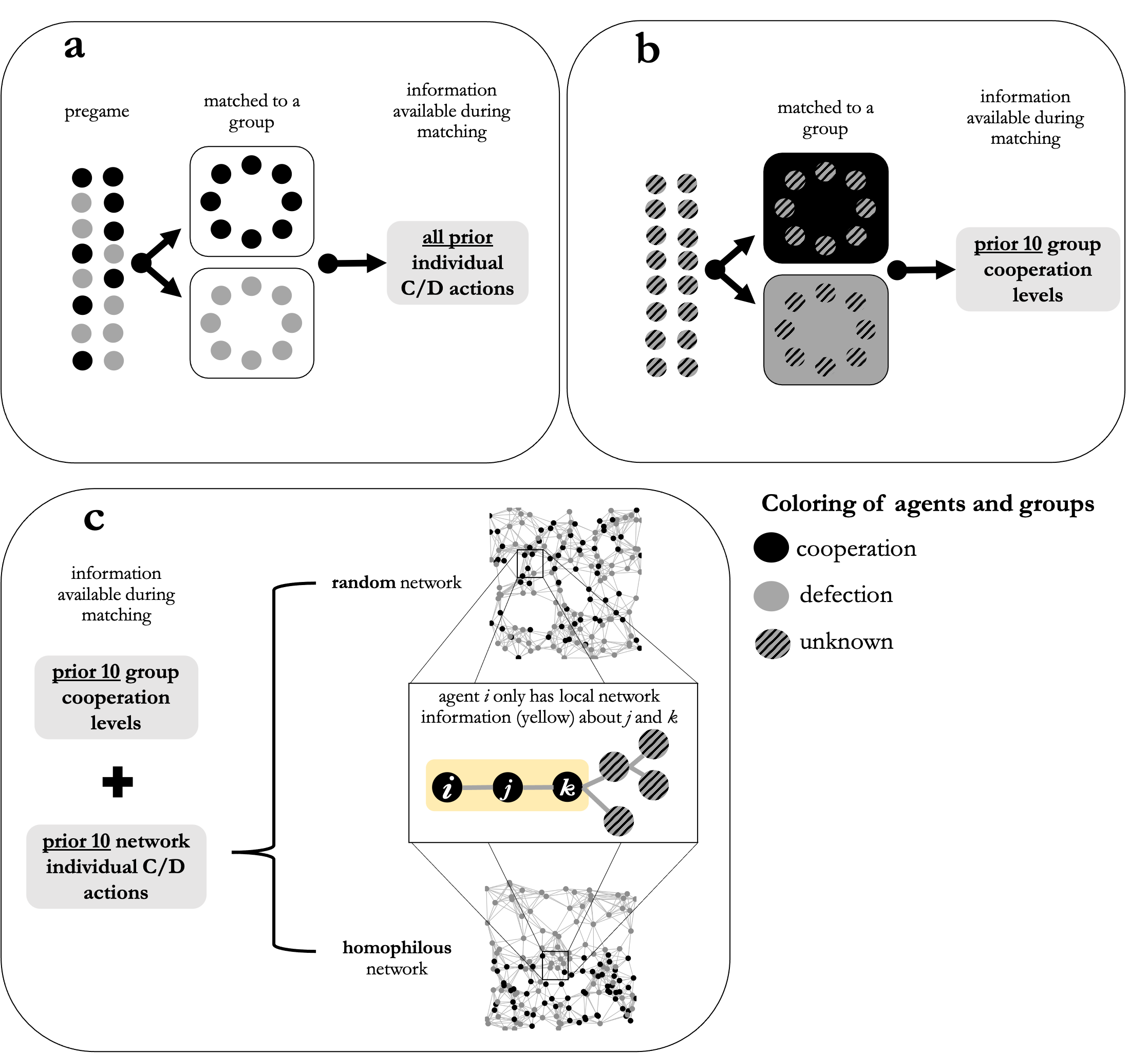
Rule 1. This rule represents our baseline scenario in which agents have complete information about all prior individual cooperative actions (Figure 4a). Agents are initially assigned to groups based on their first cooperation decision, which is itself determined based on the agent’s initial threshold. This approach limits initial mismatching. Prosocials initially have a 70 percent chance to cooperate, whereas proself agents have a 30 percent chance to cooperate.
Rule 2. This rule allows us to test intuition 1. Agents are randomly matched to groups and no reputational information from the network is available for assessing their individual merit in rematching decisions (Figure 4b). To further model incomplete information of agents in other groups, merit assessments are entirely based on the recent level of group cooperation (\(G_{10}\)) of an agent’s past group (Duca & Nax 2018). This rule tests whether mismatched cooperative agents can get away from defective groups if agents in other groups know the average level of cooperation in the group.1
Rule 3. With this rule, we add the possibility that agents in other groups can use individual reputational information from the network. Thus, agents are now embedded into two contexts (Figure 4c). Agents in other groups rely during matching on the combination of social network information and group merit to assess an agent’s merit: \(GC_{10}= (C_{10,sn} + G_{10}) / 2\), where agents store their last 10 social network decisions in \(C_{10,sn}\), while \(G_{10}\) represents the average cooperation of the last 10 iterations in their previous group. But there is a caveat: agents only rely on \(GC_{10}\) when local network information is available (yellow pane in Figure 4c) and use \(G_{10}\) when network information is unknown. Agents thus do not have global network information. Local network information may not be available if members of the receiving group do not belong to the social vicinity of an applicant. To be precise, agents know \(C_{10,sn}\) only if they are alters or alters’ alters of an applicant. Otherwise, they can only use \(G_{10}\). The addition of network information is interesting because \(G_{10}\) allows prosocial agents with low \(G_{10}\) to increase their chances to join better groups when \(C_{10,sn}\) is high. The contrary is also true. It may be detrimental for agents with a high \(G_{10}\) to incorporate a low \(C_{10,sn}\). There are two network implementations under rule 3: a random and homophilous network, allowing us to test intuition 2 and 3 respectively (Figure 4c).
Simulation experiment
To check whether our intuitions for the model are correct, we conducted simulation experiments via BehaviorSpace in NetLogo (Wilensky 1999). Our most important experimental outcome is cooperation levels reached for prosocials, but we also zoom in on proself and collective cooperation levels. We choose a scenario roughly inspired by 2 consecutive academic years, divided into 4 semesters, in which students are grouped for a project and can self-organize new project groups after each semester.
We model a population with \(n = 160\) agents, placed in \(G = 20\) equally sized groups. The population contains a minority of 40% prosocial students (\(PA = 0.4\)). Agents play an iterated \(n\)-person PD for \(400\) iterations in the groups with rematching occurring after \(X = 100\), \(200\), and \(300\) iterations. This assures groups that remain fixed for a sufficiently long period to develop stable cooperation levels. The network contains 800 social ties, where each agent has at least 5 network alters. A network is either formed with all dyads being equally likely or based on homophily.
Regarding the threshold model, we assume a moderate degree of learning (\(l = 0.5\)) and randomness (\(m = 5\)), following earlier work (Macy 1991a). The full parametrization of the model can be found in Table A1 in Appendix A5. Appendix A9 reports the various robustness checks of our findings.
Findings
Investigating intuitions 1 – 3
Figure 5 reports mean cooperation levels over time, averaged over 100 simulation runs for prosocials, proselfs, and the entire population (collective) per matching rule.
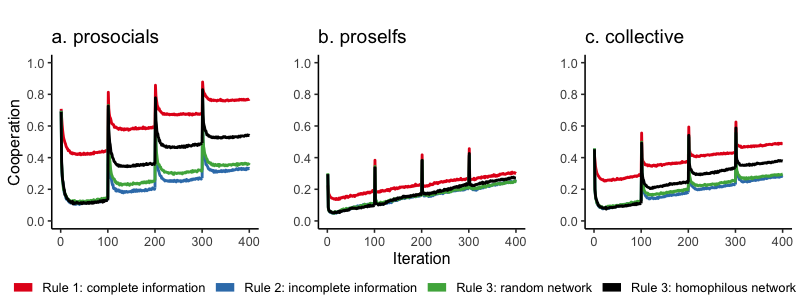
The spikes in Figure 5a after matching show prosocial agents initially cooperating with high frequency in accordance with their initial thresholds. However, cooperation tends to soon decline to lower levels than right after the matching moment. The cooperative intentions of prosocials are to no avail in some groups. The loss of cooperative potential after matching points to the presence of mismatched prosocials.
Intuition 1 is corroborated by our model. Comparing matching rules 1 (red) and 2 (blue) in Figure 5a indicates that mismatched prosocials are less able to cooperate if meritocratic matching is based on agents’ prior group performance.2 Proself agents are slightly better off when complete individual information is available, but we need to stress that differences between cooperation levels reached under complete and incomplete information rules are marginal (Figure 5b). Our model does thus not support what is considered an important strength of meritocratic matching – proselfs do not behave significantly more cooperative over time when their individual merits are visible. In sum, our simulation findings suggest that cooperative agents end up in less-than-ideal groups when matching is based on incomplete information.
Our results show also that incomplete information jeopardizes the collective efficiency of meritocratic matching. Figure 5c shows that cooperation rates are highest under complete information, which is collectively optimal under the social dilemma game groups play (Figure 5c). What is more, Figure 5b suggests that collective cooperation levels are not driven by egoistic agents overcoming their innate inclination to defect. Rather, Figure 5a shows that prosocials who cooperate under Rule 1 and Rule 3 (homophily) drive cooperation at the collective level. Consequences of removing meritocratic matching broken down for prosocials, proselfs, and the collective are reported in the Appendix A7. Without matching and network information, the model with only a \(n\)-person PD suggests that the collective fares best when agents in the group, irrespective of group composition, interact for over 10000 iterations without matching to another group (Appendix A7, Figure A2f).
We analyzed whether random or homophilous networks help restore the effectiveness of meritocratic matching in a world of imperfect information. On the one hand, intuition 2 proposed that individual information derived from dyadic interactions in a randomly formed network mitigates the bad barrels problem (green line in Figure 5a). Formerly mismatched cooperative agents are better able to signal their prosociality and, therefore, improve their chances to move into more cooperative groups. However, there is only a marginal increase from the incomplete information rule 2 (blue) and rule 3 in which additional individual network information is available in random networks (green). We cannot confirm intuition 2 for random networks.
On the other hand, the picture changes radically when homophily is implemented in the network, consistent with intuition 3. The black line in Figure 5a shows how cooperative agents increasingly cooperate when information is incomplete, due to the possibility to escape from defective groups. In particular, adding homophily increases cooperation rates only for prosocials and not for proselfs (Figure 5b). The difference to the random network condition shows the underlying mechanism. Prosocials cooperate more because due to homophilous networks they more often succeed in leaving bad barrels and joining groups in which they more readily cooperate. Our findings also suggest that there is still some loss of efficiency due to imperfect information, demonstrated by the large difference between cooperation levels when information is complete or incomplete (red vs. black line in Figure 5a).
In the next two sections, we explore underlying reasons why homophily is an important driver for prosocials’ cooperation. In a nutshell, we point to prosociality segregation and the impact of homophily on dyadic interactions as underlying reasons for the findings reported in Figure 5.
Prosociality segregation
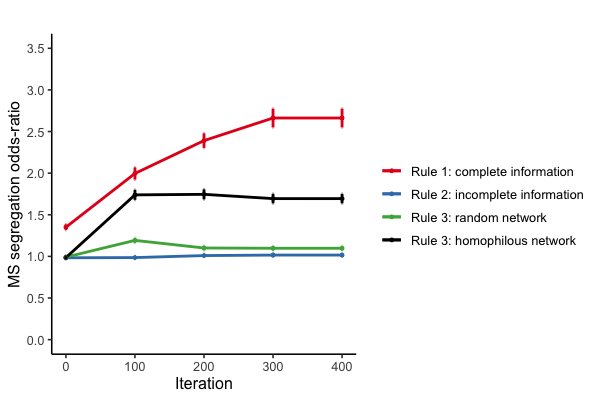
One feature that facilitates cooperation of prosocial agents is the presence of similar others in the group. Thus, the occurrence or absence of prosociality segregation – i.e. more prosocials in cooperative and proselfs in defective groups – may be an important explanans for the reported cooperation levels in Figure 5. In Figure 6, we use the gross-segregation index (MS) to measure the odds of being matched with similar types in the group context (Moody 2001).
Segregation in the group context is highest when complete information is available (red line in Figure 6). Both prosocials and proselfs are three times as likely to be grouped with their own type. What is more, the MS odds ratio value at iteration 0 for complete information shows that initial mismatching is less prevalent compared to incomplete information conditions. Even if a cooperative agent is spoiled by the mere presence in an uncooperative group, a cooperative effort at the early stages of the game still serves as a signal to others when complete individual information is available. This signal, in turn, positively affects prosocials’ chances to escape the uncooperative environment and to match to a more cooperative group.
Figure 6 shows that when agents are embedded in homophilous networks, the odds to join forces with similar others are around 1.5. Harvesting individual information from a homophilous network allows cooperators to team up, leaving defectors only their own types to be matched with. For prosocials, assorting with similar others promotes more chances to cooperate (Figure 5a), while the opposite counts for proselfs. The increases of cooperation in Figure 5a appear to be largely driven by mismatched prosocials leaving bad groups and moving to more cooperative groups with many similar others. The contrary is true for incomplete information settings when matching is initially imperfect and remains to be so. “Spoiled” cooperative types may then have a hard time escaping from unproductive groups due to the low performance of the group they reside in which makes it hard for them to demonstrate their genuine cooperativeness to other groups (green and blue line in Figure 6).
Impact of homophily
Here we zoom into how homophily affects cooperative behavior in dyadic interactions and – thereby – the information agents can obtain about potential new group members from their network interactions. In Figure 7, we compare a single run of cooperation levels in a random and homophilous network. The full simulation experiments provide a similar picture (Appendix A8). Strikingly, homophily does not so much increase cooperation of prosocials (Figure 7a), but it reduces cooperation of proselfs in dyadic interactions (Figure 7b). Agents have no other choice in random networks than to play the 2-person PD. Such a 2-person interaction scheme in random networks – where there is a 50/50 chance to link to other-type agents – is particularly beneficial for proself agents to learn to cooperate when they have repeated interactions with cooperating others (most likely prosocials). Namely, when interacting with prosocials, proselfs will quickly generate a probability to cooperate of \(0.5 \, (1 / \{1 + exp[5(1-1)]\})\), in which a random walk from defection to cooperation leads to locking into cooperation. Figure 7, green line, shows the tendency towards all-out cooperation in random networks, which, as a result, makes it hard to differentiate between more prosocial and proself agents. While prosocials maintain higher levels of cooperation than proselfs even in random networks (Figures 7a and 7b, green lines), the difference in cooperation rates is small. As a result, dyadic interactions in random networks provide insufficient information to separate prosocials from proselfs. Consequently, dyadic interactions in random networks do not lead to more cooperation in the group context among both prosocials and proselfs (Figures 5a and 5b). As such, information derived from random networks does not serve more as an exclusionary mechanism compared to information derived from homophilious networks and therefore does not lead to more cooperation in the group context among prosocials and proselfs.
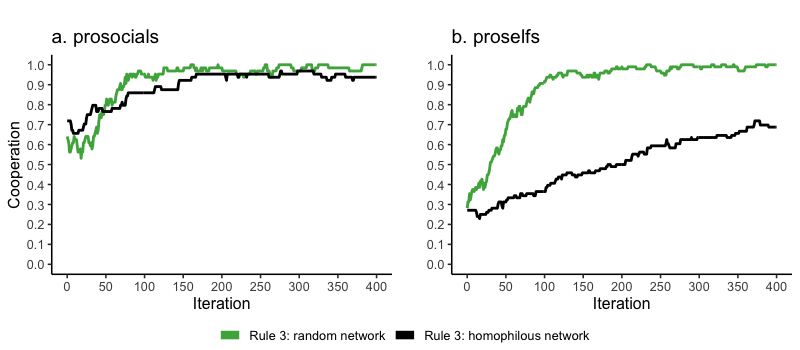
However, the picture changes when we inspect cooperation levels of proselfs in a homophilous network (Figure 7, black line). In such networks, agents mainly have network ties to similar others and similarly-behaving agents preferentially interact with each other. Cooperators – most likely prosocials – tend to receive cooperative acts in return, while defectors receive mostly defection. The context in homophilous networks has a downside for proselfs as a result of their limited interaction with cooperative others. Proselfs have little opportunity to learn cooperative behavior from interactions with others since the other is most likely a proself type. Meanwhile, homophilous networks enable prosocials to signal that they are cooperative regardless of the group context into which they have been matched. This allows prosocials who find themselves in a bad barrel to nonetheless identify themselves as cooperative. Thus, homophilous networks make prosocials more likely to be identified as good cooperation partners and proselfs less likely to be considered desirable group members. Overall, individual information derived from homophilous networks enables agents to distinguish more readily between prosocial and proself types, and consequently allows prosocials more easily to join forces (Figure 6) and cooperate more often (Figure 5a). As such, homophily serves as an exclusionary mechanism, clearly differentiating between prosocials and proselfs. Our work, reflecting ideas from earlier research on homophily in networks (McPherson et al. 2001), stresses the importance of homophily as a structural and behavioral process operating in social networks. The pervasiveness of homophily in informal social networks elucidates to what degree cooperative acts, as well as information on others’ cooperative behavior, flow locally among similar others, contrasting randomly formed networks.
Sensitivity analysis
We implemented several robustness checks inspecting under which conditions our simulation findings are robust. First, we explored various learning rates (\(l\)), since learning dynamics play a pivotal role in solving the problem of cooperation (Macy & Flache 2002). Second, the presence of more prosocial agents may increase chances to team-up with similar others; thus we inspect the impact of the proportion of prosocials (\(PA\)) in the population. Third, noise in the behavioral decision-making model (indicated by \(m\)) is bound to play an important role when agents make decisions in threshold models (Macy & Evtushenko 2020; Mäs & Opp 2016). We inspect the consequences of more or less noise. Fourth, noise also has a role in the leave-stay procedure in which a proportion of agents who were happy with group performance and therefore stayed in the group will wrongly be put in the leavers pool. On a similar note, we test the consequences of altering input for the leave-stay procedure, either \(\tau_{i}\), \(1-\tau_{i}\), or 0.5 in relation to \(G_{10}\). Finally, we vary the rate \(r\) at which dyadic interactions rather than group interactions occur.
Appendix A9 provides a comprehensive taxonomy of the various robustness checks with a total of 42600 simulation runs. Our simulation findings regarding cooperation and prosociality segregation turn out to be fairly robust to changes in the proportion of prosocials present in the population (Appendix A9.1), for learning rates below 0.9 (Appendix A9.1), and for variations in the leave-stay procedure (Appendix A9.2-A9.3). Notably, a high learning rate (\(l = 0.9\)) allows agents to quickly learn how to cooperate, providing a different solution than meritocratic matching for cooperation to thrive (Appendix A9.1). Moreover, we find that the bad barrels problem and homophilous network solution are more pronounced when \(m = 5\) and \(r < 0.25\) compared to when \(m = 1\) or \(10\) and \(r = 0.25\) or \(0.5\). The sensitivity analyses raise a few points. First, the simulation findings are sensitive to more or less noise in the decision-making model, showing two cooperation equilibria (Appendix A9.1). More noise (\(m = 1\)) leads to a self-correcting equilibrium where cooperation levels steadily hover around 0.34, whereas less noise (\(m = 10\)) leads to a self-reinforcing equilibrium where cooperative agents quickly lock into cooperation (Macy & Flache 2002). Second, the importance of complete information rules for prosocials to cooperate is robust to changes in network dyad selection (\(r\)), but our incomplete-information-with-network-information solution is not. Figure A10 in Appendix A9.4 shows when chances for dyad selection increase to values of 0.25 and higher, individual information from homophilous networks does not contribute to prosocials’ chances to cooperate more often or to join more cooperative groups with similar others. The reason for model sensitivity to \(r\) is found in the inability to differentiate between proself and prosocial agents regarding network cooperation. When \(r \geq 0.25\), proselfs more readily learn to cooperate at similar levels as prosocials, even when proselfs are embedded in parts of the social network where initial defection prevails. Finally, we also tested whether model results change qualitatively when we abandon the assumption that homophily is not only affecting the network structure but also who interacts with whom (see Appendix 9.5). While effects become smaller quantitatively, they remain unchanged qualitatively.
Discussion
Our work has uncovered a limitation of meritocratic matching. The availability of information strongly affects the ability of the matching mechanism to generate cooperative groups. Complete information on individual predispositions provides ideal conditions for meritocratic matching. To analyze the consequences of incomplete information on model outcomes, we introduced several matching rules. When only group-level information is available for the matching mechanism, prosocials end up not fully exploiting their cooperative potential, hindering cooperation in general. We also asked whether social network information can solve the bad barrels problem. Our simulations show that if prosocial agents have access to individual information derived from homophilous networks they can mobilize more of their cooperative potential. Homophilous networks improve the functioning of meritocratic matching systems by allowing cooperators to identify other cooperators. Agents preferentially connect to and interact with similarly behaving others in the network: cooperators mainly interact with cooperators while defectors are left to interact with other defectors. This creates ideal conditions for mismatched prosocial agents to display their cooperative tendencies, as they do not have to fear exploitation by uncooperative network partners. Dyadic interactions thus increase differentiation between prosocials and proselfs. In addition, homophilous networks create groups of prosocial agents who are aware of each other’s behavior. The stronger this prosociality segregation is, the better prosocials are able to cooperate in the group context. The availability of information on prosocial others and the relative effectiveness of behavior in homophilous dyadic network interactions helps prosocials group up, resulting in more cooperation in the group context.
Our study comes with limitations which suggest avenues for future research. One limitation pertains to the comparison of the value of network cooperation to group cooperation, which may be context-dependent. Our robustness checks showed that differentiation in the frequency of interactions (\(r\)) matters. But the goals of work-related teams may also differ from the social goals of inter-employee friendships. Some may even not want a spillover between the friendship and work domain. This may limit the extent to which networks help solving the “bad barrels” problem. The problem further perpetuates when merit information from the group context surpasses the importance of network-based merit. However, for important contexts, it seems plausible that network information is sufficiently reliable and relevant to improve selection decisions. For example, a scientific department recruiting new staff may want to mobilize informal collaboration networks of employees with many ties to applicants working in the discipline, to collect more individual information about applicants. Especially, when work-related information is lacking or unreliable.
An important topic highlighted by our model is the tension between what is individually or collectively optimal in meritocratic matching. Prosocials fare better under meritocratic matching, but proselfs – and thereby the collective – may need more time to follow suit. This tension, i.e., maximizing collective benefits that arise out of cooperation and minimizing individual differences in benefits, finds its roots in the classical societal problem which the meritocratic system aims to attenuate: inequality. One way to suppress inequality as an outcome is to bolster equality in opportunities—a core tenet of meritocratic matching since it leads to equal opportunities in principle. But meritocratic matching may also perpetuate inequality by shifting it to merit-based inequality. For instance, the ideal situation occurs when proselfs quickly recognize that they need to cooperate in order to advance. However, our model also suggests that proselfs need time to learn to cooperate and they learn faster in the presence of prosocials (Appendix A7). When meritocratic matching functions optimally, prosocials and proselfs are quickly segregated. One may question whether it is fair to condemn proselfs to defective collectivities. The consequence is that meritocratic matching is beneficial for prosocials and harmful to proselfs. The question is whether such a cleavage between cooperative and defective groups is collectively optimal. For example, in the context of higher education, our model suggests that it is best for cooperative students to join forces with other cooperative types, leaving non-cooperative students astray. But this risks writing off groups of proselfs who are not by definition incorrigible defectors. Thus, meritocratic matching can also have negative externalities for non-cooperative types who initially fell of the cooperative wagon, exacerbating societal inequality.
Also, future work may want to inspect conditions under which the network works as an exclusionary mechanism. For instance, our model shows how random networks operate as an exclusionary mechanism in dividing prosocials and proselfs only under certain conditions. Especially in the early stages of interactions in random networks, proselfs are relatively less attractive than prosocials. On the whole, we find that this does not translate to a radical change in cooperation rates in the group context compared to the condition of homophilous networks. A follow-up study may entail exploring network conditions under which the exclusionary mechanism in cooperative relations in homophilious networks increases the exclusion of non-cooperators also in the group context. A further intriguing possibility to explore could be that heterophilous networks – networks in which prosocials are preferentially connected to proselfs – can lead to better chances for proselfs to escape from low-cooperation groups because they can learn more effectively to cooperate also in the relational context.
Finally, although we already introduced some potential model extensions in Appendix A10, our model necessarily makes assumptions about the way individuals process and respond to the information obtained from group and dyadic interactions. As a first step towards testing the practical implications of our model, it is important to test these behavioral assumptions in laboratory experiments or empirical settings. We envision settings in which participants are embedded in group and network contexts and use information concerning merits from one context to inform others in another context. Furthermore, the homophily solution in a world where meritocratic matching is based on imperfect information does not particularly exacerbate the problem for proselfs. A reason why proselfs do not experience a backfire effect of homophily may be the static nature of the network in our model. A dynamic network in which agents preferentially form and dissolve ties with (dis)similar cooperative others may eventually result in a cooperative cluster in which prosocials reside while proselfs are condemned to interact with similar others in a defective cluster. Then homophily may be detrimental for the chances of proselfs to cooperate in the group context. Our model already incorporates interaction dynamics (via parameter \(r\)), but dynamic networks may introduce another mechanism that separates defectors from cooperators.
In summary, we showed that meritocratic matching systems in which merit is assessed based on group-level outcomes suffer from what we termed the “bad barrels” problem. Persons with cooperative intentions (the “good apples”) end up in uncooperative groups (the “bad barrels”). They are unable to single-handedly change the nature of the group and are forced to behave more uncooperatively themselves in order to avoid exploitation. The good apples are thus spoiled by the bad barrels in which they find themselves. Matching systems which rely on group-level information are unable to identify these spoiled good apples, resulting in collectively inefficient outcomes.
As a potential solution, information from informal social networks can be used to improve the functioning of meritocratic matching systems. Informal social networks, particularly when these networks show homophily on traits that relate to cooperativeness, allow individuals to show their merit without being constrained by group-level interdependence. Imagine again the student context discussed earlier. At the start of an academic year, students are randomly grouped to work together in project teams. The course ends at some point and all groups receive a collective grade. A students’ true value as a potential contributor in future project teams may not be reflected by the group grade, but social relations with similar others who also generally invest a lot of time and effort into their studies is a way out for students who have more to offer. Our findings are in sync with the five rules for cooperation to arise proposed by Nowak (2006); that is, we show that reciprocity within groups in the long haul (Appendix A7), (in)direct reciprocity in network interactions, and network clustering via homophily foster cooperation. However, our work also uncovered a potential downside of homophily: segregation of proselfs limits their possibility to learn cooperative behavior over time in interactions with prosocials. This raises an intriguing possibility for future work: identifying an optimal degree of meritocratic matching that balances the benefits for prosocials with the benefits for the overall population.
Acknowledgments
The first, second, and fourth author acknowledge that this study is part of the research program Sustainable Cooperation – Roadmaps to Resilient Societies (SCOOP) funded by NWO and the Dutch Ministry of Education, Culture, and Science (OCW) in its 2017 Gravitation Program (grant number 024.003.025). The second and third author acknowledge financial support by the Netherlands Organization for Scientific Research (NWO) under the 2018 ORA grant ToRealSim (464.18.112). We want to stipulate that this work has benefitted from enriching discussions with the members of the “Norms and Networks Cluster” at the Department of Sociology at the University of Groningen as well as with members of the Interuniversity Center for Social Science Theory and Methodology (ICS).Model Documentation
The model is written and built in NetLogo. The full NetLogo code, model, and summarized ODD protocol is stored on the CoMSES Computational Model Library under the following URL: https://www.comses.net/codebase-release/66d84cb4-c45f-46bb-bef6-b9e298758fa5/. The data was analyzed using R. The data and R-script can be found on the Open Science Framework (OSF) via the following URL: https://osf.io/2qpdn/?view_only=1a2bc9f55af145cbaaaaada22bdf9993.Notes
- Note that Figure A1 in Appendix A6 elucidates that relying on the last 10 individual cooperation decisions in the group context does not alter cooperation levels reached under rule 2.↩︎
- An additional incomplete information rule – see Appendix A6 – corroborates that solely observations of agents’ individual behavior in the context of that group also lead to similar lower cooperation levels as under rule 2.↩︎
Appendix and Supplementary Materials
The Appendix and Supplementary Materials can be accessed at: https://www.jasss.org/25/1/6/6SIFile.pdf.References
AXELROD, R. (1984). The Evolution of Cooperation. New York, NY: Basic Books.
BACHARACH, M., & Gambetta, D. (2001). 'Trust in signs.' In K. Cook (Ed.), Trust in Society (pp. 148–184). New York, NY: Russel Sage Foundation.
BALLIET, D., Parks, C. D., & Joireman, J. (2009). Social value orientation and cooperation in social dilemmas: A meta-analysis. Group Processes and Intergroup Relations, 12(4), 533–547. [doi:10.1177/1368430209105040]
BIANCHI, F., Flache, A., & Squazzoni, F. (2020). Solidarity in collaboration networks when everyone competes for the strongest partner: A stochastic actor-based simulation model. Journal of Mathematical Sociology, 44(4), 249–266. [doi:10.1080/0022250x.2019.1704284]
BOWLES, S., & Gintis, H. (2004). The evolution of strong reciprocity: Cooperation in heterogeneous populations. Theoretical Population Biology, 65(1), 17–28. [doi:10.1016/j.tpb.2003.07.001]
BROUWER, J., Flache, A., Jansen, E., Hofman, A., & Steglich, C. E. G. (2018). Emergent achievement segregation in freshmen learning community networks. Higher Education, 76(3), 483–500. [doi:10.1007/s10734-017-0221-2]
BUSKENS, V., & Raub, W. (2002). Embedded trust: Control and learning. Advances in Group Processes, 19, 167–202. [doi:10.1016/s0882-6145(02)19007-2]
CHATTOE-BROWN, E. (1998). Just how (un)realistic are evolutionary algorithms as representations of social processes? Journal of Artificial Societies and Social Simulation, 1(3), 2: https://www.jasss.org/1/3/2.html. [doi:10.18564/jasss.1819]
CHAUDHURI, A. (2011). Sustaining cooperation in laboratory public goods experiments: A selective survey of the literature. Experimental Economics, 14(1), 47–83. [doi:10.1007/s10683-010-9257-1]
DAWES, R. M. (1980). Social dilemmas. Annual Review of Psychology, 31, 169–193.
DUCA, S., Helbing, D., & Nax, H. H. (2018). Assortative matching with inequality in voluntary contribution games. Computational Economics, 52(3), 1029–1043. [doi:10.1007/s10614-017-9774-5]
DUCA, S., & Nax, H. H. (2018). Groups and scores: The decline of cooperation. Journal of the Royal Society Interface, 15(144), 20180158. [doi:10.1098/rsif.2018.0158]
FANG, H., & Moro, A. (2011). 'Theories of statistical discrimination and affirmative action: A survey.' In J. Benhabib, A. Bisin, & M. O. Jackson (Eds.), Handbook of Social Economics, (pp. 133–200). Amsterdam: North-Holland. [doi:10.1016/b978-0-444-53187-2.00005-x]
GAMBETTA, D. (2009). 'Signalling.' In P. Hedström & P. Bearman (Eds.), The Oxford Handbook of Analytical Sociology (pp. 168–194). Oxford: Oxford University Press. [doi:10.1093/oxfordhb/9780199215362.013.8]
GROW, A., Flache, A., & Wittek, R. P. M. (2017a). A model of global diversity and local consensus in status beliefs. CoMSES Computational Model Library, (Version 1.2.0). Retrieved from: https://www.comses.net/codebases/5493/releases/1.2.0/. [doi:10.15195/v4.a25]
GROW, A., Flache, A., & Wittek, R. P. M. (2017b). Global diversity and local consensus in status beliefs: The role of network clustering and resistance to belief change. Sociological Science, 4(25), 611–640. [doi:10.15195/v4.a25]
GUIDO, A., Robbett, A., & Romaniuc, R. (2019). Group formation and cooperation in social dilemmas: A survey and meta-analytic evidence. Journal of Economic Behavior and Organization, 159, 192–209. [doi:10.1016/j.jebo.2019.02.009]
GUNNTHORSDOTTIR, A., Houser, D., & McCabe, K. (2007). Disposition, history and contributions in public goods experiments. Journal of Economic Behavior and Organization, 62(2), 304–315. [doi:10.1016/j.jebo.2005.03.008]
HECKATORN, D. D. (1996). Dynamics and dilemmas of collective action. American Sociological Review, 61(2), 250–277.
HÖGLINGER, M., & Wehrli, S. (2017). 'Measuring social preferences on Amazon Mechanical Turk.' In B. Jann & W. Przepriorka (Eds.), Social Dilemmas, Institutions, and the Evolution of Cooperation (pp. 527–546). Oldenbourg: de Gruyter.
KEIJZER, M. A., Mäs, M., & Flache, A. (2018). Communication in online social networks fosters cultural isolation. Complexity, 2018, 9502872. [doi:10.1155/2018/9502872]
LAZARSFELD, P. F., & Merton, R. K. (1954). 'Friendship as social process: Substantive and methodological analysis.' In M. Berger, T. Abel, & C. H. Page (Eds.), Freedom and Control in Modern Society (pp. 18–66). NewYork, NY: Van Nostrand.
MACY, M. W. (1991a). Chains of cooperation: Threshold effects in collective action. American Sociological Review, 56(6), 730–747. [doi:10.2307/2096252]
MACY, M. W. (1991b). Learning to cooperate: Stochastic and tacit collusion in social exchange. American Journal of Sociology, 97(3), 808–843. [doi:10.1086/229821]
MACY, M. W., & Evtushenko, A. (2020). Threshold models of collective behavior II: The predictability paradox and spontaneous instigation. Sociological Science, 7(26), 628–648. [doi:10.15195/v7.a26]
MACY, M. W., & Flache, A. (2002). Learning dynamics in social dilemmas. Proceedings of the National Academy of Sciences, 99(suppl 3), 7229–7236. [doi:10.1073/pnas.092080099]
MARWELL, G., & Ames, R. E. (1981). Economists free ride, does anyone else? Experiments on the provision of public goods, IV. Journal of Public Economics, 15(3), 295–310. [doi:10.1016/0047-2727(81)90013-x]
MÄS, M., & Opp, K. D. (2016). When is ignorance bliss? Disclosing true information and cascades of norm violation in networks. Social Networks, 47, 116–129.
MCPHERSON, J. M., Smith-Lovin, L., & Cook, J. M. (2001). Birds of a feather: Homophily in social networks. Annual Review of Sociology, 27(1), 415–444. [doi:10.1146/annurev.soc.27.1.415]
MELAMED, D., Munn, C. W., Simpson, B., Abernathy, J. Z., Harrell, A., & Sweitzer, M. (2020). Homophily and segregation in cooperative networks. American Journal of Sociology, 125(4), 1084–1127. [doi:10.1086/708142]
MOODY, J. (2001). Race, school integration, and friendship segregation in America. American Journal of Sociology, 10(3), 679–716. [doi:10.1086/338954]
NAX, H. H., Murphy, R. O., Duca, S., & Helbing, D. (2017). Contribution-based grouping under noise. Games, 8(4), 50. [doi:10.3390/g8040050]
NAX, H. H., Murphy, R. O., & Helbing, D. (2017). 'Nash dynamics, meritocratic matching, and cooperation.' In B. Jann & W. Przepriorka (Eds.), Social Dilemmas, Institutions, and the Evolution of Cooperation (pp. 447–469). Oldenbourg: de Gruyter. [doi:10.1515/9783110472974-021]
NAX, H. H., Perc, M., Szolnoki, A., & Helbing, D. (2015). Stability of cooperation under image scoring in group interactions. Scientific Reports, 5(1), 12145. [doi:10.1038/srep12145]
NAX, H. H., & Rigos, A. (2016). Assortativity evolving from social dilemmas. Journal of Theoretical Biology, 395, 194–203. [doi:10.1016/j.jtbi.2016.01.032]
NOWAK, M. A. (2006). Five rules for the evolution of cooperation. Science, 314(5805), 1560–1563. [doi:10.1126/science.1133755]
NOWAK, M. A., & Sigmund, K. (1998). Evolution of indirect reciprocity by image scoring. Nature, 393(6685), 573–577. [doi:10.1038/31225]
OLSON, M. (1965). The Logic of Collective Action: Public Goods and the Theory of Groups. Cambridge, MA: Harvard University Press.
RAUB, W., & Weesie, J. (1990). Reputation and efficiency in social interactions: An example of network effects. American Journal of Sociology, 96(3), 626–654. [doi:10.1086/229574]
ROSS, L. (1977). The intuitive psychologist and his shortcomings: Distortions in the attribution process. Advances in Experimental Social Psychology, 10, 173–220. [doi:10.1016/s0065-2601(08)60357-3]
SIMPSON, B., & Willer, R. (2015). Beyond altruism: Sociological foundations of cooperation and prosocial behavior. Annual Review of Sociology, 41, 43–63. [doi:10.1146/annurev-soc-073014-112242]
SPENCE, M. (1973). Job market signaling. The Quarterly Journal of Economics, 87(3), 355–374.
THIELMANN, I., Spadaro, G., & Balliet, D. (2020). Personality and prosocial behavior: A theoretical framework and meta-analysis. Psychological Bulletin, 146(1), 30–90. [doi:10.1037/bul0000217]
WILENSKY, U. (1999). NetLogo. Center for connected learning and computer-based modeling, Northwestern University.
WITTEK, R. P. M., Snijders, T. A. B., & Nee, V. (2013). 'Introduction: Rational choice social research.' In R. P. M. WITTEK, T. A. B. Snijders, & V. Nee (Eds.), The Handbook of Rational Choice Social Research (pp. 1–30). Stanford, CA: Stanford University Press.
WONG, L. H., Pattison, P., & Robins, G. (2006). A spatial model for social networks. Physica A: Statistical Mechanics and Its Applications, 360(1), 99–120. [doi:10.1016/j.physa.2005.04.029]