An Agent-Based Model to Support Infection Control Strategies at School

Introduction

Physical distancing measures enforced to control the spread of COVID-19 were adopted by many governments to avoid the collapse of often fragile and overloaded health care systems. School closures were often considered as unavoidable control measures to reduce the transmission of SARS-CoV-2, because educational settings were considered potentially high-risk activities. Schools are characterized by close-contact settings, with students spending many hours close to each other in confined and enclosed spaces. In addition, compared with adults, children and adolescents infected with SARS-CoV-2 tend to be more commonly asymptomatic or have mild, non-specific symptoms, escaping early identification and isolation and potentially favouring the spread of the virus both inside and outside the school (Comar et al. 2021).

By late spring 2020, 80% of EU countries had fully or partially closed preschools, 90% had closed primary schools and 100% secondary schools or higher education establishments (ECDC, European Center for Disease Prevention and Control 2020). However, following the first two pandemic waves, it was generally observed that SARS-CoV-2 transmission in school settings was not the primary determinant of community transmission, leading to the hypothesis that cases observed in school settings mainly reflect SARS-COV-2 transmission in the general population (ECDC, European Center for Disease Prevention and Control 2021; Ludvigsson 2020). Furthermore, school closures are not cost-free and can, in turn, have dramatic social, economical, and health consequences. School closures can have detrimental effects on children’s physical and mental health and wellbeing and have the potential to increase inequality. School systems also provide significant social support, particularly for single parent and economically disadvantaged households (Maani 2020).

In the light of emerging epidemiologic evidence and potential social impact of school closures, governments implemented various non-pharmaceutical interventions (NPIs) in school settings, such as face masks, restricted entry to school, daily symptom checking, and reduced class sizes. These policies aimed to reduce the risk of transmission, leaving closure as an extreme and last resource.

However, large outbreaks in schools were observed, especially when prevention strategies were not fully implemented (Kampe et al. 2020; Stein-Zamir et al. 2020). The upsurge of new highly transmissible SARS-CoV-2 variants, such as the Delta variant, together with an elevated proportion of susceptible individuals among children, not fully targeted by the 2021 vaccination campaign, may have lead to an increase infection among children (Riley et al. 2021). Thus, a combination of NPI measures is still considered imperative to keep the risk of SARS-CoV-2 transmission as low as reasonably achievable in the educational settings. Thus, passive (syndromic) and active (molecular) surveillance strategies in schools have also been suggested to ensure the isolation of cases, tracing and quarantine of their contacts. Here, we used Agent-Based Modelling (ABM), which is particularly well-suited in cases of systems requiring a highly granular description of the population, to simulate the behaviour of a school environment. These modelling approaches have been already exploited to study the SARS-CoV-2 pandemic from different points of view (Lorig et al. 2021). This is especially so within school environment, such as (Phillips et al. 2021) where virus transmission was modelled considering schools and households in Ontario, or (Panovska-Griffiths et al. 2020) in which different school and society reopening strategies were simulated in the UK. Therefore, with our ABM, we aimed to evaluate the risk of infection associated with school activities and the effect of possible control strategies by simulating the behaviour of a school environment after the introduction of one infective case under various control strategies scenarios.

Material and Methods

Model description

Agent-based models (ABMs) are defined as data structures, where agents are modelled by a set of variables and interaction rules stated consistently with the programming language used for the simulations, in which they act and adapt their internal and external behaviour. These rules are defined by the modeller to obtain realistic simulations of behaviour within the system under consideration. Furthermore, ABMs can also include a description of the spatial domain, either discrete or continuous. In such cases, agents might be allowed to move throughout the environment and to interact with other agents depending on their physical proximity. Providing an accurate description of the scenario through rules, agents and environmental variables, we aimed to study the individual (micro) and aggregate (macro) effects that emerge from agents’ activities and interactions.

This paper proposes an ABM, developed in the multi-agent programmable modeling environment NetLogo version 6.1.1 (Wilensky 1999), to study the spread of COVID-19 infections within an explanatory scholastic environment, and to evaluate the effectiveness of non-pharmaceutical interventions (NPIs), such as distancing requirements, screening testing, and environment ventilation in such an environment.

The model components include:

• the environment including both physical spaces and social contact structure of the population,
• the COVID-19 progression model,
• the NPIs’ logic modeled to contain the COVID-19 spread.

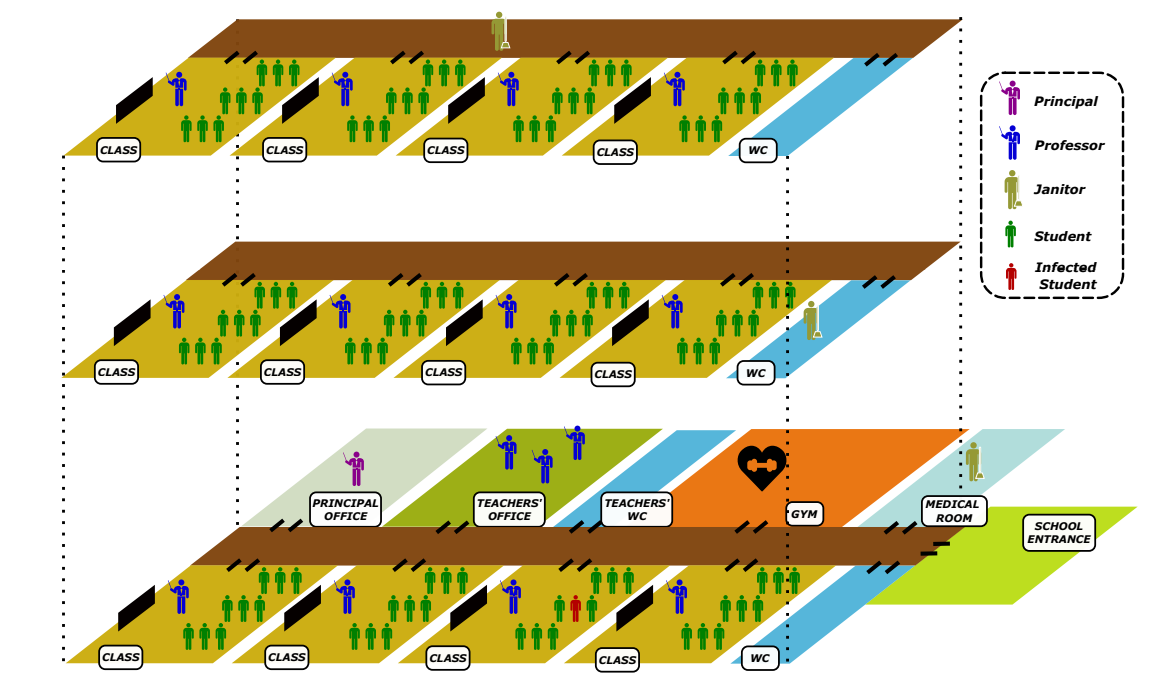
The aim of this paper is to understand the effects of contacts arising in a typical school environment as the disease spreads, and to provide insights on possible containment policies. To accomplish this aim, we did not target a specific school but modelled a typical Italian middle-sized secondary school. For generality, the modelled environment is a school of 12 classrooms (arranged on three floors), shared spaces (i.e., entrance, gym, corridors, bathrooms, stairs, medical room, teachers’ office and the principal’s office). More specifically, each floor consisted of one corridor connecting all the rooms and one bathroom only for students. The school entrance, the medical room, the gym, the principal’s office, the teachers’ office and the teachers’ bathroom are all on the first floor. Moreover, each classroom is characterized by twenty-four desks (equally distanced from each other), one teacher’s desk and the blackboard. A graphical representation of the environment and agents’ categories (i.e., students, teachers, principal and janitors) is shown in Figure 1.

In our study, the school is open from Monday to Friday and students can arrive at school from 7.35 a.m, with the first class beginning at 8:10 a.m. A school day consists of six lessons of 50 minutes each and two breaks. The first break is between the second and the third lessons, while the second one is after the fourth lesson.

Following the organization of middle schools in Italy, students stay in the same classroom and with the same classmates all day long. To limit social interaction we defined the behaviour of the agent as follows: While in class, students stay at their desks unless the teacher asks them to go to the blackboard. Other movements are not allowed. Outside classrooms, the only activity allowed is movement to the gym and to the principal’s office. Teachers move from classroom to classroom according to the class schedule. They can also go to the staffroom when they have no scheduled classes in the upcoming hour. Teachers and students can go to the bathroom on the same floor. Moreover, during breaks, students can stay in their classrooms or hallways close to their classroom and go to the bathroom. Janitors are responsible for checking students’ body temperature in addition to their usual tasks. Therefore, at the beginning of each school day they are in the medical room, while during classes they deal with their usual activities, such as cleaning and mopping floors. Table 2 reports all rates associated with agents’ actions.

At the beginning of each simulation, depending on the agent-order generation, students are allocated to classrooms (i.e., the first twenty agents are allocated to one classroom, and so on), and this association lasts for the whole simulation. Timetables for teachers are chosen in the same way following global scheduling, which is an adapted version of real teachers’ scheduling. This defines the weekly scheduling of classes for all teachers.

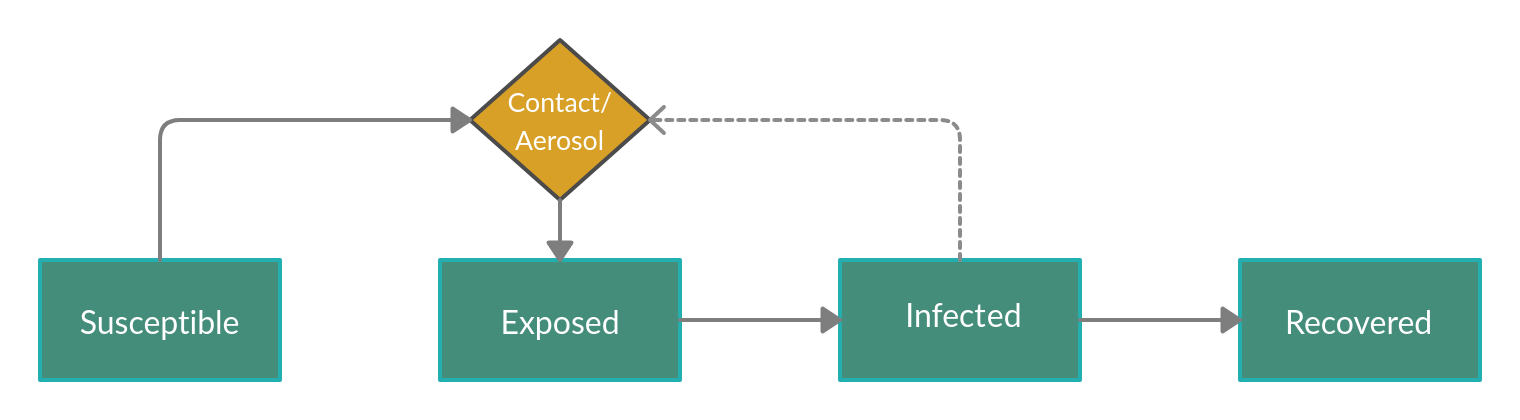
The next component of the ABM is the COVID-19 progression model, which is based on the Susceptible-Exposed-Infected-Recovered (SEIR) (Pernice et al. 2020) epidemiological model, showed in Figure 2. Thus, each agent is labeled with a specific status of the disease progression, which is updated as follows: (1) from the susceptible state to the exposed one, and consequently to virus exposure, (2) from the exposed state to the infection when the incubation period ends, and agents become contagious, (3) from an infected state to recovered one when the infectious period ends. Specifically, there is no distinction between symptomatic and asymptomatic infections, because we are interested in representing the worst-case scenario in which all infected students are asymptomatic. In Figure 2 solid lines represent transitions in disease progression, while the dashed line indicates that a susceptible individual can catch the infection only from already infected individuals. Clearly, such interaction represents the main requirement for the infection to spread. Specifically, the virus exposure is modelled through two different drivers: either close-range contacts (Hoertel et al. 2020) between susceptible and infected agents, or through aerosol (Gkantonas et al. 2021), within an indoor environment.

Considering the former case, the probability of successful contagious contact is associated with each susceptible agent (\(S_i\)) when it remains in an area (\(\mathbf{A}\)) of \(4.41 m^2\) around an infected agent. This probability is defined by the following function (Hoertel et al. 2020):

\[P_{S_{i}} = c_{r}\frac{C_{S_{i}}}{\mathbf{A} }\]

\[(1)\]

where c_r is the contamination risk, and \(C_{S_{i}}\) is the total time (in minutes) during which the \(S_{i}\) agent stays in the area of an infected one.

On the other hand, the pathogen’s spread by aerosol is computed from the quanta concentration in each room. A quanta is defined as the dose of airborne droplet nuclei required to cause infection in 63% of susceptible people (Buonanno et al. 2020). Therefore, based on (Gkantonas et al. 2021), we counted the number of quanta inhaled in a specific room (e.g., classrooms, bathrooms, etc.) by each agent to obtain the probability of being infected without directly entering in contact with an infected agent, which is defined by the following function:

\[P_{S_i} = 1 - e^{- \dfrac{N_{\text{virus}}}{k_p}}\]

\[(2)\]

where \(k_p\) represents the reciprocal of the probability that a single pathogen will initiate the response (Gkantonas et al. 2021; Watanabe et al. 2010), and \(N_{virus}\) is the quantity of inhaled quanta by each susceptible agent in a time interval \(\Delta t\). Its value is described by solving in \(\Delta t\) the differential equation 3:

\[ d N_{virus} = (1 - \eta_{mask}f_{\text{mask}})\ C(t)Q_{inh}\ dt\]

\[(3)\]

where \(\eta_{mask}\) is the masks efficacy, \(f_{mask}\) is the proportion of agents that wear correctly the mask, \(C(t)\) is the quanta concentration at time \(t\) and \(Q_{inh}\) is the inhalation rate. Note that quanta concentration at time \(t\) mainly depends on the number of people within a room, the number of infections and the room’s ventilation.

The third model component is related to NPIs. As suggested from Equation 3, the modeled NPIs are: distancing requirements, masks and increasing rooms’ air ventilation. In particular, we assumed in all the experiments that masks are used correctly for all school time (i.e. \(f_{mask}=1\)), and a ventilation process to replace contaminated with clean air is carried out constantly at a constant pace of 3 Air Changes per Hour (ACH). This airflow is maintained by keeping the door and windows of a classroom open (without ventilation systems), to reduce quanta concentrations in classrooms.

Various strategies for screening tests were considered in the model to control COVID-19 spread in the school by providing early detection of infected students. Moreover, we evaluated how different levels of efficacy in teachers’ vaccination (e.g., due to the spread of different variants) could impact COVID-19 spread in the school. Indeed, teachers in various classrooms might be important vectors of diffusion between classrooms, playing the role of shortcuts as in Watts-Strogatz’s model of random graphs (Watts & Strogatz 1998).

Verification and validation

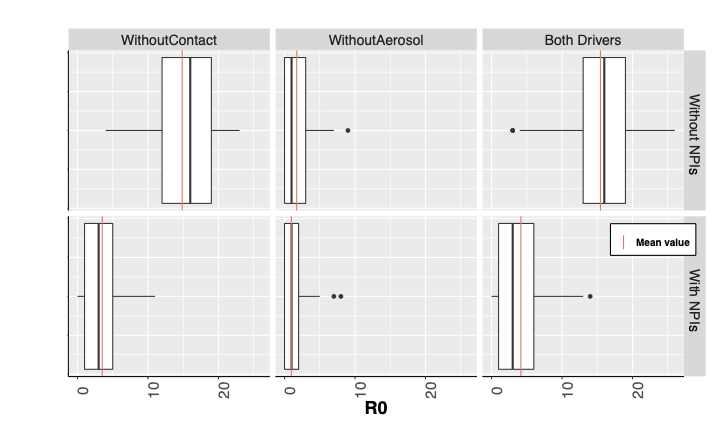
Model validation and verification are two essential steps to make a model suitable to support high-consequence decision-making. The former aims to evaluate how the model accurately represents the typical behaviour of the system under study. To validate the logic describing the complex phenomena represented in the model, we analysed our model under extreme parameter configuration. For instance, we found that if no infected agents were initially introduced into the system, then no outbreak would ever occur. In the second step, the model verification, we ensured that the parameters fed into the model would produce the expected outcomes. For instance, we verified that the average exposition time and infection time obtained by our model agreed with the literature, see Table 2. Different scenarios considering only one of the two virus infection drivers (via contact or aerosol) were performed to identify the primary infection driver in the model. In accordance with the information released by the World Health Organization (WTO), we observed that aerosol transmission is the primary infection driver. The first two boxplots in the first row of Figure 4 report the \(R_0\) variability over 200 simulation traces for the two drivers, clearly showing the greater strength of aerosol transmission compared to the transmission due to direct contacts.

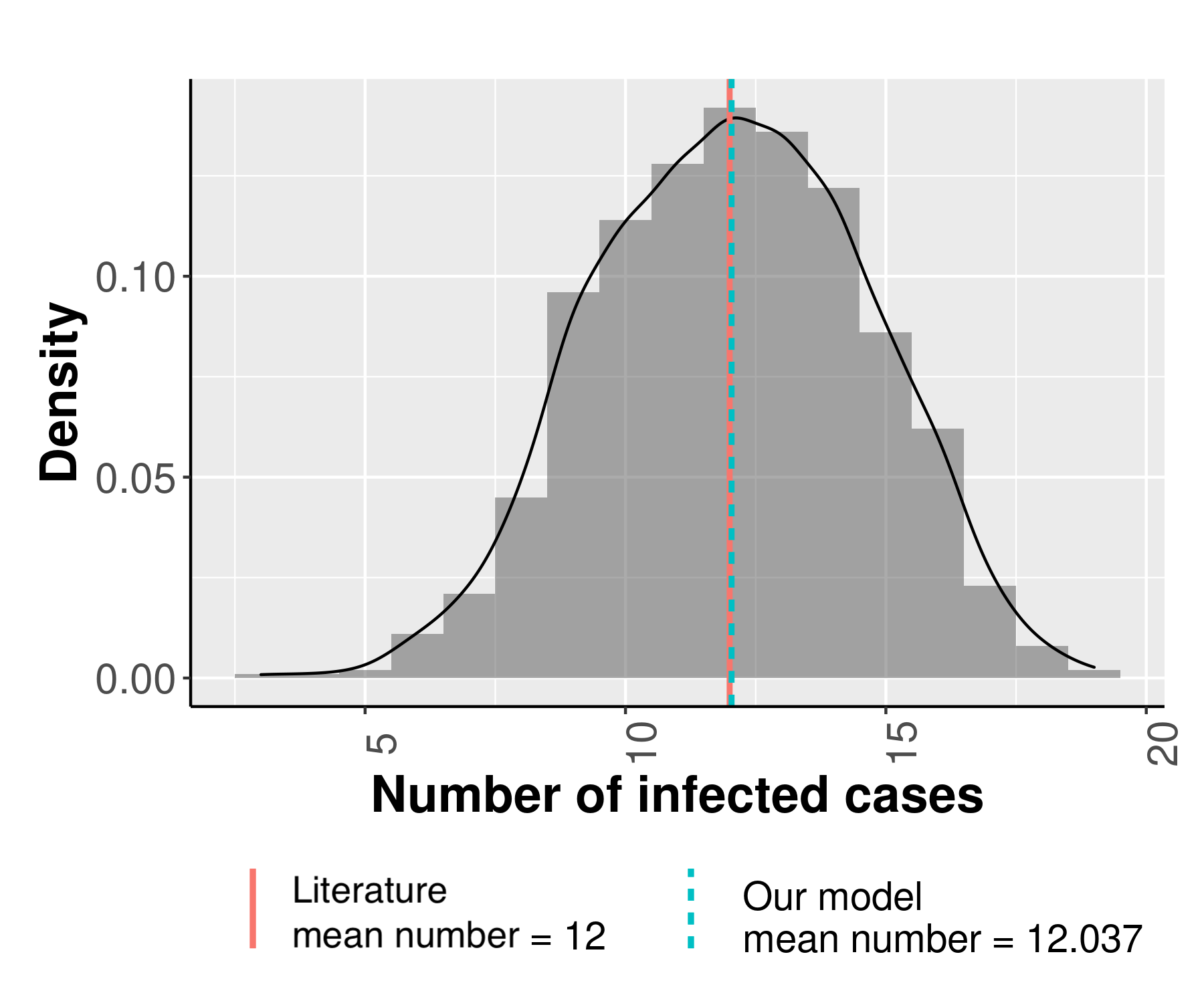
However, during the model validation phase, we measured the predictive accuracy of our model comparing its outcomes with empirical data and results already reported in the literature. First, we validated the aerosol transmission in our model compared to that proposed in Gkantonas et al. (2021) reproducing the same settings in our ABM. Indeed, Figure 3 compares the number of infected individuals after two hours lessons in a room with 20 participants and with only the teacher being infected obtained by our model compared to that reported by Gkantonas et al. (2021). More specifically, the red line and histogram represent the mean and empirical distribution of such a measure derived by 1000 simulation traces of our model, while the dashed blue line represents the mean computed in Gkantonas et al. (2021). From this, it is clear that the two measures strongly agreed. Secondly, to evaluate the overall infection process, we decided to verify the accuracy of the basic reproduction number \(R_0\) estimated by our model. Unfortunately, to the best of our knowledge, we did not find any other work studying R\(_0\) in a similar context, therefore we decided to compare our results with those proposed in Rocklöv et al. (2020) and Lai et al. (2021), in which the basic \(R_0\) is estimated considering the data generated by the COVID-19 outbreak in Diamond Princess Cruise Ship. Of course, the environment and age of the populations in these two works are quite different, although we believe that similar remarks on \(R_0\) values could be applied in our model. Specifically, both these works strongly suggest the \(R_0\) of this disease in the enclosed areas should be higher compared with that estimated by the WHO ranging from 2 to 3. Indeed, both works report that an \(R_0\) between 2 and 3 would not be able to account for the soaring number of infection cases reported in the short period of the Diamond Princess Cruise Ship. Thus, these works using different modelling approaches estimated greater \(R_0\) values (i.e., ranging from 4 to 7 in Lai et al. (2021) and 15 in Rocklöv et al. (2020)) justified by the fact that people in tightly enclosed environments can easier gather and enter into contact. The \(R_0\) values obtained by our model for different scenarios are showed in Figure 4. The three boxplots in the first row report the \(R_0\) variability over 200 simulation traces considering the following three different scenarios: (i) Without Contact, the close-range contacts are not considered and NPIs measures are not used, (ii) Without Aerosol, the infection via aerosol is not considered and NPIs measures are not used, and (iii) Both Drivers, both the drivers are considered and NPIs measures are not used. These results wholly agree with the consideration proposed in Rocklöv et al. (2020) and Lai et al. (2021). For instance, the Both Drivers scenario is characterized by a mean \(R_0\) around 15.

Experiment Design

The results presented here consider the spread of COVID-19 infections in a school and aim to evaluate the effectiveness of NPIs in this environment. To achieve this, we analyzed 21 different scenarios obtained as reported in Table 1 by considering or not the use of face masks and room ventilation, and varying the screening policy, the number of participants to the screening and the vaccination effectiveness for the teachers. Specifically, we considered the following three screening test strategies:

• Policy \(A1\): to test on all participants every week;
• Policy \(D1\): to test on 1/4 of the participant in each class every week, on a rotating basis (i.e., all students enrolled in the screening would be tested over a month);
• Policy \(D2\): to test on 1/4 of the participant in each class every week, on a rotating basis, divided into two weekly days.

We should note that, to make these screening strategies independent of the starting day, we considered the average values obtained by repeating the simulations varying the starting day of the strategy (Monday, Tuesday, etc).
For each strategy, we evaluated their impact varying the number of participants at the screening test from 100% to 25%, and two different efficacy levels in teacher vaccination: i) the vaccine is completely effective, and ii) the vaccine is effective only in 75% of cases. We also assumed that all people who enter into the school wear face masks in all scenarios, except the first one. This design choice was twofold: it allowed us to model a more realistic scenario and mitigated the effect of the screening campaign. Furthermore, we considered only asymptomatic infections that could be detected by screening tests.

Finally, all our results were computed on high performance computing infrastructures described in Aldinucci et al. (2017, 2018), and all the model parameters are summarized in Table 2. Furthermore, the time in the simulation experiments was discrete and each tick corresponds to one minute. Detail on the model code and documentation is included in Section Model Documentation.

Table 1: Summary of the scenarios simulated.

				Screening Policy			Screening participants			Vaccination Effectiveness
	Mask	Ventilation	None	A1	D1	D2	25%	50%	100%	75%	100%
1			x								x
2	x	x	x								x
3	x	x		x			x				x
4	x	x		x				x			x
5	x	x		x					x		x
6	x	x			x		x				x
7	x	x			x			x			x
8	x	x			x				x		x
9	x	x				x	x				x
10	x	x				x		x			x
11	x	x				x			x		x
12	x	x	x							x
13	x	x		x			x			x
14	x	x		x				x		x
15	x	x		x					x	x
16	x	x			x		x			x
17	x	x			x			x		x
18	x	x			x				x	x
19	x	x				x	x			x
20	x	x				x		x		x
21	x	x				x			x	x

Table 2: Model parameters

Parameter	Value	Reference
Number of classrooms	12	Assumed
Students per classroom	20	Assumed
Number of initial infected (students)	1	Assumed
Vaccine efficacy	100/75%	Assumed
Average number of days of incubation	3	(Zaki & Mohamed 2021), (World Health Organization 2020)
Average number of days of infection	7	(Byrne et al. 2020)
Duration of quarantine in days	14	(Regione Piemonte 2020)
Ventilation	3 ACH	Assumed
Mask type	Surgical	Assumed
Screening adhesion	0/25/50/100%	Assumed
Screening policy	W0/A1/D1/D2	(Baccini & Cereda 2021)
Fraction of population wearing mask	100%	Assumed
Distance learning	0%	Assumed
Probability of going to the bathroom (per minute)	8e-4	Assumed
Probability of going to the blackboard (per minute)	6e-4	Assumed
Probability of going to the principal office (per minute)	1.4e-4	Assumed
Probability of going into the hall during interval	0.532	Assumed
Contamination risk (cr)	0.024	(Hoertel et al. 2020)
Duration of the lessons in minutes	50	Assumed
Simulated days for each run	35	Assumed
Number of runs for each experiment	1000	Assumed

Results

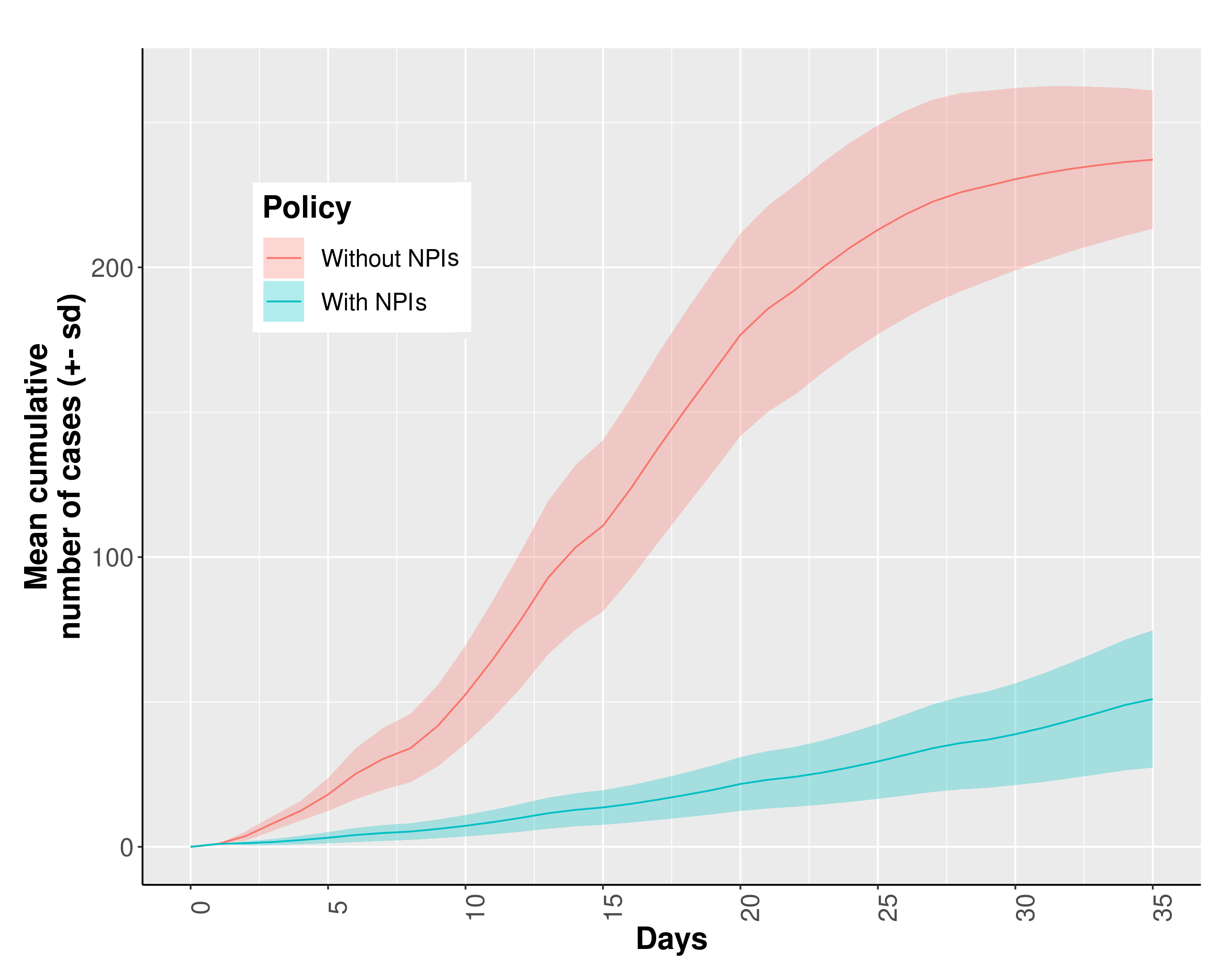
In the first experiment, we studied how the use of two NPIs, i.e., facemasks and room ventilation, can mitigate the spread of infection in a school. Figure 5 shows day by day the cumulative number of infected students both when face-masks and ventilation of the rooms are not considered (i.e., red line) and when they are taken into account (i.e., blue line). The higher number of infected students when these two interventions are not implemented is clearly evident. Indeed, after 35 days, most of the students (i.e., 237 out of a total of 240) were exposed. On the other hand, the use of these two NPIs allowed the average cumulative number of infected students to decrease from 237 to 50 cases. Moreover, in the third column of Figure 4 the R\(_0\) variability obtained by simulations with and without these two interventions is plotted. The use of face-masks and ventilation reduced the average \(R_0\) from 15 to 4. Thus, these results highlighted that these two NPIs are a mandatory requirement to slow infection, allowing screening campaigns to be effective.

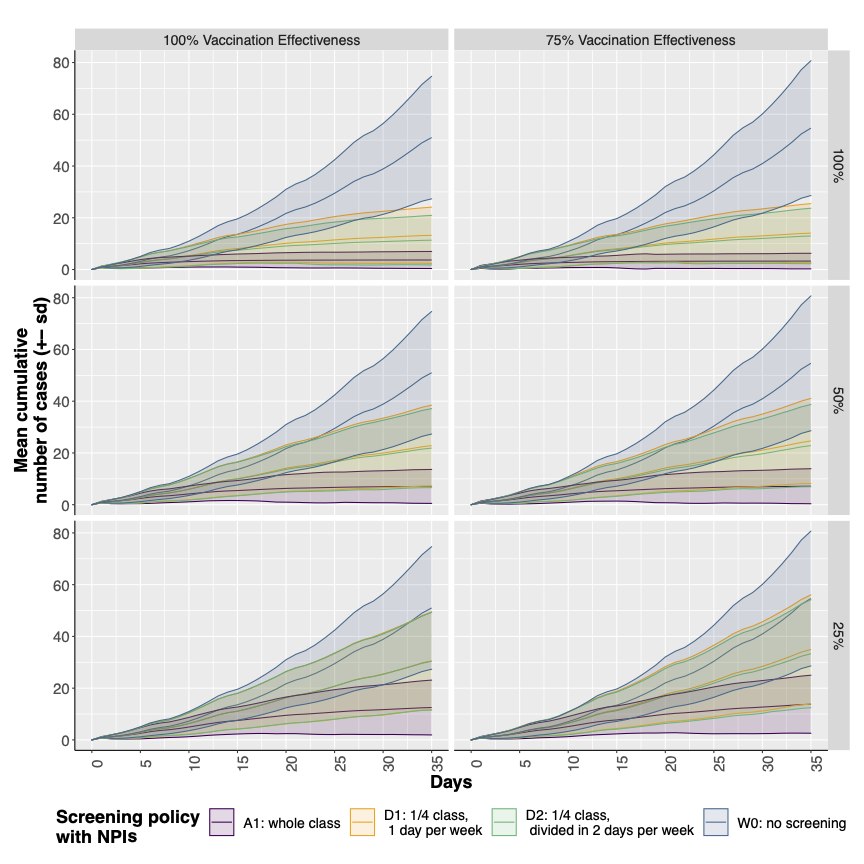
We then considered the use of face masks and ventilation of rooms as a baseline scenario (i.e., namely \(W0\)), in which a third NPI representing a screening campaign is introduced. Figure 6 compares our baseline scenario with different scenarios in which the three screening policies described in the previous section are implemented (i.e., \(A1\), \(D1\) and \(D2\)) varying the number of participants to the screening campaign in rows and the vaccination efficacy in columns.

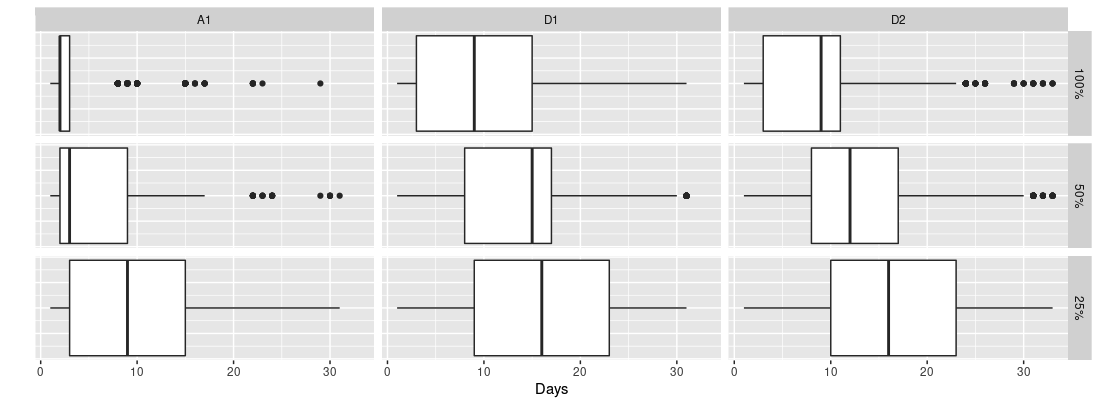
Focusing on scenarios with all students involved in the screening campaign (i.e., \(100\%\)) and 100% vaccination effectiveness, i.e., the first plot on the left, it is clear that all screening policies reduced the incidence of infection in the population compared with \(W0\). Furthermore, although \(D1\) policy performed worst, it still halved the cumulative number of infections at the end of the observation period. A slight improvement can be obtained by splitting the screening test performed in the \(D1\) policy on two different days of the week as in \(D2\) policy. This design choice allowed us to identify some infections earlier. Indeed, anticipating the discovery of infected pupils reduced the period in which their classmates were exposed, thus reducing their probability to be infected. Similar observations were made when the number of students taking part in the screening test was reduced (i.e. only 75% and 25% respectively) as shown in Figure 6, the first column and second and third rows. In particular, these results highlighted that even with a very limited number of tests, it was possible to control the spread of the infection. For instance, in the case of student participation of 25% the policy \(D1\), testing only five students for a week, can halve the total number of infected students w.r.t. \(W0\). Moreover, Figure 7 shows the distribution of the average number of days needed to detect an infected student for the different screening policies and varying the number of participants to the screening policies. From the results showed, we can state clearly that policy \(A1\) had the lowest total number of infected individuals.

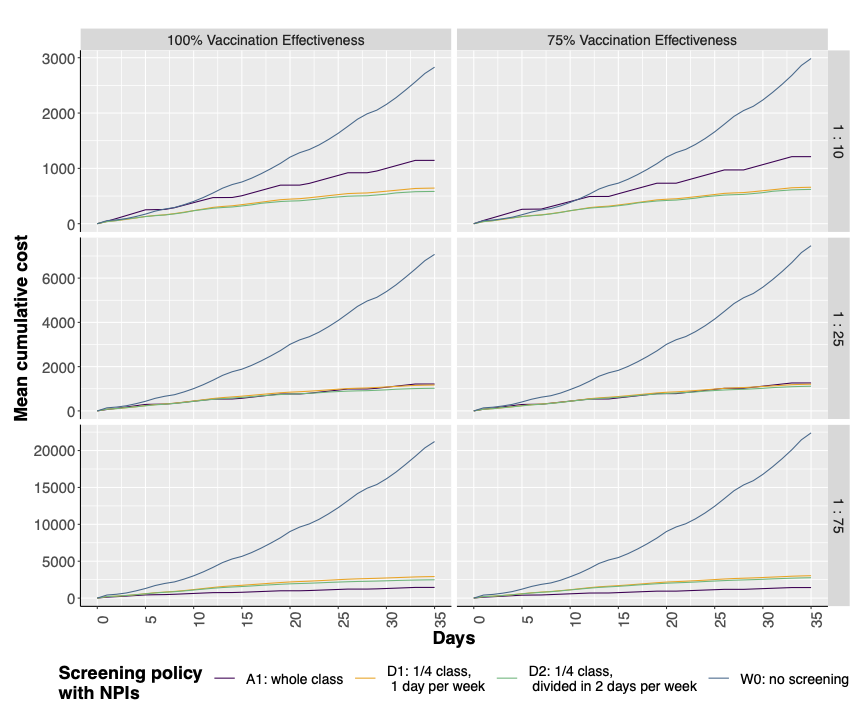
However, for policy-makers, the number of infected individuals is only one of many aspects to be considered when they make a decision. We therefore carried out a cost-benefit analysis defining a function that took into account the costs of new infections and overall costs (monetary and psychological) of performing swabs as follows:

\[\chi\left(t\right) = k_1 \tau n_i(t) + k_2 n_s(t), \]

\[(4)\]

where \(k_1\) and \(k_2\) are constants, \(\tau\) is the meantime necessary to unveil a new infected individual, and \(n_i(t)\), \(n_s(t)\) are the number of infected cases at time \(t\) and the number of students under screening at time \(t\) respectively. Thus, this cost function measures the performance of a particular screening policy in terms of the meantime of identification \(\tau\), the number of infected cases and the number of swabs. Figure 8 reports the assessment of this cost function varying the \(k_2:k_1\) ratio for each considered screening policy and the efficacy levels in teachers’ vaccination. More specifically, from upper to bottom the \(k_2:k_1\) ratio decreases, thus increasing the costs of new infections, while from left to right efficacy in the teachers’ vaccination is reduced by 25%.

It is interesting to note that independently of the level of efficacy in teacher’s vaccination, when the ratio between the two costs \(k_2\) and \(k_1\) is greater than \(\frac{1}{25}\) (i.e., the leftmost plot) the policies with a smaller number of swabs are more profitable compared to \(A1\) policy. Differently, when this ratio is smaller than \(\frac{1}{25}\), as the impact of new infections increases, \(A1\) becomes the most effective.

Discussion

In this study, we evaluated the impact of various NPI policies for reducing COVID-19 infections in the school environment using an ABM approach. Overall, we observed that the combination of different NPIs can drastically reduce the virus transmission in the school environment after the introduction of an infected case. Our model showed that, in the absence of containment measures, the introduction of a single infective case can lead to the infection of the majority of school students. However, the combination of mask wearing and room ventilation can drastically reduce, on average, viral transmission. In our simulation, after the introduction of one infected student, the use of these two NPIs decreased the cumulative number of infected students by 79% (from 237 to 50). We also tested the effect of three screening policies under different participation levels (25%, 50%, 100%). Our model suggests that screening can further reduce viral transmission through early identification and isolation of infective cases. In addition, we found that even with a low participation, screening can still have a non-negligible impact in terms of COVID-19 cases avoided.

One of the interesting features of the proposed model is that it considers students, teachers and the principal’s behaviour both in the classroom and in shared spaces, allowing the simulation of the whole school environment, rather than the infection dynamics of a single class. In addition, the model incorporates two different ways of viral transmission, namely direct viral transmission occurring through the close-range contacts and the viral quanta diffusion through aerosolization. Our findings are consistent with the literature. For instance, in the validation analysis, our model suggests that the viral transmission in the school environment is mainly due to the aerosolization of viral quanta as already suggested by other studies (Gkantonas et al. 2021). Furthermore, the estimated effects of mask-wearing and indoor ventilation is consistent with results found in other modelling studies (Chu et al. 2020).

Different screening plans in the school environment have been compared through a stochastic compartmental model by Baccini & Cereda (2021) and found that testing half of the class on rotation every week was better than testing all students every two weeks, allowing earlier detection of cases, especially when the rate of contagion in the class is high. Less expensive strategies, such as a weekly test of one-fourth of the students gave comparable results in terms of sensitivity. The latter is one of the strategies tested using our model. Mass testing and school screening have been criticized (McCartney 2020) by experts, mostly on the basis of insufficient test accuracy and the risk that the false reassurance of a negative test may lead to more risky behaviour than would have occurred without the test. However, screening campaigns similar to that modelled in this study have been adopted and implemented in the real world (Berke et al. 2021; Volpp et al. 2021). In North-West Italy, a regional screening programme targeting second and third grade students in first level secondary schools and based on voluntary participation was implemented in the first quarter of 2021 (Farina et al. 2021). In the study period, the cumulative incidence in schools participating in the program was nearly 4 times lower than that in non-participating schools. Models such as the one proposed here may provide insight into under which circumstances school screenings can result in less quarantined classes and a lower loss of school days.

The main strength of our model lies in its flexibility and ability to investigate the spread of infection and the efficacy of its containment under different epidemiological scenarios and control strategies. In the current model, we did not take into account vaccination coverage among school students because until the end of 2021 a large part of the pediatric population (subjects < 12 years of age) had not been targeted by the vaccination campaign, and even when it is launched, vaccine hesitancy of children’s parents may result in a high proportion of unvaccinated children. Far from being a limitation, the effects of different vaccination coverage proportions could be easily explored using this model. Similarly, the model could be extended to explore varying initial conditions, such as a set of schools varying in current disease prevalence in the community, and so with a changing probability of the introduction of one or more infectious agents at any given time. Furthermore, extending the model beyond school activities by including additional elements describing the external environment, would allow us to investigate the reciprocal influence of different social activities. For instance, studying the correlation between the prevalence of the infection at school and its spread within students’ families would be seminal for many other considerations, such as the connection between student illness to parental employment. A further interesting correlation that could be investigated is between the neighbourhood where students live and the school they attend. Such a correlation certainly has had an impact on the spread of the disease in any given geographical area. However, the focus of this work was to investigate the effect of containment measures and actions that can be performed by schools to control internal spread. A broader investigation would require introducing several aspects that could describe interactions among agents outside the school, which is outside our research scope. Approaching more complex yet more realistic scenarios, the cost-benefit analysis proposed in this paper could provide extremely useful information about the feasibility and impact of different screening policies.

Conclusion

The significance of risk reduction through the policies assessed here is of potential relevance for public health authorities and school administrators both at a local and national level. Implementation of standard preventive measures such as mask-wearing and environmental ventilation should be considered necessary in phases of low viral circulation. Active preventive measures such as screening campaigns can be seen as additional measures to be implemented to reduce the viral transmission in the school environment during high viral circulation period to avoid massive school closures.

References

ALDINUCCI, M., Bagnasco, S., Lusso, S., Pasteris, P., Rabellino, S., & Vallero, S. (2017). OCCAM: A flexible, multi-purpose and extendable HPC cluster. Journal of Physics: Conference Series, 898(8), 082039. [doi:10.1088/1742-6596/898/8/082039]

ALDINUCCI, M., Rabellino, S., Pironti, M., Spiga, F., Viviani, P., Drocco, M., Guerzoni, M., Boella, G., Mellia, M., Margara, P., Drago, I. and, Marturano, R., Marchetto, G., Piccolo, E., Bagnasco, S., Lusso, S., Vallero, S., Attardi, G., Barchiesi, A., … Galeazzi, F. (2018). HPC4AI: An AI-on-demand federated platform endeavour. Proceedings of the 15th ACM International Conference on Computing Frontiers. [doi:10.1145/3203217.3205340]

BACCINI, M., & Cereda, G. (2021). Screening plans for SARS-CoV-2 based on sampling and rotation: An example in the school setting. PLoS ONE, 16(9), e0257099. [doi:10.1371/journal.pone.0257099]

BERKE, E. M., Newman, L. M., Jemsby, S., Bhalla, N., Sheils, N. E., Oomman, N., Reppas, J., Hyde, B., Verma, P., & Cangelosi, G. A. (2021). Pooling-in-a-pod: A strategy for COVID-19 testing to facilitate safe return to school. Public Health Reports, 136(6), 2021. [doi:10.1177/00333549211045816]

BUONANNO, G., Stabile, L., & Morawska, L. (2020). Estimation of airborne viral emission: Quanta emission rate of SARS-CoV-2 for infection risk assessment. Environment International, 141, 105794. [doi:10.1016/j.envint.2020.105794]

BYRNE, A. W., McEvoy, D., Collins, A. B., Hunt, K., Casey, M., Barber, A., Butler, F., Griffin, J., Lane, E. A., McAloon, C., O’Brien, K., Wall, P., Walsh, K. A., & More, S. J. (2020). Inferred duration of infectious period of SARS-CoV-2: Rapid scoping review and analysis of available evidence for asymptomatic and symptomatic COVID-19 cases. BMJ Open, 10(8). [doi:10.1101/2020.04.25.20079889]

CHU, D. K., Akl, E. A., Duda, S., Solo, K., Yaacoub, S., Schünemann, H. J., El-harakeh, A., Bognanni, A., Lotfi, T., Loeb, M., & COVID-19 Systematic Urgent Review Group Effort (SURGE) study authors. (2020). Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: A systematic review and meta-analysis. The Lancet, 395(10242), 1973–1987. [doi:10.1016/j.jvs.2020.07.040]

COMAR, M., Benvenuto, S., Lazzerini, M., Fedele, G., Barbi, E., Amaddeo, A., Risso, F. M., Strajn, T., Di Rocco, P., Stefanelli, P., & Rezza, G. (2021). Prevalence of SARS-CoV-2 infection in Italian pediatric population: A regional seroepidemiological study. Italian Journal of Pediatrics, 47(1), 1–6. [doi:10.1186/s13052-021-01074-9]

ECDC, European Center for Disease Prevention and Control. (2020). COVID-19 in children and the role of school settings in COVID-19 transmission.

ECDC, European Center for Disease Prevention and Control. (2021). COVID-19 in children and the role of school settings in transmission - Second update. Available at: https://www.ecdc.europa.eu/en/publications-data/children-and-school-settings-covid-19-transmission.

FARINA, E., Eboli, I., Spadea, T., Saugo, C., Richiardi, L., Maule, M., Presti, P., & Bena, A. (2021). ’Scuola sicura’: A school screening testing programme to prevent the spread of COVID-19 in students in Piedmont. Epidemiologia E Prevenzione, 45. [doi:10.21203/rs.3.rs-864946/v1]

GKANTONAS, S., Zabotti, D., Mesquita, L. C., Mastorakos, E., & de Oliveira, P. M. (2021). airborne.cam: A risk calculator of SARS-CoV-2 aerosol transmission under well-mixed ventilation conditions. Available at: https://airborne.cam.

HOERTEL, N., Blachier, M., Blanco, C., Olfson, M., Massetti, M., Rico, M. S., Limosin, F., & Leleu, H. (2020). A stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nature Medicine, 26(9), 1417–1421. [doi:10.1038/s41591-020-1001-6]

IM Kampe, E. O., Lehfeld, A.-S., Buda, S., Buchholz, U., & Haas, W. (2020). Surveillance of COVID-19 school outbreaks, Germany, March to August 2020. Eurosurveillance, 25(38), 2001645.

LAI, C.-C., Hsu, C.-Y., Jen, H.-H., Yen, A. M.-F., Chan, C.-C., & Chen, H.-H. (2021). The Bayesian Susceptible-Exposed-Infected-Recovered model for the outbreak of COVID-19 on the Diamond Princess Cruise Ship. Stochastic Environmental Research and Risk Assessment, 35(7), 1–15. [doi:10.1007/s00477-020-01968-w]

LORIG, F., Johansson, E., & Davidsson, P. (2021). Agent-based social simulation of the Covid-19 pandemic: A systematic review. Journal of Artificial Societies and Social Simulation, 24(3), 5: https://www.jasss.org/24/3/5.html. [doi:10.18564/jasss.4601]

LUDVIGSSON, J. F. (2020). Children are unlikely to be the main drivers of the COVID-19 pandemic - A systematic review. Acta Paediatrica, 109(8), 1525–1530. [doi:10.1111/apa.15371]

MAANI, N. (2020). The true costs of the COVID-19 pandemic. Available at: https://blogs.scientificamerican.com/observations/the-true-costs-of-the-covid-19-pandemic/.

MCCARTNEY, M. (2020). Christmas covid-19 testing for students needs independent oversight. Available at: https://blogs.bmj.com/bmj/2020/12/01/margaret-mccartney-christmas-covid-19-testing-for-students-needs-independent-oversight/. [doi:10.1136/bmj.h6655]

PANOVSKA-GRIFFITHS, J., Kerr, C. C., Stuart, R. M., Mistry, D., Klein, D. J., Viner, R. M., & Bonell, C. (2020). Determining the optimal strategy for reopening schools, the impact of test and trace interventions, and the risk of occurrence of a second COVID-19 epidemic wave in the UK: A modelling study. The Lancet Child & Adolescent Health, 4(11), 817–827. [doi:10.1016/s2352-4642(20)30250-9]

PERNICE, S., Castagno, P., Marcotulli, L., Maule, M. M., Richiardi, L., Moirano, G., Sereno, M., Cordero, F., & Beccuti, M. (2020). Impacts of reopening strategies for COVID-19 epidemic: A modeling study in Piedmont region. BMC Infectious Diseases, 20(1), 798. [doi:10.1186/s12879-020-05490-w]

PHILLIPS, B., Browne, D. T., Anand, M., & Bauch, C. T. (2021). Model-based projections for COVID-19 outbreak size and student-days lost to closure in Ontario childcare centres and primary schools. Scientific Reports, 11(1), 1–14. [doi:10.1038/s41598-021-85302-6]

REGIONE Piemonte. (2020). Coronavirus e scuola, le indicazioni. Available at: https://www.regione.piemonte.it/web/temi/coronavirus-piemonte/coronavirus-scuola-indicazioni.

RILEY, S., Wang, H., Eales, O., Haw, D., Walters, C. E., Ainslie, K. E. C., Atchison, C., Fronterre, C., Diggle, P. J., Page, A. J., Prosolek, S. J., Trotter, A. J., Le Viet, T., Alikhan, N.-F., Jackson, L. M., Ludden, C., Consortium, T. C.-1. G. U. (COG-UK), Ashby, D., Donnelly, C. A., … Elliott, P. (2021). REACT-1 round 12 report: Resurgence of SARS-CoV-2 infections in England associated with increased frequency of the Delta variant. [doi:10.1101/2021.06.17.21259103]

ROCKLÖV, J., Sjödin, H., & Wilder-Smith, A. (2020). COVID-19 outbreak on the Diamond Princess cruise ship: Estimating the epidemic potential and effectiveness of public health countermeasures. Journal of Travel Medicine, 27(3), taaa030.

STEIN-ZAMIR, C., Abramson, N., Shoob, H., Libal, E., Bitan, M., Cardash, T., Cayam, R., & Miskin, I. (2020). A large COVID-19 outbreak in a high school 10 days after schools’ reopening, Israel, May 2020. Eurosurveillance, 25(29), 2001352. [doi:10.2807/1560-7917.es.2020.25.29.2001352]

VOLPP, K. G., Kraut, B. H., Ghosh, S., & Neatherlin, J. (2021). Minimal SARS-CoV-2 transmission after implementation of a comprehensive mitigation strategy at a school — New Jersey, August 20-November 27, 2020. Morbidity and Mortality Weekly Report, 70(11), 377. [doi:10.15585/mmwr.mm7011a2]

WATANABE, T., Bartrand, T. A., Weir, M. H., Omura, T., & Haas, C. N. (2010). Development of a dose-response model for SARS coronavirus. Risk Analysis: An International Journal, 30(7), 1129–1138. [doi:10.1111/j.1539-6924.2010.01427.x]

WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of small-world networks. Nature, 393(6684), 440–442. [doi:10.1038/30918]

WILENSKY, U. (1999). NetLogo. Center for connected learning and computer-based modeling, Northwestern University, Evanston, IL. Available at: http://ccl.northwestern.edu/netlogo/.

WORLD Health Organization. (2020). Coronavirus disease 2019 (COVID-19): Situation report, 73. Available at: https://www.who.int/publications/m/item/situation-report---73.

ZAKI, N., & Mohamed, E. A. (2021). The estimations of the COVID-19 incubation period: A scoping reviews of the literature. Journal of Infection and Public Health, 14(5), 638–646. [doi:10.1016/j.jiph.2021.01.019]