Confirmation Bias as a Mechanism to Focus Attention Enhances Signal Detection

,
and
University of Graz, Austria
Journal of Artificial
Societies and Social Simulation 26 (1) 2
<https://www.jasss.org/26/1/2.html>
DOI: 10.18564/jasss.4954
Received: 12-May-2022 Accepted: 13-Nov-2022 Published: 31-Jan-2023
Abstract
Confirmation bias has been traditionally seen as a detrimental aspect of the human mind, but recently researchers have also argued that it might be advantageous under certain circumstances. To test this idea, we developed a minimally complex agent-based model in which agents detect binary signals. Compared to unbiased agents, biased agents have a higher chance to detect the signal they are biased for, and a lower chance to detect other signals. Additionally, detecting signals is associated with benefits, while missing signals is associated with costs. Given this basic assumptions, biased agents perform better than unbiased agents in a wide variety of possible scenarios. Thus, we can show that confirmation bias increases the fitness of agents in an evolutionary algorithm. We conclude that confirmation bias sensitizes agents towards a certain type of data, which allows them to detect more signals. We discuss our findings in relation to topics such as polarization of opinions, the persistence of first impressions, and the social theory of reasoning.Introduction
Background
Humans have a tendency to prefer information that confirms their presupposed ideas, theories, or opinions, and to interpret ambiguous information in a way that is supportive of their already existing beliefs. This tendency can be the cause for an increased attentiveness towards such information (Jonas et al. 2001) and can also result in a better memory for supportive information (Frost et al. 2015). Such behaviors are manifestations of a phenomenon called “Confirmation Bias”, which comes in many different forms (Nickerson 1998) and by many different names such as “confirmatory bias” (Mahoney 1977) or “myside bias” (Hugo Mercier 2016). Furthermore, information that contradicts people’s beliefs is more likely to be ignored, scrutinized or neglected (Kappes et al. 2020; Lord et al. 1979).
Historically, the principle of confirmation bias was already described in the 17th century by Francis Bacon (Bacon 1620), and had a mostly negative connotation. In fact, confirmation bias can be a hindrance in the pursuit of truth, as it was elegantly demonstrated in Wason’s experiments on the determination of rules (Wason 1960). It was observed that participants primarily try to confirm a certain rule they had in mind, instead of trying to rule out (i.e., falsify) alternatives (Wason 1968). Therefore, confirmation bias does not only interfere with the process of hypothesis forming, but also with hypothesis testing.
Nickerson points out that - from a scientific perspective - confirmation bias has a problematic property: “People sometimes see in data the patterns for which they are looking, regardless of whether the patterns are really there” (Nickerson 1998, p. 181). Ergo, bias in the selection of data can transform the process of data mining into a task of “data minding”. Because of this, confirmation bias is usually seen as an obstacle that needs to be overcome by the scientific method (Schumm 2021) or with the aid of computer programs (Silverman 1992). Among others, forensic science is a field that is especially concerned about confirmation bias (to name just a few examples, Cole 2013; Kassin et al. 2013; Kukucka et al. 2020; O’Brien 2009; Perez Peña 2014).
Despite all this, recent research interest also grew around the counter-intuitive idea that confirmation bias could be advantageous (Austerweil & Griffiths 2011; Dardenne & Leyens 1995; Mercier & Sperber 2011; Rollwage & Fleming 2021). Tversky & Kahneman (1974) showed that individual bias engenders both costs and benefits and are associated with certain advantages in problem solving under uncertainty. Specifically, people do their best to focus on the representativeness of inputs, context, and good reference points. Some authors even argue for an evolutionary explanation of the confirmation bias (Dardenne & Leyens 1995; Mercier & Sperber 2011; Peters 2020; Rollwage & Fleming 2021). On an individual level, confirmation bias may help to frame life situations and lets us connect them with past experiences. On the other side, collective problem solving has further properties not reducible to the individual case. When solving complex problems that go beyond the capacity of a single individual, such as political or societal decisions, the integration of the input of individuals with cognitive bias may lead to better solutions (Krause et al. 2010). On a population level, it may help to establish a cognitive division of labor, so that the cognitive resources of a group can be used to investigate a higher number of possible solutions (Sperber et al. 2010).
Motivation
Our Motivation stems from the fact that confirmation bias seems to be detrimental, yet is ubiquitous. As Nickerson put it, it is the case that “If one were to attempt to identify a single problematic aspect of human reasoning that deserves attention above all others, the confirmation bias would have to be among the candidates for consideration” (Nickerson 1998, p. 175). And indeed, researchers were able to show why and in which way confirmation bias is problematic. However, given the ubiquitous nature of this bias, a question arises: how has this “problematic aspect” evolved and how does it still persist in the human mind? This intriguing question was the main research target of this study.
There are some studies that show beneficial aspects of confirmation bias (Austerweil & Griffiths 2011; Dardenne & Leyens 1995; Mercier & Sperber 2011; Rollwage & Fleming 2021) and implicitly argue that the potential benefits of confirmation bias could outweigh the costs. Such narratives are certainly compelling and come with plausible explanations. Despite this, it often remains unclear how exactly confirmation bias can be beneficial in concrete scenarios. Computational models are useful to simulate such scenarios, and some work in this direction has been done.
The already existing literature on computational models addressing confirmation bias shows a notable gap between highly abstract models (Pouget & Villeneuve 2012), and models that target very specific topics such as the financial market (Cafferata & Tramontana 2019), attitudes related to climate change policies (Cafferata et al. 2021), or cyber-social networks (Mao et al. 2020). Usually, abstract models implement very idealized agents and cannot encapsulate all aspects of specific scenarios, which are the subject of the latter models. The specific and more detailed models however, cannot be generalized well beyond their original scope. Only few works reside within this gap, such as models that aim at having realistic agents acting in an abstract scenario, namely the prisoner’s dilemma (Pericherla et al. 2018). One motivation of this paper is therefore to contribute to further closing this gap by developing and analyzing an abstract model that is sufficiently extendable and adaptable to answer specific questions.
The purpose of this study is twofold. First, we are interested if confirmation bias can improve performance in a simple signal detection task. Theoretically, confirmation bias may enhance the detection rate of confirmatory signals at the cost of all other signals. It is important to explore this trade off scenario and evaluate in which, if any, scenarios it is beneficial for individual agents. We chose a simple signal detection task, as it is fundamental for humans (and almost all other organisms) to use information obtained from the environment in order to inform decisions. If confirmation bias decreases performance on such an elementary and important task, we would obtain indication for it being indeed a “problematic” aspect of the human mind.
A second motivation is to study if the ability to form a strong confirmation bias could develop incrementally in an agent population. If confirmation bias has beneficial effects for agents, and can develop gradually in the population, then that would be indication that the ability to form such a bias may be an evolved feature, and could perhaps even be described as adaptive (Dardenne & Leyens 1995; Rollwage & Fleming 2021).
Methodology
What the model represents
The model aims at simulating minimally complex scenarios in which confirmation bias is relevant. For this, we assume that there are two different signals in the world: A-signals and B-signals. We further make the trivial assumption that detecting signals is better than missing signals. We integrate empirical findings such as that confirmation bias leads to selective attention towards one type of signal (Frost et al. 2015; Jonas et al. 2001; Talluri et al. 2018) at the cost of lowering attention for the other type (Koivisto et al. 2004). We suggest that such a paradigm is representative for relevant problems of humans and other animals, which is why it is the core of our model. As an example, we consider a scenario in which humans avoid anacondas while foraging for berries. Assumably, anacondas (A) can be spotted by paying attention to certain signals: the sounds they make, the tracks they leave behind, or even their bodies that can be seen (A-signals). Similarly, berries (B) have signals that can be detected by attentive foragers, such as a fragrant smell or their color (B-signals). Detecting or missing these signals is associated with benefits and costs, example values are shown in Table 1.
| Event | Detected or Missed? | Consequence | Influence on \(\Omega\) |
|---|---|---|---|
| Anaconda | Detected | Warn allies, get respect | Benefit (+2) |
| Anaconda | Missed | Get attacked, others need to help | Cost (-10) |
| Berry | Detected | Forage berry, gain energy | Benefit (+1) |
| Berry | Missed | Opportunity missed, lost energy while searching | Cost (-1) |
The last relevant factor is the relative abundance of anacondas and berries (\(\alpha\)). In an area where there are no anacondas, it is not useful to devote cognitive resources to detecting them. However, when anacondas are common, the same behavior is a necessity for survival. When beginning to forage in a new area, agents may be unbiased: they pay equal attention to anacondas as to berries. After seeing an anaconda, they may be more inclined to think that this area is an “anaconda area” and focus less on detecting berries. In Figure 1 we show the first few steps of how such a scenario is computed in the model.
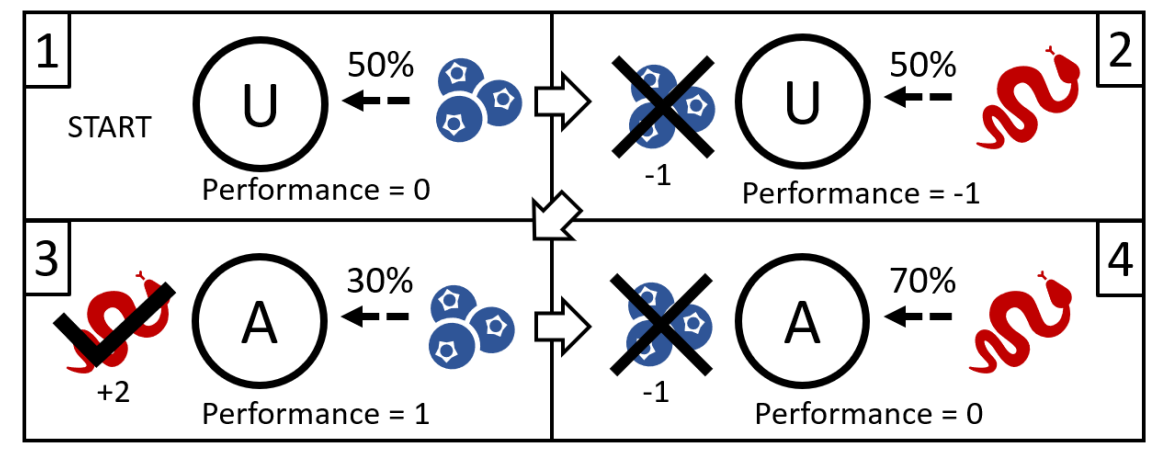
However, it could be the case that the rest of the area is very safe, and no anacondas are here. In this case, the foragers would be overly anxious about the anacondas and waste cognitive resources trying to detect them. This comes at the cost of being worse at detecting berries and returning with less food. This may be a small price to pay in this specific scenario, but there is an almost infinite number of scenarios with varying costs and benefits and various frequencies of relevant events. Thus, it is a challenging problem to answer our following research question: Is it generally useful or detrimental for agents to focus attention on the first type of signal they detect? Or with other words: Is confirmation bias advantageous in tasks such as the one that we describe?
Basic structure of the model
We created a non-spatial agent-based model in which, as opposed to a spatial model, space does not matter. Agents do neither move, nor have a position in space. This was done to keep the model as simple as possible, and because we are only interested in the perceptual mechanisms of the agents. They are confronted with a stream of signals, which they either detect or miss. Agents perceive this environment, but do not change or interact with it, and they neither perceive nor interact with other agents. At each step in the model, an event (a signal) is generated. This event is either event “A” or event “B”. In a given stream of \(nr\_events\) events, a proportion of \(\alpha\) signals are A, while all the other signals in the stream are B. The order in which the events appear is randomized, except in the experiment shown in Figure 7. Agents are minimally complex and, as shown in Table 2, have only three properties: 1) A base detection rate (\(\gamma\)) which influences how likely unbiased agents detect signals, 2) One out of three bias settings (bias), unbiased, bias toward A, or bias toward B, and 3) a bias strength (\(\beta\)), which determines how strongly the base detection rate (\(\gamma\)) gets modified.
| Parameter | Owner | Description | Values Tested |
|---|---|---|---|
| \(nr\_agents\) | World | Number of agents in the system | 1, 100 |
| \(nr\_events\) | World | Number of signals agents can perceive | 10, 30, 100 |
| \(\alpha\) | World | Proportion of signal A | 0, 0.1, 0.2... 1 |
| \(\beta\) | Agents | Determines strength of bias | 0, 0.1, 0.2... 1 |
| \(\gamma\) | Agents | Standard detection chance without bias | 0, 0.1, 0.2... 1 |
| \(Bias\) | Agents | Determines if and how agents are biased | U, A, B |
| \(cost_A\) | World | Cost of missing signal A | -1, -2, ...-10 |
| \(cost_B\) | World | Cost of missing signal B | -1, -2, ...-10 |
| \(benefit_A\) | World | Benefit of detecting signal A | 1, 2, ...10 |
| \(benefit_B\) | World | Benefit of detecting signal B | 1, 2, ...10 |
Agents are initially unbiased and perceive events happening in the environment. Each event can either be detected or missed by the agents with a certain probability. Unbiased agents detect a given event with a “base detection rate” (\(\gamma\)), and miss it with the probability of 1 - \(\gamma\). The probability with witch unbiased agents detect events is the same for A- and B-events. This represents agents without a bias that do not prefer any kind of information over another. Conversely, biased agents have two different detection probabilities: one for events that fit their bias, and one for events that do not fit their bias. The type of bias an agent has is determined by the first event that this agent detects. If an initially unbiased agent detects an A-event, it will develop a bias for A, and analogously for B if it detects a B-event while being unbiased. The probability for biased agents to detect an event that fits their bias is \(\gamma\) + \(\beta\), while the probability to detect an event that does not confirm their bias is \(\gamma\) - \(\beta\). This represents the fact that confirmatory evidence is searched for more attentively (Jonas et al. 2001), and contradicting evidence is discounted or at least viewed more critically (Kappes et al. 2020; Lord et al. 1979). It could alternatively be interpreted as a higher rate in remembering the former, and a higher rate of forgetting the latter (Frost et al. 2015). Thus, it can be understood as an influence on the memory structure of the agents, or even as a combination of an influence on the searching behavior and on the memory structure. To compare the success in detecting signals of agents and agent populations, we calculate a measurement called “performance” (\(\Omega\)). This \(\Omega\) of an agent is the sum of all acquired costs and benefits of an agent. We assume that detecting a signal is associated with a certain benefit, while missing a signal comes with a certain cost. The respective parameters are \(cost_A\), \(cost_B\), \(benefit_A\) and \(benefit_B\). We show the first few steps of an example agent in a potential simulation run in Figure 1. The mentioned performance measurement \(\Omega\) serves as the fitness function for the evolutionary algorithm, which is described in more detail in Section 2.9.
Justification of model parameters
Because we are interested in the question if confirmation bias can be generally useful in the task that we propose, we tested a large number of possible values. The parameter \(\alpha\) represents which proportion of the signals in the environment are A-signals and is used to test different potential environments. These range from completely uniform worlds (only A- or only B-signals) to balanced worlds (containing as many A- signals as there are B-signals). The parameter \(\beta\) defines how much being biased toward a type of signal increases the detection rate of that type of signal, and how much it lowers the detection rate for other signals. Parameter \(\gamma\) defines the standard detection rate, that is, the detection rate for unbiased agents, which is modified in biased agents. We performed parameter sweeps starting from the lowest (0) up to the the highest (1) logically possible values for \(\alpha\), \(\beta\), and \(\gamma\). We want to stress here that the model is not particularly sensitive to any of the parameters. Increasing the number of signals agents can perceive (the number of steps), or increasing the number of agents in the agent population, only changes the results quantitatively, but not qualitatively. We also used different two different reward schemes for the experiments, which made no qualitative difference in the reported results. The two reward schemes are described in Section 2.7. Table 2 shows all the parameters used in the model.
Standard procedure of the experiments
Unless otherwise specified, the following procedure is used for all experiments. 100 Agents are created and then get confronted with one observable signal per step for 10 steps. For each signal, the agents then either miss or detect it, and their \(\Omega\) is calculated. We conduct two sorts of experiments: in simple experiments, we evaluate the \(\Omega\) agents after 10 or 100 time steps, while we use the evolutionary algorithm in the other experiments. Often, we are interested in comparing biased and unbiased agents. Unless the \(\beta\) of agents is specified, their \(\beta\) is a random number between 0 and 1. Unbiased agents function the same as biased agents but have a \(\beta\) of 0.0. We use a simple reward scheme called “simple rewards” in most of the experiments, which consists of \(cost_A\) = \(cost_B\) = -1, and \(benefit_A\) = \(benefit_B\) = 1. For the experiments shown in Figure 4 and 10 we also use “random rewards”, consisting of a random number between -1 and -10 for \(cost_A\) and \(cost_B\), as well es a random number between 1 and 10 for \(benefit_A\) and \(benefit_B\) in each run.
We conduct at least 100 runs for each parameter setting and report mean values. For statistical analysis of the results shown in Figure 4, we used a two-sided t-test with Bonferroni correction.
Description of the evolutionary algorithm
There are varying degrees of being biased: one could be almost neutral, having only a small preference for a certain type of signals, but perceiving other signals almost equally well; but one could also be totally biased, being effectively blind to anything but one type of signal. Because we are interested in the question if - and to what degree - confirmation bias could develop within our agent population, we wrote an evolutionary algorithm (EA). Such algorithms are stochastic search algorithms that mimic natural evolution (Bartz-Beielstein et al. 2014). They can be used for parameter optimization (Bäck & Schwefel 1993) and created a simple EA to find an optimum amount of bias strength (\(\beta\)) for our agents. Technically, our algorithm is a form of EA called ES (Evolution Strategy) (Beyer & Schwefel 2002).
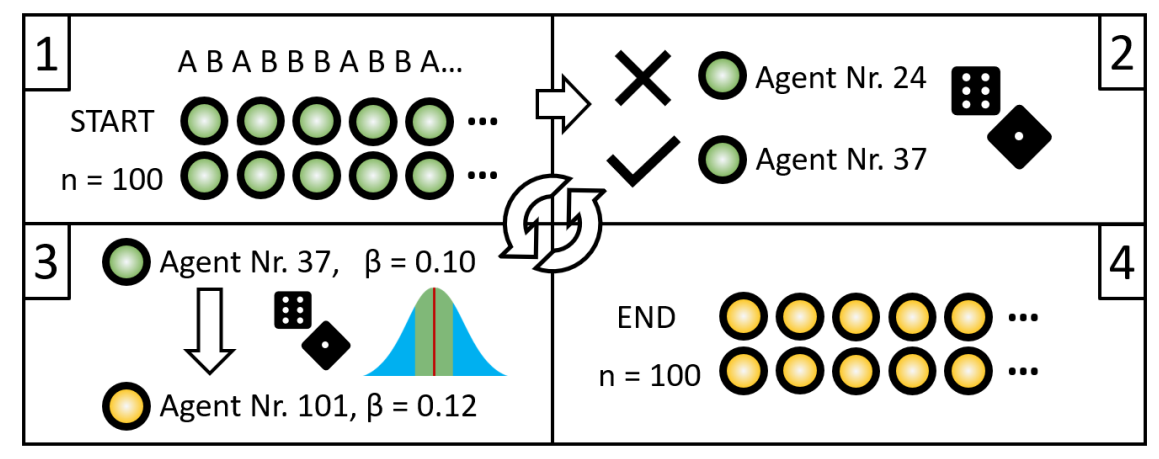
The evolutionary algorithm functions as follows: 100 agents behave the same as in the simple experiments, but the experiment does not end after 10 steps. Instead, we use the performance value \(\Omega\) of the agents as the fitness function: The best performing 20% of agents, that is, those with the highest performance \(\Omega\), are selected to serve as possible parents for new agents. Out of this pool of possible parent agents, one is randomly drawn (with repeats) to serve as a parent of a new agent. This new agent gets initialized in the same way as the agents of the first generation, but receives a new \(\beta\) value. This \(\beta\) value is based on the \(\beta\) value of the parent agent: the new \(\beta\) is a normally random distributed number with the \(\beta\) of the parent as the mean and the standard deviation being a fixed mutation rate of 0.005. This means that the bias strength of the offspring is similar, but most likely not equal to that of the parent: it is likely a bit smaller or a bit higher. The type of bias is not inherited, only the ability to form a bias is. This process of creating new agents is repeated until the number of new agents is equal to the number of agents at the start of the run. After that, the previous generation of agents gets deleted, and the new generation goes through the experimental procedure. The whole algorithm is repeated for 200 generations and is shown in Figure 2.
We conducted the experiments shown in this study also with an evolutionary algorithm that uses fitness proportionate selection. In the EA with fitness proportionate selection, the probability for an agent to be a parent is directly proportional to its performance value \(\Omega\). We received the same qualitative results as we did with the algorithm described in this Section.
Description of conducted experiments
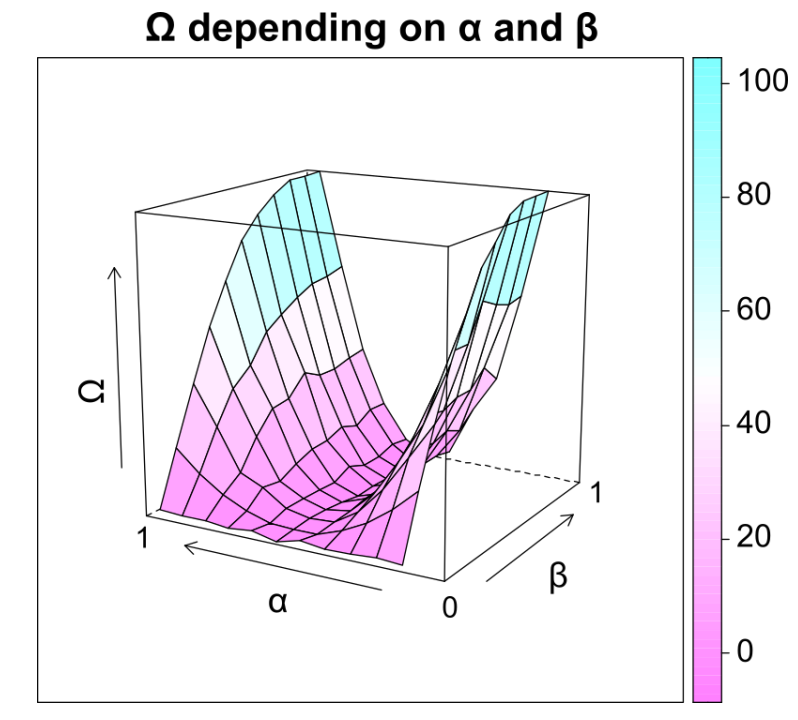
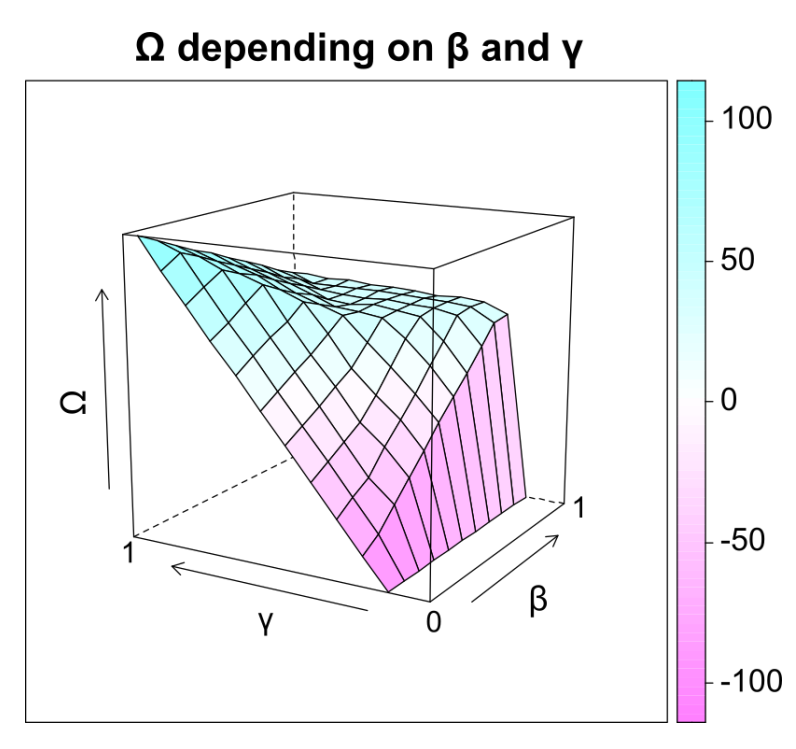
Our model allowed us now to investigate our research questions by conducting the experiments described below. Unless otherwise specified, the standard procedure described in Section 2.6 is used. First, we were interested on the interaction between the parameters \(\alpha\) and \(\beta\) and their influence on performance. The more \(\alpha\) deviates from 0.5, the more the proportion of A-signals to B-signals deviates from 0.5, and a high \(\beta\) indicates a strong effect of the bias. This is interesting, because an imbalanced world (e.g., high proportion of A-signals) makes it possible for agents with the wrong kind of bias to miss a lot of signals, but also potentially enhances the performance of correctly biased agents. Results of this experiment are shown in Figure 3. A similar experiment shows the interaction between the parameters \(\beta\) and \(\gamma\) and is shown in Figure 5. This is done to see if there is any relevant interaction between the two parameters, since it could be the case that a high \(\beta\) may not be beneficial if \(\gamma\) is also high, resulting in a saturation effect.
Secondly, to compare the performance of biased and unbiased agents in this task in the most general way possible, we compared the two types of agents observing a low number of events (10) in a simple reward scheme. The same is done for agents observing a high number of events (100), and the results are illustrated in Figure 4.
Thirdly, we were not only interested in the performance of agents, but also in what kinds of signals they observe. Intuitively, biased agents would observe a higher amount of signals that fit their bias. To test this, we compared the amount of A-signals agents observe in a balanced environment (same number of A-signals and B-signals). The results of this experiment are shown in Figure 6. Given that the bias influences the agents performance, and the bias is determined by the first type of signal detected, we analyzed the influence of the first element and show the results in Figure 7.
Lastly, we were interested in the evolution of confirmation bias in our agents. Starting with an unbiased population, we investigated the \(\beta\) that evolves after 200 generation under varying \(\gamma\) values (see Figure 8) and under varying \(\alpha\) values (see Figure 9). To see if the number of the events observed by agents leads to a qualitative difference in the results, and to see if confirmation bias would also develop just by random chance, we conducted the experiment shown in Figure 10.
Results
Comparisons of unbiased and biased agents
We made a set of experiments in which agents observe a number of events and then we measure their performance as defined by \(\Omega\) to see if confirmation bias can increase the performance of agents. We found that the more \(\alpha\) deviates from 0.5, the higher the \(\Omega\) of biased agents observing 100 events. This effect is greatly enhanced with increasing \(\beta\). The overall highest \(\Omega\) is observed when \(\alpha\) is 0 or 1 and \(\beta\) is 1. A high \(\beta\) does not increase nor decrease \(\Omega\) of agents significantly when \(\alpha\) is close to 0.5, see Figure 3.
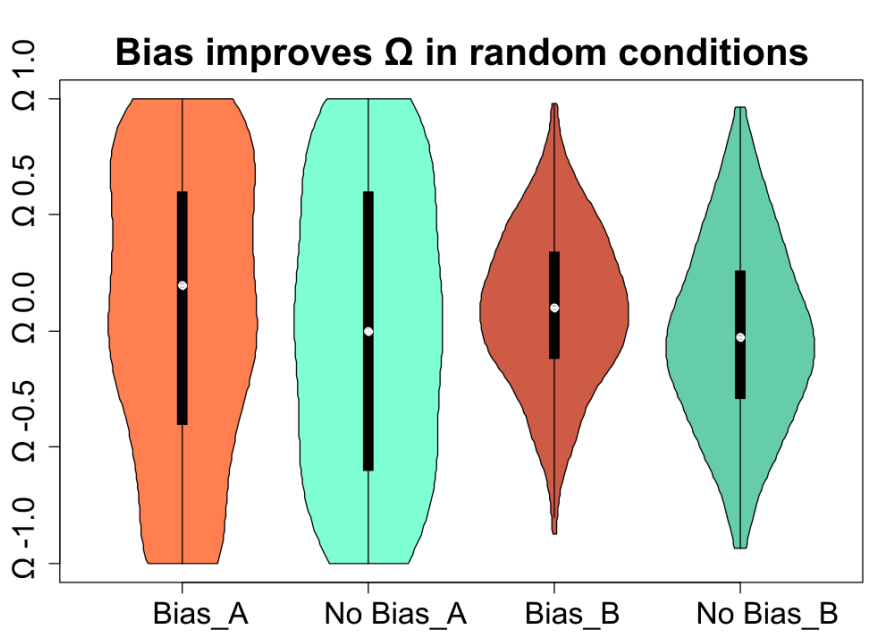
We compared biased agents (Bias) and unbiased agents (No Bias) in random conditions to see if confirmation bias can enhance the performance of agents in this task: in each run, \(\alpha\), \(\gamma\), and \(\beta\) are set to be a uniformly random number between 0 and 1. Agents without bias (turquoise) have lower mean \(\Omega\) than biased agents (orange), see Figure 4. This difference is statistically significant between randomly biased agents (RB) and unbiased agents (NB) observing 10 events with a simple reward scheme (_A) as well as between those with a random reward scheme (_B): t (Bias_A vs No Bias_A) = 2.15, t (Bias_B vs No Bias_B) = 5.11, p \(<\) 0.025, (998 degrees of freedom).
We performed a parameter sweep and measured the performance \(\Omega\) of agents to see if there is a relevant interaction between the parameters \(\beta\) and \(\gamma\). Averaging across all possible values for \(\alpha\), a high \(\gamma\) and a low \(\beta\) results in the highest \(\Omega\) of agents observing 100 events. If the \(\gamma\) is not high, increasing bias effect improves \(\Omega\), until it plateaus. Beyond this, a higher \(\beta\) is not associated with higher \(\Omega\), see Figure 5.
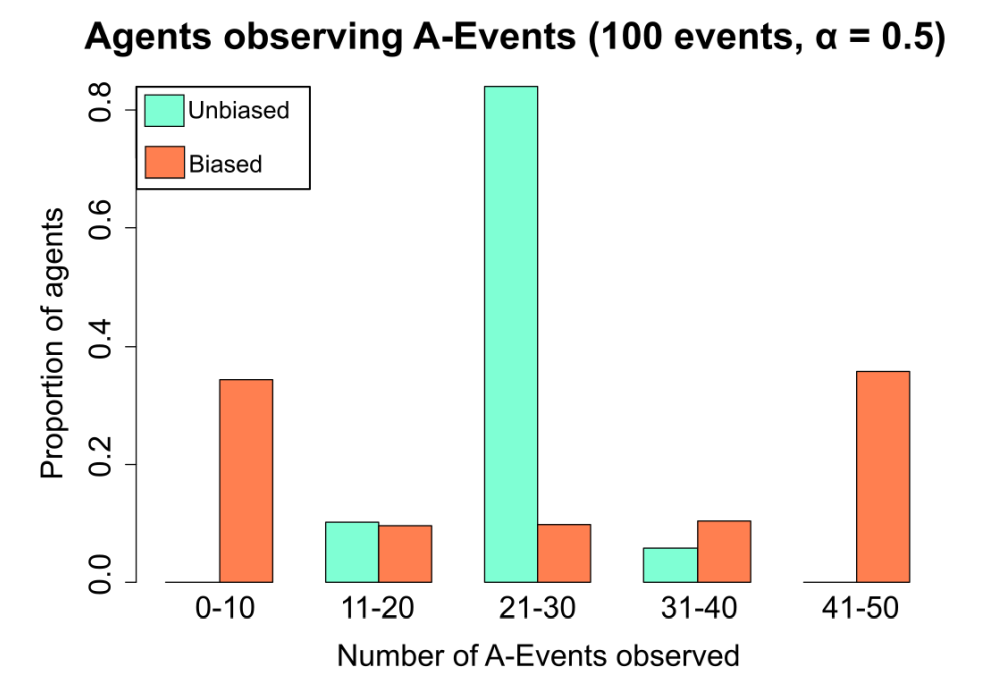
We show an example case with 150 agents, each potentially observing 100 events, of which 50 are A-events to see if confirmation bias has a significant effect on the type of signals detected by agents. Compared to unbiased populations, biased populations have a significantly higher proportion of agents that have a very low, as well as a very high number of observations of A-events. In unbiased populations, more than 80% of agents have made 21-30 observations of A-events, see Figure 6.
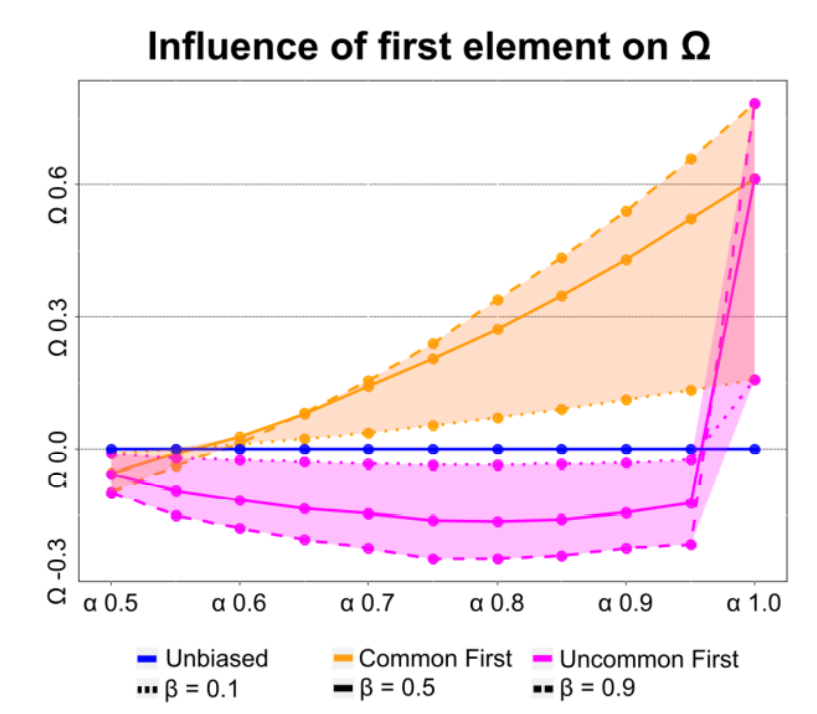
We analyzed differences between runs in which either the common, or the uncommon type of signal is the first one presented to agents, since the bias of agents in the model is formed based on the first type of signal they detect. The \(\Omega\) of biased agents is dependent on the first event presented to them, see Figure 7. Biased agents have higher \(\Omega\) after 100 events when the more common type of event is shown first (orange) compared to when the less common type of event is the first one (pink). Dashed lines represent very strongly biased agents (\(\beta\) = 0.9), solid lines represent moderately biased agents (\(\beta\) = 0.5), and dotted lines represent weakly biased agents (\(\beta\) = 0.1). The filled in colors between the dashed and the dotted lines represent results from agents with \(\beta\) \(>\) 0.1 and \(\beta\) \(<\) 0.9. The blue line shows the results of unbiased agents, whose \(\Omega\) is not influenced by the order in which the events happen or the value of \(\alpha\).
Results of experiments involving the evolutionary algorithm
We used an evolutionary algorithm to see if unbiased agents (agents with an initial \(\beta\) of 0.0) evolve into agents that have a significant bias.
Varying values for \(\beta\) developed after 200 generations when \(\alpha\) is a new random value in each generation. This is highly dependant on \(\gamma\) and we observed a drop in the evolved bias effect when the detection rate (\(\gamma\)) was below 0.1 or above 0.8, see Figure 8.
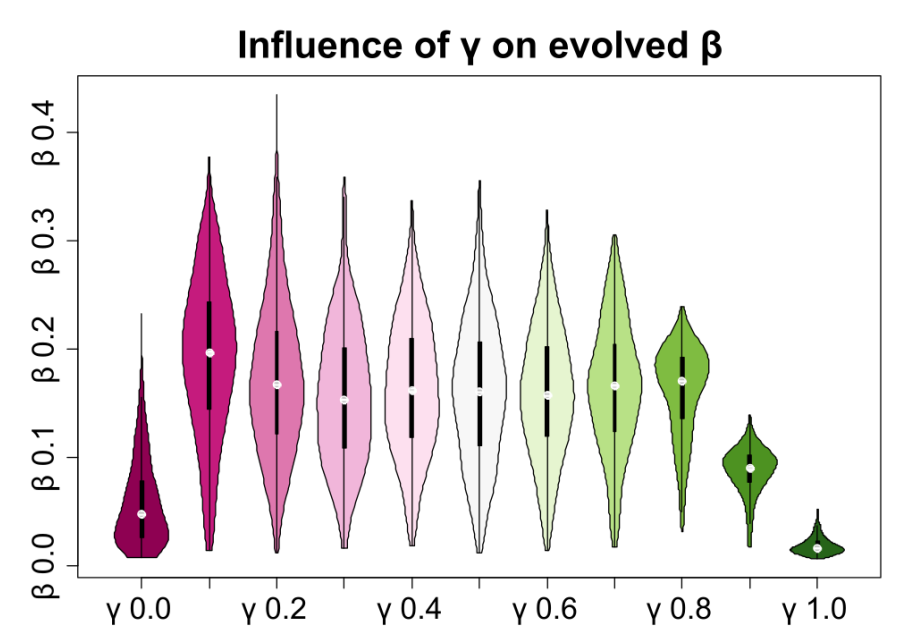
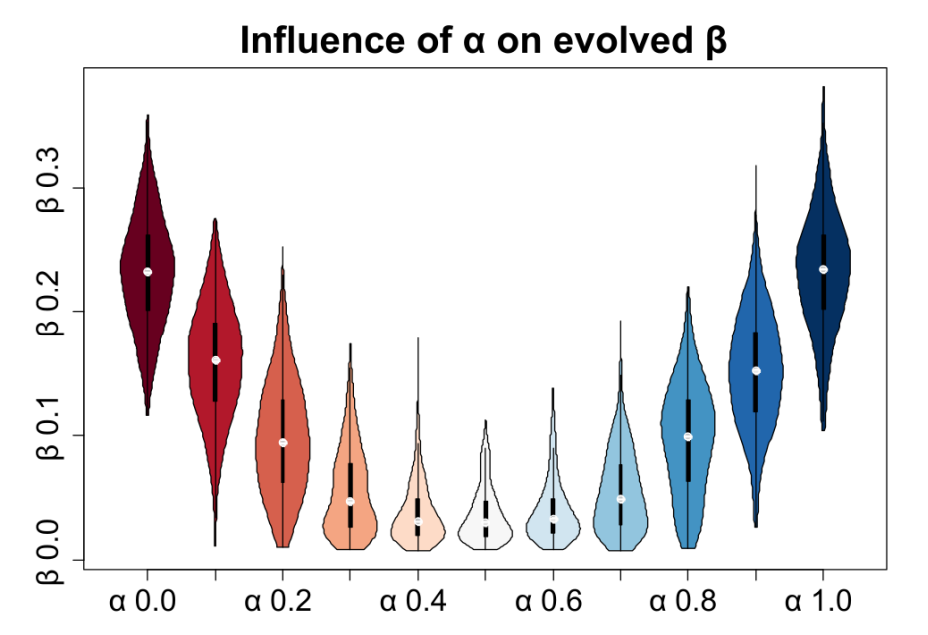
The value of \(\alpha\) also has an influence on the \(\beta\) that evolves in the agents. The closer \(\alpha\) was to 0.5, the lower the mean bias effect that evolved among the agents after 200 runs, see Figure 9. For each generation, \(\gamma\) was set to a random value.
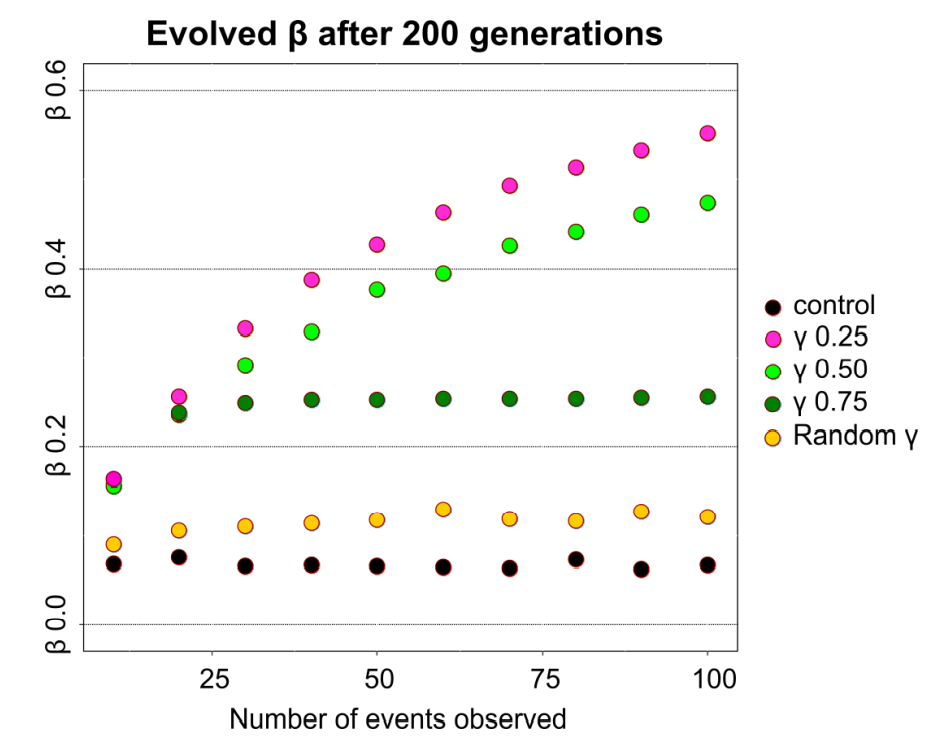
We also tested scenarios with random conditions, that is, each generation of agents was in a world that has a random reward scheme and a random \(\alpha\). We found that a significant bias evolves, especially if agents observed a high number of events before the next generation was initialized and if \(\gamma\) was low. We found a higher bias in agents that have a new random \(\gamma\) in each generation (yellow dots) compared to the control group where no selection pressure was applied, see Figure 10.
Discussion
Relevance of the model
This model aims at a certain sweet spot between highly abstract models that are not easily adaptable to concrete questions, as well as those that are highly specialized, being tailored to specific topics and settings. It improves our general understanding of confirmation bias by demonstrating how this bias can enhance performance in a signal detection task. We also provide an evolutionary algorithm in which initially unbiased agents evolve stronger biases over time and find conditions under which weaker and stronger biases evolve.
General discussion
We used an agent-based model to investigate the impact of confirmation bias on agents in a minimally complex scenario. The scenario consists of a stream of “A” and “B” signals (events), that can either be detected or missed by agents. Agents form a confirmation bias based on the first observation they make, i.e., the first signal they successfully detect. This confirmation bias increases their chances to detect confirming signals, while it decreases their chances to detect disconfirming signals.
Given these microscopic properties, we made several findings on a macroscopic level that are resistant to changes of parameters and thus seem to be the result of said microscopic properties. For example, even with a random reward scheme, a random base detection rate, as well as a random bias strength, biased agents outperformed unbiased agents. Significant differences in performance can be observed after 10 steps already, and those differences accumulate with a higher number of steps.
One of our key findings can be described as follows: as soon as there is a tendency for one event over the other, i.e., if A and B are not equally likely, then confirmation bias increases the number of observations that agents make. This can be explained by how confirmation bias is implemented in our model: agents are biased towards the first observation they make. Statistically, it is more often the case that the first event observed by an agent is the more common event. Thus, in most cases, confirmation bias biases agents to the type of event that is more common. Consequently, agents can make more observations, and if those observations are connected to benefits, they accumulate more benefits. This is shown in Figure 7, in which biased agents have higher performance than unbiased agents, but only if the first event that the agents can perceive is of the more common type. When the order of signals is artificially manipulated so that the unlikely event is presented first, a higher number of agents form a “wrong” bias. However, it is statistically likely that the first event presented is a likely event. Thus, confirmation bias could be seen as a system that adjusts agents’ attention towards what is most common. This is necessary, since cognitive resources - such as attention - are limited (Posner & Boies 1971; Sweller et al. 2011). Confirmation bias may be a heuristic that decides what should be the things one focuses on. All else being equal, what biased people focus on is the same for everyone: it is that, which confirmation bias dictates. But, it is also different for everyone: some come in contact with wildly different data or experiences, develop other hypotheses, and thus focus on different things. Interestingly, to focus the attention on the most common type of data, agents do not need to know what the most common type of data is. Instead, they can simply focus on the first thing they observe, and chances are that they then are focused on the most common type of data, which is beneficial in our task. Results shown in Figure 3 and in Figure 4 support this: agents that are biased have higher performance in most of the situations, and therefore a bias can evolve even in wildly fluctuating conditions. The only situations that agents cannot exploit by focusing on the first type of observation they make, are those situations in which the proportion of A-signals in the stream (\(\alpha\)) is close to 0.5. In such cases, A-signals and B-signals are equally common and thus, a focus on one over the other is not beneficial - given that A and B are also connected with the same costs and benefits. Consequently, no significant bias evolves in such situations, see Figure 9. Importantly, if A and B are equally important, i.e., if the costs and benefits of missing the respective signals are equal, then the bias does not lower performance either. We think that this is an interesting finding, as it suggests that confirmation bias might not only have higher benefits than costs in some scenarios, but sometimes might have no costs associated with it at all. This gets clear with an example: In a world where A and B are equally likely, does not matter if one detects 50% of all signals, as an unbiased agent would, or 70% of A signals and 30% of B signals, as an agent biased for A would. Both agents would detect 50% of all signals. In this example, we assume that the base detection rate (\(\gamma\)) is 50%. However, this is not necessarily the case. It could be that an important signal is difficult to detect, and thus, the \(\gamma\) is low. Especially for lower values of the \(\gamma\), an increased strength in the bias (\(\beta\)) can enhance performance. This is shown in Figure 8, where up to a certain \(\gamma\), higher \(\beta\) results in better performance. However, beyond this point, a high \(\beta\) reduces performance. For example, if the \(\gamma\) is, 0.8, then \(\beta\) values such as 0.3 are detrimental: The detection chance for confirming events (\(\gamma\) + \(\beta\)) would theoretically be 1.1, but in practice cannot exceed 1 (100%). However, the detection chance for disconfirming events (\(\gamma\) - \(\beta\)) is lowered to 0.5. This asymmetry results in a disadvantage for strongly biased agents when the \(\gamma\) is high, and consequently, agents evolve lower values for \(\beta\) in such scenarios, see Figure 8. This is consistent with the parameter sweep shown in Figure 5, in which increasing \(\beta\) is beneficial for low base detection rates, but detrimental for high base detection rates.
Given that the performance of agents on our task depends on the base detection rate (\(\gamma\)), the proportion of A-signals relative to B-signals (\(\alpha\)), and how strongly bias modifies the perception of agents (\(\beta\)), one could ask the question: Should agents be biased or not? Surprisingly, this hardly depends on the specifics, and the general answer is “yes”. This is shown in Figure 4, in which biased agents outperform unbiased agents in 5500 runs, with each of those having different random conditions. Further, this difference in performance is sufficient so that the bias evolves over 200 generations, see Figure 10. This was surprising to us, but, as mentioned above, the fact that confirmation bias enhances the chance to detect the type of signal agents detected first, together with the fact that they are likely to detect the more common type of signal first, helps to explain this finding.
Confirmation bias and social reasoning
One of the explanations for the persistence of confirmation bias uses and evolutionary perspective. The idea that “confirmation bias makes it possible to arrive at an efficient division of cognitive labour” (Sperber et al. 2010, p. 378) is supported by our model. In our model, biased agents increase the number of observations they make, while also having viewpoint diversity within the group. Confirmation bias may be a mechanism that leads individuals of a group to have more heterogeneous opinions; without confirmation bias, the opinions within a group are more homogeneous, see Figure 6. Together with the rather obvious assumption that observations made by agents influence their behavior, it is reasonable to assume that a population with biased agents exhibits a greater variety of behaviors. This indicates that confirmation bias could be a mechanism that increases exploratory behavior of a group. Further, Sperber and colleagues suggest that the “function of reasoning is to find arguments to convince others” and therefore “should exhibit a strong confirmation bias” (Sperber et al. 2010, p. 378). The results from our model also support this idea. The mechanism of confirmation bias indeed drives agents to find (detect) evidence (signals) in accordance to their beliefs, e.g. because of selective attention (Jonas et al. 2001). Within a social group, this may promote discourse and a broader investigation of problem spaces, as well as a wider array of different solutions (Mercier 2016; Mercier & Sperber 2011).
Confirmation bias and first impressions
Humans sometimes judge others on the basis of very little information, such as often surprisingly accurate first impressions (for a review see, Breil et al. 2021). However, it is not clear why first impressions are so stable and not easily overwritten or corrected by second or third impressions (Kenny et al. 1992). We suggest confirmation bias as one of the (possibly many) mechanisms that make first impressions quite stable. Other people are complex beings in the sense that they behave often in irregular and ambiguous ways. For example, extroverted people do not behave extroverted all the time: sometimes they display introverted behaviors as well. In a sense, they send a mix of A (extroverted) and B (introverted) signals. Given that the stream of signals in our model can be interpreted a such signals coming from one person, our model could be interpreted as agents evaluating a person. Our model suggests that the first impression establishes a bias, and that this bias influences how future information is processed. Interestingly, a first step in this direction has been done as it was shown that a specific first impression can at least lead to an underweighting of rare events (Holtz 2015). However, we suggest that it is not necessarily an underweighting, but perhaps a complete failure to detect signals towards one is not biased to. Our suggestion of such a simple mechanism playing a key role in first impressions is a valuable addition that comes with another testable hypothesis: Do people holding opinions based on first impressions simply not detect signals that would falsify the impression?
Confirmation bias and polarization
Confirmation bias has been found to lead to polarization (Alvim et al. 2021; Del Vicario et al. 2017). However, most models showing this effect model social interactions, by using approaches such as the DeGroot model or the Bounded Confidence Model. In contrast, our model shows that a mere difference in perception or directed attention is enough to lead agents to make different observations, see Figure 6. Thus, to the degree that agents base opinions on their observations, confirmation bias influences opinions. Resulting polarization in populations of biased agents means that many of those agents have “opinions” that are not accurate: they either overestimate or underestimate the rate of one event relative to the other. This is especially relevant, as one could interpret the stream of events produced in our model alternatively as a noisy environment. If agents, or real people, have a bias that lets them overlook signals and instead lets them detect primarily noise, they may find an actually nonexistent pattern within this noise. However, a population may also benefit from some agents that overestimate the rate of certain events. For example, there could be a threshold of signals that needs to be reached, before an agent takes a specific action; one does not call the fire department whenever they have the mere feeling that they smell smoke. However, if some agents are biased towards signals that indicate danger, they may be able to detect a sufficient number of signals, and then warn the group about a potentially dangerous event. This idea is in line with the “smoke detector principle” that states that it is better to overestimate, than to underestimate the chances of dangerous events, such as fires (Nesse 2005).
Conclusion
We developed a model that evaluates the influence of confirmation bias on agents in a minimally complex scenario. We suggest that agents form a bias based on the first observation that they make as a simple core mechanism. This bias influences them so that they are more likely to detect signals that confirm their beliefs, and are less likely to detect signals that would contradict their beliefs. We found that such a simple mechanism increases the overall benefits of agents by biasing them towards the most common type of data. Thus, the bias evolves over generations, almost regardless of the event landscape. The only scenario in which such a bias is not helpful is when there is no “most common type of data”, i.e., when two types of events are equally likely. Further, confirmation bias is only detrimental in our task when the base detection rate of signals is so high, that it can not be substantially improved by being biased, or if agents are typically confronted with unlikely events before they have formed their bias. Nevertheless, the bias held by agents increases their chances to detect signals, but obviously also gives them a biased sample. Therefore, their opinion of the world may be skewed, and they are hindered in their pursuit of the truth. Given that for this specific task, confirmation bias is generally, i.e., in almost all variations of the task, useful it would be interesting to find other tasks that make narrative sense and investigate the impact of confirmation bias on those.
Limitations
Our study has limitations that could be mitigated by extending the model. First, we use the term “confirmation bias” intentionally loosely. Strictly speaking, confirmation bias involves the attempt to confirm a preposition held by an agent. Modelling this in detail would require modeling epistemic contents and intentions of agents. To bypass this, we model as if agents formed a hypothesis about which signal is more common after detecting one. Another limitation is that agents have their bias fixed: after their first observation, they acquire a bias that does not change for the rest of the run. In reality, it is conceivable that at least a certain proportion of people change their biases over time. This could be modulated via a confidence variable, as recent research has shown that the stability of confirmation bias is related to confidence (Rollwage et al. 2020). A simpler approach is to make agents change their bias towards the type of signal, for which they have collected more evidence: for example, if an agent has a bias for events of the type “A”, but then sees many events of the type “B”, it may change its bias towards “B”. Lastly, the signals are identified by agents completely reliably ,i.e, if they in fact get received, they get received correctly. There is no chance to mistake a signal of “A” as “B” or similar.
Acknowledgements
We thank anonymous reviewers for helpful comments that improved the manuscript. This study is supported by the Field of Excellence COLIBRI (Complexity of Life in Basic Research and Innovation) of the Karl-Franzens University of Graz. The authors acknowledge the financial support by the University of Graz.Model Documentation
In order to make the model accessible for everyone interested, we uploaded it to the CoMSES database. The full model is available at: https://www.comses.net/codebase-release/92f8f985-fc9a-43af-92e9-8052de5e36f2/.References
ALVIM, M. S., Amorim, B., Knight, S., Quintero, S., & Valencia, F. (2021). A multi-agent model for polarization under confirmation bias in social networks. Formal Techniques for Distributed Objects, Components, and Systems: 41st IFIP WG 6.1 International Conference, FORTE 2021, Held as Part of the 16th International Federated Conference on Distributed Computing Techniques, DisCoTec 2021, Valletta, Malta, June 14-18, 2021, Proceedings. [doi:10.1007/978-3-030-78089-0_2]
AUSTERWEIL, J. L., & Griffiths, T. L. (2011). Seeking confirmation is rational for deterministic hypotheses. Cognitive Science, 35(3), 499–526. [doi:10.1111/j.1551-6709.2010.01161.x]
BACON, F. (1620). Instauratio Magna (Novum Organum).
BARTZ-BEIELSTEIN, T., Branke, J., Mehnen, J., & Mersmann, O. (2014). Evolutionary algorithms. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 4(3), 178–195. [doi:10.1002/widm.1124]
BÄCK, T., & Schwefel, H.-P. (1993). An overview of evolutionary algorithms for parameter optimization. Evolutionary Computation, 1(1), 1–23.
BEYER, H.-G., & Schwefel, H.-P. (2002). Evolution strategies - A comprehensive introduction. Natural Computing, 1(1), 3–52.
BREIL, S. M., Osterholz, S., Nestler, S., & Back, M. D. (2021). 'Contributions of nonverbal cues to the accurate judgment of personality traits.' In T. D. Letzring, J. S. Spain, S. M. BREIL, S. Osterholz, S. Nestler, & M. D. Back (Eds.), The Oxford Handbook of Accurate Personality Judgment (pp. 193–218). Oxford: Oxford University Press. [doi:10.1093/oxfordhb/9780190912529.013.13]
CAFFERATA, A., Dávila-Fernández, M. J., & Sordi, S. (2021). Seeing what can(not) be seen: Confirmation bias, employment dynamics and climate change. Journal of Economic Behavior & Organization, 189, 567–586. [doi:10.1016/j.jebo.2021.07.004]
CAFFERATA, A., & Tramontana, F. (2019). A financial market model with confirmation bias. Structural Change and Economic Dynamics, 51, 252–259. [doi:10.1016/j.strueco.2019.08.004]
COLE, S. (2013). Implementing counter-measures against confirmation bias in forensic science. Journal of Applied Research in Memory and Cognition, 2, 61–62. [doi:10.1016/j.jarmac.2013.01.011]
DEL Vicario, M., Scala, A., Caldarelli, G., Stanley, H. E., & Quattrociocchi, W. (2017). Modeling confirmation bias and polarization. Scientific Reports, 7(1), 1–9. [doi:10.1038/srep40391]
FROST, P., Casey, B., Griffin, K., Raymundo, L., Farrell, C., & Carrigan, R. (2015). The influence of confirmation bias on memory and source monitoring. The Journal of General Psychology, 142(4), 238–252. [doi:10.1080/00221309.2015.1084987]
HOLTZ, B. C. (2015). From first impression to fairness perception: Investigating the impact of initial trustworthiness beliefs. Personnel Psychology, 68(3), 499–546. [doi:10.1111/peps.12092]
JONAS, E., Schulz-Hardt, S., Frey, D., & Thelen, N. (2001). Confirmation bias in sequential information search after preliminary decisions: An expansion of dissonance theoretical research on selective exposure to information. Journal of Personality and Social Psychology, 80, 557–571. [doi:10.1037/0022-3514.80.4.557]
KAPPES, H., Harvey, A., Lohrenz, T., Montague, P., & Sharot, T. (2020). Confirmation bias in the utilization of others’ opinion strength. Nature Neuroscience, 23, 130–137. [doi:10.1038/s41593-019-0549-2]
KASSIN, S. M., Dror, I. E., & Kukucka, J. (2013). The forensic confirmation bias: Problems, perspectives, and proposed solutions. Journal of Applied Research in Memory and Cognition, 2(1), 42–52. [doi:10.1016/j.jarmac.2013.01.001]
KENNY, D., Horner, C., Kashy, D., & Chu, L.-c. (1992). Consensus at zero acquaintance: Replication, behavioral cues, and stability. Journal of Personality and Social Psychology, 62, 88–97. [doi:10.1037/0022-3514.62.1.88]
KOIVISTO, M., Hyönä, J., & Revonsuo, A. (2004). The effects of eye movements, spatial attention, and stimulus features on inattentional blindness. Vision Research, 44(27), 3211–3221. [doi:10.1016/j.visres.2004.07.026]
KRAUSE, J., Ruxton, G. D., & KRAUSE, S. (2010). Swarm intelligence in animals and humans. Trends in Ecology & Evolution, 25(1), 28–34. [doi:10.1016/j.tree.2009.06.016]
KUKUCKA, J., Hiley, A., & Kassin, S. M. (2020). Forensic confirmation bias: Do jurors discount examiners who were exposed to task-Irrelevant information? Journal of Forensic Sciences, 65(6), 1978–1990. [doi:10.1111/1556-4029.14546]
LORD, C. G., Ross, L., & Lepper, M. R. (1979). Biased assimilation and attitude polarization: The effects of prior theories on subsequently considered evidence. Journal of Personality and Social Psychology, 37(11), 2098–2109. [doi:10.1037/0022-3514.37.11.2098]
MAHONEY, M. J. (1977). Publication prejudices: An experimental study of confirmatory bias in the peer review system. Cognitive Therapy and Research, 1(2), 161–175. [doi:10.1007/bf01173636]
MERCIER, H. (2016). 'Confirmation bias–myside bias.' In Cognitive Illusions (pp. 109–124). Hove, UK: Psychology Press.
MERCIER, H. (2016). The argumentative theory: Predictions and empirical evidence. Trends in Cognitive Sciences, 20(9), 689–700. [doi:10.1016/j.tics.2016.07.001]
MERCIER, H., & Sperber, D. (2011). Why do humans reason? Arguments for an argumentative theory. Behavioral and Brain Sciences, 34(2), 57–74; discussion 74–111. [doi:10.1017/s0140525x10000968]
NESSE, R. M. (2005). Natural selection and the regulation of defenses: A signal detection analysis of the smoke detector principle. Evolution and Human Behavior, 26(1), 88–105. [doi:10.1016/j.evolhumbehav.2004.08.002]
NICKERSON, R. S. (1998). Confirmation bias: A ubiquitous phenomenon in many guises. Review of General Psychology, 2(2), 175–220. [doi:10.1037/1089-2680.2.2.175]
O’BRIEN, B. (2009). Prime suspect: An examination of factors that aggravate and counteract confirmation bias in criminal investigations. Psychology, Public Policy, and Law, 15, 315–334.
PEREZ Peña, J. R. (2014). Confronting the forensic confirmation bias. Available at: https://ylpr.yale.edu/confronting-forensic-confirmation-bias.
PERICHERLA, S. R., Rachuri, R., & Rao, S. (2018). Modeling confirmation bias through egoism and trust in a multi agent system. 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC). [doi:10.1109/smc.2018.00205]
PETERS, U. (2020). What is the function of confirmation bias? Erkenntnis, 87, 1572–8420. [doi:10.1007/s10670-020-00252-1]
POSNER, M. I., & Boies, S. J. (1971). Components of attention. Psychological Review, 78(5), 391. [doi:10.1037/h0031333]
POUGET, S., & Villeneuve, S. (2012). A mind is a terrible thing to change: Confirmatory bias in financial markets. Review of Financial Studies, 30. [doi:10.1093/rfs/hhw100]
ROLLWAGE, M., & Fleming, S. M. (2021). Confirmation bias is adaptive when coupled with efficient metacognition. Philosophical Transactions of the Royal Society B, 376(1822), 20200131. [doi:10.1098/rstb.2020.0131]
ROLLWAGE, M., Loosen, A., Hauser, T., Moran, R., Dolan, R., & Fleming, S. (2020). Confidence drives a neural confirmation bias. Nature Communications, 11. [doi:10.1038/s41467-020-16278-6]
SILVERMAN, B. G. (1992). Modeling and critiquing the confirmation bias in human reasoning. IEEE Transactions on Systems, Man, and Cybernetics, 22(5), 972–982. [doi:10.1109/21.179837]
SPERBER, D., Clement, F., Heintz, C., Mascaro, O., Mercier, H., Origgi, G., & Wilson, D. (2010). Epistemic vigilance. Mind & Language, 25(4), 359–393. [doi:10.1111/j.1468-0017.2010.01394.x]
SWELLER, J., Ayres, P., & Kalyuga, S. (2011). Cognitive Load Theory. Berlin Heidelberg: Springer. [doi:10.1007/978-1-4419-8126-4_6]
TALLURI, B. C., Urai, A. E., Tsetsos, K., Usher, M., & Donner, T. H. (2018). Confirmation bias through selective overweighting of choice-consistent evidence. Current Biology, 28(19), 3128–3135. [doi:10.1016/j.cub.2018.07.052]
TVERSKY, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185(4157), 1124–1131. [doi:10.1126/science.185.4157.1124]
WASON, P. C. (1960). On the failure to eliminate hypotheses in a conceptual task. Quarterly Journal of Experimental Psychology, 12(3), 129–140. [doi:10.1080/17470216008416717]
WASON, P. C. (1968). Reasoning about a rule. Quarterly Journal of Experimental Psychology, 20(3), 273–281. [doi:10.1080/14640746808400161]