Polarization in Social Media: A Virtual Worlds-Based Approach

and
aPrinceton University, United States; bInstitute of Technology Futures, Karlsruhe Institute of Technology, Germany
Journal of Artificial
Societies and Social Simulation 26 (3) 11
<https://www.jasss.org/26/3/11.html>
DOI: 10.18564/jasss.5170
Received: 06-Aug-2022 Accepted: 15-May-2023 Published: 30-Jun-2023
Abstract
As social media becomes increasingly integrated within the fabric of our digital lives, it is clear that these platforms have a great impact on our mental well-being and interpersonal relationships. However, recent events and studies suggest that these changes are not always for the better as social media might contribute to social polarization. In this work, we leverage agent-based modelling (ABM) techniques to simulate the associated opinion dynamics of polarization in social media platforms. To accomplish this, we first develop a methodology for distinguishing between different types of polarization. This enables a more nuanced investigation into the interplay between behavior online and behavior offline. We next expand on the public-private split model by introducing a novel “virtual worlds” framework for representing an online social media platform. Agents from the neighbor constrained “real world” can “log-in” to these virtual worlds with a certain probability and participate in a complete network; this reflects the unique socioeconomic and geographic anonymity provided through social media. Additionally, global homophilic influence is incorporated and its relationship with local virtual world structure is considered. We finally perform a sensitivity analysis over a set of model parameters, and find that the incorporation of virtual worlds can result in the simultaneous presence of different types of polarization in the real and virtual worlds. These findings align with studies on social media from the literature, and suggest that the online platform provided by social media poses unique challenges with regards to investigating the presence of polarization.Introduction
Social media platforms such as Facebook and Twitter have come under scrutiny lately as the spread of conspiracy theories and misinformation becomes increasingly apparent. The potential danger inherent in these platforms is clear to their parent companies as well. For instance, an internal report at Facebook discovered that \(64\%\) of users in extremist groups arrived through recommendation algorithms, and social media corporations acknowledged that AI-driven algorithms played a role in the 2016 Myanmar genocide (Hao 2021; Orlowski 2020). While steps have been taken by corporate entities to address this emerging issue, such as the creation of the Responsible AI team by Facebook, these groups have been tasked with considering topics involving bias in AI instead of the potential polarization such software can bring (Hao 2021). Investigative work has suggested that such sentiments are partially intentional. In the 2020 Netflix documentary film The Social Dilemma, software engineers, ethics specialists, and critics were inquired as to their individual perspectives on social media and polarization; the majority agreed that associated corporations have found polarization to be profitable (Orlowski 2020). The investigation of what specific factors contribute the most to polarization is thus critical.
Unfortunately, a direct analysis of social media algorithms is difficult given they are the intellectual property of their respective corporations. Occasionally, relevant publications become available for public access. For instance, Ahlgren et al. (2020) at Facebook recently documented the “WES” simulation platform. This software is designed to simulate interaction among AI-driven Facebook bots and determine potential pitfalls of the social media platform. However, because these types of sources are sanitized through the corporate approval process, pivotal details/social concerns pertinent to the study are likely to be absent. It is thus important to consider general modeling techniques which can provide an effective proxy for analyzing these problems independent of the actual commercial algorithm itself. An additional benefit of such a method is the opportunity it provides to investigate the time evolution of different types of polarization in a standardized manner. Indeed, a blend of computational opinion dynamics, agent-based modeling (ABM), and social analysis suggests a possible avenue.
Existing literature has considered several approaches to perform this kind of analysis. For instance, the social premise of homophily has been used in ABM studies to emulate the effect of social media algorithms (Baumann et al. 2020; Keijzer & Mäs 2022; Mäs & Bischofberger 2015). The computational implementation of this premise has varied: some interpretations use a probabilistic distribution which takes into account the relative similarity between participants, while others incorporate a fixed threshold (Baumann et al. 2020; Ben-Naim et al. 2003; Keijzer & Mäs 2022; Mäs & Bischofberger 2015). The structure and topology of social media networks has also been subject to study, with some works considering a disjoint set of online and offline agents (Dong et al. 2021) and others leveraging multi-layered/multiplexed models (Hristova et al. 2014; Peng & Porter 2022). Nevertheless, a systematic investigation into the types of polarization in social media through an agent-based representation of social media platform structure can be further explored.
To this end, we take a more sophisticated approach which is reflective of real-life social interaction. We first aim to distinguish among different types of polarization. Two important variants are structural and un-structural polarization: the former is characterized by the presence of relatively large/organized clusters of convictions, while the latter involves agents with varying convictions dispersed throughout the network (i.e., fragmentation). Note that in structural polarization the majority of individual agents will have fully concordant neighbors, leading to an “illusion of consensus” that is not present in un-structural polarization. This microscopic perspective allows for the development of mesoscopic congruence measures which can differentiate among the two types. We next introduce a novel virtual worlds framework to represent a social media platform from an ABM perspective. Agents “log-in” to virtual worlds with probability \(\lambda\) and can participate in a complete social network; this reflects the relative socioeconomic and geographic anonymity of social media (Suler 2004). After additionally integrating homophily as a social premise through a parameter \(h\), we perform a sensitivity analysis with 4400 total independent simulation trials. We then investigate which model parameters are most relevant in the development of different types of polarization and outline a social commentary. Our results reveal that increasing the strength of homophily can lead to a fundamental asymmetry of polarization, where the real world demonstrates un-structural polarization while the virtual worlds feature structural polarization. These results agree with findings from previous studies, suggesting that this kind of superposition is a unique characteristic of social media platforms (Bakshy et al. 2015; Conover et al. 2011; Keijzer & Mäs 2022).
Social Media Characterizations
We consider a brief overview of social media platforms to motivate later discussions and modeling techniques. The basic principles underlying the technology were established under the Web 2.0 era, when increased computational power and new technologies enabled a philosophical transition of the internet towards “applied services” (Dijck 2013 pg. 6). In the mid-2000s, Facebook and Twitter were released and began to take advantage of this medium for social communication (Dijck 2013 pg. 7). These platforms have since achieved great success, with more than half the global human population currently users (Kemp 2022).
Social media algorithms, structure, and polarization
To help engage their userbase, social media platforms leverage a variety of algorithms and AI-driven technologies (Dijck 2013; Vosoughi et al. 2018). For instance, Facebook uses proprietary EdgeRank and GraphRank algorithms to collect data and determine what each user should be shown on their News Feed (Dijck 2013 pg. 49). Empirical research on the News Feed feature revealed the presence of homophilic tendencies and concluded that there exists a tangible susceptibility of these algorithms to polarization (Bakshy et al. 2015). However, this study suggested that individual action was more pivotal in maintaining such boundaries, a claim supported by the analysis of other platforms such as YouTube (Cho et al. 2020).
Another important aspect of social media platforms is subgroup structure. On one hand, these can emerge naturally through large-scale discussion on divisive issues. The presence of this in Twitter was empirically investigated through a cluster analysis (Conover et al. 2011; Gaisbauer et al. 2021). While “community structure” and political polarization were found in the retweet network, the mentions network was more unstructured. On the other hand, subgroups can be artificially delineated. For instance, on the popular site Reddit users are free to create their own communities (dubbed “subreddits”) for different topics. The role of polarization in these settings is less clear.
The human impact of social media
Some of the observed human impacts of social media platforms can be summarized into the following two concepts. The first is the possibility for addiction. Turel et al. (2014) used magnetic resonance imaging (MRI) to reveal that platforms such as Facebook share “some neural features with substance and gambling addictions”. Given that reward-based systems are key to the neurology underlying human impulsiveness, it becomes clear that social media platforms have the effect of disrupting the usual process underlying human motivation for rewards (Turel et al. 2014).
The second concept is disinhibition. Online environments are intrinsically different from those offline: for instance, users may use an anonymous pseudonym in several social media platforms (Tucker et al. 2018 pg. 11). As a result, some users may feel emboldened and cultivate a persona distinct from their offline personality. Suler (2004) coins this phenomenon as online disinhibition and defines it through a set of six distinct yet mutually interacting factors. An important theme throughout Suler’s analysis is the understanding that the virtual setting of social media platforms fundamentally strips human interaction of socioeconomic behavioral cues (i.e., body language, wealth, authority, etc.) leading to a state where individuals can effectively ignore the limitations of their usual offline identity and interpersonal relationships (Suler 2004).
Agent-Based Modeling of Opinion Dynamics
In this section, we consider the basics of agent-based modeling (ABM) of opinion dynamics, a popular choice for simulating polarization. In this type of model, a graph represents a collection of “agents” and connections. Making a parallel to reality, agents represent individuals and connections represent acquaintances, while the graph represents a social network. Each agent can express an arbitrary set of opinions, although in several models these are limited to two options for simplicity. In general, agent opinions aim to mirror those of human individuals and can be expressed to various degrees of confidence, with the level of granularity implementation dependent; common options include nominal/discrete values or a continuous interval (Flache et al. 2017). Over time, the state of the model regularly updates during discrete events called time steps and the opinions of agents may change.
Modeling classes and premises
There are three major classes of agent-based models used for opinion dynamics. They are assimilative models, similarity-biased models, and repulsive models (Flache et al. 2017).
Assimilative models operate under the underlying assumption that interacting agents seek to reduce opinion differences. This is the orthodox perspective and is supported by empirical literature and cognitive consistency theories (Cartwright & Harary 1956; Festinger 1957; Friedkin & Johnsen 2011; Heider 1967; Vinokur & Burnstein 1978). Computationally, these models are characterized by the use of scaled weights between agents to capture mutual socioeconomic influence. The resultant system state often depends on the granularity of agent opinions. For instance, continuous models update through a process of social averaging and typically end with a final system state of consensus (DeGroot 1974). On the other hand, nominal interpretations (such as the voter model) have the potential for more sophisticated outcomes. General limitations of this modeling paradigm include the inability to track the development of opinion diversity (Axelrod 1997; Hegselmann & Krause 2002).
Similarity-biased models assume agents prefer interaction with like-minded neighbors. This paradigm is also supported by classic literature, such as social judgement theory and homophily (Lazarsfeld & Merton 1954; McPherson et al. 2001; Sherif & Hovland 1961). Computational implementations include probabilistic homophily and bounded confidence, the strength of which can be modified through the presence of tunable parameters. The final outcome of the model depends on these parameter choices as well as on the opinion change function that the model implements. For instance, if bounded confidence is coupled with assimilation dynamics a narrow margin for agreement will lead to fragmentation, while larger confidence thresholds result in opinion clustering or global consensus (Deffuant et al. 2000; Flache et al. 2017; Hegselmann & Krause 2002). Despite its versatility, limitations of these models involve sensitivity to noise (Flache et al. 2017; Flache & Macy 2011). Averaging models are also not capable of producing extreme outcomes without further assumptions on the presence of stubborn “extremists” or more complex opinion structures (Banisch & Olbrich 2021; Deffuant et al. 2002; Mäs & Flache 2013; Tian & Wang 2017).
The final major category are repulsive models, which assume that it is possible for differentiation to occur. This is more of a revisionist perspective which reframes some of the social theories mentioned above to allow for negative influence (Baldassarri & Bearman 2007; Flache et al. 2017; Jager & Amblard 2005). Computationally, this is represented by allowing weights to be negative. Repulsive models demonstrate the widest variety of final system states, including fragmentation, extreme consensus, and structural polarization. Nevertheless, a fundamental limitation is high sensitivity to initial conditions (Flache et al. 2017). There is also limited contemporary empirical justification for the underlying social premises. For instance, Takács et al. (2016) observed that opinion difference and general dislike did not cause negative influence in a controlled online communication setting.
Alternative modeling classes also exist. One such approach involves argument-based models. These assume that the opinion of an agent is defined by a set of pro and con arguments which are exchanged in interaction (Banisch & Shamon 2021; Betz 2022; Mäs & Flache 2013; Taillandier et al. 2021). Another modeling class, which we dub the public-private split model, is unique in that it distinguishes between public expressions of and private convictions in opinions. In these models individuals express their opinion and react to approval and disapproval by their peers (Banisch & Olbrich 2019). Interactions between agents on the same side of the opinion spectrum lead to increased private confidence, while interactions between agents that express opposing opinions decrease it. A motivation for this approach is the sociological concept of pluralistic ignorance, which involves the dissonance between public expression and private opinions caused by social pressure (Asch 1955; Huang & Wen 2014; Mitsutsuji & Yamakage 2020). This, for instance, is relevant in the opinion dynamics of war-moods (Mitsutsuji & Yamakage 2020). Computational implementations of the approach differ. Martins (2008) leveraged a combination of Bayes rule and random walk theory to propose the CODA model, which can additionally be integrated with bounded confidence (Martins 2008; Zhan et al. 2022). Recently, Banisch & Olbrich (2019) proposed an implementation inspired by reinforcement learning/reward driven techniques and neurobiology studies (cf. Banisch et al. 2022). Note that despite not leveraging similarity-bias or negative influence, this model class is able to demonstrate a variety of outcomes such as polarization, consensus, and extreme convictions.
We decide to extend the public-private split model from Banisch & Olbrich (2019) for analysis due to its theoretical alignment with concepts from the Social Media Characterizations section. Specifically, the split between public and private expressions can be interpreted as an abstraction of the disinhibition effect, while the reward-driven neurological inspiration of the model parallels the underlying neural theory of social media platforms.
Representing social media computationally
In ABM, a common approach for representing social media has been through similarity-biased models and homophily. In general, homophily represents the social phenomenon in which individuals with similar opinions, personalities, or cultures are more likely to communicate with each other (McPherson et al. 2001). Within the context of ABM for opinion dynamics, homophilic interactions are often represented through a tunable numeric parameter which limits the extent to which agents can engage with discordant neighbors. The most common forms of computational implementation are probabilistic homophily, where interaction probabilities are weighted according to the relative similarity of a given neighbor, and bounded confidence, where neighbors beyond a specified upper bound for opinion difference are ignored (Banisch et al. 2010; Baumann et al. 2020; Carley 1991; Hegselmann & Krause 2002; Keijzer & Mäs 2022; Mäs & Bischofberger 2015).
We first outline probabilistic homophily, which often involves representing homophily as a continuous probabilistic distribution (Axelrod 1997; Carley 1991). For instance, in a popular variant by Axelrod (1997) different agents are assigned a “culture” with five traits. The probability distribution is then derived through a “similarity score,” which is a discrete metric directly proportional to the number of matched traits (Axelrod 1997). Other variations have been designed specifically to model the effects of social media. Mäs & Bischofberger (2015) accounted for the presence of personalization in social media through a power law decay implementation of probabilistic homophily, and Baumann et al. (2020) modeled social media algorithms using a similar approach; the latter was empirically verified through Twitter data.
The bounded confidence implementation differentiates itself by being more binary in nature (Hegselmann & Krause 2002). The concept was introduced by Hegselmann & Krause (2002), and involves a numerical threshold \(\gamma\) for a given agent. During the update step, all potential neighbors with an opinion difference greater than \(\gamma\) are ignored. The relative simplicity of this method has made it an object of analysis across several studies. For instance, Ben-Naim et al. (2003) observed that varying \(\gamma\) has a complex impact on the final system state. Others have developed extensions upon the basic premise to model social interactions online (Del Vicario et al. 2017; Sîrbu et al. 2019).
The structure of social media has been less accounted for in the literature; nevertheless, there are some relevant studies. For instance, Dong et al. (2021) characterizes social media interactions by considering a disjoint set of online and offline agents. Another approach includes using multi-layered/multiplexed models, which incorporate an ensemble of agent networks to represent alternative communication channels (Hristova et al. 2014; Peng & Porter 2022). In this study, we introduce a novel “virtual worlds” framework similar in concept to multi-layered models; this involves a set of online parallel agent networks which agents from the offline “real world” can “log in” to with probability \(\lambda\). The virtual worlds are complete, which reflects the general absence of socioeconomic influence and the erosion of geographic limitations due to the disinhibition effect (Suler 2004). The virtual exploration rate parameter \(\lambda\) provides a variable abstraction of the addiction effect in social media; a higher \(\lambda\) represents a greater ability for the platform to distract users. We additionally incorporate homophily, and to account for the empirical results discussed in Bakshy et al. (2015) it is used as a general social premise at both the real world and virtual world levels. The implementation of probabilistic homophily from Mäs & Bischofberger (2015) is adopted due to its ease-of-use and reliability.
Methodology
In this section, we first outline the public-private split model by Banisch & Olbrich (2019), which serves as a computational basis for this work. Next, we introduce the virtual worlds framework and detail how it represents an abstraction of an online social media platform. We then describe relevant parameters in our analysis, such as \(\alpha\) (learning rate) and \(\varepsilon\) (exploration rate) from the original model and \(h\) from the computational implementation of probabilistic homophily. We finally discuss metrics used to quantitatively analyze simulation runs and additionally conceptualize the notions of structural and un-structural polarization.
Theoretical framework
Public-private split model
The public-private split model is a novel ABM implementation which leverages reinforcement learning concepts in addition to the standard framework for opinion updates (Banisch & Olbrich 2019). In this model, each agent \(a_i\) expresses a publicly visible opinion \(o_i \in \{-1, 1\}\)1 and carries an associated private confidence for both opinions \(Q_i(1), Q_i(-1) \in [-1, 1]\). The publicly visible opinion follows:
| \[o_i = arg\,max \: Q_i(o) \text{, where } o \in \{-1, 1\}\] | \[(1)\] |
This means that the opinion with higher confidence is expressed in agent interactions. Occasionally however the agent may choose to express the opposite opinion with probability \(\varepsilon\); this parameter is called the exploration rate. While the exploration rate is a fixed parameter in Banisch & Olbrich (2019), in this work we will incorporate a more adaptive variant in which \(\varepsilon\) becomes smaller as agents become more convinced in their opinions. This extension will be discussed more in detail in the Public-private split parameters section.
After specifying the values of relevant parameters, the simulation begins by creating a random graph of agents and then progresses for \(n\) time steps. At a given time step \(t\), an agent \(a_i\) is randomly selected. Among potential candidates, an agent \(a_j\) is randomly matched and the pair play a “game.” The public opinions \(o_i\) and \(o_j\) are compared: if the agents agree (i.e., \(o_i = o_j\)), then \(a_i\) had a “positive” experience and \(a_i\)’s private confidence increases. Otherwise, the opposite occurs (Banisch & Olbrich 2019). The update step can be defined according to the Q-learning update canonical form as:
| \[ \left[\begin{array}{c}Q_i(o_i) \\ Q_i(o_i')\end{array}\right] \leftarrow \begin{cases} \left[\begin{array}{c}Q_i(o_i) + \alpha \left(o_i o_j - Q_i(o_i)\right) \\ Q_i(o_i')\end{array}\right] & \text{w.p. } 1 - \varepsilon \\ \\ \left[\begin{array}{c}Q_i(o_i) \\ Q_i(o_i') + \alpha \left(o_i' o_j - Q_i(o_i')\right) \end{array}\right] & \text{else} \end{cases}\] | \[(2)\] |
Here, \(o_i\) is the public opinion of \(a_i\) (either 1 or -1) and \(o_i'\) is the other opinion; in general, agents favor agreement over disagreement. The parameters \(\alpha\) and \(\varepsilon\) are the learning rate and exploration rate respectively and are discussed more in depth in the later Public-private split parameters section.
Spatial random graph
Agent-based models are typically initialized using scale-free graphs and small-worlds graphs (Flache & Macy 2011). The implementation from Banisch & Olbrich (2019) is unique in that it leverages a spatial random graph topology, which is a special case of the Erdos-Renyi random graph. A description is as follows: suppose we assign the 2D spatial coordinates \((x_i,\ y_i)\) to agent \(a_i\). We define \(E\) as the set of all possible edges, and additionally define \(C\subseteq E\) as the subset of edges which exist. Then, the probability of the edge \(e_{ij} \in E\) which connects agent \(a_i\) and agent \(a_j\) existing is:
| \[P\{e_{ij} \in C\} = \begin{cases} 1 & \text{if} \sqrt{(x_i - x_j)^2 + (y_i - y_j)^2} < r \\ 0 & \text{otherwise} \end{cases}\] | \[(3)\] |
In other words, if the distance between two agents is less than a previously defined radius \(r\), then the connecting edge will be created. The primary motivation for this topology over others is that it generates a spatial clustering which mimics the impact that sociodemographic factors have on spatial filtering and community formation. This is an appropriate model for the primary network/real world in our study as it captures the vast sociodemographic diversity present among potential social media platform users.
Virtual worlds
We introduce a novel virtual worlds infrastructure for representing online social media interaction. This is implemented through an additional set of \(m\) parallel agent networks, each of which is complete. We enforce this characteristic due to the relative socioeconomic and geographic anonymity provided by social media, which contrasts the primary network/real world described in the Spatial random graph section (Suler 2004).
A set of \(m\) virtual worlds begin empty and become populated as the simulation progresses (intuitively akin to subreddits on the social media site Reddit). At time step \(t\), the chosen agent \(a_i\) decides to enter a virtual world with probability \(\lambda\) instead of immediately choosing a match as described in the Public-private split model section. The agent then evaluates the \(m\) parallel virtual worlds based on the ratio of publicly concordant members to publicly discordant members. For instance, consider the \(k^{th}\) virtual world \(v_k\). Additionally, let \(o_i \in \{-1, 1\}\) represent the public opinion for agent \(a_i\) and let \(o_i'\) be the other opinion. We define the number of members with opinion \(o = o_i\) as \(f_{agree}\) and the number of members with opinion \(o = o_i'\) as \(f_{disagree}\). Then the evaluation \(\chi_k\) of the \(k^{th}\) virtual world \(v_k\) is:
| \[\chi_k = \frac{f_{agree} + 1}{f_{disagree} + 1}\] | \[(4)\] |
Adding one to the numerator and denominator smooths the metric and prevents the possibility of a division by zero (i.e., this can occur if the virtual world is homogeneous in opinion or it is completely empty). This type of evaluation of the virtual worlds is inspired by social identity theory, which posits that individuals compare their ingroup and outgroup in relative rather than absolute terms (Brewer 1999; Tajfel & Turner 2004; Weisel & Böhm 2015).
The agent \(a_i\) then generates a probability \(p_k\) for the \(k^{th}\) virtual world \(v_k\) according to the softmax function:
| \[p_k = \frac{e^{\chi_k}}{\sum_{i=1}^{m}e^{\chi_i}}\] | \[(5)\] |
After randomly selecting a virtual world \(v_r\) according to the softmax probability distribution, the agent \(a_i\) “creates an account” if it has not visited \(v_r\) before by establishing links with every other agent in \(v_r\); this link creation step enforces the complete nature of the virtual worlds. Otherwise, the agent \(a_i\) simply “logs-in” and does not create any additional links. The agent \(a_i\) then continues with the game described in the Public-private split model section, albeit limited to randomly matching with neighbors in \(v_r\). In the edge case where \(v_r\) is empty (i.e., \(a_i\) is the first to join), \(a_i\) defaults to interacting with its usual set of neighbors from the real world.
Model summary
In this study, we simulate a set of \(N\) agents \(\mathcal{A} = \{a_i : 1 \leq i \leq N\}\). Each agent \(a_i\) will follow the opinion model described in the Public-private split model section; specifically, every agent will have a private confidence and a public opinion, and opinion updates after matching will leverage Equation 2.
The topology of the simulation is described in Figure 1. We incorporate a primary network/real world according to the structure discussed in the Spatial random graph section and an additional \(m\) virtual worlds according to the form detailed in the Virtual worlds section. Note that the the set of agents \(\mathcal{A}\) is constant throughout both the real world and virtual worlds; essentially, the purpose of the \(m + 1\) total worlds is to dynamically adjust the matching process before two agents interact with each other.

Computational framework
Public-private split parameters
We briefly consider two important parameters in the public-private split model: the exploration rate \(\varepsilon\) and the learning rate \(\alpha\).
The exploration rate \(\varepsilon\) is a probability (restricted to \(0 \leq \varepsilon \leq 1\)) which dictates whether an agent \(a_i\) during an interaction expresses the opposite to their current public viewpoint \(o_i\). The sociological objective of this parameter is to parallel the uncertainty individuals have in their own opinions, while the computational objective is to allow the confidence level associated with the opposing viewpoint to update periodically as per reinforcement learning theory. In the original public-private split model, the exploration rate is immutable (Banisch & Olbrich 2019). The exploration rate is modified in this work to be more adaptive by using a softmax-like function:
| \[\varepsilon = \frac{e^{\beta\cdot Q(o_i')}}{e^{\beta\cdot Q(o_i')} + e^{\beta\cdot Q(o_i)}}\] | \[(6)\] |
This implementation acknowledges that strongly convinced agents are less likely to change their opinions. A parameter \(\beta\) is introduced to dictate how soft or hard the max is.
The learning rate \(\alpha\) is a positive scaling factor that controls the amount to which interactions among agents can adjust private confidence levels (Banisch & Olbrich 2019). For instance, a large learning rate corresponds to a situation in which disagreements among agents greatly impact confidence values, making opinion flipping more likely.
Probabilistic homophily parameter
As discussed in the Representing social media computationally section, our model incorporates probabilistic homophily. We adapt the variant from Mäs & Bischofberger (2015), where the probability \(p_{j, t}\) that an agent \(a_i\) will contact an adjacent agent \(a_j\) at time step \(t\) follows:
| \[sim_{ij, t-1} = 1-\frac{|\Delta Q_{i, t-1}-\Delta Q_{j, t-1}|}{4}\] | \[(7)\] |
| \[p_{j, t} = \frac{\left(sim_{ij, t-1}\right)^h}{\sum_{j=1, j\neq i}^{N}\left(sim_{ij, t-1}\right)^h}\] | \[(8)\] |
Here we define \(\Delta Q_{i, t-1} = Q_{i, t-1}(1)-Q_{i, t-1}(-1)\) as the agent’s conviction, with notation borrowed from the Theoretical framework section. \(\Delta Q_{j, t-1}\) is defined analogously. An extra factor of \(\frac{1}{2}\) is introduced in the similarity metric to account for the fact that \(\Delta Q_{i,\ t-1}, \Delta Q_{j, t-1}\in[-2, 2]\). In general, the probability of a connection decreases as the difference in agent conviction increases.
The parameter \(h\) is of interest, as it directly impacts the extent to which concordant interactions are favored. Specifically, a greater value of \(h\) exponentially increases the weight of similar neighbors and vice versa. By tuning this, we can adjust underlying social assumptions about the innate propensity for individuals to seek out like-minded neighbors. Given the persistence of human-driven homophily in social media platforms (which is possibly enhanced by social media algorithms), we incorporate these effects in both the real world and virtual worlds (Bakshy et al. 2015; Baumann et al. 2020; Mäs & Bischofberger 2015). Note that from a computational perspective, this replaces the uniform probabilistic distribution assumed with the original public-private split model (Banisch & Olbrich 2019).
Virtual exploration rate parameter
The virtual exploration rate \(\lambda \in [0, 1]\) is a parameter which represents the probability an agent \(a_i\) decides to explore virtual worlds. We leverage the modeling assumption that \(\lambda\) is probabilistically independent of each individual \(p_k\) generated, using notation from the Virtual worlds section. This reflects how the act of opening a social media application does not eventually impact the actual content consumed.
Code availability
Banisch & Olbrich (2019) have provided MATLAB code that implements the model from the Public-private split model section. We expand on this framework and write code to represent the virtual worlds data structure and probabilistic homophily implementation. The model code can be found at CoMSES through https://www.comses.net/codebases/731b221c-438c-4ffa-b2c1-006a253a5999/releases/1.0.0/ or at GitHub via https://github.com/djapp18/VirtualWorlds-ABM/tree/main.
Simulation metrics
The model proposed in this paper may give rise to global consensus or opinion bi-polarization depending on the model parameters. In the context of the model, polarization means that agents develop and stabilize on strong convictions in opposing opinions. However, the model features two distinct types of bi-polarization which we refer to as structural and un-structural polarization. They differ with respect to how diverging opinions are distributed over the spatial random graph (see Figure 2). Therefore, in addition to standard measures that distinguish between a uni-modal consensus and a bi-modal polarized distribution (Bramson et al. 2016; DiMaggio et al. 1996), we implement a network-based measure to distinguish between these two different forms of polarization.
Consensus versus polarization
In order to differentiate consensus from bi-polarized opinion profiles we follow previous work (Banisch & Olbrich 2019; Bramson et al. 2016; DiMaggio et al. 1996; Mäs & Flache 2013) and consider the dispersion metric, which is the variance over the distribution of convictions
| \[\sigma^2=\frac{1}{N-1}\sum_{i=1}^N\left(\Delta Q_i-\Delta\bar{Q}\right)^2.\] | \[(9)\] |
Another characteristic that we track to characterize the emergent model distributions is the magnitude of average conviction (absolute value of the mean) which characterizes the shift of the distribution
| \[ |\Delta\bar{Q}| = \left|\frac{1}{N}\sum_{i=1}^N \Delta Q_i \right|.\] | \[(10)\] |
Structural versus un-structural polarization
While the distributions of convictions is sufficiently characterized by its mean and variance, a mesoscopic view on the system is needed to distinguish between structural and un-structural polarization. Here the question is how agents with opposing opinions are distributed over the network. The social feedback model by (Banisch & Olbrich 2019) predicts polarization along structural holes between different network communities. As illustrated on the left of Figure 2, structural polarization is characterized by within-community alignment and across community alienation. On the other hand, models of homophily or bounded confidence (Deffuant et al. 2000; Hegselmann & Krause 2002) predict polarization even in completely connected graphs. On a network with communities, this leads to un-structural polarization in the sense that opinions of opposing sign co-exist within structural groups (i.e. network communities). This is illustrated on the right of Figure 2.
Notice that the spatial distribution of opinions over the network has a strong impact on how individuals perceive the current state of the system. Under structural polarization most neighbors share the same opinion creating an "illusion of consensus" for agents at both sides of the opinion spectrum. In the latter case of un-structural polarization instead, many agents have close neighbors with whom they disagree and thus agents have the impression of a polarized opinion landscape.
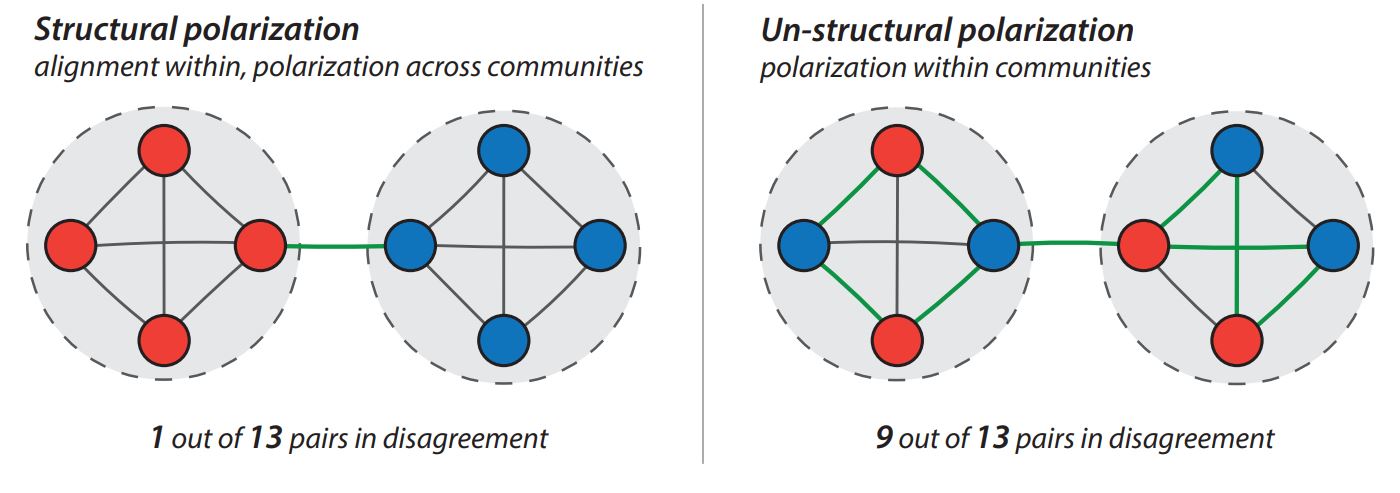
We quantify this aspect by the relative number of neighbors that are in disagreement. Let us denote as \(o_i = \text{sign}(\Delta Q_i)\) the opinion of agent \(i\). If the total number of undirected edges in the network is \(|E|\), the relative number of linked agent pairs with different opinions is:
| \[n_d = \frac{1}{|E|} \sum_{(i,j) \in E}^{} \frac{1}{2}(1-o_i o_j)\] | \[(11)\] |
The two examples shown in Figure 2 illustrate how the total effective antagonism differentiates between structural and un-structural polarization. On the left, there is only one connection that links agents with opposing opinions (green). 12 out of 13 edges connect agents that agree to one another so that the total effective antagonism becomes very low (\(n_d = 1/13\)). On the right-hand side of Figure 2 instead 9 out of 13 agent pairs connected by the graph are at disagreement leading to \(n_d = 9/13\). The measure is bound to the unit interval \(n_d \in [0,1]\) but extremal values of zero or one become possible in special cases. For instance, the measure is zero in the case of global consensus or if different opinions coexist in disconnected communities of the graph. On the other hand, it may reach one in low-dimensional lattices, for instance, on rings with an even number of nodes and opinions switching from node to node.
On a SRG with random assignment of opinions (initial condition) \(n_d \approx 0.5\) meaning that around half of the edges are between unequal and the other half between equal opinions. Under the model dynamics the total effective antagonism does not reach higher values, but reduces to values close to zero if polarization becomes structural (see, e.g. Figures 4 b and 6 b). A low value of effective antagonism hence characterizes a high level of structural polarization.
Virtual worlds metrics
We also compute the following virtual world metrics at the end of each simulation run. Specifically, we introduce a metric designed to track polarization among a set of \(m\) virtual worlds called virtual world dispersion.
| \[\sigma_V^2=\frac{1}{m-1}\sum_{k=1}^m\left(\Delta\bar{Q}_{v_k}-\Delta\bar{Q}_{v}\right)^2.\] | \[(12)\] |
Each \(\Delta\bar{Q}_{v_k}\) represents the average over the convictions in virtual world \(v_k\), and is computed similarly to Equation 10 but without taking the absolute value.
Additionally,
| \[\Delta\bar{Q}_{v} = \frac{1}{m}\sum_{k = 1}^m \Delta\bar{Q}_{v_k}\] | \[(13)\] |
Social analysis framework
We will also determine the social theoretical implications of social media platforms by analyzing the data from our model. One manifestation of this method involves assigning social representations to key parameters within a computational model/algorithm and considering the impact of different tunings on final outcomes. Rieder (2012) leverages this kind of methodology while investigating Google’s PageRank algorithm. He first evaluates the algorithm within its broader historical context, and then actively adjusts a “damping factor” parameter to observe how the algorithm reacts (Rieder 2012). He concludes by remarking on the hypothetical state of the internet if different values were chosen for the damping factor. This serves as an important reference by demonstrating how to systematically interpret quantitative results based on different social assumptions of how users interact with software.
Results
Equivalency testing
As discussed in the Public-private split parameters section, we adjust the exploration rate parameter so that it now follows an adaptive softmax implementation instead of a constant value. To ensure that this adjustment preserves the social outcomes associated with the original model, in this section we check for consistency in the final system states of the two implementations. We perform this check to ensure that the modelling and social assumptions encoded within the original public-private split model are still valid for the adjusted model. Indeed, if final system states were vastly different, this would imply that the addition of the softmax implementation destructively interferes with the remainder of the original model; as a result, a more through investigation into the sociological cause for such a difference would be required.
We leverage exemplary parameter settings of \(\alpha = 0.1\), \(N = 100\), and \(r = 0.225\) for both implementations. Additionally, for this specific experiment we have \(m = 0\) virtual worlds in order to maintain compatability with the original model (Banisch & Olbrich 2019). The simulations run for \(n = 20000 \cdot N\) time steps. Despite the innate inability to draw a direct equivalency between the parameters \(\varepsilon\) and \(\beta\), we set \(\varepsilon = 0.1\) and \(\beta = 1\); the choice of the latter ensures at maximum conviction the adaptive exploration rate reaches a minimum of \(0.1192 \approx 0.1\). Additionally, while comparing simulations we ensure that both models encounter the same pseudo-random events. Intuitively, we expect to see some similarities between the final system states of both implementations. This is because as discussed previously, at maximum conviction the adaptive exploration rate approximates the constant implementation. When conviction is low, the adaptive exploration rate will be much higher than the constant implementation; however, at this point the associated agent is primed to flip its opinion regardless.
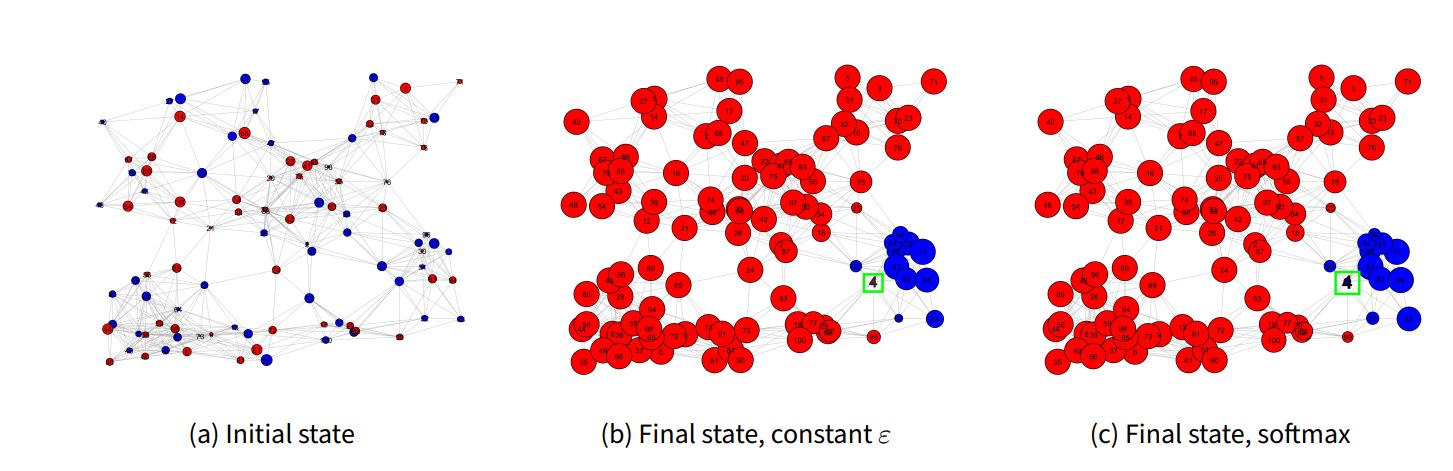
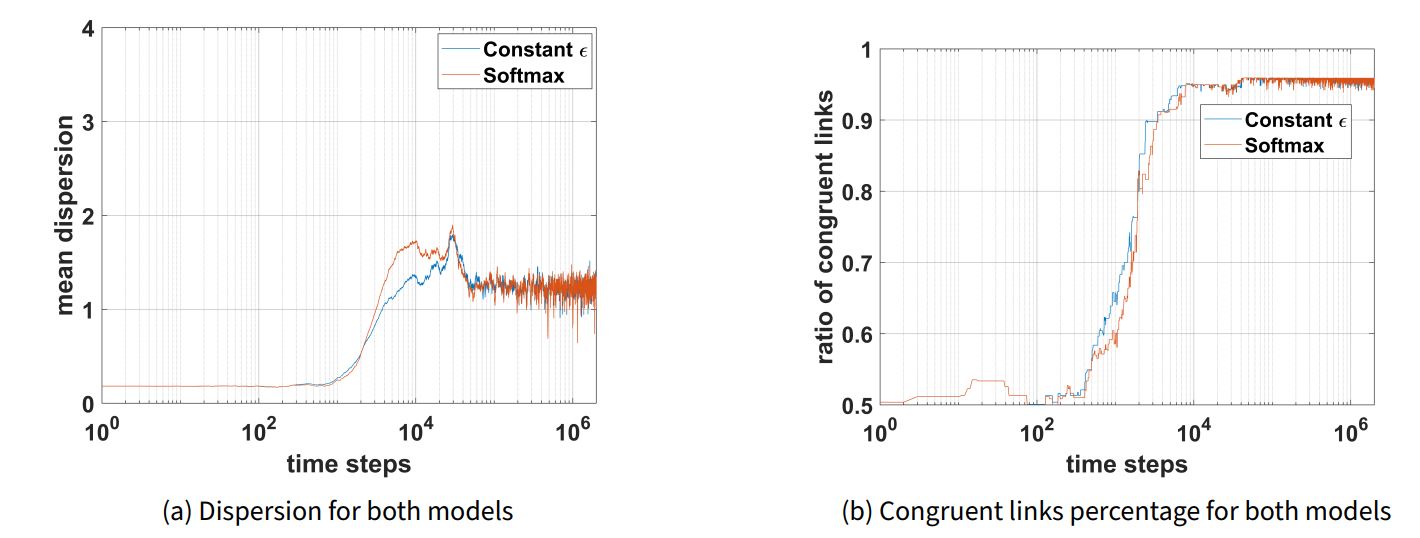
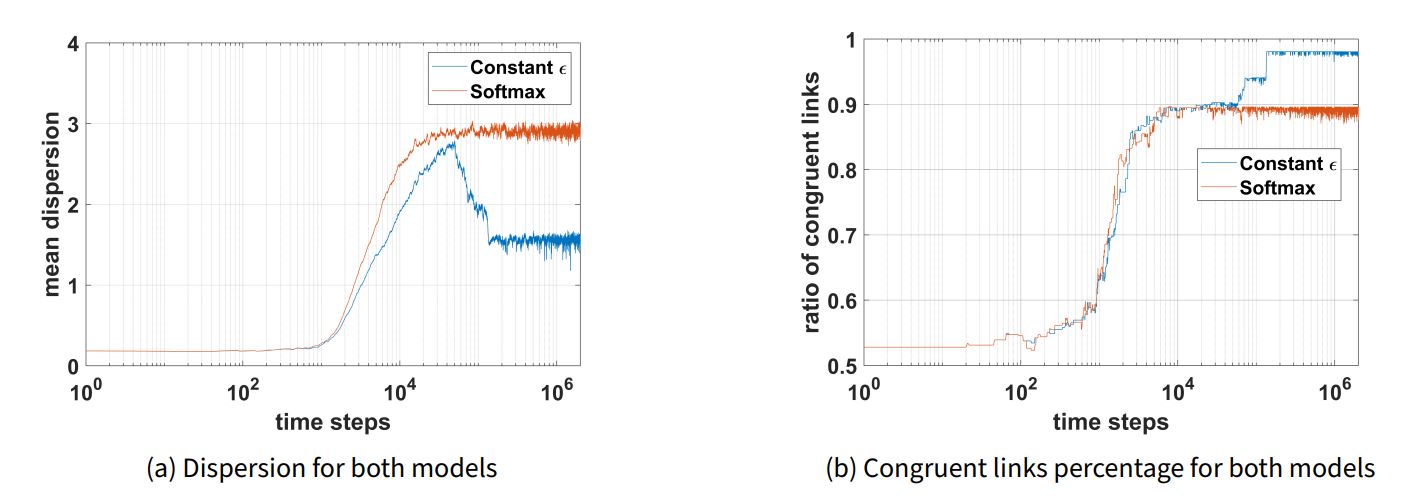
After running simulations for both implementations, we found that they often demonstrated similar quantitative and qualitative results. Figure 3 shows a case in which the results were similar and end in structural polarization. In both models the final system state is qualitatively the same, except for a few agents (i.e., agent 4 is opinion “red” in the constant exploration rate model, but is opinion “blue” in the softmax model). Quantitative agreement among the two implementations is also clear when inspecting the polarization metrics in Figure 4. For instance, dispersion in both models peaks at \(~30000\) time steps with a value of \(~1.87\), then declines and stabilizes around \(1.25\) (see Figure 4 a). Congruent links percentage in both models demonstrates a sharp increase, followed by stabilization at \(~40000\) time steps around a value of \(96\%\) (see Figure 4 b). Note that final dispersion is high, and final congruent links percentage is high (but not \(100\%\)) as expected for structural polarization. In general, the softmax implementation seems to fluctuate more, possibly because of its adaptive nature.
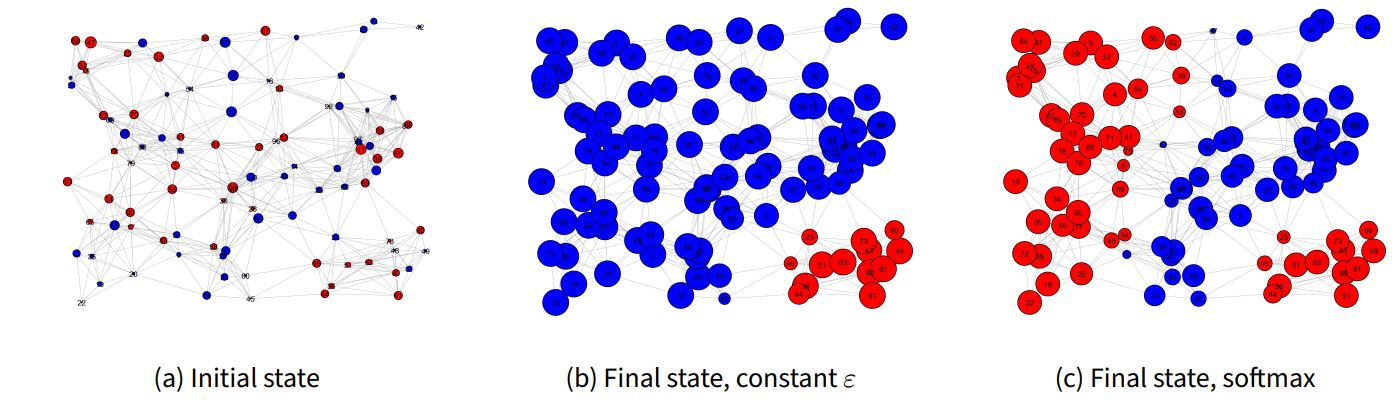
On the other hand, occasionally the two implementations demonstrated different results. Figure 5 shows such a case in which both models lead to structural polarization, although the final structures are different. Qualitatively, the constant exploration rate model features a large opinion “blue” cluster with a small opinion “red” cluster, while the softmax model features a medium opinion “blue” cluster and two disconnected opinion “red” clusters. Additionally, a comparison of the polarization measures in Figures 6 a and 6 b reveals quantitative disagreement among the two implementations. For instance, dispersion stabilizes around \(1.6\) for the constant exploration rate model but stabilizes around \(2.9\) for the softmax model. For congruent links percentage, stabilization occurs around \(98\%\) for the constant exploration rate model but \(89\%\) for the softmax model. Note that despite visual differences in final system state, there is still internal consistency among the qualitative and quantitative metrics for both models. Final dispersion is low and final congruent links percentage is high (but not \(100\%\)) for the constant exploration rate model, which agrees with the qualitative observation of a final system state close to consensus. Additionally, final dispersion is high and final congruent links percentage is low for the softmax model, which aligns with the qualitative observation of a final system state in structural polarization with disconnected groups. Unlike the previous example, fluctuations occur in the polarization metrics for both models.
To determine which of the cases above is more common, we systematically checked for general quantitative and qualitative agreement across several trials. Specifically, we applied a simple heuristic which considered the two models to be equivalent if at least \(95\%\) of agents demonstrated the same public opinion. This cutoff was chosen as it enabled some leniency for opinion flips on boundaries, but prevented the possibility for major structural differences in the final system states. After running 100 simulations, it was found that \(63\%\) of cases ended with the two models in agreement. Given that the same common parameter settings are used in subsequent analysis, we consider the two models to be equivalent for the purposes of this work. A more rigorous statistical investigation is not within the scope of this paper.
Virtual worlds testing
We now demonstrate an illustrative run of the virtual worlds framework, with \(m = 2\) virtual worlds. We set \(\alpha = 0.01\), \(\beta = 1\), \(N = 100\), and \(r = 0.225\). Additionally, we set \(h = 4\) and \(\lambda = 0.4\). The simulation runs for \(n = 20000 \cdot N\) time steps.
Figure 7 shows the initial and final states of the model and Figure 8 shows relevant time-series data. Note that the final system state does not seem to have large clusters, suggesting the presence of un-structural polarization in the real world; this is supported quantitatively by a high final dispersion around \(3.8\) and a low final congruent links percentage around \(52\%\). Simultaneously, there is structural polarization in the virtual worlds; this is clear as the virtual world evaluation ratio \(\chi_1\) stabilizes around \(1.25\) while \(\chi_2\) ends around \(-1.20\). Interestingly, the congruent links percentage and the virtual world ratios are constant from \(~160000\) time steps onward. This aligns with the qualitative observation that only three agents ultimately flip their public opinion by the final system state (agents 45, 47, 93).
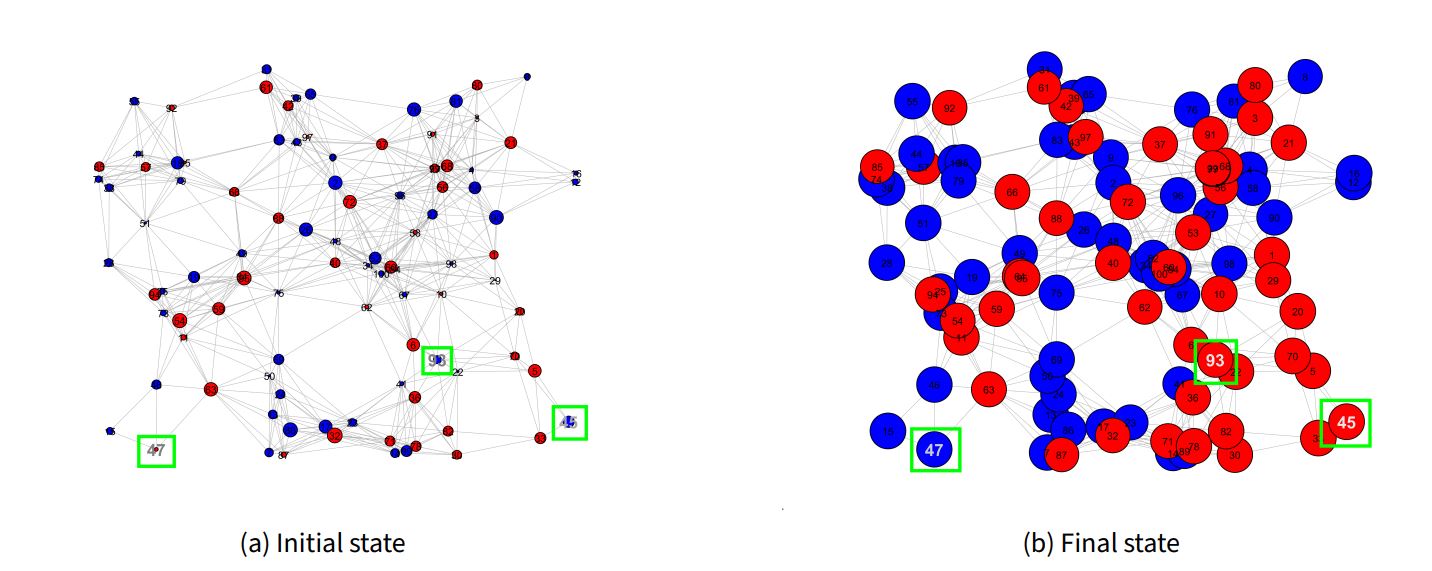
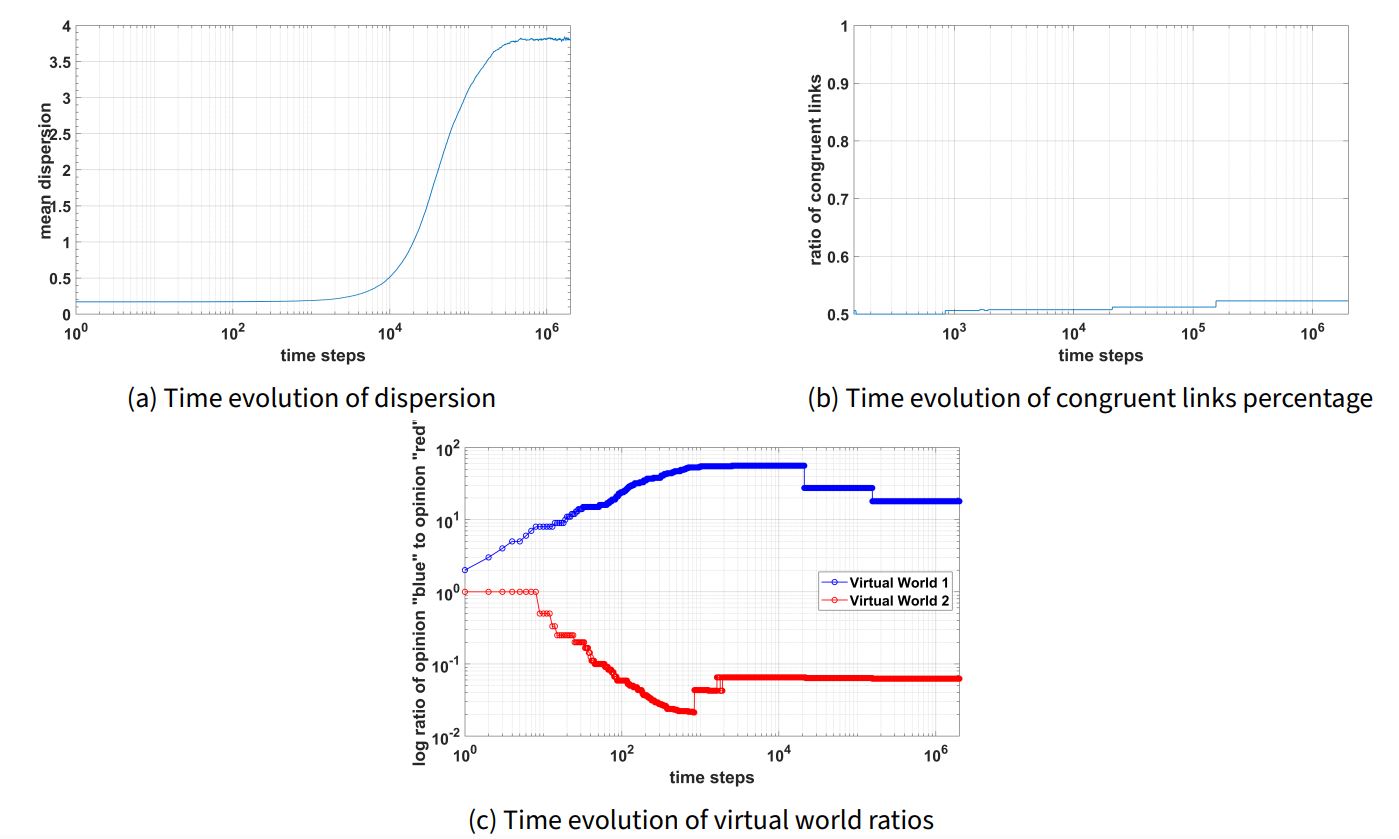
The sample run outlined here reveals the possibility for structural polarization to form at the virtual world level despite the underlying peer influence level demonstrating un-structural polarization. It suggests that agents can engage in a broader society with a tangible number of discordant contacts (i.e., this corresponds to the relatively low final congruent links percentage) and yet simultaneously participate in a social media platform which is clearly bipolarized. Additionally, the observation that few agents flip their public opinion by the end implies that the dynamics of this type of polarization is “in situ”: the presence of homophily and a social media platform has the combined effect of making initial convictions more extreme.
\(h - \lambda\) grid search
We now perform a \(h - \lambda\) grid search to determine the impact of these parameters on polarization and gain further insight into our model. We continue to let \(m = 2\), \(\alpha = 0.01\), \(\beta = 1\), \(N = 100\), \(r = 0.225\) and run simulations for \(n = 20000 \cdot N\) time steps. Within the grid we vary \(h \in \{0, 2, 4, 6\}\) and \(\lambda \in \{c \cdot 0.05 : 0 \leq c \leq 10, c \in \mathbb{Z}\}\), with 100 trials for each point.
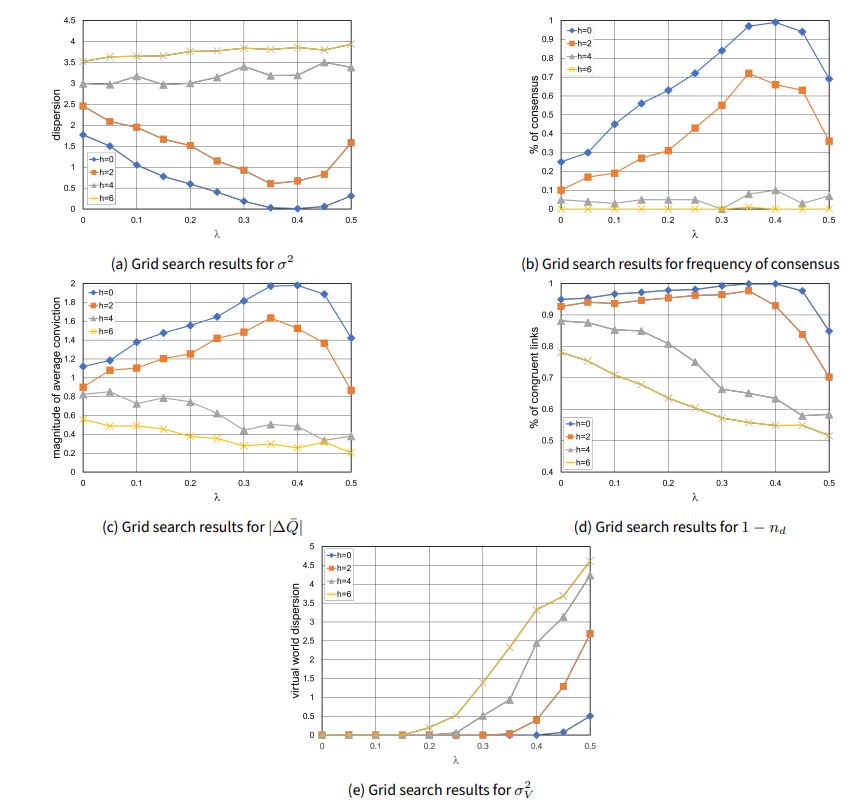
Figure 9 shows the results of this computational experiment. We note that in general an increase in \(h\) leads to higher dispersion and reduced chance of consensus (see Figures 9 a, 9 b, and 9 c). Interestingly, \(\lambda\) seems to impact the metrics differently depending on the value of \(h\). For instance, when \(h \leq 2\), increasing \(\lambda\) leads to less dispersion until the inflection point of \(\lambda = 0.4\); this is possibly due to the complete nature of the virtual worlds overcoming weak homophily and leading to consensus (i.e., in general a complete network tends towards consensus as demonstrated in Banisch & Olbrich (2019)). On the other hand, when \(h \geq 4\), increasing \(\lambda\) consistently leads to greater dispersion; it is likely that in this regime the homophily is strong enough to overcome the complete nature of the virtual worlds.
The metrics also reveal important information about the types of polarization occurring during the simulations. In the real world, increasing \(\lambda\) has the general effect of reducing the congruent links percentage and making polarization more un-structural (see Figure 9 d). For instance, when \(h \leq 2\) there is a pivot in final system state from extreme consensus to un-structural polarization at the inflection point \(\lambda = 0.4\). When \(h \geq 4\), a transition from structural polarization to un-structural polarization is prominent around \(\lambda = 0.2\) to \(\lambda = 0.3\). In the virtual worlds, increasing \(\lambda\) makes the virtual world dispersion greater and introduces structural polarization; this effect is most pronounced when homophily is also high (see Figure 9 e). Indeed, congruent links percentage being low and virtual world dispersion being high when \(\lambda\) and \(h\) are both high gives further validation for the single run analysis performed in the Virtual worlds testing section.
Discussions
By analyzing the impact of virtual exploration \(\lambda\) and homophily \(h\) on polarization metrics from the previous section, we can leverage the methodology described in Rieder (2012) and perform a social commentary. We reference the discussions from the Representing social media computationally section and consider \(\lambda\) to represent the extent to which a social media platform is addictive and \(h\) to represent the propensity of individuals to prefer concordant perspectives.
When homophily is not present, increasing \(\lambda\) results in no polarization at the virtual world level and increases the chance of consensus at the peer influence level. Thus, under the social assumption that agents do not demonstrate preferences for their interactions, this implies that the more addictive a particular social media platform is the more likely agents arrive at consensus. Indeed, under such an assumption the presence of a social media platform simply provides agents the capability to interact with a larger body of neighbors beyond the restrictive space defined by \(r\); coupled with the social assimilative features encoded within the original public-private split model, the trend in consensus aligns with expectation.
Different trends are observed when homophily is present. As \(\lambda\) increases, structural polarization begins to appear at the virtual world level and un-structural polarization becomes more common at the peer influence level. Thus, a relatively addictive social media platform coupled with homophilic preferences has the combined effect of leading to a situation in which agents may be individually exposed to discordant perspectives but nevertheless contribute to structural polarization at the virtual worlds level. A possible intuition is that when a social media platform is addictive, agents are less likely to connect with possibly discordant real world neighbors and instead will log-in to social media. Here, high homophily augments initial convictions and leads to a positive feedback mechanism in which agents begin to prefer the virtual world with the higher evaluation ratio \(\chi\). This leads to structural polarization at the virtual worlds level. Simultaneously, agents become strongly convinced in their initial opinions leading to un-structural polarization at the peer influence level. In summary, agents become more distant from their real world neighbors due to the “illusion” of consensus in the virtual worlds. Note that the presence of the inflection point around \(\lambda = 0.4\) for \(h \leq 2\) implies that this behavior takes precedence over the model’s natural drive towards consensus. There is thus an imbalance between the influence of \(\lambda\) and \(h\) on the model, with \(\lambda\) having a greater impact. Essentially, the presence of virtual worlds causes the social assimilative features of the original public-private split model to be swapped for repulsion and xenophobia.
Thus, our model suggests that it is possible for agents in a social network to participate in cross-cutting ties while still contributing to structural polarization. The value of our modeling framework becomes more apparent when considering connections to previous studies. For instance, Conover et al. (2011) showed that the social network associated with Twitter is structurally polarized; this result is consistent with our findings within the specific computational regime of \(h \geq 4\) and \(\lambda \geq 0.3\) (i.e., a combination of high homophily and high addictiveness respectively). On the other hand, Bakshy et al. (2015) claimed that the presence of cross-cutting ties among users on Facebook supported the theory that social media platforms are not responsible for polarization (Keijzer & Mäs 2022). The fundamental disconnect between the empirical studies outlined here is that they consider social media platforms from two different frames of reference. The former performs an analysis from a global view, while the latter focuses on the role of individuals and not the platform itself. While resolving this debate will certainly require additional empirical investigation, the results from our computational experiment imply that the innate structure of social media platforms is uniquely conducive to the co-existence of multiple forms of polarization.
Indeed, one important practical implication of our analysis is that un-structural polarization implies the possibility for a society to feature cross-cutting ties (i.e., interaction among those with discordant perspectives) despite the overall presence of bi-polarization. On the other hand, as discussed in Structural versus un-structural polarization, structural polarization means that at the microscopic level most individual agents will experience an “illusion of consensus.” For future work it might not be enough to simply consider the immediate topology; certain types of polarization may only be evident when investigating the relationships among agents from different perspectives (i.e., global vs. group-level vs. individual scale).
Conclusions
In this paper, we expanded on the recently proposed public-private split model by Banisch & Olbrich (2019) through a novel virtual worlds framework in order to investigate polarization in social media platforms. After performing a sensitivity analysis, we discovered that an increase in the addictiveness of a platform can cause structural polarization at the virtual world level with un-structural polarization at the peer influence level. While previous studies disagree on the presence of polarization in social media, our results show that the innate structure of these platforms mandates analysis of resultant opinion dynamics from different perspectives (Bakshy et al. 2015; Conover et al. 2011; Keijzer & Mäs 2022). Indeed, the possibility for different types of polarization to co-exist implies that fixation on any particular frame of reference will ignore key observations.
In general, we note that these results demonstrate the possibility for social media platforms to generate unique forms of polarization. There is thus a need for more ethically designed platforms which are conscious of their innate design. Possible approaches involve associated corporations organizing specialized committees dedicated to analyzing the impact of platforms from a social lens or investigating methods to proactively limit the extent of polarization.
The computational methodology in this study also offers several promising avenues for future work. First, the properties of structural virtual world polarization with un-structural peer influence polarization can be studied further from a theoretical perspective. One approach is to model agent interactions using random processes and perform a sensitivity analysis similar to that in Banisch & Olbrich (2019). Next, we note that the virtual worlds framework was incorporated as an extension to the original public-private split model with little difficulty. One takeaway from this is that the general robustness of the public-private split model in our experimentation has established it as a plausible canonical model. This signals the importance of pivoting to more localized interpretations of social networks in future agent-based models. Another takeaway is that the modular nature of the virtual worlds framework could enable it to be used with other base models to test alternative social assumptions and theories. Finally, an interesting direction to consider is the possibility of online “lurkers” who read but do not participate. In real life several social media platforms do not require users to have an account in order to read content; it will be interesting to simulate scenarios in which these users become polarized without directly engaging with rest of the social network.
Acknowledgements
The first author would like to acknowledge Dr. William Penman at Princeton University for discussions and guidance. We also acknowledge funding from the European Union’s Horizon Europe program under grant agreement No 101094752 (SoMe4Dem -- Social Media for Democracy) for the finalization of the paper.
Notes
In all figures, \(o_i = 1\) is represented by opinion “blue” and \(o_i = -1\) is represented by opinion “red”↩︎
References
AHLGREN, J., Berezin, M. E., Bojarczuk, K., Dulskyte, E., Dvortsova, I., George, J., Gucevska, N., Harman, M., Lämmel, R., Meijer, E., Sapora, S., & Spahr-Summers, J. (2020). WES: Agent-based User Interaction Simulation on Real Infrastructure. Proceedings of the IEEE/ACM 42nd International Conference on Software Engineering Workshops [doi:10.1145/3387940.3392089]
ASCH, S. E. (1955). Opinions and social pressure. Scientific American, 193(5), 31–35. [doi:10.1038/scientificamerican1155-31]
AXELROD, R. (1997). The dissemination of culture: A model with local convergence and global polarization. The Journal of Conflict Resolution, 41(2), 24. [doi:10.1177/0022002797041002001]
BAKSHY, E., Messing, S., & Adamic, L. (2015). Supporting materials for exposure to ideologically diverse news and opinion on Facebook. Science, 348(6239), 35. [doi:10.1126/science.aaa1160]
BALDASSARRI, D., & Bearman, P. (2007). Dynamics of political polarization. American Sociological Review, 72(5), 784–811. [doi:10.1177/000312240707200507]
BANISCH, S., Araújo, T., & Louçã, J. (2010). Opinion dynamics and communication networks. Advances in Complex Systems, 13(1), 95–111. [doi:10.1142/s0219525910002438]
BANISCH, S., Gaisbauer, F., & Olbrich, E. (2022). Modelling spirals of silence and echo chambers by learning from the feedback of others. Entropy, 24(10), 1484. [doi:10.3390/e24101484]
BANISCH, S., & Olbrich, E. (2019). Opinion polarization by learning from social feedback. The Journal of Mathematical Sociology, 43, 76–103. [doi:10.1080/0022250x.2018.1517761]
BANISCH, S., & Olbrich, E. (2021). An argument communication model of polarization and ideological alignment. Journal of Artificial Societies and Social Simulation, 24(1), 1. [doi:10.18564/jasss.4434]
BANISCH, S., & Shamon, H. (2021). Biased processing and opinion polarisation: Experimental refinement of argument communication theory in the context of the energy debate. SSRN preprint. Available at: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3895117 [doi:10.2139/ssrn.3895117]
BAUMANN, F., Lorenz-Spreen, P., Sokolov, I. M., & Starnini, M. (2020). Modeling echo chambers and polarization dynamics in social networks. Physical Review Letters, 124(4), 048301. [doi:10.1103/physrevlett.124.048301]
BEN-NAIM, E., Krapivsky, P. L., & Redner, S. (2003). Bifurcations and patterns in compromise processes. Physica D: Nonlinear Phenomena, 183(3–4), 190–204. [doi:10.1016/s0167-2789(03)00171-4]
BETZ, G. (2022). Natural-Language multi-Agent simulations of argumentative opinion dynamics. Journal of Artificial Societies and Social Simulation, 25(1), 2. [doi:10.18564/jasss.4725]
BRAMSON, A., Grim, P., Singer, D. J., Fisher, S., Berger, W., Sack, G., & Flocken, C. (2016). Disambiguation of social polarization concepts and measures. The Journal of Mathematical Sociology, 40(2), 80–111. [doi:10.1080/0022250x.2016.1147443]
BREWER, M. B. (1999). The psychology of prejudice: Ingroup love and outgroup hate? Journal of Social Issues, 55(3), 429–444. [doi:10.1111/0022-4537.00126]
CARLEY, K. (1991). A theory of group stability. American Sociological Review, 56(3), 331–354. [doi:10.2307/2096108]
CARTWRIGHT, D., & Harary, F. (1956). Structural balance: A generalization of Heider’s theory. The Psychological Review, 63(5), 277–293. [doi:10.1037/h0046049]
CHO, J., Ahmed, S., Hilbert, M., Liu, B., & Luu, J. (2020). Do search algorithms endanger democracy? An experimental investigation of algorithm effects on political polarization. Journal of Broadcasting & Electronic Media, 64(2), 150–172. [doi:10.1080/08838151.2020.1757365]
CONOVER, M. D., Ratkiewicz, J., Francisco, M., Goncalves, B., Flammini, A., & Menczer, F. (2011). Political polarization on Twitter. Proceedings of the International AAAI Conference on Web and Social Media, 5(1), 89–96. [doi:10.1609/icwsm.v5i1.14126]
DEFFUANT, G., Amblard, F., Weisbuch, G., & Faure. (2002). How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation, 5(4), 1.
DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 03, 87–98. [doi:10.1142/s0219525900000078]
DEGROOT, M. (1974). Reaching a consensus. Journal of the American Statistical Association, 69(345), 118–121. [doi:10.1080/01621459.1974.10480137]
DEL Vicario, M., Scala, A., Caldarelli, G., Stanley, H. E., & Quattrociocchi, W. (2017). Modeling confirmation bias and polarization. Scientific Reports, 7(1), 40391. [doi:10.1038/srep40391]
DIJCK, J. van. (2013). The Culture of Connectivity: A Critical History of Social Media. Oxford: Oxford University Press.
DIMAGGIO, P., Evans, J., & Bryson, B. (1996). Have american’s social attitudes become more polarized? American Journal of Sociology, 102(3), 690–755. [doi:10.1086/230995]
DONG, Y., Ding, Z., Chiclana, F., & Herrera-Viedma, E. (2021). Dynamics of public opinions in an online and offline social network. IEEE Transactions on Big Data, 7(4), 610–618. [doi:10.1109/tbdata.2017.2676810]
DUGGINS, P. (2017). A psychologically-Motivated model of opinion change with applications to american politics. Journal of Artificial Societies and Social Simulation, 20(1), 13. [doi:10.18564/jasss.3316]
ESTEBAN, J.-M., & Ray, D. (1994). On the measurement of polarization. Econometrica, 62(4), 819. [doi:10.2307/2951734]
FESTINGER, L. (1957). A Theory of Cognitive Dissonance. Palo Alto, CA: Stanford University Press.
FLACHE, A., & Macy, M. W. (2011). Small worlds and cultural polarization. The Journal of Mathematical Sociology, 35(1–3), 146–176. [doi:10.1080/0022250x.2010.532261]
FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2. [doi:10.18564/jasss.3521]
GAISBAUER, F., Pournaki, A., Banisch, S., & Olbrich, E. (2021). Ideological differences in engagement in public debate on Twitter. PLOS ONE, 16(3), 18. https://doi.org/10.1371/journal.pone.0249241 [doi:10.1371/journal.pone.0249241]
HAO, K. (2021). He got Facebook hooked on AI. Now he can’t fix its misinformation addiction. MIT Technology Review. Available at: https://www.technologyreview.com/2021/03/11/1020600/facebook-responsible-ai-misinformation/
HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence: Models, analysis and simulation. Journal of Artifical Societies and Social Simulation, 5(3), 2.
HRISTOVA, D., Musolesi, M., & Mascolo, C. (2014). Keep your friends close and your Facebook friends closer: A multiplex network approach to the analysis of offline and online social ties. Proceedings of the International AAAI Conference on Web and Social Media, 8(1), 206–215. [doi:10.1609/icwsm.v8i1.14544]
HUANG, C.-Y., & Wen, T.-H. (2014). A novel private attitude and public opinion dynamics model for simulating pluralistic ignorance and minority influence. Journal of Artificial Societies and Social Simulation, 17(3), 8. [doi:10.18564/jasss.2517]
JAGER, W., & Amblard, F. (2005). Uniformity, bipolarization and pluriformity captured as generic stylized behavior with an agent-Based simulation model of attitude change. Computational & Mathematical Organization Theory, 10(4), 295–303. [doi:10.1007/s10588-005-6282-2]
JDRZEJEWSKI, A., Chmiel, A., & Sznajd-Weron, K. (2015). Oscillating hysteresis in the q-neighbor Ising model. Physical Review E, 92(5), 8.
KEIJZER, M. A., & Mäs, M. (2022). The complex link between filter bubbles and opinion polarization. Data Science, 5(2), 139–166. [doi:10.3233/ds-220054]
KEMP, S. (2022). TikTok gains 8 new users every second (and other mind-Blowing stats). Hootsuite. Archived at: https://web.archive.org/web/20220718042345/https://blog.hootsuite.com/simon-kemp-social-media/
KRAPIVSKY, P. L., Redner, S., & Ben-Naim, E. (2010). A Kinetic View of Statistical Physics. Cambridge: Cambridge University Press.
LAZARSFELD, P., & Merton, R. (1954). Friendship as a social process: A substantive and methodological analysis. In M. Berger, T. Abel, & C. Page (Eds.), Freedom and Control in Modern Society (pp. 18–66). D. Van Nostrand Company, Inc.
LORENZ, J., Neumann, M., & Schröder, T. (2021). Individual attitude change and societal dynamics: Computational experiments with psychological theories. Psychological Review, 128(4), 623–642. [doi:10.1037/rev0000291]
MARTINS, A. C. R. (2008). Continuous opinions and discrete actions in opinion dynamics problems. International Journal of Modern Physics C, 19(04), 617–624. [doi:10.1142/s0129183108012339]
MÄS, M., & Bischofberger, L. (2015). Will the personalization of online social networks foster opinion polarization? SSRN Electronic Journal
MÄS, M., & Flache, A. (2013). Differentiation without distancing. Explaining bi-Polarization of opinions without negative influence. PLoS ONE, 8(11), e74516.
MCPHERSON, M., Smith-Lovin, L., & Cook, J. M. (2001). Birds of a feather: Homophily in social networks. Annual Review of Sociology, 27(1), 415–444. [doi:10.1146/annurev.soc.27.1.415]
MITSUTSUJI, K., & Yamakage, S. (2020). The dual attitudinal dynamics of public opinion: An agent-based reformulation of L. F. Richardson’s war-moods model. Quality & Quantity, 54(2), 439–461. [doi:10.1007/s11135-019-00938-x]
PENG, K., & Porter, M. A. (2022). A majority-Vote model on multiplex networks with community structure. arXiv preprint.
RIEDER, B. (2012). What is in PageRank? A historical and conceptual investigation of a recursive status index. Computational Culture, 2, 17.
SÎRBU, A., Pedreschi, D., Giannotti, F., & Kertész, J. (2019). Algorithmic bias amplifies opinion fragmentation and polarization: A bounded confidence model. PLoS ONE, 14(3), e0213246.
STAUFFER, D. (2007). Opinion dynamics and sociophysics. arXiv preprint. Available at: http://arxiv.org/abs/0705.0891
SULER, J. (2004). The online disinhibition effect. CyberPsychology & Behavior, 7(3), 321–326. [doi:10.1089/1094931041291295]
TAILLANDIER, P., Salliou, N., & Thomopoulos, R. (2021). Introducing the argumentation framework within agent-Based models to better simulate agents’ cognition in opinion dynamics: Application to vegetarian diet diffusion. Journal of Artificial Societies and Social Simulation, 24(2), 29. [doi:10.18564/jasss.4531]
TAJFEL, H., & Turner, J. (2004). An integrative theory of intergroup conflict. In M. Jo Hatch & M. Schultz (Eds.), Organizational Identity: A Reader (pp. 56–65). Oxford: Oxford University Press.
TAKÁCS, K., Flache, A., & Mäs, M. (2016). Discrepancy and disliking do not induce negative opinion shifts. PLoS ONE, 11(6), 1–21.
TIAN, Y., & Wang, L. (2017). Opinion dynamics in social networks with stubborn agents: An issue-based perspective. arXiv preprint. Available at: https://arxiv.org/abs/1609.03465
TUREL, O., He, Q., Xue, G., Xiao, L., & Bechara, A. (2014). Examination of neural systems sub-Serving Facebook “Addiction”. Psychological Reports, 115(3), 675–695. [doi:10.2466/18.pr0.115c31z8]
VINOKUR, A., & Burnstein, E. (1978). Depolarization of attitudes in groups. Journal of Personality and Social Psychology, 36(8), 872–885. [doi:10.1037/0022-3514.36.8.872]
VOSOUGHI, S., Roy, D., & Aral, S. (2018). The spread of true and false news online. Science, 359(6380), 1146–1151. [doi:10.1126/science.aap9559]
WEISEL, O., & Böhm, R. (2015). “Ingroup love” and “outgroup hate” in intergroup conflict between natural groups. Journal of Experimental Social Psychology, 60, 110–120. [doi:10.1016/j.jesp.2015.04.008]
ZHAN, M., Kou, G., Dong, Y., Chiclana, F., & Herrera-Viedma, E. (2022). Bounded confidence evolution of opinions and actions in social networks. IEEE Transactions on Cybernetics, 52(7), 7017–7028. [doi:10.1109/tcyb.2020.3043635]