Superiority Bias and Communication Noise Can Enhance Collective Problem Solving

and
University of California Merced, United States
Journal of Artificial
Societies and Social Simulation
<https://www.jasss.org/26/3/14.html>
DOI: 10.18564/jasss.5154
Received: 29-Nov-2022 Accepted: 22-May-2023 Published: 30-Jun-2023
Abstract
Error affects most human judgments and communications. Here we consider two types of error: unbiased noise and directional biases, and consider their effects in the context of collective problem solving. We studied an agent-based model of networked agents collectively searching for solutions to simple and complex problems on an NK landscape. We implemented superiority bias as a reluctance to adopt solutions used by others unless they were substantially better than one’s own solution. We implemented communication error by injecting noise into solutions learned from others. These factors both reduce the short-term efficiency of social learning, as individuals are less likely to faithfully copy superior solutions. We find that when a team faces complex problems, both communication noise and superiority bias have a positive effect on the overall quality of the team’s collective solution, at the cost of increased time and resource usage. We find that when a team faces simple problems, a moderate level of communication noise leads to a decrease in the required time and resources for a team. We discuss these results in terms of tradeoffs between the quality of a collective solution and the time and resources needed to reach that solution.Introduction
Cooperative teams can often search for solutions more effectively and efficiently than individuals searching in isolation. A large body of research has identified a number of factors that affect the performance of problem-solving teams, including problem complexity (Lazer & Friedman 2007; Levinthal 1997; Rivkin 2000), restrictions on available resources (Kanfer & Ackerman 1989; Porter et al. 2010), the characteristics and strategies of individual team members (Barkoczi & Galesic 2016; Baumann et al. 2019; Boroomand & Smaldino 2021; Yahosseini & Moussaïd 2020), as well as the characteristics of the overall team such as its size, diversity, and network structure (Boroomand & Smaldino 2021; Derex & Boyd 2016; Gomez & Lazer 2019; Lazer & Friedman 2007).
We follow much of this work by modeling collective problem-solving as a population of networked agents searching for solutions in high-dimensionality solution space represented by an NK landscape (Lazer & Friedman 2007). While many variants of this model have been explored, most studies have made two strong assumptions about how agents communicate and process social information. First, they assume that communication is error-free, such that individuals always receive perfect information about others’ solutions. And second, they assume that individuals are purely greedy and unbiased problem solvers, such that they will always adopt a solution that is even the slightest bit better than their current solution. In this paper, we investigate the effects of relaxing these assumptions. In particular, we study the effects of communication noise, in which transmitted solutions contain errors, and superiority bias, in which individuals refrain from adopting a superior solution they have learned from others unless it is a substantial improvement over their current solution. Both of these factors introduce error at the individual level.
Noise and bias are two interrelated factors that influence collective problem-solving, both being judgmental errors (Kahneman et al. 2021). Noise refers to random or inaccurate information that interferes with the problem-solving process, while bias involves directional errors in judgment or decision-making, often originating from cognitive, social, or emotional factors. Both noise and bias contribute to the total error during professional judgment. Consequently, reducing noise and bias has a similar effect on minimizing this total error in collective problem-solving efforts (Kahneman et al. 2021).
We will show that, when teams are solving complex problems, these errors can actually improve the quality of team solutions, though at the cost of prolonging the time to consensus. We build directly on previous research (Boroomand & Smaldino 2021) in which we explored variation in individual search strategies on collective problem solving, focusing on agents that were either hard-working (and could explore more solutions per unit time) or risk-taking (and could entertain large deviations from their current solution, rather than relying on single-move hill climbing). That study found that both these strategies could improve solutions to complex problems, with risk-taking proving the larger benefit at the cost of increased time to consensus. We show here that although a team expressing superiority bias needs more time and resources to achieve consensus, adopting a risk-taking strategy can help to reduce the time and resources needed to reach consensus. Finally, we consider how errors affect collective solutions on different network architectures. Previous work has shown that, in the absence of error, sparser networks improve collective problem-solving (Fang et al. 2010; Lazer & Friedman 2007). Here we likewise find that densely connected networks reduce the quality of solutions, but also that they can reduce the time and resources for the teams to reach a consensus.
In the remainder of the paper, we review the literatures on communication noise and superiority bias, which form the basis for our model extension, and then briefly review the use of the NK landscape as a model of problem space. We then describe our model, present the results of our agent-based simulations, and discuss the implications of our results for understanding factors affecting collective problem-solving.
Communication Noise
A main advantage of solving problems in teams is that individuals can take advantage of information obtained by others. High-quality solutions can therefore spread rapidly as individuals avoid the costs of trial-and-error learning (Kendal et al. 2018). Despite the benefits of teamwork, challenges can arise when communication noise disrupts the transfer of knowledge within teams. This can result in misunderstandings, confusion, duplicated efforts, wasted resources, and processing delays (London & Sessa 2006).
When problems are complex, however, and problem components interact non-additively, overreliance on social learning can lead a population to converge too quickly on a suboptimal solution (Smaldino et al. 2023). In particular, although increasing the communication efficiency in a team improves the diffusion of solutions, it can also limit the team’s capacity to generate innovative solutions (Diehl & Stroebe 1987; Fang et al. 2010; Lazer & Friedman 2007; Shore et al. 2015). Approaches that maintain the diversity of solutions allow individuals to explore possible solutions for longer time periods and give them more opportunities to find better solutions (Smaldino et al. 2023). Mediating information flow by using an inefficient communication network is one of the common approaches to maintaining the solution’s diversity (Derex & Boyd 2016; Lazer & Friedman 2007).
Previous studies have focused on “communication efficiency” primarily in terms of network density. This factor operates at the level of team organization. Here, our focus is on mechanisms that operate at the level of individuals or dyads - errors in the transmission or learning of solutions Empirical studies indicate that allowing individuals to learn only partial solutions from one another can maintain higher solution diversity (Caldwell et al. 2016; Derex et al. 2015). In our modeling approach, we introduced errors into the solutions learned from other individuals during copying.
Superiority Bias
Superiority bias, or overrating one’s positive qualities and abilities, has been discussed under many names, including: “superiority complex” (Adler 1927), “superior conformity of the self” (Codol 1975), “leniency error” (Meyer 1980), “sense of relative superiority” (Headey & Wearing 1988), the “better-than-average-effect” (Dunning et al. 1989; Zell et al. 2020), the Dunning-Kruger effect (Dunning 2011), and “illusory superiority” (Hoorens 1993). Empirical studies show that self-evaluations are often distorted in a direction favorable to oneself (Alicke & Sedikides 2011; Dunning 2012; Judge et al. 2009; Sutin et al. 2009). Individuals with superiority bias display specific behaviors, such as the inclination to compare themselves favorably and a disregard for others’ opinions. They often dismiss or undervalue the opinions, ideas, or feedback from others (Alicke & Sedikides 2011).
In most models of collective problem solving, individuals can readily identify the quality of a considered solution, and agents greedily adopt any solution that is at all better than their current solution. We operationalize superiority bias by introducing a threshold, such that a solution adopted by someone else must be better than the agent’s current solution by at least that threshold amount in order to be copied. At least two possible interpretations of this bias are possible. First, agents may misperceive their own solution to be of higher relative quality than it really is, as discussed in the previous paragraph. However, an alternative interpretation is that agents are accurately perceiving the solution scores of themselves and others, but may be rationally reluctant to incur the costs or risks associated with switching to a new solution unless the benefits of doing so justify such a change. Thus, agents may exhibit a sort of “behavioral inertia,” requiring sufficient incentives to alter their behavior. In terms of modeling, there is no difference between superiority bias and behavioral inertia so framed, and we will generally restrict our discussion of the phenomenon to the first interpretation. The role of behavioral inertia in collective problem solving is discussed in greater detail by Smaldino et al. (2023).
It might seem that superiority bias would be detrimental to collective problem-solving, as agents stubbornly refuse to abandon their own solutions in favor of ones that are demonstrably better. Certainly, it will increase the time required for team consensus. But superiority bias also allows for a greater diversity of solutions to persisting for longer in the population, which is likely to improve overall solution quality (Smaldino et al. 2023). Evidence for this hypothesis was recently provided by Gabriel & O’Connor (2021), who studied networked agents using both individual and social learning to solve a two-armed bandit problem using Bayesian updating. Their agents exhibit “confirmation bias,” in which they are unlikely to incorporate evidence that is at odds with their prior beliefs. This design differs from ours in terms of how we model learning and problem space, but it is functionally similar to our model in that agents are less likely to learn about, and therefore adopt, information about superior solutions. We, therefore, investigate here whether superiority bias, which restricts individuals’ likelihood of adopting better solutions in the short run, may nevertheless improve solutions at the team level in the long run. Baumann & Martignoni (2011) also indicated that a slight pro-innovation bias can enhance performance by prompting firms to explore broadly, identify better solutions, and potentially outperform those with unbiased evaluation processes.
Representing Solutions to Collective Problems
We model the problems that our teams of agents tackle as NK landscapes (Kauffman & Weinberger 1989; Lazer & Friedman 2007). This widely used model allows for a multidimensional solution structure, in which problem elements can exhibit interdependencies.
It is possible to represent the complexity of a problem by mapping the entire set of possible solutions to that problem into an evaluation space (also called a fitness landscape) which indicates the quality of each solution (Levinthal 1997; Wright 1932). Indeed, the extent to which the contribution of each solution element depends on the other elements is often described as the problem’s complexity, such that the simplest problems are those in which each solution element can be optimized independently (Levinthal & March 1981; Siggelkow & Levinthal 2003). Simple problems correspond to “smooth” landscapes, as they can be solved via simple hill climbing, while complex problems are akin to “rugged” landscapes, as multiple simultaneous changes may be needed to improve one’s solution. In the NK model, the variable \(N\) represents the number of elements in each solution, while \(K\) represents the number of interdependencies involved in those solutions. We describe the model in more detail below (see also Csaszar 2018).
The NK model has widely been used to study collective problem-solving (Barkoczi & Galesic 2016; Boroomand & Smaldino 2021; Lazer & Friedman 2007; Shore et al. 2015; Yahosseini & Moussaïd 2020). In our model, individuals explore the landscape independently but can also compare solutions with those in their social networks and thereby adopt superior solutions. We compare the performance of teams of agents who exhibit various levels of superiority bias and communication noise in solving complex and simple problems.
Model
We modeled the process of collective problem-solving as a team of networked agents searching over a smooth or rugged NK landscape for the highest quality solution. Each agent is initialized with a random solution at the beginning of each simulation. Agents typically searched the solution-space by making small changes to their current solution, a search strategy often referred to as hill climbing. As is typical in these models, we assumed that agents’ solutions were observable to other agents with whom they shared network ties. The ability to learn socially allows populations to achieve solutions unlikely to be found by individual hill climbing alone. An agent always employs only one solution (a location on the NK landscape) at a time, represented as an \(N\)-dimensional binary vector associated with a score. The same solution can be employed by several agents simultaneously. Agents are not able to see the entire landscape, and indeed have no memory–they can only compare other possible solutions with their current solution. The simulation proceeds in discrete time steps. In each simulation, in a random order, agents consider whether to adopt a new solution based on social or individual learning.
Our work builds directly on the analyses presented in Boroomand & Smaldino (2021). This model included agents employing hard-working and risk-taking search strategies (described below). We include these strategies here to understand how individual search strategies might interact with communication noise and superiority bias. Unless otherwise stated, we used a ring lattice network with degree four as the communication network for our team of agents. Past research has indicated that densely connected networks may perform best for simple problems while sparsely connected networks perform best for complex problems (Fang et al. 2010; Lazer & Friedman 2007). We will compare the results from our moderately connected ring network with a more sparsely connected linear network (equivalent to a ring lattice of degree 2 and one broken link) and a more densely connected complete graph (in which all nodes are connected).
Below, we describe the model incrementally, describing first the behaviors of individual agents, followed by a detailed description of the NK landscape, and concluding with a description of our implementation of communication noise and superiority bias. We then discuss our outcome metrics before presenting the results of our agent-based simulations.
Agent behavior
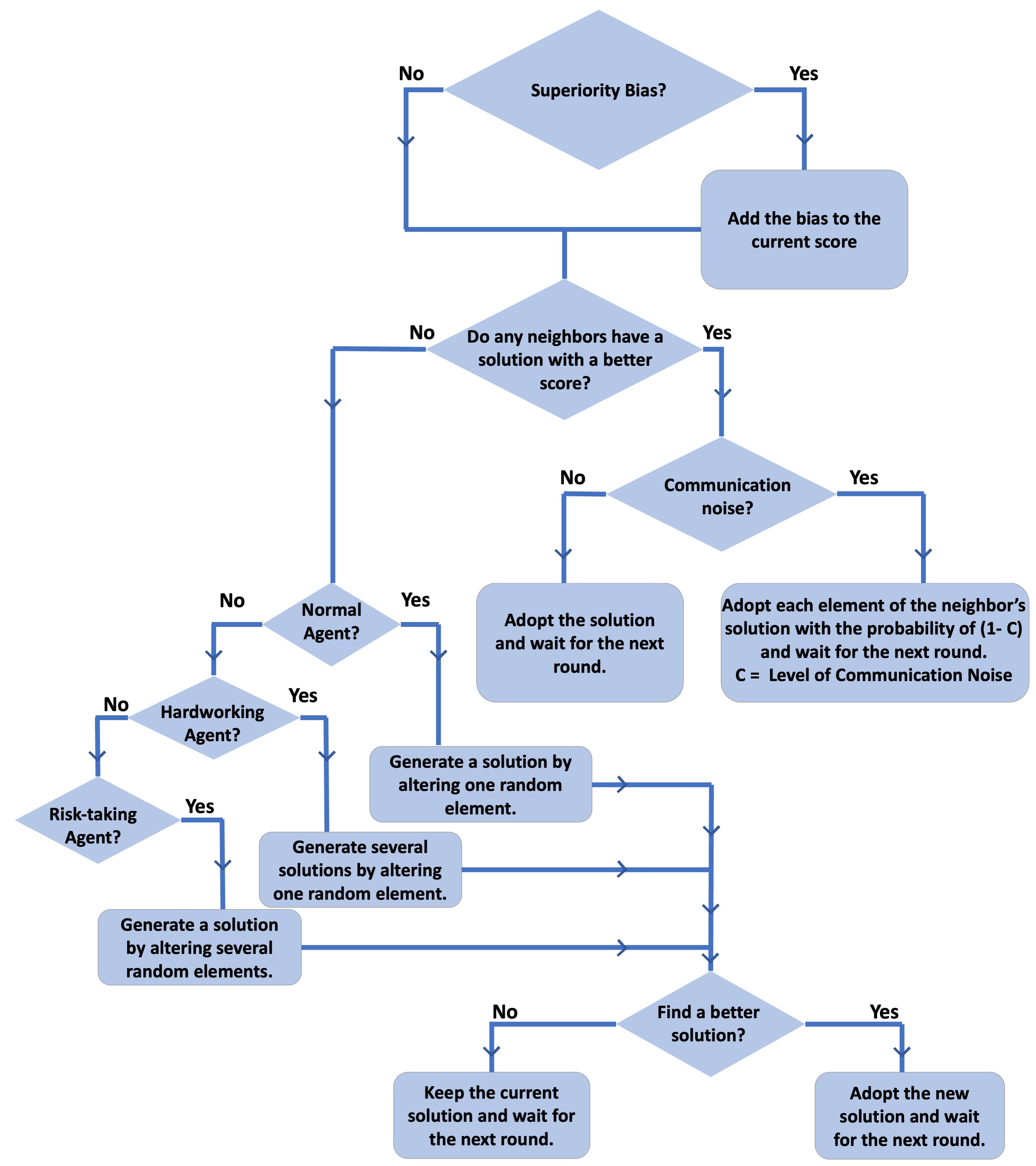
Agents can engage in either social learning (i.e., by adopting a better solution from other agents) or individual learning (i.e., generating new solutions). Employing a conditional social learning strategy, agents imitate a neighbor’s solution if it is better than their own current solution, otherwise, they try individual learning to find a better solution. A complete flowchart describing agent behavior is shown in Figure 1.
At each time step, an agent initially attempts social learning, in which the score of the current solution is compared to that of each of their network neighbors. If any neighbors have a better solution, the agent adopts the solution with the highest score. If no neighbors have a better solution than the one the agent currently uses, the agent employs individual learning and generates one or more new solutions to consider. If any of these solutions are better than the current solution the agent adopts the solution with the highest score. If neither social nor individual learning yields a better solution, the agent maintains its current solution. By involving social learning first, and if this fails, then involving individual learning, agents can be viewed as trying to avoid the cost of individual learning, which is often described as a major contributor to the evolution of social learning (Boyd & Richerson 1985; Kendal et al. 2018).
Agent type
Following Boroomand & Smaldino (2021), we consider three behavioral strategies for individual learning: normal, hard working, and risk taking agents (Figure 2).
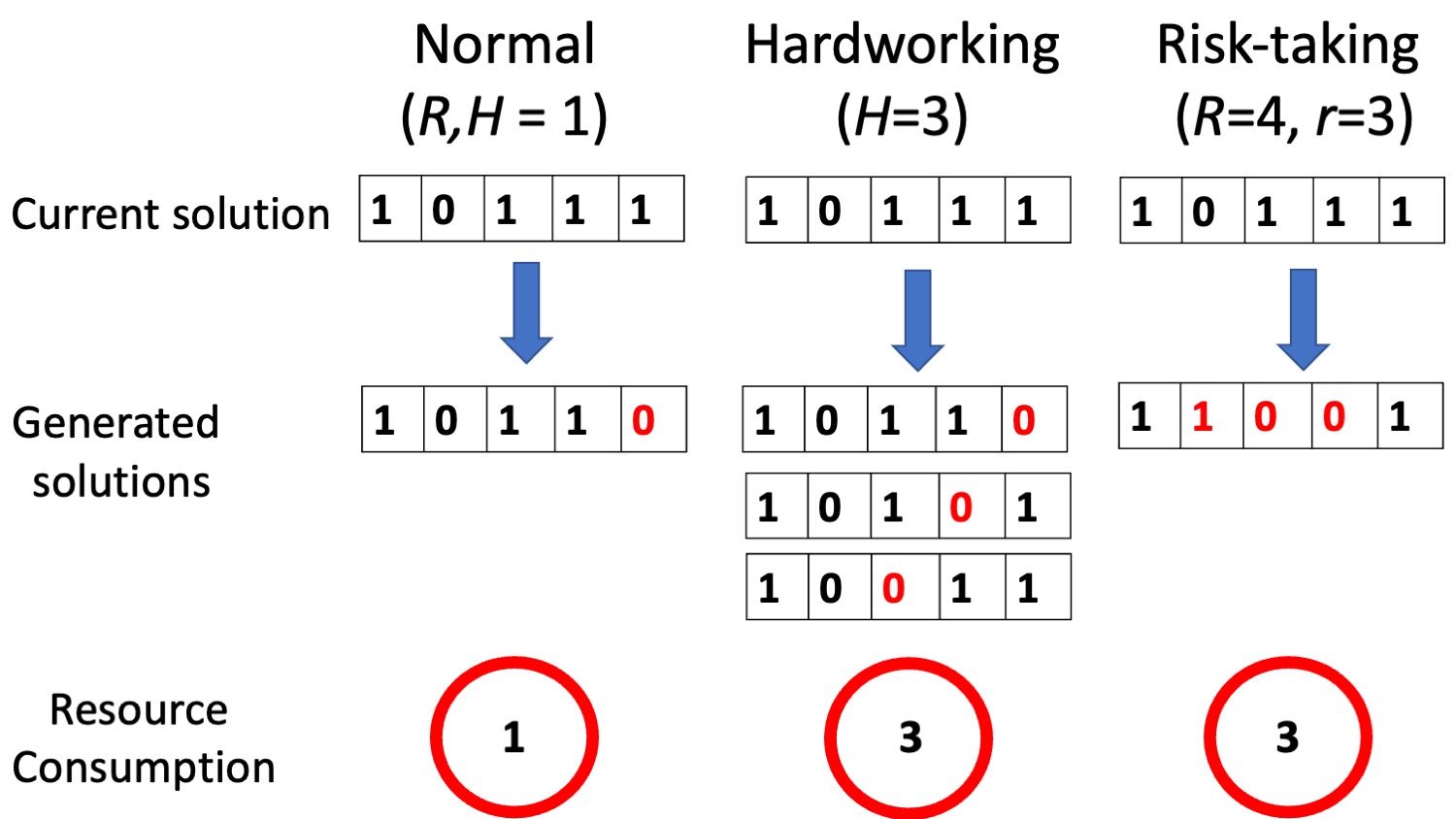
Hardworking agents generate multiple new solutions simultaneously and choose the solution with the highest score. They generate solutions by altering only one dimension of their current solution at a time, resulting in a set of new solutions that all have a Hamming distance of 1 from the agent’s current solution. The number of new solutions a hardworking agent generates in each round of individual learning is determined by its hardworking level \(H > 1\).
Risk-taking agents alter multiple solution elements at once, which reduces the correlation in score between their current and considered solutions. The extent of risk taking is given by the integer \(R > 1\). At each time step, the agent selects a random integer \(r \in [1; R]\), and explores a new solution by flipping \(r\) randomly chosen elements of its current solution. If \(r > 1\), a given element may be flipped more than once. The Hamming distance between the current solution and the considered solution can therefore vary between zero and \(r\).
Normal agents explore the landscape in each run by randomly selecting one dimension of its current solution and altering it. This is how individual learning is usually implemented in models of collective problem solving employing NK landscapes. Normal agents are equivalent to hardworking or risk-taking agents with \(H = R = 1\).
All teams eventually reach consensus on a shared solution, at which point the simulation ends. The consensus solution is not necessarily the global maximum solution (the best possible solution), as they may instead get stuck on a suboptimal local maximum. Because risk-taking agents are capable of escaping from local maxima, they will always eventually find the global maximum, though this can take an arbitrarily long time (Boroomand & Smaldino 2021). In many cases, managers look for a “good enough” solution (Johnston et al. 2002) and allow teams to stop exploring when they reach that level. Therefore, the simulations stop when either (A) the team reaches the global maximum or (B) a total of 200 time steps have passed. We chose 200 because in our previous analyses, teams generally reached a long-term consensus well before 200 time steps (Boroomand & Smaldino 2021).
NK landscape
The NK landscape is essentially a function or look-up table that evaluates a solution’s score. A solution S is a binary vector (a string of 0’s and 1’s) length \(N\):
| \[ S = [S_{1}, S_{2}, \dots, S_{N}], S_{i} \in \{0, 1\}\] | \[(1)\] |
At the start of each simulation run, each solution is assigned a score, which remains constant during the simulation. Each solution can be considered a location on the NK landscape. Two locations are adjacent neighbors if the Hamming distance of their associated solutions is 1 (they differ in only one dimension). When there is no interdependency between solution dimensions (\(K=0\)), the contribution of each element to the solution score does not depend on the state of other elements. Otherwise, the contribution of each element to the solution score is determined by its own state (0 or 1) as well as the states of \(K\) other elements which are randomly chosen at the beginning of a simulation and kept unchanged during the simulations. In this study, we fix \(N = 20\) and define simple problems as \(K = 0\) and complex problems as \(K = 10\).
To compute the score of a solution, we create \(N\) interdependency vectors (\(V_{i}\)), one for each element of the solution (\(S_{i}\)). Each interdependency vector contains the solution element and \(K\) other randomly chosen elements. The contribution value of a solution element is determined by the score of each interdependency vector. To calculate the score of an interdependency vector (\(V_{i}\)), we consider the consecutive elements of the vector as the digits in a binary number and then transform it to base 10. This latter number represents the position index in the score list, a list of random integers drawn from a uniform distribution in the range of 0 to 1000 at the start of each run. The score of each interdependency vector is the value chosen by the position index from the score list. The average score of all interdependency vectors of a solution determines the score of that solution. An example of calculating a solution score is demonstrated in the appendix. To expand the score distribution and better identify high scores from low scores, we raised all scores to the power of 8 in accordance with previous studies (Barkoczi & Galesic 2016; Boroomand & Smaldino 2021; Lazer & Friedman 2007). We standardized the results in [0, 1], with one being the maximum possible score in a particular run, in order to allow comparisons of scores across simulation runs.
Modeling communication noise
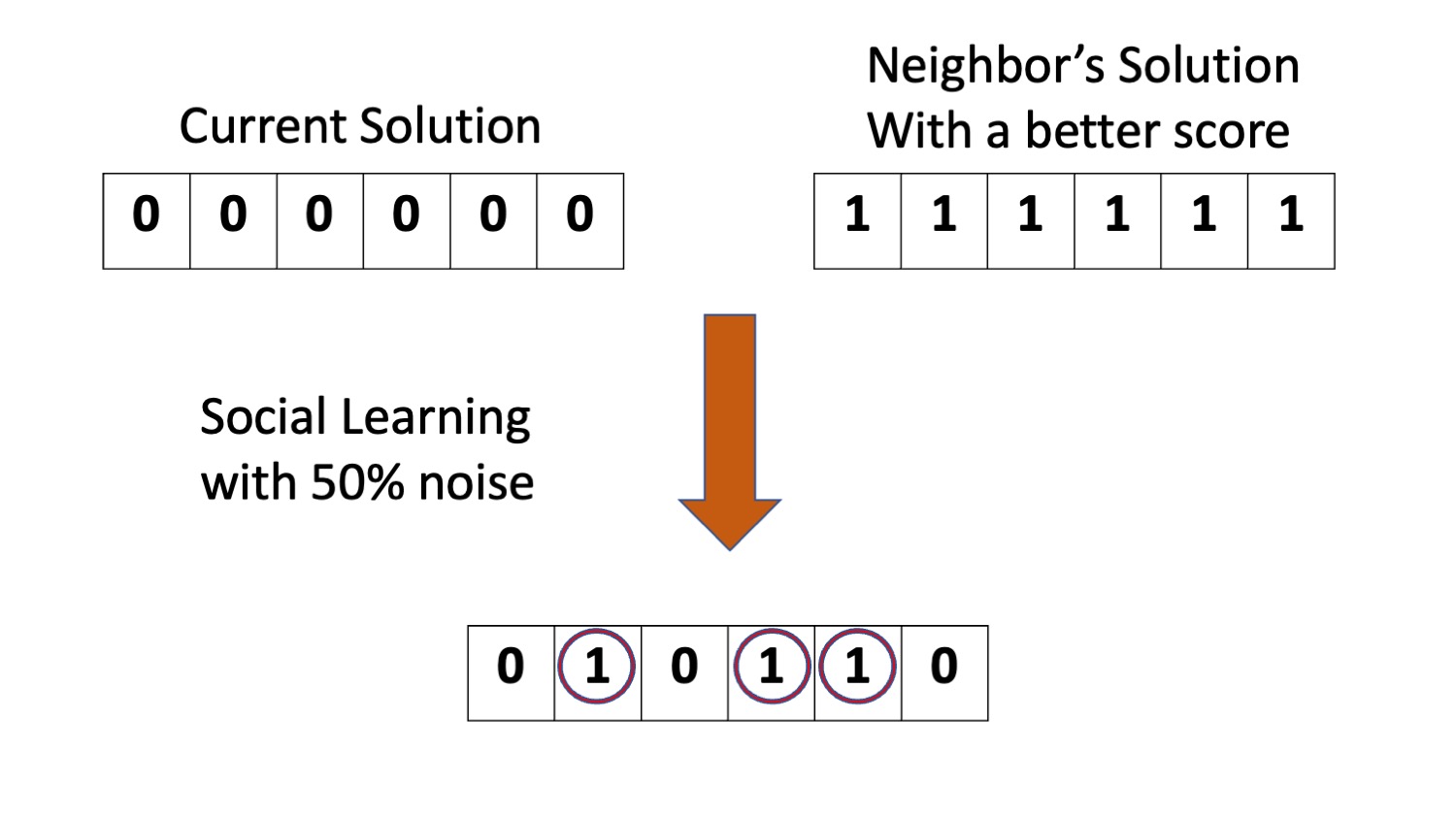
When an agent engages in social learning, it compares the score of its current solution to those of its network neighbors. If a neighbors’ solution is better than his own current solution, it adopts the neighbor’s solution with the highest score. Here we consider the possibility that the communication of this solution is not always 100% transparent. We define the communication noise \(C\) as the probability that each element of an agent’s current solution remains unchanged (and therefore is not influenced by the copied solution) during social learning. Figure 3 illustrates an example with \(N=6\) and \(C = 0.5\).
Modeling superiority bias
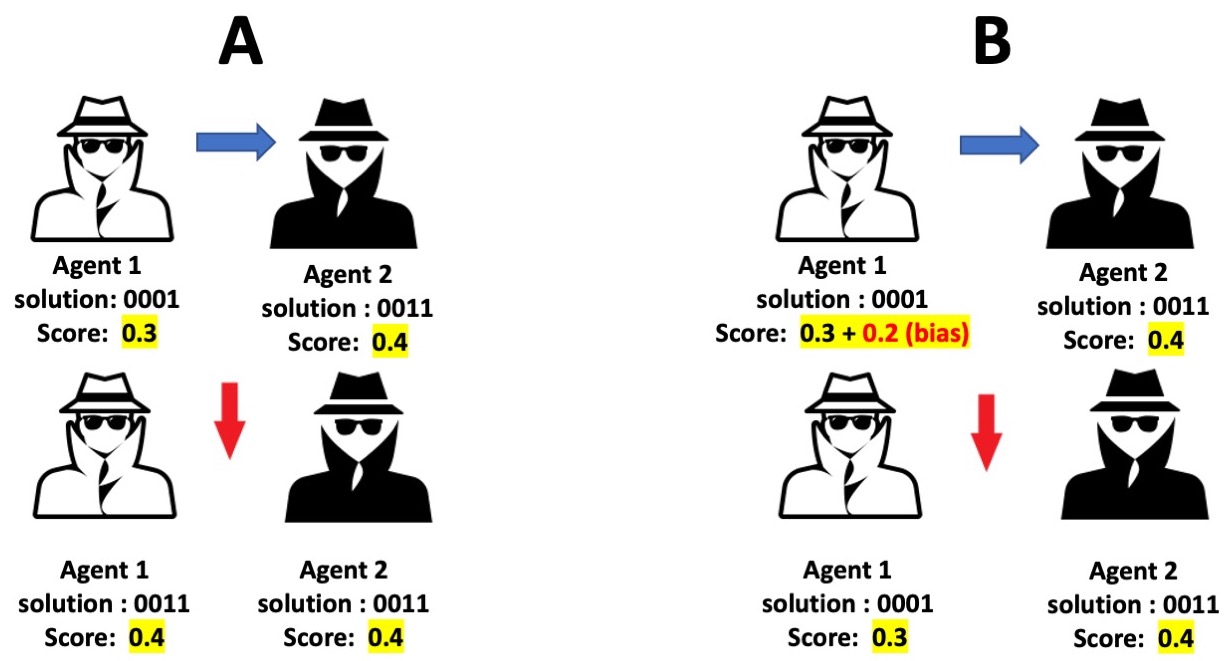
In the absence of superiority bias, agents engaging in social learning will copy another agent’s solution as long as it has a higher score than the agent’s current solution. Agents with superiority bias copy their neighbors’ solutions only when the neighbor’s score is sufficiently better than the agent’s current solution. Superiority bias is characterized by the quantity \(B_{Max}\). At initialization, each agent is assigned its own characteristic bias, \(B_{i}\), which is a real random number drawn from the uniform distribution [0, \(B_{Max}\)]. Whenever an agent considers copying another agent’s solution, it does so only if the difference between the scores of its current solution and its neighbor’s solution is greater than \(B_{i}\). This dynamic is illustrated in Figure 4.
Model evaluation
We evaluate the performance of teams in three ways. First, by the highest score they reach (either at consensus or 200 time steps); second, the time it takes for them to reach consensus (truncated at 200 times steps); and finally, the resources they use to explore the problem space. The first two metrics are fairly self-explanatory. The third metric is based on the idea that search can be costly in terms of both time and the resources needed to try to solutions (e.g., building new technologies). Agents involved in individual learning generated new solutions for the problem by flipping elements (bits) of their current solution. We define the resources that an agent consumes during each time step as the number of elements flipped during individual learning (Figure 1). This will vary depending on the search strategy used by an agent. For example, for normal agents, it is equal to one, for hardworking agents it is equal to \(H\), and for risk-taking agents it is equal to \(r\) in individual learning. The total resource usage is the sum of resource usage for all agents across the length of the simulation.
Computational Experiments
For all our runs we used teams of \(n = 100\) agents. We modeled solution space as a landscape with \(N = 20\), where \(K = 0\) or \(K = 10\). We ran simulations with normal, hardworking, and risk-taking agents, using \(H = 5\) for the hardworking agents and \(R = 5\) for the risk-taking agents.
We varied both superiority bias (\(B_{Max}\)) and communication noise (\(C\)) from 0 to 0.5. We ran 100 simulations for each combination of parameters tested and report the average metrics from across these simulations. Table 1 summarizes the model parameters and displays the default values used in our computational experiments. The NetLogo code is available at: https://www.comses.net/codebases/bc594be6-53dc-415b-859f-7d716edabaf1/releases/1.0.0/
| Parameter | Definition | Default value |
|---|---|---|
| \(n\) | Team size | 100 |
| \(N\) | Number of problem elements | 20 |
| \(K\) | Problem complexity | \(\{0, 10\}\) |
| \(H\) | Hardworking level | \(\{0, 5\}\) |
| \(R\) | Risk-taking level | \(\{0, 5\}\) |
| \(B_{Max}\) | Superiority bias | \([0, 0.5]\) |
| \(C\) | Communication noise | \([0, 0.5]\) |
Results
Superiority bias
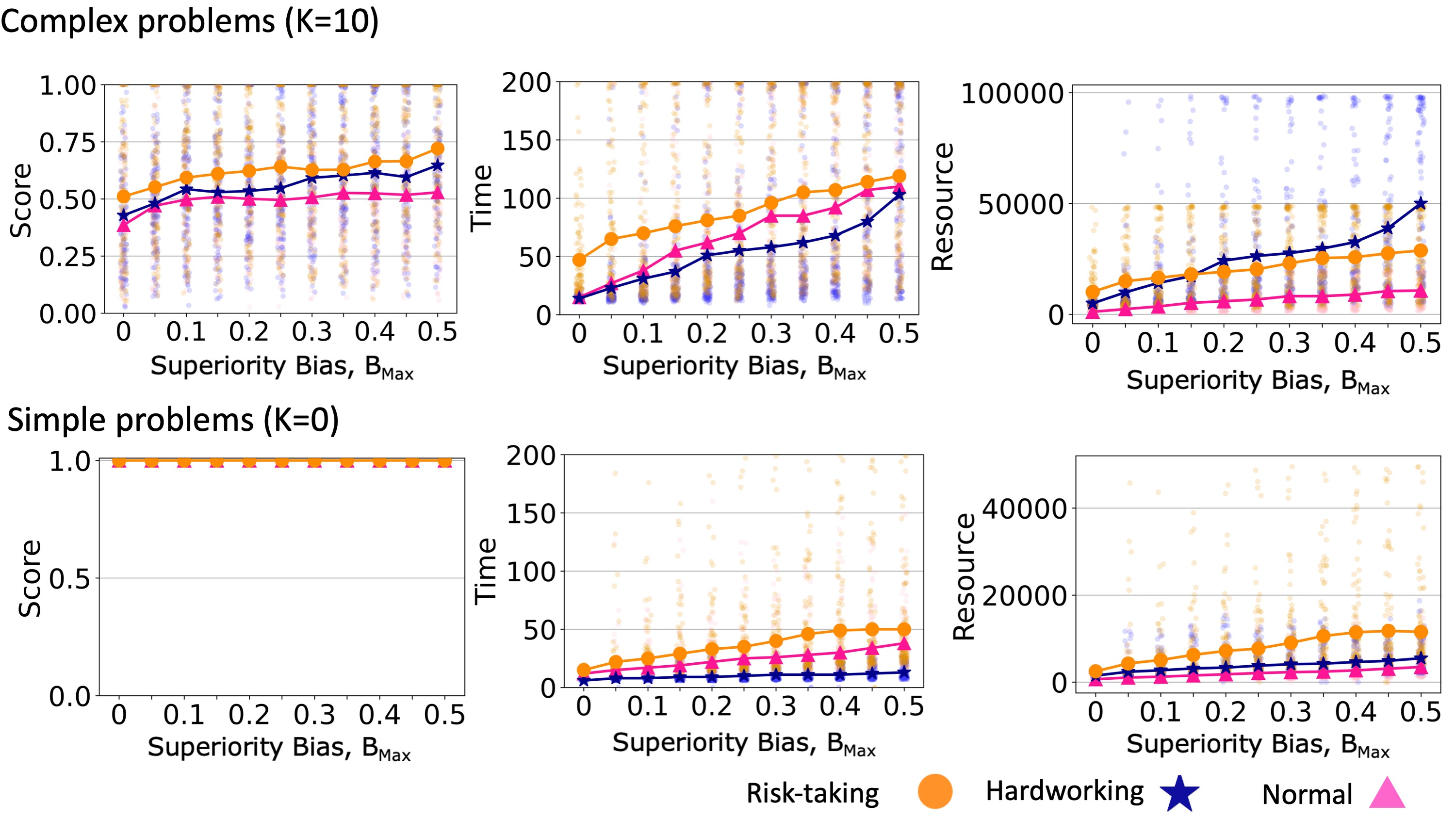
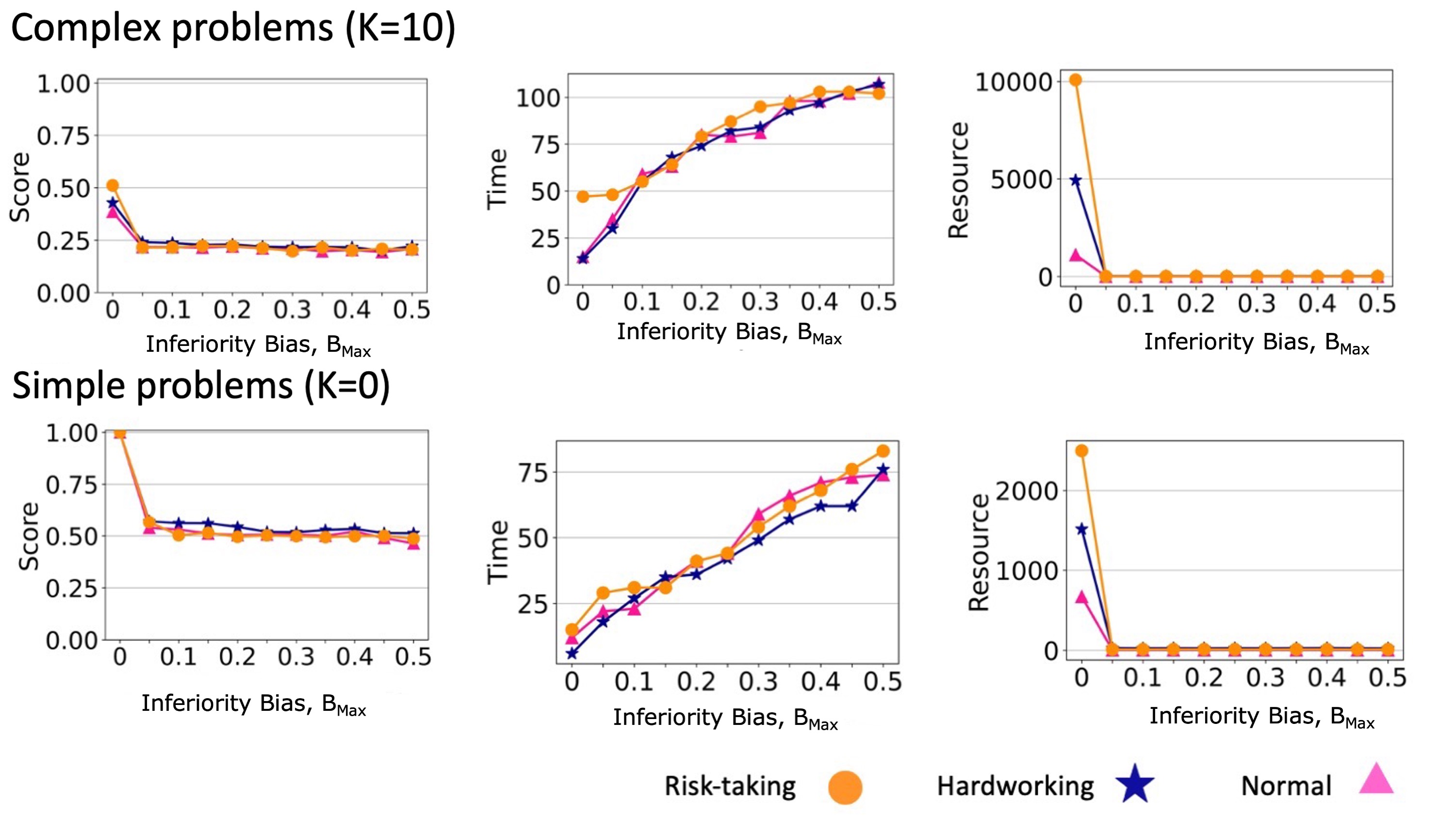
Higher levels of superiority bias led to teams reaching solutions with higher scores when solving complex problems (Figure 5, top row). Because agents only copied solutions from a neighbor when that neighbor’s solution score was better than the agent’s own score by at least \(B_{i}\). Increasing the superiority bias level decreased the probability of social learning in the team. This maintained the diversity of solutions for longer and gave agents more opportunities to learn via individual learning and avoid reaching a consensus too soon. Accordingly, increasing superiority bias also increased the time needed to reach a consensus and the number of element changes explored during individual learning (resource usage). As in Boroomand & Smaldino (2021), we found that risk-taking and hardworking agents could reach higher scores than normal agents, in that order, and we found that these effects were approximately additive when combined with superiority bias. For simple problems that can be solved via hill climbing, superiority bias increased the time and resources needed to reach a consensus without yielding any advantage in solution quality (Figure 5, bottom row).
Superiority bias and network structure
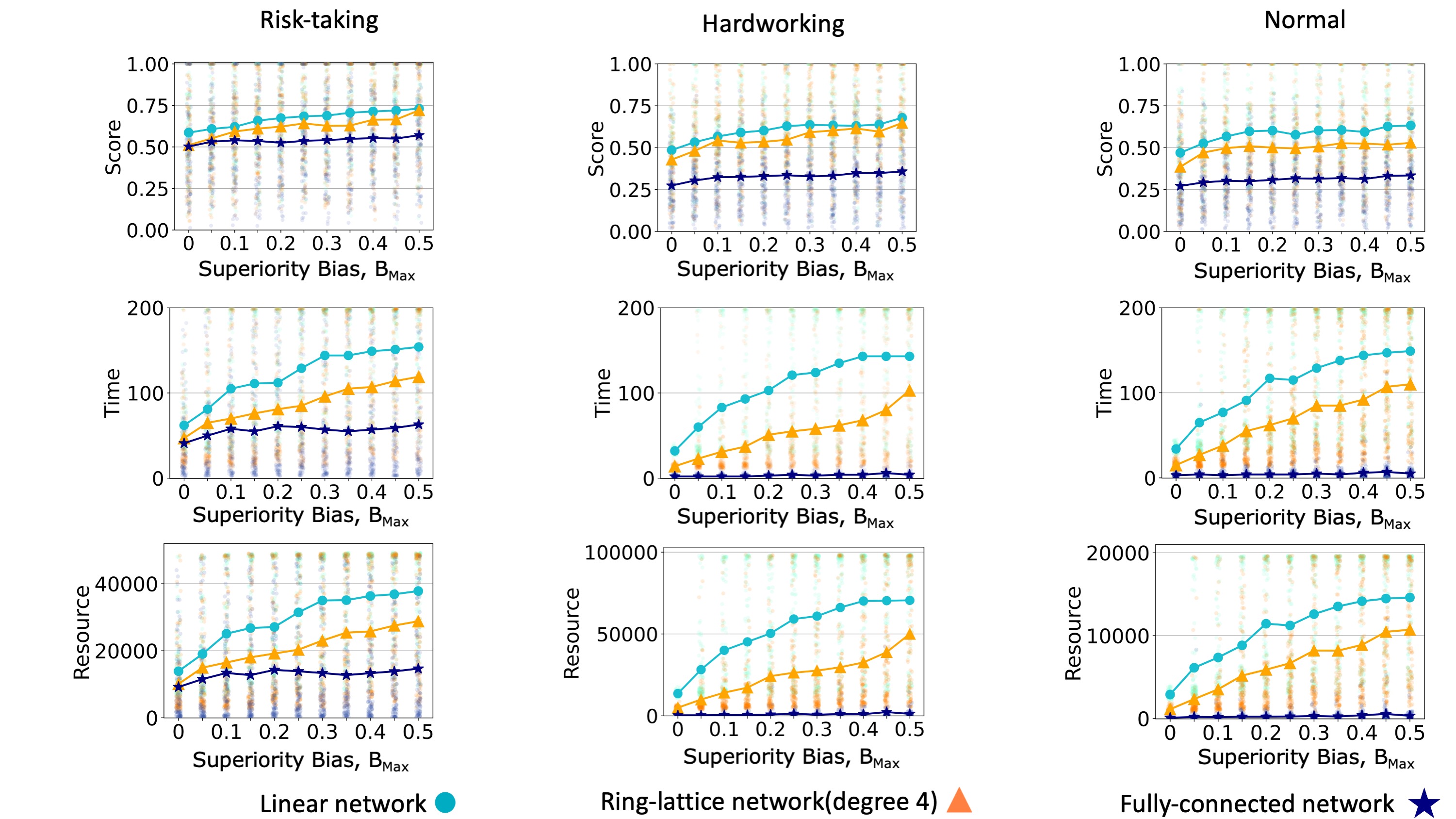
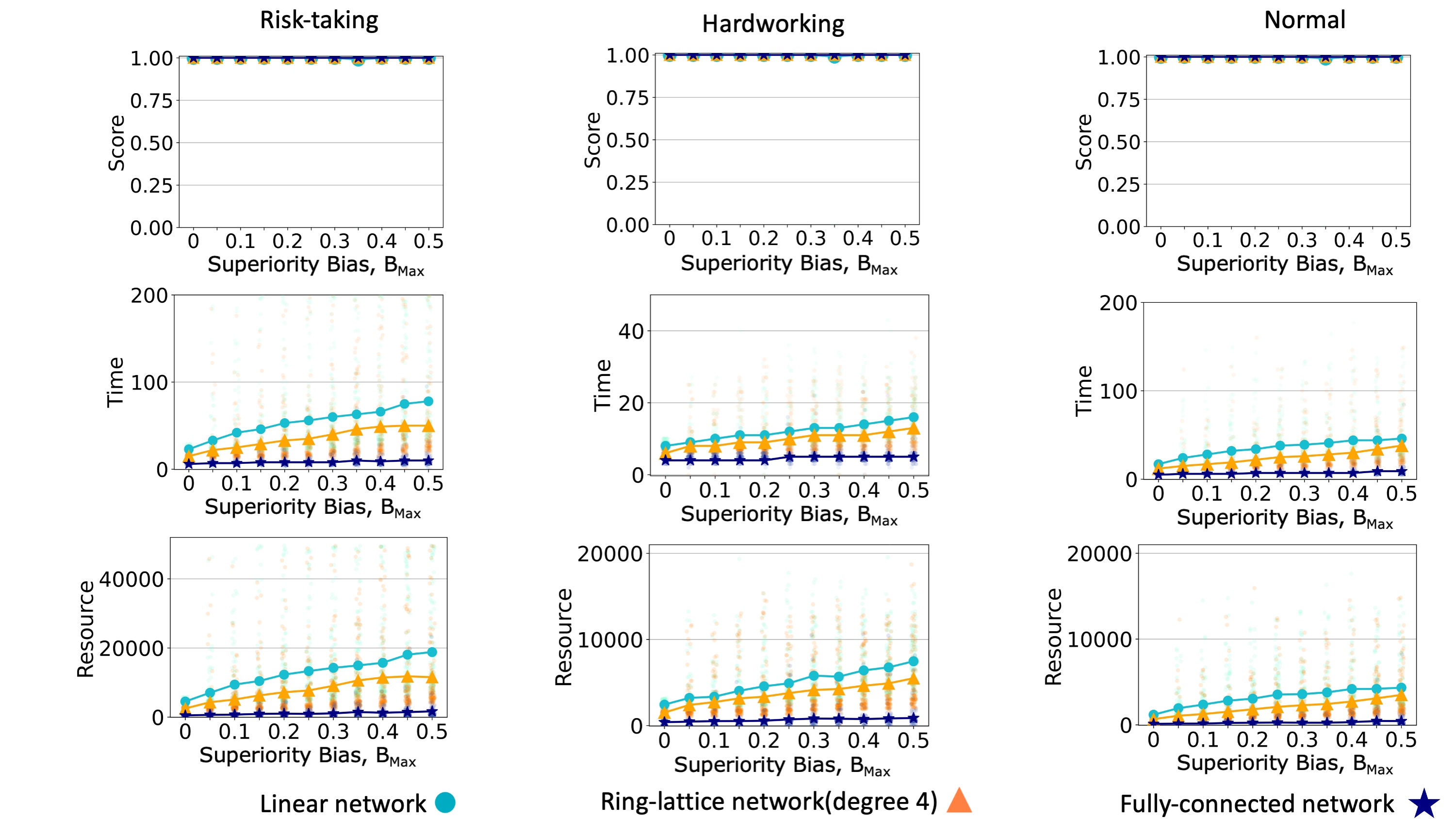
We compare the performance of the model on a linear network, a ring lattice, and a fully-connected network. In accordance with many other studies of dynamics on networks (Lind & Herrmann 2007), we find that teams converge faster when the communication network is more connected. A more connected communication network leads a team to spend less time and resources reaching a consensus (Figures 6 and 7, middle and bottom rows). When teams face simple problems, all teams can reach the global maximum (Figure 7). When teams face complex problems, a more connected communication network leads to a decrease in the quality of the solution converged upon (Figure 6). In general, superiority bias has a negative effect on the required time and resources to reach a consensus solution, and these effects seem to be more severe in sparse networks.
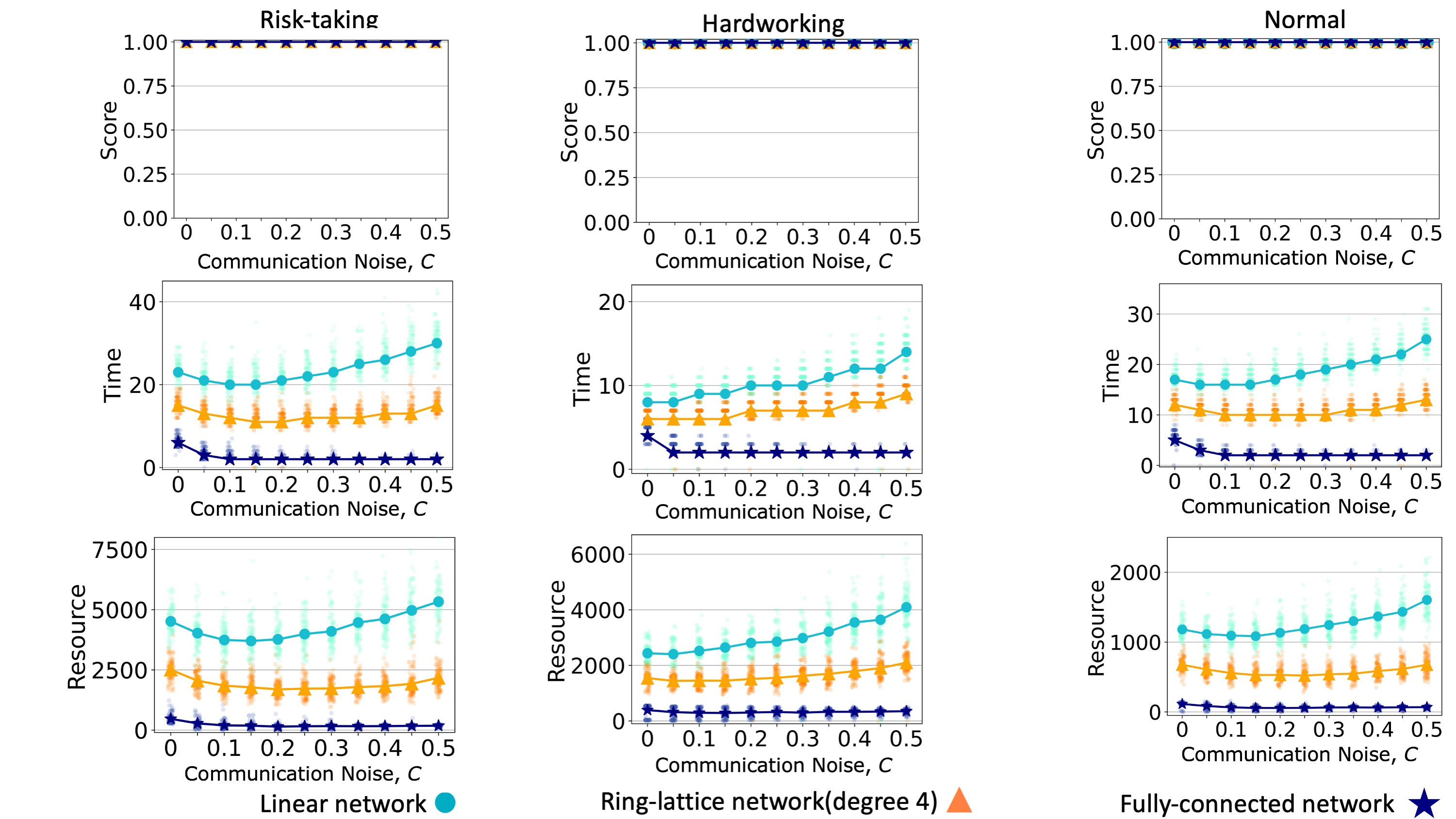
Communication noise
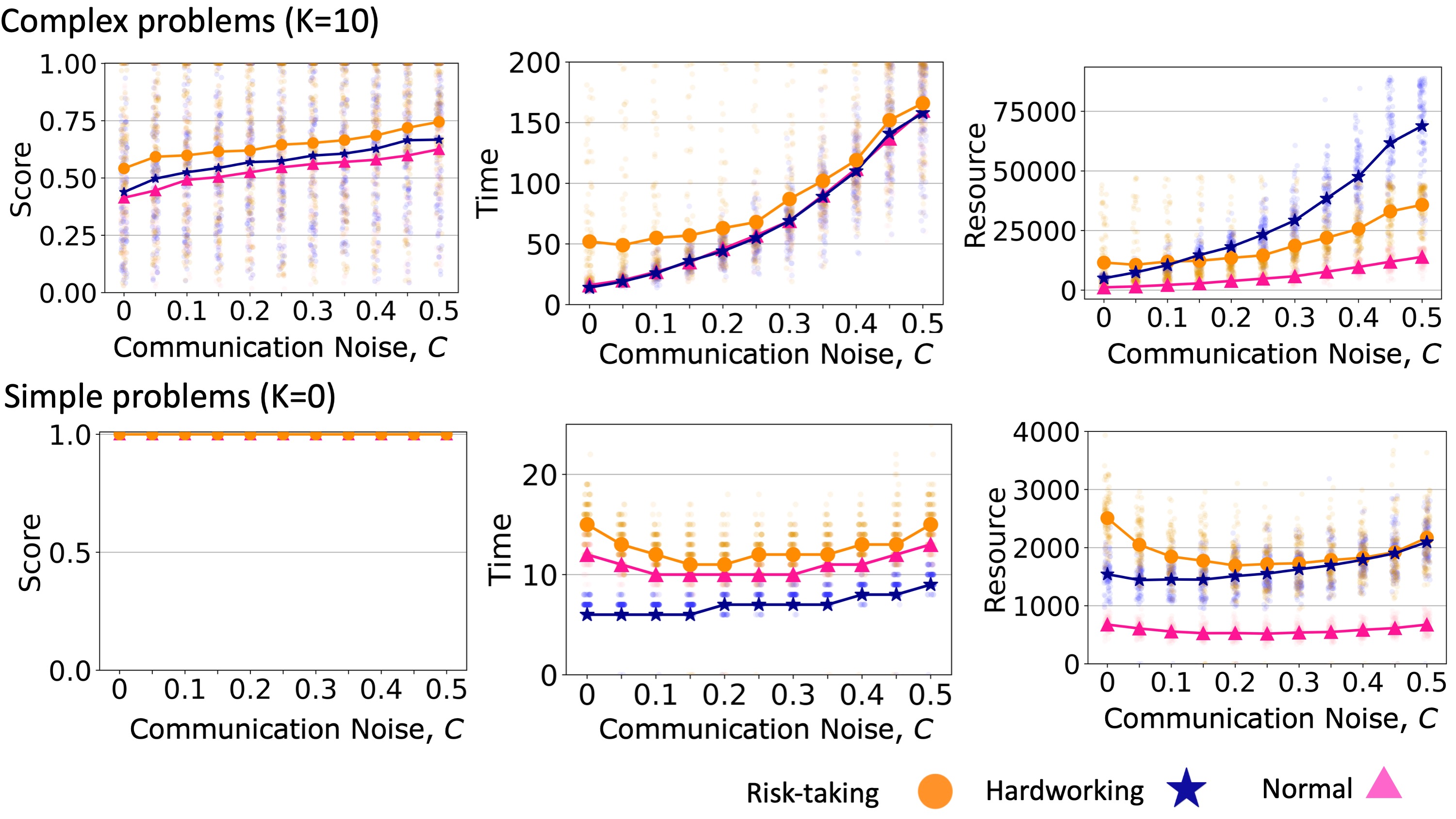
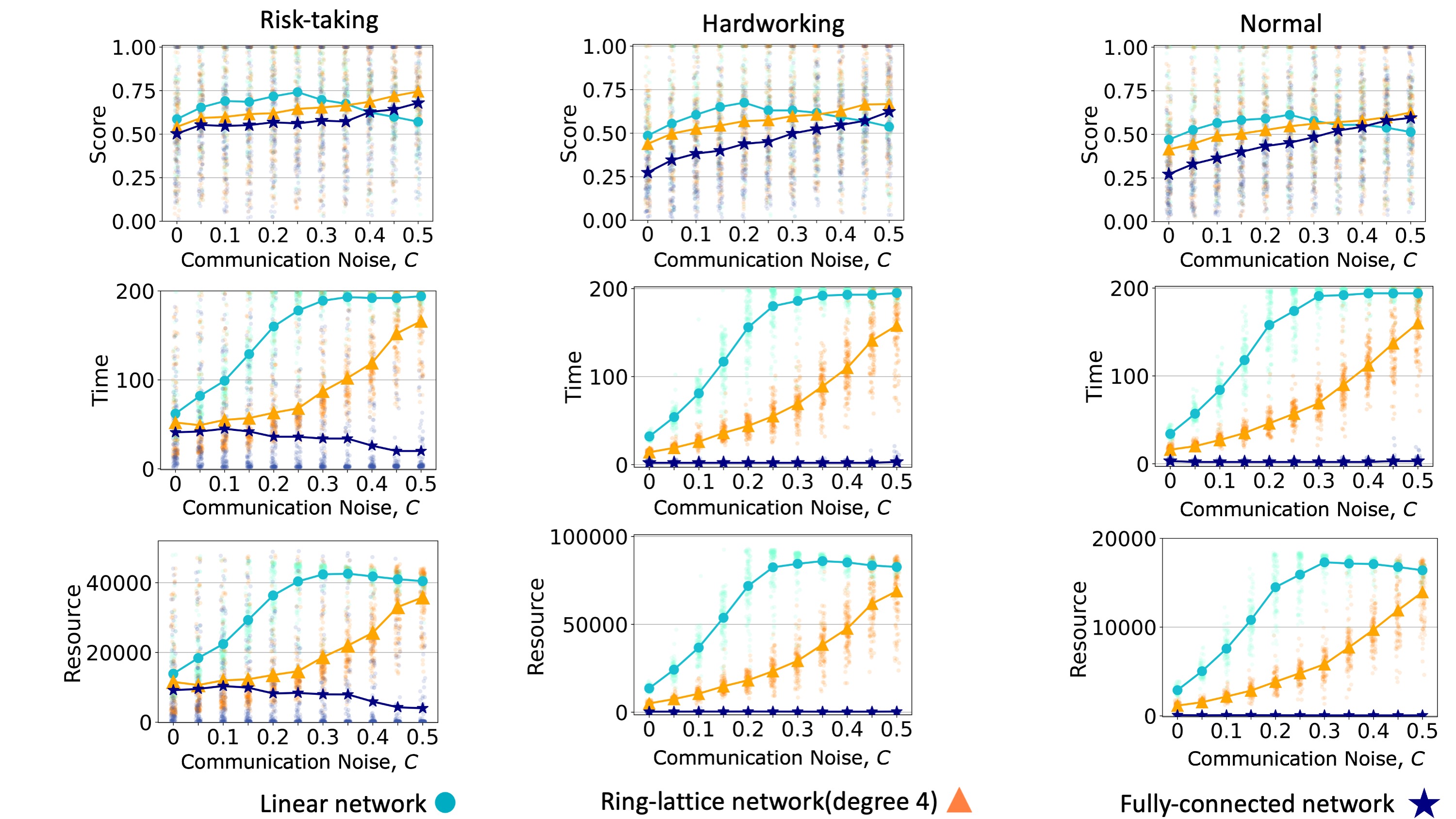
Increasing the communication noise level, \(C\), increased teams; final scores for complex problems (Figure 8, top left). This is because communication noise impeded teams from quickly reaching a consensus and allowed them to engage in the more exploratory (and less purely greedy) searches. On the other hand, Teams with noisier communication required more time and resources to reach a consensus (Figure 8, top row). In a situation with low communication noise, a hardworking team could consume fewer resources than risk-taking teams, while this relationship was reversed for higher communication noise (Figure 8, top right). As usual, teams could always reach the global maximum solution for simple problems. We find that increasing the communication noise could have a U-shaped effect on the time and resources required for teams to reach a consensus (Figure 8, bottom row). This is due to a similarly-shaped relationship between communication noise and the diversity of solutions. We explain this result below.
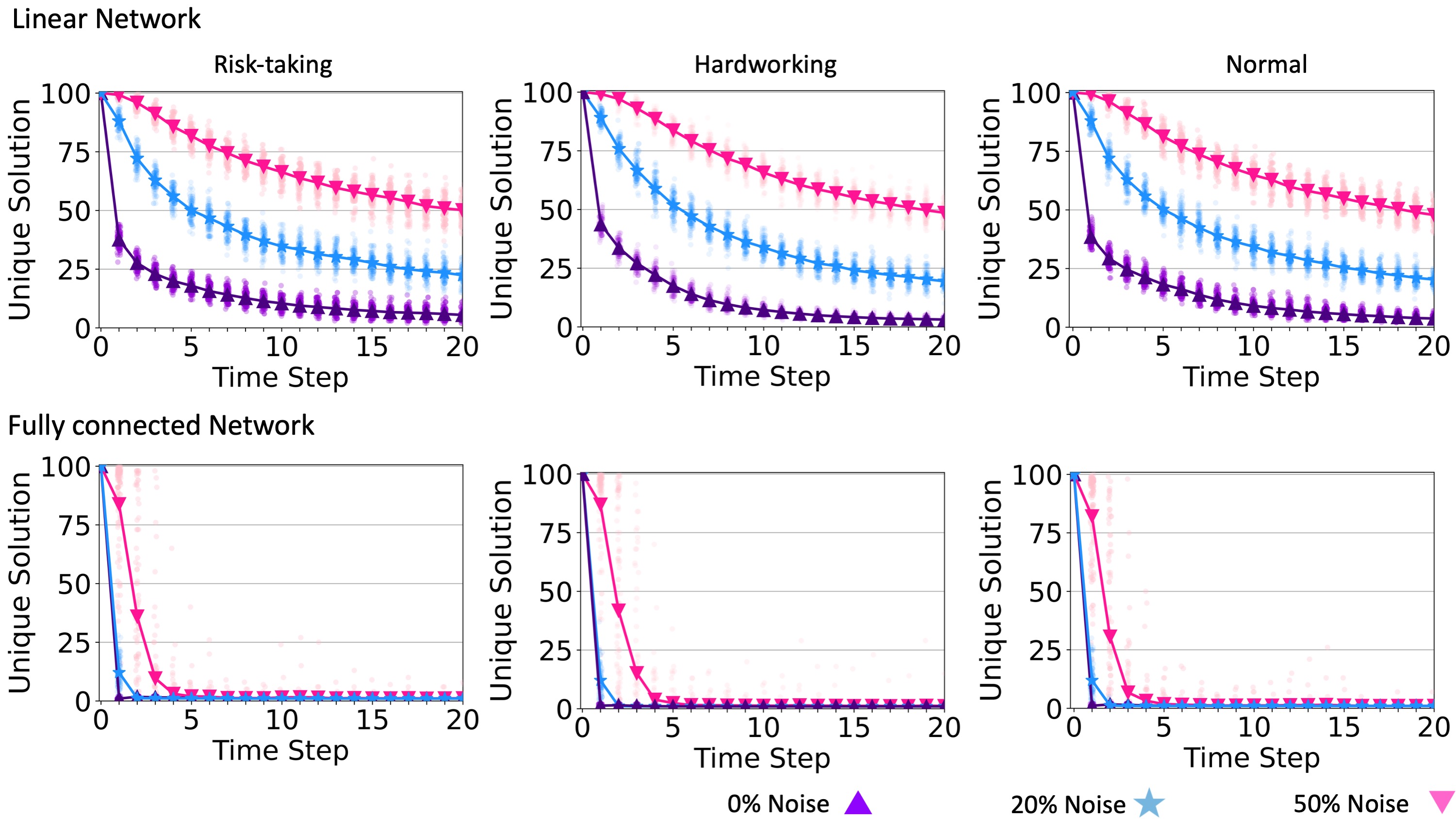
Communication noise slows the process that leads to team consensus, which increases the probability that the team will find a higher-quality solution. We illustrate this in Figure 9, which shows that in all cases, communication noise helps teams to maintain a larger number of unique solutions and therefore explore a wider area of the solution landscape. The effect holds regardless of problem complexity or individual search strategy.
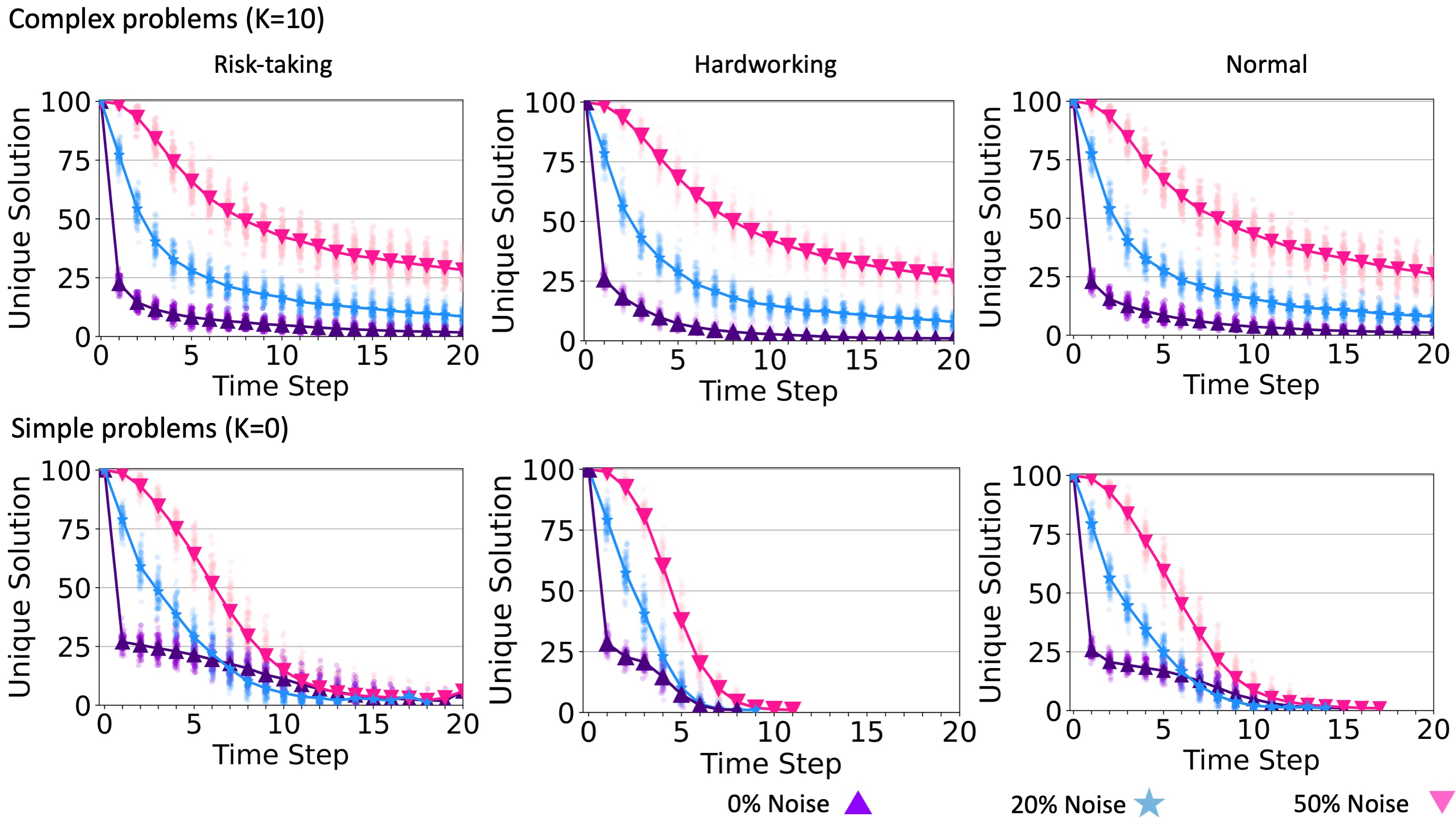
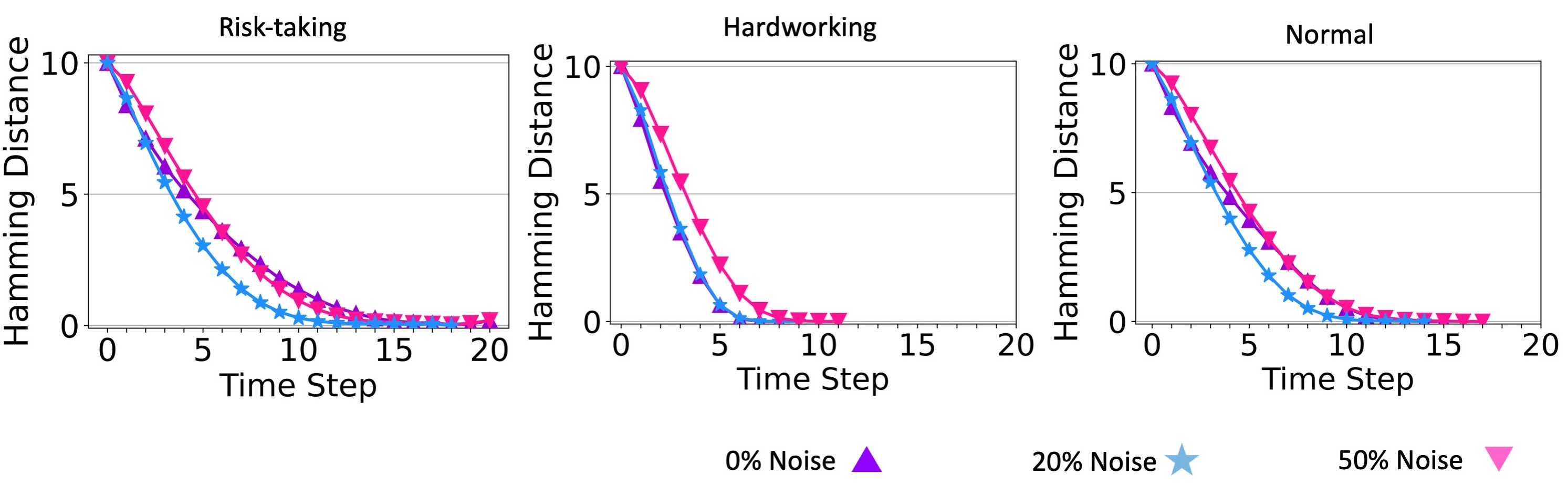
Recall that for teams solving simple problems, a moderate level of communication noise reduced the required time and resources to reach a consensus. Here we explain this result and also the U-shaped relationship between communication noise and time to consensus for simple problems. To characterize the diversity of the solutions considered by team members at any given time step, we calculated the average Hamming distance between all pairs of solutions. The results of this analysis are shown in Figure (???). Notice that a noise level of \(C = 0.2\) decreases this diversity faster than either zero noise or maximum noise (\(C = 0.5\)). This is likely because small levels of noise enabled agents to take larger leaps toward the global maximum.
We once again find that more connected communication networks lead to faster and less resource-intensive consensus to the global optimum, regardless of communication noise (see Figure 17). However, the relationship between communication noise and network structure is more complicated when teams solve complex problems (Figure 11). With low communication noise, we reproduce the result that sparse networks allow for higher quality solutions, as before. However, as communication noise increases, it takes over the role in maintaining greater diversity of solutions previously achieved by network sparseness. Sparse networks then become so inefficient that the team often ran out of time before it could reach a consensus or even find a high-quality solution (Figure 11, middle row). Accordingly, the effect of communication noise is stronger in denser networks, and with high levels of communication noise, dense networks can actually outperform sparse networks since they allow more efficient percolation of high-quality solutions, and the communication noise acts to maintain solution diversity. This result echoes previous studies that found that dense networks are preferable to sparse networks for collective solving of complex problems when other mechanisms that prolong solution diversity are present, including conformist learning (Barkoczi & Galesic 2016) and strong prior beliefs (Zollman 2010). As communication noise increases and thereby maintains greater diversity of solutions in a team (Figure 18), teams reach better solutions but increase the required time and resources needed to reach a consensus.
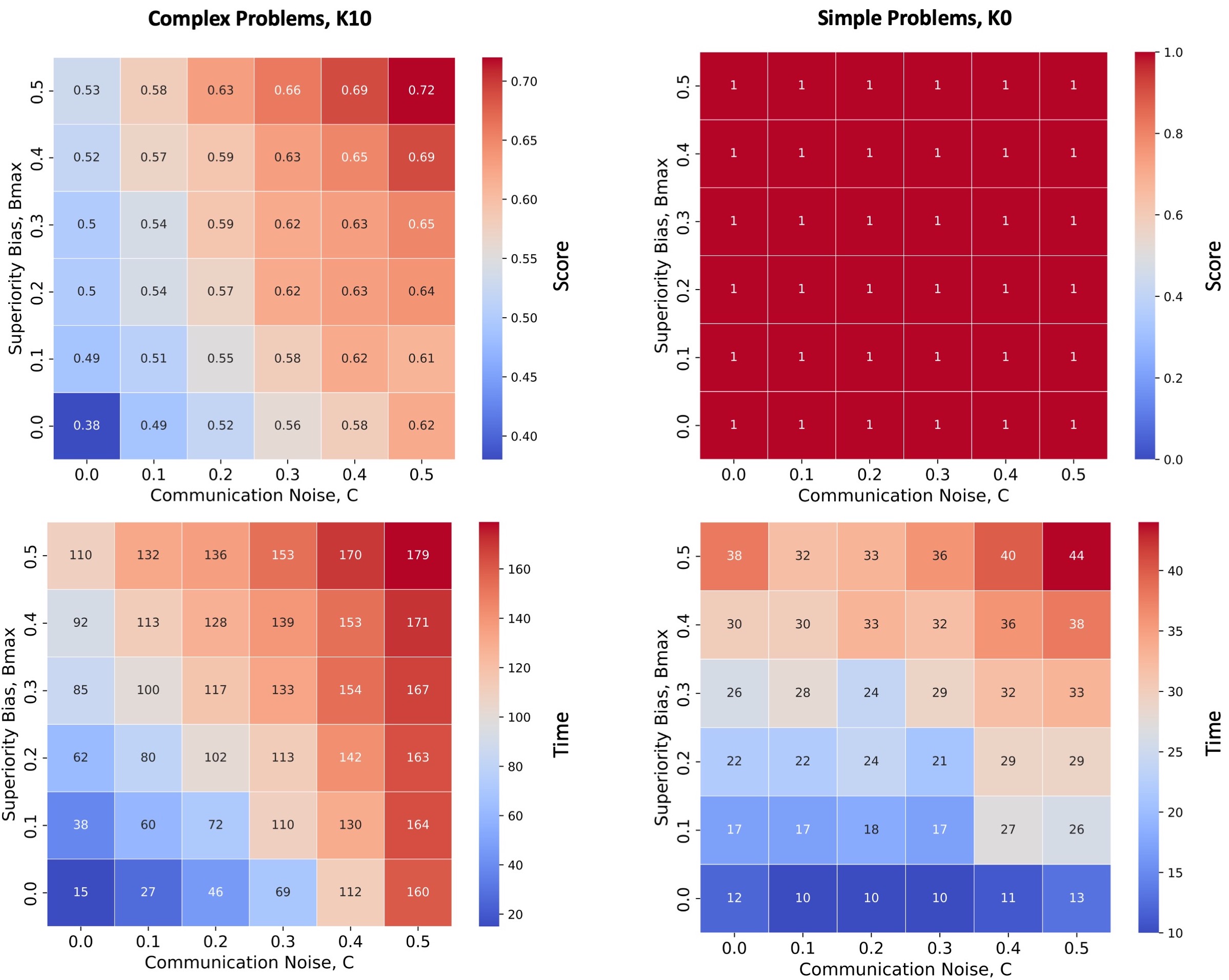
Interplay of superiority bias and communication noise
The confluence of superiority bias and communication noise demonstrates an additive effect on team performance, as illustrated in Figure 12. This suggests that when both superiority bias and communication noise are present, their combined impact on team performance metrics, such as score and time, is essentially the sum of their individual effects. This occurs because both noise and bias represent errors, sharing a similar nature, and both contribute to increasing the solution diversity within a team.
Discussion
Superiority bias and communication noise both make social learning less efficient in the short term. Agents exhibiting superiority bias ignore information about solutions that are marginally better than their current solutions, only switching when switching carries a large benefit. Agents experiencing communication noise fail to correctly copy better solutions, introducing random error that is likely to decrease rather than increase the quality of their solution. Yet each of these mechanisms, when operating at the group level, leads teams to reach a consensus on higher quality solutions than they reach when the mechanisms are absent. Each mechanism, though procedurally distinct at the psychological or communicative level, creates a benefit in the same way: by prolonging the diversity of solutions in the population and allowing a wider area of the solution space to be explored, they increase the chance that the team will discover a high-quality solution. This work contributes to an increasingly larger literature on collective problem solving, spread across several disciplines, and using several different models, showing that nearly any mechanism that increases the transient diversity of solutions will increase the quality of solutions to complex problems discovered by cooperative teams (reviewed in Smaldino et al. (2023)).
The contributions of superiority bias or communicative noise are not, however, unequivocally positive. For simple problems in which hill-climbing approaches work well and for which a determined individual is likely to reach the optimal solution, diversity-increasing processes simply prolong the time and resources needed to reach that solution. This is related to the well-known tradeoff between speed and accuracy in the judgment and decision-making literature, though that work usually focuses only on individual-level processes. It is also the case that the contribution of either superiority bias or communicative noise may interact with other mechanisms that increase or prolong diversity, including the sparseness of the social network. When added together, too much diversity may prevent a team from reaching a consensus in a timely fashion—a point previously made by Zollman (2010) in his study of networked Bayesian learners solving a two-armed bandit problem. Here we conceptually replicate this result for NK landscape models of collective problem-solving.
It is unclear how actionable the conclusions of this paper are at this time. While communication noise can be controlled to some extent, changing superiority bias is likely to be more difficult, as it reflects the psychological characteristics of individual team members. Our results also only apply to cases for which our broad model assumptions hold. These include the assumptions that problems are well-defined with a finite space of possible solutions, that solutions are readily assessable and rankable, and that team members share goals and will therefore readily share information. These assumptions are common to many models of collective problem-solving (Smaldino et al. 2023), but nevertheless do not always hold in real-life problem-solving conditions. For example, agents may have competing interests, and the quality of a solution is not always immediately apparent. So-called “wicked” problems (Buchanan 1992) may not even be easily defined in the first place, and so do not lend themselves to the sort of meandering search processes modeled here. Our model also ignores the roles of leadership, hierarchy, division of labor, and creativity that often guide collective problem-solving. Nevertheless, this work helps to flesh out work modeling factors that contribute to our understanding of collective problem-solving.
Acknowledgments
We appreciate the constructive feedback from Suzanne Sindi, Alexander Petersen, and Justin Yeakel. This work was partly funded by a grant from the Templeton World Charity, TWCF0715. Computational experiments were run on the Multi-Environment Computer for Exploration and Discovery (MERCED) cluster at UC Merced, which were funded by the National Science Foundation (NSF) Grant ACI-1429783. We thank Joshua Becker for publicly sharing the NetLogo code that formed the basis for our model code.
Appendix
Example of computing a solution’s score
\(N = 6\), \(K = 2\). The Solution:
| \[S = \{1,1,0,0,1,1\}\] | \[(2)\] |
Interdependency vectors \(V_{i}\):
| \[V_{1} = \{1,1,1\}, V_{2}= \{1,0,1\}, V_{3} = \{0,1,1\}, V_{4} = \{0,1,0\}, V_{5} = \{1,1,0\}, V_{6} = \{1,0,0\}\] | \[(3)\] |
We consider each interdependency vector as a binary number:
| \[V_{i} \Rightarrow \text{binary number} \; \; V_{1} \Rightarrow 111\] | \[(4)\] |
We convert the binary number of each interdependency vector into a decimal number:
| \[V_{i} \Rightarrow \text{binary number} \Rightarrow \text{decimal number}\; \; V_{1} \Rightarrow 111 \Rightarrow 7\] | \[(5)\] |
The score contribution of \(V_{1}\) is 143, which is the 7th element of the score in the list (indices starting at zero). The score list is a list of \(2^{(K+1)}\) random numbers from 0 to 1000.
| \[Score list: \{14,406,341,459,520,831,721,143\}\] | \[(6)\] |
| \[V_{1} \Rightarrow 143\] | \[(7)\] |
The score contribution of all interdependency vectors:
| \[\begin{aligned} V_1 & \Rightarrow 111 \Rightarrow 7 \Rightarrow 143 \\ V_2 & \Rightarrow 101 \Rightarrow 5 \Rightarrow 831 \\ V_3 & \Rightarrow 011 \Rightarrow 3 \Rightarrow 459 \\ V_4 & \Rightarrow 010 \Rightarrow 2 \Rightarrow 341 \\ V_5 & \Rightarrow 110 \Rightarrow 6 \Rightarrow 721 \\ V_6 & \Rightarrow 100 \Rightarrow 4 \Rightarrow 510 \\ \end{aligned}\] | \[(8)\] |
The solution score is the average score of all the interdependency vectors:
| \[\frac{1}{N} \sum_{i = 1}^{N} V_{i} = \frac{143 + 831 + 459 + 341 + 721 + 510}{6} = 500.83\] | \[(9)\] |
We raise all scores to power 8 and normalize them in the range of 0 to 1. With this range, we compute the scores of all solutions in the NK landscape and consider the highest score as 1.
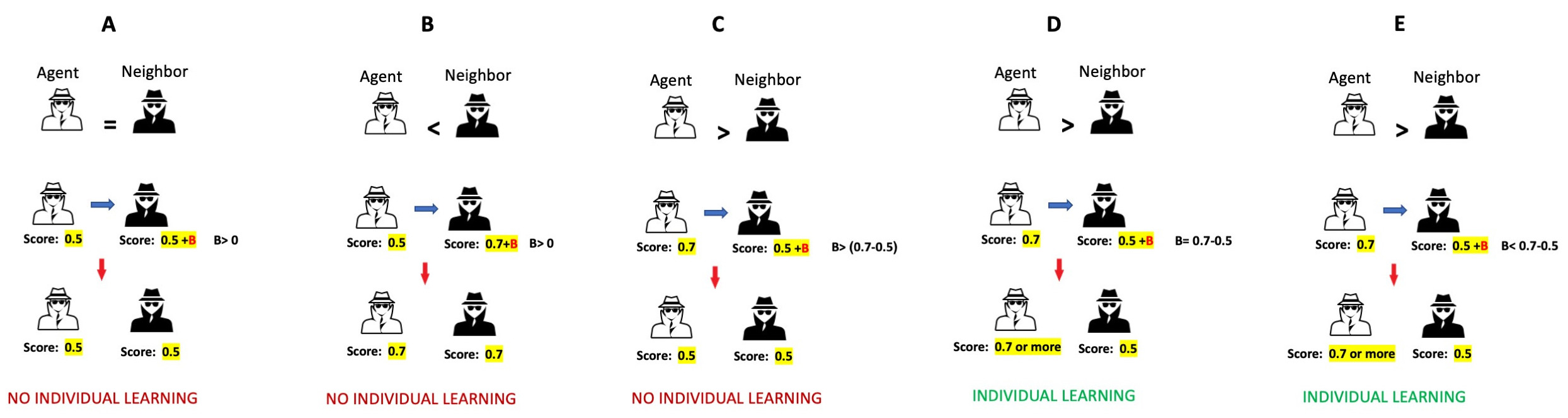
Inferiority bias
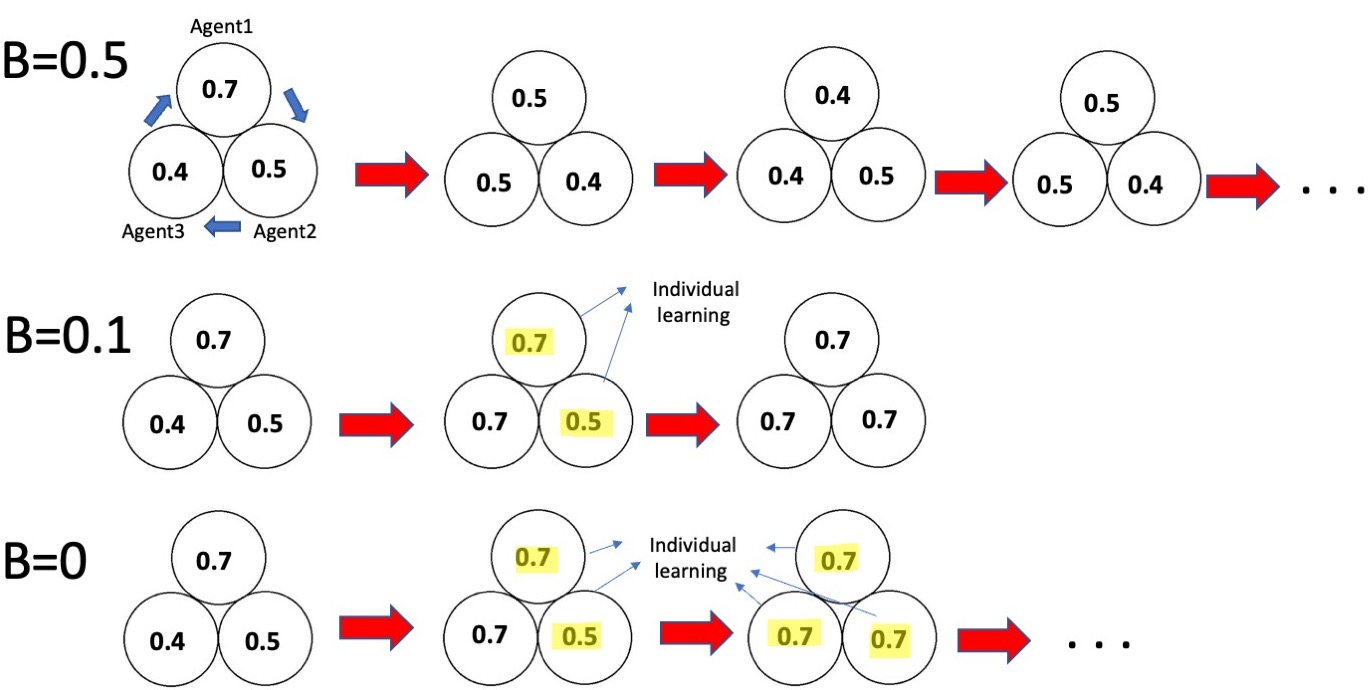
Inferiority bias is the perception of an individual belief of being inferior to others (American Psychological Association 2007). We modeled inferiority bias by adding a bias to the solution’s score of neighbor agents through social learning (Figure 13). In the social learning process, the agent considers its neighbor’s score as its actual score plus bias value (\(B_{i}\)). \(B_{i}\) is a random number between 0 and the perception level (\(B_{Max}\)). \(P\) is determined by the user. Each agent has its \(B\).

The inferiority bias dramatically decreases individual learning. In most cases, agents can find a neighbor with a score they perceive better than their scores (Figure 6). Therefore, agents adopt their neighbor’s solution and are not confident enough to explore the landscape through individual learning. This leads a team to converge quickly.
With inferiority bias, it is less likely for an agent who has already done social learning to be involved in individual learning (Figure 14). No two neighbors with the same score can be involved in individual learning because they perceive their neighbor (each others) better than themselves and imitate it (Figure 15). In our model, we consider the time as the first time a team reaches its highest score. The team score does not always increase with an inferiority bias (Figures 16, 17).
References
ADLER, A. (1927). Individual psychology. Journal of Abnormal and Social Psychology, 22(2), 116–122.
ALICKE, M. D., & Sedikides, C. (2011). Handbook of Self-Enhancement and Self-Protection. New York, NY: Guilford Press.
AMERICAN Psychological Association. (2007). APA Dictionary of Psychology. American Psychological Association Washington, DC
BARKOCZI, D., & Galesic, M. (2016). Social learning strategies modify the effect of network structure on group performance. Nature Communications, 7, 13109.
BAUMANN, O., & Martignoni, D. (2011). Evaluating the new: The contingent value of a pro-Innovation bias. Schmalenbach Business Review, 63(4), 393–415.
BAUMANN, O., Schmidt, J., & Stieglitz, N. (2019). Effective search in rugged performance landscapes: A review and outlook. Journal of Management, 45(1), 285–318.
BOROOMAND, A., & Smaldino, P. E. (2021). Hard work, risk-Taking, and diversity in a model of collective problem solving. Journal of Artificial Societies and Social Simulation, 24(4), 10.
BOYD, R., & Richerson, P. J. (1985). Culture and the Evolutionary Trocess. Chicago, IL: University of Chicago Press.
BUCHANAN, R. (1992). Wicked problems in design thinking. Design Issues, 8(2), 5–21.
CALDWELL, C. A., Cornish, H., & Kandler, A. (2016). Identifying innovation in laboratory studies of cultural evolution: Rates of retention and measures of adaptation. Philosophical Transactions of the Royal Society of London Series B, Biological Sciences, 371(1690).
CODOL, J.-P. (1975). On the so-Called “superior Conformity of the Self” behavior: Twenty experimental investigations. European Journal of Social Psychology, 5(4), 457–501.
CSASZAR, F. A. (2018). A note on how NK landscapes work. Journal of Organization Design, 7, 15.
DEREX, M., & Boyd, R. (2016). Partial connectivity increases cultural accumulation within groups. Proceedings of the National Academy of Sciences, 113(11), 2982–2987.
DEREX, M., Feron, R., Godelle, B., & Raymond, M. (2015). Social learning and the replication process: An experimental investigation. Proceedings Biological Sciences / the Royal Society, 282(1808), 20150719.
DIEHL, M., & Stroebe, W. (1987). Productivity loss in brainstorming groups: Toward the solution of a riddle. Journal of Personality and Social Psychology, 53(3), 497–509.
DUNNING, D. (2011). The dunning-Kruger effect: On being ignorant of One’s own ignorance. Advances in Experimental Social Psychology, 44, 247–296.
DUNNING, D. (2012). Self-Insight: Roadblocks and Detours on the Path to Knowing Thyself. New York, NY: Psychology Press.
DUNNING, D., Meyerowitz, J. A., & Holzberg, A. D. (1989). Ambiguity and self-Evaluation: The role of idiosyncratic trait definitions in self-Serving assessments of ability. Journal of Personality and Social Psychology, 57(6), 1082–1090.
FANG, C., Lee, J., & Schilling, M. A. (2010). Balancing exploration and exploitation through structural design: The isolation of subgroups and organizational learning. Organization Science, 21(3), 625–642.
GABRIEL, N., & O’Connor, C. (2021). Can confirmation bias improve group learning. Available at: http://cailinoconnor.com/wp-content/uploads/2022/04/Confirmation_Bias_Project-ArXiV.pdf
GOMEZ, C. J., & Lazer, D. M. J. (2019). Clustering knowledge and dispersing abilities enhances collective problem solving in a network. Nature Communications, 10(1), 5146.
HEADEY, B., & Wearing, A. (1988). The sense of relative superiority - Central to well-Being. Social Indicators Research, 20(5), 497–516.
HOORENS, V. (1993). Self-Enhancement and superiority biases in social comparison. European Review of Social Psychology, 4(1), 113–139.
JOHNSTON, R., Brignall, S., & Fitzgerald, L. (2002). “Good Enough” performance measurement: A trade-off between activity and action. Journal of the Operational Research Society, 53(3), 256–262.
JUDGE, T. A., Hurst, C., & Simon, L. S. (2009). Does it pay to be smart, attractive, or confident (or all three)? Relationships among general mental ability, physical attractiveness, core self-Evaluations, and income. The Journal of Applied Psychology, 94(3), 742–755.
KAHNEMAN, D., Sibony, O., & Sunstein, C. R. (2021). Noise: A Flaw in Human Judgment. New York, NY: Little Brown Spark.
KANFER, R., & Ackerman, P. L. (1989). Motivation and cognitive abilities: An integrative/aptitude-treatment interaction approach to skill acquisition. Journal of Applied Psychology, 74(4), 657.
KAUFFMAN, S. A., & Weinberger, E. D. (1989). The NK model of rugged fitness landscapes and its application to maturation of the immune response. Journal of Theoretical Biology, 141(2), 211–245.
KENDAL, R. L., Boogert, N. J., Rendell, L., Laland, K. N., Webster, M., & Jones, P. L. (2018). Social learning strategies: Bridge-building between fields. Trends in Cognitive Sciences, 22(7), 651–665.
LAZER, D., & Friedman, A. (2007). The network structure of exploration and exploitation. Administrative Science Quarterly, 52(4), 667–694.
LEVINTHAL, D. A. (1997). Adaptation on rugged landscapes. Management Science, 43(7), 934–950.
LEVINTHAL, D., & March, J. G. (1981). A model of adaptive organizational search. Journal of Economic Behavior & Organization, 2(4), 307–333.
LIND, P. G., & Herrmann, H. J. (2007). New approaches to model and study social networks. New Journal of Physics, 9(7), 228.
LONDON, M., & Sessa, V. I. (2006). Continuous learning in organizations: A living systems analysis of individual, group, and organization learning. Multi-level issues in social systems (Vol. 5, pp. 123-172). Emerald Group Publishing Limited
MEYER, H. H. (1980). Self-Appraisal of job performance. Personnel Psychology, 33(2), 291–295.
PORTER, C. O. L. H., Gogus, C. I., & Yu, R. C. F. (2010). When does teamwork translate into improved team performance? A resource allocation perspective. Small Group Research, 41(2), 221–248.
RIVKIN, J. W. (2000). Imitation of complex strategies. Management Science, 46(6), 824–844.
SHORE, J., Bernstein, E., & Lazer, D. (2015). Facts and figuring: An experimental investigation of network structure and performance in information and solution spaces. Organization Science, 26(5), 1432–1446.
SIGGELKOW, N., & Levinthal, D. A. (2003). Temporarily divide to conquer: Centralized, decentralized, and reintegrated organizational approaches to exploration and adaptation. Organization Science, 14(6), 650–669.
SMALDINO, P. E., Moser, C., & Pérez Velilla, A. (2023). Maintaining transient diversity is a general principle for improving collective problem solving. Perspectives on Psychological Science - In press
SUTIN, A. R., Costa Jr, P. T., Miech, R., & Eaton, W. W. (2009). Personality and career success: Concurrent and longitudinal relations. European Journal of Personality, 23(2), 71–84.
WRIGHT, S. (1932). The roles of mutation, inbreeding, crossbreeding, and selection in evolution. Available at: http://www.esp.org/books/6th-congress/facsimile/contents/6th-cong-p356-wright.pdf
YAHOSSEINI, K. S., & Moussaïd, M. (2020). Comparing groups of independent solvers and transmission chains as methods for collective problem-Solving. Scientific Reports, 10(1), 3060.
ZELL, E., Strickhouser, J. E., Sedikides, C., & Alicke, M. D. (2020). The better-than-Average effect in comparative self-Evaluation: A comprehensive review and meta-Analysis. Psychological Bulletin, 146(2), 118–149.
ZOLLMAN, K. J. (2010). The epistemic benefit of transient diversity. Erkenntnis, 72(1), 17–35.