How Polarization Extends to New Topics: An Agent-Based Model Derived from Experimental Data

, , ,
and
University of Limerick, Ireland
Journal of Artificial
Societies and Social Simulation 26 (3) 2
<https://www.jasss.org/26/3/2.html>
DOI: 10.18564/jasss.5105
Received: 03-May-2022 Accepted: 07-Apr-2023 Published: 30-Jun-2023
Abstract
Polarization is a key phenomenon which has been linked to increasing disliking between people of opposite political groups. Furthermore, polarization can extend to new topics such as the debate on COVID-19 vaccines, making it more complex to coordinate efforts for such a problem. The social identity approach (SIA) offers a robust theoretical framework for understanding identity-based social processes. This approach suggests that people’s perceptions and behaviour depend on their group identity (e.g. Democrat vs Republican). In this article, we developed an opinion-dynamics model integrating SIA to explore how polarization can extend to new topics. Furthermore, we developed this model from experiments with human participants. This allows us to use already validated micro-dynamic rules in the model. Empirical results show lack of repulsive effects, more attraction during in-group interactions and a new effect: increased stubbornness when people are exposed to opinions of an out-group member. The model was built mimicking the interaction structure of the experiment. At each iteration, an agent observes the opinion of another agent. Depending on their respective groups the agent will experience a stronger or weaker attractive force, together with some noise. This model was able to produce polarization without the use of repulsive forces. Furthermore, the sensitivity analysis tells us that polarization in new topics can appear when all the following conditions are satisfied: (1) each person recognizes who is belonging to which political group, (2) there are more in-group than out-group interactions and (3) there is some initial asymmetry on the topic.Introduction
Political polarization (i.e., the ideological distance between democrats and republicans) has been identified as a modern issue undermining social cohesion and developing hatred between different political groups (Iyengar et al. 2019; Pew Research Center 2014). Furthermore, it has shown the ability of extending also to new topics, such as climate change and COVID vaccination, strongly limiting the ability of our society to face major challenges (Farrell 2016)1.
Two predominant approaches exist in explaining polarization: the social comparison approach (Myers et al. 1980) and the informational influence/persuasive argument approach (Vinokur & Burnstein 1978) related to the common information effect (Stasser & Titus 1985). Neither approach, however, can fully account for polarization (Isenberg 1986). A two-process model has been proposed to overcome this limitation, but the social identification approach has been suggested as a more comprehensive explanation of polarization (Hogg et al. 1990; Sherman et al. 2009). The self-categorization approach posits that information will only be accepted as valid if they come from an ingroup member, and provides a singular explanation for polarization that encompasses both the informational influence and social comparison approaches (Hogg et al. 1990; McGarty 1999; Sherman et al. 2009).
The Social Identification Approach (SIA) is an important framework for understanding polarization, as it provides a comprehensive explanation of how attitudes become properties of social groups and how polarization develops. This approach claims that people perceive themselves and others fundamentally as members of social groups, and this transforms their perceptions and behaviour (Sherif 1937; Tajfel et al. 1971). Indeed, SIA is a framework that encompasses both self-categorization theory (a theory of cognition) and social identity theory (a theory of emotion/affect) (Hogg et al. 1990; McGarty 1999; Sherman et al. 2009). The framework is crucial in understanding how attitudes become a property of social groups, as people categorize themselves as group members and then internalize the group’s attitudes, leading to a desire to distance themselves from opposing outgroups (Sherman et al. 2009).
This approach is supported by extensive empirical evidence and has also been shown to be an excellent candidate for understanding phenomena such as steadily increasing political polarization (Bliuc et al. 2021). While the theoretical basis for the social identity approach is radically dynamical, for example arguing that "mind and society, individual and group, are mutual preconditions, and simultaneous emergent properties of each other," (Turner & Oakes 1986) its empirical support is largely from cross-sectional experiments (i.e., not including multiple time points) and surveys poorly adapted to investigating dynamic processes.
Opinion dynamics, on the other side, is a sub-field of agent-based modelling (ABM) which analyzes the dynamic evolution of people’s opinions (Flache et al. 2017). One of the most common approaches in this field is to simplify our society to a set of agents interacting in pairs or small groups (Castellano et al. 2009; Flache et al. 2017; Pineda et al. 2013). Usually agents do not have perceptions of broader social structures. Rather, their behavior depends uniquely on the agent (or small number of agents) they are interacting with or are adjacent to (Axelrod 1997; Deffuant et al. 2001; Hegselmann & Krause 2002). To give an example, two people may have an opinion both on Disney’s movie "Frozen" and on politics. Despite both being personal opinions (as commonly treated in many opinion dynamics models), the politics-related opinion is also related to social groups, so that one can identify the other person as Democrat or Republican (in the context of the US). This is not the case of the movie-related preference where people do not usually think in terms of "Frozeners" and "anti-Frozeners." Therefore, there is potential for studying how polarization can extend to novel from pre-defined categories (e.g., Democrats and Republicans) by including SIA into the opinion dynamics approach.
Recently, there have been calls for stronger connections between ABM and empirical work to validate models and address potential problems in theoretical models, as seen in studies like Chattoe-Brown & Gabbriellini (2021) and Edmonds (2005). Furthermore, strengthening this connection will also make ABM more accessible to fields with a strong empirical focus, such as psychology (Carpentras 2021), and increase the overall impact of ABM on the rest of the scientific community.
In the present work, we develop an agent-based model of opinion dynamics based on SIA from empirical experiments (notice that here we will use the word "experiment" to mean "experiments with human participants," instead of meaning "simulations" as sometimes done in the ABM literature). The use of experiments will be important both for (1) validating the micro-dynamic rule of the opinion dynamics model and (2) making the present work more accessible to the psychological literature which is more familiar with experiments in SIA.
This paper is divided in two parts: in the first one we will focus on the experimental procedure. Specifically, we will discuss how we designed an experiment which is both in line with SIA experiments and, at the same time, similar to the processes usually modeled in opinion dynamics. Then we will discuss the experimental findings, together with their significance for building the model. In the second part we will focus on the opinion dynamics model describing its properties and its connection to the data. Then, through manual exploration and, especially, through sensitivity analysis, we will discuss which conditions are required for observing polarization in novel topics. Finally, in the discussion section we will discuss how the conditions for polarization are fostered by online interactions as well as exploring possibilities for future studies.
The present study aims to derive an opinion dynamics model from empirical observations and to examine its implications. Our main research question centers on the exploration of how social identity influences the formation of opinions on new topics. In line with the "Keep it simple, stupid" (KISS) approach, the model we develop is designed to be straightforward, while also incorporating elements of social identity theory.
The study aims to yield insights into three key points: (1) the model is expected to reveal both congruences and novel perspectives with the SIA, (2) it will contribute to the understanding of polarization and its effect on opinion formation, and (3) it will advance the field of OD literature by providing a validated model.
Experimental Setup
Motivation and overview
As mentioned in the previous section, we included an experimental setup to both validate the micro dynamic rule and to make the current work more accessible to empirically oriented fields. Because of that, in the next subsection we will describe the experiment in detail according to the standards of classical SIA literature. In this subsection, instead, we want to provide an more intuitive overview for people working in ABM or, in general, for people more interested in the model and less in the details of the experiment.
Experiments in SIA often use as a control group that is usually referred to as "minimal groups paradigm." Minimal groups are groups that do not exist in everyday life, and are limited to the duration of the experiment (Diehl 1990; Tajfel et al. 1971). One popular example is making people choose between two paintings: Klee’s Temple Gardens or Kandinsky’s composition VIII and then grouping them based on their choice (Tajfel et al. 1971).
In our experiment we collected data both in the case of minimal groups and in the case of political groups (i.e., Republicans and Democrats), to observe how people’s dynamic behavior changed in different conditions. Specifically, we expect people to exhibit stronger attraction to in-group members in the case of political groups.
As mentioned, we are interested in how groups can influence the dynamics of novel attitudes and especially, in producing an experiment that can easily be translated into an agent-based model. Because of that, we asked participants their opinion on a novel topic both before and after showing them the opinion of a fellow participant. Furthermore, we also showed the participant’s group identity to test how in-group and out-group affected the choice of the opinion at time 2. We also collected the opinion in such a way that it can be directly translated into a "continuous" variable between -1 and 1, similarly to how opinions are often modeled in opinion dynamics models (Deffuant et al. 2001).
Data collection process
Participants were recruited through the online platform Prolific, receiving a total compensation of 1 British Pound (GBP) (i.e., 9.10 pounds per hour). As previously mentioned, we collected data from two groups: experimental and control group. The two differed only with regard to the salient group membership (i.e., arbitrary minimal groups vs. political groups). To ensure a balanced recruitment of self-identified Democrats and self-identified Republicans, we distributed two different Prolific samples with Republicans and Democrats as additional inclusion criteria. The overall sample consisted N=505 fluent English speakers from the United States ranging in age from 18 to 70 years old (women=62%, \(m_{age}\)=27.9, sd=8.5). Participants were divided into a control group (N=204) and an experimental group (N=301). Since this experiment includes groups (e.g., Republican and Democrats) within groups (experimental vs control), to avoid confusion, we will refer to the latter with the word "setting" (e.g., "experimental setting" or "control setting").
Participants were initially informed that the survey involved “working alongside others in real time to learn about each other’s attitudes on a range of different topics”. To underline this cover story, we created a "lobby" which was filled by four more players (two ingroup and two outgroup members). The text informed them also that participation involved engaging in decision-making tasks. In reality, however participants received bogus responses from pseudo participants. This was done to simplify the experimental procedure as it did not require to have all the participants active at the same time. Notice however that this does not change the type of interaction they would have experienced with real participants. Indeed, as we will discuss in a few lines, to keep the experiment similar to opinion dynamics models, we provided very minimal and standardized interaction between participants; thus making it impossible to distinguish between interactions with real participants and with a bogus participant.
For the control setting, we used the so-called "minimal group paradigm" which makes use of groups whose existence is limited to the experiment and have little or no meaning in everyday life (Diehl 1990; Tajfel et al. 1971). Following Tajfel and colleagues classic method, we choose minimal groups that categorize individuals based on aesthetical preferences, consistent with a classic minimal group design in social psychology, the Klee vs Kandinsky groups. Indeed, one group consists of the people who selected Klee’s Temple Gardens painting as an avatar, while the other consists of people who selected Kandinsky’s composition VIII. Indeed, participants were asked to "choose the Avatar you feel most affinity with." Furthermore, they were also instructed that, based on their choice, they will be joining the relative group.
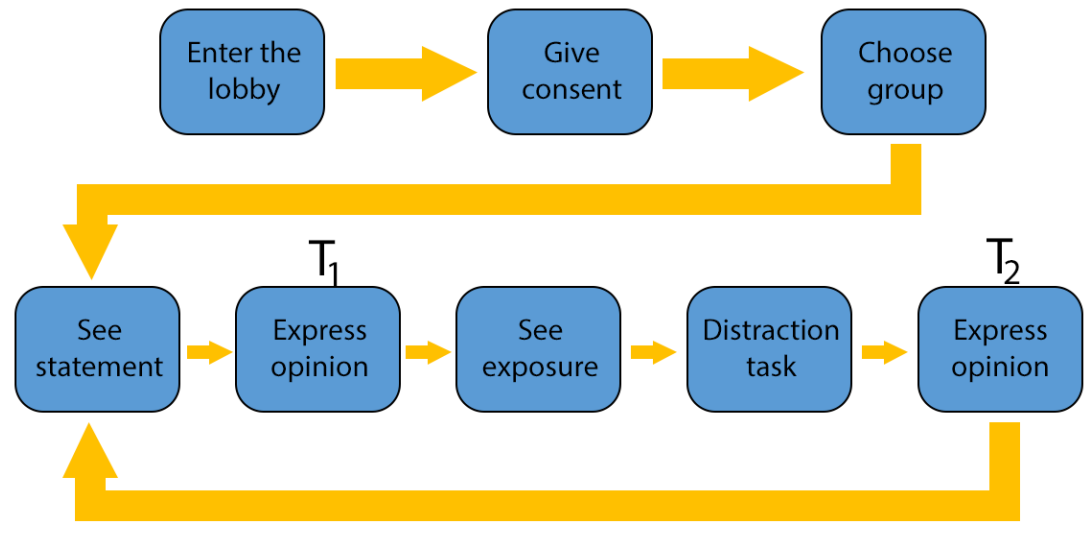
On the contrary, for the experimental setting we selected two opposing groups which are well known and relevant in America’s social life: Democrats and Republicans (represented in the avatar by the respective symbols).
During the experiment, participants were presented with a statement to which they could either agree or disagree. Furthermore, they were asked to express, on a scale from 1 to 10, how certain they were of their view. This was done as the certainty will be used to produce the final opinion.
Statements were selected among "novel attitudes" based on pre-tested arbitrary attitudes (e.g., circle is a noble shape) (Maher et al. 2020). These statements were carefully developed to have the same properties as attitude statements commonly used in scientific studies, but to be new to the person and unaffected by pre-existing attachments (whether personal or ideological). This was done to study people’s behavior on completely new topics. In this way, the observed dynamic should hold maximum internal validity and not depend on previous personal experience, other personal traits, or ideological connections to relevant identities. While some readers may think that these attituded as non-sensical statements, in Carpentras et al. (2022) it has been shown how people can easily distinguish between them and non-sensical statements.
For example, asking people their opinion about "gun control" may elicit different dynamics depending on personal characteristics, such as for people of different gender, or for people strongly versus weakly interested in politics. Similarly, such opinions are aligned to social identities, such as being Republican versus Democrat, and identity-related opinion dynamics may be different for different combinations of topic and identity. For example, male participants may behave in one way when discussing gun control and in a different way when discussing vegetarianism. Although we sacrifice some realism and ecological validity, novel attitude statements escape these confounding factors, therefore allowing us to combine them together during the data analysis (Carpentras et al. 2022; Maher et al. 2020).
Each participant reported her agreement and certainty both before and after exposure to a fellow participant’s agreement. That is, participants could see whether the other participant agreed or disagreed with the statement, but not their certainty level. This limitation was introduced to make interactions more similar to real life and social media interactions, where people express their agreement (e.g., through a like button), without adding a number to represent their certainty. In order to elicit group-based social influence, during the interaction, the participant could see also the group identity of the other participant. These were the only pieces of information accessible during the interaction, thus making impossible for the participants to distinguish between a real and a bogus participants. Besides making interactions more similar to interactions in an ABM, these limitations helped also in avoiding the introduction of additional confounds.
For each person, this process was repeated for four novel topics and organized in such a way that every time the participant would be exposed to one of the four possible conditions:
- ingroup - same agreement level
- ingroup - different agreement level
- outgroup - same agreement level
- outgroup - different agreement level
Where "same agreement level" means that both the participant and the exposure either both agree or both disagree with the presented statement. Instead "different agreement level" represents the case in which one agrees and the other disagrees with the presented statement.
Finally, participants read a closing statement debriefing them on the nature of the study. This research study has received ethical approval from the University of Limerick, Education and Health Sciences Research Ethics Committee (2019_06_19_EHS).
Data analysis
As mentioned before, we want to produce an empirical experiment that can be easily translated into an opinion dynamics model. Many models of opinion dynamics represent opinions as a continuous variable on a limited interval (Deffuant et al. 2001; Flache et al. 2017; Hegselmann & Krause 2002). As mentioned in the previous section, we collected both participants agreement (expressed as either "agree" or "disagree") and their certainty (expressed as a number between 1 and 10). In order to produce an opinion variable similar to classic models in opinion dynamics firstly we coded agree and disagree as respectively +1 and -1. Then we combined it with the certainty using the following formula:
| \[ o = \frac{a * c}{10}\] | \[(1)\] |
where \(o\) is the opinion, \(a\) is the agreement value, and \(c\) is the certainty value. While the obtained opinion is not purely continuous (in the mathematical sense) it is still a variable between +1 (representing full agreement) and -1 (representing full disagreement) with steps of 0.1.
Having calculated the opinion, we can also calculate how this opinion changes over time. We call the absolute difference \(\Delta_{a}\) calculated as:
| \[ \Delta_{a} = o(t_2)-o(t_1)\] | \[(2)\] |
Furthermore, we define the relative opinion difference as:
| \[ \Delta_r = \Delta_a * a_{exp}\] | \[(3)\] |
where \(a_{exp}\) is the agreement level (i.e., +1 or -1) of the exposure of the bogus participant. Notice that \(\Delta_r\) is positive if the participant is moving in the direction of the exposure (i.e., attraction) and negative if, instead, the participant is moving her opinion in the opposite direction (i.e., repulsion).
Finally, similar to standard procedures in experimental psychology we want to separate the "effect" from "random variations." To make this procedure more compatible with the model, we measured both the average of \(\Delta_r\) and its mean error. As we will see later, in the model these values will be represented respectively as a deterministic opinion shift and random noise, therefore we will refer to them with the terms "shift" and "noise".
Experimental results
As can be seen from table 1, we did not observe repulsive forces (i.e., all the relative shifts are positive). That is, on average, people tended to move in the direction of the opinion they were exposed to. Therefore, people exposed with +1, will tend to move in the direction of +1, while people exposed with -1 will move towards -1. This happened regardless of whether the other participant was an in-group or out-group member, and regardless of whether the relevant identity was related to minimal or political groups. While this contrasts with some arguments in SIA, as they would expect people to maximize their differences with outgroup members (Doosje et al. 1999), and thus move away from them, this is still in agreement with other experiments which did not find repulsive forces even when people’s opinions are at the opposite extremes of the opinion spectrum (Moussaïd et al. 2013; Takács et al. 2016).
Notice also that the effect of the noise is bigger than the shift. This consistent with previous studies using weak social influence (Carpentras et al. 2022) where the effect is significant and present, but people still tend to have big random fluctuations. Indeed, it has been shown how these random fluctuations are part of the self-reflection process (i.e., they appear just by asking the same opinion twice, even in the absence of any external influence). This means that a person influenced with a positive opinion (+1) may still move towards the opposite direction (-1). This is the reason why both here and in the following agent-based model we decided to not neglect the noise, but to include it as a fundamental part of the dynamic process.
However, our results also clearly show two effects which are consistent with SIA. Firstly, in-group exposure resulted in a stronger shift (i.e., people are more influenced by in-group members than by out-group members). Through t-testing we found that, while this difference is not significant for the minimal groups, it shows a significant difference (p<0.05) for the political groups. The second important effect that we can observe is that, while minimal groups still can produce a shift, this is significantly smaller (p<0.01) compared to the one produced by the political groups.
We also noticed an unexpected result: while the noise (i.e., the random component of the opinion change) is roughly the same in three conditions, it is significantly lower in the case of out-group exposure in the experimental setting (p<0.001, obtained through bootstrapping the people and checking for its impact on the noise). Thus, the presence of political out-group members seems to “solidify” someone’s opinion, not in the sense that their opinion would become more extreme, but in the sense that they would be less likely to change their own opinion (i.e., appearing more stubborn). This observation agrees with social identity theory, which holds that people perceive homogeneity in out-group members, and (usually) more variability in in-group members (Doosje et al. 1999).
In this section we observed that people tend to move in the direction of the opinion they were exposed to, regardless of whether the source was an in-group or out-group member, or if the relevant identity was related to minimal or political groups. We found two consistent results with social identity theory: stronger shifts for in-group exposure and a smaller shift for minimal groups compared to political groups. An unexpected result was that the noise was significantly lower in the case of out-group exposure, indicating that the presence of political out-group members solidified a person’s opinion, making them less likely to change it.
| Minimal groups | Political groups | |||
|---|---|---|---|---|
| Shift | Noise | Shift | Noise | |
| Ingroup | 0.022 | 0.17 | 0.068 | 0.17 |
| Outgrup | 0.003 | 0.17 | 0.033 | 0.11 |
Agent-Based Model
Model properties
Following the previous results, we built an agent-based model to reproduce the observed behavior and see which kind of dynamics it can generate in case of repeated interactions. The main purpose of this model is to study how polarization can appear in novel topics and its relationship with social groups. As previously mentioned, the biggest advantage of building a model from experimental data lies in the fact that the micro-dynamic rule (i.e., how agents update their own opinion) is already validated. Indeed, as we will discuss, most of the parameter values used in the model come from the values summarized in Table 1 and the interaction process itself comes from the experimental design.
We coded the model in python. The code is available at https://www.comses.net/codebase-release/8fc4ed37-572f-4494-86ec-1571d89e4da6/ in the form of a Jupyter notebook (a computing platform for the Python language) for ease of exploration. For the simulations, we used 1,000 agents divided into two groups of 500 each (called group A and group B). For each model iteration, two agents are selected randomly. They firstly check if they belong to the same group and, therefore, if they will have an in-group or an out-group interaction. Afterwards, they update their opinion using the values of shift and noise belonging to the type of interaction. As previously mentioned, shift is modeled as a constant opinion change. Therefore if the initial opinion is -0.3 and the agent is exposed with agreement (i.e., +1), for a shift of 0.068, the agent will update her opinion to -0.3+0.068=-0.232. On top of the shift, each agent will also experience some noise in the interaction, modeled as a uniform distribution of amplitude specified by the type of interaction. Notice that, due to the size of the noise, this will mean that people may move in the direction of the exposure, as well as in the opposite direction. However, the average movement will coincide with the shift value (i.e., an attractive force). This will mimics all the measured properties of the empirical data.
The values representing shift and noise are obtained from the experimental data in the following conditions: (1) "Minimal groups" uses the values of the table for the control setting (i.e., Klee and Kandinsky) and (2) "Political groups" instead uses the values from the experimental setting (i.e., Republicans and Democrats).
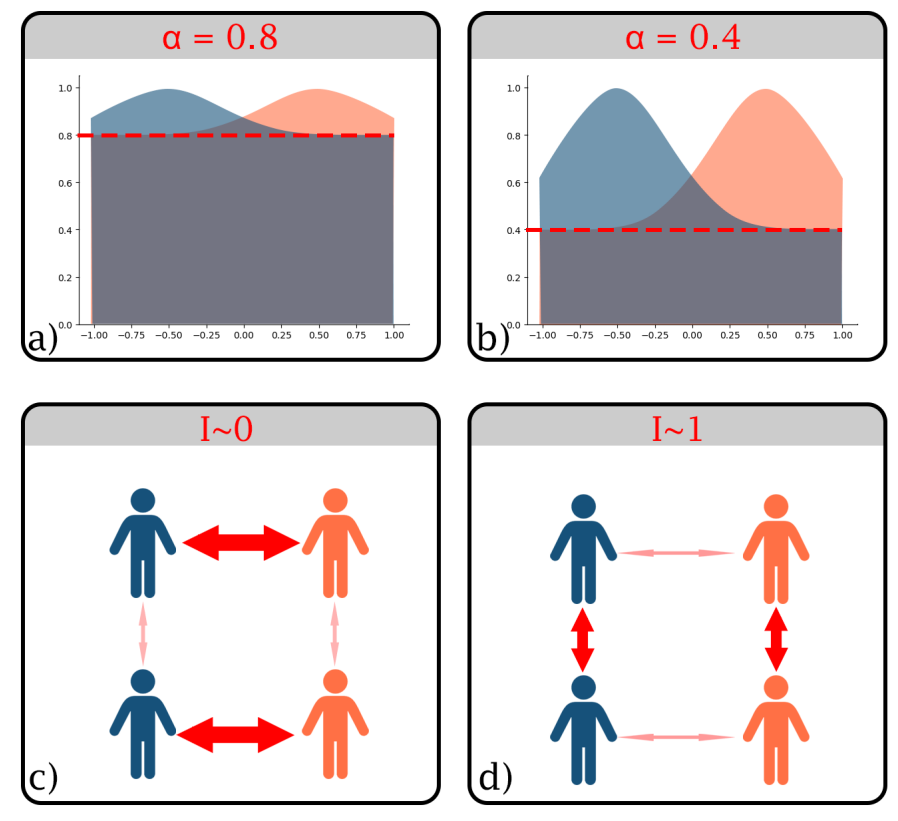
Besides these conditions, we introduced two other parameters for exploring the model. The first one is the initial opinion distribution. Indeed, while in opinion dynamics it is common to assume uniform distributions for the initial opinion, in this case would be interesting to know what happens if there is an initial bias (or, similarly a correlation) between the two groups and the expressed opinion. This will allow us to see how this will impact the appearance of polarization in new topics.
To produce this asymmetric distribution, we used a combination of both a normal and a uniform distribution (see Figure 2). We chose these functions as they are the most well-known distributions and therefore they allow for simple modelling of the intial distribution. In formula:
| \[ f(o) = (1-\alpha) * N(o)_{\mu,\sigma} + \alpha*U(o)\] | \[(4)\] |
where \(f(o)\) is the overall opinion distribution, \(N(o)\) is the normal distribution, and \(U(o)\) is the uniform distribution. While for \(\sigma\) we selected 0.5 for both groups, we choose \(\mu=0.5\) for group A and \(\mu=-0.5\) for group B to produce the initial asymmetry in the data. In this way, when \(\alpha=1\) the two distributions would be perfectly identical (i.e., two uniform distributions). Instead, for \(\alpha=0\) we would have two normal distributions centered in +0.5 and -0.5, thus maximizing initial asymmetry.
The final parameter that we would like to study is the amount of in-group interactions (as opposed to the amount of out-group interactions). We formalized this into the parameter \(I\) which represents the probability of having in-group interactions. Therefore, for \(I=1\) agents will only interact with in-group members, for \(I=0\) they will interact only with out-group members, and for \(I=0.5\) we will have equal probability of having in-group and out-group interactions.
For each run we let the model evolve for 100,000 iterations (i.e., every agent on average will interact 200 times, as in every interaction two agents are involved) as this was sufficient for the model to reach convergence.
Model convergence and sensitivity analysis
In this section, we will explore the difference between the case of minimal groups versus the case of political groups. Before moving to the sensitivity analysis, we preferred to run an intermediate phase of manual exploration of the model (Bommel et al. 2016). This helped in the interpretation of the results from the sensitivity analysis. In this phase, we found three main possible final distributions, which we will refer to as bi-polarization, mono-polarization and uniform (see Figure 3).
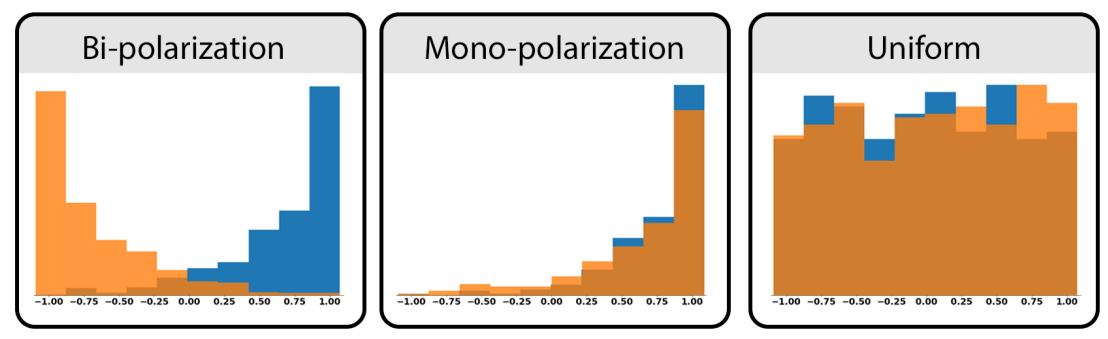
Bi-polarization happens when the two distributions move to opposite extremes (Figure 3). Qualitatively this configuration also coincides with the common interpretation of political polarization (Lelkes 2016). As we will discuss after the sensitivity analysis, this configuration appears often when people interact mostly with in-group members.
Mono-polarization, instead represents the case in which both groups move to the same extreme. This configuration appears mostly when agents interact with out-group members. Indeed, due to the lack of repulsive forces, out-group members are still able to influence each other and, with enough interactions, behave as a unique cohesive group. Notice also that, while they both move to the extreme, the concept of "being extreme" is actually contextual. Indeed, several positions that may have been extreme in the past, are today given as granted (e.g., opposing slavery). This could be modeled including concepts such as Overton Window (Overton 2023), even if this falls beyond the scope of this article. Notice also that in our model, mono-polarization can happen in both directions with equal probability. To verify this we run 100 runs with \(\alpha=1\) and found 49 times monopolarization at +1 and 51 times monopolarization at -1. This results in a p-value of 0.92, therefore, clearly not rejecting the hypothesis of equiprobability of the two outcomes.
Finally, the uniform case appears when the interaction between agents is too weak with respect to the effect of noise. In this case dominated by noise, both groups "converge" to a uniform distribution. As can be seen in Figure 3 this will not produce a perfectly uniform distribution. Indeed, due to random fluctuations we will constantly have the formation of temporary peaks.
Finally, we run the sensitivity analysis to better understand how the selected parameters will influence the final outcome. Every point in Figure 4 is the average of 10 runs, meaning that we repeated each simulation 10 times without changing the values of \(\alpha\) and \(I\), but re-initializing the simulation each time.
Since our main goal is to study the appearance of political polarization in novel topics, we introduced the polarization measurement as the difference of the mean of the two final distributions, as it is often calculated in the literature (Lelkes 2016; Pew Research Center 2014). In formula:
| \[ P = |Mean_A -Mean_B|\] | \[(5)\] |
To provide more insight, we offered an alternative measure \(P_{th}\) which represented the probability that \(P\) would be above a threshold of 0.3 at the end of the simulation. We introduced this value to test if some parameter combinations can actually generate situations in which for some runs we have strong polarization, while for other runs (still having the same parameters) we have little or no polarization.
Finally, we introduced the uniformity parameter \(u\). We introduced it for distinguishing cases of mono-polarization from cases in which both distributions are roughly uniform (as in both cases the polarization parameter would be close to 0). We calculated \(u\) for a distribution \(D\) as:
| \[ u(D) = \sum_{bins} |h(D)-mean(h(D))|\] | \[(6)\] |
where \(h\) is the histogram of the distribution \(D\). Therefore we will observe \(u=0\) when the histogram is flat (i.e., uniform distribution). This value will become progressively bigger as the distribution deviates from the uniform one.
The top part of Figure 4 shows the results for the case of political groups (i.e., using the values of shift and noise for the experimental setting). As seen, when I<0.5 (i.e., people interact mostly with out-group members) polarization cannot appear. However, as people start interacting more and more with their in-group members, initial asymmetry can give rise to the appearance of polarization. In the extreme case in which people interact only with in-group members, even in the case of two initially uniform distributions, polarization can still appear simply by random fluctuations. Furthermore, by observing the plot of the \(u\) parameter, we see that with political groups we always achieve either bi- or mono-polarization.
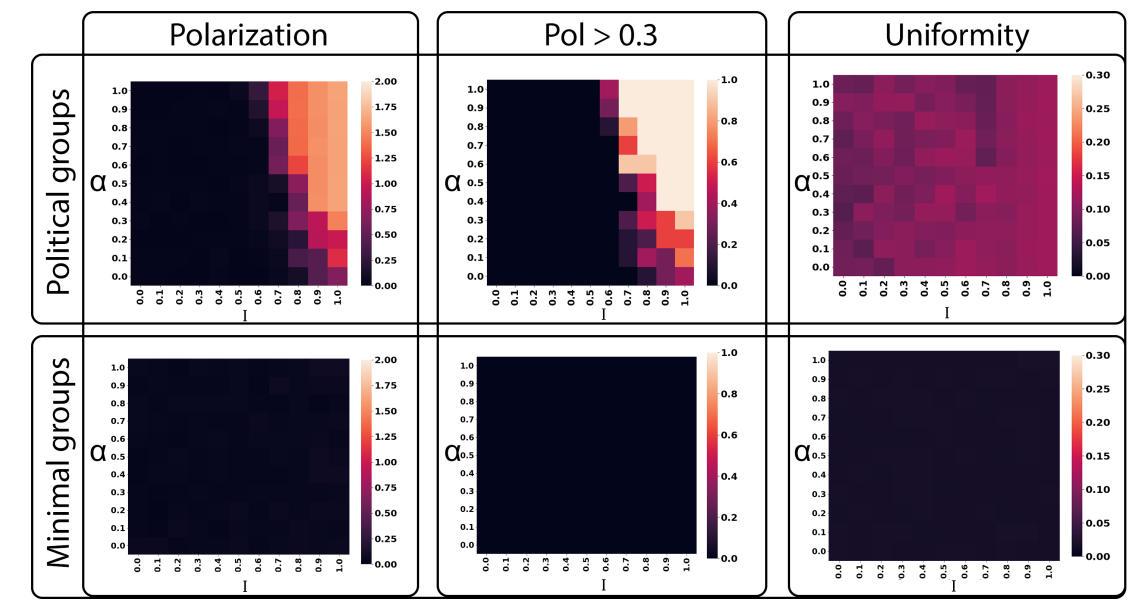
The situation is very different when, instead, we used the minimal groups configurations. In this case, the attraction between agents is so weak that the entire dynamic is dominated by the random movement. Because of that, no configuration is sufficient for producing polarization. This is also confirmed by the fact that the \(u\) parameter is way smaller than the one for political groups.
Discussion
Political polarization and its steady increase has been identified as a major threat for the stability of western democracies (Iyengar et al. 2019; Pew Research Center 2014). Indeed, it has been shown to play an important role also in new and imminent issues (e.g., vaccination or climate change) whose solution would be based on social cohesion (Farrell 2016). In this article we developed a model aimed at showing how polarization can extend from social groups into new topics. Furthermore, we rely on experimental data to validate the micro-dynamic rule. Notice, that, as there is quite some confusion in the literature with the terms "validation" and "calibration" here we refer to a very specific type. Indeed, in this study, we derived the entire model from an experiment, contrary to many other models which are first developed and then calibrated or validated on the data.
Using values from the minimal groups paradigm we observe no polarization, independently on other parameters. This tells us that even if people can form groups based on things such as aesthetic preferences, these groups are not strong enough to produce polarization in novel topics.
On the contrary, when people can recognize each other as members of political groups, polarization can appear also in new topics. However, our simulations inform us that this is not always the case. Indeed, polarization needs: 1) more interactions with in-group members than with out-group members and 2) some degree of initial asymmetry in the distribution. This second parameter is especially important when we have similar probability of in-group and out-group interactions (i.e., \(I \sim 0.5\) ).
It is also important to notice that this model can produce polarization without having to introduce repulsive forces, which has been identified as an important goal for opinion dynamics models (Flache et al. 2017). Indeed, there have been little evidence so far empirically supporting the idea of repulsive forces in social interactions (Flache et al. 2017; Mäs et al. 2013). Notice however that here we are not claiming the impossibility of having repulsive forces.
The appearance of polarization without repulsion is possible in our model as people interact only expressing their agreement but not their certainty level. Therefore, it is possible for a person with opinion +0.3 to push a person with opinion +0.7 closer to 1. While some may argue that this can still be represented mathematically as some kind of repulsion, this will not really represent the idea at the basis of repulsive forces. Notice also that this work should be seen more as a first step in analyzing polarization in novel topics, instead of as a conclusive work. Indeed, it presents several limitations that should be addressed in future works.
The first limitation is that, while this model is based on experimental data (in line with the current call on integrating empirical data in models) (Castellano et al. 2009; Flache et al. 2017; Hassan et al. 2008) the collected data refers to only two time steps. Instead, the model’s results are based on multiple iterations (on average 200 per agent). This can be seen as an advantage of modelling, as it allows to extract data from a limited dataset. However, in future works would be interesting to observe if people’s behavior on novel topics can change after multiple exchanges. Similarly, the data collection has focused on novel attitudes, making sure that these topics are completely new to the participants. However, new topics (such as bitcoin) after some time become more and more grounded in society and may become more associated to particular identities, possibly changing the interaction dynamics. Therefore, in future studies would be interesting also to include how people update their opinion on other type of topics. Similarly, future studies can also explore how more aspects of SIA can be integrated expanding the model.
Notice also how both in the experiment and in the model people are interacting with strangers. While this is partially true in our day and age (such as in social media), people tend to actually have repeated interactions with people they know.
In conclusion, our model shows how polarization can appear in new topics due to 1) the presence in the debate of political groups 2) initial asymmetry in the distributions and 3) more in-group than out-group interactions. As in the era of social media people are allowed or even pushed to interact with like-minded people and news (with phenomena such as filter bubbles and echo chambers) (Cinelli et al. 2021; Pariser 2011) this model can shine new light on how political polarization can so easily spread to other topics such as climate change and vaccination.
Acknowledgements
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie (grant agreement No 891347) and from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 802421).
Notes
The phenomenon of polarization in the United States over the past two decades has been a topic of debate, with some suggestions that it has been exaggerated. Despite this, it remains a relevant issue to consider. An important contribution to the discussion was made by (Lelkes 2016), who concluded that polarization was primarily driven by "partisans". Additionally, there is strong evidence to support the idea of "sorting", whereby individuals increasingly affiliate with like-minded individuals. (Abramowitz 2010) analyzed responses to policy items in the American National Election Studies (ANES) data and coded them as liberal (-1), conservative (1), or moderate (0). The results revealed an increased bimodality in the scale, indicating a trend towards polarization. These findings demonstrate the need for continued investigation and analysis of polarization in the US and highlight the importance of considering both the sources and mechanisms driving this phenomenon.↩︎
References
ABRAMOWITZ, A. (2010). The Disappearing Center: Engaged Citizens, Polarization, and American Democracy. Yale University Press. [doi:10.12987/9780300162882]
AXELROD, R. (1997). The dissemination of culture: A model with local convergence and global polarization. Journal of Conflict Resolution, 41(2), 203–226. [doi:10.1177/0022002797041002001]
BLIUC, A.-M., Bouguettaya, A., & Felise, K. D. (2021). Online intergroup polarization across political fault lines: An integrative review. Frontiers in Psychology, 12, 4744. [doi:10.3389/fpsyg.2021.641215]
BOMMEL, P., Becu, N., Le Page, C., & Bousquet, F. (2016). Cormas: An agent-based simulation platform for coupling human decisions with computerized dynamics. In Simulation and Gaming in the Network Society, 387–410. Springer. [doi:10.1007/978-981-10-0575-6_27]
CARPENTRAS, D. (2021). Challenges and opportunities in expanding ABM to other fields: The example of psychology. Available at: https://rofasss.org/2021/12/20/challenges/.
CARPENTRAS, D., Maher, P. J., O’Reilly, C., & Quayle, M. (2022). Deriving an opinion dynamics model from experimental data. Journal of Artificial Societies and Social Simulation, 25(4), 4. [doi:10.18564/jasss.4947]
CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2), 591. [doi:10.1103/revmodphys.81.591]
CHATTOE-BROWN, E., & Gabbriellini, S. (2021). How to improve network science: The potential of (empirically calibrated and validated) agent-Based modelling. SocArXiv preprint. Available at: https://osf.io/preprints/socarxiv/bym74/ [doi:10.31235/osf.io/bym74]
CINELLI, M., De Francisci Morales, G., Galeazzi, A., Quattrociocchi, W., & Starnini, M. (2021). The echo chamber effect on social media. Proceedings of the National Academy of Sciences, 118(9), e2023301118. [doi:10.1073/pnas.2023301118]
DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2001). Mixing beliefs among interacting agents. Advances in Complex Systems, 1(01–04), 87–98. [doi:10.1142/s0219525900000078]
DIEHL, M. (1990). The minimal group paradigm: Theoretical explanations and empirical findings. European Review of Social Psychology, 1(1), 263–292. [doi:10.1080/14792779108401864]
DOOSJE, B., Spears, R., Ellemers, N., & Koomen, W. (1999). Perceived group variability in intergroup relations: The distinctive role of social identity. European Review of Social Psychology, 10(1), 41–74. [doi:10.1080/14792779943000017]
EDMONDS, B. (2005). Assessing the safety of (numerical) representation in social simulation. Available at: https://www.academia.edu/2578378/Assessing_the_safety_of_numerical_representation_in_social_simulation.
FARRELL, J. (2016). Corporate funding and ideological polarization about climate change. Proceedings of the National Academy of Sciences, 113(1), 92–97. [doi:10.1073/pnas.1509433112]
FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2. [doi:10.18564/jasss.3521]
HASSAN, S., Antunes, L., Pavon, J., & Gilbert, G. (2008). Stepping on earth: A roadmap for data-driven agent-Based modelling. Proceedings of the 5th Conference of the European Social Simulation Association (ESSA08)
HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence: Models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2.
HOGG, M. A., Turner, J. C., & Davidson, B. (1990). Polarized norms and social frames of reference: A test of the self-categorization theory of group polarization. Basic and Applied Social Psychology, 11(1), 77–100. [doi:10.1207/s15324834basp1101_6]
ISENBERG, D. J. (1986). Group polarization: A critical review and meta-analysis. Journal of Personality and Social Psychology, 50(6), 1141. [doi:10.1037/0022-3514.50.6.1141]
IYENGAR, S., Lelkes, Y., Levendusky, M., Malhotra, N., & Westwood, S. J. (2019). The origins and consequences of affective polarization in the United States. Annual Review of Political Science, 22, 129–146. [doi:10.1146/annurev-polisci-051117-073034]
LELKES, Y. (2016). Mass polarization: Manifestations and measurements. Public Opinion Quarterly, 80(S1), 392–410. [doi:10.1093/poq/nfw005]
MAHER, P. J., MacCarron, P., & Quayle, M. (2020). The likes that bind: Group identification and attitude strength. University College Dublin, UCD Politics Spring Seminar Series.
MÄS, M., Flache, A., Takács, K., & Jehn, K. A. (2013). In the short term we divide, in the long term we unite: Demographic crisscrossing and the effects of faultlines on subgroup polarization. Organization Science, 24(3), 716–736.
MCGARTY, C. (1999). Categorization in Social Psychology. Thousand Oaks, CA: Sage.
MOUSSAÏD, M., Kämmer, J. E., Analytis, P. P., & Neth, H. (2013). Social influence and the collective dynamics of opinion formation. PLoS One, 8(11), e78433.
MYERS, D. G., Bruggink, J. B., Kersting, R. C., & Schlosser, B. A. (1980). Does learning others’ opinions change one’s opinions? Personality and Social Psychology Bulletin, 6(2), 253–260. [doi:10.1177/014616728062011]
OVERTON, J. P. (2023). Overton Window. Available at: https://www.mackinac.org/OvertonWindow.
PARISER, E. (2011). The Filter Bubble: What the Internet Is Hiding From You. London: Penguin UK.
PEW Research Center. (2014). Political polarization in the american public. Available at: https://www.pewresearch.org/politics/2014/06/12/political-polarization-in-the-american-public/.
PINEDA, M., Toral, R., & Hernández-Garc, E. (2013). The noisy hegselmann-krause model for opinion dynamics. The European Physical Journal B, 86(12), 1–10. [doi:10.1140/epjb/e2013-40777-7]
SHERIF, M. (1937). An experimental approach to the study of attitudes. Sociometry, 1(1–2), 90–98. [doi:10.2307/2785261]
SHERMAN, D. K., Hogg, M. A., & Maitner, A. T. (2009). Perceived polarization: Reconciling ingroup and intergroup perceptions under uncertainty. Group Processes & Intergroup Relations, 12(1), 95–109. [doi:10.1177/1368430208098779]
STASSER, G., & Titus, W. (1985). Pooling of unshared information in group decision making: Biased information sampling during discussion. Journal of Personality and Social Psychology, 48(6), 1467. [doi:10.1037/0022-3514.48.6.1467]
TAKÁCS, K., Flache, A., & Mäs, M. (2016). Discrepancy and disliking do not induce negative opinion shifts. PLoS One, 11(6), e0157948.
TURNER, J. C., & Oakes, P. J. (1986). The significance of the social identity concept for social psychology with reference to individualism, interactionism and social influence. British Journal of Social Psychology, 25(3), 237–252. [doi:10.1111/j.2044-8309.1986.tb00732.x]
VINOKUR, A., & Burnstein, E. (1978). Novel argumentation and attitude change: The case of polarization following group discussion. European Journal of Social Psychology, 8(3), 335–348. [doi:10.1002/ejsp.2420080306]