When "I" Becomes "We": Modelling Dynamic Identity on Autonomous Agents

, , ,
and
INESC-ID, Instituto Superior Técnico, Portugal
Journal of Artificial
Societies and Social Simulation 26 (3) 9
<https://www.jasss.org/26/3/9.html>
DOI: 10.18564/jasss.5146
Received: 02-May-2022 Accepted: 27-Apr-2023 Published: 30-Jun-2023
Abstract
Individuals change who they are in response to their social environment. In other words, one's identity is dynamic, varying according to context (e.g., individuals present, place, task). Identity has a significant impact on an individual's behaviour. Researchers have been interested in understanding how contextual aspects shape identity and, in turn, how identity influences behaviour. Agent-based simulation models are great tools to identify and predict behaviour associated with these identity processes. In addition, agents can employ identity-related mechanisms based on social theories to become more socially believable and similar to humans. The Social Identity Approach (SIA) is one of the most influential theories covering social aspects of one's identity, with many of its concepts being applied in social simulation research. This paper formalizes the Dynamic Identity Model for Agents (DIMA), an existing agent-based model based on SIA, providing a detailed theoretical foundation of the model, as well as an overview of its integration as a component into a social agent architecture. In DIMA, agents perceive themselves either as distinct individuals (personal identity) or as members of a social group (social identity), acting according to their context-dependent active identity. Two simulation scenarios are presented here to illustrate the use of this model, one based on the Dictator Game and the other on a trash collection task. This work aims to guide other researchers who want to enhance their agents with the DIMA's identity salience mechanism. As a result, they would not only be able to assess how this mechanism influences behaviour based on the context, but they would also be able to explore the dynamics between personal and social identities.Introduction
People adjust who they perceive themselves to be in response to the social environment they find themselves in, using their identity to regulate their thoughts, feelings, and behaviours (Markus & Kunda 1986; Smith & Mackie 2000). However, identity is a complex concept that has taken on many different meanings over the last century. While some define it as the personal characteristics and attributes that distinguish a person from their peers (e.g., being creative or honest), others see it as similarities shared by a group (e.g., nationality or gender). Moreover, others see identity as a combination of these two perspectives, causing one to be both different and similar to others. Nevertheless, there is a consensus that identity is primarily a social concept (Fearon 1999; Packer & Van Bavel 2014), and therefore how we define ourselves will always be related to others, as well as additional components of the social environment (e.g., place, task).
In this manner, social behaviour corresponds to responses of one’s identity to their social environment (Smith & Mackie 2000; Swann & Bosson 2010). Identity-related phenomena, such as identity shifts and group formation, have interested researchers, who want to understand their causes and impact on behaviour, being agent-based simulation models appropriate for studying these processes. As such, realistic agent behaviour can be modelled using identity-related concepts based on social theories. The Social Identity Approach (SIA) is one of the most influential theories addressing the social aspects of one’s identity, with many of its concepts being used in social simulation research. It corresponds to a collection of theories, the Social Identity and Self-Categorization theories, proposed by Tajfel and Turner (Tajfel et al. 1971, 1979; Turner et al. 1987, 1994). According to these theories, a person’s identity is neither static nor free of influences (Turner et al. 1994). However, several social contextual factors can influence an individual’s identity and behaviour (Mackie & Smith 1998).
SIA postulates that one’s identity can be both personal and social (Turner et al. 1987, 1994). Personal identity refers to the features that differentiate an individual from their peers. In turn, social identity reflects shared characteristics between the members of a group against other relevant groups. Personal identity usually becomes salient in settings with only in-group members (the social group of people to which a person feels connected and shares similar characteristics), whereas social identity may become salient when one is in the presence of members of an out-group (the group of people that are external to the in-group) (Turner et al. 1994). For the latter, the perception of the self as a member of a group strengthens, as one tends to focus their perception on the shared features with other in-group members and starts “seeing the other as an embodiment of the out-group prototype” (Stets & Burke 2000 p. 231) as well. Salience is defined by how accessible a particular social identity is and how well it fits the current social context (Bruner 1957; Oakes 1987; Turner et al. 1994). Upon perceiving themselves and others as members of a social group, one may adopt the prototypical behaviour of their in-group (Trepte & Loy 2017), if the associated social identity is active and highly salient. This behaviour may be more or less prototypical depending on the salience value of the social identity. Group behaviours could manifest, for example, as social bias (Hennessy & West 1999; Otten & Moskowitz 2000; Tajfel 1970; Tajfel et al. 1971), reflecting in-group vs out-group behaviours (e.g., cooperation within in-group members vs discrimination towards out-group ones).
As previously stated, identity should play a role in the development of believable autonomous agents, particularly in the fields of agent-based social simulation and human-agent interaction. In reality, there are multiple examples of agent-based models using SIA (or related) concepts. Personal and social identities have been studied independently in previous research on autonomous agents, with personality models being used for the former (Doce et al. 2010; Prada et al. 2010) and shared cultural features being used for the latter (Mascarenhas et al. 2013; Rehm et al. 2008). Other researchers have also explored the dynamics of two or more social identities and how they influence one another, for example, to better understand group formation (Smaldino et al. 2012) and opinion dynamics (Grier et al. 2008). Nonetheless, these approaches fail to address the dynamics between personal and social identities, which should adjust to context changes in socially dynamic environments.
The main focus of this paper is the formalization and demonstration of the Dynamic Identity Model for Agents (DIMA) (Dimas et al. 2013; Dimas & Prada 2013), an existing agent-based model based on SIA, where agents perceive themselves either as members of a social group - social identity - or as unique individuals - personal identity - depending on the social context. Previous DIMA papers provided a broad overview of the social theory underlying it; however, a formal description of the model, how to incorporate it on social agents, and a simulation scenario exploring identity dynamics and demonstrating the DIMA flow were lacking. Formalization standardizes the input, output, and main functions of the DIMA model, simplifying its incorporation into agents by other researchers. As a result, DIMA can be integrated into a social agent architecture as a separate component that does not interfere with any other modules the agent may have.
This research delivers four main results: 1) formalization of DIMA with a clear link between SIA literature and the model, 2) integration of DIMA with perception and decision-making modules in a social agent architecture, 3) two social simulation scenarios, one based on the Dictator Game (Kahneman et al. 1986) and the other on a trash collection scenario, as examples of the model configuration, and 4) an open access implementation of the DIMA model with a step-by-step tutorial outlining its flow. With this said, the intention of this work is to be a guide for researchers who want to include DIMA’s identity salience mechanism in their agents and, consequently, enhance their realism. As such, they would be able to assess the impact of this mechanism on agents’ identity and behaviour under various contextual conditions.
Related Work
A person’s expressed identity can be established by either their distinct characteristics or those shared with other members of a social category they perceive themselves to belong to. Considering this, researchers have focused not only on identity models based on personality theories (Carbonell 1980; Doce et al. 2010; Magalie Ochs 2009; Prada et al. 2010; Rizzo et al. 1997), but also on creating agents whose identities are based on shared cultural features (De Rosis et al. 2004; Mascarenhas et al. 2009, 2013; Rehm et al. 2007, 2008). Thus, these two components of identity - personal and social - have been explored alongside to create realistic agent-agent and user-agent interactions. However, studying them independently is not enough in itself; one should also contemplate group behaviour and inter-group relations, rather than just roles and how they are performed within a group, as in identity theory (Stets & Burke 2000). The interplay between personal and social identities, as well as between social identities and other social identities, their salience and how it can vary given contextual influences, should be considered. This is where social identity theories come into play: a third group of researchers has focused on models applying a few concepts of these theories (Fridman & Kaminka 2009; Grier et al. 2008; Kopecky et al. 2010; Salzarulo 2006; Smaldino et al. 2012), creating agents whose social identities shift dynamically, which is highly relevant to this work. In particular, the social identity concept has been modelled in the context of social simulation scenarios to investigate, among other things, the influence of one’s social identity on others’ active identity and behaviour. The adjustment to the social context and personal and social identities dynamics were still missing from these models.
Aiming to create distinct and unique agents, a few researchers have implemented personality models that include sets of goals representing different personality types. These could be linked to specific actions (Carbonell 1980) or preferences on plans to achieve them (Rizzo et al. 1997). Computational models of personality inspired by the well-known Five Factor Model of Personality (Digman 1990) have also been developed, in particular for agents interacting within small teamwork scenarios (Prada et al. 2010), as well as for agents displaying different emotions (Doce et al. 2010). Moreover, Magalie Ochs (2009) developed a model based on personality and social roles, in which personality-related emotions influenced the development of social relationships of non-player characters in games.
Regarding the implementation of cultural features, De Rosis et al. (2004) proposed an embodied animated agent capable of generating culturally appropriate behaviour in a doctor-patient environment. Similarly, Rehm et al. (2007) and Rehm et al. (2008) built a system based on Hofstede’s five-dimensional model of culture (Hofstede & Hofstede 2001) for an embodied conversational agent. Additionally, (Mascarenhas et al. 2009, 2013) developed a culturally-adaptable model, enabling agents to express different cultural behaviours through the use of rituals.
Concerning the development of dynamic identities, most authors have been modelling a social identity concept for simulations of crowd behaviour (Fridman & Kaminka 2009). Others have been using it to understand group formation dynamics (Smaldino et al. 2012), as well as opinion dynamics, particularly in the political field, such as opinion influence (Grier et al. 2008), multiple affiliation conflicts (Kopecky et al. 2010) or pressure toward conformity (Salzarulo 2006).
Salzarulo (2006) developed and proposed a continuous opinion dynamics model based on the Meta-Contrast principle of the Self-Categorization Theory (i.e., maximization of the ratio of perceived intergroup differences to intragroup differences). In his model, agents’ opinions could be influenced by interactions with other agents based on their social identities. In particular, agents could gravitate toward identities, and, consequently, prototypical opinions, with which they identified more strongly (attraction forces) or move away from those with whom they did not identify (repulsion forces). Thus, this model allows the production of collective phenomena such as polarization of opinions, consensus and extremism in groups of agents.
In a similar work, Grier et al. (2008) developed an ABM of political opinion dynamics called Simulation of Cultural Identities for Prediction of Reactions (SCIPR). In their model, agents changed their opinions based on demographic similarities, as well as bounded confidence models, which were related to how easily agents could be influenced by others, in regards to their set of beliefs. The agents’ main goal was to get other agents closer to their ideals or beliefs, and, consequently, affect their political party identification.
Fridman & Kaminka (2009)’s model was based on the Social Comparison Theory (Festinger 1954). These authors presented an ABM able to generate imitation behaviour in loosely-coupled groups, in which agents minimized the differences between other similar agents by engaging in processes of imitation and contagion.
Developed by Kopecky et al. (2010), the Social Identity Land Look-Ahead Simulation (SILAS) was a model centred on conflicts of identities, that could predict how individuals with multiple affiliations acted when more than one social identity was active.
Smaldino et al. (2012) developed an ABM, based on the Optimal Distinctiveness Theory (Brewer 1991), where agents decided whether to join or leave a given group, according to their neighbours’ social identities, in the attempt of belonging to an optimally distinct group (i.e., “groups that are both sufficiently inclusive and sufficiently distinct” Leonardelli et al. 2010 p. 67).
All of these models did not have at least one of the following elements: contextual influences, personal identity, and social identity. In personality models, the authors do not consider social influence on an agent’s behaviour, but in models that included cultural features, researchers took into account the impact of social context. Nevertheless, both of these approaches lacked all of the dynamics and attributes of one’s identity, such as the salience. Concerning the approaches inspired by theories of social identity, they mostly focused on the dynamics between two or more social identities, or the influence of one’s social identity on others, overlooking the impact of the dynamic between social and personal identities, and failing to address the ability of one’s identity to adjust to the social context.
Dynamic Identity Model for Agents
The Dynamic Identity Model for Agents (DIMA) is based on the Social Identity Approach (SIA), aiming to provide agents with multi-faceted and context-dependent identities. At the core of the model is the identity salience mechanism, which uses agents’ perceived information regarding their social environment to determine the salience of social identities. Agents can then perceive themselves as unique individuals (personal identity) or as members of a social group (social identity). Consequently, each agent’s active identity will regulate their decisions in any given situation.
In previous DIMA publications (Dimas et al. 2013; Dimas & Prada 2013), it was unclear how to incorporate the model into a social agent architecture. Specifics regarding the structure of its input and output were also missing. Nonetheless, the authors did a good job introducing the main SIA concepts associated with DIMA, but it was difficult to grasp why and how they chose to model certain aspects of this theory. In particular, they did not provide a formal description of DIMA. Hence, details concerning the connection between the literature and the model formalization were lacking. Additionally, the model was never publicly available online for other modellers and social scientists to apply it to their agents.
Given these shortcomings, the following subsections describe not only the integration of DIMA into a social agent architecture but also its formalization. The third subsection, in particular, summarizes the main functions of a DIMA agent, including their input and output, working as a support for other researchers looking to add DIMA as an independent component into their own agent-based models and simulations. In this sense, they can be aware of the type of input this model anticipates and the outcome it will provide. A Python implementation of the model is available on GitHub.1 This repository also includes a Jupyter Notebook with a step by step description of the model, adding more details about its formalization and setup.
Additional details on what has changed in the current work can be provided to readers who are familiar with earlier DIMA papers. The formulas presented here demonstrate and relate to the SIA literature more effectively, making the model easier to understand and adapt to a specific scenario. In particular, we removed the weighting values from the comparative fit function and considered all intra-group differences (not only the in-group ones but also the out-group). Moreover, in contrast to previous DIMA descriptions, no specific formula was defined in the social identity’s accessibility update function. As a result, other modellers can now select the appropriate formula for their scenario, which only needs to be based on the previous accessibility value of the corresponding social identity, its salience, and an optional value based on the outcome evaluation of the action performed using this identity. Other DIMA processes (e.g., clustering, normative fit) were also properly formalized in this paper.
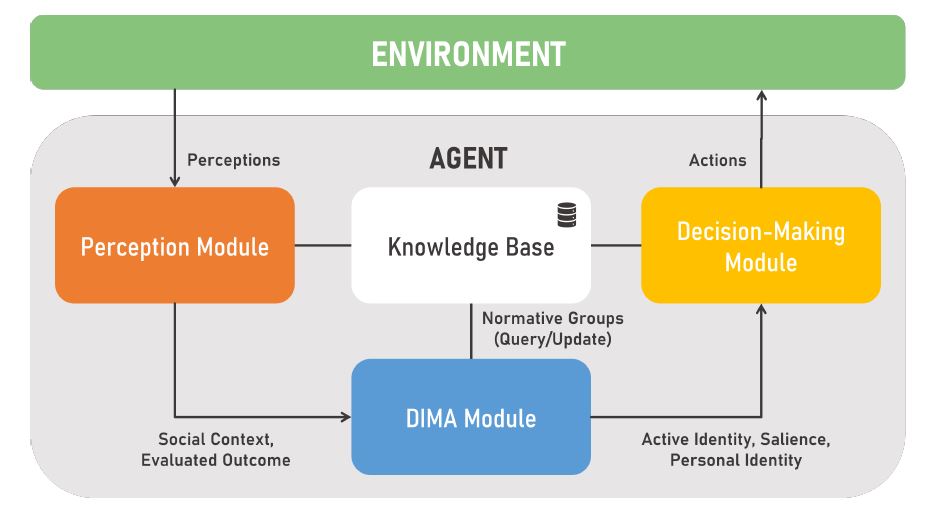
Model integration in social agent architecture
One can incorporate DIMA as a module in a social agent architecture, as shown in Figure 1, together with perception and decision-making modules, as well as the agent’s knowledge base. This architecture is depicted as a cycle, which can be executed by an agent for a specific number of steps during the simulation of a society of agents. Within the perception module, the agent identifies the social context and the characteristics of the agents in the environment, which are, in turn, sent as input to the DIMA module. If the perception module is not implemented, this input can be manually provided to DIMA in a JSON file or generated randomly, depending on the agent’s purpose. Given this input, the agent follows the DIMA steps illustrated in Figure 2, which will be further explained in the following subsection, outputting an active identity and a salience value. By default, the agent’s personal identity is also returned. The DIMA output is then sent to the decision-making module, where the agent decides how to act based on the previous parameters, performing a context-aware action in the environment. Each action has an outcome that the agent can evaluate in the perception module, resulting in a value given as input to the DIMA module. This value is used to update a specific parameter of the agent’s active identity - the accessibility, as discussed further.
Model formalization
According to Tajfel et al. (1979), “Social categorizations (...) provide a system of orientation for self-reference” (p.40), allowing individuals to easily understand and process information provided by their surroundings, categorizing people into different social groups depending on the context, as well as helping in the management of their social interactions (Trepte 2006; Trepte & Loy 2017). Self-categorization is considered a type of social categorization (Trepte & Loy 2017), in which the individual also categorizes themselves within a social group. Self-categorization Theory (Turner et al. 1987, 1994) differentiates between two levels of self-categorization: personal and social identity. While in some situations, an individual could be portrayed based on their personal characteristics (personal identity), in others, they could perceive themselves, and the ones in their social environment, as members of a group rather than unique individuals (social identity). When a person highly identifies as a member of a group, they use their salient social identity to guide their actions, which corresponds to the social category that is easier to retrieve from memory and that best matches a given context (Turner et al. 1994).
Following the SIA literature, in DIMA, an agent’s identity can go from being entirely influenced by their personal identity, when no social identity is salient, to being fully determined by a social identity if it becomes strongly salient. As the salience of their social identity increases, individuals tend to define their self-concept in accordance with the prototypical characteristics of the group they belong to (Turner et al. 1994). This results in an active identity that works as a frame of reference for the agent’s actions and decisions based on the salience of their identity Turner & others (1984). Hence, as the social context varies, so does the active identity, potentially leading to changes in the agent’s behaviour. To illustrate this, Figure 2 depicts the steps of an agent in the DIMA module, including its input and output.
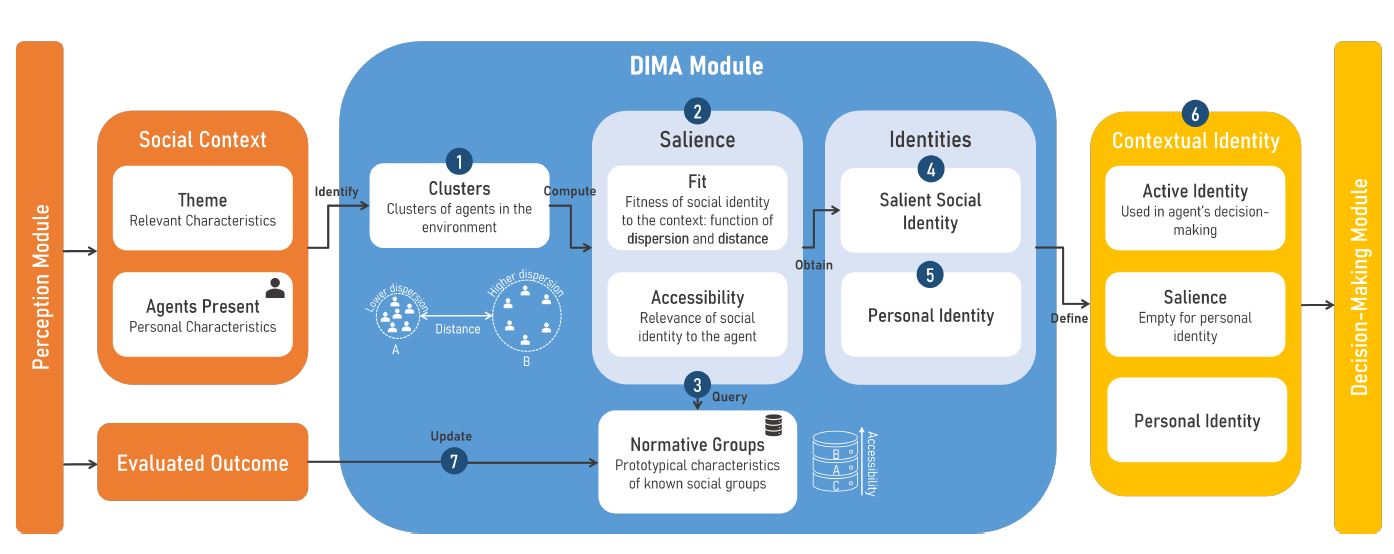
The following sections provide a formal description of the steps and elements of the DIMA module. Initially, a formalization of the model input (social context and agents) is given. The normative social groups, which belong to each agent’s knowledge base, are also formalized. These elements are used throughout the identity salience mechanism, which begins with the clustering phase and ends once the active identity is obtained. Then, a formalization of the identity salience computation is presented, focusing on the fitness and accessibility values of the social identity. These sections include a running example that illustrates how to setup the input for the model and showcases the impact of the DIMA steps on the behaviour of the agents.
Social context
As stated by Turner et al. (1994), a “perceiver gains identity from being placed in context” (p.458). A variety of contextual factors can thus influence how strongly an agent identifies with a particular identity and, consequently, how they behave towards other agents (Mackie & Smith 1998). Therefore, in the model, the social context \(Ctx = (A, T)\) consists of a finite set of agents \(A = \{{a}_{1}, ...,{a}_{n}\}\) present in the current social environment, and the theme \(T = \{({c}_{1}, {w}_{1}), ...,({c}_{n}, {w}_{n})\}, c \in C, w \in [0, 1], \sum\limits_{i=1}^{n} {w}_{i} = 1\), which highlights the characteristics that are relevant for the current situation. Each characteristic of the theme can be assigned a weight \(w\), allowing to prioritize some characteristics of the context over others. If these weights are not specified, they are assumed to be equal for all characteristics.[section:context]
\(C = \{{c}_{1}, ...,{c}_{n}\}, n > 0\) corresponds to the set of characteristics that are known to the model. Ideally, this set should include a sufficient number of characteristics to describe a diverse range of social contexts, having no predetermined maximum. There should be an overlap between \(C\) and \(T\) such that all the characteristics in \(T\) are present in \(C\), enabling the agents to identify the clusters in the environment. However, not all characteristics in \(C\) need to be present in \(T\).
As previously mentioned, the context can be inferred by the agents if a perception module is implemented. Otherwise, it can be provided directly as input to the model. In the former case, each agent may be able to identify other agents virtually present in their space or simply brought into their social context by being referenced in a conversation. Concerning the theme’s characteristics, they can be identified depending on a place, a conversation topic, an event or a task. For example, as suggested by Mackie & Smith (1998), if agents are at work, relevant characteristics could be “efficiency” or “productivity”. Alternatively, if a group participates in a group activity, such as soccer, the theme might include “speed” and “stamina” instead. Table 1 provides examples of how to define DIMA’s social context based on different situations. These situations will be used to illustrate the remaining model components and processes.
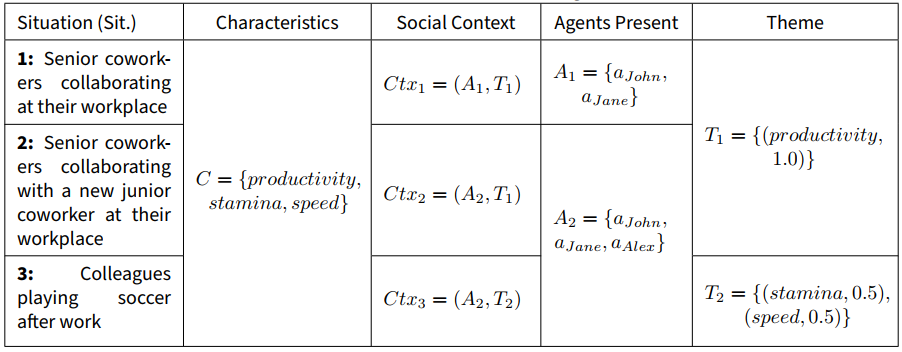
Agents
As for the agents, each agent \(a = (P_{a},{NSG}_{a}), a \in A\) is initialized with a finite set of personal characteristics \(P_a\), and a collection of known social groups \({NSG}_a\). Depending on the context’s theme, agents will focus their perception on the relevant characteristics drawn from the collection of personal characteristics of each agent present, including their own (i.e., focus on a context-filtered version of \(A\), as formalized in 3.19.
Personal characteristics \(P_a = \{({c}_{1}, {v}_{1}), ...,({c}_{n}, {v}_{n})\}, c \in C, v \in [0, 1]\) correspond to a finite collection of traits and psychological processes that define the agents. According to the Self-Categorization Theory, this set “refers to self-descriptions regarding personal attributes” (Trepte & Loy 2017 p. 6). These characteristics are associated with numerical values to simplify model computations, influencing the agents’ decision-making and behaviour generation processes.
These values often differ from agent to agent, resulting in a heterogeneous population. For example, an extroverted agent would present high values for a set of personal characteristics such as “assertiveness” and “sociability”, whereas the values of the same characteristics for an introverted agent would be lower. These different characterizations could have an impact on the agents’ decisions, leading to extroverted agents interacting with other agents more frequently than introverted ones, for instance, (Prada et al. 2010).
Normative social groups
The collection of normative social groups \(NSG_a = \{{sg}_{1}, ..., {sg}_{n}\}\) consists of a finite set of social groups known by the agents, according to each agent’s perspective and knowledge about the social reality. It is then included in each agent’s knowledge base. A social group is defined by Tajfel et al. (1979) as a “collection of individuals who perceive themselves to be members of the same social category” (p.40). Thus, given the perception of each agent, there will be “certain expectations, hopes and fears about people belonging to social categories” (Trepte 2006 p. 257). For this reason, in the model, each social group \(sg= (PT_{sg}, acc_{sg}), acc \in [0, 1]\) is defined mainly by its associated prototypical characteristics \(PT_{sg}\).
Prototypical characteristics \(PT_{sg} = \{({c}_{1}, {v}_{1}), ...,({c}_{n}, {v}_{n})\}, c \in C, v \in [0, 1]\) are, therefore, the expected characteristics of a typical member of a social group, being defined, similar to personal characteristics, by a name and a value. As an example, for the social group “researcher” stored as a normative group, prototypical characteristics could be “methodicalness” = 0.76, “inquisitiveness” = 0.94, and “credulity” = 0.05.
Each social group also has an accessibility value \(acc_{sg}\) indicating how easy it is for the agent to recall it from memory based on prior experiences.
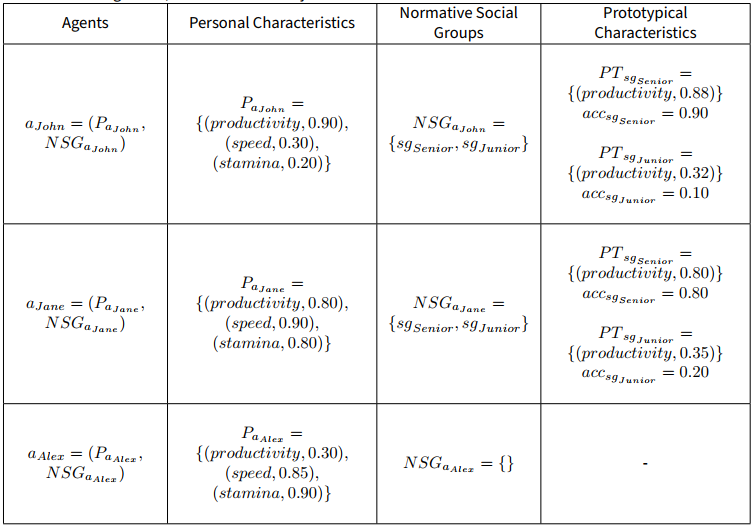
Table 2 provides examples of how to configure the agents in the DIMA model based on the situations outlined in Table 1. This table includes information on the agents’ personal characteristics, normative social groups (if applicable), and the corresponding prototypical characteristics associated with each group.
Clustering
Each DIMA agent starts by identifying the clusters present in the social environment. The clustering stage, defined in Equation 1, receives as input the current context and the personal characteristics of all agents. During this step, agents consider a filtered version of \(A\), \(A_{Ctx}\), in which each present agent \(a_{Ctx}\) is represented only by the personal characteristics that are relevant in the context, \(P_{a_{Ctx}} = \{({c}_{1}, {v}_{1}), ...,({c}_{n}, {v}_{n})\}, c \in T_{Ctx}, v \in [0, 1]\). The function’s output \(Cl = \{cl_1, ..., cl_n\}\) represents the clusters that emerge in the context, corresponding to disjoint subsets of \(A_{Ctx}\). Each agent will thus perceive whether they are in the presence of one or more clusters, as well as the cluster they belong to.
| \[ Cl = Clustering(Ctx, A) = \{cl_1, ..., cl_n\}, cl \subseteq A_{Ctx}, \bigcap_{i=1}^{n}{cl}_{i} = \emptyset\] | \[(1)\] |
The clustering function can be implemented with a typical clustering algorithm. In our example, an iterative K-Means algorithm was used, which starts with one \(K\) cluster and then determines whether or not there is at least one agent whose distance to their cluster is higher than a given distance threshold value \(tClustering\). If so, \(K\) is incremented and one more cluster is added, forcing the clustering process to restart. This process is repeated until the distance threshold heuristic is satisfied for all agents. As a result, agents will be able to obtain the centroids of the identified clusters, in addition to their members.
Salience and active identity
Following the clustering phase, each agent is able to determine which of the present agents share similar characteristics with them (i.e., belonging to the in-group) and which do not (i.e., belonging to the out-group). Turner et al. (1994) stated that “social identity tends to become more salient in intergroup contexts and personal identity in intragroup contexts” (p.456). Considering this, the agent’s active identity in the model can be defined depending on certain conditions. When the agent is exclusively in the presence of members of their own social group, identifying a single cluster in the environment (\(|Cl| = 1\)), no social identity is salient and they will perceive themselves and others as individuals. In this situation, the agent’s active identity is going to be defined by their personal identity \(PI\), whose characteristics correspond to the projection of the agent’s personal characteristics in the context \(P_{a_{Ctx}}\). However, when in the presence of an out-group, a social identity may become salient. [section:personalIdentity]
For each agent to be able to identify their salient social identity \(SSI\), they must compute the salience of each one of the identified clusters, and select the one with the highest value, as seen in Equation 2. In the Self-Categorization Theory, the salience of a particular social identity is seen as a function of fit (See Salience: Fit) and accessibility (See Salience: Accessibility) (Turner et al. 1994), as defined in Equation 3. In specific, Oakes (1987) proposes expressing this salience function as a product of fit and accessibility. This formula was inspired by Bruner (1957)’s work, in which it is stated that “given a sensory input with equally good fit to two non-overlapping categories, the more accessible of the two categories would capture the input” (p.132). With this in mind, in order to compute the salience of an identity, each agent will be required to determine how well a social identity fits the social context (i.e., the fit), as well as how useful and relevant that same identity is for them, based on “past experience, present expectations, and current motives, values, goals, and needs” (Turner et al. 1994 p. 455) (i.e., the accessibility). [section:salientSocId]
| \[ SSI = argmax(\forall_{cl \in Cl} Salience(cl))\] | \[(2)\] |
| \[ Salience(cl_i) = f ({fit}({si}_i), {acc}({si}_i)) = fit(si_{i}) \times acc(si_{i}), cl \in Cl, si \in NSG, 0 \leq Salience \leq 1\] | \[(3)\] |
Given these identities, the active identity \(AI\) can be determined according to Equation 4, being defined by the salient social identity only if its salience is higher than a certain threshold \(tSalience\). When a social identity becomes active, an individual’s self-concept becomes “depersonalized” (Turner et al. 1987): the agent sees the self as a representation of the in-group prototype instead of a unique individual, as well as other agents, which are seen as an embodiment of the out-group prototype (Stets & Burke 2000). An identity’s level of “depersonalization” will influence the degree of group behaviour an individual exhibits (Trepte & Loy 2017). This process, however, “is not a loss of personal identity but a change in identity” (McGarty 1999 p. 124). Thus, rather than modifying their personal attributes, which are always present by default, agents can simply define their self-concept based on a cognitive representation of the defining characteristics associated with their in-group (i.e., its prototypical member) (Hogg et al. 1995).
| \[ AI = {ActiveIdentity(PI, SSI)} = \begin{cases} PI\text{,} & \text{if } SSI == \emptyset \text{ or } Salience(SSI) \leq tSalience \\ SSI \text{,} & \text{otherwise} \\ \end{cases}\] | \[(4)\] |
Table 3 shows the effects of the clustering and salience steps in the DIMA model, as well as the influence of the active identity on the behaviour of the agent John in the situations outlined in Table 1.
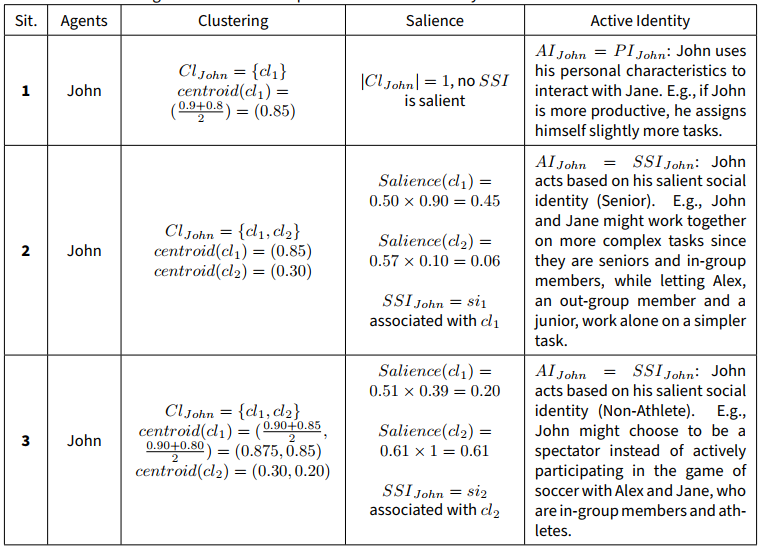
Salience: Fit
Returning to the salience function, the fit of a social identity in a social context is composed by two aspects according to the Self-Categorization Theory (Turner et al. 1987, 1994): the comparative fit, which refers to how noticeable a category is against a contrasting background; and the normative fit, which stands for how well the content of a categorization goes in accordance with what one might expect it to be (i.e., the norm).
If any expectations about a social group exist within the knowledge of an individual, the attributes of that group should be “consistent with the normative beliefs and theories about the substantive social meaning of the social category” (Turner et al. 1994 p. 455). Normative beliefs, in this sense, represent one’s beliefs about the stereotypical features and behaviour that are expected of a certain social group. Following this definition, each agent in the model will perform the normative fit by determining if they are in the presence of a social group that they already know and have experience with (i.e., if any of the agent’s known social groups has a normative fit in the current context). As a result, all of the agent’s normative groups are checked for similarity with the previously identified clusters of agents.
The centroids of each cluster are then compared to the projection in the context of the prototypical characteristics of each normative social group, \(PT_{sg_{Ctx}}\). According to Equation 5, a cluster is defined as an instance of its closest normative social group only if their distance is lower than a specific threshold \(tNormative\). In this case, the values of reference will correspond to the ones of the normative group, implying that the agent recalls the prototypical member of the social group through a simple stereotyping process. Moreover, during this process, the agent may be able to identify additional characteristics of the agents that were not initially observed.
| \[ si_i = {NormativeFit(cl_i)} = \begin{cases} argmin(distance(cl_i, \forall_{sg \in NSG} sg))\text{, if $distance < tNormative$} \\ \emptyset\text{, otherwise} \\ \end{cases}\] | \[(5)\] |
If no match is found, it is because the agent is in the presence of an ad-hoc social group (i.e., the agent does not have previous knowledge or past experiences with this group). Thus, given that no accessibility value is available, the salience computation of this cluster will be computed as the fitness multiplied by a value indicating how close the agent is to that cluster: the complement of the distance between the agent’s context-filtered personal characteristics and the cluster’s centroid. For future situations, the agent’s collection of normative social groups should also be updated with this unknown cluster, as defined in Equation 6, with its centroid value representing the prototypical characteristics of the group and the initial accessibility value corresponding to the previously computed value of closeness to the cluster.
| \[ NSG = NSG \cup newsg: newsg = (centroid(cl_i) , {acc}_{t=0})\] | \[(6)\] |
For instance, imagine an agent that just started as a player in a football team and is in the presence of other team members. Initially, no similarity is found with any of the agent’s normative groups (such as “Tennis Player” or “Swimmer”). Therefore, this agent will rely on information perceived from the current context rather than information from previous experiences. If the situation occurs again, the agent will have this group already stored as normative (e.g., “Football Player”), with assigned prototypical characteristics based on the ones defined by the centroid of the cluster from the previous situation.
The comparative fit is defined by the principles of the Meta-Contrast Theory (Turner et al. 1987), which states that a “collection of stimuli is more likely to be categorized as an entity (a higher order unit) to the degree that the average differences perceived between those stimuli are less than the average differences perceived between them and the remaining stimuli that make up the frame of reference”, meaning that “any collection of people will tend to be categorized into distinct groups to the degree that intragroup differences are perceived as smaller, on average, than intergroup differences within the relevant comparative context” (Turner et al. 1994 p. 455).
The comparative fit was formalized in a similar manner to how the meta-contrast principle was formalized by Salzarulo (2006), where the fit of a social categorization was determined by the difference between intergroup differences and intragroup differences. In DIMA, the comparative fit of a particular social identity, defined in Equation 7, also depends on the intergroup differences, as well as the intragroup differences. The former corresponds to the distance between the in-group \(sg_{in}\), and any other out-groups \(sg_{out}\) in a given context. The latter represents the dispersion of these social groups. When establishing this fitness function, it was assumed that social groups with a small dispersion (i.e., more homogeneous) and presenting a greater distance from other social groups will have higher fitness values, following the Meta-Contrast Theory’s rationale. Furthermore, it was considered that the fitness should increase if out-groups in the environment present higher dispersion values.
| \[ \begin{aligned} &{fit}({si_i})= f(distance(sg_{in}, sg_{out}), dispersion(sg_{in}), dispersion(sg_{out})) = \\ &\frac{distance(sg_{in},sg_{out})}{2} + \frac{(1 - dispersion{(sg_{in})}) + dispersion{(sg_{out})}}{4}:0 \leq fit \leq 1 \end{aligned}\] | \[(7)\] |
To better understand the computations performed by the DIMA model to obtain the salience of an identity, in particular how it computes the corresponding fitness and accessibility values, Table 4 provides a detailed example for the agent John in the situations outlined in Table 1.

The distance between the groups present in the social context can be computed through the normalized difference between their centroids (or their context-filtered prototypical characteristics, if they are normative groups). This formula is defined in Equation 8. If more than one out-group is found, the agent will merge them all in one large out-group, using as a value the mean of all out-groups’ centroids (or filtered prototypical characteristics).
| \[ distance{(sg_{in},sg_{out})} = \left|centroid({sg_{out}}) - centroid({sg_{in}}) \right|\] | \[(8)\] |
The dispersion of a social group can be measured by calculating the normalized average of absolute differences between the projection of the personal characteristics of each group member in the context and the group’s centroid (or context-filtered prototypical characteristics, as in the distance formula), as shown in Equation 9. The less dispersion the groups present, the more homogeneous they are, having more impact in the increase of the social identity salience.
| \[ dispersion{(sg_{i})} = \frac{\sum\limits_{x=1}^{n} \left|P_{{a_x}_{Ctx}} - centroid({sg_{i}}) \right|}{n}, n = |A_{sg_i}|, a \in A_{sg_i}\] | \[(9)\] |
Salience: Accessibility
Bruner (1957) stated that “the accessibility of categories reflects the learned probabilities of occurrence of events in the person’s world. The more frequently in a given context instances of a given category occur, the greater the accessibility of the category” (p.132). Therefore, in DIMA, during the accessibility update, it was considered that when agents act in accordance with their salient social identity, the accessibility of this identity should be updated according to a function depending on the previous value of accessibility and the salience of their identity, as shown in Equation 10. This function works as a reinforcement mechanism, so that each time an identity is used in a specific context, the agent’s willingness to use this social identity in similar situations increases in proportion to the value of its salience. Furthermore, in this step, the accessibility values of all identities present in the agent’s normative groups must be normalized, implying that when one identity’s accessibility increases, all the others suffer a decay. As a result, the agent’s collection of normative groups will resemble a ranking of identities, which corresponds to Blanz (1999)’s assumption that a perceiver has an internal hierarchy, in which social categorizations are ordered by their accessibility.
| \[ \begin{split} &acc_{(SSI)_{t+1}} = f(acc_{(SSI)_{t}}, Salience{(SSI)_{t}}, opt_{evaluatedOutcome}):0 \leq acc \leq 1 \end{split}\] | \[(10)\] |
Additionally, accessibility can “reflect the search requirements imposed by my needs, my ongoing activities, my defenses, etc.” (Bruner 1957 p. 132). To apply this definition, the incorporation of an agent’s mechanism in the model to assess whether the actions or decisions they made using a given identity satisfied their goals, needs, or expectations would have to be ensured. If implemented, the outcome of each agent’s action would be evaluated, returning a value that should be included in the accessibility update of their salient social identity, being this represented in the previous function as an optional parameter. With that said, depending on the type of scenario implemented, different accessibility functions can be used.
Overview of model integration and formalization
Given the architecture displayed in Figure 1 and the previous DIMA formalization, Table 5 displays the main functions required to incorporate DIMA within a social agent architecture, with their input and output specified and organized by module. The main goal is to assist researchers in easily understanding the order of events in this cycle, as well as the arguments required for the functions in each module, when connecting perception and decision-making modules to DIMA. Here, additional parameters, easy to configure, are also listed, being used as thresholds for specific functions in the DIMA module. Moreover, the function \(AccUpdate\) was added to this table, which is related to Equation 10. Besides the salient social identity, the evaluated outcome from the perception module was taken as an input and represented as a value between 0 and 1, even though this is optional. A final remark on the decision-making module’s function: given that DIMA outputs the agent’s personal identity by default, it is possible to consider the personal characteristics alongside with the characteristics and salience of the active social identity when modelling the agent’s behaviour. However, this is dependent on the modeller’s goal (e.g., study conflicts of personal and social identity). For readers to easily assess the impact of each one of these functions, the Jupyter notebook mentioned earlier includes a simple example that involves ten agents and two context characteristics as input to the model, which can be modified by readers to explore other scenarios.
| Module | Function | Input | Output | Other Param. |
|---|---|---|---|---|
| Perception | \(IdentifyContext\) | \(Environment\) | \(Ctx\) | - |
| Perception | \(IdentifyAgents\) | \(Environment\) | \(A\) | - |
| DIMA | \(Clustering\) ( 1) | Ctx, A | Cl | tClustering |
| DIMA | \(Salience\) ( 3) | \(cl \in Cl\) | \([0,1]\) | \(tNormative\) |
| DIMA | \(ActiveIdentity\) ( 4) | \(PI, SSI\) | \(AI\) | \(tSalience\) |
| Decision-Making | \(Act\) | \(AI, Salience(SSI), PI\) | \(Action\) | - |
| Perception | \(EvaluateOutcome\) | \(Outcome\) | \([0,1]\) | - |
| DIMA | \(AccUpdate\) ( 10) | \(SSI,\) \(evaluatedOutcome\) | - | - |
Use Case: Dictator Game
Following DIMA integration, this section demonstrates how to apply the model for a specific use case, which is executed as a social simulation, where the social environment was manipulated to test a set of hypotheses. We intended to showcase the effects of the identity salience mechanism, specifically, the influence of active identity, in the agent’s decision-making processes. This case is available on GitHub with the model, so that other researchers can run and modify the code to obtain the corresponding simulation plots.
The current scenario is centred on a well-known economic game, the Dictator Game (Kahneman et al. 1986). Economic games are simple ways to measure social effects, and this particular game has been extensively studied within experimental economics to gain insights on human fairness and altruism, two topics that are strongly connected to SIA (e.g., in-group and out-group bias). Moreover, there is experimental research linking the Dictator Game and the concept of social identity (Chang et al. 2019), in which different game treatments affect the salience of one’s identity, evoking identity-specific social norms when it is more salient, and thus changing a person’s re-distributions.
This game involves two players: a “dictator" and a”receiver". The dictator receives a certain amount of money, having the option of donating a portion of it to the receiver, who has no choice other than to accept the dictator’s offer. Despite the fact that the most rational choice, in economic terms, would be for the dictator to keep all of the money, the results of several experiments with humans playing this game provide evidence of the opposite. In standard conditions, the average offer by people who play the dictator role is around 20% of the amount initially given (List 2007; Lucas et al. 2008). To simplify the current demonstration, each donation is "anonymous," and the recipient is always chosen at random, which means that one’s donation has no effect on future behaviours, making each interaction in this scenario independent of the others. Nevertheless, other configurations of the dictator game can be further explored to verify if different behaviours emerge (e.g., players could be informed of other agents’ donations, which could, consequently, influence their decision).
The agents were configured to play the Dictator Game in the following manner: At each interaction step, each agent was given a fixed amount of money (\(=100\)€) to play the dictator role, while another agent in the environment was randomly selected to play as the receiver. Following this, the dictator agent decided how much money they were going to give to the receiver. If their salient social identity was active, the agent’s offer would follow Equation 11, in which the \(inGroupBias\) depended on whether or not the receiver was a member of the dictator’s group (in-group member). Otherwise, if their personal identity was active, the dictator agent would not use any bias to determine their offer. Then, they would simply use a baseline offer, a fixed value that represented a percentage of the initial amount given to the dictator (\(baselineOffer = 20\%\)). After the dictator agent decided how much to give to the receiver, the remaining portion was added to their wealth.
| \[ \begin{split} &offer_{t} = f(baselineOffer, inGroupBias, Salience{(SSI_{dictator})_{t}}) = \\ &baselineOffer \times (1 + inGroupBias \times Salience{(SSI_{dictator})_{t}}): 0 \leq Salience \leq 1\\ &inGroupBias = \begin{cases} 1\text{,} & \text{if ${receiver} \in SSI_{dictator}$} \\ -1\text{,} & \text{otherwise} \end{cases} \end{split}\] | \[(11)\] |
The rationale behind this equation was the in-group favouritism and out-group discrimination that has been found in past sociological studies (Hennessy & West 1999; Otten & Moskowitz 2000; Tajfel 1970; Tajfel et al. 1971). Essentially, the higher the salience of the agent’s social identity, the more generous they will be to in-group members and the less generous they will be to out-group agents. Then, an agent can allocate money ranging from 0% (to out-group members when their social identity salience is 1) to 40%. (to in-group members when their social identity salience is 1) of their initial amount.
Given the described formalization of the Dictator Game scenario, two hypotheses based on empirical research were tested:
H1: Group performance increases with the salience of the group identity. (Allen et al. 2004; Campo et al. 2019)
H2: Group-based behaviour increases performance compared to individualistic behaviour. (Gundlach et al. 2006)To verify these hypotheses, we ran a simulation with five distinct settings (empty context, equal groups with static context, different group dispersion with static context, different group size with static context, adaptive vs. non-adaptive agents with variable context), varying the context’s theme (i.e., the relevant characteristics of the environment the agents are in), the agents’ personal characteristics, and how adaptive to the context they were. The agents’ performance was measured according to the average accumulated wealth during the game.
In terms of the simulation variables, we defined the number of interaction steps in a single run (\(numSteps = 100\)) and the number of times the simulation can be repeated (\(numRuns = 50\)).
The agent’s perception module was not added. Instead, for the DIMA input, the values of the personal attributes of the agents (\(N=50\)) were randomized at each run, depending on how close we intended agents to be to the prototypical member of their in-group (i.e., the cluster centroid, which is visible to all agents), this being related to the group dispersion. Additionally, the context’s theme, shared by all agents, could be empty or include a finite set of relevant characteristics (in this scenario, it had only two), depending on the settings we were analyzing. In particular, for the context-variable configuration, we alternated between these two themes in each interaction step. The experimental design (i.e., context configuration) was then responsible for the emergence of one or more groups in the environment. We opted to provide names without semantics to the relevant characteristics of the context, like “Characteristic 1” and “Characteristic 2”.
Concerning the DIMA module, we specified the values of the thresholds applied in their functions (\(tClustering = tNormative = tSalience = 0.2\)). In terms of the accessibility of the salient social identity, which denotes how easy it is to recall it based on prior experience, it was updated according to Equation 10, using a constant growth factor (\(=0.01\)).
Finally, the decision-making module was defined according to Equation 11, as well as the parameters indicated in the formula description. The results of the simulation were recorded at each step of the interaction, and averaged out across the different repeated runs.
Results and discussion
Empty context and similar groups
The first and second experiments served as the baseline. In the first experiment, the context’s theme was empty, meaning that there were no relevant characteristics in the context, so only one cluster emerged. This means that the agents used their personal identity to decide how much to offer to other agents. The average accumulated wealth of each agent in this cluster was \(Wealth_{cl_1} = 10000\), in \(Step = 100\).
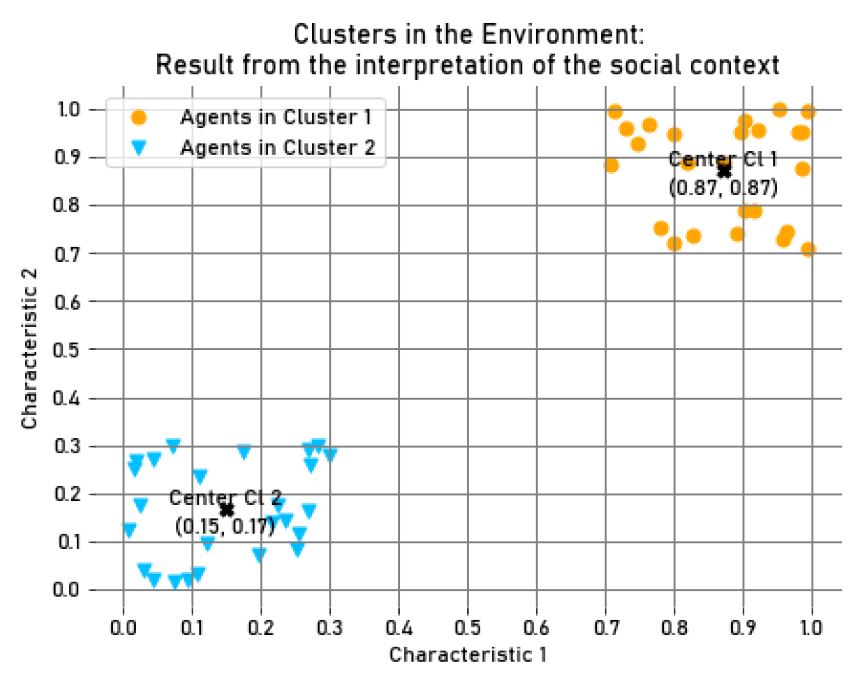
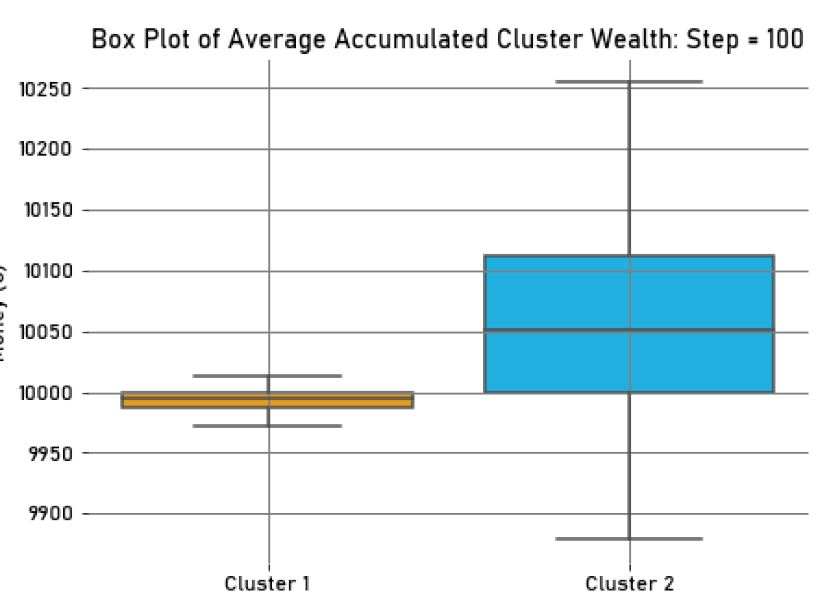
During the second experiment, the context’s theme included the two relevant characteristics. Given the values of the agents’ characteristics, two clusters with equal size (25 agents each) and a similar dispersion emerged in the environment (See Figure 3). In their decisions, agents would then use their salient social identities. These identities had similar salience values for agents in both clusters (in \(Step = 100, M_{{Salience}_{cl_1}} = M_{{Salience}_{cl_2}} = 0.58, SD_{{Salience}_{cl_1}} = 1.07*10^{-2}, SD_{{Salience}_{cl_2}} = 1.08*10^{-2}\)), as well as accessibility values (in \(Step = 100, M_{{Accessibility}_{cl_1}} = M_{{Accessibility}_{cl_2}} = 0.98, SD_{{Accessibility}_{cl_1}} = 1.92*10^{-3}, SD_{{Accessibility}_{cl_2}} = 1.85*10^{-3}\)). Additionally, regarding the average accumulated wealth of each agent in the clusters, there was almost no difference between the gathered wealth in both clusters (in \(Step = 100, M_{Wealth_{{cl}_1}} = 10002.08, SD_{Wealth_{{cl}_1}}=25.89,\) and \(M_{Wealth_{{cl}_2}} = 9997.92, SD_{Wealth_{{cl}_2}}=25.89\)). This is easy to verify in Figure 4, where we present a box plot of the average wealth for each cluster in \(Step=100\).
Different group dispersion
In the third experiment, we maintained the same group size in each cluster, as well as the two characteristics of the context’s theme. However, agents in one of the clusters were assigned characteristics closer to the centroid of their in-group, compared to the agents in the other cluster, implying that the former cluster (Cluster 2) presented a lower dispersion, being more homogeneous, than the latter one (Cluster 1), as seen in Figure 5. The salience value of the salient social identity associated with the second cluster, the more homogeneous one, was higher than the salience of the social identity linked to the first cluster (in \(Step = 100, M_{{Salience}_{cl_1}} = 0.46, SD_{{Salience}_{cl_1}} = 1.59*10^{-2},\) and \(M_{{Salience}_{cl_2}} = 0.74, SD_{{Salience}_{cl_2}} = 1.42*10^{-2}\)). Regarding the accessibility value, it revealed slightly higher values for the second social identity (in \(Step = 100, M_{{Accessibility}_{cl_1}} = 0.97, SD_{{Accessibility}_{cl_1}} = 8.71*10^{-3},\) and \(M_{{Accessibility}_{cl_2}} = 0.99, SD_{{Accessibility}_{cl_2}} = 1.52*10^{-3}\)).
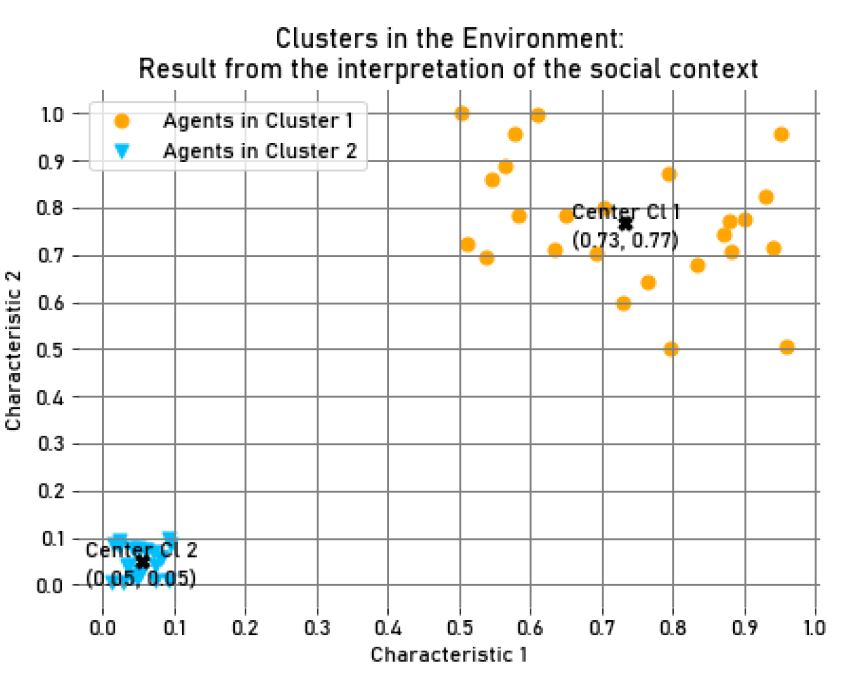
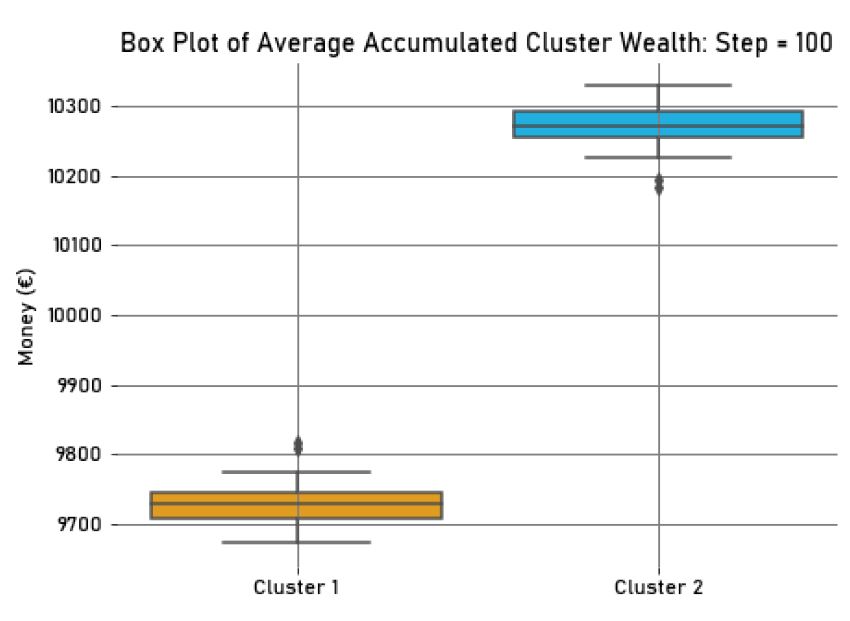
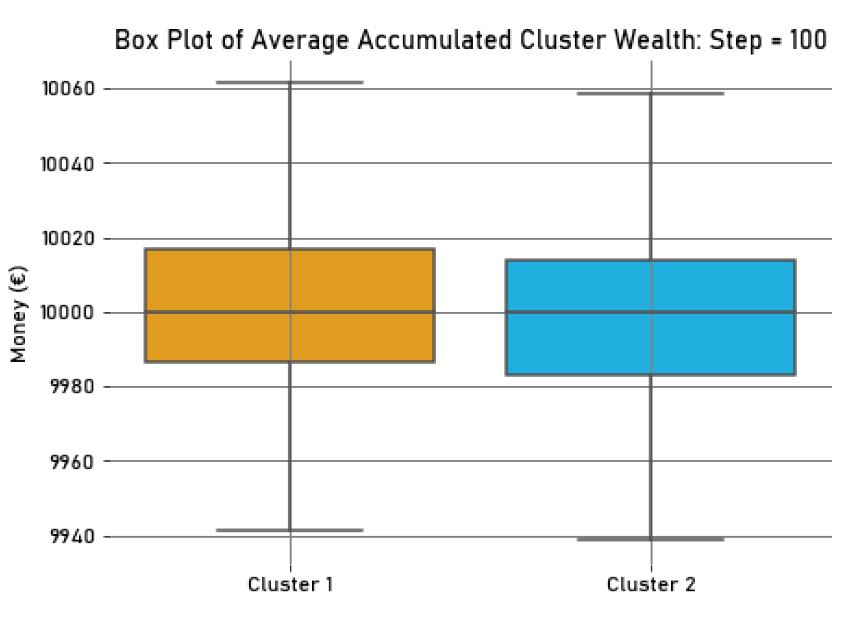
The average accumulated wealth of the agents in the second cluster, which was less dispersed and more homogeneous, was greater than the one in the first cluster (in \(Step = 100, M_{Wealth_{{cl}_1}} = 9727.65, SD_{Wealth_{{cl}_1}}=29.13,\) and \(M_{Wealth_{{cl}_2}} = 10272.35, SD_{Wealth_{{cl}_2}}=29.13\)), being this difference evident in the box plot in the Figure 6, for \(Step=100\). Concerning the average offers of each agent to in-group and out-group agents in each interaction step, agents belonging to the second cluster offered more money to their in-group members compared to agents in the first cluster, which was less homogeneous (in \(Step = 100, M_{OfferI_{{cl}_1}} = 29.18, SD_{OfferI_{{cl}_1}}=0.24,\) and \(M_{OfferI_{{cl}_2}} = 34.52, SD_{OfferI_{{cl}_2}}=0.29\)). Agents in the second cluster offered less money to out-group members compared to agents in the other cluster (in \(Step = 100, M_{OfferO_{{cl}_1}} = 10.82, SD_{OfferO_{{cl}_1}}=0.24,\) and \(M_{OfferO_{{cl}_2}} = 5.48, SD_{OfferO_{{cl}_2}}=0.29\)).
Agents belonging to the group that was more homogeneous displayed a higher value of salience of their active social identity. Consequently, these agents revealed higher levels of in-group favouritism and out-group discrimination in their behaviour, and offered more to in-group agents and less to out-group ones. With this in mind, we verified that the average accumulated wealth for agents in less dispersed and more homogeneous groups was higher compared to agents in groups with higher dispersion, implying that the agents in groups with a higher identity salience outperformed the agents in groups with a lower identity salience, as stated by hypothesis H1.
Different group size
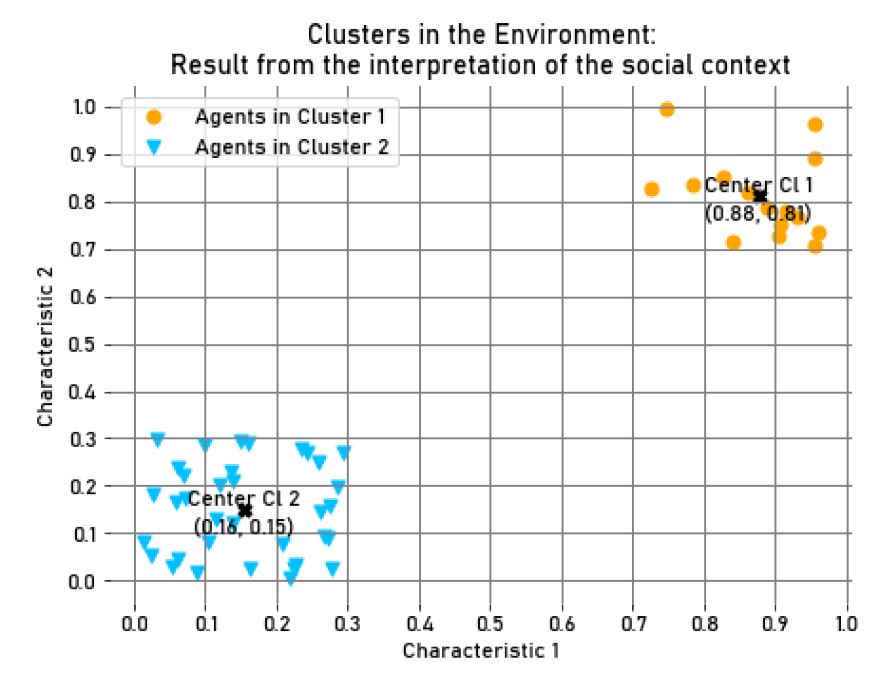
The fourth experiment was similar to the second, however we varied the values of the agents’ characteristics to obtain two clusters of different size and a similar dispersion in the environment (See Figures 7 and 9), intending to verify if there were any wealth disparities between groups with a different number of elements in the same environment.
In Figure 7, we can see two clusters, the first cluster with 15 agents (30%), and the second one with 35 agents (70%). The salience value of the social identity associated with the smallest cluster, the first one, was slightly higher compared to the larger group (in \(Step = 100, M_{{Salience}_{cl_1}} = 0.58, M_{{Salience}_{cl_2}} = 0.57, SD_{{Salience}_{cl_1}} = 1.22*10^{-2}, SD_{{Salience}_{cl_2}} = 1.19*10^{-2}\)). In terms of accessibility, these clusters presented similar values (in \(Step = 100, M_{{Accessibility}_{cl_1}} = M_{{Accessibility}_{cl_2}} = 0.98, SD_{{Accessibility}_{cl_1}} = 2.17*10^{-3}, SD_{{Accessibility}_{cl_2}} = 2.12*10^{-3}\)). Additionally, concerning the average accumulated wealth of each agent in the clusters, the smaller group accumulated slightly more wealth than the other (in \(Step = 100, M_{Wealth_{{cl}_1}} = 10009.08, SD_{Wealth_{{cl}_1}}=39.34,\) and \(M_{Wealth_{{cl}_2}} = 9995.87, SD_{Wealth_{{cl}_2}}=16.86\)). This can be seen in the box plot of the average wealth for each cluster in \(Step=100\), presented in Figure 8.
In Figure 9, two clusters can be seen in the environment, the first one with 45 agents (90%) and the second one with 5 agents (10%). The salience of the active social identity of members of the smallest cluster, the second one, was higher compared to the salience value associated with the larger group (in \(Step = 100, M_{{Salience}_{cl_1}} = 0.59, M_{{Salience}_{cl_2}} = 0.62, SD_{{Salience}_{cl_1}} = 1.88*10^{-2}, SD_{{Salience}_{cl_2}} = 1.90*10^{-2}\)). The same behaviour applied to the accessibility values, but this difference was minor (in \(Step = 100, M_{{Accessibility}_{cl_1}} = 0.98, M_{{Accessibility}_{cl_2}} = 0.99, SD_{{Accessibility}_{cl_1}} = 2.17*10^{-3}, SD_{{Accessibility}_{cl_2}} = 2.12*10^{-3}\)). Additionally, in terms of the average accumulated wealth of each agent in the clusters, the smaller group accumulated more wealth than the larger one (in \(Step = 100, M_{Wealth_{{cl}_1}} = 9993.91, SD_{Wealth_{{cl}_1}}=8.66,\) and \(M_{Wealth_{{cl}_2}} = 10054.84, SD_{Wealth_{{cl}_2}}=77.93\)). This can be verified in Figure 10, where we present a box plot of the average wealth for each cluster in \(Step=100\).
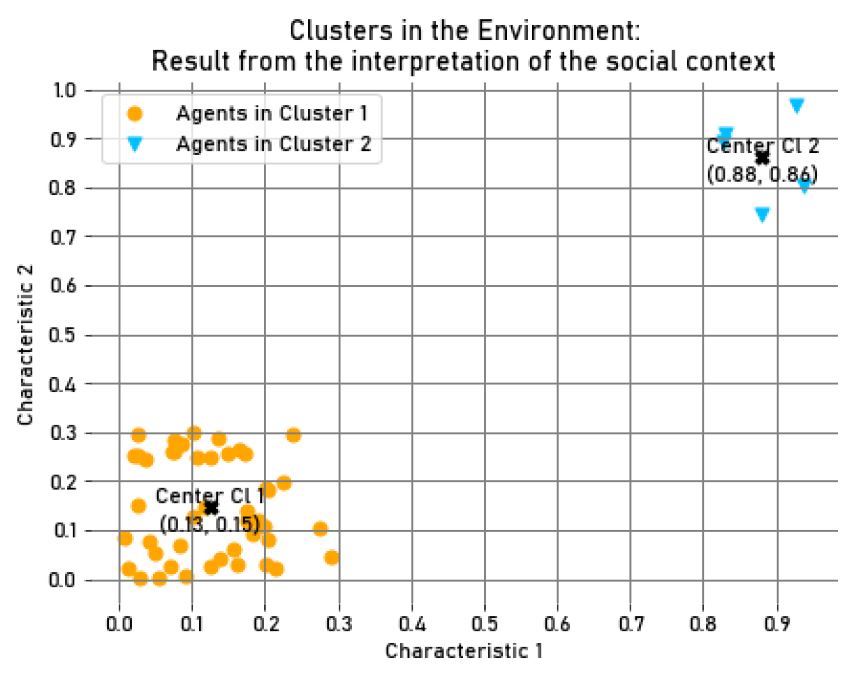
Even though we randomized the characteristics of the agents so that the clusters had a similar dispersion between them, the smallest group was more frequently less dispersed than the larger one. Given that this group had fewer elements, its members were less likely to be attributed characteristics that were distant from one another, making them perceive themselves as more similar to the prototypical member of the group (i.e., the centroid of the cluster). As seen in the third experiment, groups that are more homogeneous (less dispersed) accumulate greater wealth. Thus, this experiment is consistent with those results: as differences in the group size increase, members of the smallest group, which is usually the least dispersed, exhibit a higher value of salience for their salient social identity, as well as a higher value of accumulated wealth. Nonetheless, these differences are not particularly noticeable because the values of group dispersion are only slightly different between the groups, since, as mentioned earlier, we randomized them to be similar using the same interval of values.
Variable context
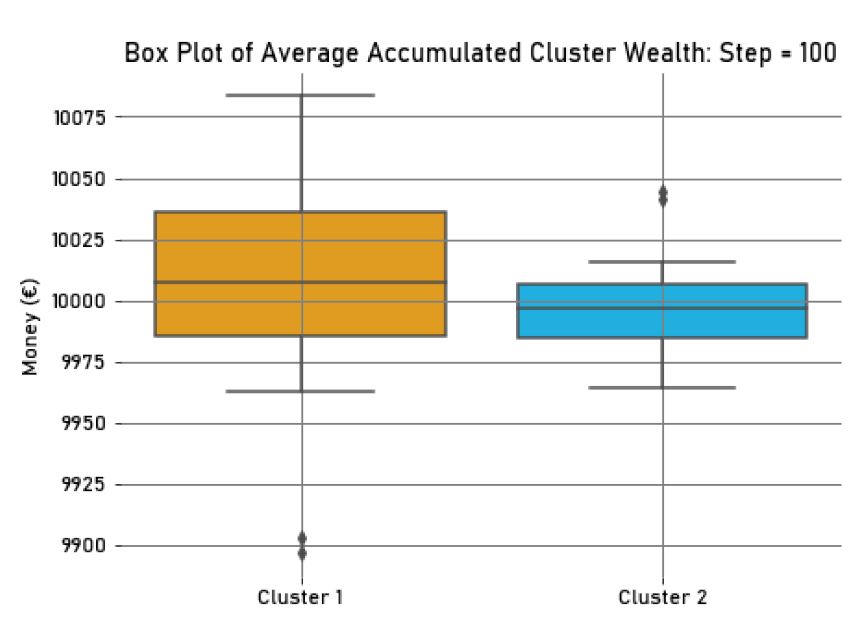
In this final experiment, we varied the context’s theme at each interaction step (empty or with two relevant characteristics), to simulate the dynamics between the personal and social identity. When there were no relevant characteristics in the context, clustering resulted in one single cluster, like in the first experiment. Otherwise, the clusters were similar to those shown in Figure 3. However, only half of the agents in the environment adapted to these context shifts, using their personal or salient social identity in their decisions, depending on the social environment (Adaptive Agents - \(A\)). On the other hand, the remaining half did not adapt to the context, always using the personal identity (Non-Adaptive Agents - \(NA\)). As a result, the average accumulated wealth for the Adaptive Agents was higher compared to the Non-Adaptive Agents (in \(Step = 100, M_{Wealth_{A}} = 10263.44, SD_{Wealth_{A}}=23.84,\) and \(M_{Wealth_{NA}} = 9736.56, SD_{Wealth_{NA}}=23.84\)). We can better visualize this wealth disparity in Figure 11, in which we present a box plot of the wealth in \(Step=100\) for the Adaptive and Non-Adaptive Agents.
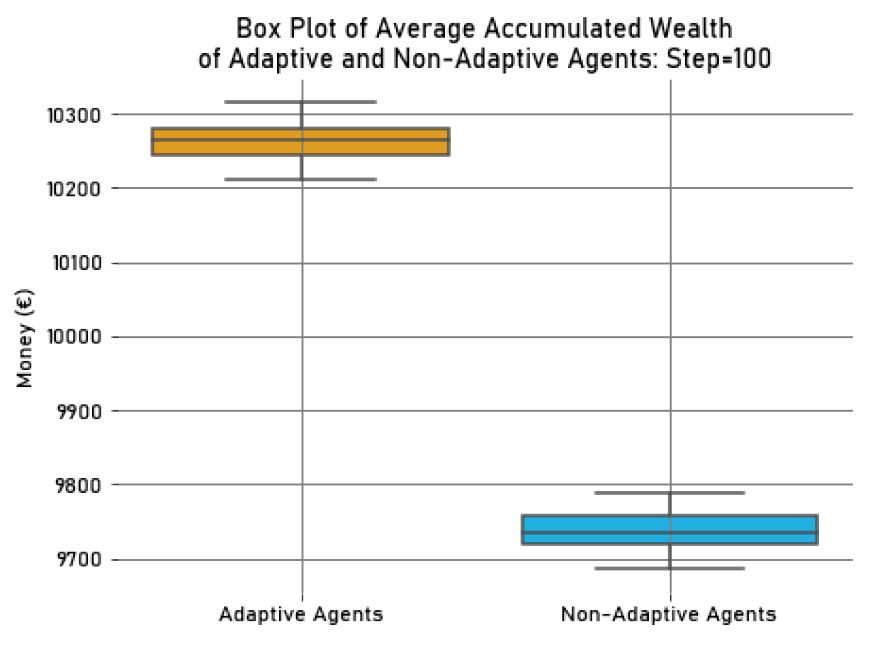
Adaptive Agents, who could shift between their identities according to the context, accumulated more wealth than Non-Adaptive Agents, who were always individualistic and never showed group-based behaviour. This indicates that, when compared to one another, group-based agents outperformed individualistic ones, as stated in hypothesis H2. Thus, the DIMA model allowed agents to behave according to the context, embodying their personal or social identity, which was beneficial for them when playing the Dictator Game.
Use Case: Trash Collection
This section describes an additional use case of the model, focusing on a trash collection simulation. The goal is to explore the interplay between personal and social identities in response to changes in the social context, aiming to show the impact of the DIMA model on the agents’ behaviour during a trash collection task. The source code for this simulation is also available on GitHub, like the previous use case.
For this use case, we drew inspiration from a driftwood collection scenario (Thebaud & Locatelli 2001), which involved exploring different behavioural strategies (aggressive/conciliatory), ranges of vision, and imitation rules of agents while they navigate a grid (a beach) and collect resources (wood). However, we adapted the scenario by replacing the wood with trash and simulating a group of work colleagues responsible for cleaning up a beach instead. The resource collection mechanism has also been simplified by allowing agents to carry an unlimited amount of resources without having to discard them into a pile.
Each agent is characterized by two personal characteristics, competitiveness and sociability, which influence their behaviour within the simulation. When there are no relevant characteristics in the context, agents behave according to the values of their personal characteristics. Agents with higher competitiveness ratings will engage in competition with their colleagues to collect more trash. When two or more agents, represented as \(collidingA\), attempt to collect the same trash item, it implies that their positions coincide within the beach environment. We refer to this event as an agent encounter or collision. In such situations, the agent with a higher competitiveness rating will claim the item, and agents with lower competitiveness ratings are likely to concede. The formalization of this behaviour is presented in Equation 12, where the variable \(collectTrash_a\) represents the decision of agent \(a\) to collect the trash.
| \[ \text{$collectTrash_a =$} \begin{cases} \text{False}, & \exists cA \in collidingA \text{ such that } competitiveness_a < competitiveness_{cA} \\ \text{True}, & \text{otherwise} \end{cases}\] | \[(12)\] |
In terms of sociability, agents with higher sociability ratings will try to seek out other agents on the beach, while those with lower sociability ratings will tend to avoid them. When there is no trash to collect in their current location, agents will explore the environment. They begin by looking at their eight adjacent cells to identify nearby agents. If an agent rates high on sociability, they will tend to move towards other agents. On the other hand, if an agent rates low on sociability, they will tend to avoid other agents and instead move towards empty positions in the environment.
Agents can also be characterized by their shirt colour, which is limited to two different colours. If the shirt colour becomes relevant to the context, the DIMA model is applied to define the agents’ behaviour. Then, agents observe their immediate environment, determine the social clusters given the current context, establish their active identity, and compute their salience value. Based on the colour of their shirt, agents will adjust their behaviour towards in-group or out-group members, following a similar idea to a previous smaller-scale simulation scenario implemented with the DIMA model (Dimas et al. 2013). Agent encounters with in-group members lead to a decrease in competitiveness, while out-group collisions lead to an increase in competitiveness. Furthermore, when surrounded by in-group members, agents prioritize being more sociable and seek out these members. Conversely, when surrounded by out-group members, agents become less sociable and try to avoid them. This in-group favouritism and out-group discrimination follows the literature mentioned in the previous use case.
When an agent’s active identity corresponds to its salient social identity, the agent’s personal characteristics undergo a shift through linear interpolation. This shift is based on the salience of the identity and the presence of in-group or out-group members in their field of view. For instance, when interacting with out-group members, an agent’s sociability value shifts from their personal sociability value to 0, while their competitiveness value shifts from their personal competitiveness value to 1, based on the salience of the identity. As a result, the agent becomes more competitive and less sociable with out-group members. Conversely, the agent’s sociability value shifts towards 1 and their competitiveness value towards 0 when interacting with in-group members. Nonetheless, if the salience of the salient identity is not strong enough or if the agent is surrounded only by in-group members, the agent will act based on their personal identity, as described earlier.
As mentioned before, the aim of this simulation is to explore the effect of the DIMA model on the behaviour of agents in a trash collection scenario. Specifically, we intend to compare the behaviour of agents when the DIMA model is inactive (i.e., when there are no relevant characteristics in the context) to when it is active (i.e., when the shirt colour is a relevant characteristic in the social context). We measure agent performance by tracking the mean trash collected by each agent, and we measure social interactions by tracking the mean number of agent encounters in each cell.
The simulation consists of three components: a \(20\times20\) grid representing the beach environment, the trash items to be collected, and the agents responsible for collecting the trash. The agents (\(N=50\)) are randomly positioned on the grid at the beginning of each run. Each cell of the grid may contain between 0 to 10 trash items, being this number randomly determined (\(N_{cell} = [0,10]\)). The simulation runs for a set number of interaction steps (\(numSteps = 500\)), and the simulation is repeated a set number of times (\(numRuns = 50\)). At each time step, agents have the option to explore the environment by moving one cell, or attempt to collect a trash item located in their current cell.
Similar to the previous use case, the agent’s perception module was not added. Thus, the DIMA input values for each agent’s personal attributes are randomized at the start of each run, with the shirt colour being randomly chosen from a set of two colours (\(shirtColours = [0, 1]\)). The context’s theme, shared by all agents, can be either empty or be defined as the shirt colour. Moreover, agents have a limited view of their surroundings and can only observe other agents in the eight adjacent cells surrounding them (\(fieldOfView=1\)), meaning that they only consider nearby agents when making decisions based on the social context.
The thresholds applied in the DIMA functions are specified as \(tClustering = tNormative = tSalience = 0.2\). The accessibility of the salient social identity is updated using a constant growth factor (\(=0.01\)), as in the previous use case.
The decision-making module is defined according to the behaviour described earlier, depending on the agents present in the agent’s field of view, and whether the shirt colour is relevant or not. The results of the simulation were recorded at each step of the interaction, and averaged out across the different repeated runs. In Figure 12, you can see an example of the trash collection grid while the simulation is running.

Results and discussion
For the following experiments, we analysed the results by classifying the agents according to their competitiveness and sociability. To make these classifications, we used threshold values of \(tCompetitiveness = 0.5\) and \(tSociability = 0.5\). An agent was considered highly competitive if its competitiveness value was greater than \(tCompetitiveness\), while an agent was considered highly sociable if its sociability value was greater than \(tSociability\).
Empty context
In the first experiment, the context had no relevant characteristics, and as a result, the DIMA model had no impact on the agents’ behaviour. Therefore, agents relied solely on their personal characteristics to make decisions during the simulation.
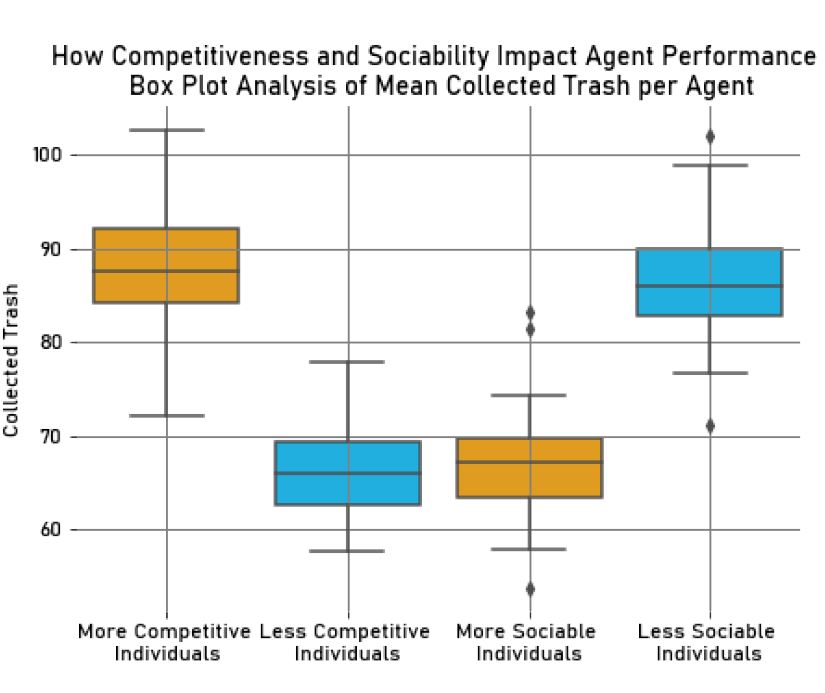
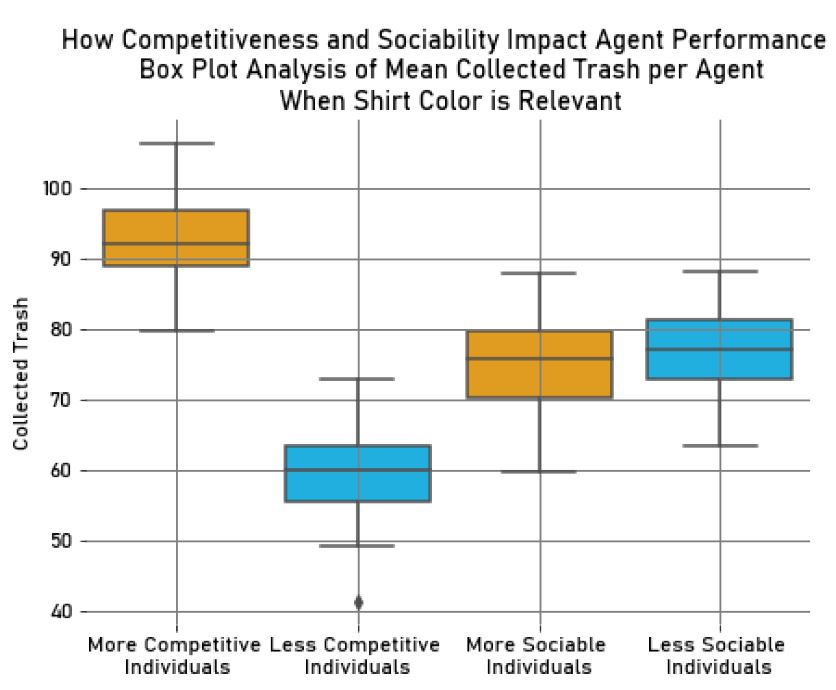
Our analysis revealed that the more competitive individuals collected, on average, more trash (\(M_{Trash_{MComp}} = 87.92, SD_{Trash_{MComp}} = 6.01\)) than the less competitive individuals (\(M_{Trash_{LComp}} = 66.18, SD_{Trash_{LComp}} = 4.79\)). This result was expected since competitive individuals "fight more" to collect the resource in a conflict with other agents.
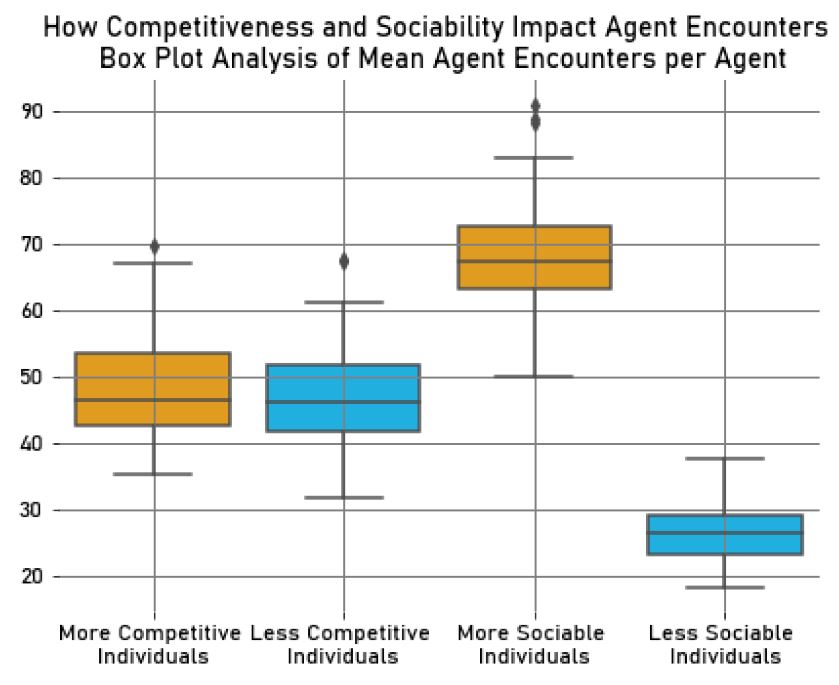
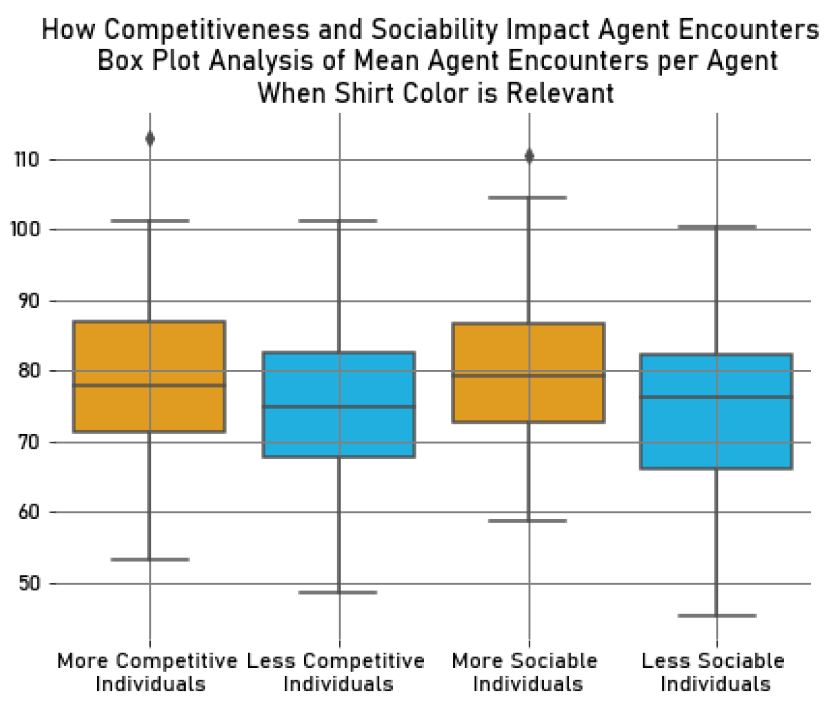
We also found that the more sociable individuals (\(M_{Trash_{MSoc}} = 67.29, SD_{Trash_{MSoc}} = 5.23\)) collected less trash than the less sociable ones (\(M_{Trash_{LSoc}} = 86.83, SD_{Trash_{LSoc}} = 6.31\)). This observation may be related to the fact that the less sociable agents tend to avoid conflicts by exploring cells where there are no other agents. As a result, they also avoid collecting trash in cells with other agents, meaning that they usually explore cells where trash is guaranteed to be collected by them. This is supported by our analysis of agent encounters, where we found, as expected, that the more sociable agents (\(M_{Collisions_{MSoc}} = 68.88, SD_{Collisions_{MSoc}} = 9.19\)) had more collisions with other agents than the less sociable agents (\(M_{Collisions_{LSoc}} = 26.96, SD_{Collisions_{LSoc}} = 4.46\)).
We have presented our findings in the box plots in Figures 13 and 14, which show the mean trash collected per agent and the mean number of agent encounters during the simulation.
Relevant shirt colour
The second experiment involved agents wearing different coloured shirts, the shirt colour being the relevant characteristic of the context. Thus, the DIMA model influenced agents’ behaviour through the dynamics between their personal and social identities.
In this experiment, the difference in performance between more competitive and less competitive individuals was greater than in the previous experiment. The results indicated that the more competitive agents collected more trash (\(M_{Trash_{MComp}} = 92.55, SD_{Trash_{MComp}} = 5.62\)) than the less competitive agents (\(M_{Trash_{LComp}} = 59.53, SD_{Trash_{LComp}} = 6.34\)). One possible explanation for the difference between the two experiments is the increase in the number of encounters per agent in comparison to the previous experiment. This could be attributed to the fact that, during the simulation, agents increased their sociability towards in-group members, according to their identity salience. Consequently, if there was no trash around them, the likelihood of following another in-group member while exploring the grid to find more trash was higher, leading these agents to reach the trash position together. In other words, there was a tendency for the agents to join together during the exploration of the environment. Then, although agents became less competitive with in-group members and more competitive with out-group members, by colliding more with other agents, there were fewer opportunities for the agents to explore the grid cells alone and collect the trash individually. This means that the more competitive agents had slightly more chances to outperform the less competitive agents in the second experiment compared to the first experiment.
The difference in performance between more sociable and less sociable agents decreased significantly compared to the previous experiment, even though the less sociable agents still collected slightly more trash on average (\(M_{Trash_{LSoc}} = 77.25, SD_{Trash_{LSoc}} = 5.84\)) than the more sociable ones (\(M_{Trash_{MSoc}} = 75.36, SD_{Trash_{MSoc}} = 6.62\)). As we mentioned before, this may be explained by the fact that agents collided with each other more frequently during this experiment, particularly with in-group members, as their sociability increased with their identity salience. Consequently, the less sociable agents ended up moving towards other agents more than in the first experiment, resulting in more agent encounters and similar trash collection to more sociable individuals. Nevertheless, the more sociable agents still had slightly more agent encounters (\(M_{Collisions_{MSoc}} = 80.04, SD_{Collisions_{MSoc}} = 11.37\)) than the less sociable ones (\(M_{Collisions_{LSoc}} = 73.98, SD_{Collisions_{LSoc}} = 12.27\)).
These results can be seen in the box plots in Figures 15 and 16, which show the mean trash collected per agent and the mean number of agent encounters.
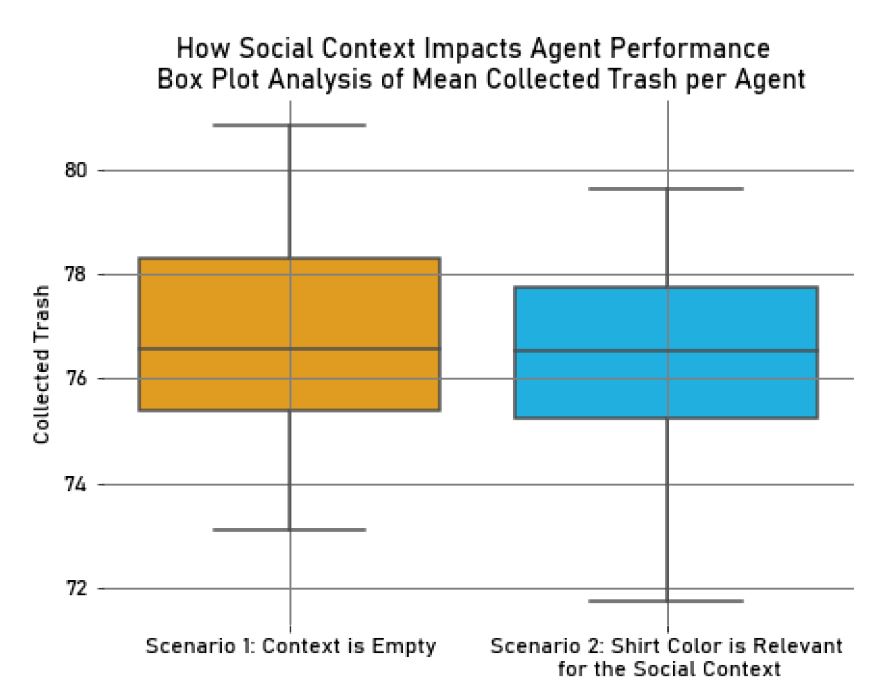
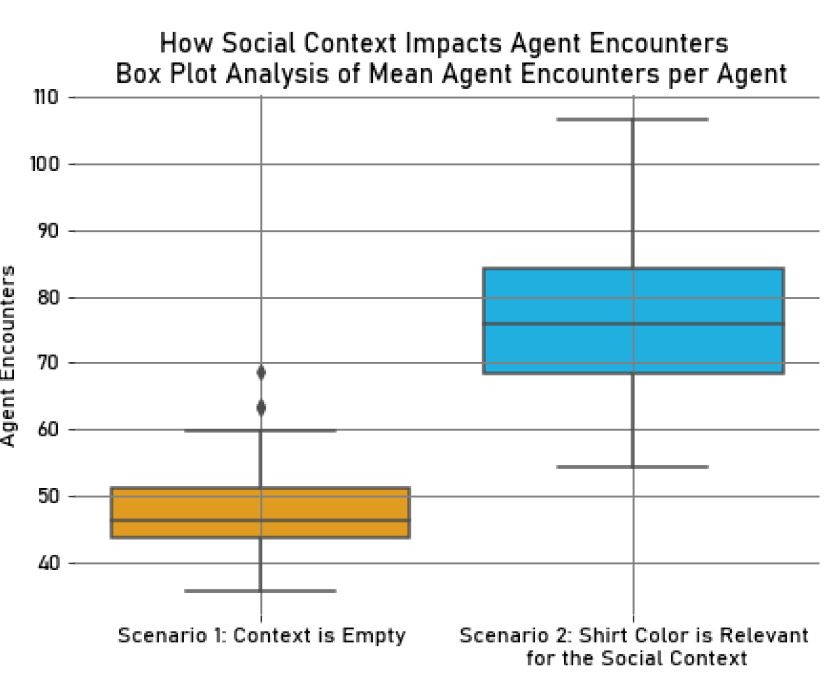
When comparing the results of the two experiments, there was a slight decrease in the mean amount of trash collected per agent in the second experiment (\(M_{Trash} = 76.37, SD_{Trash} = 1.90\)) compared to the first one (\(M_{Trash} = 76.86, SD_{Trash} = 1.87\)). However, the number of agent encounters increased in the second experiment (\(M_{Collisions} = 76.98, SD_{Collisions} = 10.73\)) compared to the first one (\(M_{Collisions} = 47.88, SD_{Collisions} = 7.17\)), suggesting a tendency for the agents to move towards other agents during the simulation, in particular with in-group members, for the reasons mentioned in the previous analysis. This could be compared to stopping to talk with other people during a group activity and taking longer to complete a task, which reflects in collecting slightly less resources in the second experiment. These trends can be observed in the box plots in Figures 17 and 18.
Conclusion and Future Work
This paper presents the formalization of the Dynamic Identity Model for Agents, an agent-based model based on the Social Identity Approach in which agents define their active identity as personal or social depending on the context. DIMA, as specified in the model section, can be integrated into existing agent architectures, like a social agent architecture with perception and decision-making modules.
The link between the model formalization and integration is provided as a reference for researchers who seek to add human-like behaviour to their agents based on identity-related processes. Then, depending on the purpose of the agent-based social simulation, DIMA’s identity salience mechanism can be added to agents to explore how contextual factors influence identity, how personal and social identities interact with one another, and how identity affects behaviour. As a demonstration of how to setup the model, a Dictator Game simulation was configured, in which agents had to distribute a specific amount of money to others based on their active identity. Different social environments were explored in this simulation to assess the impact of identity on agents’ behaviour and performance. Additionally, a simulation using a trash collection scenario was conducted to study how agents with different levels of competitiveness and sociability behave with and without the impact of the DIMA model, taking into account the colour of their shirts as a relevant characteristic. Our goal was to explore the interplay between the agents’ personal and social identities, focusing on the shift of their personal characteristics considering in-group and out-group bias, and to observe how these dynamics change agent behaviour, performance and social interactions.
These use cases not only illustrate how DIMA works for different scenarios, but also how it may be beneficial for modelling and studying cooperation using economic games or resource gathering tasks. This allows us to see the effects of a more salient group identity on the performance of agents in a group, the benefits of being context-aware vs. always using the personal identity, and the dynamics of personal and social identities and how they impact behaviour and outcomes. Nevertheless, this model can be used for more complex scenarios by including different accessibility functions (e.g., that incorporate emotions given the outcome of an action with a specific social identity) or by exploring how different social settings affect simulation results (e.g., changing the agents’ field of view).
Now that the formalization-integration connection has been defined and the model and scenario are published online, other modellers and social scientists should be able to enhance their models and simulations by including DIMA in their agents. Given the context-dependent identities of the agents, this modification may strengthen agents’ believability, allowing researchers to observe and forecast identity-related behaviour.
In future work, it should be possible for agents in the model to have multiple social identities active at the same time, to allow researchers to explore conflicts of identities and how they reinforce one another (Kopecky et al. 2010). It would also be interesting to explore scenarios with conflicts between the personal and the social identities, given that the individual goals, needs and values of an agent may conflict with those of their social identity. Finally, with the current scenario, there are a few things that could still be explored: implement a function that evaluates the outcome of an agent’s action to be used in the accessibility update (e.g., dependent on payoff), compare the performance of agents with humans in a similar game scenario, experiment a different initialization of the agents’ normative social groups (e.g., different initial accessibility levels), and so on.
Acknowledgements
This work was supported by national funds through Fundação para a Ciência e a Tecnologia (FCT) with reference UIDB/50021/2020. It was partially supported by the INVITE project (ref. UTA-Est/MAI/0008/2009) funded by FCT under the UT-Austin/Portugal cooperation agreement and by national funds through FCT, under project PEst-OE/EEI/LA0021/2011, the PIDDAC Program funds. Inês Lobo acknowledges her FCT grant (2021.04796.BD). Diogo Rato acknowledges his FCT grant (SFRHBD/131024/2017).
Notes
References
ALLEN, K., Bergin, R., & Pickar, K. (2004). Exploring trust, group satisfaction, and performance in geographically dispersed and co-located university technology commercialization teams. VentureWell. Proceedings of Open, the Annual Conference, 201. National Collegiate Inventors & Innovators Alliance.
BLANZ, M. (1999). Accessibility and fit as determinants of the salience of social categorizations. European Journal of Social Psychology, 29(1), 43–74. [doi:10.1002/(sici)1099-0992(199902)29:1<43::aid-ejsp913>3.0.co;2-z]
BRUNER, J. S. (1957). On perceptual readiness. Psychological Review, 64(2), 123.
CAMPO, M., Champely, S., Louvet, B., Rosnet, E., Ferrand, C., Pauketat, J. V., & Mackie, D. M. (2019). Group-based emotions: Evidence for emotion-performance relationships in team sports. Research Quarterly for Exercise and Sport, 90(1), 54–63. [doi:10.1080/02701367.2018.1563274]
CARBONELL, J. G. (1980). Towards a process model of human personality traits. Artificial Intelligence, 15(1), 49–74. [doi:10.1016/0004-3702(80)90022-3]
CHANG, D., Chen, R., & Krupka, E. (2019). Rhetoric matters: A social norms explanation for the anomaly of framing. Games and Economic Behavior, 116, 158–178. [doi:10.1016/j.geb.2019.04.011]
DE Rosis, F., Pelachaud, C., & Poggi, I. (2004). Transcultural believability in embodied agents: A matter of consistent adaptation. In S. Payr & R. Trappl (Eds.), Agent culture: Human-Agent interaction in a multicultural world (pp. 75–106). London: Routledge.
DIGMAN, J. M. (1990). Personality structure: Emergence of the five-factor model. Annual Review of Psychology, 41(1), 417–440. [doi:10.1146/annurev.ps.41.020190.002221]
DIMAS, J., Lopes, P., & Prada, R. (2013). One for all, all for one: Agents with social identities. Proceedings of the Annual Meeting of the Cognitive Science Society
DIMAS, J., & Prada, R. (2013). Dynamic identity model for agents. International Workshop on Multi-Agent Systems and Agent-Based Simulation [doi:10.1007/978-3-642-54783-6_3]
DOCE, T., Dias, J., Prada, R., & Paiva, A. (2010). Creating individual agents through personality traits. Intelligent Virtual Agents [doi:10.1007/978-3-642-15892-6_27]
FEARON, J. D. (1999). What is identity (as we now use the word). Unpublished manuscript, Stanford University, Stanford, California. Available at: https://www.researchgate.net/profile/James_Fearon2/publication/229052754_What_is_identity_(as_we_now_use_the_word)/links/0f31752e689dc3f2a7000000.pdf.
FESTINGER, L. (1954). A theory of social comparison processes. Human Relations, 7(2), 117–140. [doi:10.1177/001872675400700202]
FRIDMAN, N., & Kaminka, G. A. (2009). Comparing human and synthetic group behaviors: A model based on social psychology. International Conference on Cognitive Modeling (ICCM-09)
GRIER, R. A., Skarin, B., Lubyansky, A., & Wolpert, L. (2008). SCIPR: A computational model to simulate cultural identities for predicting reactions to events. Proceedings of the Second International Conference on Computational Cultural Dynamics
GUNDLACH, M., Zivnuska, S., & Stoner, J. (2006). Understanding the relationship between individualism–collectivism and team performance through an integration of social identity theory and the social relations model. Human Relations, 59(12), 1603–1632. [doi:10.1177/0018726706073193]
HENNESSY, J., & West, M. A. (1999). Intergroup behavior in organizations: A field test of social identity theory. Small Group Research, 30(3), 361–382. [doi:10.1177/104649649903000305]
HOFSTEDE, G. H., & HOFSTEDE, G. (2001). Culture consequences: Comparing values, behaviors, intitutions, and organizations across nations. SAGE Publications, Incorporated.
HOGG, M. A., Terry, D. J., & White, K. M. (1995). A tale of two theories: A critical comparison of identity theory with social identity theory. Social Psychology Quarterly, 58(4), 255–269. [doi:10.2307/2787127]
KAHNEMAN, D., Knetsch, J. L., & Thaler, R. H. (1986). Fairness and the assumptions of economics. Journal of Business, 59(4), S285–S300. [doi:10.1086/296367]
LEONARDELLI, G. J., Pickett, C. L., & Brewer, M. B. (2010). Optimal distinctiveness theory: A framework for social identity, social cognition, and intergroup relations. In M. P. Zanna (Ed.), Advances in experimental social psychology (Vol. 43, pp. 63–113). Amsterdam: Elsevier. [doi:10.1016/s0065-2601(10)43002-6]
LIST, J. A. (2007). On the interpretation of giving in dictator games. Journal of Political Economy, 115(3), 482–493. [doi:10.1086/519249]
LUCAS, M. M., Wagner, L., & Chow, C. (2008). Fair game: The intuitive economics of resource exchange in four-year olds. Journal of Social, Evolutionary, and Cultural Psychology, 2(3), 74. [doi:10.1037/h0099353]
MACKIE, D. M., & Smith, E. R. (1998). Intergroup relations: Insights from a theoretically integrative approach. Psychological Review, 105(3), 499. [doi:10.1037/0033-295x.105.3.499]
MAGALIE Ochs, V. C., Nicolas Sabouret. (2009). Simulation of the dynamics of nonplayer characters’ emotions and social relations in games. IEEE Transactions on Computational Intelligence and AI in Games, 1(4), 281–297. [doi:10.1109/tciaig.2009.2036247]
MARKUS, H., & Kunda, Z. (1986). Stability and malleability of the self-concept. Journal of Personality and Social Psychology, 51(4), 858. [doi:10.1037/0022-3514.51.4.858]
MASCARENHAS, S., Dias, J., Afonso, N., Enz, S., & Paiva, A. (2009). Using rituals to express cultural differences in synthetic characters. Proceedings of The 8th International Conference on Autonomous Agents and Multiagent Systems-Volume 1
MCGARTY, C. (1999). Categorization in social psychology. Thousand Oaks, CA: Sage.
OAKES, P. J. (1987). The salience of social categories. In J. C. Turner, M. A. Hogg, P. J. OAKES, S. D. Reicher, & M. S. Wetherell (Eds.), Rediscovering the social group: A Self-Categorization theory (pp. 117–141). Oxford: Blackwell.
OTTEN, S., & Moskowitz, G. B. (2000). Evidence for implicit evaluative in-group bias: Affect-biased spontaneous trait inference in a minimal group paradigm. Journal of Experimental Social Psychology, 36(1), 77–89. [doi:10.1006/jesp.1999.1399]
PACKER, D., & Van Bavel, J. J. (2014). The dynamic nature of identity: From the brain to behavior. In K. J. Reynolds & N. R. Branscombe (Eds.), The psychology of change: Life contexts, experiences, and identities (pp. 225–245). London: Psychology Press.
PRADA, R., Camilo, J., & Nunes, M. A. S. N. (2010). Introducing personality into team dynamics. ECAI
REHM, M., Bee, N., Endrass, B., Wissner, M., & André, E. (2007). Too close for comfort? Adapting to the user’s cultural background. Proceedings of the International Workshop on Human-Centered Multimedia [doi:10.1145/1290128.1290142]
REHM, M., Nakano, Y., André, E., & Nishida, T. (2008). Culture-specific first meeting encounters between virtual agents. Intelligent virtual agents [doi:10.1007/978-3-540-85483-8_23]
RIZZO, P., Veloso, M., Miceli, M., & Cesta, A. (1997). Personality-driven social behaviors in believable agents. Proceedings of the AAAI Fall Symposium on Socially Intelligent Agents
SALZARULO, L. (2006). A continuous opinion dynamics model based on the principle of meta-contrast. Journal of Artificial Societies and Social Simulation, 9(1), 13.
SMALDINO, P., Pickett, C., Sherman, J., & Schank, J. (2012). An agent-based model of social identity dynamics. Journal of Artificial Societies and Social Simulation, 15(4), 7. [doi:10.18564/jasss.2030]
STETS, J. E., & Burke, P. J. (2000). Identity theory and social identity theory. Social Psychology Quarterly, 63(3), 224–237. [doi:10.2307/2695870]
SWANN, W. B., & Bosson, J. K. (2010). Self and identity. In S. T. Fiske, D. T. Gilbert, & G. Lindzey (Eds.), Handbook of social psychology (pp. 589–628). Hoboken, NJ: John Wiley & Sons.
TAJFEL, H. (1970). Experiments in intergroup discrimination. Scientific American, 223(5), 96–102. [doi:10.1038/scientificamerican1170-96]
TAJFEL, H., Turner, J. C., Austin, W. G., & Worchel, S. (1979). An integrative theory of intergroup conflict. Organizational Identity: A Reader, 56(65), 94–109.
THEBAUD, O., & Locatelli, B. (2001). Modelling the emergence of resource-sharing conventions: An agent-based approach. Journal of Artificial Societies and Social Simulation, 4(2), 3.
TREPTE, S. (2006). Social identity theory. In J. Bryant & P. Vorderer (Eds.), Psychology of entertainment (pp. 255–272). Mahwah, NJ: Lawrence Erlbaum Associates Publishers.
TURNER, J. C., Hogg, M. A., Oakes, P. J., Reicher, S. D., & Wetherell, M. S. (1987). Rediscovering the social group: A self-Categorization Theory. Oxford: Basil Blackwell.
TURNER, J. C., Oakes, P. J., Haslam, S. A., & McGarty, C. (1994). Self and collective: Cognition and social context. Personality and Social Psychology Bulletin, 20(5), 454–463. [doi:10.1177/0146167294205002]