Validating Argument-Based Opinion Dynamics with Survey Experiments

and
aInstitute of Technology Futures, Karlsruhe Institute of Technology, Germany; bForschungszentrum Jülich, Germany
Journal of Artificial
Societies and Social Simulation 27 (1) 17
<https://www.jasss.org/27/1/17.html>
DOI: 10.18564/jasss.5305
Received: 15-Nov-2022 Accepted: 19-Dec-2023 Published: 31-Jan-2024
Abstract
The empirical validation of models remains one of the most important challenges in opinion dynamics. In this contribution, we report on recent developments on combining data from a survey experiment with an argument-based computational model of opinion formation in which biased processing is the principle mechanism. We first review the development of argument-based models, and extend a model with confirmation bias by noise mimicking an external source of balanced information. We then study the behavior of this extended model to characterize the macroscopic opinion distributions that emerge from the process. A new method for the automated classification of model outcomes is presented. In the final part of the paper, we describe and apply a multi-level validation approach using the micro and the macro data gathered in the survey experiment. We revisit previous results on the micro-level calibration using data on argument-induced opinion change, and show that the extended model matches surveyed opinion distributions in a specific region in the parameter space. The estimated strength of biased processing given the macro data is highly compatible with those values that achieve high likelihood at the micro level. The model provides a solid bridge from the micro processes of individual attitude change to macro level opinion distributions.Introduction
Opinion dynamics is a field that develops theoretical models of collective opinion processes to understand the mechanisms behind the emergence of consensus, polarization and conflict. It uses agent-based computational models (ABMs) to simulate the evolution of opinions in a population of artificial agents. These agents are placed in a social environment typically consisting of an interaction network defining who can interact with whom. In the course of a simulation neighboring agents interact and exchange opinions according to some simple rules. Opinion dynamics studies the properties of these complex dynamical systems to identify basic mechanisms behind different collective phenomena from consensus to different forms of polarization.
A lot of modeling work in the last two decades has been inspired by the so-called "puzzle of polarization" frequently referring to Abelson (1964) and Axelrod (1997).1 The motivating question has been: How does a population with moderate initial opinions diverge into groups of agents that strongly support opposing views? Early models (DeGroot 1974; French 1956; Friedkin & Johnsen 1990) implementing positive social influence by which opinions assimilate in interaction predict consensus whenever the interaction network is a single connected component. Research in the last 20 years has revealed quite a few mechanisms that may solve the puzzle of persistent opinion plurality including bounded confidence (Deffuant et al. 2000; Hegselmann & Krause 2002) introduced in the two papers to which this special issue is in some sense devoted. Other models targeting bi-polarization dynamics draw on more sophisticated forms of homophily (Carley 1991; Mäs & Flache 2013), negative influence (Baldassarri & Bearman 2007; Flache & Macy 2011; Jager & Amblard 2005; Mäs et al. 2014), opinion reinforcement (Banisch & Olbrich 2019; Martins 2008), biased assimilation (Banisch & Shamon 2023; Dandekar et al. 2013; Mueller & Tan 2018), and combinations of those. Most of these models are covered by the review of Flache et al. (2017) in this Journal and the social influence wiki (Social-Influence-WIKI 2022) initiated by its authors.
Nowadays, 20 years later, many models exist that provide possible explanations of collective bi-polarization and we are facing the problem to select the most relevant mechanisms given more specific questions. The field is ripe to take a further step beyond the mere theoretical exploration of how qualitatively different idealized macro phenomena, such as consensus and polarization, may arise from different basic micro-level assumptions. As a matter of fact, there is a great need for more realistic models. Especially in an era where collective communication is more and more engineered, where social network algorithms guide what becomes visible to whome, simulation tools are needed to rigorously inquire and predict the potential impact of algorithmic filters and platform choices. Recent work on algorithmic personalization and filter bubbles has shown that different combinations of micro mechanisms may lead to conflicting predictions concerning the impact of algorithm-induced homophily on opinion dynamics (Keijzer & Mäs 2022; Mäs & Bischofberger 2015). This is a big obstacle when using model results as a basis for science-based policy recommendations. In order to draw rigorous conclusions from simulation models we have to decide which of these principal mechanisms are most prevalent given an empirical case.
In order to advance towards applied opinion dynamics, the empirical validation of opinion models remains a major challenge for the field (Flache et al. 2017; Sobkowicz 2009).2 Data usually does not fit well with the idealized world of opinion models and in fact there are only few topics on which real opinions compare to the stylized pattern of bi-polarization that emerges in most of the models (Duggins 2017). In this paper, we aim to advance the state of the art of empirical validation in opinion dynamics by combining a survey experiment (Shamon et al. 2019) on argument persuasion with argument-based models of opinion formation (Banisch & Olbrich 2021; Mäs & Flache 2013; Taillandier et al. 2021). The experiment provides micro-level data on attitude change and macro-level data on opinions with respect to six different technologies for electricity production. This opens the possibility to calibrate the micro-level mechanisms of the ABM and to compare resulting opinion distributions to real opinions on the same topics. The main objective is to empirically interrogate argument communication theory (ACT) (Mäs & Flache 2013) so that models developed within this paradigm can be confidently applied to real problems such as the impact of online policies on opinion dynamics.
To achieve that, the present paper extends previous work that introduced biased argument processing into argument communication models and showed that this mechanism can explain experimentally observed opinion changes better than previous models (Banisch & Shamon 2023). While this first paper has focused on calibrating the micro mechanism with experimental data on argument-induced opinion change, the present paper concentrates on the macro-level comparison of model outcomes to the survey data gathered in the experiment. The main contribution of this paper, is to show that the argument communication model with biased processing also reproduces macro-level data on opinions with high accuracy if we control for the impact of social influence. Namely, we extend the model by assuming a certain level of unbiased external information that supplies the system with random arguments (as opposed to arguments brought up by peers). We analyze the impact of this form of noise on the model behavior and show that in a regime of moderate biased processing and a relatively high level of noise opinion data is matched remarkably well by its stationary distribution.
The model hence provides a consistent link between empirical observations at the micro and the macro level. It provides an empirically-grounded explanation that bridges from individual patterns of attitude change to the resulting distributions of surveyed opinions. We believe that this is an important step towards empirically validated argument-based models which prepares them for more specific applications.
The paper is structured as follows. The next section presents background and the current state of research. We discuss binary and continuous opinion models as the two major traditional model classes, and sketch the development of argument-based opinion dynamics as a combination of those. The next section introduces the model and provides details on the computational analysis. Section 4 provides results regarding the general behavior of the model in different regions of the parameter space. Section 5 presents the overall validation approach, discusses associated terminology and describes the survey experiment. Section 6 finally revisits previous results on model calibration, provides the results regarding the comparison of model outcomes to the empirical opinion distributions, and compares the two. We conclude with a discussion on validation in opinion dynamics and the potential contributions of this work.
Argument Communication Theory: Predecessors and Theoretical Development
Opinion dynamics is an interdisciplinary endeavor that has attracted researchers from physics, computer science and mathematics as well as sociologists, political science and communication scholars. At a very basic level, one can distinguish different models with respect to what they treat as an agent’s opinion. While the physics community has mostly concentrated on binary (or discrete) state models in which the opinion is a single nominal variable, the idea that an opinion is a metric variable on a continuous opinion scale from -1 to 1 is prevailing in the social simulation community. Argument communication theory (henceforth ACT) combines aspects of both binary choice and continuous space models. Therefore, we provide a brief and selective overview of modeling work within these two paradigms. A more encompassing review on both model classes has been provided in Sı̂rbu et al. (2017). See also Lorenz (2007), Flache et al. (2017) for reviews on continuous opinion models and Galam (2008), Castellano et al. (2009) for physics-inspired models.
Binary and continuous opinion dynamics
Binary state opinion models
In binary state models agents are characterized by a single binary variable, say \(o_i \in \{0,1\}\). In the interaction process, an agent \(i\) is chosen and updates its opinion according to opinions in its neighborhood. Models mainly differ with respect to how this update is conceived. The most simple and well-studied binary opinion model – the voter model – originated in theoretical biology as a model for the spatial conflict of two species (Kimura & Weiss 1964). In the voter model, a single neighbor \(j\) is chosen at random out of the neighbors set of \(i\) and \(i\) copies the state of \(j\) (i.e., \(o_i \leftarrow o_j\)) (Banisch 2016; Holley & Liggett 1975). In majority rule models (Chen & Redner 2005; Galam 1986, 2008), \(i\) sees the states of all neighbors and updates its opinion by following the local majority. These models are therefore closely related to early threshold models (Granovetter 1978; Schelling 1973) where opinion update takes place when a certain fraction of neighbors assumes an alternative state. More complex forms of frequency dependence have been studied with so-called non-linear voter models (Schweitzer & Behera 2009) or the Sznajd model (Sznajd-Weron & Sznajd 2000). Notice finally that also the social impact model introduced in 1990 by Nowak et al. (1990) falls into the category of binary models.
The main reason for which binary state opinion dynamics has attracted so much attention from the physics community is their analogy to spin systems. Networks of agents that switch between two opinion states by following the choices of neighbors resemble physical systems of ferromagnetically coupled Ising spins (Ising 1925). For this reason, the concepts and tools of statistical physics can be applied to study – often analytically – the dynamical behavior of a model (Castellano et al. 2009; Lewenstein et al. 1992). One very central concept is the so-called Hamiltonian that assigns an energy to each possible configuration of the system according to the network of social coupling. A computational model that implements local opinion alignment can then be seen as a relaxation dynamics approaching the (local or global) minima in this energy landscape. A second important idea that the engagement of physicists with opinion dynamics models brought into the field is that of a phase transition, and associated critical points. A phase transition indicates that the behavior of a model undergoes a qualitative change as model parameters change. In binary opinion dynamics this often means a transition from consensus (all agents aligned) to a disordered state under increasing levels of noise (Hołyst et al. 2000; Nowak & Sznajd-Weron 2020), contrarian agents (Banisch 2014; Galam 2004; Krueger et al. 2017) or zealots (Crokidakis & de Oliveira 2015; Mobilia 2003). Especially close to the transition point the models often exhibit very interesting long-lasting mesoscopic patterns such as non-stationary local clusters of agents with aligned opinions (Schweitzer & Behera 2009). It is noteworthy, that the relation between opinion dynamics and statistical mechanics has been productive in both directions. Problems of social dynamics have motivated significant research on how to tackle heterogeneous and complex networks with physics tools such as mean field approximations (Sood & Redner 2005; Vazquez & Eguı́luz 2008) and has played a big role in the development of pair and higher-order approximation techniques (Gleeson 2013; Schweitzer & Behera 2009).
Binary state dynamics over complex networks can be seen as a blueprint of a complex dynamical system and therefore these models have seen applications in all fields that have embraced the turn to complexity in the last decades. The wide applicability derives from the fact that the two possible states are open to many interpretations, including the absence or presence of biological species as in the original voter model by Kimura & Weiss (1964). In the context of opinion dynamics, they can relate to beliefs and opinions, but also to alternative behaviors as in the literature on complex contagion (Centola & Macy 2007; Ugander et al. 2012) and games on networks (Galeotti et al. 2010; Szabó & Fath 2007).
Continuous opinion dynamics
While the previous class of models originated in theoretical biology, the origins of continuous opinion dynamics can be traced back to early research in mathematical social psychology on consensus formation in small groups (see the first two chapters in Friedkin & Johnsen 2011 for a historical perspective). Here an agent’s opinion is represented as a continuous variable which typically represents a degree of favor versus disfavor (i.e. an attitude \(o_i = [-1,1]\)), or a subjective probability or belief (\(o_i \in [0,1]\)). In these early models a crucial construct has been the social influence matrix \(W\) that encodes the relative influence an individual \(j\) exerts on any other individual \(i\). In the dynamical process, the new opinion of an agent is given as the weighted average of an agent’s own current opinion (weighted by \(w_{ii}\)) and those of its neighbors (\(o_i \leftarrow \sum_j w_{ij} o_j\)). This is referred to as positive or assimilative social influence. Formally, this repeated averaging process can be written as a linear system \(o^{t+1} = W o^t = W^t o^1\) where \(o\) is the evolving \(N\)-dimensional vector with the opinions of all agents (French 1956). Such systems converge to a consensual final state (i.e., \(o_i = o_j \ \forall i,j\)) whenever the matrix of interpersonal influences \(W\) consists of a single connected component (DeGroot 1974).
Bounded confidence models (Deffuant et al. 2000; Hegselmann & Krause 2002) have been invented against this background to show how multiple opinion groups can persist under social influence dynamics. The idea is simple: two agents with opinions \(o_i\) and \(o_j\) influence one another only when they are already close enough in opinion space, that is, when the distance between \(o_i\) and \(o_j\) is below a certain confidence threshold. (Hegselmann & Krause 2002) describe very well that this extension to social influence network models formally leads to a non-linear system in which the influence matrix \(W\) changes through time. Since then, most work within the continuous opinion paradigm is based on computer simulation (see Friedkin 2015; Friedkin et al. 2016 for notable exceptions). If the threshold is low enough, the influence network features isolated groups of individuals within a certain range of opinions that converge to a group consensus independently from other groups. The number of groups depends on the confidence threshold in non-trivial ways3, but the model can lead to complete fragmentation into many opinion groups, to the persistence of two opposing opinion groups, or to consensus.
Like in binary opinion dynamics many different social and psychological assumptions have been integrated into the models in subsequent work. First, more realistic forms of relative homophily take into account that the probability of interaction depends on how many similar agents are available (Baumann et al. 2020; Carley 1991; Mäs & Flache 2013). Second, negative social influence has been proposed as an additional mechanism by which agents differentiate from other agents that are already different when they interact (Baldassarri & Bearman 2007; Flache & Macy 2011; Jager & Amblard 2005). The repulsive forces implemented by negative influence may somewhat trivially lead to extreme bi-polarization, but the empirical relevance of the mechanism is disputed (Takács et al. 2016). Another mechanism that leads to extreme bi-polarization is opinion reinforcement by which pairs of agents strengthen their conviction if they are on the same side of the attitude scale (Banisch & Olbrich 2019; Martins 2008). There are different processes that may lead to such an opinion reinforcement including argument communication under homophily (Mäs et al. 2013; Mäs & Flache 2013) (cf. Flache et al. 2017 par. 2.67), social feedback (Banisch & Olbrich 2019; Gaisbauer et al. 2020) and contagion (Lorenz et al. 2021). In terms of micro-level justification, opinion reinforcement can therefore draw on a rich body of psychological research on group polarization (Myers & Lamm 1976; Sunstein 2002) as well as on neuroscientific experiments on social reward processing (cf. Banisch et al. 2022). However, a recent experiment aimed at a direct measurement of opinion reinforcement through social approval has been inconclusive (Sarközi et al. 2022). Finally, also biased processing – the central mechanism in this paper – has been introduced in continuous state models (Dandekar et al. 2013; Deffuant & Huet 2007; Lorenz et al. 2021). The existence of cognitive biases in the processing of information has been proven to be a robust mechanism across various empirical experiments on different issues (e.g., Taber & Lodge 2006; Corner et al. 2012; Druckman & Bolsen 2011; Taber et al. 2009; Teel et al. 2006) including the one used in this paper (Shamon et al. 2019).
It is noteworthy that models usually implement combinations of these core mechanisms and study how the model outcomes are affected by varying the mixture. The biased assimilation model by Dandekar et al. (2013), for instance, combines biased processing with homophily to generate bi-polarization. Other researchers have started to systematically address the micro-macro problems involved when drawing societal level conclusions from competing micro assumptions (Keijzer & Mäs 2022; Mäs & Bischofberger 2015). This research has shown, for instance, that filter bubbles and increasing personalization (modeled as homophily) lead to completely different conclusions depending on whether they are combined with argument-based opinion exchange or negative influence. Several authors have started to increase the psychological realism of models by more explicitly drawing on established psychological theories within a continuous opinion setting (Banisch & Olbrich 2019; Duggins 2017; Lorenz et al. 2021). The model by Duggins (2017), for instance, integrates positive and negative social influence, conformity, distinction and commitment to previous beliefs as well as social networks to show that increased micro-level complexity is needed to generate realistic opinion distributions characterized by strong diversity. Lorenz et al. (2021) advance towards model synthesis – the second main challenge identified in the review by Flache et al. (2017) – by drawing on a generalized attitude change function derived as an attempt to synthesize different psychological theories of attitude change (Hunter et al. 2014).
Argument communication theory (ACT)
ACT has been introduced in Mäs et al. (2013) and Mäs & Flache (2013) as a possible explanation for the emergence of opinion bi-polarization that does not draw on negative influence. The models combine aspects from binary opinion dynamics and continuous models by relying on a two-layered concept of opinion. That is, an agents’ opinions (\(o_i\)) is assumed to be determined by an underlying string of binary arguments (\(\vec{a}_i\)) that may support a positive or a negative evaluation of an attitude object. Processes of information exchange in social interaction take place at the lower level of arguments by adopting arguments from peers. Opinions follow from that and change whenever a new argument is obtained. But opinions also become functional in the repeated exchange process as they structure lower-level information uptake by guiding partner selection (homophily) (Mäs & Flache 2013) or opinion revision (biased processing) (Banisch & Shamon 2023).
Original model by Mäs & Flache (2013)
ACT has been inspired by psychological work on group polarization in the 1970ies and 80ies (Isenberg 1986; Myers & Lamm 1976; Vinokur & Burnstein 1978) that observed that discussions may reinforce initial opinions of a group (see also Sunstein 2002). At that time, negative influence had become a frequent modeling choice in order to model a process of increasing divergence and the emergence of two increasingly opposing opinion camps at the extremes of an opinion scale. The model by Mäs & Flache (2013) showed that repeated processes of argument exchange in which agents locally assimilate may lead to polarization dynamics under homophily. This is possible through a more complex multi-layered conception of opinions as attitudes that rely on an underlying set of pro and con arguments. The argument exchange mechanism acts on the underlying level of arguments. But homophily acts at the upper layer of opinions defined as the number of pro versus con arguments. Under homophily, opinions act as social filters so that agents that already hold many pro (con) arguments will encounter other agents holding other pro arguments that further support a positive (negative) stance.
In their model, the number of arguments is relatively large, 30 pro and 30 con arguments. But agents can only "remember" a subset of 10 salient arguments which is actualized in interaction. Arguments are ranked according to their recency. If an agent receives a new argument from an interaction partner, that argument is activated (\(a_{ik}=1\)) and ranked first in recency. In turn, another argument of least recency is dropped (\(a_{ik} = 0\)). In this way, the model accounts for limited memory capacities and a higher accessibility of recent information. Opinions are then defined by the number of pro and con arguments that are currently salient.
In Mäs & Flache (2013) and subsequent papers (Keijzer & Mäs 2022; Mäs et al. 2013; Mäs & Bischofberger 2015) homophily is implemented as biased partner selection following earlier work by Carley (1991). It is a relative conception of homophily. First, an agent \(i\) is chosen and then the interaction partner \(j\) is drawn from all other agents with a probability that depends in a non-linear way on the opinion similarity between \(i\) and \(j\). The degree of favoring the most similar others is governed by a free parameter \(h\) and the system polarizes if \(h\) becomes large. As opposed to bounded confidence where the interaction probability of two agents \(i\) and \(j\) depends only on the opinion of the two involved agents, in these works the interaction probabilities depend on the opinions of all agents in the population. While this is plausible compared to the hard threshold of bounded confidence, it implicitly assumes that the opinions of all agents are known at each step. Moreover, the population-relative interaction probabilities have to be recomputed at each step which is very costly from the computational point of view.
Model simplifications
Against this background, it has been shown in Banisch & Olbrich (2021) that the qualitative behavior of the Mäs-Flache model is preserved under more simple choices regarding the number of arguments, the exchange mechanism and homophily. In their model only 3 pro and 3 con arguments are used. Agents can either believe that an argument is true (\(a_{ik} = 1\)) or false (\(a_{ik} = 0\)). Opinions are then defined as in Mäs & Flache (2013) as the number of pro versus con arguments that an agent beliefs to be true. In the interaction process, two agents, a sender and a receiver, are chosen at random and the receiver copies a randomly chosen argument from the sender. Without homophily this corresponds to a multi-dimensional voter model (see above) where agents converge to a common state independently along each dimension. While all agents converge to a common argument string (and hence opinion) without homophily, the system will polarize under strong opinion homophily. This basic polarization dynamics is preserved if the relative homophily of the original model is replaced with bounded confidence.
The introduction of ACT of bi-polarization in Mäs & Flache (2013), Mäs et al. (2013) has also inspired new socio-physics models of opinion dynamics such as the M model by La Rocca et al. (2014). In this model, the layer of arguments is not explicitly modeled. In our reading of the theory it is not an ACT model. But the two mechanism of persuasion and compromise that the model uses to define opinion change mimic the opinion changes that would be observed under argument exchange. Enabling the application of statistical physics, this approach is very useful for a better and more rigorous understanding of the statistical properties and phase transitions of ACT models that remain with a more complex structure of underlying arguments.
Interacting arguments
One great benefit of increasing complexity at the level of individual opinion is the possibility to more explicitly represent issues of real debate as well as involved argumentation processes. In Taillandier et al. (2021) a model has been presented in which opinions on vegetarian diet are represented by an underlying argument network. The model formalizes Dung (1995)’s argumentation graphs in which arguments may attack other arguments. In terms of interaction and homophily the paper follows Mäs & Flache (2013). But using the theoretical concepts of argumentation graphs it implements argument choice by the sender and acceptance by the receiver based on consistency computations on the argument attack network. This can be seen as a form of biased processing. The model studied in Taillandier et al. (2021) is empirically-informed by real arguments and attack relations, drawing on a set of 145 arguments on vegetarian diet. Closely following the computational design of Mäs & Flache (2013), the study shows that interacting arguments have an impact on the consensus-polarization transition caused by increasing homophily.
Multiple interrelated issues
Another attempt to more realistically capture the complexity of real debates has been made in Banisch & Olbrich (2021). There are no links between arguments, but a bipartite network that links arguments to multiple issues of opinion. These cognitive-affective networks entail evaluative associations in a way closely related to psychological theories of attitude structure and associated measurements (Ajzen 2001; Fishbein 1963; Fishbein & Raven 1962). In this setting, arguments may be relevant to more than one issue such as trading one versus the other. Based on a simplified argument exchange process (see above), the model accounts for polarization in terms of ideological alignment or opinion sorting on various issues. This kind of opinion alignment is a robust empirical fact, for instance, political dimensions such as "left" versus "right" are only meaningful only because of specific patterns of attitudinal correlations (Laver 2014; Laver & Budge 1992; Olbrich & Banisch 2021). Also for this model attempts to derive realistic argument-opinion relations from textual data have been made (Willaert et al. 2022). In this paper, we focus on a single-issue model with the aim to link micro-level assumptions about argument uptake to data from a survey experiment.
Incorporation of biased processing
In empirical research, there are various randomized experiments that have investigated the influence of the exchange of arguments on opinions and whose design is very close to the conceptualization of the ACT (e.g., Taber & Lodge 2006; Corner et al. 2012; Druckman & Bolsen 2011; Shamon et al. 2019; Taber et al. 2009; Teel et al. 2006). These empirical experiments have in common that participants are first asked about their opinion towards a certain issue under investigation. Then, they are sequentially exposed to arguments in favor of or against the issue and, finally, asked one more time on their opinion on the investigated issue. In this way, the empirical experiments measure opinion changes among participants as a result of exposure to pro- and con-arguments. In contrast to the ACT, however, the opinion change is not measured again after each argument exposure, but at the end of the confrontation with all arguments. Even more important, these experiments find empirical evidence for a cognitive mechanism, called biased processing, that is not addressed by ACT-assumption. Biased processing refers to a person’s tendency to inflate the quality of arguments that are compatible with his or her existing opinion on an issue whereas the quality of those arguments that speak against a person’s prevailing opinion are downgraded. This empirical robust cognitive mechanism challenges ACT’s assumption of argument adaption at a constant rate independent of the current opinion.
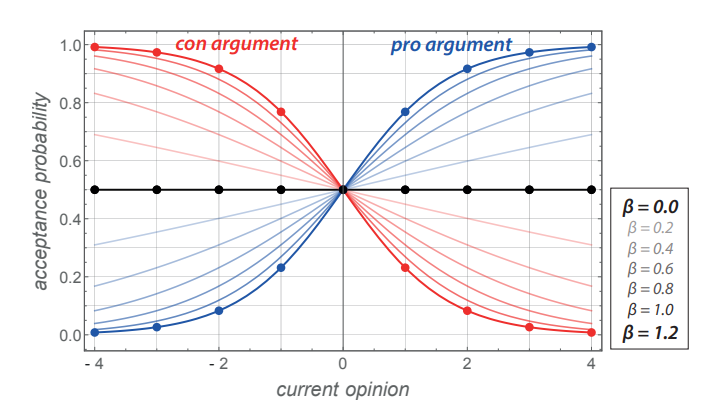
Biased processing has been incorporated into ACT in Banisch & Shamon (2023). The model operates with 4 pro and 4 con arguments which are copied in interaction. However, the probability to accept a new argument depends in a non-linear way on the current opinion of the receiver. This is modeled by a soft-max (or Fermi) function that contains a parameter \(\beta\) which accounts for the strength of biased processing. If \(\beta\) is zero, arguments are accepted with equal probability independent of the opinion. If \(\beta\) is large arguments that speak against the current opinion are rejected whereas arguments that further support the current stance are accepted with a probability close to one. In Banisch & Shamon (2023) \(\beta\) has been estimated from experimental data (see below) and moderate values (\(\beta \approx 0.5\)) have been found. The computational analysis of the model has shown that biased processing has a strong effect on the behavior of the argument model. First, as soon as \(\beta > 0\), the stability of moderate consensus is lost and group converge to one or the other extreme on the opinion scale. Second, strong biased processing (\(\beta > 1\)) may lead to a meta-stable state of bi-polarization even in the absence of homophily. In this paper, we study this version of the argument model with noise and provide a more detailed model description in the next section.
Argument Model with Biased Processing and Noise
In this paper, we extend the model of Banisch & Shamon (2023) by introducing an external source of information that supplies the system with random arguments. This corresponds to a form of unbiased noise by which individuals are exposed to a random binary signal instead of receiving an argument from a neighbor. Our model hence comes with an additional parameter \(\rho\) which governs the level of noise in the system. In this section, we describe the model, show a series of paradigmatic model realizations, and describe what we treat as a model outcome for comparison to data. We also provide details on the computational strategy and the implementation.
Model description
We model a system of \(N\) agents that exchange arguments about a single opinion item in repeated interaction. If not stated otherwise we will use \(N = 500\) agents. Here we describe the iterative process following the order in which the different steps are performed. We start with the opinion structure.
Opinion structure. Models within the framework of ACT rely on a two-layered conception of opinions. They assume that the opinion \(o_i\) of an agent \(i\) is determined by an underlying layer of pro and con arguments that the agents holds. In our model, each agent is endowed with a string of \(K\) binary variables which we call arguments or beliefs. We denote the argument string of a single agent \(i\) as \(\vec{a}_{i}\) (with \(\vec{a}_{i} = (a_{i1}, \ldots, a_{iK}) \in \{0,1\}^K\)). These beliefs are updated during the interaction process and signal whether agent \(i\) currently beliefs an argument \(k\) to be true (\(a_{ik} = 1\)) or false (\(a_{ik}=0\)). Homogeneously for the entire population, we assume that the first \(K/2\) arguments are pro arguments and the latter half (\(k > K/2\)) are counter arguments. See Figure 1. For further convenience we introduce a \(K\)-dimensional vector of evaluations \(e_k\) where the first \(K/2\) elements are \(+1\) (pro arguments) and the second \(K/2\) arguments are \(-1\) (con arguments) (see Banisch & Olbrich 2021 for a psychological motivation). An agent’s opinion, defined as the number of pro versus con arguments (\(n_+\) and \(n_-\)), can then be defined as
| \[o = \sum_{k=1}^{K} a_k e_k = n_{+} - n_{-} \] | \[(1)\] |
Hence, if an agent believes a pro argument to be true (\(a_{ik} = 1, k \leq K/2\)), this will contribute an amount of \(+1\) to a positive opinion (\(o_i\)). Vice versa, an argument \(a_{ik} = 1, k > K/2\) contributes an amount of \(-1\) to a negative stance. In this paper, we set the number of arguments to \(K = 8\) to align the opinions in the computational model with the 9-point answer scale that was used in the survey experiment. This avoids distortions that may arise when scales of different ranges are being applied in both the empirical measurement and the ABM (cf. e.g. Carpentras & Quayle 2023).
Initial conditions. At start (\(t=0\)), the system is initialized by assigning random arguments to all the agents. That is, for each single argument \(a_{ik}\) there is a fifty-to-fifty chance that \(a_{ik} = 0\) or \(a_{ik} = 1\). Consequently, the initial distribution of opinions follows a binomial distribution as shown on the left-hand side in Figure 4. Throughout the paper, we focus on the stationary dynamics of the model reducing the impact of different initial conditions.
Partner selection and update schedule. Following Banisch & Shamon (2023) we use the following schedule to update the system. At each time step, we draw \(N/2\) random agent pairs (without replacement). All agent pairs have an equal probability to be chosen and their is no interaction network or homophily (random mixing). The first agent \(s\) is considered as a sender and the second agent as a receiver (denoted respectively as \(r\)). This means that in a single simulation step (\(t \rightarrow t+1\)) each agent is chosen either as a sender or a receiver. In other words, in our model implementation one time step corresponds to \(N/2\) update events.
Argument exposure: social influence versus noise. In the original model by Banisch & Shamon (2023), for each pair, the receiver \(r\) is exposed to an argument randomly drawn from the argument string \(\vec{a}_s\) of the sender. That is, the articulated argument \(a'_k = a_{sk}\) with \(k\) drawn uniformly from \((1,\ldots,K)\). We refer to this as social influence condition. Here, we extend this model by assuming that \(r\) receives an argument from an external source with a certain probability \(\rho\). This parameter allows to control for the impact of social influence (\(1-\rho\)) versus noise (\(\rho\)). Hence, for each pair, we first decide whether \(r\) receives an argument from the sender \(s\) or a random argument from an external source. In the social influence condition (with probability \(1-\rho\)), we randomly choose an argument from \(\vec{a}_s\). In the noise condition (\(\rho\)), we also randomly select a \(k\) uniformly from \((1,\ldots,K)\), but assign a random binary value to \(a'_k\). The receiver \(r\) receives \(a'_k\) and the decision to adopt the argument is equal in the two influence conditions, and subject to biased processing in both cases.
Argument adoption. Under biased processing the probability that \(r\) accepts the new argument \(a'_k\) depends on \(r\)’s current opinion \(o_r\) such that information that confirms the current opinion is accepted at a higher rate. The strength of this confirmation bias – sometimes referred to as "my-side" bias (Baccini et al. 2023) – is governed by a second parameter \(\beta\).
We model this tendency to favor coherence over incoherence in the argument acceptance probabilities using a softmax or Fermi function. That is, an argument \(a'_k\) is accepted with
| \[p_{\beta}(o_r,a'_k) = \frac{1}{1 + e^{-\beta o_r (2 a'_k -1)e_k}}, \] | \[(2)\] |
Model summary. Figure 3 summarizes the argument communication model used in this paper. At each step, we randomly draw \(N/2\) agent pairs and assign them the roles of sender and receiver \((s,r)\). For each pair we perform the following steps:
- random choice of an argument index \(k\) in \((1,\ldots,K)\)
- social influence condition: with probability \(1-\rho\) take \(a'_k = a_{sk}\) from the sender \(s\)
- external influence condition: with probability \(\rho\) take \(a'_k \in \{0,1\}\) with equal probability
- receiver \(r\) accepts the argument \(a_{rk} = a'_k\) with probability \(p_{\beta}(o_r,a'_k)\)
- update of \(r\)’s opinion if the argument has change
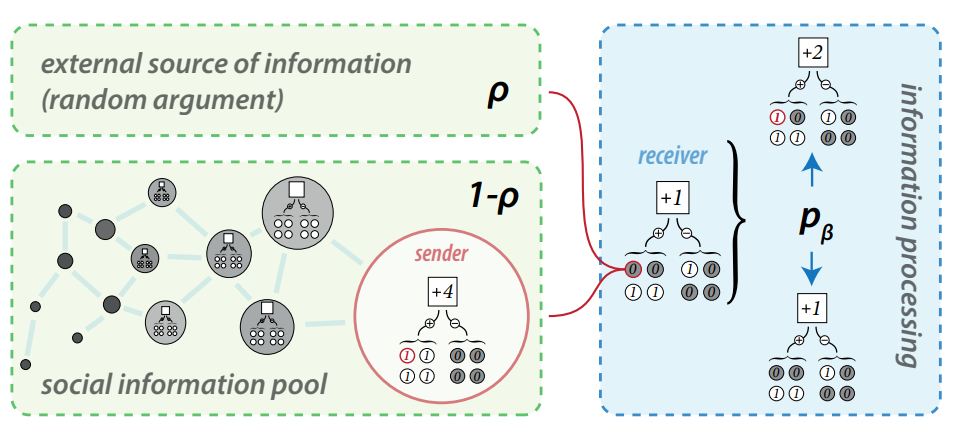
Simplifying assumptions. Notice that in this paper we do not incorporate realistic social networks but rely on the complete graph as an underlying topology. We match agent pairs completely at random so that any pair is equally likely (random mixing). As opposed to e.g., Mäs & Flache (2013), our model does not include biased partner selection (Flache et al. 2017) in form of homophily. There is also no particular mechanism behind choosing the argument \(k\) (point 1), so to incorporate motivated reasoning. The focus in this paper is on a self-confirmatory bias of information processing, and the impact of an unbiased external signal modeled as a form of noise that supplies random arguments to the system. We differentiate a social influence from an external influence condition and the parameter \(\rho\) decides on the respective probabilities. That is, \(\rho\) determines the relative importance of peer influence versus external influence which we may consider as a very simple model for an unbiased media channel. In this regard, we do also not assume biases in information selection or attention which could be integrated by assuming that an agent more likely chooses confirmatory arguments (Deffuant et al. 2023). Notice finally that agents do not remember arguments held in the past and that \(r\)’s opinion does not change (point 4) if the argument \(a'_k\) confirms an argument \(r\) already holds. In this case, the argument string does not change and \(o_r\) is not affected.
Paradigmatic simulation runs
The model exhibits a rich dynamical behavior which we approach by three exemplary simulation runs. They are shown in Figure 4. We use \(N = 500\) and \(\rho = 1/2\) meaning that receivers get a random argument in 50 percent of the cases. The first 10000 time steps of the simulation are shown. From top to the bottom, we increase \(\beta\) from \(0.3\) to \(1.2\). In all three case, the initial opinion distribution is shown on the left. In the center, the temporal evolution of the opinion distribution under the model is shown along with the respective mean opinion (blue) and the standard deviation (orange) as a measure of opinion divergence. Finally, at the right-hand side of the plots the opinion distribution averaged over the last 7500 steps is shown. We will treat this distribution as the model outcome (see below).
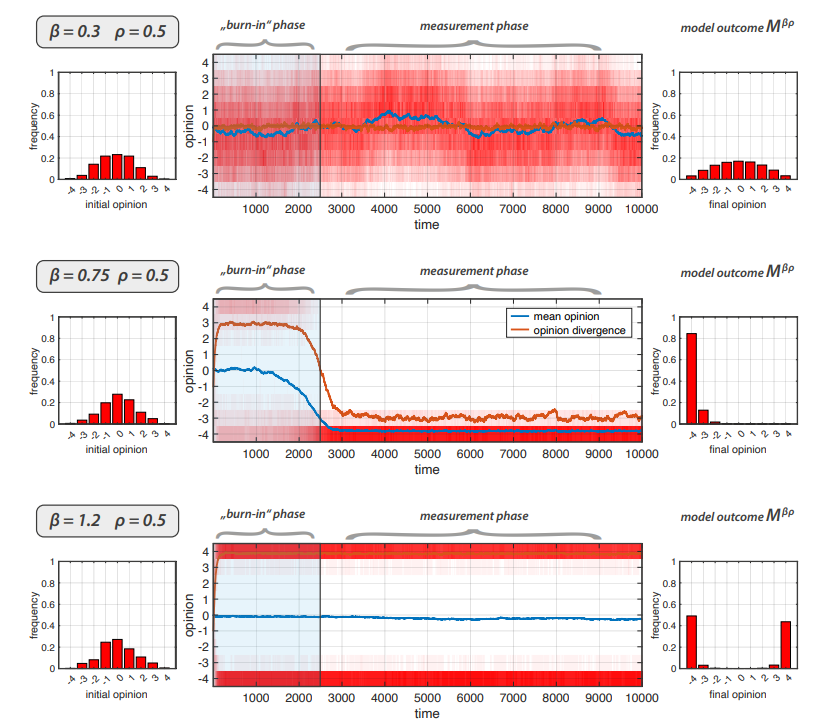
If \(\beta\) is low (top) we observe that the opinion distribution remains centered at \(o = 0\) and fluctuates slightly around it as time proceeds. In this case the dynamical behavior is driven by noise as the arguments do not completely settle. As opposed to the model without bias and noise (\(\beta = 0\) and \(\rho = 0\)) in which all agent approach the same opinion and converge to one and the same argument string, the distribution remains rather broad and dynamic. For an increased \(\beta = 0.75\) (middle) we observe a quick transition into an initial period of bi-polarization that persists for around 2000 steps. In the period around \(2000 < t < 3000\) this state resolves in a collective choice shift towards a negative opinion ("extreme consensus"). In this final situation, all agents mainly share all con arguments (\(a_{ik} = 1\) for \(k > K/2\)) and do not belief pro arguments (\(a_{ik} = 0\) for \(k \leq K/2\)). Notice that with symmetric initial conditions the shift takes place to either side with equal probability. If \(\beta\) grows large, this meta-stable bi-polarized regime persists throughout the entire 10000 time steps considered in Figure 4. In such a bi-polarized state, approximately one half of the agents will share almost all pro arguments while dismissing con arguments, and vice versa for the other half of the population. This bi-polarized opinion regime may last very long, especially when \(\beta\) increases further, but eventually also this realization will collapse into a one-sided consensual profile (cf. Banisch & Shamon 2023).
What do we treat as a model outcome?
The main aim of this paper is to provide a global picture on the opinion profiles that emerge from the model in order to identify parameters \(\beta\) and \(\rho\) for which empirical opinion data is reproduced. We treat the model as a data generating procedure and have to identify the typical opinion distribution generated by the model given the amount of biased processing \(\beta\) and the relative importance of external unbiased news \(\rho\). In this, we have to be clear about what precisely we consider as the outcome of a model. Given the complex temporal patterns briefly discussed in the previous section, this is a non-trivial task that may involve decisions that are to some extent arbitrary.
For the subsequent analyses in this paper we will closely follow previous work on systematic model analysis by Lorenz et al. (2021). That is, we analyze the model with \(N = 500\) agents and run simulations for 10000 steps. The first 2500 steps are neglected as a "burn-in phase" needed to reach a stationary profile. The remaining 7500 steps are considered as a measurement phase. The distribution of opinions over this period define the model outcome \(\mathcal{M}^{\beta \rho}\) for a single simulation.4 The burn-in phase, the measurement phase and the resulting outcome distribution are shown in Figure 4.
Systematic simulations
We perform a systematic computational analysis with respect to the strength of biased processing \(\beta = 0,0.02,\) \(0.04, \ldots , 1.4\) (71 sample points) and the relative influence of the external signal \(\rho = 0,0.02,0.04, \ldots , 1\) (51 sample points). For each of these \(71 \times 51 = 3621\) sample points \((\beta,\rho)\), we run 25 simulations and store these 25 outcome distributions \(\mathcal{M}^{\beta \rho}\) for subsequent analyses. By considering multiple runs per parameter constellation, we depart from the setting of Lorenz et al. (2021) who base their statistics on a single run.
Model and code availability
Supplementary material for the reproduction of all analyses in this article on the Open Science Framework under https://osf.io/5tz6g/. For interactive exploration (e.g., with the calibrated parameters), we provide an online version at http://universecity.de/demos/ModelExplorer.html, cited as Banisch (2022) throughout the paper.
Characterization and Categorization of Emergent Opinion Profiles
Characterization of emergent opinion distributions
In the original model of Banisch & Shamon (2023) without noise, three different outcomes are possible. First, a moderate consensus is observed if \(\beta = 0\). Second, the population converges to an extreme consensus for moderate biased processing. Third, a meta-stable state of extreme bi-polarization persists throughout a long transient period if \(\beta\) is large, but finally collapses into a one-sided consensus. With the introduction of noise, the argument model features persistent or "strong" diversity (Duggins 2017) in the sense of smooth distributions of opinions that may cover the entire range of opinions from \(-4\) to \(+4\). However, as opposed to, for instance, Duggins (2017) and Lorenz et al. (2021), our model does not lead to outcome distributions with multiple peaks except for extreme bi-polarization. One reason is that we define the model outcome \(M^{\beta \rho}\) as the average over a long measurement period and not as the distribution at a certain point in time. That is, the possible outcomes of the model are (i) a random distribution centered at the neutral opinion, (ii) a distribution strongly inclined towards one side of the opinion scale, and (iii) a smoothly bi-polar distribution that persists over the measurement period.
Consequently, we can characterize the distributions \(\mathcal{M}\) that emerge from the model by looking at the extent to which they are shifted toward one side and the amount of diversity or polarization. The latter is captured by the standard deviation of the distribution and allows to distinguish consensus profiles from diversified or polarized profiles. The sidedness of the distribution is captured by the absolute value of its mean which allows to distinguish between an extreme consensus on the one hand and bi-polarized and moderate consensus profiles on the other hand. In Figure 5, the absolute mean value and standard deviation of the outcome distribution are shown for all parameter combinations \((\beta,\rho)\) in the considered ranges \((\beta \in [0,1.4],\rho \in [0,1])\).
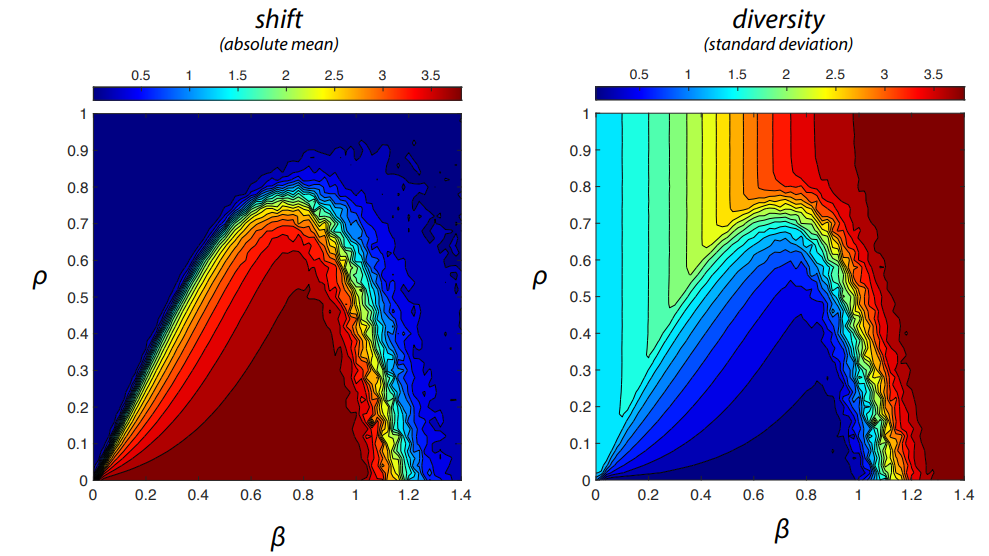
At the global scale, we observe a shift from a moderately diversified neutral distribution (close to normal) to a bi-polarized opinion distribution as \(\beta\) increases. If the influence of the unbiased media channel is large (\(\rho > 0.7\)), there is a gradual increase of diversity while the shift remains close to zero. This indicates a soft transition from a normal, to a uniform to a more and more polarized distribution. For values below (\(\rho < 0.7\)) we observe another intermediate opinion regime in which an one-sided consensus emerges. This regime is characterized by a large shift and low diversity. As the impact of social argument exchange increases (diminishing \(\rho\)), this extreme consensus becomes a prevalent outcome over a wide range of biased processing strength \(\beta\). Note that in the limiting case \(\rho = 0\) (only argument exchange) we recover the transition studied in Banisch & Shamon (2023).
Within-sample variability of shift and diversity
Figure 5 shows the mean shift and diversity over 25 simulation runs with the same parameter combination \((\beta,\rho)\). We would typically expect that in parameter regions of transition from one qualitative model regime to another, there is higher variation in the model outcomes. To control for this effect, Figure 6 shows the in-sample variability measured as the standard deviation of both observables over the 25 runs.
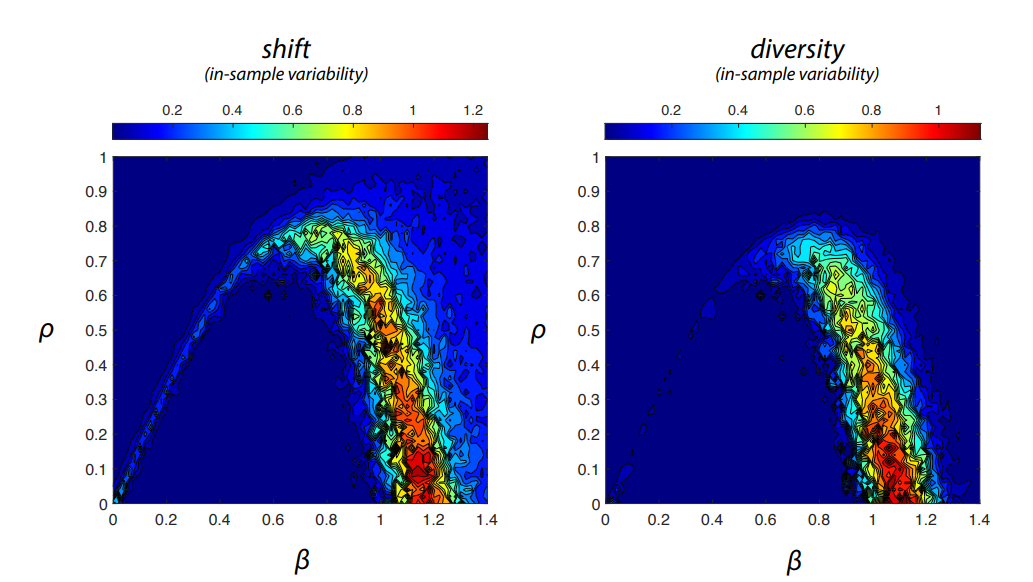
The largest variability in both measures is observed in the transition region between one-sided consensus and bi-polarization. This can be associated to the fact that bi-polarization is a meta-stable, transient phenomena in the model which becomes more persistent with increasing \(\beta\) (Banisch & Shamon 2023). In the band of high variability between \(0.8 < \beta < 1.2\) and \(\rho < 0.8\), a bi-polarized opinion profile may persist for many iterations, others may more quickly fall into the stable state of one-sided consensus. Then, while zero mean and high variance is assessed for the former, the latter is characterized by a large mean and low variance.
Interestingly, the transition from a neutral opinion profile (normal or uniform distribution) to a strongly one-sided one is not associated with very large fluctuations. This indicates a rather sharp transition from moderate opinion profiles to one-sided, extreme profiles that reveal a clear collective preference for or against the issue.5
Automatic categorization of different opinion regimes
In order to classify the model outcomes into qualitatively different opinion regimes, Lorenz et al. (2021) propose an automated procedure based on these distributional measures including the mean, the variance but also more complex measures for the peakedness of a distribution. In this paper we take a different approach and compare the outcome distributions to a series of stylized distributions using the Jensen-Shannon divergence (JS divergence). The same approach has been used by Duggins (2017) to show that the outcomes of his ABM come very close to opinion data on American politics.
Let’s denote a target opinion distribution by \(\mathcal{D}\) and, as before, a model distribution with parameters \(\beta\) and \(\rho\) by \(\mathcal{M^{\beta \rho}}\). The JS divergence generalizes the Kullback-Leibler (KL) divergence and defines a distance between the two distributions by:
| \[d_{JS}(\mathcal{M},\mathcal{D}) = \frac{1}{2} d_{KL}(\mathcal{M},M) + \frac{1}{2} d_{KL}(\mathcal{D},M)\] | \[(3)\] |
| \[d_{KL}(\mathcal{M},\mathcal{D}) = \sum_{o = -4}^{+4} \mathcal{M}(o) \log \frac{\mathcal{M}(o)}{\mathcal{D}(o)}\] | \[(4)\] |
For this purpose, we compute the JS divergence between a set of stylized distributions and the model outcomes \(\mathcal{M}^{\beta \rho}\) for different \(\beta\) and \(\rho\). The six idealized distributions (\(\mathcal{D}^{i}\)) used for comparison are shown on the left of Figure 7.6 For each parameter constellation \((\beta,\rho)\) we compute \(d_{JS}(\mathcal{M}^{\beta \rho},\mathcal{D}^{i})\) between the model outcome and these six distributions. We make use of the fact that the JS divergence is a proper distance and defines a metric in the space of opinion distributions (as opposed to the KL divergence on which it is based). This allows to identify which of these idealized distributions (indexed by \(i\)) is closest to the model outcome given some \(\beta\) and \(\rho\). Notice that later on, we will use the same procedure to compare the model outcomes to the empirical survey data.
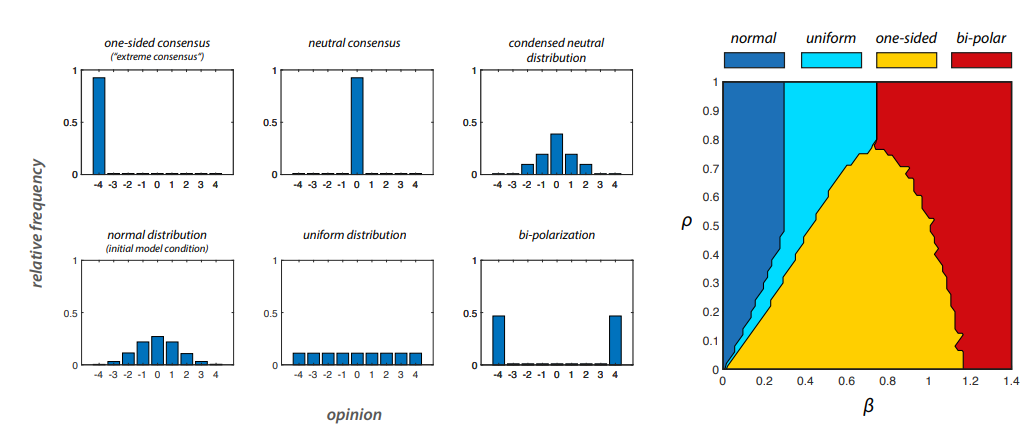
Over the entire parameter range \((\beta \in [0,1.4],\rho \in [0,1])\) only four of the six toy distributions are identified as "closest match" by this procedure. As already seen in Figure 5, a large \(\rho\) leads from an approximately normal distribution centered at the neutral opinion (dark blue) to one that is close to the uniform distribution (light blue) as \(\beta\) increases. For \(\beta > 0.7\) the distribution is already closer to the idealized bi-polarized distribution (red). When \(\rho\) is not too large \(\rho < 0.7\), an entire range of model outcomes is clearly classified as one-sided consensus (yellow), compare Figure 5. The shape of this yellow region reveals a surprising trend. When noise is introduced and its impact increases, opinion bi-polarization becomes more likely at lower values of \(\beta\). This means that less biased processing can lead to polarization in the presence of unbiased external information. When biased processing is large, complete information diversity "enforced" by a constant inflow of an equal share of pro and con arguments does not prevent and may even foster bi-polarization.
Notice that the moderate consensus and the more condensed neutral distribution are nowhere closest to the model outcome. The reason is that in the parameter space considered here moderate consensus is rare.7 In fact, it only occurs at \(\beta = 0\) and \(\rho = 0\). As soon as \(\beta\) becomes non-zero, opinions evolve into a one-sided consensus (Banisch & Shamon 2023). When \(\rho > 0\), opinions at a particular time may be condensed (only if \(\rho\) is very small). But they drift through the opinion space as time proceeds, and taking the average distribution over a period of time will be close to the normal distribution. This points to a deficit of our definition of model outcomes.
Notice also that we do not differentiate whether one-sided consensus occurs at the negative or positive extreme. In the model both cases occur with equal probability. To deal with this fact, we compare the idealized distributions with the actual model outcome \(\mathcal{M}^{\beta \rho}\) as well as with the inverse distribution mirrored at the neutral point at \(o = 0\). The minimal JS divergence among these two cases is selected for the classification.
Validation Approach
Terminology
The purpose of validation is to increase the trustworthiness of a theory or a model. Recently, it has been pointed out that validation is an ambiguous concept in the context of ABM and opinion dynamics in particular, because it may relate to very different activities (Chattoe-Brown 2022). On the other hand, key terminology for establishing the credibility in simulation models more generally has been developed more than 40 years ago by Schlesinger (1979) and the "Society for Computer Simulation". These concepts, further developed by e.g., Sargent (2010) and Sargent & Balci (2017), are now established in the computer science literature on verification and validation (V&V), and they may serve as an orientation for different validation activities in the context of ABMs (David 2009).
According to the V&V literature, different activities to assess model credibility are related to different phases of the model development cycle: from the real phenomena of interest, to a conceptual model of the problem, to a simulation model, the outcomes of which are again confronted with empirical reality (Sargent 2010). This view entails the idea that simulation models are iteratively refined to capture intended phenomena with higher accuracy. On that basis, we can distinguish the following activities:
- the objective of conceptual model qualification is to show that the conceptual model is a qualified representation of the reality of interest. This process mainly concerns the assumptions at the conceptual level as it has to show that the theories and assumptions underlying the conceptual model are correct and that the model representation of the problem entity is "reasonable" for the intended purpose of the model (Sargent 2010 p. 168).
- computerized model verification is the process which makes sure that a computer model accurately represents the developer’s conceptual description. In the computational sciences this is also concerned with a mathematical study of the numeric algorithms involved into a simulation program, stability and sensitivity analyses and robustness tests. In the agent–based community, model to model comparison (M2M) (Axtell et al. 1996; Hales et al. 2003) and model replication (Edmonds & Hales 2003; Rouchier 2003; Wilensky & Rand 2007) is a widely accepted method for model verification.
- finally, model validation is the "substantiation that a computerized model within its domain of applicability possesses a satisfactory range of accuracy consistent with the intended application of the model" (Schlesinger 1979 p. 104). Model validation is done by carrying out different confirmation experiments to support the model by evidence, i.e., to confirm its assumptions on the model setup and its interaction rules. Therefore, the concept of empirical confirmation plays an important role and will be the guiding principle in this work.
The established terminology of "verification" and "validation" is controversial in the simulation literature and beyond. In their article on different philosophical positions on model validation, Kleindorfer et al. (1998) argue that "the term validation, that is, ‘to make valid’, is already loaded with a philosophical commitment that a satisfactory model be rendered absolutely ‘true’" (p. 1089). This "either/or" logic is not only problematic from a philosophical viewpoint, it is also hardly feasible in practice. As pointed out prominently by Oreskes and colleagues in the context of Earth climate modeling, models cannot be validated in this absolute sense, since "in practice, few (if any) models are entirely confirmed by observational data, and few are entirely refuted" (Oreskes et al. 1994 p. 643). However, with each confirming observation, the confidence in a model is increased, or, as Oreskes et al. (1994) put it:
"[t]he greater the number and diversity of confirming observations, the more probable it is that the conceptualization embodied in the model is not flawed" (p.643).
Here we report two very different empirical confirmation tests, one at the micro and another one at the macro level, and argue that the consistency between the two with respect to biased processing is a viable sign for its empirical relevance in argument-based opinion models.
Validation as consistent micro and macro calibration
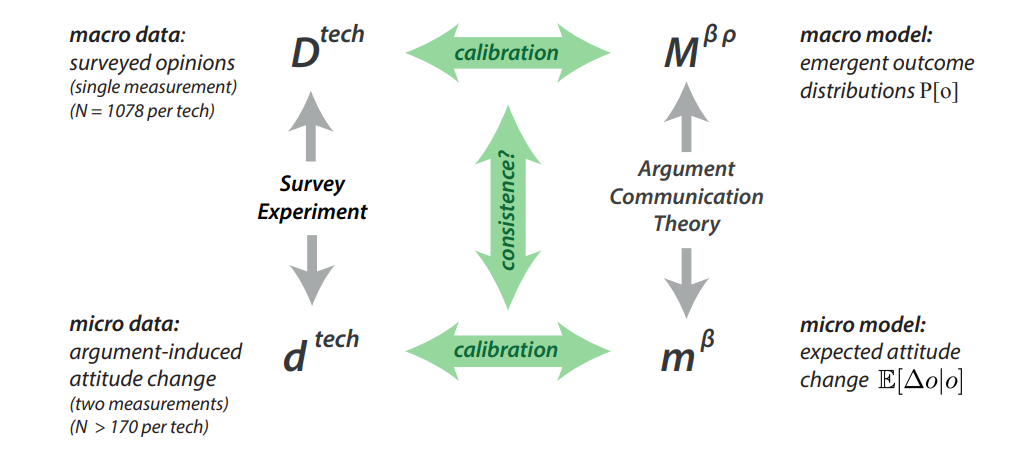
This paper deals with the empirical confirmation of argument communication theory. Confidence in the theory is increasing if the outcomes of computational models devised on the basis of the theory satisfactorily fit with observational data in the intended application domain. As pointed out in Troitzsch (2004), "[v]alidation of simulation models is thus the same (or at least analogous) to validation of theories" (p.5). The paper encompasses two different empirical tests based one two different models both derived on the basis of ACT:
- a microscopic model (\(m^{\beta}\)) of an artificial experiment to predict how individuals change their opinion when they receive arguments. This computational model of the experimental setting is conceptually aligned to the experimental part of the empirical study,
- a macroscopic ABM (\(M^{\beta,\rho}\)) of collective opinion formation to study to what extent and under which parameters the emergent opinion distributions fit those observed in the survey part of the empirical study.
With a micro model intended to capture individual attitude change by exposure to balanced arguments we show that a certain level of biased processing (\(\beta\)) explains short-term attitude changes with high accuracy. This has been the focus of the predecessor paper aiming at a refinement of ACT micro assumptions Banisch & Shamon (2023). It confirms that a considerable level of biased processing is involved and renders previous neutral assumption invalid. he macro model (ABM) is intended to realistically capture empirical opinion distributions observed in the survey part of the experiment. The main focus of this paper is to show that the ABM can reproduce these macro level data with high accuracy for similar values of \(\beta\).
Following the suggestion to invent names for the involved validation methods (Chattoe-Brown 2022), our approach could be named MiMaCo for "Micro and Macro Confirmation". However, the way in which the empirical confirmation tests are designed resembles more a parameter estimation approach. It is hence more closely related to empirical model calibration. Our claims about the empirical validity of ACT reside in the fact that the estimation results at the micro and the macro level are highly consistent. For this reason we could also refer to our approach as CoMMCal meaning "Consistent Micro and Macro Calibration". The overall validation pipeline is illustrated in Figure 8.
The survey experiment
In 2017, Shamon et al. (2019) performed a survey experiment to examine biased processing and argument-induced attitude change in the context of different electricity generating technologies. The main aim has been to address the "puzzle of polarization" in social psychology. Namely, previous experimental work (e.g., Lord et al. 1979; Corner et al. 2012; Druckman & Bolsen 2011; Taber et al. 2009; Taber & Lodge 2006; Teel et al. 2006) has lead to mixed evidence on whether exposure to balanced arguments leads to attitude moderation or polarization. Notice that in psychology attitude polarization refers to the individual-level tendency that subjects develop more extreme opinions after exposure to information. To address this puzzle in an experiment, an expert panel has developed a set of 84 arguments comprising 7 pro and 7 con arguments for six different electricity generating technologies (coal power stations, gas power stations, wind power stations (onshore), wind power stations (offshore), open-space photovoltaic, biomass power plants). Participants of the online survey were recruited from a voluntary-opt-in panel of a non-commercial German access panel operator.8 In the experiment, 1078 participants reported their opinion on all the six technologies (\(D^{tech}\) in Figure 8). Then they were randomly assigned to one of the technologies (N > 170) to receive the 14 balanced arguments tailored to that technology. Respondents were asked to rate, among other things, each argument’s persuasiveness as well as to state their perceived familiarity with each argument. The research design allowed to assess not only to what extent initial attitudes affect persuasiveness ratings of arguments but also to what extent respondents’ initial attitudes change after the exposure to the balanced set of 14 arguments.
The structure of the experiment is highly compatible with ACT and provides micro and macro data needed to conduct the CoMMCal validation procedure. The setting provides subgroup data on individual attitude change (\(d^{tech}\)) and macro opinion data on all topics from the complete set of participants (\(D^{tech}\)). At the subgroup level it provides two subsequent opinion measurements for at least 170 individuals for six different opinion items (technologies). Opinions have been measured before and after exposure to the 7 pro and 7 con arguments and the time in between these two measurements was very short. The purpose has been to identify the effect of a single exposure treatment on opinion revision.
Empirical confirmation at the micro and the macro level
Micro-level calibration
Out of the principles of ACT, Banisch & Shamon (2023) have developed a micro model directed at covering these short-term opinion changes. The main idea is to build an artificial version of the experiment which allows to predict how individual agents change their opinion when receiving an equal number of pro and con arguments. From the data, we obtain for each participant her previous opinion and the opinion change after exposure. In the micro model, agents initialized with a certain argument string (and hence opinion) are exposed to all arguments at once and we compute how many of the arguments are adopted according to the rules of ACT. Biased processing has been incorporated as a free parameter \(\beta\) that governs how much this adoption probability is biased by the initial opinion (Equation 2). The expected attitude change for any given initial opinion can be analytically computed.
This combination of experimental setup and artificial experiment allowed Banisch & Shamon (2023) to calibrate the modified version of ACT with respect to the biased processing parameter (\(\beta\)) by comparing participants’ observed attitude change in the empirical experiment with the model-based predictions on expected attitude change for their artificial twins, i.e., the agents. More precisely, Banisch & Shamon (2023) calculated the mean squared error (MSE) on the basis of the 1078 comparisons for different parameter values of \(\beta \in [0, 1.2]\). The resulting function was u-shaped and exhibited a global minimum for MSE at \(\beta \approx 0.5\) which lead the authors to the conclusion "that the argument adoption process refined with biased processing more appropriately captures argument-induced opinion changes" (Banisch & Shamon 2023 p. 9). Furthermore, they replicated this procedure for each of the six different issues (i.e., different electricity generating technologies) separately and found that, along each of the six issues, a non-zero parameter value of \(\beta\) improves the model predictions compared to models without processing bias.
These previous results are revisited in the final part of this section where we confront the micro- and macro-level estimation results.
Macro-level calibration
Empirical opinion distributions
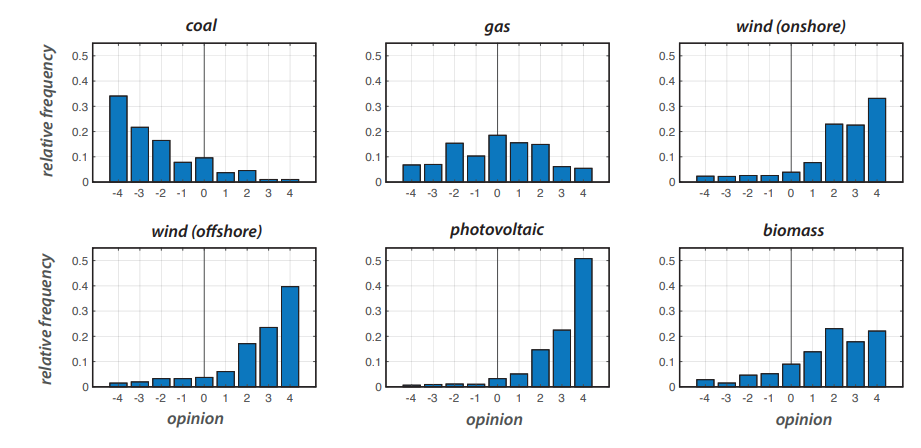
In the survey experiment of Shamon et al. (2019), \(N = 1078\) individuals reported their opinion on six different electricity-producing technologies. The six issues are coal power stations, gas power stations, wind power stations (onshore), wind power stations (offshore), open-space photovoltaic, and biomass power plants. The survey operated with a 9-point attitude scale such that an opinion of -4 indicates a very negative opinion and +4 a very positive one. In Figure 9 the respective opinion distributions are shown. These distributions will be the target of our analysis and we will assess how well the model fits this data under different parameter combinations of \(\beta\) and \(\rho\).
In our sample9, there is a clear negative opinion tendency on coal power plants whereas wind power plants, open-space photovoltaic and biomass power plants are positively evaluated by the participants. The distribution on gas power is neutral but relatively broad. Given our previous analysis of the model behavior this already indicates that the model may fit these data (except gas) well with parameters that lead to a one-sided consensus (Figure 7).
Comparing model outcomes to survey data
For each of the six technologies, we identify the regions in the parameter space \((\beta,\rho)\) of the model where the emergent opinion distributions match best with the empirical distribution of the survey. For this purpose, we compute the JS divergence between the model outcome \(\mathcal{M}^{\beta \rho}\) and the empirical target distribution \(\mathcal{D}^{tech}\). Notice that, as for the classification above, we are interested in the shape of the distribution and do not differentiate whether the opinion profile is drawn to one or the other side. We therefore compute \(d_{JS}\) also with respect to the mirrored model distribution and take the minimal divergence as the result. The test is performed on the computational data generated by the model sampling procedure described above (Section "Systematic simulations"). That is, we sample through the parameter space of the model varying the strength of biased processing \(\beta = 0,0.02,\) \(0.04, \ldots , 1.4\) (71 sample points) and the level of noice \(\rho = 0,0.02,0.04, \ldots , 1\) (51 sample points). We compute the JS divergence \(d_{JS}(\mathcal{M}^{\beta \rho},\mathcal{D}^{tech})\) for all 25 within-sample outcomes independently and take the mean value as the final result. The mean JS divergence over different parameters is shown in Figure 10.
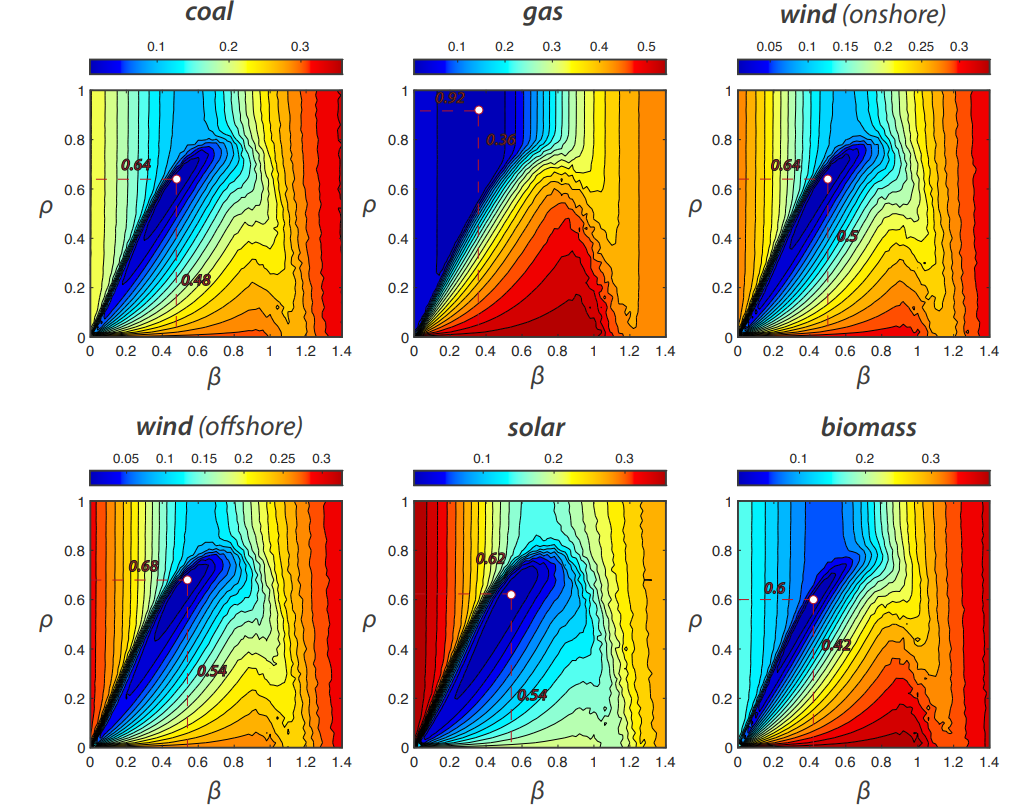
We hence adopt a statistical approach to model validation akin to calibration. We treat the expected outcome of a model as a prediction \(\mathcal{M}^{\beta \rho}\) of an empirical target distribution \(\mathcal{D}\). The model contains two parameters \(\beta\) (strength of biased processing) and \(\rho\) (noise level), and we "construct" a series of model predictions \(\mathcal{M}^{\beta \rho}\) by sampling through the parameter space \((\beta,\rho)\). Using the JS divergence, we asses the goodness of fit10 of \(\mathcal{M}^{\beta \rho}\) and identify those parameter combinations \((\beta^*,\rho^*)\) that match best with the data. Formally:
| \[(\beta^*,\rho^*) = \arg \min_{(\beta, \rho)} d_{JS}(\mathcal{M}^{\beta \rho},\mathcal{D}^{}).\] | \[(5)\] |
In Figure 10, the respective "optimal parameters" are highlighted by a white dot and the numbers \((\beta^*,\rho^*)\) are shown in red.
The comparisons between model outcomes and the six empirical opinion distributions are shown in Figure 10. The analysis reveals that the model is capable of reproducing empirical distributions with high accuracy. In all cases there is a parameter combination \((\beta^*,\rho^*)\) with which the JS divergence is almost zero indicating an almost perfect fit. The analysis shows that these values are global minima within a relatively well-defined energy landscape (no local minima). This is very important from the point of view of model estimation because a unique, well-defined basin of minimal values is a signature that (i.) the model contains relevant information about the empirical case, and (ii.) that suitable model parameters are clearly discerned from suboptimal ones. For those technologies that are one-sided (all except gas power plants), there is a narrow band of parameter values with accurate model fit which is close to the transition region from a broad (uniform) distribution to one-sidedness (cf. Figure 7). These results are of course very similar as the empirical distributions are very close. For gas, the best fit is obtained for high levels of noise in the opinion regime where the model continuously shifts from a normal-like to a uniform-like distribution.
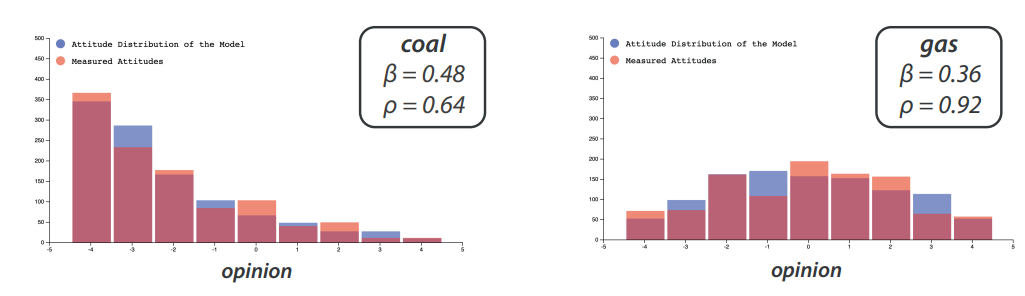
To further illustrate the capability of the model to generate the observed opinion distributions we have run experiments in our online application (Banisch 2022) using the respective parameters \((\beta^*,\rho^*)\) as an input. For coal and gas, the empirical and model distributions are shown in Figure 11. The reader is invited to test the goodness of fit for the other cases in the online tool.
Consistency between micro- and macro-level estimation results
The previous section shows that the empirical distributions are matched with high accuracy for an ABM with moderate biased processors. This is consistent with the micro level estimation of \(\beta\) in (Banisch & Shamon 2023) where moderate values in between 0.25 and 0.7 have been identified. In Figure 12, we show the estimation results for both analyses. The blue curves are taken from (Banisch & Shamon 2023). They show the mean squared error between experimentally observed opinion changes and the expected opinion change of artificial agents after reception of a balanced mix of arguments. The respective minimal value is highlighted. The orange curves show the JS divergence based on Figure 10. As the noise level \(\rho\) has a non-trivial impact on the results, here we show the minimal JS divergence over all parameter values \(\rho \in [0,1]\). Noise mimicking an external information source is a property of the collective-level ABM has no direct correspondence at the level of individual agents. Taking the minimum of each column in the Figure 10 ensures that the best possible match for a given \(\beta\) is considered.
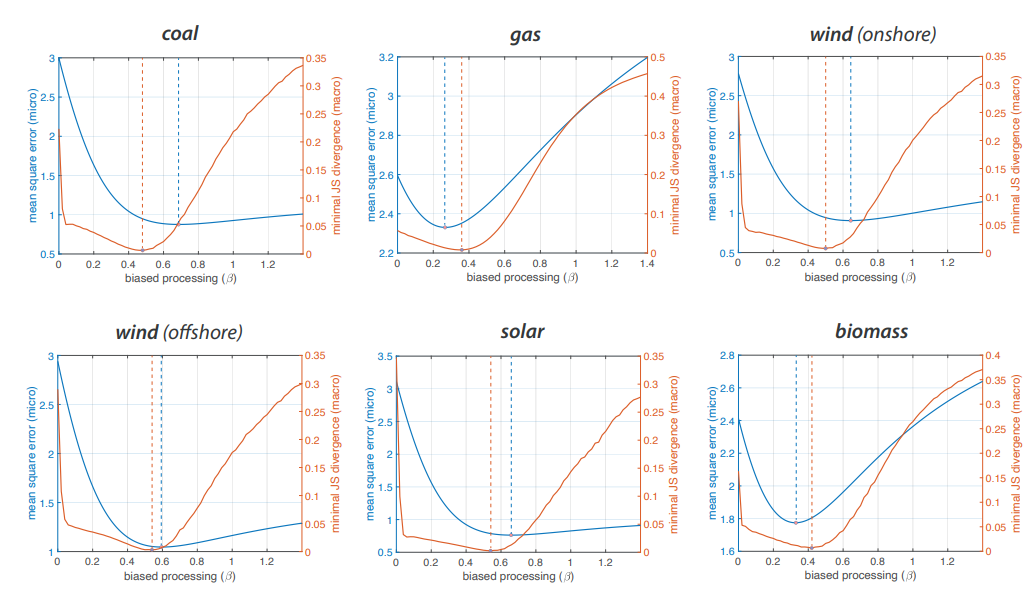
We observe in both cases moderate biased processing and the optimal values are not far apart. This means that a model calibrated at the micro level is capable of generating stationary opinion profiles very close to those observed in the survey part of the experiment. To our point of view this justifies that a moderate level of biased processing \(\beta\) enhances the empirical adequacy of argument-based models. The ABM provides a consistent link from micro data on individual attitude change to macro data in form of opinion distributions when agents are assumed to moderately favor consistent over inconsistent arguments.
Notice that the two issues (gas and biomass) for which \(\beta\) is significantly lower in the micro analysis are also lowest in the macro comparison presented in this paper. Beyond that, however, the ranking of optimal \(\beta\)’s does not match. Hence, we do observe important differences. On the other hand, the correlation between the two sets of estimated \(\beta\) parameters is very high (0.88). Moreover, even if the two estimations slightly depart from one another, the model calibrated at the micro level still generates opinion distributions that are very close to the empirical ones, as will be shown in the next section. Therefore, a central point can be made: moderate biased processing increases the empirical fit of the argument model both at the micro and the macro level.
Classical calibration-validation setting and sensitivity to initial conditions
We conclude this section with an experiment that shows how the CoMMCal setting relates to the more classical approach of reproducing macro data with a model that has been calibrated at the micro level. That is, we compare the empirical opinion distributions with the distributions that emerge from the model when using the \(\beta\)’s obtained from the micro level analysis. The respective \(\beta\)-values are \(0.686, 0.266, 0.644, 0.595, 0.658\) and \(0.329\) for coal, gas, onshore wind, offshore wind, solar power and biomass respectively. As before, we run the model for \(\rho = 0,0.02,0.04, \ldots , 1\) (51 sample points) using 25 runs per sample point. The initial state of the model is defined by a random assignment of arguments. The respective JS divergence between the model outcome and the empirical distribution is shown by the bold lines in Figure 13. Notice that this information is contained in Figure 12 and corresponds to a vertical slice at the respective value of \(\beta\).
In addition, we include into the experiment a check for robustness concerning the initial conditions of the model. For this purpose, we run an additional set of 10 simulations per sample point using an initial condition in which the population is perfectly bi-polarized. These results are shown by the shaded dots in Figure 13 as well. As can be seen, the overlap is nearly perfect showing that the validation results are not affected if the initial population is polarized. For \(\rho > 0\), we also found no significant alterations when using neutral consensus (e.g. all arguments are zero) or extreme consensus (all agents belief pro but not con arguments, or vice versa) are used to initialize the model (not shown).
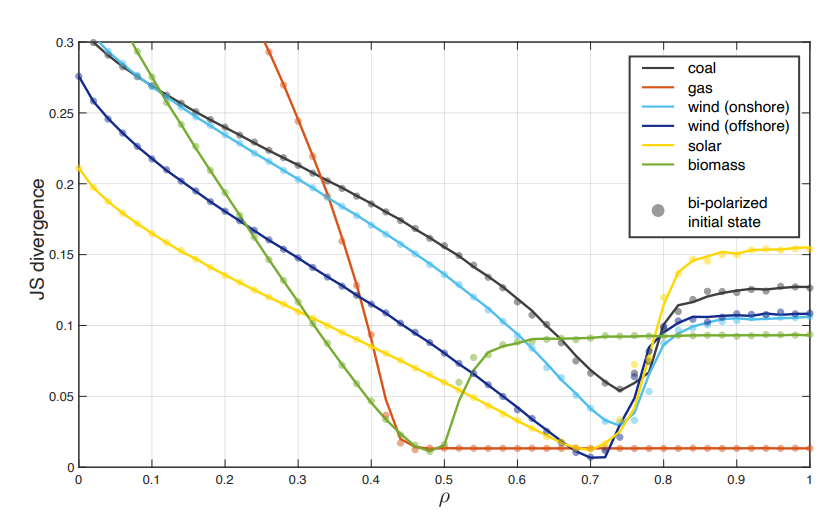
In general, we observe that the empirical distribution are within the output space of the micro-calibrated model for a considerable level of noise. For coal, wind (onshore and offshore) and solar power the fit is most accurate at a noise level of 0.7 to 0.75 meaning that social influence amounts for only about 25 % of the exchange dynamics. For biomass we find that a noise level slightly below 0.5 reproduces data best, and the distribution of opinions on gas (broad and centered) are well-reproduced for \(\rho > 0.5\). In relation to the micro-macro comparison (Figure 12), we observed that the JS-divergence remains slightly larger in the two cases (coal and onshore wind) where we found least consistency between the micro and the macro level estimates. From the methodological point of view, this supports that the CoMMCal approach is a viable tool for testing the extend to which an ABM can provide a consistent link between micro and macro data on opinions.
We should be careful, however, not to over-interpret the estimated noise level \(\rho\) in terms of meso- or macro-mechanisms. The model developed in this paper, does not include any particular assumptions about the structure of external influences, and no attempt to empirically ground the noise assumption has been undertaken. In recent years, it has become common to incorporate questions on media consumption into surveys which will provide a more nuanced basis for future model development.
Concluding discussion
Our paper uses a survey experiment to assess the validity of an argument-based model of opinion formation. Based on this experiment previous work has established biased processing (with strength \(\beta\)) as a viable micro assumption on how individuals change their opinion when exposed to new arguments (Banisch & Shamon 2023). In this work, we have concentrated on the macro-level validation by comparing model outcomes to the opinion profiles of the same surveyed population. For this purpose, the model has been extended by a noisy external signal the strength of which is governed by a second parameter \(\rho\). The resulting ABM generates stationary opinion profiles that come remarkably close to the surveyed opinions in a well-defined region of the parameter space. Throughout the six empirical cases, moderate biased processing provides the best fit which is consistent with the micro analysis.
As shown in the previous section, his consistency of micro- and macro level estimates in the CoMMCal setting entails the more typical calibration-validation approach in which a model calibrated at the micro level is shown to reproduce macro patterns. Consistent estimates of \(\beta\) imply that the experimentally calibrated ABM is capable of matching the surveyed opinion distributions at the macro level for some noise level \(\rho\). The approach adopted in this paper follows the route envisioned in the Flache et al. (2017) review:
"Calibrating models to resemble patterns observed in opinion surveys will be most fruitful if agent-based modelers at the same time assess to what extent those models that best fit macro-level patterns also contain assumptions that are compatible with empirical evidence available about micro-level processes of social influences and meso-structural conditions" (Par. 3.23)
From that angle, the main methodological contribution of this research is to show that the mixture of survey experiments and agent-based modeling is well-suited to advance further towards empirically-grounded opinion models. Survey experiment provide data at both the micro- and the macro level, and in a CoMMCal consistent calibration setting the empirical value of an ABM can be judged with respect to how well it can explain both data.
ACT is particularly suited to enable such a comparison, because it provides a clear theoretical link between persuasion experiments, used to assess individual level change, and opinion models, used to assess emergent macroscopic effects from repeated interactions. Especially in opinion dynamics empirical measurement is a very hard task, and ACT relies on a formal experimental design rooted in argument persuasion research, which has – in turn – been the main inspiration for the original development of ACT (Mäs & Flache 2013). For this reason, a high conceptual alignment between empirical experiment and model has been obtained. In particular, the empirically measured and the modeled opinions both lie on a 9-point scale, allowing for a direct comparison without further transformation. The argument model with moderate biased processing relies on agents which adjust opinions realistically when put into experimental conditions, and is at the same time capable of reproducing the distributions of surveyed opinions. For the specific subject pool and the considered topics it provides a consistent explanatory link between micro-level data on individual attitude change and macro-level data on opinions. At both levels, it rules out the previous assumption of neutral argument processing (Banisch & Olbrich 2021; Feliciani et al. 2021; Keijzer & Mäs 2022; Mäs et al. 2013; Mäs & Bischofberger 2015; Mäs & Flache 2013).
An intensive discussion of what validation may mean in the context of ABMs and opinion dynamics has emerged during the last two years (see e.g. Chattoe-Brown 2022; Keijzer 2022; Neumann 2023). While most researchers probably agree that validation involves quantitative comparisons of a model to experimental or survey data, also qualitative and interpretative approaches to model validation have been envisioned (Neumann (2023); see also Kleindorfer et al. (1998)). We have argued (Section: ) to view the question of validity not as a binary one of either yes or no. Step by step we have to gather empirical support for a model, and to demarcate where it does not apply. This naturally means to become more specific in terms of the application context of the model and the phenomena it aims to explain. When it comes to model validation, there is no reason in seeking "grand theory of societal polarization", the empirical case studies pursued in validation work will enforce a smaller scope. However, once we have a model that can reasonably be confronted with data, each step – whether successful or not – can inform new experimental hypotheses and necessary model refinements to be tested and integrated in subsequent steps. In this way, we may widen the range of validity and approach what Robert K. Merton called middle-range theories (Merton & Merton 1968) of collective opinion dynamics.
The above quote by Flache et al. (2017) also points to current limitations our study that should be overcome in the future. We have not assessed structural conditions relating to social networks or patterns of media consumption. We have also not modeled meso-level structure. The model studied in this paper is extremely simple with regard to the social composition of groups (no social network), the mechanisms of partner selection (no homophily), and the implementation of an external information channel mimicking an unbiased media source (just noise). In the light of the current experiment, we can justify these choices by the fact that we do not have sufficient knowledge on the relevant interactions and temporal processes within the surveyed population and their practices of media consumption. In that sense, we use randomness to account for factors we do not know. This strongly reduces the complexity of the social influence model to a single parameter \(\rho\). The aim is to provide a base line by showing that already this simple model may explain micro and macro opinion data if biased information processing is integrated into an argument-based ABM.
Based on the two empirical confirmation tests that we report in this paper we are (i.) rather confident that moderate biased processing is a viable assumption and should be included in future argument models. We are, however, (ii.) less confident in the influence processes modeled with the current ABM, because other models might do equally well on fitting the data we have used. More and other data is needed to assess process validity, and to address the non-uniqueness problem related to "alternative model realisations" (Oreskes & Belitz 2001 p. 24).
Most importantly, future iterations of the survey experiment should include opinion measurements some weeks after the experiment. At the moment, we have no data on opinion changes on the timescale of the ABM. In order to address meso-level conditions, many aspects can be systematically varied in survey experiments, and there is an extensive body of previous experimental research on aspects such as source effects, expertise and argument quality as well as values and identities as mediators of opinion change (Feldman 2003; Nelson & Garst 2005; Petty & Cacioppo 1986; Terry 2001). To further increase confidence with respect to biased processing (\(\beta\)), the experiment should be reproduced on a different population and issues which show different degrees of polarization. Argument communication theory makes precise predictions on the expected level of biased processing and the respective expected opinion change. At the macro level, one promising direction is to focus on group-level correlations between opinions on different issues. One the one hand, ideological patterns of opinion sorting are probably the most stable empirical signature of collective polarization (DellaPosta 2020; Dimock et al. 2014). On the other hand, the emergence of opinion alignment has already been shown within the ACT modeling framework (Banisch & Olbrich 2021), albeit without yet taking into account biased processing.
With an ACT model that withstands these empirical tests, we may more reliably address practical problems such as the impact of online social networks and algorithmic filters on polarization trends. In this regard, the model analysis has revealed a counter-intuitive effect of an ideal external channel that provides discussion groups a balanced mix of pro and con information – quite the opposite of a filter bubble. While intuitively one would expect that polarization reduces in such a scenario of perfect opinion diversity, more confrontation with balanced information may even be counter-productive and increase polarization tendencies (cf. Deffuant et al. 2023). This effect will likely interact with homophily on which previous conceptions of personalized recommender systems have been based (Keijzer & Mäs 2022; Mäs & Bischofberger 2015; Sı̂rbu et al. 2019). However, while the "complex link between filter bubbles and opinion polarization" (Keijzer & Mäs 2022) may appear even more complex, we note that ACT with biased processing entails positive and negative influence at the phenomenological level of opinions (Banisch 2023). Aside from empirical model validation, future theoretical work on model synthesis is needed to clarify the relation between biased processing and these previous core modeling assumptions.
Acknowledgements
This project has received funding from the European Union’s Horizon 2020 and Horizon Europe programmes under grant agreement No 732942 (Odycceus) and grant agreement No 101094752 (SoMe4Dem).Notes
- Abelson (1964): "Since universal ultimate agreement is an ubiquitous outcome of a very broad class of mathematical models, we are naturally led to inquire what on earth one must assume in order to generate the bimodal outcome of community cleavage studies." Axelrod (1997): "If people tend to become alike in their beliefs, attitudes, and behavior when they interact, why do not all such differences eventually disappear?"↩︎
- See Chattoe-Brown (2022) and Keijzer (2022), as well as Chattoe-Brown (2022), Carpentras (2023) and Neumann (2023) for recent discussions on the topic.↩︎
- This point has been emphasized in a recent talk by R. Hegselmann at the annual meeting of the German Physical Society in Regensburg 2022.↩︎
- Notice that the Jensen-Shannon divergence used for empirical comparison involve the logarithm and it is usually favorable to have distributions with full support, meaning that there is a non-zero probability for any \(o\). We ensure full support by adding to the model output a single instance of a population with random opinions uniformly distributed in \(\{-4,4\}\). The impact of this adjustment on the shape of the distribution is neglectable (\(\approx 1/2500\)).↩︎
- This transition is an interesting object for future research.↩︎
- Notice that a small base probability (\(0.0093\)) is assigned to all possible opinion values in \(\{-4,4\}\). The peak in the consensus profiles, for instance, is \(0.9259\), not one, and the remaining probability is equally distributed over the other opinion values. The technical purpose is to avoid taking a logarithm of zero in the computation of the JS divergence.↩︎
- This is actually an intriguing observation given that until now the main question for opinion dynamics has been "how does polarization come about" (Abelson 1964; Axelrod 1997; Flache et al. 2017). Similar findings concerning the marginality of moderate consensus have been made in Feliciani et al. (2021) and Lorenz et al. (2021) so that the focus in the future might shift back to "given that so many mechanism polarize, how can we remain moderate?"↩︎
- The analytical sample consists of 1,078 persons who indicated to have a residential address (principal address) in Germany. Respondents’ average age in the analytical sample is 40.8 years (SD=15.7), and 49.3 percent of respondents are female, 49.4 percent are male, and 1.3 percent refused to classify their gender. Furthermore, 77.7 percent of the respondents had received a secondary school leaving certificate and 5.3 percent stated that they are employed in the energy sector.↩︎
- Participants of the online survey were recruited from a voluntary-opt-in panel of a non-commercial German access panel operator. The analytical sample consists of 1,078 persons who indicated to have a residential address (principal address) in Germany. Respondents’ average age in the analytical sample is 40.8 years (SD = 15.7), and 49.3 percent of respondents are female, 49.4 percent are male, and 1.3 percent refused to classify their gender. Furthermore, 77.7 percent of the respondents had received a secondary school leaving certificate and 5.3 percent stated that they are employed in the energy sector.↩︎
- We have also computed the log likelihood to compare model results with data. The results and inferred parameters are the same. In fact, the JS divergence is closely related to the log likelihood and serves the purposes of the analysis.↩︎
References
ABELSON, R. P. (1964). Mathematical models of the distribution of attitudes under controversy. Contributions to Mathematical Psychology, 3, 1–54.
AJZEN, I. (2001). Nature and operation of attitudes. Annual Review of Psychology, 52(1), 27–58. [doi:10.1146/annurev.psych.52.1.27]
AXELROD, R. (1997). The dissemination of culture: A model with local convergence and global polarization. Journal of Conflict Resolution, 41(2), 203–226. [doi:10.1177/0022002797041002001]
AXTELL, R., Axelrod, R., Epstein, J. M., & Cohen, M. D. (1996). Aligning simulation models: A case study and results. Computational & Mathematical Organization Theory, 1, 123–141. [doi:10.1007/bf01299065]
BACCINI, E., Christoff, Z., Hartmann, S., & Verbrugge, R. (2023). The wisdom of the small crowd: Myside bias and group discussion. Journal of Artificial Societies and Social Simulation, 26(4), 7. https://www.jasss.org/26/4/7.html [doi:10.18564/jasss.5184]
BALDASSARRI, D., & Bearman, P. (2007). Dynamics of political polarization. American Sociological Review, 72(5), 784–811. [doi:10.1177/000312240707200507]
BANISCH, S. (2014). From microscopic heterogeneity to macroscopic complexity in the contrarian voter model. Advances in Complex Systems, 17(05), 1450025. [doi:10.1142/s0219525914500258]
BANISCH, S. (2016). Markov Chain Aggregation for Agent-Based Models. Berlin Heidelberg: Springer.
BANISCH, S. (2022). Interactive exploration of opinion models, model explorer. An interactive online version of the model and the data is available at: http://universecity.de/demos/ModelExplorer.html
BANISCH, S. (2023). “One mechanism to rule them all!” A critical comment on an emerging categorization in opinion dynamics. Review of Artificial Societies and Social Simulation, 26 Apr 2023. https://rofasss.org/2023/04/26/onemechanism/
BANISCH, S., Gaisbauer, F., & Olbrich, E. (2022). Modelling spirals of silence and echo chambers by learning from the feedback of others. Entropy, 24(10), 1484. [doi:10.3390/e24101484]
BANISCH, S., & Olbrich, E. (2019). Opinion polarization by learning from social feedback. The Journal of Mathematical Sociology, 43(2), 76–103. [doi:10.1080/0022250x.2018.1517761]
BANISCH, S., & Olbrich, E. (2021). An argument communication model of polarization and ideological alignment. Journal of Artificial Societies and Social Simulation, 24(1), 1. https://jasss.soc.surrey.ac.uk/24/1/1.html [doi:10.18564/jasss.4434]
BANISCH, S., & Shamon, H. (2023). Biased processing and opinion polarisation: Experimental refinement of argument communication theory in the context of the energy debate. Sociological Methods and Research, 0. [doi:10.1177/00491241231186658]
BAUMANN, F., Lorenz-Spreen, P., Sokolov, I. M., & Starnini, M. (2020). Modeling echo chambers and polarization dynamics in social networks. Physical Review Letters, 124(4), 048301. [doi:10.1103/physrevlett.124.048301]
CARLEY, K. (1991). A theory of group stability. American Sociological Review, 56(3), 331–354. [doi:10.2307/2096108]
CARPENTRAS, D. (2023). Why We Are Failing at Connecting Opinion Dynamics to the Empirical World.
CARPENTRAS, D., & Quayle, M. (2023). The psychometric house-of-mirrors: The effect of measurement distortions on agent-based models’ predictions. International Journal of Social Research Methodology, 26(2), 215–231. [doi:10.1080/13645579.2022.2137938]
CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2), 591. [doi:10.1103/revmodphys.81.591]
CENTOLA, D., & Macy, M. (2007). Complex contagions and the weakness of long ties. American Journal of Sociology, 113(3), 702–734. [doi:10.1086/521848]
CHATTOE-BROWN, E. (2022). If you wantto be cited, don’t validate your agent-based model: Atentative hypothesis badly in need of refutation. Review of Artificial Societies and Social Simulation. Available at: https://rofasss.org/2022/02/01/citing-od-models/
CHATTOE-BROWN, E. (2022). Today we have naming of parts: A possible way out of some terminological problems with ABM. Review of Artificial Societies and Social Simulation. Available at: https://rofasss.org/2022/01/11/naming-of-parts/
CHEN, P., & Redner, S. (2005). Majority rule dynamics in finite dimensions. Physical Review E, 71(3), 036101. [doi:10.1103/physreve.71.036101]
CORNER, A., Whitmarsh, L., & Xenias, D. (2012). Uncertainty, scepticism and attitudes towards climate change: Biased assimilation and attitude polarisation. Climatic Change, 114(3), 463–478. [doi:10.1007/s10584-012-0424-6]
CROKIDAKIS, N., & de Oliveira, P. M. C. (2015). Inflexibility and independence: Phase transitions in the majority-rule model. Physical Review E, 92(6), 062122. [doi:10.1103/physreve.92.062122]
DANDEKAR, P., Goel, A., & Lee, D. T. (2013). Biased assimilation, homophily, and the dynamics of polarization. Proceedings of the National Academy of Sciences, 110(15), 5791–5796. [doi:10.1073/pnas.1217220110]
DAVID, N. (2009). Validation and verification in social simulation: Patterns and clarification of terminology. In F. Squazzoni (Ed.), Epistemological Aspects of Computer Simulation in the Social Sciences (pp. 117–129). Berlin Heidelberg: Springer. [doi:10.1007/978-3-642-01109-2_9]
DEFFUANT, G., & Huet, S. (2007). Propagation effects of filtering incongruent information. Journal of Business Research, 60(8), 816–825. [doi:10.1016/j.jbusres.2007.02.001]
DEFFUANT, G., Keijzer, M. A., & Banisch, S. (2023). Regular access to constantly renewed online content favors radicalization of opinions. arXiv preprint. Available at: https://arxiv.org/abs/2305.16855
DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(01n04), 87–98. [doi:10.1142/s0219525900000078]
DEGROOT, M. H. (1974). Reaching a consensus. Journal of the American Statistical Association, 69(345), 118–121. [doi:10.1080/01621459.1974.10480137]
DELLAPOSTA, D. (2020). Pluralistic collapse: The “oil spill” model of mass opinion polarization. American Sociological Review, 85(3), 507–536. [doi:10.1177/0003122420922989]
DIMOCK, M., Doherty, C., Kiley, J., & Oates, R. (2014). Political polarization in the American public. Pew Research Center.
DRUCKMAN, J. N., & Bolsen, T. (2011). Framing, motivated reasoning, and opinions about emergent technologies. Journal of Communication, 61(4), 659–688. [doi:10.1111/j.1460-2466.2011.01562.x]
DUGGINS, P. (2017). A psychologically-Motivated model of opinion change with applications to American politics. Journal of Artificial Societies and Social Simulation, 20(1), 13. https://jasss.soc.surrey.ac.uk/20/1/13.html [doi:10.18564/jasss.3316]
DUNG, P. M. (1995). On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games. Artificial Intelligence, 77(2), 321–357. [doi:10.1016/0004-3702(94)00041-x]
EDMONDS, B., & Hales, D. (2003). Replication, replication and replication: Some hard lessons from model alignment. Journal of Artificial Societies and Social Simulation, 6(4), 11. https://www.jasss.org/6/4/11.html
FELDMAN, S. (2003). Values, ideology, and the structure of political attitudes. In D. O. Sears, L. Huddy, & R. Jervis (Eds.), Oxford Handbook of Political Psychology (pp. 477–508). Oxford: Oxford University Press. [doi:10.1093/oxfordhb/9780197541302.013.19]
FELICIANI, T., Flache, A., & Mäs, M. (2021). Persuasion without polarization? Modelling persuasive argument communication in teams with strong faultlines. Computational and Mathematical Organization Theory, 27(1), 61–92. [doi:10.1007/s10588-020-09315-8]
FISHBEIN, M. (1963). An investigation of the relationship between beliefs about an object and the attitude toward that object. Human Relations, 16(3), 233–239. [doi:10.1177/001872676301600302]
FISHBEIN, M., & Raven, B. H. (1962). The AB scales: An operational definition of belief and attitude. Human Relations, 15(1), 35–44. [doi:10.1177/001872676201500104]
FLACHE, A., & Macy, M. W. (2011). Small worlds and cultural polarization. The Journal of Mathematical Sociology, 35(1-3), 146–176. [doi:10.1080/0022250x.2010.532261]
FLACHE, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2. https://jasss.soc.surrey.ac.uk/20/4/2.html [doi:10.18564/jasss.3521]
FRENCH, J. R. (1956). A formal theory of social power. Psychological Review, 63(3), 181.
FRIEDKIN, N. E. (2015). The problem of social control and coordination of complex systems in sociology: A look at the community cleavage problem. IEEE Control Systems, 35(3), 40–51.
FRIEDKIN, N. E., Proskurnikov, A. V., Tempo, R., & Parsegov, S. E. (2016). Network science on belief system dynamics under logic constraints. Science, 354(6310), 321–326. [doi:10.1126/science.aag2624]
GAISBAUER, F., Olbrich, E., & Banisch, S. (2020). Dynamics of opinion expression. Physical Review E, 102(4), 042303. [doi:10.1103/physreve.102.042303]
GALAM, S. (1986). Majority rule, hierarchical structures, and democratic totalitarianism: A statistical approach. Journal of Mathematical Psychology, 30(4), 426–434. [doi:10.1016/0022-2496(86)90019-2]
GALAM, S. (2004). Contrarian deterministic effects on opinion dynamics: "The hung elections scenario". Physica A: Statistical Mechanics and Its Applications, 333, 453–460. [doi:10.1016/j.physa.2003.10.041]
GALAM, S. (2008). Sociophysics: A review of Galam models. International Journal of Modern Physics C, 19(03), 409–440. [doi:10.1142/s0129183108012297]
GALEOTTI, A., Goyal, S., Jackson, M. O., Vega-Redondo, F., & Yariv, L. (2010). Network games. The Review of Economic Studies, 77(1), 218–244. [doi:10.1111/j.1467-937x.2009.00570.x]
GLEESON, J. P. (2013). Binary-state dynamics on complex networks: Pair approximation and beyond. Physical Review X, 3(2), 021004. [doi:10.1103/physrevx.3.021004]
GRANOVETTER, M. (1978). Threshold models of collective behavior. American Journal of Sociology, 83(6), 1420–1443. [doi:10.1086/226707]
HALES, D., Rouchier, J., & Edmonds, B. (2003). Model-to-model analysis. Journal of Artificial Societies and Social Simulation, 6(4), 5. https://jasss.soc.surrey.ac.uk/6/4/5.html
HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2. https://www.jasss.org/5/3/2.html [doi:10.18564/jasss.5257]
HOLLEY, R. A., & Liggett, T. M. (1975). Ergodic theorems for weakly interacting infinite systems and the voter model. The Annals of Probability, 3(4), 643–663. [doi:10.1214/aop/1176996306]
HOŁYST, J. A., Kacperski, K., & Schweitzer, F. (2000). Phase transitions in social impact models of opinion formation. Physica A: Statistical Mechanics and Its Applications, 285(1-2), 199–210.
HUNTER, J. E., Danes, J. E., & Cohen, S. H. (2014). Mathematical Models of Attitude Change: Change in Single Attitudes and Cognitive Structure. New York, NY: Academic Press. [doi:10.1515/9783112470084-007]
ISENBERG, D. J. (1986). Group polarization: A critical review and meta-analysis. Journal of Personality and Social Psychology, 50(6), 1141. [doi:10.1037//0022-3514.50.6.1141]
ISING, E. (1925). Beitrag zur Theorie des Ferromagnetismus. Zeitschrift Für Physik A Hadrons and Nuclei, 31(1), 253–258. [doi:10.1007/bf02980577]
JAGER, W., & Amblard, F. (2005). Uniformity, bipolarization and pluriformity captured as generic stylized behavior with an agent-Based simulation model of attitude change. Computational & Mathematical Organization Theory, 10(4), 295–303. [doi:10.1007/s10588-005-6282-2]
KEIJZER, M. A. (2022). If you want to be cited, calibrate your agent-based model: A reply to Chattoe-Brown. Review of Artificial Societies and Social Simulation. Available at: https://rofasss.org/2022/03/09/keijzer-reply-to-chattoe-brown/ [doi:10.18564/jasss.1819]
KEIJZER, M. A., & Mäs, M. (2022). The complex link between filter bubbles and opinion polarization. Data Science, 5(2), 139–166. [doi:10.3233/ds-220054]
KIMURA, M., & Weiss, G. H. (1964). The stepping stone model of population structure and the decrease of genetic correlation with distance. Genetics, 49(4), 561. [doi:10.1093/genetics/49.4.561]
KLEINDORFER, G. B., O’Neill, L., & Ganeshan, R. (1998). Validation in simulation: Various positions in the philosophy of science. Management Science, 44(8), 1087–1099. [doi:10.1287/mnsc.44.8.1087]
KRUEGER, T., Szwabiński, J., & Weron, T. (2017). Conformity, anticonformity and polarization of opinions: Insights from a mathematical model of opinion dynamics. Entropy, 19(7), 371. [doi:10.3390/e19070371]
LA Rocca, C. E., Braunstein, L. A., & Vazquez, F. (2014). The influence of persuasion in opinion formation and polarization. EPL (Europhysics Letters), 106(4), 40004. [doi:10.1209/0295-5075/106/40004]
LAVER, M. (2014). Measuring policy positions in political space. Annual Review of Political Science, 17, 207–223. [doi:10.1146/annurev-polisci-061413-041905]
LAVER, M. J., & Budge, I. (1992). Measuring policy distances and modelling coalition formation. In M. J. Laver & I. Budge (Eds.), Party Policy and Government Coalitions (pp. 15–40). Springer. [doi:10.1007/978-1-349-22368-8_2]
LEWENSTEIN, M., Nowak, A., & Latané, B. (1992). Statistical mechanics of social impact. Physical Review A, 45(2), 763. [doi:10.1103/physreva.45.763]
LORD, C. G., Ross, L., & Lepper, M. R. (1979). Biased assimilation and attitude polarization: The effects of prior theories on subsequently considered evidence. Journal of Personality and Social Psychology, 37(11), 2098. [doi:10.1037//0022-3514.37.11.2098]
LORENZ, J. (2007). Continuous opinion dynamics under bounded confidence: A survey. International Journal of Modern Physics C, 18(12), 1819–1838. [doi:10.1142/s0129183107011789]
LORENZ, J., Neumann, M., & Schröder, T. (2021). Individual attitude change and societal dynamics: Computational experiments with psychological theories. Psychological Review, 128(4), 623–642. [doi:10.1037/rev0000291]
MARTINS, A. C. R. (2008). Continuous opinions and discrete actions in opinion dynamics problems. International Journal of Modern Physics C, 19(04), 617–624. [doi:10.1142/s0129183108012339]
MÄS, M., & Bischofberger, L. (2015). Willthe personalization of online social networks foster opinion polarization? Available at SSRN 2553436 [doi:10.2139/ssrn.2553436]
MÄS, M., & Flache, A. (2013). Differentiation without distancing. Explaining bi-polarization of opinions without negative influence. PLoS One, 8(11), e74516.
MÄS, M., Flache, A., & Kitts, J. A. (2014). Cultural integration and differentiation in groups and organizations. In V. Dignum & F. Dignum (Eds.), Perspectives on Culture and Agent-Based Simulations (pp. 71–90). Berlin Heidelberg: Springer.
MÄS, M., Flache, A., Takács, K., & Jehn, K. A. (2013). In the short term we divide, in the long term we unite: Demographic crisscrossing and the effects of faultlines on subgroup polarization. Organization Science, 24(3), 716–736.
MOBILIA, M. (2003). Does a single zealot affect an infinite group of voters? Physical Review Letters, 91(2), 028701. [doi:10.1103/physrevlett.91.028701]
MUELLER, S. T., & Tan, Y.-Y. S. (2018). Cognitive perspectives on opinion dynamics: The role of knowledge in consensus formation, opinion divergence, and group polarization. Journal of Computational Social Science, 1(1), 15–48. [doi:10.1007/s42001-017-0004-7]
MYERS, D. G., & Lamm, H. (1976). The group polarization phenomenon. Psychological Bulletin, 83(4), 602. [doi:10.1037//0033-2909.83.4.602]
NELSON, T. E., & Garst, J. (2005). Values-based political messages and persuasion: Relationships among speaker, recipient, and evoked values. Political Psychology, 26(4), 489–516. [doi:10.1111/j.1467-9221.2005.00428.x]
NEUMANN, M. (2023). The challenge of validation. Review of Artificial Societies and Social Simulation. Available at: https://rofasss.org/2023/04/18/the-challenge-of-validation/
NOWAK, A., Szamrej, J., & Latané, B. (1990). From private attitude to public opinion: A dynamic theory of social impact. Psychological Review, 97(3), 362. [doi:10.1037//0033-295x.97.3.362]
NOWAK, B., & Sznajd-Weron, K. (2020). Symmetrical threshold model with independence on random graphs. Physical Review E, 101(5). [doi:10.1103/physreve.101.052316]
OLBRICH, E., & Banisch, S. (2021). The rise of populism and the reconfiguration of the German political space. Frontiers in Big Data, 4, 83. [doi:10.3389/fdata.2021.731349]
ORESKES, N., & Belitz, K. (2001). Philosophical issues in model assessment. Model Validation: Perspectives in Hydrological Science, 23, 23–41.
ORESKES, N., Shrader-Frechette, K., & Belitz, K. (1994). Verification, validation, and confirmation of numerical models in the earth sciences. Science, 263(5147), 641–646. [doi:10.1126/science.263.5147.641]
PETTY, R. E., & Cacioppo, J. T. (1986). The elaboration likelihood model of persuasion. In Advances in Experimental Social Psychology (Vol. 19, pp. 1–24). [doi:10.1016/s0065-2601(08)60214-2]
ROUCHIER, J. (2003). Re-implementation of a multi-agent model aimed at sustaining experimental economic research: The case of simulations with emerging speculation. Journal of Artificial Societies and Social Simulation, 6(4), 7. http://jasss.soc.surrey.ac.uk/6/4/7.html
SARGENT, R. G. (2010). Verification and validation of simulation models. Proceedings of the 2010 Winter Simulation Conference [doi:10.1109/wsc.2010.5679166]
SARGENT, R. G., & Balci, O. (2017). History of verification and validation of simulation models. 2017 Winter Simulation Conference (WSC) [doi:10.1109/wsc.2017.8247794]
SARKÖZI, M., Jütersonke, S., Banisch, S., Poppe, S., & Berger, R. (2022). The effects of social feedback on private opinions. Empirical evidence from the laboratory. PLoS One, 17(10), e0274903.
SCHELLING, T. C. (1973). Hockey helmets, concealed weapons, and daylight saving: A study of binary choices with externalities. Journal of Conflict Resolution, 17(3), 381–428. [doi:10.1177/002200277301700302]
SCHLESINGER, S. (1979). Terminology for model credibility. Simulation, 32(3), 103–104.
SCHWEITZER, F., & Behera, L. (2009). Nonlinear voter models: The transition from invasion to coexistence. The European Physical Journal B, 67(3), 301–318. [doi:10.1140/epjb/e2009-00001-3]
SHAMON, H., Schumann, D., Fischer, W., Vögele, S., Heinrichs, H. U., & Kuckshinrichs, W. (2019). Changing attitudes and conflicting arguments: Reviewing stakeholder communication on electricity technologies in Germany. Energy Research & Social Science, 55, 106–121. [doi:10.1016/j.erss.2019.04.012]
SÎRBU, A., Loreto, V., Servedio, V. D., & Tria, F. (2017). Opinion dynamics: Models, extensions and external effects. In L. Loreto, M. Haklay, A. Hotho, V. D. P. Servedio, G. Stumme, J. Theunis, & F. Tria (Eds.), Participatory Sensing, Opinions and Collective Awareness (pp. 363–401). Berlin Heidelberg: Springer.
SÎRBU, A., Pedreschi, D., Giannotti, F., & Kertész, J. (2019). Algorithmic bias amplifies opinion fragmentation and polarization: A bounded confidence model. PLoS One, 14(3), e0213246.
SOBKOWICZ, P. (2009). Modelling opinion formation with physics tools: Call for closer link with reality. Journal of Artificial Societies and Social Simulation, 12(1), 11. https://www.jasss.org/12/1/11.html
SOOD, V., & Redner, S. (2005). Voter model on heterogeneous graphs. Physical Review Letters, 94(17), 178701. [doi:10.1103/physrevlett.94.178701]
SUNSTEIN, C. R. (2002). The law of group polarization. Journal of Political Philosophy, 10(2), 175–195. [doi:10.1111/1467-9760.00148]
SZABÓ, G., & Fath, G. (2007). Evolutionary games on graphs. Physics Reports, 446(4–6), 97–216.
SZNAJD-WERON, K., & Sznajd, J. (2000). Opinion evolution in closed community. International Journal of Modern Physics C, 11(06), 1157–1165. [doi:10.1142/s0129183100000936]
TABER, C. S., Cann, D., & Kucsova, S. (2009). The motivated processing of political arguments. Political Behavior, 31(2), 137–155. [doi:10.1007/s11109-008-9075-8]
TABER, C. S., & Lodge, M. (2006). Motivated skepticism in the evaluation of political beliefs. American Journal of Political Science, 50(3), 755–769. [doi:10.1111/j.1540-5907.2006.00214.x]
TAILLANDIER, P., Salliou, N., & Thomopoulos, R. (2021). Introducing the argumentation framework within agent-Based models to better simulate agents’ cognition in opinion dynamics: Application to vegetarian diet diffusion. Journal of Artificial Societies and Social Simulation, 24(2), 6. https://jasss.soc.surrey.ac.uk/24/2/6.html [doi:10.18564/jasss.4531]
TAKÁCS, K., Flache, A., & Mäs, M. (2016). Discrepancy and disliking do not induce negative opinion shifts. PLoS One, 11(6), e0157948.
TEEL, T. L., Bright, A. D., Manfredo, M. J., & Brooks, J. J. (2006). Evidence of biased processing of natural resource-related information: A study of attitudes toward drilling for oil in the Arctic National Wildlife Refuge. Society and Natural Resources, 19(5), 447–463. [doi:10.1080/08941920600561140]
TERRY, D. J. (2001). Attitudes, behavior, and social context. Social Influence: Direct and Indirect Processes, 3, 253.
TROITZSCH, K. G. (2004). Validating simulation models. Proceedings of the 18th European Simulation Multiconference
UGANDER, J., Backstrom, L., Marlow, C., & Kleinberg, J. (2012). Structural diversity in social contagion. Proceedings of the National Academy of Sciences, 109(16), 5962–5966. [doi:10.1073/pnas.1116502109]
VAZQUEZ, F., & Eguı́luz, V. M. (2008). Analytical solution of the voter model on uncorrelated networks. New Journal of Physics, 10(6), 063011. [doi:10.1088/1367-2630/10/6/063011]
VINOKUR, A., & Burnstein, E. (1978). Depolarization of attitudes in groups. Journal of Personality and Social Psychology, 36(8), 872. [doi:10.1037//0022-3514.36.8.872]
WILENSKY, U., & Rand, W. (2007). Making models match: Replicating an agent-based model. Journal of Artificial Societies and Social Simulation, 10(4), 2. https://jasss.soc.surrey.ac.uk/10/4/2.html
WILLAERT, T., Banisch, S., Van Eecke, P., & Beuls, K. (2022). Tracking causal relations in the news: Data, tools, and models for the analysis of argumentative statements in online media. Digital Scholarship in the Humanities, 37(4), 1358–1375. [doi:10.1093/llc/fqab107]